Изобретение относится к электроизмерительной технике, в частности к измерению спектра несинусоидальных сигналов.
Известен способ определения количества гармоник несинусоидальных сигналов, основанный на использовании разложения функции в ряд Фурье с определением гармонических составляющих с помощью формул (см., например, Бессонов Л. А. Теоретические основы электротехники. М.: Высшая школа, 1973, с. 225). Недостатком способа является трудоемкость расчетов при необходимости определения только ширины спектра, т.е. количества гармонических составляющих без определения их амплитудных значений. Кроме этого, не всякий несинусоидальный сигнал можно представить аналитической формулой.
Наиболее близким к предлагаемому является способ определения количества гармоник несинусоидальных сигналов, основанный на разложении заданной функции в ряд Фурье при использовании выборок мгновенных значений несинусоидального сигнала (фиг. 1) с последующим использованием приближенных формул (см. там же, с. 229), который принят в качестве прототипа.
К недостаткам известного способа можно отнести большой объем вычислений в тех случаях, когда необходимо определить только количество гармонических составляющих сигнала без определения их амплитудных значений, а также снижение точности вычислений при невыполнении условия определения оптимального числа n выборок мгновенных значений несинусоидального сигнала.
Сущность решения состоит в стремлении получить технический результат, заключающийся в снижении объема вычислений при определений числа N гармонических составляющих несинусоидального сигнала и повышении точности этого определения путем выбора оптимального числа n выборок мгновенных значений сигнала.
Указанный технический результат достигается тем, что в известном способе определения количества гармоник несинусоидальных сигналов, включающем определение n выборок мгновенных значений напряжения при одинаковом шаге между выборками, равном 360o/n, особенность заключается в том, что рассчитывают действующее значение сигнала путем возведения выборок в квадрат, их суммирования, деления на n, извлечения квадратного корня, затем повторяют описанную процедуру расчета действующего значения, увеличивая n на единицу каждый раз, до тех пор, пока действующее значение не будет равно предыдущему значению с заданной погрешностью, при этом количество N гармоник несинусоидального сигнала определяют из выражения: N=(n-1)/2.
Проведенный анализ уровня техники позволил установить, что заявителем не обнаружено аналога, характеризующегося признаками, тождественными всем признакам заявленного изобретения, а определение из перечня аналогов прототипа позволило выявить совокупность существенных по отношению к усматриваемому заявителем техническому результату отличительных признаков в заявленном способе, изложенных в формуле изобретения. Следовательно, заявляемое изобретение соответствует условию "новизна".
Для проверки соответствия заявленного изобретения условию "изобретательский уровень" заявитель провел дополнительный поиск известных решений, чтобы выявить признаки, совпадающие с отличительными от прототипа признаками заявленного способа. Результаты поиска показали, что заявленное изобретение не вытекает для специалиста явным образом из известного уровня техники, поскольку из уровня техники, определенного заявителем, не выявлено влияние предусматриваемых существенными признаками заявленного изобретения преобразований на достижение технического результата. Следовательно, заявленное изобретение соответствует условию "изобретательский уровень".
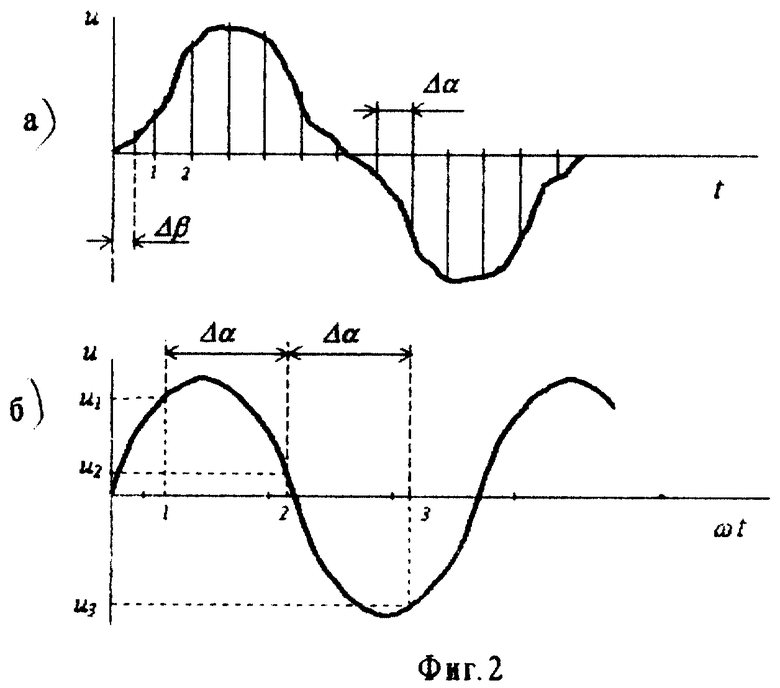
На фиг. 1 и 2 изображены временные диаграммы напряжений, на фиг.3 изображены напряжения на комплексной плоскости, поясняющие предлагаемый способ.
Рассмотрим некоторые новые положения, касающиеся определения действующего (эффективного) значения несинусоидальных сигналов на примере электрического напряжения.
Известно, что это значение определяется выражением: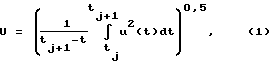
где для периодических сигналов разность (tj+1-tj) равна периоду сигнала. При приборной реализации выражения (1) интеграл заменяется суммой квадратов выборок мгновенных значений uj напряжения u(t) в моменты времени tj (фиг.1):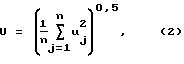
где n - число выборок, причем считается, что формула (2) является приближенной (т. е. погрешность определения действующего значения по ней стремится к нулю только при n_→∞
Несинусоидальное напряжение можно представить суммой гармоник: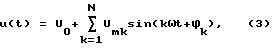
поэтому рассмотрим синусоидальный сигнал, представляющий собой k-ю гармонику ряда (3):
u = Umsin(ωt), (4)
где для упрощения анализа начальная фаза принята равной нулю.
Формула (1) для синусоидального сигнала, как известно, дает следующий результат при определении эффективного значения: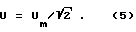
Определим n выборок мгновенных значений напряжения (4), каждая из которых равна:
uj = Umsin(Δβ+(j-1)Δα), (6)
где Δα = 360/n шаг между выборками;
Δβ- фаза при определении первой выборки (фиг. 2,а).
Подставим (6) в (2):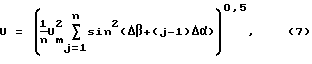
Учтем, что sin2x = 0,5(1-cos2x), тогда (7) можно записать в виде: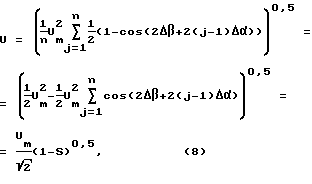
где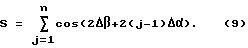
Перейдем в область комплексных изображений, приняв для упрощения выражений: 2Δβ = 0, тогда формула (9) запишется в виде: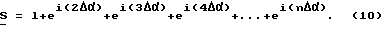
Геометрически 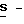 это сумма векторов единичной длины на комплексной плоскости, которые сдвинуты между собой на угол 2Δα (фиг.3, а). Поэтому при условии, что шаг между выборками
это сумма векторов единичной длины на комплексной плоскости, которые сдвинуты между собой на угол 2Δα (фиг.3, а). Поэтому при условии, что шаг между выборками
Δα = const, (11)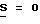 при минимальном значении n= 3 (фиг.3, б), что определяет минимальное значение числа n выборок мгновенных значений напряжения, при котором формула (8) дает результат (5), т.е. методическая погрешность при использовании способа (2) измерения действующего значения напряжения синусоидальной формы становится равной нулю.
при минимальном значении n= 3 (фиг.3, б), что определяет минимальное значение числа n выборок мгновенных значений напряжения, при котором формула (8) дает результат (5), т.е. методическая погрешность при использовании способа (2) измерения действующего значения напряжения синусоидальной формы становится равной нулю.
Это означает, что справедливо следующее утверждение: при определении эффективного значения несинусоидального напряжения, содержащего N гармоник, с помощью способа (2) методическая погрешность равна нулю при выборе количества выборок мгновенных значений напряжения, равного n=2N+1. Например, при N= 1 (для синусоидального напряжения) n=3 (фиг.2, б).
Справедливо также обратное утверждение: если с помощью способа (2) при n выборках мгновенных значений получено точное значение эффективного значения несинусоидального напряжения с ограниченным спектром, то это напряжение содержит N=(n-1)/2 гармоник.
Это утверждение положено в основу предлагаемого способа определения количества гармоник несинусоидального сигнала. Его реализация заключается в определении действующих значений Ui несинусоидального напряжения по формуле (2) при постепенном увеличении числа выборок (i,i+1,...) до некоторых значений n, n+1, для которых выполняется условие
Un - Un+1 = 0. (12)
Отметим, что при всех j<n действующее значение меняется при каждом j.
Что касается функций с неограниченным спектром, то известно, что спектральная плотность уменьшается с увеличением частоты гармоник, поэтому влияние гармоник с номерами k>N незначительно. Количество гармоник N в этом случае определяется из измененного условия (12);
Un-Un+1 = ε,
где ε - заданная погрешность, которая может быть выбрана сколь угодно малой.
При практической реализации предложенного решения, выполняемые процедуры могут быть выполнены на основе использования известных средств, например, измерение мгновенных значений - с помощью устройств выборки-хранения, а операции возведения в квадрат, суммирования и извлечения квадратного корня - с помощью ЭВМ.
Таким образом, изложенные сведения свидетельствуют о выполнении при использовании заявленного изобретения следующей совокупности условий:
средство, воплощающее заявленный способ при его осуществлении, предназначено для использования в электроизмерительной технике, в частности для определения количества гармоник несинусоидальных сигналов;
для заявленного способа в том виде, как он охарактеризован в формуле изобретения, подтверждена возможность его осуществления с помощью известных средств.
Следовательно, заявленное изобретение соответствует условию "промышленная применимость".

Изобретение относится к электроизмерительной технике, в частности к определению количества гармоник несинусоидальных сигналов. Технический результат заключается в снижении объема вычислений при определении числа гармонических составляющих несинусоидального сигнала и повышении точности этого определения путем выбора оптимального числа выборок мгновенных значений сигнала. Это достигается тем, что результатом измерения выборок мгновенных значений напряжения определяется действующее значение напряжения, причем количество выборок мгновенных значений сигнала постепенно увеличивается до некоторого значения, при котором действующее значение перестает изменяться. 3 ил.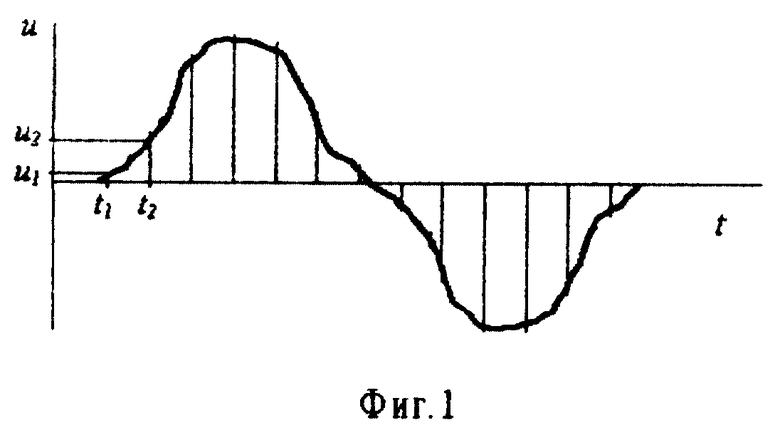
Способ определения количества гармоник несинусоидальных сигналов, включающий определение n выборок мгновенных значений напряжения при одинаковом шаге между выборками, равном 360o/n, отличающийся тем, что рассчитывают действующее значение сигнала путем возведения выборок в квадрат, их суммирования, деления на n и извлечения квадратного корня, затем повторяют описанную процедуру расчета действующего значения, увеличивая n на единицу каждый раз, до тех пор, пока действующее значение не будет равно предыдущему значению с заданной погрешностью, при этом количество N гармоник несинусоидального сигнала определяют из выражения N=(n-1)/2.
| БЕССОНОВ Л.А | |||
| Теоретические основы электротехники | |||
| - М.: Высшая школа, 1973, с | |||
| Приспособление для подачи воды в паровой котел | 1920 |
|
SU229A1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ ЧАСТОТЫ ЭЛЕКТРИЧЕСКОЙ СЕТИ | 1995 |
|
RU2110804C1 |
| СПОСОБ ИЗМЕРЕНИЯ КОЭФФИЦИЕНТА НЕЛИНЕЙНЫХ ИСКАЖЕНИЙ СИГНАЛА | 1993 |
|
RU2090900C1 |
| КОМПОЗИЦИЯ ДЛЯ ИЗГОТОВЛЕНИЯ БИОДЕСТРУКТИРУЮЩИХ ОРТОПЕДИЧЕСКИХ ИМПЛАНТАТОВ | 1992 |
|
RU2074738C1 |
| US 4978911 А, 18.12.1990. | |||
Авторы
Даты
2002-08-10—Публикация
2000-09-29—Подача