Изобретение относится к области оптической контрольно-измерительной техники и может быть использовано для измерения толщины остаточных пленок в окнах малых (~ 1 мкм) размеров, полученных путем вытравливания их (или любым другим способом) в произвольной многослойной структуре на подложке с известными оптическими характеристиками (например, на кремнии), в различных отраслях промышленности, использующих тонкопленочную технологию (широкое применение способ найдет в микроэлектронике, где в связи с непрерывным уменьшением размера элементов очень остро стоит вопрос о неразрушающем контроле полноты вскрытия окон субмикронных размеров).
Известен способ [1] определения полноты вскрытия отверстий в маскирующих слоях на полупроводниковой подложке, основанный на высаживании паров воды на охлажденные до температуры ниже точки росы контролируемые структуры с последующим повышением температуры до образования зародышевых капель. О полноте вскрытия судят по плотности распределения и форме зародышевых капель конденсата деионизованной воды в отверстиях и на поверхности маскирующих слоев (поверхность кремния гидрофобная и не смачивается жидкостью в отличие от гидрофильной поверхности двуокиси кремния, которая смачивается жидкостью).
Недостатками этого способа являются сложность реализации, ограничения по номенклатуре контролируемых изделий (отличие в смачиваемости исходной и вытравленной структур), ограничения по величине контролируемых отверстий (необходимость визуального контроля степени смачивания поверхности малых отверстий).
Наиболее близким техническим решением к предлагаемому изобретению является метод эллипсометрии [2-3], заключающийся в помещении измеряемого образца на предметный столик, в освещении контролируемого окна пучком монохроматического излучения, измерении эллипсометрических параметров ψ, Δ для этого окна, вычислении по этим параметрам толщины пленки в окне и позволяющий проводить измерение толщины остаточных пленок в окнах с помощью серийно выпускаемых стандартных эллипсометров для локальных измерений (отечественный эллипсометр ЛЭФ-801, эллипсометры фирм Rudolpn Research, CRL Laurl) Industries из США и др. ). По сравнению с аналогом этот метод прост, не имеет принципиальных ограничений по номенклатуре контролируемых изделий.
Однако как и аналог, он имеет ограничения по величине контролируемых окон (отверстий), так как все выпускаемые в настоящее время эллипсометры обладают в лучшем случае локальностью 5•10 мкм2.
Примечание 1. Эллипсометрические параметры ψ, Δ характеризуют изменение состояния поляризации света при его взаимодействии с исследуемой структурой и зависят от всех геометрических и оптических характеристик этой структуры (в том числе от толщины остаточной пленки при контроле окон).
Задачей настоящего изобретения является достижение технического результата, заключающегося в уменьшении размера окон (~1 мкм), в которых возможен контроль толщины остаточных пленок при использовании метода эллипсометрии, реализуемого на эллипсометрах с локальностью ~5•10 мкм2, за счет использования комбинат стандартных измерений с последующей обработкой результатов измерений по специальному алгоритму. Выполнение этой задачи позволит расширить номенклатуру изделий, при выпуске которых может быть реализован непосредственно на рабочих пластинах контроль толщины остаточных пленок в окнах малых (~1 мкм) размеров, вытравленных в произвольной многослойной структуре на подложке с известными оптическими характеристиками (к примеру, на кремнии), что должно привести к увеличению процента выхода годных изделий.
Для достижения названного технического результата предлагается метод эллипсометрии [2-3], включающий:
а) помещение пластины с измеряемой структурой на предметный столик,
б) освещение монохроматическим излучением не менее четырех рядом расположенных участков структуры со сформированными в ней окнами, имеющих различное соотношение площадей "исходная многослойная структура-окна",
в) измерение эллипсометрических параметров ψj, Δj (j=1, 2, 3, 4) света для каждого из этих участков в нулевом порядке дифракции для полностью перемешанных пучков света, отраженных от исходной многослойной структуры и окон,
г) вычисление эллипсометрических параметров ψ, Δ для окон по измеренным для четырех участков эллипсометрическим параметрам ψj, Δj с помощью специального алгоритм,.
д) вычисление по найденным знчениям ψ, Δ толщины остаточной пленки в окне стандартным способом.
Примечание 2. Термин "полностью перемешанные пучки света" здесь и в дальнейшем используется для краткого обозначения пучков света, которые попадают в точку измерения в результате отражения от каждой точки исследуемых участков. К примеру, одним из способов достижения такого перемешивания может быть использование однородных по сечению расходящихся пучков света. Используемые в стандартных эллипсометрах лазеры удовлетворяют этому условию и позволяют при малой расходимости ~7 угловых минут получить на фотоприемнике эллипсометра, находящемся на расстоянии ~50 см от образца и измеряющем интенсивность отраженного от исследуемого образца света, пятно размером ~1 мм, в каждой точке которого происходит вышеупомянутое полное перемешивание пучков света.
Примечание 3. Эллипсометрические параметры ψj, Δj по-прежнему характеризуют изменение состояния поляризации света при его взаимодействии с иследуемой структурой, однако в данном случае эта структура является сложной (состоит из смеси исходной многослойной структуры и вытравленных в ней окон) и измеряемые параметры ψj, Δj зависят в том числе и от параметров ψ, Δ для окон, которые в конечном итоге могут быть вычеслены по предлагаемому в заявке способу из полученных уравнений для ψj, Δj.
Таким образом, отличительными признаками настоящего изобретения являются действия б), в), г):
б) освещение монохроматическим излучением не менее четырех рядом расположенных участков структуры со сформированными в ней окнами, имеющих различное соотношение площадей "исходная многослойная структура-окна",
в) измерение эллипсометрических параметров ψj, Δj (j=1, 2, 3, 4) света для каждого из этих участков для полностью перемешанных пучков света, отраженных от исходной многослойной структуры и окон,
г) вычисление эллипсометрических параметров ψ, Δ для окон по измеренным для четырех участков эллилсометрическим параметрам ψj, Δj с помощью специального алгоритма.
Выполнение этих отличительных признаков при использовании серийных эллипсометров с локальностью 5•10 мкм2 позволяет осуществлять измерение толщины остаточных пленок в окнах размером ~1 мкм.
Проведенные патентные исследования показали, что в литературе отсутствует указание на использование вышеперечисленной совокупности отличительных признаков для решения задачи об измерении толщины остаточных пленок в окнах малых размеров, что подтверждает новизну данного изобретения.
Рассмотрим более подробно суть предложенного способа.
Пусть на произвольную подложку с известными оптическими характеристиками (показателями преломления и поглощения) нанесена многослойная структура, состоящая из прозрачных и непрозрачных на используемой длине волны света (наиболее распространены эллипсометры на длину волны 0,6328 мкм) слоев, и в такой структуре проведено вытравливание до подложки малых (порядка единицы микрона) произвольно расположенных окон с различной конфигурацией (смотри чертеж, на котором заштрихованными и незаштрихованными областями обозначены соответственно участки исходной структуры и вытравленные участки). Ставится задача о контроле полноты вскрытия таких окон, т.е. об измерении в них толщины остаточной пленки (последний слой, остаточная толщина которого определяется, должен быть прозрачным либо в случае, когда он непрозрачен, для него должны быть известны оптические характеристики).
Проведем измерение зллипсометрических параметров Δ1 и ψ1 в так называемом нулевом порядке дифракции для света, отраженного от области структуры, содержащей участок исходной структуры площадью S1 1 и участок с вытравленной до подложки (предположительно) структурой площадью S1 2 (на чертеже эта область обведена пунктиром и обозначена цифрой 1). Следует отметить, что в состав измеряемой области может входить несколько участков того и другого типа, важно только, чтобы в измеряемую область не входили участки какого-либо третьего типа. Точно таким же образом проведем измерение эллипсометрических параметров (Δ2, ψ2), (Δ3, ψ3) и (Δ4, ψ4) для областей 2, 3 и 4 (на чертеже показаны области 2 и 3), по возможности наиболее сильно отличающихся друг от друга и от области 1 соотношением площадей участков с исходной и вытравленной структурами. Если диаметр анализирующего пучка света позволяет провести измерение эллипсометрических параметров для исходной (невытравленной) структуры, то одно из вышеуказанных измерений может быть проведено на таком однородном участке.
Пример 1. Соотношение площадей участков с исходной и вытравленной структурнами для областей 1-4 может, к примеру, состовлять 0.2, 0.4, 0.6, 0.8. Уменьшение разности между значениями соотношений площадей приводит к увеличению погрешности при вычислении толщины остаточной пленки.
Пример 2. Для правильного измерения эллипсометрических параметров ψj, Δj (j= 1, 2, 3, 4) в нулевом порядке дифракции используемый эллипсометр, к примеру, должен быть снабжен диафрагмой, препятствующей прохождению на фотоприемник эллипсометра лучей во всех порядках дифракции, кроме нулевого.
Следует отметить, что ввиду неоднородности исследуемой структуры для правильного получения эллипсометрических параметров ψj, Δj света, отраженного от такой структуры, необходимо, чтобы эти параметры определялись для полностью перемешанных пучков света, отраженных от исходной многослойной структуры и окон (примечание 2). Для измеренных вышеуказанным способом эллипсометрических параметров ψj, Δj справедливы следующие уравнения эллипсометрии [4]:
φ = 4πhλ-1cosϕ, Sj = S
где r0p,r0s и rр, rs - амплитудные коэффициенты отражения света для р- и s- поляризаций соответственно на границах раздела воздух-исходная структура и воздух-вытравленная структура,
Sj - отношение площадей участков с вытравленной и исходной структурами (все параметры относятся к областям 1, 2, 3, 4 соответственно при j=1, 2, 3, 4),
h-высота ступеньки исходная-вытравленная структуры,
λ - длина волны света,
φ - угол падения света на структуру.
В выражении (1) не учитывается вклад отраженного излучения от областей, находящихся вблизи границы исходная-вытравленная структуры, в которых коэффициент отражения отличен от r0p, r0s, rp, rs (наличие таких областей приводит к некоторой модельной погрешности, однако имеются способы ее уменьшения практически до нуля).
Введя обозначения uj = tgψjexp(iΔj) для j=1, 2, 3, 4 получаем из (1) систему четырех уравнений:
ujSjr's-Sjr'p=r0p-ujr0s, где  (2)
(2)
из которых нетрудно получить следующие выражения
S21=(S2/S1)=(u0-u2)(u1-u)(u0-u1)-1(u2-u)-1, (3)
S31=(S3/S1)=(u0-u3)(u1-u)(u0-u1)-1(u3-u)-1, (4)
S41=(S4/S1)=(u0-u4)(u1-u)(u0-u1)-1(u4-u)-1, (5)
где u0=(r0p/r0s);
u = (rp/rs) = tgψexp(iΔ)- (6)
искомая комплексная величина, позволяющая найти эллипсометрические параметры Δ, ψ для участка с остаточной пленкой, по которым нетрудно по имеющимся программам вычислить толщину остаточной пленки.
Исключая из уравнений (3)-(5) u0, получаем два уравнения, содержащие величину u:
(S31-1)(S21-1)-1=(ul-u3)(u2-u)(u1-u2)-1(u3-u)-1, (7)
(S41-1)(S21-1)-1=(ul-u4)(u2-u)(u1-u2)-1(u4-u)-1, (8)
Из уравнений (7), (8) получаем два уравнения для определения комплексной величины u:
lm[(u1-u3)(u2-u)(u1-u2)-1(u3-u)-1]=0, (9)
lm[(u1-u4)(u2-u)(u1-u2)-1(u4-u)-1]=0, (10)
где значки lm обозначают вычисление мнимой части от соответствующего выражения.
Кроме того, если из уравнении (7), (8) исключить искомый комплексный параметр u, то из полученного выражения
(1-S31)(S21-S41)(1-S41)-1(S21-S31)-1= (u1-u3)(u4-u2)(u1-u4)-1(u3-u2)-1 (11)
следует условие, которому должны удовлетворять измеряемые комплексные параметры uj(j=1, 2, 3, 4)
lm[(u1-u3)(u4-u2)(u1-u4)-1(u3-u2)-1]=0 (12).
Это условие в дальнейшем используется при решении системы уравнений (9), (10).
Представляя комплексные величины в уравнениях (9),(10) в виде
uj=vj+iwj(j=1, 2, 3, 4), u=v+jw, (13)
получаем два действительных уравнения для определения v и w
a1|u|2+b1v+c1w+d1 = 0, (14)
a2|u|2+b2v+c2w+d2 = 0, (15)
где |uj|2 = v
a1=v1(w3-w2)+v2(w1-w3)+v3(w2-w1) (16)

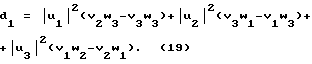
Параметры a2, b2, c2,d2 получаются из a1, b1, c1, d1 путем замены индекса 3 на индекс 4.
Простые, но довольно громоздкие преобразования показывают, что условие (12) соответствует условию
b1c2=b2c1 (20)
Умножая (14) на с2, (15) на с1 и вычитая их друг из друга с использованием условия (20), получаем следующее выражение для нахождения эллипсометрического параметра ψ для вытравленных участков:
|u|2 = tg2ψ = (d2c1-d1c2)(a1c2-a2c1)-1,
из которого находим:
ψ = arctg[(d2c1-d1c2)1/2(a1c2-a2c1)-1/2] (21)
Точно так же, умножая (14) на b2, (15) на b1 и вычитая их друг из друга с использованием условия (20), получаем выражение:
|u|2 = tg2ψ = (b1d2-b2d1)(a1b2-a2b1)-1,
из которого находим:
ψ = arctg[(b1d2-b2d1)1/2(a1b2-a2b1)-1/2] (22)
Нетрудно показать с использованием (20), что правые части выражений (21) и (22) совпадают. Однако в реальных условиях при использовании выражений (21) и (22) для вычисления ψ по измеренным величинам uj (j=1, 2, 3, 4) будут получаться разные значения для ψ и эта разница будет характеризовать суммарную модельную и экспериментальную погрешности этого метода (наличие склонов на ступеньках, влияние дифракции, наличие реальных погрешностей конкретных используемых эллипсометров, наличие областей с коэффициентами отражения, отличными от r0р, r0s, rр, rs). В связи с изложенным в принципе можно пользоваться любым из уравнений (21), (22) для вычисления ψ, однако для уменьшения погрешности лучше провести вычисление по двум формулам и результаты усреднить.
Подставляя (21) в (14), а (22) в (15), получаем систему уравнений для вычисления v и w:
vb1+wc1+c1(a1d2-a2d1)(a1c2-a2c1)-1=0 (23)
vb2+wc2+c2(a1d2-a2d1)(a1b2-a2b1)-1=0 (24)
Эти уравнения линейно зависимы (следует из (20)), поэтому получить из них v и w не представляется возможным. Однако можно использовать явные выражения для v и w
v = tgψcosΔ, w = tgψsinΔ, (25)
подставить их, а также (21), (22) соответственно в (23),(24) и получить после несложных преобразований уравнения для нахождения эллипсометрического параметра Δ для вытравленных участков: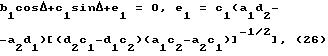

Используя условие (20), нетрудно показать, что выполняется соотношение
b1e2=b2e1, (28)
т.е. при отсутствии модельной и экспериментальной погрешностей уравнения (26) и (27) совпадают. Однако на практике представляет интерес получить решения из двух вышеуказанных уравнений, чтобы оценить реальное значение этих погрешностей и провести усреднение полученных для Δ значений для уменьшения погрешности.
Из уравнений (26),(27) получаем по два решения для Δ:
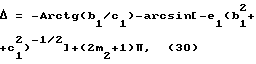

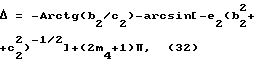
где значения α1 = Arctg(b1/c1) и α2 = Arctg(b2/c2) находятся в диапазоне от 0 до 2π и определяются с учетом знаков b1(b2) и с1(с2), совпадающих со знаками sinα1(α2) и cosα1(α2) соответственно;
m1 (j= 1,2,3,4) - целые числа, выбираемые из условия получения значений для Δ в пределах от 0 до 2π.
К сожалению, из пары решений (29)-(30) или (31)-(32) математически нельзя выбрать одно, соответствующие исследуемой структуре. Однако, если после стравливания структуры до подложки остается тонкая остаточная пленка, меньшая нескольких сотен ангстрем, то из двух решений выбирается то, которое близко к истинному значению Δ для такой пленки (или к Δ для чистой подложки) и по полученным таким образом значениями Δ и ψ (из формул (21), (22)) находится реальное значение толщины (для любых используемых в производстве пленок на реальных подложках со стабильными характеристиками (кремний, арсенид галлия и др.) диапазон значений Δ и ψ для малых толщин этих пленок известен). Если же обе пары решений для Δ далеки от истинных значений Δ для малых толщин пленок, то это говорит о том, что в окне осталась тонкая пленка (окно не вскрыто).
Точно таким же образом можно показать, что имеется еще пять пар уравнений типа (14), (15) для нахождения Δ и ψ. Эти уравнения получаются из исходной системы уравнений (2) путем использования вместо S21, S31, S41 (уравнения (3)-(5)) других соотношений (например, S21, S23, S24). При этом в этих новых уравнениях (14), (15) меняются только входящие в них параметры a1, b1, c1, d1, a2, b2, c2, d2, причем эти параметры имеют тот же вид, как в формулах (16)-(19) для подробно изложенного случая, выражаются через те же измеренные величины uj, vj, wj, но индекс j, который, как указывалось выше, может принимать значения от 1 до 4, в новых формулах принимает другие значения по сравнению с приведенными в тексте формулами (14), (15). Входящие в шесть пар уравнений (14), (15) (с учетом пары уравнений, вывод которой изложен выше) параметры a1, b1, c1, d1, a2, b2, c2, d2, можно записать в компактном виде следующим образом:
а1=ajkl=vk(wj-wl)+vj(wl-wk)+vl(wk-wj), (33)


a2=amnp, b2=bmnp, c2=cmnp, d2=dmnp, (37)
где uj= vj+iwj, vj = tgψjcosΔj, wj = tgψjsinΔj и такие же соотношения справедливы для всех других индексов (k, l, m, n, p);
наборы индексов (j,k,l) и (m,n,p) могут принимать значения от 1 до 4 и их конкретные значения для каждой из шести пар уравнений (14), (15) выбираются из таблицы (для первой пары уравнений - из второго столбца таблицы (эти индексы соответствуют уравнениям, изложенным в тексте), для второй пары - из третьего столбца и т.д., при этом из верхней и нижней строк столбца выбираются значения индексов соответственно для (j, k, l) и (m, n, p)).
Соотношения (37) в компактном виде могут быть переписаны в виде
(a, b, c, d)2=(a, b, c, d)mnp (38)
Пример 3. Для второй пары уравнений (14), (15) из третьего столбца таблицы получаем для наборов индексов (j, k, l) и (m, n, p) значения (1, 3, 2), (1, 3, 4) и из формул (33), (37) получаем для a1, a2 выражения:
a1=a132=v3(w1-w2)+v1(w2-w3)+v2(w3-w1).
a2=a134=v3(w1-w4)+v1(w4-w3)+v4(w3-w1);
точно таким же способом из формул (34)-(37) получаем выражения для других параметров (b1, c1, d1, b2, c2, d2).
Из дополнительных пяти пар уравнений получаются еще по пять пар решений (21), (22) для ψ и по пять пар выбранных вышеуказанным способом решений (29)-(32) для Δ (входящие в эти формулы параметры a1, b1, c1, d1, a2, b2, c2, d2 описываются формулами (33)-(37)). Все эти уравнения и их решения совпадают друг с другом при отсутствии модельных и экспериментальных погрешностей, однако, как указывалось выше, имеет смысл найти все эти решения, для уменьшения погрешности провести усреднение шести пар значений Δ и ψ и по найденным средним значениям этих параметров методом стандартной эллипсометрии вычислить толщину остаточной пленки в малых окнах. Отклонение найденных шести пар значений Δ и ψ от полученных средних значений будет характеризовать величину суммарной модельной и экспериментальной погрешностей.
Примечание 4. Усреднение для параметров Δ и ψ можно проводить по любому количеству из шести пар найденных значений Δ и ψ, однако результирующая погрешность уменьшается при увеличении количества усредняемых параметров.
Примечание 5. Имеется всего шесть пар уравнений типа (14), (15) для нахождения Δ и ψ (эти уравнения, как указано выше, отличаются параметрами a1, b1, c1, d1, a2, b2, c2, d2, описываемыми формулами (33)-(37) с использованием шести наборов пар индексов (j, k, l) и (m, n, p)). Это утверждение легко доказать, если учесть следующие обстоятельства:
- индексы в каждом из наборов (j, k, l) и (m, n, p) принимают значения от 1 до 4;
- индексы в каждом из наборов (j, k, l) и (m, n, p) не должны совпадать друг с другом;
- для каждой пары уравнений набор индексов (m, n, p) получается из набора индексов (j, k, l) путем замены одного из индексов в наборе (j, k, l) на оставшийся, не входящий в этот набор ( например, если набор (j, k, l) имеет вид (1, 2, 3), то набор (m, n, p) может быть (4, 2, 3), (1, 4, 3), (1, 2, 4));
- уравнения не меняются, если в любом из наборов индексов (j, k, l) или (m, n, p) поменять местами любые два индекса (например, уравнения (14), (15) для наборов индексов (j, k, l) и (m, n, p), имеющих вид (1, 2, 3), (1, 2, 4) и (2, 1, 3), (1, 2, 4) (поменяли местами только индексы 1 и 2 в наборе (j, k, l)), совпадают);
- пары уравнений (14), (15) не меняются, если поменять местами наборы (j, k, l) и (m, n, p) (при этом меняются местами только уравнения, сохраняя свой вид).
Примечание 6. В описании приведены уравнения и их решения для Δ и ψ для случая, когда измерения проводятся на четырех участках. Все изложенное остается в силе для случая использования измерений на большем количестве участков - уравнения (14) и (15) и решения для Δ и ψ имеют тот же вид, а изменяются только наборы индексов (j, k, l) и (m, n, p), так как каждый из индексов теперь принимает значения в большем интервале (для случая измерений на пяти участках - от 1 до 5) и количество пар наборов индексов существенно возрастает.
В качестве примера приведем результаты оценки погрешности, получаемой при реализации предложенного способа на стандартных эллипсометрах. С этой целью были проведены специальные модельные расчеты:
- для структуры SiO2-Si с толщиной пленки 0,30 мкм с вытравленными в ней окнами размером 0,5•1,0 мкм2 (толщина остаточной пленки в окнах выбиралась равной 0,01 мкм) проведено вычисление эллипсометрических параметров ψj, Δj для четырех областей с разным соотношением площадей с исходной пленкой и окнами (0,2; 0,4; 0,6; 0,8) без учета модельных погрешностей, вызванных наличием областей с коэффициентами отражения, отличными от коэффициентов отражения для исходной и вытравленной структур;
- с помощью полученных эллипсометрических параметров, в которые были введены реальные экспериментальные погрешности для эллипсометров (0,1 и 0,2 угловых градуса соответственно для ψj, Δj), по предложенному в заявке алгоритму была вычислена толщина пленки в окнах.
Максимальная погрешность, полученная для толщины при различных комбинациях вышеуказанных погрешностей, введенных в четыре пары ψj, Δj (с учетом знаков этих погрешностей), составляла ±0,6 нм. Дополнительную погрешность в толщину будет давать модельная погрешность (несоответствие реальной модели структуры модели, принятой в заявке при разработке алгоритма вычислений), однако имеются способы уменьшения этой погрешности практически до нуля.
Пример 4. Модельная погрешность может быть уменьшена, к примеру, следующими способами:
- путем использования для измерений участков структуры с вытравленными областями, имеющими вытянутость в каком-либо направлении (такие области можно готовить в специально создаваемой тестовой ячейке), при этом плоскость падения пучка света должна совпадать с этим направлением;
- путем освещения измеряемых участков структуры таким образом, чтобы суммарная протяженность границ раздела исходная структура - вытравленная структура, находящихся со стороны падающего пучка света и перпендикулярных плоскости падения (при расположении участков вдоль плоскости падения), была минимальной;
- при исследовании окон в структурах с минимальной величиной ступеньки (чем меньше глубина окна, тем меньше площадь области, в которой коэффициенты отражения отличны от r0р,r0p,rp,rs).
Для уменьшения вышеуказанной погрешности для толщины (±0,6 нм), которая вызвана экспериментальной погрешностью используемого эллипсометра и которая будет практически такой же во всем диапазоне малых толщин пленок (от единиц до десятков нанометров), необходимо уменьшать абсолютную погрешность эллипсометрических измерений, используя серийно выпускаемые более точные эллипсометры (имеются эллипсометры с погрешностью, на порядок меньшей по сравнению с использованной в вышеприведенных расчетах). Приведенные результаты расчетов подтверждают принципиальную возможность контроля толщины остаточных пленок в окнах малых размеров по предложенному в заявке способу с погрешностью, которая зависит от абсолютной погрешности применяемых для контроля эллипсометров.
Источники информации
1. Подольский В.А., Алферов А.Н., Нечипоренко А.П., Щербинин А.А., Кокин В. Н. , Круглов Р.Н. Способ определения полноты вскрытия отверстий в маскирующих слоях на полупроводниковой подложке и устройство для его осуществления // Авторское свидетельство 1189201 от 01.07.85 г.
2. Ржанов А.В., Свиташев К.К., Семененко А.И. и др. Основы эллипсометрии // Новосибирск, 1979. - 422 с.
3. Аззам Р., Башара М. Эллипсометрия и поляризованный свет // М., 1981. - 583 с.
4. Биленко Д.И., Казакова Н.П., Полянская В.П. Определение толщины слоев в локальных эпитаксиальных структурах // Микроэлектроника, 1983, т.12, 1, с. 70-75.
| название | год | авторы | номер документа |
|---|---|---|---|
| СПОСОБ ИЗМЕРЕНИЯ ВЫСОТЫ СТУПЕНЕК В ПРОИЗВОЛЬНЫХ МНОГОСЛОЙНЫХ СТРУКТУРАХ | 2003 |
|
RU2270437C2 |
| Способ профилирования состава при эпитаксиальном формировании полупроводниковой структуры на основе твердых растворов | 2019 |
|
RU2717359C1 |
| СПОСОБ СОЗДАНИЯ ИЗОЛЯЦИИ В ПРОИЗВОДСТВЕ ИС | 1995 |
|
RU2108638C1 |
| СПОСОБ ИЗГОТОВЛЕНИЯ ТОНКОПЛЕНОЧНЫХ ТРАНЗИСТОРОВ МАТРИЦ ЖИДКОКРИСТАЛЛИЧЕСКИХ ЭКРАНОВ | 1994 |
|
RU2069417C1 |
| БИКМОП-ПРИБОР И СПОСОБ ЕГО ИЗГОТОВЛЕНИЯ | 1996 |
|
RU2106719C1 |
| СПОСОБ ФОРМИРОВАНИЯ ПЕРЕХОДНЫХ КОНТАКТНЫХ ОКОН | 2001 |
|
RU2202136C2 |
| СПОСОБ ИЗГОТОВЛЕНИЯ БИПОЛЯРНОГО ТРАНЗИСТОРА | 1995 |
|
RU2099814C1 |
| СПОСОБ ИЗГОТОВЛЕНИЯ ИНТЕГРАЛЬНЫХ СХЕМ НА КМОП-ТРАНЗИСТОРАХ | 2000 |
|
RU2185686C2 |
| СПОСОБ ФОРМИРОВАНИЯ СЛОЕВ ПОЛИКРИСТАЛЛИЧЕСКОГО КРЕМНИЯ | 2000 |
|
RU2191847C2 |
| СХЕМА УСКОРЕННОГО ПЕРЕНОСА (ВАРИАНТЫ) | 1999 |
|
RU2149443C1 |


Изобретение относится к оптической контрольно-измерительной технике и может быть использовано для измерения толщины остаточных пленок в окнах малых (~1 мкм) размеров, полученных любым способом в произвольной многослойной структуре на подложке с известными оптическими характеристиками Сущность изобретения заключается в измерении стандартным методом эллипсометрии эллипсометрических параметров в нулевом порядке дифракции для по крайней мере четырех рядом расположенных участков структуры со сформированными в ней окнами, имеющих различное соотношение площадей "исходная многослойная структура-окна", с последующим вычислением с их помощью толщины остаточной пленки в окнах по специальному алгоритму. Технический результат: расширение номенклатуры изделий, при выпуске которых может быть реализован контроль толщины остаточных пленок в окнах малых (~1 мкм) размеров, что приводит к увеличению процента выхода годных изделий. 1 ил., 1 табл.
Способ измерения толщины остаточных пленок в окнах малых размеров, полученных любым способом в произвольной многослойной структуре на подложке с известными оптическими храктеристиками, включающий помещение образца со структурой на столик, освещение исследуемого однородного участка пластины со структурой пучком монохроматического излучения, измерение эллипсометрических параметров ψ,Δ для этого участка, вычисление по этим параметрам толщины пленки на этом участке, отличающийся тем, что освещают монохроматическим излучением не менее четырех рядом расположенных участков структуры со сформированными в ней окнами, имеющих различное соотношение площадей "исходная многослойная структура-окна", измеряют эллипсометрические параметры ψj,Δj (j= 1, 2, 3, 4) для этих участков в нулевом порядке дифракции для полностью перемешанных пучков света, вычисляют для окон параметры ψ,Δ по формулам
ψ= arctg[(d2c1-d1c2)1/2(a1c2-a2c1)-1/2] ,
ψ= arctg[(b1d2-b1d1)1/2(a1b2-a2b1)-1/2] ,



где значения α1= Arctg(b1/c1) и α2= Arctg(b2/c2) находятся в диаппзоне 0 - 2π и определяются с учетом знаков b1(b2) и с1(с2), совпадающих со знаками sinα1(α2) и cosα1(α2) соответственно;
mj (j = 1, 2, 3, 4) - целые числа, выбираемые из условия получения значений для Δ в пределах 0 - 2π;
a1= ajkl= vk(wj-wl)+vj(wl-wk)+vl(wk-wj);
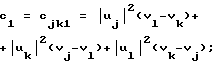

(a. b, c, d)2= (a, b, c, d)mnp;
e1= с1(a1d2-a2d1)[(d2с1-d1с2)(a1с2-a2с1)] -1,2;
e2= b2(a1d2-a2d1)[(d2b1-d1b2)(a1b2-a2b1)] -1,2;
uj= vj+iwj (i - мнимая единиц),
vj = tgψjcosΔj, wj = tgψjsinΔj (j= 1, 2, 3, 4) и такие же соотношения справедливы для всех других индексов (k, l, m, n, p),
вычисляют параметры ψ и Δ для шести пар наборов индексов (j, k, l) и (m, n, p), выбираемых последовательно из шести столбцов таблицы (см. графическую часть),
находят параметр ψ для окон путем усреднения любого количества из шести полученных по вышеприведенным формулам пар для параметра ψ, выбирают из четырех значений, полученных для параметра Δ для каждой пары индексов (j, k, l) и (m, n, p), по два таких, значения которых наиболее близки к известным параметрам Δ для исследуемой структуры с полностью вытравленным в ней окном, находят параметр Δ для окон путем усреднения любого количества из шести полученных таким образом пар для параметра Δ.
| СПОСОБ ЭЛЛИПСОМЕТРИЧЕСКОГО ИССЛЕДОВАНИЯ ТОНКИХ ПЛЕНОК НА ПЛОСКИХ ПОДЛОЖКАХ | 1997 |
|
RU2133956C1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ ЭЛЛИПСОМЕТРИЧЕСКИХ ПАРАМЕТРОВ ОБЪЕКТА | 1991 |
|
RU2008652C1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ ЭЛЛИПСОМЕТРИЧЕСКИХ ПАРАМЕТРОВ ОБЪЕКТА (ВАРИАНТЫ) | 1997 |
|
RU2149382C1 |
| US 5018863 А, 28.05.1991. | |||
Авторы
Даты
2002-11-20—Публикация
2000-01-26—Подача