Изобретение относится к измерениям электропроводящих величин вещества. Поскольку электропроводность является обратной величиной электрического сопротивления, то в качестве аналога взят способ оценки полного электрического сопротивления металла (ρполн) [1], включающий измерение остаточного сопротивления (ρост), связанного с технологией изготовления данного образца металла и не зависящего от температуры и электрического сопротивления идеальной решетки данного металла (ρид), обусловленное рассеянием на фотонах и сильно зависящее от температуры, которое описывается формулой Блоха- Грюнайзера:
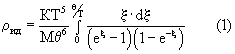
где k - постоянная, связанная с удельным объёмом металла;
М - атомная масса;
θ - характеристическая температура - параметр металла, характеризующий максимальную частоту колебаний решетки (hωmax ≅ kθ).
Недостатком этого способа является трудность достоверного определения ряда входящих в формулу (1) параметров (К, θ, ξ), а также возможности описания электропроводности других веществ - полупроводников и диэлектриков.
Также известен способ оценки электропроводности вещества (в частности, горных пород) путём определения лабораторными или промыслово-геофизическими методами макроскопических параметров, включающих коэффициенты различных видов пористости, влагонасыщения, содержания примесей, удельного сопротивления воды, степени извилистости пор и учёт их при определении электропроводности по формуле:
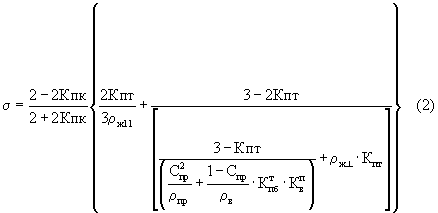
где Кпк - кавернозная пористость;
Кпт - трещинная пористость;
ρв - удельное электрическое сопротивление воды в межзерновых порах;
Спр - объёмное содержание примесей ;
ρж⊥, ρж|| - удельные электрическое сопротивления воды в трещинах, расположенных ⊥ и || к направлению токовых линий;
Кпб - коэффициент межзерновой (блоковой) пористости;
Кв - коэффициент водонасыщенности вещества;
т - показатель степени пористости;
п - показатель степени водонасыщенности;
ρпр - удельное электрическое сопротивление примеси.
Недостатком этого технического решения является отсутствие учета типа кристаллической решетки основообразующего материала вещества и его межмолекулярной пористости, а также отсутствие возможности получения достоверной информации об электропроводности вещества при переходе в сверхпроводящее состояние.
Техническим решением задачи является получение достоверной информации об электропроводности всего класса веществ, в том числе при переходе в сверхпроводящее состояние.
Поставленная задача достигается тем, что в способе оценки электропроводности всего класса веществ, в том числе с учетом перехода в сверхпроводящее состояние путём определения лабораторными или промыслово-геофизическими методами макроскопических параметров, включающих коэффициенты различных видов пористости, влагонасыщения, содержания примесей, удельного сопротивления воды, степени извилистости пор, учитывают микроскопические параметры вещества, включающие коэффициенты межмолекулярной пористости, структурного параметра кристаллической решетки, удельное электрическое сопротивление потока электронов (электронной жидкости), отношение площадей фотонных оболочек электронов к сечению межмолекулярных пор, которые определяют физическими методами на основании размеров атомно-молекулярного строения вещества и определяют электропроводность по формуле, которая учитывает наличие всех возможных каналов для движения электронов проводимости и ионов солей.
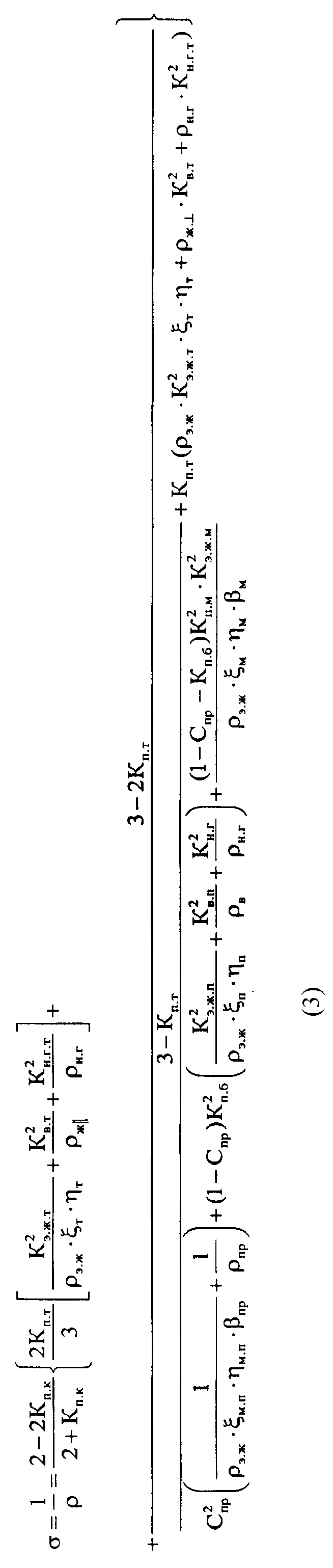
где βм, βпр - структурный параметр кристаллической решетки основного минерала и минерала примесей;
Кпк - кавернозная пористость (пористость изолированных в блоке пор);
Кпт - трещинная пористость;
Кпб - пористость блока вещества или межзерновая пористость;
Кпм - межмолекулярная пористость;
Спр - содержание примесей в веществе в долях от общего объема;
Квп, Квт - коэффициент водонасыщения пор, трещин;
Кнг, Кнгт - коэффициент нефтегазонасыщения пор, трещин;
Кэ.ж.п, Кэ.ж.м, Кэ.ж.т - коэффициент насыщения электронной жидкостью межгранулярных пор, межмолекулярных пор и трещин;
ρпр, ρэ.ж - удельное электрическое сопротивление примесей вещества и электронной жидкости;
ρв - удельное электрическое сопротивление воды в порах блока породы;
ρнг - удельное электрическое сопротивление нефтегазовой смеси;
ρж||, ρж⊥ - удельное электрическое сопротивление электропроводящей жидкости в трещинах, параллельных и перпендикулярных току;
ξм, ξм.п., ξп - степень извилистости или пережатости каналов межмолекулярных пор основного элемента, межмолекулярных пор примесей и межгранулярных пор;
ηм; ηмп; ηп; ηт - соотношение площади фотонных оболочек электрона Sф и сечений межмолекулярных пор в блоке (Sм), в примесях (Sм.п), межгранулярных пор (Sп) и трещин (Sт) или просветлость соответствующих пор для электронов:
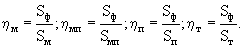
Анализ уравнения (3) показывает, что на электропроводность вещества наибольшее влияние оказывает наличие свободных каналов для движения электронов проводимости, т.к. ρэ.ж<<ρв, ρж||, ρж⊥, ρпр, степень извилистости или непрерывности (пережатости) (ξ) каналов, заполненных электронной жидкостью, параметр η, характеризующий просветлостъ каналов для электронов, и структурный параметр β кристаллической решетки основного вещества и примесей.
В каких диапазонах изменяются параметры ξ, η и β?
Извилистость каналов разной категории проводимости обусловлена размерами атомов основного вещества и примесей, зерен скелета и длиной трещин. Так параметр
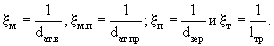
Если принять, что диаметры атомов основного вещества и примесей (dат.в; dат.пр) в среднем равны ~3·10-10 м, то
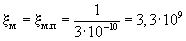
Если вещество представлено отдельными зернами, то по аналогии с горными породами можно принять диапазон изменения диаметра зерен
dзep=(10-6-10-3) м, и, следовательно,
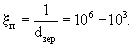
Длину трещин можно принять от 1 мм до 1 м и тогда
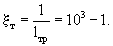
С понижением температуры будет более упорядоченное и устойчивое состояние атомов в кристаллической решетке, т.к. снижаются их колебания около положения равновесия, поэтому извилистость межмолекулярных каналов кристаллической решетки будет уменьшаться наиболее вероятно по формуле
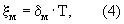
где δ - коэффициент пропорциональности.
Из формулы (4) следует, что для межмолекулярных пор
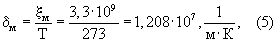
Таким образом, за счет упорядоченности колебания атомов в кристаллической решетке основного элемента и примесей извилистость межмолекулярных каналов снижается с 3,3·109 при Т=273К до 1,208·107 при T=1К.
Для межзерновой и трещинной пористости фактор влияния температуры на величину извилистости каналов оказывает существенно меньшее влияние и параметры δп и δт соответственно будут равны:

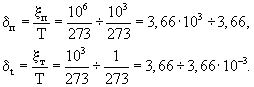
Для расчета параметров ηм, ηмп, ηп, ηт необходимо оценить вероятный диапазон изменения сечения межмолекулярных пор и трещин, а также диапазон изменения площади фотонных оболочек вокруг электрона проводимости, т.е. размера электрона с учетом влияния внешних условий.
В зависимости от характера упаковки атомов в кристаллической структуре вещества радиус межмолекулярных пор, по которым возможно перемещение электронов проводимости, может изменяться в широком диапазоне от (0,41rат) практически до нуля. При благоприятных условиях кубической упаковки атомов rпмmах=0,41rат. Можно принять, что в нормальных условиях (Т=273 К) радиус электронов проводимости близок к минимальному размеру межмолекулярных пор, т.е. ηм=1, а зависимость параметра ηм от температуры описывается функцией
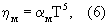
что в общем согласуется с формулой Блоха-Грюнайзера для электрического сопротивления идеальной решетки металла [1]. Здесь αм - коэффициент пропорциональности, характеризующий величину параметра ηм при температуре 1°К, при этом:
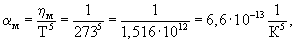
В температурных условиях, близких к абсолютному нулю (Т=1К), межмолекулярные поры будут практически освобождены от фотонных оболочек электронов ионов кристаллической решетки и их максимальный размер можно принять 0,41rат, а радиус электрона практически без фотонных оболочек на один-два порядка меньше радиуса ядра, т.е rэ=(10-17-10-16) м.
Тогда 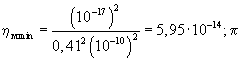
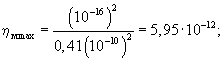
Среднее значение из этих величин дает ηм=5,95·10-13=αм, что хорошо согласуется с величиной αм, рассчитанной первым способом. При дальнейших расчетах примем значение αм=6,6·10-13.
В чем физический смысл активного влияния температуры на параметр ηм? Он определяется, с одной стороны, существенным уменьшением диаметров электронов проводимости при снижении температуры за счет излучения вращающихся вокруг электронов проводимости фотонов и, с другой стороны, - изменением размеров межмолекулярных пор, каналов проводимости электрического тока также за счет излучения фотонов с электронов, вращающихся вокруг ядер атомов и ионов кристалла. Таким образом, можно однозначно утверждать, что размер электрона не является постоянным, а зависит от температуры, причем, чем выше температура, тем больше диаметр электрона за счет увеличивающегося количества вращающихся вокруг электрона фотонов. Если исходить из условия, что радиус электрона при Т=1К составляет 5·10-17 м, а радиус межгранулярных пор изменяется в пределах 0,41rзерен, т.е. rпор=0,41(10-6-10-3) м, то для межгранулярных пор величина
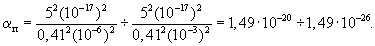
Как видно, параметр αп существенно меньше параметра αм и это свидетельствует о том, что при наличии вакуума в межгранулярных порах электросопротивление вещества будет резко снижаться и обуславливаться в основном электропроводностью межгранулярных пор, так как размер их значительно больше, чем межмолекулярных пор в веществе.
Для трещин, раскрытость которых обычно сопоставила с величиной межгранулярных пор, можно принять αт ≅ 1,49·10-24. Таким образом, используя зависимость (6) и для межгранулярных и трещинных пор, можно оценить величины ηп, ηт для Т=273К, т.е.
ηп=(1,49·10-20-1,49·10-26)2735=2,26·10-8-2,26·10-14
ηт=1,49·10-24·2735=2,26·10-12.
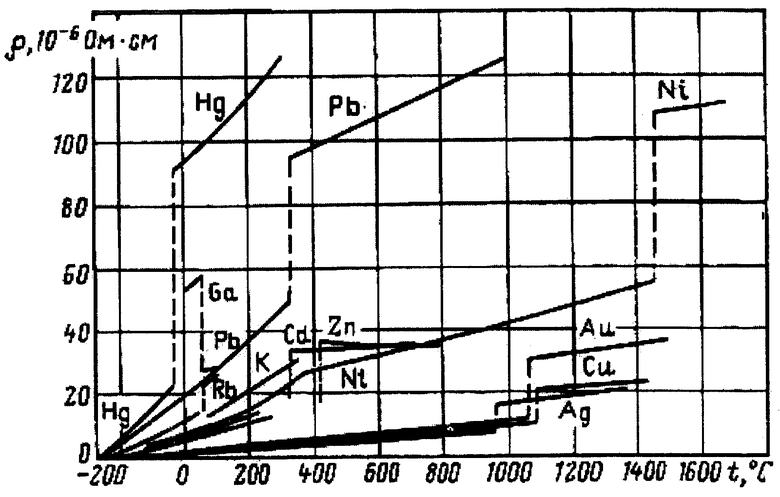
Как отмечено выше, на электропроводность определенное влияние оказывает структура кристаллической решетки, т.е. параметр β. Это наглядно подтверждается сдвигом кривой зависимости электрического сопротивления от температуры металлов при температурах фазовых переходов (чертеж) по данным [1]. Анализ величин средних значений электрических сопротивлений металлов, кристаллизующихся в различных сингониях, показывает, что минимальное среднее значение электросопротивления (ρ≈5·10-4 Ом·м) характерно для гранецентрированной кубической сингонии (ГЦК), для которой при Т=273К предлагается принять β=1. Относительно ГЦК сингонии в соответствии со средними значениями электросопротивлений можно принять для:
тетрагональной сингонии (ТЕТ) - β=2;
объемно-центрированной кубической сингонии (ОЦК) - β=3;
кубической сингонии (КУБ), простой кубической сингонии (ПК),
гексагональной (ГЕК) - β=10;
ромбоэдрической (РМЭ) - β=15.
Сущность изобретения поясняется чертежом, где представлен график изменения сопротивления в зависимости от температуры некоторых металлов в твердом и жидком состояниях (по данным [1]).
Для обоснования параметра β для полупроводников необходимо сопоставить удельное электрическое сопротивление алмаза (ρ=1012-1014 Ом·м, для расчетов можно принять среднее значение ρ=1013 Ом·м) и среднее значение удельного электрического сопротивления металлов гранецентрированной кубической сингонии ρ=5·10-4 Ом·м. Таким образом, параметр β для полупроводников равен
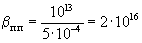 при Т=273К
при Т=273К
На величину структурного показателя полупроводников существенное влияние оказывает температура. По аналогии с формулой Блоха-Грюнайзера [1] для полупроводников примем зависимость
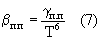
Таким образом, для полупроводников коэффициент γп.п, характеризующий величину структурного параметра βп.п при Т=1К, будет равен
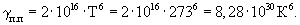
Для металлов параметр кристаллической решетки β для разных сингоний изменяется в небольших пределах. Для основных кристаллических структур (ГЦК, ОЦК, ТЕТ, ГЕК) параметр β=1-10, а при фазовых переходах сохраняется параллельность кривых ρ=f(Т) (чертеж). Все это дает основание считать, что для металлов зависимость параметра β от температуры незначительна и влияние температуры на параметр β в первом приближении можно не учитывать.
Для обоснования удельного электрического сопротивления электронной жидкости предположим предельный случай, что все атомы имеют по одному валентному электрону и все валентные электроны являются электронами проводимости, т.е. в 1 м3 находится 5,69·1028 электронов проводимости. Примем, что к проводнику длиной l=1 м приложено напряжение U=1 В и скорость движения электронов под действием приложенного напряжения ν=С, тогда минимальное сопротивление определим из условия:
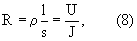
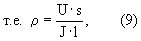
где R, ρ - общее и удельное сопротивление проводника; l, s - его длина и площадь поперечного сечения; U, J - напряжение и сила тока.
Сила тока 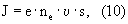
Здесь е - заряд электрона; nе - концентрация электронов проводимости в веществе; υ - скорость движения электронов и s - площадь сечения образца вещества.
При скорости движения (υ) электронов равной скорости света (с) уравнение (9) преобразуется к виду.
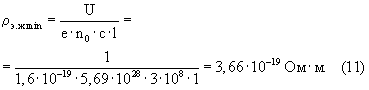
Фактически в каждом конкретном случае ρэ.ж должно соответствовать тем условиям, при которых происходит измерение сопротивления для данного вещества, т.е. эта величина переменная так же, как и ρв, зависит от концентрации солей и температуры и, следовательно, в каждом случае для каждого элемента надо оценить величину ρэ.ж. Концентрация подвижных (свободных) электронов может меняться в пределах от 5,69·1028 м-3 до нуля, а скорость их направленного поступательного движения от нуля до скорости света (3·108·м/с).
Скорость направленного движения электронов зависит от соотношения площадей сечения фотонных оболочек электронов к площади сечения пор 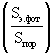 и силы, действующей со стороны электрического поля (Е) на свободные электроны,
и силы, действующей со стороны электрического поля (Е) на свободные электроны,
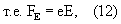
здесь е - заряд электрона.
Количество же оторванных от атомов электронов зависит отсоотношения сил теплового воздействия:
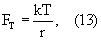
где к - постоянная Больцмана;
T - абсолютная температура, К;
r - радиус вращения электрона вокруг атома, т.е. радиус атома.
Им противодействует кулоновская сила притяжения электрона к ядру:
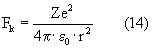
здесь Z - заряд ядра атома;
ε0 - электрическая постоянная.
Таким образом, количество электронов проводимости приближенно можно оценить по формуле:
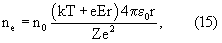
где n0 - концентрация валентных электронов.
Причем величина n0 может меняться от элемента к элементу и определяется плотностью вещества и его молекулярной (атомной) массой. Например, ниже в таблице 1 приведен расчет параметра n0 для некоторых элементов - металлов.
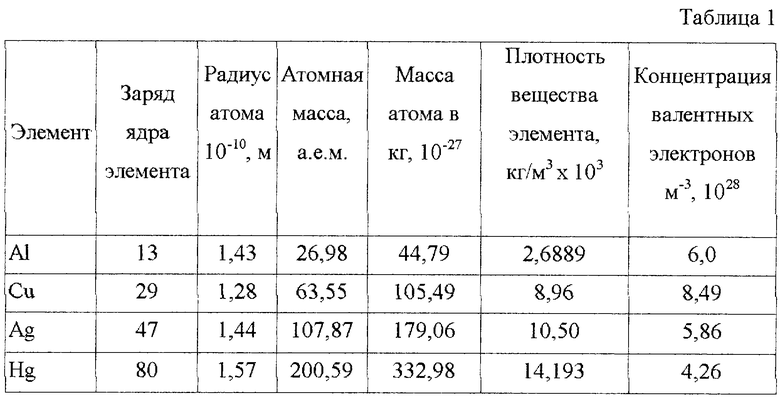
Анализ уравнения (15) показывает, что концентрация электронов проводимости существенно зависит от температуры, а также параметров Е, r, Z, причем наибольшее влияние оказывает параметр T. Например, для меди со средней величиной радиуса атома r=1,28·10-10 м, Z=29, при постоянном Е=100 В/м, параметр nе равен:
при Т=1К ne=2,69·10-7n0=2,28·1022 м-3
при Т=300К ne=8,07·10-5n0=6,85·1024 м-3
при Т=103 К ne=2,69·10-4n0=2,28·1025 м-3
при T=104 К ne=2,69·10-3n0=2,28·1026 м-3
при Т=105 К ne=2,69·10-2n0=2,28·1027 м-3.
При постоянстве Т=300К и изменении напряженности электрического поля параметр nе изменяется следующим образом:
при Е=100 В/м ne=8,07·10-5n0=6,85·1024 м-3
при Е=105 В/м ne=8,07·10-5n0=6,85·1024 м-3
при Е=108 В/м ne=1,21·10-4n0=1,03·1025 м-3
при E=1010 В/м ne=4,14·10-3n0=3,51·1026 м-3.
Как видно, концентрация электронов проводимости при разных ситуациях существенно ниже концентрации валентных электронов, но все равно очень велика, чтобы обеспечить электропроводность вещества.
Безусловно, необходимо иметь в виду, что на валентный электрон будут действовать не только все протоны ядра, но и проявлять экранирующее (отталкивающее) влияние другие электроны, расположенные ближе к ядру. Кроме того, изменение радиуса вращения валентных электронов носит вероятностный характер, однако учет всех этих факторов сложен и в данной работе не проводится.
Подставив выражение (15) вместо n0 в (11), получим уравнение, описывающее приближенно величину удельного электрического сопротивления потока электронов (электронной жидкости) в веществе конкретного элемента с учетом концентрации свободных электронов проводимости и условий измерения.
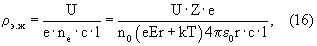
Расчет величин ρэ.ж по формуле (16) для ряда металлов при условии T=273К, U=1 В и Е=1 В/м дает следующие результаты:
ρ
ρ
ρ
ρ
Новизна заявляемого предложения заключается в том, что учитываются все параметры вещества как макроскопические, которые определяются лабораторными или промыслово-геофизическими методами, так и микроскопические, определяемые физическими приемами, например с помощью рентгена. В результате такого учета обеспечивается объективная оценка электропроводности вещества.
Заявленный способ обладает изобретательским уровнем, поскольку из данных научно-технической и патентной литературы не известна аналогичная заявляемой совокупность признаков, обеспечивающей достижения поставленной задачи.
Изобретение нашло применение при исследовании электропроводности вещества при переходе в сверхпроводящее состояние в лабораторных условиях, возможно использование и в промышленных условиях при создании сверхпроводников. С учетом вышеизложенного можно судить о промышленной применимости предложения.
Для рассмотрения конкретных примеров осуществления способа оценки электропроводности вещества, в том числе при переходе в сверхпроводящее состояние, проанализируем выражение (3).
При изучении различных материалов на предмет сверхпроводимости, как правило, их образцы не характеризуются явно выраженной кавернозной и трещинной пористостью (т.е. можно принять Кпк=Кпт=0), поэтому выражение (3) для этого случая преобразуется к виду:
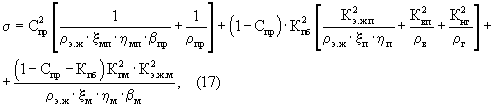
Более того, исследуемые образцы, как правило, являются сухими и поры их не насыщены водным раствором (Kвп=0) или углеводородами (Кнг=0), поэтому последнее уравнение упрощается к виду:
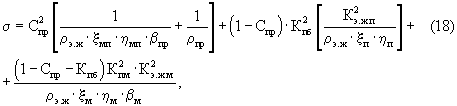
Если вещество однородное, т.е. не содержит примесей (Cnp=0), то:
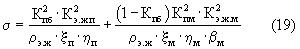
Последнее уравнение будет справедливо только в том случае, если не только в межмолекулярных, но и в межгранулярных порах будет “электронная жидкость” с сопротивлением ρэ.ж. Однако это возможно только в условиях глубокого вакуума, когда из межгранулярных пор полностью удалены не только жидкие компоненты - поровая вода и углеводороды - нефть и газ, но и воздух. Наличие даже молекул воздуха в межгранулярных порах будет существенно сдерживать движение электронов, и они будут двигаться преимущественно по межмолекулярным порам. Если же создать глубокий вакуум и откачать из межгранулярных пор образца (вещества) воздух, то резко увеличится его проводимость и он при значительно более высоких температурах проявит состояние сверхпроводимости. В обычных условиях, когда межгранулярные поры заполнены воздухом (Кэ.ж.п=0), а межмолекулярные полностью “электронной жидкостью” (Кэ.ж.м=1), электропроводность образца обусловлена только межмолекулярными порами и описывается простым выражением.
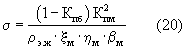
С использованием зависимостей параметров ρэ.ж, ξм, ηм, и βм от температуры уравнение (20) для кристаллических структур металлов принимает вид:
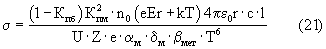
После подстановки исходных данных ε0=8,85·10-12 ф/м; с=3·108 м/с; e=1,6·10-19 Кл; αм=6,6·10-13 К-5; δм=1,208·107 м-1 К-1 уравнение (21) для электропроводности металлов преобразуется к виду:
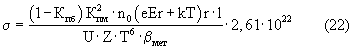
Таким образом, расчеты по формуле (22), например, для металла серебра (Z=47, n0=5,86·1028 м-3, r=1,44·10-10 м, βмет=1 (с учетом того, что кристаллическая структура серебра имеет ГЦК сингонию), принимая Кпб=0; Кпм=0,4; l=1 м; U=1 В; E=1 В/М, дают следующие результаты.
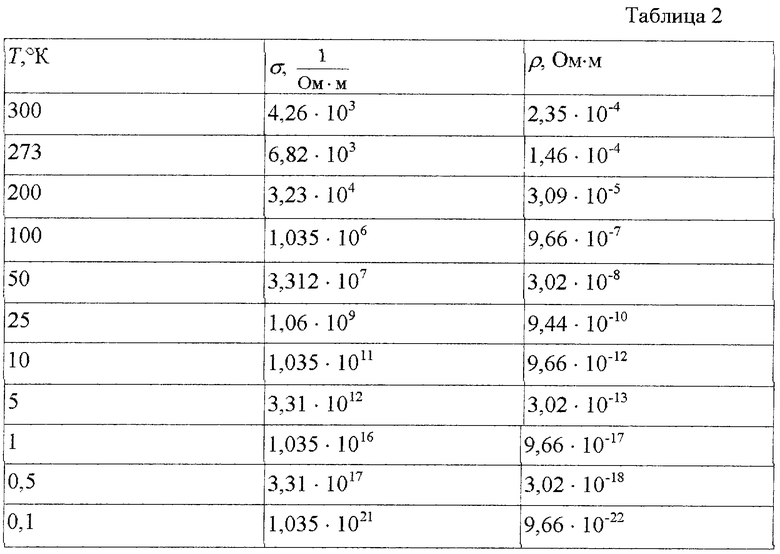
Как видно, рассчитанное значение удельного электрического сопротивления при температуре T=273К , ρ=1,46·10-4 Ом·м, а по табличным данным [1] удельное электрическое сопротивление серебра при этой температуре ρ=1,49·10-4 Ом·м, т.е. величины практически идеально совпадают. С понижением температуры рассчитанные значения удельного электрического сопротивления существенно снижаются, что соответствует экспериментальным данным.
Для полупроводников уравнение электропроводимости принимает вид:
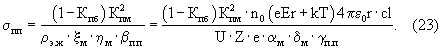
После подстановки исходных параметров, в том числе αм=6,6·10-13К-5; δм=1,208·107; γпп=8,28·1030К6.
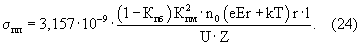
Расчеты по формуле (24) для полупроводников, например для кремния (Z=14, n0=5,79·1028 м-3, r=1,18·10-10 м), принимая те же условия, что и для металлов, т.е. Кпб=0; Кпм=0,4; l=1 м; U=1 B; e=1 В/м, дают следующие результаты:
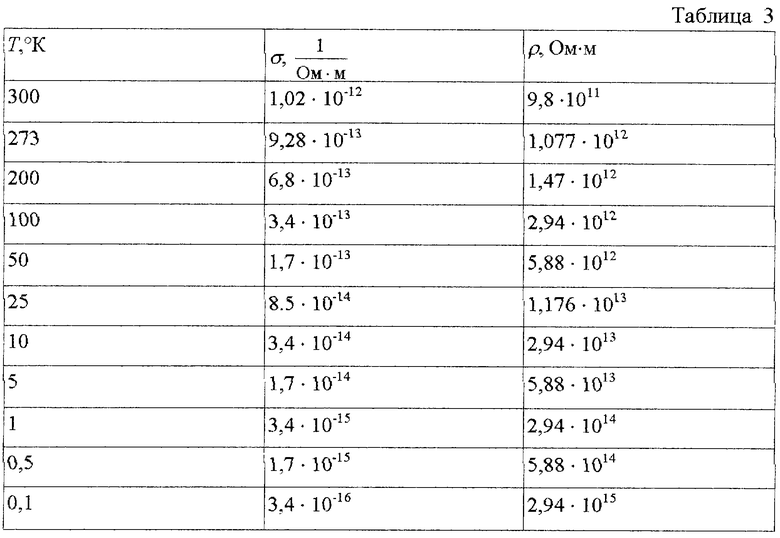
Как видно, расчетные данные удельного электрического сопротивления соответствуют как по величинам, так и по характеру зависимости удельного электрического сопротивления от температуры экспериментальным данным для полупроводников.
Если изготовить методом спекания из металлического порошка в виде гранул по технологии порошковой металлургии образцы, которые будут содержать как межмолекулярные поры в гранулах, так и межгранулярные поры, и предположить, что по части межгранулярных пор возможно движение электронов проводимости, то уравнение электропроводности такого образца в соответствии с формулой (3) будет иметь вид
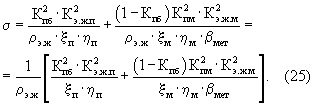
Если подставить выражение (16) для ρэ.ж, то уравнение (25)преобразуется к виду:
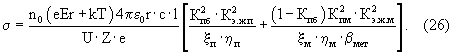
При расчетах по формуле (26) принимаем Кпб=0,3; Кпм=0,4; Кэ.ж.м=1 (коэффициент заполнения электронной жидкостью межмолекулярных пор), Кэ.ж.п=1·10-6-5·10-1 (коэффициент заполнения электронной жидкостью межгранулярных пор); 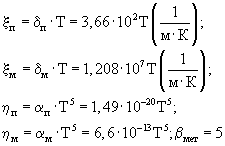
(среднее значение для всех сингоний кристаллических структур металлов); n0=6·1028 м-3; U=1 В; l=1 м; Е=1 В/м; Z=30; T=(300-0,1)К. После подстановки исходных данных в уравнение (26)
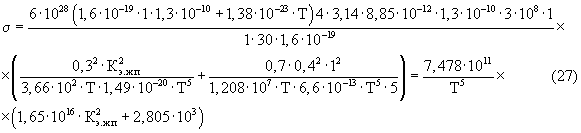
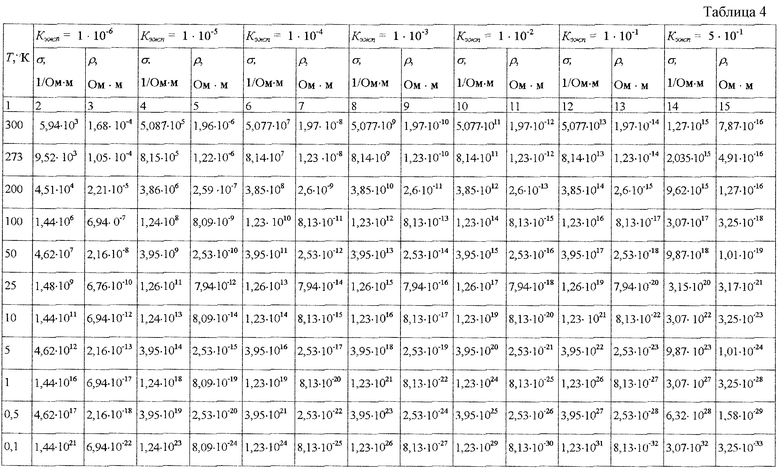
Как видно, первое слагаемое в скобках, даже при высоких температурах Т=300 К и низких Kэ.ж.п ≥ 1·10-5, существенно превалирует над вторым, т.е. при небольшой доле заполнения межгранулярных пор электронной жидкостью, ее роль в электропроводности вещества становится главенствующей и только лишь в условиях очень низкого процента (<0,001%) заполнения межгранулярных пор электронной жидкостью, т.е. при Кэ.ж.п<10-5 первое слагаемое становиться сопоставимо со вторым. По расчетным данным получены следующие результаты (таблица 4).
Высокотемпературные сверхпроводники в своем составе имеют элементы металлов и керамику и кроме межмолекулярной пористости характеризуются также межгранулярной пористостью. Причем для высокотемпературных сверхпроводников на основе керамики многими исследователями отмечается связь между наличием межгранулярных пор повышенного размера и повышением температуры перехода в сверхпроводящее состояние. Вероятно, это объясняется тем, что некоторая доля межгранулярных пор доступна для свободного движения электронов проводимости. В связи с этим рассмотрим уравнение проводимости вещества при наличии элементов металлов и элементов полупроводников, с одной стороны, и наличии межмолекулярных и межгранулярных пор, с другой стороны, причем межгранулярные поры в основном насыщены воздухом и частично электронной жидкостью. В соответствии с уравнением (3) получим:
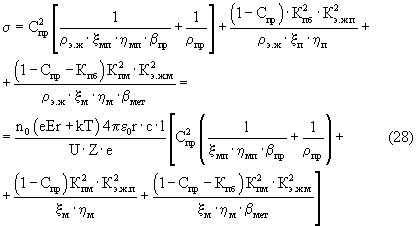
При расчетах но формуле (28) принимаем, что межгранулярная пористость блока вещества (Кп.б) как в металлическом веществе (Кп.б.м) так и в веществе полупроводника [Кп.б.п.п), а также пористость межмолекулярных пустот (Кп.м) в металлическом веществе (Кпм.м) и в веществе полупроводника {Кп.м.п.п) соответственно одинаковы, т.е. Кп.б.м=Кп.б.п.п=Кп.б; Кп.м.п.п=Кп.м, при этом Кп.б=0,3; Кп.м=0,4; Кэ.ж.м=1; Кэ.ж.п=(1·10-6-5·10-1);
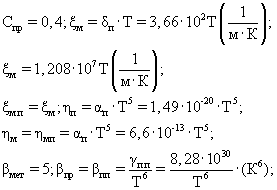
βпр=1013 Ом·м; r=1,3·10-10 м; n0=6·1028 м-3; Z=30; U=1В; l=1м; E=1В/м; T=(300-0,1)К.
После подстановки исходных данных в уравнение (28) получили
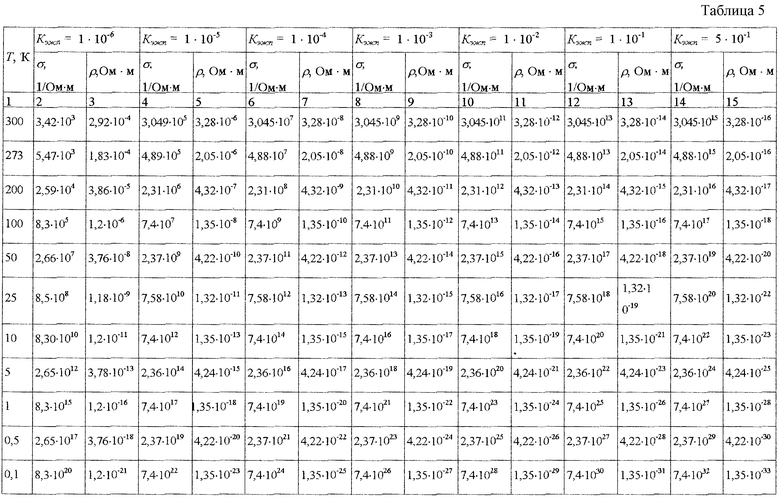
 После подстановки параметров Т=(300-0,1)К и Кэ.ж.п=(1·10-6-5·10-1) получены следующие результаты (табл.5). Сравнение данных таблиц 5 и 4 показывает, что замена 40% металла на керамику (полупроводник) с высоким электрическим сопротивлением несущественно (менее чем в 2 раза) увеличивает электрическое сопротивление образца при тех же параметрах Т и Кэ.ж.п и именно частичное заполнение межгранулярных пор электронной жидкостью приводит к снижению электрического сопротивления. Так, например, при T=100K результаты расчета электросопротивления свидетельствуют о явлении сверхпроводимости при Кэ.ж.п>1·10-1, т.е. всего-навсего при более чем 10% заполнении межгранулярных пор электронной жидкостью.
После подстановки параметров Т=(300-0,1)К и Кэ.ж.п=(1·10-6-5·10-1) получены следующие результаты (табл.5). Сравнение данных таблиц 5 и 4 показывает, что замена 40% металла на керамику (полупроводник) с высоким электрическим сопротивлением несущественно (менее чем в 2 раза) увеличивает электрическое сопротивление образца при тех же параметрах Т и Кэ.ж.п и именно частичное заполнение межгранулярных пор электронной жидкостью приводит к снижению электрического сопротивления. Так, например, при T=100K результаты расчета электросопротивления свидетельствуют о явлении сверхпроводимости при Кэ.ж.п>1·10-1, т.е. всего-навсего при более чем 10% заполнении межгранулярных пор электронной жидкостью.
Наличие трещинной пористости вдоль распространения электрического тока при условии, что трещины частично заполнены электронной жидкостью, по аналогии с исследованиями горных пород методами промысловой геофизики, будет еще более интенсивно снижать электрическое сопротивление вещества, так как в трещинах еще более снижается степень извилистости канала проводимости электрического тока. Общее уравнение проводимости при наличии межмолекулярной, межгранулярной и трещинной пористости вдоль распространения тока и частичном заполнении трещин и межгранулярных пор электронной жидкостью в соответствии с (3) принимает вид:
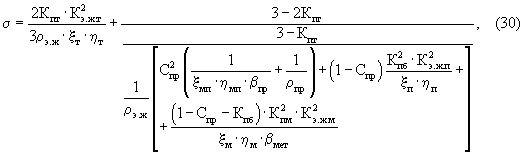
С учетом того, что величина Кпт обычно мала и (3-2 Kпт)≅(3-Kпт), а ρэж описывается выражением (16), уравнение (30) преобразуется к виду:
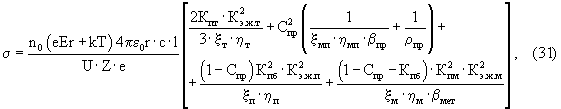
В расчетах по формуле (31) принимаем: Kпт=1·10-2-1·10-4; Kэ.ж.т=1·10-4-1; ξт=δ·Т=3,66Т; ηт=αт·Т5=1,49·10-24Т5.
Остальные исходные данные те же, что и при расчетах по формуле (28). После подстановки исходных данных в уравнение (31) получили:
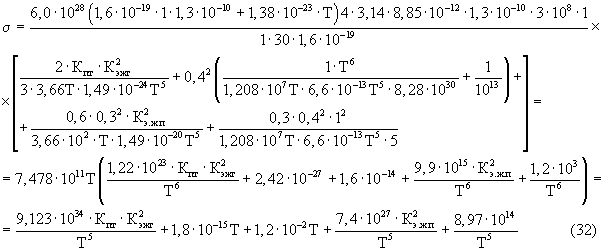
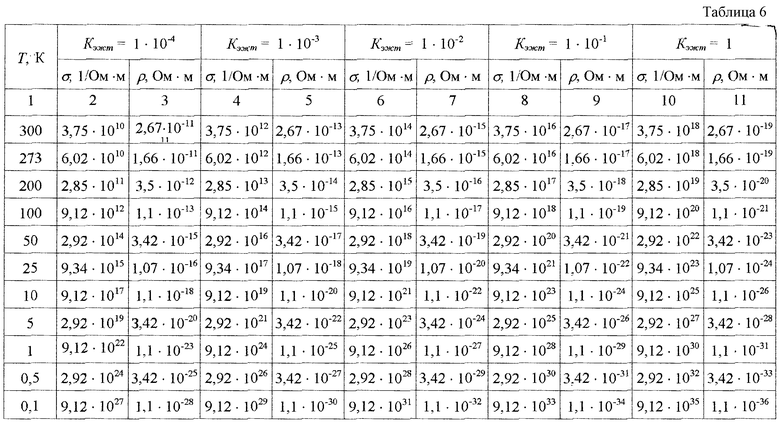
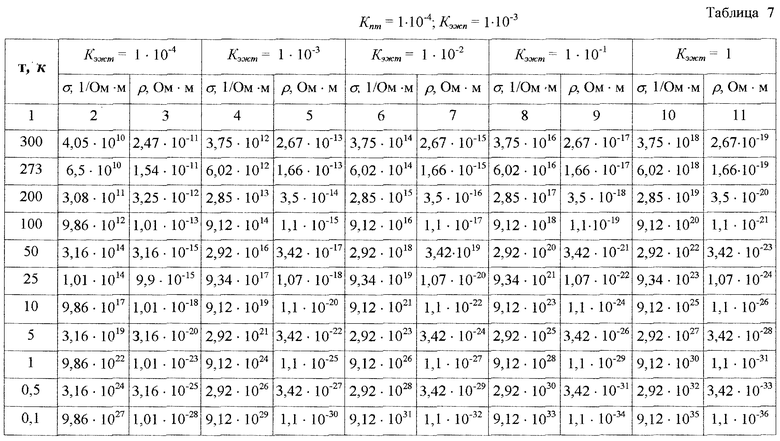
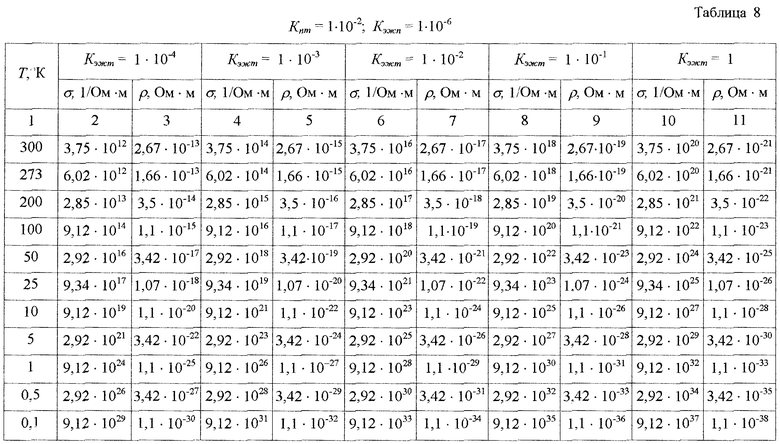
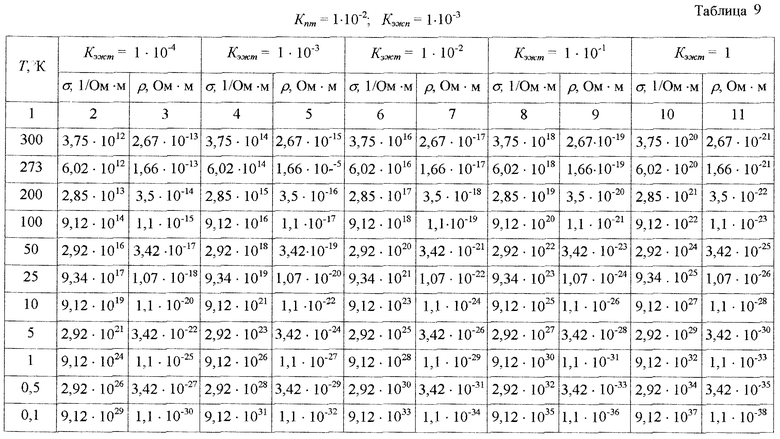
После подстановки исходных данных Т, Кпт, Кэжт, Кэжп получили следующие результаты (таблицы 6-9).
Анализ таблиц 6-9 и таблицы 5 показывает, что наибольшее влияние на электросопротивление оказывает электронная жидкость, находящаяся в трещинных порах. Даже при величине трещинной пористости Кпт=1·10-4, т.е. 0,01% от объема вещества и заполнении этих трещин только на одну сотую процента (Кэжт=1-10-4) электронной жидкостью электрическое сопротивление вещества снижается на семь порядков, а при полном заполнении этих трещин электронной жидкостью вещество становится сверхпроводящим даже при температуре Т=(200-300)К (таблицы 6, 7). С увеличением трещинной пористости до 1% (Кпт=1·10-2) и полном заполнении трещин электронной жидкостью удельное электрическое сопротивление снижается при этих температурах до 10-22-10-21 Ом·м.
ЛИТЕРАТУРА
1. Физические величины. Справочник. Под редакцией И.С.Григорьева, Е.З.Мейлихова. М.: Энергоатомиздат,1991г., с.437-438.
2. Александров Б.Л. Изучение карбонатных коллекторов геофизическими методами. М.: Недра, 1979г., с.33-34.
| название | год | авторы | номер документа |
|---|---|---|---|
| СПОСОБ ИЗГОТОВЛЕНИЯ ВЫСОКОТЕМПЕРАТУРНЫХ СВЕРХПРОВОДЯЩИХ ИЗДЕЛИЙ (ВАРИАНТЫ) | 2002 |
|
RU2231149C2 |
| КВАНТОВО-РАДИОИЗОТОПНЫЙ ГЕНЕРАТОР ПОДВИЖНЫХ НОСИТЕЛЕЙ ЗАРЯДА И ФОТОНОВ В КРИСТАЛЛИЧЕСКОЙ РЕШЕТКЕ ПОЛУПРОВОДНИКА | 2015 |
|
RU2654829C2 |
| ЭЛЕКТРОД ДЛЯ ИСПОЛЬЗОВАНИЯ В ЭЛЕКТРОХИМИЧЕСКОМ КОНДЕНСАТОРЕ С ДВОЙНЫМ ЭЛЕКТРИЧЕСКИМ СЛОЕМ (ВАРИАНТЫ) | 2007 |
|
RU2483383C2 |
| ПОЛУПРОВОДНИКОВЫЙ КЕРАМИЧЕСКИЙ МАТЕРИАЛ | 2004 |
|
RU2279729C2 |
| СПОСОБ ОПРЕДЕЛЕНИЯ КОЭФФИЦИЕНТА ДИФФУЗИИ В ПОРОШКОВЫХ МАТЕРИАЛАХ И СПОСОБ ОПРЕДЕЛЕНИЯ ТОЛЩИНЫ И ПОКАЗАТЕЛЯ ЦЕЛОСТНОСТИ ПОКРЫТИЯ НА ЧАСТИЦАХ ПОРОШКОВЫХ МАТЕРИАЛОВ | 2012 |
|
RU2522757C1 |
| КЕРАМИЧЕСКИЙ МАТЕРИАЛ ДЛЯ ИНТЕРКОННЕКТОРОВ ТОПЛИВНЫХ ЭЛЕМЕНТОВ И СПОСОБ ЕГО ПОЛУЧЕНИЯ | 2015 |
|
RU2601436C1 |
| Способ определения геологических свойств терригенной породы в около скважинном пространстве по данным геофизических исследований разрезов скважин | 2003 |
|
RU2219337C1 |
| ТРОЙНОЙ МОЛИБДАТ РУБИДИЯ, ЛЮТЕЦИЯ И ГАФНИЯ В КАЧЕСТВЕ ПОЛУПРОВОДНИКА | 2007 |
|
RU2367054C1 |
| ЭЛЕКТРОПРОВОДНЫЙ КОМПОЗИЦИОННЫЙ УГЛЕРОДСОДЕРЖАЩИЙ МАТЕРИАЛ И СПОСОБ ЕГО ПОЛУЧЕНИЯ | 2008 |
|
RU2398312C2 |
| Квантово-размерный нанокристалл | 2023 |
|
RU2833477C1 |
Изобретение относится к измерениям электропроводящих величин вещества. Сущность: способ осуществляется путем определения лабораторными или промыслово-геофизическими методами макроскопических параметров, включающих коэффициенты различных видов пористости, влагонасыщения, содержания примесей, удельного сопротивления воды, степени извилистости пор. Учитывают микроскопические параметры вещества, включающие коэффициенты межмолекулярной пористости, структурного параметра кристаллической решетки, удельное электрическое сопротивление потока электронов (электронной жидкости), отношение площадей фотонных оболочек электронов к сечению межмолекулярных пор, которые определяют физическими методами на основании размеров атомно-молекулярного строения вещества. Электропроводность определяют по расчетной формуле, которая учитывает наличие всех возможных каналов для движения электронов проводимости и ионов солей. Техническим результатом изобретения является получение достоверной информации об электропроводности всего класса веществ, в том числе при переходе в сверхпроводящее состояние. 9 табл., 1 ил.
Способ оценки электропроводности при переходе вещества в сверхпроводящее состояние путем определения лабораторными или промыслово-геофизическими методами макроскопических параметров, включающих коэффициенты различных видов пористости, влагонасыщения, содержания примесей, удельного сопротивления воды, степени извилистости пор и учет их при определении электропроводности, отличающийся тем, что определяют физическими методами на основании размеров атомарно-молекулярного строения вещества его микроскопические параметры, включающие коэффициенты межмолекулярной пористости, структурный параметр кристаллической решетки, удельное сопротивление потока электронов (электронной жидкости), отношение площадей фотонных оболочек электронов к сечению межмолекулярных пор и определяют электропроводность по формуле

где βм, βпр – структурный параметр кристаллической решетки основного минерала и минерала примесей;
Кп.к – кавернозная пористость (пористость изолированных в блоке пор);
Кп.т – трещинная пористость;
Кп.б – пористость блока вещества или межзерновая пористость;
Кп.м – межмолекулярная пористость;
Спр – содержание примесей в веществе в долях от общего объема;
Кв.п, Кв.т – коэффициент водонасыщения пор, трещин;
Кнг, Кнг.т – коэффициент нефтегазонасыщения пор, трещин;
Кэ.ж.п, Кэ.ж.м, Кэ.ж.т – коэффициент насыщения электронной жидкостью межгранулярных пор, межмолекулярных пор и трещин;
ρпр, ρэ.ж – удельное электрическое сопротивление примесей вещества и электронной жидкости;
ρв – удельное электрическое сопротивление воды в порах блока породы;
ρнг – удельное электрическое сопротивление нефтегазовой смеси;
ρж||, ρж⊥ – удельное электрическое сопротивление электропроводящей жидкости в трещинах, параллельных и перпендикулярных току;
ξм, ξм.п, ξп – степень извилистости или пережатости каналов межмолекулярных пор основного элемента, межмолекулярных пор примесей и межгранулярных пор;
ηм, ηм.п, ηп, ηт – соотношение площади фотонных оболочек электрона Sф и сечений межмолекулярных пор в блоке (Sм), в примесях (Sм.п), межгранулярных пор (Sп) и трещин (Sт) или просветлость соответствующих пор для электронов:
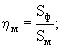
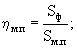
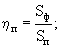
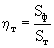
| АЛЕКСАНДРОВ Б.Л | |||
| Изучение карбонатных коллекторов геофизическими методами | |||
| - М.: Недра, 1979, с.33 и 34 | |||
| SU 1300369 A1, 30.03.1983 | |||
| WO 9115755 A2, 17.10.1995. |
Авторы
Даты
2004-05-27—Публикация
2002-08-22—Подача