Изобретения относятся к области определения значений параметров, характеризующих физико-химические свойства материалов, например коэффициентов диффузии, по величине электропроводности, и могут найти применение в порошковой металлургии, в изучении процессов самораспространяющегося высокотемпературного синтеза, в материаловедении и физике твердого тела.
Исследование свойств порошковых материалов по величине электропроводности всегда осложнено влиянием неоднородности химического состава и сильной зависимостью электропроводности от степени уплотнения материалов. Эти особенности значительно затрудняют проведение количественных определений величин, связанных с проводящими свойствами порошков, несмотря на то, что точность измерения самой электропроводности может быть весьма высокой.
Известен способ определения параметров диффузии, определяющих значения коэффициента диффузии при различных температурах, по величине электросопротивления (Бялик О.М., Иванчук Д.Ф., Голуб Л.В., Шаповал А.И. Способ определения параметров диффузии газов в металле. А.с. №1073671, МКИ G01N 27/02, БИ №6, 1984).
Способ основан на определении характера диффузионного насыщения образца металла газом с помощью измерения электропроводности между поперечными зондами, установленными в направлении течения газа с известным расстоянием между ними. Электропроводность измеряют между соседними зондами при стационарном потоке газа через определенные промежутки времени и о диффузионном изменении содержания газа на отдельных участках судят при помощи сравнения измеренных значений электропроводности с электропроводностью дегазированного образца.
Недостатком способа является то, что с его помощью нельзя определять коэффициент диффузии кислорода в порошковом металле. В способе предусмотрено изучение взаимодействия металла с «внешним» газом в диффузионном режиме, при этом процесс ведут до полного насыщения им образца. Кислород же образует на поверхности металлических частиц оксидное покрытие, которое тормозит или препятствует окислению частиц образца, и в исследуемом диапазоне температур процесс не доходит до полного насыщения. Кроме того, образование и рост оксида при взаимодействии металла с кислородом определяется не коэффициентом диффузии кислорода в металле, а коэффициентами диффузии кислорода в оксиде или металла в оксиде (Кофстад П. Высокотемпературное окисление металлов. Пер. с англ. М.: Мир, 1969, 392 с). Еще одним недостатком является то, что в способе не предусмотрен учет зависимости электропроводности от плотности (пористости), которая может сильно изменяться при диффузионном взаимодействии (насыщении) материала с внешним газом.
Наиболее близким решением - прототипом заявляемого способа определения коэффициента диффузии - является способ определения параметров диффузии кислорода в поликристаллических ферритах (Суржиков А.П., Притулов A.M., Гынгазов С.А., Полякова Т.С. Применение метода измерения температурной зависимости электропроводности для изучения диффузии кислорода в поликристаллических ферритах. Перспективные материалы. 1998, №4, с.66).
Способ основан на том, что концентрация диффузанта (в данном случае - кислорода) в межзеренных прослойках значительно выше, чем в объеме зерен поликристаллического материала, и ее изменение после отжига за счет диффузии кислорода из воздуха в объем образца сказывается как на величине самой электропроводности, так и на величине энергии активации, определяемой по ее температурной зависимости. Поэтому измерение электропроводности при различных температурах и по глубине образца позволяет определять значения энергии активации электропроводности, связывать ее с изменением концентрации ионов кислорода по глубине образца, определяемой, в свою очередь, решением уравнения диффузии (закона Фика), и устанавливать таким образом значение коэффициента диффузии. Использование такого подхода при различных температурах диффузионного отжига и последующая аппроксимация температурной зависимости коэффициента диффузии прямыми линиями в аррениусовских координатах: логарифм величины коэффициента диффузии - обратная температура (InD - 1/T), позволяют получать значения постоянных параметров коэффициента диффузии (энергии активации E и предэкспоненциального множителя D0) по закону Аррениуса:
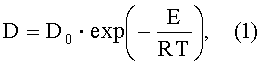
где R - универсальная газовая постоянная.
Известный способ имеет ряд недостатков, не позволяющих его использовать для порошковых материалов в различном или в неопределенном диапазоне степени уплотнения. Кроме того, он весьма сложен в осуществлении, и точность его может быть недостаточно высокой из-за того, что при реализации способа не учитывается тот факт, что на величину электропроводности и ее энергии активации влияет не только содержание диффузанта в межзеренных прослойках, но и возможность их разрушения с образованием проводящих контактов между материалом частиц (зерен), неэкранированных покрытием (Мокрушин В.В. Закономерность изменения обобщенной проводимости нагружаемых порошковых материалов. Доклады Академии наук, 1997, №3, том 357, с.332-334). Площадь поверхности проводящих контактов в материале, а следовательно, и электропроводность зависят от пористости (степени уплотнения) образца. При диффузионном отжиге образцов в межзеренных прослойках не просто снижается концентрация диффузанта (кислорода), а изменяется толщина поверхностной фазы, которая экранирует электропроводность по основному веществу материала. Кроме того, при определенной степени уплотнения экранирующее покрытие на частицах материала может разрушаться, и при этом в межчастичных контактах образуется часть проводящей поверхности по основному веществу, которая возрастает по мере дальнейшего уплотнения материала. Эти процессы совокупно приводят к изменению величины электропроводности порошкового материала и, соответственно, энергии активации электропроводности. В связи с этим, параметры электропроводности, которые связаны с изменением концентрации диффузанта в межзеренных прослойках, т.е. с возможностью определения коэффициента диффузии по изменению электропроводности для порошковых материалов, не могут быть определены без учета степени уплотнения, сведений об изменении толщины покрытия и его целостности.
К недостаткам способа следует отнести и то, что в нем предусмотрены температурные воздействия различного характера: отжиг для спекания; вакуумный отжиг с целью выравнивания концентрации диффузанта (кислорода); целевой (диффузионный) отжиг для осуществления диффузионного массопереноса ионов диффузанта; нагрев для получения температурной зависимости электропроводности. В условиях, когда в окружающей газовой среде (вакуум, воздух или инертный газ) имеются окислительные компоненты, как примесные или остаточные, так и входящие в состав атмосферы (кислород, азот, влага), термическое воздействие приводит к изменению химического состава и структуры поверхности образца и его глубинных слоев, что также сказывается на результатах измерения, снижает точность способа и усложняет его проведение.
Кроме того, существенным недостатком способа в отношении его применения к порошковым материалам является то, что при проникновении диффузанта в образец процесс контролируется диффузией в объем частиц через покрытие на их поверхности, образующее межчастичные прослойки. При этом проникновение диффузанта и его распределение по глубине образца характеризуются коэффициентом диффузии в покрытии, которое в значительной степени отличается от материала по химическому составу, и, как правило, представляет собой другое вещество (например, оксид). В этой связи попытки реализация способа, например, для порошковых металлов могут привести к определению коэффициента диффузии кислорода в оксиде, а не в металле, который представляет собой основу материала (Кофстад П. Высокотемпературное окисление металлов. М.: Мир, 1969, 392 с.).
Методический подход заявляемого способа определения коэффициента диффузии в порошковых материалах заключается в следующем. Чтобы осуществить и проконтролировать целевой диффузионный процесс, следует исходить из того, что диффузант входит в химический состав покрытия на частицах материала, составляющих межзеренные прослойки. Далее необходимо исключить (значительно снизить) приток диффузанта извне и провести измерение параметра, величина которого связана с изменением количества диффузанта в покрытии после диффузионного отжига. В этом случае при отжиге градиент концентрации диффузанта между фазами, составляющими покрытие и основное вещество частицы, приведет к диффузионному оттоку диффузанта из покрытия в объем частиц материала, т.е. к снижению содержания диффузанта в покрытии именно за счет диффузии ионов исследуемого диффузанта в исследуемом материале. Такой процесс приведет к диффузионному размытию границы между материалом и покрытием по содержанию диффузанта, и можно считать, что граница концентрации, соответствующей химическому составу вещества покрытия, сдвигается в направлении от центра к поверхности частиц по сравнению с исходным (до отжига) состоянием. Самым важным при этом является то, что снижение содержания диффузанта в фазе покрытия часто приводит к резкому изменению ее проводящих свойств. Так, например, у многих металлов диэлектрическими или полупроводниковыми свойствами с большим удельным сопротивлением при комнатной температуре обладают высшие оксиды, в то время как низшие оксиды имеют металлическую электропроводность, и их удельное сопротивление незначительно отличается от удельного сопротивления металла. Все твердые растворы кислорода в металле имеют металлический тип электропроводности с низким удельным сопротивлением. Соответственно снижение содержания диффузанта в покрытии часто в прямом смысле приводит к уменьшению толщины покрытия, обладающего выраженными экранирующими свойствами для протекания электрического тока по частицам порошкового материала. Поэтому такое диффузионное явление по отношению к изменению электропроводности можно связывать с изменением толщины экранирующего покрытия. Хотя, например, в металлах из поверхностного оксида диффундирует и растворяется за счет диффузии только кислород. Однако при этом постадийно образуются сначала низшие оксиды и затем твердый раствор, а граница его концентрации, соответствующей высшему оксиду, как бы сдвигается в направлении от центра к поверхности частицы, т.е. слой высшего оксида утоняется.
Отметим, что с точки зрения резистометрии (кондуктометрии) порошковых материалов, этот метод будет чувствителен к подобному «движению» межфазовых границ только при сильном различии фаз по физическим свойствам, в частности по электропроводности (Блошенко В.Н., Бокий В.А., Боровинская И.П. О растворении окисной пленки металла в процессе синтеза карбида титана. Физика горения и взрыва, 1984, №6, с.87-90).
Кроме того, в порошковых материалах электропроводность сильно зависит от степени уплотнения ((Мокрушин В.В. Закономерность изменения обобщенной проводимости нагружаемых порошковых материалов. Доклады Академии наук, 1997, №3, том 357, с.332-334), которая влияет на состояние покрытия в местах контакта частиц и заметно изменяется после диффузионного отжига прессованных образцов, например, за счет спекания и теплового расширения твердых тел. Эти явления вносят неопределенный вклад в изменение электропроводности прессованного образца материала с фиксированной плотностью и сказываются на точности и воспроизводимости измерения. В этой связи важными обстоятельствами являются проведение диффузионного отжига материала в насыпном виде, а измерение электропроводности до и после отжига - при различной степени уплотнения с целью определения электропроводности собственно материала в его беспористом состоянии (Баландин В.А., Голубев В.А., Мокрушин В.В., Ярошенко В.В. Способ определения электрофизического параметра порошкообразных материалов. Авторское свидетельство №1540482, МКИ G01N27/02, 1989. БИ №23, 1999).
Для количественных определений значений коэффициентов диффузии требуется определение и контроль изменения толщины экранирующего покрытия на поверхности микроскопических частиц порошковых материалов, при этом необходимо учитывать и возможность разрушения покрытия в местах контакта частиц и последующее изменение (после диффузионного отжига) площади проводящей поверхности в местах контакта частиц за счет изменения толщины покрытия (Мокрушин В.В. Теория обобщенной проводимости гетерогенных систем и резистометрическое исследование окисления порошковых металлов в пористом состоянии. Труды всероссийской конференции "Процессы горения и взрыва в физикохимии и технологии неорганических материалов". М., 24-27 июня 2002 г., Редакционно-издательский отдел ИСМАН, Черноголовка, 2002, с.268-274).
Из вышесказанного следует, что необходимо определять среднестатистическую толщину насыщенного диффузантом покрытия (для частиц металлических порошков, например, - оксидных пленок), а также величину контактной поверхности, неэкранированной покрытием, и анализировать их изменение после диффузионного отжига. Поскольку в основе заявляемого способа определения коэффициента диффузии лежит измерение электропроводности материала до и после отжига, то для порошковых материалов следует отжиг проводить в насыпном виде, а электропроводность измерять при различной степени уплотнения, чтобы исключить влияние ее изменения в процессе отжига на измеряемые параметры и конечный результат.
Определение толщины покрытия на частицах порошковых материалов, кроме того, является самостоятельной задачей в порошковом материаловедении и в других областях науки, техники и технологии, где используются порошки и поликристаллические материалы на их основе.
Наиболее близким и принятым за прототип способа определения толщины и показателя целостности покрытия на частицах порошковых материалов является способ определения толщины покрытия на частицах порошковых материалов (Баландин В.А., Бережко П.Г., Голубев В.А., Мокрушин В.В., Ярошенко В.В. Способ определения толщины покрытия на частицах порошкообразных материалов. Авторское свидетельство №1598600, МКИ G01B 7/06, 1990, БИ №23, 1999). Способ основан на том, что измерения проводятся при различной степени уплотнения и определяется индивидуальная для порошкового материала зависимость электропроводности от степени уплотнения. С помощью ее математической обработки определяется электропроводность материала в беспористом состоянии и величина критической плотности (пористости), при которой разрушается покрытие в местах контакта частиц с образованием доли проводящей поверхности, неэкранированной покрытием. Дополнительное определение величины относительной площади проекции (на площадь поперечного сечения образца) суммарной проводящей поверхности между частицами материала в местах разрушения покрытия дает возможность установить объемное содержание материала и покрытия на основании преобразования формулы Оделевского (Оделевский В.И. Расчет обобщенной проводимости гетерогенных систем. Журнал технической физики, 1951, том 21, вып.6, с.667-677) и рассчитать его толщину. Следует отметить, что изменение толщины покрытия и величины относительной площади проекции проводящей поверхности частиц - взаимосвязанные между собой явления, и изменение одного параметра приводит к изменению другого.
Недостатком способа является то, что определять оба эти параметра по величине электропроводности одновременно невозможно без наличия сведений об их функциональной взаимозависимости, например, по физической формуле, основанной на геометрической модели структуры материала, и значений других параметров, определяющих такую взаимосвязь. Кроме того, в прототипе не предусмотрен надежный подход для определения относительной площади проекции проводящей поверхности между частицами, неэкранированной покрытием, в качестве показателя целостности покрытия, что приводит к недостаточной точности определения толщины покрытия. В расчетную формулу входит параметр σП - удельное сопротивление (величина обратная электропроводности) покрытия, определять которое очень трудно, например, из-за переменного состава вещества покрытия, что также сказывается на точности определения.
Идеология заявляемого способа определения толщины покрытия и показателя его целостности основана прежде всего на том, что вводится не только понятие о том, что относительная площадь проекции неэкранированной покрытием контактной поверхности частиц материала в беспористом состоянии является показателем целостности покрытия в местах контакта частиц порошкового материала, но и предлагается надежный подход к ее определению путем измерения электропроводности материала с покрытием и без покрытия. Кроме того, между толщиной покрытия и показателем его целостности устанавливается функциональная взаимосвязь и взаимозависимость, позволяющая судить об изменении одного параметра по изменению другого, что важно с точки зрения использования резистометрических методов для количественного исследования свойств порошковых материалов. Важным обстоятельством является также и то, что определение толщины покрытия проводится по электропроводности материала при дополнительном определении гранулометрических и структурных параметров: насыпной плотности и среднестатистического координационного числа проводящих контактов между соседними частицами порошкового материала, которые также в сильной степени влияют на проводящие свойства порошков.
При реализации способа определения коэффициента диффузии достигаются следующие технические результаты: расширение области применения способа, его упрощение, повышение достоверности и точности определения.
Указанные технические результаты достигаются тем, что в способе определения коэффициента диффузии в порошковых материалах, заключающемся в том, что измеряют электропроводность материала в исходном состоянии для определения начального содержания диффузанта в покрытии на его частицах, подвергают материал диффузионному отжигу, охлаждают, измеряют электропроводность для определения измененного содержания диффузанта в покрытии, определяют коэффициент диффузии по выражению, полученному решением уравнения Фика; указанную последовательность действий повторяют при различных температурах отжига материала для получения температурной зависимости коэффициента диффузии, по которой в соответствии с законом Аррениуса определяют его постоянные параметры, новым является то, что отжиг материала проводят в насыпном виде, а измерение электропроводности - при различной степени уплотнения, дополнительно определяют толщину покрытия и показатель его целостности, с учетом которых определяют изменение содержания диффузанта в покрытии при постоянном значении его концентрации.
Отжиг порошкового материала в насыпном виде и измерение электропроводности материала (до и после отжига) при различной степени уплотнения проводят для того, чтобы учесть сильную зависимость проводящих свойств порошков от пористости с помощью определения электропроводности собственно материала в его беспористом состоянии. Указанные дополнительные операции позволяют судить об изменении содержания диффузанта по изменению толщины экранирующего покрытия, и показателя его целостности в местах контактов частиц без определения изменения концентрации, используя лишь его значение для исходного материала с покрытием, которое остается постоянным.
Описываемый подход к возможности использования измерений электрофизических величин для определения параметров структуры порошковых материалов и их изменения после отжига позволяет распространить резистометрические методы на количественное определение значений коэффициента диффузии. Такая возможность основывается на том, что покрытие и материал в сильной степени отличаются по электропроводности, например материал - электронный проводник, а покрытие - полупроводник или диэлектрик.
При этом покрытие будет экранировать всю или часть контактной поверхности частиц до тех пор, пока концентрация диффузанта на поверхности частиц соответствует концентрации в покрытии, обладающем низкими проводящими свойствами. Как только концентрация на поверхности снизится до значения, при котором свойства покрытия перестают быть изолирующими или экранирующими, можно говорить о том, что поверхность очистилась от экранирующего покрытия за счет растворения диффузанта, в том смысле, что оно перестало обладать заметным отличием от материала частиц по электропроводности. Например, если на поверхности частиц порошкового титана концентрация кислорода в диоксиде титана TiO2, обладающем полупроводниковыми свойствами с очень малой при комнатной температуре электропроводностью, снизится до концентрации, соответствующей монооксиду (TiO) с металлическим типом электропроводности, то можно говорить о растворении оксидного покрытия с изменением его толщины и целостности, полагая значение концентрации диффузанта в покрытии постоянным до момента резкого изменения проводящих свойств. В этом случае параметры, характеризующие целевой диффузионный процесс, протекающий в материале при диффузионном отжиге, можно количественно определять по изменению электропроводности, с учетом изменения толщины и целостности покрытия.
Для последующего расчета коэффициента диффузии по значениям параметров, устанавливаемых с помощью электрофизических измерений, может быть использовано известное одномерное решение уравнения Фика, которое получено для постоянной концентрации диффузанта на поверхности раздела фаз (Кофстад П. Высокотемпературное окисление металлов. М: Мир, 1969, 392 с):
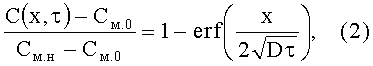
где C(x, τ) - текущая концентрация диффузанта в материале; x - координата; τ - время диффузионного отжига; См.0 - исходная (до отжига) концентрация диффузанта в материале; См.н - насыщенная концентрация диффузанта в материале (на поверхности раздела фаз «основное вещество - покрытие»).
Интегрирование уравнения (1) и последующее преобразование для определенных геометрических форм (например, полубесконечный цилиндр или шар) позволяет получить выражение для растворенной части диффузанта, а затем получить зависимость, характеризующую изменение толщины покрытия при постоянной концентрации диффузанта в нем (Ham J.L. Mechanism of Surface Oxide Removal from Metal in Space. Aerospace Engineering, vol.20, №.5, 1961, pp.20-54; / МокрушинВ.В. Теория обобщенной проводимости гетерогенных систем и резистометрическое исследование окисления порошковых металлов в пористом состоянии. Труды всероссийской конференции "Процессы горения и взрыва в физикохимии и технологии неорганических материалов". М., 24-27 июня 2002 г., Редакционно-издательский отдел ИСМАН, Черноголовка, 2002, с.268-274):
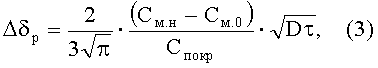
где Δδр=δ0-δ1 - изменение толщины покрытия за счет диффузии; Спокр -концентрация диффузанта в покрытии; δ0 - толщина покрытия на исходном (до отжига) материале; δ1 - толщина покрытия после отжига.
Если считать, что в исходном (до отжига) материале диффузант в объеме частиц отсутствует (или его содержание пренебрежимо мало), т.е. весь диффузант содержится в покрытии, тогда в выражении (3) См.0≈0, и коэффициент диффузии рассчитывается по изменению толщины покрытия по формуле:
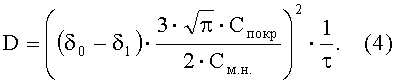
Повторное проведение отжига и выполнение операций по определению значения толщины покрытия δ1 при различных температурах отжига дает возможность определить значения D в зависимости от температуры и после выполнения расчетных процедур установить параметры D0 и E, определяющие коэффициент диффузии по уравнению Аррениуса (1).
Таким образом, при реализации способа обеспечивается достижение указанных технических результатов, а именно:
- способ определения коэффициента диффузии используют для порошковых материалов независимо от их пористости (степени уплотнения), чем достигается расширение области использования и упрощение измерительных операций;
- электропроводность материала для способа определения коэффициента диффузии определяют с учетом ее зависимости от пористости (степени уплотнения), что повышает точность определения;
- для выполнения способа определения коэффициента диффузии определяют толщину покрытия на поверхности частиц с учетом нарушения его целостности, показатель которой определяют по измерению электропроводности материала без покрытия, а искомый параметр определяют через величины, связанные с ним напрямую по решению уравнения Фика, что повышает точность и достоверность определяемой величины;
- образец подвергают однократному термическому воздействию (вакуумному отжигу) с целью осуществления целевого диффузионного переноса, что существенно упрощает способ, снижает загрязнение образца побочными примесями и повышает точность измерений.
Технический результат, достигаемый при выполнении способа определения толщины и показателя целостности покрытия на частицах порошковых материалов, заключается в повышении точности определения.
Это достигается тем, что образец материала сжимают, измеряют его электропроводность при различной степени уплотнения, определяют электропроводность и относительную площадь проекции неэкранированной покрытием контактной поверхности частиц материала в беспористом состоянии, характеризующую целостность покрытия, и с учетом полученных параметров определяют толщину покрытия. Новым в способе является то, что дополнительно измеряют удельную поверхность материала и электропроводность материала без покрытия, определяют среднестатистическое координационное число проводящих контактов частиц, а искомые параметры рассчитывают по соотношениям:
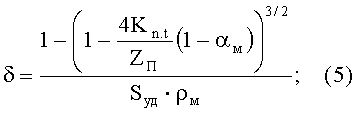
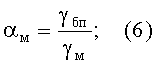
где δ - толщина покрытия на частицах порошкового материала; Kn.t - эмпирический коэффициент, связанный с геометрической неидеальностью контактов и с туннельным эффектом электропроводности в покрытии; ZП - среднестатистическое координационное число проводящих контактов частиц материала в беспористом состоянии; Sуд - удельная поверхность порошкового материала; ρм - кристаллическая плотность материала; αм - относительная площадь проекции неэкранированной покрытием контактной поверхности частиц материала в беспористом состоянии - показатель целостности покрытия; γбп - электропроводность порошкового материала с покрытием в беспористом состоянии; γм - электропроводность порошкового материала без покрытия в беспористом состоянии.
При выполнении способа определения толщины покрытия и показателя его целостности дополнительно измеряют и определяют те величины, которые так же, как и искомые параметры, влияют на величину электропроводности материала, а именно: электропроводность материала без покрытия, удельную поверхность порошкового материала и координационное число проводящих контактов, что в значительной степени сказывается на точности способа.
Показатель целостности покрытия - относительную площадь проекции неэкранированной покрытием контактной поверхности частиц αм - определяют отношением электропроводностей материала в беспористом состоянии с покрытием и без покрытия соответственно (см. формулу (6)). Основанием для этого является аналогия с закономерностью изменения проводимости порошковых материалов при их уплотнении (Мокрушин В.В. Закономерность изменения обобщенной проводимости нагружаемых порошковых материалов. Доклады Академии наук, 1997, №3, том 357, с.332-334), в которой относительная площадь проекции проводящей поверхности αП материала равна отношению электропроводности пористого материала γ к электропроводности в беспористом состоянии γбп.
Необходимость и достаточность определения дополнительных параметров: удельной поверхности материала Sуд и среднестатистического координационного числа проводящих контактов ZП частиц материала в беспористом состоянии - параметров, характеризующих гранулометрические и структурные свойства материала, - вытекает из другой, по сравнению с прототипом, модели структуры порошкового материала, частицы которого покрыты менее проводящей фазой. В данном случае принимается во внимание сферическая модель зерен материала и рассматривается строение единичного контакта, поверхность которого частично экранирована покрытием (см. фиг.1).
По схеме на фиг.1 видно, что
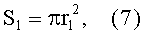
где S1 - площадь проводящего (неэкранированного покрытием) контакта; r1 - радиус проводящего контакта.
С другой стороны, параметр S1 может быть выражен отношением площади всей поверхности частицы к числу контактирующих с ней соседних частиц, т.е. к координационному числу (количеству проводящих контактов) ZП, умноженным на долю проводящей контактной поверхности, которая тождественна параметру αм:
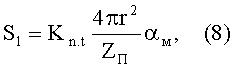
где r - радиус частицы, Kn.t - эмпирический коэффициент, учитывающий геометрическую неидеальность контактов, контактные углы (углы наклона межчастичных контактов) и электропроводность в покрытии, обусловленную туннельным эффектом.
Физический смысл коэффициента Kn.t определяется из выражения (8) как отношение относительного геометрического размера площади единичного проводящего контакта к его относительной площади проекции, определяемой через электропроводность.
Площадь реального проводящего контакта меньше площади идеализированного проводящего контакта в сферической геометрической модели. Это вытекает из того, что в реальных системах размер частиц неодинаков, сами частицы - не идеальные сферы, а форма контактных площадок - не круглая. Но более важным является то, что разрушение покрытия хотя и приводит к образованию контактов между материалом частиц в единичном контакте, но в значительно меньшей степени, чем это показано на геометрической схеме, изображенной на фиг.1, и часть тока протекает через материал покрытия за счет туннельного эффекта (Живер И. Туннельный переход в системе металл - изолятор - металл. В сб. «Туннельные явления в твердых телах». Под ред. Бурштейна Э. и Лундквиста С. Пер. с англ. М.: Мир. 1973, с.25-35.).
Аналогичные рассуждения для целого единичного контакта между частицами с площадью поверхности S2 дают соотношения:
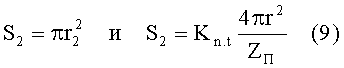
Из выражений (7)-(9) следует, что
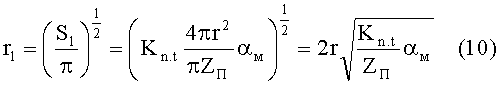
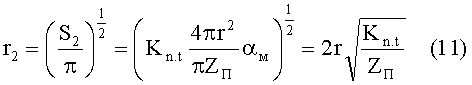
Продолжение анализа геометрической схемы единичного проводящего контакта (см. фиг.1) позволяет установить взаимосвязь между радиусами r, r1, r2 и радиусом основы частицы, состоящей из вещества материала rм:
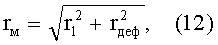
где rдеф - деформационный радиус частицы в беспористом образце или радиус сближения двух частиц, также определяемый соотношением, вытекающим из анализа схемы на фиг.1:
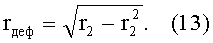
Комбинация выражений (10)-(13) дает формулу для rм:
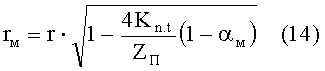
Определим среднестатистическую объемную долю покрытия в каждой частице как отношение объема покрытия к объему частицы, тогда с учетом выражения (14) получим:
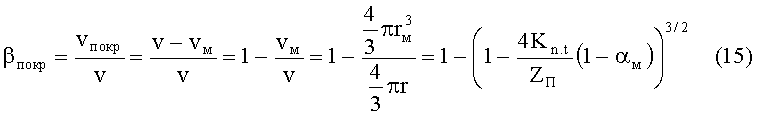
С другой стороны, объемная доля покрытия в материале может быть определена через брутто-параметры как отношение удельного объема фазы покрытия 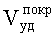
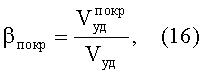
которые могут быть выражены, в свою очередь, через удельную поверхность и кристаллическую плотность материала:
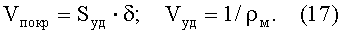
Преобразование выражений (15)-(17) относительно параметра δ дает формулу (5) для расчета толщины покрытия на частицах порошкового материала, в которой взаимосвязаны параметры структуры и проводимости порошковой гетерогенной системы.
Кроме того, через электропроводность порошковой системы, гранулометрические и структурно-механические параметры определяются следующие параметры, характеризующие проводящие свойства и состав материала:
- объемное содержание чистого (активного) материала
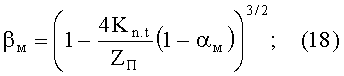
- доля площади поверхности поперечного сечения образца материала, образованная частицами материала
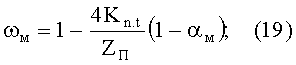
- доля площади поверхности поперечного сечения образца материала, образованная фазой покрытия (межчастичными прослойками) в беспористом состоянии
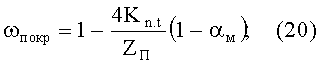
- доля площади поверхности поперечного сечения материала, экранированная покрытием
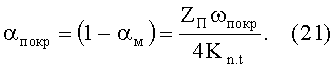
Из выражения (21) вытекает еще один физический смысл коэффициента
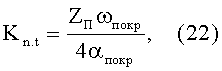
который показывает, во сколько раз проекция поверхности единичного контакта, экранированной покрытием, больше части площади поперечного сечения частицы, образованной покрытием.
В заявляемом способе показатель целостности покрытия - относительная площадь проекции проводящей поверхности частиц в беспористом состоянии αм - определяется простым отношением электропроводности порошкового материала в беспористом состоянии γбп к электропроводности материала без покрытия γм также в беспористом состоянии, в то время как в прототипе (а.с. №1598600) надежного способа определения этого параметра предложено не было. Обоснование и использование соотношения (6) для определения величины показателя целостности αм существенно повышает точность определения.
Кроме того, между толщиной покрытия и показателем его целостности устанавливается функциональная взаимосвязь через теоретически обоснованную физическую формулу, что также повышает точность заявляемого способа. Достижению этого же технического результата служит использование брутто-параметра - удельной поверхности материала - вместо величины среднестатистического размера частиц для характеристики гранулометрических свойств порошкового материала.
На фиг.1 представлена схема единичного контакта двух частиц с покрытием в сферической геометрической модели проводящей системы порошкового материала, которая иллюстрирует вывод формулы (5).
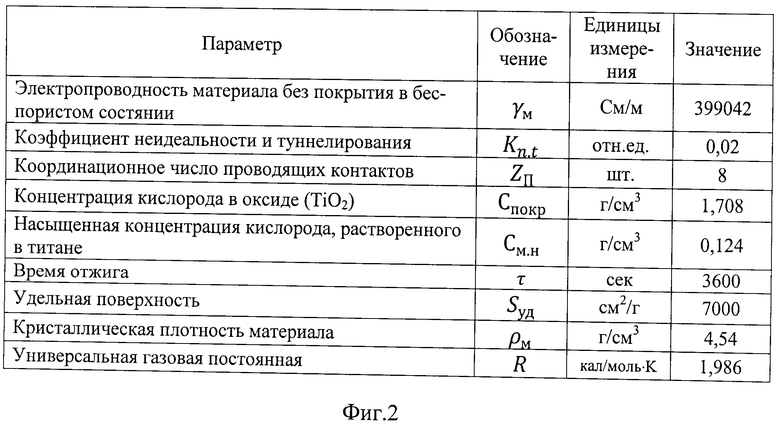
На фиг.2 приведены справочные данные, исходные и измеренные параметры, необходимые для реализации способов определения коэффициента диффузии, толщины и показателя целостности покрытия для порошкового титана, выбранного для примера 1 использования заявляемых способов.
На фиг.3 представлены результаты определения толщины оксидного покрытия, показателя его целостности и коэффициента диффузии кислорода в порошковом титане.
На фиг.4 приведен график зависимости логарифма коэффициента диффузии кислорода в порошковом титане от обратной температуры в качестве иллюстрации примера 1 выполнения заявляемых способов.
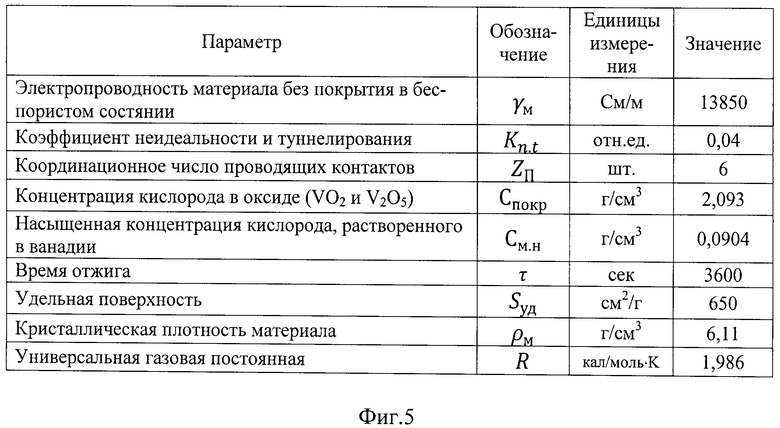
На фиг.5 приведены справочные данные, исходные и измеренные параметры, необходимые для выполнения способов определения коэффициента диффузии, толщины и показателя целостности покрытия для порошкового ванадия.
На фиг.6 представлены результаты определения толщины оксидного покрытия, показателя его целостности и коэффициента диффузии кислорода в порошковом ванадии.
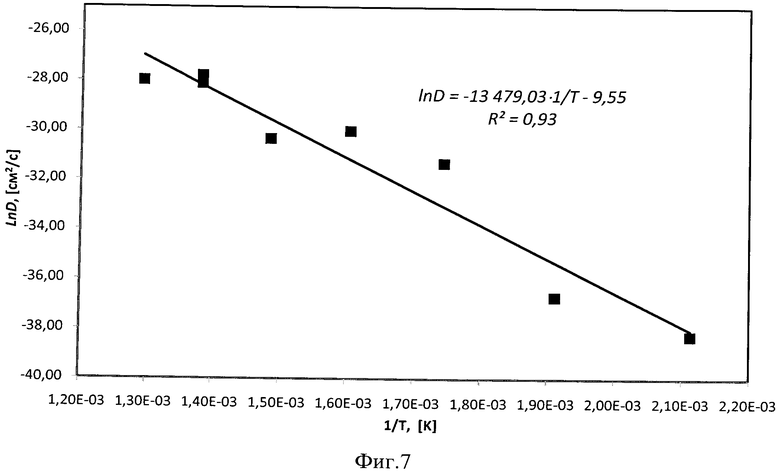
На фиг.7 приведен график зависимости логарифма коэффициента диффузии кислорода в порошковом ванадии от обратной температуры в качестве иллюстрации примера 2 выполнения заявляемых способов.
Способ определения коэффициента диффузии в порошковых материалах, как и способ определения толщины и показателя целостности покрытия на частицах порошковых материалов могут использоваться независимо друг от друга. Способы реализуются при условии, что электропроводность вещества покрытия значительно превышает электропроводность основного вещества материала.
При осуществлении способа определения коэффициента диффузии в порошковых материалах сначала измеряют электропроводность исходного (до диффузионного отжига) материала при различной степени уплотнения образца. Материал в насыпном виде подвергают вакуумному отжигу с фиксированной длительностью и температурой с целью осуществления целевого диффузионного процесса. Вакуум используют для ограничения доступа воздуха и уменьшения влияния дополнительного окисления на покрытие материала. Затем материал охлаждают, отбирают пробу материала в перчаточном боксе с инертной средой и измеряют электропроводность образца при различной степени уплотнения. Анализируя полученные зависимости электропроводности образцов от плотности, определяют удельную электропроводность материала в беспористом состоянии до и после отжига.
Диффузионный вакуумный отжиг материала в насыпном виде, его охлаждение, отбор проб, измерения электропроводности образцов в зависимости от степени уплотнения и определение электропроводности материала в беспористом состоянии повторяют для других температур отжига.
Затем определяют показатель целостности покрытия и его толщину как для исходного материала, так и для материала, подвергнутого диффузионному отжигу при различных температурах. Следует отметить, что для определения указанных параметров может быть использован способ, описанный в а.с. №1598600.
На следующем этапе по изменению значений толщины и показателя целостности покрытия до и после диффузионного отжига с различной температурой и с известной длительностью определяют значения коэффициентов диффузии по формуле (4), полученной решением уравнения Фика. Полученную таким образом зависимость коэффициентов диффузии от температуры отжига аппроксимируют в аррениусовских координатах lnD - 1/T прямой линией в соответствии с уравнением, к которому преобразуется закон Аррениуса (формула (1)) после логарифмирования:
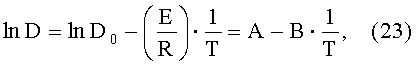
что позволяет определить его постоянные коэффициенты A, B и затем рассчитать параметры коэффициента диффузии:
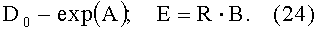
При осуществлении способа определения толщины и показателя целостности покрытия измерительные процедуры выполняют по алгоритму, описанному в изобретении (а.с. №1540482). Образец порошкового материала с известной массой помещают в матрицу из изоляционного материала, сжимают, измеряют его электропроводность и плотность, например, с использованием приспособления, описанного в прототипе (а.с. №1598600). Затем, анализируя зависимость электропроводности от степени уплотнения с использованием известной закономерности (Мокрушин В.В.. Закономерность изменения обобщенной электропроводности нагружаемых порошковых материалов. Доклады Академии наук, 1997, №3, том 357, с.332-334), определяют электропроводность материала в беспористом состоянии γбп. Далее таким же образом определяют электропроводность материала без покрытия γм в беспористом состоянии, например, после очистки поверхности частиц (с использованием вакуумно-термических или химических методов). Если на материал специально наносили покрытие, то значение γм определяется до нанесения покрытия.
По формуле (6) рассчитывают показатель целостности покрытия - относительную площадь проекции неэкранированной покрытием контактной поверхности частиц αм. Затем измеряют удельную поверхность порошкового материала, например, с использованием метода БЭТ (Герман Р. Порошковая металлургия от А до Я. Долгопрудный: Издательский Дом «Интеллект», 2009, с.127). С помощью оптической или электронной микроскопии определяют среднее координационное число ZП проводящих контактов между соседними частицами в образце при степени уплотнения 0,6-0,8, при достижении которой практически отсутствует смещение частиц и образование новых контактов. Подбирают величину эмпирического коэффициента Kn.t с помощью сведений о содержании примесей, входящих в покрытие, или данных о содержании основного вещества в порошковом материале. После этого рассчитывают значение среднестатистической толщины покрытия на частицах порошкового материала 8 по формуле (5).
ПРИМЕР 1. Определение коэффициента диффузии, толщины и показателя целостности покрытия на частицах порошкового титана.
Заявляемые способы реализованы при исследовании порошка титана, аналогичного использованному в работе (Артемова Л.Н., Власова М.П., Голубев А.В., Крекнин Д.А., Селезенев А.А. Влияние температуры отжига на кинетику взаимодействия титана с водородом. Известия Академии наук СССР. Металлы. 1989. №5. С.200-201).
В данном случае покрытие на поверхности частиц - оксидное, диффузант - кислород, для которого определяется коэффициент диффузии по растворению (уменьшению толщины) оксидной пленки из TiO2.
На фиг.2 приведены справочные и исходные данные, необходимые для использования способов определения коэффициента диффузии, толщины и показателя целостности покрытия для порошкового титана, а на фиг.3 представлены результаты определения толщины оксидного покрытия, показателя его целостности, а также значений коэффициента диффузии кислорода в порошковом титане при различных температурах отжига.
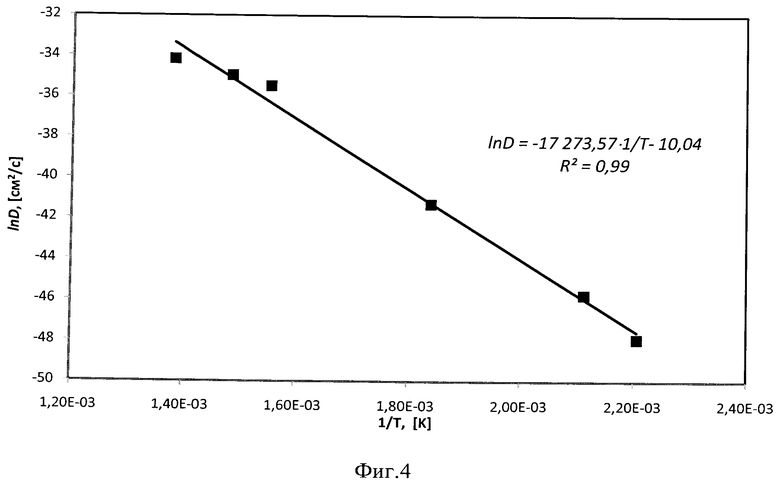
На фиг.4 зависимость значений lnD от обратной температуры 1/Т представлена в виде графика, на котором точки - это экспериментальные значения, а линия - аппроксимирующая прямая. Там же приведено уравнение этой прямой линии, по которому определяется значение предэкспоненциального множителя (см. выражения (24)):
D0=exp(-10,04)=4,36·10-5 [см2/с],
и энергия активации коэффициента диффузии:
E=17273,6·1,986=34305 [кал/моль·К].
Представление полученных значений согласно закону Аррениуса (см. формулу (1)) и округление значения энергии активации до трех значащих цифр дает следующий вид температурной зависимости для коэффициента диффузии кислорода в порошковом титане:
D=4,36·10-5·ехр(-34300/RT).
Для сравнения следует указать, что значение коэффициента диффузии в альфа-титане, установленное по внутреннему трению, по данным монографии (Кофстад П. Высокотемпературное окисление металлов. М.: Мир, 1969, 392 с.) равно:
D=1,80·10-3·ехр(-35900/RT).
Различие в значениях предэкспоненциального множителя несущественно, т.к. оно определяется геометрией конкретной рассматриваемой системы (Пешков В.В., Рыжков Ф.Н. и др. О кинетике растворения окисных пленок в титане. Журнал физической химии, том 59, вып.5, 1985, с.1244-1246). Значения же энергии активации в сильной степени зависят от чистоты исследуемого материала и от метода исследования, однако несмотря на это сравниваемые значения энергии активации достаточно близки.
ПРИМЕР 2. Определение коэффициента диффузии, толщины и показателя целостности покрытия на частицах порошка электролитического ванадия марки ВЭЛ-2.
На фиг.5 приведены справочные и исходные данные, необходимые для осуществления способов определения коэффициента диффузии, толщины и показателя целостности покрытия, состоящего из оксидов VO2 и V2O5, для порошкового ванадия. На фиг.6 представлены результаты определения толщины оксидного покрытия, показателя его целостности, а также значений коэффициентов диффузии кислорода в порошковом ванадии при различных температурах отжига.
На фиг.7 представлена зависимость логарифма коэффициента диффузии кислорода в ванадии от обратной температуры, а также полуэмпирическое уравнение аппроксимирующей линейной зависимости, по которому определяется значение предэкспоненциального множителя (см. выражения (24)):
D0=ехр(-9,55)=7,12·10-5 [см2/с]
и энергии активации:
Е=13479,03·1,986=26770 [кал/моль·K].
Округление и запись полученных значений в виде формулы (1), описывающей закон Аррениуса, дает:
D=7,12·10-5·ехр(-26800/RT).
Для сравнения приведем значение коэффициента диффузии в ванадии по данным монографии (Кофстад П. Высокотемпературное окисление металлов. М.: Мир, 1969, 392 с.), установленное релаксационным методом:
D=1,30·10-2·ехр(-29000/RT).
Если учесть, что различия в значениях предэкспоненциального множителя определяются геометрией конкретной изучаемой системы и тот факт, что используются разные методы определения, можно считать, что полученные коэффициенты диффузии достаточно согласуются между собой.
| название | год | авторы | номер документа |
|---|---|---|---|
| СПОСОБ ОПРЕДЕЛЕНИЯ КОЭФФИЦИЕНТОВ ДИФФУЗИИ В ПЛЕНОЧНЫХ МАТЕРИАЛАХ | 2002 |
|
RU2212027C1 |
| Способ определения коэффициента диффузии | 1981 |
|
SU1117491A1 |
| Способ определения коэффициента диффузии в твердом материале | 1985 |
|
SU1359721A1 |
| МЕТАЛЛОПОКРЫТИЕ С ПОВЫШЕННОЙ АДГЕЗИЕЙ К МАТЕРИАЛУ ПОДЛОЖКИ И СПОСОБ ЕГО ИЗГОТОВЛЕНИЯ | 2007 |
|
RU2358034C2 |
| Способ определения диффузионной проницаемости материалов | 1978 |
|
SU787956A1 |
| Способ определения коэффициента диффузии в порошковых спеченных соединениях | 1990 |
|
SU1721473A1 |
| Способ получения конструкционной порошковой стали | 1991 |
|
SU1803264A1 |
| СПОСОБ ИЗГОТОВЛЕНИЯ ПОРОШКОВОГО КОМПОЗИТА Сu-Cd/Nb ДЛЯ ЭЛЕКТРОКОНТАКТНОГО ПРИМЕНЕНИЯ | 2013 |
|
RU2516236C1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ ДИФФУЗИОННЫХ КОНСТАНТ В ПОЛИКРИСТАЛЛИЧЕСКИХ ТЕЛАХ | 1999 |
|
RU2169914C2 |
| СПОСОБ ОПРЕДЕЛЕНИЯ ДИФФУЗИОННЫХ КОНСТАНТ В ПОЛИКРИСТАЛЛИЧЕСКИХ МАТЕРИАЛАХ | 2004 |
|
RU2260787C1 |


Изобретения относятся к области определения значений параметров, характеризующих физико-химические свойства материалов, например коэффициентов диффузии, по величине электропроводности, и могут найти применение в порошковой металлургии, в изучении процессов самораспространяющегося высокотемпературного синтеза, в материаловедении и физике твердого тела. В способе определения коэффициента диффузии измеряют электропроводность материала в исходном состоянии для определения начального содержания диффузанта в покрытии на его частицах. Затем подвергают материал в насыпном виде диффузионному отжигу, охлаждают и измеряют электропроводность для определения измененного содержания диффузанта в покрытии. Измерение электропроводности материала до и после отжига проводят при различной степени уплотнения, а также до и после отжига определяют толщину покрытия и показатель его целостности, с учетом которых определяют изменение содержания диффузанта в покрытии при постоянном значении его концентрации и определяют коэффициент диффузии по выражению, полученному решением уравнения Фика. Указанную последовательность действий повторяют при различных температурах отжига материала для получения температурной зависимости коэффициента диффузии, по которой в соответствии с законом Аррениуса определяют его постоянные параметры: предэкспоненциальный множитель и энергию активации. При осуществлении способа определения толщины и показателя целостности покрытия образец материала сжимают, измеряют его электропроводность при различной степени уплотнения, определяют электропроводность материала в беспористом состоянии. Дополнительно измеряют удельную поверхность материала и электропроводность материала без покрытия, определяют среднестатистическое координационное число проводящих контактов частиц. Затем рассчитывают относительную площадь проекции неэкранированной покрытием контактной поверхности частиц материала в беспористом состоянии, характеризующую целостность покрытия, и толщину покрытия. Техническим результатом является повышение точности и достоверности определения, упрощение способа, расширение области применения. 2 н.п. ф-лы, 7 ил.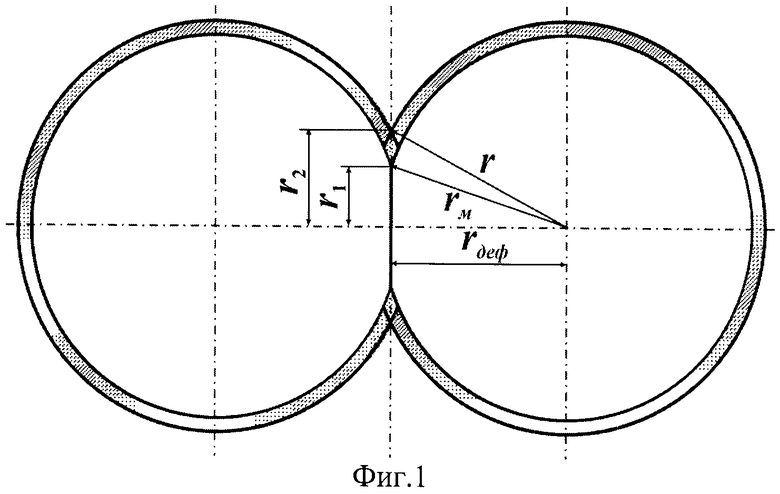
1. Способ определения коэффициента диффузии в порошковых материалах, заключающийся в том, что измеряют электропроводность материала в исходном состоянии для определения начального содержания диффузанта в покрытии на его частицах, подвергают материал диффузионному отжигу, охлаждают, измеряют электропроводность для определения измененного содержания диффузанта в покрытии, определяют коэффициент диффузии по выражению, полученному решением уравнения Фика; указанную последовательность действий повторяют при различных температурах отжига материала для получения температурной зависимости коэффициента диффузии, по которой в соответствии с законом Аррениуса определяют его постоянные параметры, отличающийся тем, что отжиг материала проводят в насыпном виде, а измерение электропроводности - при различной степени уплотнения, дополнительно определяют толщину покрытия и показатель его целостности до и после отжига, с учетом которых определяют изменение содержания диффузанта в покрытии при постоянном значении его концентрации.
2. Способ определения толщины и показателя целостности покрытия на частицах порошковых материалов, заключающийся в том, что образец материала сжимают, измеряют его электропроводность при различной степени уплотнения, определяют электропроводность и относительную площадь проекции неэкранированной покрытием контактной поверхности частиц материала в беспористом состоянии, характеризующую целостность покрытия, и с учетом полученных параметров определяют толщину покрытия, отличающийся тем, что дополнительно измеряют удельную поверхность материала и электропроводность материала без покрытия, определяют среднестатистическое координационное число проводящих контактов частиц, а искомые параметры рассчитывают по соотношениям:
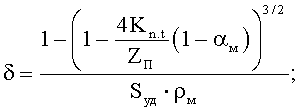
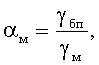
где δ - толщина покрытия на частицах порошкового материала;
Kn.t - эмпирический коэффициент, связанный с геометрической неидеальностью контактов и с туннельным эффектом электропроводности в покрытии;
ZП - среднестатистическое координационное число проводящих контактов частиц материала в беспористом состоянии;
Sуд - удельная поверхность порошкового материала;
ρм - кристаллическая плотность материала;
αм - относительная площадь проекции неэкранированной покрытием контактной поверхности частиц материала в беспористом состоянии - показатель целостности покрытия;
γбп - электропроводность порошкового материала с покрытием в беспористом состоянии;
γм - электропроводность порошкового материала без покрытия в беспористом состоянии.
| Суржиков А.П | |||
| и др., Применение метода измерения температурной зависимости электропроводности для изучения диффузии кислорода в поликристаллических ферритах | |||
| Приспособление для соединения пучка кисти с трубкою или втулкою, служащей для прикрепления ручки | 1915 |
|
SU66A1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ ДИФФУЗИОННЫХ КОНСТАНТ В ПОЛИКРИСТАЛЛИЧЕСКИХ МАТЕРИАЛАХ | 2004 |
|
RU2260787C1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ ДИФФУЗИОННЫХ КОНСТАНТ В ПОЛИКРИСТАЛЛИЧЕСКИХ ТЕЛАХ | 1999 |
|
RU2169914C2 |
| СПОСОБ ОПРЕДЕЛЕНИЯ ТОЛЩИНЫ ПОКРЫТИЯ НА ЧАСТИЦАХ ПОРОШКООБРАЗНЫХ МАТЕРИАЛОВ | 1988 |
|
SU1598600A1 |
| JPH06129976 A 13.05.1994 | |||
Авторы
Даты
2014-07-20—Публикация
2012-12-27—Подача