Предлагаемое изобретение относится к измерительной технике, в частности к измерению температур.
Известен способ измерения температуры термометром сопротивления [а. с.№ 1332158], который приводят в контакт с объектом контроля. Подают на термометр сопротивления мощность P1 и в момент времени t1 измеряют первое значение температуры θ 1 и увеличивают мощность до величины Р2. В моменты времени t2 и t3 проводят второе и третье измерение температуры θ 2 и θ 3. Измерение температур организовано так, что t2-t1=t3-t2. Значение измеряемой температуры рассчитывается по формуле
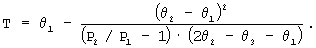
Недостатками данного метода является низкая точность измерения вследствие не учета нелинейности ВАХ терморезистора, непостоянства значения измерительного тока при разных значениях сопротивления датчика, нелинейная зависимость выходного напряжения от сопротивления датчика.
За прототип принят способ измерения температуры полупроводниковым терморезистором [а.с.№1364911], при измерении его сопротивления. Для этого через терморезистор пропускают электрический ток, который производит его нагрев. Температуру дополнительного нагрева контролируют сравнением полученного сопротивления с первоначальным сопротивлением. Измеряют второе значение сопротивления. Измеряют ток нагрева, соответствующий второму значению сопротивления терморезистора, и определяют рассеиваемую на нем электрическую мощность. Определяют температуру нагрева терморезистора из уравнения теплового баланса. Постепенно увеличивают температуру нагрева ступенчатыми изменениями тока нагрева с регистрацией изменения сопротивления терморезистора. Процесс увеличения тока нагрева прекращают, если изменение сопротивления терморезистора становится незначительным по сравнению с предыдущим состоянием. Измеряют третье значение сопротивления терморезистора. По результатам измерения трех значений сопротивления терморезистора и по току нагрева находят температуру Т контролируемой среды по формуле
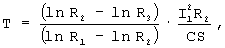
где R1 - сопротивление терморезистора при температуре контролируемой среды, R2 - сопротивление терморезистора, дополнительно нагретого измерительным током, I1 - ток дополнительного нагрева терморезистора, С - коэффициент рассеивания тепла нагретым терморезистором, S - поверхность охлаждения терморезистора.
Недостатками прототипа являются погрешность измерений, обусловленная отсутствием отражающей физику происходящих процессов зависимости сопротивления терморезистора от тока нагрева, определение температуры по неинформативным параметрам, зависящим от пропускаемого через терморезистор тока, свойств контролируемой среды и других неконтролируемых параметров, а также длительным временем измерения температуры, в течение которого температура контролируемой среды может поменяться.
Технической задачей способа является повышение точности определения температуры.
Поставленная техническая задача достигается тем, что:
1. В способе определения температуры полупроводниковый терморезистор приводят в тепловой контакт с объектом, терморезистор включается в цепь регулируемого источника постоянного тока с начальным значением тока, при котором измеряют падение напряжения на терморезисторе, изменяют ток и измеряют второе падение напряжения на терморезисторе, затем, в отличие от прототипа, по двум значениям тока и напряжения рассчитывают диффузионное сопротивление, а температуру Т контролируемой среды находят по формуле
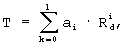
где Rd - диффузионное сопротивление терморезистора, ai - постоянные коэффициенты, l – степень полинома.
2. В способе по п.1 определение диффузионного сопротивления осуществляют по оптимальным режимным параметрам для конкретного терморезистора, которые находят при сопоставлении экспериментальной и моделируемых вольт-амперных характеристик при различных соотношениях токов, для которых погрешность минимальна.
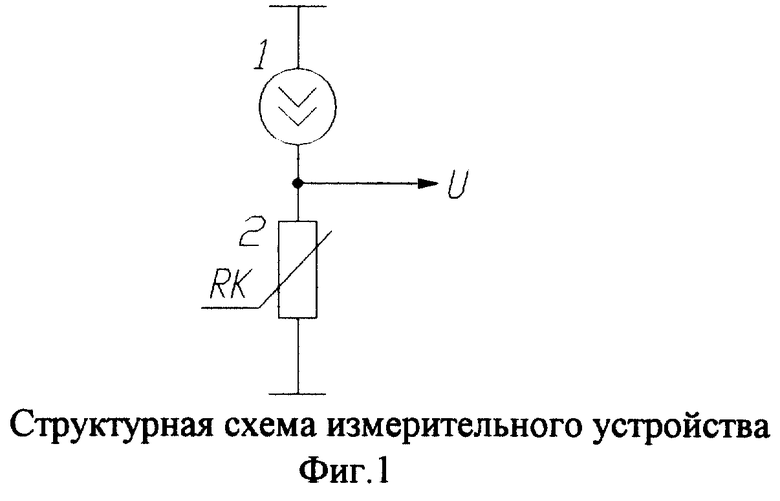
Сущность предлагаемого способа поясняется на фиг.1-4. Предлагаемый способ включает 2 этапа:
1) измерение диффузионного сопротивления терморезистора;
2) определение диффузионного сопротивления осуществляется по оптимальным режимным параметрам при известных температурах.
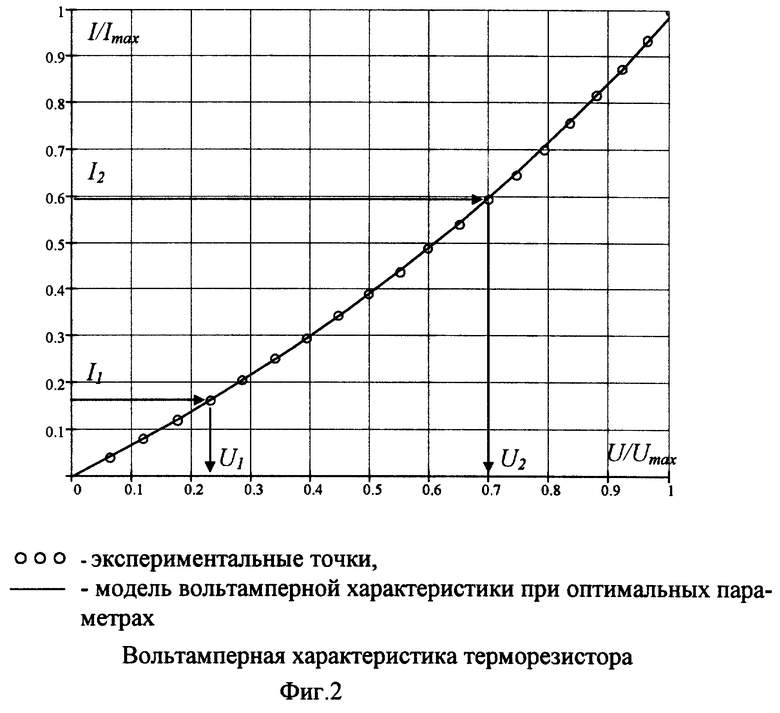
1. Температура определяется за счет измерения диффузионного сопротивления терморезистора. Терморезистор 2, помещенный в контролируемую среду, включают в цепь управляемого источника постоянного тока 1 (фиг.1). Устанавливается начальный ток I1, при котором измеряют падение напряжения U1, устанавливают ток I2 и измеряют второе падение напряжение U2 на терморезисторе, по двум токам I1 и I2 и двум напряжениям U1 и U2 находят диффузионное сопротивление Rd терморезистора (фиг.2).
Вольт-амперная характеристика терморезистора имеет нелинейный характер, а ток изменяется по экспоненциальному закону (фиг.2)
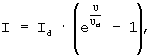
где I - значение измерительного тока через терморезистор, U - падение напряжения на терморезисторе, Id - диффузионный ток, обусловленный движением электронов и дырок в полупроводнике терморезистора до начала пропускания через него измерительного тока, Ud - диффузионное напряжение терморезистора, возникшее вследствие протекания диффузионного тока Id.
Диффузионное сопротивление полупроводника определяется по закону Ома:
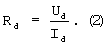
Диффузионное сопротивление обладает уникальным свойством, заключающимся в отсутствии зависимости его значения от величины проходящего через терморезистор тока и приложенного напряжения, при постоянной температуре. Поэтому диффузионное сопротивление является информативным параметром температуры.
Диффузионное сопротивление Rd можно определить по зависимости (2) из системы уравнений:
для двух значений токов I1, I2 запишем:
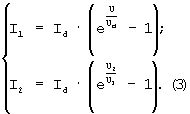
Приведем систему (3) к виду, удобному для логарифмирования:
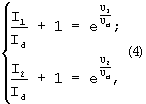
и, поделив одно уравнение системы (4) на другое, получим выражение:
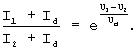
Прологарифмируем уравнение:
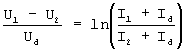
и выразим Ud:
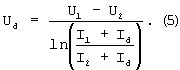
Для нахождения Id выразим его из первого уравнения системы (3)
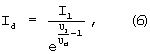
и подставим выражение (5) в формулу (6):
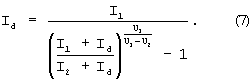
Полученное решение (7) относительно тока Id получено в неявном виде и имеет решение только при численном моделировании по итерационному алгоритму, поэтому перепишем его для итеративного расчета в виде:
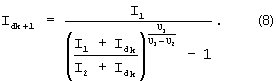
По соотношениям (8) и (5) рассчитаем величину тока Id и напряжения Ud.
Для расчета диффузионного тока, приведенного в неявном виде (8), введем критерий оценки адекватности последующего Idk+1 с предыдущим значением Id (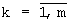 - число итераций):
- число итераций):
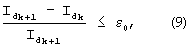
где ε 0=0.0001 - допустимая погрешность.
Алгоритм расчета формулы (8) заключается в следующем:
- первоначальное значение Id0 находим по формуле (8) при Idk=0 (k=1);
- последующее значение Idk+1 получим из выражения (9) при использовании
Idk(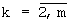 ),
),
- по критерию (9) сравниваем точность вычисления Id с мерой ε 0;
- если соотношение (9) выполняется, то расчет Id по формуле (8) прекращается и последний результат итерации Idk+1 принимают за действительное значение диффузионного тока Id терморезистора;
- если соотношение (9) не выполняется, то осуществляется следующая (k+1) итерация.
По найденному значению диффузионного тока Id определяют по формулам (5 и 2) диффузионное напряжение Ud и диффузионное сопротивление Rd.
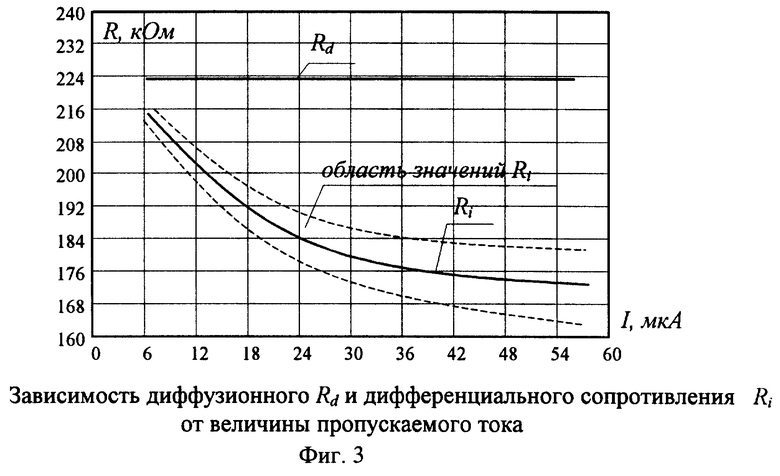
Диффузионное сопротивление Rd по предложенной методике является информативным параметром температуры и не зависит от протекающего через терморезистор тока (см. фиг.3), тогда как сопротивление Ri убывает по экспоненте (см. эффективность по точности п.1).
Температуру контролируемой среды определяют по формуле:
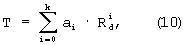
где Rd - диффузионное сопротивление терморезистора, аi - постоянные коэффициенты, k - степень полинома (10). Значения коэффициентов аi определяются в процессе аппроксимации значений диффузионного сопротивления Rd, полученных при известных температурах.
2. Определение диффузионного сопротивления осуществляется по оптимальным режимным параметрам, которые находят при сопоставлении экспериментальной и моделируемых ВАХ при различных значениях токов, с минимальной погрешностью.
Для определения оптимальных режимных параметров получают вольт-амперную характеристику путем измерения значений падения напряжения на терморезисторе при пропускании через него токов Ii=I1·i, где 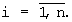 Осуществляется процесс нормировки значения шкал экспериментальной ВАХ (фиг.2) и последующий анализ ведется с применением алгоритма расчета информативных параметров, описанного выше.
Осуществляется процесс нормировки значения шкал экспериментальной ВАХ (фиг.2) и последующий анализ ведется с применением алгоритма расчета информативных параметров, описанного выше.
В процессе поиска оптимальных режимных параметров предложенного способа построено ряд ВАХ на основе перебора значений тока, где номер выбранного значения тока, относительно которого происходит перебор, является постоянным до последнего значения (i=1; j=i+1,... ,n). Аналогично выбирается следующее значение, относительно которого также осуществляется перебор токов (i=2; j=i+1,... ,n). Этот процесс осуществляется до тех пор, пока постоянным значением окажется предпоследний номер тока (i=n-1; j=n).
Погрешность адекватности моделируемых ВАХ с экспериментом рассчитывается для каждой пары токов и напряжений по среднеквадратическому отклонению σ :
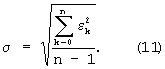
где 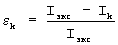 - относительная погрешность отклонения модели ВАХ от экспериментальных данных.
- относительная погрешность отклонения модели ВАХ от экспериментальных данных.
На фиг.2 показано оптимальное сближение кривых в режимных условиях i=6, j=11-13, где среднеквадратическое отклонение не превышает 2%.
Докажем эффективность по точности по отношению к прототипу.
Для доказательства эффективности определим погрешности, возникающие при нахождении температуры с использованием дифференциальных сопротивлений Ri и по диффузионному сопротивлению Rd, которые по закону Ома определяются отношениями:
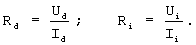
В аналогах и прототипе измеряют сопротивления, не принимая во внимание нелинейность ВАХ, тогда в ходе эксперимента, например, при пропускании токов I1 или I2 сопротивления 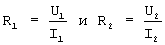 отличны между собой и не соответствуют диффузионному сопротивлению Rd, которое не зависит от величины пропускаемого тока. Визуально эффективность можно оценить на фиг.3, где видно, что диффузионное сопротивление Rd, в отличие от дифференциального сопротивления Ri, не зависит от проходящего через терморезистор тока.
отличны между собой и не соответствуют диффузионному сопротивлению Rd, которое не зависит от величины пропускаемого тока. Визуально эффективность можно оценить на фиг.3, где видно, что диффузионное сопротивление Rd, в отличие от дифференциального сопротивления Ri, не зависит от проходящего через терморезистор тока.
На базе предложенного способа определим коэффициент информативности электрофизических характеристик терморезистора, используя следующий аналитический подход:
введем обозначения для кратных токов 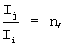 принимая
принимая 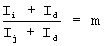 и перепишем систему (6 и 8) с учетом введенных обозначений
и перепишем систему (6 и 8) с учетом введенных обозначений
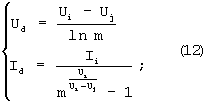
согласно закону Ома из формулы (2) найдем Rd, поделив первое уравнение системы на второе:
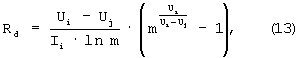
после несложных преобразований, с учетом того, что Ri=Ui/Ii, получим:
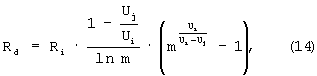
тогда коэффициент информативности:
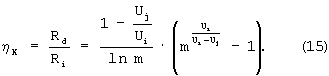
Найдем диффузионное сопротивление Rd по закону Ома и по формуле (14) (Rd*), определяемые характеристики и используемые параметры для минимального, максимального и среднего значений измерительного тока и занесем в таблицу:
Анализ таблицы показывает, что дифференциальное сопротивление R не является информативным параметром температуры, меняя свое значение при изменении протекающего тока, в то время как диффузионное сопротивление Rd остается стабильным. Верность утверждения Rd≅Rd* наглядно показывает, что данный информативный параметр невосприимчив к воздействию текущих электрофизических характеристик (фиг.3).
Докажем эффективность разработанного способа по отношению к прототипу путем сравнения методических погрешностей определения температуры. С целью упрощения рассуждении запишем методическую погрешность прототипа и предлагаемого метода в общем виде:
- для прототипа dT1=а1∂R1+а2∂R2+а3∂R3+а4∂I;
- для разработанного способа dT2=b∂ Rd.
Введем коэффициент эффективности по точности:
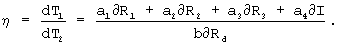
Каждое из слагаемых погрешности прототипа и погрешность предлагаемого метода являются величинами одного порядка, поэтому η =4. Таким образом, методическая погрешность предлагаемого метода в 4 раза ниже погрешности прототипа.
При исследованиях использовались полупроводниковые бусинковые терморезисторы типа СТ1-18 и СТЗ-18. Реализация предлагаемого способа осуществлена на базе измерительно-вычислительной системы для контроля комплекса теплофизических свойств твердых материалов “ТЕМП-075”, построенной на базе персонального компьютера, что позволило за счет повышения точности измерения температуры повысить точность контроля комплекса теплофизических свойств.
Таким образом, предлагаемый способ определения температуры по диффузионному сопротивлению терморезистора, в отличие от известных решений, позволяет повысить эффективность по точности измерения температуры в 4 раза.
| название | год | авторы | номер документа |
|---|---|---|---|
| СПОСОБ ДЛЯ ОПРЕДЕЛЕНИЯ ВЛАЖНОСТИ ДРЕВЕСИНЫ | 2002 |
|
RU2240545C2 |
| СПОСОБ ДЛЯ ОПРЕДЕЛЕНИЯ ВЛАЖНОСТИ КАПИЛЛЯРНО-ПОРИСТЫХ МАТЕРИАЛОВ | 2000 |
|
RU2187098C2 |
| СПОСОБ ОПРЕДЕЛЕНИЯ ВЛАЖНОСТИ КАПИЛЛЯРНО-ПОРИСТЫХ МАТЕРИАЛОВ | 2003 |
|
RU2240546C1 |
| СПОСОБ ИДЕНТИФИКАЦИИ КОМПЛЕКСА ТЕПЛОФИЗИЧЕСКИХ ХАРАКТЕРИСТИК ТВЕРДЫХ МАТЕРИАЛОВ | 2004 |
|
RU2263306C1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ ТЕМПЕРАТУРЫ ПОЛУПРОВОДНИКОВЫМ ТЕРМОРЕЗИСТОРОМ | 2004 |
|
RU2269102C1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ НЕРАВНОМЕРНОСТИ ТЕМПЕРАТУРНОГО ПОЛЯ | 1992 |
|
RU2051342C1 |
| СПОСОБ И УСТРОЙСТВО ОПРЕДЕЛЕНИЯ ВЛАЖНОСТИ ПО ВОЛЬТ-АМПЕРНОЙ ХАРАКТЕРИСТИКЕ МАТЕРИАЛОВ | 2008 |
|
RU2374633C1 |
| СПОСОБ ИЗМЕРЕНИЯ ПОСЛЕДОВАТЕЛЬНОГО СОПРОТИВЛЕНИЯ БАЗЫ ПОЛУПРОВОДНИКОВОГО ДИОДА | 2013 |
|
RU2548925C1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ УРОВНЯ ЖИДКОСТИ И УСТРОЙСТВО ДЛЯ ЕГО ОСУЩЕСТВЛЕНИЯ | 2006 |
|
RU2336502C2 |
| СПОСОБ ОПРЕДЕЛЕНИЯ ВЛАЖНОСТИ КАПИЛЛЯРНО-ПОРИСТЫХ МАТЕРИАЛОВ | 2007 |
|
RU2341788C1 |
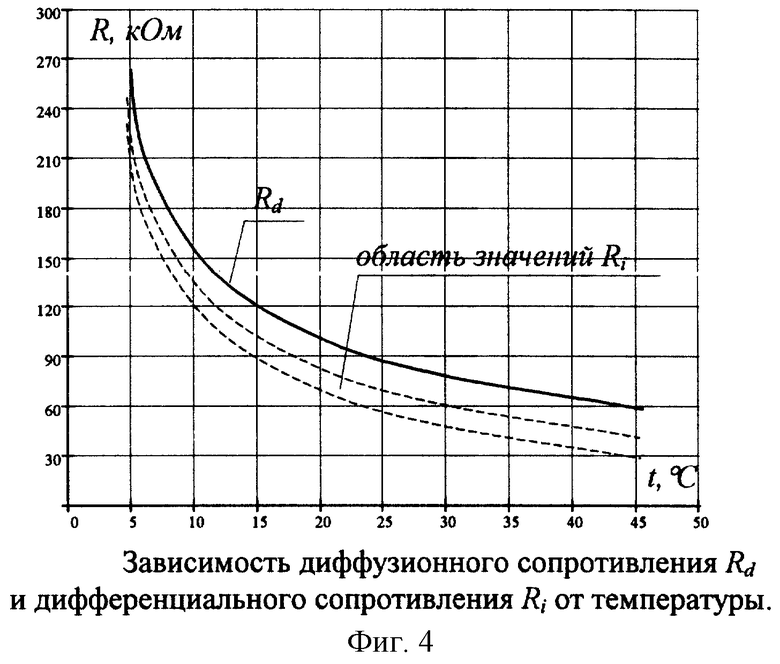
Изобретение относится к измерительной технике, в частности к измерению температур. Способ включает пропускание тока через размещенный в контролируемой среде полупроводниковый терморезистор и определение его сопротивления. Сопротивление терморезистора определяют путем измерения на нем падения напряжения. После чего изменяют пропускаемый ток и измеряют второе значение падения напряжения. По двум токам и напряжениям находят диффузионное сопротивление терморезистора, по которому определяют температуру. Изобретение позволяет повысить точность определения температуры. 1 з.п. ф-лы, 1 табл., 4 ил.
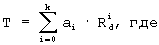
Rd - диффузионное сопротивление терморезистора,
ai - постоянные коэффициенты,
k - степень полинома,
значения коэффициентов аi определяются в процессе аппроксимации значений диффузионного сопротивления, полученных при известных температурах по оптимальным режимным параметрам, которые находят при сопоставлении экспериментальной и моделируемых вольтамперных характеристик для различных соотношений токов, для которых погрешность минимальна.
| Способ определения температуры | 1986 |
|
SU1364911A1 |
| Способ определения температуры | 1973 |
|
SU481795A1 |
| ПОЛУПРОВОДНИКОВЫЙ ДАТЧИК ТЕМПЕРАТУРЫ | 1994 |
|
RU2090953C1 |
| СПОСОБ ДЛЯ ОПРЕДЕЛЕНИЯ ВЛАЖНОСТИ КАПИЛЛЯРНО-ПОРИСТЫХ МАТЕРИАЛОВ | 2000 |
|
RU2187098C2 |
Авторы
Даты
2005-04-10—Публикация
2003-06-16—Подача