Изобретение можно отнести к классу информационно-измерительных устройств и может быть использовано в самых различных областях науки и техники.
Рассмотрим временной ряд 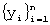 , который представляет собой последовательность N значений y1, y2, ... , yn некоторой функции ƒ (ti), полученные в равноотстоящие моменты времени t1, t2, ... , tn.
, который представляет собой последовательность N значений y1, y2, ... , yn некоторой функции ƒ (ti), полученные в равноотстоящие моменты времени t1, t2, ... , tn.
Рассматриваемый временной ряд представляет собой аддитивную смесь некоторой систематической составляющей (детерминированная составляющая, полезный сигнал, тренд) S(t) и случайной составляющей (шум, погрешности измерений и др.) u(t):
y(t)=S(t)+u(t).
Относительно случайной составляющей u(t) будем предполагать, что Мut=0, Dut=σ 2 и, кроме того, ее значения в разные моменты времени некоррелированы (т.е. cov(ut,us)=0, t≠ S), хотя эти условия не являются существенными.
Основная решаемая задача - выделение полезного сигнала (тренда) в условиях недостаточной априорной информации о статистических характеристиках аддитивного шума и функции полезного сигнала (тренда) при наличии единственной реализации измеряемого процесса. Априорно предполагается известным, что выделяемая функция полезного сигнала является гладкой ([1], с.61), т.е. выделяемая функция на некоторых не слишком малых интервалах времени может быть достаточно точно аппроксимирована некоторым многочленом P(t). Рассматриваемая задача может возникать: в работе приемо-передающих устройств дальней или космической связи; в экономических расчетах при выделении основной тенденции развития каких-либо показателей и принятии решения об удалении результатов воздействия случайных факторов; в метеорологии, при измерении различных характеристик состояния атмосферы и т.д.
В случаях, когда полезный сигнал имеет вполне определенную структуру (т.е. функция S(t) принадлежит известному классу функций) и определяется конечным числом параметров, используются параметрические методы оценивания (сюда входят методы регрессионного анализа, основу которых составляет классическая теория наименьших квадратов). В тех же случаях, когда отсутствует информация о функции полезного сигнала, для оценивания тренда используются непараметрические методы, такие как сглаживание. Известно, что наилучший способ сглаживания - усреднение по ансамблю (семейству) реализации yj(t) (или yjt) исходного процесса ([2], с.35-36). Однако на практике, как правило, мы располагаем лишь единственной реализацией измеряемого процесса. В этом случае целесообразно пользоваться способами сглаживания (фильтрации), которые “работают” с единственной реализацией, либо способами, позволяющими “размножать” имеющуюся реализацию изучаемого процесса.
Известен такой способ выделения полезной составляющей как усреднения по ансамблю реализаций ([3], с.22). Для его применения необходимо иметь N реализаций исходного процесса. Каждая реализация представляет собой временной ряд результатов 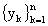 наблюдений (измерений) процесса y(t), полученных в n равноотстоящих моментов времени t1, t2, ... , tn. Эти результаты наблюдений можно представить в виде матрицы реализаций:
наблюдений (измерений) процесса y(t), полученных в n равноотстоящих моментов времени t1, t2, ... , tn. Эти результаты наблюдений можно представить в виде матрицы реализаций:

где yj1, yj2, ... , yjn - j-я реализация исходного процесса, представляющая собой сумму функции полезного сигнала S(t) и шумовой составляющей u(t).
Способ усреднения по ансамблю реализаций предполагает:
- запоминание N входных реализаций Уj1, yj2, ... , yjn, (j=1, 2, ... , N), полученных в n равноотстоящих моментов времени;
- вычисление среднего арифметического значения этих реализаций в каждый момент времени;
- замену значений исходных реализаций случайного процесса полученной усредненной оценкой.
При применении данного способа вычисляются средние арифметические по столбцам матрицы реализаций (1):
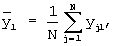
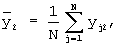 ... ,
... , 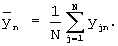
В результате получаем сглаженный временной ряд 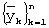 .
.
Признаки способа-аналога, совпадающие с признаками заявляемого технического решения, следующие: дискретизация сигнала по времени, запоминание цифрового сигнала, нахождение среднего арифметического, замена исходного временного ряда сглаженным.
Недостатками известного способа-аналога являются:
- для применения способа-аналога необходимо иметь несколько реализаций.
Причины, препятствующие достижению требуемого технического результата, заключаются в следующем: особенности способа-аналога не позволяют обрабатывать единственную реализацию исходного процесса, а также не позволяют применить его к уже сглаженным значениям (в отличие от способов, “работающих” с единственной реализацией); результат обработки нескольких реализаций существенно зависит от количества реализаций.
Структурная схема устройства, реализующего рассмотренный способ-аналог, содержит для n реализаций n буферных блоков, входы которых являются информационными входами устройства, а выходы подключены через коммутаторы ко входам блоков хранения результатов измерений, выходы которых подсоединены ко входам арифметического устройства также через коммутаторы, выходы которых подключены ко входу регистра хранения тренда, а выход регистра является информационным выходом устройства.
В заявке №2000127308 от 30.10.2000 (патент №2207622 опубликован в Б.И. №18 27.06.2003 г.) был предложен метод размножения оценок при ограниченном объеме априорных данных и единственной реализации исходного процесса.
Рассматриваемый способ предполагает:
1) запоминание входной реализации 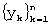 ;
;
2) разбиение временного отрезка [t1,tn] (длительность реализации) на m промежутков, случайными числами, подчиненых равномерному закону распределения;
3) проверку того, что промежутки разбиения включают не менее l значений исходной реализации;
4) нахождение для каждого промежутка разбиения коэффициентов 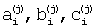 аппроксимирующего полинома
аппроксимирующего полинома 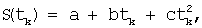 (k∈ [1,n], j∈ [1,N], i∈ [1,m]) методом наименьших квадратов;
(k∈ [1,n], j∈ [1,N], i∈ [1,m]) методом наименьших квадратов;
5) повторение процедур, описанных в пунктах 2) - 4) N раз;
6) нахождение сглаживающей (аппроксимирующей) функции как среднего арифметического значения “кусочно-квадратичных” аппроксимирующих функций в каждом сечении tk, полученных для каждого разбиения временного отрезка [t1, tn].
Сначала с помощью генератора (датчика) случайных чисел, равномерно распределенных в интервале (0;1), получают m-1 чисел 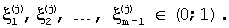 Затем по формуле у=t1+(tn-t1)х, осуществляющей отображение промежутка (0;1) на промежуток (t1;tn), получают соответствующее разбиение числами
Затем по формуле у=t1+(tn-t1)х, осуществляющей отображение промежутка (0;1) на промежуток (t1;tn), получают соответствующее разбиение числами 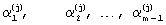 промежутка (t1;tn) на m частей, где
промежутка (t1;tn) на m частей, где
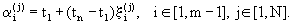
Промежутки разбиения обозначают:
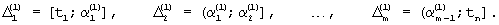
Проверяется выполнение условия: каждый промежуток 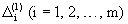 должен содержать не менее l значений из набора {y1, y2, ... , yn}. Если это условие не выполнено, то отбрасываются числа
должен содержать не менее l значений из набора {y1, y2, ... , yn}. Если это условие не выполнено, то отбрасываются числа  и генерируем следующие.
и генерируем следующие.
Наличие этого условия означает, что, по крайней мере, l m≤ n. Далее, повторяется N раз процедура разбиения отрезка [t1,tn] на m промежутков случайной длины (с проверкой вышеуказанного условия). В результате получается набор разбиений временного отрезка [t1;tn]:
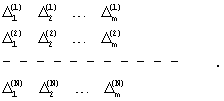
Для каждого промежутка 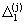 методом наименьших квадратов находим оценки
методом наименьших квадратов находим оценки 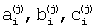 коэффициентов аппроксимирующего полинома a+bt+ct2.
коэффициентов аппроксимирующего полинома a+bt+ct2.
Результатом действия описанного алгоритма (“размножения” оценок 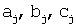 коэффициентов этого полинома) будет набор определенных на отрезке [t1;tn] сглаживающих функций S(j)(t) (j=1, 2, ... , N), каждая из которых является “кусочно-квадратичной”:
коэффициентов этого полинома) будет набор определенных на отрезке [t1;tn] сглаживающих функций S(j)(t) (j=1, 2, ... , N), каждая из которых является “кусочно-квадратичной”:
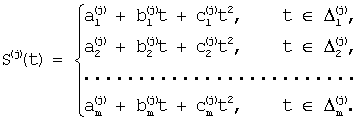
Аппроксимирующая функция 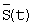 находится как среднее арифметическое функций
находится как среднее арифметическое функций 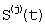 (по всем N разбиениям отрезка [t1;tn]):
(по всем N разбиениям отрезка [t1;tn]): 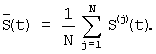
Признаки способа-аналога, совпадающие с признаками заявляемого технического решения, следующие: дискретизация сигнала по времени, запоминание цифрового сигнала, аппроксимация по методу наименьших квадратов, нахождение среднего арифметического, замена исходного временного ряда сглаженным.
Недостатками известного способа являются:
- для обработки реализации необходимо запоминать всю выборку;
- невозможно провести обработку исходной реализации в реальном масштабе времени;
- рост ошибки выделения с неограниченным увеличением размножения исходной реализации.
Причины, препятствующие достижению требуемого технического результата, заключаются в следующем:
- из-за того, что перед обработкой исходной реализации необходимо иметь в наличии всю выборку, возможности использования метода размножения оценок в реальном масштабе времени крайне ограничены;
- предположение о том, что на каждом интервале разбиения исходной реализации полезный сигнал можно описать полиномом второй степени, приводит к росту ошибки выделения полезного сигнала и росту шумовой составляющей, с уменьшением длины интервала разбиения.
Структурная схема устройства, реализующего рассмотренный способ-аналог, содержит буферный блок, вход которого является информационным входом устройства, а выход подключен к информационным входам блоков хранения результатов измерений, к управляющим входам которых через коммутаторы подключены выходы блока разбиения исходной реализации, который содержит генератор случайных чисел, распределенных по равномерному закону, выход которого подключен ко входу блока устранения связанных значений, выход которого подсоединен ко входу блока ранжирования, к выходу которого подключен регистр хранения выборки случайных чисел, чей выход является информационным выходом блока разбиения; к выходам блоков хранения подключены входы блоков аппроксимации, выходы которых подключены ко входам регистров хранения оценок исходной функции, выходы которых подключены ко входам арифметического суммирующего устройства, выход которого подключен ко входу регистра хранения тренда, чей выход является информационным выходом устройства. Синхронность работы устройства обеспечивается генератором тактовых импульсов.
Известен способ экспоненциального сглаживания временных рядов ([4], с.262). Его особенность заключается в том, что в процедуре нахождения сглаженного значения используются только предшествующие значения исходного ряда, взятые с определенным “весом”, причем “вес” измерения уменьшается по мере удаления его от момента времени, для которого определяется сглаженное значение ряда. Для применения этого способа достаточно одной реализации 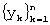 исходного процесса.
исходного процесса.
Способ экспоненциального сглаживания предполагает запоминание входной реализации y1, y2, ... , yn случайного процесса, выбор параметра сглаживания α , характеризующего “вес” текущего (самого нового) наблюдения (0<α <1), выбор величины Q0, характеризующей начальные условия, вычисление сглаженных значений временного ряда по рекуррентным формулам
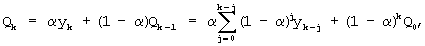
(где k=1, 2, ... , n), замену исходных значений y1, y2, ... , yn временного ряда сглаженными значениями Q1, Q2, ... , Qn.
Сначала при применении экспоненциального сглаживания для временного ряда определяется начальное значение Q0 сглаженного ряда и параметр сглаживания α . В зависимости от выбора параметра α (в частности, если α близко к нулю) начальное значение Q0 сглаженного ряда может оказать существенное воздействие на результат обработки временного ряда. В практических рекомендациях по применению экспоненциального сглаживания ([5], с.156) предлагается брать в качестве начального значения Q0 либо первое значение ряда, либо среднее арифметическое нескольких первых членов ряда, например, Q0=(y1+y2+y3)/3. С другой стороны, влияние выбора уменьшается с увеличением длины ряда и становится несущественным при большом числе измерений (наблюдений).
После выбора Q0 и α вычисляются сглаженные значения временного ряда, которыми заменяются исходные значения:
Q1=α y1+(1-α )Q0,
Q2=α y2+(1-α )Q1=α y2+α (1-α )y1+(1-α )2Q0,
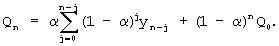
Признаки способа-аналога, совпадающие с признаками заявляемого технического решения, следующие: дискретизация сигнала по времени, запоминание цифрового сигнала, представление значений сглаженного ряда в виде многочлена от значений исходного ряда, замена исходного временного ряда сглаженным.
Недостатками известного способа являются:
- неопределенность выбора параметра сглаживания α ; в отдельных случаях предлагается (необоснованно) определять величину α исходя из длины сглаживаемого ряда: α =2/(n+1) ([5], с.156); на практике параметр сглаживания часто отыскивают с помощью “сетки”, т.е. возможные значения параметра разбиваются “сеткой” с определенным шагом; например, рассматривается сетка значений от α =0,1 до α =0,9 с шагом 0,1, а затем выбирается α , для которого сумма квадратов остатков является минимальной;
- неопределенность выбора начального значения Q0, что часто приводит к необходимости многократного повторного применения способа экспоненциального сглаживания при другом выборе α и Q0.
Причины, препятствующие достижению требуемого технического результата, заключаются в следующем: способ экспоненциального сглаживания не является “самонастраивающимся” способом, поскольку выбор параметров α и Q0 осуществляется субъективно и зависит от опыта и практических навыков исследователя.
Структурная схема устройства, реализующего рассмотренный способ-аналог, содержит генератор тактовых импульсов, коммутатор, блок управления, регистр хранения, сумматор, блок умножения, выходной регистр хранения сглаженного ряда исходной реализации.
Существует метод медианного сглаживания ([6], с.56). Для применения этого способа достаточно одной реализации y1, y2, ... , yn исходного процесса. Основное достоинство медианного сглаживания - устойчивость к выбросам. В основе способа лежит вычисление скользящей медианы.
Способ медианного сглаживания предполагает следующую последовательность шагов:
- запоминание отрезка 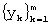 реализации временного ряда
реализации временного ряда 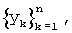 где m<n (ширины “скользящего окна");
где m<n (ширины “скользящего окна");
- ранжирование (упорядочивание по возрастанию) выбранного отрезка ряда 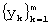 ;
;
- определение медианы 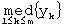 (центрального члена) ранжированного отрезка временного ряда;
(центрального члена) ранжированного отрезка временного ряда;
- замену центрального (до ранжирования) из значений выбранного отрезка 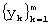 найденной медианой
найденной медианой 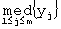 ;
;
- сдвиг “скользящего окна” на одно значение вправо (т.е. выбор вместо отрезка 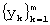 ряда другого отрезка
ряда другого отрезка 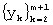 из
из 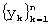 ).
).
Описанный алгоритм выполняется до тех пор, пока не будет достигнут правый конец временного ряда 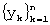 .
.
Априорно для временного ряда определяется интервал сглаживания, т.е. “скользящее окно” протяженностью m отсчетов, где m<n. Количество отсчетов рекомендуется брать нечетным (m=2р+1), хотя медианное сглаживание можно проводить и при четной ширине “окна”. Для первых m значений временного ряда вычисляется их медиана; это будет сглаженное значение временного ряда, находящееся в середине интервала сглаживания. При этом заметим, что медиана ряда во временном интервале определяется как центральный член вариационного ряда - последовательности значений ряда, входящих в этот временной интервал, упорядоченной по возрастанию, а именно операция медианной фильтрации последовательности значений сигнала характеризуется соотношением
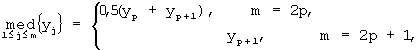
где фиксированное значение р=1, 2, ... определяет ширину “окна”. Затем интервал сглаживания сдвигается на одно значение вправо, повторяется вычисление медианы и снова центральное значение интервала сглаживания заменяется вычисленной медианой. Таким образом, для того чтобы найти значение скользящей медианы в точке с порядковым номером j, вычисляется медиана значений ряда во временном интервале [j-p, j+p].
Признаки способа-аналога, совпадающие с признаками заявляемого технического решения, следующие: дискретизация сигнала по времени, запоминание только первых m значений цифрового сигнала, выделение временных отрезков, замена исходного временного ряда сглаженным.
Недостатками известного способа являются:
- первые р и последние р значений ряда теряются (не сглаживаются);
- вследствие нелинейности нельзя строго разграничить влияние медианной фильтрации на сигнал и шум (при наличии свойства линейности такая задача решается сравнительно просто);
- медианное сглаживание можно рассматривать как эффективный метод предварительной обработки временного ряда (сигнала) в условиях импульсных помех, но при отсутствии явных выбросов этот метод приводит к более “зубчатым” кривым (чем сглаживание скользящим средним);
- медианное сглаживание не позволяет использовать веса, т.е. адаптивные возможности у этого метода отсутствуют.
Причины, препятствующие достижению требуемого технического результата, заключаются в следующем:
- если ширина окна сглаживания равна 2p+1, то первые p и последние p значений ряда не подвергаются обработке;
- при медианной фильтрации не выполняется свойство аддитивности (а значит, медианная фильтрация не обладает свойством линейности):
med{yj (1)+yj (2)}≠ med{yj (1)}+mеd{yj (2)};
- медианный фильтр сохраняет монотонно изменяющиеся участки сигнала (и поэтому при малой ширине “скользящего окна” сглаживание недостаточно эффективно).
Структурная схема устройства, реализующего рассмотренный способ-аналог, содержит генератор тактовых импульсов, коммутатор, блок управления, регистр хранения, блок ранжирования, блок выбора среднего значения, выходной регистр, где хранится сглаженный ряд исходной реализации.
Из известных способов выделения тренда наиболее близким по технической сущности к заявляемому является способ скользящего среднего ([5], с.154, 170). Это один из самых простых методов механического сглаживания временных рядов. Рассмотрим этот способ в качестве прототипа. Для применения этого метода достаточно одной реализации у1, y2, ... , yn исходного процесса.
Способ скользящего среднего предполагает следующую последовательность шагов:
- запоминание реализации 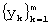 случайного процесса, где m<n (ширины “скользящего окна”) ряда
случайного процесса, где m<n (ширины “скользящего окна”) ряда 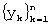 , для которых будет вычисляться среднее значение
, для которых будет вычисляться среднее значение 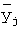 по ряду
по ряду 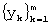 ;
;
- замена центрального из значений 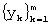 найденным средним
найденным средним 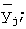
- сдвиг “скользящего окна” на одно значение вправо (т.е. выбор вместо отрезка 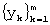 ряда следующего отрезка
ряда следующего отрезка 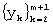 из
из 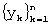 ).
).
Описанный алгоритм выполняется до тех пор, пока не будет достигнут правый конец ряда 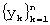 .
.
Априорно для временного ряда определяется интервал сглаживания m, т.е. натуральное число m<n. Если необходимо сгладить мелкие беспорядочные колебания, то интервал сглаживания берут по возможности больше; интервал сглаживания уменьшают, если нужно сохранить более мелкие колебания. Для первых m значений временного ряда вычисляется их среднее арифметическое значение; это будет сглаженное значение временного ряда, находящееся в середине интервала сглаживания. Затем интервал сглаживания сдвигается на одно значение вправо, повторяется вычисление среднего арифметического и т.д. По этой причине этот способ называют методом скользящего среднего, т.к. при выполнении процедуры происходит скольжение окном шириной 2р+1 по всему ряду от начала до конца. Ширину окна обычно берут нечетной, т.к. теоретическое значение рассчитывается для центрального значения. Отсюда получаем формулу для вычисления сглаженных значений временного ряда:
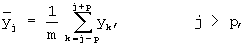
где р=(m-1)/2 (m - нечетное число).
В результате такой процедуры получаются n-m+1 сглаженных значений ряда. Среднее квадратичное отклонение σ m сглаженного ряда равно:
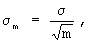
где через σ обозначено среднее квадратичное отклонение исходных членов ряда. Поэтому чем больше интервал сглаживания, тем сильнее усреднение данных и менее изменчива выделяемая тенденция. Чаще всего сглаживание производят по трем, пяти и семи членам исходного ряда. При этом следует учитывать следующие особенности скользящего среднего: если рассмотреть ряд с периодическими колебаниями постоянной длины, то при сглаживании на основе скользящего среднего с интервалом сглаживания, равным или кратным периоду, колебания полностью устраняться. Нередко сглаживание на основе скользящего среднего столь сильно преобразует ряд, что выделенная тенденция проявляется лишь в самых общих чертах, а более мелкие, но важные для анализа детали (волны, изгибы и т.д.) исчезают. После сглаживания мелкие волны могут иногда поменять направление на противоположное - на месте “пиков” появляются “ямы” и наоборот. Все это требует осторожности в применении простого скользящего среднего и заставляет искать более точные методы выделения тренда.
Признаки способа-прототипа, совпадающие с признаками заявляемого технического решения, следующие: дискретизация сигнала по времени, запоминание только первых m значений цифрового сигнала, замена исходного временного ряда сглаженным.
Недостатками известного способа являются:
- первые p и последние p значений ряда теряются (не сглаживаются); этот недостаток особенно заметно сказывается в случае, когда длина ряда невелика, или же если необходимо провести экстраполяцию за пределы рассматриваемого временного интервала с целью решения задачи прогнозирования;
- способ недостаточно эффективен, поскольку не учитывает мелкие детали тренда;
- применяют для временных рядов, имеющих линейную тенденцию;
- использование данного способа вызывает автокорреляцию остатков, даже если она отсутствовала в исходном ряду, т.е. в сглаженном временном ряде возникает взаимозависимость соседних значений ряда (эффект Слуцкого-Юла).
Причины, препятствующие достижению требуемого технического результата, заключаются в следующем:
- если ширина окна сглаживания равна 2p+1, то первые p и последние р значений ряда не подвергаются обработке;
- поскольку центральное значение окна (отрезка) сглаживания вычисляется как среднее арифметическое соседних, то новые значения временного ряда становятся зависимыми;
- замена центрального значения окна (отрезка) сглаживания средним арифметическим соседних значений будет заметным (существенным) лишь в том случае, когда центральное значение существенно отклоняется от среднего, и практически не скажется на результате, когда центральное значение колеблется около среднего значения.
Структурная схема устройства, реализующего рассмотренный способ-аналог, содержит генератор тактовых импульсов, коммутатор, блок управления, первый и второй регистры, сумматор, выход которого подключен к информационному входу первого регистра, выход которого соединен с первым информационным входом коммутатора, второй выход которого является входом устройства (авт. св. №1 193 688).
Существует разновидность рассмотренного способа-прототипа - способ взвешенного скользящего среднего. Он отличается от предыдущего способа сглаживания тем, что значения временного ряда, входящие в интервал сглаживания, суммируются с разными весами ([5], с.155). Здесь для вычисления сглаженных значений временного ряда 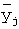 применяется формула взвешенного среднего арифметического:
применяется формула взвешенного среднего арифметического:
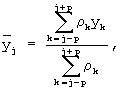
причем веса ρ k определяются с помощью метода наименьших квадратов. Эти веса рассчитываются для различных степеней аппроксимирующего полинома и различных интервалов сглаживания. Так, для полиномов второго и третьего порядков числовая последовательность весов при интервале сглаживания m=5 имеет вид {-3;12;17;12;-3}, а при m=7 имеет вид {-2;3;6;7;6;3;-2}.
Для взвешенного скользящего среднего недостатком по-прежнему является невозможность сгладить значения временного ряда на концах. Кроме того, применение этого способа без отрицательных весов вызывает автокорреляцию остатков, т.е. имеет место эффект Слуцкого-Юла.
Предлагаемый способ исходит из наличия единственной дискретной реализации исследуемого процесса 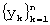 , где yk=y(tk), k=1, 2, ... ,n, представляющего собой сумму полезной и шумовой составляющих, т.е. y(t)=S(t)+u(t). Априорная информация об исследуемом процессе заключается в том, что на выбранном интервале m<n/2 полезный сигнал достаточно точно описывается полиномом второй степени:
, где yk=y(tk), k=1, 2, ... ,n, представляющего собой сумму полезной и шумовой составляющих, т.е. y(t)=S(t)+u(t). Априорная информация об исследуемом процессе заключается в том, что на выбранном интервале m<n/2 полезный сигнал достаточно точно описывается полиномом второй степени:
S(t)=a+bt+ct2
Рассматриваемый способ предполагает следующую последовательность шагов:
- запоминание реализации 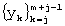 (j=1, 2, ... , n-m+1) случайного процесса, где m<n/2 (m - ширина “скользящего окна”), на котором будет производиться аппроксимация полиномом второй степени по методу наименьших квадратов;
(j=1, 2, ... , n-m+1) случайного процесса, где m<n/2 (m - ширина “скользящего окна”), на котором будет производиться аппроксимация полиномом второй степени по методу наименьших квадратов;
- замена ряда 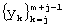 значениями аппроксимирующей функции
значениями аппроксимирующей функции 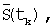 в результате чего получается ряд
в результате чего получается ряд 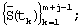
- сдвиг “скользящего окна” на одно значение вправо (т.е. выбор вместо отрезка 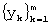 ряда следующего отрезка
ряда следующего отрезка 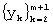 из
из 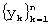 );
);
- повторение процедур, описанных выше, пока не будет достигнут правый конец ряда, т.е. j=n-m+1.
Сначала определяем ширину “скользящего окна” m<n/2, на котором будет производиться аппроксимация полиномом второй степени по методу наименьших квадратов. Определив число m, запоминаем первый отрезок исходного ряда 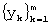 . Из условия минимума суммы квадратов отклонения:
. Из условия минимума суммы квадратов отклонения:
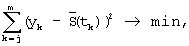
определяем коэффициенты 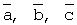 аппроксимирующего полинома:
аппроксимирующего полинома:
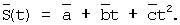
Находим оценку аппроксимирующей функции 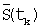 на отрезке ряда
на отрезке ряда 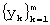 и запоминаем ее. Сдвигаем на один отсчет “скользящее окно” и получаем новый отрезок исходного ряда
и запоминаем ее. Сдвигаем на один отсчет “скользящее окно” и получаем новый отрезок исходного ряда 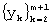 . Заново производим аппроксимацию полиномом второй степени по методу наименьших квадратов, находим оценку
. Заново производим аппроксимацию полиномом второй степени по методу наименьших квадратов, находим оценку 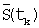 и запоминаем ее. Таким образом, мы получим r=n-m+1 отрезков исходного ряда и r их оценок. Отрезки исходного ряда можно представить в виде матрицы размерностью m× r:
и запоминаем ее. Таким образом, мы получим r=n-m+1 отрезков исходного ряда и r их оценок. Отрезки исходного ряда можно представить в виде матрицы размерностью m× r:
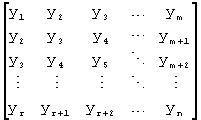
Тогда матрица оценок запишется следующим образом:

Находим аппроксимирующую функцию 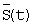 усреднением по побочным диагоналям:
усреднением по побочным диагоналям:

Сущность предлагаемого способа и устройства поясняется чертежом.
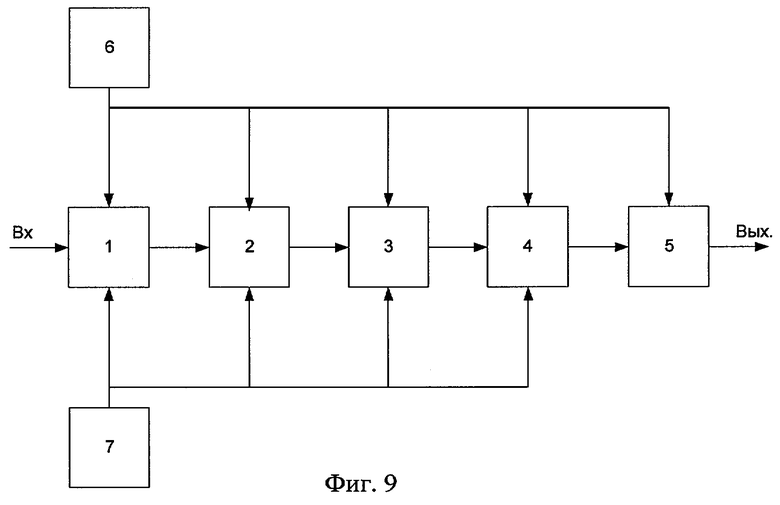
Устройство, для выделения тренда результатов измерений физической величины методом скользящего размножения оценок (“КРОТ”) его единственной дискретной исходной реализации, содержит (фиг.9) буферный блок хранения результатов измерения (напряжения, тока, сопротивления, температуры и т.д.) 1, вход которого является информационным входом устройства, выход которого подключен к блоку задержки 2, выход которого подключен ко входу блока аппроксимации по методу наименьших квадратов 3, выход которого является информационным входом блока хранения оценок тренда 4, выход которого подключен ко входу блока усреднения 5, выход которого является информационным выходом устройства, к дополнительным информационным входам блоков 1, 2, 3, 4, 5 подключен блок управления 6. Синхронность работы устройства обеспечивается генератором тактовых импульсов 7.
Устройство для выделения тренда работает следующим образом. В буферный блок записывается первый m значений исходной дискретной реализация результатов измерений (m является шириной “скользящего окна”), значение m задается блоком управления. По окончании записи в буферный блок производится аппроксимация поступивших m значений по методу наименьших квадратов (МНК) полиномом второй степени.
Полученные оценки первых m значений исходной дискретной реализации записываются в блок хранения оценок тренда. После каждого последующего поступившего на вход значения результата измерений в блоке аппроксимации по МНК производится оценка последних m отсчетов, записанных в буферном блоке, и запись их в блок хранения тренда со сдвигом в один отсчет относительно начала реализации. Полученные оценки по методу среднего арифметического суммируются в каждый момент времени дискретизации исходной дискретной реализации результатов измерений, и окончательная оценка тренда поступает на выход устройства.
Такой метод выделения тренда реализуется следующим образом. В блоке управления 6 задается ширина скользящего окна m, информация о котором поступает на дополнительные информационные входы регистра хранения измерений 1, блока задержки 2, блока аппроксимации 3, блока хранения оценок 4 и блока усреднения 5. В регистр хранения измерений 1 записывается первые m значений дискретной последовательности результатов измерений. С помощью блока задержки 2 осуществляется задержка поступления данных в блок 3 на m-1 тактов. После получения m-го значения данные блока регистра хранения 1 поступают в блок 3, где осуществляется их аппроксимация по методу наименьших квадратов полиномом второй степени. Оценки, полученные в блоке 3, записываются в блок 4. После каждого последующего поступившего на вход значения результата измерений в блоке аппроксимации по МНК производится оценка последних m отсчетов и запись их со сдвигом в один отсчет относительно начала реализации в блок 4. Данные, записанные в блоке 4, поступают в блок 5, где по методу среднего арифметического в каждый момент времени определяется усредненная оценка тренда, выход блока 5 является информационным выходом устройства.
Технический результат - уменьшение погрешности оценки функции полезного сигнала (тренда) при ограниченном объеме априорной информации о статистических характеристиках аддитивного шума и функции полезного сигнала (тренда), которая достигается с помощью обработки в реальном масштабе времени единственной исходной реализации результатов измерений “размножением” оценок аппроксимирующих полиномов и последующего усреднения полученных оценок функции полезного сигнала.
Технические особенности применения предлагаемого способа на этапе “размножения” оценок аппроксимирующих полиномов состоят в следующем. Пусть yk - значения временного ряда, попавшие в промежуток 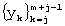 (j=1, 2, ... , n-m+1) и отвечающие отсчетам времени tk. Тогда оценки a, b, с коэффициентов аппроксимирующего полинома:
(j=1, 2, ... , n-m+1) и отвечающие отсчетам времени tk. Тогда оценки a, b, с коэффициентов аппроксимирующего полинома:
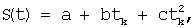
определяются из условия минимизации суммы квадратов отклонений элементов ряда yk, попавших в промежуток 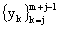 (j=1, 2, ... , n-m+1), от значений полинома S(tk) в соответствующих точках, т.е. из условия
(j=1, 2, ... , n-m+1), от значений полинома S(tk) в соответствующих точках, т.е. из условия
Σ (yk-S(tk))2→min,
где суммирование распространяется на все значения уk, попавшие в указанный промежуток разбиения. Для определения оценок 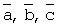 получаем систему линейных уравнений
получаем систему линейных уравнений
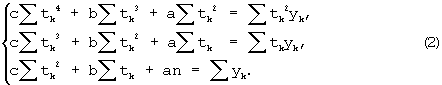
Вводя обозначения:
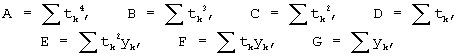
перепишем систему (2) (относительно неизвестных а, b, с) в виде
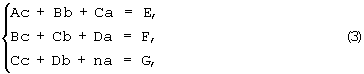
Решая систему (3), получим:
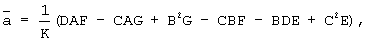
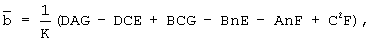
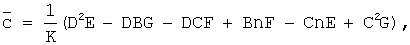
где K=AD2-AnC+B2n-2BCD+C3.
Посредством имитационного моделирования было установлено, что предлагаемый способ обладает следующими преимуществами:
- Средняя квадратичная погрешность оценки функции полезного сигнала (тренда) значительно меньше погрешностей оценки при использовании других ранее рассмотренных способов при ограниченном объеме априорной информации об исследуемом процессе.
- Прелагаемый способ позволяет осуществлять обработку исходных данных в реальном масштабе времени.
- Оценка функции полезного сигнала (тренда) независимо от вида исходной функции полезного сигнала (тренда) и статистических характеристик аддитивного шума и достаточно полно отображает основные закономерности изменения полезного сигнала (тренда).
- Отсутствие краевых эффектов.
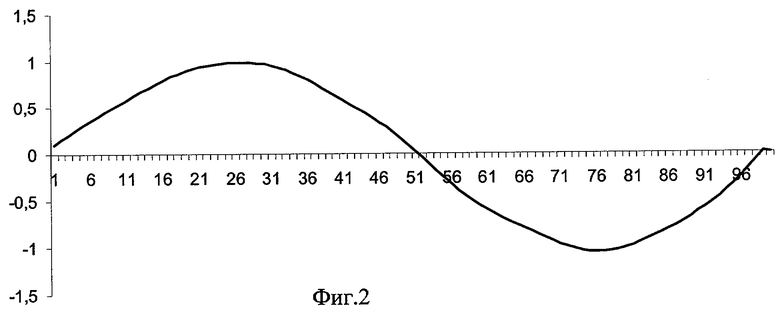
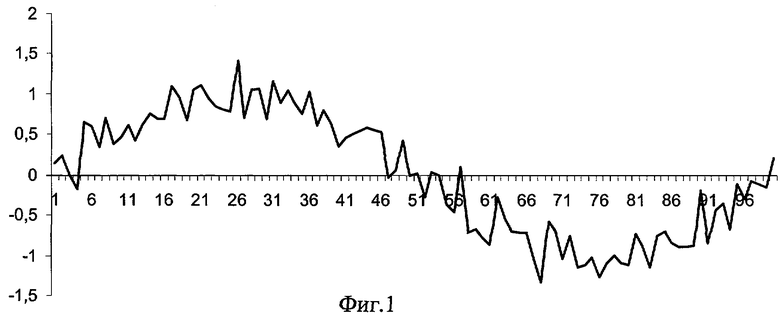
На фиг.1 приведена исходная функция измеряемого процесса, представляющая собою аддитивную смесь гармонического сигнала (тренда) и шума, распределенного по закону Гаусса. Как видно из исследуемой модели, исходная функция полезного сигнала (тренда) существенно отличается от функции, описывающейся полиномом второй степени. Несмотря на это полученная оценка, приведенная на фиг.2 практически полностью повторяет исходную функцию. Обработка проводилась при следующих исходных данных: ширина окна m равна 16.
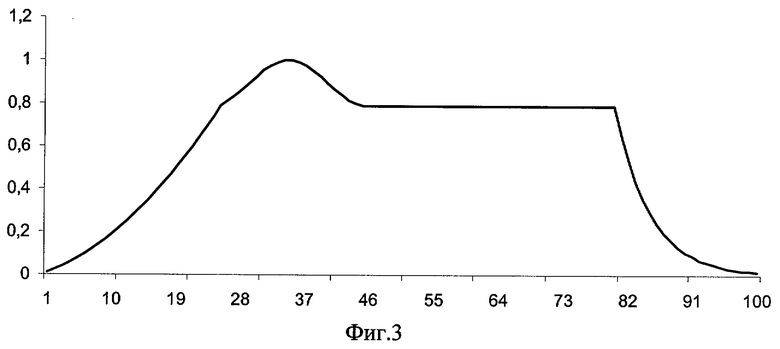
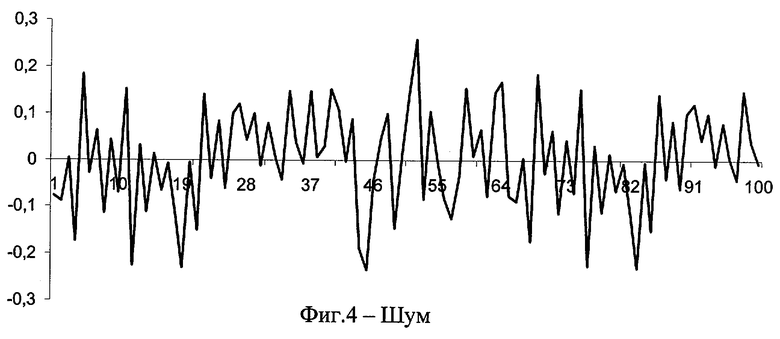
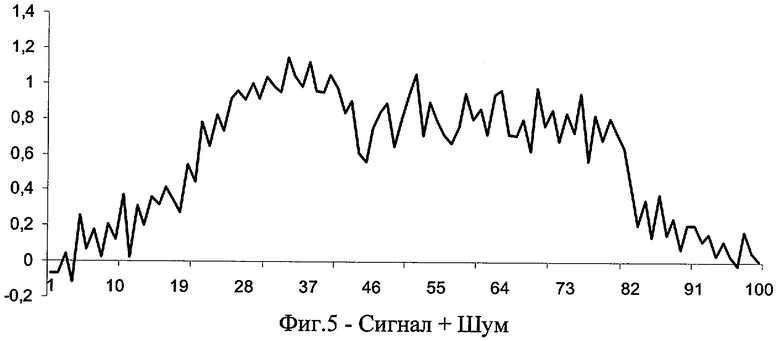
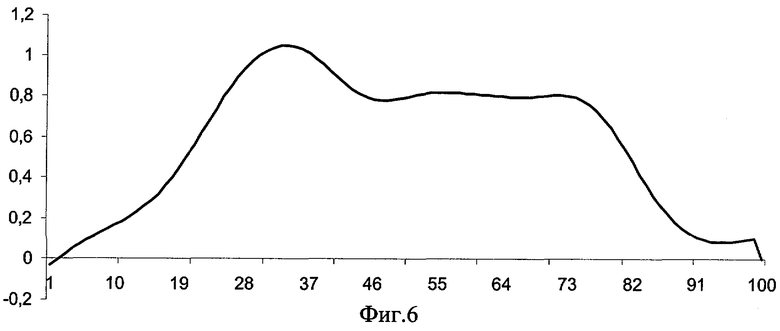
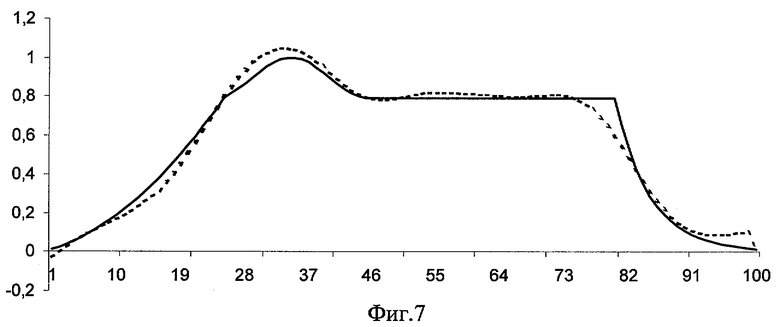
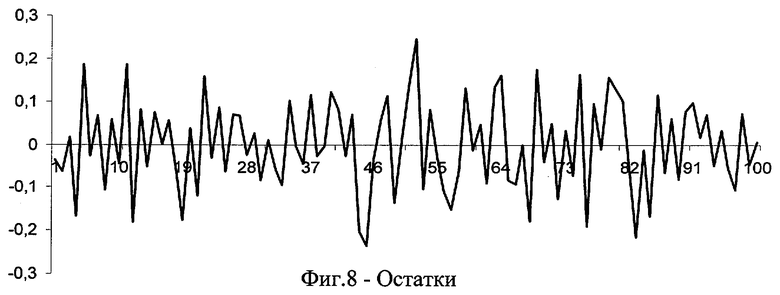
На фиг.3 приведен сложный сигнал, состоящий из параболы, синусоиды, постоянной и экспоненты; на фиг.4 показана шумовая составляющая, а на фиг.5 - сигнал с аддитивным шумом. В результате обработки сигнала (фиг.6) заявляемым способом (“КРОТ”) выделен полезный сигнал (тренд), сравнение которого с исходным сигналом приведено на фиг.7. График остатков приведен на фиг.8.
Список литературы
1. Андерсон Т. Статистический анализ временных рядов. - М.: Мир, 1976. - 765 с.
2. Переверткин С.М. и др. Бортовая телеметрическая аппаратура космических летательных аппаратов. - М.: Машиностроение, 1977. - 208 с.
3. Бендат Дж., Пирсол А. Прикладной анализ случайных данных. - М.: Мир, 1989. - 540 с.
4. Колемаев В.А., Калинина В.Н. Теория вероятностей и математическая статистика. - М.: ИНФРА-М, 1997. - 302 с.
5. Экономико-математические методы и прикладные модели: Учеб. пособие для вузов./ Под ред. В.В.Федосеева. - М.: ЮНИТИ, 1999. - 399 с.
6. Васильев В.Н., Гуров И.П. Компьютерная обработка сигналов в приложении к интерферометрическим системам. - СПб.: БХВ - Санкт-Петербург, 1998. - 240 с.
7. Дубров А.М., Мхитарян B.C., Трошин Л.И. Многомерные статистические методы: Учебник. - М.: Финансы и статистика, 1998. -352 с.
| название | год | авторы | номер документа |
|---|---|---|---|
| СПОСОБ ВЫДЕЛЕНИЯ ТРЕНДА ПУТЕМ РАЗМНОЖЕНИЯ ОЦЕНОК ЕГО ЕДИНСТВЕННОЙ ИСХОДНОЙ РЕАЛИЗАЦИИ (РАЗОЦ) И УСТРОЙСТВО ДЛЯ ЕГО ОСУЩЕСТВЛЕНИЯ | 2000 |
|
RU2207622C2 |
| УСТРОЙСТВО ВЫДЕЛЕНИЯ ПОЛЕЗНОГО СИГНАЛА НА ФОНЕ ШУМОВ С МИНИМИЗАЦИЕЙ КОНЦЕВЫХ ЭФФЕКТОВ СПОСОБОМ КУСОЧНОГО РАЗМНОЖЕНИЯ ОЦЕНОК | 2007 |
|
RU2365980C1 |
| СПОСОБ УМЕНЬШЕНИЯ ПОГРЕШНОСТИ ОЦЕНКИ ПОЛЕЗНОЙ СОСТАВЛЯЮЩЕЙ В УСЛОВИЯХ АПРИОРНОЙ НЕОПРЕДЕЛЕННОСТИ И УСТРОЙСТВО, ЕГО РЕАЛИЗУЮЩЕЕ | 2013 |
|
RU2541916C1 |
| УСТРОЙСТВО ДЛЯ ВЫДЕЛЕНИЯ ПОЛЕЗНОГО СИГНАЛА С ЛИКВИДАЦИЕЙ ТОЧЕК РАЗРЫВА ПРИ ИСПОЛЬЗОВАНИИ СПОСОБА РАЗМНОЖЕНИЯ ОЦЕНОК | 2006 |
|
RU2313826C1 |
| УСТРОЙСТВО ДЛЯ ВЫДЕЛЕНИЯ ПОЛЕЗНОГО СИГНАЛА ПРИ ОДНОСТОРОННЕМ ЗАКОНЕ РАСПРЕДЕЛЕНИЯ АДДИТИВНОЙ ШУМОВОЙ СОСТАВЛЯЮЩЕЙ | 2007 |
|
RU2368002C2 |
| СПОСОБ ПОВЫШЕНИЯ ТОЧНОСТИ АППРОКСИМАЦИИ ПРИ ВЫДЕЛЕНИИ ПОЛЕЗНОГО СИГНАЛА В УСЛОВИЯХ АПРИОРНОЙ НЕОПРЕДЕЛЕННОСТИ И УСТРОЙСТВО, ЕГО РЕАЛИЗУЮЩЕЕ | 2013 |
|
RU2541919C1 |
| АДАПТИВНЫЙ ДВУМЕРНЫЙ СПОСОБ РАЗМНОЖЕНИЯ ОЦЕНОК И УСТРОЙСТВО, ЕГО РЕАЛИЗУЮЩЕЕ | 2010 |
|
RU2461874C2 |
| УСТРОЙСТВО ДЛЯ ОБРАБОТКИ ИЗОБРАЖЕНИЙ НА ОСНОВЕ ДВУМЕРНОГО СПОСОБА РАЗМНОЖЕНИЯ ОЦЕНОК | 2009 |
|
RU2406130C1 |
| ПОСЛЕДОВАТЕЛЬНО-ПАРАЛЛЕЛЬНОЕ УСТРОЙСТВО ОБРАБОТКИ СИГНАЛОВ | 2007 |
|
RU2321053C1 |
| ИТЕРАЦИОННЫЙ СПОСОБ ВЫДЕЛЕНИЯ ТРЕНДА СИГНАЛА ПРИ НАЛИЧИИ ГРУБЫХ ИЗМЕРЕНИЙ, ОСНОВАННЫЙ НА МЕТОДЕ НАИМЕНЬШИХ МОДУЛЕЙ | 2005 |
|
RU2290688C2 |
Изобретение относится к информационно-измерительным устройствам, вычислительной технике, устройствам систем управления. Техническим результатом является уменьшение погрешности оценки функции полезного сигнала (тренда) при ограниченном объеме априорной информации о статистических характеристиках аддитивного шума и функции полезного сигнала (тренда). Для этого устройство содержит блок хранения результатов измерения физической величины, блок задержки, блок усреднения, блок управления, блок генератора тактовых импульсов, блок аппроксимации по методу наименьших квадратов, блок хранения оценок тренда. 9 ил.
Устройство для выделения тренда методом скользящего размножения оценок его единственной исходной реализации, содержащее блок хранения результатов измерения физической величины, вход которого является информационным входом устройства, а выход подсоединен к входу блока задержки, блок усреднения, выход которого является информационным выходом устройства, блок управления, выход которого подключен к управляющим входам блоков хранения результатов измерения физической величины, задержки, усреднения, блок генератора тактовых импульсов, выход которого подключен к синхронизирующим входам блоков хранения результатов измерения физической величины, задержки, усреднения, отличающееся тем, что в устройство введен блок аппроксимации по методу наименьших квадратов, вход которого подключен к выходу блока задержки, а выход подключен к входу блока хранения оценок тренда, выход которого подключен к входу блока усреднения, к управляющим входам блоков аппроксимации по методу наименьших квадратов и хранения оценок тренда подключен выход блока управления, а к синхронизирующим входам блоков аппроксимации по методу наименьших квадратов и хранения оценок тренда подключен выход блока генератора тактовых импульсов.
| СПОСОБ ВЫДЕЛЕНИЯ ТРЕНДА ПУТЕМ РАЗМНОЖЕНИЯ ОЦЕНОК ЕГО ЕДИНСТВЕННОЙ ИСХОДНОЙ РЕАЛИЗАЦИИ (РАЗОЦ) И УСТРОЙСТВО ДЛЯ ЕГО ОСУЩЕСТВЛЕНИЯ | 2000 |
|
RU2207622C2 |
| RU 2001119757 A1, 27.06.2003 | |||
| Устройство для прогнозирования надежности, учитывающее тренд случайного воздействия | 1977 |
|
SU714362A1 |
| Устройство для вычисления скользящего среднего | 1984 |
|
SU1193688A1 |
| СПОСОБ АНАЛИЗА НЕСТАЦИОНАРНОГО ПРОЦЕССА | 1998 |
|
RU2159956C2 |
| RU 98116830 A1, 20.08.2000 | |||
| US 4534041 A, 08.06.1985. | |||
Авторы
Даты
2005-07-27—Публикация
2003-11-03—Подача