Предлагаемое изобретение относится к способам статистической обработки информации и может быть использовано для выделения полезного сигнала при обработке сигналов с импульсными выбросами.
Пусть наблюдается временной ряд y1, y2,...,yn, представляющий собой последовательность результатов измерений. Рассматриваемая модель временного ряда представляет собой сумму некоторой систематической составляющей (детерминированная составляющая, полезный сигнал, тренд) S(t) и случайной составляющей (шум, погрешности измерений и др.)
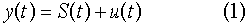
Относительно случайной составляющей принимается стандартное предположение о нулевом среднем Eu(f)=0 и конечной дисперсии Du(t)<∞.
Основная решаемая задача - выделение полезного сигнала (тренда) в условиях недостаточной априорной информации о статистических характеристиках аддитивного шума, о наличии импульсных выбросов в сигнале, а также о функции полезного сигнала (тренда), при условии наличия для обработки единственной реализации измеряемого процесса. Априорно предполагается известным, что исходная функция полезного сигнала является гладкой по Андерсону ([2], с.61), т.е. исходная функция на некоторых, не слишком малых интервалах времени может быть достаточно точно аппроксимирована полиномом не выше второй степени.
Известным аналогом предлагаемого способа является способ обработки по методу наименьших квадратов [10]. Метод наименьших квадратов в задачах оценивания неизвестных параметров состоит в том, что из всех возможных оценок выбирается оценка, минимизирующая норму (сумму квадратов компонент) вектора ошибок (вектора невязок). Общим со способом-аналогом является достаточность единственной дискретной реализации процесса, а также предположение относительно полезного сигнала, состоящее в том, что он с допустимой точностью приближается полиномом некоторой степени на всем участке аппроксимации.
Для описания аналога рассмотрим систему уравнений второго порядка, то есть квадратичный полином, как один из основных возможных вариантов приближенного описания полезного сигнала:
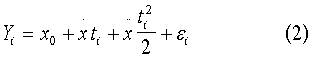
где ti=iΔt (Δt - временной шаг).
Способ-аналог состоит в построении оценок коэффициентов аппроксимирующего полинома методом наименьших квадратов для полиномиальной модели.
В матричном виде модель имеет вид:

МНК-оценка коэффициентов аппроксимирующего полинома вычисляется по формуле:

Соответствующие матрицы метода являются следующими:
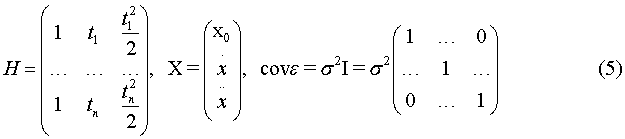
Признаки способа-аналога, совпадающие с признаками предлагаемого способа: дискретизация сигнала по времени; нахождение МНК-оценки сигнала; замена исходного сигнала сглаживающим полиномом.
Недостатки способа-аналога:
- необходимо знать аналитическое выражение для функции полезного сигнала;
- на концах участков аппроксимации погрешность аппроксимации существенно возрастает;
- оценки полезного сигнала по методу наименьших квадратов чувствительны к наличию выбросов в сигнале.
Из известных способов выделения тренда наиболее близким к заявляемому способу является Итерационный способ выделения тренда (Патент RU 2222824 С2. - 7 G 06 F 17/18) [9], принятый в качестве прототипа.
Прототип предполагает наличие единственной дискретной реализации исследуемого процесса y1, y2,...,yn, где yj=y(tj), j=1, 2, ...,n, представляющего собой сумму полезного сигнала и шума, т.е. y(t)=S(t)+u(t).
Априорная информация об исследуемом процессе заключается в том, что на подынтервалах Δj⊂[t1, tn] полезный сигнал с допустимой погрешностью (описывается полиномом второй степени [2, с.456]:
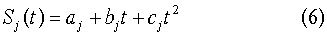
Способ-прототип состоит в выполнении следующих операций:
1) обнаружение участков нестационарности f(yj) внутри интервала [t1, tn], где находится входная реализация y1, y2,...,yn,
2) нахождение для обнаруженных участков нестационарности f(yj) коэффициентов аппроксимирующего полинома Sj(t)=aj+bjt+cjt2 методом наименьших квадратов;
3) запоминание полученного аппроксимирующего полинома S(tj) как оценки входной реализации первого шага итерации;
4) получение остатков путем вычисления разности входной реализации и оценки первого шага итерации поразрядно y(tj)-S1(tj);
5) итерационная обработка остатков по пунктам 1-4, причем оценки второго S2(tj) и последующих Sl(tj) шагов итерации поразрядно суммируются с результатами первого шага для уточнения оценки исследуемого процесса;
6) число необходимых шагов итерации ограничивается, с одной стороны, погрешностью способа обнаружения участков нестационарности [10; с.15-18], с другой стороны, возможностью перерегулирования (связанной с аппроксимацией аддитивной шумовой составляющей).
Алгоритм итерационного способа выделения тренда изображен на фиг.1. Сходимость по вероятности выделенного итерационным методом сигнала к истинному сигналу обладает свойством:
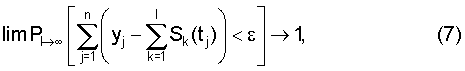
где l - число итерационных шагов, ε - погрешность выделения (порог признания процесса нестационарным).
Таким образом, полученную итерационным методом оценку реализации можно записать в следующем виде:
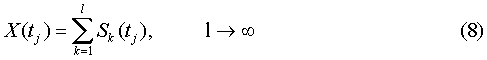
Видно, что оценка, полученная итерационным способом, является асимптотически состоятельной с точностью до порога признания процесса нестационарным.
В операторной форме оценка записывается следующим образом:
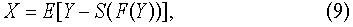
где Х - выходная оценка, функционал определения нестационарности разности исходной реализации и полученных оценок.
Оценка среднего квадратичного отклонения аппроксимирующей функции находится по формуле:
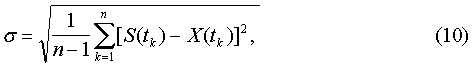
где S(t} - исходная функция полезного сигнала.
Недостатки способа-прототипа:
- способ ориентирован, с использованием полиномиальной модели, на анализ обрабатываемой последовательности на нестационарность, причем стационарные участки подвергаются обработке обычным методом наименьших квадратов, принятым за прототип, а нестационарные -итерационно с применением того же метода в каждой итерации;
- различие в методах обработки на различных участках сигнала обусловливает зависимость результатов обработки от субъективного уровня критерия нестационарности, усложнение процедуры обработки, а также порождает на различных участках пограничный эффект Слупкого-Юла;
- не обеспечивается робастность процедуры обработки при наличии в серии обрабатываемых данных выбросов, так называемых "сорных" измерений [3]; в соответствии с описанием способа-прототипа, он соотносит такие выбросы с проявлением нестационарности и осуществляет статистическое сглаживание по квадратичной модели, описывающей выброс, то есть без снижения его влияния.
Предлагаемый итерационный способ выделения тренда при наличии грубых измерений-выбросов, основанный на методе наименьших модулей, предполагает заимствованные из прототипа:
- обработку измерений в группах по 2m+1 измерений;
- определение значения выборочной медианы для каждой группы;
- решение задачи с применением МНК с n измерениями на полиномиальных моделях, отражающих закономерности изменения тренда;
- итеративную процедуру вычисления оценок, выполняемую до достижения модулем разности между двумя последовательными приближениями заданного порогового уровня.
Задачей предлагаемого способа является выделение тренда при наличии грубых измерений без специальной процедуры предварительной отбраковки замеров.
Итерационный способ выделения тренда сигнала при наличии грубых измерений, основанный на методе наименьших модулей, реализованном в процедуре вариационно-взвешенных квадратичных приближений метода наименьших квадратов, заключающийся в том, что исходную реализацию нестационарного случайного процесса, представляющую сумму полезного сигнала и шума, поступающую в буферный блок, обрабатывают в блоке аппроксимации на интервале длины 2m+1 по методу наименьших квадратов, в результате чего получают начальное приближение оценки полезного сигнала, с ее итерационным уточнением, отличающийся тем, что обработка осуществляется на скользящем интервале, а последующие приближения полезного сигнала, в каждом положении скользящего интервала, формируются в блоке последовательной аппроксимации в результате итеративного применения метода наименьших квадратов к полученным оценкам с весовыми матрицами метода вариационно-взвешенных квадратичных приближений до тех пор, пока разница между последовательными приближениями, поступающими в регистр хранения оценок, не станет меньше заданного порогового уровня.
Новыми в предлагаемом способе являются переход от последовательности групп по 2m+1 измерений к скользящему окну размером 2m+1 измерений и робастная комбинация МНК и МНМ, обеспечивающая оптимальность процедуры обработки для распределений как Гаусса, так и Лапласа, без априорного знания, к какому из этих типов распределений относится обрабатываемый сигнал, и приводящая для этих распределений к оценкам квазиправдоподобия с минимальной дисперсией. Эти оценки являются состоятельными и эффективными [9].
Таким образом, предлагаемый способ, наряду с основным назначением - уменьшением влияния стохастического рассеяния при обработке первичных данных измерения, оказывается одновременно средством подавления влияния сорных измерений, без применения специальной процедуры отбраковки [3, 4, 5, 6, 8].
В связи с этим, применением предлагаемого способа решается проблемный вопрос практики - отбраковки сорных измерений с отказом от специальной процедуры такой отбраковки в пользу предлагаемого способа, основанного на робастной комбинации МНК и МНМ.
Для обеспечения процедурной реализации с минимальными объемом вычислений и затратами времени метод вариационно-взвешенных квадратичных приближений реализуется по схеме, приведенной на фиг.1:.
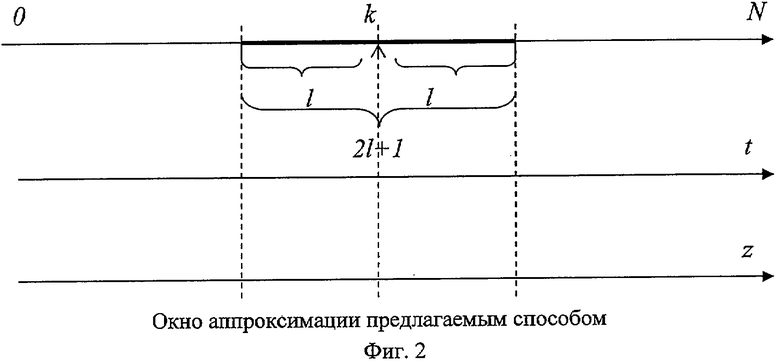
1) на множестве N членов временного ряда вводится скользящее симметричное окно размером 2l+1 (значения сигнала на котором записываются в буферный блок) с центральной точкой аппроксимации - нормальным местом, индексируемым номером k, с возможностью изменения положения на мерном интервале в очевидных пределах k=l+1,...,N-l (фиг.2);
2) в буферном блоке формируются векторы:
узлов времени

и измерений на окне

3) формируется матрица размерности (2k+l)×m членов полинома степени m:
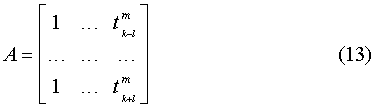
4) в блоке последовательной аппроксимации, представляющем собой последовательность из регистра хранения весовой матрицы, вычитателя, блока вычисления разностей последовательных приближений, блока аппроксимации по методу наименьших квадратов и регистра хранения остатков, формируется начальное приближение

5) вместо функции (7) вводится ее аналог вида
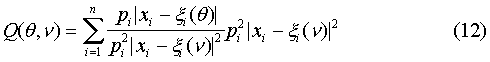
с векторной весовой функцией
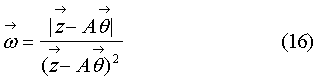
6) поскольку последовательные приближения могут вызвать появление в знаменателе нуля, эта весовая функция преобразовывается добавлением к знаменателю пренебрежимо малого для результата значения ε≈10-k (k=3-7):
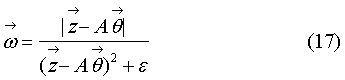
7) на начальном шаге итераций значение 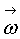 вычисляется при θ0;
вычисляется при θ0;
8) теперь задача отыскания минимизирующего векторного параметра коэффициентов 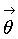 сводится к методу взвешенных наименьших квадратов, осуществляемому в блоке последовательной аппроксимации:
сводится к методу взвешенных наименьших квадратов, осуществляемому в блоке последовательной аппроксимации:

9) осуществляется переход к пункту (5) с формированием начального приближения первой итерации при 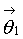 ;
;
10) итерационные вычисления по пунктам 5-9 выполняются до тех пор, пока модуль разности 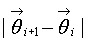 между двумя последовательными приближениями в буферном блоке блока вычисления разностей последовательных приближений не станет меньше заданного порогового уровня;
между двумя последовательными приближениями в буферном блоке блока вычисления разностей последовательных приближений не станет меньше заданного порогового уровня;
11) итоговая оценка обобщенного измерения в точке аппроксимации - нормальном месте tk отыскивается путем свертки

Таким образом, МНМ реализуется с помощью процедуры МНК, что определяет вычислительную компактность и быстродействие способа.
Практическая значимость предлагаемого способа состоит в его стандартности (метод взвешенных наименьших квадратов), быстрой сходимости к оценкам МНМ и сравнительной вычислительной простоте, которая дает сокращение времени вычислений в 50-60 раз по сравнению со стандартной процедурой вычисления оценок МНМ.
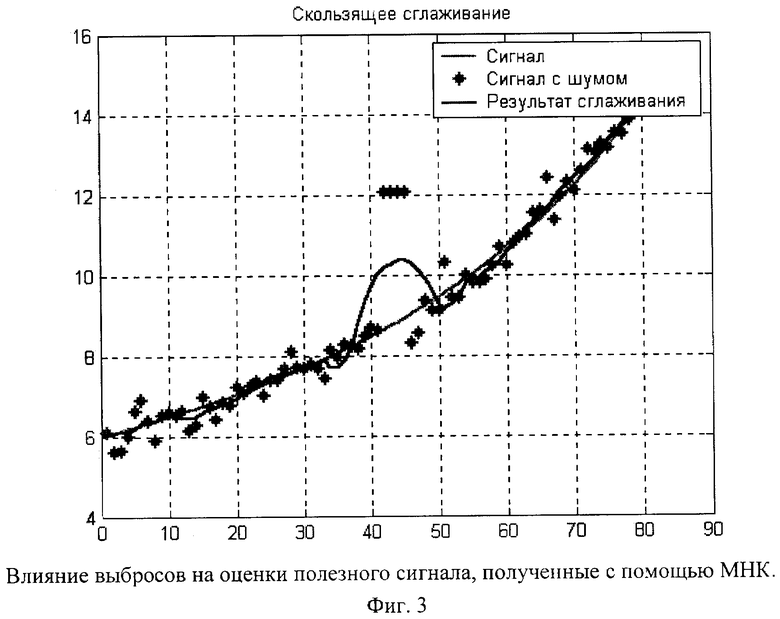
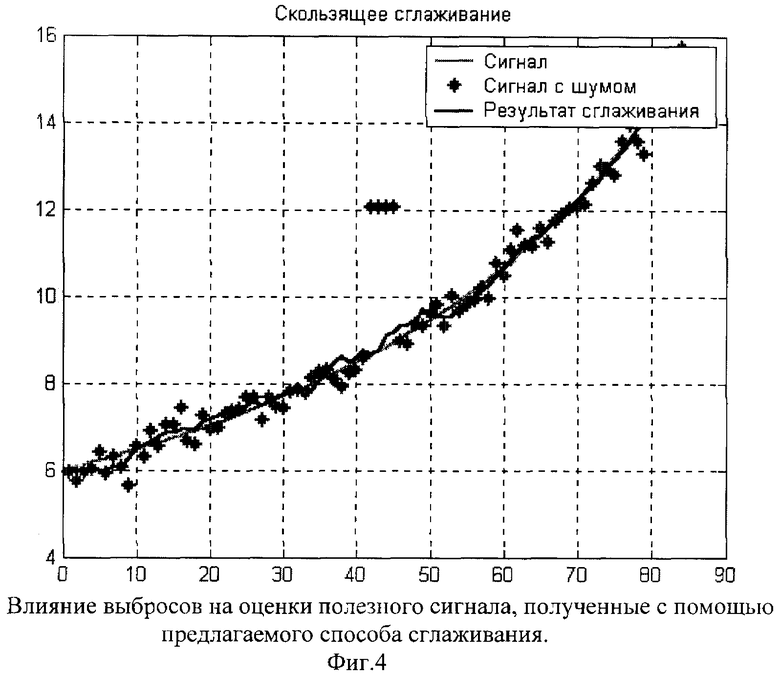
Результаты реализации сглаживании измерений с временной моделью изменения по закону арктангенса приводятся:
- для способа-прототипа на фиг.3;
- предлагаемым способом на фиг.4.
Итоговые СКО полученных оценок для МНК и МНМ соотносятся как 3:1.
Таким образом, предлагаемый способ демонстрирует устойчивость к сорным измерениям, с существенным снижением СКО обобщенных оценок - существенным преимуществом даже над уже испытанным способом квадратичного сглаживания на середину мерного интервала, а также приемлемыми затратами времени на обработку данных.
Список литературы
1. Акимов П.С. Обнаружители радиосигналов. Радио и связь., 1989. - 288 с.: ил.
2. Андерсон Т. Статистический анализ временных рядов. - М: Мир, 1976. - 765 с.
3. Бендат Дж., Пирсол А. Прикладной анализ случайных данных. - М.: Мир, 1989. - 540 с.
4. Васильев В.Н., Гуров И.П. Компьютерная обработка сигналов в приложении к интерферометрическим системам. - СПб.: БХВ - Санкт-Петербург, 1998. - 240 с.
5. Дубров А.М., Мхитарян B.C., Трошин Л.И. Многомерные статистические методы: Учебник. - М.: Финансы и статистика, 1998. - 352 с.
6. Колемаев В.А., Калинина В.Н. Теория вероятностей и математическая статистика. - М.: ИНФРА - М, 1997. - 302 с.
7. Мудров В.И., Кушко В.Л. Методы обработки измерений: Квазиправдоподобные оценки. - М.: Радио и связь, 1983. - 304 с.
8. Экономико-математические методы и прикладные модели: Учеб. пособие для вузов. / Под ред. В.В. Федосеева. - М.: ЮНИТИ, 1999. - 399 с.
9. RU 2222824 С2. - 7 G 06 F 17/18 - прототип.
10. SU 4639668/00-24 88 12 05/A1 1824479 - аналог.
| название | год | авторы | номер документа |
|---|---|---|---|
| СПОСОБ ПОВЫШЕНИЯ ТОЧНОСТИ АППРОКСИМАЦИИ ПРИ ВЫДЕЛЕНИИ ПОЛЕЗНОГО СИГНАЛА В УСЛОВИЯХ АПРИОРНОЙ НЕОПРЕДЕЛЕННОСТИ И УСТРОЙСТВО, ЕГО РЕАЛИЗУЮЩЕЕ | 2013 |
|
RU2541919C1 |
| СПОСОБ ВЫДЕЛЕНИЯ ТРЕНДА МЕТОДОМ СКОЛЬЗЯЩЕГО РАЗМНОЖЕНИЯ ОЦЕНОК ТРЕНДА ЕГО ЕДИНСТВЕННОЙ ИСХОДНОЙ РЕАЛИЗАЦИИ ("КРОТ") И УСТРОЙСТВО ДЛЯ ЕГО ОСУЩЕСТВЛЕНИЯ | 2003 |
|
RU2257610C1 |
| СПОСОБ ВЫДЕЛЕНИЯ ТРЕНДА ПУТЕМ РАЗМНОЖЕНИЯ ОЦЕНОК ЕГО ЕДИНСТВЕННОЙ ИСХОДНОЙ РЕАЛИЗАЦИИ (РАЗОЦ) И УСТРОЙСТВО ДЛЯ ЕГО ОСУЩЕСТВЛЕНИЯ | 2000 |
|
RU2207622C2 |
| СПОСОБ УМЕНЬШЕНИЯ ПОГРЕШНОСТИ ОЦЕНКИ ПОЛЕЗНОЙ СОСТАВЛЯЮЩЕЙ В УСЛОВИЯХ АПРИОРНОЙ НЕОПРЕДЕЛЕННОСТИ И УСТРОЙСТВО, ЕГО РЕАЛИЗУЮЩЕЕ | 2013 |
|
RU2541916C1 |
| СПОСОБ ПРОГНОЗИРОВАНИЯ РЕЗУЛЬТАТОВ ИЗМЕРЕНИЙ И УСТРОЙСТВО ЕГО РЕАЛИЗУЮЩЕЕ | 2008 |
|
RU2374682C2 |
| ПОСЛЕДОВАТЕЛЬНО-ПАРАЛЛЕЛЬНОЕ УСТРОЙСТВО ОБРАБОТКИ СИГНАЛОВ | 2007 |
|
RU2321053C1 |
| АДАПТИВНЫЙ ДВУМЕРНЫЙ СПОСОБ РАЗМНОЖЕНИЯ ОЦЕНОК И УСТРОЙСТВО, ЕГО РЕАЛИЗУЮЩЕЕ | 2010 |
|
RU2461874C2 |
| УСТРОЙСТВО ВЫДЕЛЕНИЯ ПОЛЕЗНОГО СИГНАЛА НА ФОНЕ ШУМОВ С МИНИМИЗАЦИЕЙ КОНЦЕВЫХ ЭФФЕКТОВ СПОСОБОМ КУСОЧНОГО РАЗМНОЖЕНИЯ ОЦЕНОК | 2007 |
|
RU2365980C1 |
| Способ выделения тренда нестационарного процесса с адаптацией интервалов аппроксимации | 2016 |
|
RU2645273C1 |
| УСТРОЙСТВО ДЛЯ ВЫДЕЛЕНИЯ ПОЛЕЗНОГО СИГНАЛА С ЛИКВИДАЦИЕЙ ТОЧЕК РАЗРЫВА ПРИ ИСПОЛЬЗОВАНИИ СПОСОБА РАЗМНОЖЕНИЯ ОЦЕНОК | 2006 |
|
RU2313826C1 |
Изобретение относится к способам статистической обработки информации. Техническим результатом является уменьшение влияния рассеяния измерений. Согласно способу получают начальное приближение оценки полезного сигнала с ее итерационным уточнением, при этом последующие приближения полезного сигнала, в каждом положении скользящего интервала, формируются в блоке последовательной аппроксимации в результате итеративного применения к полученным оценкам метода наименьших квадратов, реализованного в процедуре вариационно-взвешенных квадратичных приближений с векторной весовой функцией метода наименьших модулей, до тех пор, пока разница между последовательными приближениями, поступающими в регистр хранения оценок, не станет меньше заданного порогового уровня. 4 ил.
Итерационный способ выделения тренда сигнала, заключающийся в том, что исходную реализацию нестационарного случайного процесса, представляющую сумму полезного сигнала и шума, поступающую в буферный блок, обрабатывают в блоке последовательной аппроксимации на скользящем интервале длины 2m+1 по методу наименьших квадратов, в результате чего получают начальное приближение оценки полезного сигнала, с ее итерационным уточнением, при котором последующие приближения полезного сигнала в каждом положении скользящего интервала формируют в блоке последовательной аппроксимации в результате итеративного применения к полученным оценкам метода наименьших квадратов, реализованного в процедуре вариационно-взвешенных квадратичных приближений, до тех пор, пока разница между последовательными приближениями, поступающими в регистр хранения оценок, не станет меньше заданного порогового уровня, отличающийся тем, что метод наименьших квадратов реализуют в процедуре вариационно-взвешенных квадратичных приближений с векторной весовой функцией метода наименьших модулей.
| ИТЕРАЦИОННЫЙ СПОСОБ ВЫДЕЛЕНИЯ ТРЕНДА И УСТРОЙСТВО ДЛЯ ЕГО ОСУЩЕСТВЛЕНИЯ | 2001 |
|
RU2222824C2 |
| СПОСОБ ВЫДЕЛЕНИЯ ТРЕНДА ПУТЕМ РАЗМНОЖЕНИЯ ОЦЕНОК ЕГО ЕДИНСТВЕННОЙ ИСХОДНОЙ РЕАЛИЗАЦИИ (РАЗОЦ) И УСТРОЙСТВО ДЛЯ ЕГО ОСУЩЕСТВЛЕНИЯ | 2000 |
|
RU2207622C2 |
| RU 200119757 A1, 27.06.2003 | |||
| Устройство для прогнозирования надежности, учитывающее тренд случайного воздействия | 1977 |
|
SU714362A1 |
| СПОСОБ АНАЛИЗА НЕСТАЦИОНАРНОГО ПРОЦЕССА | 1998 |
|
RU2159956C2 |
| RU 98116830 A1, 20.08.2000 | |||
| US 4534041 A, 08.06.1985. | |||
Авторы
Даты
2006-12-27—Публикация
2005-03-14—Подача