Изобретение относится к областям радиотехники и акустики и может быть использовано для обнаружения нелинейных объектов и исследования нелинейности преобразования ими сигналов.
Известны способы исследования нелинейности преобразования сигналов объектом, заключающиеся в том, что исследуемый объект подвергают воздействию синусоидального сигнала с последующей оценкой в сигнале-отклике от объекта спектральных составляющих на частотах гармоник или одновременному воздействию двух синусоидальных сигналов, имеющих разные частоты, с последующей оценкой сигнала на комбинационных частотах [1]. Их недостатком является то, что с их помощью нельзя исследовать нелинейность преобразования объектом импульсных или шумоподобных сигналов (нелинейность объектов проявляется по-разному при воздействии на них разных сигналов).
Известен способ исследования нелинейности преобразования сигналов объектом, заключающийся в том, что исследуемый объект подвергают воздействию тестового узкополосного шума, и в сигнале-отклике от объекта проводят анализ возникающих в результате нелинейного преобразования спектральных составляющих вне полосы частот тестового шума [2]. Недостатком данного способа является то, что тестовый шум занимает только часть анализируемой полосы частот (использование широкополосных, занимающих всю анализируемую полосу частот, тестовых сигналов невозможно).
Известен также способ исследования нелинейности преобразования сигналов объектом, заключающийся в том, что на исследуемый объект воздействуют тестовым сигналом, образованным изменяющимся во времени каким-либо физическим фактором, и в исследуемом отклике определяют величину физического фактора на частоте или частотах одного или нескольких локальных нулей спектральной плотности мощности исходного тестового сигнала [3]. Недостатком этого способа является то, что регистрации доступна только небольшая часть продуктов нелинейного преобразования в окрестности одного или нескольких нулей спектральной плотности мощности исходного тестового сигнала.
Наиболее близким по технической сущности к заявляемому способу исследования нелинейности преобразования сигналов объектом является способ, заключающийся в воздействии на объект тестовым сигналом и регистрации разности тестового сигнала и сигнала-отклика от объекта [4]. Недостатком способа-прототипа является то, что при использовании этого способа требуется компенсация линейных искажений тестового сигнала объектом, что реально только для стабильных во времени линейных искажений с простой частотной зависимостью.
Технический результат, на достижение которого направлено предлагаемое решение, - создание способа, позволяющего исследовать нелинейность преобразования сигналов объектами, вносящими сложные линейные искажения сигнала, в том числе изменяющиеся во времени.
Это достигается тем, что в известном способе исследования нелинейности преобразования сигналов объектом, включающем воздействие на него тестовым сигналом и прием от объекта сигнала-отклика на тестовый сигнал, после окончания сигнала-отклика на объект воздействуют дополнительным тестовым сигналом, осуществляют задержку сигнала-отклика на тестовый сигнал в линии задержки, время запаздывания сигнала в которой выбирают равным интервалу времени между началом тестового сигнала и началом дополнительного тестового сигнала, затем выходной сигнал линии задержки пропускают через первый линейный фильтр, а сигнал-отклик объекта на дополнительный тестовый сигнал пропускают через второй линейный фильтр и регистрируют разность сигналов на выходе первого и второго линейных фильтров, при этом отношение передаточных характеристик первого и второго линейных фильтров выбирают равным отношению спектров дополнительного тестового сигнала и тестового сигнала, причем при вычислении спектра тестового сигнала за нулевой момент времени принимают начало тестового сигнала, а при вычислении спектра дополнительного тестового сигнала за нулевой момент времени принимают начало дополнительного тестового сигнала. В частном случае разность выходных сигналов первого и второго линейных фильтров пропускают через третий линейный фильтр.
Использование двух тестовых сигналов позволяет отличить их нелинейное преобразование от линейного, в том числе и в случае, когда линейные искажения тестового сигнала объектом имеют сложную частотную зависимость и нестабильны во времени. Ниже приводится обоснование этого утверждения.
Нелинейность преобразования сигнала в частотной области проявляется в виде отклонения от уравнения линии:
u(ω)=К(ω)х(ω),
где u(ω) и х(ω) - спектры Фурье сигнала-отклика от объекта и тестового сигнала соответственно, К(ω) - постоянный на каждой конкретной частоте комплексный коэффициент (передаточная характеристика объекта), ω - круговая частота.
Воздействуем на объект двумя сигналами - тестовым x1(t) и дополнительным тестовым x2(t), где t - время. Сигналы-отклики объекта u1(t) и u2(t) (на тестовый сигнал и на дополнительный тестовый сигнал соответственно) пропустим через линейные фильтры с передаточными характеристиками К1(ω) и К2(ω) соответственно и найдем разность ε(ω) выходных сигналов фильтров:
ε(ω)=K1(ω)u1(ω)-K2(ω)u2(ω), (1)
где u1(ω) и u2(ω) - спектры Фурье сигналов-откликов на тестовый сигнал и на дополнительный тестовый сигнал соответственно.
Если
K1(ω)/K2(ω)=x2(ω)/x1(ω), (2)
то ε(ω) можно использовать в качестве характеристики нелинейности преобразования сигналов объектом, поскольку при линейном преобразовании сигналов объектом ε(ω)=0. Если преобразование сигналов линейно, то
ε(ω)=K1(ω)u1(ω)-К2(ω)u2(ω)=K1(ω)K(ω)x1(ω)-K2(ω)K(ω)х2(ω);
ε(ω)+K2(ω)K(ω)x2(ω)=K1(ω)K(ω)x1(ω);
ε(ω)/[K(ω)K2(ω)x1(ω)]+x2(ω)/x1(ω)=K1(ω)/K2(ω).
При выполнении (2)
ε(ω)/[K(ω)K2(ω)x1(ω)]=0. (3)
Если исключить физически нереальный случай K(ω)K2(ω)x1(ω)=∝, то из (3) следует ε(ω)=0.
Ограничений на передаточную характеристику объекта, кроме ее постоянства в течение времени измерения, не накладывается, поэтому предлагаемый способ позволяет отличить нелинейное преобразование тестового сигнала от линейного и исследовать нелинейность преобразования сигнала при наличии сложных линейных искажений сигнала, причем допустимо, чтобы к моменту следующего измерения линейные искажения изменились. На тестовые сигналы не устанавливается ограничений, поэтому тестовые сигналы могут быть широкополосными.
Если почленно взять обратное преобразование Фурье от (1), то получим временнýю зависимость сигнала ε(t):
ε(t)=h1(t)*u1(t)-h2(t)*u2(t). (4)
Здесь h1(t) и h2(t) - импульсные характеристики первого и второго линейных фильтров соответственно, * - символ свертки, h1(t)*u1(t) и h2(t)*u2(t) - сигналы на выходе первого и второго линейного фильтров соответственно при подаче на их входы соответственно сигналов-откликов объекта на тестовый сигнал и на дополнительный тестовый сигнал.
Сигналы-отклики объекта на тестовый и дополнительный тестовый сигналы необходимо регистрировать раздельно, поэтому воздействие дополнительным тестовым сигналом начинают после окончания сигнала-отклика на тестовый сигнал, а для того, чтобы зарегистрировать разность пропущенных через фильтры откликов в соответствии с (4), сигнал-отклик на тестовый сигнал подают на вход первого линейного фильтра через линию задержки, время запаздывания в которой выбирают равным интервалу времени между началом тестового сигнала и началом дополнительного тестового сигнала.
В частном случае сигнал ε(t) пропускают через третий линейный фильтр. С помощью этого фильтра преобразуют форму сигнала ε(t) (например, концентрируют сигнал во времени), для того чтобы он стал более наглядным или лучше заметным на фоне шумов. Также этот фильтр используют для подавления появляющихся в результате нелинейного преобразования спектральных составляющих, лежащих выше исследуемого диапазона частот, наличие которых нежелательно при регистрации сигнала ε(t) с помощью аналого-цифрового преобразователя.
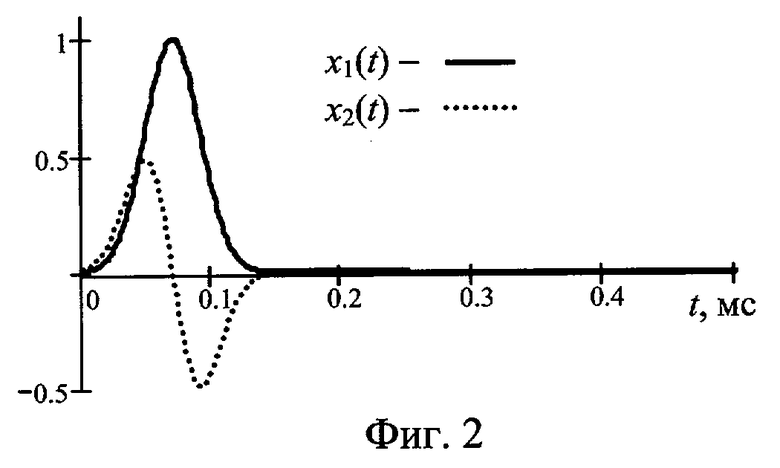
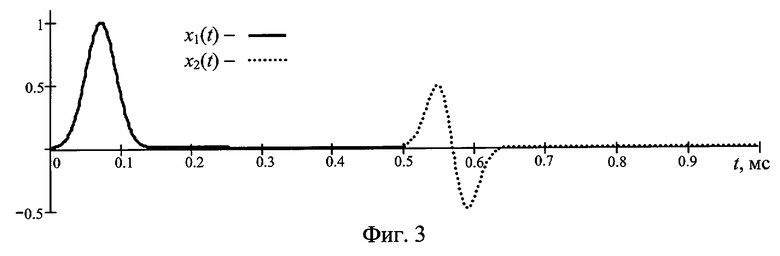
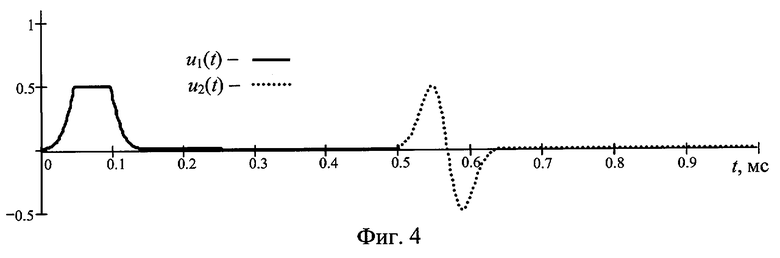
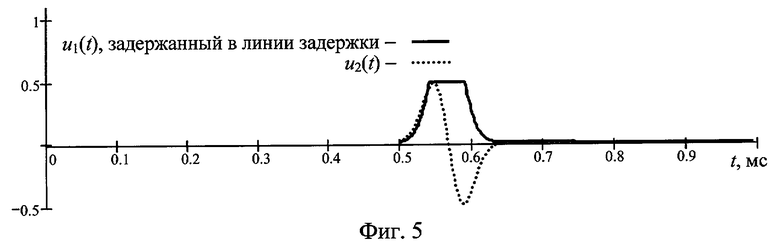
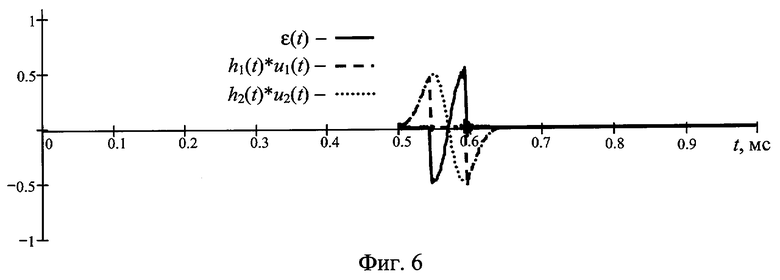
На фиг.1 представлена амплитудная характеристика, на фиг.2 - тестовые сигналы, на примере которых иллюстрируется предложенный способ, на фиг.3 тестовые сигналы представлены последовательно во времени так, как они воздействуют на объект, на фиг.4 представлены отклики объекта на тестовые сигналы фиг.3, на фиг.5 представлены задержанный в линии задержки отклик объекта на тестовый сигнал и отклик объекта на дополнительный тестовый сигнал (входные сигналы первого и второго линейных фильтров соответственно) и на фиг.6 проиллюстрировано получение сигнала ε(t). Сплошной линией на фиг.2 и 3 представлен тестовый сигнал, пунктирной линией - дополнительный тестовый сигнал. Сплошной линией на фиг.4 обозначен отклик объекта на тестовый сигнал, пунктирной линией - отклик объекта на дополнительный тестовый сигнал. На фиг.5 сплошной линией обозначен задержанный в линии задержки отклик объекта на тестовый сигнал, пунктирной линией - отклик объекта на дополнительный тестовый сигнал. На фиг.6 штриховой линией обозначен сигнал на выходе первого линейного фильтра, пунктирной линией - сигнал на выходе второго линейного фильтра и сплошной линией - разность сигналов на выходах первого и второго линейных фильтров.
Ниже приведен пример осуществления изобретения.
В качестве тестового сигнала выбираем импульс Гаусса x1(t)=exp[-((t-t0)/τ1)2]. При τ1=30 мкс, t0=70 мкс получим сигнал, показанный на фиг.2 сплошной линией. В качестве дополнительного тестового сигнала выбираем первую производную импульса Гаусса x2(t)=-[2τ(t-t0)/τ1 2]exp[-((t-t0)/τ1)2]. При τ=17 мкс получим сигнал, представленный на фиг.2 пунктирной линией. Соотношение спектров дополнительного тестового и тестового сигналов x2(ω)/x1(ω)=jωτ. Для выполнения (2) выбираем передаточную характеристику первого линейного фильтра K1(ω)=jωτ и передаточную характеристику второго линейного фильтра К2(ω)=1.
Тестовые сигналы генерируем в электрическом виде генератором и последовательно во времени так, как представлено на фиг.3. Интервал времени между началом тестового сигнала и началом дополнительного тестового сигнала выбираем равным 0,5 мс. Затем подаем тестовый и дополнительный тестовый сигналы на преобразователь, который преобразует их в физический фактор, воздействующий на объект.
Природа физического фактора может быть различна. Если исследуется нелинейность преобразования сигналов проходными электро- и радиотехническими устройствами (четырехполюсниками), то в качестве физического фактора используется ток или напряжение. Если решается задача дистанционного обнаружения объекта с нелинейными свойствами, то в качестве физического фактора выступает электрическое или магнитное поле. Если исследуются нелинейности преобразования звуковых волн в жидкостях или газах, то в качестве физического фактора используются акустические колебания. Сигналы-отклики объекта преобразуются в электрические сигналы соответствующим преобразователем.
Действие способа рассмотрим на примере объекта с амплитудной характеристикой u(х):
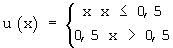
представленной на фиг.1, где х и u - тестовый сигнал и отклик объекта на него соответственно.
Принимаем сигналы-отклики от объекта. Преобразованные в электрический вид сигналы-отклики объекта на тестовый сигнал и дополнительный тестовый сигнал (представлены на фиг.4) подаем соответственно на вход линии задержки и вход второго линейного фильтра. Время запаздывания сигнала в линии задержки выбираем равным интервалу времени между началом тестового сигнала и началом дополнительного тестового сигнала, то есть 0,5 мс. На фиг.5 представлены сигнал-отклик на дополнительный тестовый сигнал и задержанный в линии задержки сигнал-отклик на тестовый сигнал. Выходной сигнал линии задержки подаем на вход первого линейного фильтра.
Поскольку передаточная функция второго линейного фильтра выбрана тождественно равной единице, выходной сигнал этого фильтра будет равен входному, то есть u2(t). Дополнительный тестовый сигнал укладывается в линейную часть амплитудной характеристики, поэтому форма сигнала-отклика объекта u2(t) (представленного на фиг.4 пунктирной линией) повторяет форму и амплитуду x2(t). Отсюда следует, что выходной сигнал второго линейного фильтра (фиг.6, пунктирная линия) будет совпадать по форме и амплитуде с x2(t). Выходной же сигнал первого линейного фильтра h1(t)*u1(t) совпадает с x2(t) только в том случае, если его входной сигнал u1(t) совпадает с x1(t):
h1(t)*u1(t)=h1(t)*x1(t)=F-1[K1(ω)x1(ω)]=F-1[(x2(ω)/x1(ω))x1(ω)]=x2(t),
где F-1 - обратное преобразование Фурье.
Однако поскольку амплитудная характеристика нелинейна, u1(t) отличается от x1(t), и выходной сигнал первого линейного фильтра (фиг.6, штриховая линия) отличается по форме от x2(t), то между выходными сигналами первого и второго линейных фильтров появляется разностный сигнал ε(t) (фиг.6, сплошная линия).
Источники информации
1. Шкритек П.Справочное руководство по звуковой схемотехнике: Пер. с нем. - М.: Мир, 1991. С.32.
2. Журавлев В. М. Метод измерения нелинейных искажений с помощью полос шума: Канд. дисс. Л.: ЛИКИ, 1967.
3. Семенов Э.В. Синтез сверхширокополосных тестовых сигналов для обнаружения нелинейного преобразования сигнала путем наблюдения за нулями его спектральной плотности мощности // Сборник докладов Всероссийской научной конференции "Сверхширокополосные сигналы в радиолокации, связи и акустике". Муром, 1-3 июля 2003 г. - Муром: Изд.-полиграфический центр МИ ВлГУ, 2003. - С.99-103.
4. Акулиничев И. Селекция сигнала искажений // Радио, 1983, №10. С.42-44 - прототип.
| название | год | авторы | номер документа |
|---|---|---|---|
| СПОСОБ ОБНАРУЖЕНИЯ НЕКАЧЕСТВЕННОГО ЭЛЕКТРИЧЕСКОГО КОНТАКТА | 2014 |
|
RU2560034C1 |
| СПОСОБ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ АСТАТИЧЕСКОГО ОБЪЕКТА | 1996 |
|
RU2103714C1 |
| УГЛОМЕРНО-БАЗОВЫЙ СПОСОБ ИЗМЕРЕНИЯ ДАЛЬНОСТИ | 2001 |
|
RU2184981C1 |
| СПОСОБ СЖАТИЯ ШИРИНЫ СПЕКТРА ИНФОРМАЦИОННЫХ ЭЛЕКТРИЧЕСКИХ СИГНАЛОВ С ОГРАНИЧЕННОЙ ПОЛОСОЙ ЧАСТОТ | 2000 |
|
RU2192708C2 |
| СИСТЕМА И СПОСОБ РАЗДЕЛЕНИЯ ЭЛЕКТРОМАГНИТНОГО ВОЛНОВОГО ПОЛЯ | 2003 |
|
RU2328756C2 |
| СПОСОБ ДИАГНОСТИРОВАНИЯ НЕИСПРАВНОСТЕЙ ДИНАМИЧЕСКИХ ОБЪЕКТОВ И УСТРОЙСТВО ДЛЯ ЕГО ОСУЩЕСТВЛЕНИЯ | 1994 |
|
RU2084945C1 |
| СПОСОБ ПОЛУЧЕНИЯ СЕЙСМИЧЕСКОГО РАЗРЕЗА | 1991 |
|
RU2022310C1 |
| СПОСОБ ДИНАМИЧЕСКИХ ИСПЫТАНИЙ КОНСТРУКЦИЙ И СИСТЕМ НА МЕХАНИЧЕСКИЕ И ЭЛЕКТРОННЫЕ ВОЗДЕЙСТВИЯ | 2014 |
|
RU2569636C2 |
| СПОСОБ НЕЗАВИСИМОГО ОЦЕНИВАНИЯ НЕИЗВЕСТНЫХ ПАРАМЕТРОВ ЛИНЕЙНЫХ ОБЪЕКТОВ | 2008 |
|
RU2399078C2 |
| СПОСОБ НЕЛИНЕЙНОЙ РАДИОЛОКАЦИИ | 2009 |
|
RU2436115C2 |
Изобретение относится к областям радиотехники и акустики и может быть использовано для обнаружения нелинейных объектов. Сущность изобретения состоит в том, что на объект воздействуют тестовым сигналом, принимают от объекта сигнал-отклик на тестовый сигнал, после окончания сигнала-отклика на объект воздействуют дополнительным тестовым сигналом, осуществляют задержку сигнала-отклика на тестовый сигнал в линии задержки, время запаздывания сигнала в которой выбирают равным интервалу времени между началом тестового сигнала и началом дополнительного тестового сигнала, затем выходной сигнал линии задержки пропускают через первый линейный фильтр, а сигнал-отклик объекта на дополнительный тестовый сигнал пропускают через второй линейный фильтр и регистрируют разность сигналов на выходе первого и второго линейных фильтров, при этом отношение передаточных характеристик первого и второго линейных фильтров выбирают равным отношению спектров дополнительного тестового сигнала и тестового сигнала, причем при вычислении спектра тестового сигнала за нулевой момент времени принимают начало тестового сигнала, а при вычислении спектра дополнительного тестового сигнала за нулевой момент времени принимают начало дополнительного тестового сигнала. В частном случае разность выходных сигналов первого и второго линейных фильтров пропускают через третий линейный фильтр. Достигаемый технический результат - исследование нелинейности преобразования сигналов объектами, вносящими сложные линейные искажения сигнала, в том числе изменяющиеся во времени. 1 з.п. ф-лы, 6 ил.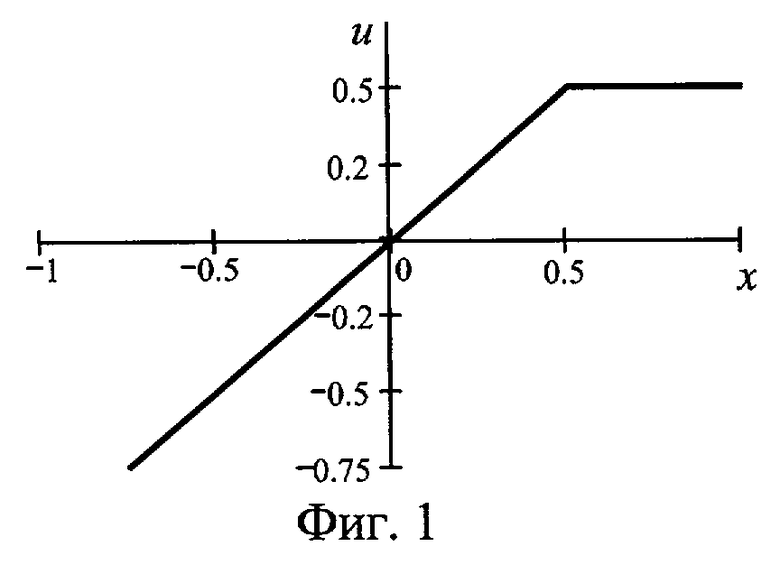
| АКУЛИНИЧЕВ И | |||
| Селекция сигнала искажений | |||
| Радио, 1983, №10, с.42-44 | |||
| RU 2002123629 А, 20.03.2004 | |||
| УСТРОЙСТВО ДЛЯ КЛАССИФИКАЦИИ МНОГОПАРАМЕТРИЧЕСКИХ ОБЪЕКТОВ | 1991 |
|
RU2049355C1 |
| СПОСОБ ОБНАРУЖЕНИЯ НЕЛИНЕЙНОГО ОБЪЕКТА С РАСПОЗНАВАНИЕМ ТИПА НЕЛИНЕЙНОСТИ | 2001 |
|
RU2205419C2 |
| СИСТЕМА ОБНАРУЖЕНИЯ И РАСПОЗНАВАНИЯ ОБЪЕКТОВ, ВКЛЮЧАЮЩИХ ЭЛЕМЕНТЫ С НЕЛИНЕЙНЫМИ ВОЛЬТАМПЕРНЫМИ ХАРАКТЕРИСТИКАМИ | 2000 |
|
RU2166769C1 |
| US 3992666 A, 16.11.1976 | |||
| ТЕЛЕЖКА ЛОКОМОТИВА С УПРАВЛЯЕМО-КИНЕМАТИЧЕСКОЙ РАДИАЛЬНОЙ УСТАНОВКОЙ КОЛЕСНЫХ ПАР (ВАРИАНТЫ) | 2002 |
|
RU2238201C2 |
Авторы
Даты
2005-11-10—Публикация
2004-04-07—Подача