СПОСОБ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ АСТАТИЧЕСКОГО ОБЪЕКТА Российский патент 1998 года по МПК G05B11/01 

Изобретение относится к автоматическому регулированию астатических систем с нелинейными корректирующими устройствами и может быть использовано в высокоточных приводах с различными типами исполнительных двигателей.

Известен способ автоматического регулирования объекта, реализованный в управляемом Пи-регуляторе [1]. По этому способу для управления соотношением пропорциональной (П) и интегральной (И) составляющих входного сигнала регулятора используют величину скорости ошибки. Чем меньше скорость, тем меньше постоянная времени интегратора и сильнее влияние И-регулятора. Малая скорость сигнала ошибки характерна для установившегося состояния системы; большая скорость - для переходных процессов.

Однако этот способ малоэффективен в установившемся движении из-за большого фазового запаздывания (-90^o) и дрейфа нуля И-регулятора, а также из-за нелинейных амплитудных свойств регулятора по причине детерминированной зависимости его параметров от абсолютной величины скорости ошибки.

Известен способ автоматического регулирования объекта, реализованный в следящем приводе [2]. По этому способу при формировании управляющего сигнала для объекта используют выходной сигнал интегратора ошибки с логическим управлением ключа цепи шунтирования выхода и входа интегратора по соотношению скоростей задающего и выходного сигналов следящей системы. Шунтирорвание интегратора эквивалентно переключению И-регулятора на П-регулятор. И-регулятор используют для повышения динамической точности следящей системы в установившихся режимах при малой разности скоростей задающего выходного сигналов, П-регулятор - для снижения колебательности переходных процессов при большой разности скоростей.

Причины низкой эффективности этого способа сходны с предыдущим случаем, а нелинейные амплитудные свойства регулятора обусловлены детерминированным пороговым значением разности абсолютных значений скоростей для переключения регулятора.

Главная задача способов [1, 2] - повышение качества переходных процессов в системе за счет ослабления И-составляющей в регуляторе. Эти способы не предназначены для достаточно распространенного в практике следящих систем режима динамического слежения за кусочно монотонным задающим сигналом (например, гармоническим или треугольным).

Известен способ автоматического регулирования астатического объекта, реализованный в следящих системах [3, 4] и следящем электроприводе [5]. Во всех системах при формировании управляющего сигнала для объекта получают и используют следующие сигналы: выходной сигнал ПИ-регулятора с логически коммутируемой обратной связью управляемого интегратора (УИ) и масштабированные ошибку и скорость ошибки в фазоопережающем фильтре (ФФ) с функцией U вида
U = K • ε + T_Д • D_ε,
где ε - ошибка следящей системы;
D_ε - скорость ошибки;
K - коэффициент пропорциональности;
Т_Д - постоянная времени дифференцирования.

Главное различие между системами [3, 4, 5] заключается в законе формирования сигнала логического управления коммутацией обратной связи УИ. По этому признаку прототипом, т.е. наиболее близким по технической сущности к предлагаемому способу, является способ реализованный в [5], по которому используют знак выходного сигнала УИ для получения сигнала управления коммутацией обратной связи УИ, а также скорость задающего сигнала системы.

Технический результат - повышение динамической точности этой следящей системы - достигают за счет переменности структуры регулятора и связанных с этим скользящих режимов. В реальных скользящих режимах всегда присутствуют автоколебания с конечными амплитудой и частотой, величины которых обусловлены нелинейностями и возмущениями объекта регулирования, что ухудшает динамическую точность следящей системы. Также этот способ не обеспечивает астатизма амплитудной частотной характеристики (АЧХ) Пи-регулятора при уменьшенном эквивалентном фазовом запаздывании. Уменьшение фазового запаздывания необходимо для повышения запасов устойчивости и уменьшения перерегулирования переходных процессов в следящей системе по сравнению с системой с линейным ПИ-регулятором.

Задача изобретения - повышение динамической точности следящей системы с астатическим объектом за счет дополнительного астатизма АЧХ псевдолинейного ПИ-регулятора с уменьшенным эквивалентным фазовым запаздыванием в рабочей частотной области (другое название такого регулятора в ТАР - нелинейный изодром (НИ)).

Задача решена тем, что ФФ управляют посредством логического переключения коэффициента К и одностороннего ограничения сверху сигнала U с переменным уровнем ограничения , после ограничения выходной сигнал ФФ подают на вход УИ с обнулением, для управления обнулением используют логическую функцию y1, для управления коэффициентом К используют логическую функцию y2
y1 = (x1 = -x4) И [(x4 = x2) ИЛИ (x4 = x3)],
y2 = (x1 = -x4) И [(x1 = x2) И (x1 = x3)],
где x1 - знак выходного сигнала УИ;
x2 - знак скорости задающего сигнала;
x3 - знак сигнала разности скорости задающего сигнала и скорости сигнала ошибки.

x4 - знак сигнала ошибки.

При равенстве единице сигнала y1 обнуляют выходной сигнал УИ, при равенстве единице сигнала у2 выбирают большее из двух значений коэффициента К, выходной сигнал ПИ-регулятора суммируют с выходным сигналом дополнительного интегратора компенсации постоянной составляющей ошибки и суммарный сигнал подают на управляющий вход астатического объекта.

На фиг.1 показана функциональная схема по способу с УИ с обнулением; на фиг.2 - функциональная схема реализации УИ с обнулением; на фиг.3 - логарифмические амплитудные частотные характеристики (ЛАЧХ) выхода к ошибке следящей системы и ЛАЧХ линейного объекта с астатизмом первого порядка; на фиг. 4 - соответствующие логарифмические фазовые частотные характеристики (ЛФЧХ) выхода к ошибке следящей системы и ЛФЧХ линейного объекта с астатизмом первого порядка; на фиг. 5 - качественные характеристики задающего сигнала ошибки и выходного сигнала регулятора при гармоническом задающем сигнале рабочей частоты в следящей системе; на фиг. 6 - качественные характеристики тех же сигналов в разомкнутой системе; на фиг. 7 - ЛФЧХ регулятора в следящей системе и разомкнутой системе; на фиг. 8 - качественные характеристики задающего сигнала, ошибки и выходного сигнала регулятора при треугольном задающем сигнале рабочей частоты в следящей системе; на фиг. 9 - функциональная схема по способу с УИ с обнулением и установкой; на фиг. 10 - функциональная схема реализации УИ с обнулением и установкой; на фиг. 11 - ЛАЧХ выхода к ошибке следящих систем с УИ с обнулением и с УИ с обнулением и установкой; на фиг. 12 - соответствующие ЛФЧХ выхода к ошибке следящих систем с УИ с обнулением и с УИ с обнулением и установкой.

На фиг. 1 функциональная схема включает в себя объект 1, содержащий последовательное астатическое звено первого порядка, измеритель ошибки 2 задающего сигнала и выходного сигнала обратной связи, дифференциаторы задающего сигнала 3 и сигнала ошибки 4, УИ 5 с обнулением, интегратор 6 компенсации постоянной составляющей ошибки, четыре определителя знаков: знака выходного сигнала УИ 7, знака скорости задающего сигнала 8, знака разности скорости задающего сигнала и скорости ошибки 9, знака сигнала ошибки 10, логический блок 11 формирования сигналов управления обнулением УИ и переключением коэффициента К ФФ, пропорциональные блоки 12, 13, 14, 15, блоки умножения 16, 17, 18, логически управляемый переключатель 19 П-цепей ФФ с двумя значениями коэффициента К, блок 20 одностороннего ограничения с управляемым уровнем ограничения сверху, элемент вычитания 21, двухвходовый сумматор 22 и трехвходовый сумматор 23.

На фиг. 1 и 2 приняты следующие обозначения параметров:
g - задающий сигнал следящей системы;
y - выходной сигнал обратной связи;
U_p - выходной сигнал регулятора;
D - оператор дифференцирования d/dt, где d - дифференциал, t - время; соответственно 1/D - оператор интегрирования;
T - постоянная времени УИ;
dI - входной сигнал УИ;
I - выходной сигнал УИ;
R - вход и логический сигнал управления обнулением УИ;
X - коэффициент, теоретически стремящийся к бесконечности (в практической реализации предельно большой коэффициент);
K₀; K₁ - значения коэффициента K ФФ соответственно при y2 = 0 (K = K₀) и y2 = 1 (K = K₁);
K_п - коэффициент П-регулятора;
T_к - постоянная времени интегратора компенсации;
W₀ - статическая часть передаточной функции объекта.

Обозначения K • ε; U; K; T_Д; x1; x2; x3; x4; y1; y2 приведены ранее.

Способ осуществляют следующим образом.

Этапу эксплуатации системы автоматического регулирования предшествует этап ее синтеза. В инженерной практике и ТАР нелинейных систем одним из самых распространенных является частотный метод синтеза, сопряженный с методом гармонической линеаризации нелинейностей объекта и регулятора.

Вначале по критерию устойчивости проводят частотный синтез следящей системы без УИ, т.е. П-регулятор с интегратором компенсации постоянной составляющей ошибки системы, вызванной исходным смещением и низкочастотным дрейфом нуля объекта, а также его статической нагрузкой. Величина T_к выбирается достаточно большой, чтобы не вносить ощутимого фазового запаздывания в ЛФЧХ регулятора в рабочей частотной области. Определяют частоту среза разомкнутой системы. По критериям достаточных запасов устойчивости и качества переходных процессов в системе частоту среза обычно выбирают в 3...5 раз меньше частоты с фазовым запаздыванием разомкнутой системы -180^o. Затем дополнительно подключают ветвь УИ и синтезируют параметры НИ. При этом в 2...3 раза уменьшают коэффициент K_п, а величину T для УИ выбирают в 2...3 раза больше величины, обратной частоте среза исходной системы без УИ. Одновременно устанавливают соотношения K₁/K₀ и T_Д/T больше единицы, но из соображений устойчивости не больше величины отношения частоты с фазой -180^o к частоте среза исходной разомкнутой системы без УИ.

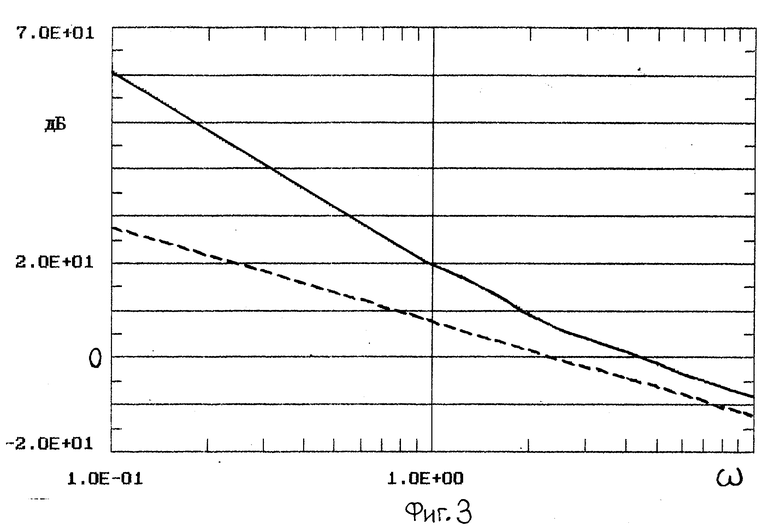
На этом синтез регулятора системы закончен. Правильно синтезированная система с НИ и линейным астатическим объектом в режиме слежения за гармоническими задающими сигналами имеет ЛАЧХ, изображенные на фиг. 3, ЛФЧХ, изображенные на фиг. 4, и временные характеристики - на фиг. 5. При получении всех характеристик соотношения K₁/K₀ и T_Д/T были выбраны равными трем.

Все графики ЛАЧХ и ЛФЧХ выполнены в традиционной манере: ЛАЧХ имеют размерность дБ, ЛФЧХ - размерность град (^o), по оси аргумента в логарифмическом масштабе отложена частота ε.

На фиг. 3 сплошной линией обозначена ЛАЧХ выхода к ошибке системы 20lg(y/ω) и штриховой линией - ЛАЧХ объекта 20lg(y/U_p), на фиг. 4 сплошной линией - ЛФЧХ выхода к ошибке системы ε , штриховой - ЛФЧХ объекта ϕ(y/ε)(y/U_p).

В рабочей частотной области очевиден дополнительный астатизм ЛАЧХ выхода к ошибке скорректированной системы с уменьшенным эквивалентным фазовым запаздыванием ЛФЧХ (в пределе -160^o вместо -180^o астатического объекта с линейным Пи-регулятором).

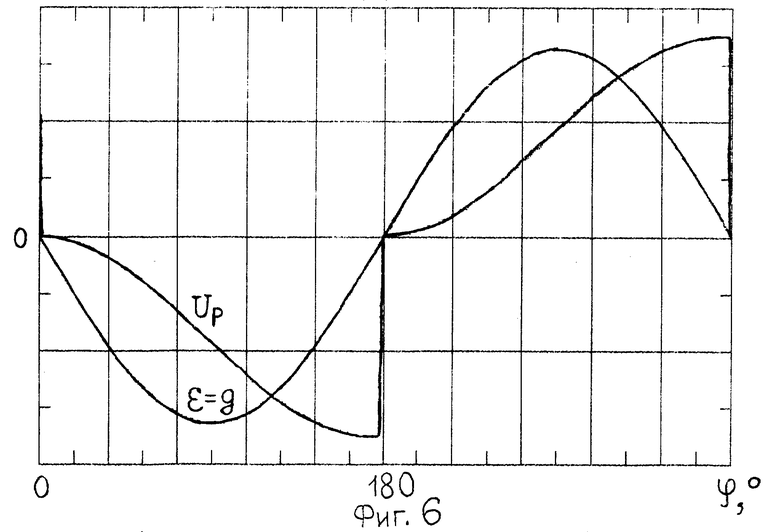
На фиг. 5, 6 и 8 сигналы g, ϕ и U_p имеют большой разброс амплитуд и для наглядности даны в разных масштабах, для обобщения аргумент времени трансформирован в аргумент фазы периодического задающего сигнала через коэффициент 360^o/T₀, T₀ - период времени повторения задающего сигнала. Для случаев фиг. 5 и 8 амплитуда ошибки ε существенно меньше амплитуды сигнала g, для случая фиг. 6 ошибка ε совпадает с сигналом g.

В реальности астатический объект является нелинейным и обычно у него есть зона нечувствительности по входу. Предельным случаем системы с таким объектом является разомкнутая система по причине полной нечувствительности объекта по входу (разомкнутую систему можно также получить за счет разрыва обратной связи). В разомкнутой системе при нулевом входном сигнале ошибка равна задающему сигналу (фиг. 6). При этом астатическая ЛАЧХ регулятора практически не изменяется (ЛАЧХ регулятора на фигуру не вынесена), а фазовое запаздывание ЛФЧХ регулятора в рабочей частотной области за счет изменения форм сигнала ошибки и выходного сигнала регулятора уменьшается с -70^o до -38^o (на фиг. 7 сплошной линией обозначена ЛФЧХ ε регулятора следящей системы, штриховой - ЛФЧХ ϕ(U_p/ε) регулятора разомкнутой системы).

Формулы коэффициентов q; q' гармонической линеаризации НИ, а также производных от них A_q = (q² + q'²)^0,5; ϕ(U_p/ε) = arctg (q'/q), полученные с учетом K_п = 1; T; ϕ_q и на основании форм сигналов ω и U_р фиг. 5, 6, соответствуют низкочастотным ассимптотам ЛАЧХ и ЛФЧХ:
для следящей системы:
ε
для разомкнутой системы:
q= 0,43/(Tω); A_q=1,43/(Tω) q'=-1,36/(Tω) ϕ_q=-72^°
Другим типовым примером динамического кусочно монотонного задающего сигнала следящей системы является треугольный сигнал. На фиг. 8 даны характеристики для случая сигнала g рабочей частоты. Сигнал U_р в установившемся движении в основном формируют за счет сигнала УИ I, много большем сигнала ПИ-регулятора q= 1,27/(Tω); A_q=1,62/(Tω) q'=-1,00/(Tω) ϕ_q=-38^°.

Главная задача УИ в режиме динамического слежения системы за кусочно монотонным сигналом в рабочей частотной области - удерживать систему в апериодическом режиме без перерегулирования при y2 = 0 и при этом активно уменьшать ошибку за счет роста собственного выходного сигнала (см. фиг. 8). Величина y2 = 1 соответствует переходу системы в нежелательное состояние перерегулирования и тогда для уменьшения перерегулирования и связанного с этим эквивалентного фазового запаздывания НИ увеличивают коэффициент П-цепи ФФ с K₀ до K₁. Средством уменьшения фазового запаздывания УИ также является одностороннее ограничение сверху выходного сигнала ФФ с управляемым уровнем ограничения K_п• ε, который разрешает дифференциальной составляющей K • ε участвовать только в уменьшении входного сигнала УИ на этапе торможения системы при стремлении ошибки к нулю.

Логическое условие y1 обнуления УИ делает невозможным переход системы в состояние неконтролируемого торможения и связанного с этим существенного дополнительного запаздывания в случае противоположности знака выходного сигнала УИ и одинаковых знаков ошибки и любой из скоростей задающего или выходного сигналов системы (скорость выходного сигнала обратной связи тождественна разности скоростей задающего сигнала и сигнала ошибки).

Дополнительный интегратор компенсирует постоянную составляющую ошибки объекта. При этом НИ становится регулятором с псевдолинейными свойствами, т. е. частотными характеристиками, зависящими от частоты и не зависящими от величин амплитуд сигналов.

Таким образом, неразрывная совокупность отличительных признаков предлагаемого способа автоматического регулирования позволяет достичь нового существенного технического результата.

Дополнительным средством борьбы с перерегулированием и уменьшения фазового запаздывания ошибки следящей системы с астатическим объектом является способ установки выходного сигнала УИ. Он заключается в том, что выходной сигнал УИ умножают на ограниченное в диапазоне от нуля до единицы частное от деления скорости задающего сигнала на скорость выходного сигнала системы, выходной сигнал УИ скачком устанавливают равным результату этого умножения в момент смены знака сигнала ошибки.

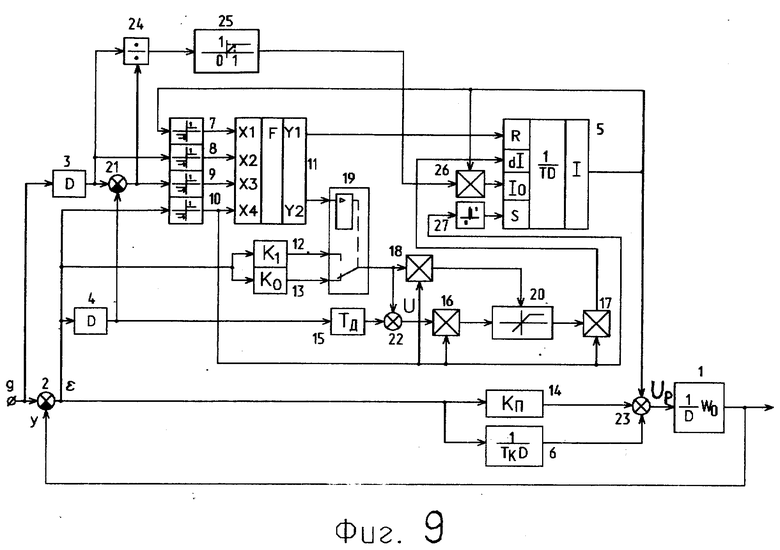
На функциональной схеме фиг. 9 вместо УИ с обнулением под номером 5 изображен УИ с обнулением и установкой. Остальные блоки с номерами от 1 до 23 фиг. 9 идентичны блокам фиг. 1, но схема фиг. 9 дополнительно имеет делитель 24, блок 25 двустороннего ограничения от нуля до единицы, блок умножения 26 и блок 27 формирования логической единицы при нуле входного сигнала блока.

На фиг. 9 и 10 дополнительно обозначены:
S - вход и логический сигнал управления установкой выхода УИ;
I₀ - вход и сигнал величины установки выхода УИ.

По схеме фиг. 9 момент смены знака ошибки фиксируют активным логическим управляющим сигналом установки выхода УИ с помощью блока 27. По схеме фиг. 10 вначале по фронту перехода сигнала управления S в активное состояние производят запоминание в элементе памяти сигнала величины установки I₀, полученного в результате умножения выходного сигнала УИ на ограниченный коэффициент отношения скоростей. Запоминание заканчивают к началу процесса установки УИ по активному уровню сигнала S. Процесс установки (в частном случае, обнуления) выхода УИ осуществляют замыканием следящей системы с задающим сигналом величины установки выхода УИ. Эту систему с предельно большим для максимальной скорости установки коэффициентом усиления прямой цепи K∞ замыкают через нормально разомкнутый контакт переключателя, управляемого объединенным сигналом, формируемым по функции ИЛИ из логических сигналов установки и обнуления. При обнулении УИ от активного управляющего сигнала обнуления R на вход следящей системы установки подключают нулевой сигнал. В отсутствии активных управляющих сигналов R и S через нормально замкнутый контакт переключателя в режиме обычного интегрирования к интегратору подключают входной сигнал УИ dI.

В режиме динамического слежения за кусочно монотонным задающим сигналом рабочей частоты при переходе в перерегулирование и смене знака ошибки скорости задающего и выходного сигналов системы обычно являются одинаковыми по знаку, но скорость выходного сигнала больше скорости задающего сигнала, и, следовательно, частное от деления скоростей будет положительным числом, большим или равным нулю, но меньшим единицы. В момент обнуления ошибки и сигнала П-регулятора K_п• ε только выходной сигнал УИ I определяет скорость выхода астатического объекта. Переход в перерегулирование свидетельствует об избытке скорости выхода и, следовательно, об избытке выходного сигнала УИ. За счет уменьшения скачком выходного сигнала УИ с помощью коэффициента отношения скоростей в момент смены знака ошибки этот избыток частично компенсируют и уменьшают последующее перерегулирование.

Ограничение коэффициента отношения скоростей в диапазоне от нуля до единицы также является существенным признаком. Если в момент смены знака ошибки знаки скоростей были противоположны, что свидетельствует о близости частоты задающего сигнала к частоте системы, ограничение нуля сделает коэффициент отношения скоростей нулевым и функция установки выходного сигнала УИ фактически станет функцией обнуления УИ. В частотной области вблизи частоты среза это также позволяет дополнительно уменьшить фазовое запаздывание регулятора за счет ослабления составляющей УИ в суммарном сигнале НИ. Ограничение единицей сверху коэффициента отношения скоростей гарантирует системе невозможность случайного (из-за шумов и погрешностей операций дифференцирования и деления) нежелательного увеличения сигнала УИ в момент смены знака ошибки.

Наглядным подтверждением сказанного являются сравнительные ЛАЧХ (фиг. 11) и ЛФЧХ (фиг. 12) выхода к ошибке следящих систем с УИ с обнулением (сплошные линии характеристик) и УИ с обнулением и установкой (штриховые линии характеристик). Во всей частотной области при практически одинаковых ЛАЧХ систем получают меньшее запаздывание ЛФЧХ системы с УИ с обнулением и установкой.

Таким образом, совокупность дополнительных отличительных признаков способа позволяет достичь технического результата дополнительного уменьшения фазового запаздывания.

Источники информации:
1. Патент ФРГ N 1673601, G 05 B 11/00, 1973.

2. Авторское свидетельство СССР N 794611, G 05 B 11/01, 1981.

2. Авторское свидетельство СССР N 1352451, G 05 B 11/01, 1987.

2. Авторское свидетельство СССР N 1425595, G 05 B 11/01, 1988.

2. Авторское свидетельство СССР N 1446600, G 05 B 11/01, 1988.

Изобретение относится к автоматическому регулированию астатических объектов с нелинейными корректирующими устройствами. Для регулирования объекта используют Пи-регулятор с управляемым интегратором и управляемым фазоопережающим фильтром входного сигнала управляемого интегратора. Формирование функций обнуления интегратора и переключения коэффициента пропорциональной ветви фильтра по логическим соотношениям знаков сигналов: ошибки выходного сигнала управляемого интегратора, скорости задающего сигнала, разности скорости задающего сигнала и скорости ошибки (разность этих скоростей тождественна скорости выходного сигнала обратной связи объекта). Одностороннее ограничение сверху выходного сигнала фильтра с переменным уровнем ограничения по текущему сигналу пропорциональной ветви фильтра. Параллельно Пи-регулятору интегратор компенсации постоянной составляющей ошибки. Дополнительная возможность установки скачком (с коррекцией по соотношению в пределах от нуля до единицы скоростей задающего и выходного сигналов системы) выхода управляемого интегратора при смене знака ошибки. Технический результат - повышение динамической точности следящей системы с астатическим объектом за счет астатизма амплитудной частотной характеристики псевдолинейного ПИ-регулятора с уменьшенным эквивалентным фазовым запаздыванием в рабочей частотной области. 1 з.п. ф-лы, 12 ил.

1. Способ автоматического регулирования астатического объекта, заключающийся в том, что при формировании управляющего сигнала для объекта получают и используют следующие сигналы: выходной сигнал ПИ-регулятора с логически управляемым интегратором, знак выходного сигнала управляемого интегратора, сигнал скорости задающего сигнала следящей системы, масштабированные сигналы ошибки и скорости ошибки в фазооперажающем фильтре с функцией U вида
U = K•ε+T_д•D_ε,
где e - ошибка следящей системы;
D_ε- скорость ошибки;
K коэффициент пропорциональности;
T_д постоянная времени дифференцирования,
отличающийся тем, что фазоопережающим фильтром управляют посредством логического переключения коэффициента K и одностороннего ограничения сверху сигнала U с переменным уровнем ограничения K•ε, после ограничения выходной сигнал фазоопережающего фильтра подают на вход управляемого интегратора с обнулением выходного сигнала, для управления обнулением используют логическую функцию y1, для управления переключением коэффициента K используют логическую функцию y2
y1 (x1 -x4) И [(x4 x2) ИЛИ (x4 x3)]
y2 (x1 -x4) И (x1 x2) И (x1 x3),
где x1 знак выходного сигнала управляемого интеграетора;
x2 знак скорости задающего сигнала;
x3 знак сигнала разности скорости задающего сигнала и скорости сигнала ошибки;
x4 знак сигнала ошибки,
при равенстве единице сигнала y1 обнуляют выходной сигнал управляемого интегратора, при равенстве единице сигнала y2 выбирают большее из двух значений коэффициента K, выходной сигнал ПИ-регулятора суммируют с выходным сигналом дополнительного интегратора компенсации постоянной составляющей ошибки и суммарный сигнал подают на вход управления объекта. 2. Способ по п. 1, отличающийся тем, что выходной сигнал управляемого интегратора умножают на ограниченное в диапазоне от нуля до единицы частное от деления скорости задающего сигнала на разность скорости задающего сигнала и скорости сигнала ошибки, выходной сигнал управляемого интегратора скачком устанавливают равным результату этого умножения в момент смены знака сигнала ошибки следящей системы.