Изобретение относится к области астрономии и может быть использовано для изучения периодических движений поверхности Земли.
Литосфера состоит из плит, образующих сплошное твердое покрытие земного шара с утолщениями в виде континентов. Плиты опираются на астеносферу - слой с повышенной текучестью. Тепловая конвекция в нем постепенно, за миллионы лет, деформирует литосферу и меняет взаимное расположение континентов (V.P.Trubitsyn, V.V.Rykov, Russian Journal of Earth Sciences, 1999, vol.1, p.87).
В среднем раз в миллион лет происходят инверсии геомагнитного поля. Поискам происхождения магнитного поля Земли посвящено много работ, в частности, по гидродинамике вращающихся жидкостей (У.Паркинсон. Введение в геомагнетизм, Москва, 1986; F.H.Busse, C.R.Carrigan, J.Fluid Mech.,1974, vol.62, p.379; K.Zhang, P.Earnshow, X.Liao, F.H.Busse, J.Fluid Mech., 2001, vol.437, p.103).
С периодами порядка одного года совершается сложное перемещение полюсов Земли, в числе причин которого обсуждается влияние Солнца и Луны (Ю.Н.Авсюк, В.В.Адушкин, В.М.Овчинников. Физика Земли, 2001, №8, с.64; Н.С.Сидоренков. Атмосферные процессы и вращение Земли, С.-Петербург, 2002).
Задача настоящего изобретения состоит в создании модели, раскрывающей механизм регулярной прецессии литосферы как целого вокруг мантии планеты в отсутствие влияния других небесных тел. Решение данной задачи существенно для оценки вязкости астеносферы, поиска закономерностей, определяющих движение ядер космических объектов, а также для определения источника геомагнитного поля. Прецессия литосферы вокруг мантии планеты в литературе не описана. Модели этого явления ранее не предлагались.
Известны устройства для испытания вращающихся тел (например, патент РФ №2131610, 1999 г., м.кл. G 01 Р 3/16) и для их применения в качестве регуляторов (например, авторское свидетельство РФ №1358605, 1996 г., м.кл. G 05 D 13/10). Эти и другие известные устройства не могут быть использованы для решения указанной задачи.
Задача, поставленная в настоящем изобретении, решена благодаря тому, что предлагаемое устройство содержит сферическую оболочку, геометрический центр которой фиксирован в пространстве и которая имеет возможность поворота относительно этого центра, в оболочке выполнено отверстие, через которое проходит вертикальный стержень, несущий шар, расположенный внутри оболочки, отверстие оболочки и сечение стержня имеют удлиненную форму.
Выступающий из оболочки конец стержня снабжен ограничителем поворота и вставлен в вертикальный канал на периферии колеса, которое установлено на основании с возможностью вращения вокруг вертикальной оси, проходящей через геометрический центр оболочки, колесо соединено с двигателем.
Оболочку поддерживают три ролика с ориентированными горизонтально цилиндрическими шипами. Шипы роликов расположены в пазах держателей, закрепленных на верхней стороне круглой платформы. Нижняя сторона платформы имеет кольцевой паз и опирается на шарики, расположенные в кольцевом пазу основания.
В оболочке находится жидкость. Для ее заливки служит горловина, закрытая пробкой. Отверстие для стержня выполнено в резиновой втулке, встроенной в стенку оболочки. Резиновая втулка скреплена по периметру с эластичным колпаком, натянутым на кольцевой выступ стержня, чем обеспечивается герметизация устройства.
Возможны варианты устройства, различающиеся положением колеса: под оболочкой (основной вариант) либо над оболочкой. В основном варианте устройства колесо имеет вал, на котором закреплены шарикоподшипник и шкив, соединенный ременной тягой со шкивом двигателя. Ограничитель поворота выполнен в виде шатуна, один конец которого скреплен со стержнем, а другой конец имеет паз, куда входит неподвижный цилиндрический штырь. Оболочка выполнена разъемной из двух полусфер. Ее стенка изготовлена из прозрачного материала.
Благодаря указанному выполнению устройства относительное перемещение его элементов достоверно передает особенности движения элементов планеты - мантии (в модели представлена шаром) и литосферы (в модели представлена оболочкой). В частности, удлиненная форма сечений стержня и отверстия, через которое стержень проходит, исключает прокручивание оболочки относительно стержня. Сочетание элементов качения двух типов - шариков и роликов - обеспечивает фиксацию геометрического центра сферической оболочки, что соответствует сохранению положения центра масс планеты при относительном движении ее частей. Шатун обеспечивает перемещение шара, близкое к поступательному, что характерно для мантии в системе координат, связанной с планетой. Вертикальная ось, проходящая через геометрический центр оболочки, соответствует оси суточного вращения планеты. В указанной системе координат ось суточного вращения фиксирована.
Сущность изобретения и выводов, основанных на его применении, поясняется следующими чертежами.
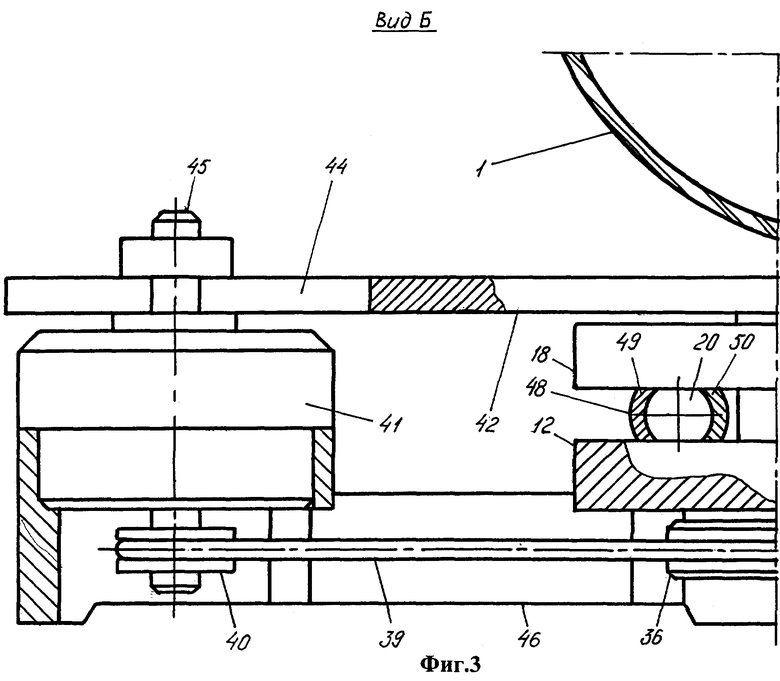
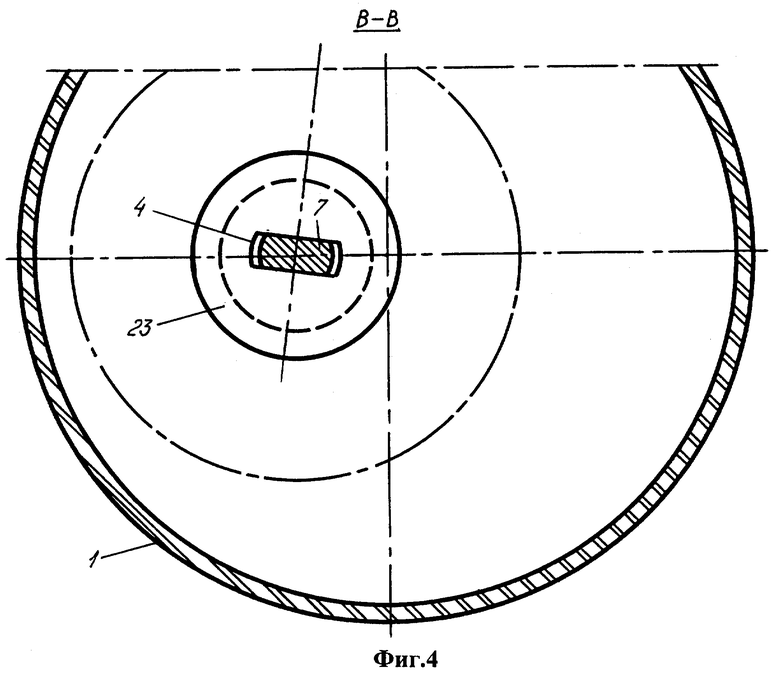
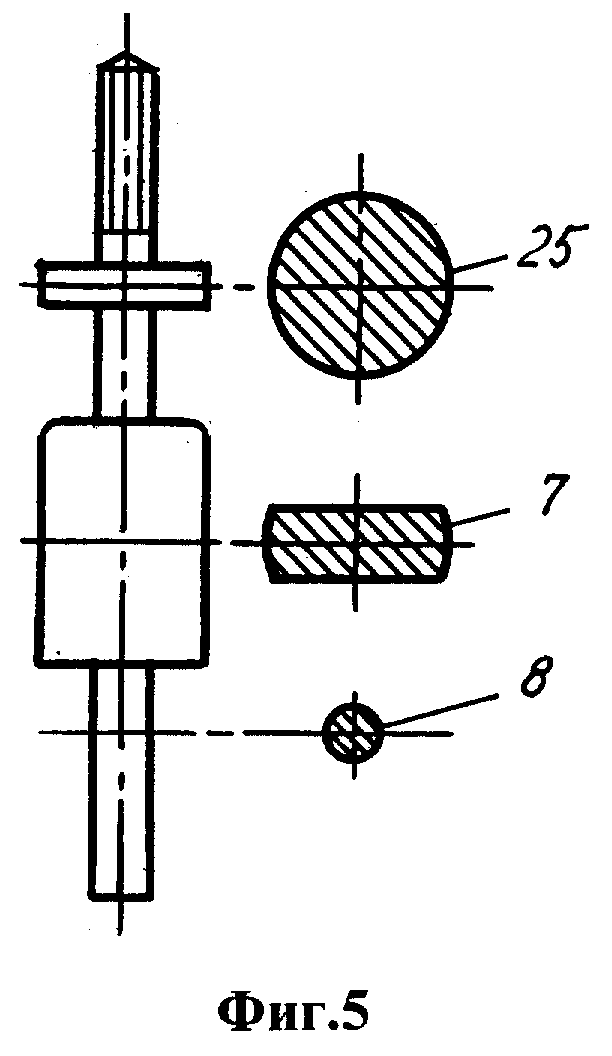
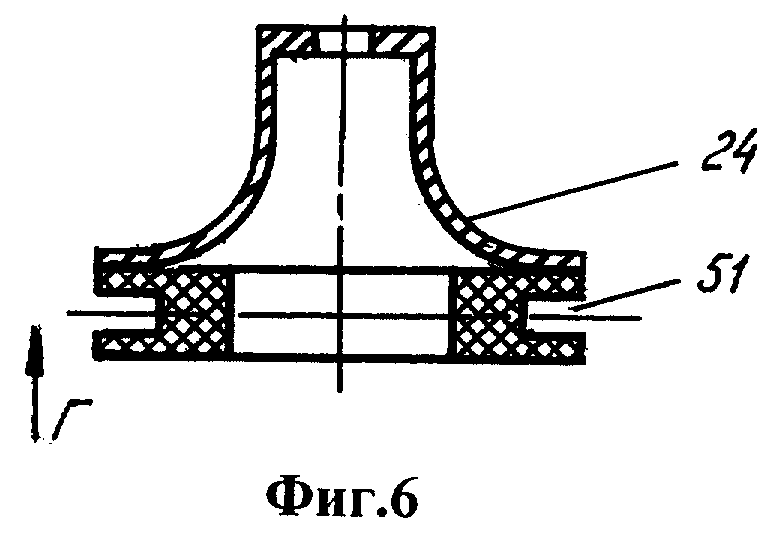
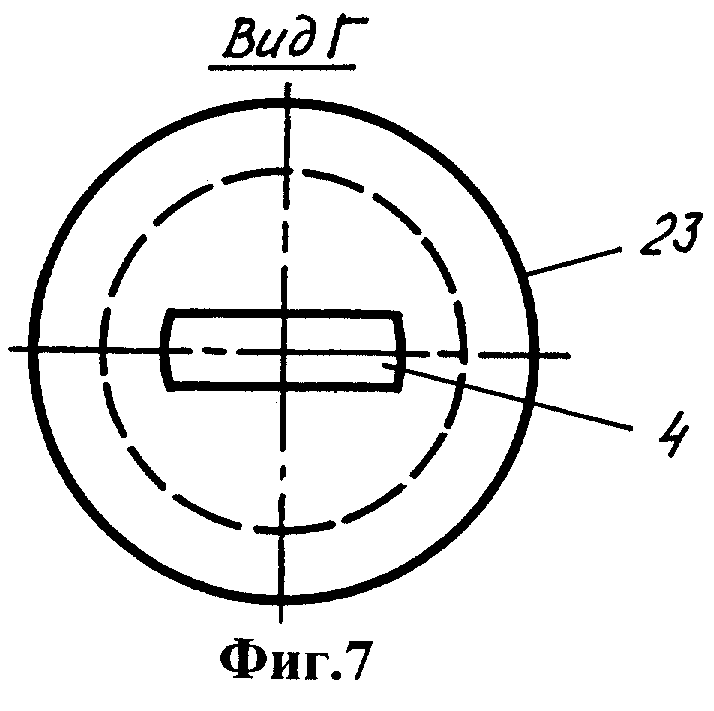
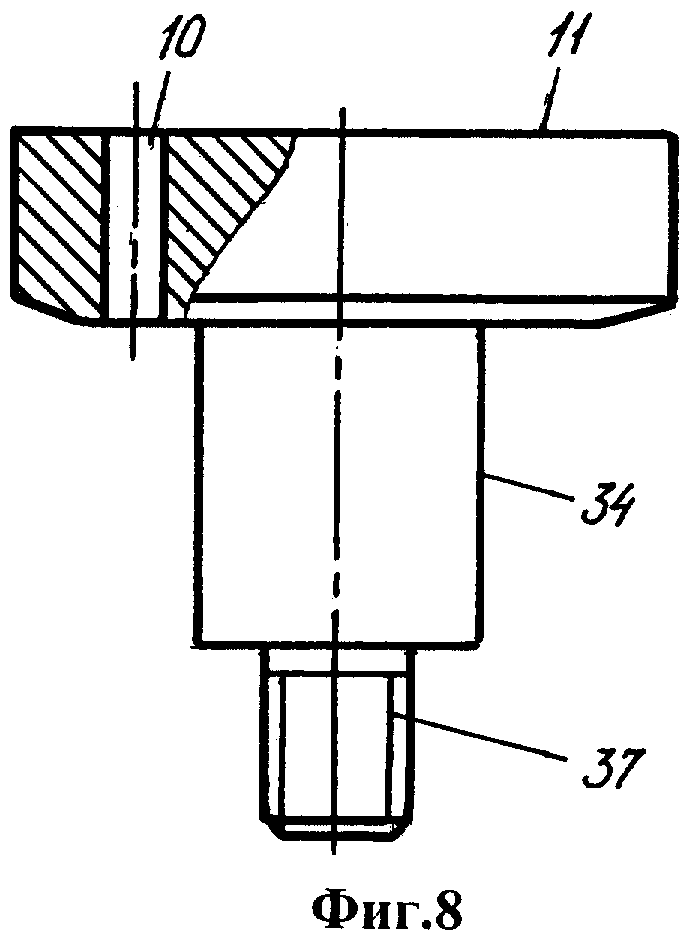
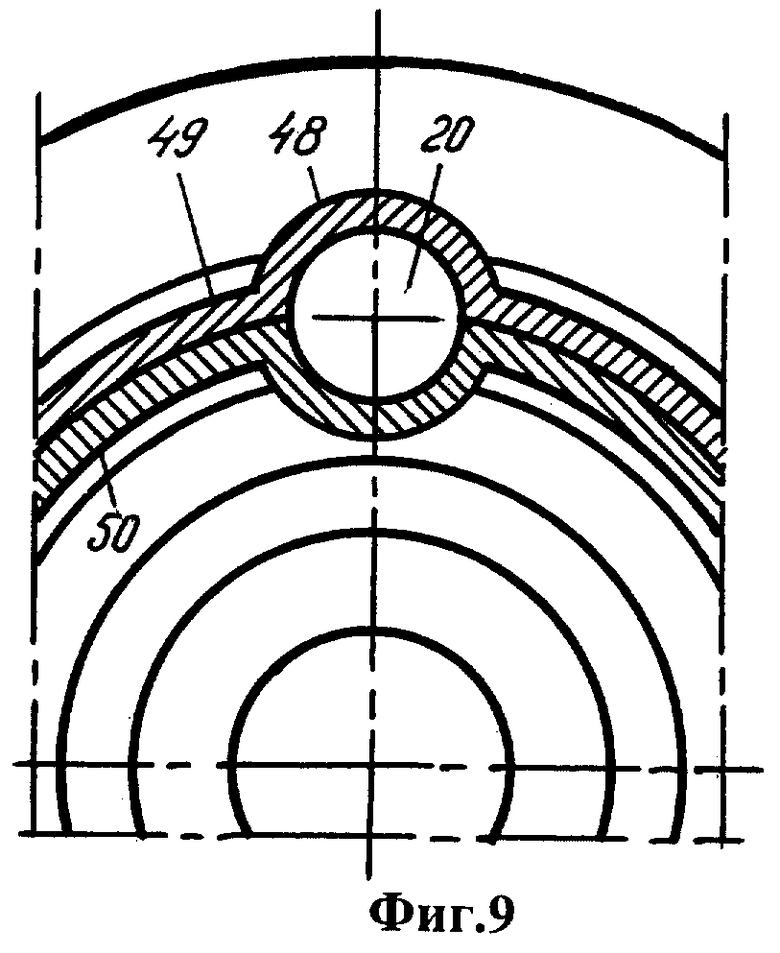
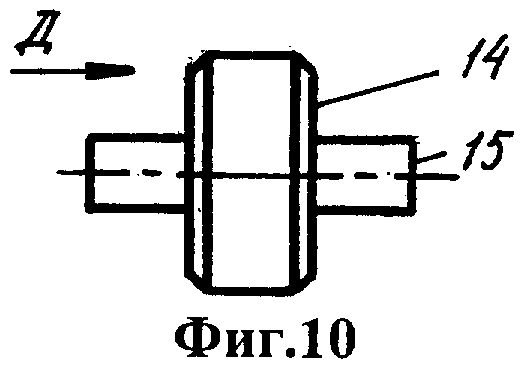
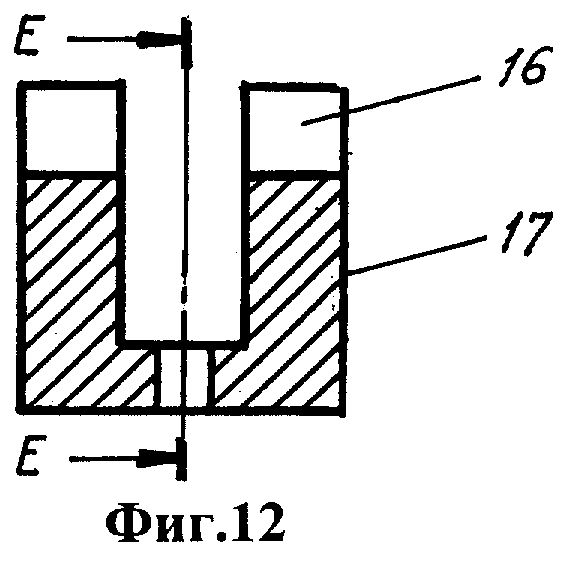
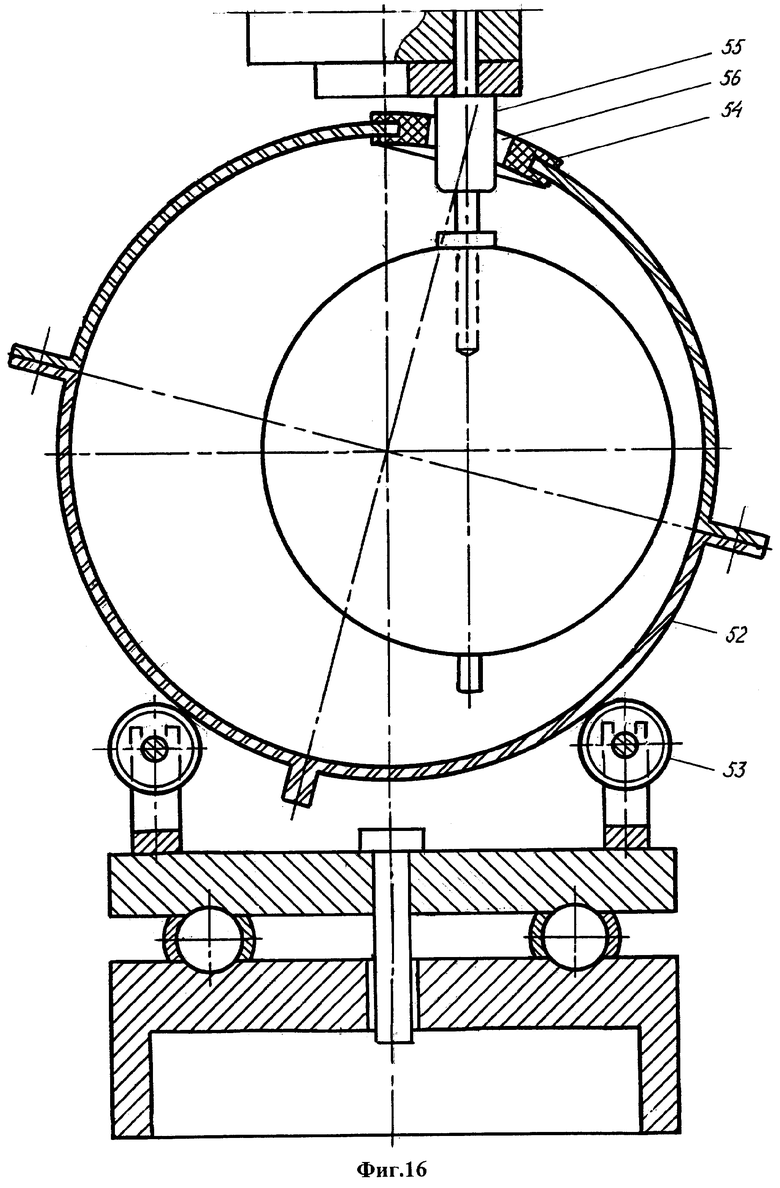
Фиг.1 - устройство для моделирования прецессии литосферы вокруг мантии, общий вид. Фиг.2 - вид А на фиг.1. Фиг.3 - вид Б на фиг.1. Фиг.4 -разрез В-В на фиг.1. Фиг.5 - стержень. Фиг.6 - втулка. Фиг.7 - вид Г на фиг.6. Фиг.8 - вал. Фиг.9 - положение сепаратора и шарика на основании. Фиг.10 - ролик. Фиг.11 - вид Д на фиг.10. Фиг.12 - держатель ролика. Фиг.13 - разрез Е-Е на фиг.12. Фиг.14 - шатун. Фиг.15 - разрез Ж-Ж на фиг.14. Фиг.16 - вариант устройства с расположением колеса над оболочкой.
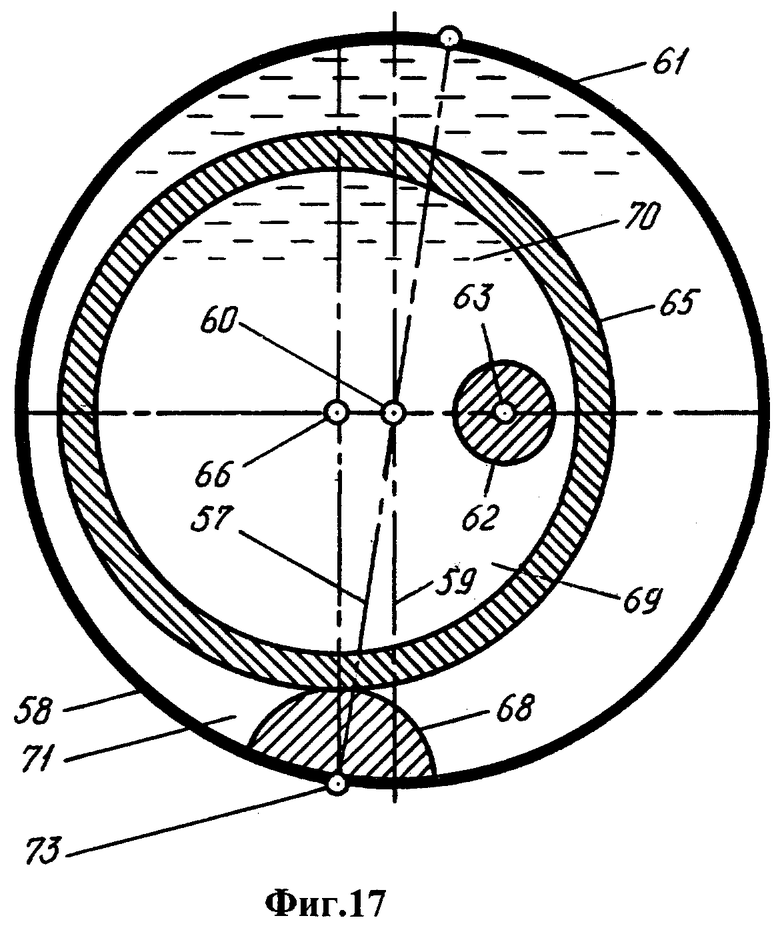
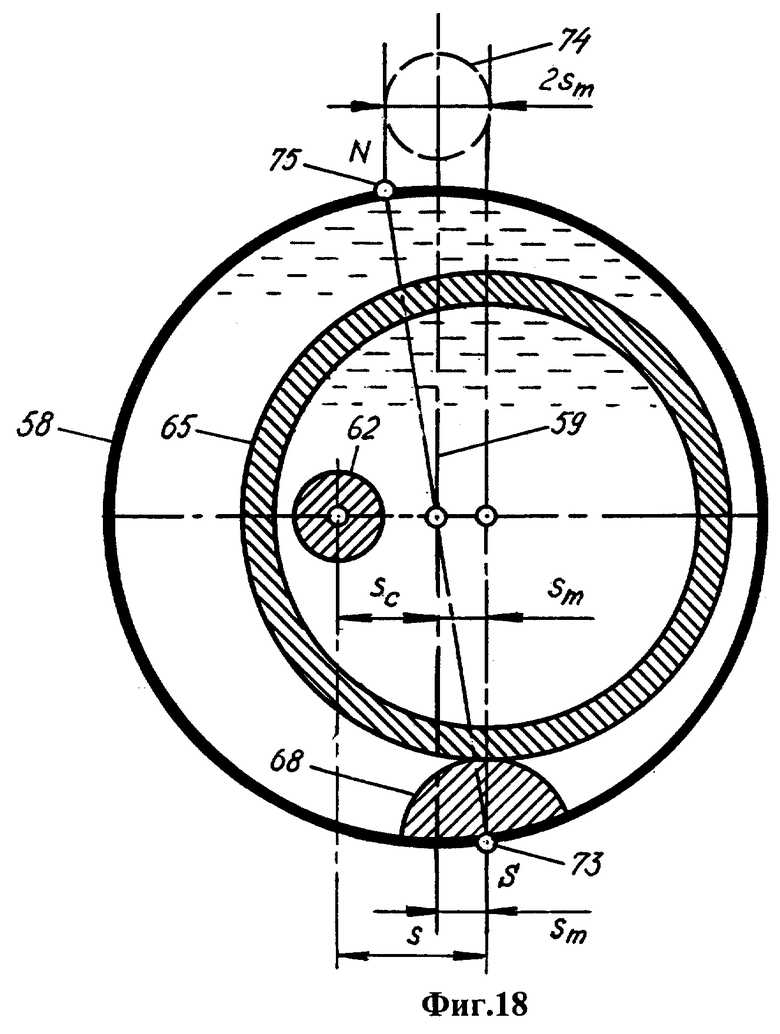
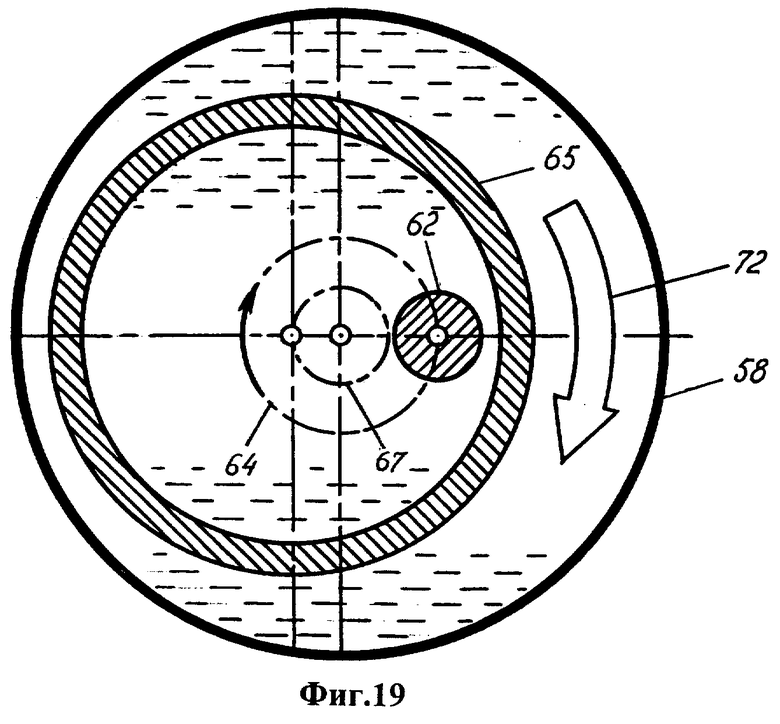
Фиг.17 и 18 - схемы последовательных положений литосферы, мантии и твердого ядра с интервалом в полупериод прецессии (меридиональное сечение планеты). Фиг.19 - схема течения астеносферы в зазоре между мантией и литосферой (экваториальное сечение планеты; течение показано белой стрелкой, орбита твердого ядра вокруг центра масс планеты показана черной стрелкой).
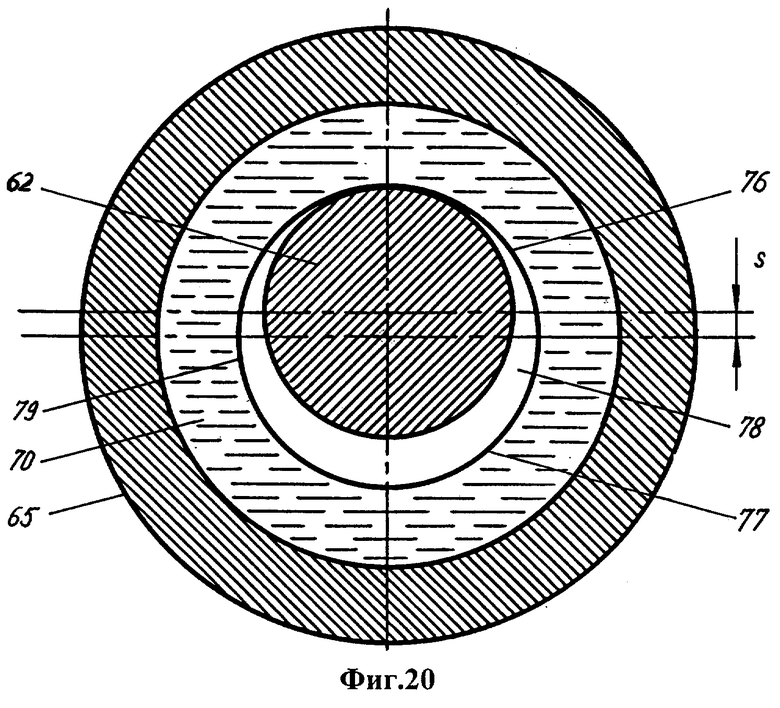
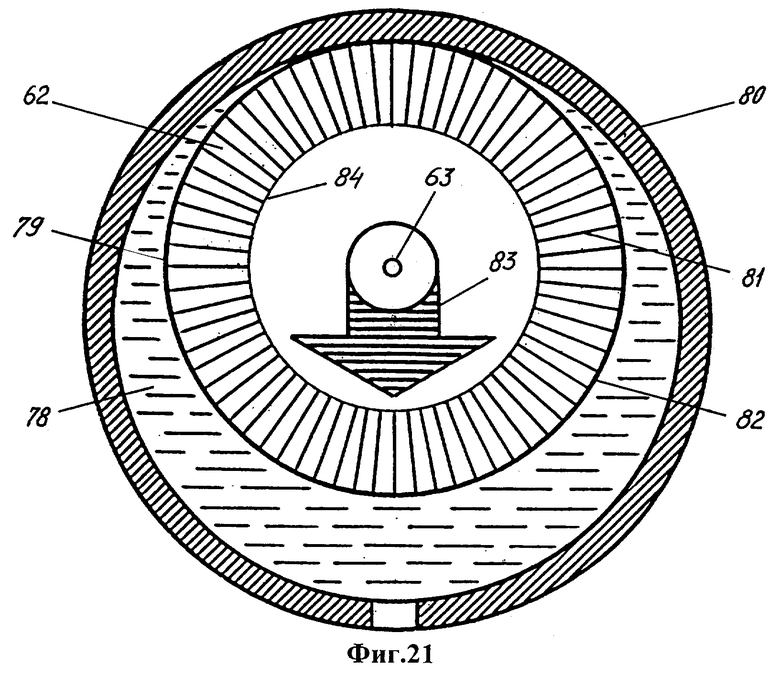
Фиг.20 - схема образования автономной центральной области в полости мантии планеты при спонтанном сдвиге твердого ядра, приводящем к прецессии литосферы. Фиг.21 - схема создания равного давления на ядро при замене свободной поверхности автономной области твердой стенкой сосуда (радиальные штрихи - эпюра давления жидкой среды на поверхность твердого ядра).
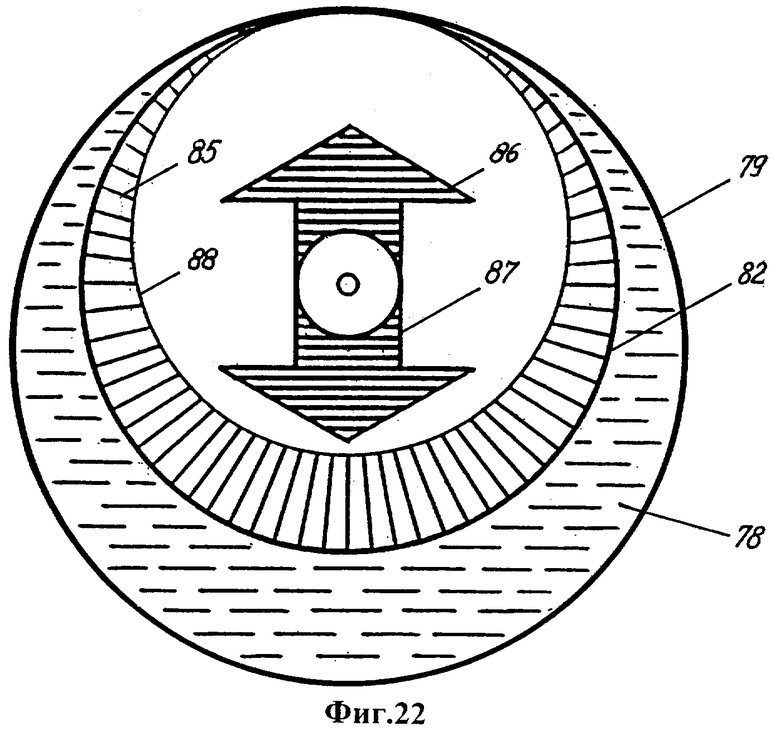
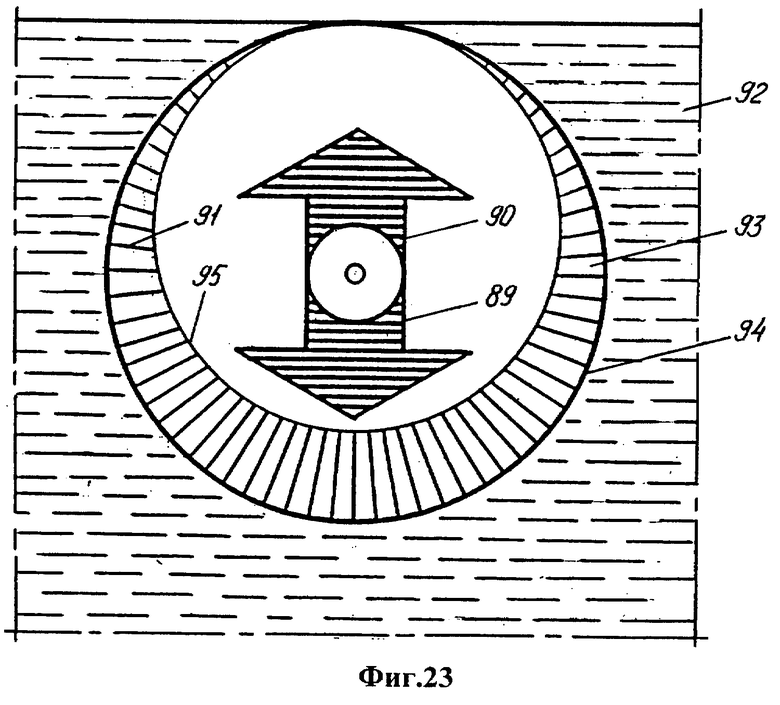
Фиг.22 - схема линейной компенсации тяготения и давления, действующих на твердое ядро в автономной области, имеющей свободную поверхность (как и на фиг.21, показана эпюра давления). Фиг.23 - схема компенсации тяготения и давления у шара, плавающего в жидкости с плотностью, близкой к плотности шара, как иллюстрация взвешенного состояния твердого ядра планеты.
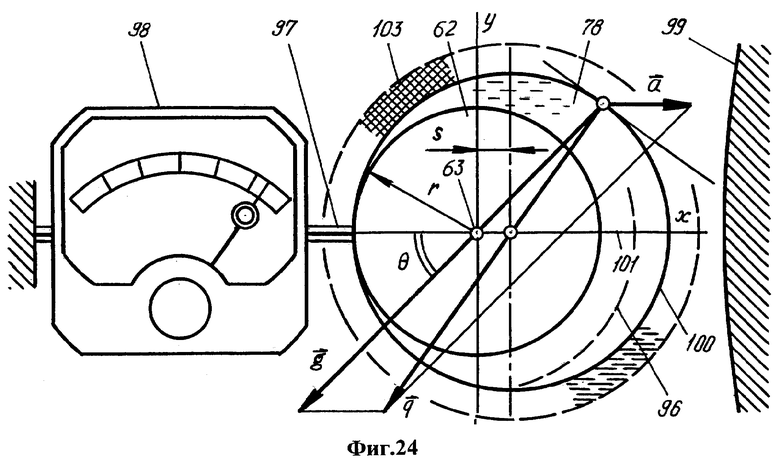
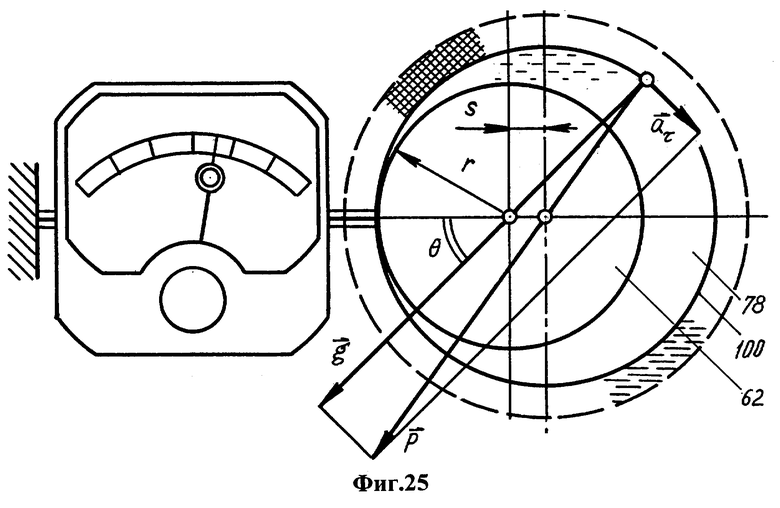
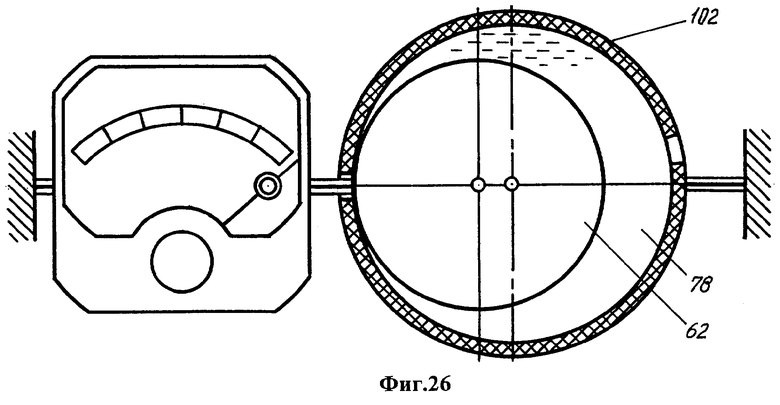
Фиг.24 - схема одностороннего прилива для оценки сверху силы притяжения ядра к жидкой среде. Фиг.25 - схема регистрации силы притяжения ядра, пропорциональной квадрату его смещения. Фиг.26 - схема роста силы притяжения при заключении ядра в закрепленный сосуд.
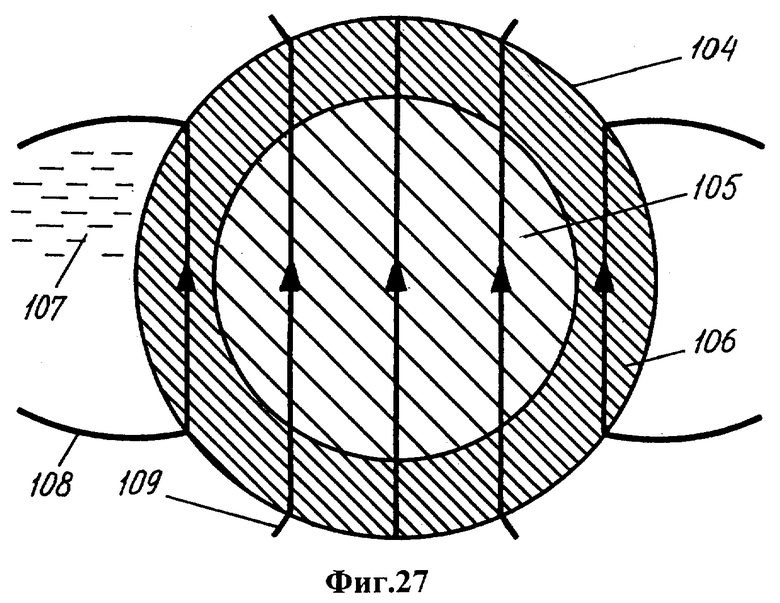
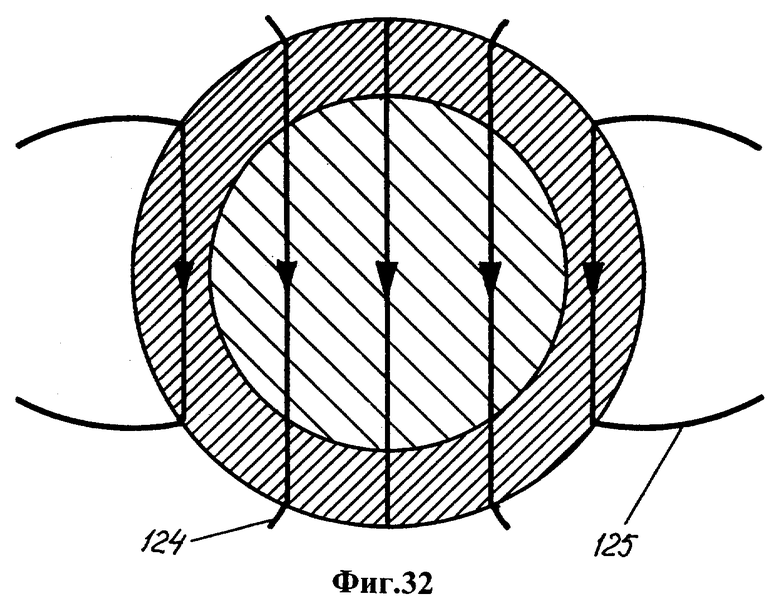
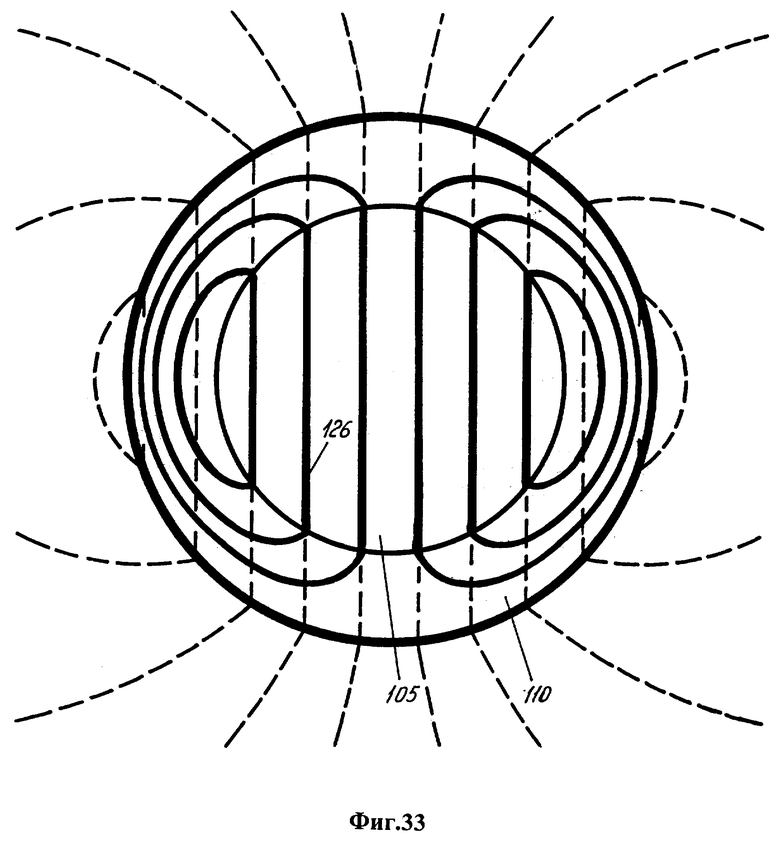
Фиг.27 - 32 - последовательные стадии инверсии геомагнитного поля, создаваемого твердым ядром; ядро состоит из железо-никелевого субъядра и баромагнитной оболочки, содержащей гидриды железа и никеля с примесью диоксида тория, который постепенно разогревает баромагнитную оболочку в результате радиоактивного распада. Фиг.33 - подтверждаемая параметрами прецессии литосферы схема инверсии геомагнитного поля: плавление наружной части твердого ядра и замыкание внутреннего магнитного поля на расплавленную наружную часть.
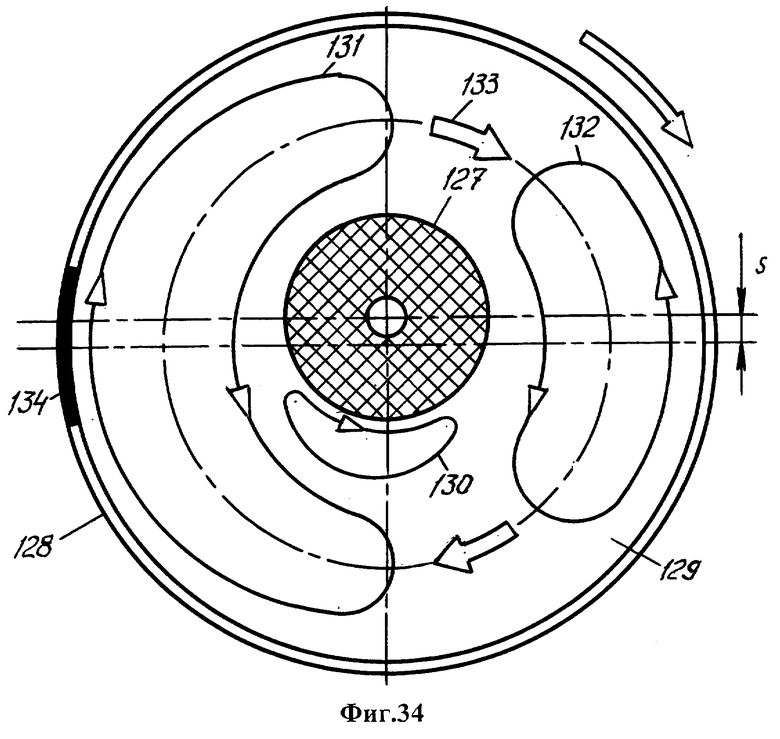
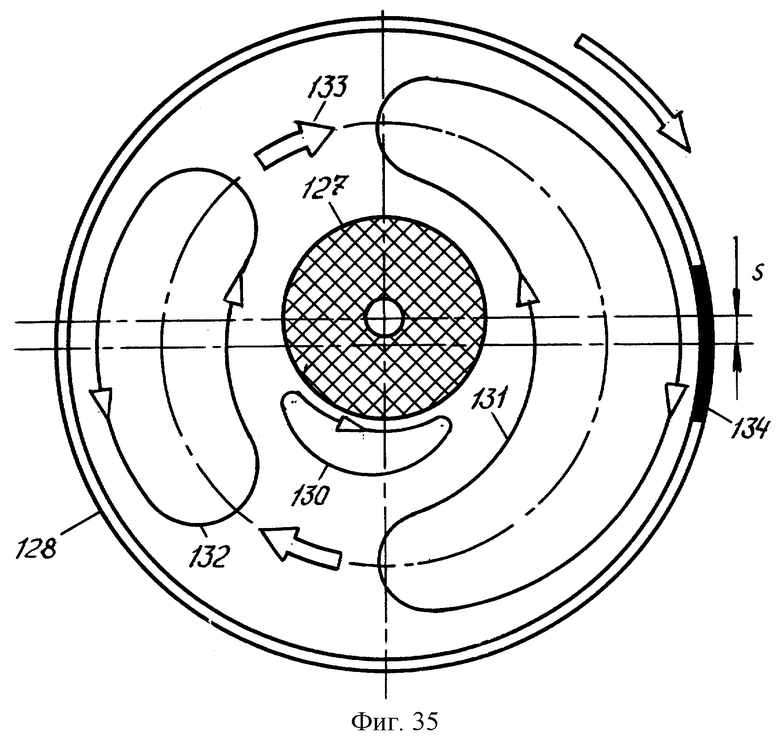
Фиг.34, 35 - фазы течения расплава в полости мантии вокруг твердого ядра при его спонтанном сдвиге от оси вращения планеты, найденные путем моделирования.
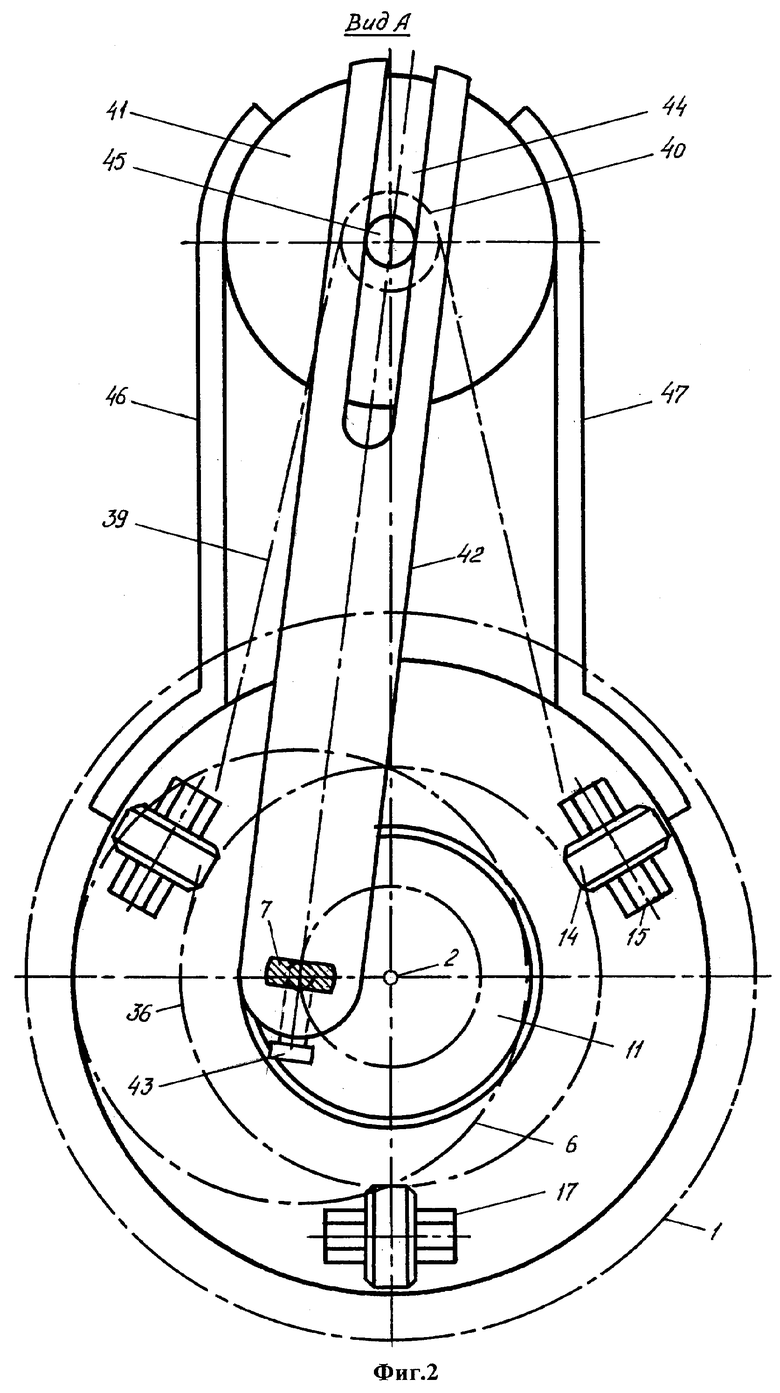
Устройство для моделирования прецессии литосферы вокруг мантии планеты содержит сферическую оболочку 1, геометрический центр 2 которой фиксирован в пространстве. Оболочка имеет возможность поворота вокруг своего геометрического центра. В стенке 3 оболочки выполнено отверстие 4, через которое проходит вертикальный стержень 5, несущий шар 6, расположенный внутри оболочки. Отверстие оболочки и сечение средней части 7 стержня имеют удлиненную форму. Нижний конец 8 стержня снабжен ограничителем 9 поворота и вставлен в вертикальный канал 10 на периферии колеса 11.
Колесо установлено на основании 12 с возможностью вращения вокруг вертикальной оси 13, проходящей через геометрический центр оболочки. Оболочка 1 поддерживается тремя роликами 14, шипы 15 которых ориентированы горизонтально и вставлены в пазы 16 держателей 17. Держатели закреплены на круглой платформе 18, которая снизу имеет кольцевой паз 19 и опирается на шесть шариков 20, расположенных в кольцевом пазу 21 основания. Снизу основание имеет полость 22.
Отверстие 4 выполнено в резиновой втулке 23, встроенной в стенку оболочки. По периметру втулки она скреплена с эластичным колпаком 24, натянутым на кольцевой выступ 25 стержня. В верхней части оболочки расположена горловина 26, закрытая пробкой 27. Оболочка выполнена разъемной из двух полусфер 28, 29, которые смыкаются фланцами 30 и имеют общую с оболочкой ось 31 симметрии, проходящую через горловину и отверстие резиновой втулки, а также через геометрический центр оболочки. На наружную поверхность оболочки нанесена метка 32 в форме выступа для регистрации изменения широты. Оболочка заполнена жидкостью 33, например водой либо глицерином.
Колесо имеет вал 34, на котором закреплены шарикоподшипник 35 и шкив 36, расположенный в полости основания. На нижнем конце вала выполнена резьба 37, на которую навинчена гайка 38, прижимающая шкив 36 к колесу. Шкив колеса соединен ременной тягой 39 со шкивом 40 двигателя 41. Ограничитель поворота выполнен в виде шатуна 42, один конец которого скреплен со стержнем с помощью винта 43, а другой конец имеет паз 44, куда входит неподвижный цилиндрический штырь 45.
Основание и двигатель скреплены боковыми пластинами 46, 47. Шарики 20 заключены в сепаратор 48, составленный из внешнего кольца 49 и внутреннего кольца 50. На боковой поверхности резиновой втулки выполнен паз 51.
В другом варианте устройства (фиг.16) оболочка 52 установлена на роликах 53. Отличие состоит в том, что резиновая втулка 54 и стержень 55, проходящий через ее отверстие 56, расположены в верхней части оболочки, что упрощает герметизацию при заполнении оболочки жидкостью.
Устройство работает следующим образом. Через ременную передачу 35 двигатель 41 приводит во вращение колесо 11 со стержнем 5, угловая ориентация которого фиксирована шатуном 42. Сцепленная со стержнем резиновая втулка 23 описывает круг, что приводит к качанию оси 31 симметрии оболочки относительно фиксированной вертикальной оси 13 в соответствии с качанием оси симметрии литосферы относительно оси вращения планеты. При этом метка 32 смещается на угол Δθ, соответствующий изменению широты, которое одинаково для всех мест литосферы. Закрепленный на стержне шар движется внутри оболочки по круговой орбите и сообщает кольцевое движение жидкости, заключенной в зазоре между шаром и оболочкой, что соответствует течению астеносферы. Ролики обкатывают наружную поверхность оболочки. Круглая платформа совершает вращательные колебания на шариках, перекатывающихся в кольцевом пазу основания.
У Земли толщина литосферы составляет в среднем 100 км, астеносферы - 300 км. Мантией в настоящем описании именуется расположенный под астеносферой относительно твердый слой толщиной около 2000 км (нижняя мантия); между этим слоем и твердым ядром расположен слой расплава такой же толщины (жидкое ядро). В упрощенном виде механизм прецессии литосферы показан на схемах фиг.17-19.
Ось симметрии 57 литосферы 58 качается относительно оси 59 вращения планеты, проходящей через центр масс 60 планеты 61. Качание обусловлено круговыми поступательными движениями двух тел - твердого ядра 62 с центром масс 63 по орбите 64 и мантии 65 с центром масс 66 по орбите 67 при постоянном сцеплении мантии с внутренним выступом 68 литосферы в южно-полярной области. Центры обеих орбит совпадают с центром масс планеты.
Радиусы орбит обозначены соответственно sc и sm. Сумма радиусов равна центробежному смещению s центра масс ядра от центра масс мантии, в которой ядро заменено вытесненным расплавом, s=sc+sm, причем sm≪sc.
Твердое ядро перемещается в полости 69 мантии, заполненной расплавом 70. Между мантией и литосферой расположена астеносфера 71 - слой относительно легкоплавких соединений, находящийся в вязкоупругом состоянии. Движение мантии создает в астеносфере течение 72.
Расположенный на литосфере южный географический полюс 73, обозначенный точкой S (фиг.18), повторяет движение центра масс мантии и перемещается по окружности 74 относительно оси 59 вращения планеты. Такую же окружность, но в противофазе, описывает северный географический полюс 75, обозначенный точкой N. Радиус sm этой окружности определяется центробежным смещением твердого ядра.
Двигаясь указанным образом в системе координат, связанной с планетой, мантия и литосфера сохраняют азимутальную ориентацию, то есть не вращаются вокруг собственных осей. По этой причине качание литосферы сопровождается периодическим изменением широты находящихся на ней предметов, чему в устройстве соответствует изменение широты метки 32.
Относительная разность полярного и экваториального радиусов Земли составляет 1/298, что с достаточным приближением позволяет считать поверхности литосферы и мантии сферическими. Спонтанный сдвиг твердого ядра 62 понижает симметрию полости мантии (фиг.20) и планеты в целом. Есть и другие нарушения симметрии планеты, в частности оцененный далее спонтанный сдвиг мантии относительно литосферы. Однако по размерам они на несколько порядков меньше радиуса Земли и практически не влияют на движение ядра внутри мантии.
Поэтому спонтанный сдвиг ядра рассчитан здесь в условиях сферической симметрии верхних слоев планеты, присоединенных к мантии.
Концентрическая с мантией минимальная сфера 76, содержащая смещенное ядро, ограничивает автономную в гравитационном отношении область 77, в которой ядро взаимодействует с серпообразным слоем 78 расплава. Характер взаимодействия определяется условиями на границе 79 автономной области.
Если бы автономная область была заключена в твердый сосуд 80, способный противостоять нагрузке (фиг.21), то давление 81 расплава было бы одинаково во всех точках поверхности 82 ядра и не давало бы вклада в действующую на ядро силу притяжения 83 (фиг.21, радиальными штрихами показана эпюра 84 давления). В данных условиях твердый сосуд подобен гидравлическому прессу, так как распространяет максимальное давление на всю поверхность ядра. Вместе с тем такое давление создается только в одном месте ядра - там, где столб жидкости достигает максимальной высоты 2s (в наиболее глубоком месте серпообразного слоя).
В соответствии с законом Гука сила притяжения 83 была бы пропорциональна смещению s центра масс ядра от центра масс мантии, как и ускорение силы тяжести. Найденная таким путем линейная по s сила притяжения в 634 раза превосходит центробежную силу, создаваемую суточным вращением Земли, откуда следует вывод об устойчивом центральном положении ядра внутри планеты.
В действительности, однако, гидравлического пресса над твердым ядром нет. Граница 79 автономной области подобна свободной поверхности и, в частности, не совершает работы при поперечном перемещении, сопровождающем движение ядра. В любом месте поверхности твердого ядра давление серпообразного слоя определяется высотой столба жидкости над этим местом. В данных условиях серпообразный слой 78 расплава создает на поверхности 82 смещенного твердого ядра неравномерное давление 85, равнодействующая 86 которого отлична от нуля и компенсирует силу 87 тяготения ядра к центру мантии (фиг.22, длина штрихов показанной эпюры 88 пропорциональна давлению).
Физической иллюстрацией данного явления может служить плавучесть - компенсация силы 89 тяжести предмета равнодействующей силой 90 гидростатического давления 91 жидкости на него снизу. Если в воду 92 погружен шар 93 с плотностью, близкой к плотности воды, то гидростатическое давление 91 распределено по его поверхности 94 так же, как и по поверхности ядра (фиг.23). Эпюра 95 гидростатического давления на плавающий шар совпадает по форме с эпюрой 88 давления на смещенное ядро планеты - в обоих случаях давление пропорционально «глубине», то есть координате, отсчитываемой в направлении силы тяготения.
В указанном смысле ядро способно плавать на притянутом к нему расплаве. Однако в отличие от обычной плавучести тяготение ядра складывается из двух компонент: линейной и квадратичной по расстоянию между центрами масс ядра и мантии. Давление расплава полностью компенсирует линейную компоненту. Остается некомпенсированной относительно малая квадратичная составляющая - активная сила тяготения, способная уравновесить центробежную силу.
Активная сила тяготения твердого ядра 62 к серпообразному слою 78 расплава может быть оценена с помощью мысленного эксперимента (фиг.24-26). Твердое ядро 62, имеющее радиус r и покрытое вначале равномерным слоем 96 расплава толщины s≪r, закрепляют тягой 97, содержащей стрелочный динамометр 98. На достаточном удалении от твердого ядра устанавливают массивный вспомогательный шар 99, гравитационное поле которого вызывает перераспределение расплава и образование приливного горба 100, воспроизводящего форму серпообразного слоя 78.
В меридиональном сечении (показанном на фиг.24) поверхность расплава удовлетворяет уравнению
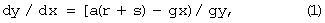
где х (абсцисса) и у (ордината) - прямоугольные координаты с началом в центре 63 масс ядра,
а - ускорение, создаваемое притяжением к вспомогательному шару вдоль оси х и действующее на частицы расплава,
g- ускорение, создаваемое притяжением к эффективной массе ядра (полная масса ядра за вычетом массы вытесненного им расплава),
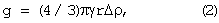
γ=6.672·10-14 м3 г-1с-2 - гравитационная постоянная, а≪g,
Δρ=ρс-ρ - разность средней плотности ρc ядра и плотности ρ расплава у его поверхности,
s - исходная толщина слоя расплава, совпадающая со смещением центра масс твердого ядра от центра масс сферической мантии (в полости которой ядро заменено вытесненным расплавом).
Приведенное уравнение означает, что сумма 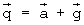 векторов соответствующих ускорений a и g направлена по нормали к поверхности расплава. Использование эффективной массы ядра соответствует вектору
векторов соответствующих ускорений a и g направлена по нормали к поверхности расплава. Использование эффективной массы ядра соответствует вектору 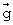 , проходящему через центр 63 масс ядра, что упрощает расчет, не снижая его точности. Использование полной массы ядра и, соответственно, ускорения силы тяжести, проходящего через общий центр масс ядра и слоя расплава, приводит к тому же результату, куда та же самая величина Δρ входит как параметр координаты общего центра масс.
, проходящему через центр 63 масс ядра, что упрощает расчет, не снижая его точности. Использование полной массы ядра и, соответственно, ускорения силы тяжести, проходящего через общий центр масс ядра и слоя расплава, приводит к тому же результату, куда та же самая величина Δρ входит как параметр координаты общего центра масс.
Решением данного уравнения является окружность исходного радиуса r+s,
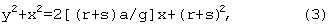
центр которой смещен от центра ядра на расстояние (r+s)a/g. В случае автономной области смещение равно s, ускорение а определяется уравнением s=(r+s)а/g. Отсюда а=(s/r)g с точностью до пренебрежимо малой величины (s/r)2g. С той же относительной точностью масса слоя расплава плотности ρ составляет ms=4πr2sρ.
Создаваемая вспомогательным шаром сила ams воспроизводит геометрию серпообразного слоя 78 (фиг.20, 24) и, следовательно, преодолевает движущую силу G взаимного притяжения ядра и расплава в условиях автономной области планеты. Такой расчет дает оценку движущей силы G сверху
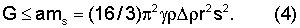
Если вспомогательный шар 99 достаточно быстро удален, горб 100 расплава некоторое время сохранит свою форму благодаря инерции (фиг.25). В данном случае та же самая движущая сила притяжения уравновешивается силами инерции, действующими на расплав вдоль поверхности ядра (нормальная составляющая сил инерции пренебрежимо мала).
Устранение внешнего воздействия дает возможность определить величину движущей силы притяжения ядра с большей точностью. Соответствующее ускорение может быть найдено по уклону свободной поверхности расплава сразу после удаления вспомогательного шара 99 либо, что эквивалентно, как тангенциальная составляющая аτ ускорения а в присутствии вспомогательного шара
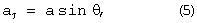
где θ - угол, отсчитываемый от экваториальной плоскости 101 твердого ядра.
Существенно, что при s≪r для образования горба 100 (той же высоты 2s и той же формы) достаточно действия только тангенциальной составляющей аτ ускорения а. Суммарный вектор 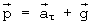 направлен по нормали к поверхности расплава, как и
направлен по нормали к поверхности расплава, как и 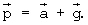 Отсюда следует избыточность нормальной составляющей силы а ms притяжения расплава к вспомогательному шару и возможность применения величины ams именно в качестве оценки сверху для движущей силы G взаимного притяжения расплава и ядра.
Отсюда следует избыточность нормальной составляющей силы а ms притяжения расплава к вспомогательному шару и возможность применения величины ams именно в качестве оценки сверху для движущей силы G взаимного притяжения расплава и ядра.
Вместе с тем, в случае достаточно малого смещения s сила G возникает только за счет тангенциального движения расплава вдоль поверхности ядра. Поскольку тангенциальная составляющая aτ полностью расходуется на остановку этого движения, то рассчитанная по ней суммарная сила торможения расплава должна быть точно равна активной силе притяжения ядра к расплаву.
Слой расплава имеет толщину h=s(1+cosθ) и может быть разбит на кольцевые элементы с объемом
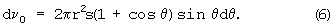
Один элемент испытывает силу притяжения dFτ=aτρdν0. Ее проекция на ось х (направление тяготения ядра) составляет sinθdFτ. На ядро при этом действует сила
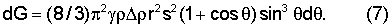
Интегрирование по θ от 0 до π дает искомую активную силу тяготения ядра:
Go(s)=(32/9)π2γρΔρr2s2, (8)
где индекс «о» показывает, что данный результат справедлив при s≪r.
Величина GO(s) в 1.5 раза ниже оценки сверху, полученной путем введения вспомогательного шара 99. С другой стороны, заключение ядра с окружающим его расплавом в закрепленный твердый сосуд 102, действующий как гидравлический пресс, должно значительно повысить силу притяжения (в соответствии со схемой фиг.26). Различие в испытываемых ядром силах схематически отражено в изменении показаний динамометра 98 (фиг.24-26).
Само по себе добавление сферической оболочки 103 (твердой или жидкой) - если она не закреплена, не притягивается к вспомогательному шару и способна перемещаться вместе со слоем расплава, сохраняющим при образовании горба свою сферическую поверхность - не меняет силы, воспринимаемой твердым ядром в данном эксперименте. Использованное неравенство s≪r обычно выполнено в условиях планеты.
Для произвольных значений смещения s движущая сила тяготения ядра может быть найдена из общего уравнения гидродинамики. При скорости жидкости, равной нулю, что соответствует началу обтекания ядра, нелинейные члены отсутствуют:
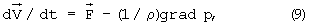
где 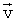 - вектор скорости жидкости, t - время,
- вектор скорости жидкости, t - время, 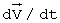 - вектор ускорения жидкости,
- вектор ускорения жидкости, 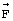 - вектор ускорения избыточной силы тяжести (создается ядром за вычетом массы вытесненной жидкости), ρ - постоянная плотность жидкости, p - избыточное давление. Постоянство плотности упрощает расчет и вместе с тем не вносит, как показано далее, существенной погрешности.
- вектор ускорения избыточной силы тяжести (создается ядром за вычетом массы вытесненной жидкости), ρ - постоянная плотность жидкости, p - избыточное давление. Постоянство плотности упрощает расчет и вместе с тем не вносит, как показано далее, существенной погрешности.
В сферических координатах с началом в центре масс ядра, расстоянием до начала λ и углом θ от оси симметрии (определен выше)
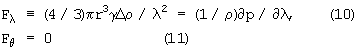
где индексы λ и θ обозначают радиальную и тангенциальную компоненты вектора. Следовательно,
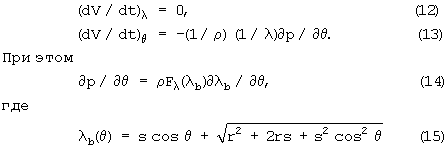
- высота столба жидкости над поверхностью ядра как функция угла θ.
На элемент массы жидкости в виде кольца с радиусом λ sin θ
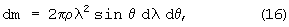
действует сила (dV/dt)θdm, направленная под углом π/2-θ к оси симметрии. Ядро воспринимает ее проекцию на ось симметрии (с обратным знаком)
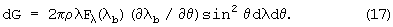
Жидкость занимает область r<λ<λb, 0<θ<π. Интегрирование dG по λ и θ в указанных пределах дает тяготение ядра при любом его сдвиге s в жидкой среде с постоянной плотностью:
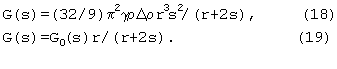
В случае переменной плотности, ρ=ρ(λ), этот результат справедлив с точностью до относительного изменения ρ в области r<λ<λb.
Например, полость мантии Земли с радиусом 3400 км допускает смещение твердого ядра с радиусом r=1670 км на расстояние s=1730 км ≈ r, При этом G(s)/GO(s)=1/3, то есть точная и приближенная формулы дают различие тяготения в 3 раза. В то же время изменение плотности расплава в полости ограничено значениями 10 г см-3<ρ<13 г см-3, то есть составляет 1/1.3 и относительно мало влияет на характер зависимости G(s).
Приведенная схема расчета применима также для точного учета функции ρ(λ). При малых s≪r зависимость G от s переходит в квадратичную, полученную выше.
Расстояние центра масс ядра до оси вращения планеты
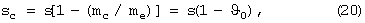
где mc=(4/3)πr3Δρ - избыточная масса ядра, Δρ - разность плотностей ядра и среды, me - масса планеты,
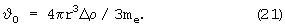
На ядро в текучей среде действует центробежная сила С=mcω2sc, где ω - угловая скорость суточного вращения планеты. Отсюда
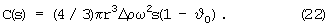
Расстояние s (между центрами масс ядра и мантии) определяется равенством отклоняющей и возвращающей сил, C(s)=G(s), или
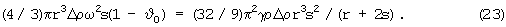
Это уравнение имеет два решения:
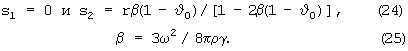
Таким образом, ядро планеты имеет два положения равновесия. Первое совпадает с центральным положением и неустойчиво при любой угловой скорости вращения планеты. Второе устойчиво и удалено от центрального положения на значительное расстояние, которое возрастает как квадрат угловой скорости.
Из полученного результата следует, что все без исключения вращающиеся массы космического происхождения, в том числе планеты и звезды, асимметричны относительно оси вращения.
В соответствии с найденным сдвигом s расстояние sc от оси вращения планеты до центра масс ядра составляет
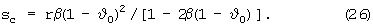
Полученные выражения дают возможность рассматривать в качестве ядра любую внутреннюю оболочку планеты, покрытую слоем жидкости:
1) твердое ядро под расплавом в полости мантии,
2) мантию под текучей средой в полости литосферы,
3) литосферу под океаном со свободной поверхностью.
Во всех трех случаях центральное положение внутренней оболочки неустойчиво, что нарушает симметрию планеты.
В первых двух случаях сдвиг внутренней оболочки мал по сравнению с толщиной слоя жидкости и практически не отражается на форме внешней оболочки. Незначительна, в частности, деформация мантии при сдвиге твердого ядра. Данное условие положено в основу проведенного расчета и обеспечивает точность найденного сдвига. Оба случая включают прецессию литосферы вокруг мантии. В третьем случае расчет применим только качественно из-за относительно малой глубины океана.
Ниже кратко охарактеризованы проявления спонтанного сдвига ядра в каждом из трех случаев.
Для внутреннего твердого ядра у известных планет выполнены условия ϑО≤0.01, β≤0.01, откуда с приемлемой точностью

Для Земли ω=0.7272·10-4 с-1, r=1.67·106 м (внутреннее ядро с твердой баромагнитной оболочкой), ρ=12·106 гм-3, ϑO=3.26·10-3
Отсюда β=0.788·10-3,
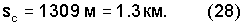
Для Юпитера значения ω=1.7585·10-4 с-1, r=8.57·106 м, ρ=4.15·106 гм-3, ϑO=1.53·10-2 дают β=1.441·10-2,
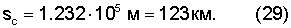
Устойчивое равновесное смещение ядра является радиусом орбиты, по которой перемещается центр масс ядра при вращении планеты вокруг собственной оси. В простейшем случае смещенное ядро неподвижно относительно планеты. При этом диаметрально противоположные точки поверхности ядра испытывают постоянную разность давлений, которая максимальна в направлении вдоль радиуса планеты. На стороне с меньшим давлением ядро плавится, а на противоположной стороне нарастает, что приводит к отставанию центра масс ядра от вращения планеты. Он перемещается по внутренней орбите относительно планеты в обратном направлении.
Инерция ядра способствует его поступательному перемещению, то есть без заметного (за один оборот по орбите) вращения вокруг собственной оси. За период обращения по орбите угол поворота ядра относительно планеты мал (в отличие, например, от Луны, совершающей полный оборот вокруг собственной оси за период обращения вокруг Земли).
Разность давлений на поверхности поступательно движущегося ядра колеблется около нуля с периодом, равным периоду относительного обращения центра масс ядра по своей орбите. Если период достаточно мал (порядка 1 года в случае Земли), разность давлений не успевает существенно повлиять на форму ядра.
Наблюдениями, начатыми в конце 19 века, было обнаружено, что Земля совершает пульсирующую прецессию, преимущественно (но не всегда) в направлении собственного вращения. Круговое перемещение полюсов приводит к колебаниям широты, измеренной по звездам. В 1891 году С.Чандлер обобщил данные многих обсерваторий и выделил колебания полюса с периодом 1.2 года (430 суток) на фоне сезонных колебаний с периодом 1 год. Относительно среднего положения полюс описывает раскручивающиеся и закручивающиеся траектории с запада на восток (за редкими исключениями) в пределах радиуса (0,40)"=12.3 м при среднем радиусе (0,14)"=4.3 м.
Чандлеровские колебания полюса происходят с биениями, уменьшаясь почти до нуля раз в 40 лет. Это указывает на присутствие двух источников колебаний с близкими частотами. Одним из источников признана прецессия оси вращения Земли, предсказанная Эйлером. Учет упругой деформации Земли, проведенный Лявом и Лармором, позволил получить согласие с наблюдаемым периодом 430 суток.
Второй источник колебаний полюса оставался до последнего времени неизвестным. В соответствии с моделированием на предложенном устройстве вторым источником колебаний полюса является прецессия литосферы вокруг мантии планеты, вызванная спонтанным сдвигом внутреннего ядра. Данная прецессия литосферы происходит в направлении, обратном прецессии оси вращения планеты, что соответствует перемещению полюса с востока на запад. Наблюдаемая траектория полюса - результат сложения двух противоположных периодических движений с незначительным преобладанием прецессии оси вращения Земли.
С точностью до отношения масс ядра и планеты (ϑ≤0.01) спонтанный сдвиг ядра Земли не зависит от размера планеты и положения двух твердых оболочек - мантии и литосферы. На него практически не влияет также скорость отставания ядра от вращения планеты. Однако отставание ядра выражается в его движении по круговой орбите внутри планеты. Колебание массы ядра раскачивает твердые оболочки, которые окружены жидкостью и потому свободны в относительном движении. Спонтанный сдвиг ядра - проявление гравитационного равновесия системы. Инерционные колебания выводят систему из этого равновесия.
Непосредственно сила инерции колеблющегося ядра воспринимается твердой мантией, внешний радиус которой равен приблизительно 5970 км. В пределах этого радиуса масса mO мантии составляет 0.9 от массы планеты.
Значительное превосходство мантии по массе над ядром и литосферой дает возможность отдельно оценить колебания мантии, вызванные ядром, и колебания литосферы, вызванные мантией.
Западный дрейф центра масс ядра по орбите с радиусом sc=1.3 км относительно общего центра масс приводит к западному дрейфу центра масс мантии по орбите с радиусом

В соответствии с литературными данными, разность средней плотности ρc твердого ядра и плотности ρ прилегающей к ядру жидкой среды, ρc-ρ=Δρ, может быть принята равной 1 г см-3. Масса Земли me=5.98·1027г, ϑО=3.25·10-3. Подстановка найденных выше значений дает радиус орбиты центра масс мантии

По круговой орбите внутри Земли мантия перемещается поступательно, что обусловлено ее значительной инерцией. Само по себе такое движение не меняет широту. Наблюдаемое изменение широты связано с дополнительным явлением - поворотом литосферы относительно мантии. Этому способствуют два фактора: 1) текучесть астеносферы, отделяющей литосферу от твердой мантии, 2) твердая перемычка 68, соединяющая литосферу с нижней мантией в южно-полярной области (функцию перемычки в описываемом устройстве выполняет стержень 5).
Двигаясь по круговой орбите, мантия увлекает за собой соединенный с нею полярный участок литосферы. Уровень литосферы относительно центра масс планеты стабилизирован течениями в астеносфере, которые восстанавливают гравитационное равновесие. Центр масс литосферы остается почти неподвижным. Проходящая через него ось симметрии литосферы наклоняется к оси вращения Земли и описывает коническую поверхность, совершая таким образом прецессию. В данных условиях амплитуда тангенциального сдвига литосферы вдоль меридиана совпадает с радиусом орбиты мантии (sm) и соответствует наблюдаемым колебаниям широты.
Перемычка 68 допускает малые меридиональные колебания литосферы, однако препятствует непрерывному вращению литосферы относительно мантии вдоль экватора. Элемент планеты с функциями перемычки существует в действительности. Исследования, проведенные недавно методом сейсмической томографии, обнаружили под Антарктидой скопление плотного материала затонувших (при субдукции) плит в виде конуса высотой более 1000 км (Fukao Y., Maruyama S., Inoue H., J.Geol.Soc.Japan, 1994, vol.100, p.7; Добрецов Н.Л., Кирдяшкин А.Г., Кирдяшкин А.А. Глубинная геодинамика, Новосибирск 2001, с. 108). Основанием конус примыкает к Антарктиде по всей ее площади, а вершиной входит глубоко в нижнюю мантию.
В системе «литосфера - астеносфера - мантия» (второй из указанных случаев) вращение планеты приводит к гравитационному равновесию со спонтанным сдвигом sc мантии. Для оценки sc в полученные выше формулы следует подставить значения: r=5970 км, ρ=3.8 г см-3, Δρ=1.7 г см-3. При этом ϑO=0.254, β=2.49·10-3, sc=8.3 км.
В результате спонтанного сдвига мантии ее центр масс постепенно перемещается внутри планеты по орбите с радиусом sc=8.3 км. Литосфера реагирует прецессией, при которой полюс описывает окружность с тем же радиусом 8.3 км. Это является причиной перемещения среднего полюса, вокруг которого совершаются чандлеровские колебания. Расстояние 14.5 м, пройденное средним полюсом за 112 лет (с 1890 по 2002 г.г.), соответствует периоду приблизительно 400 тысяч лет для обращения центра масс мантии по орбите, что связано с относительно высокой вязкостью астеносферы.
Спонтанный сдвиг мантии вносит существенный вклад в различие между главными экваториальными моментами инерции планеты А и В:
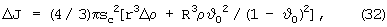
где R - радиус планеты. В условиях Земли ΔJ=0.76·1035 г м2.
Для спутниковой гравиметрии такая величина находится на пределе разрешающей способности из-за сложности расчета системы многих тел и влияния магнитного поля планеты. Из формы геопотенциала рассчитаны, в частности, следующие значения главных моментов инерции Земли (Ж.С.Ержанов, А.А.Калыбаев. Общая теория вращения Земли, Москва, 1984, с.214): А=8.010015·1040 г м2, В=8.010131·1040 г м2, C=8.036381·1040г м2, B-A=12·1035г м2≈10-5A без гарантированной точности.
По порядку величины значение ΔJ, обусловленное сдвигом мантии, близко к измеренной разности В-А и составляет ее заметную часть.
Третий случай относится к спонтанному сдвигу литосферы и означает, что планета не может быть покрыта сплошным океаном равной глубины. Для дна сферической формы различие в глубинах должно быть меньше средней глубины, что исключает образование острова только за счет сдвига литосферы. Однако в сочетании с внутренней активностью планеты сдвиг литосферы может привести к образованию материка только в одном месте океана.
Современные континенты отделились от единого суперконтинента «Гондваны», который 500 миллионов лет назад находился в зоне экватора с одной стороны земного шара и был окружен океаном. В определенной степени образование суперконтинента могло быть связано с описанным выше спонтанным сдвигом.
Тенденция к изменению среднего уровня дна океана вдоль экватора просматривается и в настоящее время, однако замаскирована тектоническими складками. На фоне местной вулканической активности спонтанный сдвиг литосферы сохраняет свое влияние на глобальное формирование дна.
Изложенный механизм колебаний полюса планеты дает возможность оценить вязкость астеносферы. При достаточно высокой вязкости, исключающей течение астеносферы, смещение мантии sm сопровождалось бы таким же смещением внешних слоев - астеносферы и литосферы - относительно центра масс планеты с появлением возвращающей их силы
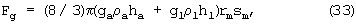
где rm - радиус мантии (с переходным слоем),
gi, ρi, hi - соответственно ускорение силы тяжести на уровне слоя, средняя плотность и толщина слоя для астеносферы (индекс a) и литосферы (индекс l). Этой силе противостоит сила Fs сопротивления вязкого течения астеносферы.
Известно (Лойцянский Л.Г. Механика жидкости и газа, Москва, 1978, с.423), что шар, перемещающийся через центр сферической полости с вязкой жидкостью, испытывает сопротивление
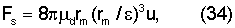
где μd - динамическая вязкость,
ε - зазор между шаром радиуса rm и стенкой полости, ε≪rm,
u - скорость шара.
В данном случае u= Ωsm,
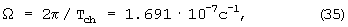
где Tch=430 суток - период качания полюса, ε=ha=300 км - толщина астеносферы, hl=100 км, rm=5970 км, ρa=3.8 г см-3, ρl=3.4 г см-3, ga=10 м с-2, gl=9.8 м с-2. При равенстве сил, Fg=Fs, течение в астеносфере способно уменьшить смещение слоев приблизительно наполовину, чему соответствует вязкость
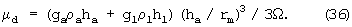
В данных условиях амплитуда колебаний поверхности литосферы порядка sm/2=2 м (наблюдаемая, например, по относительным колебаниям уровня океана) давала бы для вязкости астеносферы оценку 4·1015 П.
Однако согласно наземным и спутниковым данным об уровне морских приливов амплитуда их составляющей с частотой Ω не превосходит 2 см (Desai S.D., J. of Georhysical Research, 2002, vol.107 (С11) р.7,1), то есть оказывается на два порядка ниже указанной величины sm/2. Отсюда следует, что вязкость расплавленной части астеносферы имеет соответственно порядок μd≈10...1014 П, что существенно ниже значения 1018 П, найденного по времени подъема земной поверхности после снятия ледовой нагрузки.
Вместе с тем, оцененная вязкость астеносферы все еще достаточно высока для проведения поперечных сейсмических волн. Полученный здесь результат относится к области астеносферы, центральной по глубине, то есть на 100...200 км глубже дна литосферы.
Соответствие рассчитанной западной компоненты качаний полюса наблюдаемым биениям позволяет использовать чандлеровский период для расчета относительной угловой скорости Ω орбитального движения центра масс ядра против вращения планеты, | Ω|≪|ω|.
При этом абсолютные угловые скорости планеты и центра масс ядра равны соответственно ω и ω- Ω. Если бы центр масс ядра перемещался вместе с планетой ( Ω=0), то мантия с расплавом в ее полости и твердое ядро вращались бы как монолитное твердое тело, то есть без углового отставания ядра. Отсюда следует, что вклад в угловой дрейф ядра дает только относительное перемещение его центра масс, описываемое параметрами Ω и s.
В условиях вращательного отрыва потока (при числах Рейнольдса Re>30) средняя по времени скорость углового отставания твердого ядра от планеты составляет
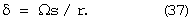
Подстановка r=1.67·106 м и найденных величин s=sc=1320 м, Ω=1.691·10-7 с-1 дает угловую скорость западного дрейфа твердого ядра
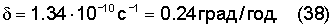
Наблюдаемая угловая скорость западного дрейфа геомагнитного поля
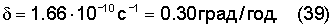
Совпадение рассчитанного и наблюдаемого дрейфа (с точностью 20%), полученное из первых принципов, показывает, что непосредственным источником геомагнитного поля является твердое ядро. В сочетании с фактом инверсий отсюда следует, что твердое ядро включает намагниченную оболочку, которая периодически разогревается до плавления и меняет полярность при повторном затвердевании.
Указанная оболочка, называемая баромагнитной, состоит в основном из гидрида железа и разогревается за счет α-распада диоксида тория, который в виде тугоплавкого песка распределен в расплаве полости мантии и при осаждении накапливается вблизи субъядра.
На современном этапе при сейсмическом зондировании баромагнитная оболочка проявляет себя как переходный слой F толщиной 460 км над железоникелевым субъядром, радиус которого составляет 1210 км. Толщина оболочки и, соответственно, слоя F определяется фазовым переходом, происходящим в гидриде железа при давлении p≈300 ГПа, которое достигается на глубине 4700 км (радиус 1670 км от центра Земли). Вероятной причиной перехода является металлизация абсорбированного водорода, что выражается в изменении характера его связи с железом.
Под давлением 300 ГПа и выше температура магнитного упорядочения вещества оболочки (температура Кюри) превосходит температуру плавления. Магнитное упорядочение обеспечивается существованием бидиполя - сочетания электрического и магнитного дипольных моментов в атоме переходного металла, в данном случае железа.
Благодаря бидиполям внешнее электрическое поле способно намагничивать металлы, не обладающие в исходном состоянии магнитным порядком, в частности, медь, серебро, титан, платину. Этот эффект обнаружен экспериментально на границе металлов с раствором электролита. Источником внешнего поля служил двойной электрический слой. Сопряженные моменты бидиполя ориентированы так, что северный магнитный полюс заряжен положительно, а южный магнитный полюс отрицательно: |S(-)(+)N〉. По отношению к внешним зарядам бидиполь ориентируется противоположным образом:
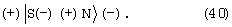
Магнитное упорядочение достигается взаимодействием электрических частей бидиполей:
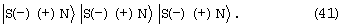
Сверхвысокое давление значительно повышает концентрацию бидиполей, что усиливает их взаимодействие благодаря сближению. Образуются некомпенсированные по спинам заполненные зоны d-электронов. Из-за роста концентрации валентных электронов с давлением уровень Ферми оказывается намного выше заполненной зоны, что ослабляет влияние температуры на магнитный порядок.
Для образования бидиполя благоприятно отсутствие внутренних радиальных узлов у 3d- волновой функции. Металлы групп 4d- и 5d- (например, родий и платина) не ферромагнитны из-за наличия узлов, соответственно, одного и двух. В электрическом поле узлы могут быть исключены, что, в частности, происходит при адсорбции водорода на металле.
Известные электромагнитные явления симметричны. В отличие от случая сегнетомагнетиков, обладающих исходным магнитным порядком, постоянное электрическое поле не может в обычных условиях создать магнитный порядок от нуля, так как это означало бы ничем не обусловленное преимущество одной ориентации магнитного поля над противоположной. В бидиполе электрическое поле предпочитает определенную ориентацию магнитного поля. В этом смысле бидиполь асимметричен (нарушена пространственная четность).
Отдельного внимания в бидиполе заслуживает его электрическая часть: возникновение электрического дипольного момента у атома, который не является водородоподобным. Такой момент обычен для молекулы, но не для атома. Электрическое диполь-дипольное взаимодействие между атомами дает определенный вклад в энергию связи между ними и является дополнительным параметром, определяющим состояние системы. Взаимодействие такого рода возможно и в отсутствие магнитного момента.
Гидрид железа, заполняющий полость мантии, теряет способность к намагничиванию при давлениях ниже 300 ГПа, то есть за пределами центральной области с радиусом 1670 км. Внутри этой области окрестность железоникелевого субъядра намагничена независимо от агрегатного состояния - до и после плавления.
В твердом состоянии вещество баромагнитной оболочки имеет однодоменную структуру, которая энергетически выгодна для намагниченных масс большого размера и обеспечивает стабильность во времени. В этих условиях оболочка служит постоянным магнитом.
При плавлении из-за разрушения дальнего структурного порядка оболочка теряет остаточную индукцию, но приобретает значительную магнитную проницаемость, характерную для магнитомягкого аморфного магнетика. Сохраняя магнитный порядок, расплавленное вещество оболочки образует мезофазу, способную при дальнейшем повышении температуры совершить фазовый переход к немагнитному состоянию.
Внутри намагниченного шара поле однородно (силовые линии параллельны), а вне шара совпадает с полем точечного диполя. В твердой намагниченной оболочке и внутри нее поле однородно при равенстве магнитных проницаемостей обеих областей, что с достаточным приближением выполнено в условиях Земли. Беспрепятственное проникание поля из твердой баромагнитной оболочки в субъядро существенно для механизма геомагнитных инверсий, в процессе которых субъядро выполняет функцию аккумулятора магнитной энергии.
Инверсии геомагнитного поля обусловлены изменением состояния твердого ядра (фиг.27-33).
Преобладающую часть времени (в интервалах между инверсиями) твердое ядро 104 Земли содержит твердое субъядро 105 и твердую баромагнитную оболочку 106, окруженную расплавом 107 полости мантии. При этом вещество оболочки является магнитотвердым и обладает собственной намагниченностью.
Субъядро не намагничено. Силовые линии 108, 109 магнитного поля оболочки (фиг.27) проходят через субъядро, расплав в полости мантии, мантию и литосферу. По величине и направлению поля на поверхности Земли однородная баромагнитная оболочка эквивалентна центральному диполю.
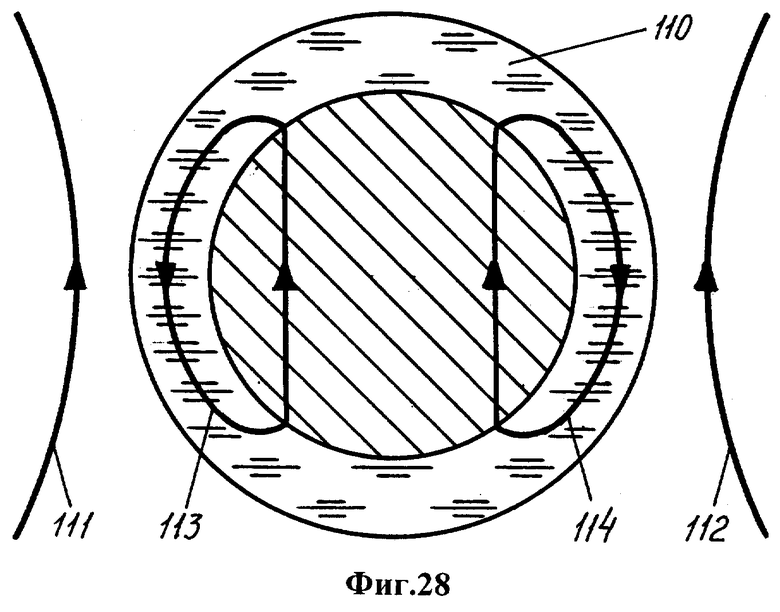
Процесс инверсии начинается плавлением твердой оболочки с образованием расплавленной оболочки 110, вещество которой становится магнитомягким (фиг.28). Связанное с этим изменение магнитного потока возбуждает в субъядре и расплаве полости мантии электрический ток, стремящийся сохранить исходное магнитное поле.
Со временем индуцированное поле рассеивается: в твердом субъядре за счет диффузии
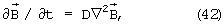
в расплаве полости мантии - за счет диффузии и конвекции
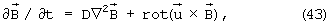
где 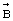 - вектор магнитной индукции,
- вектор магнитной индукции,
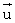 - вектор скорости расплава относительно твердого субъядра,
- вектор скорости расплава относительно твердого субъядра,
D=1/σμ - магнитная вязкость (коэффициент диффузии магнитного поля),
σ - электропроводность,
μ - магнитная проницаемость.
Твердое субъядро и окружающий его расплав имеют различные σ и μ. Проницаемость субъядра равна магнитной постоянной μ0=4π·10-7 Гн м-1 расплавленной баромагнитной оболочки μ>μ0.
Есть основания полагать, что металлическое субъядро имеет более высокую электропроводность, чем гидридный расплав.
В данных условиях независимо от точных значений σ и μ решающим является конвективный член 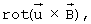 , который обусловлен перемешиванием расплавленной оболочки с ее окрестностью в полости мантии. Благодаря такой конвекции магнитное поле в расплаве оболочки рассеивается значительно быстрее, чем в субъядре. Время сохранения магнитного поля в субъядре приблизительно совпадает с длительностью процесса инверсии, которая, согласно данным палеомагнетизма, имеет порядок 104 лет.
, который обусловлен перемешиванием расплавленной оболочки с ее окрестностью в полости мантии. Благодаря такой конвекции магнитное поле в расплаве оболочки рассеивается значительно быстрее, чем в субъядре. Время сохранения магнитного поля в субъядре приблизительно совпадает с длительностью процесса инверсии, которая, согласно данным палеомагнетизма, имеет порядок 104 лет.
Последнее дает возможность оценить электропроводность субъядра σs. Время диффузионного рассеяния поля в области с характерным размером Ld составляет τd≈Ld 2/D=Ld 2 σ/μ.
При Ld≈600 км (наружный слой субъядра толщиной в половину его радиуса), τd≈104 лет и μ=μ0 отсюда следует σs=7·105 См м-1. Это значение на порядок ниже электропроводности железа в нормальных условиях:1.1·10 См м-1
При рассеянии исходного поля расплавленной оболочки силовые линии 111, 112 перемещаются из нее в глубь жидкого ядра (фиг.28). По завершении конвекции сохранившееся поле субъядра замыкается на расплавленную оболочку и создает в ней - как в шунте - поле противоположного направления с силовыми линиями 113, 114.
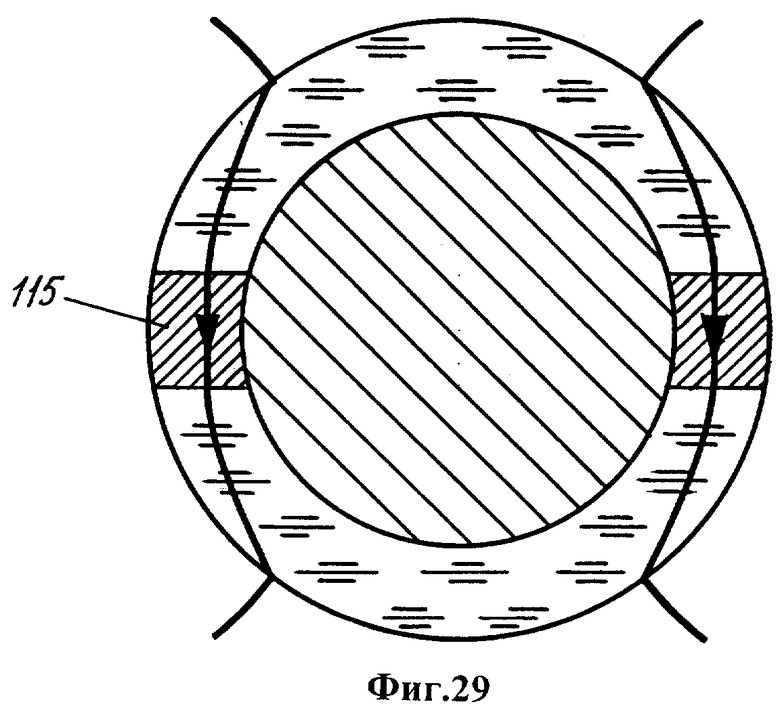
На границе с мантией в поверхностном слое расплава существует течение, направленное от полюсов к экватору. Субъядро от этой границы отделяют 2200 км, и течение до субъядра непосредственно не доходит. Однако оно способствует относительному понижению температуры во всем экваториальном сечении полости мантии. По этой причине в процессе охлаждения расплавленной оболочки наиболее низкая температура достигается на ее экваторе.
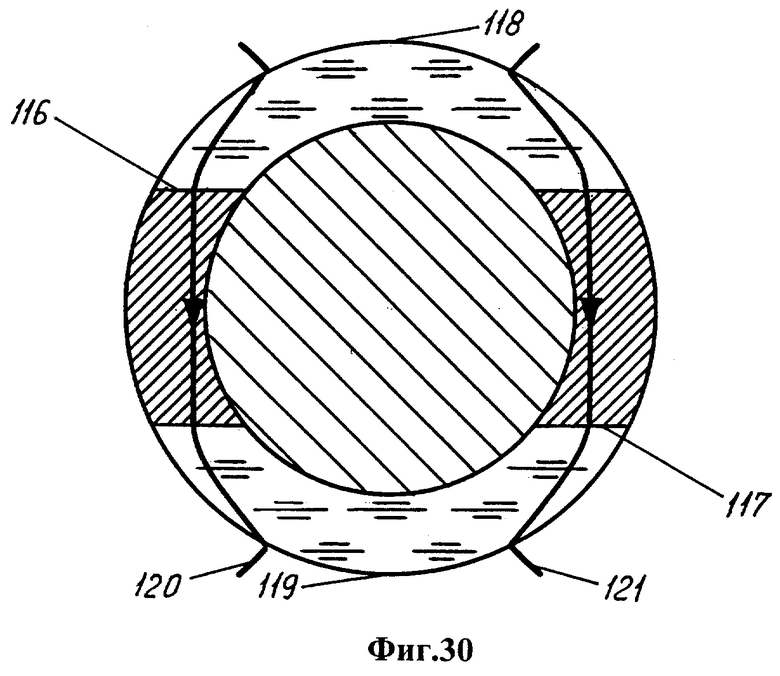
Первой затвердевает экваториальная область 115 оболочки, приобретающая постоянную намагниченность в направлении наведенной намагниченности расплавленного шунта (фиг.29). Исходное поле субъядра постепенно ослабевает. Фронт затвердевания 116, 117 оболочки распространяется к ее полярным областям 118, 119.
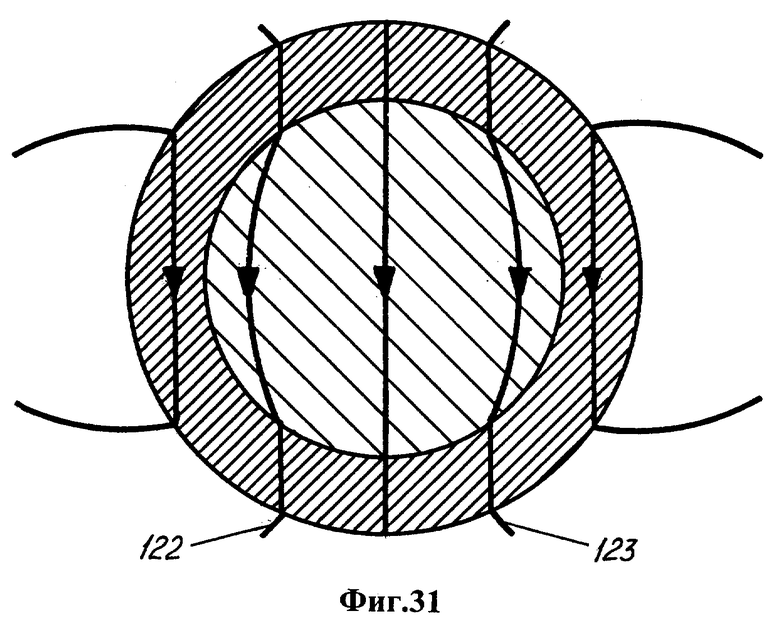
В затвердевшей части оболочки силовые линии 120, 121 магнитного поля сохраняют направление, заданное экваториальной областью (фиг.30). Полное затвердевание оболочки сопровождается прониканием в субъядро новых силовых линий 122, 123 (фиг.31).
Процесс инверсии заканчивается формированием стационарного в среднем магнитного поля твердого ядра с направлением силовых линий 124, 125, противоположным исходному (фиг.32). Затвердевшая оболочка обладает значительной коэрцитивностью, которая обеспечивает длительное сохранение поля установившегося направления.
Кульминационной фазой описанного процесса инверсии является замыкание силовых линий 126 магнитного поля субъядра 105 на расплавленную баромагнитную оболочку 110 (фиг.33). Затвердевание оболочки замораживает поле, наведенное в ней как в шунте. Ориентация поля воспроизводится на фронте затвердевания благодаря безузловому упорядочению, поддерживающему параллельность спинов затвердевшей и жидкой фаз, что возможно без наложения внешнего поля. При разогреве затвердевшей баромагнитной оболочки описанный цикл повторяется и заканчивается очередной переориентацией магнитного диполя Земли.
В соответствии с изложенным моделирование прецессии литосферы и западного дрейфа твердого ядра планеты содействует решению проблем тяготения в жидкой среде и происхождения магнитного поля Земли.
При моделировании обнаружен вращательный отрыв потока - явление, важное для гидродинамики. Им вызвано движение ядра 127, свободно взвешенного во вращающемся сферическом сосуде 128 с жидкостью 129 (фиг.34, 35). Сосуд выполняет роль мантии.
Механизм вращательного отрыва потока состоит в том, что при смещении неподвижного центра масс ядра от оси вращения сосуда у поверхности ядра образуется область 130 обратного течения, размер которой увеличивается со смещением s. Обратное течение тормозит вращение ядра. С помощью электродов, чувствительных к скорости течения, выявлены два вихря 131 и 132, переносимые течением 133 вокруг ядра с периодом, который точно равен периоду вращения сосуда. Вихри как бы прикреплены к определенным местам 134 сосуда и неограниченное время следуют за ними, несмотря на отсутствие заметных отклонений формы сосуда от симметрии тела вращения. После перерыва во вращении места локализации вихрей в сосуде воспроизводятся. Вихрь 131, вращающийся в направлении вращения сосуда, в два раза больше по размеру вдоль экватора, чем вихрь 132, вращающийся в противоположном направлении.
В цилиндрическом сосуде - в отличие от сферического - синхронизация вихрей с вращением сосуда отсутствует.

Изобретение может быть использовано в качестве наглядного пособия в учебных программах и для анализа астрономических явлений в научных исследованиях. Изобретение направлено на обеспечение возможности моделирования прецессии литосферы вокруг мантии планеты и содержит сферическую оболочку, геометрический центр которой фиксирован в пространстве и которая имеет возможность поворота. В оболочке выполнено отверстие, через которое проходит вертикальный стержень, несущий шар, расположенный внутри оболочки. Отверстие оболочки и сечение стержня имеют удлиненную форму. Выступающий из оболочки конец стержня снабжен ограничителем поворота и входит в вертикальный канал на периферии колеса, установленного с возможностью вращения вокруг вертикальной оси, проходящей через геометрический центр оболочки. Колесо соединено с двигателем. Оболочка заполнена жидкостью и установлена на трех роликах с ориентированными горизонтально цилиндрическими шипами. Держатели шипов закреплены на верхней стороне круглой платформы. Нижняя сторона платформы имеет кольцевой паз и опирается на шарики, расположенные в кольцевом пазу основания. Отверстие для стержня выполнено в резиновой втулке, расположенной в стенке оболочки. Ограничитель поворота выполнен в виде кривошипа, один конец которого скреплен со стержнем, а другой конец имеет паз, куда входит неподвижный цилиндрический штырь. При моделировании оболочка воспроизводит движение литосферы планеты, а шар внутри оболочки - движение мантии, обусловленное центробежным смещением твердого ядра. Стержень соответствует перемычке, соединяющей литосферу с мантией в южно-полярной области планеты. Поступательное движение мантии по круговой орбите преобразуется посредством перемычки в качания литосферы. Период качания литосферы равен времени обращения твердого ядра по орбите внутри мантии. Рассчитанный по этому параметру западный дрейф твердого ядра совпадает с наблюдаемым дрейфом геомагнитного поля. Данное совпадение раскрывает причину инверсий геомагнитного поля. Они обусловлены периодическим плавлением намагниченного покрытия твердого ядра и замыканием магнитного поля, аккумулированного во внутренней части твердого ядра, на расплавленное покрытие. Западный дрейф твердого ядра сопровождается вращательными автоколебаниями расплава в полости мантии с периодом, равным времени обращения твердого ядра по орбите. Из параметров прецессии литосферы следует оценка вязкости астеносферы порядка 1014 П. 13 з.п.ф-лы, 35 ил.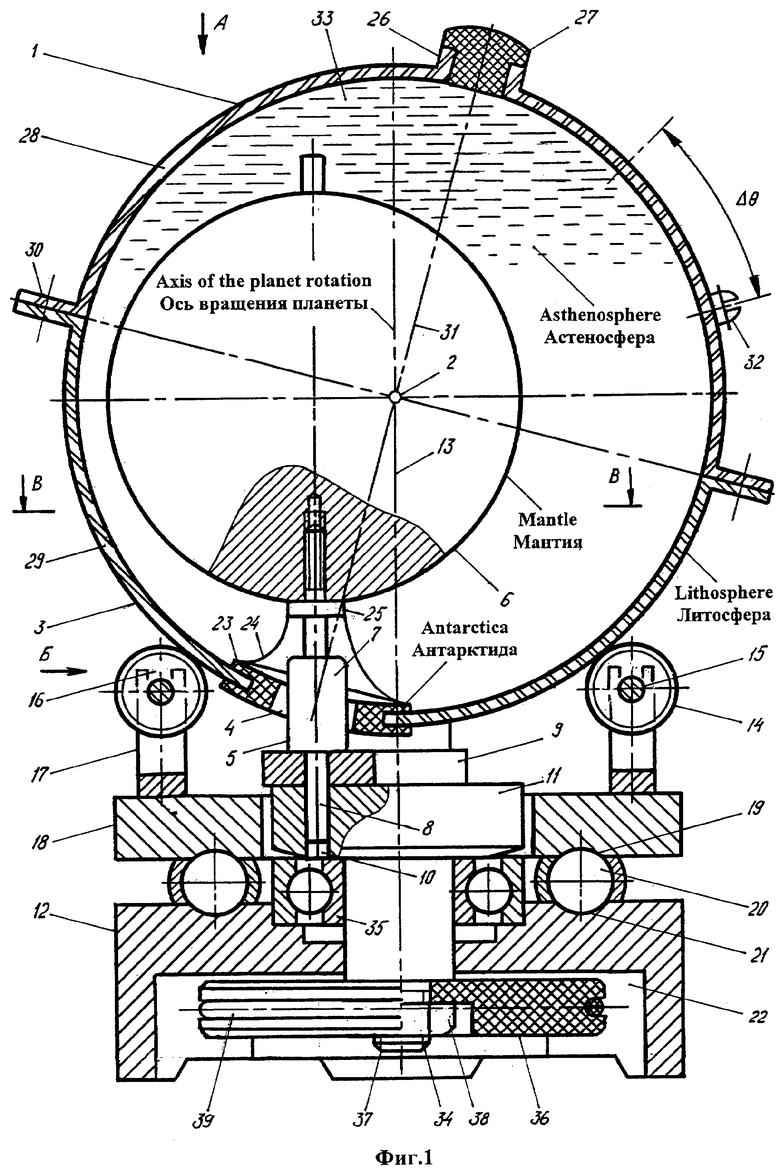
| СПОСОБ ОПРЕДЕЛЕНИЯ КРИТИЧЕСКОГО ЗНАЧЕНИЯ ОКРУЖНОЙ СКОРОСТИ ЦЕНТРА МАССЫ ТВЕРДОГО ТЕЛА НА СООТВЕТСТВУЮЩЕМ РАДИУСЕ ЕГО ВРАЩЕНИЯ | 1997 |
|
RU2131610C1 |
Авторы
Даты
2005-11-10—Публикация
2004-06-18—Подача