Изобретение относится к области радиолокации, в частности к первичной обработке эхо-сигналов в радиолокационной станции (РЛС), и может быть использовано при обнаружении полезных сигналов на фоне шума.
Качество обнаружения полезных сигналов на фоне шума в значительной степени зависит от эффективности средств фильтрации приемного тракта РЛС, в частности, на участке между фазовым и амплитудным детекторами, где осуществляется когерентная обработка сигналов. В связи с этим важнейшей задачей синтеза обработки сигналов на фоне шума является выбор способа фильтрации, позволяющего эффективно накопить энергию сигнала, ослабив при этом маскирующее влияние шума (см. Справочник по радиолокации. Под ред. М. Сколника. М., "Советское радио", 1979, т.3, с.162-163).
Известны способы аналоговой обработки радиолокационных сигналов, основанные на использовании оптимального аналогового фильтра, максимизирующего отношение сигнал-шум. Передаточную характеристику К(ω) такого фильтра с точностью до не оказывающего на качество фильтрации влияния постоянного коэффициента (при этом коэффициент в дальнейшем в соотношениях будем опускать) определяют по формуле

где ω - частота;
S*(ω) - комплексно-сопряженный спектр полезного сигнала;
N(ω) - спектральная плотность мощности шума (см., например, книгу Кука Ч. и Бернфельда М. Радиолокационные сигналы. Теория и применение. Пер. с англ. М., "Советское радио", 1971, с.34, равенство 2.19а).
Несомненным достоинством аналоговой фильтрации является независимость обеспечиваемого качества обнаружения от времени прихода полезного сигнала. Однако, при практической реализации аналоговые фильтры обладают рядом значительных недостатков, таких как большое затухание сигнала в линии задержки, сложность перестройки параметров и др. Особенно эти недостатки ощутимы при обработке сигналов со сложными законами внутриимпульсной модуляции: фазоманипулированных сигналов, сигналов с различными законами частотной модуляции и т.д.
Гораздо большими возможностями в отношении устранения указанных недостатков обладает дискретная обработка сигналов, обычно реализуемая на основе цифровых устройств, обладающих повышенной надежностью, технологической гибкостью, оперативностью перестройки параметров и другими преимуществами. В качестве примера дискретной обработки можно сослаться на обработку, основанную на использовании оптимального дискретного фильтра, максимизирующего выходное отношение сигнал-шум, и характеризующуюся во временной области весовым вектором W, который определяют по формуле

где Ф - корреляционная матрица шума;
S - вектор полезного сигнала
(см. книгу Ширмана Я.Д. и Манжоса В.Н. Теория и техника обработки радиолокационной информации на фоне помех, М., "Радио и связь", 1981, с.23, равенство 3.17).
Однако, когда исходный процесс после фазового детектора, подлежащий обработке, является непрерывным во времени (аналоговым), дискретная обработка не может быть реализована в "чистом" виде. Она предполагает временную дискретизацию аналогового процесса, которая осуществляется после предварительного ограничения полосы частот, занимаемой входной смесью сигнала и шума. Такое ограничение реализуется с помощью полосового аналогового фильтра и необходимо для приведения полосы частот исходного аналогового процесса в соответствие с шагом временной дискретизации согласно условиям теоремы Котельникова (см. указанную в наст. описании книгу Ширмана Я.Д. и Манжоса В.Н., с.147). Таким образом, вся обработка в целом является аналого-дискретной (см. также книгу Цикина И.А. Дискретно-аналоговая обработка сигналов. М., "Радио и связь", 1982, с.126). При этом вид вектора S, фигурирующего в приведенном в настоящем описании соотношении (2), зависит от времени прихода аналогового полезного сигнала, а точнее, от его положения относительно моментов временной дискретизации.
Для пояснения этого временное положение аналогового полезного сигнала Δt можно представить в виде

где Δt - шаг временной дискретизации;
N - целое число;
τ - часть временной задержки, принимающая значения из интервала 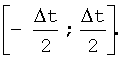
Очевидно, что вид вектора S зависит только от составляющей τ полной задержки. Поэтому в дальнейшем имеет значение только эта зависимость, а составляющая N×Δt без потери общности полагается равной нулю.
С учетом изложенного в качестве прототипа выбран способ аналого-дискретной обработки радиолокационных сигналов, поступающих на видеочастоте с фазового детектора, включающий аналоговую фильтрацию с помощью фильтра нижних частот, предназначенную для приведения ширины спектра процесса в соответствие с шагом последующей временной дискретизации, аналого-дискретное преобразование процесса с некоторым временным шагом Δt и многоканальную дискретную обработку, каждый из каналов которой содержит дискретный фильтр с весовым вектором W вида (2), соответствующий определенному времени прихода полезного сигнала, и устройство некогерентной обработки, которое кроме амплитудного детектора может содержать устройства межпериодной обработки пачки импульсов. Выходные сигналы устройств некогерентной обработки объединяют в блоке отбора максимального из них, последний затем сравнивают с заданным порогом обнаружения для принятия решения о наличии или отсутствии во входной смеси полезного сигнала (см. указанную в наст. описании книгу Ширмана Я.Д. и Манжоса В.Н., с. 146-150).
Основным недостатком этого способа обработки является многоканальность дискретной фильтрации (см. книгу Ширмана Я.Д. и Манжоса В.Н., с.149), которая вытекает из общей теории оптимального обнаружения (см. эту же книгу Ширмана Я.Д. и Манжоса В.Н., с.304-306), что с учетом последующей некогерентной обработки, а также необходимости отбора максимума, приводит к значительным аппаратурным затратам при практической реализации.
Техническим результатом предлагаемого изобретения является снижение аппаратурных затрат на обработку радиолокационных сигналов при минимальном значении возникающих потерь в отношении сигнал-шум.
Указанный технический результат достигается тем, что в способе аналого-дискретной обработки радиолокационных импульсных сигналов с неизвестным временным положением, поступающих в приемном тракте с фазового детектора на видеочастоте, путем когерентной обработки, включающей предварительную аналоговую фильтрацию, аналого-цифровое преобразование и дискретную фильтрацию, с последующей некогерентной обработкой и сравнением с заданным порогом обнаружения, формируют аналого-дискретный фильтр с общей передаточной характеристикой К(ω) и с помощью его проводят указанную когерентную обработку сигналов, при этом передаточную характеристику К(ω) сформированного аналого-дискретного фильтра определяют по формуле
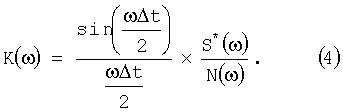
Предлагаемый способ позволяет параллельный набор дискретных фильтров заменить единственным дискретным фильтром с оптимизацией пары аналоговый фильтр - дискретный фильтр как единого аналого-дискретного фильтра (АДФ) по критерию максимума среднего по времени прихода полезного сигнала выходного отношения сигнал-шум, что приводит к оптимальной по этому критерию передаточной характеристике К(ω) АДФ, определяемой по формуле (4).
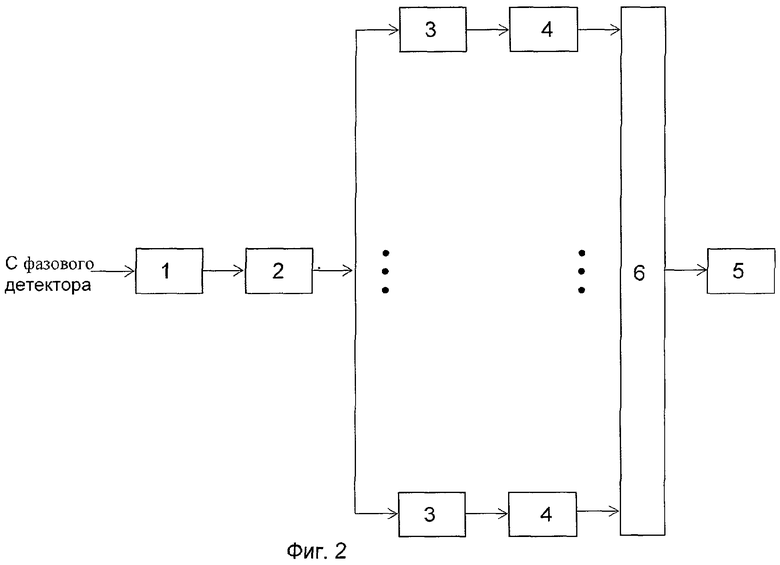
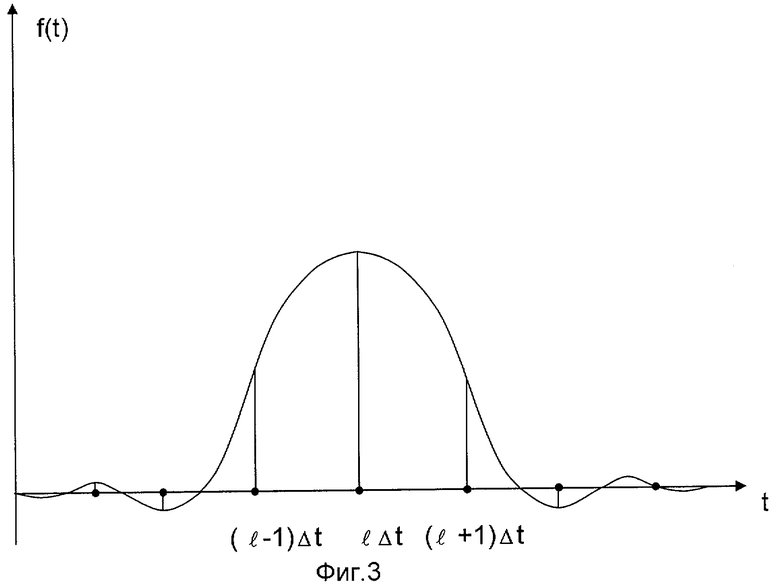
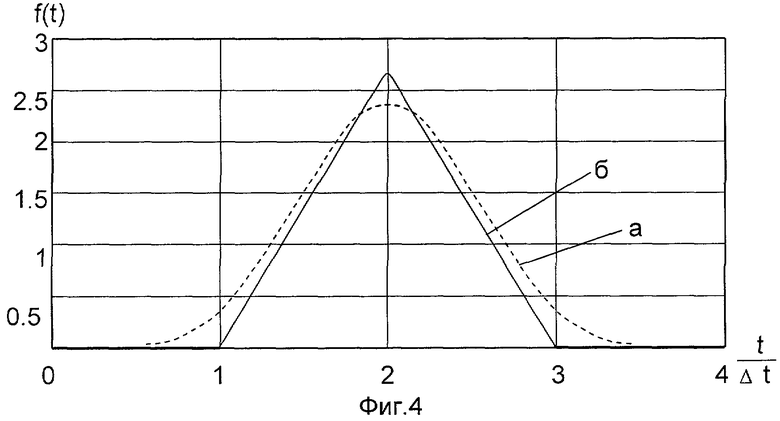
На фиг.1 и 2 представлены структурные схемы устройств, реализующих, соответственно, заявляемый способ аналого-дискретной обработки радиолокационных импульсных сигналов и способ по прототипу; на фиг.3 - кривая функции, модулирующей по амплитуде отсчеты полезного сигнала на выходе АДФ в соответствии с выражением (22), поясняющая расчетное обоснование заявляемой одноканальной обработки; на фиг.4 - кривые функций, модулирующих по амплитуде отсчеты полезного сигнала на выходе оптимального (кривая а) и согласованного (кривая б) АДФ при обнаружении прямоугольного импульса на фоне белого шума, иллюстрирующие выигрыш в среднем по времени прихода полезного сигнала выходном отношении сигнал-шум, обеспечиваемом оптимальным АДФ.
Устройство, реализующее предлагаемый способ, содержит последовательно соединенные аналоговый фильтр нижних частот 1, аналого-дискретный преобразователь, в частности, аналого-цифровой (АЦП) 2, дискретный фильтр 3, устройство некогерентной обработки 4 и пороговое устройство 5 (см. фиг.1).
Способ аналого-дискретной обработки радиолокационных импульсных сигналов осуществляют следующим образом.
Сигналы с фазового детектора на видеочастоте поступают на вход аналогового фильтра нижних частот 1 и после приведения в нем полосы частот, занимаемой входным процессом (после фазового детектора), в соответствие с шагом временной дискретизации согласно теореме Котельникова, подвергаются дискретизации по времени в АЦП 2 и подаются на вход дискретного фильтра 3, по выходу из которого осуществляется некогерентная обработка сигналов в устройстве 4 с последующим сравнением с заданным порогом обнаружения в пороговом устройстве 5.
Что касается первого аспекта достигаемого технического результата, а именно, сокращения объема аппаратурных затрат по сравнению со способом прототипом, то он вытекает из сравнения приведенных на фиг.1 и 2 структурных схем устройств, реализующих сравниваемые способы обработки.
Действительно, устройство для реализации способа-прототипа (см. фиг.2) так же, как и устройство для заявляемого способа, содержит последовательно соединенные аналоговый фильтр нижних частот 1, аналого-дискретный преобразователь 2, но в отличие от заявляемого способа - параллельный набор дискретных фильтров 3 и устройств некогерентной обработки 4, выходы которых объединяются в блоке отбора максимума 6, подсоединенном выходом к входу порогового устройства 5. При этом для оптимальной реализации способа-прототипа, строго говоря, требуется, чтобы совокупность дискретных фильтров образовывала континуум (непрерывное множество) в зависимости от значений временной задержки τ аналогового полезного сигнала. На практике, естественно, ограничиваются некоторым конечным набором дискретных фильтров, расставленных с некоторым шагом по τ. Но даже при этом многоканальная схема дискретной фильтрации с учетом тиражирования еще и некогерентной обработки, а также последующего отбора максимума требует с очевидностью значительно больших аппаратурных затрат по сравнению с заявляемой одноканальной схемой, приведенной на фиг.1.
Покажем, что АДФ с передаточной характеристикой К(ω), определяемой выражением (4), действительно обеспечивает максимум среднего по времени прихода τ выходного отношения сигнал-шум, что послужит обоснованием второго аспекта получаемого технического результата, а именно, что при уменьшении аппаратурных затрат, обусловленных переходом от многоканального дискретного фильтра в способе-прототипе к способу, в котором используется единственный дискретный фильтр, заявляемый способ вносит минимальные потери в отношении сигнал-шум.
Обозначим через H(ω) и F(ω) передаточные характеристики аналогового и дискретного фильтров, соответственно, а спектр полезного сигнала представим в виде
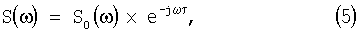
где 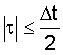 - параметр, характеризующий временное положение полезного сигнала;
- параметр, характеризующий временное положение полезного сигнала;
S0(ω) - спектр полезного сигнала при τ=0.
Ниже для получения отношения сигнал-шум на выходе АДФ будут использоваться известные соотношения (см. указанную в наст. описании книгу Цикина Л.А., с.122-129, 151, 152), связывающие входные и выходные спектры таких устройств, как аналоговый фильтр, дискретный фильтр, аналого-дискретный преобразователь, причем влиянием амплитудного квантования пренебрегаем.
В соответствии с введенными обозначениями получаем, что на выходе аналогового фильтра спектр сигнала равен
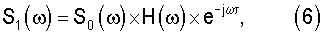
а спектральная плотность мощности шума
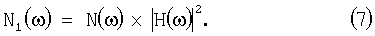
Временная дискретизация приводит к периодическому повторению k с периодом 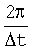 спектральных функций (6) и (7) в соответствии с выражениями
спектральных функций (6) и (7) в соответствии с выражениями
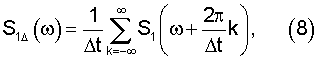
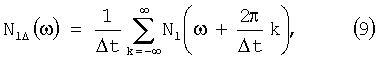
где S1Δ(ω) - спектр полезного сигнала, а N1Δ(ω) - спектральная плотность мощности шума на выходе аналого-дискретного преобразователя.
И, наконец, на выходе дискретного фильтра спектр сигнала имеет вид
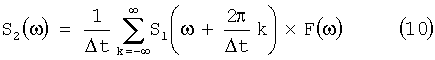
и спектральную плотность мощности шума
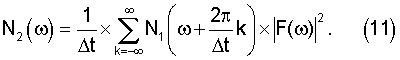
Поскольку F(ω) является периодической функцией с периодом 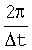 , то слагаемые в суммах (10) и (11) можно представить в виде
, то слагаемые в суммах (10) и (11) можно представить в виде
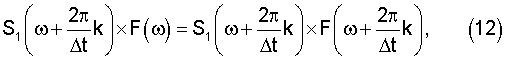
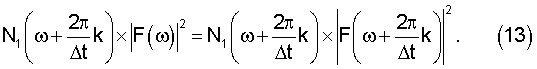
С учетом (12) и (13) выражения (10) и (11) принимают вид
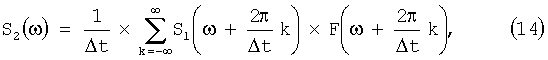
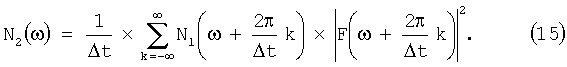
Переходя во временную область, согласно (14) и (15) получаем на выходе АДФ отсчеты сигнала
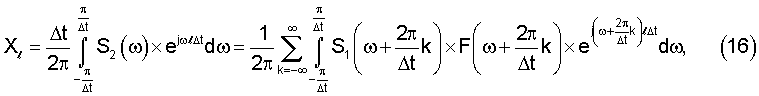 и мощность шума
и мощность шума
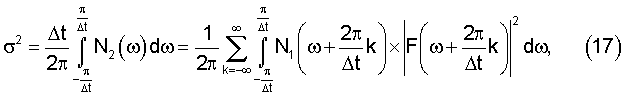
При получении (16) учтено, что еjωlΔt периодична с периодом 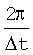 , вследствие чего правомерна замена в этой функции ω на
, вследствие чего правомерна замена в этой функции ω на 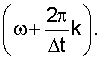
Если провести замену переменной вида 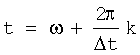 в интегралах выражений (16) и (17), то получим
в интегралах выражений (16) и (17), то получим
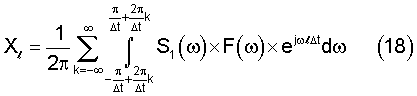
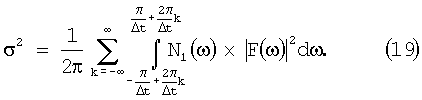
Нетрудно видеть, что интервалы интегрирования суммируемых интегралов примыкают друг к другу, покрывая всю числовую ось. Поэтому сумму интегралов в (18) и (19) можно заменить одним интегралом с бесконечными пределами интегрирования, что с учетом (6) и (7) приводит выражения (18) и (19) к виду
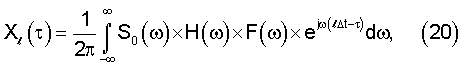
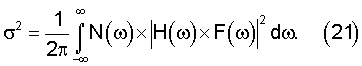
Как следует из (20), отсчеты сигнала на выходе АДФ можно представить как результат временной дискретизации в моменты (lΔt-τ) кривой
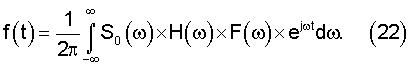
Характерный вид такой кривой при оптимальной (или близкой к оптимальной) обработке приведен на фиг.3, где показаны также отсчеты сигнала при τ=0.
Функция f(t) имеет ярко выраженный главный пик шириной порядка Δt, что является необходимым условием эффективности обработки, поскольку позволяет сконцентрировать энергию полезного сигнала в одном выходном отсчете, доминирующем при всех τ над остальными отсчетами, максимально выделяя тем самым сигнал из шума. В связи с этим оптимизация АДФ будет проводиться на классе таких произведений H(ω)×F(ω), для которых функция f(t), определяемая выражением (22), обладает вышеуказанным видом.
Если, например, подставить в (22) вместо H(ω)×F(ω) передаточную характеристику (1), то кривая f(t) будет, очевидно, соответствовать выходному сигналу оптимального аналогового фильтра. При этом, как известно, достигается максимально возможное отношение сигнал-шум в точке, соответствующей максимуму кривой f(t), но, вообще говоря, не обеспечивается максимально возможное среднее значение отношения сигнал-шум в окрестности 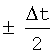 от этой точки. Для достижения такого максимума необходимо провести "коррекцию" формы главного пика кривой f(t), соответствующей передаточной характеристике (1) оптимального аналогового фильтра с тем, чтобы перераспределить часть энергии сигнала от максимальной точки кривой к прилегающим точкам. Эта задача сводится к отысканию такого произведения H(ω)×(ω), которое обеспечивало бы для отсчета, расположенного в интервале
от этой точки. Для достижения такого максимума необходимо провести "коррекцию" формы главного пика кривой f(t), соответствующей передаточной характеристике (1) оптимального аналогового фильтра с тем, чтобы перераспределить часть энергии сигнала от максимальной точки кривой к прилегающим точкам. Эта задача сводится к отысканию такого произведения H(ω)×(ω), которое обеспечивало бы для отсчета, расположенного в интервале 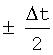 от максимума кривой f(t) (для конкретности будем полагать его номер равным l) выполнение равенства
от максимума кривой f(t) (для конкретности будем полагать его номер равным l) выполнение равенства
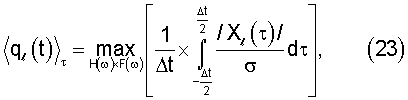
где ql(τ) - отношение сигнал-шум для l-го отсчета при конкретном 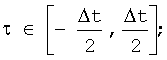
<>τ - обозначение статистического усреднения по τ.
Закон распределения параметра τ в (23) полагается равномерным.
Как видно из фиг.3, фигурирующий в (23) отсчет сигнала не меняет своего знака при изменении параметра τ (смена знака характерна для отсчетов, соответствующих боковым лепесткам кривой f(t)). Поэтому операции интегрирования и взятие модуля в выражении (23) можно поменять местами, после чего оно с учетом (20) и (21) примет вид 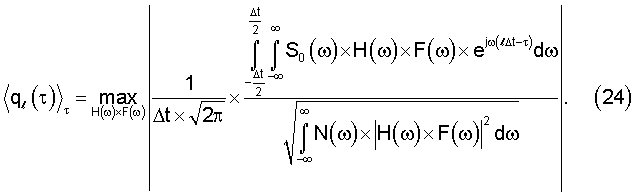
Полагая, что выполнены известные условия регулярности, позволяющие менять порядок интегрирования в двойном интеграле, и проводя в (24) интегрирование по τ, получаем
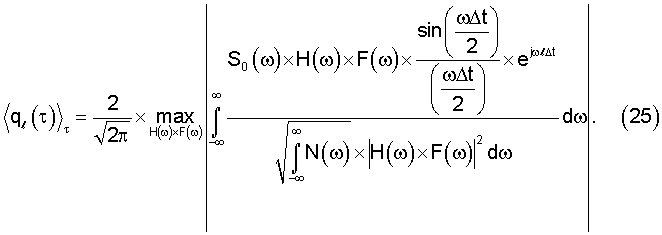
Для отыскания максимума выражения (25) воспользуемся неравенством Коши-Шварца, одна из форм записи которого определяется выражением
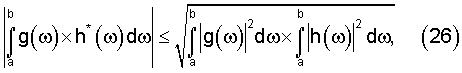
где g(ω) и h(ω) - любые функции, квадратично интегрируемые на интервале [а, b] (см. книгу Корна Г. и Корна Т. Справочник по математике. Пер. с англ. М., "Наука", 1974, с.129, 457). Причем равенство в (26) достигается тогда и только тогда, когда выполнено условие
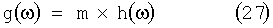
где m - любая не зависящая от ω величина.
Представим подинтегральное выражение в правой части (25) в виде произведения двух сомножителей 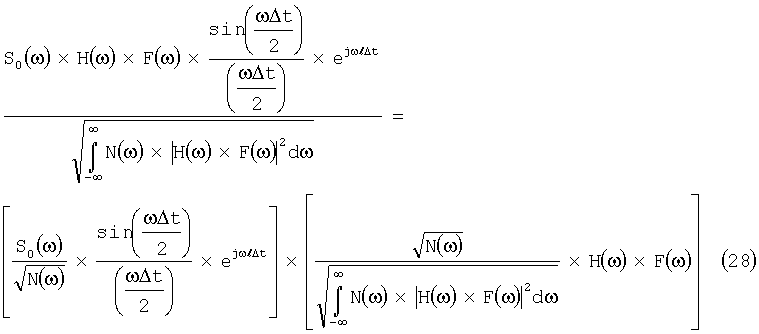
Полагая в качестве g(ω) первый из сомножителей в правой части (28), а в качестве h*(ω)- второй, т.е.
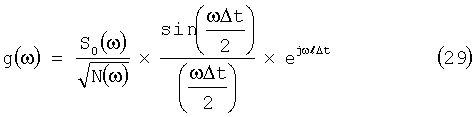
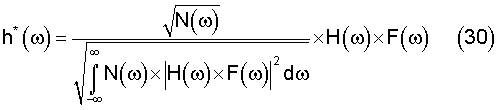
и применяя после этого к правой части (25) неравенство Коши-Шварца (26), получаем
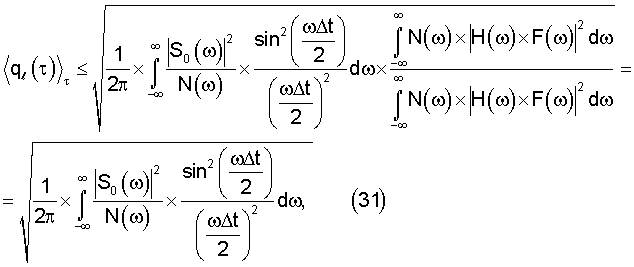
а максимальное среднее по времени прихода сигнала отношение сигнал-шум, равное правой части (31), достигается согласно (27), (29) и (30) при передаточной характеристике АДФ, определяемой (с точностью до константы) выражением
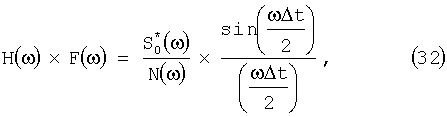
что и требовалось доказать.
В качестве иллюстрации на фиг.4 приведены кривые (а и б) f(t) при аналого-дискретной фильтрации прямоугольного импульса длительностью Δt на фоне белого шума, т.е. при 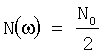 , где N0 - постоянная.
, где N0 - постоянная.
Кривая (б) соответствует согласованной фильтрации, когда
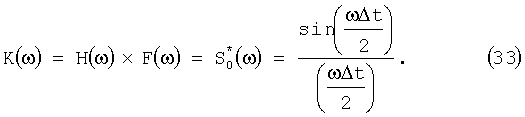
Кривая (а) соответствует оптимальной фильтрации согласно выражению (32), т.е.
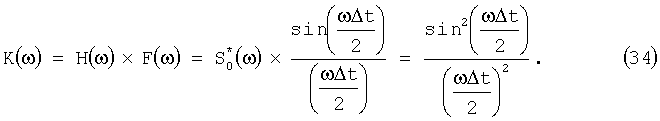
Для того, чтобы сравнение было корректным, передаточные характеристики (33) и (34) перед подстановкой в (22) нормировались в соответствии с выражением
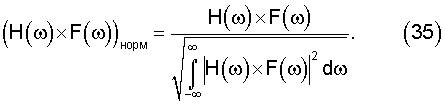
При таком нормировании мощность шума на выходах фильтров становится одинаковой, что позволяет сравнивать обеспечиваемое ими качество обнаружения по соотношению кривых f(t). Как видно на фиг.4, при согласованной фильтрации функция f(t) имеет треугольную форму с длительностью 2×Δt по основанию. При этом для самого неблагоприятного времени прихода полезного сигнала 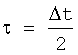 потери в отношении сигнал-шум составляют 6 дБ. При фильтрации же в соответствии с передаточной характеристикой (34), кривая f(t) имеет более пологий характер, несколько проигрывая случаю (33) в максимуме и ближайшей его окрестности, но превышая сплошную кривую на остальной части интервала
потери в отношении сигнал-шум составляют 6 дБ. При фильтрации же в соответствии с передаточной характеристикой (34), кривая f(t) имеет более пологий характер, несколько проигрывая случаю (33) в максимуме и ближайшей его окрестности, но превышая сплошную кривую на остальной части интервала 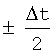 от максимума, обеспечивая наибольшее среднее значение функции f(t) на этом интервале.
от максимума, обеспечивая наибольшее среднее значение функции f(t) на этом интервале.
В заключение оценим потери в отношении сигнал-шум, возникающие при замене способа-прототипа (см. фиг.2) на предлагаемый способ (см. фиг.1). При этом ввиду сложности анализа многоканальной схемы с коррелированными шумами проведем сравнение заявляемого способа с оптимальной аналоговой обработкой, которая заведомо не уступает по качеству способу-прототипу. И хотя полученная величина потерь может оказаться при этом несколько завышенной, ее можно взять за основу при сравнении эффективности заявляемого способа и прототипа.
Оптимальная аналоговая обработка получается из обработки, приведенной на фиг.1 при замене АДФ на оптимальный аналоговый фильтр с передаточной характеристикой (1). Поскольку обе сопоставляемые схемы одноканальные, их сравнение можно провести на основе отношения сигнал-шум на выходе фильтров, т.е. на входе некогерентной обработки. Для простоты шум будем считать белым с двухсторонней спектральной плотностью 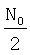 .
.
Известно (см. указанную в наст. описании книгу Кука Ч. и Бернфельда, М., с. 17,18), что отношение сигнал-шум (по амплитуде) на выходе оптимального фильтра равно 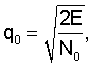 где Е - энергия сигнала, при этом с учетом теоремы Парсеваля (см. эту же книгу, с.46), связывающей энергию сигнала с его спектром, это отношение можно записать в виде
где Е - энергия сигнала, при этом с учетом теоремы Парсеваля (см. эту же книгу, с.46), связывающей энергию сигнала с его спектром, это отношение можно записать в виде
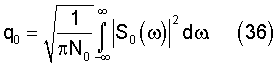
Тогда в соответствии с (31) получаем выражение для среднего значения потерь
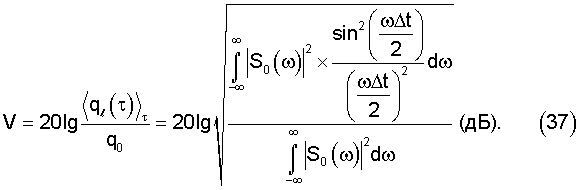
Например, для рассмотренного выше случая фильтрации прямоугольного импульса длительности Δt V≈-1,76. Если учесть, что эта величина характеризует потери АДФ с передаточной характеристикой К(ω) в соответствии с выражением (4) по отношению к аналоговому оптимальному фильтру с К(ω) в соответствии с выражением (1), т.е. является завышенной, то плата за существенное уменьшение объема аппаратуры при замене способа-прототипа на предлагаемый способ может оказаться вполне приемлемой для многих практических применений.
| название | год | авторы | номер документа |
|---|---|---|---|
| СПОСОБ ФОРМИРОВАНИЯ И ОБРАБОТКИ РАДИОЛОКАЦИОННЫХ МОДИФИЦИРОВАННЫХ ФАЗОМАНИПУЛИРОВАННЫХ СИГНАЛОВ | 2015 |
|
RU2635875C2 |
| СПОСОБ ОБРАБОТКИ НЕКОГЕРЕНТНОГО ПАКЕТА РАДИОИМПУЛЬСОВ | 1992 |
|
RU2054691C1 |
| СПОСОБ СЕЛЕКЦИИ ДВИЖУЩИХСЯ ЦЕЛЕЙ | 2015 |
|
RU2593276C1 |
| СПОСОБ ОБРАБОТКИ ВИДЕОСИГНАЛА В ПЗС-КОНТРОЛЛЕРЕ ДЛЯ МАТРИЧНЫХ ПРИЕМНИКОВ ИЗОБРАЖЕНИЯ | 2011 |
|
RU2480717C1 |
| СПОСОБ АНАЛОГО-ЦИФРОВОЙ ОБРАБОТКИ СИГНАЛА РАДИОМЕТРИЧЕСКОГО ДАТЧИКА | 2009 |
|
RU2386209C1 |
| КОМПЕНСАЦИОННЫЙ СПОСОБ ИЗМЕРЕНИЯ РАЗНОСТИ ФАЗ СЛУЧАЙНЫХ СИГНАЛОВ | 2002 |
|
RU2227306C2 |
| Способ обнаружения воздушных объектов при зондировании сверхкороткими радиоимпульсами | 2022 |
|
RU2791275C1 |
| ЦИФРОВОЙ ПРИЕМНИК ДИСКРЕТНО-НЕПРЕРЫВНЫХ ФАЗОМАНИПУЛИРОВАННЫХ СИГНАЛОВ С АДАПТАЦИЕЙ ЧАСТОТЫ ДИСКРЕТИЗАЦИИ | 2007 |
|
RU2365036C2 |
| КВАЗИОПТИМАЛЬНЫЙ ПРИЕМНИК ДИСКРЕТНО-НЕПРЕРЫВНЫХ ФАЗОМАНИПУЛИРОВАННЫХ СИГНАЛОВ | 2005 |
|
RU2300173C1 |
| СПОСОБ СПЕКТРАЛЬНОГО АНАЛИЗА ЭЛЕКТРИЧЕСКОГО СИГНАЛА | 2010 |
|
RU2431853C1 |
Изобретение относится к области радиолокации, в частности к первичной обработке эхо-сигналов в радиолокационной станции, и может быть использовано при обнаружении полезных сигналов на фоне шума. Технический результат предлагаемого изобретения - снижение аппаратурных затрат на обработку радиолокационных сигналов при минимальном значении возникающих потерь в отношении сигнал-шум. Для достижения технического результата в способе аналого-дискретной обработки радиолокационных импульсных сигналов с неизвестным временным положением, поступающих в приемном тракте с фазового детектора на видеочастоте, путем когерентной обработки, включающей предварительную аналоговую фильтрацию, аналого-цифровое преобразование и дискретную фильтрацию с последующей некогерентной обработкой и сравнением с заданным порогом обнаружения, формируют аналого-дискретный фильтр с общей передаточной характеристикой К(ω) и с помощью его проводят указанную когерентную обработку сигналов, при этом передаточную характеристику К(ω) сформированного аналого-дискретного фильтра определяют по формуле
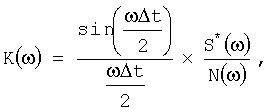
где ω - частота; Δt - шаг временной дискретизации; S*(ω) - комплексно-сопряженный спектр полезного сигнала; N(ω) - спектральная плотность мощности шума. 4 ил.
Способ аналого-дискретной обработки радиолокационных импульсных сигналов с неизвестным временным положением, поступающих в приемном тракте с фазового детектора на видеочастоте, путем когерентной обработки, включающей предварительную аналоговую фильтрацию, аналого-цифровое преобразование и дискретную фильтрацию с последующей некогерентной обработкой и сравнением с заданным порогом обнаружения, отличающийся тем, что когерентную обработку проводят с помощью аналого-дискретного фильтра, передаточную характеристику которого формируют по формуле
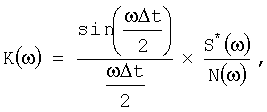
где ω - частота;
Δt - шаг временной дискретизации;
S*(ω) - комплексно-сопряженный спектр полезного сигнала;
N(ω) - спектральная плотность мощности шума.
| ШИРМАН Я.Д.Б, МАНЖОС В.Н | |||
| Теория и техника обработки радиолокационной информации на фоне помех | |||
| Москва, Радио и связь, 1981, с.23 | |||
| АДАПТИВНОЕ УСТРОЙСТВО ЗАЩИТЫ РАДИОЛОКАЦИОННОЙ СТАНЦИИ ОТ ПАССИВНЫХ ПОМЕХ | 1994 |
|
RU2097781C1 |
| СПОСОБ ИЗМЕРЕНИЯ МАЛЫХ ОТНОШЕНИЙ СИГНАЛ/ШУМ И УСТРОЙСТВО ДЛЯ ЕГО ОСУЩЕСТВЛЕНИЯ | 1993 |
|
RU2072522C1 |
| ЕР 0650261 А, 26.04.1995 | |||
| US 5982315, 09.11.1999. | |||
Авторы
Даты
2007-01-10—Публикация
2004-09-15—Подача