Изобретение относится к области измерения потока гамма-излучения и может быть использовано в радиометрической дефектоскопии толстостенных изделий с переменной толщиной.
Процесс дефектоскопии радиометрическим методом осуществляется путем непрерывного или дискретного сканирования. Первый способ предпочтителен для громоздких крупногабаритных объектов, когда возникают значительные механические нагрузки при пуске и торможении. Дискретное сканирование имеет свои преимущества, связанные с устранением динамических погрешностей. Дискретному методу сканирования посвящен ряд современных работ [Недавний О.И., Солодушкин В.И. Сравнительный анализ эффективности применения счетного и аналогового режимов регистрации излучения в радиометрических системах радиационной толщинометрии. - Дефектоскопия, 2002, №7, с.70-81. Оценка эффективности счетного метода обработки информации в многоканальных радиометрических системах контроля. - Дефектоскопия, 2005, №2, с.79-90], где рассмотрены вопросы выбора оптимальных режимов регистрации радиометрических сигналов счетным или аналоговым методом.
Задача фильтрации сигналов при непрерывном сканировании имеет более давнюю историю [Таточенко Л.К. Радиоактивные изотопы в приборостроении. - М.: Атомиздат, 1960. - 366 с.]. Обычно в аналоговом радиометрическом дефектоскопе сигнал сглаживается RC-фильтром, при этом выбирается оптимальная постоянная времени для достижения максимального отношения сигнал/шум (ОСШ). Очевидно, RC-фильтр не является оптимальным для решения подобной задачи. Наибольшее значение ОСШ достигается, если импульсная функция отклика фильтра является зеркальным отражением сигнала от дефекта [Тихонов В.И. Статистическая радиотехника. - М.: Советское радио, 1966. - 681 с.]. Теоретически такое решение является оптимальным для обнаружения сигнала детерминированной формы на фоне белого шума, каковым практически является радиометрический сигнал до фильтрации. На самом деле, сигналы от различных дефектов имеют неодинаковую форму. Обычно дефектоскоп настраивают так, чтобы обнаруживать минимальные выявляемые дефекты, полагая, что дефекты большего объема будут обнаружены и при неоптимальной фильтрации. Размер окна коллиматора в направлении сканирования выбирают приблизительно равным линейному размеру минимального выявляемого дефекта. Форма сигнала S(t) от подобного дефекта близка к треугольной:
 ,
,
где А - амплитуда сигнала, Т - длительность.
На фиг.1 представлены результаты компьютерного моделирования сигналов от дефектов кубической и сферической формы, где 1 - сигналы от дефектов кубической формы, 2 - сферической, 3 - те же сигналы при наличии шума.
Полагаем, что источник излучения моноэнергетический, пучок излучения узкий, а объект состоит из однородного материала. Тогда среднее число нерассеянных квантов, регистрируемых детектором за объектом в процессе сканирования, определяется выражением:
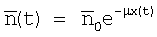 ,
,
где x - толщина поглотителя, µ - линейный коэффициент ослабления, n0 - число квантов, регистрируемых при отсутствии объекта. Сигнал с детектора представляет собой случайную последовательность импульсов, которые имеют случайную амплитуду:
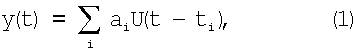
где U(t) - форма импульса, ai - его амплитуда. Полагаем, что длительность импульса τ0 значительно меньше длительности сигнала от дефекта Т. Количество импульсов n, регистрируемых в интервале времени Δt, распределено по закону Пуассона: 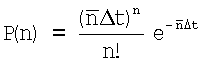 , где n - среднее число импульсов в единичном интервале времени. Амплитуда импульса имеет непрерывное распределение ξ(а), которое определяется процессом взаимодействия гамма-квантов в кристалле, развитием сцинтилляционной вспышки, светосбором на фотокатод и рядом других факторов.
, где n - среднее число импульсов в единичном интервале времени. Амплитуда импульса имеет непрерывное распределение ξ(а), которое определяется процессом взаимодействия гамма-квантов в кристалле, развитием сцинтилляционной вспышки, светосбором на фотокатод и рядом других факторов.
Оптимальная аналоговая фильтрация, позволяющая получить максимальное отношение сигнал/шум (ОСШ), в данном случае определяется выражением:
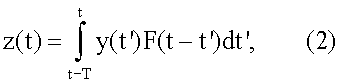
где y(t) - сигнал с детектора, F(t) - импульсная характеристика согласованного фильтра. Она удовлетворяет условию:
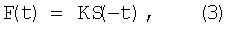
где k - произвольный коэффициент.
Определим дисперсию сигнала z(t). Для этого сначала представим исходный сигнал (1) в следующем виде:
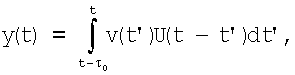
где 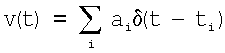 представляет собой пуассоновский поток δ-импульсов.
представляет собой пуассоновский поток δ-импульсов.
Тогда с учетом (3) перепишем выражение (2):
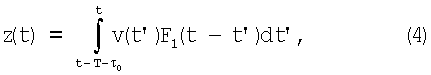
где F1 (t) - функция отклика объединенного фильтра:
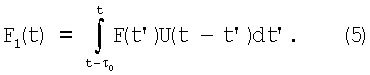
Если выполняется оговоренное выше условие τ0<<Т и форма импульса U(t) нормирована, то можно допустить с высокой точностью, что F1(t)≈F(t).
Можно показать [Овчаренко A.M., Недавний О.И., Капранов Б.И. Представление случайного процесса на выходе сцинтилляционного детектора. - Дефектоскопия, 1973, №5, с.50-55], что при условии малого изменения 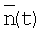 в течение времени Т действия фильтра дисперсия сигнала (4) имеет вид:
в течение времени Т действия фильтра дисперсия сигнала (4) имеет вид:
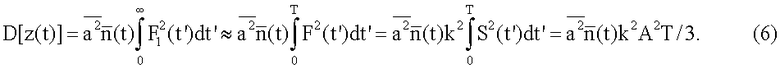
Далее вычислим амплитуду сигнала от дефекта после фильтрации. Максимальное значение сигнала возникает в момент, когда интервалы действия сигнала и согласованного фильтра совпадают.
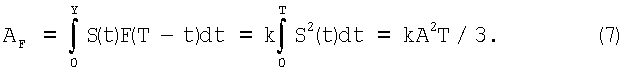
Теперь с учетом выражений (6) и (7) можно записать выражение для ОСШ:
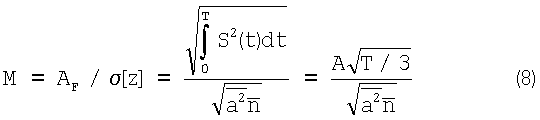
где 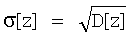 - среднеквадратическое отклонение.
- среднеквадратическое отклонение.
Амплитуду А сигнала от дефекта можно оценить следующим образом. Предположим, что появлению дефекта соответствует эквивалентное изменение просвечиваемой толщины, равное Δх, тогда амплитуда сигнала может быть определена как соответствующая вариация интенсивности регистрируемого излучения:
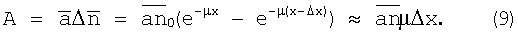
Выражение (9) получено при условии µΔx<<1.
Подставив (9) в (8), окончательно получим:
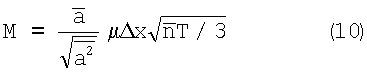
Представленный результат является идеальным решением задачи, условия которой оговорены выше, но получен он в аналоговом виде. Реализация оптимального фильтра в виде аналогового электронного устройства в настоящее время не является лучшим решением, более удобным и простым является использование цифрового фильтра. Применение же цифровых методов приведет к уменьшению ОСШ из-за ошибок квантования.
Цель данной работы направлена на решение вопросов выбора параметров аналого-цифрового преобразования и алгоритма обработки для минимизации ошибок квантования по времени и амплитуде. Кроме того, в работе обращается внимание на возможность потери статистических данных при квантовании стохастического сигнала по времени, что тоже приводит к уменьшению ОСШ.
Стандартный подход к цифровой реализации формулы (2) заключается в выполнении следующей последовательности операций: аналоговая фильтрация верхних частот сигнала y(t) до частоты среза f0, дискретизация по времени с частотой не менее 2f0 (условие Котельникова - Найквиста), квантование по амплитуде в интервале целых чисел от 0 до 2N-1 и цифровая фильтрация [6]:
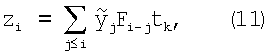
где zi - результат цифровой фильтрации, 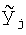 - сигнал с детектора с отфильтрованными верхними частотами, квантованный по времени и амплитуде, Fj - функция отклика фильтра, дискретизированная по времени с той же частотой, что и сигнал, но не квантованная по амплитуде (тип real), tk - период дискретизации.
- сигнал с детектора с отфильтрованными верхними частотами, квантованный по времени и амплитуде, Fj - функция отклика фильтра, дискретизированная по времени с той же частотой, что и сигнал, но не квантованная по амплитуде (тип real), tk - период дискретизации.
Другой подход заключается в применении иного способа аналоговой фильтрации с последующим вычислением суммы:
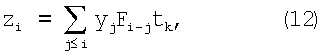
где 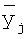 - предварительно отфильтрованные аналоговым способом, дискретизированные по времени и амплитуде значения исходного сигнала. Аналоговая фильтрация должна минимизировать дисперсии отсчетов
- предварительно отфильтрованные аналоговым способом, дискретизированные по времени и амплитуде значения исходного сигнала. Аналоговая фильтрация должна минимизировать дисперсии отсчетов 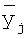 и сохранить их независимость как случайных величин. Последнее условие требуется, чтобы не исказить согласованный фильтр Fj. Такому условию удовлетворяет аналоговый фильтр, осуществляющий скользящее среднее по интервалу, равному периоду дискретизации. Вместо скользящего среднего можно применить просто интегрирование по тому же интервалу, что дает тот же результат после дискретизации по времени.
и сохранить их независимость как случайных величин. Последнее условие требуется, чтобы не исказить согласованный фильтр Fj. Такому условию удовлетворяет аналоговый фильтр, осуществляющий скользящее среднее по интервалу, равному периоду дискретизации. Вместо скользящего среднего можно применить просто интегрирование по тому же интервалу, что дает тот же результат после дискретизации по времени.
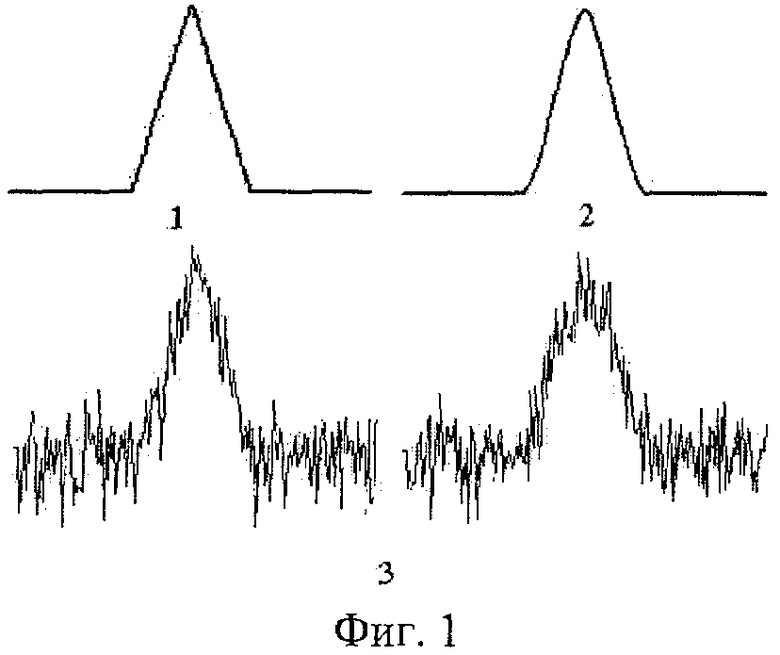
В аналоговой электронике реализовать скользящее усреднение достаточно сложно по сравнению, например, с RC-фильтром. В качестве более простого аналогового фильтра можно применить RC-фильтр или какой-либо другой, у которого функция отклика быстро спадает во времени. Во всех перечисленных случаях аналоговый фильтр характеризуется временем сглаживания ta. Эта величина определена точно для фильтра, осуществляющего скользящее среднее. В случае RC-фильтра полагают ta=RC, но действие фильтра распространяется и за этот интервал, уменьшаясь экспоненциально. Для фильтра верхних частот полагают ta=1/f, где f - максимальная частота в спектре отфильтрованного сигнала. Здесь функция отклика тоже отличается от нуля за пределами интервала ta. Функции импульсного отклика этих фильтров изображены на Фиг.2, где 4 - RC-фильтр, 5 - фильтр скользящего усреднения, 6 - фильтр верхних частот.
Постоянная времени ta аналогового фильтра, применяемого перед АЦП, имеет конечную величину, которая определяется формой полезного сигнала. Величина ta должна быть такой, чтобы результат цифровой фильтрации незначительно уступал аналоговой. Если постоянная времени ta аналогового фильтра достаточно мала по сравнению с постоянной времени Т цифрового фильтра, а период квантования по времени tk<<ta, то в пределе при уменьшении ta мы получим такой же результат, как при оптимальной аналоговой фильтрации, независимо от вида предварительного аналогового фильтра (по крайней мере, из перечисленных выше).
В случае применения стандартного подхода после аналоговой фильтрации верхних частот проводится квантование по времени с периодом ta/2, a затем квантование по амплитуде. Если применить скользящее среднее, то период квантования можно выбрать равным ta, при этом ОСШ не уменьшится. Для доказательства определим ОСШ для сигнала (12). Дисперсии величин 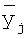 , полученных путем интегрирования исходного сигнала y(t) по интервалу ta, равна
, полученных путем интегрирования исходного сигнала y(t) по интервалу ta, равна 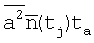
(tj - моменты времени аналого-цифрового преобразования). Как и прежде, полагаем, что интенсивность регистрируемого излучения мало меняется на интервале Т, кроме того, τ0<<ta<<Т. При оговоренных условиях случайные величины 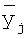 можно считать независимыми, а дисперсия фильтрованного сигнала z имеет вид:
можно считать независимыми, а дисперсия фильтрованного сигнала z имеет вид:
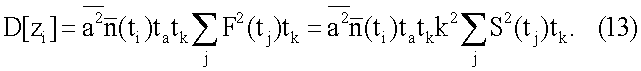
Полученное значение дисперсии отличается от (6) дополнительным множителем tatk и дискретной формой вычисления интеграла. Аналогично проводится расчет амплитуды сигнала от дефекта в дискретном виде:
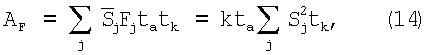
где 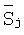 - значение сигнала от дефекта, усредненное по интервалу ta. Выражение (14) отличается от (7) множителем ta и дискретным способом вычисления интеграла. Если интервал интегрирования ta равен периоду дискретизации tk, то ОСШ для дискретного сигнала имеет вид:
- значение сигнала от дефекта, усредненное по интервалу ta. Выражение (14) отличается от (7) множителем ta и дискретным способом вычисления интеграла. Если интервал интегрирования ta равен периоду дискретизации tk, то ОСШ для дискретного сигнала имеет вид:
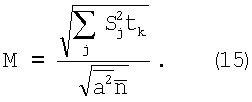
ОСШ (15) для квантованного сигнала отличается от максимального значения (8) лишь дискретной формой вычисления интеграла от достаточно гладкой функции. Погрешность этого вычисления стремится к нулю при уменьшении ta. Рассмотрим, как будет изменяться ОСШ, если сделать период квантования tk больше или меньше времени усреднения. В обоих случаях дисперсии величин 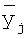 останутся те же. В случае превышения периода квантования tk>ta сохраняется независимость
останутся те же. В случае превышения периода квантования tk>ta сохраняется независимость 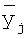 , а следовательно, и выражение для дисперсии (13). Выражение для ОСШ теперь имеет следующий вид:
, а следовательно, и выражение для дисперсии (13). Выражение для ОСШ теперь имеет следующий вид:
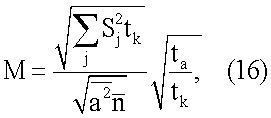
следовательно, ОСШ уменьшится пропорционально 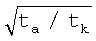 . Это явление объясняется тем, что уменьшается эффективная интенсивность регистрируемого излучения - образуются интервалы времени, когда регистрации не производится.
. Это явление объясняется тем, что уменьшается эффективная интенсивность регистрируемого излучения - образуются интервалы времени, когда регистрации не производится.
В противоположном случае tk<ta величины 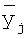 становятся коррелированными и выражение для дисперсии (13) будет несправедливым. Оценку дисперсии фильтрованного сигнала можно получить в предположении, что интервал tk<<ta. В этом случае можно рассматривать итоговый сигнал как результат аналоговой фильтрации исходной последовательности импульсов y(t) двумя фильтрами: первый интегрирует по интервалу ta, а второй имеет функцию отклика, равную F(t). Если время действия ta первого фильтра много меньше второго - ta<<Т, то объединенный фильтр (как уже оговаривалось ранее) по форме незначительно отличается от последнего:
становятся коррелированными и выражение для дисперсии (13) будет несправедливым. Оценку дисперсии фильтрованного сигнала можно получить в предположении, что интервал tk<<ta. В этом случае можно рассматривать итоговый сигнал как результат аналоговой фильтрации исходной последовательности импульсов y(t) двумя фильтрами: первый интегрирует по интервалу ta, а второй имеет функцию отклика, равную F(t). Если время действия ta первого фильтра много меньше второго - ta<<Т, то объединенный фильтр (как уже оговаривалось ранее) по форме незначительно отличается от последнего:
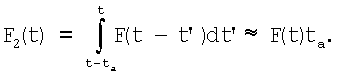
Результат действия такого фильтра уже известен (см. (10)), коэффициент пропорциональности ta не меняет ОСШ. Из последнего результата следует, что уменьшение периода дискретизации относительно времени аналогового усреднения не приводит к уменьшению статистической погрешности.
Рассмотрим, к каким потерям приведет применение RC-фильтра вместо скользящего среднего на этапе предварительного аналогового сглаживания. Как и в предыдущем случае полагаем, что длительность полезного сигнала значительно превышает время аналогового сглаживания: Т>>τ=RC. Задача состоит в выборе периода дискретизации tk сигнала, сглаженного RC-фильтром. Как и ранее, определим ОСШ сигнала, обработанного таким образом: сглаживание RC-фильтром с постоянной времени τ, дискретизация по времени с периодом tk.
Сглаженный RC-фильтром сигнал (1) при условии τ>>τ0 можно представить в следующем виде:
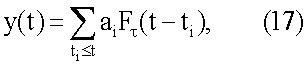
где 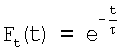 - функция отклика RC-фильтра.
- функция отклика RC-фильтра.
Воспользовавшись выражением (6), вычислим дисперсию шума после RC-фильтра
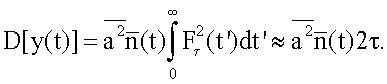
После квантования по времени проводим цифровую фильтрацию аналогично (II):
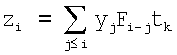 .
.
Случайные величины yi - значения сигнала (16) в дискретные моменты времени ti, отсчитываемые через интервал tk. В отличие от фильтрации скользящим средним, они теперь не являются независимыми, поскольку RC-фильтр имеет неограниченную во времени функцию отклика. Независимыми их можно считать приближенно, если интервал дискретизации значительно превосходит τ. Амплитуда сигнала от дефекта после цифровой фильтрации имеет следующий вид:
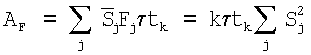 ,
,
где 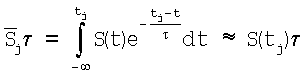 .
.
Вычисление дисперсии случайной величины zi при произвольном времени дискретизации tk затруднительно в аналитическом виде. Расчет легко произвести для двух предельных случаев: tk<<τ и tk>>T. В первом варианте получаем оценку дисперсии непрерывного сигнала, представляющего белый шум, сглаженный фильтром с импульсной функцией F2(t):
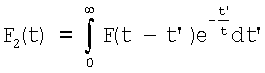 .
.
При условии τ<<Т получим F2(t)≈F(t)τ. С учетом этих допущений видим, что объединенный фильтр F2(t) удовлетворяет условию согласованности (3), а ОСШ принимает максимальное значение (8).
Следовательно, если перед аналого-цифровым преобразованием сигнал в виде белого шума сгладить RC-фильтром с постоянной времени τ значительно меньшей, чем длительность полезного сигнала Т, а дискретизацию по времени произвести с периодом tk значительно меньшим τ, то при последующей оптимальной цифровой фильтрации получим ОСШ, близкое к максимальному.
В противоположном случае, когда τ<<tk, но при этом tk<<T полагаем, что случайные величины yj в (17) являются независимыми, тогда можно вычислить дисперсию сигнала zi, амплитуду сигнала от дефекта после фильтрации и ОСШ:
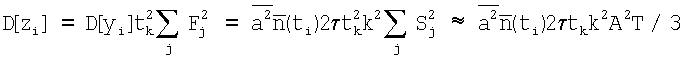 ,
,
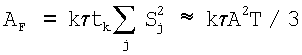 ,
, 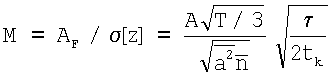 .
.
Последнее выражение меньше максимального (8) в 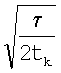 . Причина этого эффекта заключается в частичной потере статистических данных аналогично тому, что мы получили при фильтрации скользящим средним и большом периоде квантования tk>ta.
. Причина этого эффекта заключается в частичной потере статистических данных аналогично тому, что мы получили при фильтрации скользящим средним и большом периоде квантования tk>ta.
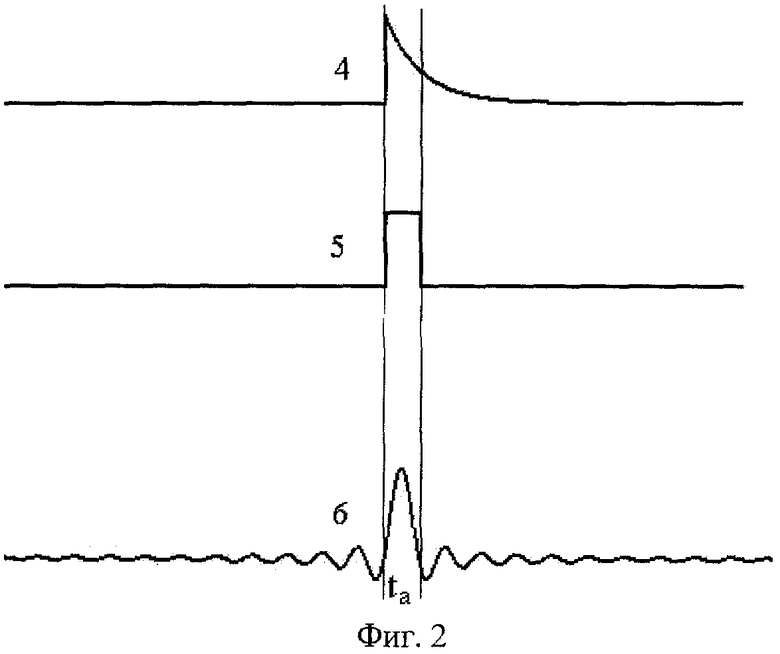
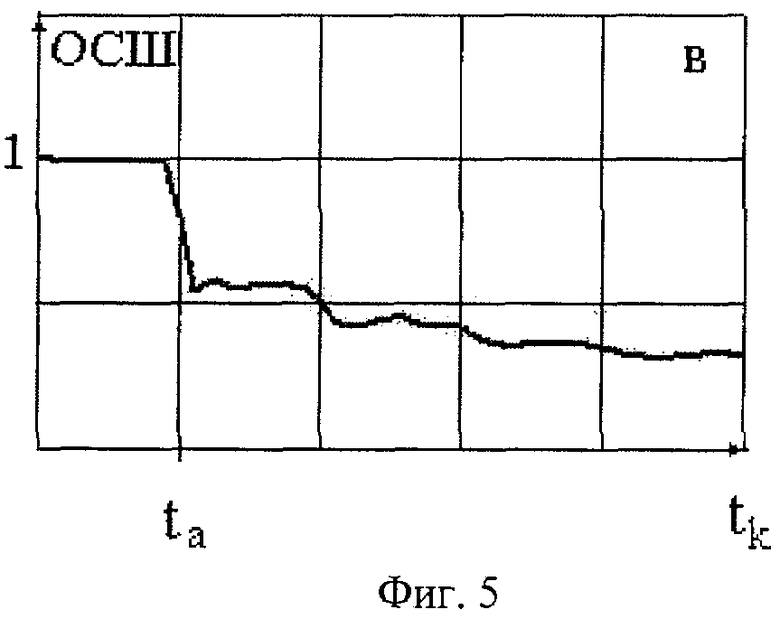
Получить промежуточные значения ОСШ в зависимости от времени квантования tk можно путем моделирования случайного процесса и последовательности его обработки. На фиг.3 представлена относительная зависимость ОСШ от периода квантования для сигнала, предварительно сглаженного RC-фильтром. ОСШ непрерывно уменьшается при возрастании периода квантования tk, и при tk=τ принимает значение 0,9 от максимальной величины, а при tk=2τ-0,8. На фиг.4 представлен результат моделирования ОСШ для сигнала, предварительно сглаженного скользящим средним. Здесь ОСШ не меняется для периода квантования от 0 до ta, а затем начинает убывать пропорционально 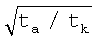 . Аналогичная зависимость получена путем моделирования для фильтра верхних частот (фиг.5). Здесь мы видим, что ОСШ начинает заметно уменьшаться при tk>0,8 ta. На фиг.3, 4, 5 видно, что период квантования сигнала, сглаженного аналоговым фильтром с постоянной времени ta, зависит от вида фильтра и согласно рассмотренным примерам не должен превышать эту величину. Для фильтра верхних частот период квантования может существенно превышать ta/2 без заметного увеличения статистической погрешности.
. Аналогичная зависимость получена путем моделирования для фильтра верхних частот (фиг.5). Здесь мы видим, что ОСШ начинает заметно уменьшаться при tk>0,8 ta. На фиг.3, 4, 5 видно, что период квантования сигнала, сглаженного аналоговым фильтром с постоянной времени ta, зависит от вида фильтра и согласно рассмотренным примерам не должен превышать эту величину. Для фильтра верхних частот период квантования может существенно превышать ta/2 без заметного увеличения статистической погрешности.
Из полученных результатов следует, что постоянная времени аналогового фильтра, применяемого перед АЦП, определяется формой полезного сигнала (обычно длительностью). Период квантования зависит от типа фильтра и не должен превышать постоянной времени ta. В противном случае происходит уменьшение отношения сигнал/шум из-за потерь статистических данных.
Следующим этапом после выбора постоянной времени фильтра и периода квантования является определение разрядности АЦП, которую можно вычислить, зная диапазон входного сигнала и минимальную вариацию сигнала, подлежащую надежной регистрации. При таком подходе к решению задачи о выборе разрядности АЦП, очевидно, что результат не зависит от параметров аналогового фильтра.
Любой из перечисленных выше способов аналого-цифровой обработки радиометрического сигнала может быть применен без значительного преимущества друг перед другом, следует лишь выбирать постоянную времени аналогового фильтра и период квантования, позволяющие минимизировать статистические погрешности. Кроме того, необходимо выбрать АЦП достаточной разрядности, чтобы надежно выявлять сигнал от дефекта.
Использование фильтра верхних частот является наиболее популярным для предварительной аналоговой фильтрации, поэтому рассмотрим способ обработки радиометрического сигнала, включающий в себя аналоговую фильтрацию верхних частот, аналого-цифровое преобразование и оптимальную цифровую фильтрацию в качестве прототипа [Солонина А.И., Улахович Д.А., Арбузов С.М., Соловьева Е.Б. Основы цифровой обработки сигналов. - Санкт-Петербург, «БХВ-Петербург», 2005. - 753 с.].
В способе, рассматриваемом в качестве прототипа, постоянная времени фильтра определяется, как было показано выше, формой полезного сигнала и никак не связана с разрядностью АЦП. В практике радиометрической дефектоскопии объектов с большим диапазоном контролируемой толщины требуется либо АЦП высокой разрядности (более 20), либо логарифмический преобразователь, который уменьшает динамический диапазон сигнала и снижает требования к АЦП. Следовательно, если применить способ, рассмотренный в качестве прототипа, то потребуется либо дорогостоящий АЦП, либо аналоговый логарифмический преобразователь, использование которого приводит к дополнительным погрешностям и увеличению габаритов датчика.
Задачей настоящего изобретения является создание такого способа аналого-цифровой обработки сигнала радиометрического датчика, который позволяет применять АЦП с меньшей разрядностью и уменьшить стоимость и габариты аппаратуры.
Поставленная задача решается способом аналого-цифровой обработки сигнала радиометрического датчика, включающим предварительную аналоговую фильтрацию посредством скользящего среднего или посредством RC-фильтра, аналого-цифровое преобразование и цифровую фильтрацию. Особенность заключается в том, что формируют аналоговый фильтр с постоянной времени, в два и более раза меньшей длительности полезного сигнала и обеспечивающей среднеквадратическое отклонение шума фильтрованного сигнала равным или большим ступени квантования аналого-цифрового преобразователя, при этом период квантования по времени выбирают меньшим или равным постоянной времени аналогового фильтра.
Покажем, что в задаче аналого-цифровой фильтрации подходящий выбор постоянной времени аналогового фильтра позволяет уменьшить число разрядов АЦП.
Сначала на примере типичной задачи радиометрической дефектоскопии рассмотрим, как определить требуемую разрядность АЦП. Предположим, что просвечиваемая толщина контролируемого объекта меняется от нуля до 10 длин пробега квантов, т.е. µxmin=0, µxmax=10, а чувствительность контроля составляет 1% от максимальной просвечиваемой толщины. Это соответствует тому, что появление дефекта эквивалентно изменению толщины Δx на 1%, следовательно, µΔ=0,1. Максимальный сигнал пропорционален 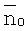 , минимальный
, минимальный 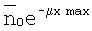 , амплитуда А сигнала от дефекта на максимальной толщине составляет в тех же единицах:
, амплитуда А сигнала от дефекта на максимальной толщине составляет в тех же единицах:
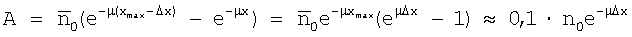 .
.
Для уверенной регистрации сигнала от дефекта в его амплитуде должно укладываться несколько ступеней квантования Δ, допустим 10, тогда 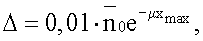 а число ступеней квантования
а число ступеней квантования 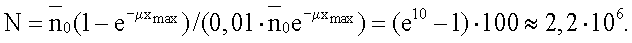 Следовательно, для радиометрической дефектоскопии объектов с диапазоном толщин от 0 до xmax=10/µ и чувствительностью 1% требуется АЦП с 21 разрядом, если не проводить предварительной компрессии сигнала, например, логарифмирования.
Следовательно, для радиометрической дефектоскопии объектов с диапазоном толщин от 0 до xmax=10/µ и чувствительностью 1% требуется АЦП с 21 разрядом, если не проводить предварительной компрессии сигнала, например, логарифмирования.
Это было бы действительно так, если бы сигнал не содержал шумовой составляющей. В результате дискретизации по времени и амплитуде сигнала, содержащего шум, и последующей цифровой фильтрации можно искусственно повысить разрядность АЦП. [http://www.atmel.com/dyn/products/app_notes.asp?family_id=607 AVR121: Enhancing ADC resolution by oversampling]. Для получения такого эффекта необходимо три условия: среднеквадратическое отклонение сигнала, поступающего на вход АЦП, должно быть сравнимо или больше ступени квантования, дискретизированные во времени значения сигнала должны быть слабо коррелированы, период квантования tk должен быть значительно меньше длительности полезного сигнала.
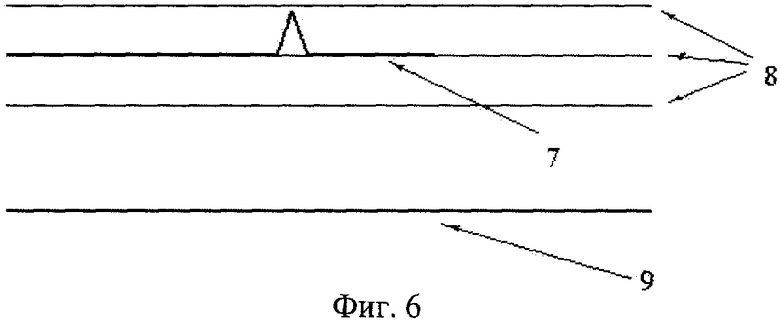
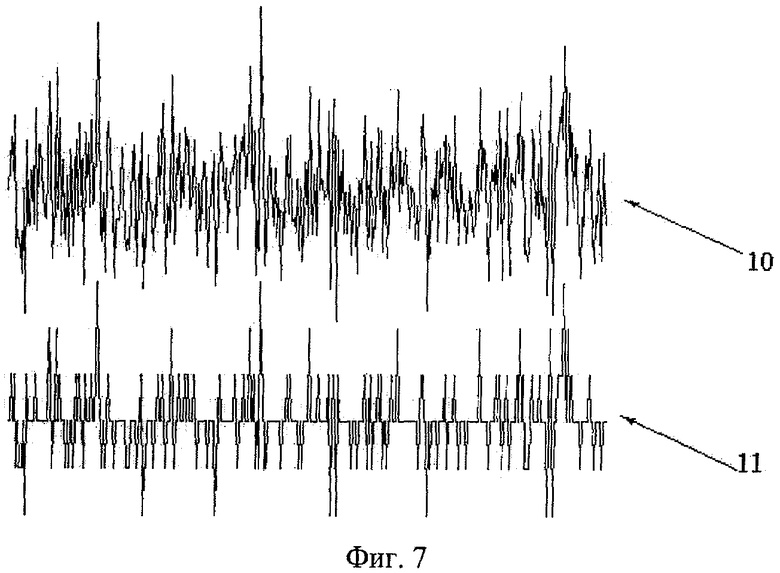
Проиллюстрируем данный эффект на примере, полученном путем компьютерного моделирования. На фиг.6 представлен сигнал 7 от дефекта без помехи (при отсутствии шума), пунктиром показаны уровни квантования 8 по амплитуде. При аналого-цифровом преобразовании незашумленного сигнала в данных обстоятельствах полезный сигнал 9 будет пропущен. На фиг.7 отображен сигнал с аддитивной помехой до и после АЦП, позиции 10 и 11 соответственно. На фиг.8 верхний график отображает первичный сигнал 12, обработанный оптимальным аналоговым фильтром. На нижнем графике представлен сигнал 13 после АЦП и цифровой фильтрации. Сравнивая эти два графика, видим, что они практически не различаются. Это означает, что в значительной мере сократились помехи квантования по амплитуде.
В простейшем случае, когда цифровой фильтр осуществляет скользящее среднее по m отсчетам, шаг квантования уменьшается в m раз. При этом арифметические операции необходимо выполнять в формате действительных чисел. В случае применения цифрового фильтра с произвольной функцией отклика сигнал на выходе будет квантован, но с неравномерным шагом квантования. Если цифровой фильтр неотрицателен и нормирован: 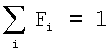 , Fi≥0, то Fi≤1. Можно показать, что в данном случае максимальная ступень квантования будет равна Δ·Fmax. Так, например, для фильтра треугольной формы длительностью m отсчетов Fmax=2/m.
, Fi≥0, то Fi≤1. Можно показать, что в данном случае максимальная ступень квантования будет равна Δ·Fmax. Так, например, для фильтра треугольной формы длительностью m отсчетов Fmax=2/m.
Полученный результат позволяет применять АЦП невысокой разрядности, при этом исключить необходимость компрессии сигнала высокого динамического диапазона.
Рассмотрим, удовлетворяет ли поставленным условиям сигнал реального радиометрического дефектоскопа с изотопным источником гамма-излучения. Предположим, что при сканировании среднее число n квантов, регистрируемых за секунду, меняется в интервале от 105 до 2,2·109 с-1, что соответствует диапазону толщины от 0 до xmax=10/µ. Появлению минимального выявляемого дефекта соответствует вариация толщины Δх в 1% от максимальной, а интенсивность изменится при максимальной толщине на величину 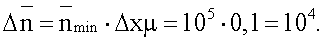 Если бы в сигнале отсутствовал шум, то для выявления сигнала от дефекта в оговоренном диапазоне потребовался бы 21-разрядный АЦП. Теперь определим, будет ли выявляться такой сигнал при аналоговой фильтрации. Пусть длительность сигнала от дефекта составляет 1 секунду. Предположим, что фильтрация производится путем интегрирования по интервалу Т=1 сек. Тогда среднеквадратическое отклонение шума на максимальной составит
Если бы в сигнале отсутствовал шум, то для выявления сигнала от дефекта в оговоренном диапазоне потребовался бы 21-разрядный АЦП. Теперь определим, будет ли выявляться такой сигнал при аналоговой фильтрации. Пусть длительность сигнала от дефекта составляет 1 секунду. Предположим, что фильтрация производится путем интегрирования по интервалу Т=1 сек. Тогда среднеквадратическое отклонение шума на максимальной составит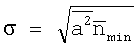 , амплитуда сигнала после фильтрации
, амплитуда сигнала после фильтрации 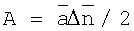 A (в предположении, что до фильтрации сигнал имел треугольную форму), а
A (в предположении, что до фильтрации сигнал имел треугольную форму), а 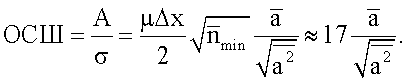 Отношение
Отношение 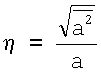 называют коэффициентом амплитудного разброса. По оценкам, проведенным в [3] для сцинтилляционного датчика η≈1,2. В итоге ОСШ≈14, следовательно, сигнал надежно выявляется.
называют коэффициентом амплитудного разброса. По оценкам, проведенным в [3] для сцинтилляционного датчика η≈1,2. В итоге ОСШ≈14, следовательно, сигнал надежно выявляется.
Теперь рассмотрим процесс предварительной аналоговой фильтрации, аналого-цифрового преобразования и цифровой фильтрации. Предполагаем, что мы сглаживаем сигнал методом скользящего среднего с временем усреднения ta, при этом фильтр нормирован: 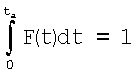 . Такой фильтр не меняет амплитуду сигнала и его диапазон. После сглаживания этим фильтром получим аналоговый сигнал
. Такой фильтр не меняет амплитуду сигнала и его диапазон. После сглаживания этим фильтром получим аналоговый сигнал 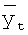 :
:
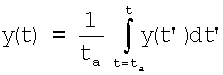 .
.
Амплитуда сигнала от дефекта останется прежней: 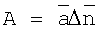 , дисперсия шума на максимальной толщине:
, дисперсия шума на максимальной толщине: 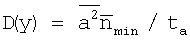 , а среднеквадратическое отклонение -
, а среднеквадратическое отклонение -
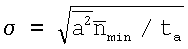 .
.
Дискретизацию сигнала произведем через интервал ta, а цифровую фильтрацию выполним подобно выше рассмотренной аналоговой - путем суммирования дискретного сигнала на интервале Т:
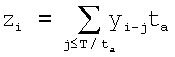 .
.
Если не учитывать квантования по амплитуде, после цифровой фильтрации амплитуда сигнала от дефекта, дисперсия и среднеквадратическое отклонение шума получаются такие же, как и при аналоговой фильтрации, с точностью погрешностей вычисления интегралов дискретным методом. Теперь обратим внимание на то, что среднеквадратическое отклонение шума σ перед аналого-цифровым преобразованием можно регулировать путем выбора подходящего времени предварительного сглаживания ta, сохраняя при этом динамический диапазон сигнала. Таким образом, при определенном значении ступени квантования можно обеспечить среднеквадратическое отклонение шума, сравнимое с этой ступенью или превосходящее ее. Так, в рассматриваемом примере при ta=10-3 сек 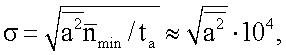 а амплитуда сигнала
а амплитуда сигнала 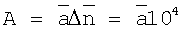 . Следовательно, предварительно отфильтрованный таким образом сигнал может быть подвержен аналого-цифровому преобразованию с периодом дискретизации 10-3 сек и ступенью квантования
. Следовательно, предварительно отфильтрованный таким образом сигнал может быть подвержен аналого-цифровому преобразованию с периодом дискретизации 10-3 сек и ступенью квантования 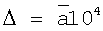 . Диапазон сигнала укладывается в интервал
. Диапазон сигнала укладывается в интервал 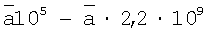 , в котором содержится 2,2·109 ступеней квантования, следовательно, для преобразования достаточно 17-разрядного АЦП. Последующее усреднение цифрового сигнала в течение 1 сек, т.е. по 103 отсчетам уменьшит ступень квантования в 103 раз, что эквивалентно искусственному повышению разрядности АЦП на 10. Это фактически сводит к нулю эффекты от квантования по амплитуде.
, в котором содержится 2,2·109 ступеней квантования, следовательно, для преобразования достаточно 17-разрядного АЦП. Последующее усреднение цифрового сигнала в течение 1 сек, т.е. по 103 отсчетам уменьшит ступень квантования в 103 раз, что эквивалентно искусственному повышению разрядности АЦП на 10. Это фактически сводит к нулю эффекты от квантования по амплитуде.
При уменьшении толщины контролируемого материала возрастает интенсивность 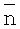 регистрируемого излучения. Сигнал от дефекта одного и того же объема увеличивается пропорционально интенсивности, а среднеквадратическое отклонение возрастает пропорционально корню из этой величины, и, следовательно, требования к разрядности АЦП снижаются.
регистрируемого излучения. Сигнал от дефекта одного и того же объема увеличивается пропорционально интенсивности, а среднеквадратическое отклонение возрастает пропорционально корню из этой величины, и, следовательно, требования к разрядности АЦП снижаются.
Таким образом, можно сделать следующие выводы: при линейной цифровой фильтрации наличие слабо коррелированного шума в сигнале позволяет снизить количество разрядов АЦП посредством выбора предварительного аналогового сглаживающего фильтра; фильтр должен быть таким, чтобы среднеквадратическое отклонение сигнала перед аналого-цифровым преобразованием превышало ступень квантования, а фильтрованный сигнал был слабо коррелирован; последующая линейная цифровая фильтрация снижает ступень квантования в число, пропорциональное количеству отсчетов, укладывающихся в длительности полезного сигнала.
| название | год | авторы | номер документа |
|---|---|---|---|
| Способ диаграммообразования в проемной цифровой антенной решетке | 2021 |
|
RU2766536C1 |
| ФИЛЬТРУЮЩИЙ АНАЛОГО-ЦИФРОВОЙ ПРЕОБРАЗОВАТЕЛЬ С ИСПОЛЬЗОВАНИЕМ ДЕЛЬТА- МОДУЛЯЦИИ | 1997 |
|
RU2125343C1 |
| СПОСОБ ОБНАРУЖЕНИЯ ДЕФЕКТОВ МАГИСТРАЛЬНЫХ ТРУБОПРОВОДОВ МЕТОДОМ АКУСТИЧЕСКОЙ ТОМОГРАФИИ | 2017 |
|
RU2681424C1 |
| Способ и устройство автоматического распознавания типа манипуляции радиосигналов | 2017 |
|
RU2665235C1 |
| СПОСОБ ИНДЕНТИФИКАЦИИ ТОНАЛЬНЫХ СИГНАЛОВ В СЕТЯХ СВЯЗИ И ЦИФРОВОЕ УСТРОЙСТВО ДЛЯ ЕГО ОСУЩЕСТВЛЕНИЯ | 2004 |
|
RU2291405C2 |
| СПОСОБ АНАЛОГО-ДИСКРЕТНОЙ ОБРАБОТКИ РАДИОЛОКАЦИОННЫХ ИМПУЛЬСНЫХ СИГНАЛОВ | 2004 |
|
RU2291463C2 |
| СПОСОБ АНАЛОГО-ЦИФРОВОГО ПРЕОБРАЗОВАНИЯ УЗКОПОЛОСНЫХ СИГНАЛОВ | 1992 |
|
RU2036558C1 |
| ВНУТРИТРУБНЫЙ ИНСПЕКЦИОННЫЙ СНАРЯД | 2002 |
|
RU2205397C1 |
| МНОГОПАРАМЕТРИЧЕСКИЙ ДЕФЕКТОСКОП | 1997 |
|
RU2123687C1 |
| Ультразвуковое устройство для измерения контактных давлений | 1990 |
|
SU1746297A1 |


Использование: в радиометрической дефектоскопии толстостенных изделий с переменной толщиной. Технический результат заключается в возможности применять аналого-цифровой преобразователь с меньшей разрядностью при уменьшении стоимости и габаритов аппаратуры. Способ включает предварительную аналоговую фильтрацию посредством скользящего среднего или посредством RC-фильтра, аналого-цифровое преобразование и цифровую фильтрацию, при этом формируют аналоговый фильтр с постоянной времени в два и более раза меньшей длительности полезного сигнала и обеспечивающей среднеквадратическое отклонение шума фильтрованного сигнала равным или большим ступени квантования аналого-цифрового преобразователя. Кроме того, период квантования по времени выбирают меньшим или равным постоянной времени аналогового фильтра. 8 ил.
Способ аналого-цифровой обработки сигнала радиометрического датчика, включающий предварительную аналоговую фильтрацию посредством скользящего среднего или посредством RC-фильтра, аналого-цифровое преобразование и цифровую фильтрацию, отличающийся тем, что формируют аналоговый фильтр с постоянной времени, в два и более раза меньшей длительности полезного сигнала и обеспечивающей среднеквадратическое отклонение шума фильтрованного сигнала равным или большим ступени квантования аналого-цифрового преобразователя, при этом период квантования по времени выбирают меньшим или равным постоянной времени аналогового фильтра.
| СПОСОБ АНАЛОГО-ДИСКРЕТНОЙ ОБРАБОТКИ РАДИОЛОКАЦИОННЫХ ИМПУЛЬСНЫХ СИГНАЛОВ | 2004 |
|
RU2291463C2 |
| УСТРОЙСТВО ДЛЯ ОБРАБОТКИ СИГНАЛОВ | 2000 |
|
RU2195014C2 |
| СПОСОБ ПРЕОБРАЗОВАНИЯ НЕПРЕРЫВНОГО СИГНАЛА В ЦИФРОВОЙ КОД | 0 |
|
SU296250A1 |
| EP 0650261 A1, 26.04.1995. | |||
Авторы
Даты
2010-04-10—Публикация
2009-01-11—Подача