Предлагаемое изобретение касается способа трехмерного моделирования некоторого свойства f (х, у, z), определяемого в геологической области, в которой формируются ячейки, адаптированные к критическим поверхностям этого подлежащего моделированию геологического объема.
Предлагаемое изобретение также касается устройства для трехмерного моделирования некоторого геологического объема, предназначенного для осуществления способа в соответствии с этим изобретением.
И наконец, предлагаемое изобретение касается программного продукта для вычислительной машины, обеспечивающего возможность функционирования программируемого устройства для трехмерного моделирования некоторого геологического объема для осуществления способа в соответствии с данным изобретением.
Известным образом моделирование некоторого геологического объема подразделяется на два крупных этапа, относящихся соответственно к построению структурной модели, а затем к построению модели свойств этого объема.
Как это показано на фиг.1, построение структурной модели состоит в разложении данного геологического пространства на систему так называемых "гомогенных" регионов, обычно ограниченных поверхностями трех типов, а именно: "поверхности излома", которые возникают вследствие сдвигов или разрушений, встречающихся обычно после оседания материалов, которые образуют геологические слои; "поверхности горизонтов", которые образуют поверхности разделения между последовательно расположенными геологическими слоями и название которых связано с тем, что они были приблизительно горизонтальными в момент оседания материалов, образующих эти слои; и граничные поверхности, введенные искусственным образом для ограничения расширения исследуемой области в боковом направлении.
Построение структурной модели зафиксировано в известном уровне техники и описано, например, в документе "Mallet J.L., 1997: Discrete Modeling for Natural Objects. Journal of Mathematical Geology, том 29, №2, стр.199-219", и поэтому не требует более подробного описания.
Для осуществления трехмерного моделирования некоторого геологического объема необходимо выполнить построение модели свойств. Действительно, земные недра могут быть охарактеризованы при помощи системы свойств, содержащей, в частности: проницаемость, пористость, плотность, скорость распространения сейсмических колебаний или вероятность принадлежности к некоторому геологическому разлому. Данное свойство обычно известно в нескольких точках наблюдения исследуемой геологической области и может быть определено в каждом однородном регионе исследуемой геологической области путем использования известных методов интерполяции, например, метода "krigeage", описанного в публикации "Deutsh С.V., and Journel А.G., GSLIB: Geostatistical Software Library and User′s Guide (второе издание (1998)), 369 страниц", изданной Oxford University Press, Нью-Йорк.
Эти методы интерполяции оказываются вполне удовлетворительными в том случае, когда данная интерполяция осуществляется и регистрируется в запоминающем устройстве вычислительной машины для каждого узла регулярной решетки с шестигранными ячейками, и когда узлы этой регулярной решетки с шестигранными ячейками располагаются параллельно горизонтам.
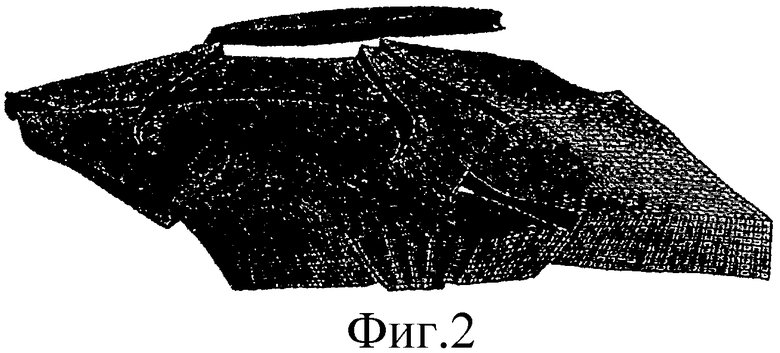
Для того чтобы сблизить два эти условия и обеспечить удовлетворительную интерполяцию, как это представлено на фиг.2, упомянутую регулярную решетку деформируют таким образом, чтобы придать ей форму, прилегающую к форме горизонтов. Основной недостаток такого сближения состоит в том, что регулярная решетка становится криволинейной; это обстоятельство заставляет обеспечивать запоминание всех координат каждого узла такой криволинейной решетки в запоминающем устройстве вычислительной машины и влечет за собой значительное и нежелательное расходование ресурсов этого запоминающего устройства.
Менее значительное расходование ресурсов запоминающего устройства вычислительной машины может быть обеспечено в том случае, когда используемый способ формирует шестигранные ячейки, вынужденные проектироваться в вертикальном направлении в форме прямолинейной решетки в горизонтальной плоскости. В патентном документе ЕР 0254325 В2 описан способ трехмерного математического моделирования некоторого ограниченного геологического объема путем построения слоев, образованных множеством ячеек. При этом геометрический объем определяется критическими поверхностями и имеет заданную слоистую структуру, которая содержит наклонные седиментарные слои. Этот способ содержит этап построения раздельной решетки для заполнения пространства, заключенного между каждой критической поверхностью, ограничивающей упомянутый объем для того, чтобы определить моделируемое пространство, являющееся репрезентативным для упомянутого объема, этап построения слоев ячеек внутри упомянутого моделируемого пространства и этап задействования атрибутов на основе точек расположения, принадлежащих упомянутому реальному объему, в ячейках, которые соответствуют, с точки зрения их положения внутри упомянутого моделируемого объема, положениям этих атрибутов в реальном геологическом объеме.
Построенные таким образом ячейки располагаются в слоях ячеек, имеющих вертикальные угловые кромки, длина которых изменяется таким образом, чтобы согласовываться с геометрией соответствующих седиментарных слоев, располагающихся в данном геологическом объеме. Упомянутые ячейки в каждом слое обладают предварительно определенной постоянной вертикальной толщиной между критическими поверхностями в любом положении, в том случае, когда данная ячейка не заканчивается на уровне критической поверхности ограничения. Реальный объем представляет собой геологический объем, обладающий слоистой геологической структурой, образованной наложенными друг на друга наклонными седиментарными осадочными слоями. Построенные таким образом решетки образуют моделируемый объем, аналогичный реальному объему. Слои ячеек размещены в моделируемом объеме вдоль вертикальных колонок ячеек и слои ячеек наклонены и уложены друг на друга таким же образом, как и осадочные слои в реальном геологическом объеме.
Упомянутые критические поверхности представляют собой критические поверхности инициализации или критические поверхности ограничения, содержащие наклонные седиментарные слои, заключенные между критическими поверхностями в стратиграфической структуре. Построенные в этом случае решетки представляют собой решетки инициализации или решетки ограничения, служащие для представления поверхности ограничения в соответствии с данной стратиграфической структурой. Эти ячейки располагаются вдоль вертикальных колонок от одного слоя к другому и эти слои ячеек построены в основном параллельно к критической поверхности инициализации и обладают постоянной высотой вдоль соответствующего им слоя.
Техническая задача данного изобретения заключается в том, чтобы предложить способ трехмерного моделирования некоторого геологического объема, применяя для этого общий метод моделирования функции, представляющей изменения некоторого заданного геологического свойства внутри исследуемой геологической области, обеспечивая при этом экономию ресурсов запоминающего устройства используемой вычислительной машины.
Другая техническая задача предлагаемого изобретения состоит в том, чтобы усовершенствовать известные технологии, описанные, например, в патентном документе ЕР 0254325 В2, таким образом, чтобы преодолеть вертикальное выравнивание ячеек и уменьшить потребный объем памяти для построенной таким образом решетки.
Еще одна техническая задача предлагаемого изобретения состоит в том, чтобы облегчить консультирование результатов моделирования, используя для этого технологии структурированного программирования.
Объектом предлагаемого изобретения является способ трехмерного моделирования некоторого геологического объема, в котором определяют ячейки, адаптированные к критическим поверхностям подлежащего моделированию геологического объема, отличающийся тем, что этот способ содержит следующие этапы:
а) определяют совокупности геологических макроячеек, адаптированных к геометрии геологических слоев подлежащего моделированию объема;
b) осуществляют определение параметров данного геологического пространства для установления соответствия исследуемой геологической области и некоторой параметрической области, связывая с некоторой точкой, принадлежащей данной геологической области, некоторое отображение, располагающееся в параметрической области;
с) определяют виртуальное разбиение упомянутых макроячеек на микроячейки, геометрия которых обеспечена путем разбиения геометрии каждой макроячейки таким образом, чтобы положение каждой микроячейки было выведено путем интерполяции из положений вершин соответствующей макроячейки, и таким образом, чтобы эти микроячейки соответствовали узлам регулярной решетки, покрывающей параметрическую область с тем, чтобы моделировать некоторую функцию, являющуюся репрезентативной для некоторого геологического свойства на регулярной решетке параметрической области, сокращая при этом количество подлежащих запоминанию данных.
В соответствии с другими альтернативными характеристиками предлагаемого изобретения:
- упомянутая параметрическая область перекрыта прямолинейной регулярной решеткой, координаты узлов которой могут быть найдены путем расчета, выполняемого на основе координат (u0, v0, w0) исходного узла и шагов упомянутой решетки в ее основных направлениях (u, v, w);
- определение параметров геологического пространства для установления соответствия между исследуемой геологической областью и параметрической областью таким образом, чтобы параметрическая координата (w) регулярной решетки параметрической области оставалась постоянной на отображении каждого горизонта, и таким образом, чтобы градиент отображений (u, v, w) оставался там не равным нулю;
- параметрические координаты (u, v, w) любой точки отображения для некоторой точки (х, у, z), располагающейся внутри макроячейки данной геологической области, рассчитываются путем интерполяции параметрических координат вершин этой макроячейки, предполагающихся предварительно рассчитанными и сохраненными в запоминающем устройстве вычислительной машины;
- данные функции f, являющейся репрезентативной для некоторого геологического свойства, наблюдаемые в точках выборки с координатами (xi, yi, zi) данной геологической области, переносятся в точки с координатами (ui, vi, wi) параметрической области;
- величина f (х, у, z) моделируемой функции "переносится" между точкой с геологическими координатами (х, у, z) и точкой с координатами (u, v, w) параметрической области;
- величина f (х, у, z) моделируемой функции может быть интерполирована в узлах регулярной решетки, покрывающей параметрическую область, или величина f (х, у, z) в геологической точке Х (х, у, z) моделируемой функции может быть получена путем считывания величины функции f, связанной с узлом с координатами (i, j, к), ближайшим к отображению (u, v, w) геологической точки Х (х, у, z) в регулярной решетке.
Объектом предлагаемого изобретения также является устройство трехмерного моделирования некоторого геологического объема, в котором определяют ячейки, адаптированные к критическим поверхностям подлежащего моделированию геологического объема, отличающееся тем, что это устройство содержит средства, предназначенные для определения макроячеек, адаптированных к геометрии подлежащих моделированию геологических слоев, средства, предназначенные для определения параметров данного геологического пространства с целью установления соответствия исследуемой геологической области и некоторой параметрической области, связывая с некоторой точкой, принадлежащей данной геологической области, некоторое отображение, располагающееся в упомянутой параметрической области, и средства, предназначенные для определения виртуального разбиения упомянутых макроячеек на микроячейки, геометрия которого обеспечена путем разбиения геометрии каждой макроячейки таким образом, чтобы положение каждой микроячейки было выведено путем интерполяции из положений вершин соответствующей макроячейки, и таким образом, чтобы эти микроячейки соответствовали узлам регулярной решетки, покрывающей упомянутую параметрическую область.
И наконец, объектом предлагаемого изобретения является программный продукт для вычислительной машины, содержащий элементы кода программы, предназначенной для выполнения перечисленных выше этапов способа в соответствии с этим изобретением, в том случае, когда упомянутая программа выполняется вычислительной машиной.
Предлагаемое изобретение будет лучше понято из приведенного ниже описания не являющегося ограничительным примера его реализации, где даются ссылки на приведенные в приложении фигуры, среди которых:
- Фиг.1 представляет собой схематический перспективный вид, иллюстрирующий структурную модель известного типа, образованную однородными регионами, ограниченными поверхностями изломов, поверхностями горизонтов и искусственными поверхностями, ограничивающими боковое распространение первой геологической области.
- Фиг.2 представляет собой схематический перспективный вид в разборе примера реализации криволинейной регулярной решетки из существующего уровня техники, покрывающей геологическую область, представленную на фиг.1.
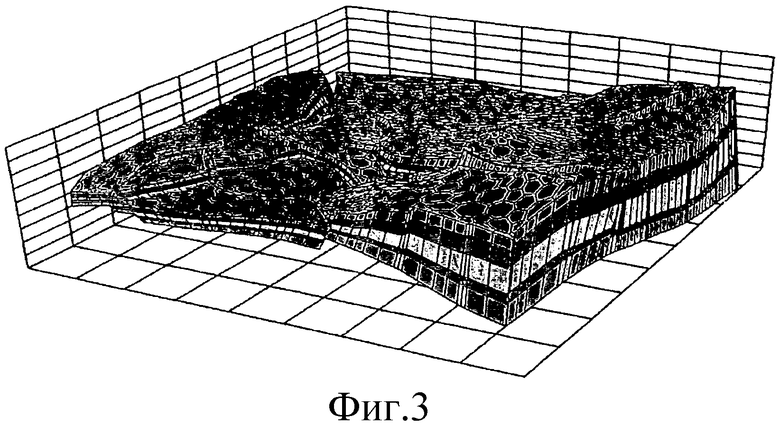
- Фиг.3 представляет собой схематический перспективный вид в разрезе примера другой геологической области G, состоящей из многогранных ячеек, в соответствии с предлагаемым изобретением, в которой ребра не пересекают упомянутые горизонты и поверхности изломов.
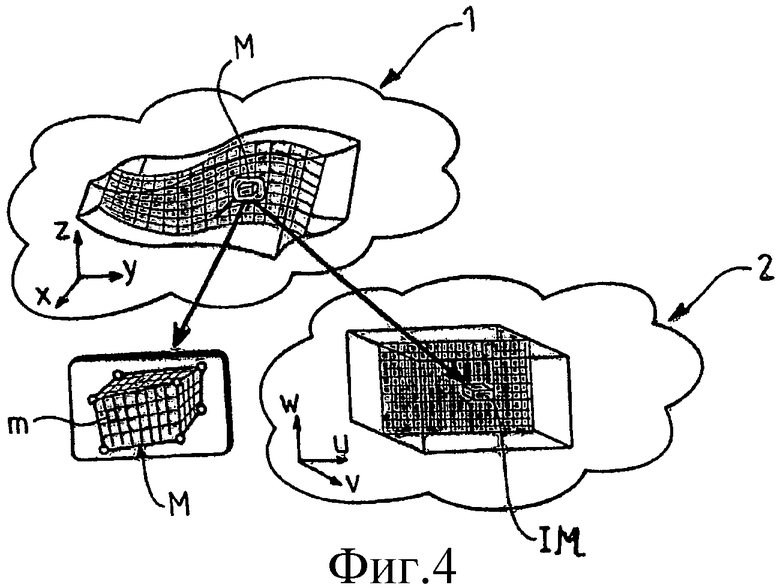
- Фиг.4 схематически иллюстрирует процесс приведения в соответствие, используемый для моделирования некоторого геологического объема при помощи способа в соответствии с предлагаемым изобретением.
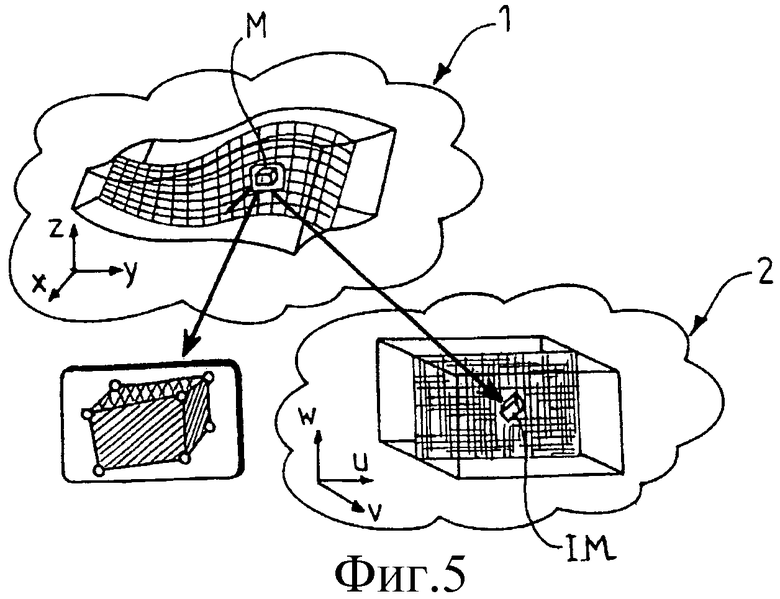
- Фиг.5 схематически иллюстрирует другой процесс приведения в соответствие, используемый для моделирования некоторого геологического объема при помощи способа в соответствии с предлагаемым изобретением.
- Фиг.6 схематически иллюстрирует процесс приведения в соответствие, используемый для моделирования некоторого геологического объема при помощи способа в соответствии с предлагаемым изобретением.
Как это можно видеть на фиг.3-6, идентичные или функционально эквивалентные элементы обозначены идентичными цифровыми позициями.
На фиг.3 схематически проиллюстрирована другая геологическая область G, которая разрезана на многогранные ячейки в соответствии с предлагаемым изобретением и в которой грани этих ячеек не пересекают горизонты и поверхности изломов.
Ячейки, полученные таким образом при помощи любого известного способа, в представленном ниже описании предлагаемого изобретения будут называться "геологическими макроячейками М", которые реализуют разбиение геологической области G на примыкающие друг к другу "геологические макроячейки М", представляющие собой небольшие элементы многогранного объема.
Это разбиение геологической области G на примыкающие друг к другу "геологические макроячейки М" предназначено, например, для обеспечения возможности исследования миграции текучих сред, складывания геологических слоев или же для разметки сейсмических регионов. Эти многогранные макроячейки М подразделяют структурную модель, проиллюстрированную на фиг.3, таким образом, чтобы ребра этих многогранных ячеек никогда не пересекали горизонты и поверхности изломов, причем грани этих многогранных ячеек либо по существу параллельны горизонтам, либо по существу перпендикулярны этим горизонтам.
Количество ячеек, необходимое для удовлетворения этих требований, зависит только от сложности геометрической конфигурации упомянутых горизонтов и поверхностей разломов. На практике такое рассечение геологической области обычно требует только относительно небольшого количества этих макроячеек М, не зависящего от сложности подлежащей моделированию функции f (х, у, z), что позволяет сохранять в запоминающем устройстве используемой в данном случае вычислительной машины только координаты (х, у, z) каждой вершины этих макроячеек в данной геометрической области G.
Если рассматривать специфическую макроячейку М, обозначенную символом С, и если координатами {Х1(С), X2(С), ...Xn(С)} обозначить вершины этой ячейки С в геологической области G, можно определить, для любой точки Х, располагающейся внутри этой ячейки С, коэффициенты {а1(Х,С), а2(Х,С), ... an(Х,С)}, соответствующие формуле
Х=а1(X,C)·X1(C)+a2(X,C)·X2(C)+...+an(X,C)·Xn(C).
Можно выбрать, в частности, для упомянутых выше параметров {а1(Х,С), а2(Х,С), ... an(Х,С)}, систему барицентрических координат Х по отношению к {Х1(С), Х2(С), ... Xn(С)}.
Если обозначить через (х, у, z) геологические координаты Х и обозначить через (xi(С), yi(С), zi(С)) координаты вершины Xi(С), приведенное выше уравнение становится эквивалентным трем следующим уравнениям.
x=а1(X,C)·x1(C)+a2(X,C)·x2(C)+...+an(X,C)·xn(C)
у=а1(X,C)·у1(C)+a2(X, C)·у2(C)+...+an(X, C)·yn(C)
z=а1(X,C)·z1(C)+a2(X, C)·z2(C)+...+an(X, C)·zn(C)
Обобщение этих уравнений позволяет обеспечить разбиение "геологических макроячеек М", которые "виртуально" разделяются на геологические микроячейки m.
Способ в соответствии с предлагаемым изобретением позволяет "виртуально" рассечь макроячейки на микроячейки, исключая необходимость сохранения в явном виде в запоминающем устройстве координат (х, у, z) вершин микроячеек, и дает возможность обеспечить значительную экономию объема памяти запоминающего устройства по сравнению с существующим уровнем техники.
Рассечение макроячеек на микроячейки остается "виртуальным", поскольку нет необходимости рассчитывать в явном виде и сохранять в запоминающем устройстве координаты (х, у, z) вершин этих микроячеек.
Действительно, согласно способу в соответствии с предлагаемым изобретением построение векторной математической функции Х (u, v, w)=[х (u, v, w), у (u, v, w), z (u, v, w)] и ее инверсии U (х, у, z)=[u (х, у, z), v (х, у, z), w (х, у, z)], связывающих взаимно однозначным образом некоторую точку с координатами (u, v, w) пространства параметрического отображения с соответствующими координатами (х, у, z) каждой точки геологического пространства.
Упомянутая функция U (х, у, z) определяется следующим образом.
- В фазе инициализации произвольным образом выбирают параметрические координаты (u, v, w) каждой точки отображения, связанной с каждой вершиной всех макроячеек М таким образом, чтобы:
* координата w была постоянной на каждой вершине всех макроячеек М, располагающихся на одном и том же геологическом горизонте;
* геологические поверхности, обратные по отношению к плоскостям постоянного значения координаты u и плоскостям постоянного значения координаты v, являются по существу перпендикулярными по отношению к упомянутым геологическим горизонтам;
* геологические поверхности, обратные по отношению к плоскостям постоянного значения координаты u и плоскостям постоянного значения координаты v, являются по существу перпендикулярными между собой.
- Затем сохраняют в запоминающем устройстве вычислительной машины параметрические координаты (u, v, w) отображений, связанных с каждой вершиной всех макроячеек М.
- Для каждой точки с координатами (х, у, z), располагающейся в макроячейке С данного геологического пространства, определяют величину U (х, у, z), как полученную путем интерполяции параметрических координат (u, v, w) отображений, связанных с вершинами С, и предварительно сохраненными в запоминающем устройстве вычислительной машины. Можно, например, осуществлять трилинейные интерполяции при помощи упомянутых выше барицентрических уравнений или другие трилинейные интерполяции, использующие только координаты (х, у, z) в первой степени.
Упомянутое параметрическое пространство отображения предпочтительным образом покрыто трехмерной ортоскопической решеткой G, узлы которой G [i, j, к] обозначены целочисленными индексами (i, j, к). Параметрические координаты u (i, j, к), v (i, j, к), и w (i, j, к) каждого узла G [i, j, к], представляют собой линейные функции индексов (i, j, к).
Геологическая точка Х (х, у, z) данного геологического пространства, соответствующая или антецедентная каждому узлу G [i, j, к], рассматривается в качестве центра "виртуальной" геологической микроячейки, располагающейся в точке Х с координатами х (u (i, j, к), v (i, j, к), w (i, j, к)); у (u (i, j, к), v (i, j, к), w (i, j, к)); z (u (i, j, к), v (i, j, к), w (i, j, к)).
В ряде случаев достаточно большое число этих "виртуальных" геологических микроячеек не зависит от размеров рассматриваемых геологических макроячеек, но зависит только от расстояния между узлами решетки G.
С каждой геологической точкой Х (х, у, z), соответствующей или антецедентной каждому узлу G [i, j, к], взятому в качестве центра "виртуальной" микроячейки данного геологического пространства, может быть связано некоторое физическое свойство, задействованное в центре этой микроячейки.
Выполняют построение трехмерной матрицы Т [i, j, к], содержащей количественные характеристики этого свойства, индексированные для того, чтобы это свойство в центре Х "виртуальной" геологической микроячейки, соответствующее или предшествующее узлу G [i, j, к], было сохранено в этой матрице Т [i, j, к].
Таким образом, только количественные характеристики данного физического свойства в центре Х (х, у, z) каждой микроячейки сохраняются в запоминающем устройстве в форме трехмерной матрицы Т [i, j, к], тогда как координаты центра Х (х, у, z) или вершин этих микроячеек никогда не сохраняются и могут быть локализованы посредством упомянутой выше функции локализации Х (u, v, w)=[х (u, v, w), у (u, v, w), z (u, v, w)], примененной к решетке G.
Таким образом, преимущество способа моделирования в соответствии с предлагаемым изобретением состоит в исключении необходимости сохранения координат (х, у, z) вершин или центров микроячеек. Из этого следует значительный выигрыш ресурсов запоминающего устройства по сравнению с известными способами, которые требуют сохранения в запоминающем устройстве по меньшей мере некоторых координат микроячеек.
В отличие от известных способов, где только одна количественная характеристика моделируемого физического свойства сохраняется в запоминающем устройстве для одной ячейки, больше нет необходимости адаптировать размеры этих ячеек к более или менее значительному локальному изменению упомянутого свойства. Таким образом, предлагаемое изобретение позволяет "разъединить" представление моделируемого физического свойства и представление геометрии ячеек и допускает разбиение данного геологического пространства на ограниченное число макроячеек обычно значительных размеров, выбираемых в функции сложности геометрии горизонтов и поверхностей разломов и не зависящих от сложности подлежащего моделированию физического свойства.
На фиг.4, 5 и 6 геологический объем, обозначенный в целом позицией 1, приведен в соответствии с пространством отображения, обозначенным в целом позицией 2, при помощи способа математического моделирования в соответствии с предлагаемым изобретением.
В существующем уровне техники в данной области один из обычных способов, предназначенных для построения геологической модели, состоит в разложении геологических слоев на систему примыкающих друг к другу трехмерных или объемных многогранных ячеек. Обычно эти ячейки имеют шестигранную форму и располагаются таким образом, чтобы две таких примыкающих друг к другу шестигранных ячейки соединялись между собой при помощи одной общей стороны или грани. Эти шестигранные ячейки располагаются равномерно таким образом, чтобы представлять верхние грани и нижние грани, являющиеся параллельными геологическим слоям. Равномерное расположение этих ячеек может быть нарушено разрывами или критическими поверхностями, соответствующими геологическим поверхностям разломов или геологическим складкам. В случае поверхностей разлома или геологических складок грани упомянутых ячеек могут быть расположены тангенциально по отношению к данной критической поверхности или же, альтернативным образом, эти ячейки могут быть распределены вдоль ломаного контура, охватывающего и аппроксимирующего критическую поверхность, соответствующую данной поверхности разлома. Геометрия построенной таким образом системы ячеек полностью определяется координатами вершин ячеек в данном геологическом пространстве. Предпочтительным образом, и в соответствии с существующим уровнем техники в данной области, края шестигранных ячеек располагаются таким образом, чтобы ориентировать ребра, связывающие верхние и нижние грани ячеек, вдоль направления, приблизительно перпендикулярного подлежащему моделированию геологическому слою. В соответствии с известным уровнем техники можно построить регулярные системы, то есть системы выстроенных по одной линии ячеек близких геометрических форм. Можно также построить нерегулярные криволинейные трехмерные системы, в которых ячейки представляют многогранную форму, эти ячейки не обязательно имеют одну и ту же форму, эти ячейки не обязательно выстроены регулярно по одной линии, но при этом примыкают друг к другу. Размеры таких ячеек предпочтительным образом выбираются достаточно малыми для того, чтобы содержать однородную геологическую фацию, представляющую по существу постоянные физические свойства, например, постоянную пористость и/или проницаемость. Для получения удовлетворительного представления изменения физических свойств в геологических слоях оказывается, таким образом, необходимым построение очень большого числа ячеек, что требует для их сохранения весьма значительных объемов памяти запоминающего устройства.
Для устранения этого недостатка в патентных документах US 4821164 и ЕР 0254325 В2 предложено строить систему ячеек таким образом, чтобы их проекции в горизонтальной плоскости образовывали регулярную ортогональную сеть. Такой подход требует, чтобы эти шестигранные ячейки имели располагающиеся по одной линии вертикальные ребра. Таким образом, эта упрощенная модель позволяет легко найти в горизонтальной проекции координаты построенных ячеек, причем единственным компонентом, который должен быть при этом сохранен в запоминающем устройстве, является вертикальная составляющая положения каждой вершины. Действительно, эта вертикальная составляющая может изменяться в функции толщины моделируемого геологического слоя.
Данное изобретение отличается от существующего уровня техники в данной области тем, что в этом изобретении предлагается техника моделирования в двух уровнях, соответствующих двум последовательным этапам моделирования.
На первом этапе моделируют вспомогательную геометрическую поверхность, определяя для этого совокупность шестигранных или многогранных ячеек, адаптированных к геометрии геологических слоев подлежащего моделированию геологического объема 1. На втором этапе определяют разбиение этих макроячеек М на шестигранные или многогранные микроячейки m, геометрия которых получается путем разбиения геометрии каждой упомянутой макроячейки.
Таким образом, данное геологическое пространство 1 разделяется на макроячейки М, располагающиеся в соответствии с криволинейной системой, при помощи известной технологии. Это определение системы примыкающих друг к другу макроячеек М позволяет определить, в случае, представленном на фиг.4, тройку координат х, у, z, однозначно определяющих вершину каждой макроячейки М, и определить таким образом координаты вершин регулярной криволинейной системы, представленной на фиг.5. Каждое отображение IM макроячейки М, представленное связанной с ним тройкой координат х, у, z, сохраняется в пространстве отображения 2, соответствующем регистрации U (х, у, z)=[u (х, у, z), v (х, у, z), w (х, у, z)] в соответствии с трехмерной матрицей данных, соответствующих рассматриваемой макроячейке.
Каждая вершина отображения IM макроячейки М индексирована в трехмерной матрице пространства отображения 2 при помощи тройки целых чисел i, j, к.
Второй этап способа в соответствии с предлагаемым изобретением состоит в "виртуальном" разбиении многогранных (или шестигранных) макроячеек М на шестигранные микроячейки m. Таким образом, каждая макроячейка равномерно и "виртуально" разбивается на целое число микроячеек m, количество которых выбирается в функции сложности изменений подлежащих моделированию физических свойств (например, проницаемости или пористости).
На практике эти микроячейки m являются достаточно малыми для того, чтобы упомянутые физические свойства оставались по существу постоянными внутри каждой такой микроячейки m. Итерация путем последовательных разбиений позволяет проверить это условие или "виртуально" увеличить количество микроячеек m внутри данной макроячейки М, если это условие не соблюдается.
Таким образом, при использовании предлагаемого изобретения упомянутая вспомогательная поверхность моделируется в виде регулярной трехмерной криволинейной системы, образованной многогранными или шестигранными макроячейками М, примыкающими друг к другу в геологическом пространстве 1. Размеры этих многогранных или шестигранных макроячеек М адаптированы к сложности геометрических характеристик основных геологических структур (основные горизонты и поверхности разломов) и не учитывают изменение физических свойств внутри этих макроячеек М. Действительно, физические свойства внутри этих макроячеек М не обязательно являются постоянными и не должны быть сохранены в запоминающем устройстве для этих макроячеек М. Единственная функция этих макроячеек М состоит по существу в разбиении геометрического пространства подлежащего моделированию геологического объема.
Эти макроячейки М могут иметь по существу многогранную или шестигранную форму, но их ребра не обязательно являются параллельными некоторому предварительно определенному направлению, и, в частности, ребра, располагающиеся в вертикальном направлении, не обязательно являются параллельными вертикальной оси координат, в отличие от указаний патентного документа US 4821164 или патентного документа ЕР 0254325 В2.
Поскольку известно, что единственная функция макроячеек М состоит в разбиении геологических слоев, разъединение между геометрией макроячеек М и изменениями физических свойств в подлежащей исследованию среде позволяет покрыть протяженное геологическое пространство при помощи ограниченного числа макроячеек М, адаптированного к особенностям геометрии геологических слоев подлежащего моделированию объема, не нарушая при этом критические поверхности типа поверхностей геологических разломов и верхних и нижних границ рассматриваемых геологических слоев.
Как это представлено более подробно в увеличенном виде на фиг.4, 5 или 6, каждая макроячейка М "виртуально" и равномерно разбивается на некоторое число микроячеек m, выбираемое в функции сложности изменений подлежащих моделированию физических свойств (например, проницаемости или пористости).
Индексирование микроячеек m может быть выполнено аналогично индексированию макроячеек М в пространстве отображения 2 путем индексирования при помощи тройки индексов i, j, к так, чтобы установить объективное соответствие между каждой микроячейкой и тройкой индексов i, j, к трехмерной матрице пространства отображения 2, и так, чтобы не нарушать свойства двух смежных микроячеек m, а именно, индексировать смежные микроячейки m смежными тройками индексов i, j, к и соответствующими геологическому положению этих микроячеек.
Таким образом, разбиение макроячеек М на микроячейки m позволяет зарегистрировать физические свойства внутри каждой микроячейки, связывая их с тройкой индексов i, j, к трехмерной матрицы пространства отображения 2.
Такое связывание представляет собой особенно предпочтительную характеристику способа моделирования в соответствии с предлагаемым изобретением, позволяя сократить общий объем памяти запоминающего устройства, необходимый для осуществления данного изобретения.
Другие специфические и предпочтительные характеристики способа моделирования в соответствии с предлагаемым изобретением являются следствием "виртуального" моделирования геометрических параметров каждой микроячейки.
Действительно, моделирование геометрических параметров каждой микроячейки m может осуществляться без регистрации геометрических положений характерных вершин микроячеек m. Достаточно вывести положение характерной вершины или центра каждой микроячейки, обращаясь к положению характерных вершин соответствующей "материнской" макроячейки.
Эта характеристика позволяет также обеспечить существенную экономию потребного объема памяти запоминающего устройства, поскольку техника геологического моделирования в соответствии с предлагаемым изобретением является более компактной по сравнению с моделированием, требующим регистрации всех характерных вершин микроячеек m, с коэффициентом, по меньшей мере равным утроенному числу микроячеек m в рассматриваемой макроячейке.
В качестве примера, в специфическом и наиболее простом случае можно рассчитать координаты криволинейных отображений u, v, w характерной вершины микроячейки, связанной с тройкой индексов i, j, к трехмерной матрицы, при помощи следующих операций.
u=I±1/2
v=j±1/2
w=к±1/2
В этих формулах трехмерная матрица представлена как совокупность точек трехмерного пространства с целочисленными координатами i, j, к; при этом криволинейные координаты u, v, w связанной регулярной решетки рассматриваются как непрерывные интерполяции местоположения координат упомянутой трехмерной матрицы.
Можно видеть, что вершины макроячеек М также представляют собой вершины некоторых микроячеек m и, следовательно, что вершины этих некоторых микроячеек m дают отображения u, v, w в параметрическом пространстве 2 вершин макроячеек М.
При этом координаты характерных вершин макроячеек М являются известными одновременно при помощи их отображений в параметрическом пространстве u, v, w и при помощи их значений в геологическом пространстве х, у, z.
Как можно видеть на фиг.6, для каждой макроячейки М можно построить непрерывную векторную функцию по кускам Х (u, v, w), связывающим каждую точку параметрического пространства с некоторой точкой геологического пространства, путем интерполяции координат вершин каждой макроячейки.
Для этого можно использовать метод интерполяции, описанный как "hyperpatches" и приведенный в работе MORTENSON, опубликованной в 1985 году под названием "Geometric Modelling" в Editions John Wiley, Нью-Йорк, или, например, метод аппроксимации или интерполяции Безье, или метод интерполяции и аппроксимации Spline.
Здесь следует отметить, что определенная таким образом при помощи этих методов функция Х (u, v, w) зависит только от координат (х, у, z) вершин данной макроячейки в трехмерном геологическом пространстве 1. Следовательно, функция Х (u, v, w) представляет собой векторную функцию, которая непосредственно может быть использована для расчета местоположения вершин микроячеек m в геологическом пространстве 1.
На фиг.5 можно видеть, что способ моделирования в двух уровнях в соответствии с предлагаемым изобретением, описанный выше, также может быть применен к регулярным криволинейным трехмерным решеткам в наиболее общем случае, когда микроячейки m и макроячейки М не располагаются на одной линии. В этом случае макроячейки М содержат переменное число микроячеек m и решетка макроячеек М разбита на подсистемы этих макроячеек М, причем каждая такая подсистема связана с различной трехмерной матрицей, содержащей микроячейки m этой подсистемы.
Единственное условие, требуемое для осуществления способа в соответствии с предлагаемым изобретением, состоит в том, чтобы иметь возможность пересчитать местоположение вершин микроячеек m на основе местоположения вершин многогранных или шестигранных макроячеек М.
Для этого, как это схематически показано на фиг.4, 5 и 6, достаточно связать локальные координаты u, v, w в параметрическом пространстве 2 с каждой вершиной макроячеек М для того, чтобы иметь возможность вывести затем, при помощи упомянутых методов интерполяции, местоположения вершин микроячеек m.
Обобщение предлагаемого изобретения, представленное на фиг.4, может быть еще расширено до более полного обобщения, обращаясь к макроячейкам М многогранной формы. В этом случае предпочтительно, чтобы микроячейки m, содержащиеся в многогранных ячейках М, представляли шестигранную форму таким образом, чтобы еще иметь возможность использовать в этом случае общее техническое решение, представленное выше для регулярных решеток.
В наиболее общем способе в соответствии с предлагаемым изобретением, примененном в этом не представленном здесь варианте реализации, можно использовать такие этапы, как:
- регистрация параметрических координат u, v, w каждой из вершин макроячеек М в пространстве отображения i, j, к трехмерных матриц, используемых для регистрации свойств шестигранных микроячеек m;
- построение векторной функции Х (u, v, w), связывающей параметрическое пространство с геологическим пространством таким образом, чтобы функция Х (u, v, w) обеспечивала интерполяцию предварительно определенных вершин решетки макроячеек М;
- использование определенной таким образом векторной функции Х (u, v, w) для расчета местоположения вершины или центра каждой микроячейки m в геологическом пространстве х, у, z.
В этом случае можно также перегруппировать многогранные макроячейки М нерегулярного разбиения в подсистему, соответствующую геологическим блокам или геологическим системам, связывая эти подсистемы с различными трехмерными матрицами пространства отображения.
Предлагаемое изобретение, описанное выше со ссылками на несколько специфических примеров его реализации, ни в коем случае не ограничивается этими примерами, но охватывает, напротив того, любую модификацию формы и любой вариант реализации способа в соответствии с этим изобретением, содержащий определение системы макроячеек М, а затем разбиение этих макроячеек М на систему микроячеек m.
Для осуществления предлагаемого изобретения предпочтительным образом используют программируемое устройство для трехмерного моделирования, содержащее средства, предназначенные для определения многогранных или шестигранных макроячеек М, адаптированных к геометрии геологических слоев подлежащего моделированию геологического объема, а также средства, предназначенные для разбиения упомянутых макроячеек на микроячейки m, геометрия которых получается путем разбиения геометрии каждой макроячейки.
Предпочтительным образом устройство трехмерного моделирования в соответствии с предлагаемым изобретением представляет собой программируемое устройство, имеющее в своем составе запоминающее устройство, предназначенное для сохранения численных величин и управляемое при помощи программного продукта вычислительной машины, реализованного специально для осуществления способа трехмерного моделирования в соответствии с предлагаемым изобретением.
Для моделирования быстрых изменений некоторого свойства f (х, у, z) при помощи очень тонкой регулярной решетки программируют моделирование в несколько этапов: определение параметров данного геологического пространства; дискретизация геологической области; моделирование некоторого свойства f (х, у, z).
При определении параметров геологического пространства используют установление соответствия между исследуемой геологической областью G и параметрической областью Р, связывая с любой точкой, имеющей координаты (х, у, z) и принадлежащей данной геологической области G, некоторое отображение, располагающееся в точке с координатами (u, v, w) в параметрической области Р.
u=u (х, у, z)
v=v (х, у, z)
w=w (х, у, z)
Функции u (х, у, z), v (х, у, z), w (х, у, z) строятся непрерывными при помощи кусков и представляют разрывы только через поверхности разломов, не нарушающие следующих ограничений:
- отображение каждого горизонта в параметрической области Р представляет собой горизонтальную плоскость: функция w (х, у, z) выбирается постоянной для любой точки с координатами (х, у, z), принадлежащей одному и тому же горизонту;
- отображение любой пары различных точек (х1, у1, z1) и (х2, у2, z2), располагающихся в геологической области G, представляет собой пару различных точек (u1, v1, w1) и (u2, v2, w2) в параметрической области Р: градиент функций u (х, у, z), v (х, у, z), w (х, у, z) выбирается таким образом, чтобы он никогда не обнулялся в исследуемой геологической области G.
Функции u (х, у, z), v (х, у, z), w (х, у, z) задаются в виде некоторого числа точек выборки (xi, yi, zi), располагающихся в геологическом пространстве, и интерполируются численным методом при помощи любого известного способа, совместимого с разрывами через поверхности разломов, например, при помощи способа krigeage или способа DSI, описанного в документе "Mallet J.L., (1992), Discrete Smooth Interpolation in Geometric Modeling, Computer-Aided Design", том 24, №4, стр.177-191.
Обозначим как F(t) выбранную произвольно строго монотонную функцию; например, можно выбрать функцию F(t)=(t0-t), где t0 представляет собой произвольно заданную константу. Для нахождения точек выборки (xi, yi, zi), принадлежащих геологической области G, для которых заданы величины u (xi, yi, zi), v (xi, yi, zi) и w (xi, yi, zi), фиксируют функцию w (xi, yi, zi)=F(к) для любой точки (xi, yi, zi), принадлежащей горизонту Нк в перечне (Н1, Н2,...Hn) горизонтов, располагающихся в геологической области G и классифицированных в порядке убывания геологического возраста; затем, используя метод, позволяющий построить систему определения параметров u (х, у, z), v (х, у, z) для каждого горизонта Н (например, метод, описанный в "Levy В. and Mallet J.L., (1998), Non-distorted texture mapping for sheared triangulated meshes, АСМ-SIGGRAPH, 1998, Conference Proceedings, Orlando, Florida, стр.343-352") рассчитывают величины u (xi, yi, zi) и v (xi, yi, zi) в любой точке выборки, располагающейся в горизонте Н.
Дискретизация геологической области осуществляется таким образом, чтобы ребра многогранных ячеек никогда не пересекали упомянутые горизонты и поверхности разломов, и таким образом, чтобы поверхности многогранных ячеек были по существу параллельными или по существу ортогональными к упомянутым горизонтам.
Для каждой вершины уменьшенного числа ячеек (макроячеек), полученных после дискретизации данной геологической области, сохраняют в запоминающем устройстве вычислительной машины координаты (х, у, z) этой вершины в геологической области G и координаты (u, v, w) отображения этой вершины в параметрической области Р.
Моделирование некоторого свойства F (х, у, z) облегчается вследствие того, что упомянутая параметрическая область покрывается регулярной трехмерной решеткой с шестигранными ячейками, ребра которых являются прямолинейными и перпендикулярными между собой, а также вследствие того, что координаты (ui, vj, wк) любого узла (i, j, к) этой решетки достаточно просто рассчитываются при помощи следующих уравнений.
ui=u0+i.Du
vj=v0+j.Dv
wк=w0+к.Dw,
где (u0, v0, w0) представляют собой координаты исходных узлов решетки, тогда как Du, Dv и Dw представляют собой шаги этой решетки соответственно в направлениях u, v и w.
Величины (u0, v0, w0) и (Du, Dv, Dw) сохраняются в запоминающем устройстве вычислительной машины для осуществления способа моделирования функции f (х, у, z).
Этот способ моделирования функции f (х, у, z) содержит следующие этапы.
1. Для каждой геологической точки Х (xi, yi, zi), где наблюдается некоторая величина F (xi, yi, zi) подлежащей моделированию функции, приступают к "переносу" этой величины в параметрическую область, в точку с координатами u (xi, yi, zi), v (xi, yi, zi), w (xi, yi, zi)) следующим образом:
а - определяют геологическую макроячейку С, содержащую точку Х (xi, yi, zi);
b - находят параметрические координаты (ui, vi, wi) точки отображения этой геологической точки Х (xi, yi, zi) в параметрической области;
с - устанавливают данные fi=f (xi, yi, zi) в точку с координатами (ui, vi, wi).
2. В параметрическом пространстве, используя, например, упомянутые выше способы интерполяции krigeage или DSI, производят интерполяцию свойства f (i, j, к) в любом узле (i, j, к) регулярной решетки и сохраняют эту величину в запоминающем устройстве вычислительной машины.
3. Для каждой точки (х, у, z) в геологической области G, где желательно знать величину функции f (х, у, z), находят эту величину f (х, у, z) следующим образом:
а - определяют макроячейку С, содержащую точку (х, у, z);
b - находят точку (u, v, w), отображающую точку (х, у, z), в параметрической области Р;
с - отыскивают индексы (i, j, к) узла регулярной решетки, ближайшего к точке (u, v, w) в параметрическом пространстве;
d - считывают величину функции f, сохраненную в запоминающем устройстве вычислительной машины и связанную с узлом (i, j, к), и присваивают эту считанную величину функции f (х, у, z), или, наоборот, рассчитывают функцию f (х, у, z) как локальную интерполяцию величин f, связанных с узлами, окружающими точку с координатами (u, v, w).
Таким образом, благодаря использованию предлагаемого изобретения сохранение координат узлов регулярной решетки становится ненужным: только величины (u0, v0, w0) и (Du, Dv, Dw) и величины исследуемой функции f подлежат сохранению в запоминающем устройстве вычислительной машины.
Предлагаемое изобретение описано со ссылками на несколько специфических объектов, ни в коем случае не являющихся ограничительными, но охватывает, напротив того, любой вариант реализации в рамках и в духе предлагаемого изобретения, причем главное состоит в том, чтобы осуществлять моделирование на двух уровнях: первый уровень геометрического моделирования не должен учитывать постоянство физических параметров в макроячейках, а второй уровень более тонкого моделирования адаптирован к стабильности (приблизительно постоянной величине) физических параметров внутри каждой микроячейки.

Изобретение относится к способам трехмерного моделирования геологического объема. Технический результат заключается в сокращении времени моделирования. Технический результат достигается за счет того, что определяют совокупность многогранных макроячеек (М), адаптированных к геометрии геологических слоев подлежащего моделированию объема и осуществляют определение параметров геологического пространства для установления соответствия исследуемой геологической области и параметрической области, связывая с точкой, принадлежащей этой геологической области, точку отображения, располагающуюся в этой параметрической области. Затем определяют виртуальное разбиение многогранных макроячеек (М) на шестигранные микроячейки (m), геометрия которых обеспечена путем разбиения геометрии каждой макроячейки (М). 3 н. и 7 з.п. ф-лы, 6 ил.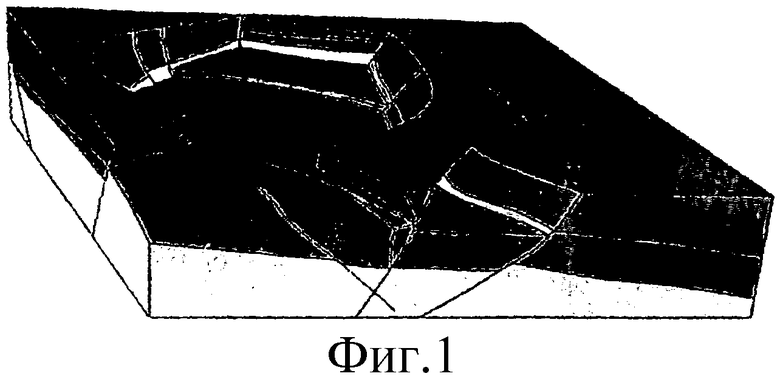
a) определяют совокупность многогранных макроячеек в геологической области, адаптированных к геометрии геологических слоев подлежащего моделированию объема;
b) осуществляют определение параметров геологического пространства для установления соответствия исследуемой геологической области и параметрической области, связывая с точкой, принадлежащей этой геологической области, точку отображения, располагающуюся в параметрической области;
c) определяют виртуальное разбиение макроячеек на микроячейки, геометрию которых получают путем разбиения геометрии каждой макроячейки таким образом, чтобы положения каждой микроячейки были выведены путем интерполяции из положений вершин соответствующей макроячейки, и таким образом, чтобы эти микроячейки соответствовали узлам регулярной решетки, покрывающей параметрическую область, с тем, чтобы моделировать некоторую функцию f (x, у, z), характеризующую геологическое свойство на регулярной решетке параметрической области, сокращая при этом количество подлежащих запоминанию данных.
| СПОСОБ ОПРЕДЕЛЕНИЯ НАЧАЛЬНЫХ И ТЕКУЩИХ ЗАПАСОВ ГАЗА ГАЗОКОНДЕНСАТНОГО МЕСТОРОЖДЕНИЯ | 1999 |
|
RU2148153C1 |
| US 5844564 A, 12.01.1998 | |||
| МОКРЫЙ ЦЕНТРОБЕЖНЫЙ СКРУББЕР | 0 |
|
SU254325A1 |
| JP 10153520, 09.06.1998 | |||
| US 6106561 А1, 22.08.2000. | |||
Авторы
Даты
2007-09-20—Публикация
2002-12-10—Подача