Изобретение относится к области моделирования 3D (трехмерных) объектов и может быть использовано в компьютерных системах при моделировании сложных структур для облегчения анализа или их проектирования, в частности, к системам и способам для генерации сеток, представляющим такие структуры.
Для решения задач гидрогеологии и гидроэкологии трехмерное моделирование заданного объекта осуществляется путем дискретизации геологической модели (построения сеточной модели) в вычислительной системе.
Особенностями, например, геологических моделей являются:
- протяженность по латерали;
- слоистая структура отложений;
- крупный масштаб по площади (до нескольких тысяч кв. км);
- неопределенность внутреннего строения (из-за ограниченности возможностей изучения пластов).
Как правило, для таких задач трехмерная модель - это слоистые сеточные модели, полученные вытягиванием двумерной сетки вдоль направления по оси аппликат.
Получение сетки на основе решетки начинается с геометрической модели, которая точно определяет внутренние и наружные границы объектов, для которых строятся сетки. Таким образом, существует необходимость в системе и методике построения сеток, чтобы облегчить анализ множества наборов данных, связанных с трехмерным объектом, и обеспечить правильное восприятие геометрических связей между данными измерений и трехмерным объектом.
Точность большинства вычислений, выполняемых на сетках, зависит от регулярности сеточных элементов. Моделирование, выполненное на треугольных сетках с высокой регулярностью, имеющих почти равносторонние треугольники, является более точным, чем то, которое выполнено на нерегулярных сетках с длинными тонкими треугольниками. Это одна причина, по которой популярна триангуляция Делоне. При заданном наборе узлов, представляющих местоположения узлов для двумерной сетки, триангуляция Делоне этих узлов по сравнению со всеми иными возможными триангуляциями дает треугольники, в наибольшей степени близкие к равносторонним. Однако триангуляция Делоне сама по себе не гарантирует регулярной сетки. Для этого необходимо тщательно выбирать местоположения узлов сетки. (Для обзора двумерной и трехмерной триангуляции Делоне в применении к проблеме построения сеток см. Bern, М., and Eppstein, D., Mesh Generation and Optimal Triangulation, in Computing in Euclidean Geometry, Du, D.-Z. and Hwang, F.K. eds., World Scientific, 1995.)
Также для описания (моделирования) сложных структурных элементов, например, геологической модели применяют неструктурированные сетки с целью повышения точности расчета вблизи геометрических особенностей. Известными примерами способов построения таких структур являются TOUGH2 (Официальный сайт компании Lawrence Berkeley National Lab. Earth Sciences Division: http://esd.lbl.gov/research/projects/tough/software), MODFLOW-USG (http://www.swstechnology.com/blog/modflow-usg-unstructured-grids-a-game-changer-for-groundwater-modeling) и др.
Одним из критериев генерации сетки является скорость построения, а также ограничения на используемую оперативную память. В силу изложенных причин на практике особый интерес вызывает построение сеток в параллельном режиме.
Для получения сеточных моделей с числом ячеек, сопоставимым с числом ячеек, например, первичной геологической модели (до нескольких миллиардов) требуется разработка способов параллельной генерации трехмерных неструктурированных сеток. Поэтому одной из важных задач в настоящее время является распараллеливание процессов генерации неструктурированных сеток, как двухмерных, так и трехмерных.
Известен способ трехмерного моделирования заданного свойства в заданном объеме (Патент РФ №2306607, приоритет от 10.12.2002, «Способ, устройство и программный продукт для трехмерного моделирования геологического объема при помощи выбора трехмерных параметров геологической области» авторов Дени Лоран, Коньо Ришар, МПК: G06T 7/60, 17/00, опубликовано 20.09.2007. Бюл. №26), заключающийся в построении регулярной сетки из шестигранников в искривленном объеме. Недостатком данного способа является то, что он предназначен для работы в последовательном режиме, а также структурированность.
Известен способ трехмерного моделирования заданного объекта (EP 2741259 «А system and method for generating a mesh», автор: SUNDARAM RAVI, МПК: G06T 7/60, 15/08, 17/00), заключающийся в построении слоевой неструктурированной в каждом слое сетки (ячейки - тетраэдры). Недостатками данного способа являются последовательный процесс построения, что увеличивает время построения сеток и увеличивает требования по используемой памяти.
Кроме того, не все способы построения двухмерных вычислительных сеток могут быть достаточно легко обобщены на трехмерный случай.
Известны несколько способов построения двухмерной неструктурированной сетки в параллельном режиме.
Известен отказоустойчивый фронтальный метод построения двухмерной неструктурированной сетки (Y. Ito, A.M. Shih, B.K. Soni. Reliable Isotropic Tetrahedral Mesh Generation based on an Advancing front method // Proceedings of the 13th International meshing roundtable, Williamsburg, VA. Pp 95-105, 2004), который применяется к областям сложной формы. К положительным качествам метода относится робастность, а к отрицательным качествам - возможность локального появления элементов сетки низкого качества, причем эти зоны нельзя предсказать заранее. Фронтальный метод не использует принципа Делоне при создании элементов, что приводит к низкому качеству получаемой сетки и требуются дополнительные корректировки.
Известен двухэтапный метод "упаковки сфер" построения двухмерной неструктурированной сетки на основе физической релаксации (Shimada K., Yamakawa A., Itoh Т., Anisotropic triangular meshing of parametric surfaces via close packing of ellipsoidal bubbles. In 6th International Meshing roundtable. Pp 375-390, 1997). Метод способен построить наиболее качественную сетку, но время для ее построение является большим и даже распараллеливание этого метода не решает проблему скорости. Сложность способа по количеству операций оценить нельзя, но существует зависимость времени построения от таких факторов как размерность задачи, тип генерируемой сетки, изотропность/анизотропность сетки, функция распределения характерного размера сфер и др.
Известен метод построения двухмерной неструктурированной сетки "откусывания сферами" К.Я. Ли, Ш.Х. Тена и А. Унгора (Li X.Y., Teng S.H., Ungor A. Bitting spheres in 3d. Submitted to the 8th International Meshing Roundtable). Достоинством метода является совмещение преимуществ метода релаксации и фронтального метода. К недостаткам метода можно отнести низкое топологическое качество получаемой неструктурированной сетки и сложность вычисления положения новой точки.
В работе Миллера и соавторов (Miller G.L., Talmor D., Teng S.H., Walkington N. A delaunnay based numerical method for three dimensions: generation, formulation and partition // In Proc 27th Annu. ACM Sympos. Theor. Comput. Pp 683-692, 1995) рассматривается также двухэтапный метод, который представляет собой генерацию точек внутри области на основе декартового адаптивного шаблона и последующей фильтрации и соединения. Этот метод хорошо распараллеливается и легко реализуется на практике, однако, сетка не будет повторять форму границ области из-за ступенчатой формы шаблона.
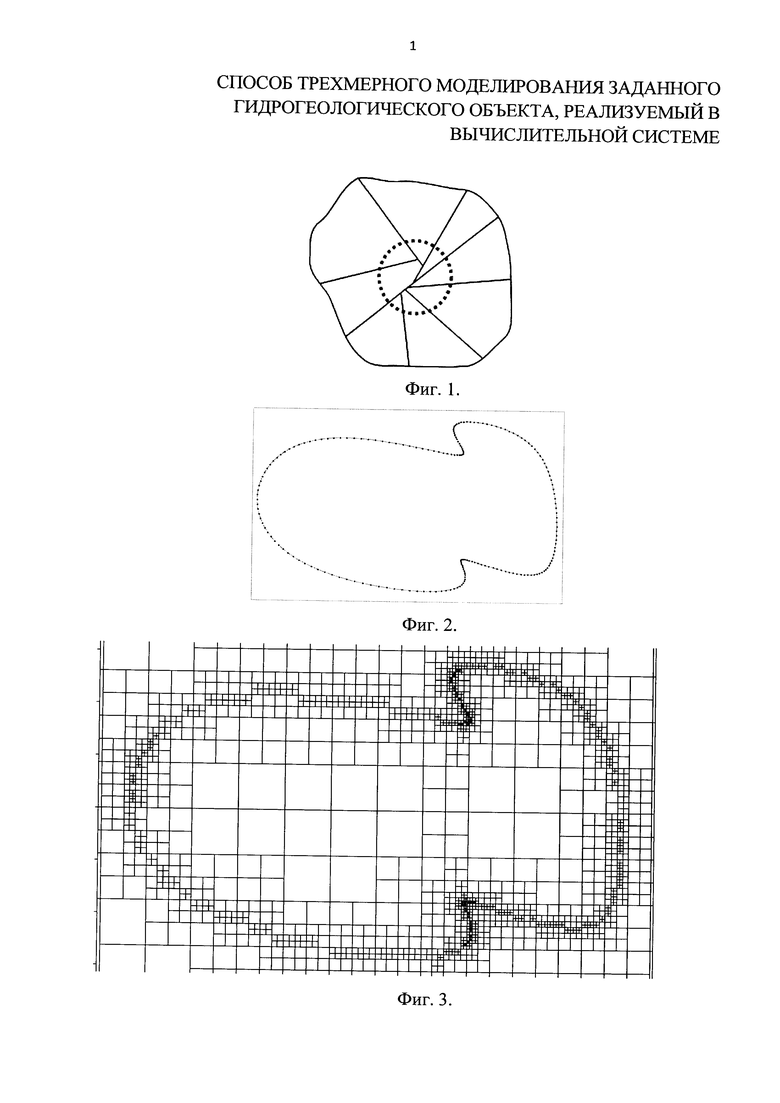
Известен способ моделирования заданного объекта, в котором применяют построение неструктурированных сеток (Е.Г. Иванов. «Автоматическая параллельная генерация неструктурированных расчетных сеток для задач вычислительной механики». Автореферат диссертации на соискание ученой степени кандидата физико-математических наук. Институт теоретической и прикладной механики им. С.А. Христиановича Сибирского отделения РАН, Новосибирск. 2007), основанный на распараллеливании способа построения неструктурированных сеток по фрагментам, когда в каждом фрагменте соответствующим процессором генерируется своя неструктурированная сетка без обмена данными между процессорами. В данном способе предварительно строится поверхностная сетка на моделируемом объеме, затем объем с помощью инерциального метода разбивается плоскостями на трехмерные фрагменты. На плоских границах генерируется совместная плоская двумерная сетка (то есть она общая для соседних фрагментов). На основании полученной поверхностной сетки каждого фрагмента строится трехмерная неструктурированная сетка. Недостатком данного способа является то, что в местах стыка более двух фрагментов может образовываться сетка неудовлетворительного качества (фиг. 1). Кроме того, результирующая сетка зависит от метода декомпозиции исходной области на фрагменты. Данный способ является наиболее близким аналогом.
Задачей, на решение которой направлено изобретение, является создание способа трехмерного моделирования заданного гидрогеологического объекта, реализуемого в вычислительной системе.
Технический результат заключается в повышении точности моделирования заданного объекта.
Дополнительным техническим результатом является увеличение скорости моделирования.
Данный технический результат достигается тем, что способ трехмерного моделирования заданного гидрогеологического объекта, реализуемый в вычислительной системе, заключается в том, что предварительно моделируемый объект виртуально разбивают на определенное количество слоев, затем определяют и сохраняют в запоминающем устройстве параметрические координаты точек граничных контуров моделируемого объекта и его образованных слоев в виде набора точек, упорядоченных по часовой стрелке, далее для каждой поверхности раздела слоев посредством соответствующих вычислительных ядер строят двухмерную неструктурированную сетку, включающую список координат узлов, списки узлов и ячеек, затем производят разбиение каждой полученной двухмерной неструктурированной сетки на подобласти и сохраняют координаты узлов, упорядоченный набор номеров узлов каждой ячейки и список номеров соседних с ней ячеек каждой образованной подобласти в памяти соответствующего вычислительного ядра; далее в параллельном режиме производят построение трехмерной вычислительной сетки заданного гидрогеологического объекта, в ходе которого одновременно посредством соответствующего вычислительного ядра из каждой ячейки каждой образованной подобласти двухмерной неструктурированной сетки, используя координаты точек контуров ячеек, вдоль оси аппликат образуют многогранник, затем одновременно в каждой подобласти определяют граничные условия для каждого образованного многогранника путем доопределения граней, являющихся общими с соседними многогранниками, после чего производят разбиение каждого многогранника определенным способом вдоль оси аппликат на определенное число ячеек, далее доопределяют граничные ячейки и грани многогранников, соприкасающихся с поверхностями раздела слоев, затем сохраняют в соответствующем вычислительном ядре координаты узлов, списки узлов граней, списки граней ячеек каждого многогранника каждой образованной подобласти трехмерной вычислительной сетки
Двухмерная неструктурированная сетка может быть построена следующим образом. Посредством вычислительных ядер с помощью заданных координат точек для граничного контура каждой поверхности раздела слоев строят первую двухмерную фоновую сетку, затем на каждой полученной первой фоновой сетке в ячейках, содержащих узлы граничного контура, определяют граничные условия I рода и решают численно уравнение Лапласа с этими условиями для определения размерной функции, посредством которой затем производят построение второй двухмерной фоновой сетки, далее вторую двухмерную фоновую сетку разбивают на подобласти, каждую из которых сохраняют в памяти соответствующего вычислительного ядра, далее определенным образом производят заполнение узлами ячеек каждой образованной подобласти второй фоновой сетки, затем одновременно посредством каждого соответствующего вычислительного ядра производят триангуляцию Делоне множества точек соответствующей подобласти с определенными ограничениями в виде заданного контура, далее производят преобразование граничных зон смежных подобластей путем осуществления обмена данными между соответствующими вычислительными ядрами для доопределение ячеек являющихся общими с ячейками соседних подобластей.
Использование всей совокупности существенных признаков позволяет произвести параллельное построение сеток в заданном объеме (как двухмерные, так и трехмерные фрагменты, на которые разбит объем) с обменом информацией между соседними вычислительными ядрами и за счет этого исключить зависимость качества результирующей сетки от формы границ фрагментов, что повышает качество результирующей сетки, за счет чего повышается точность моделирования заданного гидрогеологического объекта.
Увеличение скорости моделирование достигается за счет параллельного построения каждой двухмерной сетки, обеспечиваемое тем, что каждая подобласть соответствующей двухмерной сетки строится посредством соответствующего вычислительного ядра одновременно.
Изобретение поясняется следующими чертежами.
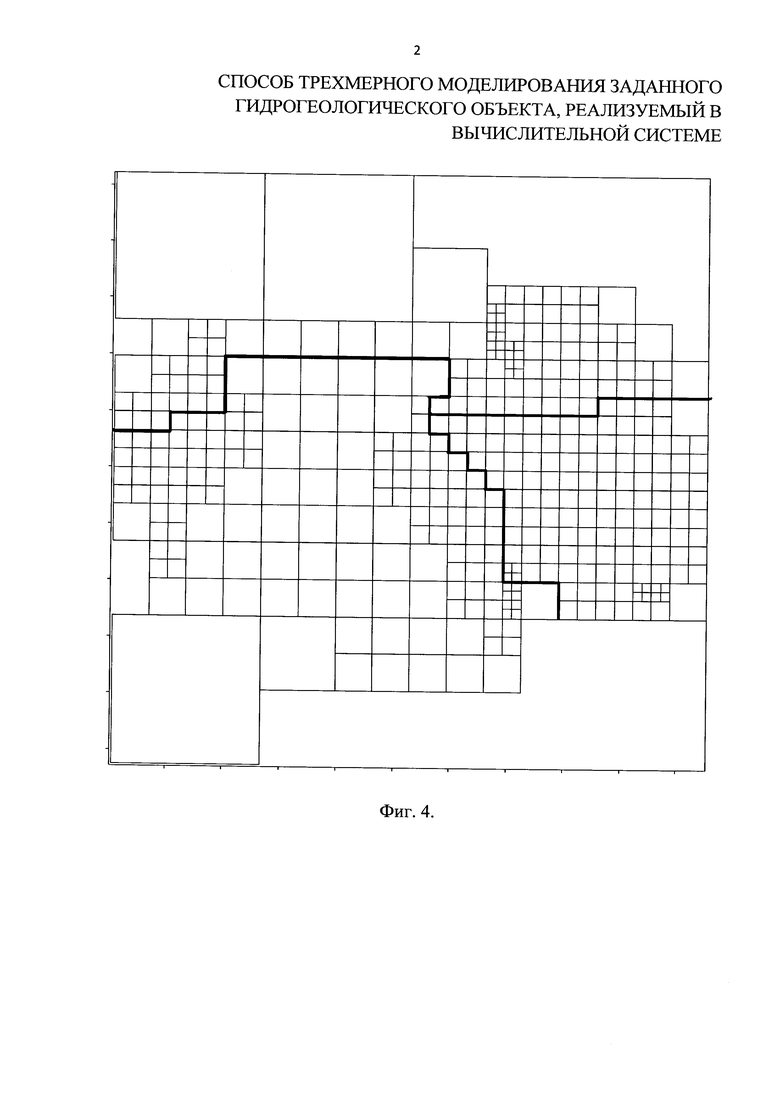
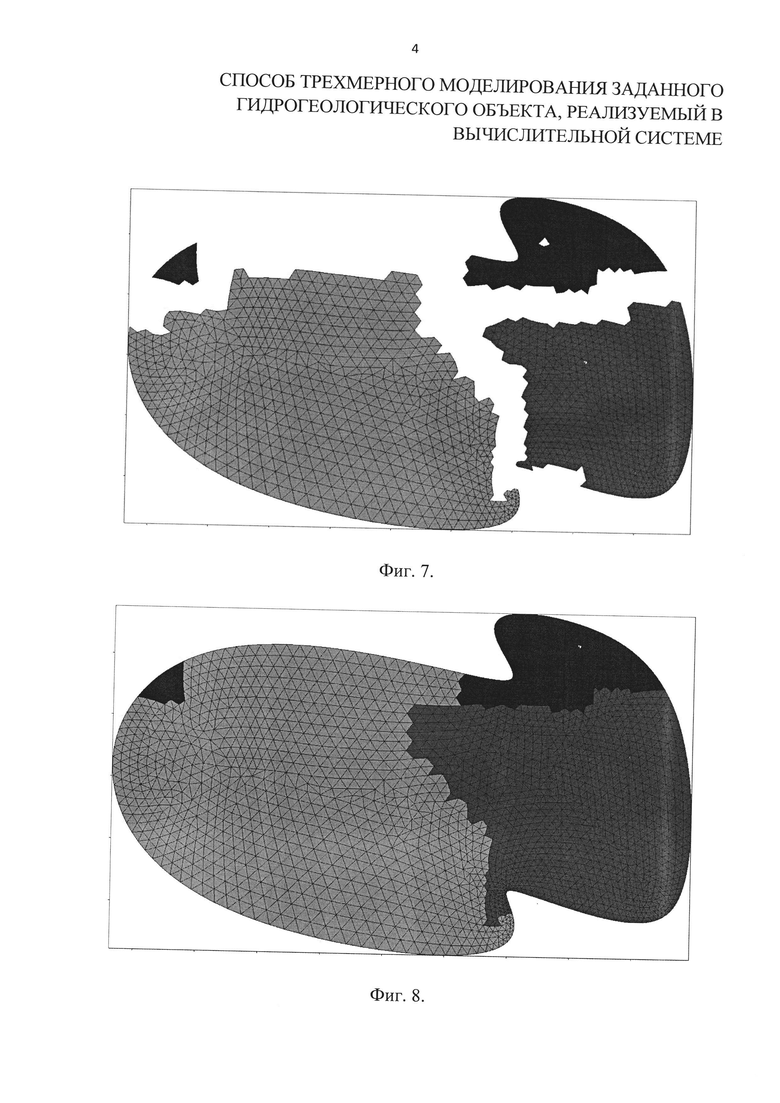
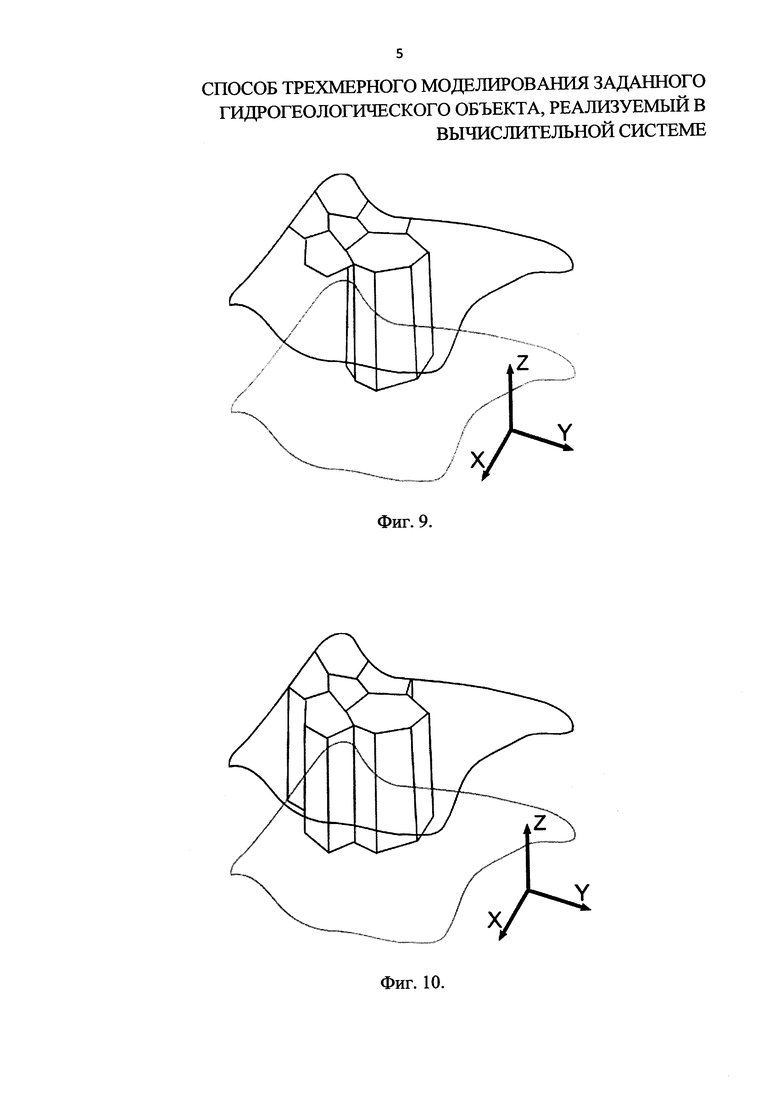
На фиг. 2 представлен вариант граничного контура поверхности раздела слоев моделируемого объекта. На фиг. 3 представлена первая двухмерная фоновая сетка. На фиг. 4 представлена вторая двухмерная фоновая сетка. На фиг. 5 - первая итерация заполнения области узлами, на фиг. 6 - результат заполнения области узлами, на фиг. 7 - результат триангуляции доопределения граничных условий смежных подобластей, на фиг. 8 - результат триангуляции (двухмерная неструктурированная сетка поверхности раздела слоев), на фиг. 9, фиг. 10 и фиг. 11 - фрагменты слоя моделируемого объекта, на фиг. 12 - трехмерная сетка слоя моделируемого объекта, на фиг. 13 - показаны трехмерные сетки соседних слоев, на фиг. 14 - трехмерная сетка моделируемого объекта.
Заявленный способ трехмерного моделирования заданного гидрогеологического объекта реализуется на вычислительных системах любого типа. Типовая вычислительная система включает в себя множество вычислительных ядер, связанное с ними запоминающее устройство, средства ввода, клавиатура и мышь, устройство вывода - дисплей.
Способ трехмерного моделирования заданного гидрогеологического объекта, реализуемый в вычислительной системе, осуществляется следующим образом.
Предварительно моделируемый объект (например, геологическую модель) виртуально разбивают на определенное количество слоев.
Далее определяют и сохраняют в запоминающем устройстве координаты точек граничных контуров моделируемого объекта и его образованных слоев в виде набора точек, упорядоченных по часовой стрелке.
Для каждой поверхности раздела слоев посредством соответствующих вычислительных ядер с помощью заданных координат точек для каждой поверхности раздела слоев строят двухмерную неструктурированную сетку следующим образом.
1. Строится первая двухмерная фоновая сетка для вычисления размерной функции (функции распределения характерного размера ребер результирующей двухмерной сетки). Контур поверхности раздела слоев (фиг. 2) искусственно делится так, чтобы размер ребра в образованном контуре был примерно равен минимальному размеру ребра в первоначальном контуре. Вокруг контура создается квадрат, и затем производится его дробление - создаются дочерние квадраты, так чтобы не осталось квадратов, содержащих более одного узла образованного контура (фиг. 3).
2. На основании длин ребер контура вычисляется размерная функция, определяемая внутри квадратов первой двухмерной фоновой сетки посредством решения уравнения Лапласа с заданным граничным условием первого рода на квадратах содержащих точки контура (Numerical Solution of Laplace Equation, Gilberto E. Urroz, October 2004);
3. На основании вычисленной размерной функции строится вторая двухмерная фоновая сетка, предназначенная для ускорения поиска ближайших точек (фиг. 4). Вокруг контура создается квадрат, и затем производится его дробление - создаются дочерние квадраты, так чтобы не осталось квадратов, содержащих менее чем Nt будущих треугольников (Nt вычисляется как отношение площади квадрата к площади равностороннего треугольника со стороной, длина которой равна значению размерной функции в данной точке пространства в ячейке первой двухмерной фоновой сетки).
4. Производится разбиение (декомпозиция) второй двухмерной фоновой сетки методом RegionGrow (Frey Р, George P.L., Mesh Generation Application To Finite Elements (Hermes Science, 2000)) с весами (вес каждой ячейки второй фоновой сетки - это предварительное количество ячеек итоговой двухмерной сетки в ячейке второй фоновой сетки). Вторую двухмерную фоновую сетку разбивают на подобласти. Количество образованных подобластей может быть больше или равно количеству изначально используемых вычислительных ядер. Каждую образованную подобласть второй двухмерной фоновой сетки сохраняют в памяти соответствующего вычислительного ядра.
5. Область, ограниченная заданным контуром, заполняется узлами, являющимися носителями сфер определенного диаметра, вычисляемого с помощью функции распределения характерного размера ребер сетки (Способ заполнения узлами может быть разным - например шаблонный (Li X.Y., Teng S.H., Ungor A. Bitting spheres in 3d. Submitted to the 8th International Meshing Roundtable.) или фронтальный (Miller G.L., Talmor D., Teng S.H., Walkington N. A delaunnay based numerical method for three dimensions: generation, formulation and partition // In Proc 27th Annu. ACM Sympos. Theor. Comput. Pp 683-692, 1995.)); (фиг. 5, 6).
6. Одновременно в каждом вычислительном ядре производится триангуляция Делоне множества узлов в ячейках соответствующей подобласти второй двухмерной фоновой сетки с определенными ограничениями (фиг. 7). Определенные ограничения это наборы точек и ребер, применение которых позволяет учесть в сетке различные объекты, характеризующие особенности моделируемого объекта. Они окажут влияние на характерный размер вблизи себя.
7. Производят преобразование граничных зон смежных подобластей путем осуществления обмена данными между соответствующими вычислительными ядрами для доопределения ячеек являющихся общими с ячейками соседних подобластей (фиг. 8). Затем может производиться сглаживание (смещение узлов по определенному критерию, не ухудшающему меру качества сетки) и локальное перестроение полученной треугольной сетки по ряду критериев, приводящих к улучшению геометрической меры качества сетки (Tian Zhou, Kenji Shimada, "An Angle Based Aproach To Two Dimensional Mesh Smoothing", Carnegie Melon University, Pitsburgh, USA 2000). Результирующая двухмерная сетка поверхности раздела слоев представлена на фиг. 8.
Этапы 1-3 выполняются на каждом вычислительном ядре для всей области без обменов. Этапы 4-7 реализованы в параллельном режиме, причем выполнение каждого из них производится локально (в своей подобласти), каждая подобласть соответствующей двухмерной сетки строится посредством соответствующего вычислительного ядра одновременно, а на границах смежных подобластей осуществляют обмены данными между вычислительными ядрами.
Двухмерная неструктурированная сетка каждой поверхности раздела слоев хранится в формате - список координат узлов, список узлов и соседних ячеек для каждой ячейки сетки.
После построения двухмерной сетки производят повторную декомпозицию (передекомпозицию), позволяющую изменить количество итоговых подобластей двухмерной сетки и варьировать количество ячеек в подобластях. Для этого производят разбиение каждой полученной двумерной неструктурированной сетки на подобласти и сохраняют координаты узлов, упорядоченный набор номеров узлов каждой ячейки и список номеров соседних с ней ячеек каждой образованной подобласти в памяти соответствующего вычислительного ядра. Количество подобластей определяется сложностью объекта, числом доступных ядер и числом ячеек двухмерной сетки.
После построения двухмерной неструктурированной сетки каждой поверхности раздела слоев в параллельном режиме проводится построение трехмерной сетки моделируемого объекта (множество пластов).
Построение трехмерной сетки каждого пласта заданного объекта происходит следующим образом:
1. Одновременно для каждой образованной подобласти посредством соответствующего вычислительного ядра из каждой ячейки подобласти двумерной неструктурированной сетки, используя координаты точек контуров ячеек, вдоль оси аппликат образуют многогранник (столбец) (фиг. 9).
2. Затем одновременно в каждой подобласти определяют граничные условия для каждого образованного многогранника путем доопределения граней, являющихся общими с соседними многогранниками (фиг. 10). То есть производят «сшивание» столбцов подобласти между собой.
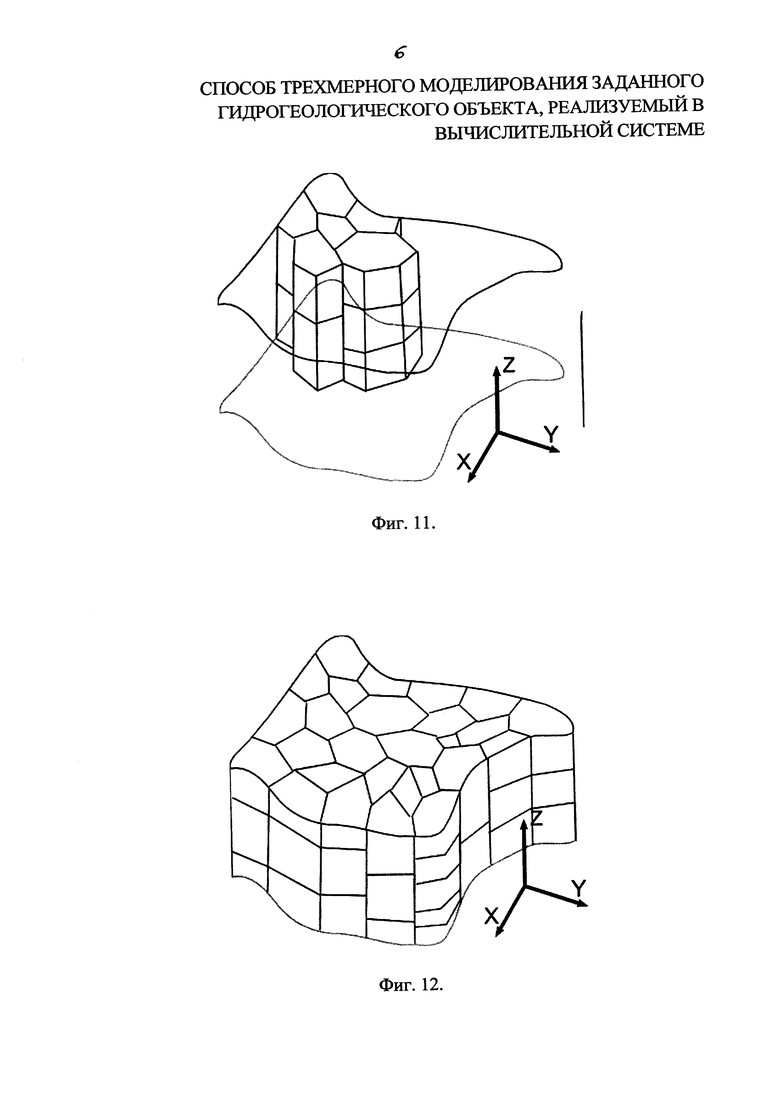
3. Производят разбиение каждого многогранника определенным способом вдоль оси аппликат на определенное число ячеек (фиг. 11) одновременно в каждой подобласти. При этом в разных местах используется разное число дробления, что позволяет адаптировать итоговую сетку в соответствии с толщиной слоя и особенностями моделируемого объекта, например, для геологической модели, особенности рельефа.
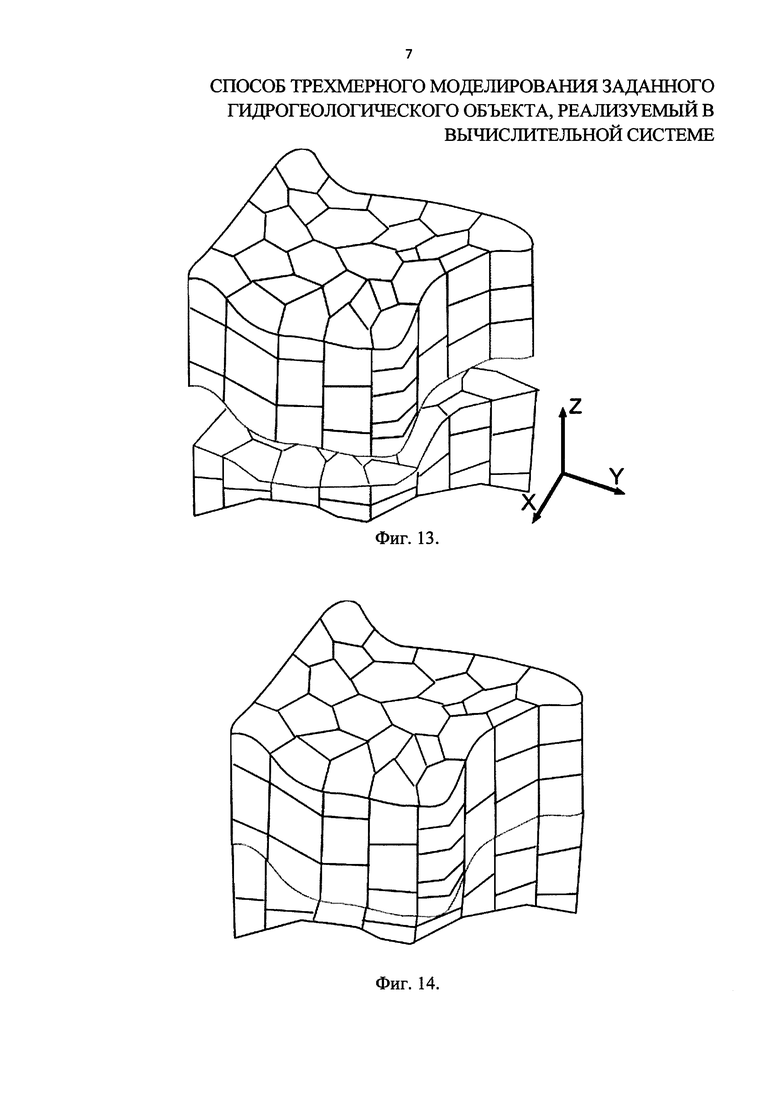
После построения трехмерных сеток каждого слоя (фиг. 12) доопределяют граничные ячейки и грани многогранников, соприкасающихся с поверхностями раздела слоев (фиг. 13, 14). То есть происходит «сшивка» слоев моделируемого объекта.
Заявленное параллельное построение вычислительных сеток в заданном объеме (как двухмерные, так и трехмерные фрагменты, на которые разбит объем) с обменом информацией между соседними вычислительными ядрами позволяет исключить зависимость качества результирующей сетки от формы границ фрагментов, что повышает качество результирующей сетки, за счет чего повышается точность моделирования заданного гидрогеологического объекта.
Затем может быть произведено разбиение образованной трехмерной вычислительной сетки моделируемого объекта на подсетки, количество которых определяется сложностью объекта, числом доступных ядер и числом ячеек двухмерной сетки. Дополнительное разбиение производят для ускорения последующих параллельных вычислений на полученной сетке. В соответствующем вычислительном ядре, сохраняют координаты узлов, списки узлов граней, списки граней ячеек каждого многогранника каждой образованной подобласти трехмерной вычислительной сетки.
Трехмерная сетка хранится в формате - список координат, списки узлов и соседних ячеек граней, списки граней для каждой ячейки сетки.

Изобретение относится к области моделирования 3D (трехмерных) объектов. Способ трехмерного моделирования заданного гидрогеологического объекта, реализуемый в вычислительной системе, заключается в том, что предварительно моделируемый объект виртуально разбивают на определенное количество слоев, затем определяют и сохраняют в запоминающем устройстве параметрические координаты точек граничных контуров моделируемого объекта и его образованных слоев в виде набора точек, упорядоченных по часовой стрелке, далее для каждой поверхности раздела слоев посредством соответствующих вычислительных ядер строят двухмерную неструктурированную сетку, включающую список координат узлов, списки узлов и ячеек, затем производят разбиение каждой полученной двухмерной неструктурированной сетки на подобласти и сохраняют координаты узлов, упорядоченный набор номеров узлов каждой ячейки и список номеров соседних с ней ячеек каждой образованной подобласти в памяти соответствующего вычислительного ядра; далее в параллельном режиме производят построение трехмерной вычислительной сетки заданного гидрогеологического объекта, в ходе которого одновременно посредством соответствующего вычислительного ядра из каждой ячейки каждой образованной подобласти двухмерной неструктурированной сетки, используя координаты точек контуров ячеек, вдоль оси аппликат образуют многогранник, затем одновременно в каждой подобласти определяют граничные условия для каждого образованного многогранника путем доопределения граней, являющихся общими с соседними многогранниками, после чего производят разбиение каждого многогранника определенным способом вдоль оси аппликат на определенное число ячеек, далее доопределяют граничные ячейки и грани многогранников, соприкасающихся с поверхностями раздела слоев, затем сохраняют в соответствующем вычислительном ядре координаты узлов, списки узлов граней, списки граней ячеек каждого многогранника каждой образованной подобласти трехмерной вычислительной сетки. Технический результат – повышение точности моделирования заданного объекта. 1 з.п. ф-лы, 14 ил.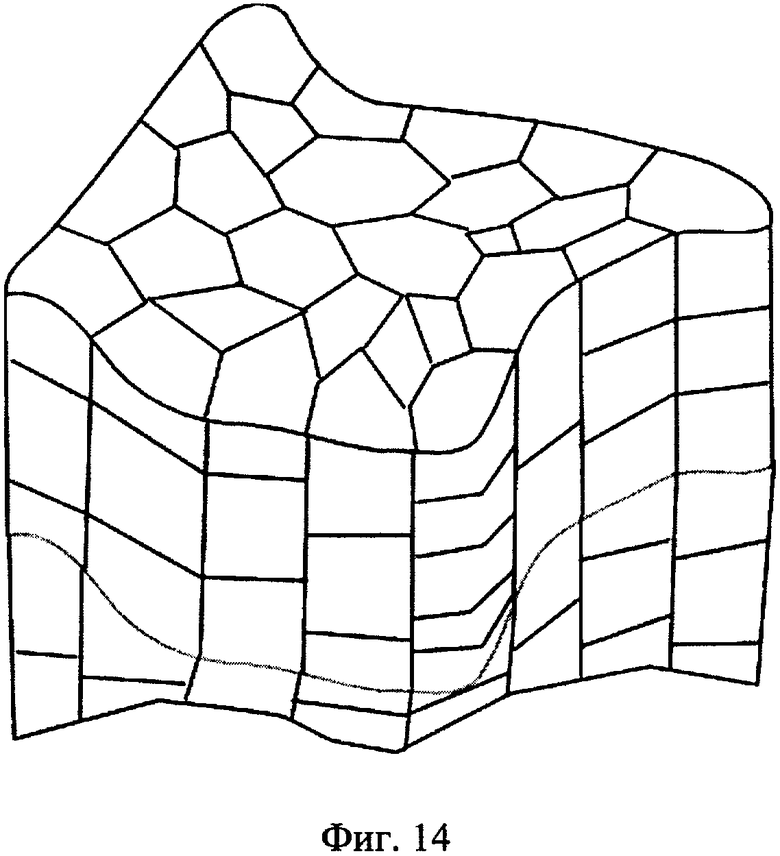
1. Способ трехмерного моделирования заданного гидрогеологического объекта, реализуемый в вычислительной системе, заключающийся в том, что предварительно моделируемый объект виртуально разбивают на определенное количество слоев, затем определяют и сохраняют в запоминающем устройстве параметрические координаты точек граничных контуров моделируемого объекта и его образованных слоев в виде набора точек, упорядоченных по часовой стрелке, далее для каждой поверхности раздела слоев посредством соответствующих вычислительных ядер строят двухмерную неструктурированную сетку, включающую список координат узлов, списки узлов и ячеек, затем производят разбиение каждой полученной двухмерной неструктурированной сетки на подобласти и сохраняют координаты узлов, упорядоченный набор номеров узлов каждой ячейки и список номеров соседних с ней ячеек каждой образованной подобласти в памяти соответствующего вычислительного ядра; далее в параллельном режиме производят построение трехмерной вычислительной сетки заданного гидрогеологического объекта, в ходе которого одновременно посредством соответствующего вычислительного ядра из каждой ячейки каждой образованной подобласти двухмерной неструктурированной сетки, используя координаты точек контуров ячеек, вдоль оси аппликат образуют многогранник, затем одновременно в каждой подобласти определяют граничные условия для каждого образованного многогранника путем доопределения граней, являющихся общими с соседними многогранниками, после чего производят разбиение каждого многогранника определенным способом вдоль оси аппликат на определенное число ячеек, далее доопределяют граничные ячейки и грани многогранников, соприкасающихся с поверхностями раздела слоев, затем сохраняют в соответствующем вычислительном ядре координаты узлов, списки узлов граней, списки граней ячеек каждого многогранника каждой образованной подобласти трехмерной вычислительной сетки.
2. Способ трехмерного моделирования заданного гидрогеологического объекта, реализуемый в вычислительной системе по п. 1, отличающийся тем, что при построении двухмерной неструктурированной сетки для каждой поверхности раздела слоев посредством вычислительных ядер с помощью заданных координат точек для граничного контура каждой поверхности раздела слоев строят первую двухмерную фоновую сетку, затем на каждой полученной первой фоновой сетке в ячейках, содержащих узлы граничного контура, определяют граничные условия I рода и решают численно уравнение Лапласа с этими условиями для определения размерной функции, посредством которой затем производят построение второй двухмерной фоновой сетки, далее вторую двухмерную фоновую сетку разбивают на подобласти, каждую из которых сохраняют в памяти соответствующего вычислительного ядра, далее определенным образом производят заполнение узлами ячеек каждой образованной подобласти второй фоновой сетки, затем одновременно посредством каждого соответствующего вычислительного ядра производят триангуляцию Делоне множества точек соответствующей подобласти с определенными ограничениями в виде заданного контура, далее производят преобразование граничных зон смежных подобластей путем осуществления обмена данными между соответствующими вычислительными ядрами для доопределения ячеек, являющихся общими с ячейками соседних подобластей.
| Иванов Е | |||
| Г | |||
| "Автоматическая параллельная генерация неструктурированных расчетных сеток для задач вычислительной механики" | |||
| Автореферат диссертации на соискание ученой степени кандидата физико-математических наук | |||
| Институт теоретической и прикладной механики им | |||
| С.А | |||
| Христиановича Сибирского отделения РАН, Новосибирск | |||
| Пресс для выдавливания из деревянных дисков заготовок для ниточных катушек | 1923 |
|
SU2007A1 |
| СПОСОБ, УСТРОЙСТВО И ПРОГРАММНЫЙ ПРОДУКТ ДЛЯ ТРЕХМЕРНОГО МОДЕЛИРОВАНИЯ ГЕОЛОГИЧЕСКОГО ОБЪЕМА ПРИ ПОМОЩИ ВЫБОРА ТРЕХМЕРНЫХ ПАРАМЕТРОВ ГЕОЛОГИЧЕСКОЙ ОБЛАСТИ | 2002 |
|
RU2306607C2 |
| US 20010006387 A1, 05.07.2001 | |||
| US 5844564 A, 01.12.1998. | |||
Авторы
Даты
2017-03-01—Публикация
2015-12-01—Подача