Изобретение относится к области кодирования и передачи криптографических ключей через открытое пространство.
Из уровня техники в данной области известен способ кодирования и передачи криптографических ключей, включающий формирование на передающей станции последовательности квантовых фотонных состояний и передачу этих состояний по открытому пространству на принимающую станцию (см. патент США №6748083 В1, кл. МКИ Н04К 001/08; G06F 001/02; G06F 007/58, опубликованный 08.06.2004 г.).
К принципиальным недостаткам известного способа можно отнести невозможность технически реализовать источник, генерирующий строго однофотонные состояния. При нестрогой однофотонности источника и затухании в пространстве, превышающем некоторую критическую величину, известный способ не гарантирует секретность передаваемых криптографических ключей. Кроме того, известный способ требует прецизионного и согласованного контроля за поляризационными степенями свободы как при кодировании, так и при детектировании однофотонных состояний на принимающей и передающей станциях. В силу указанных принципиальных недостатков известный способ не позволяет обеспечивать секретность передаваемых криптографических ключей на большие расстояния, долговременную стабильность системы и минимизировать поток ошибок на принимающей станции.
Технический результат, на достижение которого направлено изобретение, заключается в обеспечении секретности криптографических ключей при передаче последних через открытое пространство на большие расстояния, включая передачу между наземными объектами и низкоорбитальными спутниками (вплоть до высот в 1000 км) в том случае, когда источник квантовых состояний не является строго однофотонным, и во время связи в пространстве имеется произвольное затухание, а также на достижение долговременной стабильности и уменьшение потока ошибок в передаваемых первичных криптографических ключах на принимающей станции.
Использование такого фундаментального принципа как принцип релятивистской причинности в квантовой криптографии позволяет сформулировать принципиально новый подход к обеспечению секретности передаваемых криптографических ключей. В данном способе кодирования и передачи криптографических ключей снимаются принципиальные трудности, имеющиеся в ранее известном способе (см. патент США №6748083 В1, кл. МКИ Н04К 001/08; G06F 001/02; G06F 007/58, опубликованный 08.06.2004 г.). Предложенный способ кодирования и передачи криптографических ключей естественно называть релятивистской квантовой криптографией. Релятивистская квантовая криптография обеспечивает секретность при передаче криптографических ключей: 1) при любом затухании во время связи (затухание снижает лишь скорость передачи ключей, но не влияет на их секретность); 2) не требует строго однофотонного источника квантовых состояний (достаточно лишь присутствие однофотонной компоненты в состояниях лишь с некоторой вероятностью. Схема остается секретной даже при сколь угодно малой доле (вероятности) однофотонной компоненты. Это означает, что квантовое состояние может иметь сколь угодно большое среднее число фотонов. Доля однофотонной компоненты влияет лишь на скорость передачи ключей, но не на их секретность).
Указанный технический результат достигается тем, что в способе кодирования и передачи криптографических ключей, включающем формирование на передающей станции последовательности квантовых фотонных состояний и передачу этих состояний по открытому пространству на принимающую станцию, предварительно измеряют расстояние между станциями и синхронизируют часы на них, затем на передающей станции преобразуют последовательности квантовых фотонных состояний в одно- или многофотонные ортогональные состояния и измеряют время их отправки, а на принимающей станции измеряют время их приема и определяют величину задержки, по которой производят декодирование для обнаружения подслушивания.
Сущность изобретения поясняется чертежами. На фиг. 1а), б), в) и 2 показаны пространственно-временные диаграммы квантовых состояний с конечной протяженностью для кодирования криптографических ключей, поясняющие неизбежность возникновения задержки по времени на принимающей станции, если были попытки подслушивания и извлечения информации при передаче ключей. На фиг.3 показан пример реализации способа.
На фиг.1:
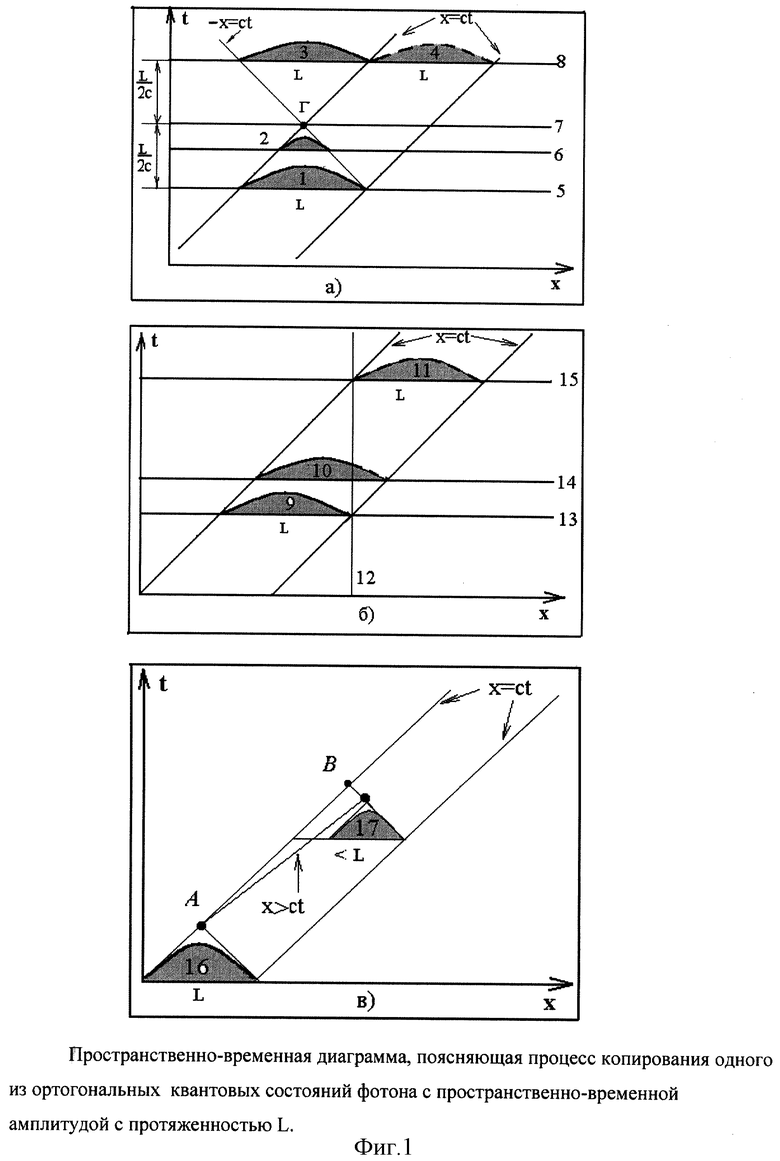
а) пространственно-временная диаграмма, поясняющая процесс копирования одного из ортогональных квантовых состояний фотона с пространственно-временной амплитудой с протяженностью L посредством его преобразования в локализованное в пространственно-временной точке Г, измерение последнего, затем преобразование обратно в квантовое состояние с той же пространственно-временной амплитудой, что и исходное состояние, но с временной задержкой, равной протяженности состояния;
б) пространственно-временная диаграмма, поясняющая процесс копирования протяженного квантового состояния фотона посредством унитарного преобразования в атомные степени свободы, измерение квантового состояния атомной системы, затем преобразование квантового состояния атомной системы в состояние фотона с той же пространственно-временной формой, что и исходное, но с временной задержкой, равной протяженности состояния;
в) пространственно-временная диаграмма, поясняющая нарушение принципа релятивистской причинности, если одно из ортогональных квантовых состояний копируется быстрее, чем это предписывается диаграммами а) и б).
На фиг.1а) приняты следующие обозначения:
1 - исходное квантовое состояние с пространственно-временной протяженностью L на временном срезе 5;
2 - промежуточное квантовое состояние с меньшей пространственно-временной протяженностью, чем исходное на более позднем временном срезе 6;
3 - копия исходного квантового состояния на временном срезе 8, но с задержкой по времени по сравнению с исходным состоянием 4, испытывающем свободное распространение со скоростью света;
7 - временной срез, на котором исходное квантовое состояние преобразовано в локализованное в точке Г. L/c - минимально необходимое время между срезами 5 и 7, которое диктуется принципом релятивистской причинности, для преобразования исходного квантового состояния в локализованное. Аналогично, L/c - минимально необходимое время между срезами 7 и 8, для преобразования локализованного квантового состояния в точке Г, в протяженное с той же пространственно-временной амплитудой, что и исходное, но задержанное по времени по сравнению с квантовым состоянием 4 со свободным распространением со скорость света.
На фиг.1б) приняты следующие обозначения:
9 - исходное квантовое состояние с пространственно-временной протяженностью L на временном срезе 13;
10 - квантовое состояние на временном срезе 14, штриховой линией показана доля нормировки состояния, которая преобразована в атомные степени свободы, локализованные в точке (пространственный срез 12);
11 - амплитуда свободно распространяющегося квантового состояния фотона на временном срезе 15.
На фиг.1в) приняты следующие обозначения.
16 - исходное квантовое состояние с пространственно-временной протяженностью L;
17 - гипотетическое преобразование исходного состояния в квантовое состояние с меньшей пространственно-временной протяженностью, нарушающее принцип релятивистской причинности.
Любые квантовые состояния имеют некоторую конечную пространственно-временную протяженность (соответственно конечную частотную полосу). В этом случае при формулировке протокола обмена в реальном времени для различения числа фотонов в линии как и для любых других измерений, требуется неизбежно конечное время, которое приводит к задержке результатов измерений на принимающей станции, что позволяет детектировать любые попытки подслушивания.
Для ортогональных квантовых состояний нет запрета на достоверное различение без их возмущения, если состояние доступно сразу как целое.
Доступ к квантовому состоянию сразу как целому неизбежно подразумевает доступ к той части пространства-времени, где отлична от нуля амплитуда (волновая функция) состояния 1 (см. фиг.1а)). Если же доступна лишь часть пространства, где отлична от нуля амплитуда состояний, то в этом случае даже ортогональные состояния невозможно достоверно скопировать или различить. Последнее более или менее очевидно, поскольку никакой процесс, в том числе копирование или различение, не может иметь вероятность исхода больше, чем доля нормировки состояний, которая набирается в доступной пространственно-временной области, и тем автоматически в доступной части гильбертова пространства. То есть, чтобы с достоверностью скопировать или различить ортогональные состояния, они нужны сразу и целиком.
В нерелятивистской квантовой механике, где нет ограничений на предельную скорость распространения сигналов, доступ к любой конечной области может быть получен мгновенно. В квантовой теории поля, где существуют ограничения на предельную скорость, доступ к квантовому состоянию целиком может быть получен лишь в том случае, если протяженное квантовое состояние предварительно преобразовано к квантовому состоянию с амплитудой, отличной от нуля лишь в сколь угодно малой пространственной области. Из-за принципа релятивистской причинности такое преобразование квантового состояния, заданного в конечной пространственно-временной области, в квантовое состояние, локализованное в сколь угодно малой пространственной области, может быть осуществлено лишь за конечное время. Минимально необходимое время определяется из условия накрытия прошлой частью светового конуса с вершиной в Г (см. фиг.1а)) исходной пространственной области, где была отлична амплитуда квантового состояния 1 (см. фиг.1а)). Вершина этого конуса находится в сколь угодно сильно локализованной области (точка Г), в которую преобразуется исходная амплитуда квантового состояния 1, 2 (см. фиг.1а)). Каждое из пары ортогональных квантовых состояний, преобразованных ("собранных") в локализованной области, могут быть после этого достоверно скопированы или различимы. Поскольку речь идет о безмассовых состояниях квантованного поля (фотонов), которые распространяются с предельно допустимой скоростью, то такое преобразование и дальнейшее копирование приведет к сдвигу (задержке) состояний в пространстве-времени по сравнению с исходной свободной эволюцией (распространением) состояний.
Данное обстоятельство позволяет детектировать любые попытки подслушивания путем измерения задержек результатов измерений на принимающей станции.
Иначе говоря, для ортогональных состояний безмассового квантованного поля (фотонов) теорема о запрете копирования звучит следующим образом. Ортогональные состояния могут быть с вероятностью, сколь угодно близкой к единице, скопированы. Но при этом в результате копирования получаются состояния с той же формой амплитуд, но сдвинутые (транслированные в пространстве-времени). Т.е. разрешен более слабый процесс по сравнению с нерелятивистским случаем
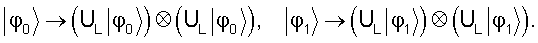
UL оператор трансляции в пространстве-времени вдоль ветви светового конуса величину L=Δ(x-t) - размер области, где отлична от нуля амплитуда состояний |ϕ0,1> (считаем, для краткости, что оба состояния отличны от нуля в одинаковой пространственно-временной области, но отличаются формой амплитуд
|ϕ0,1(x-t)>).
Аналогично модифицируется теорема о различении ортогональных состояний, разрешен лишь более слабый процесс по сравнению с нерелятивистским случаем
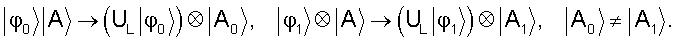
Сказанное удобно пояснить при помощи фиг.1а), б).
Поскольку амплитуда состояний безмассового квантованного поля (фотонов), распространяющихся в одном направлении оси x, зависит лишь от разности x-t, то можно фиксировать время и считать переменной координату, либо наоборот. Сделаем это для обоих случаев. Этими двумя случаями исчерпываются все ситуации. Пусть задано одно из ортогональных состояний с амплитудой |ϕ0,1(x-t)>, распространяющихся со скоростью света (выбрана система единиц, когда с=1, индекс состояния 0 или 1 для краткости пока опустим). Пусть состояние 1,9 сосредоточено в области L (рис.1а), б)).
Чтобы иметь сразу все значения амплитуды состояния при всех x, в момент t0 в той области, где она отлична от нуля, необходимо совершить унитарное преобразование сразу над всем состоянием. Пусть унитарное преобразование над амплитудой состояния - U ϕ0,1(x-t0)=ϕ0,1(x-t)(t>t0), амплитуда нового состояния ϕ0,1(x'-t) может быть отлична от нуля уже в меньшей пространственной области. По существу, минимальный размер области по x' к моменту t диктуется релятивистским принципом причинности. К моменту времени не ранее чем L/c амплитуда исходного состояния может быть унитарным образом преобразована в состояние со сколь угодно сильно локализованной амплитудой в окрестности Г (см. фиг 1а)). Принципиально важно, что это будет уже другое состояние, чем исходное ϕ0,1(x-t0). К моменту Г доступны значения амплитуды состояния при всех x сразу (мгновенно). Теперь можно мгновенно получить исход измерения и иметь полную (с вероятностью единица) информацию о состоянии. Если пара исходных состояний была ортогональна, то можно унитарным преобразованием получить также пару ортогональных состояний к моменту Г и, соответственно, достоверно отличить одно от другого. Подчеркнем еще раз, что это будут уже другие ортогональные состояния, отличные от исходных. "Восстановление" или копирование состояния также может быть реализовано обратным унитарным преобразованием, "направленным" вперед во времени. Состояние 3 с той же формой амплитуды, как исходное, может быть получено к моменту не ранее, чем это диктуется релятивистской причинностью (см. фиг.1а)). Амплитуда состояния, с той же формой, как у исходного, находится в передней части светового конуса, выпущенного из точки Г. Полученное состояние 3 (фиг.1а)) также другое по сравнению с исходным 4 (фиг.1а)), в том смысле, что оно запаздывает по времени по отношению к исходному состоянию, которое успело бы распространиться вперед по x к моменту L/c, как раз на величину L/c, если бы не было попыток копирования или получения информации о нем. Пока речь шла о получении информации о состояниях в канале с вероятностью единица. Те же самые рассуждения годятся для получения информации с вероятностью, меньшей единицы. При этом задержка по времени, вносимая подслушивателем будет меньше L/c (фиг.1а), б)), но неизбежно будет отлична от нуля.
Аналогично можно показать, когда состояние унитарным образом преобразуется в состояние вспомогательной локализованной системы (см. фиг.1б)) Пример такого унитарного преобразования имеет место при "остановке" света. Данное унитарное преобразование переводит состояние фотонного поля в вакуумное состояние из-за его безмассовости и невозможности иметь нулевую скорость распространения, а состояние атомной системы - в некоторое новое состояние. Преобразование, будучи унитарным, также требует доступа ко всем значениям амплитуды фотонного пакета в точке локализации атомной системы 12 (см. фиг.1б)). Такой доступ достигается естественным образом по мере распространения пакета со скоростью света и достижения им локализованной атомной системы ("вхождение" пакета целиком в атомную систему). Данный процесс, если речь идет о получения результата с вероятностью единица, также требует времени L/c (однофотонный пакет должен целиком "войти" в атомную систему). Процесс "вхождения" показан на фиг.1б) - промежуточное состояние 10. При этом фотонное поле оказывается в другом - вакуумном состоянии, а вспомогательная система - в новом состоянии в зависимости от входного фотонного состояния. К моменту времени L/c с вероятностью единица можно выяснить, что это за состояние и приготовить такое же, но с неизбежной задержкой на L/c, которая будет иметь место по сравнению со свободным распространением исходного пакета 11 (фиг.1б)).
Таким образом, любое получение информации об одном из ортогональных состояний приводит к неизбежной их модификации - трансляции в пространстве-времени (задержке по времени).
Также важно, что никакая эволюция безмассового квантованного поля, взаимодействующего с окружением (другими квантовыми и классическими степенями свободы в канале), не может привести к "сжатию" состояния, в том смысле, что нормировка состояния будет набираться в меньшей пространственной области, выходящей за световой конус по сравнению со свободным распространением (см. фиг.1в)). Как правило, такое взаимодействие приведет к тому, что состояние будет смешанным, но носитель матрицы плотности в пространстве-времени не может быть "сжат" и выведен за световой конус (фиг.1б) - состояние 16). В противном случае это бы давало возможность передавать информацию при помощи квантовых состояний быстрее скорости света. Действительно, пусть имеется одно из пары ортогональных квантовых состояний (фиг.1в) - 16 - состояние протяженностью L накрывается прошлой частью светового конуса, выпущенного из точки А. В точке А можно извлечь классическую информацию из квантового состояния не ранее чем в момент времени, определяемый условием накрытия амплитуды состояния прошлой частью светового конуса. После этого он может передать уже классическую информацию к точке В (см. фиг.1в)). Такая передача не может быть сделана быстрее, чем со скоростью света (наблюдатели соединены ветвью светового конуса фиг.1в)). Если бы в результате эволюции квантового состояния в канале оно могло "сжаться" таким образом, чтобы при накрытии состояния прошлой частью светового конуса, вершина этого конуса оказывалась в пространственно-подобной области по отношению к световому конусу с вершиной в точке А, одна из ветвей которого проходит через точку В (см. фиг.1в)). В этом случае в точке В можно извлечь классическую информацию из квантового состояния раньше, чем ее можно было передать со скоростью света из точки А, поскольку вершина светового конуса, накрывающего "сжатое" квантовое состояние, выходит в пространственно-подобную область 17 (см. фиг.1в)).
Для криптографии сказанное означает, что шум в канале не дает подслушивателю ни скопировать, ни получить информацию о состоянии раньше, чем это диктуется диаграммами на фиг.1а), б) (величина ошибки подслушивателя при условии прохождения временного теста на задержку не может быть меньше, чем L/c).
Это обстоятельство принципиально важно для секретности релятивистской квантовой криптографии, которая остается секретной при любом затухании. Поскольку в нашем случае секретность основана на релятивистском принципе причинности для эволюции квантовых состояний, то затухание, какое бы оно ни было, не может отменить ограничения, диктуемые релятивистской причинностью.
Данный способ кодирования и передачи секретных криптографических ключей через открытое пространство гарантирует детектирование подслушивателя и получение секретных ключей даже если квантовое фотонное состояние излучения не является строго однофотонным. Величиной, которая отвечает за обнаружение подслушивателя, является величина δОК Е - вероятность для подслушивателя узнать передаваемый бит и пройти тест на задержку на принимающей станции в зависимости от величины задержки р(δТ), которую подслушиватель может выбирать произвольно, и среднего числа фотонов в квантовом состоянии. Существует оптимальная для подслушивателя величина задержки, которая зависит от среднего числа фотонов в состоянии.
При малом среднем числе фотонов μ=0.1 величина δОК Е, как видно из таблицы 1, составляет δОК Е=0.565, что лишь на 0.065 превосходит вероятность простого угадывания подслушивателем передаваемого бита информации (напомним, что вероятность простого угадывания составляет 0.5 и является самой невыгодной для подслушивателя). Для дальнейшего будет удобнее использовать минимальную вероятность ошибки для подслушивателя δЕ=1-δОК Е. Данная величина имеет следующий смысл.
Поскольку на принимающей станции в точке В оставляют только те посылки, которые дали исход в нужном временном окне, то для подслушивателя это означает, что вероятность ошибки, с которой он знает биты в принятых в точке В позициях, прошедших тест, составляет δЕ. Даже при среднем число фотонов в когерентном состоянии вплоть до μ=5 вероятность ошибки для подслушивателя 30%, это означает, что подслушиватель знает принятые легитимными пользователями биты примерно в 70% позиций. При длинной принятой последовательности N легитимными участниками в точках А и В может быть извлечено 0.3 N секретных.
При большом среднем числе фотонов величина δОК Е стремится к единице (соответственно, вероятность ошибки δЕ стремится к 0, но никогда не становится нулевой). Оптимальная для подслушивателя задержка также стремится к нулю, но никогда не становится нулевой. Хотя доля нормировки р(δТ), набирающаяся во временном окне измерения δТ, стремится к нулю (при μ=100, при этом р(δТ)=0.04), тем не менее эта малость компенсируется большим числом фотонов, которые могут дать отсчет в окне δТ. При больших μ>>1 имеет место классическая ситуация, два состояния электромагнитного поля с неперекрывающимися частотными полосами могут быть достоверно идентифицированы мгновенно без задержки.
Тот факт, что можно использовать когерентные состояния со средним числом μ=1-3, где величина δЕ еще велика, для экспериментальных реализации означает, что не требуется ослабления лазерного излучения до уровня μ=0.1-0.3, как это обычно имеет место. При среднем числе фотонов μ=3 холостые посылки, когда в канале присутствует лишь вакуумная компонента, практически отсутствуют, что позволяет увеличить скорость генерации ключа в 10 раз (см. таблицу 1).
Ответ для вероятности δЕ, no существу, не зависит от исходной ширины частотной полосы δk, а зависит только от безразмерного параметра δk δT. Поэтому при любой частотной полосе всегда можно выбрать требуемую величину временного окна, в которую состояние фотонного поля "помещается" целиком. Величина δЕ зависит только от структуры состояний и максимальна для чистого состояния (не статистической смеси состояний с разным числом фотонов) однофотонного пакета, распространяющего со скоростью света.
Состояние однофотонного пакета отвечает предельно квантовой релятивистской ситуации, и в этом случае величина δЕ носит универсальный характер и является, в определенном смысле, мировой константой, поскольку при ее выводе ничего, кроме нормировки амплитуды квантового состояния и факта распространения состояния со скоростью света, не использовалось.
Вероятность δ0K E для атаки с расщеплением многофотонного состояния лазерного излучения в зависимости от коэффициента светоделителя η и среднего числа фотонов μ приведена в таблице 2. В таблице 2 приведена максимальная величина δОК Е для оптимального η.
При малых средних числах фотонов μ=0.1 для подслушивателя вероятность узнать состояние и остаться незамеченным близка к 0.5 (при этом δОК Е=0.502, что лишь незначительно превышает вероятность простого угадывания подслушивателем передаваемого бита информации). Данный результат качественно понятен, поскольку при μ=0.1 (за вычетом вероятности вакуумной компоненты) в канале, в основном, находится один фотон. Вероятности появления двух и более фотонов существенно меньше. Поэтому после светоделителя однофотонное состояние может быть зарегистрировано либо подслушивателем, либо легитимным пользователем на принимающей станции, но никогда обоими.
При больших числах заполнения μ>10 фотонов состояние близко к классическому, поэтому можно "отщепить" половину состояния (η=0.5), при этом вероятность одновременных отсчетов у подслушивателя и легитимного пользователя на принимающей будет близка к единице.
Временная эволюция состояний поясняется на пространственно-временной диаграмме фиг.2.
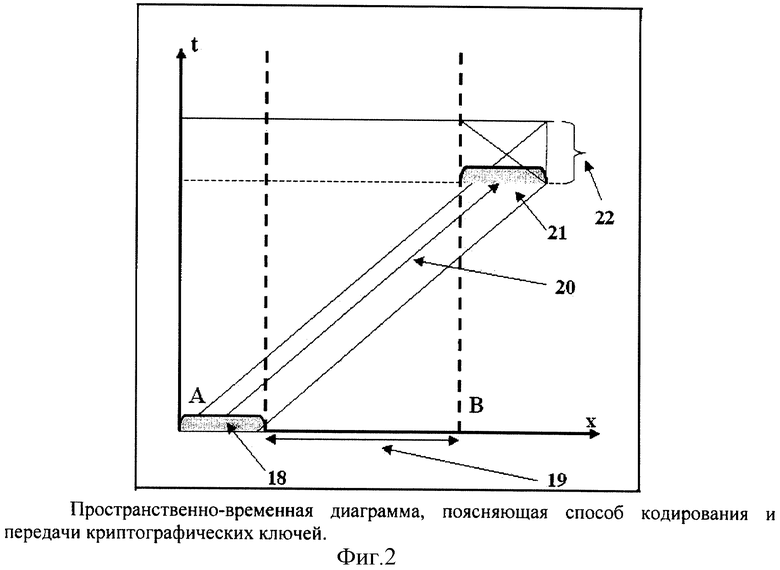
На фиг.2 показана пространственно-временная диаграмма, поясняющая способ кодирования и передачи криптографических ключей.
Процесс распространения квантовых состояний с синхронизацией часов на принимающей и передающей станциях. Квантовые состояния приготавливаются на передающей станции (А), измерения происходят на принимающей станции (В) в определенное временное окно.
На фиг.2 приняты следующие обозначения:
18 - квантовое фотонное состояние на передающей станции А;
19 - длина канала связи;
20 - эволюция квантового состояния в пространстве-времени (передача состояния от передающей станции А к принимающей станции В;
21 - квантовое фотонное состояние на принимающей станции;
22 - временное окно детектирования на принимающей станции. Только фотоотсчеты в этом временном окне дают вклад в криптографический ключ.
На фиг.3 показана экспериментальная реализация способа кодирования и передачи криптографических ключей через открытое пространство. Протяженные ортогональные квантовые состояния, в которые кодируется информация о передаваемых ключах, формируют путем "вырезания" оптическими фильтрами состояний с узкими не перекрывающимися частотными полосами, центрированными вокруг длин волн λ1 и λ2.
На фиг.3 приняты следующие обозначения:
23 - лазеры генерирующие когерентные квантовые состояния;
24 - оптический фильтр с центральной длиной волны λ1 и частотной полосой пропускания δk;
25 - оптический фильтр с центральной длиной волны λ2 и частотной полосой пропускания δk;
26 - оптические призмы;
27 - оптические фотодетекторы;
28 - расстояние между станциями;
29 - направление распространения сигнала.
Способ осуществляют следующим образом (см. фиг.3). Предварительно измеряют расстояние 28 (см. фиг.3) между передающей и принимающей станциями и синхронизируют часы.
Затем на передающей станции преобразуют последовательности квантовых фотонных состояний в одно- или многофотонные ортогональные состояния и измеряют время их отправления.
На передающей станции показаны два лазера 23 (см. фиг.3). Включение лазера с несущей длиной волны λ1 отвечает передаче на принимающую станцию логического бита, равного 0, соответственно включение лазера с несущей длиной волны λ2 отвечает передаче логического бита, равного 1.
В некоторый момент времени начала протокола случайно запускают один из лазеров, предварительно фиксируют его мощность и получают одно- или многофотонные квантовые состояния. Лазер выдает оптический импульс с широким спектром δω1 и, соответственно, короткий по времени δt˜1/δω1$. Момент включения лазера является временем отправления состояний. Впоследствии время отправления состояний сообщают через общедоступный (открытый) классический канал связи на принимающую станцию. Часы синхронизируют с точностью ˜δt. Далее широкополосное состояние направляют на вход фильтров 24, 25 (фиг.3). Каждый фильтр вырезает из широкого спектра δω ортогональные (не перекрывающиеся по частоте) состояния с узкой частотной полосой δk квантовые фотонные состояния. Регулируют мощность на выходе лазера (задают среднее число фотонов μ), и тем самым формируют одно- или многофотонные состояния. Далее состояния направляют на оптическую призму 26 (фиг.3), обеспечивающую отклонение фотонных состояний, центрированных вокруг разных длин волн, и затем посылают через открытое пространство на принимающую станцию.
Вырезание узкой частотной полосы шириной δk приводит к формированию квантовых состояний пространственной протяженностью сδТ˜c/δk. Точность времени отправки протяженного квантового состояния в открытое пространство известна с высокой точностью δt<<cδT. Соответственно, длительность фотонного состояния с узким частотным спектром δk много больше времени δt, с которым синхронизируют часы на передающей и принимающей станциях. По известному расстоянию между станциями, времени отправки и протяженности фотонных состояний вычисляют время прибытия переднего фронта состояния на принимающую станцию. По известной протяженности фотонных состояний и времени прибытия переднего фронта фотонного состояния вычисляют временное окно на принимающей станции 22 (фиг.2), в котором должны происходить отсчеты в фотодетекторах 27 (фиг.3) от незадержанных состояний.
На принимающей станции точно такие же оптические фильтры 24, 25 (фиг.3), как и на передающей, пропускает на детекторы 27 (фиг.3) фотонные состояния только с узкой частотной полосой δk, соответственно, с пространственной протяженностью не меньшей, чем сδТ˜c/δk. Детекторы работают в ждущем режиме. Требуется, чтобы постоянная времени лавинного фотодиода τD была много меньше длительности состояния (τD<<δТ). Пользователь на принимающей станции осуществляет декодирование, которое сводится к тому, что он оставляет только те посылки, в которых срабатывание было во временном окне 22 (фиг.2). В зависимости от того, какой из фотодетекторов сработал, пользователь на принимающей станции записывает логический 0 или 1 и формирует криптографический ключ.
Фильтры 24, 25 (фиг.3) на принимающей станции перед детекторами 27 (фиг.3) нужны для того, чтобы исключить перепосылку подслушивателем фотонных состояний, более коротких по времени, чем δТ (соответственно, фотонных состояний с широким частотным спектром), что могло бы скомпенсировать задержку, вносимую подслушивателем при измерении протяженного фотонного состояния длительностью δТ.
Если подслушиватель измеряет передаваемые фотонные состояния (соответственно, логические биты 0 или 1), то он неизбежно вызывает задержку фотонных состояний. Задержка фотонных состояний приведет к возникновению фотоотсчетов вне временного окна 22 (фиг.2). По фотоотсчетам вневременного окна 22 (фиг.2) на принимающей станции обнаруживают подслушивателя. Все посылки, в которых были фотоотсчеты вне временного окна 22 (фиг.2), на принимающей станции отбрасывают и не учитывают при формировании криптографического ключа.
| название | год | авторы | номер документа |
|---|---|---|---|
| СПОСОБ КВАНТОВОГО КОДИРОВАНИЯ И ПЕРЕДАЧИ КРИПТОГРАФИЧЕСКИХ КЛЮЧЕЙ | 2010 |
|
RU2427926C1 |
| СПОСОБ КВАНТОВОГО КОДИРОВАНИЯ И ПЕРЕДАЧИ КРИПТОГРАФИЧЕСКИХ КЛЮЧЕЙ | 2012 |
|
RU2507690C1 |
| СПОСОБ КОДИРОВАНИЯ И ПЕРЕДАЧИ КРИПТОГРАФИЧЕСКИХ КЛЮЧЕЙ | 2005 |
|
RU2302085C1 |
| СПОСОБ ВЫЯВЛЕНИЯ АТАКИ НА КВАНТОВЫЕ СОСТОЯНИЯ В КВАНТОВОМ КАНАЛЕ СВЯЗИ | 2019 |
|
RU2730554C1 |
| Способ обнаружения атаки с ослеплением детекторов в системах квантовой криптографии с поляризационным кодированием | 2021 |
|
RU2783977C1 |
| Способ квантового распределения ключей в однопроходной системе квантового распределения ключей | 2018 |
|
RU2706175C1 |
| Система релятивистской квантовой криптографии | 2017 |
|
RU2667755C1 |
| Устройство квантовой криптографии (варианты) | 2015 |
|
RU2622985C1 |
| СЕТЬ КВАНТОВОГО РАСПРЕДЕЛЕНИЯ КЛЮЧЕЙ | 2015 |
|
RU2621605C2 |
| Система квантовой криптографии на запутанных поляризационных состояниях фотонов с активным выбором базиса измерения | 2023 |
|
RU2814445C1 |
Изобретение относится к области кодирования и передачи криптографических ключей через открытое пространство. Способ включает формирование на передающей станции последовательности квантовых фотонных состояний для кодирования криптографических ключей и передачу этих состояний по открытому пространству на принимающую станцию, причем предварительно измеряют расстояние между передающей и принимающей станциями и синхронизируют часы на них, затем на передающей станции преобразуют последовательности квантовых фотонных состояний в одно- или многофотонные ортогональные состояния и измеряют время их отправки, которое сообщают на принимающую станцию, а на принимающей станции измеряют время приема последовательности одно- или многофотонных ортогональных квантованных состояний, определяют величину задержки, по которой осуществляют их декодирование и обнаружение подслушивания. Технический результат - обеспечение секретности криптографических ключей при их передаче через открытое пространство на большие расстояния и достижение долговременной стабильности и уменьшение потока ошибок в передаваемых криптографических ключах на принимающей станции. 3 ил., 2 табл.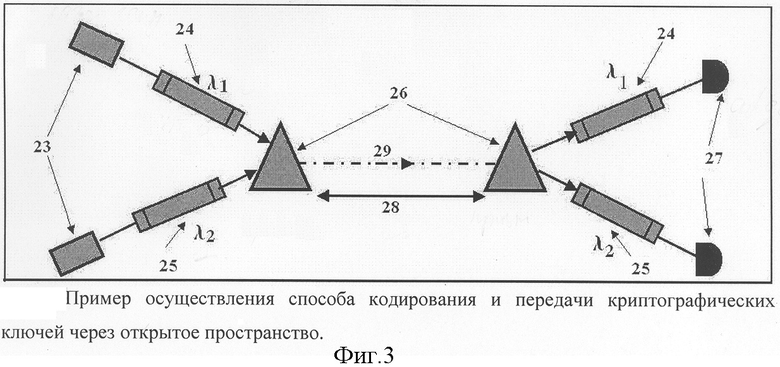
Способ кодирования и передачи криптографических ключей, включающий формирование на передающей станции последовательности квантовых фотонных состояний для кодирования криптографических ключей и передачу последовательности квантовых фотонных состояний по открытому пространству на принимающую станцию, отличающийся тем, что предварительно измеряют расстояние между передающей и принимающей станциями и синхронизируют часы на них, затем на передающей станции преобразуют последовательности квантовых фотонных состояний в одно- или многофотонные ортогональные квантовые состояния и измеряют время их отправки, которое сообщают на принимающую станцию, а на принимающей станции измеряют время приема последовательности одно- или многофотонных ортогональных квантовых состояний, определяют величину задержки, по которой осуществляют их декодирование и обнаружение подслушивателя.
| US 6748083 В2, 08.06.2004 | |||
| СПОСОБ ФОРМИРОВАНИЯ КЛЮЧА ШИФРОВАНИЯ/ДЕШИФРОВАНИЯ | 2000 |
|
RU2171012C1 |
| US 5515438 A, 07.05.1996 | |||
| СПОСОБ КРИПТОГРАФИЧЕСКОГО ПРЕОБРАЗОВАНИЯ ДВОИЧНЫХ ДАННЫХ | 2001 |
|
RU2226041C2 |
| УСТРОЙСТВО СИНХРОНИЗАЦИИ ЧАСОВ | 2000 |
|
RU2177167C2 |
Авторы
Даты
2008-05-20—Публикация
2006-06-06—Подача