Изобретение относится к области физики магнетизма и электроники, в частности к системам автоматической стабилизации напряжения постоянного тока, вырабатываемого непосредственным преобразованием тепловой энергии внешней среды, например водных бассейнов, и может быть использовано в экологически чистой электроэнергетике.
Известно прямое преобразование тепловой энергии в электрическую постоянного тока на основе эффекта Зеебека - возникновения в электрической цепи, состоящей из нескольких разнородных проводников, контакты между которыми имеют различные температуры [1-3], например, на основе спая проводников «константан (-38 мкВ./°К) - хромель (+24 мкВ/°К)» или соединений «висмута (-68 мкВ/°К) с сурьмой (+43 мкВ/°К)». На основе эффекта Зеебека разработаны термоэлектрические генераторы, в состав которых входят термобатареи, набранные из полупроводниковых термоэлементов (аморфных или стеклообразных), соединенных последовательно или параллельно. Идея использования полупроводниковых термоэлементов вместо металлических термопар принадлежит академику А.Ф. Иоффе (СССР). Однако эти устройства пока не нашли применения в электроэнергетике по целому ряду объективных причин.
Представляет интерес использовать термомагнитные явления для получения механической работы, а именно магнитокалорический эффект в ферромагнетиках в сочетании с известными их свойствами - магнитной вязкости, снижения магнитной восприимчивости в насыщающих магнитных полях (кривая Столетова), возникновения фазового перехода первого рода в насыщающих магнитных полях (с адекватным уменьшением удельной теплоемкости ферромагнетика), нарушения симметрии в процессах нагревания при намагничивании и охлаждения при размагничивании в динамике взаимодействия движущегося ферромагнетика относительно локализованного насыщающего магнитного поля. Совокупность названных свойств позволяет синтезировать параметрический термомагнитный генератор для выработки механической энергии, в котором вращающееся магнитное поле заменено вращающимся распределением магнитной восприимчивости синхронно с вращающимся ферромагнитным кольцом, небольшая часть которого помещена в неподвижное локализованное в пространстве насыщающее магнитное поле (принцип эквивалентности вращений). При этом центр намагниченности движущегося внутри магнитного зазора ферромагнетика в таком постоянно действующем во времени распределении отстает от центра притяжения внутри магнитного зазора, в силу чего возникает постоянно действующая втягивающая сила, вектор которой направлен по касательной к ферромагнитному кольцу в сторону его вращения, что поддерживает указанное вращательное движение, если вращательный момент не меньше момента трения и присоединенной нагрузки. При этом затрачивается внутренняя тепловая энергия ферромагнитного кольца при его намагничивании с результирующим охлаждением ферромагнитного кольца, восполняемая тепловой энергией внешней среды в механизме теплопроводности.
На указанном сочетании известных свойств ферромагнетиков автором предложены способ получения энергии и целый ряд устройств, основанных на данном способе и его модификациях [4-13].
Ближайшим аналогом заявляемого технического решения (прототипом) может быть названо «Устройство автоматического управления электрогенератором» [13], ранее предложенное автором, содержащее ферромагнитное кольцо, механически связанное с осью вращения через траверсы, часть ферромагнитного кольца помещена в насыщающее магнитное поле сильного постоянного магнита, снабженного катушкой подмагничивания, а другая его часть связана с тепловыделяющей средой, например очищенной водой, забираемой из соответствующего водного бассейна, с осью вращения механически связан трехфазный генератор переменного тока, подключенный к трехфазному выпрямителю и к электрической нагрузке, выход трехфазного выпрямителя через блок управления подмагничиванием связан с катушкой подмагничивания сильного постоянного магнита, вход блока управления подмагничиванием подключен к выходу последовательно соединенных генератора опорного напряжения, фазочувствительного выпрямителя и фильтра нижних частот (или интегратора), отличающееся тем, что с осью вращения ферромагнитного кольца механически связан тахогенератор, выход которого подключен ко второму входу фазочувствительного выпрямителя, а магнитный зазор сильного постоянного магнита выполнен из двух частей, первая из которых образует однородное магнитное поле с напряженностью, обеспечивающей на длине L этой части магнитного зазора доведение магнитной восприимчивости ферромагнетика до максимального значения, а вторая часть магнитного зазора длиной L образует насыщающее магнитное поле в начале этой части магнитного зазора и далее в направлении движения ферромагнитного кольца линейно возрастающее по напряженности магнитное поле к концу магнитного зазора, причем угловая скорость ω* вращения ферромагнитного кольца, соответствующая максимуму возникающего в нем вращательного момента определена условием ω*=L/λRτ, где λ=1,23 и R - средний радиус ферромагнитного кольца, τ - постоянная времени релаксации магнитной вязкости ферромагнетика, из которого выполнено ферромагнитное кольцо.
Данное устройство работает на основе потребления тепловой энергии внешней среды, поступающей к охлаждающемуся при вращении ферромагнитному кольцу, и в задачу этого устройства входит поддержание неизменным (мало изменяющимся) значения частоты вырабатываемого переменного тока при изменении потребляемой мощности в присоединенной нагрузке.
Целями заявляемого технического решения являются стабилизация напряжения постоянного тока при вариации внешней нагрузки и увеличение срока действия и надежности функционирования генерирующего электроэнергию прибора.
Указанные цели достигаются в заявляемом устройстве автоматического управления электрогенератором, содержащем ферромагнитное кольцо, механически связанное с осью вращения через траверсы, часть ферромагнитного кольца совмещена с насыщающим магнитным полем сильного постоянного магнита, а другая его часть связана с тепловыделяющей средой, например очищенной водой, забираемой из соответствующего водного бассейна, а также последовательно соединенные фильтр нижних частот (или интегратор) и блок управления подмагничиванием, выходом соединенный с катушкой подмагничивания, при этом магнитный зазор сильного постоянного магнита выполнен из двух частей, первая из которых образует однородное магнитное поле с напряженностью Н*, обеспечивающей на длине L этой части магнитного зазора доведение магнитной восприимчивости ферромагнетика до максимального значения, а вторая часть магнитного зазора длиной L снабжена катушкой подмагничивания и образует насыщающее магнитное поле в начале этой части магнитного зазора и далее в направлении движения ферромагнитного кольца линейно возрастающее по напряженности магнитное поле к концу магнитного зазора, причем угловая скорость ω* вращения ферромагнитного кольца, соответствующая максимуму возникающего в нем вращательного момента за счет возникающей силы втягивания ферромагнетика, определена условием ω*=L/λRτ, где λ=1,23 и R - средний радиус ферромагнитного кольца, τ - постоянная времени релаксации магнитной вязкости ферромагнетика, из которого выполнено ферромагнитное кольцо, отличающимся тем, что ось вращения механически связана с измерителем частоты вращения оси с цифровым табло и бесколлекторным генератором постоянного тока, подключенным к нагрузке и включающем раздельные рабочую обмотку и обмотку подмагничивания, рабочая обмотка подключена к буферному источнику постоянного тока в виде аккумуляторной батареи, к внешней нагрузке, к источнику опорного напряжения, к блоку управления подмагничиванием и к первому входу устройства сравнения, обмотка подмагничивания генератора подключена к аккумуляторной батарее через переключатель перемены полярности постоянного тока, выход источника опорного напряжения подключен ко второму входу устройства сравнения, выход которого соединен с управляющим входом блока управления подмагничиванием через фильтр нижних частот (или интегратор).
Достижение поставленных целей объясняется действием статической (астатической в случае применения интегратора, вместо фильтра нижних частот) системы авторегулирования и применением бесколлекторного генератора постоянного тока. Сигнал ошибки регулирования формируется на выходе устройства сравнения путем вычитания из фиксированного напряжения с выхода источника опорного напряжения известной части напряжения на выходе бесколлекторного генератора постоянного тока, величина которого пропорциональна угловой скорости оси вращения. При этом увеличение напряжения на выходе рабочей обмотки бесколлекторного генератора постоянного тока приводит к снижению угловой скорости оси вращения, а при снижении заданного значения напряжения в нагрузке, наоборот, к увеличению угловой скорости оси вращения. Отсутствие в электрогенераторе коллектора якоря генератора и щеток повышает срок службы и надежность функционирования электрогенератора постоянного тока.
Структурная схема заявляемого технического решения представлена на рис.1. Магнитная система показана на рис.2. На рис.3-7 рассматриваются графики, поясняющие работу устройства, объясняющие вращение ферромагнитного кольца. На рис.8 приведена схема бесколлекторного генератора постоянного тока, которым запускается начальное вращение ферромагнитного кольца, когда этот генератор работает в режиме двигателя от буферного источника постоянного тока - аккумуляторной батареи. На рис.9 указан центральный разрез генератора, ортогональный его оси вращения. На рис.10 показано разложение силы Лоренца на составляющие части, приложенные к ротору и статору в режиме работы генератора как двигателя.
Устройство на рис.1 содержит:
1 - ферромагнитное кольцо, ширина которого много меньше его среднего радиуса,
2 - сильный постоянный магнит из двух совмещенных частей с однородным и неоднородным насыщающим магнитными полями,
2а - первая часть с однородным магнитным полем напряженностью Н*,
2б - вторая часть с насыщающим неоднородным магнитным полем НО≤Н≤НМАХ, НО>>НО,
3 - катушка подмагничивания второй части магнита 2б,
4 - ось вращения ферромагнитного кольца 1,
5 - траверсы связи ферромагнитного кольца 1 с осью вращения 4,
6 - измеритель частоты вращения оси 4 с цифровым табло,
7 - бесколлекторный генератор постоянного тока,
8 - устройство сравнения,
9 - фильтр нижних частот (или интегратор),
10 - блок управления подмагничиванием,
11 - источник опорного напряжения,
12 - аккумуляторная батарея с коммутатором - буферный источник постоянного тока,
13 - переключатель перемены полярности буферного источника постоянного тока 12 при переключении бесколлекторного генератора постоянного тока в режимы двигателя или генератора.
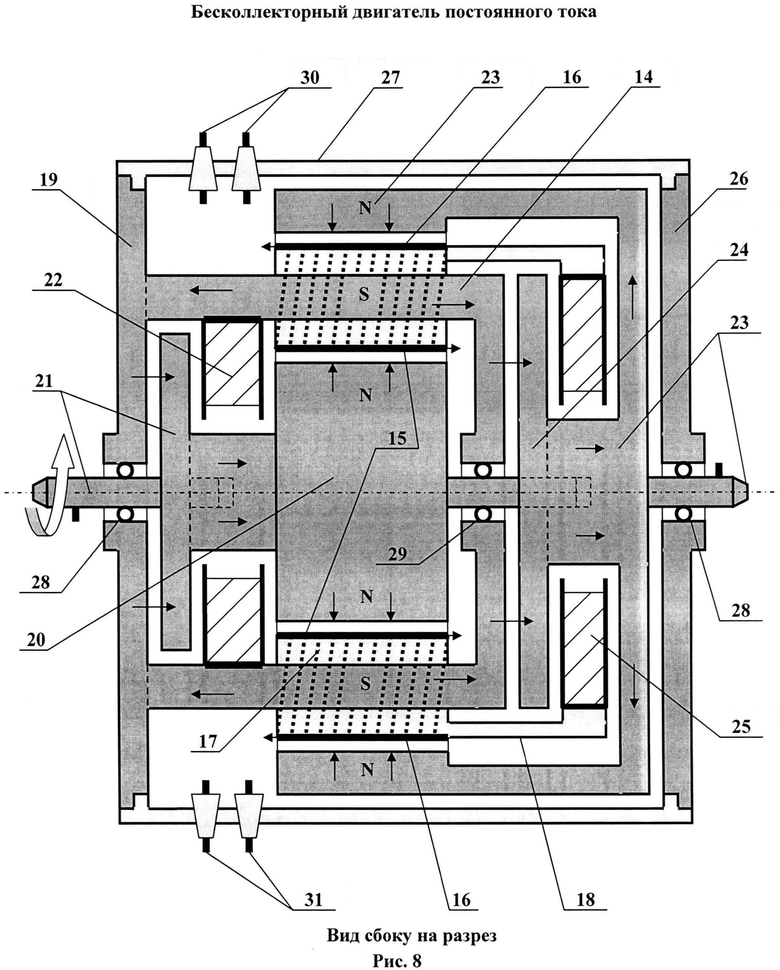
На рис.8 представлен центральный разрез бесколлекторного генератора постоянного тока 7, включающий следующие элементы:
14 - неподвижный, связанный с корпусом двигателя тороидальный статор с его магнитопроводящей крышкой (на рис.8 слева, позиция 19),
15 - полувитки рабочей обмотки тороидального статора 14, расположенные вблизи поверхности вращающегося безобмоточного ротора, его внутренней части,
16 - полувитки рабочей обмотки тороидального статора 14, расположенные вблизи поверхности безобмоточного ротора, его внешней части, выполненного в форме полого магнитопроводящего цилиндра,
17 - немагнитный (диэлектрический) цилиндр, вплотную прилегающий к внутренней поверхности магнитного полюса тороидального статора,
18 - дополнительный немагнитный (диэлектрический) цилиндр, вплотную прилегающий к внешней поверхности магнитного полюса тороидального статора с цилиндрическим выносом (вправо на рис.1) для крепления к нему дополнительной катушки подмагничивания внешней части ротора,
19 - магнитопроводящая крышка тороидального статора (на рис.8 слева),
20 - вращающаяся внутренняя часть безобмоточного ротора относительно тороидального статора 14 с осесимметричным цилиндром подмагничивания,
21 - магнитопроводящая шайба внутренней части ротора 20, закрепленная на тугой посадке с цилиндром подмагничивания, с выносной осью вращения (слева),
22 - катушка подмагничивания внутренней части ротора 20, закрепленная в теле тороидального статора 14,
23 - вращающаяся внешняя часть безобмоточного ротора, жестко закрепленная на оси вращения путем тугой посадки его с отрезком оси,
24 - магнитопроводящая шайба, закрепленная с цилиндром подмагничивания внешней части ротора 23,
25 - дополнительная катушка подмагничивания внешней части ротора 23, жестко закрепленная с телом неподвижного тороидального статора 14 через вынос немагнитного (диэлектрического) цилиндра 18, включена последовательно с катушкой подмагничивания 22,
26 - крышка корпуса двигателя (справа на рис.8),
27 - полый немагнитный цилиндрический корпус двигателя с посадочными канавками для связи с крышкой 26 и магнитопроводящей крышкой 19 тороидального статора 14,
28 - наружные подшипники генератора,
29 - внутренний подшипник генератора,
30 - выводы рабочей обмотки (ее полувитков 15 и 16) тороидального статора 14,
31 - выводы последовательно соединенных катушек подмагничивания 22 и 25 частей безобмоточных роторов 20 и 23 соответственно (подводящие проводники на рис.8 не указаны).
Рассмотрим действие заявляемого технического решения.
Целесообразно сначала рассмотреть работу термомагнитного двигателя на основе ферромагнитного кольца 1 с осью вращения 4 и магнитной системы 2, а затем рассмотреть работу системы авторегулирования и конструкцию бесколлекторного генератора постоянного тока 7.
В основе работы термомагнитного двигателя на ферромагнитном кольце 1 и сильном постоянном магните 2 лежит известный принцип работы электромагнитного двигателя с использованием силового взаимодействия между намагниченными ротором и статором, в котором магнитное поле статора вращается, увлекая за собой ротор, вращающийся вместе с вращающимся магнитным полем статора. Так работают, например, синхронные и асинхронные электродвигатели переменного тока. В заявляемом техническом решении магнитное поле статора неподвижно, будучи образовано неподвижно расположенным сильным постоянным магнитом. Однако в силу принципа эквивалентности вращающееся в обратную сторону относительно физического вращения ферромагнитного кольца (как ротора) распределение намагниченности в ферромагнитном кольце также приводит к силовому взаимодействию за счет отставания центра намагниченности ферромагнитного кольца внутри магнитного зазора сильного постоянного магнита от его центра магнитного притяжения. В результате такого силового взаимодействия ферромагнитное кольцо вращается под действием втягивающей силы, стремящейся совместить указанные центры намагниченности и магнитного притяжения. Таким образом, остается обеспечить указанное отставание центра намагниченности той части ферромагнитного кольца, которая находится в зазоре сильного постоянного магнита, от центра магнитного притяжения последнего. При этом имеется в виду, что вращение указанного распределения намагниченности на ферромагнитном кольце в системе координат, связанной с ферромагнитным кольцом, обратно синхронно вращению ферромагнитного кольца, что приводит к постоянно действующей картине распределения намагниченности внутри магнитного зазора в системе координат, связанной с неподвижным сильным постоянным магнитом, и сила втягивания является постоянно действующей. Эта задача решается благодаря использованию свойства магнитной вязкости ферромагнетика, из которого изготовлено ферромагнитное кольцо, в динамике вращения последнего под действием приложенного к ферромагнитному кольцу пускового момента импульса достаточной величины, после чего ферромагнитное кольцо будет поддерживать режим вращения при условии, что момент трения и присоединенной нагрузки не больше вращательного момента, возникающего от указанного силового взаимодействия, а компенсация потерь энергии при таком вращении ферромагнитного кольца осуществляется за счет притока из внешней среды тепловой энергии к ферромагнитному кольцу, которое охлаждается при размагничивании выходящей из магнитного зазора части ферромагнитного кольца согласно известному магнитокалорическому эффекту.
Одним из важных применительно к рассматриваемому техническому решению свойств ферромагнитных материалов является их так называемая магнитная вязкость, магнитное последействие - отставание по времени намагниченности ферромагнетика от изменения напряженности магнитного поля. В наиболее простых случаях изменение намагниченности ΔJ в зависимости от времени t описывается формулой
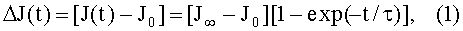
где J0 и J∞ - соответственно значения намагниченности непосредственно после изменения напряженности Н магнитного поля в момент t=0 и после установления нового равновесного состояния, τ - константа, характеризующая скорость процесса и называемая постоянной времени релаксации. Значение τ зависит от природы магнитной вязкости и в различных материалах может изменяться от 10-9 с до нескольких десятков часов.
Различают два вида магнитной вязкости: диффузионный (рихтеровский) и термофлуктуационный (иордановский). В первом из них магнитная вязкость определяется диффузией примесных атомов или дефектов кристаллической структуры. Объяснение роли примесей было дано J. Snock, а более строгая теория построена L. Neel и базируется на предположении о преимущественной диффузии примесных атомов в те межатомные промежутки кристалла, которые определенным образом ориентированы относительно направления спонтанной намагниченности. Это создает локальную наведенную анизотропию, приводящую к стабилизации доменной структуры. Поэтому после изменения магнитного поля новая доменная структура устанавливается не сразу, а после диффузного перераспределения примеси, что и является причиной магнитной вязкости.
Второй вид магнитной вязкости более универсален и наблюдается практически во всех ферромагнетиках, особенно в области магнитных полей, сравнимых с коэрцитивной силой. Неелем был предложен термофлуктуационный механизм для объяснения этого вида магнитной вязкости. Тепловые флуктуации способствуют преодолению доменными стенками энергетических барьеров в магнитных полях, меньших критического поля. В высококоэрцитивных сплавах, состоящих из однодоменных областей, наблюдается особенно большая магнитная вязкость, так как в этом случае термические флуктуации сообщают дополнительную энергию для необратимого вращения спонтанной намагниченности тех частиц, потенциальная энергия которых во внешнем магнитном поле недостаточна для их перемагничивания.
Кроме этих основных механизмов магнитной вязкости, существуют и другие. Например, в некоторых ферритах вклад магнитной вязкости дает перераспределение электронной плотности (диффузия электронов между ионами разной валентности). С магнитной вязкостью тесно связаны такие явления в ферромагнетиках, как потери на перемагничивание, временной спад относительной магнитной восприимчивости χ ее частотная зависимость [14-16].
Заявляемое техническое решение, как уже было указано, основано на использовании динамического взаимодействия ферромагнитного вещества с магнитным полем, создаваемым сильным постоянным магнитом. Ферромагнитное вещество характеризуется достаточно сложной зависимостью его магнитной восприимчивости χ от величины действующего на него магнитного поля напряженностью Н согласно известной кривой Столетова. В отсутствие магнитного поля ферромагнитное вещество имеет начальную магнитную восприимчивость χНАЧ, а по мере увеличения напряженности магнитного поля сначала магнитная восприимчивость возрастает, доходит до своей максимальной величины χМАХ при напряженности магнитного поля Н*, после чего вновь уменьшается, и в области насыщения магнитной индукции (при парапроцессе) ее произведение с величиной напряженности магнитного поля остается практически неизменным, определяя намагниченность насыщения JPAC(∞)=µОχ(Н)ННАС≈const (Н) в диапазоне насыщающих магнитных полей НО≤ННАС≤НМАХ, реализуемых во второй (рабочей) части магнитного зазора, как показано на рис 2; при этом µО=1,256·10-6 Гн/м - константа, называемая абсолютной магнитной проницаемостью вакуума. Указанное значение намагниченности насыщения устанавливается экспоненциально во времени, поэтому значение JHAC(∞) имеет место в установившемся режиме, теоретически при t→∞, а практически за некоторое число m постоянных релаксации τ с учетом соотношения (1), когда ΔJ(mτ)→0.
Работа устройства, представленного на рис.1, заключается в предварительном повышении магнитной восприимчивости ферромагнитного кольца 1 до максимальной ее величины χмах, для чего используется первая часть магнитного зазора с напряженностью однородного магнитного поля в ней, равной Н*, как видно из рис.2, после чего осуществляется процесс магнитного втягивания ферровещества во вторую (рабочую) часть магнитного зазора сильного постоянного магнита 2, намагничивание до насыщения ферромагнетика, а по его выходе из магнитного зазора - его размагничивание с понижением магнитной восприимчивости до начальной величины χНАЧ с охлаждением, после чего ферромагнитное вещество (вне действия магнитного поля) вновь нагревается тепловой энергией из внешней среды в механизме теплопроводности, и цикл действия повторяется вновь и вновь, обусловливая непрерывное вращение ферромагнитного кольца.
Известная кривая Столетова с достаточной степенью точности аналитически может быть задана непрерывной функцией вида χ(Н):
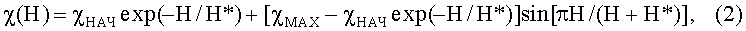
так что при Н=0 имеем χ(0)=χНАЧ, при Н=Н* имеем χ(Н*)=χМАХ, а при Н→∞ имеем χ(∞)→0, что соответствует концепции Столетова.
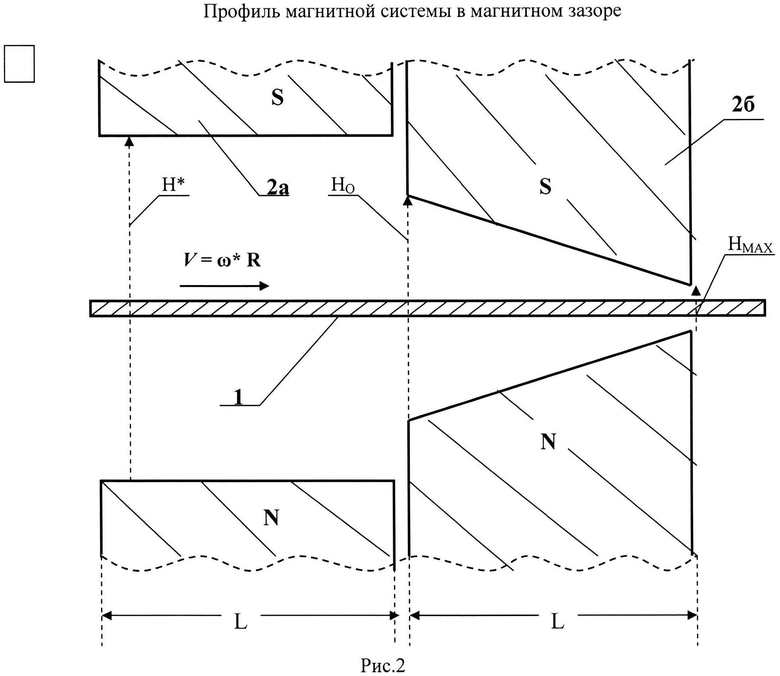
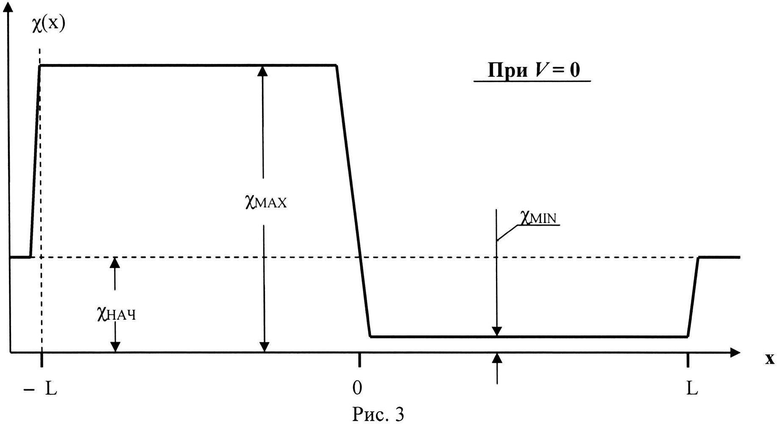
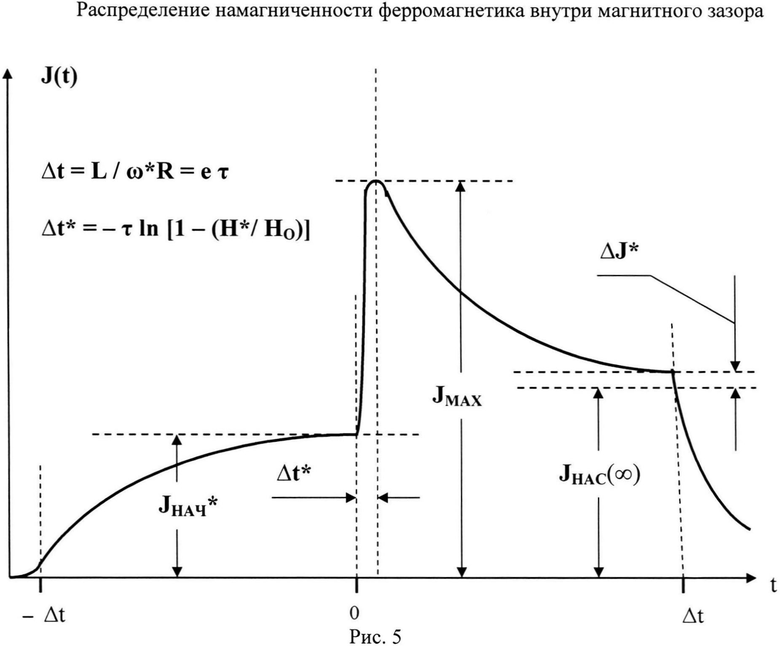
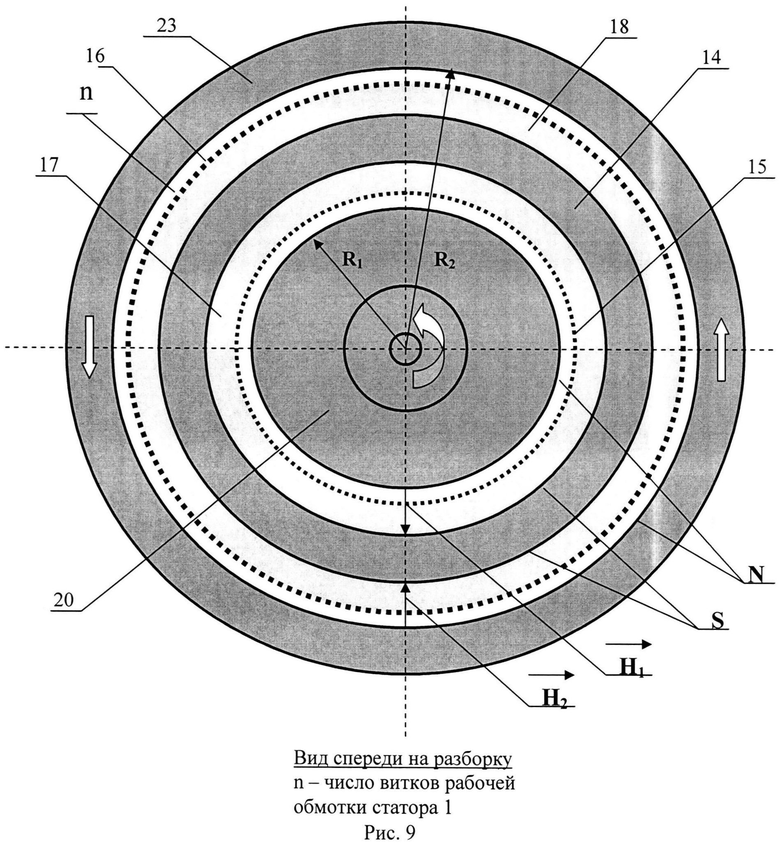
На рис.3 представлен график для значений магнитной восприимчивости ферромагнетика на различных координатах х магнитного зазора в диапазоне - L≤x≤L при неподвижном ферромагнитном кольце (ω=0), то есть в установившемся режиме. Видно, что в первой половине магнитного зазора (рис.2) устанавливается максимальная магнитная восприимчивость χMAX, а во второй - минимальная χMIN, при которой намагниченность является насыщающей JHAC(∞), как это видно на рис.5. Переходы от χНАЧ до χМАХ и далее до χMIN и снова до χНАЧ, хотя и резкие, но не скачкообразные, что определяется влиянием краевых эффектов на границах переходов магнитного поля в магнитном зазоре.
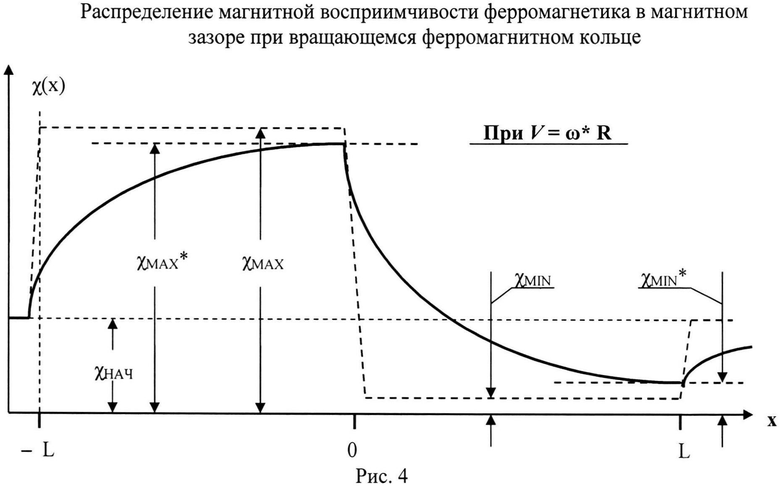
В первой части магнитного зазора длиной L при протяжке ферромагнитного вещества вдоль оси х со скоростью V=ω*R за время Δt=L/ω*R магнитная восприимчивость ферромагнетика будет экспоненциально возрастать до максимально возможной при данной скорости протяжки величины χМАХ*, как это видно из рис.4. Как будет показано ниже, угловая скорость вращения ферромагнитного кольца ω*, соответствующая максимуму вращательного момента в кольце, равна ω*=L/Δt R=L/λτR. Поэтому величина χМАХ(Н*) зависит от значения угловой скорости вращения ферромагнитного кольца и при ω=0, то есть при неподвижном ферромагнитном кольце, χМАХ(Н*)|ω=0=χМАХ>χМАХ*. хотя превышение χМАХ относительно величины χМАХ* незначительно - всего около 6,6%.
Величина намагниченности ферромагнетика к концу первой половины магнитного зазора JНАЧ* достигает величины:
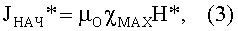
как это видно на рис.5.
Поскольку во второй части магнитного зазора сильного постоянного магнита 2 имеется неоднородное линейно возрастающее вдоль координаты х магнитное поле, которое имеет аналитический вид:
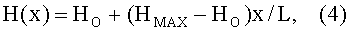
где 0≤х≤L, L - длина второй части магнитного зазора, то намагниченность J(х) ферромагнитного вещества, находящегося во второй части магнитного зазора, вычисляется на основе рекуррентных соотношений. Для этого разобьем промежуток L на n малых и одинаковых отрезков, безразмерную величину отношения х/L=ε обозначим в дискретном представлении целочисленным индексом i, а отношение (НМАХ-НО)/НО обозначим, как и раньше, через параметр градиента магнитного поля р, тогда выражение (4) запишется в индексной форме как:

и при i=n имеем Hn=НМАХ.
Поскольку состояние ферромагнетика к началу его взаимодействия с магнитным полем второй части магнитного зазора уже сформировалось и магнитная восприимчивость доведена до наибольшего значения χМАХ* в магнитном поле Н*, а магнитное поле в начале этой части магнитного зазора скачком увеличивается до величины НО>>Н*, то при анализе намагниченности ферромагнетика внутри магнитного зазора рабочего постоянного магнита следует учитывать в выражении (2) только его ниспадающую часть кривой Столетова в индексном представлении:
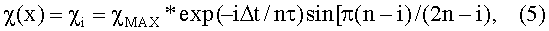
что соответствует рис.5, и при i=n имеем χn=χMIN*>χMIN, и указанное превышение χMIN* над χMIN незначительно (порядка 6,6%).
При анализе динамики намагничивания ферромагнетика, определяемого общим выражением J=µOχН, следует иметь в виду, что временное изменение этой величины зависит только от временного изменения магнитной восприимчивости, которая обладает свойством магнитной вязкости, то есть не может изменяться скачком, как в данном устройстве практически скачком изменяется напряженность магнитного поля на границе первой и второй части магнитного зазора - от Н* до HO. Это объясняет наличие выброса намагниченности с коротким фронтом порядка Δt*=-τln[1-(Н*/HO)], как это видно на рис.5, стремящегося к величине JMAX=µOχМАХ*HO, но не доходящего до нее из-за одновременного действия насыщающего магнитного поля, уменьшающего значение магнитной восприимчивости во времени, после чего намагниченность экспоненциально уменьшается для установившегося режима до величины намагниченности насыщения, равной JHAC(∞), а в данном случае до величины JHAC(∞)+ΔJ*, которая превышает намагниченность насыщения для установившегося режима на величину ΔJ*. Поскольку намагниченность дифференциального объема ферромагнитного кольца dv=Sdx (S - поперечное сечение ферромагнитного кольца внутри магнитного зазора), находящегося на какой-либо координате х в интервале 0≤х≤L в произвольный момент времени, определяется как J(х)=µOχ[Н(х)]Н(х), где Н(х) задана выражением (4), то, учитывая (1), отмечаем, что для ее нахождения необходимо найти ее предыдущее значение на координате (х-dx) или, что то же самое при достаточно большом числе разбиений отрезка L на n равных частей, для нахождения намагниченности в i-м интервале, надо сначала ее найти на (i-1) интервале, тогда имеем:
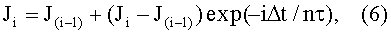
Но чтобы найти значение J(i-1) необходимо сначала найти значение J(i-2) и т.д. до J1, величина которого определяется просто:
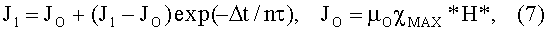
Отметим, что в скобках выражений (6) и (7), а также последующих аналогичных выражений для разностей (Ji-J(i-1)) используются установившиеся значения этих величин, а не мгновенные значения в текущем времени.
Тогда приходим к системе рекуррентных уравнений вида:
J1=JO+(J1-JO)exp(-Δt/nτ),
J2=J1+(J2-J1)exp(-2Δt/nτ),
J3=J2+(J3-J2)exp(-3Δt/nτ),
……………………………………………
Jк=Jк-1+(Jк-J(к-1))exp(-кΔt/nτ),
……………………………………………
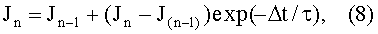
На основании (8) общее выражение для намагниченности в к-м интервале промежутка 0≤х≤L (или, что то же, 0≤ε≤1 - для безразмерного обозначения переменной) можно записать в виде:
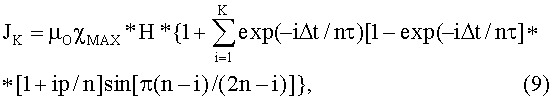
В выражении (9) известный сомножитель µOχМАХ*Н* - величина постоянная, поэтому представляет интерес безразмерная функция, стоящая в фигурных скобках, и равная:
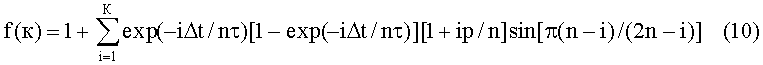
Для вычисления распределения этой функции в интервале i=1, 2, 3,… n с использованием компьютерной программы Mathcad необходимо представить эту функцию в интегральном виде, то есть с использованием непрерывных функций параметра ε=x/L. Тогда получим:
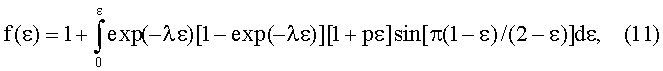
где λ=Δt/τ, и р=(НМАХ-НО)/НО, а переменная лежит в пределах 0≤ε≤1.
Как показывает анализ функции f(ε) на экстремум приравниванием нулю ее производной по параметру λ, то есть ∂f(ε)/∂λ=0, функция максимальна при λ=1,23 независимо от текущего значения переменной ε., откуда находим оптимальное значение угловой скорости ω* вращения ферромагнитного кольца, при которой достигается максимум вращательного момента:
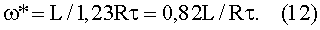
Обратимся к вопросу, как расставлены друг от друга центры магнитного притяжения ХН и намагниченности XJ вдоль криволинейной оси х в направлении протяжки ферромагнитного вещества в магнитном зазоре. Для определения центра магнитного притяжения внутри второй части магнитного зазора по программе Mathcad с помощью оператора root запишем уравнение, из решения которого находится значение относительного центра магнитного притяжения α:
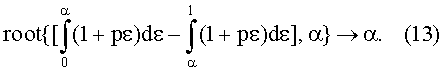
Можно построить график относительного положения центра магнитного притяжения α как функции параметра р, а также таблицу некоторых значений α(р). Видно, что положение центра магнитного притяжения ХН=(0,5…0,707)L. Так, для наиболее подходящих значениях р=5…10 имеем ХН=(0,66…0,68)L, то есть существенно дальше от середины второй части магнитного зазора при х=L/2.
Для нахождения центра намагниченности ферромагнетика XJ, находящегося внутри второй части магнитного зазора длиной L, воспользуемся модифицированным выражением (11) для относительного распределения намагниченностей ферромагнетика f(ε) при некоторых конкретно заданных условиях: р=10, τ=5·10-4 сек, λ=1,23, и введенного значения σ=JHAC(∞)/JНАЧ*=2…4 и конкретно σ=2.
Модифицированное уравнение может быть записано в форме:
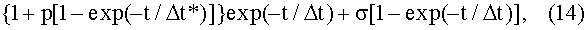
где Δt*=-τln[1-(H*/HO)]=-5·10-4ln0,9=5,27·10-5 с, Δt=1,23·5·10-4=6,15·10-4 с. Отношение Δt/Δt*=11,67. При этом уравнение (14) при заданных величинах принимает вид:
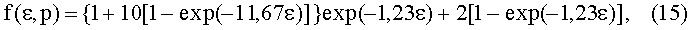
которое при ε=0 равно единице, а при ε=1 принимает значение σ=2, что и соответствует условиям задачи.
Можно также построить график для рассматриваемого примера. При этом максимум относительной функции намагниченности ферромагнетика прижат к началу второй части магнитного зазора, поэтому центр намагниченности XJ явно смещен к началу этой части зазора относительно ее центра х=L/2. Точное значение этого центра рассчитывается по формуле:
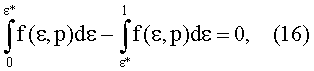
решением для которой методом последовательных приближений находим значение ε*, определяющее положение центра намагниченности XJ=ε*L, Решение (16) с учетом (15) при угловой скорости ω* вращения ферромагнитного диска имеет вид ε*=0,445, так что центр намагниченности находится на координате XJ=0,445 L.
Сравнивая средние значения положений центров магнитного притяжения и намагничивания, видим, что они разделены интервалом ΔХ=ХН-XJ=(0,67-0,45)L=0,22 L, следовательно, должна возникать сила втягивания F(ω*) ферромагнетика в магнитный зазор, и ферромагнитный диск получает вращательный момент МВР*=F(ω*)R под действием этой силы.
Известно, что дифференциал силы dF(ω), действующей со стороны неоднородного магнитного поля с градиентом напряженности вдоль оси х, равным grad HX на дифференциальный ферромагнитный объем dv с магнитным моментом J(x) dv, равна:
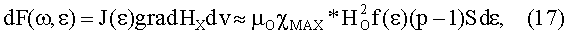
так как dv=Sdx, x/L=ε, dx=Ldε и grad HX=HO(р-1)/L.
Отметим, что знак приблизительного равенства взят в связи с тем, что выброс намагниченности в начале второй части магнитного зазора на самом деле не достигает величины µOχМАХ*HO, как было указано ранее. Так, максимум функции f(ε) составляет 0,86 от ожидаемой величины, что следует учитывать в точных оценках энергетики устройства. Для рассмотренного примера реализации устройства точное выражение для (17) соответствует dF(ω,ε)=0,86µOχМАХ*HO 2f(ε)*(p-1)Sdε.
В выражении (17) множитель µOχМАХ*НО 2(р-1)S=const(ε), а переменная часть этого выражения df(ε)=f(ε)dε, где дифференциал относительной силовой функции определяется из (11). Распределение сил для дифференциальных объемов dv, находящихся на координатах х или безразмерных координатах ε (что то же), находится из уравнения:
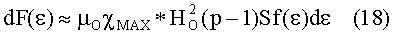
и эти дифференциалы сил для соответствующих дифференциальных объемов ферромагнитного кольца внутри второй части магнитного зазора измеряются в ньютонах [н].
Максимальное значение силы втягивания ферромагнетика второй частью магнитного зазора F(ω*) определяется разностью интегралов:
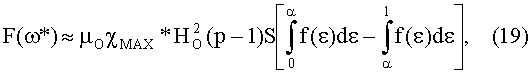
где α=ХН/L - относительное положение центра магнитного притяжения второй части магнитного зазора.
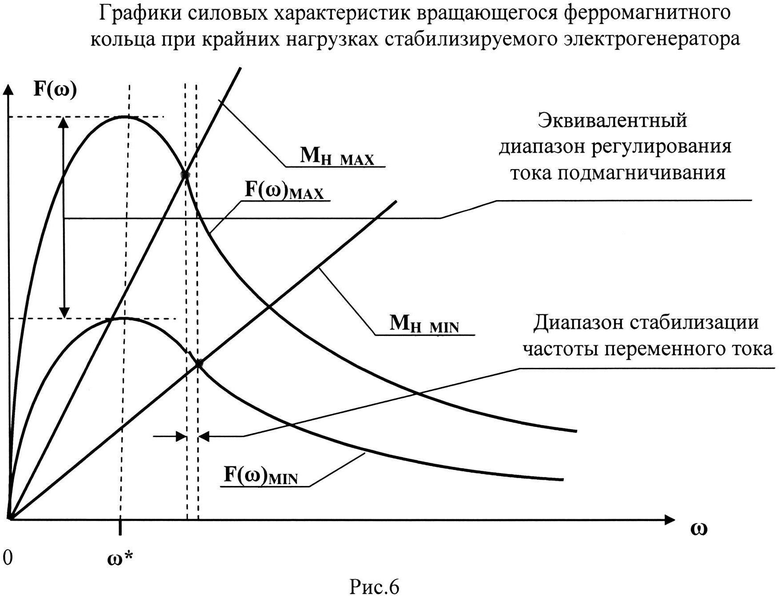
Подставляя в подынтегральные выражения (19) значение функции из (11), получим явное выражение для максимальной силы втягивания F(ω*), распределение для которой в функции угловой скорости ω показано на графиках рис.6 при двух разных значениях HO.
Можно записать следующие выражения для (10) при следующих параметрах: α=0,67, λ=1,23, р=2
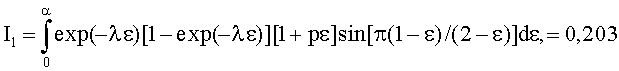
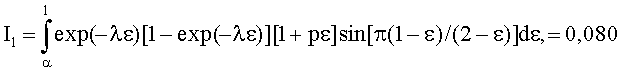
и тогда, подставляя эти выражения в (19), получим максимум втягивающей силы F(ω*) при оптимальной скорости вращения ферромагнитного кольца ω*, равный
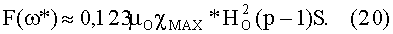
Для рассмотренного примера (20) имеет место решение 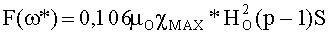
Рассмотрим пример.
Пусть χMAX*=1000, HO=104 А/м, р=9 и S=6·10-5 м2 (при толщине ферромагнитного кольца 3 мм и его ширине 2 см), тогда F(ω*)=0,106·1,256·10-6·103·108·9·6·10-5=7,19 н. Если средний радиус ферромагнитного кольца R=0,1 м, то вращательный момент МВР=F(ω*)R=0,719 н*м. Если L=0,02 м и τ=5.10-4, то оптимальная угловая скорость вращения ферромагнитного кольца равна ω*=L/1,23Rτ=400 рад/с=63,7 об/с. Максимальная мощность на валу РМАХ=МВРω*=287,6 Вт. Тепловую мощность устройство должно потреблять из окружающей среды, например, из воды соответствующего водного бассейна. Вариацией параметров L и R можно получить иные угловые скорости вращения ферромагнитного кольца, чтобы обеспечить скорость вращения вала электрогенератора 7 (рис.1) равной, например, 50 об/с.
Из теории автоматического управления известно, что присоединенная нагрузка и трение снижают скорость оси вращения 4, и устойчивое состояние режима ее вращения достигается в точке пересечения кривой силовой характеристики F(ω) с нагрузочной прямой обратной связи, когда производные этих характеристик имеют противоположные знаки. Момент нагрузки определяется тангенсом угла наклона прямой обратной связи, и производная нагрузочной прямой положительна, следовательно, устойчивое состояние в системе автоматического управления достигается на нисходящей ветви силовой характеристики F(ω), как это видно на рис.6. Поэтому вращательный момент на оси 4 оказывается всегда меньше максимального МВР=F(ω*))R, и скорость установившегося процесса вращения будет всегда выше величины ω*. Для рассмотренного примера при максимальной нагрузке МН МАХ мощность на оси вращения может достигать величины порядка 200 Вт при соответствующем подборе размеров L и R при скорости вращения оси порядка 50 об/с при учете параметра τ. При этом такая мощность теплового потока должна поступать к ферромагнитному кольцу из внешней среды. Это означает, что при перепаде температуры воды в процессе нагревания ферромагнетика в 1°С потребный поток воды составит приблизительно 50 г/с или 180 л/час.
Для увеличения интенсивности теплопередачи целесообразно ферромагнитное кольцо погружать в нагревающую его жидкость, например, очищенную воду или иную жидкость с циркуляцией ее по замкнутому циклу с радиатором нагревания и насосом для обеспечения циркуляции (радиатор при этом может быть погружен в проточную воду). Для снижения потерь на трение в качестве циркулирующей жидкости можно выбрать нитробензол, имеющий небольшую по сравнению с водой вязкость.
Другим решением теплопередачи к ферромагнитному кольцу из водной среды без погружения ферромагнитного кольца в очищенную воду является предложение автора, известное из его патента [11]. В этом случае траверсами 5 служат тонкие диски из медной фольги, на краях которых напылены тонкие слои ферромагнетика. Совокупность склеенных между собой таких медных дисков образует прекрасный теплопроводник. При этом полая ось вращения 4 выполняется из медной трубки с пайкой к ней стопы медных дисков, а внутри трубки образуется водный поток (необязательно очищенный) непосредственно из водного бассейна (озера, реки, моря). Для образования протока воды в этой трубке - оси вращения 4, внутри нее могут располагаться винтообразные лопасти, при вращении которых создается требуемый поток, и ферромагнитное кольцо быстро нагревается теплотой внешней (водной) среды.
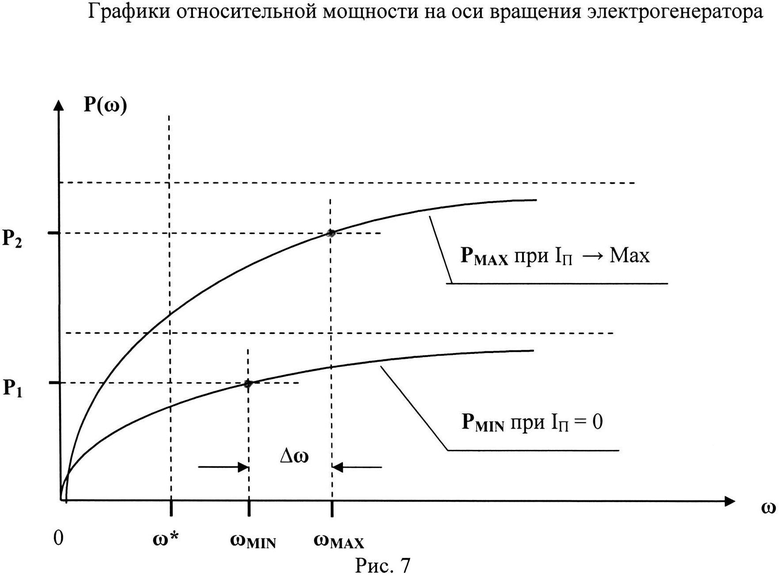
Как видно на рис.7, мощность Р(ω) на оси вращения растет с увеличением угловой скорости вращения оси 4, асимптотически приближаясь к соответствующим пороговым уровням. Это означает, что снижение угловой скорости вращения ферромагнитного кольца понижает мощность, поэтому это снижение компенсируют увеличением числа ферромагнитных колец и связанных с ними сильных постоянных магнитов в единой конструкции и с единой осью вращения [17-18]. Сильный постоянный магнит, используемый в рассматриваемой системе, выполняется из магнитожестких ферритов, например SmCo3, NdFeB или AlNiCo, имеющих высокую индукцию остаточной намагниченности - до 1,6 Тл≈1,3*106 А/м (для NdFeB).
Следует специально остановиться на рассмотрении магнитокалорического эффекта, благодаря которому осуществляется работа устройства.
Пусть в исходном состоянии ненамагниченный ферромагнетик имеет температуру TO и удельную теплоемкость cO. Для рассматриваемой массы ферромагнетика m имеем его внутреннюю тепловую энергию QO=cOmTO. Если плотность ферромагнетика ρ, то объем указанной массы m равен v=m/ρ. Если указанный объем поместить в магнитный зазор постоянного магнита, создающего магнитное поле с напряженностью Н, то энергия магнитного поля, запасенная в этом объеме, как известно, равна W=µOµvH2/2, где µ=χ+1 - относительная магнитная проницаемость ферромагнетика. При этом возникает его намагничивание, и закон сохранения энергии выражается соотношением:
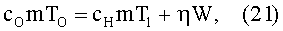
где cH - удельная теплоемкость намагниченного ферромагнетика (cH<cO), T1 - температура его объема v в процессе квазиадиабатического намагничивания, причем T1>TO (при намагничивании, как известно, ферромагнетик нагревается), η - так называемый коэффициент магнито-калорической активности (термин введен автором), зависящий от свойств ферромагнетика и учитывающий потери тепловой энергии, расходуемой на организацию вращательного движения ферромагнитного кольца. Можно показать, что η=1-[LF(ω)/W]. После выхода объема v ферромагнетика из указанного магнитного зазора в процессе его квазиадиабатического размагничивания происходит охлаждение этого объема, и закон сохранения энергии записывается как для адиабатического размагничивания
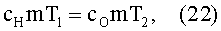
где Т2 - температура рассматриваемого объема ферромагнетика при его адиабатическом размагничивании (строго говоря, имеет место квазиадиабатическое размагничивание).
Покажем, что Т2<TO, то есть внутренняя тепловая энергия данного объема ферромагнетика, который сначала намагничивается в магнитном зазоре, а затем покидает его, размагничиваясь в адиабатическом процессе (за счет вращения ферромагнитного кольца), уменьшается на величину
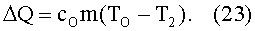
Согласно (21) можно для значения cH записать выражение
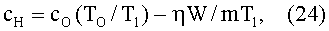
Подставляя (24) в (22), получим
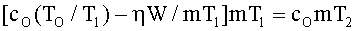
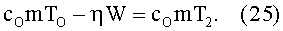
Из (25) следует, что
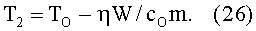
Поскольку ηW/cOm=µOηµvH2/2cOm=µOηµН2/2ρcO>0, то действительно имеем неравенство TO-T2>0, то есть TO>T2, и конечная температура Т2 рассматриваемого объема ферромагнетика оказывается ниже его исходной температуры TO (до входа в магнитный зазор с магнитным полем Н). С учетом значения коэффициента η, указанного выше, численное значение разностной температуры TO-Т2=LF(ω)/cOm=F(ω)/ρcOS, где S - поперечное сечение ферромагнитного кольца, охваченное насыщающим магнитным полем.
Изменение внутренней тепловой энергии рассматриваемого объема ферромагнетика в процессах его квазиадиабатического намагничивания и размагничивания определено в (23). Это изменение как раз и соответствует производимой при вращении ферромагнитного кольца механической работе. Тогда мощность на оси вращения 4 может быть записана как Р(ω)=ωМВР=ωF(ω)R=dQ/dt, где dQ/dt - скорость теплового потока, поглощаемого ферромагнитным кольцом из внешней среды.
Важно отметить, что энергия нагревания ферромагнетика, находящегося в состоянии покоя, при наложении насыщающего магнитного поля в точности равна энергии охлаждения его в процессе размагничивания. Однако с учетом динамики вращения ферромагнетика под действием сил магнитного взаимодействия величина энергии нагревания становится меньше за счет совершаемой работы сил втягивания ферромагнитного кольца во вторую часть магнитного зазора, чем энергия охлаждения ферромагнитного кольца при его размагничивании по мере выхода из магнитного зазора, что и приводит к охлаждению ферромагнитного кольца до его стационарной температуры TO>Т2, и при этом температура То оказывается меньшей температуры внешней среды ТВН, что вызывает в свою очередь теплопередачу тепловой энергии от внешней среды к ферромагнитному кольцу со скоростью dQ/dt. При этом безразмерный коэффициент η показывает, какая часть энергии магнитного поля, передаваемая в магнитном зазоре ферромагнитному веществу, расходуется на появление втягивающей силы во вращающемся ферромагнитном кольце, поддерживая его движение в процессе непосредственного преобразования тепловой энергии в механическую работу. В рассматриваемом процессе преобразования соблюдается универсальный физический закон сохранения и превращения энергии.
Рассмотрим процесс автоматического управления электрогенератором 7 по схеме рис.1. Цель такого управления состоит в поддержании величины выходного напряжения во внешней нагрузке с разбросом напряжения в небольших допустимых пределах при вариации величины нагрузки (потребляемой от электрогенератора мощности). Для выполнения этой задачи автоматическое управление током подмагничивания в катушках сильных постоянных магнитов приводит к соответствующему изменению напряженности магнитного поля Но в магнитном зазоре, значение которого сомножителем входит в выражение (20). Эффективность такого управления связана с тем, что величина Но в этом выражении возводится в квадрат. Например, для увеличения мощности в четыре раза ток подмагничивания увеличивают лишь вдвое или даже меньше, учитывая собственную намагниченность сильного постоянного магнита - его второй части 26 (т.е. без тока подмагничивания). На рис.6 приведены графики для силы втягивания F(ω) для наибольшей нагрузки электрогенератора (MH MAX) и наименьшей (MH MIN). Подмагничивающие токи выбраны так, что независимо от нагрузки на электрогенератор постоянное напряжение на концах его рабочей обмотки поддерживается почти постоянным, например с точностью порядка ±0,1 В. Из рис.6 усматривается, что изменением подмагничивающего тока в катушке подмагничивания 3 (рис.1) можно получить с достаточно высокой точностью постоянную скорость вращения ферромагнитного кольца 1 с его осью 4, как это важно для поддержания частоты генерируемых колебаний в устройстве-прототипе с генератором переменного тока [13].
В рассматриваемом техническом решении стабилизации подвергается не частота переменного тока, как в прототипе, а напряжение на выходе бесколлекторного генератора постоянного тока, изменение которого в зависимости от присоединенной внешней нагрузки таково, что требует работы этого генератора в расширенном диапазоне угловых скоростей оси вращения 4 (обратная задача по отношению к решению-прототипу). Так, при снижении напряжения UВЫХ на концах рабочей обмотки генератора требуется увеличить угловую скорость вращения оси 4, и, наоборот, при повышении этого напряжения следует снижать скорость вращения оси 4, как это вытекает из принципа действия генераторного устройства. Это видно на рис.7 для работы генератора при различных нагрузках P1 и Р2, причем разброс частот вращения оси 5 для указанных нагрузок Δω может оказаться достаточно большим, а сами угловые скорости вращения оси 4 всегда больше круговой частоты ω*. Частота вращения оси 4 регистрируется измерителем частоты вращения 6 (рис.1) и высвечивается на его цифровом табло.
Управление скоростью вращения ферромагнитного кольца осуществляется соответствующей вариацией тока подмагничивания в катушке 3 магнитной системы 2 от блока управления подмагничиванием 10, питание к которому подается от аккумуляторной батареи 12, параллельно соединенной с рабочей обмоткой генератора 7 по сигналам управления с выхода фильтра нижних частот (или интегратора) 9, вход которого соединен с выходом устройства сравнения 8. В последнем происходит вычитание напряжений с выходов источника опорного напряжения 11 и известной части напряжения, действующего на зажимах рабочей обмотки генератора 7. Выходной сигнал устройства сравнения 8 фильтруется либо фильтром нижних частот 9 (в схеме статического типа регулирования с остаточными ошибками), либо интегратором, вместо фильтра нижних частот (при этом схема регулирования является астатической с нулевой остаточной ошибкой, но с пониженным быстродействием).
Нетрудно понять, что для увеличения скорости вращения ферромагнитного кольца с целью увеличения выходного напряжения генератора 7 следует соответственно увеличить ток подмагничивания в катушке подмагничивания 3, что отвечает повышенной внешней нагрузке. На рис.7 видно, что мощность на оси вращения 4 также при этом возрастает.
В исходном состоянии коммутатор аккумуляторной батареи 12 отключает последнюю от обмоток генератора, и ферромагнитное кольцо 1 находится в состоянии покоя. Для пуска устройства в работу по выработке электроэнергии от генератора 7 необходимо последний использовать в режиме двигателя, чему соответствует положение переключателя 13 в указанном на рис.1 положении, после чего включают коммутатор батареи аккумуляторов и ферромагнитное кольцо начинает раскручиваться, например, в направлении против часовой стрелки, как показано на рис.1. На цифровом табло измерителя частоты вращения 6 отмечаются текущие значения скорости вращения оси вращения 4. Когда значение угловой скорости вращения оси превысит значение ω* переключатель 13 приводят в положение, соответствующее режиму работы устройства 7 как генератора постоянного тока. Поскольку при этом меняется на противоположную полярность напряжения, прикладываемого к обмотке подмагничивания, то самоподдерживающееся вращение ферромагнитного кольца за счет работы термомагнитного двигателя будет вызывать э.д.с. на концах рабочей обмотки генератора той же полярности, что и при работе его в качестве двигателя. При этом коммутатор аккумуляторной батареи может быть выключен, если не стоит задача подзаряда аккумуляторной батареи 12.
Кратко остановимся на конструкции и принципе действия бесколлекторного генератора (двигателя) постоянного тока 7, вид которого в ортогональных разрезах показан на рис 8 и 9.
Возможность построения бесколлекторных двигателей и генераторов показана ранними работами М. Фарадея в 1821 году и на примере колеса Барлоу (1824 г.), а также показана в работах [19-22] и основана на законе М. Фарадея об электромагнитной индукции и третьем законе И. Ньютона о разнонаправленных силах действия и противодействия, приложенных к физическим телам.
Ранее автором был заявлен бесколлекторный двухроторный двигатель постоянного тока, содержащий вращающийся намагниченный безобмоточный ротор и неподвижный тороидальный статор с наложенной на нем рабочей обмоткой, а также закрепленную на статоре катушку подмагничивания ротора, отличающийся тем, что в него введен жестко связанный с осью вращения ротора дополнительный безобмоточный ротор в форме магнитопроводящего цилиндра с дополнительной катушкой его подмагничивания, закрепленной к телу статора, оба вращающихся ротора с общей их осью вращения расположены их одноименными магнитными полюсами соответственно с внутренней и наружной поверхностями тороидального статора с образованием двух цилиндрических магнитных зазоров, внутри которых установлены прилегающие к тороидальному статору немагнитные цилиндры, на которые намотана рабочая обмотка тороидального статора, витки которой пропускаются через отверстия в последнем, а соответствующие полувитки рабочей обмотки находятся в непосредственной близости (с минимально допустимым зазором) от цилиндрических поверхностей обоих вращающихся роторов, обе катушки подмагничивания роторов и рабочая обмотка тороидального статора подключены последовательно или параллельно к источнику постоянного тока, причем образованные две независимые магнитные цепи «ротор - тороидальный статор» и «дополнительный ротор - тороидальный статор» замыкаются через магнитно связанные с их роторами магнитопроводящие шайбы, закрепленные с телами их роторов, с минимально допустимьми зазорами с неподвижными магнитопроводящими стенками тороидального статора; при этом толщина стенок немагнитных цилиндров выбрана в пять-десять раз большей зазора между проводниками рабочей обмотки тороидального статора и цилиндрическими поверхностями вращающихся роторов.
Такой двигатель может работать и как генератор постоянного тока, что очевидно. Рассмотрим сначала действие заявляемого бесколлекторного двухроторного двигателя постоянного тока (БДДПТ). Его состав был указан выше при описании рис.8. и рассмотрен в [23].
По правилу «левой руки» в поперечном магнитном поле с напряженностью магнитного поля Н (в амперах на метр) на проводник длиной L (в метрах) с током I (в амперах) действует парциальная сила Лоренца F, равная F=µOLIH (в ньютонах), где µо=1,256·10-6 Гн/м - магнитная постоянная. Следовательно, в обозначениях на рис.3 имеем F1=µOLIH1 и F2=µOLIH2.
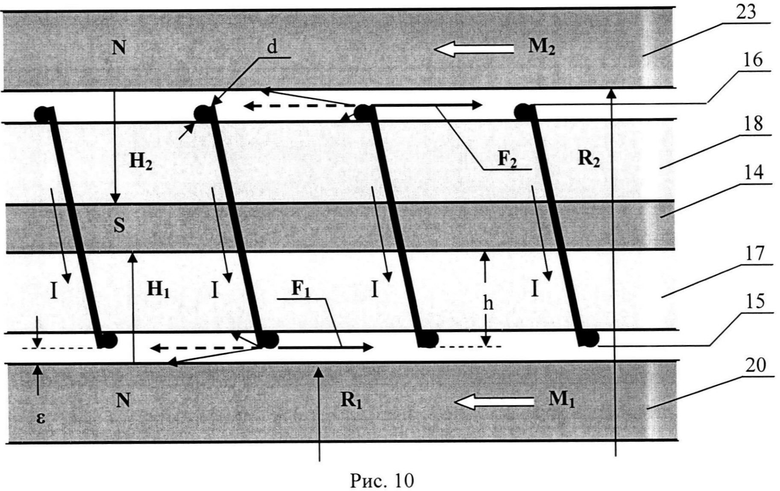
В соответствии с третьим законом Ньютона (сила действия равна и противоположна силе противодействия) силы действия F1 и F2 на полувитки 15 и 16 рабочей обмотки статора 14 (см. рис.8) определяют такие же по величине, но противоположно направленные силы противодействия, приложенные к источникам поперечных магнитных полей H1 и H2 - соответственно к статору 14 и обоим роторам 20 и 23. Эти силы противодействия как равнодействующие разлагаются на существенно не равные по величине составляющие FPOT - роторную и FCT - статорную, где FPOT>>FCT, так как h>>ε, как это видно на рис.10.
Нетрудно понять, что 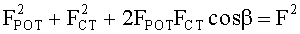
FPOT≈F{1+cos[π(ε+d/2)/(h+ε)]}/2 и
FCT≈F{1-cos[π(ε+d/2)/(h+ε))]/2 с учетом близости β→π/2,
где 0≤ε+d/2≤h+ε, где h+ε - расстояние между полюсами магнитных зазоров для независимых систем «ротор-статор».
Тогда суммарная сила FPOTΣ1, действующая по касательной на ротор 20 (внутренний), равна FPOTΣ1=nFPOT1=nµOLIH1{1+cos[π(ε+d/2)/(h+ε)]}/2, а суммарная сила, действующая по касательной на дополнительный ротор 23 (внешний), равна FPOTΣ2=nµOLIH2*{1+cos[π(ε+d/2)/(h+ε)]}/2.
Легко понять, что вращательный момент M1, приложенный к ротору 20, определяется как M1=R1FPOTΣ1, а момент вращения М2, приложенный к дополнительному ротору 23, равен M2=R2FPOTΣ2. Поскольку оба этих вращательных момента совпадают по направлению, то общий вращательный момент МΣ на оси вращения двигателя равен сумме моментов M1 и М2, то есть имеем MΣ=nµOLI(R1H1+R2H2){1+cos[π(ε+d/2)/(h++ε)]}/2. Если в первом приближении считать, что cos[π(ε+d/2)/(h+ε)]≈1, то для МΣ получаем МΣ≈nµOLI(R1H1+R2H2).
При выполнении однослойной намотки рабочей обмотки тороидального статора 14 виток к витку с диаметром проводника d на внутреннем диаметре немагнитного цилиндра 17 умещается число витков, равное n=2π(R1+ε)/d≈2πR1/d, так как R1>>d. Тогда имеем для MΣ≈2πR1µOLI(R1H1+R2H2)/d. Если ампервитки в дополнительной катушке подмагничивания 25 по отношению к ампервиткам катушки подмагничивания 22 выбрать так, что будет выполняться равенство R1H1=R2H2, что, безусловно, всегда выполнимо, то получим упрощенное выражение для полного вращательного момента на оси двигателя, равного 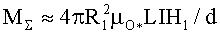
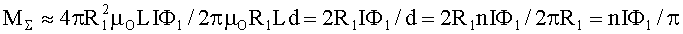
Анализируя полученное выражение для MΣ≈пIФ1/π, отмечаем, что вращательный момент непосредственно не зависит от геометрии ротора 7 - его длины L и радиуса R1, а определяется лишь ампервитками рабочей обмотки тороидального статора 1 и магнитным потоком Ф1, создаваемым катушкой подмагничивания 22, который, в свою очередь, определяется ампер-витками этой катушки подмагничивания.
Однако произведение n I определяется допустимой плотностью тока j в рабочей обмотке (для медного проводника можно принимать, что j=10 А/мм2) и радиусом R1, поскольку n=2πR1/d. Для тока I имеем выражение I=πjd2/4. Тогда для произведения n I получим n I=(2πR1/d)(πjd2/4)=π2jR1d/2 (значения R1 и d берутся в миллиметрах).
Следовательно, MΣ≈пIФ1/π=πjR1dФ1/2,то есть полный вращательный момент на оси двигателя пропорционально возрастает с увеличением радиуса R1 при заданной величине диаметра d применяемого медного проводника и заданном значении магнитного потока Ф1, создаваемого катушкой подмагничивания 22. Те же рассуждения относятся и ко второму магнитному контуру из тороидального статора 14 и дополнительного ротора 23 в предположении равенства R1H1=R2H2, а также при Ф1=Ф2.
Полезная мощность на оси вращения двигателя равна РОСИ=ω|MΣ|, где ω - круговая частота вращения роторов 20 и 23
Как уже указывалось выше, рабочая обмотка тороидального статора 14 может подключаться к источнику постоянного тока независимо от питания катушек подмагничивания (обычно включенных между собой последовательно) или последовательно с этими катушками. В последнем случае проводники всех обмоток выполняются из одного и того же медного проводника (по его сечению), что минимизирует потери на подводящих проводниках от единого источника постоянного тока.
Рассмотренный тип бесколлекторного двухроторного двигателя постоянного тока выгодно отличается от всех известных коллекторных двигателей отсутствием ненадежного их элемента - коллектора со щетками - и вообще отсутствием каких-либо скользящих контактов, снижающих надежность и долговечность функционирования известных двигателей. В коллекторных двигателях одномоментно работает только одна из множества секций обмотки ротора. В рассматриваемом типе двигателя работает постоянно вся рабочая обмотка тороидального статора, что увеличивает энергетику двигателя. При его работе отсутствуют переходные процессы, характерные для коллекторных двигателей постоянного тока из-за высокочастотного переключения секций обмотки его ротора. Это способствует увеличению скорости вращения роторов заявляемого двигателя и отсутствию излучений в широком спектре радиопомех. Кроме того, это приводит к увеличению удельной полезной мощности на валу двигателя на единицу его объема (веса).
В бесколлекторном двигателе постоянного тока все его обмотки включают последовательно (сериесный вариант) или параллельно (шунтовой вариант) при последовательном соединении обмоток подмагничивания 22 и 25. Понятно, что для реверса вращения ротора в таком двигателе достаточно изменить полярность подключения к источнику постоянного тока либо рабочую его обмотку, либо обмотки подмагничивания. Это обстоятельство использовано в заявляемом техническом решении, для которого необходимо сначала включить устройство (рис.8) в режим работы двигателя, а после соответствующего раскрута ферромагнитного кольца - в режим генерирования постоянного тока. При переходе из режима двигателя в режим генератора направление тока в обмотках подмагничивания следует изменить на противоположное, Тогда в режиме генерирования ферромагнитное кольцо как поставщик механической работы будет продолжать вращаться в том же направлении, в котором оно вращалось в режиме двигателя. При этом направление тока в рабочей обмотке изменится на противоположное при сохранении той же полярности на ее концах.
Интересное решение по построению бесколлекторного двигателя (генератора) постоянного тока предложено в [24] с тороидально-цилиндрическими ротором и статором, которое отличается повышенным к.п.д. вследствие практически полного использования проводника рабочей обмотки, намотанной на неподвижном статоре.
Заявляемое техническое решение может быть успешно применено в промышленных изделиях и в бытовой технике в качестве поставщика электрической энергии с отбором тепловой энергии водных бассейнов, которая восполняется непрерывно солнечной радиацией. Такие источники энергии являются экологически чистыми и уменьшают опасные последствия глобального потепления нашей планеты при широком применении таких устройств.
Данное устройство может быть изготовлено на предприятиях радиопромышленности с привлечением организаций, связанных с технологией изготовления ферроматериалов и сильных постоянных магнитов.
Литература
1. Ландсберг Г.С. Оптика, 5 изд., М., 1976, гл. 31;.
2. Ельяшевич М.А., Атомная и молекулярная спектроскопия, М., 1962;
3. Фриш С.Э. Оптические спектры атомов, М. - Л., 1963;
4. Меньших О.Ф., Магнитовязкий маятник. Патент РФ №2291546, опубл. №01 от 10.01.2007;
5. Меньших О.Ф. Ферромагнитовязкий ротатор. Патент РФ №2309527, опубл. №30 от 27.10.2007;
6. Меньших О.Ф. Магнитный двигатель. Патент РФ №2310265, опубл. №31 от 10.11.2007;
7. Меньших О.Ф. Магнитовязкий ротатор. Патент РФ №2325754, опубл. №15 от 27.05.2008;
8. Меньших О.Ф. Способ получения энергии и устройство для его реализации. Патент РФ №2332778, опубл. №24 от 17.08.2008;
9. Меньших О.Ф. Ферромагнитовязкий двигатель. Патент РФ №2359398, опубл. №17 от 20.06.2009;
10. Меньших О.Ф. Устройство стабилизации частоты генератора. Патент РФ №2368073, опубл. №26 от 20.09.2009;
11. Меньших О.Ф. Ротор ферромагнитовязкого двигателя. Патент РФ №2412524, опубл. в №5 от 20.02.2011;
12. Меньших О.Ф. Способ получения энергии и устройство для его реализации, Патент РФ №2452074, опубл. в №15 от 27.05.2012;
13. Меньших О.Ф. Устройство автоматического управления электрогенератором, Патент РФ №2444802, опубл. в №7 от 10.03.2012 (прототип);
14. Kronmuller H., Nachwirkung in Ferromsgnetika, 1968;
15. Вонсовский С.В. Магнетизм, М., 1971;
16. Мишин Д.Д. Магнитные материалы, М., 1981;
17. Вольфарт Э. Магнитно-твердые материалы, пер. с англ., М. - Л., 1963.
18. Меньших О.Ф. Способ производства постоянных магнитов. Патент РФ №2483380, опубл. в №15 от 27.05.2013;
19. Электрические униполярные машины, под ред. Л.А. Суханова, М., ВНИИЭМ, 1964, с.14;
20. «Электричество», №8,1991, с.6-7, рис.8;
21. Патент Великобритании №2223628 А;
22. Меньших О.Ф. Бесколлекторный двигатель постоянного тока. Патент РФ №2391761, опубл. в №16 от 10.06.2010.
23. Меньших О.Ф. Бесколлекторный двухроторный двигатель постоянного тока. Заявка №2013115807/07 (023441) с приоритетом от 08.04.2013;
24. Меньших О.Ф. Бесколлекторный двигатель постоянного тока. Заявка №2013124383/07 (035957) с приоритетом от 27.05.2013.
Отчет о патентном поиске
Изобретение относится к электротехнике, к системам автоматической стабилизации напряжения постоянного тока, вырабатываемого непосредственным преобразованием тепловой энергии внешней среды, например водных бассейнов, и может быть использовано в экологически чистой электроэнергетике. Технический результат состоит в стабилизации напряжения постоянного тока при вариации внешней нагрузки и увеличении срока действия и надежности. Устройство автоматического управления электрогенератором содержит ферромагнитное кольцо, механически связанное с осью вращения через траверсы, одна часть которого совмещена с насыщающим магнитным полем сильного постоянного магнита, а другая связана с тепловыделяющей средой. Фильтр нижних частот, или интегратор, последовательно соединен с блоком управления подмагничиванием, выход которого соединен с катушкой подмагничивания. Магнитный зазор сильного постоянного магнита выполнен из двух частей, первая из которых образует однородное магнитное поле с напряженностью, обеспечивающей на длине L этой части зазора доведение магнитной восприимчивости ферромагнетика до максимального значения, а вторая длиной L снабжена катушкой подмагничивания и образует насыщающее магнитное поле в начале этой части зазора и далее в направлении движения ферромагнитного кольца линейно возрастающее по напряженности магнитное поле к концу зазора. Ось вращения механически связана с измерителем частоты вращения оси и бесколлекторным генератором постоянного тока, подключенным к нагрузке и включающем раздельные рабочую обмотку и обмотку подмагничивания. Рабочая обмотка подключена к аккумуляторной батарее, к внешней нагрузке, к источнику опорного напряжения, к блоку управления подмагничиванием и к первому входу устройства сравнения. Обмотка подмагничивания подключена к аккумуляторной батарее через переключатель перемены полярности постоянного тока. Выход источника опорного напряжения подключен ко второму входу устройства сравнения, выход которого соединен с управляющим входом блока управления подмагничиванием через фильтр нижних частот. 10 ил.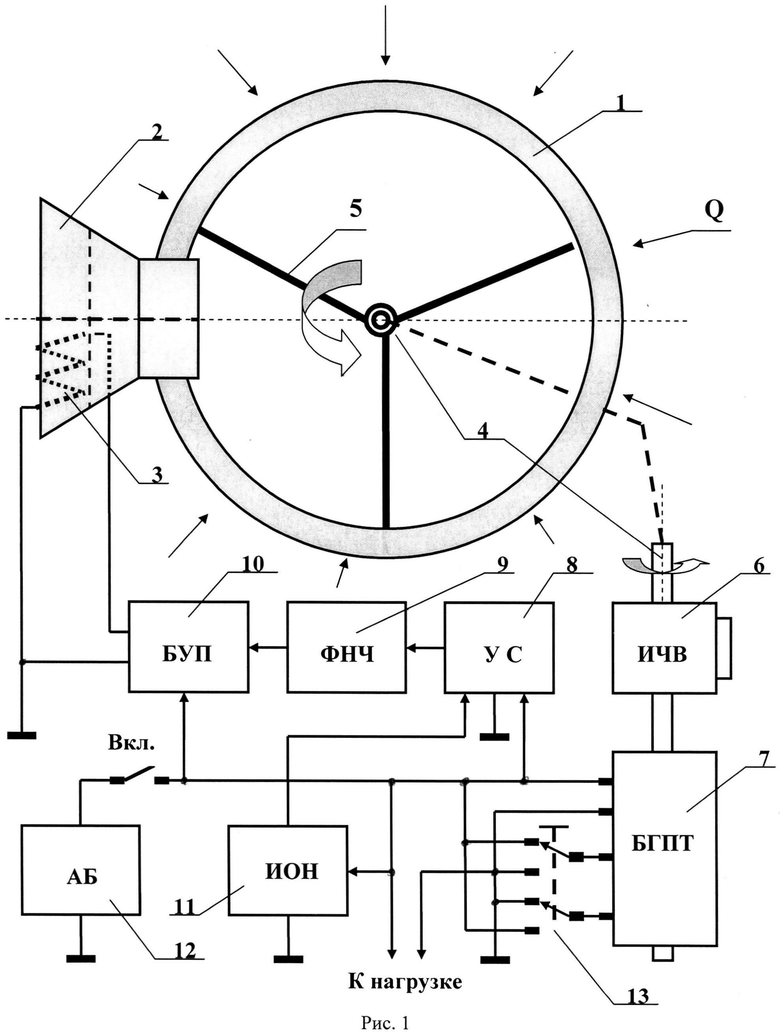
Устройство автоматического управления электрогенератором, содержащее ферромагнитное кольцо, механически связанное с осью вращения через траверсы, часть ферромагнитного кольца совмещена с насыщающим магнитным полем сильного постоянного магнита, а другая его часть связана с тепловыделяющей средой, например, очищенной водой, забираемой из соответствующего водного бассейна, а также последовательно соединенные фильтр нижних частот (или интегратор) и блок управления подмагничиванием, выходом соединенный с катушкой подмагничивания, при этом магнитный зазор сильного постоянного магнита выполнен из двух частей, первая из которых образует однородное магнитное поле с напряженностью Н*, обеспечивающей на длине L этой части магнитного зазора доведение магнитной восприимчивости ферромагнетика до максимального значения, а вторая часть магнитного зазора длиной L снабжена катушкой подмагничивания и образует насыщающее магнитное поле в начале этой части магнитного зазора и далее в направлении движения ферромагнитного кольца линейно возрастающее по напряженности магнитное поле к концу магнитного зазора, причем угловая скорость ω* вращения ферромагнитного кольца, соответствующая максимуму возникающего в нем вращательного момента за счет возникающей силы втягивания ферромагнетика, определена условием ω*=L/λRτ, где λ=1,23 и R - средний радиус ферромагнитного кольца, τ - постоянная времени релаксации магнитной вязкости ферромагнетика, из которого выполнено ферромагнитное кольцо, отличающееся тем, что ось вращения механически связана с измерителем частоты вращения оси с цифровым табло и бесколлекторным генератором постоянного тока, подключенным к нагрузке и включающем раздельные рабочую обмотку и обмотку подмагничивания, рабочая обмотка подключена к буферному источнику постоянного тока в виде аккумуляторной батареи, к внешней нагрузке, к источнику опорного напряжения, к блоку управления подмагничиванием и к первому входу устройства сравнения, обмотка подмагничивания генератора подключена к аккумуляторной батарее через переключатель перемены полярности постоянного тока, выход источника опорного напряжения подключен ко второму входу устройства сравнения, выход которого соединен с управляющим входом блока управления подмагничиванием через фильтр нижних частот (или интегратор).
| УСТРОЙСТВО АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ ЭЛЕКТРОГЕНЕРАТОРОМ | 2010 |
|
RU2444802C1 |
| УСТРОЙСТВО СТАБИЛИЗАЦИИ ЧАСТОТЫ ГЕНЕРАТОРА | 2007 |
|
RU2368073C2 |
| Способ электрической контактной сварки | 1932 |
|
SU32649A1 |
| JPH 10146074 A, 29.05.1998 | |||
| EP 1476933 A1, 17.11.2004 | |||
Авторы
Даты
2015-01-10—Публикация
2013-07-24—Подача