Изобретение относится к области физики магнетизма и электроники, в частности к системам автоматической стабилизации частоты переменного тока, вырабатываемого непосредственным преобразованием тепловой энергии внешней среды, например водных бассейнов, с использованием известных физических свойств ферромагнетиков, динамически взаимодействующих с насыщающим магнитным полем, и может найти применение в экологически чистой электроэнергетике.
Известно прямое преобразование тепловой энергии в электрическую постоянного тока на основе эффекта Зеебека - возникновения в электрической цепи, состоящей из нескольких разнородных проводников, контакты между которыми имеют различные температуры [1-3], например, на основе спая проводников «константан (-38 мкВ/К) - хромель (+24 мкВ/К)» или соединений «висмута (-68 мкВ/К) с сурьмой (+43 мкВ/К)». На основе эффекта Зеебека разработаны термоэлектрические генераторы, в состав которых входят термобатареи, набранные из полупроводниковых термоэлементов (аморфных или стеклообразных), соединенных последовательно или параллельно. Идея использования полупроводниковых термоэлементов, вместо металлических термопар, принадлежит академику А.Ф. Иоффе (СССР). Однако эти устройства пока не нашли применения в электроэнергетике по целому ряду объективных причин.
Представляет интерес использовать термомагнитные явления для получения механической работы, а именно магнитокалорический эффект в ферромагнетиках в сочетании с известными их свойствами - магнитной вязкости, снижения магнитной восприимчивости в насыщающих магнитных полях (кривая Столетова), возникновения фазового перехода первого рода в насыщающих магнитных полях (с адекватным уменьшением удельной теплоемкости ферромагнетика), нарушения симметрии в процессах нагревания при намагничивании и охлаждения при размагничивании в динамике взаимодействия движущегося ферромагнетика относительно локализованного насыщающего магнитного поля. Совокупность названных свойств позволяет синтезировать параметрический термомагнитный генератор для выработки механической энергии, в котором вращающееся магнитное поле заменено вращающимся распределением магнитной восприимчивости синхронно с вращающимся ферромагнитным кольцом, небольшая часть которого помещена в неподвижное локализованное в пространстве насыщающее магнитное поле (принцип эквивалентности вращений). При этом центр намагниченности движущегося внутри магнитного зазора ферромагнетика в таком постоянно действующем во времени распределении отстает от центра притяжения внутри магнитного зазора, в силу чего возникает постоянно действующая втягивающая сила, вектор которой направлен по касательной к ферромагнитному кольцу в сторону его вращения, что поддерживает указанное вращательное движение, если вращательный момент не меньше момента трения и присоединенной нагрузки. При этом затрачивается внутренняя тепловая энергия ферромагнитного кольца при его намагничивании с результирующим охлаждением ферромагнитного кольца, восполняемая тепловой энергией внешней среды в механизме теплопроводности.
На указанном сочетании известных свойств ферромагнетиков автором предложены способ получения энергии и целый ряд устройств, основанных на данном способе и его модификациях [4-13].
Ближайшим аналогом заявляемого технического решения (прототипом) может быть взято «Устройство автоматического управления электрогенератором» [13], ранее предложенное автором, содержащее ферромагнитное кольцо, механически связанное с осью вращения через траверсы, часть ферромагнитного кольца помещена в насыщающее магнитное поле сильного постоянного магнита, снабженного катушкой подмагничивания, а другая его часть связана с тепловыделяющей средой, например очищенной водой, забираемой из соответствующего водного бассейна, с осью вращения механически связан трехфазный генератор переменного тока, подключенный к трехфазному выпрямителю и к электрической нагрузке, выход трехфазного выпрямителя через блок управления подмагничиванием связан с катушкой подмагничивания сильного постоянного магнита, вход блока управления подмагничиванием подключен к выходу последовательно соединенных генератора опорного напряжения, фазочувствительного выпрямителя и фильтра нижних частот (или интегратора), отличающееся тем, что с осью вращения ферромагнитного кольца механически связан тахогенератор, выход которого подключен ко второму входу фазочувствительного выпрямителя, а магнитный зазор сильного постоянного магнита выполнен из двух частей, первая из которых образует однородное магнитное поле с напряженностью, обеспечивающей на длине L этой части магнитного зазора доведение магнитной восприимчивости ферромагнетика до максимального значения, а вторая часть магнитного зазора длиной L образует насыщающее магнитное поле в начале этой части магнитного зазора и далее в направлении движения ферромагнитного кольца линейно возрастающее по напряженности магнитное поле к концу магнитного зазора, причем угловая скорость ω* вращения ферромагнитного кольца, соответствующая максимуму возникающего в нем вращательного момента, определена условием ω*=L/λRτ, где λ=1,23 и R - средний радиус ферромагнитного кольца, τ - постоянная времени релаксации магнитной вязкости ферромагнетика, из которого выполнено ферромагнитное кольцо.
Данное устройство работает на основе потребления тепловой энергии внешней среды, поступающей к охлаждающемуся при вращении ферромагнитному кольцу, и в задачу этого устройства входит поддержание неизменным (мало изменяющимся) значения частоты вырабатываемого переменного тока при изменении потребляемой мощности в присоединенной нагрузке.
Целями заявляемого технического решения являются стабилизация частоты вырабатываемого переменного тока при вариации внешней нагрузки и увеличение срока действия и надежности функционирования генерирующего электроэнергию прибора.
Указанные цели достигаются в заявляемом стабилизированном генераторе переменного тока, содержащем ферромагнитное кольцо, механически связанное с осью вращения через траверсы, часть ферромагнитного кольца совмещена с насыщающим магнитным полем сильного постоянного магнита, а другая его часть связана с тепловыделяющей средой, например очищенной водой, забираемой из соответствующего водного бассейна, а также последовательно соединенные фильтр нижних частот (или интегратор) и управляемый источник тока подмагничивания, выходом соединенный с катушкой подмагничивания, при этом магнитный зазор сильного постоянного магнита выполнен из двух частей, первая из которых образует однородное магнитное поле с напряженностью H*, обеспечивающей на длине L этой части магнитного зазора доведение магнитной восприимчивости ферромагнетика до максимального значения, а вторая часть магнитного зазора длиной L образует насыщающее магнитное поле в начале этой части магнитного зазора и далее в направлении движения ферромагнитного кольца линейно возрастающее по напряженности магнитное поле к концу магнитного зазора, причем угловая скорость ω* вращения ферромагнитного кольца, соответствующая максимуму возникающего в нем вращательного момента за счет возникающей силы втягивания ферромагнетика определена условием ω*=L/λRτ, где λ=1,23 и R - средний радиус ферромагнитного кольца, τ - постоянная времени релаксации магнитной вязкости ферромагнетика, из которого выполнено ферромагнитное кольцо, ось вращения ферромагнитного кольца механически связана с измерителем частоты вращения оси с цифровым табло и генератором переменного тока, например трехфазным, подключенным к электрической нагрузке, а также содержащем устройство управления током подмагничивания указанной электромагнитной системы из подключенного к управляемому источнику тока подмагничивания через фильтр нижних частот (или интегратор) фазочувствительного выпрямителя, входы которого подключены соответственно к выходам измерителя частоты вращения и генератора опорного напряжения, отличающемся тем, что на ферромагнитное кольцо намотана катушка из проводника, связанная с аккумуляторной батареей через установленные на его оси кольцевые скользящие контакты и силовой диод в цепи заряда аккумуляторной батареи, питающей управляемый источник тока подмагничивания.
Достижение поставленных целей объясняется действием статической (астатической в случае применения интегратора, вместо фильтра нижних частот) системы авторегулирования для поддержания практически неизменной скорости вращения оси ферромагнитного кольца. Сигнал ошибки регулирования формируется на выходе фазочувствительного выпрямителя путем сравнения частоты генератора опорного напряжения и с выхода измерителя частоты вращения. Отличительные признаки заявляемого технического решения обеспечивают выработку постоянного тока заряда аккумуляторной батареи от катушки из проводника, намотанной на ферромагнитном кольце при его вращении относительно продольной составляющей магнитного поля, образующейся во второй части электромагнитной системы с насыщающим магнитным полем.
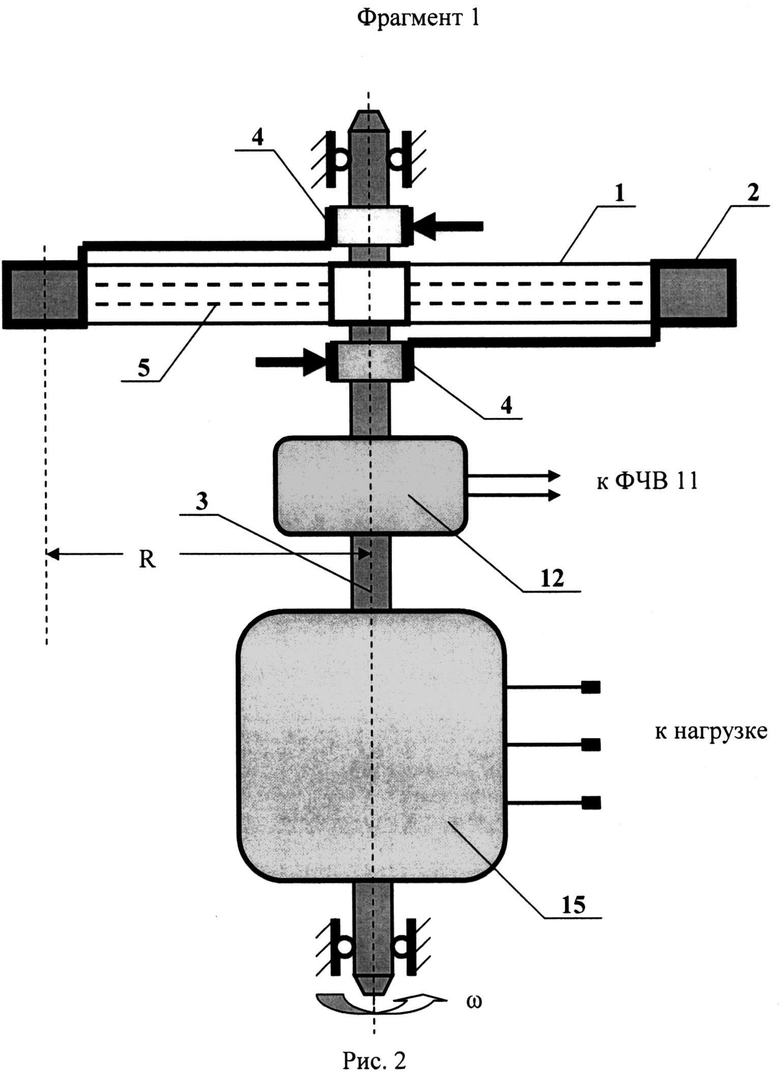
Структурная схема заявляемого технического решения представлена на рис.1. На рис.2 представлен фрагмент 1 с расположенными на оси вращения ферромагнитного кольца с кольцевыми электродами, подключенными к катушке, намотанной на ферромагнитном кольце, измерителя частоты вращения и трехфазного генератора переменного тока. На рис.3 приведен фрагмент 2 структуры магнитных зазоров электромагнитной системы относительно части ферромагнитного кольца с намотанной на него катушкой из проводника. На рис.4 (фрагмент 3) рассмотрена структура магнитной системы с ее катушкой подмагничивания. На рис.5 показан эксперимент возбуждения ЭДС индукции в катушке, размещенной на ферромагнитном стержне, относительно которого вдоль него перемещается намагниченный тороид с некоторой скоростью. На рис.6 представлены силовые и нагрузочные характеристики ферромагнитовязкого двигателя при двух крайних значениях присоединенной к двигателю нагрузки.
На рис.1 заявляемое устройство состоит из следующих элементов.
1 - ферромагнитное кольцо со средним радиусом R,
2 - намотанная на кольце 1 катушка из проводника (например, однослойная виток к витку),
3 - ось вращения ферромагнитного кольца,
4 - пара кольцевых электродов, закрепленных на оси вращения 3 и соединенных с катушкой из проводника 2,
5 - траверсы соединения ферромагнитного кольца 1 с осью вращения 3,
6 - комбинированный магнит с подмагничиванием,
7 - катушка подмагничивания комбинированного магнита 6,
8 - силовой диод,
9 - аккумуляторная батарея (подзаряжается через силовой диод 8 от катушки 2),
10 - управляемый источник тока подмагничивания,
11 - фазочувствительный выпрямитель,
12 - измеритель частоты вращения (с цифровым табло),
13 - генератор опорного напряжения (с фиксированной частотой),
14 - фильтр нижних частот (или интегратор) системы авторегулирования,
15 - трехфазный генератор переменного тока.
На рис.1 также показан процесс теплопередачи из внешней среды к ферромагнитному кольцу 1, охлаждающемуся при вращении, с мощностью теплового потока Р, потребляемого охлаждающимся ферромагнитным кольцом 1.
На рис.2 (фрагмент 1) часть устройства представлена следующими элементами, указанными на рис.1, - ферромагнитным кольцом 1 с намотанной на него катушкой из проводника 2, осью вращения 3 с подшипниковой парой, парой кольцевых электродов 4, связанных с катушкой 2, траверсами 5, измерителем 12 частоты вращения оси 3 и трехфазным генератором переменного тока 15.
На рис.3 (фрагмент 2) представлен разрез комбинированного магнита с подмагничиванием 6, из двух секций - с однородным магнитным полем H* и неоднородным, возрастающим по напряженности от HO до HMAX, а также часть ферромагнитного кольца 1 с намотанной на него катушкой 2, движущегося в магнитном поле с линейной скоростью V=ωR при вращении ферромагнитного кольца 1 с угловой скоростью ω при среднем радиусе кольца R. Длина секций магнита 6 одинакова и равна L.
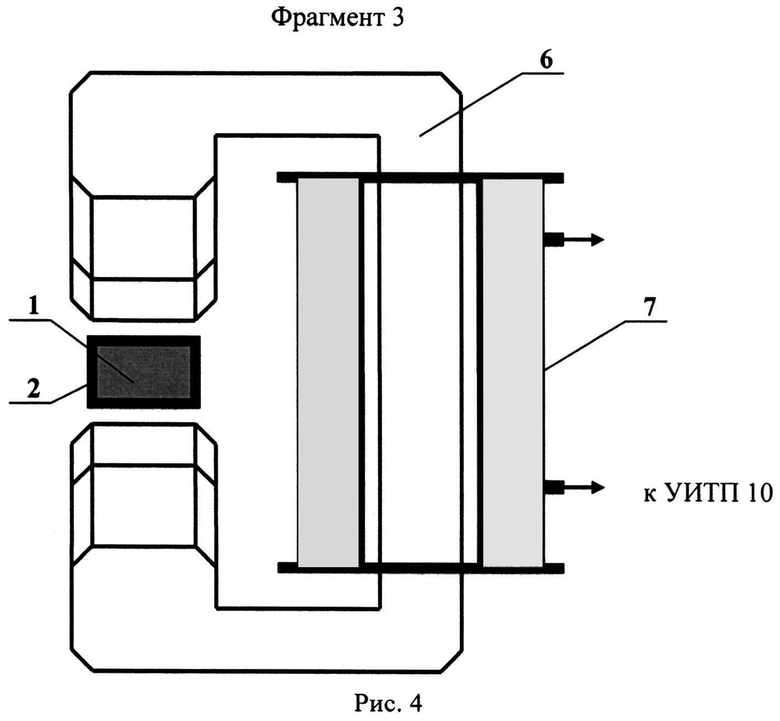
На рис.4 (фрагмент 3) показан вид на комбинированный магнит 6 с его катушкой подмагничивания 7, связанной с управляемым источником тока подмагничивания 10.
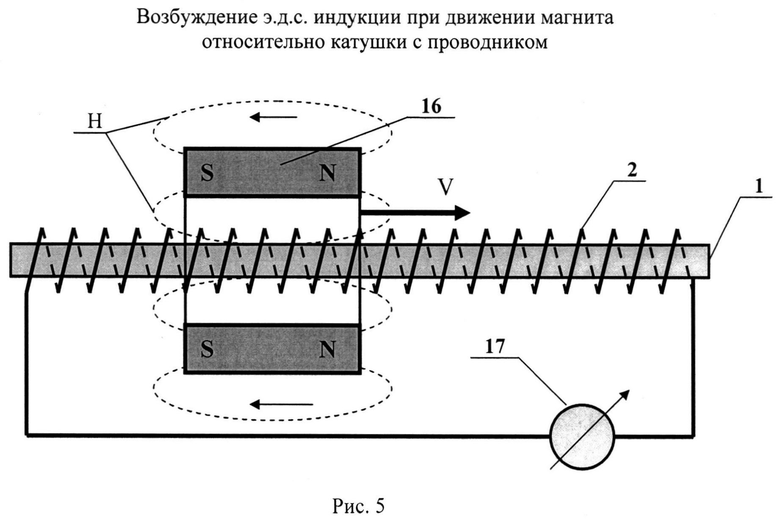
На рис.5 показана схема возбуждения ЭДС индукции в катушке с проводником 2, намотанной на ферромагнитном стержне 1 (части ферромагнитного кольца 1), при движении тороидального магнита 16 вдоль оси катушки 2 со скоростью V. При этом ток в катушке 2 регистрируется магнитоэлектрическим прибором 17, а его направление в катушке меняется при изменении знака вектора скорости V.
На рис.6 представлены две силовые характеристики ферромагнитовязкого двигателя - зависимости действующей на ферромагнитное кольцо 1 силы F(ω) в направлении его вращения (то есть совпадающей с вектором V) в функции угловой скорости ω вращения оси 3 при двух крайних значениях тока подмагничивания в катушке 7 комбинированного магнита 6. На этом же рисунке даны соответственно две нагрузочные характеристики для соответствующих двух крайних нагрузок на трехфазный генератор переменного тока 15 (минимально и максимально допустимых), определяемых моментами нагрузки MH MIN и MH MAX. Видно, что максимум силовой характеристики в ферромагнитовязком двигателе достигается при угловой скорости вращения ферромагнитного кольца, равной ω*, а работа устройства всегда осуществляется при угловых скоростях ω>ω*. Точки пересечения соответствующих силовых и нагрузочных характеристик соответствуют точкам устойчивого равновесия системы авторегулирования, а разброс проекций этих точек на ось абсцисс сводится к минимуму в статической системе авторегулирования (при использовании фильтра нижних частот 14) или к нулевому значению для астатической системы авторегулирования (при замене ФЧВ 14 на интегратор), хотя применение астатической системы авторегулирования понижает ее быстродействие.
Рассмотрим действие заявляемого устройства.
В основе работы термомагнитного двигателя на ферромагнитном кольце 1 и сильном комбинированном постоянном магните 6 с подмагничиванием лежит известный принцип работы электромагнитного двигателя с использованием силового взаимодействия между намагниченными ротором и статором, в котором магнитное поле статора вращается, увлекая за собой ротор, вращающийся вместе с вращающимся магнитным полем статора. Так работают, например, синхронные и асинхронные электродвигатели переменного тока. В заявляемом техническом решении магнитное поле статора неподвижно, будучи образовано неподвижно расположенным сильным постоянным магнитом. Однако в силу принципа эквивалентности вращающееся в обратную сторону относительно физического вращения ферромагнитного кольца (как ротора) распределение намагниченности в ферромагнитном кольце также приводит к силовому взаимодействию за счет отставания центра намагниченности ферромагнитного кольца внутри магнитного зазора сильного постоянного магнита от его центра магнитного притяжения. В результате такого силового взаимодействия ферромагнитное кольцо вращается под действием втягивающей силы, стремящейся совместить указанные центры намагниченности и магнитного притяжения. Таким образом, остается обеспечить указанное отставание центра намагниченности той части ферромагнитного кольца, которая находится в зазоре сильного постоянного магнита, от центра магнитного притяжения последнего. При этом имеется в виду, что вращение указанного распределения намагниченности на ферромагнитном кольце в системе координат, связанной с ферромагнитным кольцом, обратно синхронно вращению ферромагнитного кольца, что приводит к постоянно действующей картине распределения намагниченности внутри магнитного зазора в системе координат, связанной с неподвижным сильным постоянным магнитом, и сила втягивания является постоянно действующей. Эта задача решается благодаря использованию свойства магнитной вязкости ферромагнетика, из которого изготовлено ферромагнитное кольцо, в динамике вращения последнего под действием приложенного к ферромагнитному кольцу пускового момента импульса достаточной величины, после чего ферромагнитное кольцо будет поддерживать режим вращения при условии, что момент трения и присоединенной нагрузки не больше вращательного момента, возникающего от указанного силового взаимодействия, а компенсация потерь энергии при таком вращении ферромагнитного кольца осуществляется за счет притока из внешней среды тепловой энергии к ферромагнитному кольцу, которое охлаждается при размагничивании выходящей из магнитного зазора части ферромагнитного кольца согласно известному магнитокалорическому эффекту.
Одним из важных применительно к рассматриваемому техническому решению свойств ферромагнитных материалов является их так называемая магнитная вязкость, магнитное последействие - отставание по времени намагниченности ферромагнетика от изменения напряженности магнитного поля. В наиболее простых случаях изменение намагниченности AJ в зависимости от времени t описывается формулой

где J0 и J∞ - соответственно значения намагниченности непосредственно после изменения напряженности Н магнитного поля в момент t=0 и после установления нового равновесного состояния, τ - константа, характеризующая скорость процесса и называемая постоянной времени релаксации. Значение τ зависит от природы магнитной вязкости и в различных материалах может изменяться от 10-9 с до нескольких десятков часов.
Различают два вида магнитной вязкости: диффузионный (рихтеровский) и термофлуктуационный (иордановский). В первом из них магнитная вязкость определяется диффузией примесных атомов или дефектов кристаллической структуры. Объяснение роли примесей было дано J. Snock, а более строгая теория построена L. Neel и базируется на предположении о преимущественной диффузии примесных атомов в те межатомные промежутки кристалла, которые определенным образом ориентированы относительно направления спонтанной намагниченности. Это создает локальную наведенную анизотропию, приводящую к стабилизации доменной структуры. Поэтому после изменения магнитного поля новая доменная структура устанавливается не сразу, а после диффузного перераспределения примеси, что и является причиной магнитной вязкости.
Второй вид магнитной вязкости более универсален и наблюдается практически во всех ферромагнетиках, особенно в области магнитных полей, сравнимых с коэрцитивной силой. Неелем был предложен термофлуктуационный механизм для объяснения этого вида магнитной вязкости. Тепловые флуктуации способствуют преодолению доменными стенками энергетических барьеров в магнитных полях, меньших критического поля. В высококоэрцитивных сплавах, состоящих из однодоменных областей, наблюдается особенно большая магнитная вязкость, так как в этом случае термические флуктуации сообщают дополнительную энергию для необратимого вращения спонтанной намагниченности тех частиц, потенциальная энергия которых во внешнем магнитном поле недостаточна для их перемагничивания.
Кроме этих основных механизмов магнитной вязкости существуют и другие. Например, в некоторых ферритах вклад магнитной вязкости дает перераспределение электронной плотности (диффузия электронов между ионами разной валентности). С магнитной вязкостью тесно связаны такие явления в ферромагнетиках, как потери на перемагничивание, временной спад относительной магнитной восприимчивости χ и ее частотная зависимость [14-16].
Заявляемое техническое решение, как уже было указано, основано на использовании динамического взаимодействия ферромагнитного вещества с магнитным полем, создаваемым сильным постоянным магнитом. Ферромагнитное вещество характеризуется достаточно сложной зависимостью его магнитной восприимчивости χ от величины действующего на него магнитного поля напряженностью Н согласно известной кривой Столетова. В отсутствие магнитного поля ферромагнитное вещество имеет начальную магнитную восприимчивость χНАЧ, а по мере увеличения напряженности магнитного поля сначала магнитная восприимчивость возрастает, доходит до своей максимальной величины χMAX при напряженности магнитного поля Н*, после чего вновь уменьшается, и в области насыщения магнитной индукции (при парапроцессе) ее произведение с величиной напряженности магнитного поля остается практически неизменным, определяя намагниченность насыщения JHAC(∞)=µOχ(Н)HHAC≈const(Н) в диапазоне насыщающих магнитных полей HO≤HHAC≤HMAX, реализуемых во второй (рабочей) части магнитного зазора, при этом µO=1,256*10-6 Гн/м - константа, называемая абсолютной магнитной проницаемостью вакуума. Указанное значение намагниченности насыщения устанавливается экспоненциально во времени, поэтому значение JHAC(∞) имеет место в установившемся режиме, теоретически при t→∞, а практически за некоторое число m постоянных релаксаций τ с учетом соотношения (1), когда ΔJ(mτ)→0.
Работа устройства, представленного на рис.1, заключается в предварительном повышении магнитной восприимчивости ферромагнитного кольца 1 до максимальной ее величины χMAX, для чего используется первая часть магнитного зазора с напряженностью однородного магнитного поля в ней, равной Н*, как видно из рис.3, после чего осуществляется процесс магнитного втягивания ферровещества во вторую (рабочую) часть магнитного зазора сильного постоянного магнита 6, намагничивание до насыщения ферромагнетика, а по его выходе из магнитного зазора - его размагничивание с понижением магнитной восприимчивости до начальной величины χНАЧ с охлаждением, после чего ферромагнитное вещество (вне действия магнитного поля) вновь нагревается тепловой энергией из внешней среды в механизме теплопроводности, и цикл действия повторяется вновь и вновь, обусловливая непрерывное вращение ферромагнитного кольца.
Известная кривая Столетова с достаточной степенью точности аналитически может быть задана непрерывной функцией вида χ(Н):
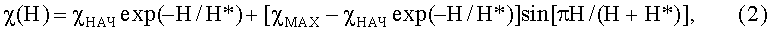
так что при Н=0 имеем χ(0)= χНАЧ, при Н=Н* имеем χ(Н*)=χМАХ, а при Н→∞ имеем χ(∞)→0, что соответствует концепции Столетова.
В первой части магнитного зазора длиной L при протяжке ферромагнитного вещества вдоль оси x со скоростью V=ω*R за время Δt=L/ω*R магнитная восприимчивость ферромагнетика будет экспоненциально возрастать до максимально возможной при данной скорости протяжки величины χMAX*. Как будет показано ниже, угловая скорость вращения ферромагнитного кольца ω*, соответствующая максимуму вращательного момента в кольце, определяется равенством ω*=L//ΔtR=L/λτR. Поэтому величина χMAX(Н*) зависит от значения угловой скорости вращения ферромагнитного кольца и при ω=0, то есть при неподвижном ферромагнитном кольце, χMAX(Н*)|ω=0=χMAX>χMAX*, хотя превышение χMAX относительно величины χMAX* незначительно - всего около 6,6%.
Величина намагниченности ферромагнетика к концу первой половины магнитного зазора JНАЧ* достигает величины:

Во второй части магнитного зазора сильного постоянного магнита 6 имеется неоднородное линейно возрастающее вдоль координаты x магнитное поле, которое имеет аналитический вид:
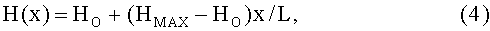
где 0≤x≤L, L - длина второй части магнитного зазора, то намагниченность J(x) ферромагнитного вещества, находящегося во второй части магнитного зазора, вычисляется на основе рекуррентных соотношений. Для этого разобьем промежуток L на n малых и одинаковых отрезков, безразмерную величину отношения x/L=ε обозначим в дискретном представлении целочисленным индексом i, а отношение (HMAX-HO)/HO обозначим, как и раньше, через параметр градиента магнитного поля p, тогда выражение (4) запишется в индексной форме как:
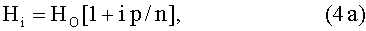
и при i=n имеем Hn=HMAX.
Поскольку состояние ферромагнетика к началу его взаимодействия с магнитным полем второй части магнитного зазора уже сформировалось, и магнитная восприимчивость доведена до наибольшего значения χMAX* в магнитном поле Н*, а магнитное поле в начале этой части магнитного зазора скачком увеличивается до величины HO>>Н*, то при анализе намагниченности ферромагнетика внутри магнитного зазора рабочего постоянного магнита следует учитывать в выражении (2) только его ниспадающую часть кривой Столетова в индексном представлении:
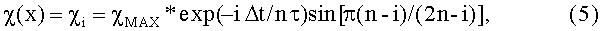
и при i=n имеем χn=χMIN*>χMIN, и указанное превышение χMIN* над χMIN незначительно (порядка 6,6%).
При анализе динамики намагничивания ферромагнетика, определяемого общим выражением J=µOχН, следует иметь в виду, что временное изменение этой величины зависит только от временного изменения магнитной восприимчивости, которая обладает свойством магнитной вязкости, то есть не может изменяться скачком, как в данном устройстве практически скачком изменяется напряженность магнитного поля на границе первой и второй части магнитного зазора - от Н* до HO. Это объясняет наличие выброса намагниченности с коротким фронтом порядка Δt*=-τln[1-(Н*/HO)], стремящегося к величине JMAX=µOχMAX*HO, но не доходящего до нее из-за одновременного действия насыщающего магнитного поля, уменьшающего значение магнитной восприимчивости во времени, после чего намагниченность экспоненциально уменьшается для установившегося режима до величины намагниченности насыщения, равной JHAC(∞), а в данном случае до величины JHAC(∞)+ΔJ*, которая превышает намагниченность насыщения для установившегося режима на величину ΔJ*. Поскольку намагниченность дифференциального объема ферромагнитного кольца dv=Sdx (S - поперечное сечение ферромагнитного кольца внутри магнитного зазора), находящегося на какой-либо координате x в интервале 0≤х≤L в произвольный момент времени, определяется как J(х)=µOχ[Н(х)]Н(х), где Н(х) задана выражением (4), то, учитывая (1), отмечаем, что для ее нахождения необходимо найти ее предыдущее значение на координате (х-dx) или, что то же самое при достаточно большом числе разбиений отрезка L на n равных частей, для нахождения намагниченности в i-ом интервале, надо сначала ее найти на (i-1) интервале, тогда имеем:
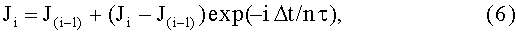
Но чтобы найти значение J(i-1), необходимо сначала найти значение J(i-2) и т.д. до J1, величина которого определяется просто:

Отметим, что в скобках выражений (6) и (7), а также последующих аналогичных выражений для разностей (Ji-J(i-1)) используются установившиеся значения этих величин, а не мгновенные значения в текущем времени.
Тогда приходим к системе рекуррентных уравнений вида:
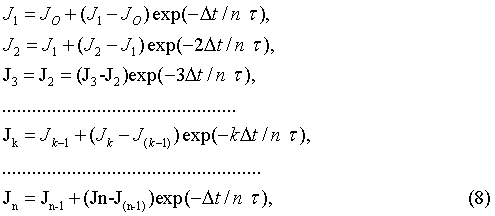
На основании (8) общее выражение для намагниченности в k-ом интервале промежутка О≤x≤L (или, что то же, 0≤ε≤1 - для безразмерного обозначения переменной) можно записать в виде:
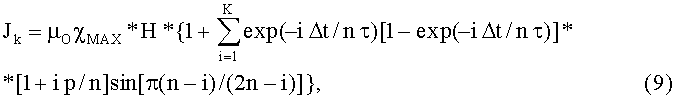
В выражении (9) известный сомножитель µO χMAX*Н* - величина постоянная, поэтому представляет интерес безразмерная функция, стоящая в фигурных скобках, и равная:
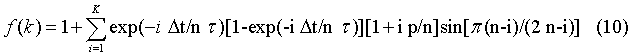
Для вычисления распределения этой функции в интервале i=1, 2, 3,… n с использованием компьютерной программы Mathcad необходимо представить эту функцию в интегральном виде, то есть с использованием непрерывных функций параметра ε=х/L. Тогда получим:
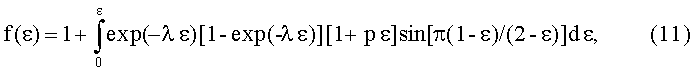
где λ=Δt/τ, и p=(HMAX-HO)/HO, а переменная лежит в пределах 0≤ε≤1.
Как показывает анализ функции f(ε) на экстремум приравниванием нулю ее производной по параметру λ, то есть ∂f(ε)/∂λ=0, функция максимальна при λ=1,23 независимо от текущего значения переменной ε, откуда находим оптимальное значение угловой скорости ω* вращения ферромагнитного кольца, при которой достигается максимум вращательного момента:
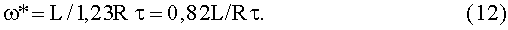
Обратимся к вопросу, как расставлены друг от друга центры магнитного притяжения XH и намагниченности XJ вдоль криволинейной оси x в направлении протяжки ферромагнитного вещества в магнитном зазоре. Для определения центра магнитного притяжения внутри второй части магнитного зазора по программе Mathcad с помощью оператора root запишем уравнение, из решения которого находится значение относительного центра магнитного притяжения α:
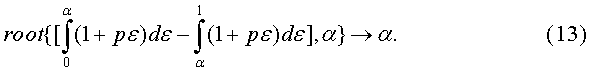
Можно построить график относительного положения центра магнитного притяжения а как функции параметра p, а также таблицу некоторых значений α(p). Видно, что положение центра магнитного притяжения XH=(0,5…0,707) L. Так, для наиболее подходящих значениях р=5…10 имеем XH=(0,66…0,68) L, то есть существенно дальше от середины второй части магнитного зазора при x=L/2.
Для нахождения центра намагниченности ферромагнетика XJ, находящегося внутри второй части магнитного зазора длиной L, воспользуемся модифицированным выражением (11) для относительного распределения намагниченностей ферромагнетика f (ε) при некоторых конкретно заданных условиях: р=10, τ=5.10-4 с, λ=1,23 и введенного значения σ=JHAC(∞)/JНАЧ*=2…4 и конкретно σ=2.
Модифицированное уравнение может быть записано в форме:
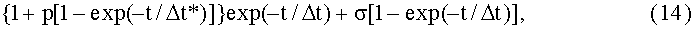
где Δt*=-τln[1-(H*/HO)]=-5.10-4ln0,9=5,27∗10-5c, Δt=1,23*5.10-4=6,15.10-4c. Отношение Δt/Δt*=11,67. При этом уравнение (14) при заданных величинах принимает вид:
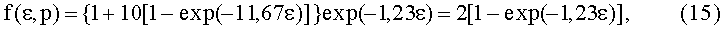
которое при ε=0 равно единице, а при ε=1 принимает значение σ=2, что и соответствует условиям задачи.
Можно также построить график для рассматриваемого примера. При этом максимум относительной функции намагниченности ферромагнетика прижат к началу второй части магнитного зазора, поэтому центр намагниченности XJ явно смещен к началу этой части зазора относительно ее центра x=L/2. Точное значение этого центра рассчитывается по формуле:
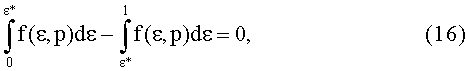
решением для которой методом последовательных приближений находим значение ε*, определяющее положение центра намагниченности XJ=ε*L. Решение (16) с учетом (15) при угловой скорости ω* вращения ферромагнитного диска имеет вид ε*=0,445, так что центр намагниченности находится на координате XJ=0,445L.
Сравнивая средние значения положений центров магнитного притяжения и намагничивания, видим, что они разделены интервалом ΔХ=XH-XJ=(0,67-0,45) L=0,22 L, следовательно, должна возникать сила втягивания F(ω*) ферромагнетика в магнитный зазор, и ферромагнитный диск получает вращательный момент МВР*=F(ω*)R под действием этой силы.
Известно, что дифференциал силы dF(ω), действующей со стороны неоднородного магнитного поля с градиентом напряженности вдоль оси x, равным grad HX, на дифференциальный ферромагнитный объем dv, с магнитным моментом J(x) dv равна:
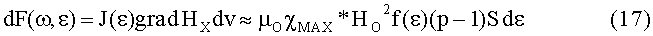
так как dv=Sdx, x/L=ε, dx=Ldε и grad HX=HO(р-1)/L.
Отметим, что знак приблизительного равенства взят в связи с тем, что выброс намагниченности в начале второй части магнитного зазора на самом деле не достигает величины µOχMAX*HO, как было указано ранее. Так, максимум функции f(ε) составляет 0,86 от ожидаемой величины, что следует учитывать в точных оценках энергетики устройства. Для рассмотренного примера реализации устройства точное выражение для (17) соответствует dF((ω,ε)=0,86 µOχMAX*HO 2f(ε)∗(p-1)Sdε.
В выражении (17) множитель µOχMAX*HO 2(р-1)S=const(ε), а переменная часть этого выражения df(ε)=f(ε)dε, где дифференциал относительной силовой функции определяется из (11). Распределение сил для дифференциальных объемов dv, находящихся на координатах x или безразмерных координатах ε (что то же), находится из уравнения:
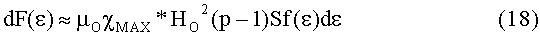
и эти дифференциалы сил для соответствующих дифференциальных объемов ферромагнитного кольца внутри второй части магнитного зазора измеряются в ньютонах [Н].
Максимальное значение силы втягивания ферромагнетика второй частью магнитного зазора F(ω*) определяется разностью интегралов:
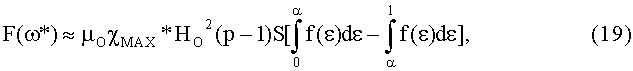
где α=XH/L - относительное положение центра магнитного притяжения второй части магнитного зазора.
Подставляя в подынтегральные выражения (19) значение функции из (11), получим явное выражение для максимальной силы втягивания F(ω*), распределение для которой в функции угловой скорости ω показано на графиках рис.6 при двух разных значениях HO.
Можно записать следующие выражения для (10) при следующих параметрах:
α=0,67, λ=1,23, p=2
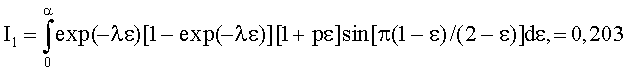
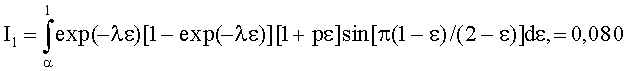
и тогда, подставляя эти выражения в (19), получим максимум втягивающей силы F(ω*) при оптимальной скорости вращения ферромагнитного кольца ω*, равный
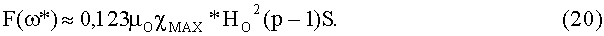
Для рассмотренного примера (20) имеет место решение F(ω*)=0,106 µOχMAX*HO 2(р-1)S. Можно показать, что на других угловых скоростях ω>ω* и ω<ω* значения сил F(ω)<F(ω*).
Рассмотрим пример. Пусть χMAX*=1000, HO=104 А/м, р=9 и S=6*10-5 м2 (при толщине ферромагнитного кольца 3 мм и его ширине 2 см), тогда F(ω*)=0,106*1,256.10-6 *103 *108 *9*6.10-5=7,19 Н. Если средний радиус ферромагнитного кольца R=0,1 м, то вращательный момент МВР=F(ω*) R=0,719 Н*м. Если L=0,02 м и τ=5.10-4, то оптимальная угловая скорость вращения ферромагнитного кольца равна ω*=L/1,23R τ=400 рад/с=63,7 об/с. Максимальная мощность на валу PMAX=МВР ω*=287,6 Вт. Тепловую мощность устройство должно потреблять из окружающей среды, например из воды соответствующего водного бассейна. Вариацией параметров L и R можно получить иные угловые скорости вращения ферромагнитного кольца, чтобы обеспечить скорость вращения вала трехфазного генератора переменного тока 15 (рис.1) равной, например, 50 об/с (стандартная частота электрической сети).
Из теории автоматического управления известно, что присоединенная нагрузка и трение снижают скорость оси вращения 3, и устойчивое состояние режима ее вращения достигается в точке пересечения кривой силовой характеристики F(ω) с нагрузочной прямой обратной связи, когда производные этих характеристик имеют противоположные знаки. Момент нагрузки определяется тангенсом угла наклона прямой обратной связи, и производная нагрузочной прямой положительна, следовательно, устойчивое состояние в системе автоматического управления достигается на нисходящей ветви силовой характеристики F(ω), как это видно на рис.6. Поэтому вращательный момент на оси 3 оказывается всегда меньше максимального МВР=F(ω*))R, и скорость установившегося процесса вращения будет всегда выше величины ω*. Для рассмотренного примера при максимальной нагрузке MH MAX мощность на оси вращения может достигать величины порядка 200 Вт при соответствующем подборе размеров L и R при скорости вращения оси порядка 50 об/с при учете параметра τ. При этом такая мощность теплового потока должна поступать к ферромагнитному кольцу из внешней среды. Это означает, что при перепаде температуры воды в процессе нагревания ферромагнетика в 1°C потребный поток воды составит приблизительно 50 г/с или 180 л/ч.
Для увеличения интенсивности теплопередачи целесообразно ферромагнитное кольцо погружать в нагревающую его жидкость, например очищенную воду или иную жидкость с циркуляцией ее по замкнутому циклу с радиатором нагревания и насосом для обеспечения циркуляции (радиатор при этом может быть погружен в проточную воду). Для снижения потерь на трение в качестве циркулирующей жидкости можно выбрать нитробензол, имеющий небольшую по сравнению с водой вязкость.
Другим решением теплопередачи к ферромагнитному кольцу из водной среды без погружения ферромагнитного кольца в очищенную воду или нитробензол является предложение автора, известное из его патента [11]. В этом случае траверсами 5 служат тонкие диски из медной фольги с центральными отверстиями, на краях которых напылены тонкие слои ферромагнетика. Совокупность склеенных между собой таких медных дисков образует прекрасный теплопроводник. При этом полая ось вращения 3 выполняется из медной трубки с пайкой к ней стопы медных дисков, а внутри трубки образуется водный поток (необязательно очищенный) непосредственно из водного бассейна (озера, реки, моря). Для образования протока воды в этой трубке - оси вращения 3, внутри нее могут располагаться винтообразные лопасти при вращении которых создается требуемый поток, и ферромагнитное кольцо быстро нагревается теплотой внешней (водной) среды.
Мощность Р(ω) на оси вращения растет с увеличением угловой скорости вращения оси 3, асимптотически приближаясь к соответствующим пороговым уровням. Это означает, что снижение угловой скорости вращения ферромагнитного кольца 1 понижает мощность, поэтому это снижение можно компенсировать увеличением числа ферромагнитных колец и связанных с ними сильных постоянных магнитов в единой конструкции и с единой осью вращения. Сильный постоянный магнит, используемый в рассматриваемой системе, выполняется из магнитожестких ферритов, например SmCo3, NdFeB или AlNiCo, имеющих высокую индукцию остаточной намагниченности - до 1,6 Тл ≈ 1,3*106 А/м (для NdFeB) [14-18].
Следует специально остановиться на рассмотрении магнитокалорического эффекта, благодаря которому осуществляется работа устройства.
Пусть в исходном состоянии ненамагниченный ферромагнетик имеет температуру TO и удельную теплоемкость cO. Для рассматриваемой массы ферромагнетика m внутри рабочего магнитного зазора с насыщающим магнитным полем имеем его внутреннюю тепловую энергию QO=cOmTO. Если плотность ферромагнетика ρ, то объем указанной массы m равен v=m/ρ. Если указанный объем поместить в магнитный зазор постоянного магнита, создающего магнитное поле с напряженностью Н, то энергия магнитного поля, запасенная в этом объеме, как известно, равна W=µOµvH2/2, где µ=χ+1 - относительная магнитная проницаемость ферромагнетика. При этом возникает его намагничивание, и закон сохранения энергии выражается соотношением:
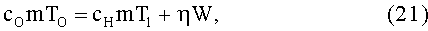
где cH - удельная теплоемкость намагниченного ферромагнетика (cH<cO), T1 - температура его объема v в процессе квазиадиабатического намагничивания, причем T1>TO (при намагничивании, как известно, ферромагнетик нагревается), η - так называемый коэффициент магнитокалорической активности (термин введен автором), зависящий от свойств ферромагнетика и учитывающий потери тепловой энергии, расходуемой на организацию вращательного движения ферромагнитного кольца. Можно показать, что η=1-[LF(ω)/W]. После выхода объема v ферромагнетика из указанного магнитного зазора в процессе его квазиадиабатического размагничивания происходит охлаждение этого объема, и закон сохранения энергии записывается как для адиабатического размагничивания

где Т2 - температура рассматриваемого объема ферромагнетика при его адиабатическом размагничивании (строго говоря, имеет место квазиадиабатическое размагничивание).
Покажем, что Т2<TO, то есть внутренняя тепловая энергия данного объема ферромагнетика, который сначала намагничивается в магнитном зазоре, а затем покидает его, размагничиваясь в адиабатическом процессе (за счет вращения ферромагнитного кольца), уменьшается на величину

Согласно (21) можно для значения cH записать выражение
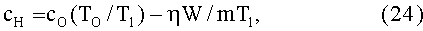
Подставляя (24) в (22), получим
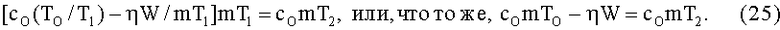
Из (25) следует, что


Поскольку ηW/cOm=µOηµvH2/2cO m=µOηµН2/2ρcO>0, то действительно имеем неравенство TO-Т2>0, то есть TO>Т2, и конечная температура Т2 рассматриваемого объема ферромагнетика оказывается ниже его исходной температуры TO (до входа в магнитный зазор с магнитным полем Н). С учетом значения коэффициента η, указанного выше, численное значение разностной температуры TO-Т2=LF(ω)/cOm=F(ω)/ρcOS, где S - поперечное сечение ферромагнитного кольца, охваченное насыщающим магнитным полем.
Изменение внутренней тепловой энергии рассматриваемого объема ферромагнетика в процессах его квазиадиабатического намагничивания и размагничивания определено в (23). Это изменение как раз и соответствует производимой при вращении ферромагнитного кольца механической работе. Тогда мощность на оси вращения 4 может быть записана как Р(ω)=ωMBP=ωF(ω)R=dQ/dt, где dQ/dt - скорость теплового потока, поглощаемого ферромагнитным кольцом из внешней среды.
Важно отметить, что энергия нагревания ферромагнетика, находящегося в состоянии покоя, при наложении насыщающего магнитного поля в точности равна энергии охлаждения его в процессе размагничивания, и магнитокалорический эффект сохраняет свою симметрию. Однако с учетом динамики вращения ферромагнетика под действием сил магнитного взаимодействия величина энергии нагревания становится меньше за счет совершаемой работы сил втягивания ферромагнитного кольца во вторую часть магнитного зазора, чем энергия охлаждения ферромагнитного кольца при его размагничивании по мере выхода из магнитного зазора, что и приводит к охлаждению ферромагнитного кольца до его стационарной температуры TO>Т2, и при этом температура TO оказывается меньшей температуры внешней среды ТBH, что вызывает, в свою очередь, теплопередачу тепловой энергии от внешней среды к ферромагнитному кольцу со скоростью dQ/dt. Таким образом, в рассмотренной динамической задаче магнитокалорический эффект обнаруживает свою несимметрию. При этом безразмерный коэффициент η показывает, какая часть энергии магнитного поля, передаваемая в магнитном зазоре ферромагнитному веществу, расходуется на появление втягивающей силы во вращающемся ферромагнитном кольце, поддерживая его движение в процессе непосредственного преобразования тепловой энергии в механическую работу. В рассматриваемом процессе преобразования соблюдается универсальный физический закон сохранения и превращения энергии.
Рассмотрим процесс автоматического управления ферромагнитовязким двигателем по схеме рис.1. Цель такого управления состоит в поддержании постоянной угловой скорости оси вращения 3 при заданном разбросе присоединенной нагрузки (потребляемой от электрогенератора мощности). Для выполнения этой задачи автоматическое управление током подмагничивания в катушках сильных постоянных магнитов приводит к соответствующему изменению напряженности магнитного поля HO в магнитном зазоре, значение которого сомножителем входит в выражение (20). Эффективность такого управления связана с тем, что величина HO в этом выражении возводится в квадрат. На рис.6 приведены графики для силы втягивания F(ω) для наибольшей нагрузки электрогенератора (MH MAX) и наименьшей (MH MIN). Подмагничивающие токи выбраны так, что независимо от нагрузки на электрогенератор частота вращения оси 3 поддерживается почти постоянной с относительной погрешностью порядка ±1%. Из рис.6 усматривается, что изменением подмагничивающего тока в катушке подмагничивания 7 (рис.1) можно получить с достаточно высокой точностью постоянную скорость вращения ферромагнитного кольца 1. Частота вращения оси 3 регистрируется измерителем частоты вращения 12 (рис.1) и высвечивается на его цифровом табло для контроля.
Управление скоростью вращения ферромагнитного кольца осуществляется соответствующей вариацией тока подмагничивания в катушке 7 магнитной системы 6 от управляемого источника тока подмагничивания 10, питание к которому подается от аккумуляторной батареи 9, соединенной с обмоткой 2 через силовой диод 8. По сигналам с выхода фильтра нижних частот 11 (или интегратора), входы которого соединены с выходами измерителя частоты вращения 12 оси 3 и генератора опорного напряжения 13 осуществляется управление током подмагничивания в катушке 7 комбинированного магнита 6. В фазочувствительном выпрямителе происходит сравнение частот переменных напряжений с выходов элементов 12 и 13 и соответственно вырабатывается управляющий сигнал ошибки регулирования. Выходной сигнал этого устройства сравнения фильтруется либо фильтром нижних частот 14 (в схеме статического типа регулирования с остаточными ошибками), либо интегратором, вместо фильтра нижних частот (при этом схема регулирования является астатической с нулевой остаточной ошибкой, но с пониженным быстродействием).
Подзаряд аккумуляторной батареи 9 осуществляется постоянным током от обмотки 2, наложенной на ферромагнитном кольце 1, через силовой диод 8. Возникновение ЭДС индукции в обмотке 2 обусловлено ее перемещением относительно продольной составляющей насыщающего магнитного поля во второй части комбинированного магнита 6 аналогично указанному на рис.5. Это соответственно увеличивает присоединенную нагрузку на двигатель.
Основы работы ферромагнито вязкого двигателя рассмотрены в работах [19, 20].
Заявляемое техническое решение может быть успешно применено в промышленных изделиях и в бытовой технике в качестве поставщика электрической энергии с отбором тепловой энергии водных бассейнов, которая восполняется непрерывно солнечной радиацией. Такие источники энергии являются экологически чистыми и уменьшают опасные последствия глобального потепления нашей планеты при широком применении таких устройств.
Данное устройство может быть изготовлено на предприятиях радиопромышленности с привлечением организаций, связанных с технологией изготовления ферроматериалов и сильных постоянных магнитов.
Литература
1. Ландсберг Г.С., Оптика, 5 изд., М., 1976, гл. 31.
2. Ельяшевич М.А., Атомная и молекулярная спектроскопия, М., 1962.
3. Фриш С.Э., Оптические спектры атомов, М. - Л., 1963.
4. Меньших О.Ф., Магнитовязкий маятник. Патент РФ №2291546, опубл. №01 от 10.01.2007.
5. Меньших О.Ф., Ферромагнитовязкий ротатор. Патент РФ №2309527, опубл. №30 от 27.10.2007.
6. Меньших О.Ф., Магнитный двигатель, Патент РФ №2310265, опубл. №31 от 10.11.2007
7. Меньших О.Ф., Магнитовязкий ротатор. Патент РФ №2325754, опубл. №15 от 27.05.2008.
8. Меньших О.Ф., Способ получения энергии и устройство для его реализации. Патент РФ №2332778, опубл. №24 от 17.08.2008.
9. Меньших О.Ф., Ферромагнитовязкий двигатель. Патент РФ №2359398, опубл. №17 от 20.06.2009.
10. Меньших О.Ф., Устройство стабилизации частоты генератора. Патент РФ №2368073, опубл. №26 от 20.09.2009.
11. Меньших О.Ф., Ротор ферромагнитовязкого двигателя. Патент РФ №2412524, опубл. в №5 от 20.02.2011.
12. Меньших О.Ф., Способ получения энергии и устройство для его реализации. Патент РФ №2452074, опубл. в №15 от 27.05.2012.
13. Меньших О.Ф., Устройство автоматического управления электрогенератором. Патент РФ №2444802, опубл. в №7 от 10.03.2012 (прототип).
14. Kronmuller H., Nachwirkung in Ferromsgnetika, 1968.
15. Вонсовский С. В., Магнетизм, М., 1971.
16. Мишин Д.Д., Магнитные материалы, М., 1981.
17. Вольфарт Э., Магнитно-твердые материалы, пер. с англ., М.-Л., 1963.
18. Меньших О.Ф., Способ производства постоянных магнитов. Патент РФ №2483380, опубл. в №15 от 27.05.2013.
19. Меньших О.Ф., Способ исследования динамики намагничивания ферромагнетика, быстро вводимого в насыщающее сверхсильное магнитное поле, Патент РФ №2488839, опубл. в №21 от 27.07.2013.
20. Меньших О.Ф., Явление динамического сверхнамагничивания ферромагнетика, Заявка на открытие, РАЕН, приоритет от 27.08.2012.
Отчет о патентном поиске
RU 2488839 С2, 27.07.2013 RU 2483380 С2, 27.05.2013 RU 2452074 С2, 27.05.2012 RU 2444802 C2, 10.03.2012 RU 2412524 С2, 20.02.2011 RU 2391761 С2, 10.06.2010 RU 2368073 С2, 20.09.2009 RU 2359398 С2, 20.06.2009 RU 2332778 С2, 17.08.2008 RU 2325754 С2, 27.05.2008 RU 2310265 C2, 10.11.2007 RU 2309527 С2, 27.10.2007 RU 2291546 С2, 10.01.2007.


Изобретение относится к физике магнетизма и электронике, к системам, вырабатывающим переменный ток непосредственным преобразованием тепловой энергии внешней среды, например водных бассейнов. Технический результат состоит в стабилизации частоты вырабатываемого переменного тока, повышении надежности. Генератор переменного тока содержит механически связанное с осью вращения через траверсы ферромагнитное кольцо, часть совмещена с насыщающим магнитным полем сильного постоянного магнита, а другая - связана с тепловыделяющей средой, например очищенной водой, забираемой из соответствующего водного бассейна. Управляемый источник тока подмагничивания выходом соединен с катушкой подмагничивания. Магнитный зазор сильного постоянного магнита выполнен из двух частей, первая из которых образует однородное магнитное поле с напряженностью H*, обеспечивающей на длине L этой части доведение магнитной восприимчивости ферромагнетика до максимального значения, а вторая длиной L - образует насыщающее магнитное поле в начале этой части магнитного зазора и далее в направлении движения ферромагнитного кольца, линейно возрастающее по напряженности магнитное поле к концу магнитного зазора. На ферромагнитное кольцо намотана катушка из проводника, связанная с аккумуляторной батареей через установленные на его оси кольцевые скользящие контакты и силовой диод в цепи заряда аккумуляторной батареи, питающей управляемый источник тока подмагничивания. 6 ил.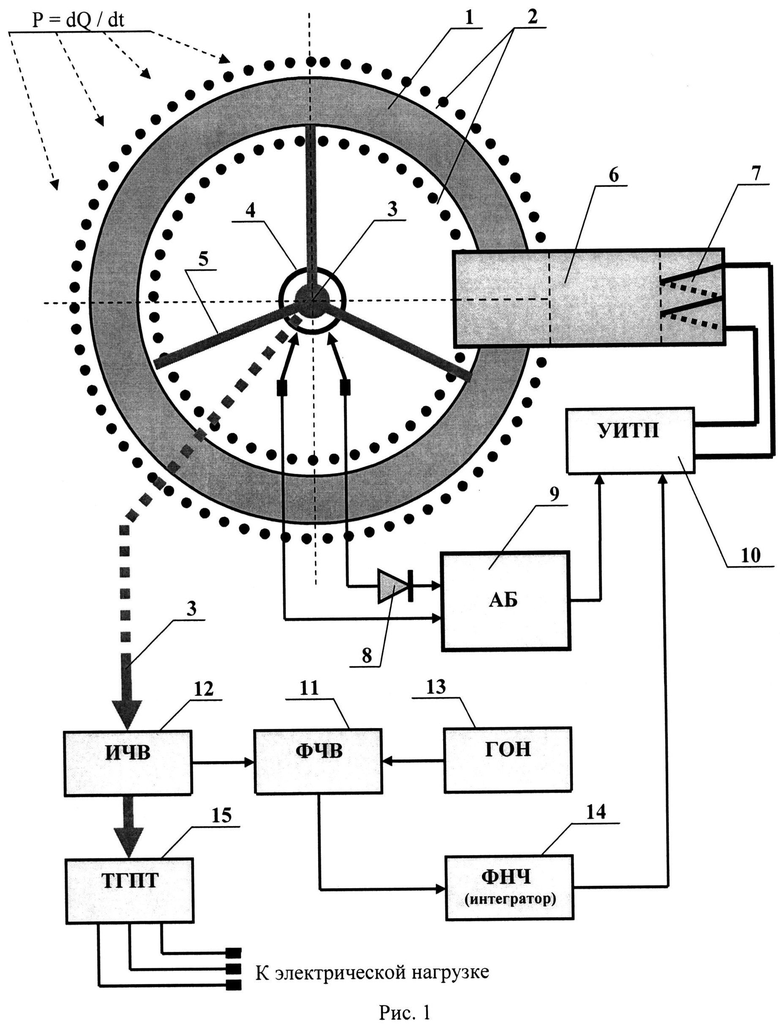
Стабилизированный генератор переменного тока, содержащий ферромагнитное кольцо, механически связанное с осью вращения через траверсы, часть ферромагнитного кольца совмещена с насыщающим магнитным полем сильного постоянного магнита, а другая его часть связана с тепловыделяющей средой, например, очищенной водой, забираемой из соответствующего водного бассейна, а также последовательно соединенные фильтр нижних частот (или интегратор) и управляемый источник тока подмагничивания, выходом соединенный с катушкой подмагничивания, при этом магнитный зазор сильного постоянного магнита выполнен из двух частей, первая из которых образует однородное магнитное поле с напряженностью Н*, обеспечивающей на длине L этой части магнитного зазора доведение магнитной восприимчивости ферромагнетика до максимального значения, а вторая часть магнитного зазора длиной L образует насыщающее магнитное поле в начале этой части магнитного зазора и далее в направлении движения ферромагнитного кольца линейно возрастающее по напряженности магнитное поле к концу магнитного зазора, причем угловая скорость ω* вращения ферромагнитного кольца, соответствующая максимуму возникающего в нем вращательного момента за счет возникающей силы втягивания ферромагнетика, определена условием ω*=LλRτ, где λ=1,23 и R - средний радиус ферромагнитного кольца, τ - постоянная времени релаксации магнитной вязкости ферромагнетика, из которого выполнено ферромагнитное кольцо, ось вращения ферромагнитного кольца механически связана с измерителем частоты вращения оси с цифровым табло и генератором переменного тока, например, трехфазным, подключенным к электрической нагрузке, а также содержащим устройство управления током подмагничивания указанной электромагнитной системы из подключенного к управляемому источнику тока подмагничивания через фильтр нижних частот (или интегратор) фазочувствительного выпрямителя, входы которого подключены соответственно к выходам измерителя частоты вращения и генератора опорного напряжения, отличающийся тем, что на ферромагнитное кольцо намотана катушка из проводника, связанная с аккумуляторной батареей через установленные на его оси кольцевые скользящие контакты и силовой диод в цепи заряда аккумуляторной батареи, питающей управляемый источник тока подмагничивания.
| УСТРОЙСТВО АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ ЭЛЕКТРОГЕНЕРАТОРОМ | 2010 |
|
RU2444802C1 |
| СПОСОБ ПОЛУЧЕНИЯ ЭНЕРГИИ И УСТРОЙСТВО ДЛЯ ЕГО РЕАЛИЗАЦИИ | 2006 |
|
RU2332778C1 |
| МАГНИТОВЯЗКИЙ РОТАТОР | 2006 |
|
RU2325754C1 |
| УСТРОЙСТВО СТАБИЛИЗАЦИИ ЧАСТОТЫ ГЕНЕРАТОРА | 2007 |
|
RU2368073C2 |
| МАГНИТОПАРАМЕТРИЧЕСКИЙ ГЕНЕРАТОР | 2008 |
|
RU2359397C1 |
| ФЕРРОМАГНИТОВЯЗКИЙ РОТАТОР | 2005 |
|
RU2309527C2 |
| US 2013106116 A, 02.05.2013 | |||
| US 2005062360 A1, 24.03.2005 | |||
| DE 4133559 A1, 24.06.1993 | |||
| JPS 5839286 A, 07.03.1983 | |||
Авторы
Даты
2015-02-27—Публикация
2013-09-13—Подача