Изобретение относится к области обработки сигналов различной природы и может быть использовано при изучении и диагностике поведения систем различной природы, включая живые системы, по временным рядам, содержащим некоторые различные характерные фазы поведения. Изобретение также может быть эффективно использовано в задачах автоматического выделения различных стадий на временных рядах электроэнцефалограмм, электрокардиограмм, соннограмм и других сигналов физиологической природы, а также при исследовании перемежающегося поведения, широко распространенного в динамических системах различной природы.
Выделение характерных фаз поведения систем важно в задачах различных областей, включая нейрофизиологию. В частности, весьма важной и актуальной технической задачей является создание способов автоматической разметки (выделения) различных стадий на электроэнцефалограммах (пик-волновые эпилептические разряды, неэпилептическая активность - сонные веретена, фоновая активность, дельта-волны и т.д.) для диагностики заболеваний центральной нервной системы.
Широко известны способы выделения характерных фаз поведения систем, основанные на анализе "текущего" периода колебаний или амплитуды колебаний системы [Берже П., Помо И., Видаль К. Порядок в хаосе. М.: Мир, 1991, Г. Шустер. Детерминированный хаос. М.: Мир, 1988 и др.]. Однако такие способы могут работать лишь тогда, когда одна из характерных фаз представляет собой сигнал, очень близкий к строго регулярному, что имеет место далеко не всегда.
Способ, основанный на анализе амплитуды системы, может быть применен только в том случае, когда одна фаза характеризуется существенно большей амплитудой колебаний по сравнению с другой характерной фазой. В этом случае задается определенное пороговое значение Δ и пока состояние системы характеризуется значением, по абсолютной величине превышающим этот порог, считается, что в системе реализуется одна из фаз, а когда значение, описывающее состояние системы оказывается ниже порогового, - другая.
Недостаток данного способа заключается в том, что в течение движения величина, характеризующая состояние системы, флуктуирует в широких пределах и многократно пересекает нулевое значение, т.е. оказывается как выше, так и ниже некоторого порогового значения. В свою очередь, это приводит к погрешности выделения характерных фаз и к появлению ошибочно диагностированных коротких фаз другого типа, так как каждая фаза оказывается искусственно разделенной на несколько частей. Таким образом возникает большая погрешность при анализе статистических свойств перемежающегося поведения.
Наиболее близким к заявляемому способу является способ исследования перемежающегося поведения с использованием непрерывного вейвлетного преобразования [Короновский А.А., Храмов А.Е., Об эффективном анализе перехода к хаосу через перемежаемость с помощью вейвлетного преобразования. Письма в ЖТФ 27(1), (2001), 3-11, Короновский А.А., Храмов А.Е., Непрерывный вейвлетный анализ и его приложения. М.: Физматлит, 2003].
Согласно данному способу над анализируемым сигналом проводится непрерывное вейвлетное преобразование и определяется число максимумов вейвлетной поверхности в каждый момент времени t. Принадлежность определенного интервала времени к ламинарной или турбулентной фазе определяется постоянством количества максимумов на вейвлетной поверхности. Фазы, в течение которых число максимумов на вейвлетной поверхности не изменяется, считаются фазами определенного типа.
Однако данный способ хорошо работает только в том случае, если поведение системы в фазе, в течение которой на вейвлетной поверхности не меняется количество максимумов, является регулярным и имеет одну и ту же структуру в любой момент времени фазы. Более того, он оказывается неприменим к широкому кругу систем, у которых амплитуда сигнала изменяется в широком диапазоне, а движения непериодичны (в этом случае число максимумов в течении фазы для любого момента времени различно) [Zhan М., Wei G.W., Lai C.H., Phys. Rev. E 65(3), (2002), 036202].
Также серьезным недостатком известных способов выделения характерных фаз поведения систем является слабая устойчивость метода к влиянию шумов, неизбежно появляющимся во временных реализациях анализируемой величины.
Задачей настоящего изобретения является разработка универсального способа, позволяющего эффективно проводить выделение характерных фаз по временным реализациям динамических систем различной природы, включая системы, подверженные флуктуациям. По сравнению с прототипом и аналогами данный способ может быть применим для анализа перемежающегося поведения различных типов в разных системах (как с непрерывным, так и дискретным временем), включая живые системы, повышена точность метода выделения характерных фаз.
Техническим результатом изобретения по сравнению с прототипом является возможность точного определения различных характерных фаз поведения хаотических систем.
Поставленная задача достигается тем, что в способе выделения характерных фаз поведения систем по временным данным, включающем снятие сигнала с системы с последующим непрерывным вейвлетным преобразованием, анализ полученных данных, в результате которого выделяют характерные фазы поведения системы, согласно решению для анализа полученных данных выбирают мгновенное и интегральное распределения энергии вейвлетного спектра по временным масштабам, определяют диапазоны характерных временных масштабов исследуемого сигнала в течении каждой из фаз, и по суммарному значению энергии вейвлетного спектра, приходящейся на выбранный диапазон характерных временных масштабов в различные моменты времени, выделяют различные фазы поведения системы.
Диапазон характерных временных масштабов выбирают на основании мгновенных распределений энергии вейвлетного спектра для различных фаз поведения системы таким образом, что в одной из фаз на выбранный характерный диапазон временных масштабов приходится большая часть энергии вейвлетного спектра.
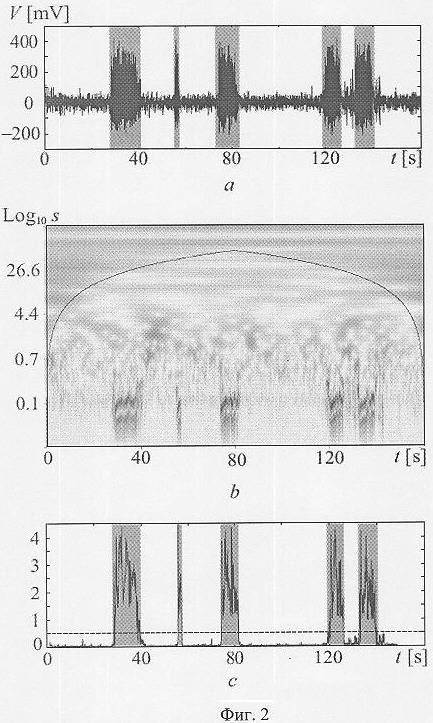
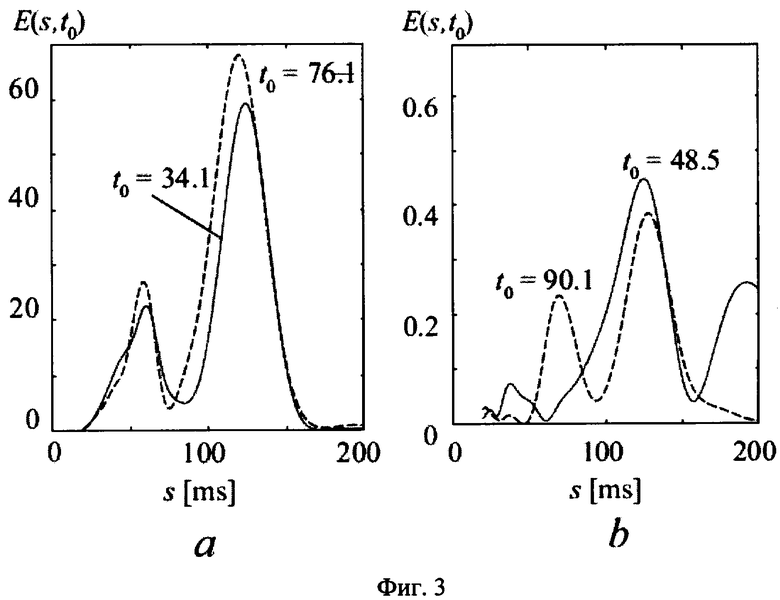
Изобретение поясняется чертежами, где на фиг.1 представлены временная реализация x(t) системы Лоренца при значении параметра r=166.14 (а); проекция вейвлетной поверхности |W(t,s)| на плоскость (t, s) для временной реализации x(t) (b), энергия вейвлетного спектра w(t), приходящаяся на диапазон характерных временных масштабов s∈(0.15,2.4), на фиг.2 - типичный фрагмент электроэнцефалограммы электрической активности мозга крыс, предрасположенных к абсанс эпилепсии, представляющий собой ламинарные фазы (нормальное поведение), перемежающиеся турбулентными всплесками (эпилептическая активность показана серыми прямоугольниками) (а), проекция вейвлетной поверхности |W(s,t)|, соответствующая электроэнцефалограмме (b), зависимость энергии w(t), приходящейся на диапазон характерных временных масштабов (s1,s2) (с), на фиг.3 - типичные распределения энергии вейвлетного спектра по временным масштабам E(s,t0) для ламинарных (а) и турбулентных (b) фаз в различные моменты времени t0 для анализируемой энцефаллограммы крыс.
На фиг.1 (b) и 2 (b) по оси абсцисс отложено время t, по оси ординат - временные масштабы s. Интенсивность градаций серого цвета пропорциональна абсолютной величине вейвлетной поверхности |W(s,t)|. Сплошная линия ограничивает область влияния краевых эффектов, достоверные данные располагаются ниже этой линии.
Заявляемый способ выделения характерных фаз поведения систем по временным данным осуществляется следующим образом.
Над исследуемым сигналом x(t) проводят непрерывное вейвлетное преобразование:
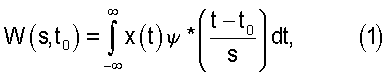
где ψ(t) - базисный вейвлет (звездочка обозначает комплексное сопряжение), s - временной масштаб, t0 - временной сдвиг вейвлетной функции вдоль оси времени. В качестве базисного вейвлета используется вейвлет Морле 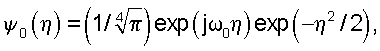 где
где 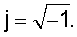 Параметр базисного вейвлета выбирается равным ω0=2π, что, с одной стороны, обеспечивает хорошее соотношение между локализациями вейвлетной функции во времени и Фурье-пространстве [Короновский А.А., Храмов А.Е., Непрерывный вейвлетный анализ и его приложения. М.: Физматлит, 2003], а с другой стороны, позволяет легко сопоставлять временные масштабы s вейвлетного преобразования (1) с частотами f спектрального представления сигнала, поскольку для данного значения параметра ω0 выполняется соотношение s≈1/f.
Параметр базисного вейвлета выбирается равным ω0=2π, что, с одной стороны, обеспечивает хорошее соотношение между локализациями вейвлетной функции во времени и Фурье-пространстве [Короновский А.А., Храмов А.Е., Непрерывный вейвлетный анализ и его приложения. М.: Физматлит, 2003], а с другой стороны, позволяет легко сопоставлять временные масштабы s вейвлетного преобразования (1) с частотами f спектрального представления сигнала, поскольку для данного значения параметра ω0 выполняется соотношение s≈1/f.
Вводят в рассмотрение мгновенное E(s)|W(s,t0)|2 и интегральное 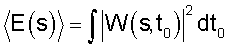 распределение энергии по временным масштабам.
распределение энергии по временным масштабам.
Поскольку поведение системы в течение различных фаз различается (для различных типов поведения и систем фазы поведения называются «ламинарными» и «турбулентными»), то и структура вейвлетной поверхности W(t,s) в области ламинарных и турбулентных фаз движения также будет существенно различна [Короновский А.А., Храмов А.Е., Письма в ЖТФ 27(1), (2001), 3-11; Короновский А.А., Храмов А.Е., Непрерывный вейвлетный анализ и его приложения. М.: Физматлит, 2003].
Затем выбирают характерный диапазон временных масштабов на основании мгновенных распределений энергии вейвлетного спектра для различных фаз перемежающегося поведения таким образом, что в одной из фаз на выбранный характерный диапазон временных масштабов приходится большая часть энергии вейвлетного спектра <E(s)>.
Энергия вейвлетного спектра E(s,t) будет распределена по характерным временным масштабам s, которые будут для разных фаз временной реализации x(t) разными, причем доля энергии, приходящейся на эти характерные временные масштабы, также будет различаться. Таким образом переходят от анализа структуры вейвлетной поверхности W(s,t) к анализу распределения энергии вейвлетного спектра по характерным временным масштабам.
Для выделения различных фаз поведения в каждый момент времени t определяют суммарное значение энергии вейвлетного спектра w(t), приходящейся на выбранный диапазон характерных временных масштабов s∈S(s1; s2):
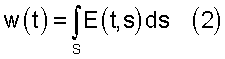
Диапазон характерных временных масштабов s, по которым будет определяться величина w(t), определяется рассматриваемой системой. В ряде случаев может сложиться ситуация, что необходимо рассматривать несколько диапазонов временных масштабов Si, которые однозначно позволяли бы охарактеризовать поведение системы. В этом случае интегрирование (2) проводится по объединению 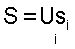 соответствующих диапазонов временных масштабов.
соответствующих диапазонов временных масштабов.
Если диапазоны характерных временных масштабов выбраны корректно, то при переходе из одной фазы в другую значение величины w(t) будет существенно меняться. В этом случае задают некоторое пороговое значение Δ. Тогда превышение величиной w(t) порога Δ будет свидетельствовать о наличии той или иной фазы поведения системы. На основе полученных данных можно получить различные статистические характеристики исследуемого сигнала от объекта, используемые при выявлении характера поведения объекта.
Примеры конкретной реализации способа
Заявляемый способ был применен для анализа перемежающегося поведения в эталонных нелинейных системах, таких как, например, система Лоренца:
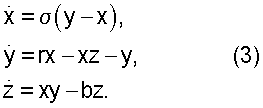
При значениях управляющих параметров σ=10, b=8/3 и при r<r* ≈166.07 временная реализация x(t) представляет собой устойчивое периодическое движение. При превышении порога r* регулярные колебания x(t) прерываются хаотическими всплесками, которые с ростом г становятся все более и более длительными, пока движение полностью не хаотизируется. Перемежаемость в данной системе классифицируется как перемежаемость I рода [Шустер Г., Детерминированный хаос. М.: Мир, 1988]. В теории перемежаемости регулярные колебания называются ламинарными фазами, хаотические всплески - турбулентными.
На фиг.1 показаны временная реализация x(t) системы Лоренца (3) при значении бифуркационного параметра r=166.14 (а), соответствующая ей проекция вейвлетной поверхности |W(t,s)| на плоскость (s,f) (b), и энергия вейвлетного спектра w(t), приходящаяся на диапазон характерных временных масштабов s∈(s1;s2) (s1=0.15, s2=2.4) (с). Наиболее темные участки проекции |W[t,s)| на плоскость (s, t) (фиг.1b) соответствуют максимумам вейвлетной поверхности, кривая на фигуре ограничивает область влияния краевых эффектов.
На проекции вейвлетной поверхности четко выделяются структуры, соответствующие ламинарной и турбулентной фазам перемежающегося поведения во временной реализации. Структура вейвлетной поверхности, соответствующая регулярной фазе движения, имеет профиль W(s)|t=const с двумя глобальными максимумами, соответствующими характерным временным масштабам sa≈0.4 и sb≈1.1. Этим максимумам вейвлетной поверхности соответствуют две темные области на проекции поверхности |W[t,s)|, расположенные параллельно оси времени. Профиль поверхности |W(t,s)| не изменяется с течением времени t в пределах ламинарной фазы. При входе системы в турбулентную фазу вид поверхности |W[t,s)| сильно изменяется. Можно сказать, что в режиме хаотической динамики наблюдается «всплеск» разномасштабных колебательных явлений. Из фиг.1b видно, что области вейвлетной поверхности, соответствующие турбулентным фазам, четко локализованы во времени [КороновскийА.А., Храмов А.Е., Письма в ЖТФ 27(1), (2001), 3-11]. Также видно, что в пределах ламинарной фазы функция w(t) имеет структуру, близкую к периодической, и совершает колебания малой амплитуды. В течение турбулентной фазы w(t) испытывает резкий провал (см. фиг.1), что позволяет точно диагностировать различные фазы движения. Моменты времени, в которые величина w(t) оказывается больше порогового значения Δ=250, считаются ламинарными фазами, а интервалы времени, для которых выполняется условие w(t)<Δ, - турбулентными.
С помощью данного способа исследована сложная реальная система, демонстрирующая перемежающееся поведение; В процессе исследования рассмотрены временные реализации записей электрической активности головного мозга крыс линии WAG/Rij. Все крысы этой линии имеют генетическую предрасположенность к абсанс эпилепсии. Судорожная активность представлена пик-волновыми разрядами, которые возникают спонтанно и не сопровождается конвульсиями [van Luijtelaar E.L., Coenen A.M., Neurosci Lett. 70(3), (1986), 393-397].
В эксперименте запись электрической активности мозга проведена с поверхности коры больших полушарий (электрокортикограмма, ЭКоГ) у интактных свободноподвижных крыс посредством хронически вживленных электродов. Частотный диапазон ЭКоГ составил 1-500 Hz, амплитуда сигнала варьировала от 25 до 800 μV. Длительность ЭКоГ записей составляла от 6 часов до 4-х суток. Использованы были как самцы (n=5), так и самки (n=6) вышеупомянутой линии крыс. Типичная ЭКоГ, регистрируемая в ходе наблюдений, представляла собой чередование низкоамплитудных (от 25 до 100 μV) полиритмических участков ЭКоГ, соответствующих "нормальному" функционированию головного мозга, и участков высокоамплитудной (от 100 до 800 μV) генерализованной активности с относительно стабильной несущей частотой от 8 до 12 Hz, соответствующих эпилептическим припадкам.
На фиг.2а приведен фрагмент типичной ЭКоГ, состоящей из фоновой активности, перемежающейся всплесками, соответствующими эпилептическим пик-волновым разрядам (серые прямоугольники на фиг.2а, с). Осуществив вейвлетное преобразование сигнала, была получена проекция вейвлетной поверхности |W(s,t)|, показанная на фиг.2b. Фрагменты вейвлетной поверхности, соответствующие различным фазам поведения, оказываются принципиально различными. На основании структуры вейвлетной поверхности W(s, i) был определен диапазон характерных временных масштабов s∈(s1, s2) (s1=70 ms, s2=110 ms). Интегральное распределение энергии вейвлетного спектра по временным масштабам показано на фиг.2с. По суммарному значению энергии вейвлетного спектра w(f), приходящейся на выбранный диапазон характерных временных масштабов в различные моменты времени, были выделены фазы поведения системы следующим образом.
В течение фазы, соответствующей «нормальному» функционированию мозга, величина w(t) превышает порог Δ=0.5, что позволяет легко выделять различные типы поведения во временной реализации. Мгновенные распределения энергии вейвлетного спектра 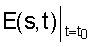 для разных участков ЭКоГ показаны на фиг.3.
для разных участков ЭКоГ показаны на фиг.3.
В результате проведенных исследований было установлено, что чередование судорожной и неэпилетической ("нормального" функционирования мозга) активностей активности может быть хорошо описано в рамках динамики on-off перемежаемости [N. Platt, E.A. Spiegel, C. Tresser. Phys. Rev. Lett. 70(3) 1993]. Такое заключение сделано на основании анализа распределений длительностей фаз "нормального" функционирования мозга, выделенных из ЭКоГ с помощью вышеописанной методики. Аналогичные результаты были получены при анализе судорожной активности данного типа на ЭКоГ всех экспериментальных животных (11 крыс).
| название | год | авторы | номер документа |
|---|---|---|---|
| СПОСОБ ВЫДЕЛЕНИЯ ВЕРЕТЕНОПОДОБНЫХ ПАТТЕРНОВ ПО ВРЕМЕННЫМ ДАННЫМ ЭЛЕКТРОЭНЦЕФАЛОГРАММ | 2014 |
|
RU2565993C1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ МОМЕНТОВ СИНХРОННОГО И АСИНХРОННОГО ПОВЕДЕНИЯ ДВУХ СВЯЗАННЫХ СИСТЕМ | 2010 |
|
RU2431857C1 |
| СПОСОБ АВТОМАТИЧЕСКОГО ВЫДЕЛЕНИЯ ФИЗИОЛОГИЧЕСКИХ СОСТОЯНИЙ МЕЛКИХ ЛАБОРАТОРНЫХ ЖИВОТНЫХ | 2020 |
|
RU2751744C1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ ОТНОСИТЕЛЬНОГО РАЗМЕРА СИНХРОННОГО КЛАСТЕРА В СЕТИ ПО ЕЕ МАКРОПАРАМЕТРАМ | 2017 |
|
RU2647677C1 |
| СПОСОБ ВЫДЕЛЕНИЯ СИГНАЛОВ ИМПУЛЬСНОГО ТИПА ПО ВРЕМЕННЫМ ДАННЫМ | 2014 |
|
RU2552183C1 |
| СПОСОБ ИССЛЕДОВАНИЯ ЭЛЕКТРОЭНЦЕФАЛОГРАММЫ ЧЕЛОВЕКА И ЖИВОТНЫХ | 2012 |
|
RU2543275C2 |
| СПОСОБ ДЕТЕКТИРОВАНИЯ СИГНАЛОВ ЯДЕРНОГО КВАДРУПОЛЬНОГО И ЯДЕРНОГО МАГНИТНОГО РЕЗОНАНСА | 2011 |
|
RU2490618C2 |
| Способ классификации сигналов ЭЭГ при воображении двигательной активности у нетренированного оператора | 2018 |
|
RU2682492C1 |
| СПОСОБ СКРЫТОЙ ПЕРЕДАЧИ ИНФОРМАЦИИ | 2012 |
|
RU2509423C2 |
| Способ выделения ритма сердечных сокращений из сигналов электрокардиограммы и/или фотоплетизмограммы на основе скелетонного анализа непрерывного вейвлетного преобразования | 2024 |
|
RU2841467C1 |
Изобретение относится к биологии и медицине и предназначено для выделения характерных фаз поведения систем по временным данным. Снимают сигнал с системы с последующим непрерывным вейвлетным преобразованием. Определяют мгновенное и интегральное распределения энергии вейвлетного спектра по временным масштабам. Выбирают диапазоны характерных временных масштабов исследуемого сигнала в течение каждой из фаз на основании мгновенных распределений энергии вейвлетного спектра для различных фаз поведения системы. Выбор производят таким образом, чтобы в одной из фаз на выбранный характерный диапазон временных масштабов приходится большая часть энергии вейвлетного спектра. По суммарному значению энергии вейвлетного спектра, приходящейся на выбранный диапазон характерных временных масштабов в различные моменты времени, выделяют различные фазы поведения системы. Предлагаемый способ позволяет уменьшить влияние шумов при выделении характерных фаз поведения систем по временным данным. 3 ил.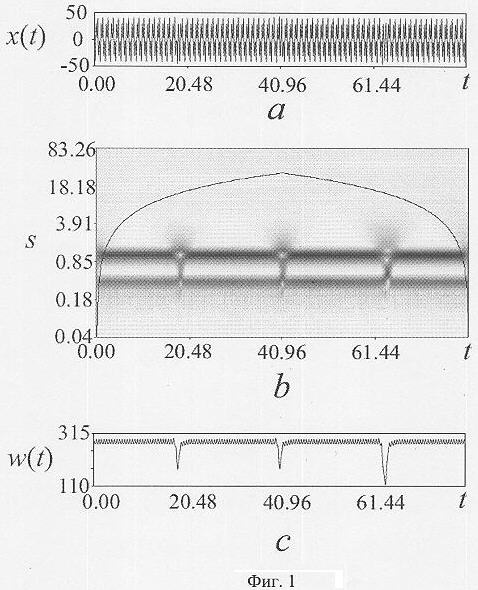
Способ выделения характерных фаз поведения систем по временным данным, при котором снимают сигнал с системы с последующим непрерывным вейвлетным преобразованием, определяют мгновенное и интегральное распределения энергии вейвлетного спектра по временным масштабам, выбирают диапазоны характерных временных масштабов исследуемого сигнала в течение каждой из фаз на основании мгновенных распределений энергии вейвлетного спектра для различных фаз поведения системы таким образом, чтобы в одной из фаз на выбранный характерный диапазон временных масштабов приходится большая часть энергии вейвлетного спектра и по суммарному значению энергии вейвлетного спектра, приходящейся на выбранный диапазон характерных временных масштабов в различные моменты времени, выделяют различные фазы поведения системы.
| КОРОНОВСКИЙ А.А | |||
| и др | |||
| Анализ хаотической синхронизации динамических систем с плохо определенной фазой | |||
| Радиотехника и электроника, 2005, т.50, №7 с.1-9 | |||
| Приспособление к горизонтально-фрезерному станку для фрезерования шестигранных изделий | 1939 |
|
SU61440A1 |
| Шлюз для улавливания золота или других россыпных полезных ископаемых | 1927 |
|
SU12293A1 |
| КОРОНОВСКИЙ А.А | |||
| и др | |||
| Исследование распределения турбулентных фаз при разрушении синхронизации с запаздыванием | |||
| Письма в ЖТФ, 2005, т.31, вып.21, | |||
Авторы
Даты
2008-11-10—Публикация
2007-04-19—Подача