МНОГОМАСШТАБНАЯ БЕСПРОВОДНАЯ СВЯЗЬ Российский патент 2008 года по МПК H04L27/00 

Область техники

Настоящее изобретение относится к беспроводной связи, в частности к беспроводной связи с помощью систем передачи волновых пакетов, в которых используется разделение как во временной, так и в частотной областях.

Уровень техники

Беспроводная связь предусматривает несколько видов модуляции сигнала до его передачи по мобильному каналу. Некоторые примеры типов обработки, входящих в модуляцию беспроводной связи, включают временную обработку (например, расширение спектра), спектральную обработку (например, мультиплексирование с ортогональным частотным разделением (OFDM)) и пространственную обработку (например, пространственно-временное кодирование). Такой вид обработки происходит в одном измерении (например, по времени, частоте или пространству) и иногда называется одномасштабной модуляцией. Как правило, используемый тип обработки выбирают на основе характеристик мобильного канала связи. Например, в мобильном канале, который не обеспечивает разноса (например, замирание в единственном тракте), иногда используют пространственную обработку. С другой стороны, мобильный канал, в котором имеет место многолучевое распространение (например, частотно-избирательное замирание), можно эффективнее обработать с использованием спектральной модуляции, например OFDM.

Многомасштабная модуляция включает обработку сигнала по двум измерением, а именно по времени и частоте. Поэтому выходной сигнал многомасштабного модулятора характеризуется как временным диапазоном, так и набором частот. Такой тип обработки сигнала способен согласоваться с двумя измерениями беспроводного канала, а не с одним.

Многомасштабную модуляцию можно визуализировать с использованием частотно-временной мозаичной диаграммы. Типовая мозаика, полученная в соответствии со ссылкой (1), приведенной ниже, изображена на фиг.1. Частотно-временная мозаика для формы сигнала, составленного из синусоиды с частотой f₀ и импульса t₀, в этом примере приводит к наличию энергии во всех поддиапазонах частотно-временной области, пересекающей как f₀, так и t₀. Частотно-временное представление сигнала может быть получено с использованием вейвлет-разложения.

Предыдущие работы были посвящены использованию вейвлет-разложения в цифровой связи. Например, Уорнел (Wornell) (8) развил концепцию фрактальной модуляции для многомасштабной связи. Кроме того, в работах, например (9) и (10), оптимальное вейвлет-разложение выбиралось для учета специфических состояний канала или недостатков передатчика. Характерной проблемой, в значительной степени присущей предыдущим работам в области многомасштабной связи, является то, что вопросу уравнивания многолучевых каналов в приемнике часто не уделялось внимания. Скорее всего это происходило из-за трудности адаптивного выравнивания канала в двух измерениях. Таким образом, было бы желательно иметь возможность согласования конкретного вейвлета с мгновенным состоянием канала при минимальном взаимодействии (то есть обратной связи) между приемником и передатчиком. Однако в известных работах не рассматривается преимущество компактной реализации больших семейств вейвлетов для согласования вейвлетов с состоянием беспроводного канала на основе выбора одной или нескольких скалярных величин. В этой работе, основанной на известных компактных вейвлет-разложениях, разработан способ параметризованной вейвлет-модуляции, в котором параметры выбирают с целью наилучшего согласования с состоянием беспроводного канала.

Вейвлет-разложения обычно определяют в непрерывной области, где из (2), (3) (см. ниже) вначале выводится так называемая масштабирующая функция φ(х)

где {c_k} - действительная последовательность. Последовательность {c_k} имеет четную длину и должна удовлетворить следующим условиям:

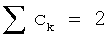
Другой важной характеристикой вейвлетов, которая определяет "гладкость", или непрерывность, последовательности, обозначенной {с_k}, является количество исчезающих моментов. Если вейвлет имеет М (М≥1) исчезающих моментов, то справедливо следующее:

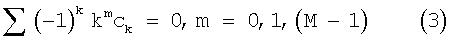
Соответствующий вейвлет теперь можно определить как

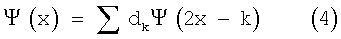
где

Таким образом, расширения и сдвиги вейвлет-функции образуют ортогональный базис:

Поскольку вейвлет имеет компактный базис, последовательность {c_k} имеет конечную длину; положим, что длина последовательности равна 2N. Тогда дискретное вейвлет-преобразование можно определить, если начать с двух последовательностей {с_k} и {d_k} одинаковой длины. Эти две последовательности можно также рассматривать как фильтры; все вместе они формируют совершенный банк фильтров восстановления.

Параметризованная конструкция для вейвлетов и масштабирующих фильтров для произвольных значений N (где М<N) исчезающих моментов была предложена в (3) и (4), см. ниже. Предположим, что для величины N коэффициенты фильтра обозначены как {с_k ^N}. При заданном наборе параметров вейвлетов длиной N {α_i} {-π≤αi<π, 0≤i<N) коэффициенты {с_k ^N} получаются рекурсией

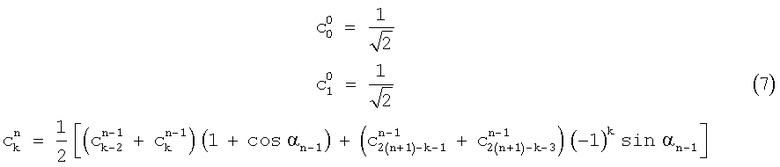
Структура вейвлетов в (7) является ограниченной в том смысле, что набор параметров в общем случае не может быть определен на континууме [-π, π]^N и все еще обеспечивать вейвлет по меньшей мере с одним исчезающим моментом. Однако Поллен (Pollen) показал, что вейвлеты могут быть определены на континууме [-π, π]^N для произвольного N (за счет гладкости). Для исследования этих типов структур для данного N определим матрицу банка фильтров F_N как

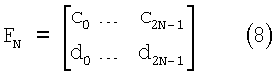
Тогда матрица банка фильтров для N=1 имеет вид

Матрицу в (9) иногда называют также матрицей вращения Гивенса (Givens). Аналогично, матрица банка фильтров для N=2 равна (см. (6)):

Выражения для банка фильтров при N=2 и N=3 иногда называют также фильтрами Поллена (Pollen), поскольку именно Поллен впервые предложил эти два представления [см. ссылку (7)]. Аналогично, матрица F₁ банка фильтров становится матрицей Хаара, когда α₀=π/4, a F2 сводится к банку фильтров Добеши с 4 отводами, когда α₀=π/6. Хотя избирательность фильтра улучшается с увеличением N, это происходит за счет необходимости определения большего набора параметров при задании вейвлетов. Это можно видеть в параметризованном выражении для {с_k ³}:

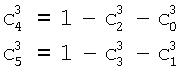
Теперь перед определением банка фильтров необходимо определить два параметра. Фактически, хотя избирательность фильтра улучшается с увеличением количества коэффициентов, сложность задания параметров, необходимых для формирования банка фильтров, также растет.

Вейвлет-разложение теперь можно определить в виде ряда банков фильтров и стадий передискретизации. Для заданной входной последовательности а_i(n) выходная последовательность может быть получена путем обработки, изображенной на фиг.2.

В современной технике процесс фильтрации выполняют в цифровой форме в вычислительной системе, например в компьютере общего назначения или в интегральной схеме, предназначенной для цифровой обработки сигналов.

Количество стадий передискретизации в вейвлет-разложении иногда называют количеством временных растяжений. Такая обработка может также быть представлена как преобразование входной последовательности унитарной матрицей. Предположим, что входная последовательность с временным индексом i, т.е. a_i(n), имеет (четную) длину К (то есть 0≤n<К), и мы хотим определить матрицу Т_K дискретного вейвлет-преобразования (DWT - Discrete wavelet transformation) размером К×К для конкретной матрицы F_N банка фильтров. Кроме того, предположим, что при преобразовании желательно провести Р временных растяжений. Тогда, используя вышеизложенную структуру, можно найти способ получения матрицы преобразования. Определяя индекс временной шкалы как I (0<I<P), можно определить матрицу К×К банка фильтров для каждой шкалы времени:

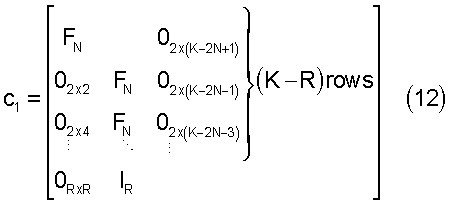
В (12) O_mxn - нулевая матрица с m строками и n столбцами, a I_R -единичная матрица с R строками и R столбцами. Для каждого растяжения можно также определить матрицу Р перестановки (1≤ν<P):

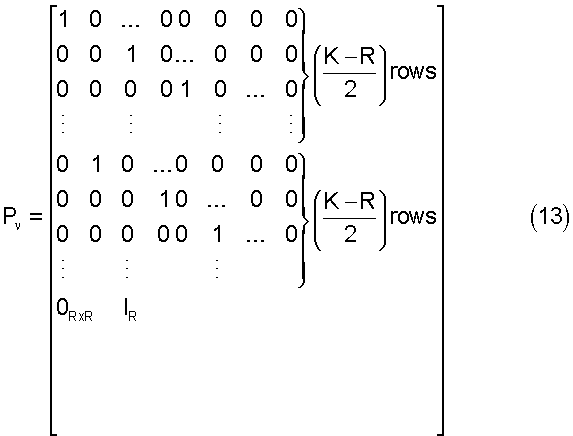
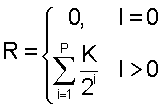
Таким образом, для Р растяжений унитарная матрица Т_K(Р) преобразования может быть определена как

Теперь эту матрицу можно использовать для модуляции входного вектора a_i=[a_i(0)...a_i(K-1)]^T (i - индекс символа). Иллюстративно элементы вектора входного сигнала а_i можно рассматривать как коэффициенты на наборе базисных функций, которые представляют данные, например речь.

Таким образом, выходная последовательность при такой модуляции может быть сформирована как результат матрично-векторного умножения x_i=Т_к ^T(Р) а_i. Как описано выше, единственная результирующая матрица Т_K(Р) представляет Р внутренних произведений вейвлетов и данных. Если мы предполагаем, что F_N является компактной вейвлет-реализацией, то мы можем также предположить, что Т_K(Р) является функцией набора {α_i} вейвлет-параметров, то есть x_i=Т_K(Р,{(α_i})а_i.

Сущность изобретения

Изобретение относится к системе связи с несколькими несущими, которая адаптивно выбирает набор вейвлетов, соответствующий условиям канала.

Особенностью настоящего изобретения является использование компактной параметризации, которая обеспечивает генерацию бесконечного числа вейвлетов и масштабирование фильтрующих пар с использованием конечного набора параметров, например количества растяжений и параметров фильтра.

Другой особенностью настоящего изобретения является устранение эквалайзера в приемнике путем изменения параметров вейвлетов с целью предварительной компенсации изменений характеристик канала.

Краткое описание чертежей

На фиг.1 показана частотно-временная зависимость в системе с волновыми пакетами.

На фиг.2 показана блок-схема вейвлетной системы передачи.

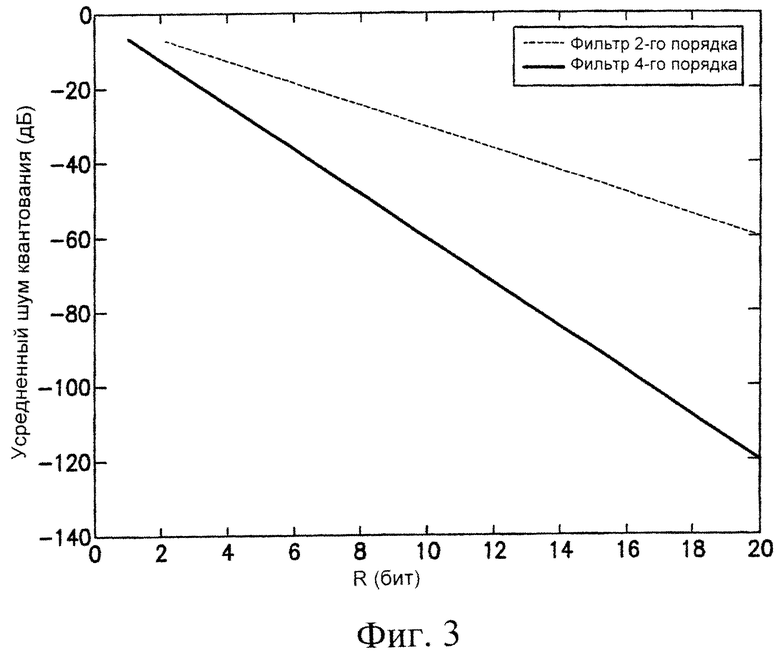
На фиг.3 показаны характеристики шумов квантования.

На фиг.4 иллюстрируется влияние обратной связи (ОС) в вейвлетной системе с двумя отводами.

На фиг.5 иллюстрируется влияние обратной связи в вейвлетной системе с четырьмя отводами.

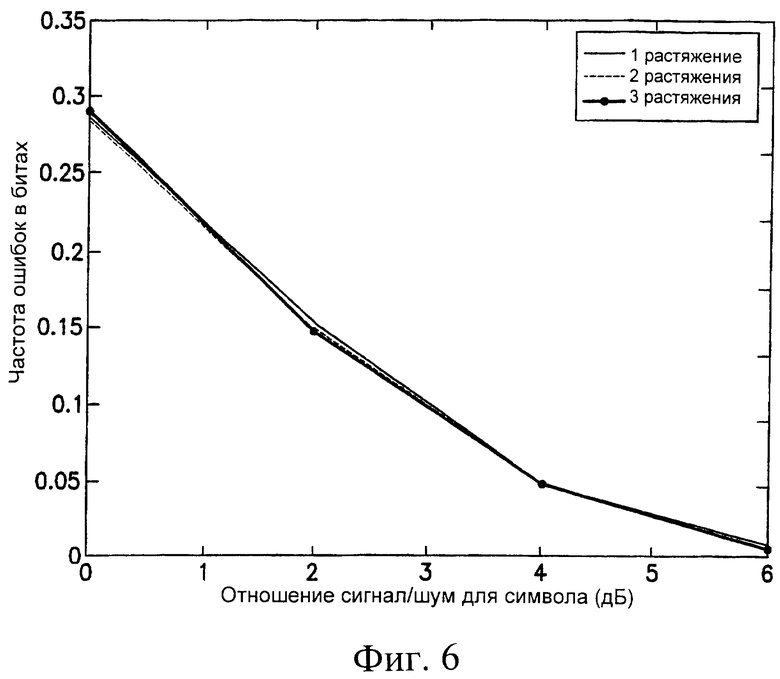
На фиг.6 иллюстрируется влияние растяжений в вейвлетной системе с двумя отводами.

На фиг.7 иллюстрируется влияние растяжений в вейвлетной системе с четырьмя отводами.

На фиг.8 иллюстрируется сравнение частоты появления ошибочных битов (BER) в вейвлетной системе и OFDM системе.

На фиг.9 иллюстрируется сравнение частоты появления ошибочных битов в фиксированной и адаптивной вейвлетных системах с двумя отводами.

На фиг.10 иллюстрируется сравнение частоты появления ошибочных битов в фиксированной и адаптивной вейвлетных системах с четырьмя отводами.

На фиг.11 иллюстрируется частота появления ошибочных битов в различных системах.

Подробное описание изобретения

Система передачи на основе вейвлетов может быть сформирована, если взять входной вектор a_i=[a_i(0).... a_i(K-1)]^T и сформировать выходной вектор x_i=T_K ^T=(P,{α_i})a_i аналогично тому, как этот имеет место в OFDM системе. Однако в отличие от OFDM систем, в которых могут использоваться простые выравнивающие структуры путем использования свойств циклической свертки базовой модуляции с дискретным преобразованием Фурье, система на основе вейвлетов может быть чувствительной к частотно-избирательным беспроводным каналам, и поэтому проблема выравнивания для вейвлетов может оказаться сложной.

Выходной вектор х передается последовательно. Если предполагается, что беспроводной канал может быть описан вектором канала с L отводами h_i=[h_i(0)...h_i(L-1)]^T (где предполагается, что h_i имеет единичную норму), то элементы у_i принятого сигнала могут быть представлены (в предположении, что L<K) как

В (15) n_i((k) представляет собой член, соответствующий аддитивному шуму. Типичные способы выравнивания для этого типа принятого сигнала основаны на поддержке принятия решения, требующего оценки предыдущего переданного символа а_i-1 для учета межсимвольной интерференции (ISI - Intersymbol interference) и оценки индивидуальных входных сигналов х_i для учета перекрестной помехи между несущими (ICI - Intercarrier interference). Это выражение можно также записать в матрично-векторной форме:

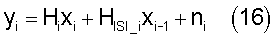
Входящие в уравнение (16) H_i, H_|S|__i и n_i описаны ниже:

n_i=[n_i(0) n_i(1)...n_i(К-1)]^T

Вместо этого для выравнивания канала предложено использовать компактную вейвлет-параметризацию. Другими словами, если имеется оценка набора параметров для данной матрицы F_N банка фильтров, которая повышает качество принятого сигнала, то эта информация может использоваться для модификации матрицы Т_K модуляции. Если предполагается, что имеется достаточно обучающих данных, чтобы сформировать оценку канала в приемнике то наилучший набор вейвлет-параметризации можно найти с использованием дополнительных обучающих данных и матрицы оценки канала размером К×К:

Очевидно, что применение унитарного преобразования не снижает мощности аддитивного гауссового шума; однако унитарное преобразование, например дискретное вейвлет-преобразование, можно применить для минимизации двух источников помех, наблюдаемых в частотных избирательных каналах многоканальной связи, а именно межсимвольной интерференции и перекрестной помехи между несущими. При использовании этой матрицы оценки канала оптимальный набор вейвлет-параметризации, который минимизирует перекрестные помехи для заданного Р, можно найти как

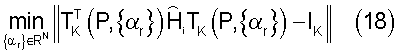
Для минимизации межсимвольной интерференции (ISI) можно ввести дополнительные критерии. Они могут включать выбор вейвлет-преобразования, которое будет делать вклады ISI от любого заданного вейвлет-символа в последующий вейвлет-символ пренебрежимо малыми. На основе ISI вкладов, очевидных из выражения (15), определяем матрицу канала размером К×К:

Таким образом, можно рассмотреть другой критерий оптимизации, который минимизирует межсимвольную интерференцию:

В дополнение к выбору вейвлета, который минимизирует перекрестную помеху между несущими и межсимвольную интерференцию, сам вейвлет нельзя рассматривать как имеющий приблизительно выровненный канал, пока энергия по результирующей диагонали не будет максимальной. Это непосредственно следует из максимизации энергии принятого сигнала. Критерий, по которому максимизируется энергия по диагонали (в предположении, что Λ - диагональный оператор), имеет следующий вид:

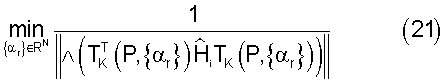
Нельзя предполагать, что единственный набор параметров минимизирует перекрестную помеху между несущими и межсимвольную интерференцию при максимизации энергии, извлеченной из канала. Таким образом, выбор вейвлет-параметра должен основываться на критерии, который минимизирует всю остаточную помеху:

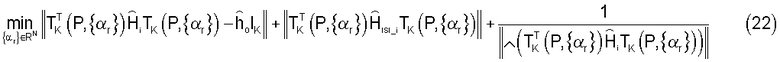И, наконец, способ передачи вейвлета иллюстрируется на фиг.2.

Подводя итоги, можем заключить, что процесс согласно настоящему изобретению включает следующее.

Начинаем с оценки матрицы канала и начального набора параметров альфа, который определяет начальный вейвлет (в предположении, что Р фиксировано).

Посылаем обучающие сигналы из передатчика (базовой станции) в приемник.

В приемнике итерируем (или вычисляем другим способом) значение регулируемых вейвлет-параметров, которые минимизируют перекрестную помеху между несущими и межсимвольную интерференцию, а также полную остаточную помеху.

Посылаем регулируемые параметры назад в передатчик по цепи обратной связи.

Используем регулируемые параметры при передаче в течение следующего периода времени до следующей регулировки.

Следует отметить, что остаточная помеха все еще может иметь место даже после выбора вейвлета. Это вызывается такими эффектами, как задержка обратной связи относительно времени когерентности канала, сужение пространства поиска параметра и т.д. В результате некоторая ограниченная форма подавления помех может потребоваться даже тогда, когда вейвлет согласован с условиями в канале наилучшим образом. Кроме того, использование метрики в уравнении (22) не максимизирует разнесение в системе; оно лишь оптимизирует перекрестную помеху между несущими и межсимвольную интерференцию.

Создание параметризованных вейвлетов ставит классическую задачу адаптивного построения формы волны для беспроводной передачи в системе, в которой приемник должен передавать в передатчик информацию об условиях в канале: как снизить пропускную способность, необходимую для ретрансляции из приемника в передатчик информации, необходимой для точного выбора структуры волны. Обычно это не является проблемой в системах с дуплексной связью с временным разделением каналов (TDD -Time division duplex), поскольку в общем случае предполагается, что TDD передатчик может оценить условия в канале, наблюдаемые в TDD приемнике, без обратной связи. Однако двухполосные системы в общем случае не имеют достаточной корреляции между частотами передачи и приема, используемыми данным приемопередатчиком. Таким образом, критичной является минимизация объема информации, которая будет ретранслироваться из приемника в передатчик для выбора структуры волны.

Однако избирательность матрицы банка вейвлет-фильтров явно повышается с возрастанием порядка 2N. Это требует большей параметризации, что, в свою очередь, потенциально увеличивает необходимую информацию обратной связи. Таким образом, при заданной максимальной полезной нагрузке R (в битах) канала обратной связи существует компромисс между увеличением избирательности банка фильтров и снижением шума квантования параметров обратной связи. Если мы предполагаем, что каждое значение в наборе {α_i} параметров равномерно квантовано между 0 и π, мы можем найти среднюю ошибку квантования как

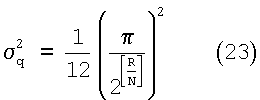
В уравнении (23) ошибка квантования получена из классического результата однородного квантования равномерно распределенной случайной переменной. К сожалению, такая дисперсия ошибки сама по себе не может дать достаточного понимания деградации системы связи на основе вейвлетов из-за ограничения пропускной способности для сигналов обратной связи при выборе вейвлет-параметров. Однако она может показать порядок оптимального банка фильтров при заданных конкретных ограничениях обратной связи. Шум квантования для фильтров порядков 2 и 4 изображен на фиг.3. В левой части кривой с ростом порядка фильтра шум квантования возрастает до недопустимого уровня. Однако в правой части кривой с ростом порядка фильтра шум квантования имеет тенденцию к уменьшению ниже неприемлемых уровней (хотя шум квантования все еще растет с ростом порядка фильтра для любого заданного значения R). Это не удивительно, поскольку понятно, что увеличение пропускаемых по каналу полезных нагрузок позволяет более точно квантовать увеличивающееся число вейвлет-параметров, а следовательно, допускает больший порядок банка фильтров.

Здесь кажется уместным вопрос, а сколько конкретно составляет "неприемлемый уровень" шума квантования, поскольку понятно, что для заданного значения R выбираемый порядок фильтра должен быть максимальным, но таким, при котором этот уровень не превышается.

На фиг.2 иллюстрируется процесс вычисления коэффициентов, которые формируют заданный вейвлет. Набор {α_i} коэффициентов сигнала, представляющего речь или другие данные, вводится слева и обрабатывается (например, системой компьютеров общего назначения) с формированием результирующих коэффициентов, которые определяют конкретные вейвлеты, используемые в передатчике.

В процессе работы системы согласно изобретению передатчик периодически посылает эталонный сигнал (обучающую последовательность) в приемник. Приемник применяет к принятому сигналу известные алгоритмы, чтобы оценить матрицу канала. Затем приемник преобразует матрицу канала с использованием различных пробных параметров и выбирает параметры, которые дают наилучшее совпадение по некоторому критерию, например, сформулированному в уравнении (22), который минимизирует перекрестную помеху между несущими и межсимвольную интерференцию.

Параметры "оптимальной подгонки" ретранслируются в передатчик по каналу обратной связи, имеющему ограниченное число битов.

После этого передатчик подготавливает пакеты с использованием параметров, посланных ему приемником, в течение периода времени.

Тестирование на профиле конкретного канала было проведено для нескольких различных типов вейвлет-разложений с целью исследовать осуществимость адаптации вейвлетов к мгновенным условиям в канале на основе их параметризации. В предположении, что входной вектор размерности 32 модулируется квадратной матрицей вейвлет-преобразования, система передачи была протестирована при скорости передачи вейвлет-символов 250 кГц (в этом случае скорость передачи символа относится к скорости, с которой передаются все 32 вейвлет-коэффициента, полученных из единственного входного вектора). Вейвлет-модели с четырьмя отводами и с двумя отводами (9) и (10) были исследованы при передаче сигналов двоичной фазовой манипуляции (BPSK) (канальный профиль распределения мощности при многолучевом распространении [0,8 0,1 0,1]) при предполагаемой частоте несущей 5 ГГц и скорости 3 км/час. При моделировании системы вейвлет-параметр выбирался каждые 50 символов. В этих условиях рабочие характеристики вейвлетов с 4 отводами и с 2 отводами в отношении квантования обратной связи приводятся на фиг.4 и 5 соответственно.

В этих условиях преимущества возрастания обратной связи естественно становятся менее превалирующими с ростом количества битов. В такой среде, хотя повышение обратной связи обеспечивает снижение шума квантования на 6 дБ, очевидно, что оно не приводит к такому же выигрышу в отношении общих рабочих характеристик. Должно также быть понятно, что результаты на графике касаются необработанного коэффициента ошибок при двоичной фазовой манипуляции; использование дополнительного кода коррекции ошибок может привести к меньшему выигрышу, достигаемому вследствие увеличения количества битов в обратной связи. Другое обстоятельство, на которое следует обратить внимание, это то, что рабочие характеристики вейвлетных систем с 4 отводами и с 2 отводами в грубом приближении были приблизительно одинаковыми.

Кроме того, количество растяжений может влиять на рабочие характеристики предложенного способа вейвлетной передачи. Вновь обратимся к результатам как для вейвлетов с 4 отводами, так и с 2 отводами в предположении 3-битового квантования обратной связи, что иллюстрируется на фиг.6 и 7 соответственно. Увеличение количества растяжений не дает большого выигрыша в улучшении рабочих характеристик системы. Наиболее вероятно, это обусловлено тем, что характеристики рассматриваемого канала уже довольно компактны по частоте и времени; наибольшее улучшение, обеспечиваемое этим способом, заключается в изменении фундаментального банка вейвлет-фильтров, а не в изменении частотно-временного разложения передаваемого сигнала.

Для лучшего понимания максимально достижимого преимущества многомасштабной связи была смоделирована система мультиплексирования с ортогональным частотным разделением (OFDM) с использованием одинаковых условий в канале и одинаковых размеров входных векторов. Сравнение с вейвлетом с 2 отводами и одним битом обратной связи приведено на фиг.8. Как видно, улучшение рабочих характеристик благодаря вейвлетной модуляции достигает 3 дБ. Учитывая, что система OFDM осуществляет квадратурную передачу, тогда как вейвлет-система не требует квадратурной передачи для сигналов с двоичной фазовой манипуляцией, понятно, что спектральная эффективность вейвлетной системы потенциально намного выше, чем системы OFDM.

Были получены дополнительные результаты для адаптивного способа в каналах с замираниями, и эти результаты сравнивались с результатами применения фиксированного способа (в данном случае, базиса Хаара и Добеши с 4 отводами). При использовании канального профиля распределения мощности [0,8 0,2], наряду со скоростью передачи символов 125 кГц и размером входного вектора 64, было проведено сравнение фиксированного и адаптивного способов в условиях замираний при частоте несущей 5 ГГц и скорости 150 км/час. Использовался сверточный код с скоростью 1/2; это означает, что входной сегмент из 32 битов кодировался во входной вектор из 64 двоичных символов (сигнал двоичной фазовой манипуляции). Результаты показаны на фиг.9 и 10.

Оба способа дают близкие результаты при низком отношении сигнал/шум. Это происходит потому, что главным источником ошибок в этой рабочей области является аддитивный белый гауссовский шум (AWGN); в этих условиях никакая адаптация не может улучшить линию связи. Кроме того, следует отметить, что оба способа действительно приводят к минимальному уровню ошибок. Для фиксированного случая это происходит благодаря тому, что для передачи используется субоптимальный вейвлет. В адаптивном случае это происходит благодаря использованию ограниченной обратной связи. Однако даже в предположении бесконечно точного квантования параметрического пространства необходимо вновь подчеркнуть, что выбранный вейвлет является аппроксимацией выравнивающего преобразования.

Вышеизложенный способ выбора вейвлета, в особенности критерий, иллюстрируемый уравнением (22), был исследован в сравнении с фиксированным способом при статическом канальном профиле [0,5 0,3 0,1 0,1]. В этом случае квантование обратной связи было увеличено до 5 битов, что позволяло более точно исследовать, выбирается ли в результате селекции действительно лучший вейвлет. Более конкретно, в предположении грубого квантования вероятность выбора правильного вейвлета с использованием указанного способа выбора вейвлета возрастает; поэтому в таких условиях точность этого способа оценить не просто. Результаты для способа с 2 отводами приведены на фиг.11. Следует отметить, что указанный способ выбора вейвлета сохраняет преимущества адаптивного способа по сравнению с использованием фиксированного вейвлета. Еще отметим, что минимальный уровень ошибки все еще присутствует, хотя и с частотой ошибочных битов между 10^-4 и 10^-3.

Хотя настоящее изобретение было описано на примере ограниченного количества вариантов его выполнения, специалистам в данной области техники понятно, что можно создать другие варианты выполнения настоящего изобретения в рамках формулы изобретения.

Источники информации

1. Vetterli, Martin and Jelena Kovacevic. Wavelets and Subband Coding. Englewood Cliffs, NJ: Prentice-Hall Inc., 1995.

2. Strang, Gilbert and Truong Nguyen. Wavelets and Filter Banks. Wellesley, MA: Wellesley-Cambridge Press, 1996.

3. Zou, Hehong and Ahmed H. Tewfik. "Parameterization of Compactly Supported Orthonormal Wavelets." IEEE Transactions on Signal Processing. Vol.41. No. 3. March 1993. pp.1428-1431.

4. Schneid, J. and S. Pittner. "On the Parameterization of the Coefficients of Dilation Equations for Compactly Supported Wavelets." Computing. Vol.51. May 1993. pp.165-173.

5. Vidakovic, Brani. "Pollen Bases and Daubechies-Lagarias Algorithm in MATLAB." Jacket's Wavelets website. http://www.isye.gatech.edii/˜brani/datasoft/DL.pdf

6. Silva, Vitor and Luis de Sa. "Analytical Optimization of CQF Filter Banks." IEEE Transactions on Signal Processing. Vol.44. No. 6. June 1996. pp.1564-1568.

7. Pollen, D. "Parameterization of Compactly Supported Wavelets." Aware Inc. technical report AD890503. May 1989.

8. Womell, Gregory W. "Emerging Applications of Multirate Signal Processing and Wavelets in Digital Communications." Proceedings of the IEEE. Vol.84. No. 4. April 1996. pp.586-603.

9. Lindsey, Alan R. "Wavelet Packet Modulation for Orthogonally Multiplexed Communication." IEEE Transactions on Signal Processing. Vol.45. No. 5. May 1997. pp.1336-1339.

10. Wong, K.-M., Wu, J., Davidson, T.N. and Jin, Q "Wavelet Packet Division Multiplexing and Wavelet Packet Design under Timing Error Effects." IEEE Transactions on Signal Processing. Vol.45. No. 12. December 1997. pp.2877-2890.

Изобретение относится к технике связи. Технический результат состоит в упрощении устройства путем устранения эквалайзера в приемнике. Многомасштабная связь, в которой используется частотно-временная обработка передаваемого сигнала, рассматривается применительно к типичным системам беспроводной связи, в которых модулирующий вейвлет согласуется с условиями в конкретном канале. Используются компактные вейвлет-базисы, и на основе их параметризации выбирается такой вейвлет, который лучше всего соответствует условиям в беспроводном канале. 8 н. и 46 з.п. ф-лы, 11 ил.

1. Передатчик, содержащий модулятор для модуляции входного сигнала с формированием модулированного выходного сигнала с использованием вейвлет-преобразования, при этом модулятор характеризуется набором параметров, конфигурированных для выбора одного из множества вейвлетов, и конфигурирован для определения вейвлет-преобразования с использованием по меньшей мере указанного набора параметров и для модификации в ответ на информацию, принятую по обратной связи, по меньшей мере части этого набора параметров, по меньшей мере частично на основе принятой информации, причем модулированный выходной сигнал пригоден для передачи по каналу.2. Передатчик по п.1, в котором вейвлет-преобразование имеет представление, соответствующее Р растяжениям.3. Передатчик по п.1, в котором вейвлет-преобразование включает К-точечное вейвлет-преобразование, определенное по меньшей мере частично, с использованием модифицированного набора параметров.4. Передатчик по п.1, в котором модулированный выходной сигнал содержит набор параллельных данных, а передатчик содержит входной порт для приема входного сигнала и параллельно-последовательный преобразователь для преобразования набора параллельных данных в набор последовательных данных, пригодных для передачи по каналу.5. Передатчик по п.4, дополнительно содержащий передающую антенну для передачи набора последовательных данных по каналу.6. Передатчик по п.1, в котором модулятор выполнен с возможностью умножать вектор, который представляет входные данные, соответствующие входному сигналу, на матрицу, представляющую вейвлет-преобразование.7. Передатчик по п.1, в котором модулятор выполнен с возможностью в течение первого периода времени модулировать входной сигнал, включающий тестовые данные, с использованием вейвлет-преобразования, определенного с использованием по меньшей мере исходного набора параметров, а в течение второго периода времени модулировать входной сигнал, содержащий другие данные, с использованием вейвлет-преобразования, определенного с использованием по меньшей мере модифицированной версии исходного набора параметров, которая определена путем модификации по меньшей мере части исходного набора параметров, по меньшей мере частично на основе принятой информации.8. Передатчик по п.1, в котором указанная информация соответствует квантованным значениям параметров по меньшей мере для части набора параметров, причем модулятор выполнен с возможностью определять на основе квантованных значений значения параметров по меньшей мере в указанной части набора параметров.9. Способ передачи сигналов, включающий определение вейвлет-преобразования с использованием по меньшей мере набора параметров, который позволяет выбрать один из множества вейвлетов; модуляцию входного сигнала с формированием модулированного выходного сигнала с использованием указанного вейвлет-преобразования, причем модулированный выходной сигнал пригоден для передачи по каналу; и модификацию в ответ на информацию, принятую по обратной связи, по меньшей мере части набора параметров, по меньшей мере частично на основе принятой информации.10. Способ по п.9, в котором вейвлет-преобразование имеет представление, соответствующее Р растяжениям.11. Способ по п.9, в котором вейвлет-преобразование включает К-точечное вейвлет-преобразование, определенное по меньшей мере частично, с использованием модифицированного набора параметров.12. Способ по п.9, в котором модулированный выходной сигнал содержит набор параллельных данных, а способ дополнительно включает прием входного сигнала и преобразование принятого входного сигнала из набора параллельных данных в набор последовательных данных, пригодных для передачи по каналу.13. Способ по п.12, дополнительно включающий передачу набора последовательных данных по каналу.14. Способ по п.9, в котором модуляция дополнительно включает умножение вектора, который представляет входные данные, соответствующие входному сигналу, на матрицу, представляющую вейвлет-преобразование.15. Способ по п.9, в котором модуляция включает до модификации модуляцию входного сигнала, содержащего тестовые данные, с использованием вейвлет-преобразования, определенного с использованием по меньшей мере исходного набора параметров, а модификация включает модификацию по меньшей мере части исходного набора параметров, по меньшей мере частично на основе принятой информации, при этом способ включает модуляцию входного сигнала, содержащего другие данные, с использованием вейвлет-преобразования, определенного с использованием по меньшей мере модифицированного исходного набора параметров.16. Способ по п.9, в котором информация соответствует квантованным значениям параметров по меньшей мере для части набора параметров, а модификация включает определение на основе этих квантованных значений значений параметров по меньшей мере в указанной части набора параметров.17. Носитель программных данных, считываемых компьютером, причем носитель содержит компьютерные команды для осуществления способа передачи сигналов по любому из пп.9-16.18. Устройство передачи сигналов, содержащее средство определения вейвлет-преобразования с использованием по меньшей мере набора параметров, позволяющего выбрать один из множества вейвлетов;

средство модуляции входного сигнала с формированием модулированного выходного сигнала с использованием указанного вейвлет-преобразования, причем модулированный выходной сигнал пригоден для передачи по каналу; и средство модификации, реагирующее на информацию, принятую по обратной связи, для модификации по меньшей мере части набора параметров по меньшей мере частично на основе принятой информации.

средство определения вейвлет-преобразования с использованием по меньшей мере набора параметров, позволяющего выбрать один из множества вейвлетов;

средство демодуляции сигнала, принятого по каналу, в соответствии с вейвлет-преобразованием с формированием демодулированного сигнала; средство модификации по меньшей мере части набора параметров на основе по меньшей мере оценки канала; и

средство создания информации, пригодной для передачи по обратной связи, на основе по меньшей мере части набора параметров.