Изобретение относится к области исследования и анализа материалов с помощью оптических средств и может быть использовано для определения фазового состава твердофазной смеси в случае необходимости выявления одного из соединений или определения состава смеси, а также для оценки наличия примесей в веществе.
Известен рентгенографический способ определения фазового состава смеси (Ковба Л.М., Трунов В.К. «Рентгенофазовый анализ», М.: изд. МГУ, 1976, с.283), в основе которого лежит уравнение Вульфа-Брэгга, связывающее набор межплоскостных расстояний кристаллической решетки, которым отвечает соответствующий набор дифракционных максимумов на дифрактограмме.
Недостатком известного способа является невозможность анализировать аморфные и плохокристаллические вещества и смеси, а также такие смеси, которые содержат фазы, рефлексы от которых на дифрактограммах совпадают или близки с таковыми для других веществ или их смесей.
Известен оптико-иммерсионный способ определения фазового состава смеси (Головкин Б.Г. «Оптико-иммерсионный метод фазового анализа», Журнал аналитической химии, 2007, т.62, №7, с.1-7), основанный на измерении показателей преломления и других оптических характеристик ее ингредиентов и сравнении их с таковыми для известных чистых веществ.
Недостатком этого способа является невозможность определять показатели преломления непрозрачных веществ и в силу этого невозможность исследовать фазовый состав смеси, содержащей такие вещества.
Наиболее близким техническим решением к предлагаемому является способ эллипсометрии (Аззам Р., Башара Н. "Эллипсометрия и поляризованный свет", Изд. «Мир», М., 1981, с.316) (прототип), в котором помещают изучаемый образец на предметный столик, освещают пучком монохроматического излучения, измеряют эллипсометрические параметры с последующими вычислениями с помощью специального алгоритма. Известный эллипсометрический способ касается изучения свойств границы раздела двух сред или находящейся между ними пленки. В этом способе используют изменение поляризации, которое имеет место, когда луч поляризованного света отражается от границы раздела или пленки или проходит через нее.
Однако недостатком известного способа является невозможность его использования для определения фазового состава твердофазной смеси в случае необходимости выявления одного из соединений или определения состава смеси, а также для оценки наличия примесей в веществе.
Таким образом, перед авторами стояла задача расширить области применения эллипсометрического способа, разработав возможность его применения для определения фазового состава твердофазной смеси.
Поставленная задача решена в предлагаемом способе определения эллипсометрических параметров, включающем помещение образца на подложку, расположенную на предметном столике эллипсометра, освещение поверхности образца под заданным углом поляризованным световым лучом, определение относительных изменений амплитуды ψ и фазы Δ линейно-поляризованной монохроматической световой волны в нескольких точках образца, в котором осуществляют 30-100 измерений эллипсометрических параметров путем сдвига образца относительно направления падения светового луча, затем вычисляют условные показатели преломления η(φ) и коэффициенты поглощения k(φ) образца в каждой точке по формуле:
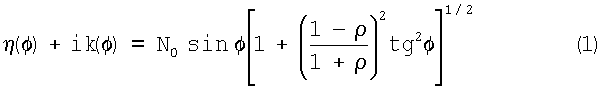 ,
,
где φ - угол падения луча относительно нормали к поверхности образца,
N0 - показатель преломления среды,
ρ=eiΔtgψ (2),
выстраивают полученные значения η(φ) и k(φ) в ряд по возрастанию, разбивают ряд на равные интервалы с шагом Н и определяют частоту ω, отвечающую количеству значений η(φ), попавших в каждый интервал, после чего строят эллипсограмму в координатах η(φ)-ω и сравнивают с эллипсограмами соответствующих чистых веществ.
Наличие в предлагаемом способе зависимости показателей преломления от угла падения светового луча позволяет получать при измерении в разных точках образца статистический набор различных значений условных показателей преломления. Выявление скрытых экстремумов в этом наборе, в свою очередь, позволяет характеризовать вещество и выявлять его присутствие среди других ингредиентов в смеси.
Предлагаемый способ может быть использован как для подтверждения индивидуальности отдельных веществ, их чистоты, так и для идентификации содержания их в различных смесях. Однако особые его преимущества проявляются в таких ситуациях, когда известные методы фазового анализа не могут дать однозначного ответа на поставленные вопросы. В частности, к таким случаям, можно отнести следующие:
1. Определение границ твердых растворов, у которых величины радиусов ионов замещающих элементов близки к таковым для замещаемых элементов (как это имеет место, например, в системе TiO2-VO2-V2O5), что ведет к практическому совпадению рентгенографических и других характеристик различных составов.
2. Идентификации сверхструктурных фаз с мало отличающимися рентгенографическими характеристиками (например, сверхструктурные фазы в системе Bi12(VxBi1-x)O19,5+x, где 0≤x≤1).
3. Идентификация соединений, дифракционные максимумы которых совпадают с таковыми для других ингредиентов смеси. Примером таких веществ являются AlPO4 и V2O5, наборы дифракционных максимумов которых трудно различимы.
Как известно, способ отражательной эллипсометрии основан на измерении состояний поляризации падающей и отраженной линейно-поляризованных световых волн. Исследования, проведенные авторами, позволили установить, что показатель преломления и коэффициент поглощения поликристаллических образцов, коими являются исследуемые объекты, зависят от угла падения φ, а именно, с увеличением угла падения, соответственно, увеличиваются и значения искомых величин. Одной из причин этого явления может быть то, что в анализатор эллипсометра попадает не только отраженный свет, но и рассеянный, который также поляризован, а интенсивность его зависит от угла падения, но формулой (1), естественно, не учитывается. И поскольку кристаллы исследованных поликристаллических образцов в большем количестве расположены параллельно столику эллипсометра, то при увеличении угла падения количество примесного рассеиваемого света соответственно увеличивается. Это и приводит к увеличению значений измеряемых эллипсометрических параметров. По этой причине величины, находимые по формулам (1, 2), авторы называют условными показателями преломления η(φ) и коэффициентами поглощения k(φ) соответственно.
Поскольку объектами исследования являются поликристаллические порошки, то углы падения светового луча по отношению к поверхности соответствующего микрокристалла могут быть самыми разными. Поэтому измеряются величины η(φ) или k(φ) в различных точках образца. После математической обработки полученного статистического набора полученных данных строятся эллипсограммы, представляющие собой кривые распределения этих величин. Сопоставление эллипсограмм для чистых веществ и исследуемых смесей позволяет выяснить, присутствуют ли данные вещества в анализируемых смесях. Обнаружение на эллипсограмме максимумов, положения которых не соответствуют ни одному из известных веществ, позволяет предполагать наличие в смеси одной или нескольких новых или неизвестных фаз.
Предлагаемый способ может быть осуществлен следующим образом. Необходима идентичность получения исследуемых смесей и ее возможных ингредиентов. Если это механические мелкокристаллические смеси из тех же самых ингредиентов, которые в данный момент имеются в распоряжении, то предыстория ингредиентов не имеет значения. Если же ингредиенты и смеси состоят из очень крупных кристаллов, агломератов или оплавленных кусков, то те и другие перед началом анализа следует подвергнуть измельчению в одинаковых условиях. Если же смеси получены в процессе какого-либо химического процесса, например вследствие химической реакции между некоторыми компонентами системы, то возможные ингредиенты образующейся при этом смеси желательно выдержать в условиях этого химического процесса для приобретения соответствующей текстуры.
Образцы для исследований с целью уменьшения светорассеяния формируют в таблетки и подвергают прессованию под давлением около 100 кг/см2. Угол падения светового луча относительно нормали к поверхности образца φ можно выбирать любой, но он, в соответствии с вышесказанным, не должен меняться в очередной серии измерений.
Отраженный (или преломленный) от поверхности образца световой луч попадает в анализатор эллипсометра, где с помощью компенсаторов определяются относительные изменения амплитуды ψ и фазы Δ. После чего образец немного сдвигают и определяют новые значения этих величин. Как правило, достаточно 30-100 измерений. Полученные значения Δ и ψ записывают в виде таблицы, проводят соответствующие математические расчеты, строят эллипсограммы и затем принимают решения о фазовом составе исследуемого образца. При математической обработке результатов величины η(φ) и k(φ) находят из условных комплексных показателей преломления
N(φ)=η(φ)+ik(φ) (3),
определяемых по формуле (1) на основании измеренных с помощью эллипсометра значений Δ и ψ, и располагают последние в виде соответствующих каталогов по возрастанию их значений. Затем разбивают упорядоченный ряд данных Xj, каковыми являются ряды ηj(φ), или kj(φ), представленные в каталогах, на K равных интервалов ΔXk с шагом H:
ΔXk=Xk+1-Xk (4)
где Xk и Xk+1 - граничные значения X этих интервалов. Затем подсчитывают в каждом К - интервале количества найденных значений Xj, называемые частотами:
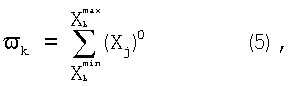
где 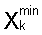 и
и 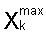 - минимальные и максимальные значения Xj в k-ом интервале. После чего строится графическая зависимость
- минимальные и максимальные значения Xj в k-ом интервале. После чего строится графическая зависимость 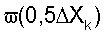 частоты
частоты 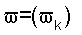 от величин 0,5ΔXk, равных значениям X, в центре k-го интервала в виде полигона или гладкой кривой, называемой эллипсограммой.
от величин 0,5ΔXk, равных значениям X, в центре k-го интервала в виде полигона или гладкой кривой, называемой эллипсограммой.
Особенностью предлагаемого способа является то, что количество пиков на эллипсограмме оказывается сильно зависящим от интервала шага. Чем больше интервал шага H, тем меньше количество шагов К уложилось в общем интервале ΔХ наблюдаемых значений Х:
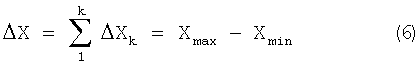
где Xmax и Xmin - максимальное и минимальное значения в каталоге всех значений Xj, тем меньше будет пиков на эллипсограмме и, следовательно, тем грубее оказываются результаты проведенного анализа. Критерий оптимальных значений H и K определяют из следующих соображений. Полагая, что каждый пик в среднем может быть зафиксирован m точками, то общее количество их на эллипсограмме равно:
К=mn (7),
а длина шага, соответственно равна:
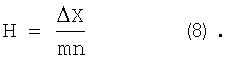
Минимальное значение m может быть равно даже 2, если Xj≠Xj+1. Более высокою гарантию экстремума дают значения m, равные от 3 до 7. При m≥6 обычно уже наблюдается расщепление, и фиксируются сателлитные пики. Точки перегиба при увеличении m могут превратиться в максимумы, а точки прогиба соответственно в минимумы. Поэтому такие точки являются потенциальными экстремумами. Сравнение эллипсограмм чистых веществ и анализируемой смеси рациональнее производить при одинаковых значениях Н. Но если это не представляется возможным, то можно использовать величины H и не совпадающие с оптимальными значениями. В этом случае появление некоторых неидентифицируемых мелких пиков может не свидетельствовать о наличии в смеси какой-либо новой неизвестной фазы.
Предлагаемый способ иллюстрируется следующим примером.
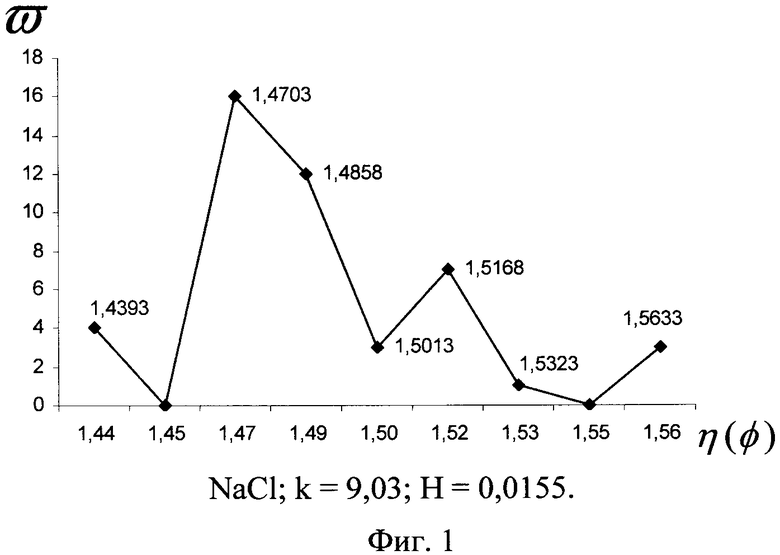
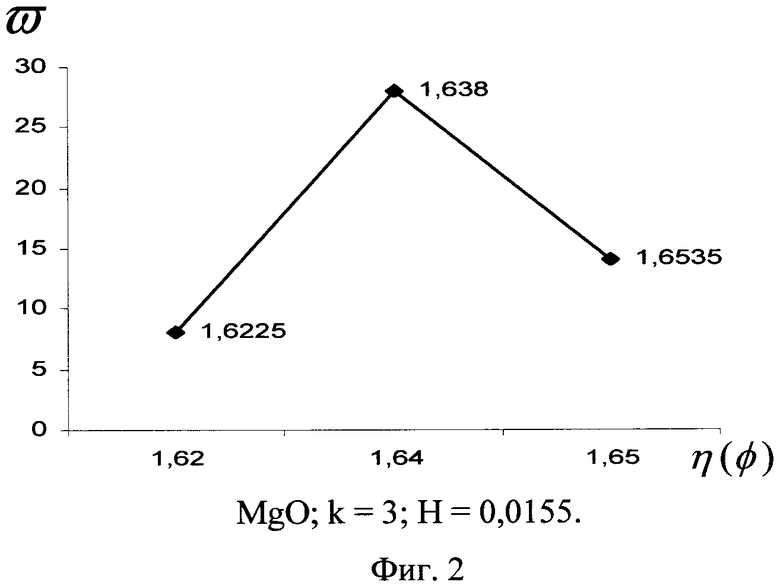
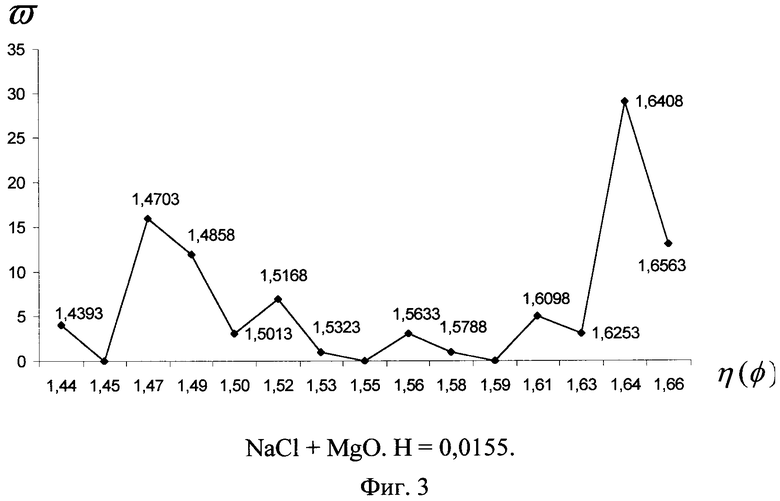
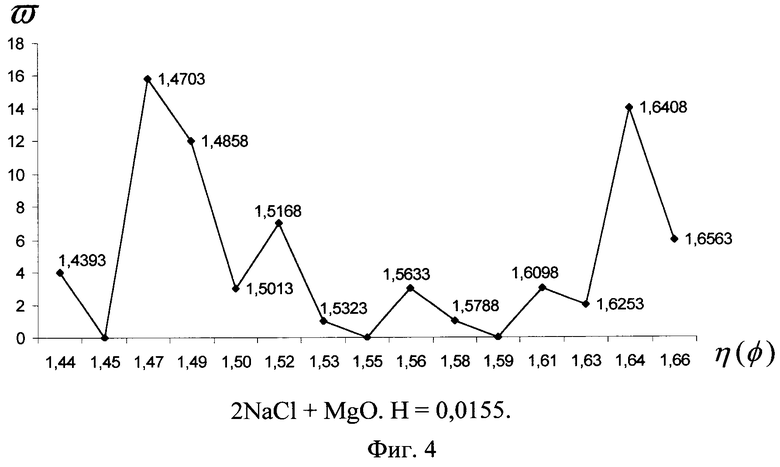
ПРИМЕР. Берут образцы механических смесей А и В, состоящих из NaCl и MgO квалификации «х.ч.», в соотношении 1:1 и 2:1 соответственно. Смеси готовят путем встряхивания стехиометрических количеств соответствующих соединений в закрытой емкости при комнатной температуре. Образцы NaCl, MgO, смесей А и В прессуют в таблетки под давлением 100 кг/см2. С помощью нуль-эллипсометра измеряют значения Δ и ψ в 50 различных точках каждого образца при угле падения φ=70°. Используя эти данные, по формуле (1) рассчитывают величины η(φ). Поскольку оба исходных соединения имеют кубическую сингонию, то на эллипсограммах исходных веществ с оптимальным значением H должно быть всего по одному пику (n=1). Обсчет данных эллипсограммы при m=3, 4; 5, что соответствует Н=0,0155; 0,0116; 0,0092 для MgO и Н=0,0466; 0,035; 0,028 для NaCl, это подтвердил. Эллипсограммы этих веществ с m≥6 действительно уже содержат сателлитные пики. Для построения эллипсограмм смесей выбирают единое значение Н. Но выше найденные значения Н для NaCl и MgO не перекрываются. Поэтому для того чтобы использовать самое большое значение n=0,0155 для MgO, необходимо взять это же самое значение и для NaCl. Величина m, вычисленная по формуле (6) для хлорида натрия, оказывается равной 9,03, и, как следует ожидать, соответствующая эллипсограмма, изображенная на фиг.1, содержит сателлиты. Фиг.2 представляет собой эллипсограмму MgO с шагом H=0,0155. Фиг.3 и 4 являются эллипсограммами смесей А и В, соответственно, с тем же шагом. Легко заметить, что пики на этих полигонах те же самые, что и у ингредиентов смесей, хотя их численные значения слегка отличаются, из чего можно однозначно заключить, что смеси А и В состоят из NaCl и MgO. Существенно отметить, что в эквимолярной смеси А наиболее представительный пик MgO выше аналогичного пика NaCl, а в смеси с большим содержанием NaCl, наоборот, меньше. Это говорит о том, что предлагаемый способ может давать информацию и об относительных количествах ингредиентов в смеси.
Важным преимуществом предлагаемого способа является возможность анализировать смеси, содержащие непрозрачные вещества, а также аморфные и плохокристаллические вещества.
| название | год | авторы | номер документа |
|---|---|---|---|
| Способ определения линейного коэффициента теплового расширения тонкой прозрачной пленки | 2018 |
|
RU2683879C1 |
| СПОСОБ КОНТРОЛЯ КАЧЕСТВА СЛОЕВ МНОГОСЛОЙНОГО ЛЕНТОЧНОГО СВЕРХПРОВОДНИКА | 2014 |
|
RU2584340C1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ ТОЛЩИНЫ ТОНКОЙ ПРОЗРАЧНОЙ ПЛЕНКИ | 2011 |
|
RU2463554C1 |
| Способ определения толщины пленки | 2021 |
|
RU2787807C1 |
| СПОСОБ ИЗМЕРЕНИЯ МАГНИТООПТИЧЕСКИХ ЭФФЕКТОВ in situ | 2014 |
|
RU2560148C1 |
| ЭЛЛИПСОМЕТР | 2005 |
|
RU2302623C2 |
| Способ профилирования состава при эпитаксиальном формировании полупроводниковой структуры на основе твердых растворов | 2019 |
|
RU2717359C1 |
| Способ определения оптических констант пленок химически активных металлов или их сплавов | 2017 |
|
RU2659873C1 |
| СПОСОБ ЭЛЛИПСОМЕТРИЧЕСКОГО ИССЛЕДОВАНИЯ ТОНКИХ ПЛЕНОК НА ПЛОСКИХ ПОДЛОЖКАХ | 1997 |
|
RU2133956C1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ ПОКАЗАТЕЛЯ ПРЕЛОМЛЕНИЯ ОПТИЧЕСКИ ПРОЗРАЧНОГО МАТЕРИАЛА | 2016 |
|
RU2629695C2 |
Изобретение относится к области исследования и анализа материалов с помощью оптических средств и может быть использовано для определения фазового состава твердофазной смеси в случае необходимости выявления одного из соединений или определения состава смеси, а также для оценки наличия примесей в веществе. Способ включает помещение образца на подложку, расположенную на предметном столике эллипсометра, освещение поверхности образца под заданным углом поляризованным световым лучом, определение относительных изменений амплитуды ψ и фазы Δ линейно-поляризованной монохроматической световой волны в нескольких точках образца. Осуществляют 30-100 измерений эллипсометрических параметров путем сдвига образца относительно направления падения светового луча, затем вычисляют условные показатели преломления η(φ) и коэффициенты поглощения k(φ) образца в каждой точке, выстраивают полученные значения η(φ) и k(φ) в ряд по возрастанию, разбивают ряд на равные интервалы с шагом Н и определяют частоту ω, отвечающую количеству значений η(φ), попавших в каждый интервал, после чего строят эллипсограмму в координатах η(φ)-ω и сравнивают с эллипсограмами соответствующих чистых веществ. Техническим результатом является расширение области использования. 4 ил.
Способ определения эллипсометрических параметров, включающий помещение образца на подложку, расположенную на предметном столике эллипсометра, освещение поверхности образца под заданным углом поляризованным световым лучом, определение относительных изменений амплитуды ψ и фазы Δ линейно-поляризованной монохроматической световой волны в нескольких точках образца, отличающийся тем, что осуществляют 30-100 измерений эллипсометрических параметров путем сдвига образца относительно направления падения светового луча, затем вычисляют условные показатели преломления η(φ) и коэффициенты поглощения k(φ) образца в каждой точке по формуле
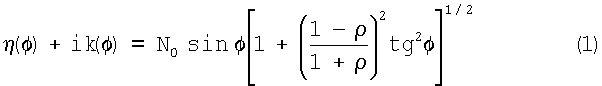 ,
,
где φ -угол падения луча относительно нормали к поверхности образца, N0 - показатель преломления среды,
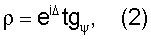
выстраивают полученные значения η(φ) и k(φ) в ряд по возрастанию, разбивают ряд на равные интервалы с шагом Н и определяют частоту ω, отвечающую количеству значений η(φ) попавших в каждый интервал, после чего строят эллипсограмму в координатах η(φ)-ω и сравнивают с эллипсограммами соответствующих чистых веществ.
| АЗЗАМ Р | |||
| и др | |||
| Эллипсометрия и поляризованный свет | |||
| - М.: Мир, 1981, с.316 | |||
| СПОСОБ ЭЛЛИПСОМЕТРИЧЕСКОГО ИССЛЕДОВАНИЯ ТОНКИХ ПЛЕНОК НА ПЛОСКИХ ПОДЛОЖКАХ | 1997 |
|
RU2133956C1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ ЭЛЛИПСОМЕТРИЧЕСКИХ ПАРАМЕТРОВ ОБЪЕКТА (ВАРИАНТЫ) | 1997 |
|
RU2149382C1 |
| FR 2860298 А1, 01.04.2005 | |||
| JP 10038694 А, 13.02.1998. | |||
Авторы
Даты
2009-03-27—Публикация
2007-06-27—Подача