Изобретение относится к области электросвязи и вычислительной техники, а конкретнее к области криптографических способов аутентификации электронных сообщений, передаваемых по телекоммуникационным сетям и сетям ЭВМ, и может быть использовано в системах передачи электронных сообщений (документов), заверенных электронной цифровой подписью (ЭЦП), представленной в виде многоразрядного двоичного числа (МДЧ). Здесь и далее под МДЧ понимается электромагнитный сигнал в двоичной цифровой форме, параметрами которого являются число битов и порядок следования их единичных и нулевых значений 1)
(1) толкование используемых в описании терминов приведено в Приложении 1).
Известен способ формирования и проверки ЭЦП, предложенный в патенте США №4405829 от 20.09.1983 и детально описанный в книгах [1. М.А.Иванов. Криптография. М., КУДИЦ-ОБРАЗ, 2001; 2. А.Г.Ростовцев, Е.Б.Маховенко. Введение в криптографию с открытым ключом. С-Петербург, Мир и семья, 2001. - с.43]. Известный способ заключается в следующей последовательности действий:
формируют секретный ключ в виде трех простых МДЧ p, q и d, формируют открытый ключ (n, е) в виде пары МДЧ n и е, где n - число, представляющее собой произведение двух простых МДЧ р и q, и е - МДЧ, удовлетворяющее условию ed=1 mod (p-1)(q-1), принимают электронный документ (ЭД), представленный МДЧ Н;
в зависимости от значения Н и значения секретного ключа формируют ЭЦП в виде МДЧ Q=S=Hd mod n;
формируют первое проверочное МДЧ А=Н;
формируют второе проверочное МДЧ В, для чего МДЧ S возводят в целочисленную степень е по модулю n: В=Sе mod n;
сравнивают сформированные проверочные МДЧ А и В;
при совпадении параметров сравниваемых МДЧ А и В делают вывод о подлинности ЭЦП.
Недостатком известного способа является относительно большой размер подписи и необходимость увеличения размера подписи при разработке новых более эффективных методов разложения числа n на множители или при росте производительности современных вычислительных устройств. Это объясняется тем, что значение элемента подписи S вычисляются путем выполнения арифметических операций по модулю n, а стойкость ЭЦП определяется сложностью разложения модуля n на множители р и q.
Известен также способ формирования и проверки подлинности ЭЦП Эль-Гамаля, описанный в книге [Молдовян А.А., Молдовян Н.А., Советов Б.Я. Криптография. - СПб, Лань, 2000. - с.156-159], который включает следующие действия:
формируют простое МДЧ р и двоичное число G, являющееся первообразным корнем по модулю р, генерируют секретный ключ в виде МДЧ х, в зависимости от секретного ключа формируют открытый ключ в виде МДЧ Y=Gx mod р, принимают ЭД, представленный в виде МДЧ Н, в зависимости от H и секретного ключа формируют ЭЦП Q в виде двух МДЧ S и R, то есть Q=(S, R);
осуществляют процедуру проверки подлинности ЭЦП, включающую вычисление двух контрольных параметров с использованием исходных МДЧ р, G, Y, H и S путем возведения МДЧ G, Y, R в дискретную степень по модулю р и сравнение вычисленных контрольных параметров;
при совпадении значений контрольных параметров делают вывод о подлинности ЭЦП.
Недостатком данного способа также является относительно большой размер ЭЦП. Это объясняется тем, что значения элементов подписи S и R вычисляют путем выполнения арифметических операций по модулю р-1 и по модулю р соответственно.
Известен также способ формирования и проверки ЭЦП, предложенный в патенте США №4995089 от 19.02.1991. Известный способ заключается в следующей последовательности действий:
формируют простое МДЧ р, такое, что р=Nq+1, где q - простое МДЧ;
формируют простое МДЧ а, такое что а≠1 и аq mod р=1;
методом генерации случайной равновероятной последовательности формируют секретный ключ в виде МДЧ х;
формируют открытый ключ в виде МДЧ y по формуле y=ax mod p;
принимают ЭД, представленный МДЧ М;
формируют ЭЦП в виде пары МДЧ (е, s), для чего генерируют случайное МДЧ t, формируют МДЧ R по формуле R=at mod р, формируют МДЧ е=f(M||R), где знак || обозначает операцию присоединения двух МДЧ и f - некоторая специфицированная хэш-функция, значение которой имеет фиксированную длину (обычно 160 или 256 бит), независим от размера аргумента, т.е. от размера МДЧ M||R, а затем формируют МДЧ s по формуле s=(t-ex) mod q;
формируют первое проверочное МДЧ А, для чего генерируют МДЧ R' по формуле R'=asys mod p и формируют МДЧ е'=f(M||R');
формируют второе проверочное МДЧ В путем копирования МДЧ е: В=е;
сравнивают сформированные проверочные МДЧ А и В;
при совпадении параметров сравниваемых МДЧ А и В делают вывод о подлинности ЭЦП.
Недостатком способа по патенту США является относительно высокая вычислительная сложность процедуры формирования и проверки ЭЦП, что связано с тем, что для обеспечения минимально требуемого уровня стойкости требуется использовать простой модуль р разрядностью не менее 1024 бит.
Наиболее близким по своей технической сущности к заявленному является известный способ формирования и проверки подлинности ЭЦП, предлагаемый российским стандартом ГОСТ Р 34.10-2001 и описанный, например, в книге [Б.Я.Рябко, А.Н.Фионов. Криптографические методы защиты информации. М., Горячая линия - Телеком, 2005. - 229 с. (см. с.110-111)], согласно которому ЭЦП формируется в виде пары МДЧ r и s, для чего генерируют эллиптическую кривую (ЭК) в виде совокупности точек, причем каждая точка представляется двумя координатами в декартовой системе координат в виде двух МДЧ, называемых абсциссой (x) и ординатой (y), затем осуществляют операции генерации точек ЭК, сложения точек ЭК и умножения точки ЭК на число, а также арифметические операции над МДЧ, после чего в результате выполненных операций формируются МДЧ r и s. Указанные операции над точками выполняются как операции над МДЧ, являющимися координатами точек, по известным формулам [Б.Я.Рябко, А.Н.Фионов. Криптографические методы защиты информации. М., Горячая линия - Телеком, 2005. - 229 с. (см. с.110-111)]. В прототипе генерируют ЭК, описываемую уравнением y2=x3+ax+b mod р, поэтому генерация ЭК состоит в генерации чисел a, b и р, являющихся параметрами ЭК и однозначно задающих множество точек ЭК как множество точек, абсцисса и ордината которых удовлетворяет указанному уравнению. Ближайший аналог (прототип) заключается в выполнении следующей последовательности действий:
генерируют эллиптическую кривую (ЭК), которая представляет собой совокупность пар МДЧ, называемых точками ЭК и обладающих определенными свойствами (см. Приложение 1, пп.15-19);
методом генерации случайной равновероятной последовательности формируют секретные ключи в виде МДЧ k1, k2, …, kn;
формируют открытые ключи в виде точек ЭК P1, Р2, …, Рn, для чего генерируют точку G, имеющую значение порядка равное q (порядком точки ЭК называется наименьшее положительное целое число q, такое что результатом умножения данной точки на число q является так называемая бесконечно удаленная точка О; результатом умножения любой точки ЭК на нуль по определениию является точка О [Б.Я.Рябко, А.Н.Фионов. Криптографические методы защиты информации. М., Горячая линия - Телеком, 2005. - 229 с. (см. с.97-130)]; см. также Приложение 1, пп.15-19) и генерируют открытые ключи путем умножения точки G на МДЧ k1, k2, …, kn, т.е. формируют открытые ключи по формулам P1=k1G, Р2=k2G, …, Рn=knG;
принимают ЭД, представленный МДЧ Н;
генерируют случайное МДЧ 0<t<q, по которому формируют точку R по формуле R=tG;
формируют ЭЦП Q в виде пары МДЧ (r, s), для чего генерируют МДЧ r по формуле r=xR mod q, где xR - абсцисса точки R, а затем генерируют МДЧ s по формуле s=(tH+rki) mod q, где 1≤i≤n;
формируют первое проверочное МДЧ А, для чего генерируют МДЧ v по формуле v=sH-1 mod q и МДЧ w по формуле w=(q-rH-1) mod q, затем генерируют точку R' по формуле R'=vG+wPi, после чего МДЧ А получают по формуле А=xR' mod q, где xR' - абсцисса точки R';
формируют второе проверочное МДЧ В путем копирования МДЧ r: В=r;
сравнивают сформированные проверочные МДЧ А и В;
при совпадении параметров сравниваемых МДЧ А и В делают вывод о подлинности ЭЦП.
Недостатком ближайшего аналога является возрастание размера коллективной ЭЦП, т.е. ЭЦП устанавливающей факт подписания некоторого заданного документа двумя и более пользователями пропорционально числу пользователей, подписывающих заданный ЭД, что обусловлено тем, что каждый пользователь формирует ЭЦП, которая не зависит от ЭЦП других пользователей.
Целью изобретения является разработка способа формирования и проверки подлинности ЭЦП, заверяющей ЭД, зависящей от произвольной совокупности секретных ключей пользователей и имеющей фиксированный размер, т.е. размер, который не зависит от числа пользователей, которым принадлежит данная коллективная подпись, благодаря чему уменьшается размер коллективной ЭЦП.
Поставленная цель достигается тем, что в известном способе формирования и проверки подлинности ЭЦП, заверяющей ЭД, заключающемся в том, что генерируют эллиптическую кривую в виде совокупности точек, каждая из которых определяется парой МДЧ, являющихся соответственно абсциссой и ординатой данной точки эллиптической кривой в декартовой системе координат, формируют совокупность из n≥2 секретных ключей в виде МДЧ k1, k2, …, kn, по секретным ключам формируют n открытых ключей в виде точек P1, Р2, …, Рn эллиптической кривой, принимают ЭД, представленный МДЧ Н, в зависимости от принятого электронного документа и от значения секретного ключа формируют ЭЦП Q в виде двух или более МДЧ, формируют первое А и второе В проверочные МДЧ, сравнивают их и при совпадении их параметров делают вывод о подлинности ЭЦП, новым является то, что дополнительно формируют коллективный открытый ключ в виде точки Р эллиптической кривой, генерируемой в зависимости от точек эллиптической кривой 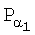 ,
, 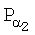 , …,
, …, 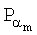 , где α1, α2, …, αm - натуральные числа, 2≤m≤n, αj≤n и j=1, 2, …, m, причем, по крайней мере, одно из проверочных МДЧ формируют в зависимости от коллективного открытого ключа Р.
, где α1, α2, …, αm - натуральные числа, 2≤m≤n, αj≤n и j=1, 2, …, m, причем, по крайней мере, одно из проверочных МДЧ формируют в зависимости от коллективного открытого ключа Р.
Новым является также то, что коллективный открытый ключ Р формируют в зависимости от точек эллиптической кривой 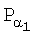 ,
, 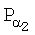 , …,
, …, 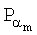 , по формуле
, по формуле 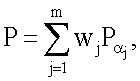
где wj - вспомогательные МДЧ.
Новым является также и то, что при формировании открытых ключей точки P1, Р2, …, Рn эллиптической кривой генерируют по формуле Рi=diG, где i=1, 2, …, n, G - дополнительно сгенерированная точка эллиптической кривой, a di=zki mod q, z>1 - натуральное число, q - порядок точки G эллиптической кривой, ЭЦП Q формируют в виде четырех МДЧ xR, yR, хZ и yZ, для чего генерируют m случайных МДЧ 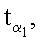
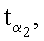 …,
…, 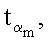 генерируют m точек
генерируют m точек 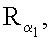
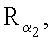 …,
…, 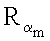 эллиптической кривой по формуле
эллиптической кривой по формуле 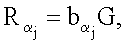 где
где  j=1, 2, …, m, после чего генерируют первое и второе МДЧ электронной цифровой подписи в виде соответственно абсциссы xR и ординаты yR точки R эллиптической кривой путем генерации точки R эллиптической кривой по формуле
j=1, 2, …, m, после чего генерируют первое и второе МДЧ электронной цифровой подписи в виде соответственно абсциссы xR и ординаты yR точки R эллиптической кривой путем генерации точки R эллиптической кривой по формуле 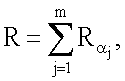 затем генерируют промежуточное МДЧ е по формуле е=хRН mod δ, где xR - абсцисса точки R и δ - вспомогательное МДЧ, генерируют m точек
затем генерируют промежуточное МДЧ е по формуле е=хRН mod δ, где xR - абсцисса точки R и δ - вспомогательное МДЧ, генерируют m точек 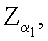
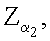 …,
…,  эллиптической кривой по формуле
эллиптической кривой по формуле 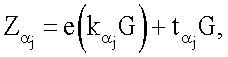 после чего генерируют третье и четвертое МДЧ электронной цифровой подписи в виде соответственно абсциссы xZ и ординаты yZ точки Z эллиптической кривой путем генерации точки Z эллиптической кривой по формуле
после чего генерируют третье и четвертое МДЧ электронной цифровой подписи в виде соответственно абсциссы xZ и ординаты yZ точки Z эллиптической кривой путем генерации точки Z эллиптической кривой по формуле 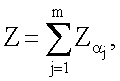 причем первое проверочное МДЧ А формируют по формуле А=xW, где xW - абсцисса точки W эллиптической кривой, вычисленной по формуле W=zZ, а второе проверочное МДЧ В формируют по формуле В=хU, где хU - абсцисса точки U эллиптической кривой, вычисленной по формуле U=еР+R.
причем первое проверочное МДЧ А формируют по формуле А=xW, где xW - абсцисса точки W эллиптической кривой, вычисленной по формуле W=zZ, а второе проверочное МДЧ В формируют по формуле В=хU, где хU - абсцисса точки U эллиптической кривой, вычисленной по формуле U=еР+R.
Новым также является и то, что при формировании открытых ключей точки P1, Р2, …, Рn эллиптической кривой генерируют по формуле Pi=diG, где i=1, 2, …, n, G - дополнительно сгенерированная точка эллиптической кривой, a di=zki, mod q, z>1 - натуральное число, q - порядок точки G эллиптической кривой, ЭЦП Q формируют в виде трех МДЧ е, xZ и yZ, для чего генерируют m случайных МДЧ 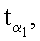
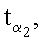 …,
…, 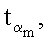 генерируют m точек
генерируют m точек 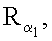
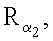 …,
…, 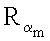 эллиптической кривой по формуле
эллиптической кривой по формуле 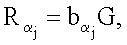 где
где 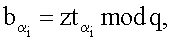 j=1, 2, …, m, генерируют точку R эллиптической кривой по формуле
j=1, 2, …, m, генерируют точку R эллиптической кривой по формуле 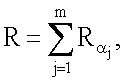 после чего формируют первое МДЧ е электронной цифровой подписи по формуле е=хRН mod δ, где xR - абсцисса точки R и δ - вспомогательное МДЧ, затем генерируют m точек
после чего формируют первое МДЧ е электронной цифровой подписи по формуле е=хRН mod δ, где xR - абсцисса точки R и δ - вспомогательное МДЧ, затем генерируют m точек 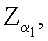
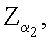 …,
…, 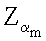 эллиптической кривой по формуле
эллиптической кривой по формуле 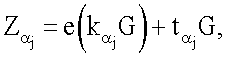 после чего генерируют второе и третье МДЧ электронной цифровой подписи в виде соответственно абсциссы xZ и ординаты yZ точки Z эллиптической кривой путем генерации точки Z эллиптической кривой по формуле
после чего генерируют второе и третье МДЧ электронной цифровой подписи в виде соответственно абсциссы xZ и ординаты yZ точки Z эллиптической кривой путем генерации точки Z эллиптической кривой по формуле 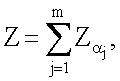 причем первое проверочное МДЧ А формируют по формуле
причем первое проверочное МДЧ А формируют по формуле
А=хR'Н mod δ,
где xR' - абсцисса точки R' эллиптической кривой, вычисленной по формуле R'=zZ-еР, а второе проверочное МДЧ В формируют по формуле В=е.
Новым также является и то, что при формировании открытых ключей точки P1, P2, …, Pn эллиптической кривой генерируют по формуле Pi=kiG, где i=1, 2, …, n, G - дополнительно сгенерированная точка эллиптической кривой, имеющая порядок q, а ЭЦП формируют в виде пары МДЧ е и s, для чего генерируют m случайных МДЧ 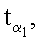
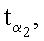 …,
…, 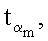 генерируют m точек
генерируют m точек 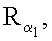
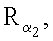 …,
…, 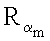 эллиптической кривой по формуле
эллиптической кривой по формуле 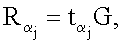 где j=1, 2, …, m, генерируют точку R эллиптической кривой по формуле
где j=1, 2, …, m, генерируют точку R эллиптической кривой по формуле 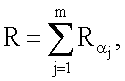 после чего формируют первое МДЧ е электронной цифровой подписи по формуле е=хRН mod δ, где xR - абсцисса точки R и δ - вспомогательное простое МДЧ, затем генерируют m МДЧ
после чего формируют первое МДЧ е электронной цифровой подписи по формуле е=хRН mod δ, где xR - абсцисса точки R и δ - вспомогательное простое МДЧ, затем генерируют m МДЧ 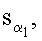 ,
, 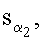 …,
…, 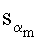 по формуле
по формуле 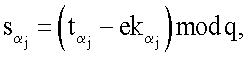 после чего генерируют второе МДЧ s электронной цифровой подписи по формуле
после чего генерируют второе МДЧ s электронной цифровой подписи по формуле 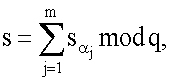
причем первое проверочное МДЧ А формируют по формуле
А=xR'H mod δ,
где хR' - абсцисса точки R' эллиптической кривой, вычисленной по формуле R'=еР+sG, а второе проверочное МДЧ В формируют по формуле В=е.
Предлагаемый способ может быть использован для числа пользователей равного n≥2. Пользователи условно обозначаются номерами i=1, 2, …, n. Этот номер используется как индекс, указывающий на то, какому пользователю принадлежит секретный и открытый ключи, или на то, какой из пользователей генерирует отмеченные индексом МДЧ или точки ЭК. Из совокупности n пользователей некоторое их подмножество, состоящее из m произвольно выбранных пользователей, может быть задано номерами пользователей входящих в данное подмножество, например номерами α1, α2, …, αm, каждый из которых выбирается из множества чисел 1, 2, …, n. Таким образом, числа αj, где j=1, 2, …, m, представляют собой выборку произвольных m номеров из множества {1, 2, …, n}, при этом m≤n. Соответственно этому совокупность открытых ключей 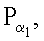
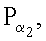 …,
…, 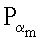 представляет собой выборку из множества всех открытых ключей P1, P2, …, Pn, а совокупность секретных ключей ka, где j=1, 2, …, m, представляет собой выборку из множества всех секретных ключей ki, где i=1, 2, …, n.
представляет собой выборку из множества всех открытых ключей P1, P2, …, Pn, а совокупность секретных ключей ka, где j=1, 2, …, m, представляет собой выборку из множества всех секретных ключей ki, где i=1, 2, …, n.
Корректность заявленного способа доказывается теоретически. Рассмотрим, например, вариант реализации способа по п.5 формулы изобретения. Коллективный открытый ключ, соответствующий подмножеству пользователей с условными номерами α1, α2, …, αm, представляет собой точку
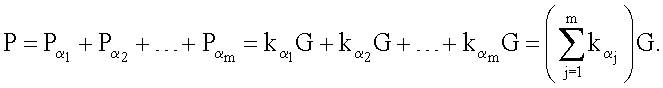
Значения 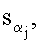 которые представляют собой «доли» пользователей в коллективной подписи, генерируются по формуле
которые представляют собой «доли» пользователей в коллективной подписи, генерируются по формуле 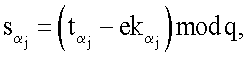 поэтому
поэтому
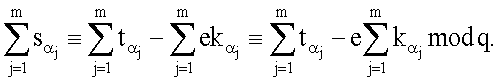
Значение точки R', используемой для формирования первого проверочного МДЧ А, генерируется по формуле R'=еР+sG, т.е. оно равно
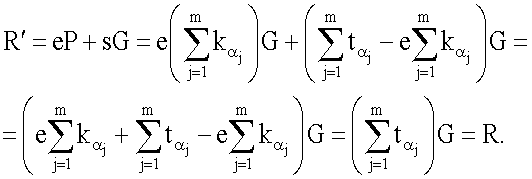
Следовательно, A=xR'Hmodδ=xRHmodδ=e=В, т.е. правильно сформированная коллективная подпись удовлетворяет процедуре проверки подписи, т.е. корректность процедур генерации и проверки ЭЦП доказана.
Рассмотрим примеры реализации заявленного технического решения с использованием ЭК, описываемой уравнением (см. Приложение 1, пп.15-19):
y2=х3+ax+bmodp,
где конкретные значения использованных параметров описаны в приводимых ниже численных примерах. Использованные в примерах ЭК были сгенерирована с помощью программы, разработанной специально для генерации ЭК, генерации точек ЭК, включая точки с заданным порядком, и выполнения операций над точками ЭК. Приводимые в примере МДЧ записаны для краткости в виде десятичных чисел, которые в вычислительных устройствах представляются и преобразуются в двоичном виде, т.е. в виде последовательности сигналов высокого и низкого потенциала.
Пример 1. Реализация заявляемого способа по п.2 формулы изобретения
В данном примере иллюстрируется п.2 формулы изобретения. В нем используется ЭК с параметрами, обеспечивающими достаточную стойкость для применения при решении реальных практических задач аутентификации информации. Этот пример иллюстрирует реальные размеры чисел, которые используются на практике при генерации и проверке подлинности ЭЦП. Особенностью данного примера является то, что принимают ЭД (представленный МДЧ Н), который состоит из двух частей, представленных МДЧ Н1 и Н2. При этом первый пользователь подписывает первую часть документа, второй пользователь - вторую, а третий пользователь подписывает весь документ целиком. Возможность реализации коллективной ЭЦП с такими свойствами обеспечивается за счет того, что при проверке ЭЦП используется коллективный открытый ключ, формируемый в зависимости от открытых ключей пользователей по формуле Р=w1P1+w2P2+w3Р3, где w1=Н1, w2=H2 и w3=Н3.
В примере 1 используется ЭК, определяемая следующими параметрами:
а=5521767865737634555390416300599776622347333359784, b=9717196 и р=5521767865737634555390416300599776622347333359787.
Данная ЭК содержит количество точек равное простому числу N=5521767865737634555390416228783886913339823841723, т.е. любая ее точка имеет порядок q, равный значению N, т.е. q=N.
Рассмотрим коллектив из трех пользователей. При формировании и проверке подлинности ЭЦП (подписью является пара чисел е и s) выполняют следующую последовательность действий:
1. Генерируют ЭК с параметрами, указанными выше.
2. Формируют секретные ключи в виде случайных МДЧ:
k1=8182108890892890101467333434019 - ключ первого пользователя;
k2=3952504539403758278808581024791 - ключ второго пользователя;
k3=9763160941600092631935520658071 - ключ третьего пользователя.
3. Формируют открытые ключи в виде точек ЭК P1, Р2, Р3, для чего
3.1. Генерируют точку G, имеющую порядок q:
G=(4058138998817699569976678358233335958495037969465,
768568926336036825718495218916308682494116144160);
3.2. Генерируют точки P1, Р2, Р3 по формуле Рi=kiG, где i=1, 2, 3:
P1=(2406767665928158899446906165821747218883574602371, 562377648521692290689031507205008060205345636991);
Р2=(348708108378027085357389414044825237922683510732, 1402026191996080196399482770468472598076052599809)
P3=(4307166077833519301063322533024162005091025020313, 5280296312549156028148905914215570655514986217509).
4. Принимают ЭД, представленный МДЧ Н и состоящий из двух частей, представленных МДЧ Н1 и H2:
Н=8925999026871145131520337612117778680659192576033;
H1=135708092215597910168314154751917220633712178686;
Н2=3812498990028819155316571350634376652814331770527.
5. Формируют ЭЦП Q в виде двух МДЧ е и s, для чего выполняют следующие действия.
5.1. Первый, второй и третий пользователи генерируют случайные МДЧ t1, t2 и t3 соответственно:
t1=2090880922625982683584460167862382379;
t2=5360383526856663700583896205266418341;
t3=7677118810723142352012317453400887449.
5.2. Затем первый, второй и третий пользователи генерируют точки R1, R2 и R3 соответственно по формуле Ri=tiG:
R1=(4533360075292446608850664400364711592205136618460, 1175061337062232179584348686477324762101164050095);
R2=(1958279223827902047379336465285895435330140185477, 8836508908256232955144234242970494318564852573);
R3=(5038616028852959877509554081789667436853794753557, 209613157933044677924551688484534713038841468913).
5.3. Генерируют точку R по формуле R=R1+R2+R3:
R=(2597097970263610863546069436833994580002105418569, 3304915040104400813802374282473985550015521973383).
5.4. Формируют МДЧ е по формуле е=xR mod δ, где xR - абсцисса точки R и δ - вспомогательное простое МДЧ (δ=7118198218659321028989011):
е=5079008233076932087473789.
5.5. Первый, второй и третий пользователи генерируют МДЧ s1, s2 и s3 соответственно по формуле si=(ti-ewiki) mod q, где i=1, 2, 3; w1=Н1; w2=H2; w3=H и q=N:
s1=133444963875333388923743187271473122915443205289;
s2=1887661653203847944710282450835612551620081427016;
s3=4850696161955991125559318084555021335580302189827.
5.6. Генерируют МДЧ s=s1+s2+s3 mod q:
s=1350034913297537903802927493878220096776002980409.
6. Формируют первое проверочное МДЧ А, для чего выполняют следующую последовательность действий.
6.1. Формируют коллективный открытый ключ в виде точки Р по формуле Р=w1P1+w2P2+w3Р3:
w1P1=(1386084349002545424511668926945575066838407867380, 4543633731958840101124845818771841004374561021017)
w2P2=(299211431532419026428141393395396288778694972469, 5300327094421154876022064946876206296853312043729)
w3Р3=(4523528487954522900878694877895556963796345154180, 4100826103480972798980996909196526199327733122181)
Р=(228426539485900338090938878090464611548638254406, 1202278174553095231135389060209649902535727110543).
6.2. Генерируют точку R'=eP+sG:
eP=(4556848179595887141400726723891321438602307875189, 2883779289574756983177387955618073719731329543379);
sG=(1360352815531577166684912233134001496389816081366, 3543269787247235781900897404104279341644752005600);
R'=(2597097970263610863546069436833994580002105418569, 3304915040104400813802374282473985550015521973383);
6.3. Генерируют МДЧ А по формуле A=xR'Hmod δ, где дополнительное МДЧ δ=7118198218659321028989011:
А=5079008233076932087473789.
7. Формируют второе проверочное МДЧ В путем копирования МДЧ е:
В=е=5079008233076932087473789.
8. Сравнивают первое А и второе В проверочные МДЧ.
Сравнение показывает, что параметры МДЧ А и В совпадают. Совпадение значений А и В означает, что коллективная ЭЦП является подлинной, т.е. относится к принятому ЭД, представленному МДЧ Н, причем первый пользователь подписал часть ЭД, представленную МДЧ Н1, второй пользователь подписал часть ЭД, представленную МДЧ H2, а третий пользователь подписал ЭД целиком.
Пример 2. Реализация заявляемого способа по п.3 формулы изобретения
Данный пример относится к реализации заявленного технического решения с искусственно уменьшенной разрядностью используемых чисел и поясняет реализацию заявляемого способа по п.3 формулы изобретения. В данном примере задается значение z=13917 и при формировании и проверке подлинности ЭЦП (подписью является пара точек ЭК, обозначенных буквами R и Z) выполняют следующую последовательность действий:
1. Генерируют ЭК с параметрами:
р=1449024649,
а=1449024646;
b=1507;
N=q=1449049321.
2. Формируют секретные ключи в виде случайных МДЧ
k1=35132631 - секретный ключ первого пользователя;
k2=567916337 - секретный ключ второго пользователя;
k3=132552971 - секретный ключ третьего пользователя.
3. Формируют открытые ключи в виде точек P1, Р2 и Р3, для чего выполняют следующие действия:
3.1. Генерируют точку G, имеющую порядок q:
G=(1080340158, 754837262).
3.2. Формируют вспомогательные МДЧ d1, d2 и d3 по формуле di=zki mod q, где i=1, 2, 3:
d1=13917·35132631 mod q=611204450;
d2=13917·567916337 mod q=576665295;
d3=13917·132552971 mod q=99911774.
3.3. Генерируют точки P1, Р2 и Р3 по формуле Рi=z(kiG)=(zki)G=diG:
P1=(1329656100, 292197808) - открытый ключ первого пользователя;
P2=(1051928635, 239761167) - открытый ключ второго пользователя;
P3=(1359744381, 928409442) - открытый ключ третьего пользователя.
4. Принимают ЭД, представленный МДЧ Н=171315687.
5. Формируют ЭЦП Q в виде четырех МДЧ xR, yR, xZ и yz, являющихся координатами точек R и Z ЭК, для чего выполняют следующие действия.
5.1. Первый, второй и третий пользователи генерируют случайные МДЧ t1, t2 и t3, соответственно:
t1=172637431;
t2=36716173;
t3=71259291.
5.2. Затем первый, второй и третий пользователи генерируют МДЧ b1, b2, и b3 соответственно по формуле bi=zti mod q:
b1=13917·172637431 mod q=71353009;
b2=13917·36716173 mod q=913618649;
b3=13917·71259291 mod q=565817283.
5.3. Затем первый, второй и третий пользователи генерируют точки R1, R2 и R3 соответственно по формуле Ri=biG:
R1=(281198047, 813455618);
R2=(1260148915, 294769180);
R3=(1391070805, 541095949).
5.4. Генерируют точку R по формуле R=R1+R2+R3:
R=(xR, yR)=(337223575, 1350626111).
5.5. Формируют вспомогательное МДЧ е по формуле е=xRHmod δ, где xR - абсцисса точки R и δ - вспомогательное МДЧ (δ=348743991):
е=337223575·171315687 mod δ=54524994.
5.6. Генерируют точки Zi по формуле Zi=e(kiG)+tiG=(eki+ti)G:
ek1+t1=54524994·35132631+172637431modq=1140036991;
ek2+t2=54524994·567916337+36716173modq=104065810;
ek3+t3=54524994·132552971+71259291modq=638476987:
Z1=(502331244, 1026983590);
Z2=(1362556964, 156518973);
Z3=(697927304, 886677154).
5.7. Генерируют точку Z по формуле Z=Z1+Z2+Z3:
Z=(xZ, yZ)=(714524287, 1037968014).
6. Формируют первое проверочное МДЧ А, для чего генерируют точку V=zZ=(1001319513, 191443386) и формируют А путем копирования абсциссы точки V:
A=1001319513.
7. Формируют второе проверочное МДЧ В, для чего выполняют следующие действия.
7.1. Формируют коллективный открытый ключ в виде точки Р по формуле Р=Р1+P2+P3:
Р=(672831345, 705469329);
7.2. Генерируют точку W=еР+R:
еР=(1146914821, 380461506);
W=(1001319513, 191443386).
7.3. Генерируют МДЧ В путем копирования абсциссы точки W:
B=1001319513.
8. Сравнивают первое и второе проверочные МДЧ. Они совпадают, поэтому подпись признается подлинной.
Отметим, что в результате выполнения п.5 примера 1 формируется ЭЦП в виде четырех МДЧ 337223575, 1350626111, 714524287 и 1037968014, которые могут быть представлены точками R=(337223575, 1350626111) и S=(714524287, 1037968014). Эти два варианта представления ЭЦП являются идентичными.
Пример 3. Реализация заявляемого способа по п.4 формулы изобретения
Данный пример относится к реализации заявленного технического решения с искусственно уменьшенной разрядностью используемых чисел и поясняет реализацию заявляемого способа по п.4 формулы изобретения. В примере 3 также задается значение z=13917 и используются те же значения параметров ЭК, секретных и открытых ключей, а также остальных используемых МДЧ, что и в примере 2. Отличие примера 3 от примера 2 состоит в том, что в примере 3 в качестве ЭЦП Q формируется тройка МДЧ е, xZ и yZ, из которых второе и третье МДЧ представляют собой координаты некоторой точки ЭК. ЭЦП может быть тождественно представлена в виде и пары (е, Z), где е - МДЧ и Z - точка ЭК. Использование ЭЦП вида (е, Z) позволяет сократить размер подписи примерно на 25% по сравнению с примером 2. При формировании и проверке подлинности ЭЦП (подписью является пара точек ЭК, обозначенных буквами R и Z) в примере 3 выполняют следующую последовательность действий.
1. Выполняют последовательность действий, предписанных пп.1, 2, 3 и 4 примера 1.
2. Формируют ЭЦП Q в виде трех МДЧ е, xZ и yZ, где xZ и yZ - координаты некоторой точки Z ЭК, которая генерируется в зависимости от секретных ключей пользователей, участвующих в формировании коллективной ЭЦП, для чего выполняют следующие действия.
2.1. Первый, второй и третий пользователи генерируют случайные МДЧ t1, t2 и t3 соответственно:
t1=172637431;
t2=36716173;
t3=71259291.
2.2. Затем первый, второй и третий пользователи генерируют МДЧ b1, b2 и b3 соответственно по формуле bi=zti mod q:
b1=13917·172637431 mod q=71353009;
b2=13917·36716173 mod q=913618649;
b3=13917·71259291 mod q=565817283.
2.3. Затем первый, второй и третий пользователи генерируют точки R1, R2 и R3 соответственно по формуле Ri=biG:
R1=(281198047, 813455618);
R2=(1260148915, 294769180);
R3=(1391070805, 541095949).
2.4. Генерируют точку R по формуле R=R1+R2+R3:
R=(337223575, 1350626111).
2.5. Формируют первое МДЧ е электронной цифровой подписи по формуле е=xRH mod δ, где xR - абсцисса точки R и δ - вспомогательное МДЧ (δ=348743991):
е=337223575·171315687 mod δ=54524994.
2.6. Генерируют точки Zi по формуле Zi=e(kiG)+tiG=(eki+ti)G:
ek1+t1=54524994·35132631+172637431 mod q=1140036991;
ek2+t2=54524994·567916337+36716173 mod q=104065810;
ek3+t3=54524994·132552971+71259291 mod q=638476987:
Z1=(502331244, 1026983590);
Z2=(1362556964, 156518973);
Z3=(697927304, 886677154).
2.7. Генерируют второе и третье МДЧ е электронной цифровой подписи в виде координат точки Z ЭК, вычисляемой по формуле Z=Z1+Z2+Z3:
Z=(xZ, yZ)=(714524287, 1037968014).
3. Формируют первое проверочное МДЧ А, для чего выполняют следующую последовательность действий.
3.1. Формируют коллективный открытый ключ в виде точки Р по формуле P=P1+P2+P3:
Р=(672831345, 705469329);
3.2. Генерируют точку R'=zS-eP=zS+(q-e)P:
zS=(1001319513, 191443386);
(q-e)P=1394524327·(672831345, 705469329)=(1146914821, 1068563143);
R'=(1001319513, 191443386)+(1146914821, 1068563143)=(337223575, 1350626111);
3.3. Генерируют МДЧ А по формуле A=xR'Hmod δ, где дополнительное МДЧ δ=348743991:
А=337223575·171315687 mod δ=54524994.
4. Формируют второе проверочное МДЧ В путем копирования МДЧ е:
В=е=54524994.
5. Сравнивают первое А и второе В проверочные МДЧ. Они совпадают, поэтому подпись признается подлинной.
Пример 4. Реализация заявляемого способа по п.5 формулы изобретения
В данном примере используется ЭК, секретные и открытые ключи пользователей такие же, как и в примере 1. В примере используется ЭК, определяемая следующими параметрами:
а=5521767865737634555390416300599776622347333359784, b=9717196 и р=5521767865737634555390416300599776622347333359787.
Данная ЭК содержит количество точек равное простому числу N=5521767865737634555390416228783886913339823841723, т.е. любая ее точка имеет порядок q, равный значению N, т.е. q=N.
Рассмотрим коллектив из трех пользователей. При формировании и проверке подлинности ЭЦП (подписью является пара МДЧ е и s.) выполняют следующую последовательность действий.
1. Генерируют ЭК с параметрами, указанными выше.
2. Формируют секретные ключи в виде случайных МДЧ
k1=8182108890892890101467333434019 - ключ первого пользователя;
k2=3952504539403758278808581024791 - ключ второго пользователя;
k3=9763160941600092631935520658071 - ключ третьего пользователя.
3. Формируют открытые ключи в виде точек ЭК P1, Р2, Р3, для чего выполняют следующие действия.
3.1. Генерируют точку G:
G=(4058138998817699569976678358233335958495037969465,
768568926336036825718495218916308682494116144160);
3.2. Генерируют точки P1, P2, P3 по формуле Рi=kiG, где i=1, 2, 3:
P1=(2406767665928158899446906165821747218883574602371, 562377648521692290689031507205008060205345636991);
P2=(348708108378027085357389414044825237922683510732, 1402026191996080196399482770468472598076052599809)
P3=(4307166077833519301063322533024162005091025020313, 5280296312549156028148905914215570655514986217509).
4. Принимают ЭД, представленный, например, следующим МДЧ Н (в качестве которого может быть взята, в частности, хэш-функция от ЭД):
H=8925999026871145131520337612117778680659192576033.
5. Формируют ЭЦП Q в виде пары МДЧ е и s, для чего выполняют следующие действия.
5.1. Первый, второй и третий пользователи генерируют случайные МДЧ t1, t2 и t3 соответственно:
t1=2090880922625982683584460167862382379;
t2=5360383526856663700583896205266418341;
t3=7677118810723142352012317453400887449.
5.2. Затем первый, второй и третий пользователи генерируют точки R1, R2 и R3 соответственно по формуле Ri=tiG:
R1=(4533360075292446608850664400364711592205136618460, 1175061337062232179584348686477324762101164050095);
R2=(1958279223827902047379336465285895435330140185477, 8836508908256232955144234242970494318564852573);
R3=(5038616028852959877509554081789667436853794753557, 209613157933044677924551688484534713038841468913).
5.3. Генерируют точку R по формуле R=R1+R2+R3:
R=(2597097970263610863546069436833994580002105418569, 3304915040104400813802374282473985550015521973383).
5.4. Формируют первое МДЧ е электронной цифровой подписи по формуле е=xRHmod δ, где xR - абсцисса точки R и δ - вспомогательное простое МДЧ (δ=7118198218659321028989011):
e=4927124871592959793329711.
5.5. Первый, второй и третий пользователи генерируют МДЧ s1, s2 и s3 соответственно по формуле si=(ti-eki) mod q, где q'=N и i=1, 2, 3:
s1=359849983424274307716254877984953159149283598626;
s2=2228471503399271451844174588034195792013686207551;
s3=3321295738385055881020248326363803564813773402448.
5.6. Генерируют второе МДЧ s электронной цифровой подписи по формуле s=s1+s2+s3 mod q:
s=387849359470967085190261563599065602636919366902.
6. Формируют первое проверочное МДЧ А, для чего выполняют следующую последовательность действий.
6.1. Формируют коллективный открытый ключ в виде точки Р по формуле Р=P1+P2+Р3:
Р=(2597097970263610863546069436833994580002105418569, 3304915040104400813802374282473985550015521973383).
6.2. Генерируют точку R'=eP+sG:
еР=(146955471348564375364922408624400975297984578370, 5067487498889971752716283347516092217397817107870);
sG=(2925357468651177964466813642233631538174971712513, 599550386022153150210626227063281723596625174740);
R'=(2597097970263610863546069436833994580002105418569, 3304915040104400813802374282473985550015521973383).
6.3. Генерируют МДЧ А по формуле А=xR'Hmod δ, где дополнительное МДЧ δ=7118198218659321028989011:
A=4927124871592959793329711.
7. Формируют второе проверочное МДЧ В путем копирования МДЧ е:
В=е=4927124871592959793329711.
8. Сравнивают первое А и второе В проверочные МДЧ.
Сравнение показывает, что параметры МДЧ А и В совпадают. Совпадение значений А и В означает, что коллективная ЭЦП является подлинной, т.е. относится к принятому ЭД, представленному МДЧ Н, и сформирована тремя пользователями, по открытым ключам которых был сформирован коллективный открытый ключ, использованный для проверки подлинности подписи.
Примеры 1, 2, 3 и 4 экспериментально подтверждают корректность реализации заявляемого способа, что дополняет математическое доказательство корректности, приведенное выше.
Таким образом показано, что заявляемый способ может быть положен в основу стойких систем ЭЦП, обеспечивающих уменьшение размера коллективной ЭЦП.
Приведенные примеры и математическое обоснование показывают, что предлагаемый способ формирования и проверки подлинности ЭЦП работает корректно, технически реализуем и позволяет достичь сформулированного технического результата.
Приложение 1
Толкование терминов, используемых в описании заявки
1. Двоичный цифровой электромагнитный сигнал - последовательность битов в виде нулей и единиц.
2. Параметры двоичного цифрового электромагнитного сигнала: разрядность и порядок следования единичных и нулевых битов.
3. Разрядность двоичного цифрового электромагнитного сигнала - общее число его единичных и нулевых битов, например число 10011 является 5-разрядным.
4. Электронная цифровая подпись (ЭЦП) - двоичный цифровой электромагнитный сигнал, параметры которого зависят от подписанного электронного документа и от секретного ключа. Проверка подлинности ЭЦП осуществляют с помощью открытого ключа, который зависит от секретного ключа.
5. Электронный документ (ЭД) - двоичный цифровой электромагнитный сигнал, параметры которого зависят от исходного документа и способа его преобразования к электронному виду.
6. Секретный ключ - двоичный цифровой электромагнитный сигнал, используемый для формирования подписи к заданному электронному документу. Секретный ключ представляется, например, в двоичном виде как последовательность цифр «0» и «1».
7. Открытый ключ - двоичный цифровой электромагнитный сигнал, параметры которого зависят от секретного ключа и который предназначен для проверки подлинности цифровой электронной подписи.
8. Хэш-функция от электронного документа - двоичный цифровой электромагнитный сигнал, параметры которого зависят от электронного документа и выбранного метода ее вычисления.
9. Многоразрядное двоичное число (МДЧ) - двоичный цифровой электромагнитный сигнал, интерпретируемый как двоичное число и представляемый в виде последовательности цифр «0» и «1».
10. Операция возведения числа S в дискретную степень А по модулю n - это операция, выполняемая над конечным множеством натуральных чисел
{0, 1, 2, …, n-1}, включающем n чисел, являющихся остатками от деления всевозможных целых чисел на число n; результат выполнения операций сложения, вычитания и умножения по модулю n представляет собой число из этого же множества [Виноградов И.М. Основы теории чисел. - М.: Наука, 1972. - 167 с.]; операция возведения числа S в дискретную степень Z по модулю n определяется как Z-кратное последовательное умножение по модулю n числа S на себя, т.е. в результате этой операции также получается число W, которое меньше или равно числу n-1; даже для очень больших чисел S, Z и n существуют эффективные алгоритмы выполнения операции возведения в дискретную степень по модулю [см. Молдовян А.А., Молдовян Н.А., Гуц Н.Д., Изотов Б.В. Криптография: скоростные шифры. - СПб, БХВ-Петербург, 2002. - с.58-61 или Б.Шнайер. Прикладная криптография. - М., изд-во «Триумф», 2002. - с.278-280] и электронные устройства, осуществляющие эту операцию с большой скоростью [У.Диффи. Первые десять лет криптографии с открытым ключом // ТИИЭР. 1988. т.76. №5. с.67-68]; выполнение операции возведения числа S в дискретную степень Z по модулю n обозначается как W=SZ mod n, где W - число являющееся результатом выполнения данной операции.
11. Функция Эйлера от натурального числа n - это число чисел, являющихся взаимно простыми с n и не превосходящими n [Виноградов И.М. Основы теории чисел. - М.: Наука, 1972. - 167 с.; Бухштаб А.А. Теория чисел. - М.: Просвещение, 1966. - 384 с].
12. Показатель q по модулю n числа а, являющегося взаимно простым с n - это минимальное из чисел γ, для которых выполняется условие aγ mod n=1, т.е. q=min{γ1, γ2, …} [Виноградов И.М. Основы теории чисел. - М.: Наука, 1972. - 167 с.].
13. Операция деления целого числа А на целое число В по модулю n выполняется как операция умножения по модулю n числа А на целое число B-1, которое является обратным к В по модулю n.
14. Порядок числа q по модулю n числа а - это показатель q по модулю n числа а.
15. Эллиптическая кривая (ЭК) - это совокупность пар МДЧ, которые удовлетворяют соотношению вида
y2=х3+ax+b mod p,
где коэффициенты а и b и модуль р определяют конкретный вариант ЭК. Над ЭК определены операция сложения пар МДЧ и операция умножения пары МДЧ на произвольное целое число. Указанные пары МДЧ записываются в виде (x, y), где x называется абсциссой точки, а y - ординатой. Операции, определенные над точками ЭК, выполняются как операции над координатами точек ЭК. В результате вычисляется пара МДЧ, которая является координатами новой точки, являющейся результатом операции. Точки ЭК называются равными, если равны их обе координаты x и y. Детальное описание ЭК можно найти в широко доступных книгах: [Б.Я.Рябко, А.Н.Фионов. Криптографические методы защиты информации. М., Горячая линия - Телеком, 2005. - 229 с. (см. с.97-130)]
16. Операция сложения двух точек А и В с координатами (хA, yA) и (xB, yB) соответственно выполняется по формулам:
xC=k2-xA-xBmod p и yC=k(xA-xC)-yAmod p,
где 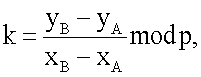 если точки А и В не равны, и
если точки А и В не равны, и 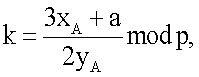 если точки А и В равны.
если точки А и В равны.
17. Операция умножения точки А на натуральное число n определяется как многократное сложение токи А:
nA=А+А+…+А (n раз).
Результатом умножения любой точки ЭК на нуль определяется точка, называемая бесконечно удаленной точкой и обозначаемой буквой О. Две точки А=(x, y) и -А=(x, -y) называются противоположными. Умножение на целое отрицательное число -n определяется следующим образом: (-n)А=n(-А). По определению принимают, что сумма двух противоположных точек равна бесконечно удаленной точке О [Б.Я.Рябко, А.Н.Фионов. Криптографические методы защиты информации. М., Горячая линия - Телеком, 2005. - 229 с. (см. с.97-130)].
18. Выполнение операций на точками ЭК осуществляется в вычислительных устройствах как действия над двоичными цифровыми электромагнитными сигналами, осуществляемыми по определенными правилам, определяемым через операции над МДЧ.
19. Порядком точки А ЭК называется наименьшее натуральное число q, такое что qA=О, т.е. такое, что результатом умножения точки А на число q является бесконечно удаленная точка.
Изобретение относится к области электросвязи, а именно к области криптографических устройств и способов проверки электронной цифровой подписи (ЭЦП). Изобретение позволяет уменьшить размер коллективной ЭЦП без снижения ее уровня стойкости. Способ генерации и проверки ЭЦП включает следующую последовательность действий: генерируют эллиптическую кривую в виде совокупности точек, каждая из которых задается двумя многоразрядными двоичными числами (МДЧ), формируют n>2 секретных ключей в виде МДЧ k1, k2, …, kn, по секретным ключам формируют n открытых ключей в виде точек P1, P2, …, Рn эллиптической кривой, принимают электронный документ, представленный МДЧ Н, в зависимости от принятого электронного документа и от значения секретного ключа формируют ЭЦП Q в виде двух или более МДЧ, формируют коллективный открытый ключ в виде точки Р эллиптической кривой, генерируемой в зависимости от точек 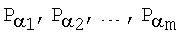 , где α1, α2, …, αm - натуральные числа, 2≤m≤n, αj≤n и j=1, 2, …, m, формируют первое А и второе В проверочные МДЧ, причем, по крайней мере, одно из проверочных МДЧ формируют в зависимости от коллективного открытого ключа Р, сравнивают МДЧ А и В. При совпадении их параметров делают вывод о подлинности электронной цифровой подписи. 4 з.п. ф-лы.
, где α1, α2, …, αm - натуральные числа, 2≤m≤n, αj≤n и j=1, 2, …, m, формируют первое А и второе В проверочные МДЧ, причем, по крайней мере, одно из проверочных МДЧ формируют в зависимости от коллективного открытого ключа Р, сравнивают МДЧ А и В. При совпадении их параметров делают вывод о подлинности электронной цифровой подписи. 4 з.п. ф-лы.
1. Способ генерации и проверки подлинности электронной цифровой подписи, заверяющей электронный документ, заключающийся в том, что генерируют эллиптическую кривую в виде совокупности точек, каждая из которых определяется парой многоразрядных двоичных чисел, являющихся соответственно абсциссой и ординатой данной точки эллиптической кривой в декартовой системе координат, формируют совокупность из n≥2 секретных ключей в виде многоразрядных двоичных чисел k1, k2, …, kn, по секретным ключам формируют n открытых ключей в виде точек P1, Р2, …, Рn эллиптической кривой, принимают электронный документ, представленный многоразрядным двоичным числом Н, в зависимости от принятого электронного документа и от значения секретного ключа формируют электронную цифровую подпись Q в виде двух или более многоразрядных двоичных чисел, формируют первое А и второе В проверочные многоразрядные двоичные числа, сравнивают их и при совпадении их параметров делают вывод о подлинности электронной цифровой подписи, отличающийся тем, что дополнительно формируют коллективный открытый ключ в виде точки Р эллиптической кривой, генерируемой в зависимости от точек эллиптической кривой 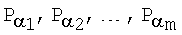 , где α1, α2, …, αm - натуральные числа, 2≤m≤n, αj≤n и j=1, 2, …, m, причем, по крайней мере, одно из проверочных многоразрядных двоичных чисел формируют в зависимости от коллективного открытого ключа Р.
, где α1, α2, …, αm - натуральные числа, 2≤m≤n, αj≤n и j=1, 2, …, m, причем, по крайней мере, одно из проверочных многоразрядных двоичных чисел формируют в зависимости от коллективного открытого ключа Р.
2. Способ по п.1, отличающийся тем, что коллективный открытый ключ Р формируют в зависимости от точек эллиптической кривой 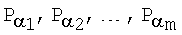 по формуле
по формуле 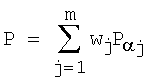 ,
,
где wj - вспомогательные многоразрядные двоичные числа.
3. Способ по п.1, отличающийся тем, что при формировании открытых ключей точки P1, P2, …, Рn эллиптической кривой генерируют по формуле Pi=diG, где i=1, 2, …, n, G - дополнительно сгенерированная точка эллиптической кривой, a di=zki mod q, z>1 - натуральное число, q - порядок точки G эллиптической кривой, электронную цифровую подпись Q формируют в виде четырех многоразрядных двоичных чисел xR, yR, xZ и yZ, для чего генерируют m случайных многоразрядных двоичных чисел 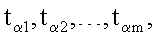 генерируют m точек
генерируют m точек 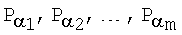 эллиптической кривой по формуле
эллиптической кривой по формуле 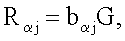 где
где 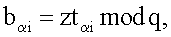 j=1, 2, …, m, после чего генерируют первое и второе многоразрядные двоичные числа электронной цифровой подписи в виде соответственно абсциссы xR и ординаты yR точки R эллиптической кривой путем генерации точки R эллиптической кривой по формуле
j=1, 2, …, m, после чего генерируют первое и второе многоразрядные двоичные числа электронной цифровой подписи в виде соответственно абсциссы xR и ординаты yR точки R эллиптической кривой путем генерации точки R эллиптической кривой по формуле  затем генерируют промежуточное многоразрядное двоичное число е по формуле е=xRН mod δ, где xR - абсцисса точки R и δ - вспомогательное многоразрядное двоичное число, генерируют m точек
затем генерируют промежуточное многоразрядное двоичное число е по формуле е=xRН mod δ, где xR - абсцисса точки R и δ - вспомогательное многоразрядное двоичное число, генерируют m точек 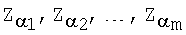 эллиптической кривой по формуле
эллиптической кривой по формуле  , после чего генерируют третье и четвертое многоразрядные двоичные числа электронной цифровой подписи в виде соответственно абсциссы xZ и ординаты yZ точки Z эллиптической кривой путем генерации точки Z эллиптической кривой по формуле
, после чего генерируют третье и четвертое многоразрядные двоичные числа электронной цифровой подписи в виде соответственно абсциссы xZ и ординаты yZ точки Z эллиптической кривой путем генерации точки Z эллиптической кривой по формуле 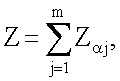 причем первое проверочное многоразрядное двоичное число А формируют по формуле A=xW, где xW - абсцисса точки W эллиптической кривой, вычисленной по формуле W=zZ, а второе проверочное многоразрядное двоичное число В формируют по формуле B=xU, где xU - абсцисса точки U эллиптической кривой, вычисленной по формуле U=eP+R.
причем первое проверочное многоразрядное двоичное число А формируют по формуле A=xW, где xW - абсцисса точки W эллиптической кривой, вычисленной по формуле W=zZ, а второе проверочное многоразрядное двоичное число В формируют по формуле B=xU, где xU - абсцисса точки U эллиптической кривой, вычисленной по формуле U=eP+R.
4. Способ по п.1, отличающийся тем, что при формировании открытых ключей точки P1, Р2, …, Рn эллиптической кривой генерируют по формуле Pi=diG, где i=1, 2, …, n, G - дополнительно сгенерированная точка эллиптической кривой, a di=zki mod q, z>1 - натуральное число, q - порядок точки G эллиптической кривой, электронную цифровую подпись Q формируют в виде трех многоразрядных двоичных чисел е, xz и yz, для чего генерируют m случайных многоразрядных двоичных чисел
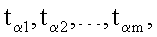 генерируют m точек
генерируют m точек 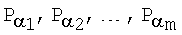 эллиптической кривой по формуле
эллиптической кривой по формуле 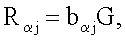 где
где 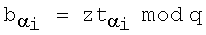 , j=1, 2, …, m, генерируют точку R эллиптической кривой по формуле
, j=1, 2, …, m, генерируют точку R эллиптической кривой по формуле 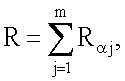 после чего формируют первое многоразрядное двоичное число е электронной цифровой подписи по формуле е=хRН mod δ, где xR - абсцисса точки R и δ - вспомогательное многоразрядное двоичное число, затем генерируют m точек
после чего формируют первое многоразрядное двоичное число е электронной цифровой подписи по формуле е=хRН mod δ, где xR - абсцисса точки R и δ - вспомогательное многоразрядное двоичное число, затем генерируют m точек 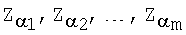 эллиптической кривой по формуле
эллиптической кривой по формуле 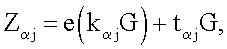 после чего генерируют второе и третье многоразрядные двоичные числа электронной цифровой подписи в виде соответственно абсциссы xZ и ординаты yZ точки Z эллиптической кривой путем генерации точки Z эллиптической кривой по формуле
после чего генерируют второе и третье многоразрядные двоичные числа электронной цифровой подписи в виде соответственно абсциссы xZ и ординаты yZ точки Z эллиптической кривой путем генерации точки Z эллиптической кривой по формуле 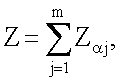 причем первое проверочное многоразрядное двоичное число А формируют по формуле A=xR'H mod δ, где xR' - абсцисса точки R' эллиптической кривой, вычисленной по формуле R'=zZ-eP, а второе проверочное многоразрядное двоичное число В формируют по формуле В=е.
причем первое проверочное многоразрядное двоичное число А формируют по формуле A=xR'H mod δ, где xR' - абсцисса точки R' эллиптической кривой, вычисленной по формуле R'=zZ-eP, а второе проверочное многоразрядное двоичное число В формируют по формуле В=е.
5. Способ по п.1, отличающийся тем, что при формировании открытых ключей точки P1, P2, …, Рn эллиптической кривой генерируют по формуле Pi=kiG, где i=1, 2, …, n, G - дополнительно сгенерированная точка эллиптической кривой, имеющая порядок q, а электронную цифровую подпись формируют в виде пары многоразрядных двоичных чисел е и s, для чего генерируют t случайных многоразрядных двоичных чисел 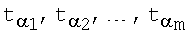 , генерируют m точек
, генерируют m точек 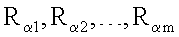 эллиптической кривой по формуле
эллиптической кривой по формуле 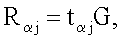 где j=1, 2, …, m, генерируют точку R эллиптической кривой по формуле
где j=1, 2, …, m, генерируют точку R эллиптической кривой по формуле 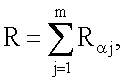 после чего формируют первое многоразрядное двоичное число е электронной цифровой подписи по формуле е=xRН mod δ, где xR - абсцисса точки R и δ - вспомогательное простое многоразрядное двоичное число, затем генерируют m многоразрядных двоичных чисел
после чего формируют первое многоразрядное двоичное число е электронной цифровой подписи по формуле е=xRН mod δ, где xR - абсцисса точки R и δ - вспомогательное простое многоразрядное двоичное число, затем генерируют m многоразрядных двоичных чисел 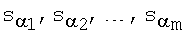 по формуле
по формуле 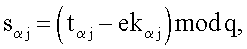 после чего генерируют второе многоразрядное двоичное число s электронной цифровой подписи по формуле
после чего генерируют второе многоразрядное двоичное число s электронной цифровой подписи по формуле 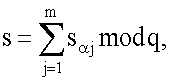 причем первое проверочное многоразрядное двоичное число А формируют по формуле A=xR'H mod δ, где xR' - абсцисса точки R' эллиптической кривой, вычисленной по формуле R'=eP+sG, а второе проверочное многоразрядное двоичное число В формируют по формуле В=е.
причем первое проверочное многоразрядное двоичное число А формируют по формуле A=xR'H mod δ, где xR' - абсцисса точки R' эллиптической кривой, вычисленной по формуле R'=eP+sG, а второе проверочное многоразрядное двоичное число В формируют по формуле В=е.
| Рябко Б.Я | |||
| и др | |||
| Криптографические методы защиты информации | |||
| Москва, Горячая линия - Телеком, 2005, с.110-111 Молдовян А.А | |||
| и др | |||
| Криптография | |||
| Санкт-Петербруг, Лань, 2000, с.156-159 | |||
| US 4995082, 19.02.1991 | |||
| US 4405829, 20.09.1983. |
Авторы
Даты
2009-05-20—Публикация
2007-08-13—Подача