Изобретение относится к области электросвязи и вычислительной техники, а конкретнее к области криптографических способов аутентификации электронных сообщений, передаваемых по телекоммуникационным сетям и сетям ЭВМ, и может быть использовано в системах передачи электронных сообщений (документов), заверенных электронной цифровой подписью (ЭЦП), представленной в виде битовой строки (БС) или нескольких БС. Здесь и далее под БС понимается электромагнитный сигнал в двоичной цифровой форме, параметрами которого являются: число битов и порядок следования их единичных и нулевых значений (толкование используемых в описании терминов приведено в Приложении 1).
Известен способ формирования и проверки ЭЦП, предложенный в патенте США №4405829 от 20.09.1983 и детально описанный также и в книгах [1. М.А.Иванов. Криптография. М., КУДИЦ-ОБРАЗ, 2001; 2. А.Г.Ростовцев, Е.Б.Маховенко. Введение в криптографию с открытым ключом. С-Петербург, Мир и семья, 2001.- с.43]. Известный способ заключается в следующей последовательности действий:
формируют секретный ключ в виде трех простых многоразрядных двоичных чисел (МДЧ)p, q и d, представленных тремя БС;
формируют открытый ключ (n, е) в виде пары МДЧ n и е, где n - число, представляющее собой произведение двух простых МДЧ p и q, и е - МДЧ, удовлетворяющее условию ed=1mod(p-l)(q-1),
принимают электронный документ (ЭД), представленный БС Н,
в зависимости от значения Н, под которым понимается значение МДЧ, представленное БС Н, и значения секретного ключа формируют ЭЦП в виде МДЧ Q=S=Hd mod n.
формируют первое проверочное МДЧ А=Н;
формируют второе проверочное МДЧ В, для чего МДЧ S возводят в целочисленную степень е по модулю n: В=Sе mod n;
сравнивают сформированные проверочные МДЧ А и В;
при совпадении параметров сравниваемых МДЧ А и В делают вывод о подлинности ЭЦП.
Недостатком известного способа является относительно большой размер подписи и необходимость увеличения размера подписи при разработке новых более эффективных методов разложения числа n на множители или при росте производительности современных вычислительных устройств. Это объясняется тем, что значение элемента подписи S вычисляются путем выполнения арифметических операций по модулю n, а стойкость ЭЦП определяется сложностью разложения модуля n на множители p и q.
Известен также способ формирования и проверки подлинности ЭЦП Эль-Гамаля, описанный в книге [Молдовян А.А., Молдовян Н.А., Советов Б.Я. Криптография. - СПб.: Лань, 2000. - с.156-159], который включает следующие действия:
формируют простое МДЧ p и двоичное число G, являющееся первообразным корнем по модулю p, генерируют секретный ключ в виде МДЧ x, в зависимости от секретного ключа формируют открытый ключ в виде МДЧ Y=Gx mod p, принимают ЭД, представленный в виде МДЧ Н, в зависимости от Н и секретного ключа формируют ЭЦП Q в виде двух МДЧ S и R, то есть Q=(S, R);
осуществляют процедуру проверки подлинности ЭЦП, включающую вычисление двух контрольных параметров с использованием исходных МДЧ р, G, Y, Н и S путем возведения МДЧ G, Y, R в дискретную степень по модулю p и сравнение вычисленных контрольных параметров;
при совпадении значений контрольных параметров делают вывод о подлинности ЭЦП.
Недостатком данного способа также является относительно большой размер ЭЦП. Это объясняется тем, что значения элементов подписи S и R вычисляют путем выполнения арифметических операций по модулю p - 1 и по модулю p, соответственно.
Известен также способ формирования и проверки ЭЦП, предложенный в патенте США №4995089 от 19.02.1991. Известный способ заключается в следующей последовательности действий:
формируют простое МДЧ p, такое что р=Nq+1, где q - простое МДЧ;
формируют простое МДЧ а, такое что а≠1 и aq mod p=1;
методом генерации случайной равновероятной последовательности формируют секретный ключ в виде МДЧ k;
формируют открытый ключ в виде МДЧ y по формуле y=ak mod p;
принимают ЭД, представленный МДЧ М;
формируют ЭЦП в виде пары МДЧ (е, s), для чего генерируют случайное МДЧ t, формируют МДЧ R по формуле R=at mod p, формируют МДЧ е=f(M||R), где знак || обозначает операцию присоединения двух МДЧ и f - некоторая специфицированная хэш-функция, значение которой имеет фиксированную длину (обычно 160 или 256 бит), независимую от размера аргумента, т.е. от размера МДЧ M||R, а затем формируют МДЧ s по формуле s=(t+ek) mod q;
формируют первое проверочное МДЧ А, для чего генерируют МДЧ R' пo формуле R'=asy -e mod p и формируют МДЧ е'=f(M||R');
формируют второе проверочное МДЧ В путем копирования МДЧ е: В=е;
сравнивают сформированные проверочные МДЧ А и В;
при совпадении параметров сравниваемых МДЧ А и В делают вывод о подлинности ЭЦП.
Недостатком способа по патенту США является относительно высокая вычислительная сложность процедуры формирования и проверки ЭЦП, что связано с тем, что для обеспечения минимально требуемого уровня стойкости требуется использовать простой модуль p разрядностью не менее 1024 бит.
Наиболее близким по своей технической сущности к заявленному является известный способ формирования и проверки подлинности ЭЦП, предлагаемый российским стандартом ГОСТ Р 34.10-2001 и описанный, например, в книге [Б.Я. Рябко, А.Н. Фионов. Криптографические методы защиты информации. М., Горячая линия - Телеком, 2005. - 229 с. (см. с.110-111)], согласно которому ЭЦП формируется в виде пары МДЧ r и s, для чего генерируют эллиптическую кривую (ЭК) в виде совокупности точек, причем каждая точка представляется двумя координатами в декартовой системе координат в виде двух МДЧ, называемых абсциссой (x) и ординатой (у), затем осуществляют операции генерации точек ЭК, сложения точек ЭК и умножения точки ЭК на число, а также арифметические операции над МДЧ, после чего в результате выполненных операций формируются МДЧ r и s. Указанные операции над точками выполняются как операции над МДЧ, являющимися координатами точек, по известным формулам [Б.Я. Рябко, А.Н. Фионов. Криптографические методы защиты информации. М., Горячая линия - Телеком, 2005.-229 с. (см. с.110-111)]. Операция сложения двух точек А и В с координатами (хA, yA) и (хB, yB), соответственно, выполняется по формулам:
xC=k2-xA-xB mod p и yC=k(xA-xC)-yA mod p,
где 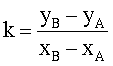 mod p, если точки А и В не равны, и
mod p, если точки А и В не равны, и 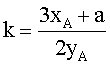 mod p, если точки А и В равны. При вычислении значения k выполняется операция деления МДЧ по модулю простого МДЧ, что ограничивает производительность формирования и проверки подлинности ЭЦП по стандарту ГОСТ Р 34.10-2001. Операция умножения точки А на натуральное число n определяется как многократное сложение точки А:
mod p, если точки А и В равны. При вычислении значения k выполняется операция деления МДЧ по модулю простого МДЧ, что ограничивает производительность формирования и проверки подлинности ЭЦП по стандарту ГОСТ Р 34.10-2001. Операция умножения точки А на натуральное число n определяется как многократное сложение точки А:
nА=А+А+…+А (n раз).
Результатом умножения любой точки ЭК на нуль определяется точка, называемая бесконечно удаленной точкой и обозначаемой буквой О. Две точки А=(х, у) и -А=(х, -у) называются противоположными. Умножение на целое отрицательное число -n определяется следующим образом: (-n)А=n(-А). По определению принимают, что сумма двух противоположных точек равна бесконечно удаленной точке О.
В прототипе, т.е. в способе формирования и проверки подлинности ЭЦП по стандарту ГОСТ Р 34.10-2001, генерируют ЭК, описываемую уравнением у2=х3+ax+b mod p, поэтому генерация ЭК состоит в генерации чисел а, b и p, являющихся параметрами ЭК и однозначно задающих множество точек ЭК, абсцисса и ордината каждой из которых удовлетворяет указанному уравнению. Ближайший аналог (прототип) заключается в выполнении следующей последовательности действий:
генерируют эллиптическую кривую (ЭК), которая представляет собой совокупность пар МДЧ, называемых точками ЭК и обладающих определенными свойствами (см. Приложение 1, пп.27-31);
методом генерации случайной равновероятной последовательности формируют секретный ключ в виде МДЧ k;
формируют открытый ключ Р в виде двух МДЧ, являющихся координатами точки ЭК Р, для чего генерируют точку G, имеющую значение порядка, равное q (порядком точки ЭК называется наименьшее положительное целое число q, такое что результатом умножения данной точки на число q является так называемая бесконечно удаленная точка О; результатом умножения любой точки ЭК на нуль по определению является точка О [Б.Я.Рябко, А.Н.Фионов. Криптографические методы защиты информации. М., Горячая линия - Телеком, 2005. - 229 с.(см. с.97-130)]; см. также Приложение 1, пп.27-31) и генерируют открытый ключ путем умножения точки G на МДЧ k, т.е. формируют открытый ключ по формуле Р=kG;
принимают ЭД, представленный МДЧ Н;
генерируют случайное МДЧ 0<t<q, по которому формируют точку R по формуле R=tG;
формируют ЭЦП Q в виде пары МДЧ (r, s), для чего генерируют МДЧ r по формуле r=xR mod q, где xR - абсцисса точки R, а затем генерируют МДЧ s по формуле s=(tH+rk) mod q;
формируют первое проверочное МДЧ А, для чего генерируют МДЧ ν по формуле ν=sH-1 mod q и МДЧ w по формуле w=(q-rH-1) mod q, затем генерируют точку R' по формуле R'=νG+wP, после чего МДЧ А получают по формуле А=xR' mod q, где xR' - абсцисса точки R';
формируют второе проверочное МДЧ В путем копирования МДЧ r: В=r;
сравнивают сформированные проверочные МДЧ А и В;
при совпадении параметров сравниваемых МДЧ А и В делают вывод о подлинности ЭЦП.
Недостатком ближайшего аналога является относительно невысокая производительность процедуры формирования и проверки ЭЦП, что связано с тем, что выполнение операций над точками ЭК включает операцию деления МДЧ по модулю простого МДЧ, которая требует времени выполнения, длительность которого более чем в 10 раз превышает время выполнения операции умножения.
Целью изобретения является разработка способа формирования и проверки подлинности ЭЦП, заверяющей ЭД, свободного от операции деления по модулю простого МДЧ, благодаря чему повышается производительность процедур формирования и проверки ЭЦП.
Поставленная цель достигается тем, что в известном способе формирования и проверки подлинности ЭЦП, заверяющей ЭД, заключающемся в том, что генерируют секретный ключ в виде, по крайней мере, одной битовой строки, по секретному ключу формируют открытый ключ Y в виде более чем одной БС, принимают ЭД, представленный БС Н1, Н2, …, Нz, где z≥1, в зависимости от принятого ЭД и от значения секретного ключа формируют ЭЦП Q в виде совокупности МДЧ е, s1, s2, …, su, где 1≤u≤8, в зависимости от открытого ключа, принятого ЭД и ЭЦП, формируют первую А и вторую В проверочные БС, сравнивают их и при совпадении их параметров делают вывод о подлинности ЭЦП, новым в заявленном изобретении является то, открытый ключ Y формируют в виде w-мерного, где 2≤m≤64, вектора путем генерации w-мерных векторов G1, G2, …, Gu, координатами каждого из которых являются БС разрядностью r, где 16≤r≤512, генерации секретного ключа в виде МДЧ k1, k2, …, ku и генерации открытого ключа Y по формуле
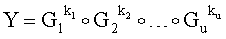 ,
,
где знак ° обозначает операцию умножения векторов.
Осуществление операций умножения векторов БС не требует выполнения операции деления МДЧ по модулю простого МДЧ, благодаря чему повышается производительность формирования и проверки подлинности ЭЦП, заверяющей ЭД. Кроме того, координаты вектора БС, являющегося результатом выполнения операции умножения векторов БС, являющихся операндами, вычисляются по координатам векторов-операндов независимо друг от друга, то имеется возможность распараллелить операцию умножения векторов БС на m независимых процессов и выполнять их параллельно, благодаря чему применение вычислений над векторами позволяет существенно повысить скорость процедур формирования и проверки подлинности ЭЦП.
Новым является также и то, что открытый ключ Y формируют в виде m-мерного, где 2≤m≤64, вектора МДЧ путем генерации m-мерных векторов МДЧ G1, G2, …, Gu, координатами каждого из которых являются МДЧ разрядностью r, где 16≤r≤512, генерации секретного ключа в виде МДЧ k1, k2, …, ku и генерации открытого ключа Y по формуле
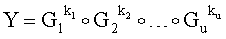 ,
,
где знак ° обозначает операцию умножения векторов МДЧ.
Использование в качестве векторов БС векторов МДЧ позволяет эффективно реализовать заявленный способ в программах для ЭВМ.
Новым является также и то, что открытый ключ Y формируют в виде m-мерного, где 2≤m≤64, вектора многочленов путем генерации m-мерных векторов многочленов G1, G2, …, Gu, координатами каждого из которых являются многочлены разрядностью r, где 16≤r≤512, генерации секретного ключа в виде МДЧ k1, k2, …, ku и генерации открытого ключа Y по формуле
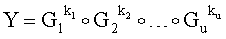 ,
,
где знак ° обозначает операцию умножения векторов многочленов.
Использование в качестве векторов БС векторов МДЧ позволяет эффективно реализовать заявленный способ в специализированных вычислительных устройствах. Выполнение операции умножения векторов БС включает выполнение над БС операций сложения и умножения по модулю простого МДЧ, если БС представляют МДЧ, или по модулю неприводимого многочлена, если БС представляют собой многочлены. В обоих случаях не требуется выполнять операцию деления по модулю простого числа или по модулю неприводимого многочлена, благодаря чему обеспечивается повышение производительности процедур формирования и проверки подлинности ЭЦП как при программной, так и при аппаратной реализации заявленного способа.
Новым является также то, что открытый ключ Y формируют в виде m-мерного, где m=2, вектора путем генерации m-мерных векторов G1 и G2, имеющих порядок, равный простому МДЧ q, генерации секретного ключа в виде МДЧ k1 и k2 и генерации открытого ключа Y по формуле
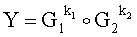 ,
,
принимают ЭД, представленный БС Н1, а ЭЦП формируют в виде трех МДЧ е, s1 и s2, для чего генерируют случайные МДЧ t1 и t2, генерируют вектор R по формуле
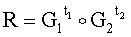 ,
,
затем в зависимости от R и Н1 формируют первое МДЧ е ЭЦП по формуле e=f(R,Н1), где f(R,Н1) - выражение, задающее правило вычисления МДЧ е, затем в зависимости от секретного ключа генерируют пару МДЧ s1 и s2 ЭЦП по формулам
s1=(t1-k1e)mod q и s2=(t2-k2e)mod q,
после чего формируют первую и вторую проверочные БС А и В по формулам
A=f(R',H1) и B=e,
где вектор R' вычисляют по формуле
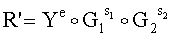 .
.
Генерация двух различных секретных ключей позволяет повысить стойкость алгоритма ЭЦП при использовании нециклических групп векторов за счет использования векторов БС G1 и G2 размерности m=2, генерирующих циклические подгруппы нециклической группы векторов, такие, что они не попадают в какую либо одну циклическую подгруппу нециклической группы векторов.
Новым является также и то, что открытый ключ Y формируют в виде m-мерного, где m=3, вектора путем генерации w-мерных векторов G1, G2 и G3, имеющих порядок, равный простому МДЧ q, генерации секретного ключа в виде МДЧ k1, k2 и k3 и генерации открытого ключа Y по формуле
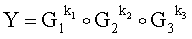 ,
,
принимают ЭД, представленный БС H1, а ЭЦП формируют в виде четырех битовых строк е, s1, s2, и s3, для чего генерируют случайные МДЧ t1, t2, и t3, генерируют вектор R по формуле
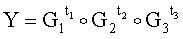 ,
,
затем в зависимости от R и Н1 формируют первое МДЧ е ЭЦП по формуле е=f(R,Н1), где f(R,H1) - выражение, задающее правило вычисления МДЧ е, затем в зависимости от секретного ключа генерируют тройку МДЧ s1, s2, и s3 ЭЦП по формулам
s1=(t1-k1e)mod q, s2=(t2-k2e)mod q
и s3=(t3-k3e)mod q,
после чего формируют первую и вторую проверочные БС А и В по формулам
A=f(R',H1) и B=e,
где вектор R' вычисляют по формуле
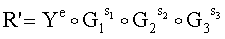 .
.
В качестве выражения e=f(R,H1) может быть, например, использована формула е=rH1mod δ, где r=(r1||r2||r3) - МДЧ, заданное конкатенацией БС, являющихся координатами вектора БС R, и δ - вспомогательное простое МДЧ. Генерация трех различных секретных ключей позволяет повысить стойкость алгоритма ЭЦП при использовании нециклических групп векторов БС за счет использования векторов БС G1, G2 и G3, размерности m=3, генерирующих циклические подгруппы нециклической группы векторов БС, такие, что они попарно не попадают в какую либо одну циклическую подгруппу нециклической группы векторов БС. Конкатенацией двух БС а и b, представленных в виде 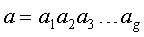 и
и 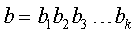 , называется БС
, называется БС 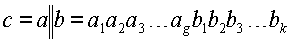 . Знак || обозначает операцию конкатенации.
. Знак || обозначает операцию конкатенации.
Новым является также и то, что открытый ключ Y формируют в виде m-мерного, где m=5, вектора путем генерации m-мерных векторов G1 и G2, имеющих порядки, равные МДЧ q1 и q2, соответственно, генерации секретного ключа в виде МДЧ k1 и k2 и генерации открытого ключа Y по формуле
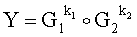 ,
,
принимают ЭД, представленный БС Н1, а ЭЦП формируют в виде трех МДЧ е, s1 и s2, для чего генерируют случайные МДЧ числа t1 и t2, генерируют вектор R по формуле
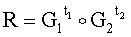 ,
,
затем в зависимости от R и Н1 формируют первое МДЧ е ЭЦП по формуле е=f(R',H1), где f(R,H1) - выражение, задающее правило вычисления числа е, затем в зависимости от секретного ключа генерируют пару МДЧ s1 и s2 ЭЦП по формулам
s1=(t1-k1e)mod q1 и s2=(t2-k2e)mod q2,
после чего формируют первую и вторую проверочные БС А и В по формулам
A=f(R',H1) и B=e,
где вектор R вычисляют по формуле
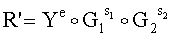 .
.
Использование векторов БС размерности m=5 позволяет снизить сложность операции умножения векторов БС по сравнению со случаями использования векторов БС меньшей размерности, сохраняя возможность получения нециклических групп векторов БС, содержащих различные циклические подгруппы, не принадлежащие какой-либо одной циклической подгруппе, что позволяет повысить стойкость алгоритмов ЭЦП путем формирования открытого ключа по двум секретным ключам.
Новым является также и то, что открытый ключ Y формируют в виде m-мерного, где m=3, вектора путем генерации m-мерного вектора G1, имеющего порядок, равный МДЧ q, генерации секретного ключа в виде МДЧ k1 и генерации открытого ключа Y по формуле 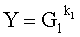 , принимают ЭД, представленный БС H1, а ЭЦП формируют в виде двух МДЧ е и s1, для чего генерируют случайное МДЧ t, генерируют вектор R по формуле R=Gt, затем в зависимости от R и Н1 формируют первое МДЧ е ЭЦП по формуле e=f(R,H1), где f(R,H1) - выражение, задающее правило вычисления числа е, затем в зависимости от секретного ключа генерируют второе МДЧ s1 ЭЦП по формуле
, принимают ЭД, представленный БС H1, а ЭЦП формируют в виде двух МДЧ е и s1, для чего генерируют случайное МДЧ t, генерируют вектор R по формуле R=Gt, затем в зависимости от R и Н1 формируют первое МДЧ е ЭЦП по формуле e=f(R,H1), где f(R,H1) - выражение, задающее правило вычисления числа е, затем в зависимости от секретного ключа генерируют второе МДЧ s1 ЭЦП по формуле
s1=(t+k1e)mod q,
после чего формируют первую и вторую проверочные БС А и В по формулам
А=f(R',Н1) и В=е,
где вектор R' вычисляют по формуле
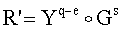 .
.
Новым является также и то, что открытый ключ Y формируют в виде m-мерного, где 2≤m≤8, вектора путем генерации m-мерных векторов G1, G2, …, Gm, имеющих порядок, равный простому МДЧ q, генерации секретного ключа в виде МДЧ k1, k2, …, km и генерации открытого ключа Y по формуле
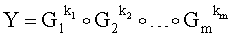 ,
,
принимают ЭД, представленный БС Н1, Н2, …, Нm, а ЭЦП формируют в виде совокупности МДЧ е, s1, s2, …, sm, для чего генерируют случайные МДЧ t1, t2, …, tm, генерируют вектор R по формуле
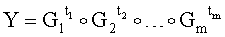 ,
,
затем в зависимости от R формируют первое МДЧ число е ЭЦП по формуле е=f(R,H), где f(R,H) - выражение, задающее правило вычисления числа е, и Н=H1||H2||H3||…||Hm, где знак || обозначает операцию конкатенации, затем в зависимости от секретного ключа генерируют m МДЧ s1, s2, …, sm ЭЦП по формулам
s1=(t1-k1e)H1 -1mod q, s2=(t2-k2e)H2 -1mod q, …,
…, sm=(tm-kme)Hm -1mod q,
после чего формируют первую и вторую проверочные БС А и В по формулам
A=f(R',H) и В=е,
где вектор R вычисляют по формуле
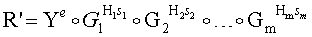 .
.
Использование секретного ключа в виде набора из нескольких МДЧ позволяет обеспечить высокую стойкость ЭЦП при использовании векторов БС, порядок которых равен простому числу сравнительно малого размера, что упрощает выбор параметров для реализации заявленного способа формирования и проверки ЭЦП, заверяющей ЭД.
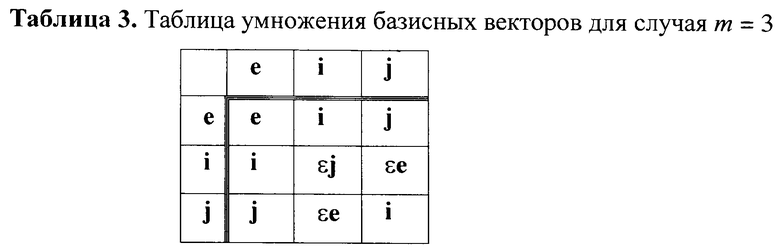
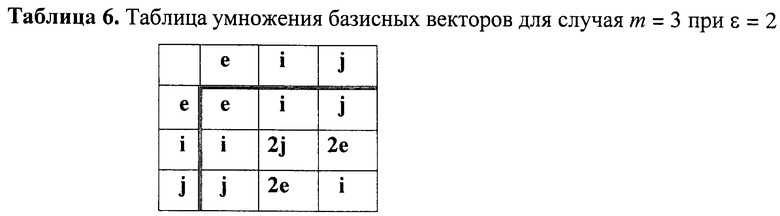
Вектор БС - это набор из двух или более БС, называемых координатами вектора БС. Вектор БС записывается различными способами, требование к которым состоит в том, чтобы они идентифицировали позиции координат вектора БС. Например, вектор БС можно записать в виде (a1, a2, …, am), где m≥2 - это размерность вектора БС, равная числу координат в векторе БС. В качестве разделителя может быть использован знак операции сложения векторов БС, определенной как сложение одноименных координат двух векторов БС, являющихся слагаемыми. При использовании такого разделителя координаты вектора идентифицируются указанием формального базисного вектора (устанавливаемого перед или после соответствующей координаты) в виде буквы латинского алфавита. Формальными базисные вектора называются потому, что им не приписывается никакого физического смысла. Они служат только для того, чтобы идентифицировать координаты вектора БС, независимо от последовательности их записи. Так, например, вектора БС Z1=523425e+3676785i+53453453j и Z2=3676785i+523425e+53453453j, в которых координатами являются МДЧ, рассматриваются как равные, т.е. Z1=Z2. Отдельные слагаемые в такой записи векторов БС называются компонентами вектора БС, поскольку они представляют собой вектора БС с одной ненулевой координатой. Размерность вектора БС - это количество БС, входящих в вектор БС в качестве его координат. В данной заявке рассматриваются конечные группы векторов БС, т.е. алгебраические группы, элементами которых являются вектора БС вида Z=ае+bi+…+cj, а групповая операция определена через операции над векторами БС как операция перемножения компонентов векторов БС, являющихся операндами, с учетом того, что возникающие при этом произведения формальных базисных векторов, заменяются по некоторой специфицированной таблице одним базисным вектором или однокомпонентным вектором, т.е. вектором, содержащим только одну ненулевую координату. Такая таблица умножения базисных векторов для случая векторов БС размерности m=3 имеет, например, следующий вид:
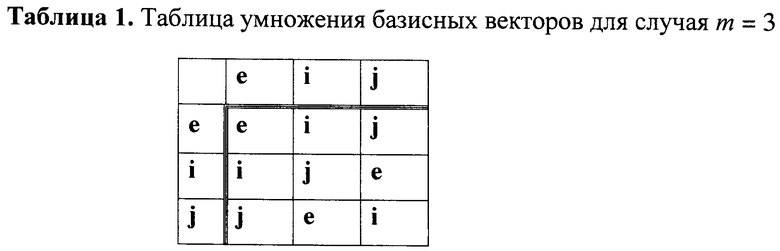
Эта таблица определяет следующее правило подстановки базисных векторов:
e·i→i, e·j→j, j·i→e, i·i→j, j·j→i и т.д.
Такие таблицы будем называть таблицами умножения базисных векторов. Например, пусть Z1=а1е+b1i+c1j и Z2=а2е+b2i+с2j тогда операция умножения векторов БС Z1 и Z2 (обозначим ее знаком «о») выполняется следующим образом:
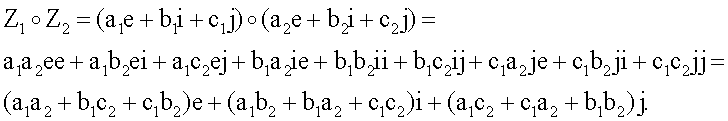
Чтобы задать конечные группы векторов БС операции сложения и умножения над БС, являющимися координатами векторов БС, задаются специальным образом, а именно, так, что координатами являются элементы конечного поля, в частности поля чисел, являющихся остатками от деления всех целых чисел на некоторое простое число р, называемое модулем. Такие поля называются простыми и обозначаются следующим образом GF(p). Число элементов простого конечного поля равно р и называется порядком поля. Другим практически важным случаем задания конечных множеств векторов БС является задание векторов БС над конечными полями многочленов. Такие поля называются расширенными конечными полями и обозначаются следующим образом GF(pd), где d - натуральное число, называемое степенью расширения простого поля характеристики р. Понятие поля хорошо известно в научно-технической литературе [см., например, А.И.Кострикин. Введение в алгебру. Основы алгебры. М.: Физматлит. 1994. - 320 с.]. Многочлен - это последовательность коэффициентов, например МДЧ, являющихся элементами поля GF(p). Над многочленами определены операции сложения многочленов и умножения многочленов, которые сводятся к выполнению действий с коэффициентами многочленов, являющихся операндами. Многочлены и правила действия над ними подробно рассмотрены в книгах [А.И.Кострикин. Введение в алгебру. Основы алгебры. М.: Физматлит. 1994. - 320 с.] и [Курош А.Г. Курс высшей алгебры. - М., «Наука», 1971. - 431 с.]. В вычислительных устройствах многочлены представляются в виде БС, в которых каждый бит или каждая подстрока битов фиксированной длины интерпретируется как один из коэффициентов многочлена, над которыми определены операции сложения и умножения коэффициентов. Элементами конечного поля многочленов являются все возможные многочлены, коэффициентами которых являются элементы простого поля GF(p) для некоторого заданного значения простого числа р. Операция умножения в поле многочленов состоит в умножение многочленов-сомножителей и взятия остатка от делении полученного произведения на некоторый заданный неприводимый многочлен. Число элементов конечного поля многочленов (порядок поля) равно pd, где d - степень неприводимого многочлена, которая совпадает с максимальным числом коэффициентов в многочленах, получаемых в качестве остатка от деления на неприводимый многочлен.
Вектора, в которых БС являются элементами конечного простого поля, т.е. многоразрядными двоичными числами, будем называть векторами МДЧ. Вектора, в которых БС являются элементами конечного расширенного поля, т.е. многочленами, будем называть векторами многочленов. Действия над конечными множествами векторов МДЧ и конечными множествами многочленов описываются одинаково, за исключением того, что действия над координатами векторов относятся к полям различного типа, а потому отличаются в этих двух случая. Действия над координатами векторов МДЧ можно описать как выполнение операций сложения и умножения по модулю простого числа р. Действия над координатами векторов многочленов можно описать как выполнение операций сложения и умножения по модулю неприводимого многочлена p. Размер модуля в обоих случаях выбирается таким, чтобы обеспечить достаточно большой порядок группы векторов МДЧ. В обоих случаях формула, описывающая действия, которые выполняются при умножении векторов БС Z1=(a1e+b1i+c1j) и Z2=а2е+b2i+с2j, имеет одинаковый вид:
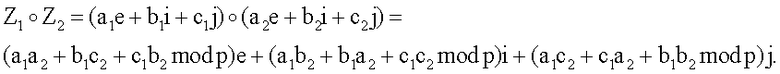
Таким образом, примеры реализации заявляемого способа формирования и проверки подлинности ЭЦП, приведенные для случая задания векторов БС над простыми полями, одновременно задают и примеры реализации заявляемого способа для случая задания векторов БС над конечными расширенными полями, т.е. полями многочленов.
В случае векторов МДЧ в качестве координат вектора МДЧ могут быть заданы целые числа из конечного кольца целых чисел, являющихся остатками от деления всех целых чисел на составное натуральное число. Возможный вариант таких случаев подробно описан в примере 6, приведенном ниже.
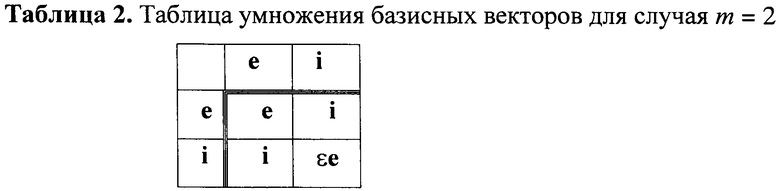
В зависимости от размерности векторов БС, над которыми определяются операции умножения, и конкретного варианта задания операции умножения векторов БС могут быть использованы различные таблицы умножения базисных векторов, например, для векторов БС размерности m=2 приемлемая таблица имеет вид таблицы 2, где 0<ε<р, а для векторов БС размерности m=3 - вид таблицы 3, где 0<ε<р. Значение параметра ε, называемого коэффициентом растяжения, может выбираться произвольно из указанного интервала. Различные значения параметра ε придают различные свойства конечной группе векторов БС при фиксированном значении размерности m и модуля р. Таблицы умножения базисных векторов для случая векторов МДЧ и векторов многочленов, представляющих частные варианты задания векторов БС, имеют одинаковый вид, за исключением того, что в случае векторов МДЧ коэффициент ε представляет собой некоторое МДЧ, а в случае векторов многочленов коэффициент ε представляет собой некоторый многочлен.
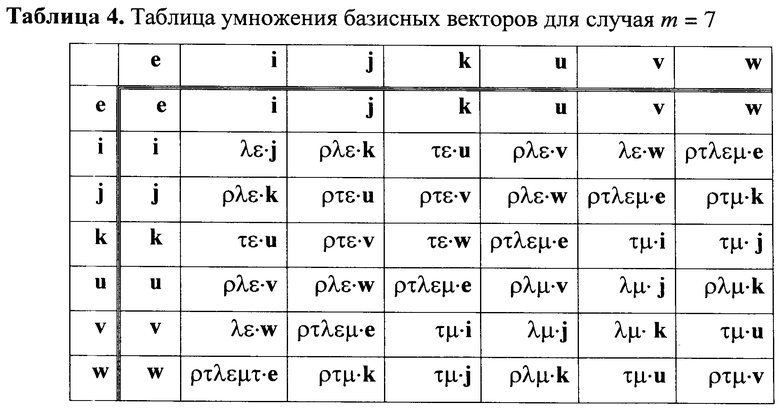
Аналогичным способом могут быть определены групповые операции над конечными группами векторов БС размерностей m=4, m=5 и т.д. Например, правила умножения базисных векторов для случая m=7 приведены в следующей таблице 4, где в качестве коэффициентов растяжения p, τ, λ, ε, µ и τ могут быть использованы произвольные шесть значений, являющихся многочленами в случае, когда вектора БС представляют собой вектора многочленов, или являющихся МДЧ в случае, когда вектора БС представляют собой вектора МДЧ.
При соответствующем выборе таблицы умножения базисных векторов и простого значения р множество векторов МДЧ является конечным и это конечное множество содержит подмножество векторов МДЧ, которое образуют группу с групповой операцией 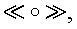 причем порядок этой подгруппы является достаточно большим. Группа - это алгебраическая структура (т.е. множество математических элементов некоторой природы), над элементами которой задана некоторая операция таким образом, что алгебраическая структура обладает следующим набором свойств: операция ассоциативна, результатом выполнения операции над двумя элементами является элемент этой же структуры, существует нейтральный элемент такой, что при выполнении операции над ним и другим некоторым элементом а группы результатом является элемент а. Детальное описание групп дано в широко доступной математической литературе, например в книгах [А.Г.Курош. Теория групп.- М., изд-во «Наука», 1967. - 648 с.] и [М.И.Каргаполов, Ю.И.Мерзляков. Основы теории групп.- М., изд-во «Наука. Физматлит», 1996. - 287 с.]. Операция, определенная над элементами группы, называется групповой операцией. Группа называется циклической, если каждый ее элемент может быть представлен в виде g=аn для некоторого натурального числа n, где а - элемент данной подгруппы, называющийся генератором или образующим элементом циклической подгруппы, и степень n означает, что над элементом а выполняются n последовательных операций, т.е.
причем порядок этой подгруппы является достаточно большим. Группа - это алгебраическая структура (т.е. множество математических элементов некоторой природы), над элементами которой задана некоторая операция таким образом, что алгебраическая структура обладает следующим набором свойств: операция ассоциативна, результатом выполнения операции над двумя элементами является элемент этой же структуры, существует нейтральный элемент такой, что при выполнении операции над ним и другим некоторым элементом а группы результатом является элемент а. Детальное описание групп дано в широко доступной математической литературе, например в книгах [А.Г.Курош. Теория групп.- М., изд-во «Наука», 1967. - 648 с.] и [М.И.Каргаполов, Ю.И.Мерзляков. Основы теории групп.- М., изд-во «Наука. Физматлит», 1996. - 287 с.]. Операция, определенная над элементами группы, называется групповой операцией. Группа называется циклической, если каждый ее элемент может быть представлен в виде g=аn для некоторого натурального числа n, где а - элемент данной подгруппы, называющийся генератором или образующим элементом циклической подгруппы, и степень n означает, что над элементом а выполняются n последовательных операций, т.е. 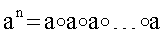 (n раз). Известно, что, если порядок группы есть простое число, то она циклическая [А.И. Кострикин. Введение в алгебру. Основы алгебры. М.: Физматлит. 1994. - 320 с.]. Важной характеристикой группы является ее порядок, который равен числу элементов в группе. Для элементов группы также применяется понятие порядка. Порядком элемента группы является минимальное значение степени, в которую нужно возвести этот элемент, чтобы результатом операции было получение нейтрального элемента группы.
(n раз). Известно, что, если порядок группы есть простое число, то она циклическая [А.И. Кострикин. Введение в алгебру. Основы алгебры. М.: Физматлит. 1994. - 320 с.]. Важной характеристикой группы является ее порядок, который равен числу элементов в группе. Для элементов группы также применяется понятие порядка. Порядком элемента группы является минимальное значение степени, в которую нужно возвести этот элемент, чтобы результатом операции было получение нейтрального элемента группы.
Обычно при разработке способов формирования и проверки ЭЦП используются циклические группы большого простого порядка или группы, порядок которых делится нацело на большое простое число [Венбо Мао. Современная криптография. Теория и практика. - М., СПб, Киев. Издательский дом «Вильямс», 2005. - 763 с.]. При соответствующем задании группы векторов БС это условие легко обеспечивается. При этом стойкость способов формирования и проверки ЭЦП определяется сложностью задачи дискретного логарифмирования, которая состоит в определении значения степени n, в которую надо возвести заданный элемент группы, чтобы результатом этой операции был некоторый другой заданный элемент группы [Молдовян НА. Практикум по криптосистемам с открытым ключом. - СПб. БХВ-Петербург, 2007. - 298 с.].
Поскольку групповая операция 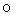 над векторами МДЧ выполняется путем выполнения модульных умножений и сложений над МДЧ, являющихся компонентами векторов МДЧ, достаточно высокая трудность задачи дискретного логарифмирования в группе векторов МДЧ достигается при сравнительно малом значении размера модуля р, благодаря чему обеспечивается сравнительно высокая производительность операции возведения векторов МДЧ в большую степень. Поскольку производительность процедур формирования и проверки ЭЦП определяется производительностью операции возведения в степень, то при использовании операций над векторами МДЧ обеспечивается сравнительно высокая производительность процедур формирования и проверки ЭЦП.
над векторами МДЧ выполняется путем выполнения модульных умножений и сложений над МДЧ, являющихся компонентами векторов МДЧ, достаточно высокая трудность задачи дискретного логарифмирования в группе векторов МДЧ достигается при сравнительно малом значении размера модуля р, благодаря чему обеспечивается сравнительно высокая производительность операции возведения векторов МДЧ в большую степень. Поскольку производительность процедур формирования и проверки ЭЦП определяется производительностью операции возведения в степень, то при использовании операций над векторами МДЧ обеспечивается сравнительно высокая производительность процедур формирования и проверки ЭЦП.
Порядком вектора БС V называется наименьшее натуральное число q, такое что Vq=1, т.е. такое, что результатом умножения вектора МДЧ Q на самого себя q раз является единичный вектор МДЧ Е=1e+0i+…+0j=(1, 0, 0,…, 0).
В частных случаях задания конечного множества векторов БС оно будет представлять расширенное поле, в котором все ненулевые вектора БС составляют циклическую мультипликативную группу [Молдовян Н.А. Алгоритмы аутентификации информации в АСУ на основе структур в конечных векторных пространствах // Автоматика и телемеханика (М., РАН), 2008]. В других частных случаях формируемые группы являются нециклическими, в которых содержится q+1 циклических подгрупп простого порядка q, где q является делителем порядка поля, над которым заданы вектора БС. При этом значение q является достаточно большим, благодаря чему нециклические группы векторов БС могут быть основой для реализации стойких алгоритмов ЭЦП даже в случае, когда размер максимального простого порядка подгрупп составляет 60-100 бит и менее. Это обеспечивается за счет того, что открытый ключ формируется на основе нескольких заданных векторов БС, входящих в разные подгруппы простого порядка, которые имеют единственный общий элемент - единичный вектор БС. Данный механизм задания открытого ключа в способах формирования и проверки ЭЦП является новым и ранее неизвестным.
Корректность заявленного способа доказывается теоретически. Рассмотрим, например, вариант реализации способа по п.9 формулы изобретения. Открытый ключ, соответствующий секретному ключу k, представляет собой вектор БС Y=Gk. Вектор БС R генерируется по формуле R=Gk, а первое МДЧ в ЭЦП (e, s) вычисляется по формуле е=f(R,H). Значение s генерируется по формуле s=(k+ex) mod q, поэтому вектор МДЧ R', генерируемый по формуле 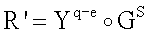 и используемый для формирования первого проверочного МДЧ А, равен
и используемый для формирования первого проверочного МДЧ А, равен
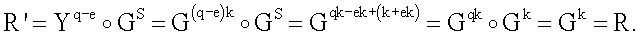
Поскольку вектора МДЧ R' и R одинаковы, то равны между собой и значения е'=f(R',H) и e=f(R,H), т.е. А=е'=е=В. Таким образом, правильно сформированная ЭЦП подпись удовлетворяет процедуре проверки подписи, т.е. корректность процедур генерации и проверки ЭЦП доказана. Аналогичным образом дается доказательство корректности и для пп.5-8 формулы изобретения.
Особенностью пп.5-7 и п.11 формулы изобретения является использование нескольких различных векторов БС G1,…, Gu (G1 и G2 в пп.5 и 7; G1, G2 и G3, в п.6; G1, G2,…, Gm в п.11), по которым вычисляется открытый ключ и которые входят в соответствующие формулы проверки подлинности ЭЦП. Этот признак является новым в области способов формирования и проверки ЭЦП и имеет принципиальное значение для случая использования конечных групп векторов БС, которые являются нециклическими. В нециклических группах векторов БС отсутствуют отдельные значения векторов БС, степени которого могут выразить любой вектор БС. Используемые различные значения G1, G2 и G3 относятся к различным циклическим подгруппам нециклической группы векторов БС, поэтому для определения секретного ключа по открытому ключу требуется вычислять секретный ключ как единое целое, т.е. нет возможности вычислять секретный ключ по частям. Это позволяет построить стойкие алгоритмы ЭЦП даже в случаях, когда порядки векторов БС G1, G2 и G3, т.е. значения МДЧ q1, q2 и q3, соответственно, имеют размер значительно меньше 160 бит. Требование безопасности состоит в том, чтобы суммарная длина значений q1, q2 и q3 была не меньше, чем 160 бит. В зависимости от параметров конечного множества векторов БС и операции умножения, с помощью которой задаются конечные группы векторов БС для формирования открытого ключа, может быть использовано одно значение G (п.9 формулы изобретения), порядок которого имеет размер 160 бит и более, также могут быть использованы два (пп.5 и 7 формулы изобретения), три (п.6 формулы изобретения), четыре и более значений Gi, i=1,2,…, u (п.11 формулы изобретения). В соответствии с этим также модифицируется уравнение проверки ЭЦП. Так в общем случае открытый ключ формируется по формуле 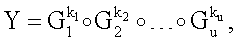 где k1, k2, …, ku - элементы секретного ключа, а подлинность ЭЦП проверяется по формуле
где k1, k2, …, ku - элементы секретного ключа, а подлинность ЭЦП проверяется по формуле 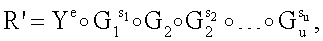 где s1, s2, …, su - элементы ЭЦП, u≤m.
где s1, s2, …, su - элементы ЭЦП, u≤m.
Пункт 10 формулы изобретения представляет частный вариант реализации заявленного способа, в котором для обеспечения безопасности ЭЦП используется сложность вычисления корней большой степени w из заданного значения вектора БС. В этом случае корректность процедуры проверки подлинности ЭЦП доказывается следующим образом. Открытый ключ, соответствующий секретному ключу, сгенерированному в виде БС К, представляет собой вектор БС Y, вычисляемый по формуле Y=Kw, где w - вспомогательное простое МДЧ. Вектор МДЧ R генерируется по формуле R=Тw, где Т - вектор БС, генерируемый по случайному закону. Первое МДЧ ЭЦП (е, S) вычисляется по формуле е=f(R, H). Вектор БС S генерируется по формуле 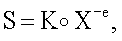 поэтому вектор МДЧ R', генерируемый по формуле
поэтому вектор МДЧ R', генерируемый по формуле 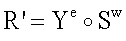 и используемый для формирования первого проверочного МДЧ А, равен
и используемый для формирования первого проверочного МДЧ А, равен
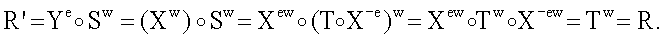
Поскольку вектора МДЧ R' и R одинаковы, то равны между собой и значения e'=f(R', H) и e=f(R, Н), т.е. A=e'=e=В. Таким образом, правильно сформированная ЭЦП удовлетворяет процедуре проверки подписи, т.е. корректность процедур генерации и проверки ЭЦП доказана и в случае частного варианта реализации заявляемого способа по п.10 формулы изобретения. Доказательство корректности проверки ЭЦП в случае п.8 включает объединение доказательств, выполненных для пп.9 и 10.
Рассмотрим примеры реализации заявленного технического решения, где конкретные значения использованных параметров описаны в приводимых ниже численных примерах. Использованные в примерах вектора МДЧ были сгенерирована с помощью программы, разработанной специально для генерации вектором МДЧ, включая вектора МДЧ с заданным порядком, и выполнения операций над векторами МДЧ. Приводимые в примере МДЧ взяты сравнительно малого размера и записаны для краткости в виде десятичных чисел. В вычислительных устройствах МДЧ представляются и преобразуются в двоичном виде, т.е. как БС в виде последовательности сигналов высокого и низкого потенциала. В реальных приложениях следует использовать вектора МДЧ, которые включают в качестве своих координат МДЧ длиной от 16 до 512 бит в зависимости от значения их размерности m векторов МДЧ. При меньшей размерности следует использовать МДЧ более высокой разрядности.
При использовании на практике заявляемого способа следует выбрать таблицу умножения базисных векторов и размер параметров р и q таким образом, чтобы разрядность значения порядка q была равна или превышала 32, 40, 64, 80 и 160 бит в зависимости от конкретного варианта реализации заявленного способа. В примерах, приводимых ниже, используются параметры с искусственно уменьшенной разрядностью, чтобы уменьшить размер примеров и сделать их более наглядными.
Пример 1.
Данный пример иллюстрирует вариант реализации заявленного способа, соответствующий п.5 формулы изобретения, в котором действия выполняются над двухкомпонентными векторами БС. Для получения конечной группы двухмерных векторов БС вида (е, b)=ее+bi БС е и b интерпретируются как МДЧ, над которыми определены операции умножения и сложения координат, выполняемые по модулю целого положительного числа М. В данном примере групповая операция 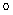 выполняется с использованием таблицы 2. В соответствии с этой таблицей умножения базисных векторов для случая размерности m=2 имеем i·i=ε, где ε∈ {1,…,М-1}. Операция умножения двухмерных БС (а, b) и (с, d) выполняется по правилу:
выполняется с использованием таблицы 2. В соответствии с этой таблицей умножения базисных векторов для случая размерности m=2 имеем i·i=ε, где ε∈ {1,…,М-1}. Операция умножения двухмерных БС (а, b) и (с, d) выполняется по правилу:
(a, b)(c, d)=((ас+εbd) mod М, (ad+bc) mod М)=g'e+h'i,
где g'=(ас+εbd) mod М и h'=(ad+bc) mod М. Легко проверить, что определенные таким образом операции сложения и умножения обладают свойствами ассоциативности и коммутативности. Среди алгебраических структур такого типа имеются конечные поля и мультипликативные группы, существенным свойством которых является наличие единицы Е=(1, 0) - нейтрального элемента по умножению, который определяет существование для каждой ненулевой пары А единственного обратного значения А-1 такого что АА-1=Е.
Группа - это алгебраическая структура с ассоциативной операцией, для которой существует обратная операция [Курош А.Г. Курс высшей алгебры.- М., «Наука», 1971.- 431 с.], т.е. уравнения
АХ=В и YA=В имеют единственное решение для любых элементов А и В. Поскольку определенная выше операция умножения является коммутативной, то указанные уравнения являются эквивалентными и можно рассматривать только одно из них. Легко показать, что однозначность решения указанных уравнений выполняется, если для каждого элемента А существует единственное обратное значение А-1, поэтому представляет интерес рассмотреть решение уравнений вида АХ=Е, которое можно представить следующим образом:
(аe+bi)(хе+yi)=((ax+εby) mod M)e+(ay+bx) mod M)i=1e+0i.
Из последней записи вытекает, что для определения обратных значений следует решать следующую систему из двух линейных сравнений с двумя неизвестными
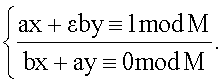
Рассмотрим существование решений этой системы для случая использования в качестве модуля простого МДЧ p, т.е. М=р. Приравнивая нулю главный определитель этой системы, получаем характеристическое уравнение
е2-εb2=0 mod р.
Значение (а, b)=(0,0) является решением характеристического уравнения для любых значений модуля, поэтому для этой пары не существует обратного значения. Значения р и s можно выбрать таким образом, что характеристическое уравнение не имеет других решений, а значит рассматриваемая система сравнений имеет единственное решение для любой пары (а, b)≠(0,0). Рассмотрим несколько важных частных случаев.
Случай 1. Значительный интерес представляет выбор в качестве параметра ε значения, которое является квадратичным невычетом по модулю р. В этом случае получаем структуру, являющуюся конечным полем GF(p2), мультипликативная группа которого имеет порядок
Ω=p2-1=(p-1)(р+1).
Задавая различные значения модуля р и параметра ε, получаем различные варианты конечного поля типа GF(p2). Для заданного значения р имеем (р-1)/2 различных вариантов поля GF(p2), включающих одно и то же множество элементов, но отличающихся видом операции умножения, соответственно числу различных квадратичных невычетов по модулю p.
Случай 2 (используется для иллюстрации частных вариантов реализации заявляемого способа по п.5 и п.8 формулы изобретения в примерах 1 и 4, соответственно). Пусть в определении операции умножения используется параметр ε, который является квадратичным вычетом по модулю р. При этих условиях характеристическое уравнение имеет, кроме (а,b)=(0,0), еще 2(р-1) следующих решений вида
(ε1/2b mod p,b) и (-ε1/2 b mod p,b),
где b∈{0,1,…,р-1}. Для пар такого вида не существуют решений системы сравнений, которые определяют значение обратных элементов. Следовательно, количество элементов, для которых существуют единственные обратные значения, равно
Ω=p2-2(p-1)-1=(p-1)2.
Эти элементы составляют мультипликативную группу, поскольку результат умножения любых двух элементов из этого множества является элементом этого же множества. Данная группа векторов БС является нециклической и содержит большое число циклических подгрупп, имеющих одно и то же значение простого порядка q, который является делителем р-1. Наибольшее значение порядка циклических подгрупп равно р-1. Выполненные нами теоретические и экспериментальные исследования показали, что группа БС, соответствующая случаю 2, содержит q+1 циклических подгрупп простого порядка q для каждого простого делителя числа р-1. При больших значениях q, размер которых превышает 80 бит, число циклических подгрупп чрезвычайно велико, что позволяет обеспечить стойкость ЭЦП соответствующей стойкости ЭЦП в случае известных аналогов при применении циклических групп простого порядка, размер которого превышает 160 бит.
Случай 3 (относится к варианту реализации заявляемого способа по п.10 формулы изобретения, иллюстрируемого ниже в примере 6). Особенностью этого случая является задание операций сложения и умножения над координатами вектора БС, выполняемых по модулю М, который не является простым. В этом случае общий анализ условий существования групп и определение их порядка является более сложным. Однако интересующий нас следующий частный случай составного модуля М=w2, где w - простое число, позволяет получить формулы для расчета порядка группы при произвольном простом МДЧ w.
Пусть используется значение М=w2, где w - простое число, в качестве модуля, а параметр ε делится на w. При этих условиях для элементов (а, b), таких что а не делится на w, характеристическое уравнение не имеет решений, поскольку w|ε, а определитель системы сравнений является взаимно простым с модулем М=w2, т.е. для каждого из указанных элементов имеются обратные значения. При этом операция умножения двух элементов дает третий элемент, в котором первая координата также не делится на М, т.е. операция умножения является замкнутой на указанном множестве пар (а, b). Следовательно, это множество векторов БС является группой, порядок которой можно определить из того факта, что число возможных значений первой координаты равно функции Эйлера от модуля φ(М)=φ(w2)=w(w-1), число возможных значений второй координаты равно М=w2. Получаем следующую формулу для значения порядка построенной мультипликативной группы
Ω=w(w-l)·w2=w3(w-1).
Опыт показал, что в построенной группе содержится циклическая группа порядка
Ω'=w2(w-1),
которая подходит для решения нашей задачи синтеза алгоритмов ЭЦП, основанных на вычислительной сложности нахождения корней большой простой степени в конечных мультипликативных группах.
В примере 1 реализуют вычисления в группе векторов БС, тип которой соответствует случаю 2, описанному выше. При этом выполняют следующую последовательность действий.
1. Генерируют простое число р, такое что р - 1 содержит большой простой множитель q, т.е. р=Nq+1, где N - четное число, и задают значение ε=225, являющееся квадратичным вычетом по модулю р:
р=3990163786012426536171919;
q=1997539432909;
2. Генерируют секретный ключ в виде пары случайных МДЧ k1 и k2:
k1=1853362791;
k2=8457313533;
3. Формируют открытый ключ в виде вектора МДЧ Y, для чего выполняют следующую последовательность действий.
3.1. Генерируют пару векторов МДЧ G1 и G2, имеющих порядок
q=1997539432909.
G1=3294504589562920276812106е+2766233567473802431338876i;
G2=1028484769067346813640211е+3852939155310569961109202i;
3.2. Генерируют вектор МДЧ 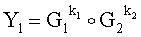 :
:
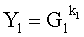 =1183619390973024467297431е+3703669051605973538784782i;
=1183619390973024467297431е+3703669051605973538784782i;
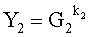 =182788774563б60856108049е+1936038364647789724421279i;
=182788774563б60856108049е+1936038364647789724421279i;
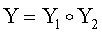 =1924471834140042300320534e+174837666126798422981001i;
=1924471834140042300320534e+174837666126798422981001i;
4. Принимают ЭД, представленный, например, следующим МДЧ Н1 (в качестве которого может быть взята, в частности, хэш-функция от ЭД):
H1=7579346783.
5. Формируют ЭЦП Q в виде трех БС е, s1 и s2, для чего выполняют следующие действия:
5.1. Формируют первую БС е ЭЦП, для чего
5.1.1. Генерируют пару случайных МДЧ t1=18357236873 и t2=38157216371.
5.1.2. Генерируют вектор БС R по формуле 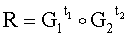 :
:
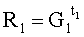 =755879295575251075473814е+440880985283782634380692i;
=755879295575251075473814е+440880985283782634380692i;
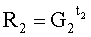 =1432490514364096482144778e+952288470467392311694046i;
=1432490514364096482144778e+952288470467392311694046i;
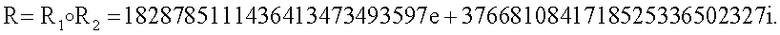
5.1.3. Генерируют БС е в виде МДЧ, вычисляемого по формуле е=r1H1 mod δ, где δ - вспомогательное простое МДЧ, например, δ=q=1997539432909; r1 - МДЧ, являющееся первой координатой вектора МДЧ R: е=1701612237557.
5.2. Формируют вторую и третью БС s1 и s2 ЭЦП в виде двух МДЧ, вычисляемых по формулам s1=t1-k1e mod q и s2=t2-k2e mod q:
s1=1767916348307; s2=1894616394985.
6. Формируют первую проверочную БС А, для чего выполняют следующие действия:
6.1. Генерируют вектор БС R' в виде вектора МДЧ, вычисляемого по формуле
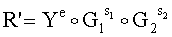 :
:
Ye=3849037943945673660459504е+3583704901879536834939540i.
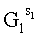 =3580532237073410771710519e+896847748485820473603568i;
=3580532237073410771710519e+896847748485820473603568i;
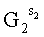 =2902157646689814295993329е+1114779150752846285743470i.
=2902157646689814295993329е+1114779150752846285743470i.
R'=1828785111436413473493597e+3766810841718525336502327i.
6.2. Генерируют БС А в виде МДЧ, вычисляемого по формуле А=r'1H1 mod q, где r'1 - МДЧ, являющееся первой координатой вектора МДЧ R':
А=1701612237557.
7. Формируют вторую проверочную БС В путем копирования МДЧ е, т.е. по формуле В=е: В=1701612237557.
8. Сравнивают первую и вторую проверочные БС: А=В.
Совпадение проверочных БС подтверждает подлинность ЭЦП.
Пример 2 (иллюстрация п.6 формулы изобретения).
В данном примере рассматривается случай использования трехкомпонентных векторов БС (m=3), в котором групповая операция о выполняется с использованием таблицы 3, задающей правило умножения базисных векторов. Выполняют следующую последовательность действий.
1. Генерируют простое число р, такое что р-1 содержит большой простой множитель q, т.е. р=Nq+1, где N - четное число, и задают значение ε=6859=193, являющееся кубичным вычетом по модулю p:
р=33888823497367; q=2376581;
2. Генерируют секретный ключ в трех случайных МДЧ k1, k2 и k3:
k1=1853362791; k2=8457313533; k3=3873059582.
3. Формируют открытый ключ в виде вектора МДЧ Y, для чего выполняют следующую последовательность действий:
3.1. Генерируют три вектора МДЧ G1, G2 и G3, имеющие порядок q=2376581.
G1=5955377462471e+28217758221981i+21380040635602j;
G2=31195950338318e+1146212670059i+19798505045659j;
G3=12169985178873e+22834221533336i+23611151771899j.
3.2. Генерируют вектор МДЧ 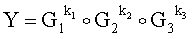 :
:
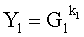 =26106362944111e+9121853491576i+7998895962567j;
=26106362944111e+9121853491576i+7998895962567j;
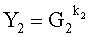 =8841482011615e+31890466083034i+31068266275905j;
=8841482011615e+31890466083034i+31068266275905j;
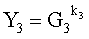 =32249398803413e+18420663759564i+31373921099158j;
=32249398803413e+18420663759564i+31373921099158j;
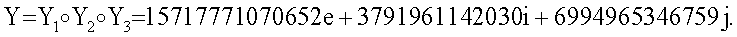
4. Принимают ЭД, представленный, например, в виде БС следующим МДЧ Н1 (в качестве которого может быть взята, в частности, хэш-функция от ЭД):
H1=1578147.
5. Формируют ЭЦП Q в виде четырех БС е, s1, s2, и s3, для чего выполняют следующие действия:
5.1. Формируют первую БС е ЭЦП, для чего
5.1.1. Генерируют три случайных МДЧ t1=16355233827, t2=9315216313 и t3=286572167.
5.1.2. Генерируют вектор МДЧ R по формуле 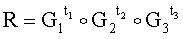 :
:
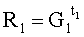 =26476756850873e+89620836256881+670851250270j;
=26476756850873e+89620836256881+670851250270j;
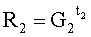 =30556526925766e+28584458265015i+8838154755582j;
=30556526925766e+28584458265015i+8838154755582j;
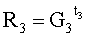 =11801846609303e+18076196032752i+32080216656488j;
=11801846609303e+18076196032752i+32080216656488j;
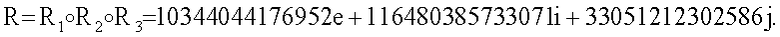
5.1.3. Генерируют БС е в виде МДЧ, вычисляемого по формуле е=(r1||r2||r3)Н1 mod δ, где δ - вспомогательное простое число, в качестве которого в данном примере берется МДЧ q, т.е. δ=q=2376581; r1||r2||r3 - МДЧ, равное конкатенации координат вектора МДЧ R: е=665438.
5.2. Формируют вторую, третью и четвертую БС s1, s2 и s3, ЭЦП в виде трех МДЧ, вычисляемых по формулам s1=t1-k1e mod q, s2=t2-k2e mod q и s3=t3-k3e mod q:
s1=56419; s2=1472355; s3=1213067.
6. Формируют первую проверочную БС А, для чего выполняются следующие действия:
6.1. Вычисляют вектор МДЧ R' по формуле 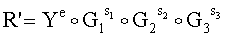 :
:
Ye=6474526780075e+26594658074693i+27807198777585j;
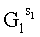 =46566596б2651е+31668525221129i+9741922667955j;
=46566596б2651е+31668525221129i+9741922667955j;
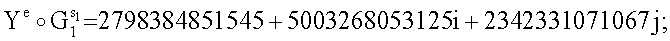
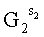 =13878539449612e+10268579457949i+25993200515657j;
=13878539449612e+10268579457949i+25993200515657j;
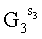 =8522604164956e+3729385407205i+6316798018014j;
=8522604164956e+3729385407205i+6316798018014j;
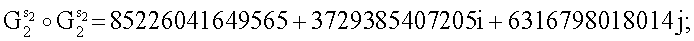
R'=10344044176952e+11648038573307i+33051212302586j.
6.2. Генерируют первую проверочную БС А в виде МДЧ, вычисляемого по формуле А=(r'1||r'2||r'3)H1 mod q: А=665438.
7. Формируют вторую проверочную БС В путем копирования МДЧ е по формуле В=е: В=665438.
8. Сравнивают первую и вторую проверочные БС: А=В
Совпадение проверочных БС подтверждает подлинность ЭЦП.
Пример 3 (иллюстрация п.7 формулы изобретения).
В данном примере рассматривается случай использования пятикомпонентных векторов БС (размерность m=5), в котором групповая операция о выполняется с использованием следующей таблицы умножения базисных векторов.

Выполняют следующую последовательность действий.
1. Генерируют простое число p, такое что р-1 содержит большой простой множитель q, т.е. р=Nq+1, где N- четное число, и задают значение ε=17377:
р=13900359797; q=820177;
2. Генерируют секретный ключ в виде двух случайных МДЧ k1 и k2:
k1=3178457367; k2=4154733715.
3. Формируют открытый ключ в виде вектора БС Y, для чего выполняют следующую последовательность действий.
3.1. Генерируют два вектора БС G1 и G2, имеющие порядок q1=820177 и g2=59403247. G1=4670230529e+6363758539i+1115493580j+11774211119k+4481291788u;
G2=7346947995e+9935549003i+571858634j+5252170971k+11375019823u.
3.2. Генерируют вектор БС 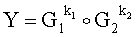 :
:
Y1=5595374136e+6222510934i+5243302038j+12338881800k+1993502504u;
Y2=8724284212e+10520629249i+37795532j+9839512858k+9802549315u;
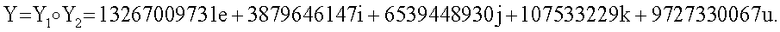
4. Принимают ЭД, представленный, например, следующим МДЧ H1 (в качестве которого может быть взята, в частности, хэш-функция от ЭД): Н1=89154314.
5. Формируют ЭЦП Q в виде трех БС е, s1 и s2, для чего выполняют следующие действия:
5.1. Формируют первую БС е ЭЦП, для чего
5.1.1. Генерируют пару случайных МДЧ k1=613352348 и k2=37591463.
5.1.2. Генерируют вектор МДЧ 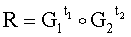 :
:
R1=2267371210e+1531475463i+11370174246j+13211765802k+10527441855u;
R2=1310809391le+3936822199i+9539524888j+5370585930k+6567932491u;
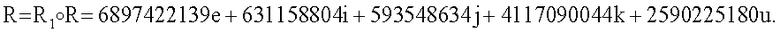
5.1.3. Генерируют БС е в виде МДЧ, вычисляемого по формуле е=(r1||r2||r3,)Н1 mod δ, где δ - вспомогательное простое число, в качестве которого в данном примере берется МДЧ δ=2376581; r1||r2||r3 - МДЧ, равное конкатенации трех МДЧ, являющихся координатами вектора МДЧ R: е=119236.
5.2. Формируют пару БС s1 и s2 в виде МДЧ, вычисляемого по формулам s1=t1-k1e mod q1 и s2=t2-k2e mod q2.
s1=626030; s2=2528952.
6. Формируют первую проверочную БС А, для чего выполняют следующие действия:
6.1. Вычисляют вектор МДЧ R' по формуле 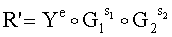 :
:
Yе=977315114е+13874743606i+10113644214j+97683587k+971368210u;
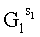 =10769096929e+2654696484i+11130937343j+3507101146k+4306145379u;
=10769096929e+2654696484i+11130937343j+3507101146k+4306145379u;
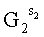 =12814278574e+7057455723i+12699485338j+1124012626k+147947960u;
=12814278574e+7057455723i+12699485338j+1124012626k+147947960u;
R'=6897422139e+631158804i+593548634j+4117090044k+2590225180u.
6.2. Генерируют БС А в виде МДЧ, вычисляемого по формуле
А=(r'1||r'2||r'3)H1 mod δ: A=119236.
7. Формируют вторую проверочную БС В путем копирования МДЧ е:
В=е=119236.
8. Сравнивают первую и вторую проверочные БС: А=В.
Совпадение проверочных БС подтверждает подлинность ЭЦП.
Пример 4.
Данный пример относится к варианту реализации заявленного способа по п.8 формулы изобретения. В данном примере используется нециклическая группа Г, содержащая циклические подгруппы, порядок которых делится на w2. Формирование такой нециклической группы описано в примере 1 как случай 2. В данном конкретном примере, относящемся к использованию группы, порядок которой выражается формулой Ω=(р-1)2, в группе Г существуют элементы порядка ω=(р-1)=Nw2, где N - четное число и w - простое число достаточно большого размера.
В данном примере в качестве модуля, по которому ведут вычисления, используется простое МДЧ р=2qw2+1, где
р=757095462971039987; q=1433729993 - простое МДЧ;
w=16249 - простое МДЧ.
Выполняют следующую последовательность действий, используя значение параметра ε=152399025, являющегося квадратом числа 12345.
1. Генерируют секретный ключ в виде двухмерного вектора БС К=(k1,k2), представленного двумя МДЧ k1 и k2, и одной БС, представленной МДЧ k:
К=(k1, k2)=(162748957475865968, 978716439507194574);
k=73678436295562.
2. Генерируют вектор БС G, порядок которого равен q:
G=(89833863138176218, 481445738651243524).
3. Формируют открытый ключ Y в виде двухмерного вектора БС, вычисляемого по формуле 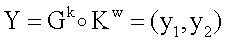 выполняя следующие действия:
выполняя следующие действия:
3.1. Вычисляют значения векторов БС Gk и Кw:
Gk=(328752664651659001, 188933597249340036);
Кw=(561576529082416854, 311520115027605902).
3.2. Генерируют открытый ключ Y=(у1,у2), для чего умножают вектор БС Gk на вектор БС Kw:
Y=(y1,y2)=(355961954073853677, y2=52073643974617679).
4. Принимают ЭД, представленный, например, следующим МДЧ H1 (в качестве которого может быть взята, в частности, хэш-функция от ЭД).
5. Формируют ЭЦП в виде четырех БС, заданных четырьмя МДЧ е, s, s1 и s2, для чего выполняют следующую последовательность действий.
5.1. Генерируют случайное МДЧ t и случайный двухмерный вектор БС, в котором координаты представляют собой МДЧ:
t=2134356456473;
Т=(64697680789267, 70914503766891).
5.2. Генерируют вектор БС R, выполняя вычисления по формуле: 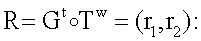
Gt=(633200307649534083,225907802600880012);
Тw=(334316797118875406,694605535104513177).
В результате перемножения векторов БС Gt и Tw генерируют следующие значения координат вектора БС R:
r1=278285084410523629; r2=476437561152596152.
5.3. Формируют первую БС е ЭЦП в виде МДЧ, вычисляемого по формуле e=f(R,H1), где f(R,Н1) - выражение, специфицирующее процедуру вычисления числа е. Пусть получено значение, равное е=874095303603.
5.4. Вычисляют двухмерный вектор БС S, координаты которого являются третьей и четвертой БС ЭЦП, по формуле 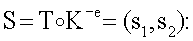
К-e=Kp-1-e=(586016270354358239, 327468169526176273);
S=(s1, s2)=(120860422228891963, 483553947421564222).
5.5. Генерируют БС s в виде МДЧ, вычисляемого по формуле
s=s1 -1(t-ke)mod q:
s1 -1=124122450; s=222387665.
6. Проверяют подлинность ЭЦП, для чего выполняют следующую последовательность действий.
6.1. Формируют вектор БС R' по формуле 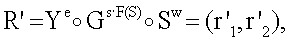 где F(S)=s1:
где F(S)=s1:
s·F(S)=26877867090397379188836395;
Gs·F(S)=(117660193869193445, 78350012648906257);
Ye=(45991950818968478, 376342549870250020);
Sw=(441809832936651938, 4975252013635854).
R'=(r'1, r'2)=(278285084410523629, 476437561152596152).
6.2. Формируют первую проверочную БС А по формуле А=f(R',H1).
Поскольку получено R'=R, то А=f(R',H1)=f(R,H1)=е, т.е. имеем:
А=874095303603.
6.3. Формируют вторую проверочную БС В по формуле В=е:
В=874095303603.
6.4. Сравнивают проверочные БС А и В.
6.5. Сравнение показывает, что параметры проверочных БС А и В совпадают, на основании чего делают вывод о подлинности ЭЦП.
Пример 5.
Случай использования трехкомпонентных векторов МДЧ (иллюстрация п.9 формулы изобретения). В данном примере рассматривается группа трехмерных векторов БС с групповой операцией 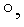 выполняемой по таблице 6 умножения базисных векторов.
выполняемой по таблице 6 умножения базисных векторов.
Данный пример показывает, что при соответствующем выборе размерности m, простого числа р и коэффициента растяжения ε значение порядка q может значительно превышать значение p. Выполняют следующую последовательность действий.
1. Генерируют простое число p, такое что число p2+р+1 содержит большой простой множитель q: р=97; q=3169.
2. Генерируют секретный ключ k в виде случайного МДЧ: k=2079.
3. Формируют открытый ключ в виде вектора БС Y, для чего выполняют следующую последовательность действий.
3.1. Генерируют вектор БС G, имеющий порядок q=3169:
G=8е+3i+93j.
3.2. Генерируют вектор БС Y=Gk: Y=87е+96i+86j.
4. Принимают ЭД, представленный, например, следующим МДЧ Н1 (в качестве которого может быть взята, в частности, хэш-функция от ЭД): Н1=5168.
5. Формируют ЭЦП Q в виде двух БС е и s, для чего выполняют следующие действия:
5.1. Формируют первую БС е ЭЦП, для чего
5.1.1. Генерируют случайное МДЧ t=5387
5.1.2. Генерируют вектор МДЧ R по формуле R=Gt=96е+56i+81j.
5.1.3. Генерируют БС е в виде МДЧ, вычисляемого по формуле е=rH1 mod δ,
где r=(r1||r2||r3) - МДЧ, равное конкатенации МДЧ, являющихся координатами вектора МДЧ R и δ=3169: e=3138.
5.2. Формируют вторую БС s ЭЦП в виде МДЧ, вычисляемого по формуле
s=t+ke mod q: s=1149.
6. Формируют первую проверочную БС А, для чего выполняются следующие действия:
6.1. Вычисляют вектор МДЧ R' по формуле 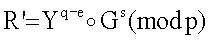
Yq-e(mod p)=75e+46i+84j
Gs(mod р)=27е+81i+81j
R'=96е+56i+81j.
6.2. Генерируют БС А в виде МДЧ, вычисляемого по формуле А=r'H1 mod δ, где r'=(r'1||r'2||r'3) МДЧ, равное конкатенации МДЧ, входящих в состав вектора МДЧ R' и δ=3169 - вспомогательное простое число: А=3138.
7. Формируют вторую проверочную БС В путем копирования МДЧ е:
В=е=3138.
8. Сравнивают первую и вторую проверочные БС: А=В
Совпадение проверочных БС подтверждает подлинность ЭЦП.
Пример 6.
Данный пример относится к варианте реализации заявленного способа по п.10 формулы изобретения. В данном примере используется нециклическая группа Г, содержащая циклические подгруппы, порядок которых делится на w2. Формирование такой нециклической группы описано в примере 1 как случай 3.
Данный конкретный пример относится к использованию группы такого типа. Порядок группы Г выражается формулой Ω=w3(w-1), где w - простое число.
В группе Г существуют элементы порядка ω=w2(w-1). Возьмем значение w=92618137318729677928546646365838873180498085133. Тогда имеем значение модуля
М=w2=8578119360391067054292626600438708965746964997146182659298964331315788956009108954679715627689
В качестве коэффициента ε возьмем значение 101w, т.е. ε=9354431869191697470783211282949726191230306598433.
Выбор группы данного конкретного вида вносит определенную специфику в синтезируемый алгоритм ЭЦП. При генерации случайного секретного ключа К=(k1,k2) ∈ Г следует делать проверку: НОД(w, k1)=l и Kw(w-1)≠1,0). Первое условие обеспечивает выбор в качестве секретного ключа элемента, принадлежащего группе Г. Второе условие обеспечивает выбор в качестве секретного ключа элемента, порядок которого делится на квадрат степени корня, что является требованием безопасности ЭЦП. Аналогичную проверку следует выполнить и при генерации случайного вектора БС Т=(t1,t2) ∈ Г. Если указанное условие не выполняется (вероятность этого события мала) для случайно выбранных координат k1 и k2 (или для координат t1 и t2), то следует выбрать новые случайные значения координат k1≤М=w2 и k2≤М=w2 (или координат t1≤M=w2 и t2≤M=w2). В данном примере выполняют следующую последовательность действий.
1. Генерируют секретный ключ К в виде двухмерного вектора БС, представленного двумя МДЧ:
К=(162748957475865968, 9787164395071945749328495).
2. Формируют открытый ключ Y в виде двухмерного вектора БС, путем выполнения операции возведения секретного ключа в степень w в соответствии с формулой Y=Кw=(y1,y2) - В результате генерируют следующие значения координат вектора БС Y:
y1=21228784879778840523736855349044078599261832125691229247376837230 26454694663820975943984437961;
y2=90646893590375535174289454483400852640445760352160962710838716809 2764835.
3. Принимают ЭД, представленный БС Н1.
4. Формируют ЭЦП в виде трех БС, заданных тремя МДЧ е, s1 и s2, для чего выполняют следующую последовательность действий.
4.1. Генерируют случайный двухмерный вектор БС, в котором пара БС интерпретируется как пара МДЧ:
Т=(96846596736586738292216171, 37586931174658693746285927).
4.2. Генерируют вектор БС R путем выполнения операции возведения вектора БС Т в степень w в соответствии с формулой R=Тw (r1, r2). В результате генерируют следующие значения координат вектора БС R:
r1=6676527716822018383957988126039278418617223915758582479614295011535668063135439573548109332464;
r2=3481231552924180293255968160466563282460623255695990065475962954205823291.
4.3. Формируют первую БС ЭЦП в виде МДЧ е, вычисляемого по формуле e=f(R,H1), где f(R,H1) - выражение, специфицирующее процедуру вычисления числа е. Пусть получено значение, равное е=75867496586968496537352193793673918466970375638.
4.4. Вычисляют двухмерный вектор БС S, координаты которого являются второй и третьей БС ЭЦП, по формуле 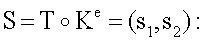
s1=8256594105547617216423939012826302237218370734284428450969373421295221722475025012259161992826;
s2=422260754784925502959681748215173239940083978470857855504330212012892903897205453209052939744.
5. Проверяют подлинность ЭЦП, для чего выполняют следующую последовательность действий:
5.1. Формируют вектор БС R' по формуле 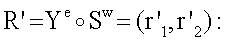
r'1=6676527716822018383957988126039278418617223915758582479614295011535668063135439573548109332464;
r'2=3481231552924180293255968160466563282460623255695990065475962954205823291.
5.2. Формируют первую проверочную БС А по формуле А=f(R',Н).
Сравнение показывает, что R'=R, поэтому А=f(R', Н)=f(R', Н)=е, т.е. А=75867496586968496537352193793673918466970375638.
5.3. Формируют вторую проверочную БС В по формуле В=е:
В=75867496586968496537352193793673918466970375638.
5.4. Сравнивают проверочные БС А и В.
5.5. Сравнение показывает, что параметры проверочных БС А и В совпадают, на основании чего делают вывод о подлинности ЭЦП.
Пример 7.
Данный пример относится к варианту реализации заявленного способа по п.11 формулы изобретения. В нем используется группа, элементами которой являются вектора БС размерности m, над которыми определена операция умножения таким образом, что порядок группы равен (р-1)m, а максимальный порядок элементов группы равен р-1, где р - характеристика конечного простого поля, над которым заданы вектора БС, причем БС интерпретируются как МДЧ, а операции над БС выполняются как операции над МДЧ. Условия построения групп данного типа описаны, например, для случая m=3, в работе [Молдовян Н.А. Группы векторов для алгоритмов электронной цифровой подписи // Вестник СПбГУ. Сер. 10. 2008]. Аналогичным способом могут быть заданы группы БС для размерностей m=4, 5, 6, …. В данном примере не приводятся конкретные значения получаемых значений БС, а описываются результаты процедур формирования и генерации БС и векторов БС в обобщенном виде для произвольного случая. Подставляя вместо буквенных обозначений конкретные численные значения, могут быть построены различные варианты численной иллюстрации п.11 формулы изобретения. В данном примере акцент делается на корректность процедуры проверки подлинности ЭЦП, которая доказывается для общего случая. Выполняется следующая последовательность действий.
1. Генерируют секретный ключ в виде МДЧ k1, k2, …,km.
…,km.
2. Формируют открытый ключ Y в виде m-мерного, где m≥2, вектора БС, для чего выполняют следующие действия.
2.1. Генерируют вектора БС G1, G2,…,Gm размерности m, имеющие порядок, равный простому МДЧ q.
2.2. Генерируют открытый ключ Y в виде вектора БС, вычисляемого по формуле 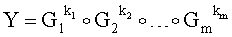 .
.
3. Принимают ЭД, представленный БС Н1, Н2,…, Hz, где z=m.
4. Формируют ЭЦП в виде совокупности БС е, s1, s2,…,sm, для чего выполняют следующие действия.
4.1. Генерируют случайные МДЧ t1,t2,…, tm.
4.2. Генерируют вектор БС R по формуле 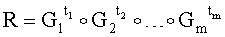 .
.
4.3. Формируют первую БС е ЭЦП в виде МДЧ, вычисляемого в зависимости от R и H по формуле e=f(R,H), где f(R,H) - выражение, задающее правило вычисления числа е, и Н=H1||Н2||…||Нz, где z=m.
4.4. Генерируют m БС s1, s2,…, sm ЭЦП в виде МДЧ, вычисляемых по формулам s1=(t1-k1e)H-1 1 mod q, s2=(t2-k2e)H-1 2 mod q…, sm=(tm-kme)H-1 m mod q.
5. Формируют первую проверочную БС А, для чего выполняют следующие действия.
5.1. Формируют вектор БС R', выполняя вычисления по формуле 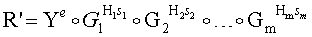 .
.
5.2. Формируют БС А по формуле А=f(R',Н), где f(R,H) - выражение, задающее правило вычисления числа е и Н=Н1||Н2||…||Нz, где z=m.
6. Формируют вторую проверочную БС В путем копирования БС е, т.е. по формуле В=е.
7. Сравнивают проверочные БС А и В.
Сравнение показывает, что параметры проверочных БС А и В совпадают, на основании чего делают вывод о подлинности ЭЦП. Тот факт, что при проверке ЭЦП, сформированной по процедуре формирования ЭЦП с использованием правильного секретного ключа, на шаге 7 будет получено совпадение параметров проверочных БС доказывается следующим образом. Подставим в формулу,
по которой формируется вектор БС R' (см. п.5.1), значения БС s1,s2,…,sm, полученные по формулам, приведенным в п.4.4. В результате получим
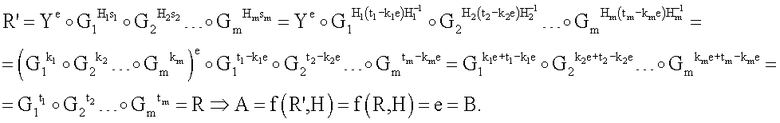
Таким образом, корректность процедуры проверки подлинности ЭЦП доказана.
Последовательность действий по формированию и проверке подлинности ЭЦП, заверяющей ЭД, описанная в примере 7, может быть выполнена также и для случая, когда БС представляют собой многочлены. При этом таблицы умножения базисных векторов при заданном значении размерности m являются такими же, как приведенные выше, за исключением того, что коэффициент растяжения ε в случае реализации заявленного способа при использовании многочленов будет представлять собой некоторый заданный многочлен, определяющий конкретный вид операции умножения векторов многочленов. Доказательство корректности процедуры проверки ЭЦП в случае, когда вектора БС представляют собой вектора многочленов, является таким же, как и приведенное выше доказательство для случая использования векторов БС, являющихся векторами МДЧ. Частные примеры реализации заявленного способа, аналогичные описанным выше примерам 1-6, также могут быть реализованы для случая использования вычислений над векторами БС, являющимися векторами многочленов. Выполнение операций сложения, умножения и деления многочленов, а также операций умножения и сложения по модулю неприводимого многочлена широко описано в научно-технической литературе. Также широко представлена реализация конечных полей многочленов и основные их свойства (см. например книги [Курош А.Г. Курс высшей алгебры. - М.: Наука, 1971. - 431 с.], [Кострикин А.И. Введение в алгебру. Основы алгебры. М.: Физматлит.1994. - 320 с], [А.Акритас. Основы компьютерной алгебры с приложениями. М.: Мир, 1994. - 544 с.] и [Л.Б.Шнеперман. Курс алгебры и теории чисел в задачах и упражнениях.- Минск, «Вышэйшая школа», 1986.- 272 с.]). Варианты построения конечных множеств векторов многочленов рассмотрены в работе [Молдовян Н.А. Группы векторов для алгоритмов электронной цифровой подписи // Вестник СПбГУ. Сер. 10. 2008].
Для практики представляют интерес различные варианты значений размерности m векторов БС. Выбор соответствующей размерности m зависит от требований конкретных применений заявленного способа формирования и проверки ЭЦП. Например, при использовании 32-разрядных процессоров для выполнения вычислений интерес представляют простые значения размерности m=5, m=7, m=11 и m=13. При аппаратной реализации в виде специализированных вычислительных устройств высокая производительность процедур формирования проверки ЭЦП может быть достигнута при значениях размерности векторов БС m=8, m=9, m=16 и m=32. Наиболее высокая производительность при аппаратной реализации может быть достигнута при использовании заявленного способа для случая использования векторов двоичных многочленов в качестве векторов БС. Это объясняется тем, что операции сложения и умножения и двоичных многочленов в конечных полях двоичных многочленов являются наиболее эффективными с точки зрения получения высокого быстродействия и уменьшения сложности аппаратной реализации.
Приведенные выше примеры показывают принципиальную реализуемость и корректность заявленного способа формирования и проверки подлинности ЭЦП, заверяющей ЭД. Аналогичным образом реализуется заявляемый способ при использовании векторов МДЧ размерности m=4, m=5, m=6 и т.д. Например, могут быть использованы следующие таблицы умножения базисных векторов, в которых значение коэффициента растяжения ε может быть выбрано в интервале 0≤ε<p, где число р выбирается таким образом, чтобы обеспечивалось значение порядка векторов МДЧ q, равное достаточно большому простому МДЧ, например, равное значению простого МДЧ разрядности 32, 40, 64, 80, 160 или 256 бит.Таблица умножения базисных векторов для задания групповой операции над четырехмерными векторами МДЧ (случай m=4) имеет вид таблицы 7.
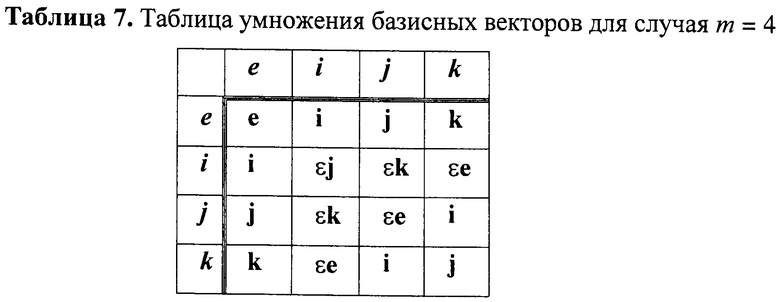
Таблица для задания групповой операции над шестимерными векторами МДЧ (случай m=6) имеет вид таблицы 8. Была разработаны программы для ЭВМ, реализующие операции умножения и возведения в большую целочисленную степень векторов МДЧ, имеющих значения размерности от m=2 до m=55 для каждого промежуточного целочисленного значения размерности. С помощью этих программ были сгенерированы приведенные выше примеры и установлено, что аналогичные примеры реализации заявленного способа с использованием векторов МДЧ размерности m=7, m=8, m=11, m=13, m=16, m=17 и др. также обеспечивают корректность процедуры проверки подлинности ЭЦП.

Таблицы умножения базисных векторов, определяющие групповые операции над векторами произвольных размерностей m, строятся по следующему общему правилу. Первоначально строится исходная таблица, которая не включает коэффициентов растяжения, путем последовательной записи строк базисных векторов таким образом, что каждая следующая строка получается из предыдущей путем циклического сдвига на одну клетку. Получаемая при этом исходная таблица умножения базисных векторов имеет стандартный вид для произвольных значений размерности векторов, поэтому ее можно назвать типовой (см. распределение базисных векторов в таблице 9). Для типовой таблицы и произвольного значения m имеется два простых и общих варианта задания распределения коэффициента растяжения по клеткам таблицы умножения базисных векторов, при которых обеспечивается ассоциативность и коммутативность операции умножения векторов БС.
Один из этих вариантов состоит в выделении квадрата, состоящего из всех клеток, не входящих в первый ряд или в первую строку, и внесении коэффициента растяжения ε в клетки этого квадрата, расположенные на диагонали, идущей из правого верхнего угла в левый нижний угол (каждая из этих клеток содержит базисный вектор е), а также во все клетки, расположенные выше этой диагонали. Второй из этих вариантов является симметричным первому относительно указанной диагонали (эта диагональ отмечена в таблице 9 серым фоном). Второй вариант распределения показан как распределение коэффициента µ, который вносится в каждую клетку диагонали, содержащей базисный вектор е и все клетки, расположенные ниже этой диагонали. Коэффициентам µ и ε может быть присвоено любое значение в интервале от 0 до р-1. При этом операция умножения векторов МДЧ будет обладать свойствами ассоциативности и коммутативности. Выбор конкретных значений коэффициентов растяжения определяет параметры групп векторов БС и должен осуществляться с привязкой к конкретным используемым значениям размерности m и числа р.
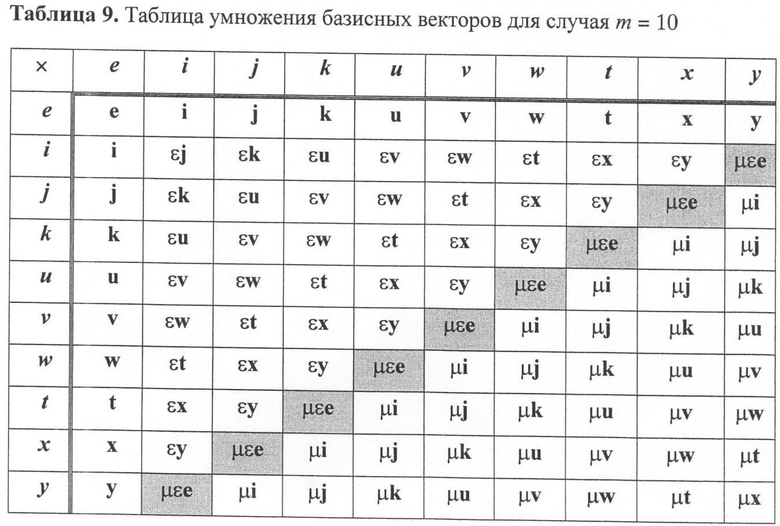
При реализации заявленного способа с использованием операций над векторами многочленов различной размерности m таблицы умножения базисных векторов строятся по указанному выше общему правилу, за исключением того, что в случае векторов многочленов коэффициенты ε и µ представляют собой многочлены. При использовании групп векторов БС, имеющих сравнительно большую размерность высокая криптографическая стойкость ЭЦП обеспечивается при меньшей разрядности МДЧ, являющихся компонентами векторов МДЧ. Например, при m=16 и m=32 разрядность указанных МДЧ может составлять 64 и 32 бита, соответственно, что позволяет повысить быстродействие процедур формирования и проверки подписи при программной реализации для выполнения программ, реализующих заявляемый способ, на 64- и 32-разрядных микропроцессорах.
Приведенные выше примеры экспериментально подтверждают корректность реализации заявляемого способа, что дополняет приведенные выше математические доказательства корректности описанных конкретных реализации заявленного способа формирования и проверки ЭЦП, заверяющей ЭД.
Таким образом, показано, что заявляемый способ может быть положен в основу стойких систем ЭЦП, обеспечивающих повышение производительности устройств и программ формирования и проверки ЭЦП.
Приведенные примеры и математическое обоснование показывают, что предлагаемый способ формирования и проверки подлинности ЭЦП работает корректно, технически реализуем и позволяет достичь сформулированного технического результата.
Приложение 1
Толкование терминов, используемых в описании заявки
1. Двоичный цифровой электромагнитный сигнал - последовательность битов в виде нулей и единиц.
2. Параметры двоичного цифрового электромагнитного сигнала: разрядность и порядок следования единичных и нулевых битов.
3. Разрядность двоичного цифрового электромагнитного сигнала - общее число его единичных и нулевых битов, например число 10011 является 5-разрядным.
4. Битовая строка (БС) - двоичный цифровой электромагнитный сигнал, представляемый в виде конечной последовательности цифр «0» и «1».
5. Электронная цифровая подпись (ЭЦП) - двоичный цифровой электромагнитный сигнал, параметры которого зависят от подписанного электронного документа и от секретного ключа. Проверка подлинности ЭЦП осуществляют с помощью открытого ключа, который зависит от секретного ключа.
6. Электронный документ (ЭД) - двоичный цифровой электромагнитный сигнал, параметры которого зависят от исходного документа и способа его преобразования к электронному виду.
7. Секретный ключ - двоичный цифровой электромагнитный сигнал, используемый для формирования подписи к заданному электронному документу. Секретный ключ представляется, например, в двоичном виде как последовательность цифр «0» и «1».
8. Открытый ключ - битовая строка, параметры которой зависят от секретного ключа и которая предназначена для проверки подлинности цифровой электронной подписи.
9. Хэш-функция от электронного документа - двоичный цифровой электромагнитный сигнал, параметры которого зависят от электронного документа и выбранного метода ее вычисления. В системах ЭЦП считается, что хэш-функция однозначно представляет ЭД, поскольку используемые хэш-функции удовлетворяют требованию коллизионной стойкости, которое означает вычислительную невозможность нахождения двух различных ЭД, которым соответствует одно и то же значение хэш-функции.
10. Многоразрядное двоичное число (МДЧ) - двоичный цифровой электромагнитный сигнал, интерпретируемый как двоичное число и представляемый в виде последовательности цифр «0» и «1».
11. Операция возведения числа S в дискретную степень А по модулю n - это операция, выполняемая над конечным множеством натуральных чисел {0, 1, 2, …, n-1}, включающем n чисел, являющихся остатками от деления всевозможных целых чисел на число n; результат выполнения операций сложения, вычитания и умножения по модулю n представляет собой число из этого же множества [Виноградов И.М. Основы теории чисел. - М.: Наука, 1972. - 167 с.]; операция возведения числа S в дискретную степень Z по модулю n определяется как Z-кратное последовательное умножение по модулю n числа S на себя, т.е. в результате этой операции также получается число W, которое меньше или равно числу n-1; даже для очень больших чисел S, Z и n существуют эффективные алгоритмы выполнения операции возведения в дискретную степень по модулю.
12. Показатель q по модулю n числа а, являющегося взаимно простым с n - это минимальное из чисел γ, для которых выполняется условие аγmodn=1, т.е. q=min{γ1, γ2, …} [Виноградов И.М. Основы теории чисел. - М.: Наука, 1972. - 167 с.].
13. Операция деления целого числа А на целое число В по модулю n выполняется как операция умножения по модулю n числа А на целое число В-1, которое является обратным к В по модулю n.
14. Порядок числа q по модулю n числа а - это показатель q по модулю n числа а.
15. Многочлен - это последовательность коэффициентов, например многоразрядных двоичных чисел (МДЧ). Над многочленами определены операции сложения многочленов и умножения многочленов, которые сводятся к выполнению действий с коэффициентами многочленов, являющихся операндами. Многочлены и правила действия над ними подробно рассмотрены в книгах [Кострикин А.И. Введение в алгебру. Основы алгебры. М.: Физматлит. 1994. - 320 с.] и [Курош А.Г. Курс высшей алгебры. - М.: Наука, 1971. - 431 с.]. В вычислительных устройствах многочлены представляются в виде битовой строки, в которой каждый бит или каждая подстрока битов фиксированной длины интерпретируется как один из коэффициентов многочлена, над которыми определены операции сложения и умножения коэффициентов.
16. Алгебраическая структура - это множество математических элементов некоторой природы. В качестве математических элементов могут выступать, например, многочлены, МДЧ, пары МДЧ, пары многочленов, тройки МДЧ, тройки многочленов, матрицы МДЧ, матрицы многочленов и т.д., над которыми заданы математические действия (операции). Математически алгебраическая структура определяется путем задания конкретного множества математических элементов и одной или нескольких операций, выполняемых над элементами.
17. Элемент алгебраической структуры - это одна битовая строка или набор из нескольких битовых строк, над которыми определена алгебраическая операция. При определении конкретного типа алгебраической структуры определяются операции над элементами алгебраической структуры, которые указывают однозначно правила интерпретации и преобразования битовых строк, представляющих эти элементы. Реализуемые в вычислительных устройствах преобразования битовых строк соответствуют операциям, выполняемым над элементами заданной алгебраической структуры.
18. Группа - это алгебраическая структура (т.е. множество элементов различной природы), над элементами которой определена одна операция и которая при заданной операции обладает заданным набором свойств: операция ассоциативна, результатом выполнения операции над двумя элементами является также элемент этой же структуры, существует нейтральный элемент такой, что при выполнении операции над ним и другим некоторым элементом а группы результатом является элемент а. Детальное описание групп дано в книгах [А.Г.Курош. Теория групп. - М.: Наука, 1967. - 648 с.] и [М.И.Каргаполов, Ю.И.Мерзляков. Основы теории групп. - М.: Наука. Физматлит, 1996. - 287 с.]. Операция, определенная над элементами группы, называется групповой операцией.
19. Кольцо - это алгебраическая структура (т.е. множество математических элементов природы), над элементами которой определены две операции, одна из которых называется сложением, а вторая - умножением. При этом при заданных операциях эта алгебраическая структура обладает заданным набором свойств: операции сложения и умножения ассоциативны и коммутативны, операция умножения является дистрибутивной относительно операции сложения, а результатом выполнения каждой из этих операций над двумя элементами является также элемент этой же структуры. Кроме того, для сложения существует нейтральный элемент, такой, что при выполнении операции над ним и другим некоторым элементом а группы результатом является элемент а. Нейтральный элемент относительно сложения называется нулевым элементом (или просто нулем). Детальное описание колец дано в книгах [Кострикин А.И. Введение в алгебру. Основы алгебры. М.: Физматлит. 1994. - 320 с.] и [Курош А.Г. Курс высшей алгебры. - М.: Наука, 1971. - 431 с.].
20. Поле - это алгебраическая структура (т.е. множество математических элементов различной природы), над элементами которой определены две операции, одна из которых называется сложением, а вторая - умножением. При этом при заданных операциях эта алгебраическая структура обладает заданным набором свойств: операции сложения и умножения ассоциативны и коммутативны, операция умножения является дистрибутивной относительно операции сложения, а результатом выполнения каждой из этих операций над двумя элементами является также элемент этой же структуры. Причем для каждой из указанных двух операций существует нейтральный элемент, такой, что при выполнении операции над ним и другим некоторым элементом а группы результатом является элемент а. Нейтральный элемент относительно сложения называется нулевым элементом (или просто нулем), а нейтральный элемент относительно умножения называется единичным элементом (или просто единицей). Кроме того, каждому ненулевому элементу а может быть сопоставлен в соответствие единственный элемент а-1, называемый обратным элементом по отношению к данному элементу, такой, что произведение а-1а (а значит, и аа-1) равно единице. Детальное описание полей дано в книгах [А.И.Кострикин. Введение в алгебру. Основы алгебры. М.: Физматлит. 1994. - 320 с.] и [Курош А.Г. Курс высшей алгебры. - М.: Наука, 1971. - 431 с.].
21. Циклическая группа - это группа, каждый элемент которой может быть представлен в виде 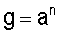 для некоторого натурального значения n, где а - элемент данной группы, называемый генератором или образующим элементом циклической группы. Степень n означает, что над элементом а выполняются n последовательных операций, т.е. выполняются вычисления по формуле
для некоторого натурального значения n, где а - элемент данной группы, называемый генератором или образующим элементом циклической группы. Степень n означает, что над элементом а выполняются n последовательных операций, т.е. выполняются вычисления по формуле 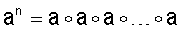 (n раз), где «°» обозначает операцию, определенную над элементами группы.
(n раз), где «°» обозначает операцию, определенную над элементами группы.
22. Циклическая подгруппа группы - это подгруппа, каждый элемент которой может быть представлен в виде 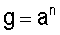 для некоторого натурального значения n, где а - элемент данной подгруппы, называющийся генератором или образующим элементом циклической подгруппы.
для некоторого натурального значения n, где а - элемент данной подгруппы, называющийся генератором или образующим элементом циклической подгруппы.
23. Вектор - это набор из двух или более элементов заданной алгебраической структуры, называемых компонентами вектора. Число элементов алгебраической структуры, над которым задан вектор, называется размерностью вектора.
24. Вектор битовых строк (вектор БС) - это набор из двух или более БС, каждая из которых представляет заданную алгебраическую структуру. Битовые строки называются координатами (или компонентами) вектора. Вектор БС записывается различными способами, требование к которым состоит в том, чтобы они идентифицировали позиции координат. Например, вектор БС можно записать в виде (а1, а2, …, аm), где m≥2 - это размерность вектора БС, означающая число координат (компонентов) в векторе БС. В качестве разделителя может быть использован знак операции, определенной над координатами (компонентами) вектора, и тогда координаты (компоненты) вектора идентифицируются указанием формальной переменной (в начале или в конце соответствующего компонента) в виде буквы латинского алфавита. Формальной называется переменная потому, что ей не приписывается никакого численного значения и она служит только для того, чтобы идентифицировать конкретную позицию координаты (компоненты) вектора БС, независимо от последовательности его записи. Так векторы БС Z1=ае+bi+cj и Z2=bi+ае+cj рассматриваются как равные, т.е. Z1=Z2. При использовании некоторых частных таблиц замены переменных формальные переменные в литературе иногда называются базисными векторами, а векторы Z1 и Z2 - векторами m-мерного пространства [Л.Б.Шнеперман. Курс алгебры и теории чисел в задачах и упражнениях.- Минск: Вышэйшая школа, 1986. - 272 с.].
25. Вектор многоразрядных двоичных чисел (векторы МДЧ) - это вектор БС, координатами которого являются МДЧ.
26. Размерность вектора БС - это количество БС, входящих в вектор БС в качестве координат.
27. Эллиптическая кривая (ЭК) - это совокупность пар МДЧ, которые удовлетворяют соотношению вида
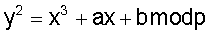 ,
,
где коэффициенты а и b и модуль р определяют конкретный вариант ЭК. Над ЭК определены операция сложения пар МДЧ и операция умножения пары МДЧ на произвольное целое число. Указанные пары МДЧ записываются в виде (х, y), где х называется абсциссой точки, а y - ординатой. Операции, определенные над точками ЭК, выполняются как операции над координатами точек ЭК. В результате вычисляется пара МДЧ, которая является координатами новой точки, являющейся результатом операции. Точки ЭК называются равными, если равны их обе координаты х и y. Детальное описание ЭК можно найти в широко доступных книгах: [Б.Я.Рябко, А.Н.Фионов. Криптографические методы защиты информации. М.: Горячая линия - Телеком, 2005. - 229 с. (см. с.97-130)].
28. Операция сложения двух точек А и В с координатами (xA,yA) и (xB,yB) соответственно выполняется по формулам:
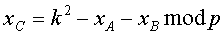 и
и 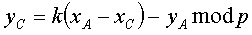 ,
,
где 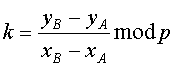 , если точки А и В не равны, и
, если точки А и В не равны, и 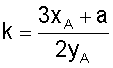
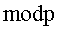 , если точки А и В равны.
, если точки А и В равны.
29. Операция умножения точки А на натуральное число n определяется как многократное сложение точки А:
nA=А+А+…+А (n раз).
Результатом умножения любой точки ЭК на нуль определяется точка, называемая бесконечно удаленной точкой и обозначаемой буквой О. Две точки А=(х, y) и -А=(х, -y) называются противоположными. Умножение на целое отрицательное число -n определяется следующим образом: (-n)А=n(-А). По определению принимают, что сумма двух противоположных точек равна бесконечно удаленной точке О [Б.Я.Рябко, А.Н.Фионов. Криптографические методы защиты информации. М.: Горячая линия - Телеком, 2005. - 229 с. (см. с.97-130)].
30. Выполнение операций над точками ЭК осуществляется в вычислительных устройствах как действия над двоичными цифровыми электромагнитными сигналами, осуществляемыми по определенным правилам, определяемым через операции над МДЧ.
31. Порядком точки А ЭК называется наименьшее натуральное число q, такое что qA=О, т.е. такое, что результатом умножения точки А на число q является бесконечно удаленная точка.
Изобретение относится к области электросвязи, а именно к области криптографических устройств и способов проверки электронной цифровой подписи (ЭЦП). Способ генерации и проверки ЭЦП включает следующую последовательность действий: генерируют секретный ключ в виде, по крайней мере, одной, битовой строки (БС) k, по секретному ключу формируют открытый ключ Y в виде вектора БС размерности m, где 2≤m<64, принимают электронный документ (ЭД), представленный МДЧ Н, в зависимости от принятого электронного документа и от значения секретного ключа формируют ЭЦП Q в виде, по крайней мере, двух БС, в зависимости от ЭЦП, ЭД и открытого ключа формируют первое А и второе В проверочные БС, сравнивают БС А и В. При совпадении их параметров делают вывод о подлинности электронной цифровой подписи. Техническим результатом, достигаемым в заявленном способе, является повышение производительности алгоритмов ЭЦП без снижения ее уровня стойкости. 7 з.п. ф-лы, 9 табл.
1. Способ формирования и проверки подлинности электронной цифровой подписи, заверяющей электронный документ, заключающийся в том, что генерируют секретный ключ в виде, по крайней мере, одной битовой строки, по секретному ключу формируют открытый ключ Y в виде более чем одной битовой строки, принимают электронный документ, представленный битовыми строками H1, H2, …, Hz, где z≥1, в зависимости от принятого электронного документа и от значения секретного ключа формируют электронную цифровую подпись Q в виде совокупности многоразрядных двоичных чисел е, s1, s2, …, su, где 1≤u≤8, в зависимости от открытого ключа, принятого электронного документа и электронной цифровой подписи формируют первую А и вторую В проверочные битовые строки, сравнивают их и при совпадении их параметров делают вывод о подлинности электронной цифровой подписи, отличающийся тем, что открытый ключ Y формируют в виде m-мерного, где 2≤m≤64, вектора путем генерации m-мерных векторов G1, G2, …, Gu, координатами каждого из которых являются битовые строки разрядностью r, где 16≤r≤512, генерации секретного ключа в виде многоразрядных двоичных чисел k1, k2, …, ku и генерации открытого ключа Y по формуле 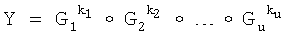 , где знак
, где знак  обозначает операцию умножения векторов.
обозначает операцию умножения векторов.
2. Способ по п.1, отличающийся тем, что открытый ключ Y формируют в виде m-мерного, где 2≤m≤64, вектора многоразрядных двоичных чисел путем генерации m-мерных векторов многоразрядных двоичных чисел G1, G2, …, Gu, координатами каждого из которых являются многоразрядные двоичные числа разрядностью r, где 1≤r≤512, генерации секретного ключа в виде многоразрядных двоичных чисел k1, k2, …, ku и генерации открытого ключа Y по формуле 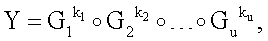 где знак
где знак  обозначает операцию умножения векторов многоразрядных двоичных чисел.
обозначает операцию умножения векторов многоразрядных двоичных чисел.
3. Способ по п.1, отличающийся тем, что открытый ключ Y формируют в виде m-мерного, где 2≤m≤64, вектора многочленов путем генерации m-мерных векторов многочленов G1, G2, …, Gu, координатами каждого из которых являются многочлены разрядностью r, где 1≤r≤512, генерации секретного ключа в виде многоразрядных двоичных чисел k1, k2, …, ku и генерации открытого ключа Y по формуле 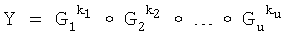 , где знак
, где знак  обозначает операцию умножения векторов многочленов.
обозначает операцию умножения векторов многочленов.
4. Способ по п.1, отличающийся тем, что открытый ключ Y формируют в виде m-мерного, где m=2, вектора путем генерации m-мерных векторов G1 и G2, имеющих порядок, равный простому многоразрядному двоичному числу q, генерации секретного ключа в виде многоразрядных двоичных чисел k1 и k2 и генерации открытого ключа Y по формуле 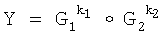 , принимают электронный документ, представленный битовой строкой H1, а электронную цифровую подпись формируют в виде трех многоразрядных двоичных чисел е, s1 и s2, для чего генерируют случайные многоразрядные двоичные числа t1 и t2, генерируют вектор R по формуле
, принимают электронный документ, представленный битовой строкой H1, а электронную цифровую подпись формируют в виде трех многоразрядных двоичных чисел е, s1 и s2, для чего генерируют случайные многоразрядные двоичные числа t1 и t2, генерируют вектор R по формуле 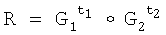 , затем в зависимости от R и H1 формируют первое многоразрядное двоичное число е электронной цифровой подписи по формуле e=f(R,H1), где f(R,H1) - выражение, задающее правило вычисления многоразрядного двоичного числа е, затем в зависимости от секретного ключа генерируют пару многоразрядных двоичных чисел s1 и s2 электронной цифровой подписи по формулам s1=(t1-k1e)modq и s2=(t2-k2e)modq, после чего формируют первую и вторую проверочные битовые строки А и В по формулам А=f(R',Н1) и B=е, где вектор R' вычисляют по формуле
, затем в зависимости от R и H1 формируют первое многоразрядное двоичное число е электронной цифровой подписи по формуле e=f(R,H1), где f(R,H1) - выражение, задающее правило вычисления многоразрядного двоичного числа е, затем в зависимости от секретного ключа генерируют пару многоразрядных двоичных чисел s1 и s2 электронной цифровой подписи по формулам s1=(t1-k1e)modq и s2=(t2-k2e)modq, после чего формируют первую и вторую проверочные битовые строки А и В по формулам А=f(R',Н1) и B=е, где вектор R' вычисляют по формуле 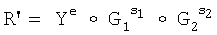 .
.
5. Способ по п.1, отличающийся тем, что открытый ключ Y формируют в виде m-мерного, где m=3, вектора путем генерации m-мерных векторов G1, G2 и G3, имеющих порядок, равный простому многоразрядному двоичному числу q, генерации секретного ключа в виде многоразрядных двоичных чисел k1, k2 и k3 и генерации открытого ключа Y по формуле 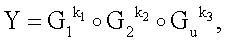 принимают электронный документ, представленный битовой строкой Н1, а электронную цифровую подпись формируют в виде четырех битовых строк е, s1, s2, и s3, для чего генерируют случайные многоразрядные двоичные числа t1, t2 и t3, генерируют вектор R по формуле
принимают электронный документ, представленный битовой строкой Н1, а электронную цифровую подпись формируют в виде четырех битовых строк е, s1, s2, и s3, для чего генерируют случайные многоразрядные двоичные числа t1, t2 и t3, генерируют вектор R по формуле 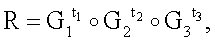 затем в зависимости от R и H1 формируют первое многоразрядное двоичное число е электронной цифровой подписи по формуле e=f(R,H1), где f(R,H1) - выражение, задающее правило вычисления многоразрядного двоичного числа е, затем в зависимости от секретного ключа генерируют тройку многоразрядных двоичных чисел s1, s2 и s3 электронной цифровой подписи по формулам s1=(t1-k1e)modq, s2=(t2-k2e)modq и s3=(t3-k3e)modq, после чего формируют первую и вторую проверочные битовые строки А и В по формулам А=f(R',H1) и В=е, где вектор R' вычисляют по формуле
затем в зависимости от R и H1 формируют первое многоразрядное двоичное число е электронной цифровой подписи по формуле e=f(R,H1), где f(R,H1) - выражение, задающее правило вычисления многоразрядного двоичного числа е, затем в зависимости от секретного ключа генерируют тройку многоразрядных двоичных чисел s1, s2 и s3 электронной цифровой подписи по формулам s1=(t1-k1e)modq, s2=(t2-k2e)modq и s3=(t3-k3e)modq, после чего формируют первую и вторую проверочные битовые строки А и В по формулам А=f(R',H1) и В=е, где вектор R' вычисляют по формуле 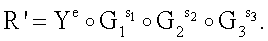
6. Способ по п.1, отличающийся тем, что открытый ключ Y формируют в виде m-мерного, где m=5, вектора путем генерации m-мерных векторов G1 и G2, имеющих порядки, равные многоразрядным двоичным числам q1 и q2 соответственно, генерации секретного ключа в виде многоразрядных двоичных чисел k1 и k2 и генерации открытого ключа Y по формуле 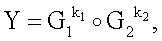 принимают электронный документ, представленный битовой строкой H1, а электронную цифровую подпись формируют в виде трех многоразрядных двоичных чисел е, s1 и s2, для чего генерируют случайные многоразрядные двоичные числа t1 и t2, генерируют вектор R по формуле
принимают электронный документ, представленный битовой строкой H1, а электронную цифровую подпись формируют в виде трех многоразрядных двоичных чисел е, s1 и s2, для чего генерируют случайные многоразрядные двоичные числа t1 и t2, генерируют вектор R по формуле 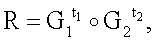 затем в зависимости от R и Н1 формируют первое многоразрядное двоичное число е электронной цифровой подписи по формуле e=f(R,H1), где f(R,H1) - выражение, задающее правило вычисления числа е, затем в зависимости от секретного ключа генерируют пару многоразрядных двоичных чисел s1 и s2 электронной цифровой подписи по формулам s1=(t1-k1e)modq1 и s2=(t2-k2e)modq2, после чего формируют первую и вторую проверочные битовые строки А и В по формулам А=f(R',H1) и В=е, где вектор R' вычисляют по формуле
затем в зависимости от R и Н1 формируют первое многоразрядное двоичное число е электронной цифровой подписи по формуле e=f(R,H1), где f(R,H1) - выражение, задающее правило вычисления числа е, затем в зависимости от секретного ключа генерируют пару многоразрядных двоичных чисел s1 и s2 электронной цифровой подписи по формулам s1=(t1-k1e)modq1 и s2=(t2-k2e)modq2, после чего формируют первую и вторую проверочные битовые строки А и В по формулам А=f(R',H1) и В=е, где вектор R' вычисляют по формуле 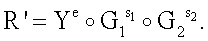
7. Способ по п.1, отличающийся тем, что открытый ключ Y формируют в виде m-мерного, где m=3, вектора путем генерации m-мерного вектора G1, имеющего порядок, равный многоразрядному двоичному числу q, генерации секретного ключа в виде многоразрядного двоичного числа k1 и генерации открытого ключа Y по формуле 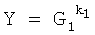 , принимают электронный документ, представленный битовой строкой Н1, а электронную цифровую подпись формируют в виде двух многоразрядных двоичных чисел е и s1, для чего генерируют случайное многоразрядное двоичное число t, генерируют вектор R по формуле R=G', затем в зависимости от R и Н1 формируют первое многоразрядное двоичное число е электронной цифровой подписи по формуле e=f(R,H1), где f(R,H1) - выражение, задающее правило вычисления числа е, затем в зависимости от секретного ключа генерируют второе многоразрядное двоичное число s1 электронной цифровой подписи по формуле s1=(t+k1e)modq, после чего формируют первую и вторую проверочные битовые строки А и В по формулам А=f(R',H1) и В=е, где вектор R' вычисляют по формуле
, принимают электронный документ, представленный битовой строкой Н1, а электронную цифровую подпись формируют в виде двух многоразрядных двоичных чисел е и s1, для чего генерируют случайное многоразрядное двоичное число t, генерируют вектор R по формуле R=G', затем в зависимости от R и Н1 формируют первое многоразрядное двоичное число е электронной цифровой подписи по формуле e=f(R,H1), где f(R,H1) - выражение, задающее правило вычисления числа е, затем в зависимости от секретного ключа генерируют второе многоразрядное двоичное число s1 электронной цифровой подписи по формуле s1=(t+k1e)modq, после чего формируют первую и вторую проверочные битовые строки А и В по формулам А=f(R',H1) и В=е, где вектор R' вычисляют по формуле 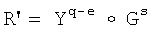 .
.
8. Способ по п.1, отличающийся тем, что открытый ключ Y формируют в виде m-мерного, где 2≤m≤8, вектора путем генерации m-мерных векторов G1, G2, …, Gm, имеющих порядок, равный простому многоразрядному двоичному числу q, генерации секретного ключа в виде многоразрядных двоичных чисел k1, k2, …, km и генерации открытого ключа Y по формуле 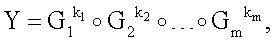 принимают электронный документ, представленный битовыми строками H1, Н2, …, Hm, а электронную цифровую подпись формируют в виде совокупности многоразрядных двоичных чисел е, s1, s2, …, sm, для чего генерируют случайные многоразрядные двоичные числа t1, t2, …, tm, генерируют вектор R по формуле
принимают электронный документ, представленный битовыми строками H1, Н2, …, Hm, а электронную цифровую подпись формируют в виде совокупности многоразрядных двоичных чисел е, s1, s2, …, sm, для чего генерируют случайные многоразрядные двоичные числа t1, t2, …, tm, генерируют вектор R по формуле 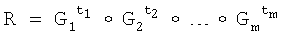 , затем в зависимости от R формируют первое многоразрядное двоичное число е электронной цифровой подписи по формуле e=f(R,H), где f(R,H) - выражение, задающее правило вычисления числа е, и H=H1||H2||…||Hm, где знак || обозначает операцию конкатенации, затем в зависимости от секретного ключа генерируют m многоразрядных двоичных чисел s1, s2, …, sm электронной цифровой подписи по формулам
, затем в зависимости от R формируют первое многоразрядное двоичное число е электронной цифровой подписи по формуле e=f(R,H), где f(R,H) - выражение, задающее правило вычисления числа е, и H=H1||H2||…||Hm, где знак || обозначает операцию конкатенации, затем в зависимости от секретного ключа генерируют m многоразрядных двоичных чисел s1, s2, …, sm электронной цифровой подписи по формулам 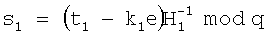 ,
, 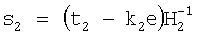 , …,
, …, 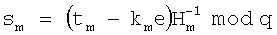 , после чего формируют первую и вторую проверочные битовые строки А и В по формулам A=f(R',H) и В=е, где вектор R' вычисляют по формуле
, после чего формируют первую и вторую проверочные битовые строки А и В по формулам A=f(R',H) и В=е, где вектор R' вычисляют по формуле 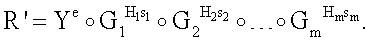
| СПОСОБ ФОРМИРОВАНИЯ И ПРОВЕРКИ ПОДЛИННОСТИ ЭЛЕКТРОННОЙ ЦИФРОВОЙ ПОДПИСИ, ЗАВЕРЯЮЩЕЙ ЭЛЕКТРОННЫЙ ДОКУМЕНТ | 2006 |
|
RU2325767C1 |
| СПОСОБ ПРОВЕРКИ ПОДЛИННОСТИ ЭЛЕКТРОННОЙ ЦИФРОВОЙ ПОДПИСИ, ЗАВЕРЯЮЩЕЙ ЭЛЕКТРОННЫЙ ДОКУМЕНТ | 2005 |
|
RU2280896C1 |
| US 2003051137 A1, 13.03.2003 | |||
| Переносная печь для варки пищи и отопления в окопах, походных помещениях и т.п. | 1921 |
|
SU3A1 |
| СПОСОБ ИДЕНТИФИКАЦИИ ПОДЛИННОСТИ КОНТРОЛИРУЕМОГО ОБЪЕКТА | 2000 |
|
RU2172015C1 |
| Приспособление в пере для письма с целью увеличения на нем запаса чернил и уменьшения скорости их высыхания | 1917 |
|
SU96A1 |
Авторы
Даты
2010-10-10—Публикация
2008-07-24—Подача