Изобретение относится к области электросвязи и вычислительной техники, а конкретнее к области криптографических способов аутентификации электронных сообщений, передаваемых по телекоммуникационным сетям и сетям ЭВМ, и может быть использовано в системах передачи электронных сообщений (документов), заверенных электронной цифровой подписью (ЭЦП), представленной в виде многоразрядного двоичного числа (МДЧ). Здесь и далее под МДЧ понимается электромагнитный сигнал в двоичной цифровой форме, параметрами которого являются: число битов и порядок следования их единичных и нулевых значений (1)толкование используемых в описании терминов приведено в Приложении 1).
Известен способ формирования и проверки ЭЦП, предложенный в патенте США №4405829 от 20.09.1983 и детально описанный также и в книгах 1. М.А.Иванов. Криптография. М., КУДИЦ-ОБРАЗ, 2001; 2. А.Г.Ростовцев, Е.Б.Маховенко. Введение в криптографию с открытым ключом. СПб.: Мир и семья, 2001. - с.43. Известный способ заключается в следующей последовательности действий:
формируют секретный ключ в виде трех простых МДЧ р, q и d, формируют открытый ключ (n, е) в виде пары МДЧ n и е, где n - число, представляющее собой произведение двух простых МДЧ р и q, и е - МДЧ, удовлетворяющее условию ed=1 mod (p-1)(q-1), принимают электронный документ (ЭД), представленный МДЧ Н,
в зависимости от значения H и значения секретного ключа формируют ЭЦП в виде МДЧ Q=S=Hd mod n;
формируют первое проверочное МДЧ А=H;
формируют второе проверочное МДЧ В, для чего МДЧ S возводят в целочисленную степень е по модулю n: В=Se mod n;
сравнивают сформированные проверочные МДЧ А и В,
при совпадении параметров сравниваемых МДЧ А и В делают вывод о подлинности ЭЦП.
Недостатком известного способа является относительно большой размер подписи и необходимость увеличения размера подписи при разработке новых более эффективных методов разложения числа n на множители или при росте производительности современных вычислительных устройств. Это объясняется тем, что значение элемента подписи S вычисляются путем выполнения арифметических операций по модулю n, а стойкость ЭЦП определяется сложностью разложения модуля n на множители р и q.
Известен также способ формирования и проверки подлинности ЭЦП Эль-Гамаля, описанный в книге Молдовян А.А., Молдовян Н.А., Советов Б.Я. Криптография. - СПб., Лань, 2000. - с.156-159, который включает следующие действия:
формируют простое МДЧ р и двоичное число G, являющееся первообразным корнем по модулю р, генерируют секретный ключ в виде МДЧ х, в зависимости от секретного ключа формируют открытый ключ в виде МДЧ Y=Gx mod р, принимают ЭД, представленный в виде МДЧ H, в зависимости от H и секретного ключа формируют ЭЦП Q в виде двух МДЧ S и R, то есть Q=(S, R);
осуществляют процедуру проверки подлинности ЭЦП, включающую вычисление двух контрольных параметров с использованием исходных МДЧ р, G, Y, H и S путем возведения МДЧ G, Y, R в дискретную степень по модулю р и сравнение вычисленных контрольных параметров;
при совпадении значений контрольных параметров делают вывод о подлинности ЭЦП.
Недостатком данного способа также является относительно большой размер ЭЦП. Это объясняется тем, что значения элементов подписи S и R вычисляют путем выполнения арифметических операций по модулю р-1 и по модулю р соответственно.
Известен также способ формирования и проверки ЭЦП, предложенный в патенте США №4995089 от 19.02.1991. Известный способ заключается в следующей последовательности действий:
формируют простое МДЧ p, такое что р=Nq+1, где q - простое МДЧ;
формируют простое МДЧ а, такое что а≠1 и aq mod р=1;
методом генерации случайной равновероятной последовательности формируют секретный ключ в виде МДЧ х;
формируют открытый ключ в виде МДЧ у по формуле у=ax mod p;
принимают ЭД, представленный МДЧ М;
формируют ЭЦП в виде пары МДЧ (е, s), для чего генерируют случайное МДЧ t, формируют МДЧ R по формуле R=at mod р, формируют МДЧ е=f(M||R), где знак || обозначает операцию присоединения двух МДЧ и f - некоторая специфицированная хэш-функция, значение которой имеет фиксированную длину (обычно 160 или 256 бит), независимо от размера аргумента, т.е. от размера МДЧ M||R, а затем формируют МДЧ s по формуле s=(t-ex) mod q;
формируют первое проверочное МДЧ А, для чего генерируют МДЧ R' по формуле R'=asye mod p и формируют МДЧ А=f(M||R');
формируют второе проверочное МДЧ В путем копирования МДЧ е: В=е;
сравнивают сформированные проверочные МДЧ А и В;
при совпадении параметров сравниваемых МДЧ А и В делают вывод о подлинности ЭЦП.
Недостатком способа по патенту США является относительно высокая вычислительная сложность процедуры формирования и проверки ЭЦП, что связано с тем, что для обеспечения минимально требуемого уровня стойкости требуется использовать простой модуль р разрядностью не менее 1024 бит.
Наиболее близким по своей технической сущности к заявленному является известный способ формирования и проверки подлинности ЭЦП, предлагаемый российским стандартом ГОСТ Р 34.10-2001 и описанный, например, в книге Б.Я.Рябко, А.Н.Фионов. Криптографические методы защиты информации. М., Горячая линия - Телеком, 2005. - 229 с. (см. с.110-111), согласно которому ЭЦП формируется в виде пары МДЧ r и s, для чего генерируют эллиптическую кривую (ЭК) в виде совокупности точек, причем каждая точка представляется двумя координатами в декартовой системе координат в виде двух МДЧ, называемых абсциссой (х) и ординатой (у), затем осуществляют операции генерации точек ЭК, сложения точек ЭК и умножения точки ЭК на число, а также арифметические операции над МДЧ, после чего в результате выполненных операций формируются МДЧ r и s. Указанные операции над точками выполняются как операции над МДЧ, являющимися координатами точек, по известным формулам [Б.Я.Рябко, А.Н.Фионов. Криптографические методы защиты информации. М., Горячая линия - Телеком, 2005. - 229 с. (см. с.110-111)]. Операция сложения двух точек А и В с координатами (xА, yA) и (xB, yB) соответственно выполняется по формулам:
xC=k2-xA-xB mod p и yC=k(xA-xC)-yA mod p,
где 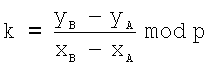 , если точки А и В не равны, и
, если точки А и В не равны, и 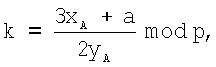 если точки А и В равны. Операция умножения точки А на натуральное число n определяется как многократное сложение точки А:
если точки А и В равны. Операция умножения точки А на натуральное число n определяется как многократное сложение точки А:
nА=А+А+…+А (n раз).
Результатом умножения любой точки ЭК на нуль определяется точка, называемая бесконечно удаленной точкой и обозначаемой буквой О. Две точки А=(х, у) и -А=(х, -у) называются противоположными. Умножение на целое отрицательное число -n определяется следующим образом: (-n)А=n(-А). По определению принимают, что сумма двух противоположных точек равна бесконечно удаленной точке О.
В прототипе, т.е. в способе формирования и проверки подлинности ЭЦП по стандарту ГОСТ Р 34.10-2001, генерируют ЭК, описываемую уравнением у2=х3+ax+b mod p, поэтому генерация ЭК состоит в генерации чисел a, b и р, являющихся параметрами ЭК и однозначно задающих множество точек ЭК, абсцисса и ордината каждой из которых удовлетворяет указанному уравнению. Ближайший аналог (прототип) заключается в выполнении следующей последовательности действий:
генерируют эллиптическую кривую (ЭК), которая представляет собой совокупность пар МДЧ, называемых точками ЭК и обладающих определенными свойствами (см. Приложение 1, пп.15-19);
методом генерации случайной равновероятной последовательности формируют секретные ключи в виде МДЧ k1, k2, …, kn;
формируют открытые ключи в виде точек ЭК P1, Р2, …, Pn, для чего генерируют точку G, имеющую значение порядка, равное q (порядком точки ЭК называется наименьшее положительное целое число q, такое, что результатом умножения данной точки на число q является так называемая бесконечно удаленная точка О; результатом умножения любой точки ЭК на нуль по определению является точка О [Б.Я.Рябко, А.Н.Фионов. Криптографические методы защиты информации. М., Горячая линия - Телеком, 2005. - 229 с. (см. с.97-130)]; см. также Приложение 1, пп.15-19), и генерируют открытые ключи путем умножения точки G на МДЧ k1, k2, …, kn, т.е. формируют открытые ключи по формулам P1=k1G, P2=k2G, …, Pn=knG;
принимают ЭД, представленный МДЧ Н;
генерируют случайное МДЧ 0<t<q, по которому формируют точку R по формуле R=tG;
формируют ЭЦП Q в виде пары МДЧ (r, s), для чего генерируют МДЧ r по формуле r=xR mod q, где xR - абсцисса точки R, а затем генерируют МДЧ s по формуле s=(tH+rki) mod q, где 1≤i≤n;
формируют первое проверочное МДЧ А, для чего генерируют МДЧ v по формуле v=sH-1 mod q и МДЧ w по формуле w=(q-rH-1) mod q, затем генерируют точку R' по формуле R'=vG+wPi, после чего МДЧ А получают по формуле А=xR' mod q, где xR' - абсцисса точки R';
формируют второе проверочное МДЧ В путем копирования МДЧ r: В=r;
сравнивают сформированные проверочные МДЧ А и В;
при совпадении параметров сравниваемых МДЧ А и В делают вывод о подлинности ЭЦП.
Недостатком ближайшего аналога является относительно невысокая производительность процедуры формирования и проверки ЭЦП, что связано с тем, что выполнение операций над точками ЭК включает операцию деления МДЧ по модулю простого МДЧ, которая требует времени выполнения, длительность которого более чем в 10 раз превышает время выполнения операции умножения.
Целью изобретения является разработка способа формирования и проверки подлинности ЭЦП, заверяющей ЭД, свободного от операции деления по модулю простого МДЧ, благодаря чему повышается производительность процедур формирования и проверки ЭЦП.
Поставленная цель достигается тем, что в известном способе формирования и проверки подлинности ЭЦП, заверяющей ЭД, заключающемся в том, что генерируют секретный ключ в виде МДЧ х, по секретному ключу формируют открытый ключ Y в виде более чем одного МДЧ, принимают ЭД, представленный МДЧ Н, в зависимости от принятого ЭД и от значения секретного ключа формируют ЭЦП Q в виде двух МДЧ, в зависимости от открытого ключа, принятого ЭД и ЭЦП, формируют первое А и второе В проверочные МДЧ, сравнивают их и при совпадении их параметров делают вывод о подлинности электронной цифровой подписи, открытый ключ Y формируют в виде вектора МДЧ размерности m, где 2≤m≤64.
Выполнение операции умножения векторов МДЧ включает выполнение над МДЧ операций сложения и умножения по модулю простого МДЧ. Благодаря тому что при выполнении операций умножения и возведения в степень векторов МДЧ не требуется выполнять операцию деления по модулю, обеспечивается повышение производительности процедур формирования и проверки подлинности ЭЦП.
Новым является также и то, что открытый ключ Y генерируют в виде вектора МДЧ размерности m=2, для чего генерируют вектор МДЧ G размерности m=2, имеющий порядок, равный МДЧ q, и открытый ключ Y формируют по
формуле Y=Gx (mod р), а ЭЦП формируют в виде пары МДЧ е и s, для чего генерируют случайное МДЧ k, генерируют вектор МДЧ R по формуле
R=Gk (mod р), где р - МДЧ, являющееся модулем, по которому выполняются операции над МДЧ, входящими в состав вектора МДЧ G при выполнении над G операции возведения в степень, затем формируют первое МДЧ е электронной цифровой подписи по формуле e=rH mod δ, где r=(r1||r2) - МДЧ, равное конкатенации МДЧ, входящих в вектор МДЧ R, и δ - вспомогательное простое МДЧ, затем генерируют второе МДЧ s электронной цифровой подписи по формуле s=(k-ex)mod q, после чего формируют первое и второе проверочные МДЧ А и В по формулам А=r'H mod δ и В=е, где r'=(r'1||r'2) - МДЧ, равное конкатенации МДЧ, входящих в вектор МДЧ R', вычисленный по формуле R'=YeGs(mod р).
Новым является также и то, что МДЧ p и q являются простыми.
Новым является также и то, что открытый ключ Y генерируют в виде вектора МДЧ размерности 3×3, для чего генерируют вектор МДЧ G размерности 3×3, имеющий порядок, равный МДЧ q, и открытый ключ Y формируют по формуле Y=Gx (mod р), где р - МДЧ, являющееся модулем, по которому выполняются операции над МДЧ, входящими в состав вектора МДЧ G при выполнении над G операции возведения в степень, а электронную цифровую подпись формируют в виде пары МДЧ е и s, для чего генерируют случайное МДЧ k, генерируют вектор МДЧ R по формуле R=Gk (mod р), затем формируют первое МДЧ е электронной цифровой подписи по формуле е=rH mod δ, где r=(r1||r2||r3) - МДЧ, равное конкатенации МДЧ, входящих в состав вектора МДЧ R, и δ - вспомогательное простое МДЧ, затем генерируют второе МДЧ s электронной цифровой подписи по формуле s=(k+ex)mod q, после чего формируют первое и второе проверочные МДЧ А и В по формулам А=r'H mod δ и В=е, где r'=(r'1||r'2||r'3) - МДЧ, равное конкатенации МДЧ, входящих в состав вектора МДЧ R', вычисленного по формуле R'=Yq-eGs(mod p).
Новым является также и то, что МДЧ р является составным, т.е. представляет собой произведение двух или более простых чисел.
Конкатенацией двух МДЧ а и b, представленных в некоторой позиционной системе исчисления в виде а=а1а2а3…ag и b=b1b2b3…bk, называется число с=а||b=а1а2а3…agb1b2b3…bk. Знак || обозначает операцию конкатенации.
Вектор многоразрядных двоичных чисел - это набор из двух или более МДЧ, называемых компонентами (вектора МДЧ). Вектор МДЧ записывается различными способами, требование к которым состоит в том, чтобы они идентифицировали позиции компонентов. Например, вектор МДЧ можно записать в виде (а1, a2, …, am), где m≥2 - это размерность вектора МДЧ, означающая число компонентов в векторе МДЧ. В качестве разделителя может быть использован знак операции, определенной над компонентами вектора, и тогда компоненты вектора идентифицируются указанием формальной переменной (в начале или в конце соответствующего компонента) в виде буквы латинского алфавита. Формальной называется переменная потому, что ей не приписывается никакого численного значения, и она служит только для того, чтобы идентифицировать компонент вектора МДЧ, независимо от последовательности его записи. Так, векторы МДЧ Z1=5е+3i+5j и Z2=3i+5e+5j рассматриваются как равные, т.е. Z1=Z2. Размерность вектора МДЧ - это количество МДЧ, входящих в вектор МДЧ в качестве компонентов. В данной заявке рассматриваются конечные группы, элементами которой являются векторы МДЧ вида Z=ае+bi+cj, где групповая операция определена через операции над векторами МДЧ как операция умножения многочленов с учетом того, что возникающие при этом произведения формальных переменных заменяются по некоторой специфицированной таблице. Такая таблица замены переменных для векторов МДЧ размерности m=3 имеет, например, следующий вид:
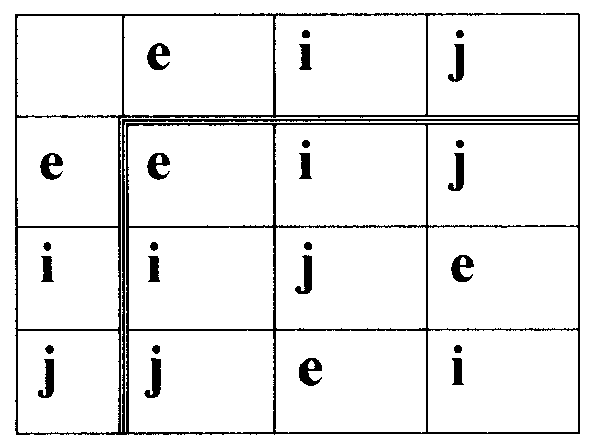
Эта таблица определяет следующее правило подстановки переменных:
e·i→i, e·j→j, j·i→e, i·i→j, j·j→i и т.д.
Например, пусть Z1=а1е+b1i+с1j и Z2=а2е+b2i+с2j, тогда операция умножения векторов МДЧ Z1 и Z2 (обозначим ее знаком 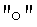 ) выполняется следующим образом:
) выполняется следующим образом:

Чтобы задать конечные группы векторов МДЧ, операции сложения и умножения над МДЧ, являющимися компонентами векторов МДЧ, задаются по модулю простого числа р, размер которого выбирается таким, чтобы обеспечить достаточно большой порядок группы векторов МДЧ:
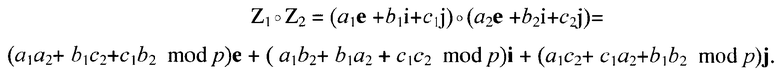
При записи формул, описывающих выполнение операций в конечной группе векторов МДЧ и заданных через операции сложения и умножения по модулю, в конце правой части формул будем указывать в скобках (mod p), где р - значение модуля. Например, операцию 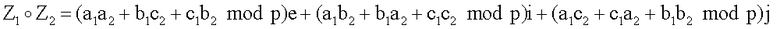 будем записывать в виде Z1Z2 (mod p), т.e.
будем записывать в виде Z1Z2 (mod p), т.e. 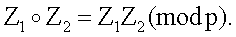 В зависимости от размерности векторов МДЧ, над которыми определяются операции умножения, и конкретного варианта операции умножения могут быть использованы различные таблицы подстановок переменных, например:
В зависимости от размерности векторов МДЧ, над которыми определяются операции умножения, и конкретного варианта операции умножения могут быть использованы различные таблицы подстановок переменных, например:
1. Для векторов размерности m=2 приемлемая таблица имеет вид
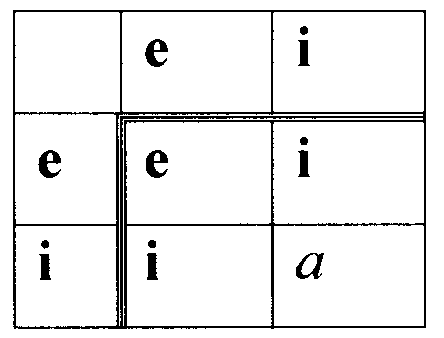
где 0<а<р.
2. Для векторов размерности m=3 приемлемая таблица имеет вид

где 0<а<р. Значение параметра а может выбираться любым из указанного интервала. Различные значения параметра а придают различные свойства конечной группе векторов МДЧ при фиксированном значении размерности m и модуля р. Аналогичным способом могут быть определены групповые операции над конечными группами векторов МДЧ размерностей m=4, m=5 и т.д.
При соответствующем выборе таблицы замены формальных переменных и простого значения р множество векторов МДЧ является конечным, и это конечное множество содержит подмножество векторов МДЧ, которое образуют группу с групповой операцией  причем порядок этой подгруппы является достаточно большим. Группа - это алгебраическая структура (т.е. множество математических элементов некоторой природы), над элементами которой задана некоторая операция таким образом, что алгебраическая структура обладает следующим набором свойств: операция ассоциативна, результатом выполнения операции над двумя элементами является также элемент этой же структуры, существует нейтральный элемент такой, что при выполнении операции над ним и другим некоторым элементом а группы результатом является элемент а. Детальное описание групп дано в широкодоступной математической литературе, например в книгах А.Г.Курош. Теория групп.- М., «Наука», 1967. - 648 с. и М.И.Каргаполов, Ю.И.Мерзляков. Основы теории групп. - М., «Наука. Физматлит», 1996. - 287 с. Операция, определенная над элементами группы, называется групповой операцией. Группа называется циклической, если каждый ее элемент может быть представлен в виде g=an для некоторого натурального числа n, где а - элемент данной подгруппы, называющийся генератором или образующим элементом циклической подгруппы, и степень n означает, что над элементом а выполняются n последовательных операций, т.е.
причем порядок этой подгруппы является достаточно большим. Группа - это алгебраическая структура (т.е. множество математических элементов некоторой природы), над элементами которой задана некоторая операция таким образом, что алгебраическая структура обладает следующим набором свойств: операция ассоциативна, результатом выполнения операции над двумя элементами является также элемент этой же структуры, существует нейтральный элемент такой, что при выполнении операции над ним и другим некоторым элементом а группы результатом является элемент а. Детальное описание групп дано в широкодоступной математической литературе, например в книгах А.Г.Курош. Теория групп.- М., «Наука», 1967. - 648 с. и М.И.Каргаполов, Ю.И.Мерзляков. Основы теории групп. - М., «Наука. Физматлит», 1996. - 287 с. Операция, определенная над элементами группы, называется групповой операцией. Группа называется циклической, если каждый ее элемент может быть представлен в виде g=an для некоторого натурального числа n, где а - элемент данной подгруппы, называющийся генератором или образующим элементом циклической подгруппы, и степень n означает, что над элементом а выполняются n последовательных операций, т.е. 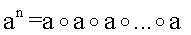 (n раз). Известно, что, если порядок группы есть простое число, то она циклическая [А.И.Кострикин. Введение в алгебру. Основы алгебры. М.: Физматлит. 1994. - 320 с.]. Важной характеристикой группы является ее порядок, который равен числу элементов в группе. Для элементов группы также применяется понятие порядка. Порядком элемента группы, является минимальное значение степени, в которую нужно возвести этот элемент, чтобы результатом операции было получение нейтрального элемента группы.
(n раз). Известно, что, если порядок группы есть простое число, то она циклическая [А.И.Кострикин. Введение в алгебру. Основы алгебры. М.: Физматлит. 1994. - 320 с.]. Важной характеристикой группы является ее порядок, который равен числу элементов в группе. Для элементов группы также применяется понятие порядка. Порядком элемента группы, является минимальное значение степени, в которую нужно возвести этот элемент, чтобы результатом операции было получение нейтрального элемента группы.
Обычно при разработке способов формирования и проверки ЭЦП используются циклические группы большого простого порядка или группы, порядок которых делится нацело на большое простое число [Венбо Мао. Современная криптография. Теория и практика. - М., СПб, Киев. Издательский дом «Вильямс», 2005. - 763 с.]. При соответствующем задании группы векторов МДЧ это условие легко обеспечивается. При этом стойкость способов формирования и проверки ЭЦП определяется сложностью задачи дискретного логарифмирования, которая состоит в определении значения степени n, в которую надо возвести заданный элемент группы, чтобы результатом этой операции был некоторый другой заданный элемент группы [Молдовян Н.А. Практикум по криптосистемам с открытым ключом. - СПб., БХВ-Петербург, 2007. - 298 с.].
Поскольку групповая операция 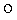 над векторами МДЧ выполняется путем выполнения модульных умножений и сложений над МДЧ, являющихся компонентами векторов МДЧ, достаточно высокая трудность задачи дискретного логарифмирования в группе векторов МДЧ достигается при сравнительно малом значении размера модуля р, благодаря чему обеспечивается сравнительно высокая производительность операции возведения векторов МДЧ в большую степень. Поскольку производительность процедур формирования и проверки ЭЦП определяется производительностью операции возведения в степень, то при использовании операций над векторами МДЧ обеспечивается сравнительно высокая производительность процедур формирования и проверки ЭЦП.
над векторами МДЧ выполняется путем выполнения модульных умножений и сложений над МДЧ, являющихся компонентами векторов МДЧ, достаточно высокая трудность задачи дискретного логарифмирования в группе векторов МДЧ достигается при сравнительно малом значении размера модуля р, благодаря чему обеспечивается сравнительно высокая производительность операции возведения векторов МДЧ в большую степень. Поскольку производительность процедур формирования и проверки ЭЦП определяется производительностью операции возведения в степень, то при использовании операций над векторами МДЧ обеспечивается сравнительно высокая производительность процедур формирования и проверки ЭЦП.
Порядком вектора МДЧ V называется наименьшее натуральное число q, такое что Vq=1, т.е. такое, что результатом умножения вектора МДЧ Q на самого себя q раз является единичный вектор МДЧ Е=1e+0i+0j=1.
Корректность заявленного способа доказывается теоретически. Рассмотрим, например, вариант реализации способа по пп.4 и 5 формулы изобретения. Открытый ключ, соответствующий секретному ключу х, представляет собой вектор МДЧ Y=Gx(mod p).
Вектор МДЧ R генерируется по формуле R=Gk (mod р), а первое МДЧ в ЭЦП (e, s) вычисляется по формуле e=rH mod δ, где r=(r1||r2||r3) - МДЧ, равное конкатенации МДЧ, входящих в вектор МДЧ R. Значение s генерируется по формуле s=(k+ex)mod q, поэтому вектор МДЧ R', генерируемый по формуле R'=Yq-eGs mod p и используемый для формирования первого проверочного МДЧ А, равен
R'=Yq-eGs(mod p)=G(q-e)xGs(mod p)=G(q-e)x+(k+ex)(mod p)=
=Gqx+k(mod p)=GqxGk(mod p)=Gk(mod p)=R.
Поскольку векторы МДЧ R' и R одинаковы, то равны между собой и значения r' и r: r'=(r'1||r'2||r'3)=r=(r1||r2||r3), следовательно, A=r'H mod δ=rH mod δ=e=В, т.e. правильно сформированная коллективная подпись удовлетворяет процедуре проверки подписи, т.e. корректность процедур генерации и проверки ЭЦП доказана. Аналогичным образом дается доказательство корректности и для пп.2 и 3 формулы изобретения.
Рассмотрим примеры реализации заявленного технического решения, где конкретные значения использованных параметров описаны в приводимых ниже численных примерах. Использованные в примерах вектора МДЧ были сгенерирована с помощью программы, разработанной специально для генерации матриц, включая векторы МДЧ с заданным порядком, и выполнения операций над векторами МДЧ. Приводимые в примере МДЧ взяты сравнительно малого размера и записаны для краткости в виде десятичных чисел. В вычислительных устройствах МДЧ представляются и преобразуются в двоичном виде, т.e. в виде последовательности сигналов высокого и низкого потенциала. В реальных приложениях следует использовать вектора МДЧ, которые включают МДЧ длиной от 16 до 512 бит в зависимости от значения их размерности m. При меньшей размерности следует использовать МДЧ более высокой разрядности.
При использовании на практике заявляемого способа следует выбрать таблицу замены переменных и размер параметров р и q таким образом, чтобы разрядность значения порядка q была равна или превышала 160 бит. В примерах, приводимых ниже, используются параметры с искусственно уменьшенной разрядностью, чтобы уменьшить размер примеров и сделать их более наглядными.
Пример 1. Случай использования двухкомпонентных векторов МДЧ (иллюстрация пп.2 и 3 формулы изобретения). В данном примере групповая операция 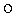 выполняется с использованием следующей таблицы замены переменных:
выполняется с использованием следующей таблицы замены переменных:
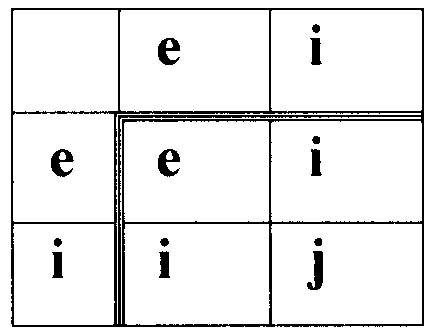
Выполняется следующая последовательность действий.
1. Генерируют простое число р, такое что p-1 содержит большой простой множитель q, т.е. р=Nq+1, где N - четное число:
р=3990163786012426536171919;
q=1997539432909;
G=2205829896139765611199743е+750652585528120205203869i;
2. Генерируют секретный ключ х в виде случайного МДЧ:
х=1853362791;
3. Формируют открытый ключ в виде вектора МДЧ Y, для чего выполняют следующую последовательность действий.
3.1. Генерируют вектор МДЧ, имеющий порядок q=1997539432909.
3.2. Генерируют вектор МДЧ Y=Gх (mod р):
Y=1170349070330824405069406е+2505690115109586035639139i;
4. Принимают ЭД, представленный, например, следующим МДЧ H (в качестве которого может быть взята, в частности, хэш-функция от ЭД):
H=635473563483.
5. Формируют ЭЦП Q в виде пары чисел (е, s) для чего выполняют следующие действия:
5.1. Формируется первый элемент ЭЦП е, для чего
5.1.1. Генерируется случайное МДЧ k=18357236873.
5.1.2. Генерируется вектор МДЧ R=Gk(mod p):
R=2057361867821351253457028е+3679538494005836479635721i.
5.1.3. Вычисляется МДЧ е по формуле е=r1h mod δ, где δ - вспомогательное простое число (например, δ=q=1997539432909), r1 - первое МДЧ в векторе МДЧ R: е=113678582682.
5.2. Формируется второй элемент ЭЦП s по формуле s=k+xe mod q:
s=139316649025.
6. Формируется первое проверочное МДЧ А, для чего выполняются следующие действия.
6.1. Вычисляется вектор МДЧ R' по формуле: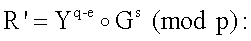
q-е=1883860850227;
Yq-e=2005499870579969554139198е+3027974868612498293037474i. Gs=1846689595470242217257892e+2845865428349522504128287i. R'=20573б1867821351253457028е+3679538494005836479635721i.
6.2. Вычисляется МДЧ А по формуле А=R'eh mod q: A=113678582682.
7. Формируется второе проверочное МДЧ по формуле В=е:
B=113678582682.
8. Сравнивают первое и второе проверочные МДЧ: А=В.
Совпадение проверочных МДЧ подтверждает подлинность ЭЦП.
Пример 2. Случай использования трехкомпонентных векторов МДЧ (иллюстрация п.4 формулы изобретения). В данном примере групповая операция 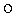 выполняется с использованием следующей таблицы замены переменных:
выполняется с использованием следующей таблицы замены переменных:

Выполняется следующая последовательность действий.
1. Генерируют простое число р, такое что p-1 содержит большой простой множитель q, т.е. р=Nq+1, где N - четное число:
р=30817; q=107;
2. Генерируют секретный ключ х в виде случайного МДЧ:
x=79.
3. Формируют открытый ключ в виде вектора МДЧ Y, для чего выполняют следующую последовательность действий.
3.1. Генерируют вектор МДЧ G, имеющий порядок q=107:
G=11297е+10799i+23186j.
3.2. Генерируют вектор МДЧ Y=Gх (mod p):
Y=Gх (mod p)=9129e+24262i+19035j.
4. Принимают ЭД, представленный, например, следующим МДЧ H (в качестве которого может быть взята, в частности, хэш-функция от ЭД): Н=68.
5. Формируют ЭЦП Q в виде пары чисел (е, s), для чего выполняют следующие действия:
5.1. Формируется первый элемент ЭЦП е, для чего
5.1.1. Генерируется случайное МДЧ k=87.
5.1.2. Генерируется вектор МДЧ R=Gk (mod p)=23203е+17932i+16380j.
5.1.3. Вычисляется МДЧ е по формуле е=rH mod δ, где r=(r1||r2||r3) - МДЧ, равное конкатенации МДЧ, входящих в состав вектора R, и δ=109 - вспомогательное простое число: е=76.
5.2. Формируется второй элемент ЭЦП s по формуле s=k+хе mod q: s=99.
6. Формируется первое проверочное МДЧ А, для чего выполняются следующие действия:
6.1. Вычисляется вектор МДЧ R' по формуле 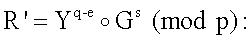
Yq-e (mod p)=16855e+6774i+24171j.
Gs (mod p)=6300e+3337i+13319j.
R'=23203e+17932i+16380j.
6.2. Вычисляется МДЧ А по формуле А=r'H mod δ, где r'=(r'1||r'2||r'3) - МДЧ, равное конкатенации МДЧ, входящих в состав вектора МДЧ R', и δ=109 - вспомогательное простое число: А=76.
7. Формируется второе проверочное МДЧ по формуле В=е: В=е=76.
8. Сравнивают первое и второе проверочные МДЧ: А=В.
Совпадение проверочных МДЧ подтверждает подлинность ЭЦП.
Пример 3. Случай использования трехкомпонентных векторов МДЧ (иллюстрация п.4 формулы изобретения). В данном примере групповая операция 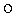 выполняется с использованием следующей таблицы замены переменных:
выполняется с использованием следующей таблицы замены переменных:
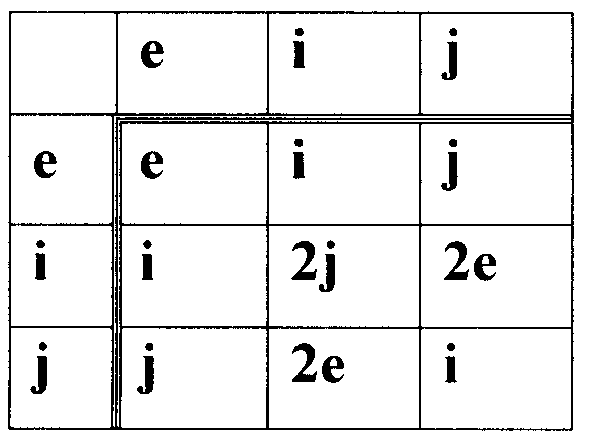
Данный пример показывает, что при соответствующем выборе простого числа р и таблицы замены переменных значение порядка q может значительно превышать значение р. Выполняется следующая последовательность действий.
1. Генерируют простое число р, такое что число p2+р+1 содержит большой простой множитель q:
p=97; q=3169.
2. Генерируют секретный ключ х в виде случайного МДЧ:
х=2079.
3. Формируют открытый ключ в виде вектора МДЧ Y, для чего выполняют следующую последовательность действий.
3.1. Генерируют вектор МДЧ G, имеющий порядок q=3169:
G=8е+3i+93j.
3.2. Генерируют вектор МДЧ Y=Gх (mod р):
Y=87е+96i+86j.
4. Принимают ЭД, представленный, например, следующим МДЧ H (в качестве которого может быть взята, в частности, хэш-функция от ЭД): Н=5168.
5. Формируют ЭЦП Q в виде пары чисел (е, s), для чего выполняют следующие действия:
5.1. Формируется первый элемент ЭЦП е, для чего
5.1.1. Генерируется случайное МДЧ k=5387.
5.1.2. Генерируется вектор МДЧ R=Gk (mod p)=96е+56i+81j.
5.1.3. Вычисляется МДЧ е по формуле е=rH mod δ, где r=(r1||r2||r3) - МДЧ, равное конкатенации МДЧ, входящих в состав вектора R, и δ=3169: е=3138.
5.2. Формируется второй элемент ЭЦП s по формуле s=k+xe mod q: s=1149.
6. Формируется первое проверочное МДЧ А, для чего выполняются следующие действия:
6.1. Вычисляется вектор МДЧ R' по формуле 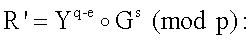
Yq-e (mod p)=75e+46i+84j
Gs(mod p)=27e+81i+81j
R'=96е+56i+81j.
6.2. Вычисляется МДЧ А по формуле А=r'H mod δ, где r'=(r'1||r'2||r'3) - МДЧ, равное конкатенации МДЧ, входящих в состав вектора МДЧ R', и δ=3169 - вспомогательное простое число: А=3138.
7. Формируется второе проверочное МДЧ по формуле В=е: В=е=3138.
8. Сравнивают первое и второе проверочные МДЧ: А=В.
Совпадение проверочных МДЧ подтверждает подлинность ЭЦП.
Пример 4. Случай использования трехкомпонентных векторов МДЧ (иллюстрация п.5 формулы изобретения). В данном примере в качестве модуля р используется составное МДЧ, а групповая операция 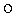 выполняется с использованием следующей таблицы замены переменных:
выполняется с использованием следующей таблицы замены переменных:
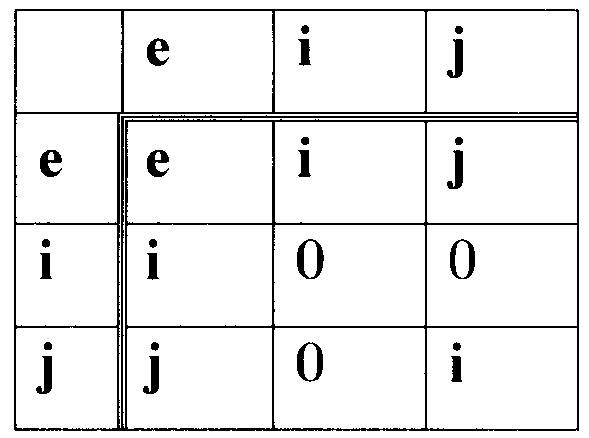
Выполняется следующая последовательность действий.
1. Генерируют составное число р, равное произведению простых чисел 11 и 457: р=5027.
2. Генерируют секретный ключ х в виде случайного МДЧ:
х=279.
3. Формируют открытый ключ в виде вектора МДЧ Y, для чего выполняют следующую последовательность действий.
3.1. Генерируют вектор МДЧ G, имеющий порядок q=457:
G=1e+4631i+4785j.
3.2. Генерируют вектор МДЧ Y=Gх (mod p):
Y=1e+2156i+2860j.
4. Принимают ЭД, представленный, например, следующим МДЧ Н (в качестве которого может быть взята, в частности, хэш-функция от ЭД): Н=168.
5. Формируют ЭЦП Q в виде пары чисел (е, s), для чего выполняют следующие действия:
5.1. Формируется первый элемент ЭЦП е, для чего
5.1.1. Генерируется случайное МДЧ k=387.
5.1.2. Генерируется вектор МДЧ R=Gk (mod p)=1e+2475i+1859j.
5.1.3. Вычисляется МДЧ е по формуле е=rH mod δ, где r=(r1||r2||r3) - МДЧ, равное конкатенации МДЧ, входящих в состав вектора R, и δ=319: е=190.
5.2. Формируется второй элемент ЭЦП s по формуле s=k+xe mod q: s=385.
6. Формируется первое проверочное МДЧ А, для чего выполняются следующие действия:
6.1. Вычисляется вектор МДЧ R' по формуле 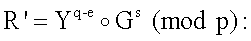
Yq-e (mod p)=1e+2475i+4543j; Gs(mod p)=1e+2937i+2343j
R'=1е+56i+81j.
6.2. Вычисляется МДЧ А по формуле А=r'H mod δ, где r'=(r'1||r'2||r'3) - МДЧ, равное конкатенации МДЧ, входящих в состав вектора МДЧ R', и δ=3169 - вспомогательное простое число: А=190.
7. Формируется второе проверочное МДЧ по формуле В=е: В=е=190.
8. Сравнивают первое и второе проверочные МДЧ: А=В.
Совпадение проверочных МДЧ подтверждает подлинность ЭЦП.
Приведенные выше примеры показывают принципиальную реализуемость и корректность заявленного способа формирования и проверки подлинности ЭЦП, заверяющей ЭД. Аналогичным образом реализуется заявляемый способ при использовании векторов МДЧ размерности m=4, m=5, m=6 и т.д. Например, могут быть использованы следующие таблицы замены формальных переменных, в которых значение параметра а может быть выбрано в интервале 0≤а<р, где число р выбирается таким образом, чтобы обеспечивалось значение порядка векторов МДЧ q, равное достаточно большому простому МДЧ, например равное значению простого МДЧ разрядности 160, 256 или 512 бит. Таблица для задания групповой операции над четырехкомпонентными векторами МДЧ (случай m=4) имеет вид:
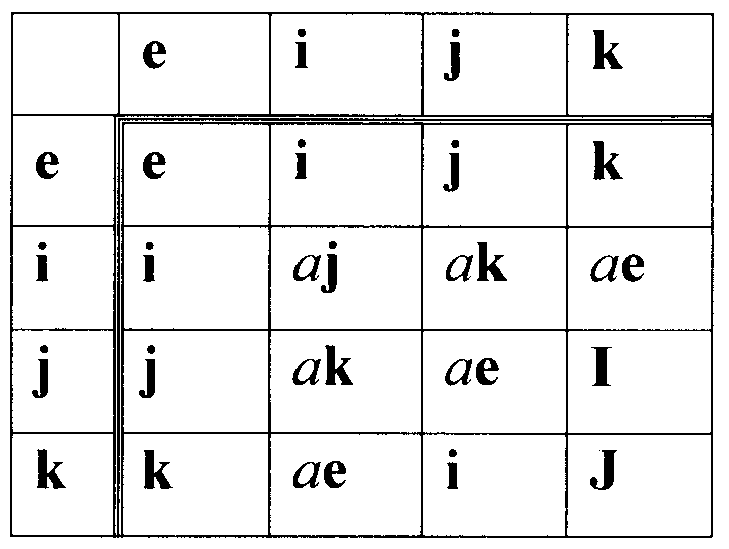
Таблица для задания групповой операции над пятикомпонентными векторами МДЧ (случай m=5) имеет вид:
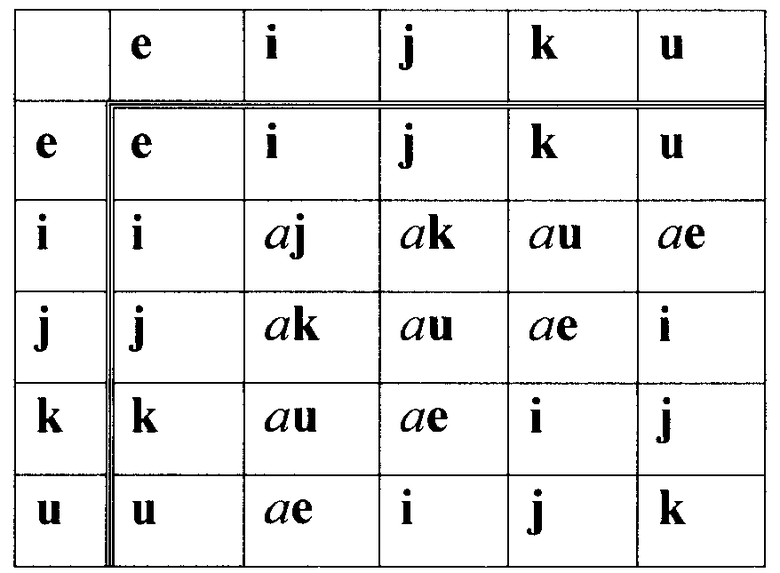
Таблица для задания групповой операции над шестикомпонентными векторами МДЧ (случай m=6) имеет вид:
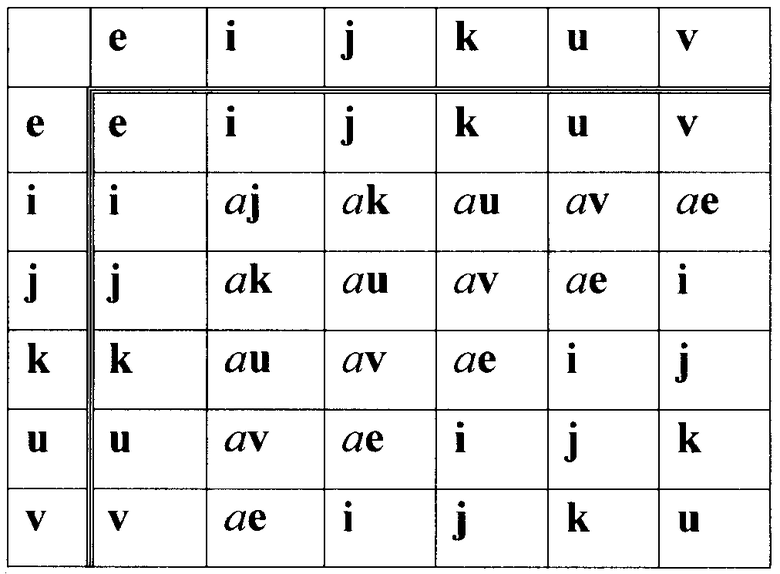
Была разработаны программы для ЭВМ, реализующие операции умножения и возведения в большую целочисленную степень векторов МДЧ, имеющих размерность m=2, m=3, m=4, m=5 и m=6. С помощью этих программ были сгенерированы приведенные выше примеры и установлено, что аналогичные примеры реализации заявленного способа с использованием векторов МДЧ размерности m=4, m=5 и m=6 также обеспечивают корректность процедуры проверки подлинности ЭЦП.
По аналогии с построением приведенных выше таблиц можно построить таблицы, определяющие групповые операции над векторами произвольных размерностей m. При этом при использовании групп векторов МДЧ, имеющих сравнительно большую размерность, высокая криптографическая стойкость ЭЦП обеспечивается при меньшей разрядности МДЧ, являющихся компонентами векторов МДЧ. Например, при m=16 и m=32 разрядность указанных МДЧ может составлять 64 и 32 бита соответственно, что позволяет повысить быстродействие процедур формирования и проверки подписи при программной реализации для выполнения программ, реализующих заявляемый способ, на 64- и 32-разрядных микропроцессорах.
Приведенные выше примеры экспериментально подтверждают корректность реализации заявляемого способа, что дополняет приведенные выше математические доказательства корректности описанных конкретных реализаций заявленного способа формирования и проверки ЭЦП, заверяющей ЭД.
Таким образом, показано, что заявляемый способ может быть положен в основу стойких систем ЭЦП, обеспечивающих повышение производительности устройств и программ формирования и проверки ЭЦП.
Приведенные примеры и математическое обоснование показывают, что предлагаемый способ формирования и проверки подлинности ЭЦП работает корректно, технически реализуем и позволяет достичь сформулированного технического результата.
Приложение 1
Толкование терминов, используемых в описании заявки
1. Двоичный цифровой электромагнитный сигнал - последовательность битов в виде нулей и единиц.
2. Параметры двоичного цифрового электромагнитного сигнала: разрядность и порядок следования единичных и нулевых битов.
3. Разрядность двоичного цифрового электромагнитного сигнала - общее число его единичных и нулевых битов, например число 10011 является 5-разрядным.
4. Электронная цифровая подпись (ЭЦП) - двоичный цифровой электромагнитный сигнал, параметры которого зависят от подписанного электронного документа и от секретного ключа. Проверка подлинности ЭЦП осуществляют с помощью открытого ключа, который зависит от секретного ключа.
5. Электронный документ (ЭД) - двоичный цифровой электромагнитный сигнал, параметры которого зависят от исходного документа и способа его преобразования к электронному виду.
6. Секретный ключ - двоичный цифровой электромагнитный сигнал, используемый для формирования подписи к заданному электронному документу. Секретный ключ представляется, например, в двоичном виде как последовательность цифр «0» и «1».
7. Открытый ключ - двоичный цифровой электромагнитный сигнал, параметры которого зависят от секретного ключа и который предназначен для проверки подлинности цифровой электронной подписи.
8. Хэш-функция от электронного документа - двоичный цифровой электромагнитный сигнал, параметры которого зависят от электронного документа и выбранного метода ее вычисления. В системах ЭЦП считается, что хэш-функция однозначно представляет ЭД, поскольку используемые хэш-функции удовлетворяют требованию коллизионной стойкости, которое означает вычислительную невозможность нахождения двух различных ЭД, которым соответствует одно и то же значение хэш-функции.
9. Многоразрядное двоичное число (МДЧ) - двоичный цифровой электромагнитный сигнал, интерпретируемый как двоичное число и представляемый в виде последовательности цифр «0» и «1».
10. Операция возведения числа S в дискретную степень А по модулю n - это операция, выполняемая над конечным множеством натуральных чисел {0, 1, 2, …, n-1}, включающем n чисел, являющихся остатками от деления всевозможных целых чисел на число n; результат выполнения операций сложения, вычитания и умножения по модулю n представляет собой число из этого же множества [Виноградов И.М. Основы теории чисел. - М.: Наука, 1972. - 167 с.]; операция возведения числа S в дискретную степень Z по модулю n определяется как Z-кратное последовательное умножение по модулю n числа S на себя, т.е. в результате этой операции также получается число W, которое меньше или равно числу n-1; даже для очень больших чисел S, Z и n существуют эффективные алгоритмы выполнения операции возведения в дискретную степень по модулю.
11. Показатель q по модулю n числа а, являющегося взаимно простым с n - это минимальное из чисел γ, для которых выполняется условие aγ mod n=1, т.е. q=min{γ1, γ2, …} [Виноградов И.М. Основы теории чисел. - М.: Наука, 1972. - 167 с.].
12. Операция деления целого числа А на целое число В по модулю n выполняется как операция умножения по модулю n числа А на целое число В-1, которое является обратным к В по модулю n.
13. Порядок числа q по модулю n числа а - это показатель q по модулю n числа а.
14. Группа - это алгебраическая структура (т.е. множество математических элементов различной природы), над элементами которой задана некоторая операция и они обладают заданным набором свойств: операция ассоциативна, результатом выполнения операции над двумя элементами является также элемент этой же структуры, существует нейтральный элемент такой, что при выполнении операции над ним и другим некоторым элементом а группы результатом является элемент а. Детальное описание групп дано в книгах А.Г.Курош. Теория групп. М., «Наука», 1967. - 648 с. и М.И.Каргаполов, Ю.И.Мерзляков. Основы теории групп. - М., «Наука. Физматлит», 1996. - 287 с. Операция, определенная над элементами группы называется групповой операцией.
15. Циклическая группа - это группа, каждый элемент которой может быть представлен в виде g=аn для некоторого натурального значения n, где а - элемент данной группы, называемый генератором или образующим элементом циклической группы. Степень n означает, что над элементом а выполняются n последовательных операций, т.е. выполняются вычисления по формуле 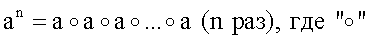 обозначает операцию, определенную над элементами группы.
обозначает операцию, определенную над элементами группы.
16. Циклическая подгруппа группы - это подгруппа, каждый элемент g которой может быть представлен в виде g=аn для некоторого натурального значения n, где а - элемент данной подгруппы, называющийся генератором или образующим элементом циклической подгруппы.
17. Вектор - это набор из двух или элементов различной природы, называемых компонентами вектора.
18. Вектор многоразрядных двоичных чисел (вектора МДЧ) - это набор из двух или более МДЧ, называемых компонентами вектора МДЧ. Вектор МДЧ записывается различными способами, требование к которым состоит в том, чтобы они идентифицировали позиции компонентов. Например, вектор МДЧ можно записать в виде (а1, а2, …, аm), где m≥2 - это размерность вектора МДЧ, означающая число компонентов в векторе МДЧ. В качестве разделителя может быть использован знак операции, определенной над компонентами вектора, и тогда компоненты вектора идентифицируются указанием формальной переменной (в начале или в конце соответствующего компонента) в виде буквы латинского алфавита. Формальной называется переменная потому, что ей не приписывается никакого численного значения, и она служит только для того, чтобы идентифицировать компонент вектора МДЧ независимо от последовательности его записи. Так, векторы МДЧ Z1=5e+3i+5j и
Z2=3i+5e+5j рассматриваются как равные, т.е. Z1=Z2. При использовании некоторых частных таблиц замены переменных формальные переменные в литературе иногда называются базисными векторами, а числа Z1 и Z2 - векторами m-мерного пространства [Л.Б.Шнеперман. Курс алгебры и теории чисел в задачах и упражнениях. - Минск, «Вышэйшая школа», 1986. - 272 с.].
19. Размерность вектора МДЧ - это количество МДЧ, входящих в вектор МДЧ в качестве компонентов.
Изобретение относится к области криптографических устройств электронной цифровой подписи (ЭЦП). Технический результат заключается в повышении производительности алгоритмов электронной цифровой подписи (ЭЦП) без снижения ее уровня стойкости. Сущность изобретения заключается в том, что способ генерации и проверки ЭЦП включает следующую последовательность действий: генерируют секретный ключ в виде многоразрядного двоичного числа (МДЧ) х, по секретному ключу формируют открытый ключ Y в виде вектора МДЧ размерности m, где 2≤m<64, принимают электронный документ (ЭД), представленный МДЧ Н, в зависимости от принятого электронного документа и от значения секретного ключа формируют ЭЦП Q в виде двух МДЧ, в зависимости от ЭЦП, ЭД и открытого ключа формируют первое А и второе В проверочные МДЧ, сравнивают МДЧ А и В. При совпадении их параметров делают вывод о подлинности электронной цифровой подписи. 4 з.п. ф-лы, 10 табл.
1. Способ генерации и проверки подлинности электронной цифровой подписи, заверяющей электронный документ, заключающийся в том, что генерируют секретный ключ в виде многоразрядного двоичного числа х, по секретному ключу формируют открытый ключ Y в виде более чем одного многоразрядного двоичного числа, принимают электронный документ, представленный многоразрядным двоичным числом Н, в зависимости от принятого электронного документа и от значения секретного ключа формируют электронную цифровую подпись Q в виде двух многоразрядных двоичных чисел, в зависимости от открытого ключа, принятого электронного документа и электронной цифровой подписи формируют первое А и второе В проверочные многоразрядные двоичные числа, сравнивают их и при совпадении их параметров делают вывод о подлинности электронной цифровой подписи, отличающийся тем, что открытый ключ Y формируют в виде вектора многоразрядных двоичных чисел размерности m, где 2≤m≤64.
2. Способ по п.1, отличающийся тем, что открытый ключ Y генерируют в виде вектора многоразрядных двоичных чисел размерности m=2, для чего генерируют вектор многоразрядных двоичных чисел G размерности m=2, имеющий порядок, равный многоразрядному двоичному числу q, и открытый ключ Y формируют по формуле Y=Gx (mod р), где р - многоразрядное двоичное число, являющееся модулем, по которому выполняются операции над многоразрядными двоичными числами, входящими в состав вектора многоразрядных двоичных чисел G при выполнении над G операции возведения в степень, а электронную цифровую подпись формируют в виде пары многоразрядных двоичных чисел е и s, для чего генерируют случайное многоразрядное двоичное число k, генерируют
вектор многоразрядных двоичных чисел R по формуле R=Gk (mod p), затем формируют первое многоразрядное двоичное число е электронной цифровой подписи по формуле е=r1Н mod δ, где r1 - первое многоразрядное двоичное число в векторе многоразрядных двоичных чисел R и δ - вспомогательное простое многоразрядное двоичное число, затем генерируют второе многоразрядное двоичное число s электронной цифровой подписи по формуле s=(k+ex)mod q, после чего формируют первое и второе проверочные многоразрядные двоичные числа А и В по формулам А=r'Н mod δ и В=е, где r'1 - первое многоразрядное двоичное число в векторе многоразрядных двоичных чисел R', вычисленном по формуле R'=Yq-eGs(mod p).
3. Способ по п.2, отличающийся тем, что многоразрядные двоичные числа р и q являются простыми.
4. Способ по п.1, отличающийся тем, что открытый ключ Y генерируют в виде вектора многоразрядных двоичных чисел размерности m=3, для чего генерируют вектор многоразрядных двоичных чисел G размерности m=3, имеющую порядок, равный многоразрядному двоичному числу q, и открытый ключ Y формируют по формуле Y=Gx (mod р), где р - многоразрядное двоичное число, являющееся модулем, по которому выполняются операции над многоразрядными двоичными числами, входящими в состав вектора многоразрядных двоичных чисел G при выполнении над G операции возведения в степень, а электронную цифровую подпись формируют в виде пары многоразрядных двоичных чисел е и s, для чего генерируют случайное многоразрядное двоичное число k, генерируют вектор многоразрядных двоичных чисел R по формуле R=Gk (mod р), затем формируют первое многоразрядное двоичное число е электронной цифровой подписи по формуле е=rН mod δ, где r=(r1||r2||r3) - многоразрядное двоичное число, равное конкатенации многоразрядных двоичных чисел, входящих в состав вектора многоразрядных двоичных чисел R, и δ - вспомогательное простое многоразрядное двоичное число, затем генерируют второе многоразрядное двоичное число s электронной цифровой подписи по формуле s=(k+ex) mod q, после чего формируют первое и второе проверочные многоразрядные двоичные числа А и В по формулам A=r'H mod δ и В=е, где r'=(r'1||r'2||r'3) - многоразрядное двоичное число, равное конкатенации многоразрядных двоичных чисел, входящих в состав вектора многоразрядных двоичных чисел R', вычисленного по формуле R'=Yq-eGs (mod p).
5. Способ по п.4, отличающийся тем, что многоразрядное двоичное число р является составным.
| ИНФОРМАЦИОННАЯ ТЕХНОЛОГИЯ | |||
| КРИПТОГРАФИЧЕСКАЯ ЗАЩИТА ИНФОРМАЦИИ | |||
| ПРОЦЕССЫ ФОРМИРОВАНИЯ И ПРОВЕРКИ ЭЛЕКТРОННОЙ ЦИФРОВОЙ ПОДПИСИ | |||
| Нивелир для отсчетов без перемещения наблюдателя при нивелировании из средины | 1921 |
|
SU34A1 |
| US 4995089, 19.02.1991 | |||
| US 4405829, 20.09.1983 | |||
| Устройство для транспортирования материалов | 2002 |
|
RU2220896C1 |
| СПОСОБ ПРОВЕРКИ ПОДЛИННОСТИ ЭЛЕКТРОННОЙ ЦИФРОВОЙ ПОДПИСИ, ЗАВЕРЯЮЩЕЙ ЭЛЕКТРОННЫЙ ДОКУМЕНТ | 2005 |
|
RU2280896C1 |
| СПОСОБ ИДЕНТИФИКАЦИИ ПОДЛИННОСТИ КОНТРОЛИРУЕМОГО ОБЪЕКТА | 1998 |
|
RU2132569C1 |
Авторы
Даты
2009-10-10—Публикация
2007-12-25—Подача