СПОСОБ ВЕРИФИКАЦИИ ДИАГНОЗОВ БОЛЕЗНЕЙ ВЕН НИЖНИХ КОНЕЧНОСТЕЙ ПО ДАННЫМ КОМБИНИРОВАННОЙ ТЕРМОМЕТРИИ НА ОСНОВЕ БАЙЕСОВСКОГО КЛАССИФИКАТОРА И АПОСТЕРИОРНЫХ ВЕРОЯТНОСТЕЙ Российский патент 2009 года по МПК A61B5/01 

Изобретение относится к медицине, а именно к хирургии, и касается диагностики заболеваний вен нижних конечностей с применением математической экспертной системы для обработки данных комбинированной термометрии.

Целью изобретения является разработка способа диагностики заболеваний вен нижних конечностей, который позволит классифицировать заболевания вен нижних конечностей по данным комбинированной термометрии и провести численную верификацию диагноза.

Наиболее близок к заявляемому нами и служит основным прототипом способ диагностики рака молочной железы по данным микроволновой радиометрии с применением математической экспертной системы. Авторы - Вайсблат А.В. и Бурдина Л.М. (1999), проанализировав большое количество термограмм больных раком молочной железы, выделили 6 характерных признаков этого заболевания, которые были формализованы:

1. Повышенное максимальное значение температуры соска по сравнению со средней температурой молочной железы.

2. Повышенная разница температур сосков правой и левой молочной железы.

3. Повышенное максимальное значение разности температур между одноименными точками правой и левой молочной железы.

4. Повышенное среднеквадратичное значение разностей температур между одноименными точками правой и левой молочной железы.

5. Повышенное среднеквадратичное значение разброса температур в одной из молочных желез вычисляется отдельно по точкам для каждой из молочных желез, рассматривается большее из двух значений.

Принцип компьютерной диагностики рака молочной железы состоит в следующем: термограммы всех верифицированных случаев рака вводятся в память компьютера. Далее в процессе диагностики программа сравнивает, насколько термограмма обследуемой пациентки, по выделенным признакам, близка к термограммам пациенток с установленным диагнозом рака молочной железы.

Однако анатомические и функциональные особенности молочной железы не позволяют применить эту экспертную систему для способа диагностики патологии вен нижних конечностей.

Поставленная нами цель достигается путем проведения последовательного измерения кожной (инфракрасной) температуры и глубокой микроволновой термометрии (РТМ) в 12 симметричных точках, расположенных по задней поверхности обеих голеней пациента. Для этого мы используем диагностический комплекс РТМ-01-РЭС, позволяющий регистрировать как инфракрасную температуру с поверхности тела, так и внутреннюю температуру тканей на глубине от 4 до 6 см по их естественному тепловому излучению в микроволновом диапазоне. В состав комплекса входят: антенна-аппликатор для регистрации микроволнового излучения, датчик регистрации инфракрасной температуры, блок обработки информации, персональный компьютер (ПЭВМ). Антенна-аппликатор устанавливается на соответствующую точку на поверхности голени плотно, без зазора между кожей и плоскостью аппликатора, без дополнительного нажима. Температура измеряется последовательно попеременно в 12-ти точках по задней поверхности правой и левой голени. Первые три точки расположены: на вершине латеральной головки икроножной мышцы (1), в подколенной ямке (2), на вершине медиальной головки икроножной мышцы (3). Второй ряд точек расположен: по центру латеральной головки икроножной мышцы (4), между головками икроножной мышцы (5) и по центру медиальной головки икроножной мышцы (6). Третий ряд точек расположен в нижней части икроножной мышцы - латерально (7), в центре (8) и медиально (9). Последние точки измерения температуры находятся на наружной стороне ахилового сухожилия в области латеральной лодыжки (10), по центру ахилового сухожилия (11) и по его внутренней поверхности в области медиальной лодыжки (12). Измерение температуры в указанных точках проводится последовательно радиодатчиком (РТМ) и датчиком температуры кожи (ИК) в положении пациента «лежа на животе» и «стоя». Результаты измерений поступают в виде постоянного напряжения на блок обработки и далее на ПЭВМ, где осуществляется фиксация данных измерений температуры, привязанных к позиции датчиков. Данные по температуре обрабатываются и могут быть отображены на мониторе или принтере в виде термограммы или в виде цветового поля температур. Все обследуемые больные имеют предварительный диагноз, поставленный на основании ультразвукового доплеровского обследования на ультразвуковом доплерографе БИОСС-1 датчиком 8 МГц с помощью проб Вальсальвы и манжеточной пробы (Market A., Meissner M., Manzo a., et al., 1994), а также ультразвукового сканирования состояния подкожных и глубоких вен в положении стоя на ультразвуковом сканере "Лоджик а-100" фирмы «Дженерал электрик».

Проведенные нами исследования здоровых конечностей у лиц различного возраста выявили определенный диапазон и закономерность распределения температур на голени здорового человека (Табл. 1, 2).

Из представленных данных видно, что для голени здорового человека характерен определенный термографический профиль, который нарушается при появлении у него острого венозного тромбоза вен (Табл. 3, 4), посттромботической болезни (Табл. 5, 6) или варикозной болезни (Табл. 7, 8). При статистической обработке данных термометрии учитывались изменения вен каждой ноги каждого пациента. Т.е., если пациент имеет правую здоровую ногу, а левую - с варикозной болезнью, то правая нога обсчитывалась в группе здоровых конечностей, а левая - в группе больных варикозной болезнью.

Для математической верификации диагноза термометрии мы представили наши исходные данные как упорядоченный набор из 48 признаков-координат, каждый из которых представляет собой температуру, измеренную в определенной точке правой и левой голени пациента в положении лежа и стоя микроволновым и инфракрасным датчиком.

В наших исследованиях мы использовали метод классификации пациентов с болезнями вен нижних конечностей на основе непараметрического оценивания плотности распределения вероятности с помощью многомерного ядра Пуассона и два алгоритма дискриминантного анализа, основанные на отношении плотностей распределения двух классов, оценки которых построены методами, описанными ниже. Наши исходные данные мы представили как упорядоченный набор из р признаков-координат (р=48), т.е. в виде матрицы:

где уⁱ выступает в качестве номера болезни 1-го наблюдения.

Обозначим X=(x₁, …, x_Р) - новое наблюдение, которое необходимо отнести к одному из имеющихся классов и причислить номер класса уⁱ.

За Hj тогда обозначим соответствующую гипотезу о принадлежности нового наблюдения к Xj-му классу.

F_j(…)=F(…|H_j) - функция распределения вектора X, принадлежащего j-му классу.

f_j(…)=f_j(…|H_j) - плотности распределения вероятностей вектора X, принадлежащего j-му классу, j=1, 4.

Основная задача дискриминантного анализа - задача отнесения нового наблюдения к одному из двух классов (частный случай нашей задачи). Она тесно связана с классической задачей проверки простой гипотезы Н₁ против альтернативной гипотезы Н₂

H₁ : X ∈ F₁

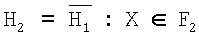
Если пространство всех возможных исходов Х обозначить как Ω, то чтобы проверить какую-либо гипотезу H₁ исходя из выборки наблюдений, мы должны разделить выборочное пространство Ω на две области. Если наблюдаемая выборочная точка Х попадает в одну из этих областей, скажем ω, то гипотеза H₁ отвергается, если же Х попадает в дополнительную область Ω/ω, то гипотеза принимается. Область ω называется критической областью критерия, a Ω/ω - областью принятия гипотезы. Если известно распределение вероятностей наблюдений, соответствующее проверяемой гипотезе H₁, то можно определить ω так, чтобы при выполнении гипотезы H₁ вероятность отвергнуть эту гипотезу (т.е. вероятность попадания Х в ω) была равна заранее заданной величине α, т.е.

P{X∈ω|H₁}=α

Число α называют уровнем значимости критерия. Ошибки, возникающие при проверке статистической гипотезы, могут быть двух типов:

1) можно ошибочно отвергнуть гипотезу, когда она верна;

2) можно ее ошибочно принять, когда она неверна.

Эти ошибки называются соответственно ошибками первого и второго рода. Вероятность ошибки первого рода равна уровню значимости. Вероятность ошибки второго рода, обозначаемая β, зависит от рассматриваемой альтернативной гипотезы Н₂. Таким образом,

Р{Х∈(Ω/ω)|H₂}=β или P{X∈ω|H₂}=1-β.

Вероятность (1-β) называется мощностью критерия для проверки гипотезы против альтернативной гипотезы Н₂.

Функция правдоподобия выборки x₁, x₂, …, 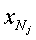определяются как

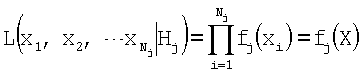
Среди всех критериев, различающих две альтернативные гипотезы H₁ и Н₂ с уровнем значимости а, наиболее мощным является критерий отношения правдоподобия, основанный на статистике

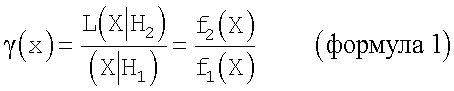
где L - функция правдоподобия. При γ(X)≤C_α, принимается гипотеза Н₁, при γ(X)>C_α - соответственно Н₂.

Введя априорные вероятности гипотез πj, которые вычисляются как отношение числа наблюдений Nj из j-го класса к общему числу наблюдений N, рассмотрим частный случай описанного критерия.

Пусть

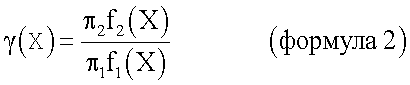
Если γ(Х)>1, принимается гипотеза Н₂, если γ(Х)≤1, соответственно принимается гипотеза H₁.

Формула 2 представляет собой байесовский классификатор, минимизирующий вероятность принятия неверного решения по поводу принадлежности нового наблюдения к той или иной болезни.

Известно, что большинство используемых на практике алгоритмов классификации строится исходя из формулы 1. При этом возможно оценивание неизвестных параметров θ предполагаемых теоретических распределений и замена их оценками θ в плотности распределения. Далее вычисляется оценка отношения :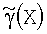

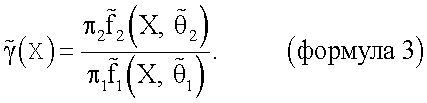
Это параметрический метод построения алгоритмов классификации.

Если нельзя сделать предположение о структуре многомерной плотности распределения вероятности, то для данной точки сразу, минуя оценку параметров, строится оценка отношения

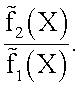
Это непараметрические методы. В нашем изобретении мы использовали непараметрический метод оценивания плотности распределения, основанный на приближении δ-образной последовательностью многомерной δ-функции Дирака.

Тогда оценка плотности для j-класса представима в виде:

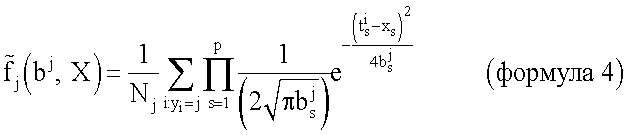
Где 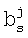- произвольные параметры сглаживания, s=1, … р.

Если различна мера разброса р признаков-координат, то предлагается в качестве параметров сглаживания b^j, j=1, … 4 рассматривать минимальное, среднее или максимальное расстояние 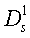, 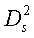… 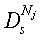от s-й координаты нового наблюдения

Х=(x1, …xs, …xp) до s-й координаты наблюдений 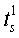, , 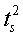… 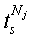из j-го класса:

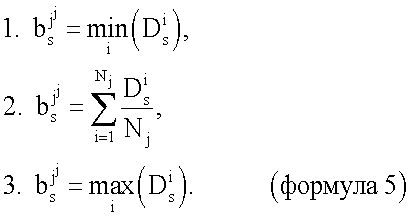
Здесь N_j - число наблюдений в j-м классе,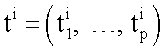

- наблюдения из базы i=1, …N_j для j-й болезни.

На практике подбор подходящего параметра сглаживания b^j производится путем численного эксперимента.

Проверка проводилась двумя алгоритмами классификации: на основе байесовского классификатора и с использованием апостериорных вероятностей.

Каждого человека из базы рассматривали как нового больного и классифицировали с помощью экспертной системы относительно остальных наблюдений. Далее сравнивали предварительный диагноз (по данным доплеровского исследования и комбинированной термометрии) с поставленным посредством разработанного способа классификации.

При проведении численных экспериментов были использованы два способа задания параметров сглаживания 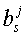: один, описанный формулой (5), другой представлял собой случай, когда 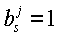, ∀j, ∀s.

Пример 1.

Первый алгоритм основан на байесовском классификаторе и на методе объединения больных в общий класс с последующим поэтапным вычленением каждой болезни.

а. На первом шаге, вычисляя для здоровых оценку плотности вероятности f_i(X) и для объединенного класса всех больных 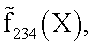находим оценку отношения

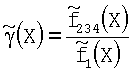
Обозначим априорные вероятности для класса здоровых π₁, для класса больных -

π₂₃₄.

Если ,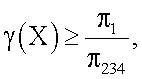

то принимается гипотеза Н₂₃₄, говорящая о том, что новый пациент принадлежит классу больных. В ином случае выполнена гипотеза Н₁ - человек из класса здоровых.

b. В случае, если новое наблюдение на первом шаге не было классифицировано как здоровый, вычисляем для класса ВБ оценку плотности вероятности 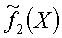, априорную вероятность π₂, для объединенного класса двух других болезней (ОВТ и ПТБ) общую оценку плотности распределения 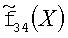и априорную вероятность π₃₄. Снова находим оценку: .

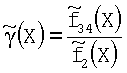Если 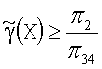, то принимается гипотеза

Н₃₄, говорящая о том, что новый пациент принадлежит классу ОВТ и ПТБ-больных. В ином случае выполнена гипотеза Н₂ - человек из класса ВБ.

с. Далее, если вновь пришедший больной не классифицирован как здоровый или ВБ-больной, то вычисляем для класса ПТБ-больных оценку плотности распределения 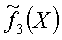, априорную вероятность

π₃ и сравниваем их с оценкой плотности распределения класса ОВ-больных 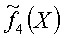, вычислив априорную вероятность ОВТ-класса π₄:

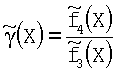
При γ(Х)≥π₃/π₄ принимается гипотеза Н₄ (болен ОВТ), в ином случае - гипотеза Н₃ (болен ПТБ).

Пример 2.

Второй алгоритм базируется на вычислении апостериорных вероятностей.

Одним из основных определений, которое будет использоваться в дальнейшем, является понятие условной (апостериорной) вероятности отнесения наблюдения к данному классу при заданном значении вектора признаков X. Используя формулу Байеса, запишем условную вероятность в виде:

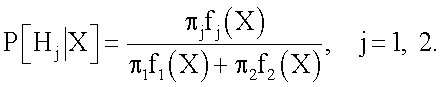
В ситуации с полной информацией решающее правило, минимизирующее условную вероятность ошибки, может быть определено в виде: объект относится к классу H₁, если выполняется неравенство

P[H₁|x]>P[H₂|x],

и к классу Н₂ в противном случае.

Обобщая на случай четырех болезней можно сказать, что тот класс, которому соответствует наибольшее значение апостериорной вероятности P[H_j|X], и будет искомым классом для наблюдения X.

Для каждого класса строится оценка

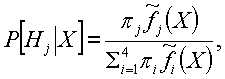
где P[H_j|x] - условная (апостериорная) вероятность появления j-го класса при заданном значении вектора признаков X, и полученные апостериорные вероятности затем сравниваются между собой.

Результаты численных экспериментов.

1. Результаты численных экспериментов для классификации "Здоров - Болен" сравнивались с базой данных диагнозов заболеваний вен нижних конечностей, полученных на предварительном обследовании пациентов: 58 человек больные, 19 человек здоровые.

1.1. Классификатор, основанный на апостериорных вероятностях со средними в качестве параметра сглаживания b, общее число людей: 77.

Классифицированные как Здоровые - 25 человек.

Классифицированные как Больные - 52 человека.

Ошибка классификации - 13 человек.

1.2. Классификатор, основанный на апостериорных вероятностях с единицей в качестве параметра сглаживания b, общее число людей: 77.

Классифицированные как Здоровые - 11 человек.

Классифицированные как Больные - 66 человек.

Ошибка классификации - 8 человек.

1.3. Байесовский классификатор со средними в качестве параметра сглаживания b, общее число людей: 77.

Классифицированные как Здоровые - 31 человек.

Классифицированные как Больные - 46 человек.

Ошибка классификации - 16 человек.

1.4. Байесовский классификатор с единицей в качестве параметра сглаживания b, общее число людей: 77.

Классифицированные как Здоровые - 16 человек.

Классифицированные как Больные - 61 человек.

Ошибка классификации - 3 человека.

Наименьшую ошибку классификации на два класса (3.89%) имеет методика анализа, построенная на байесовском классификаторе с параметром сглаживания b, равным единице.

Вычислим чувствительность, точность и специфичность разработанного метода с наименьшей ошибкой классификации.

По результатам данной методики, заболевания вен нижних конечностей были подтверждены у 58 человек (истинно положительный диагноз). Обозначим это число Nip.

Ни один человек с верифицированным диагнозом болезней вен нижних конечностей не был классифицирован как здоровый (ложноотрицательный диагноз). Обозначается это число N_LQ.

У 16 человек (NIQ) с неварикозными заболеваниями их характер был подтвержден (истинноотрицательный диагноз).

У 3 человек (N_Lp) с неварикозными заболеваниями были найдены признаки варикоза (ложноположительный диагноз).

Обозначим общее число людей через N.

Чувствительность метода (выявляемость заболеваний вен), вычисляемая по формуле 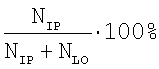для разработанного метода составила 100%.

Точность метода, вычислим как

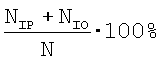
Для нашей методики она составила 96.1%.

Специфичность метода, вычисляемая как

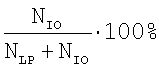
в нашем случае равна 84.2%.

Приведем для сравнения чувствительность, точность и специфичность экспертной системы по дифференциальной диагностике рака молочной железы у женщин: чувствительность обследования составляет 89.7%; точность - 86.4%; специфичность метода - 81.8%.

2. Результаты решения задачи, когда необходимо поставить точный диагноз (более широкая задача), класс "Больные" разбиваются на три болезни: ВБ, ПТБ и ОВТ

Результаты также сравнивались с клиническими данными: 19 здоровых, 20 человек с диагнозом ВБ, 22 человека - ПТБ, 16 человек - ОВТ.

2.1. Классификатор, основанный на апостериорных вероятностях со средними в качестве параметра сглаживания b, общее число людей: 77.

Классифицированные как Здоровые - 28 человек.

Классифицированные как ВБ - 18 человек.

Классифицированные как ПТБ - 20 человек.

Классифицированные как ОВТ - 11 человек.

Ошибка

классификации - 16 человек.

2.2. Классификатор, основанный на апостериорных вероятностях с единицей в качестве параметра сглаживания b, общее число людей: 77.

Классифицированные как Здоровые - 14 человек.

Классифицированные как ВБ - 21 человек.

Классифицированные как ПТБ - 25 человек.

Классифицированные как ОВТ - 17 человек.

Ошибка

классификации - 5 человек.

2-3. Байесовский классификатор со средними в качестве параметра сглаживания b, общее число людей: 77.

Классифицированные как Здоровые - 31 человек.

Классифицированные как ВБ - 16 человек.

Классифицированные как ПТБ - 0 человек.

Классифицированные как ОВТ - 30 человек.

Ошибка

классификации - 36 человек.

2.4. Байесовский классификатор с единицей в качестве параметра сглаживания b, общее число людей: 77.

Классифицированные как Здоровые - 16 человек.

Классифицированные как ВБ - 21 человек.

Классифицированные как ПТБ - 10 человек.

Классифицированные как ОВТ - 30 человек.

Ошибка классификации - 25 человек.

Наименьшую ошибку классификации на четыре класса (6.5%) имеет методика анализа, основанная на апостериорных вероятностях с единицей в качестве параметра сглаживания b.

Нами получены следующие результаты.

1. В случае, когда все признаки-координаты измеряются в одной температурной шкале (в нашем случае эта шкала температур в С°), наилучший результат классификации достигается, если в качестве параметров сглаживания выступают единицы (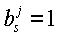, ∀j, ∀s).

2. Предложенная методика, основанная на байесовском классификаторе, с 3.89% ошибкой классифицирует новое наблюдение к одному из двух классов: "Здоров" или "Болен". Чувствительность данной методики составляет 100%, точность и специфичность превосходит запатентованную и разрешенную к применению в медицинской практике экспертную систему по дифференциальной диагностике рака молочной железы у женщин на 8.7% и 2.4% соответственно.

3. Применение разработанных методик для более точной классификации с указанием конкретного диагноза пациента дает немного худшие результаты (ошибка классификации 6.4%). Экспертная система в этом случае базируется на вычислении апостериорных вероятностей, т.к байесовский классификатор выдает ошибку классификации 33.7%.

Таким образом, предлагаемый нами способ диагностики на основе байесовского классификатора и апостериорных вероятностей с единицей в качестве параметра сглаживания по данным комбинированной термометрии имеет высокую точность (максимальная ошибка классификации 6,4%) и может быть предложен в качестве базы для разработки интеллектуальной экспертной компьютерной системы диагностики заболеваний вен нижних конечностей.

Использованная литература

1. Кендалл М., Стьюарт А. "Статистические выводы и связи." М.: Наука. 1973 г.

2. Айвазян С.А., Бухштабер В.М., Епюков И.С. Мешалкин Л.Д. "Прикладная статистика: Классификация и снижение размерности: Справ, изд." Под ред. Айвазяна С.А. - М.: Финансы и статистика, 1989 г.

3. Колмогоров А.Н., Фомин СВ. "Элементы теории функций и функционального анализа." М.: Наука, 1972.

4. Деврой Л., Дьерфи Л. "Непараметрическое оценивание плотностей. L1-подход". М.: Мир, 1988 г.

5. Дуда Р., Хард П. "Распознавание образов и анализ сцен." Изд. "Мир", Москва, 1976 г.

6. Фукуиага К. "Введение в статистическую теорию распознавания образов". М.: Наука, 1979 г.

7. Бурдина Л.М., Хайленко В.А., Кижаев Е.В., Легков А.А., Пинхосевич Е.Г., Мустафип Ч.К., Вайсблат А.В., Веснин С.Г., Тихомирова Н.Н. "Применение радиотермометра диагностического компьютеризированного интегральной глубинной температуры ткани для диагностики рака молочной железы". - Пособие для врачей. - М.: 1999 г.

8. Вайсблат А.В., Веснин С.Г., Конкин М.А. «Использование микроволновой радиотермометрии в диагностике рака молочной железы». - www.resltd.ru

Таблица №1
Среднее значение инфракрасного (ИК) и микроволнового (РТМ) датчиков температуры в различных точках голени у здоровых лиц в положении лежа Точка исследования 1 2 3 4 5 6 7 8 9 10 11 12 Среднее значение температуры кожи (ИК) 30,83 31,61 31,30 31,12 31,18 31,20 30,80 30,69 30,70 30,39 30,17 30,33 Дисперсия 1,95 1,62 1,69 1,70 1,66 1,77 2,06 2,21 2,12 1,97 1,96 2,38 Среднее значение глубокой температуры (РТМ) 33,4 34,06 33,81 33,9 33,7 33,81 33,63 33,27 33,23 32,7 32,55 32,58 Дисперсия 0,75 0,79 1,07 0,59 0,78 0,96 0,91 1,19 1,38 1,37 1,34 1,39

Таблица №2
Среднее значение инфракрасного (ИК) и микроволнового (РТМ) датчиков температуры в различных точках голени у здоровых лиц в положении стоя Точка исследования 1 2 3 4 5 6 7 8 9 10 11 12 Среднее значение температуры кожи (ИК) 30,83 31,46 31,22 31,01 30,98 31,16 30,80 30,48 30,78 30,25 30,16 30,29 Дисперсия 2,32 1,90 2,22 2,12 2,26 2,13 2,37 2,39 2,26 2,42 2,47 2,35 Среднее значение глубокой температуры (РТМ) 33,31 33,88 33,51 33,68 33,52 33,45 33,39 33,14 33,13 32,44 32,44 32,24 Дисперсия 0,73 0,64 0,75 0,59 0,78 0,73 0,89 0,94 0,93 1,06 1,27 1,15

Таблица №3
Среднее значение инфракрасного (ИК) и микроволнового (РТМ) датчиков температуры в различных точках голени у больных с ОВТ в положении лежа Точка исследования 1 2 3 4 5 6 7 8 9 10 11 12 Среднее значение температуры кожи (ИК) 31,39 31,82 32,19 31,80 31,93 32,31 31,82 31,74 31,6 31,41 31,76 31,64 Дисперсия 4,53 3,86 3,39 3,74 3,95 2,74 4,22 3,56 3,56 3,45 6,57 4,70 Среднее значение глубокой температуры (РТМ) 34,11 34,46 34,65 34,82 32,5 34,5 34,7 34,43 34,38 34,01 33,92 34,06 Дисперсия 1,36 0,59 0,61 0,59 0,93 0,49 0,92 0,88 1,11 0,83 1,24 1,50

Таблица №4
Среднее значение инфракрасного (ИК) и микроволнового (РТМ) датчиков температуры в различных точках голени у больных с ОВТ в положении стоя Точка исследования 1 2 3 4 5 6 7 8 9 10 11 12 Среднее значение температуры кожи (ИК) 31,42 31,81 32,17 31,61 31,75 32,28 31,78 31,46 31,95 31,21 31,26 31,59 Дисперсия 3,60 2,78 2,51 3,22 2,65 2,25 2,85 2,68 3,53 2,71 2,91 3,63 Среднее значение глубокой температуры (РТМ) 34,65 34,84 34,63 34,60 34,58 34,70 34,71 34,48 34,32 33,92 34,03 33,76 Дисперсия 1,66 1,19 0,86 0,73 0,47 0,66 1,26 1,65 0,94 1,53 1,50 2,22

Таблица №5
Среднее значение инфракрасного (ИК) и микроволнового (РТМ) датчиков температуры в различных точках голени у больных посттромботической болезнью в положении лежа Точка исследования 1 2 3 4 5 6 7 8 9 10 11 12 Среднее значение температуры кожи (ИК) 31,47 31,85 32,22 31,87 32,08 32,32 31,96 31,84 32,15 31,55 31,49 32,03 Дисперсия 2,88 2,24 2,25 1,94 3,24 2,39 2,37 2,51 2,70 1,99 1,99 3,39 Среднее значение глубокой температуры (РТМ) 33,77 34,29 34,43 34,45 34,41 34,54 34,41 34,15 34,27 33,71 33,78 33,91 Дисперсия 0,96 0,97 0,64 0,82 1,11 0,88 0,71 1,06 0,94 1,07 0,90 1,41

Таблица №6
Среднее значение инфракрасного (ИК) и микроволнового (РТМ) датчиков температуры в различных точках голени у больных посттромботической болезнью в положении стоя Точка исследования 1 2 3 4 5 6 7 8 9 10 11 12 Среднее значение температуры кожи (ИК) 31,34 31,82 32,07 31,74 31,72 32,15 31,74 31,6 32,11 31,40 31,38 31,73 Дисперсия 2,39 1,75 1,99 2,06 1,68 2,09 1,89 2,43 2,03 1,57 1,69 2,17 Среднее значение глубокой температуры (РТМ) 34,03 34,34 34,41 36,29 34,30 34,48 34,35 34,15 34,31 33,7 33,91 33,7 Дисперсия 0,72 0,66 0,94 297,33 0,77 0,92 0,58 0,86 0,89 1,22 0,80 1,32

Таблица №7
Среднее значение инфракрасного (ИК) и микроволнового (РТМ) датчиков температуры в различных точках голени у больных варикозной болезнью в положении лежа Точка исследования 1 2 3 4 5 6 7 8 9 10 11 12 Среднее значение температуры кожи (ИК) 30,3 30,95 31,59 30,76 30,91 31,78 30,9 31,08 31,74 31,04 30,87 31,68 Дисперсия 2,48 2,23 1,82 2,55 2,34 2,22 3,11 2,76 1,91 3,12 3,21 2,84 Среднее значение глубокой температуры (РТМ) 33,18 33,7 33,96 33,70 33,60 34,03 33,61 33,44 33,65 33,18 33,1 33,47 Дисперсия 1,56 1,65 1,26 1,58 1,41 1,23 1,57 1,55 0,98 2,04 2,04 1,27

Таблица №8
Среднее значение инфракрасного (ИК) и микроволнового (MB) датчиков температуры в различных точках голени у больных варикозной болезнью в положении стоя Точка исследования 1 2 3 4 5 6 7 8 9 10 11 12 Среднее значение температуры кожи (ИК) 30,19 31,04 31,74 30,72 30,83 31,96 30,85 30,88 31,64 30,90 30,67 31,45 Дисперсия 3,24 2,52 2,51 2,29 2,44 2,12 2,50 2,49 2,35 2,73 2,53 1,95 Среднее значение глубокой температуры (РТМ) 33,23 33,73 33,97 33,46 33,43 33,91 33,36 33,23 33,59 32,9 32,91 33,04 Дисперсия 2,36 1,73 1,30 1,30 1,29 1,25 1,56 1,42 1,32 1,93 1,88 1,49

Изобретение относится к медицине и может быть использовано для верификации диагнозов болезней вен нижних конечностей по данным комбинированной термометрии на основе байесовского классификатора и апостериорных вероятностей. Для этого измеряют поверхностные и глубокие температуры тканей голени пациентов. Затем для классификации пациентов применяют математическую экспертную систему на основе байесовского классификатора и апостериорных вероятностей с единицей в качестве параметра сглаживания. На основе полученных данных диагностируют заболевания вен нижних конечностей. Заявленный способ позволяет достигнуть высокой точности верификации диагнозов болезней вен нижних конечностей и может быть использован в качестве базы для разработки интеллектуальной экспертной компьютерной системы диагностики заболеваний вен нижних конечностей. 8 табл.

Способ диагностики заболеваний вен нижних конечностей по изменению поверхностной и глубокой температуры тканей голени пациентов, отличающийся применением для классификации пациентов математической экспертной системы на основе байесовского классификатора и апостериорных вероятностей с единицей в качестве параметра сглаживания.