Изобретение относится к области измерения физических констант, а именно к измерению пространственных (радиус) и энергетических (энергия связи) констант.
Известны методы измерения радиусов атомов и ионов, в том числе: 1) рефрактометрический, который основан на измерении рефракции (Иоффе Б.В. Рефрактометрические методы химии. - Л.: Химия, 1983; с.98); 2) рентгеноструктурный, который основан на явлении дифракции рентгеновского излучения на соответствующих микрочастицах (Бацанов С.С. Структурная химия. - М., 2000, с.139); 3) волюметрический, который основан на определении атомного объема (Регель А.Р., Глазов В.М. Периодический закон и физические свойства электронных расплавов. - М.: Наука, 1978, с.5); 4) столкновительные, которые основаны на определении сечения столкновения атомов и молекул (Берд Г., Молекулярная газовая динамика. - М.: Мир, 1981, с.17) и др. Широко распространен также рефрактометрический метод измерения радиуса атомов а, который основан на связи диэлектрической проницаемости или показателя преломления с поляризуемостью α микрочастиц (Фрелих Г. Теория диэлектриков. - М., 1960, с.218) в соответствии с уравнением Клаузиуса-Моссотти.
Недостатком данного метода является то, что радиус микрочастиц рассчитывается через атомный объем, который в свою очередь определяется через плотность вещества; это означает, что атомный объем является функцией параметров состояния вещества и характера межатомных взаимодействий и потому не может выступать в качестве атомной константы.
Наиболее близким к предлагаемому методу измерения радиуса атомов и ионов является метод, основанный на измерении его поляризуемости α в соответствии с соотношением 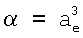 (Потапов А.А. Деформационная поляризация. - Новосибирск: Наука, 2004).
(Потапов А.А. Деформационная поляризация. - Новосибирск: Наука, 2004).
Недостатком данного метода является то, что он не учитывает зависимость радиуса атомов и ионов от их электронной конфигурации, а также наличие систематической погрешности измерения, обусловленной конечными размерами остова атомов и ионов.
К числу наиболее распространенных энергетических параметров атомов и ионов относится энергия ионизации (Бацанов С.С. Структурная химия. - М., 2000, с.6). Основными методами измерения энергии ионизации являются: 1) спектроскопический; 2) метод электронного удара; 3) фотоионизации (Веденеев В.И. и др. Энергии разрыва химических связей. Потенциалы ионизации и средство к электрону. - М., 1962, с.26-32).
Энергия ионизации равна работе вырывания электрона из атома или иона и тем самым характеризует прочность связи электрона в атоме или ионе. Однако связь между энергией ионизации и энергией связи внешних электронов с ядром атома (иона) неоднозначна. Энергия ионизации складывается из двух составляющих - энергии отрыва электрона и энергии, освобождаемой за счет перестройки электронной оболочки после удаления электрона. Это означает, что всем методам измерения энергии ионизации присуща систематическая погрешность, обусловленная трудноучитываемым эффектом перестройки электронной оболочки в результате отрыва одного из внешних электронов.
Наиболее близким к предлагаемому методу измерения энергии связи атомов является метод, основанный на присущей атомам взаимосвязи между энергией связи атома и его радиусом (Потапов А.А. Деформационная поляризация. - Новосибирск: Наука, 2004) 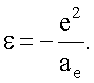
Недостатком данного метода измерения является наличие у него систематической погрешности, обусловленной принятым здесь отождествлением радиуса атома с действительным расстоянием между взаимодействующими зарядами остова атома и внешних электронов.
Следует также отметить, что известные методы измерения энергии ионизации и методы измерения радиуса атомов и ионов на практике применяются независимо друг от друга, хотя по своей сути они причинно взаимосвязаны и взаимообусловлены. В силу центральной симметрии энергия связи электронов с ядром зависит только от радиуса. Примером тому является основополагающее выражение для энергии связи εн атома водорода, которая однозначно определяется его радиусом аБ, так что 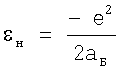 ,
,
где е - элементарный заряд электрона, аБ - боровский радиус.
Предлагаемое изобретение позволяет устранить отмеченные выше недостатки.
В основе предлагаемого способа измерения лежит фундаментальное явление поляризации вещества, проявляющееся во взаимодействии внешнего (анализирующего) электрического поля с электрическими зарядами атомов и ионов. Результатом такого взаимодействия является индуцируемые внешним полем Е электрические моменты атомов и ионов данного вещества, которые детектируются с помощью диэлектрических величин, таких как диэлектрическая проницаемость или диэлектрическая восприимчивость и показатель преломления. Фундаментальность явления поляризации обязана поляризуемости - основополагающему свойству атомов и ионов, заключающемуся в способности их электронных оболочек к упругой деформации во внешних электрических полях. Автором установлено, что поляризуемость атомов и ионов причинно связана с эффективными размерами внешней электронной оболочки и энергией связи ε. Данное обстоятельство принимается в качестве концептуального положения, лежащего в основании предлагаемого изобретения.
Сущность предлагаемого изобретения.
Предшествующий анализ и многочисленные исследования подтверждают простую связь между поляризуемостью и радиусом атомов и ионов [1, с.348]

где κ - коэффициент, зависящий от электронной конфигурации атомов или ионов, α и а - электронная поляризуемость и радиус атомов или ионов соответственно.
Такую связь можно объяснить тем, что в силу сферической симметрии атомов, у них проявляется один единственный вид поляризации - электронный. По той же причине для описания их структуры достаточно лишь одного параметра - радиуса.
По имеющимся литературным данным коэффициент κ в (1) может быть как равным, так и меньшим и большим единицы. Наибольшее распространение на практике имеет случай κ=1, для которого имеется косвенное обоснование в виде моделей Бора и Томсона для атома водорода. Неопределенность коэффициента κ в значительной мере обусловлена неопределенностью входящей в (1) величины а. Действительно, на практике имеет место широкое хождение различных радиусов, таких как ван-дер-ваальсовы, кинетические, орбитальные, ковалентные и др. Каждый из них несет вполне определенный физический смысл, соответствующий выбранному методу наблюдения или принимаемой модели описания соответствующей микросистемы.
В данном семействе радиусов отсутствует понятие поляризационного радиуса ае, что объясняется фактическим отсутствием в настоящее время соответствующего метода как инструмента изучения внутри атомной структуры. Более того, действует негласный запрет на применение соотношения 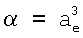 (частный случай уравнения (1), при κ=1), которое следует из модели Бора и Томсона [1, с.334], поскольку квантомеханическое описание дает величину κ=4, 5 [2]. Такое разительное различие коэффициентов зачастую принимается как основание для вывода о несостоятельности классического описания.
(частный случай уравнения (1), при κ=1), которое следует из модели Бора и Томсона [1, с.334], поскольку квантомеханическое описание дает величину κ=4, 5 [2]. Такое разительное различие коэффициентов зачастую принимается как основание для вывода о несостоятельности классического описания.
Предлагаемый метод позволяет разрешить данное противоречие. Дело в том, что при квантово-механических расчетах используется орбитальный радиус а0 [3], а при классических - поляризационный радиус ае. Т.е. в формуле (1) различие радиусов а0 и ае должно учитываться введением различных коэффициентов κ.
В этой связи обратимся к рассмотрению сущности поляризационного радиуса, который фактически предопределяет постановку его измерения на основе явления поляризации микрочастиц во внешнем электрическом поле.
В общем случае атомную систему можно представить в виде мгновенного диполя р, образуемого связанными между собой эффективным зарядом q+ положительного ядра и эффективным зарядом q- валентных электронов, которые находятся на расстоянии ае друг от друга. Во внешнем поле Е на эти заряды действует пара сил F+=q+E, F-=q-E, которые вызывают соответствующие смещения Δа+ и Δа-. Причем в каждый момент времени эти силы разнонаправлены и приводят к растяжению (или сжатию) диполя р на (Δа++Δа-). С другой стороны, мгновенный диполь определяется как p=аеq (в приближении q+=q-=q). Отсюда следует, что точками приложения сил F± должны выступать точечные заряды q±, которые находятся на расстоянии ае между ядром и валентными электронами. У атомов с симметричным расположением электронов на внешней оболочке (и потому не имеющих собственных дипольных моментов) индукционный механизм поляризации не отличается от рассмотренного выше. Точками приложения сил внешнего поля Е являются заряды, положение которых задается радиусом ае, также как у атомов с дипольной структурой. Отсюда следует важный вывод - в уравнении (1) должен входить не безымянный радиус а, а вполне конкретный радиус, определяемый данным методом детектирования поляризации, а именно поляризационный радиус ае.
Чтобы воспользоваться уравнением (1) для расчета поляризационных радиусов атомов, необходимо определиться с коэффициентом κ. Во внешнем электрическом поле Е атомы и ионы приобретают индуцированные дипольные моменты

где pi=q2Δa.
В результате возмущения водородоподобных атомов исходное равновесное состояние системы зарядов q+ и q- нарушается и новое равновесное состояние атома достигается благодаря противодействию возвращающей силы со стороны заряда остова
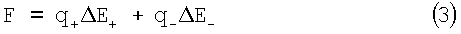
где q+ - квазиточечные заряды q+ остова, q- - заряды внешних электронов, ΔE+ и ΔE- - изменения напряженностей полей зарядов q+ и q-. Природа возвращающей силы F по (3) связана с перераспределением зарядов q+ и q- (из-за смещения электронов на Δа- и ядер Δa+), которые приводят к изменению исходных напряженностей полей в атоме ΔE+ и ΔЕ-, так что
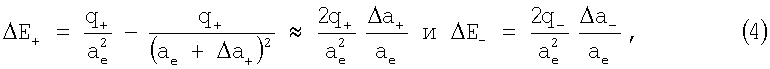
где ае - эффективный радиус атома в исходном состоянии. Т.о., с одной стороны, на водородоподобный атом действует пара сил внешнего поля F±=q±E, а с другой, - возвращающая сила по (3). Решение уравнения баланса F=F± приводит к выражению для поляризуемости

В силу структурного подобия данное выражение для поляризуемости α можно распространить на водородоподобные атомы (на атомы щелочных металлов в приближении их жестких остовов). С этой целью обратимся к теореме Гаусса, согласно которой заряд на поверхности сферы равен сумме всех зарядов внутри данной сферы, причем результирующий заряд эквивалентен точечному заряду, помещенному в центре сферы [4]. В отношении к водородоподобным атомам это означает, что заряд их остова равен квазиточечному заряду +е как результату суммы заряда ядра +eZ и заряда электронов на всех внутренних оболочках -e(Z-1). Отсюда следует, что атомы первой группы таблицы Менделеева имеют электронную конфигурацию такую же как у атома водорода, и к ним может быть применено уравнение (1).
Близкий к (5) результат ранее был получен для атома водорода с помощью квантовомеханического расчета [1-3]

где аБ - боровский радиус.
Рассчитываемая по формуле (5) и (6) поляризуемость согласуется с экспериментально определяемой величиной αн=0,67Å3 с погрешностью около 10%. Отсюда следует, что между классическим и квантовомеханическим описанием обозначенного выше противоречия нет. Просто уравнения (5) и (6) содержат в себе разные радиусы аБ и ае. С одной стороны, боровский радиус по определению представляет собой наиболее вероятное положение электрона относительно ядра [3], а, с другой, - поляризационный радиус - это действительное расстояние между ядром и электроном. Кстати, ранее было установлено, что между орбитальным радиусом а0 (для атома водорода а0=аБ) и поляризационным радиусом ае выполняется соотношение 2a0=ae [1]. Подстановка ae=2aБ в (6) дает 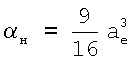 , что практически совпадает с (5).
, что практически совпадает с (5).
Можно показать, что для остальных (неводородоподобных) атомов таблицы Менделеева в приближении изотропного распределения зарядов атомов уравнение баланса сил имеет вид
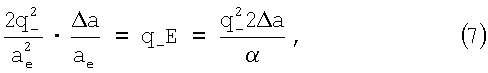
из которого следует уравнение связи

Уравнения (5) и (8) выступают в качестве исходных уравнений для установления связи между поляризуемостью и радиусом атомов. По мере уточнения электронной конфигурации атомов численное значение коэффициента κ, входящего в (1), также будет уточняться.
Сферическая симметрия, характерная для атомов, сохраняется и у их ионов. Как в случае атомов, так и в случае ионов ядро предопределяет центральный характер взаимодействия его с внешними электронами. Тоже относится и к явлению поляризации; индукционный механизм поляризации одинаков у атомов и ионов. Данное обстоятельство предполагает возможность применения формул (5) и (8) к описанию связи поляризуемости с радиусом ионов.
При всей значимости уравнений (5) и (8) они отражают скорее наличие принципиальной связи между поляризуемостью и размерами атомов и ионов. При этом надо иметь в виду то, что они получены в приближении точечных зарядов и, строго говоря, применимы только к атому водорода и водородоподобным ионам. У реальных атомов и ионов следует учитывать их оболочечное строение и конечные размеры остовов атомов и ионов. Дело в том, что связь внешних электронов с ядром осуществляется лишь косвенно. В действительности эта связь формируется в результате кулоновского притяжения их к положительно заряженному остову (согласно теореме Гаусса). Это означает, что наблюдаемая в эксперименте энергия связи внешних электронов в атомах или ионах определяется расстоянием d между внешними электронами и их остовом (но не их ядром). Поэтому в приведенных выше уравнениях баланса сил F и F± следует заменить радиус ае на эффективное расстояние d между зарядами остова и внешней оболочкой. Эти расстояния связаны соотношением

где аост. - радиус остова атома или иона.
Замена ае на d приводит к замене (5) на

и (8) на выражение

Из соотношения (9) следует, что для определения радиуса атома (или иона) необходимо знать радиус остова аост., который, очевидно, складывается из радиуса первой К-оболочки и суммы межоболочечных расстояний d1-2, d2-3, d3-4, …, т.е.
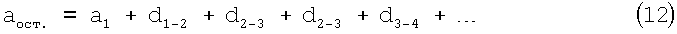
Радиус а1 К-оболочки определяется в результате прямого кулоновского взаимодействия ядра атома (или иона) с его внешними электронами. Данное обстоятельство позволяет найти выражение для энергии K-оболочки ε1, в общем виде

где Z - порядковый номер атома, аБ - боровский радиус, е - элементарный заряд.
Выражение (13) получено с учетом взаимного отталкивания электронов К-оболочки аналогично известному уравнению для энергии связи водородоподобных атомов и ионов 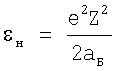 .
.
С другой стороны, энергия ε1 связана с радиусом а1 универсальным образом через посредство соотношения 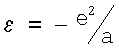 (см. ниже), так что
(см. ниже), так что
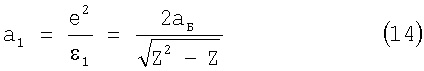
Здесь также учтен эффект кулоновского сжатия оболочки, который наглядно отражается известным соотношением для водородоподобных атомов и ионов 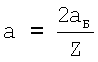 . Входящие в (12) межоболочечные расстояния можно найти, используя эмпирический закон Мозли [5], представленный в виде
. Входящие в (12) межоболочечные расстояния можно найти, используя эмпирический закон Мозли [5], представленный в виде
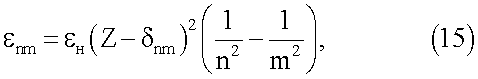
где εн - энергия связи атома водорода; εnm - энергия внутриатомного перехода n→m между соответствующими оболочками; δnm - константа перехода.
Выражение (15) можно интерпретировать следующим образом. Оно представляет разность энергий, соответствующих состоянием n и m. Каждая из этих энергий - это результат кулоновского взаимодействия положительного заряда (Z-δ)e на соответствующей оболочке и заряда электронов (Z-δ)e, находящихся за пределами данной оболочки, разделяемых расстоянием 2аБn2 (или 2аБm2). Такое понимание закона Мозли является следствием теоремы Гаусса, согласно которой заряды на оболочках (Z-δ)e можно рассматривать как точечные заряды.
Энергия перехода εnm и соответствующее ему межоболочечное расстояние dnm как уже отмечалось выше взаимосвязаны между собой наподобие (14)
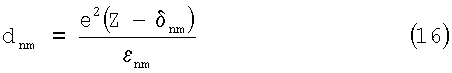
Распишем выражение (16) для искомых переходов:
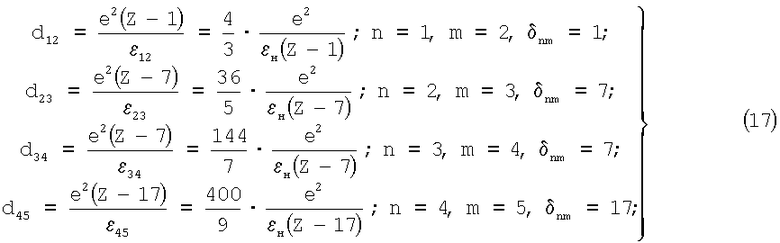
На основании формул (9), (14) и (17) для примера были рассчитаны радиусы ряда атомов, которые представлены в таблице, отличие этих данных от полученных ранее в работе [1] минимально для атомов 2-го и 3-го периодов (около 10%) и возрастает для более «тяжелых» атомов, достигая 50% для ксенона. При этом основной вклад в радиус вносит расстояние между внешними электронами и остовом атома; внутренние межоболочечные расстояния выступают как поправки к величине dn.
Рассмотрим сущность предлагаемого метода измерения в отношении энергии связи атомов и ионов. Исходным для рассмотрения является уравнение для энергии связи атома водорода
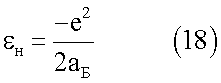
Аналогичное (18) соотношение было получено для связи между обратным орбитальным радиусом и энергией связи (или потенциалом ионизации). Оно характерно для большинства атомов [3, с.49]. В работе [1] показано, что закономерности в поведении величин α(N) и 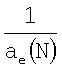 являются следствием присущей всем элементам таблицы Менделеева обусловленности свойств а (поляризуемости) их структурой (радиус). В свою очередь структура атома предопределяет величину его энергии связи. Примером тому служит основополагающее в атомной физике уравнение (18).
являются следствием присущей всем элементам таблицы Менделеева обусловленности свойств а (поляризуемости) их структурой (радиус). В свою очередь структура атома предопределяет величину его энергии связи. Примером тому служит основополагающее в атомной физике уравнение (18).
Принимая во внимание линейность зависимости энергии связи от величины 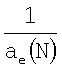 , уравнение (18) можно обобщить на многоэлектронные атомы, так что
, уравнение (18) можно обобщить на многоэлектронные атомы, так что

где dn - расстояние между остовом атома и его внешними электронами, подстрочный индекс n соответствует номеру периода. Данное выражение представляет рассмотренную выше двухзарядовую модель атома или иона, согласно которой энергия связи определяется кулоновскими силами, взаимодействуя между зарядами остова и внешними электронами. Отличие (19) от предложенного ранее выражения
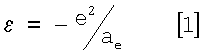 ,
,
заключается в замене ае на dn отражает более реальную оболочечную модель атомов и ионов. Надо отметить, что в формулу (19) также как и в (18) входят не эффективные, а единичные заряды. Объяснить такое упрощение модели атома можно на основании следующего. Внешние электроны не различимы между собой и к ним вполне применимо хорошо известное в атомной физике приближение независимых электронов. Поэтому в силу сферической симметрии энергия взаимодействия эффективного заряда остова атома с каждым из электронов внешней оболочки одинакова для всех электронов. Эта означает, что один из зарядов в (19) представляет собой заряд электрона е-. В соответствии с оболочечной моделью атома и на основании теоремы Гаусса [4, с.44] действующий на внешние электроны заряд ядра равен q+=Ne, где N - число электронов на внешней оболочке. Энергия взаимодействия между ними равна 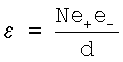 ,
,
где d - расстояние между зарядами q+ и е-. Это выражение тождественно уравнению (19) в приближении 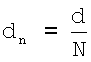 ,
,
где dn - эффективное (измеряемое) расстояние между остовом и внешними электронами.
Уравнение (19) было принято для расчета энергии связи атомов (см. таблицу 1), по которым в свою очередь построены зависимости энергии связи элементов от порядкового номера Nn, т.е. εn(N) в соответствующем n-ом периоде таблицы Менделеева (см. чертеж). Величины εn, рассчитанные по уравнению (19), находятся в неплохом согласии с данными по потенциалам ионизации I [6]. У отдельных элементов имеются относительно большие расхождения между этими величинами, но они имеют достаточно регулярный характер. Зависимости εn(Nn) выглядят как результат спрямления зависимостей I(N) (см. чертеж). Такое соответственное поведение величин ε и I указывает на их единую природу.
Различие между ε и I имеет простое объяснение. Энергия связи ε определяется методом измерения, согласно которому энергетический уровень отсчета в процессе измерения поляризуемости остается неизменным. А при определении потенциала ионизации I происходит значительная перестройка энергетического уровня конечного (ионизированного) состояния атома или иона за счет перестройки электронной оболочки в результате удаления электрона. Поэтому потенциал ионизации зависит не только от действительной энергии связи электрона с ядром, но и от энергии конечного состояния ионизированного атома. Данное положение подтверждается заметными отклонениями энергии Δ=(ε-I) у атомов разных групп таблицы Менделеева. Т.е., между энергией связи и потенциалом ионизации при их количественном различии имеется качественное соответствие. Зависимости ε(N) и I(N) коррелированы между собой, отражая их единство в самом важном аспекте нашего рассмотрения - стабильности и устойчивости атомов и ионов. Они не тождественны друг другу, но взаимодополнительны. Т.е., уравнение (19) имеет не только эмпирическое обоснование (на уровне погрешности соответствия между энергией связи и потенциалом ионизации атомов таблицы Менделеева), но и правильно отражает концептуальное положение оболочечной модели атома.
Таким образом, к существенным признакам предлагаемого изобретения можно отнести: 1) новое в атомной физике понятие - поляризационный радиус аn атомов и ионов как радиус сферы, имеющей максимально возможное расстояние электронов внешней оболочки от ядра, рассчитываемое по данным измерения поляризуемости α этих атомов и ионов; он определяется путем суммирования всех межоболочечных расстояний; 2) уравнение связи между поляризуемостью и межоболочечным расстоянием, в котором коэффициент пропорциональности зависит от внутриатомной структуры; 3) энергия связи и межоболочечное расстояние взаимосвязаны и взаимообусловлены, а их произведение представляет инвариант εd=е2=inv; 4) измерительные процедуры и их последовательность, направленные на определение энергии связи и радиуса атомов и ионов.
Таким образом, предложен способ определения радиуса аn и энергии связи εn атомов и ионов, основанный на взаимосвязи этих величин с поляризуемостью, отличающийся тем, что измеряют поляризуемость α атома исследуемого вещества в газовой фазе при давлении, соответствующем идеальному состоянию вещества, а также измеряют энергии его внутриатомных переходов εnm, рассчитывают расстояние между внешними электронами и остовом данного атома dn, межоболочечные расстояния dnm и радиус первой К-оболочки а1, по формулам
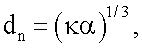
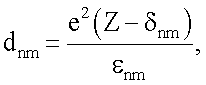
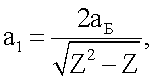
где κ - коэффициент, равный 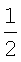 для атомов I группы таблицы Менделеева и κ=1 для остальных атомов, δnm - константа внутриатомных переходов n→m; Z - порядковый номер элемента; е - элементарный заряд, аБ - боровский радиус, затем определяют радиус атома или иона по формуле
для атомов I группы таблицы Менделеева и κ=1 для остальных атомов, δnm - константа внутриатомных переходов n→m; Z - порядковый номер элемента; е - элементарный заряд, аБ - боровский радиус, затем определяют радиус атома или иона по формуле
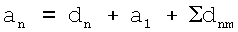
и его энергию связи по формуле
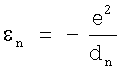 .
.
Решаемые задачи
1. Появилась принципиальная возможность получения достоверной информации о размерах атомов и ионов, а также их стабильности и устойчивости. Эта информация до настоящего времени размывалась и терялась из-за неопределенности сложившегося понятия "радиус атома" и в условиях, когда в хождении находятся многочисленные виды атомных радиусов, такие как ван-дер-ваальсовы, кинетические, ковалентные, металлические, онсагеровские, орбитальные, средние и т.п. Введение понятия "поляризационный радиус" обосновано тем, что данные радиусов являются результатом прямых измеринй поляризуемости. Поляризационный радиус претендует на роль "абсолютного" радиуса, поскольку он причинно предопределен величиной мгновенного дипольного момента атома, т.е. самой природой явления диэлектрической поляризации. Точность измерения радиуса в пределе определяется точностью измерения поляризуемости атома, которая в настоящее время достигает 0,02% [1].
2. Понятие поляризационного радиуса может быть распространено и на ионы, имеющие также как и атомы сферическую симметрию в распределении их электронного заряда. Явление поляризации, лежащее в основе метода измерения радиуса и энергии связи, в одинаковой мере применимо к атомам и ионам.
3. Поляризационный радиус атома как атомная константа предопределяет величину энергии связи внешних электронов атома с его ядром, являясь количественной мерой устойчивости и стабильности атомов. Метод измерения энергии связи атомов и ионов сводится к определению энергии связи электронов внешней оболочки с ядром (остовом атома) практически в невозмущенном состоянии атома или иона. В этом отношении предлагаемый метод измерения энергии связи свободен от систематических погрешностей, присущих потенциалам ионизации. В методическом отношении представляется также важным то, что появился новый независимый и теоретически обоснованный метод измерения такой важной атомной константы, как энергия связи.
4. Величины радиусов и энергий связи являются исходными для формирования физических и химических свойств веществ. Данное обстоятельство предполагает на основании новых данных аn и εn возможность построения более совершенных моделей вещества и более корректных теорий электронного строения вещества.
5. Настоящее изобретение может быть использовано при разработке теоретических основ нанотехнологии, поскольку "эксплуатационные" свойства наноустройств и свойствами их исходных структурных элементов - атомов и ионов.
6. Существенным компонентом изобретения является его эвристическая ценность, которая видится в осуществлении экспериментального подхода к получению новой информации об атомном строении.
Описание чертежей
На чертеже приведены зависимости энергии связи ε (I-IV) и потенциала ионизации I (Ia-IVa) от порядкового номера N элемента в разных периодах (I-IV) для ns- и np-элементов.
Осуществление изобретения
Предлагаемое изобретение может быть осуществлено с применением стандартных и общепринятых методов и средств измерения поляризуемости [1, 7] и рентгеноструктурного анализа [8]. Измерение энергии внутриатомных переходов εmn, так что εmn,=hνmn, где h - постоянная Планка [см. также: Физический энциклопедический словарь. - М.: Сов. энциклопедия, 1983, с.41; 637, 638].

ЛИТЕРАТУРА
1. Потапов А.А. Деформационная поляризация. - Новосибирск: Наука, 2004. - 511 с.
2. Слэтер Дж. Диэлектрики. Полупроводники. Металлы. - М.: Мир, 1969.
3. Годовиков А.А. Кристаллохимия простых веществ. - Новосибирск: Наука, 1989. - 181 с.
4. Парселл Э. Электричество и магнетизм. - М.: Наука, 1975. - 440 с.
5. Робертсон Б. Современная физика в прикладных науках. - М.: Мир, 1985. - 272 с.
6. Бацанов С.С. Экспериментальные основы структурной химии. - М.: Изд-во стандартов. 1986. - 240 с.
7. Потапов А.А. Молекулярная диэлькометрия. - Новосибирск: Наука, 1994. - 285 с.
8. Физическая энциклопедия / Рентгеновская спектральная аппаратура. - М.: Сов. энциклопедия, 1994. - Т.4. - С.351-353; 361-363.
Изобретение относится к измерению атомных констант - радиуса и энергии связи валентных электронов атомов и ионов. Способ основан на деформации электронных оболочек атомов во внешних электрических полях. Согласно изобретению измеряют поляризацию атомов вещества, находящегося в состоянии идеального газа, и по выражениям, полученным для оболочечной модели атома, находят радиус атома и энергию связи валентных электронов. При этом предполагается, что поляризуемость атомов и ионов причинно связана с эффективными размерами внешней электронной оболочки и энергией связи валентных электронов. Данные по радиусам и энергиям связи, полученные согласно изобретению, могут быть использованы для уточнения теорий электронного строения вещества и могут быть полезны в нанотехнологии. 1 ил., 1 табл.
Способ измерения радиуса an и энергии связи εn атомов и ионов, основанный на взаимосвязи этих величин с поляризуемостью, отличающийся тем, что измеряют поляризуемость α атома исследуемого вещества в газовой фазе при давлении, соответствующем идеальному состоянию вещества, а также измеряют энергии его внутриатомных переходов εnm, рассчитывают расстояние между внешними электронами и остовом данного атома dn, межоболочечные расстояния dnm и радиус первой К - оболочки а1, по формулам
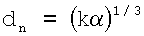 ,
, 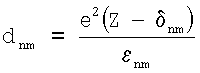 ,
, 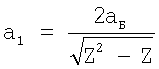 ,
,
где k - коэффициент, равный 2 для атомов I группы таблицы Менделеева и k=1 для остальных атомов; δnm - константа внутриатомных переходов n→m; Z - порядковый номер элемента; е - элементарный заряд, аБ - боровский радиус, затем определяют радиус атома или иона по формуле
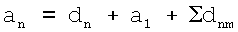
и его энергию связи по формуле
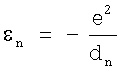 .
.
| RU 2005104213 А, 27.07.2006 | |||
| СПОСОБ ОЦЕНКИ РАДИУСОВ АТОМОВ ХИМИЧЕСКИХ ЭЛЕМЕНТОВ В РАЗЛИЧНОМ ЭНЕРГЕТИЧЕСКОМ СОСТОЯНИИ | 2004 |
|
RU2273058C1 |
| СПОСОБ ИЗМЕРЕНИЯ ЭНЕРГИИ МЕЖАТОМНЫХ И МЕЖМОЛЕКУЛЯРНЫХ ВЗАИМОДЕЙСТВИЙ И КООРДИНАЦИОННОГО ЧИСЛА АТОМНЫХ И МОЛЕКУЛЯРНЫХ ВЕЩЕСТВ | 2005 |
|
RU2287153C2 |
| СПОСОБ ОЦЕНКИ СТЕПЕНИ ИОННОСТИ ХИМИЧЕСКОЙ СВЯЗИ АТОМОВ В МОЛЕКУЛЕ | 2004 |
|
RU2272279C1 |
| Домовый номерной фонарь, служащий одновременно для указания названия улицы и номера дома и для освещения прилежащего участка улицы | 1917 |
|
SU93A1 |
| US 5420805 A, 30.05.1995 | |||
| БЛОХИНЦЕВ Д.И | |||
| Основы квантовой механики, изд | |||
| Кипятильник для воды | 1921 |
|
SU5A1 |
| Планшайба для точной расточки лекал и выработок | 1922 |
|
SU1976A1 |
Авторы
Даты
2009-06-20—Публикация
2007-02-26—Подача