Область техники, к которой относится изобретение
Настоящее изобретение относится, в общем, к блочному основанному на преобразовании сжатию цифрового мультимедиа (к примеру, видео и изображений).
Предшествующий уровень техники
Блочное основанное на преобразовании кодирование
Кодирование с преобразованием - это методика сжатия, используемая во многих системах сжатия звука, изображений и видео. Несжатое цифровое изображение или видео в типичном случае представляется или захватывается в качестве выборок элементов картинки или цветов в местах в изображении или видеокадре, организованных в соответствии с двумерной (2D) сеткой. Это упоминается как представление в пространственной области изображения или видео. Например, типичный формат для изображений состоит из потока 24-битных выборок элементов цветной картинки, размещенных как сетка. Каждая выборка - это число, представляющее цветовые компоненты в местоположении пиксела в сетке в рамках цветового пространства, такого как RGB или YIQ, помимо прочего. Различные системы изображений и видео могут использовать различные цветовые, пространственные и временные разрешения при взятии выборок. Также цифровое аудио в типичном случае представляется как дискретизированный по времени поток звуковых сигналов. Например, типичный формат аудио состоит из потока 16-битных выборок по амплитуде звукового сигнала, взятых с постоянным интервалом времени.
Несжатые цифровые сигналы звука, изображений и видео могут потреблять значительную емкость при хранении и передаче. Кодирование с преобразованием уменьшает размер цифрового аудио, изображений и видео посредством преобразования представления сигнала в пространственной области в представление в частотной области (или другой аналогичной области преобразования) и последующего уменьшения разрешения определенных, в общем, менее воспринимаемых частотных компонентов представления в области преобразования. Это обычно приводит к гораздо менее воспринимаемому ослаблению цифрового сигнала по сравнению с уменьшением цветового или пространственного разрешения изображений или видео в пространственной области или звука во временной области.
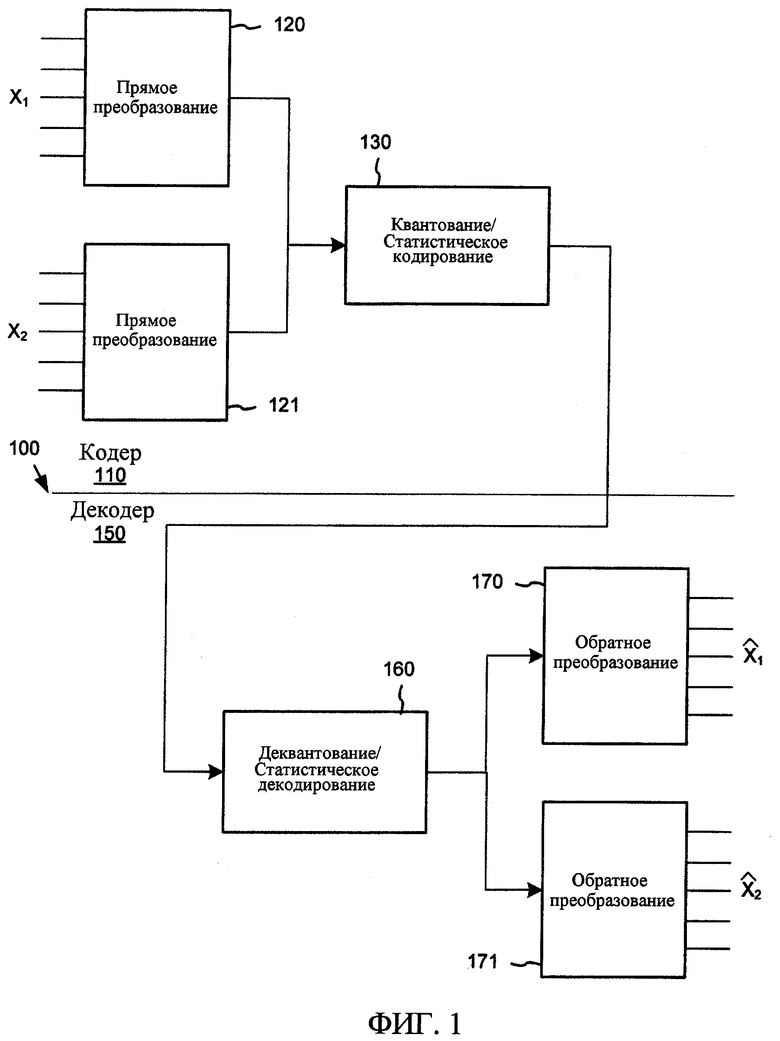
Более конкретно, типичный блочный основанный на преобразовании кодек 100, показанный на фиг. 1, делит пиксели несжатого цифрового изображения на двумерные блоки фиксированного размера (X1,..., Xn), при этом каждый блок, возможно, перекрывается другими блоками. Линейное преобразование 120-121, которое выполняет анализ пространственных частот, применяется к каждому блоку, что преобразует разнесенные выборки в рамках блока к набору коэффициентов частот (или преобразования), обычно представляющих интенсивность цифрового сигнала в соответствующих полосах частот по блочному интервалу. Для сжатия коэффициенты преобразования могут быть выборочно квантованы 130 (т.е. уменьшено их разрешение, например, посредством отбрасывания наименее значимых битов значений коэффициентов или иного отображения значений в числовом множестве с более высоким разрешением на меньшее разрешение), а также закодированы 130 статистическим кодированием или кодированием с переменной длиной в сжатый поток данных. При декодировании коэффициенты преобразования обратно преобразуются 170-171, чтобы приблизительно восстановить исходный дискретизованный по цвету/пространству сигнал изображения/видео (восстановленные блоки 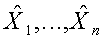 ).
).
Блочное преобразование 120-121 может быть задано как математическая операция над вектором x размера N. Более часто операцией является линейное умножение, генерирующее выход области преобразования y = Mx, где M - матрица преобразования. Когда входные данные имеют произвольную длину, они сегментируются на N векторов определенной длины, и блочное преобразование применяется к каждому сегменту. Для целей сжатия данных выбираются обратимые блочные преобразования. Другими словами, матрица M является обратимой. В нескольких измерениях (к примеру, для изображения и видео) блочные преобразования в типичном случае реализуются как раздельные операции. Матричное умножение применяется раздельно вдоль каждого измерения данных (т.е. и строк, и столбцов).
Для сжатия коэффициенты преобразования (компоненты вектора y) могут быть выборочно квантованы (т.е. уменьшено их разрешение, например, посредством отбрасывания самых младших битов значений коэффициентов или иного отображения значений в числовом множестве с более высоким разрешением на меньшее разрешение), а также закодированы статистическим кодированием или кодированием с переменной длиной в сжатый поток данных.
При декодировании в декодере 150 инверсия этих операций (деквантование/статистическое декодирование 160 и обратное блочное преобразование 170-171) применяется на стороне декодера 150, как показано на фиг. 1. При восстановлении данных обратная матрица M -1 (обратное преобразование 170-171) применяется в качестве множителя к данным области преобразования. При применении к данным области преобразования обратное преобразование приблизительно восстанавливает исходное цифровое мультимедиа временной области или пространственной области.
Во многих приложениях кодирования на основе блочного преобразования желательно, чтобы преобразование было обратимым, чтобы поддерживать кодирование как с потерями, так и без потерь в зависимости от коэффициента квантования. При отсутствии квантования (обычно представляемого как коэффициент квантования 1), например, кодек, использующий обратимое преобразование, может точно воспроизводить входные данные при декодировании. Тем не менее, требование обратимости в этих приложениях ограничивает выбор преобразований, на основе которых может быть разработан кодек.
Многие системы сжатия изображений и видео, такие как MPEG и Windows Media, помимо прочих, используют преобразования на основе дискретного косинусного преобразования (DCT). DCT, как известно, имеет подходящие свойства энергетического сжатия, что приводит к практически оптимальному сжатию данных. В этих системах сжатия обратное DCT (IDCT) используется в циклах восстановления как в кодере, так и в декодере системы сжатия для восстановления отдельных блоков изображений. DCT описано в публикации N. Ahmed, T. Natarajan и K.R. Rao "Discrete Cosine Transform", IEEE Transactions on Computers, C-23 (январь 1974), на стр. 90-93. Примерная реализация IDCT описана в"IEEE Standard Specification for the Implementations of 8x8 Inverse Discrete Cosine Transform", IEEE Std. 1180-1990, 6 декабря 1990 г.
Традиционные преобразования данных, используемые, чтобы реализовать средство обратимого сжатия двумерных данных, в общем, имели один или более следующих основных недостатков.
1. Неравные нормы между коэффициентами преобразования, требующие сложных схем статистического кодирования.
2. Неточные аппроксимации к оптимальным преобразованиям, таким как DCT.
3. Высокая вычислительная сложность.
Традиционная реализация двумерного преобразования
Раздельное двумерное преобразование в типичном случае реализуется посредством выполнения одномерных преобразований над строками данных, после чего следует одномерное преобразование над столбцами данных (или наоборот). См. публикацию A. K. Jain "Fundamentals of Digital Image Processing". Prentice Hall, 1989. В матричном представлении, пусть T представляет матрицу преобразования, а X является двумерными данными. Раздельное двумерное преобразование с помощью T задано Y в следующем уравнении:
Y = T X T' (1)
На самом деле построчные и постолбцовые преобразования могут отличаться. Например, матрица данных может быть не квадратной (скажем, размера 4×8), либо построчные и постолбцовые преобразования могут быть DCT и дискретным синусным преобразованием (DST) соответственно. В этом случае и множители умножения справа и слева отличаются (скажем, T 1 и T 2), и преобразование задается как
Y = T 1 X T' 2 (2)
Например, фиг. 2 показывает двумерное DCT 4×4, реализованное в две стадии. На первой стадии столбцы матрицы данных преобразуются с помощью 4-точечного одномерного DCT. На второй стадии четырехточечные одномерные DCT применяются вдоль строк. С бесконечной арифметической точностью это упорядочивание может быть переключено без изменений в выходе.
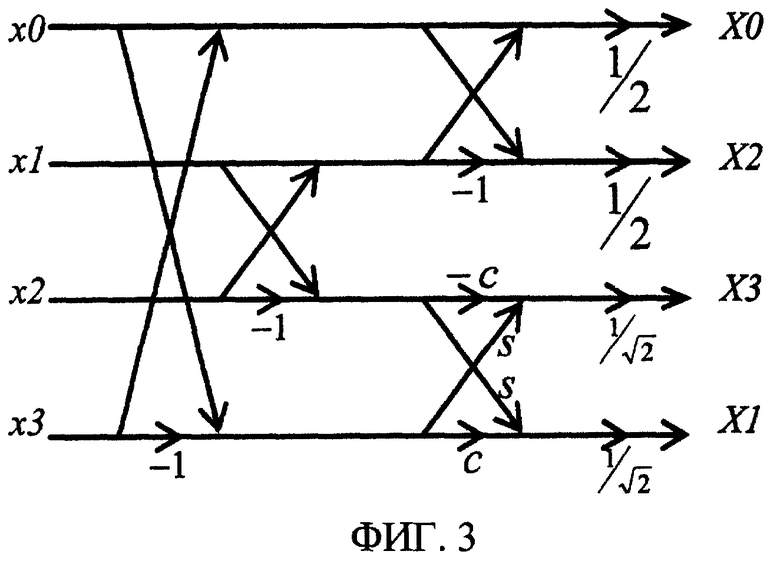
Четырехточечное одномерное DCT может быть реализовано как последовательность операций умножения и сложения над 4 значениями входных данных, как представлено на сигнальном ориентированном графе, показанном на фиг. 3. Значения c и s в этом схеме являются соответственно косинусом и синусом π/8. Подход раздельного преобразования хорошо подходит для кодека с потерями данных. Кодеки без потерь более сложно реализовать. Даже при квантовании с коэффициентом единица не гарантируется, что описанное выше раздельное двумерное DCT совместно с раздельным обратным DCT или IDCT обеспечит точное до бита совпадение с исходным вводом. Это обусловлено тем, что делители на фиг. 3 вызывают ошибки округления, которые могут не быть скомпенсированы между кодером и декодером.
Лифтинг-преобразование
Чтобы добиться сжатия без потерь с помощью блочного основанного на преобразовании кодека, необходимо заменить вышеописанное двумерное DCT 4×4 на преобразование без потерь. Раздельное преобразование может быть использовано только в том случае, если каждое одномерное преобразование выполняется без потерь или является обратимым. Хотя существует несколько вариантов для обратимых одномерных преобразований, основанные на "лифтинг-преобразовании" (схеме преобразования сигнала, заключающейся в сокращении числа его выборок за счет удаления коррелирующих значений при сохранении определенных скалярных характеристик) являются наиболее желательными. Лифтинг-преобразование - это процесс выполнения матрично-векторного умножения с помощью последовательных "сдвигов". Сдвиг задается как умножение вектора-операнда на матрицу, которая является единичной матрицей, плюс один ненулевой недиагональный элемент. Перемена знака одного или более векторных коэффициентов может осуществляться где-либо в ходе этого процесса без потери общности.
Лифтинг-преобразование ранее реализовывалось посредством структур лестничного или решетчатого фильтра. Основанные на лифтинг-преобразовании или последовательном сдвиге методики использовались в графике. См. публикацию A. Tanaka, M. Kameyama, S. Kazama и O. Watanabe. "A rotation method for raster image using skew transformation". Proc IEEE Confon Computer Vision and Pattern Recognition, страницы 272-277, июль 1986 г.; и A. W. Paeth "A fast algorithm for general raster rotation". Proceedings of Graphics Interface '86, стр. 77-81, май 1986 г. Фактически можно утверждать, что исключение Гаусса-Джордана - это демонстрация лифтинг-преобразования. Одной простой двухточечной операцией является преобразование Адамара, заданное матрицей преобразования
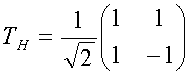 .
.
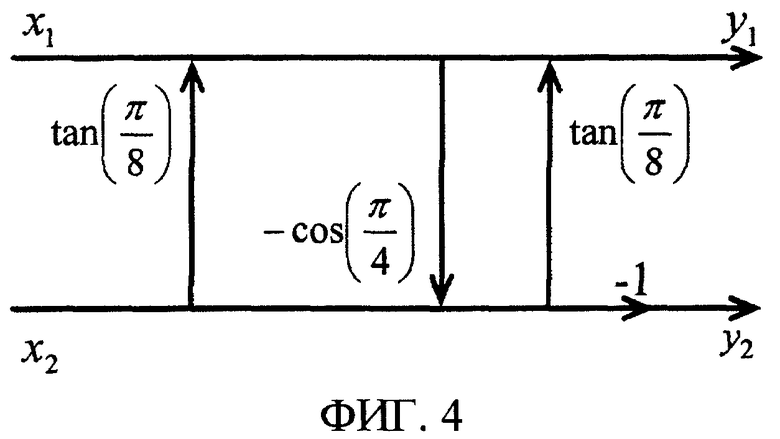
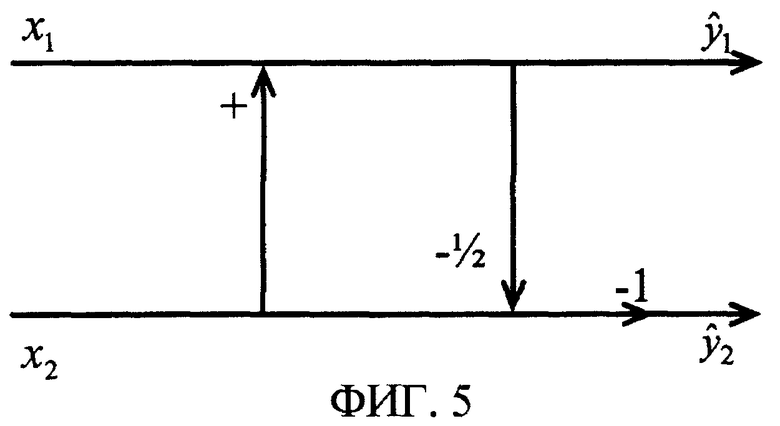
Два подхода, как правило, используются для реализации основанного на лифтинг-преобразовании (обратимого) одномерного преобразования Адамара. Первый заключается в том, чтобы реализовать нормированное или безмасштабное преобразование Адамара по этапам лифтинг-преобразования, как показано на фиг. 4. Второй подход заключается в том, чтобы разрешить масштабам различаться между двумя коэффициентами преобразования, как показано на фиг. 5.
Проблемы при лифтинг-преобразовании
Лифтинг-преобразование имеет свои проблемы. В первом подходе преобразования Адамара, показанном на фиг. 4, два коэффициента преобразования нормированы. Это желательно для реализации многостадийных преобразований, таких как четырех- или восьмиточечное DCT. Тем не менее, эта реализация имеет два основных недостатка - во-первых, каждое двухточечное преобразование Адамара требует трех нетривиальных (т.е. с большим объемом вычислений) этапов лифтинг-преобразования, а во-вторых, ошибки округления на этапах лифтинг-преобразования обуславливают "перетекание" низкочастотной энергии в высокочастотный терм, приводя к снижению эффективности сжатия. В этом первом подходе использование аппроксимации 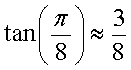 и
и 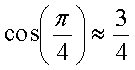 приводит к базисной функции переменного тока (АС) [0,75-0,7188]. Хотя расхождение с требуемым [0,7071-0,7071] не кажется слишком большим, сигнал постоянного тока (CD) амплитуды 64 генерирует АС отклик тока в 2 единицы, который перетекает в требующий больших ресурсов для кодирования диапазон высоких частот.
приводит к базисной функции переменного тока (АС) [0,75-0,7188]. Хотя расхождение с требуемым [0,7071-0,7071] не кажется слишком большим, сигнал постоянного тока (CD) амплитуды 64 генерирует АС отклик тока в 2 единицы, который перетекает в требующий больших ресурсов для кодирования диапазон высоких частот.
Второй подход (фиг. 5) использует этапы тривиального лифтинг-преобразования. Тем не менее, терм низких частот увеличивается на коэффициент 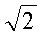 , тогда как терм высоких частот уменьшается на 1/
, тогда как терм высоких частот уменьшается на 1/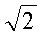 (или наоборот). Разрешение двух коэффициентов отличается на один бит. В двух измерениях терм "высокие-высокие" меньше по разрешению на 2 бита по сравнению с термом "низкие-низкие". Стадии каскадного преобразования только увеличивают это расхождение. Статистическое кодирование более сложно реализовать вследствие отличающихся диапазонов коэффициентов.
(или наоборот). Разрешение двух коэффициентов отличается на один бит. В двух измерениях терм "высокие-высокие" меньше по разрешению на 2 бита по сравнению с термом "низкие-низкие". Стадии каскадного преобразования только увеличивают это расхождение. Статистическое кодирование более сложно реализовать вследствие отличающихся диапазонов коэффициентов.
Обобщая, при основанных на лифтинг-преобразовании преобразованиях без потерь возникают следующие проблемы.
1. Возможно неравное масштабирование между коэффициентами преобразования, приводящее к более сложным механизмам статистического кодирования.
2. Неточные аппроксимации к требуемым базисным функциям преобразования, которые могут вызвать нежелательные эффекты, такие как перетекание DC частот в АС частоты.
3. Потенциально высокая вычислительная сложность, особенно если основанная на лифтинг-преобразовании реализация предназначена, чтобы хорошо аппроксимировать необходимое преобразование.
Сущность изобретения
Система кодера/декодера цифрового мультимедиа основана на раздельном двумерном блочном преобразовании, которое имеет множество реализаций, описанных в данном документе, которые разрешают вышеуказанные проблемы и недостатки преобразований предшествующего уровня техники. В частности, описанная реализация пары раздельного двумерного преобразования и его инверсии имеет последовательность этапов лифтинг-преобразования, предназначенных для снижения вычислительной сложности (т.е. уменьшения числа нетривиальных операций). Эта пара преобразования имеет свойства энергетического сжатия, аналогичные DCT, и также выполняется без потерь и является безмасштабной. Термин "без потерь" означает, что исходный целочисленный ввод в преобразование может быть восстановлен без ошибки посредством обратного преобразования на основе его целочисленных коэффициентов преобразования, предполагая отсутствие квантования. "Безмасштабное" относится к тому, что базисные функции пары преобразования имеют одинаковый масштаб, что также означает, что результирующая матрица преобразования является ортогональной.
Одной описанной реализацией этой пары преобразования является преобразование 4×4, но оно также может быть расширено до других размеров (к примеру, 8×8 и т.д.). Более того, каскады пары преобразования могут быть использованы, чтобы реализовать иерархические пирамиды и более крупные преобразования. Например, одна описанная реализация использует двухуровневый каскад преобразования. На второй стадии преобразования преобразование применяется к 16 DC коэффициентам, сгенерированным в рамках макроблока. Поскольку преобразование аналогично DCT, оно может быть использовано, чтобы реализовать кодек цифрового мультимедиа без потерь и с потерями (т.е. кодек, чей параметр квантования может быть варьирован от настройки без потерь до настроек с потерями) с хорошими рабочими характеристиками искажения в зависимости от скорости передачи и эффективностью сжатия.
Дополнительные признаки и преимущества станут более явными из последующего подробного описания вариантов осуществления, которое осуществляется со ссылками на прилагаемые чертежи.
Краткое описание чертежей
Фиг. 1 - блок-схема традиционного блочного основанного на преобразовании кодека согласно предшествующему уровню техники.
Фиг. 2 - блок-схема двумерного DCT 4×4, реализованного в две стадии, также согласно предшествующему уровню техники.
Фиг. 3 - сигнальный ориентированный граф одномерного DCT 4×4, также согласно предшествующему уровню техники.
Фиг. 4 - сигнальный ориентированный граф нормированного 2-точечного преобразования Адамара с использованием лифтинг-преобразования, также согласно предшествующему уровню техники.
Фиг. 5 - сигнальный ориентированный граф тривиального 2-точечного преобразования Адамара, также согласно предшествующему уровню техники.
Фиг. 6 - блок-схема работы кодера, основанного на усовершенствованном обратимом двумерном преобразовании.
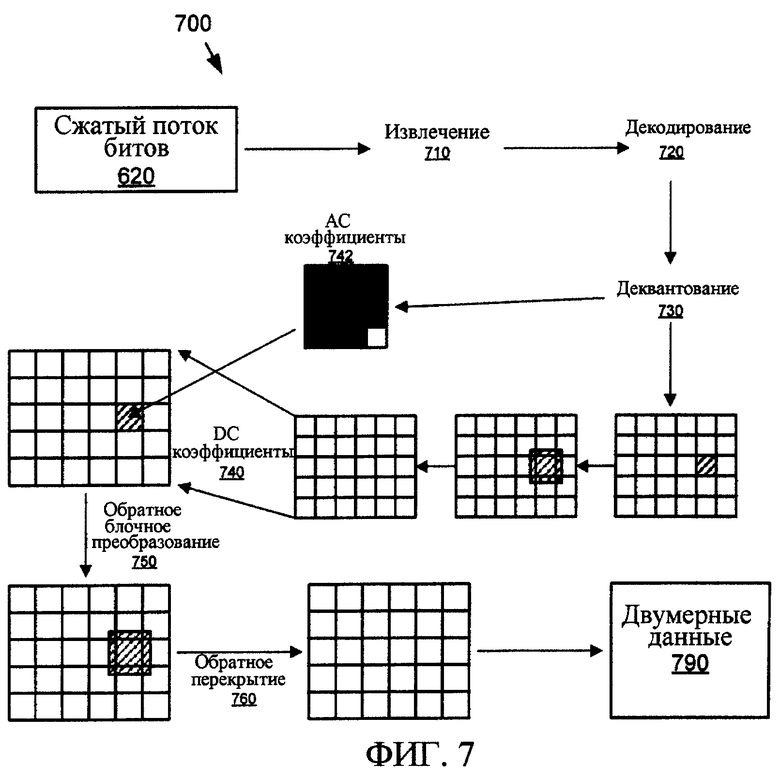
Фиг. 7 - блок-схема работы декодера, основанного на усовершенствованном обратимом двумерном преобразовании.
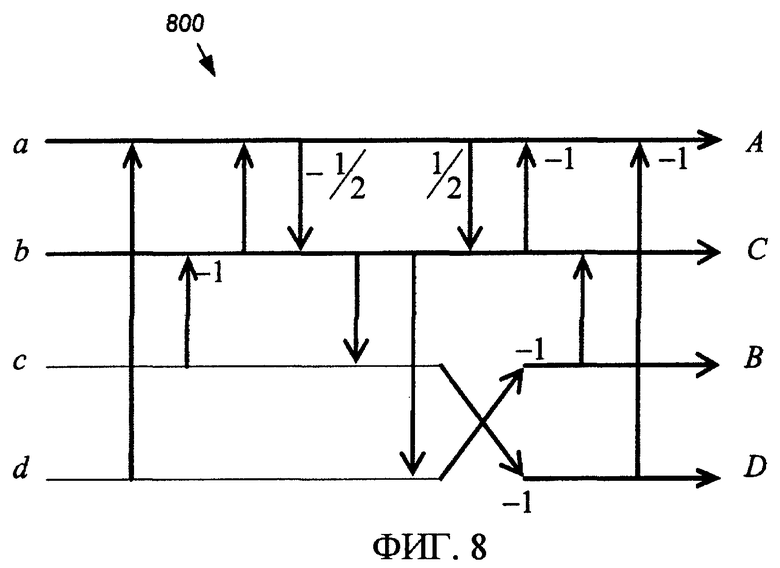
Фиг. 8 - сигнальный ориентированный граф нормированной основанной на лифтинг-преобразовании реализации обратимого преобразования Адамара 2×2.
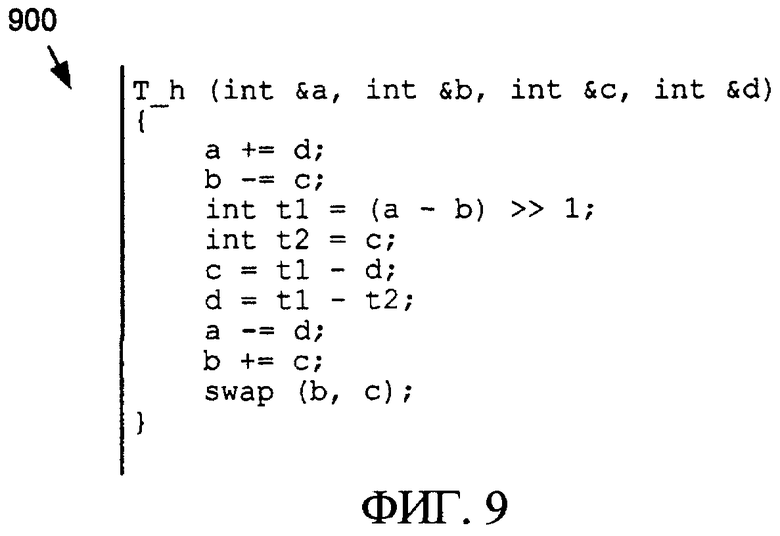
Фиг. 9 - листинг программы на языке программирования C для реализации нормированного обратимого преобразования Адамара 2×2 по фиг. 8.
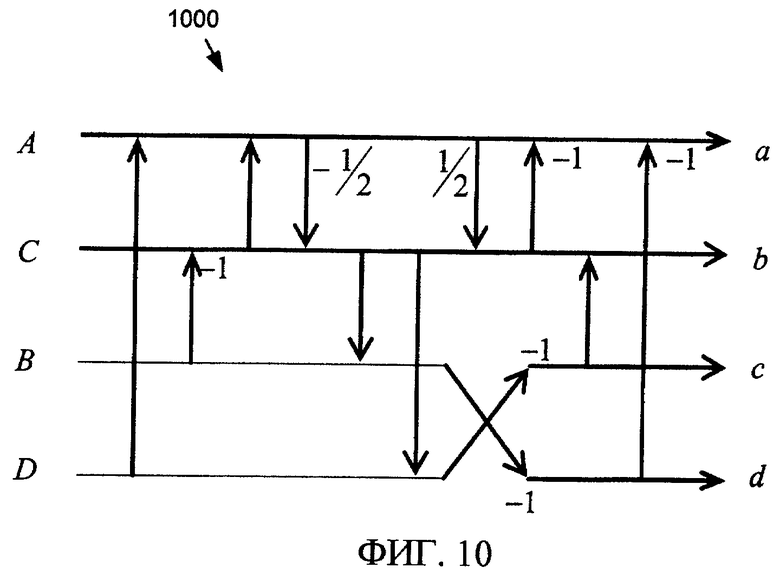
Фиг. 10 - сигнальный ориентированный граф нормированного обратимого преобразования Адамара по фиг. 8.
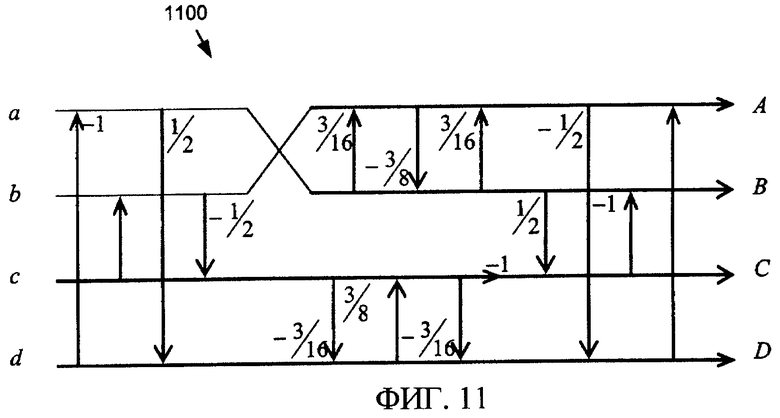
Фиг. 11 - график потока сигналов ориентированный граф нормированной основанной на лифтинг-преобразовании реализации преобразования Todd.
Фиг. 12 - листинг программы на языке программирования C для реализации нормированного преобразования Todd по фиг. 11.
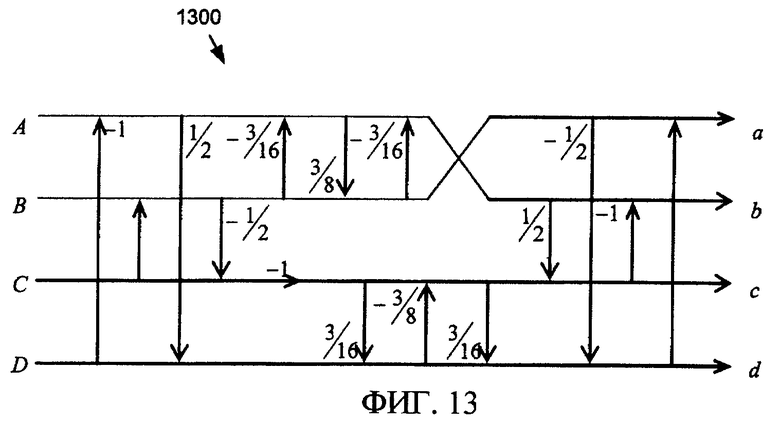
Фиг. 13 - сигнальный ориентированный граф нормированной основанной на лифтинг-преобразовании версии инверсии преобразования Todd по фиг. 11.
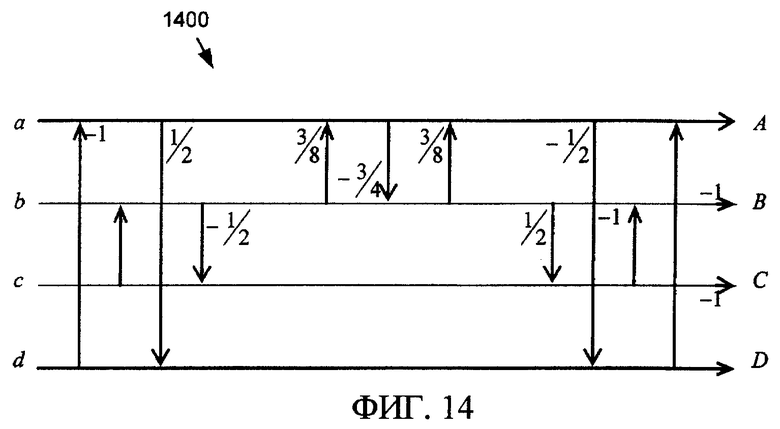
Фиг. 14 - сигнальный ориентированный граф нормированной основанной на лифтинг-преобразовании реализации преобразования Todd-odd.
Фиг. 15 - листинг программы на языке программирования C для реализации нормированного преобразования Todd-odd по фиг. 14.
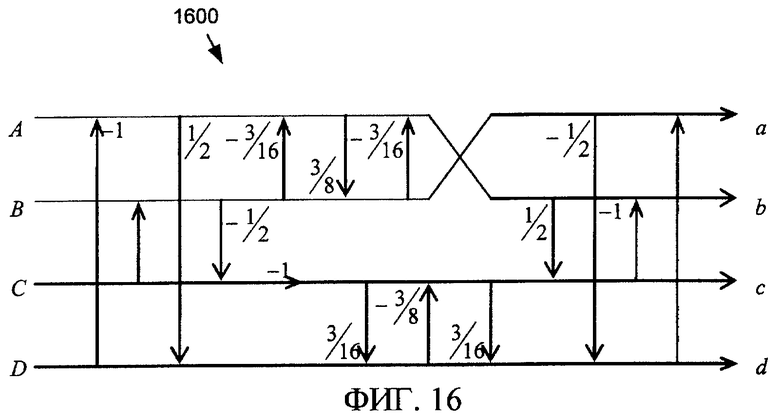
Фиг. 16 - сигнальный ориентированный граф нормированной основанной на лифтинг-преобразовании версии инверсии преобразования Todd-odd по фиг. 14.
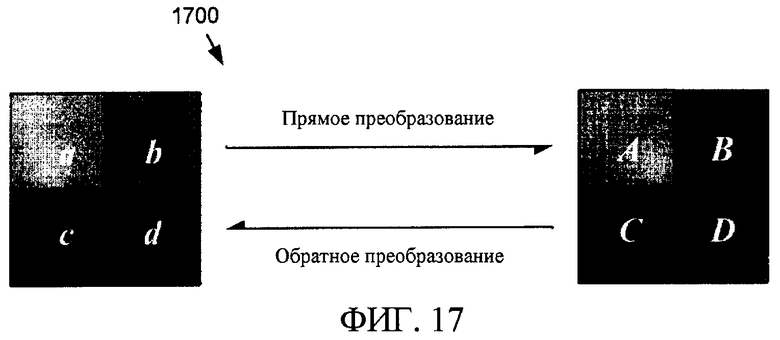
Фиг. 17 - схема, иллюстрирующая упорядочивание данных 2×2 в приведенных здесь иллюстрациях операций преобразования и обратного преобразования.
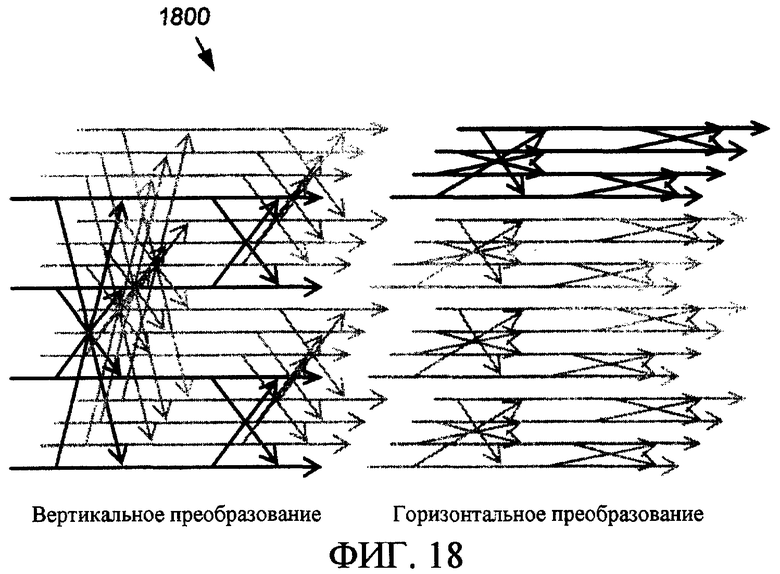
Фиг. 18 - график потока сигналов ориентированный граф, иллюстрирующий двумерное DCT, реализованное раздельно как одномерное вертикальное DCT и одномерное горизонтальное DCT, примененное к столбцам и строкам соответственно, ввода данных 4×4.
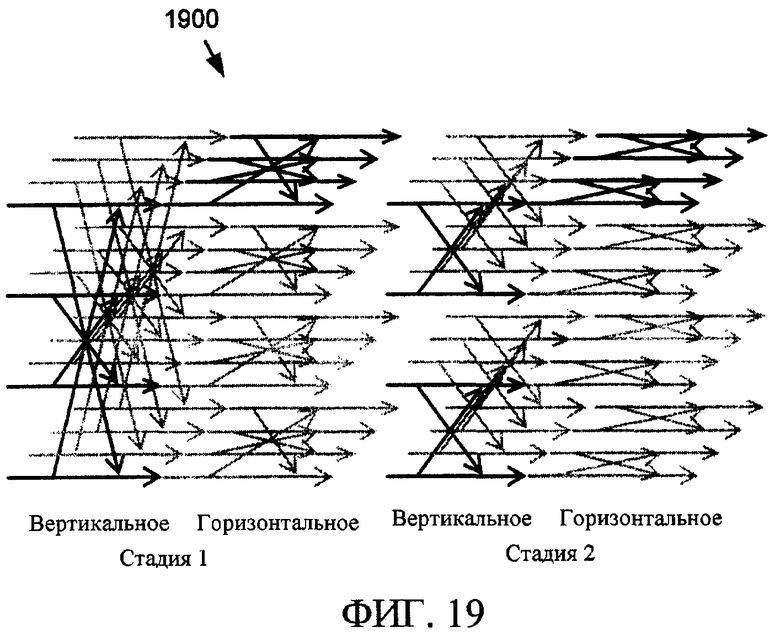
Фиг. 19 - сигнальный ориентированный граф, иллюстрирующий обратимое безмасштабное двумерное преобразование, реализованное посредством чередования операций горизонтального и вертикального преобразования в две стадии.
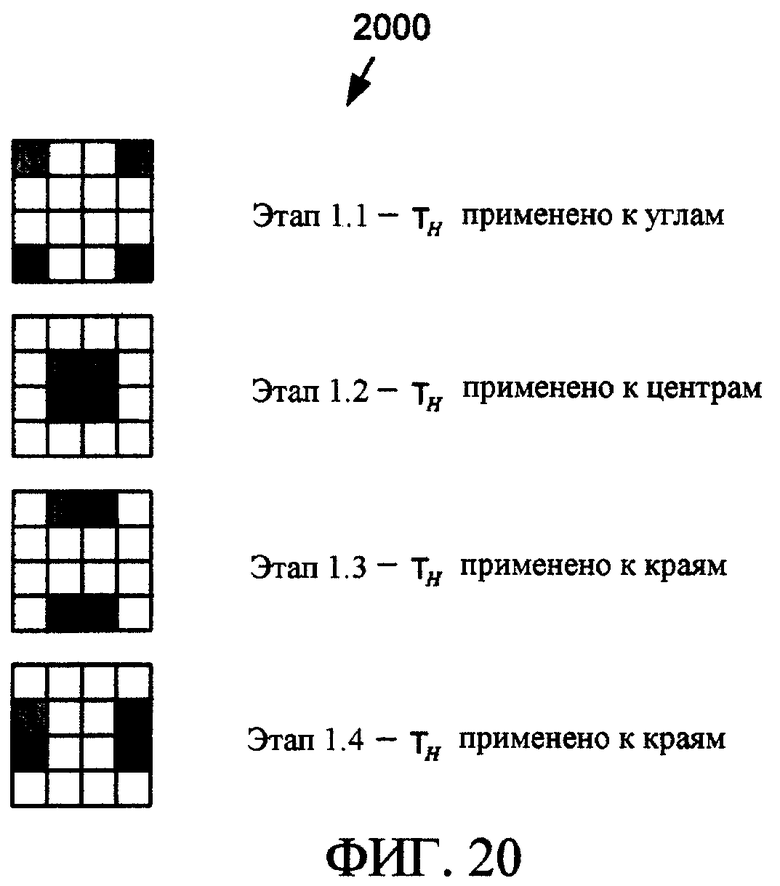
Фиг. 20 - схема, иллюстрирующая точки блока данных 4×4, к которому применено преобразование Адамара 2×2 по фиг. 8 на первой стадии усовершенствованного обратимого двумерного преобразования в кодере по фиг. 6.
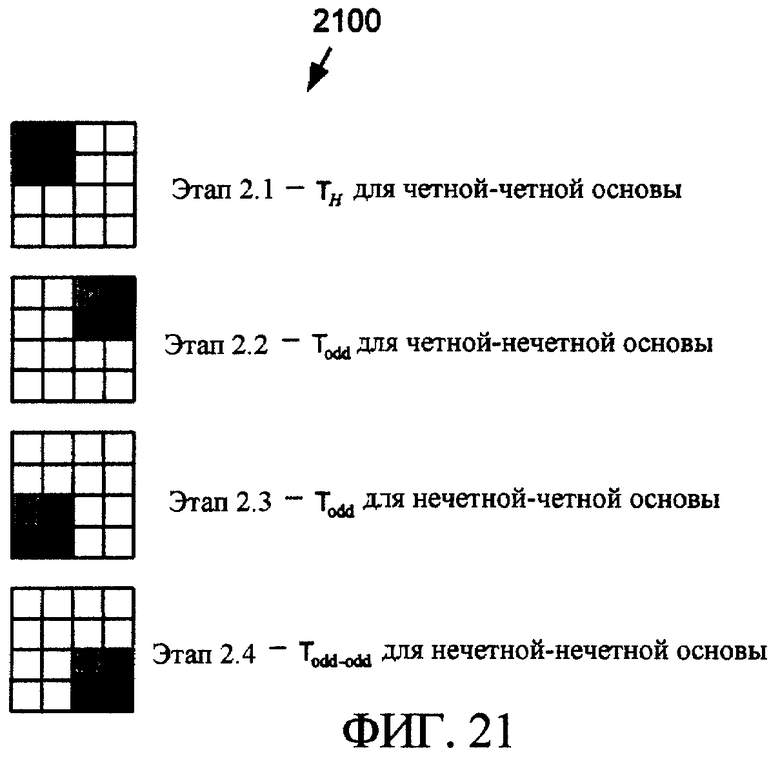
Фиг. 21 - схема, иллюстрирующая точки блока данных 4×4, к которому применено преобразование Адамара 2×2 по фиг. 8, преобразование Todd по фиг. 11 и преобразование Todd-odd по фиг. 14 на второй стадии реализации усовершенствованного обратимого двумерного преобразования в кодере по фиг. 6.
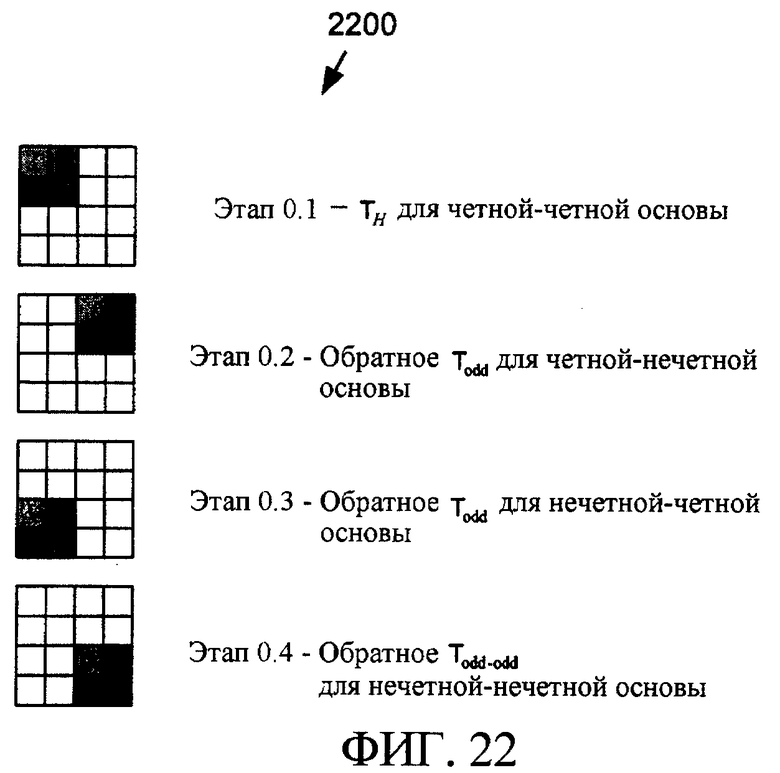
Фиг. 22 - схема, иллюстрирующая точки блока коэффициентов преобразования 4×4, к которому применено преобразование Адамара 2×2 по фиг. 8, преобразование Todd по фиг. 11 и преобразование Todd-odd по фиг. 14 на первой стадии реализации обратимого двумерного преобразования в декодере по фиг. 7.
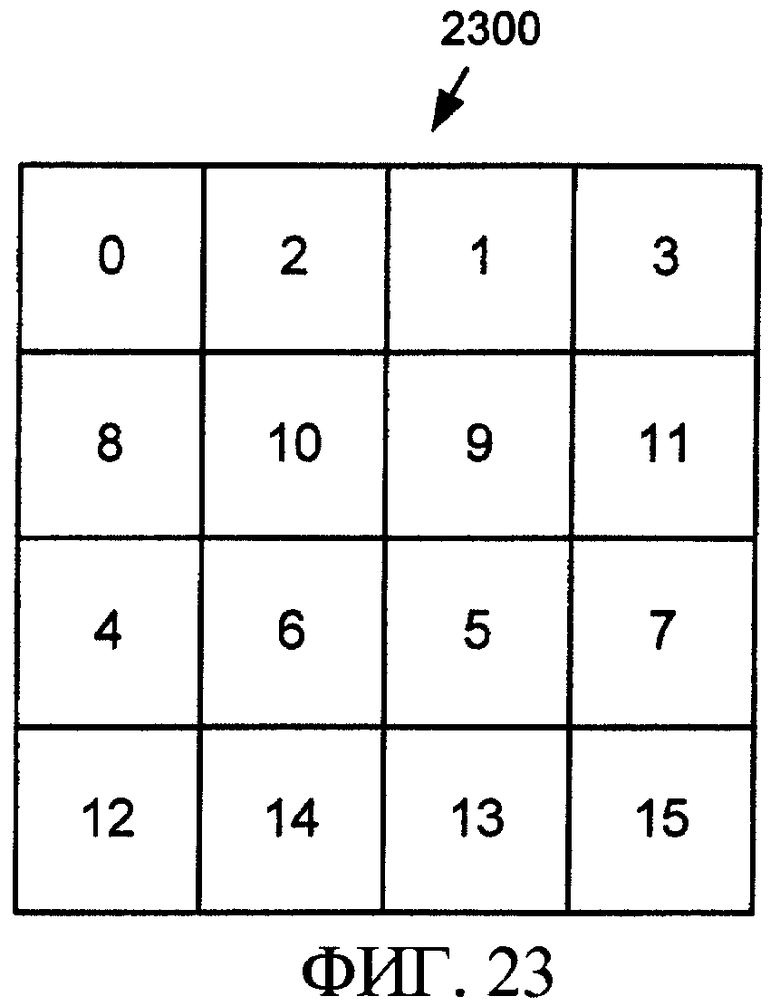
Фиг. 23 - схема, иллюстрирующая упорядочивание коэффициентов преобразования для прямого и обратного двумерного преобразования в кодере по фиг. 6 и декодере по фиг. 7.
Фиг. 24 - блок-схема подходящей вычислительной среды для реализации блочного основанного на преобразовании кодека с усовершенствованным перекрывающимся преобразованием пространственной области по фиг. 6 и 7.
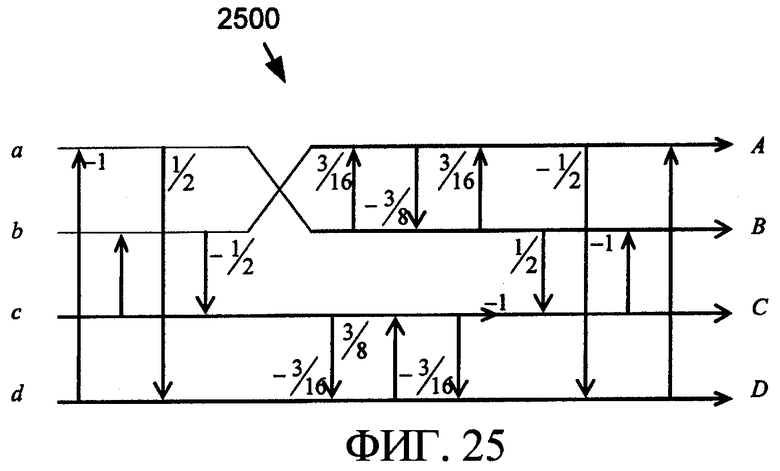
Фиг. 25 - сигнальный ориентированный граф структуры нормированной основанной на лифтинг-преобразовании реализации обратимых двумерных преобразований, показанных на фиг. 11 и 14.
Подробное описание изобретения
Последующее описание относится к системе сжатия или кодеку цифрового мультимедиа, который использует усовершенствованное обратимое безмасштабное двумерное преобразование. В целях иллюстрации вариантом осуществления системы сжатия, содержащей в себе усовершенствованное преобразование, является система сжатия изображений или видео. Альтернативно, усовершенствованное преобразование также может быть включено в системы сжатия или кодеки для других двумерных данных. Преобразование не требует, чтобы система сжатия цифрового мультимедиа кодировала сжатые цифровые мультимедийные данные в конкретном формате кодирования.
1. Кодер/декодер
Фиг. 6 и 7 - это обобщенная диаграмма процессов, используемых в репрезентативном кодере 600 и декодере 700 двумерных (2D) данных, основанном на усовершенствованном обратимом безмасштабном двумерном преобразовании 650, подробно описанном ниже. Эти схемы представляют обобщенную или упрощенную иллюстрацию использования и применения данного преобразования в системе сжатия, включающей в себя кодер и декодер двумерных данных. В альтернативных кодерах, основанных на этом преобразовании, дополнительное или меньшее число процессов, чем проиллюстрировано в репрезентативном кодере и декодере, может быть использовано для сжатия двумерных данных. Например, некоторые кодеры/декодеры могут также включать в себя цветовое преобразование, форматы цветов, масштабируемое кодирование, кодирование без потерь, режимы макроблоков и т.д. Усовершенствованное двумерное преобразование разрешает системе сжатия (кодеру и декодеру) предоставлять кодирование двумерных данных без потерь и/или с потерями, в зависимости от квантования, которое может быть основано на параметре квантования, варьирующемся от режима “без потерь” до режима “с потерями”.
Кодер 600 двумерных данных генерирует сжатый поток 620 битов, который является более компактным представлением (для типичного ввода) двумерных данных 610, представляемых в качестве входа кодеру. Например, вводом двумерных данных может быть изображение, кадр видеопоследовательности или другие данные, имеющие два измерения. Кодер двумерных данных разбивает 630 входные данные на макроблоки, которые имеют размер 16×16 пикселей в данном репрезентативном кодере. Кодер двумерных данных дополнительно разбивает макроблок на блоки 632 4×4. Оператор 640 "прямого перекрытия" применяется к каждому краю между блоками, после чего каждый блок 4×4 преобразуется с помощью обратимого безмасштабного преобразования 650. Далее DC коэффициент 660 каждого блока преобразования 4×4 подлежит аналогичной цепочке обработки (разбиение, прямое перекрытие, за которым следует преобразование блоков 4×4). В отношении результирующих DC коэффициентов преобразования выполняются квантование 670, статистическое кодирование 680 и пакетирование 690.
Декодер выполняет обратный процесс. На стороне декодера биты коэффициентов преобразования извлекаются 710 из своих соответствующих пакетов, на основе которых сами коэффициенты декодируются 720 и деквантуются 730. DC коэффициенты 740 регенерируются посредством применения обратного преобразования, и плоскость DC коэффициентов "перекрывается в обратном порядке" с помощью подходящего сглаживающего оператора, применяемого по краям блока DC. В дальнейшем все данные регенерируются посредством применения обратного преобразования 750 4×4 к DC коэффициентам, и АС коэффициенты 742 декодируются из потока битов. Наконец, края блока в плоскостях результирующих изображений фильтруются 760 с помощью обратного перекрытия. Это дает на выходе восстановленные двумерные данные.
2. Реализация усовершенствованного обратимого безмасштабного преобразования
Как описано, к примеру, в A. K. Jain "Fundamentals of Digital Image Processing". Prentice Hall, 1989 г., раздельное двумерное преобразование может быть реализовано как одномерное преобразование, работающее в отношении данных, упорядоченных одномерно, генерируя также упорядоченный векторный результат. Матрица эквивалентного преобразования генерируется произведением Кронекера умножения справа и слева множителей, используемых в раздельном случае. Если x и y означают векторы данных и преобразования, переупорядоченные из своего двумерного представления в (2), их соотношение задается следующим образом:
y=Tx, (3)
где T = Kron(T 1, T 2).
Хотя раздельная реализация двумерного преобразования, показанная в уравнении (2), вычислительно более эффективна (в асимптотическом смысле), чем в уравнении (3), существуют определенные случаи, когда последнее представление приводит к требуемым свойствам. Например, реализация, основанная на уравнении (3), имеет меньшую задержку, чем в уравнении (2), благодаря одностадийному перемножению матриц (которое является операцией, поддерживаемой изначально на нескольких процессорах цифровых сигналов (DSP)). Для усовершенствованного обратимого безмасштабного преобразования, описанного в данном документе, одномерное представление этапов 2×2 приводит к безмасштабной обратимой структуре.
Более того, раздельное двумерное преобразование может быть реализовано как каскад более простых одномерных преобразований. Предположим, что матрицы преобразования T 1 и T 2 могут быть разложены на составные части следующим образом:
T 1 = T 1A T 1B
T 2 = T 2A T 2B
Ассоциативность операции перемножения матриц может быть использована, чтобы переупорядочить двумерное преобразование (2) следующим образом:
= T
1A
T
1B X T'
2B
T'
2A =
= T
1A (T
1B
X T'
2B)T'
2A
приводя к каскадной одномерной реализации
Преобразования, такие как DCT, могут быть сформулированы как каскад элементарных двухточечных операций поворота. Двумерное DCT может быть сформулировано с помощью структуры (6), чтобы обладать определенными требуемыми свойствами, которые подробнее описаны далее.
А. Двумерное преобразование Адамара
Двумерное преобразование Адамара, реализованное как одномерная операция, генерируется произведением Кронекера,
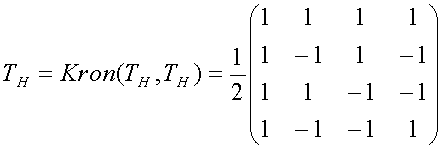
Интересно, что можно реализовать безмасштабное обратимое преобразование, соответствующее уравнению (7), используя только этапы тривиального лифтинг-преобразования. Реализация этой формы показана в качестве сигнального ориентированного графа 800 на фиг. 8. Соответствующий код C++, исключая некоторые избыточные операции, показан на фиг. 9. В этом листинге 900 кода функция "swap(x,y)" - это функция, которая меняет значения своих аргументов.
Из вышеописанного можно видеть, что нормированное обратимое двумерное преобразование Адамара может быть сформулировано только с помощью этапов тривиального лифтинг-преобразования, хотя это невозможно для, вероятно, "более простого" случая одномерного преобразования Адамара! Хотя матрица преобразования сама является инволютивной (т.е. T H совпадает с собственной обратной матрицей), восстановление без потерь требует, чтобы этапы лифтинг-преобразования были тщательно реверсированы так, чтобы точно генерировать любые эффекты округления. Инверсия 1000 структуры 800 на фиг. 8 представлена на фиг. 10 - структура 1000 идентична прямому преобразованию в данном случае. Заметим, что коэффициенты преобразования B и C переставлены в сигнальных ориентированных графах.
Обратимое безмасштабное двумерное преобразование 650 в кодере 600 по фиг. 6 использует аппроксимацию к DCT 4×4. Последующее описание демонстрирует, что весь процесс преобразования 650 может быть реализован как каскад трех элементарных операций преобразования 2×2, которые являются преобразованием Адамара 2×2, и следующие:
Нечетное (odd) преобразование поворота: Y = T R X T' H
Нечетное-нечетное (odd-odd) преобразование поворота:
где двухточечная матрица вращения TR задана как
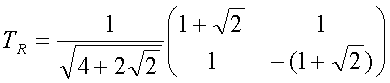
одномерные реализации уравнения (8) получаются посредством вычисления произведения Кронекера матриц преобразования (аппроксимированных до четырех десятичных знаков), являющихся множителями слева и справа

и
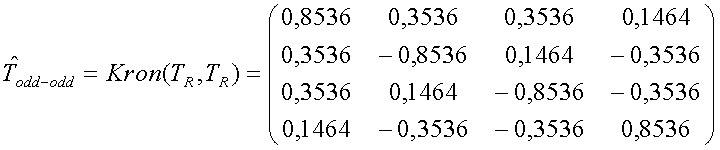
Символ “^” означает требуемую матрицу преобразования. Преобразования, получающиеся из фактических реализаций, не имеют этого символа. Для преобразования Адамара 2×2 требуемая матрица преобразования и ее аппроксимация идентичны. Поэтому TH используется, чтобы означать преобразование Адамара 2×2, реализованное одномерно, без какой-либо неопределенности. Далее мы рассмотрим реализацию лифтинг-преобразования в Todd и Todd-odd.
B. Реализация T odd
Безмасштабная основанная на лифтинг-преобразовании реализация преобразования 1100 Todd показана как сигнальный ориентированный граф на фиг. 11 и в листинге 1200 программы кода C++ на фиг. 12. Можно видеть, что первая и последняя стадии лифтинг-преобразования идентичны случаю преобразования Адамара. Помимо тривиальных сдвигов два нетривиальных поворота с лифтинг-преобразованием применяются на промежуточных стадиях. Каждый нетривиальный поворот реализован в трех этапах, с умножением на 3 и битовым сдвигом на 3 или 4 бита. Поэтому Todd может быть реализовано обратимым безмасштабным способом посредством использования 6 этапов нетривиального лифтинг-преобразования.
Получившаяся матрица Todd одномерного преобразования показана ниже (12), она находится в близком соответствии с исходной формулировкой ^Todd в (10). Можно видеть, что вторая и четвертая строки получившейся матрицы преобразования в сумме дают ноль, что означает, что нет перетекания постоянного тока в полосы переменного тока. Это требуемое свойство получается несмотря на то, что требуемые двумерные вращения просто аппроксимированы в структуре.
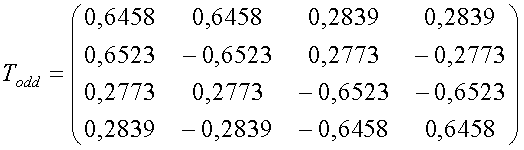
Хотя матрица преобразования Todd является инволютивной (т.е. совпадает с собственной инверсией), ошибки округления не компенсируются в двух последовательных применениях сигнального ориентированного графа или кода. Инверсия Todd без потерь получается посредством реверсирования этапов лифтинг-преобразования либо в сигнальном ориентированном графе, либо в коде C++, чтобы реплицировать ошибки округления при прямом преобразовании. Сигнальный ориентированный граф инверсии 1300 Todd показан на фиг. 13 - код может быть получен аналогично.
C. Реализация T odd-odd
Преобразование 1400 Todd-odd составлено из двух поворотов, ни один из которых не является преобразованием Адамара. Интересно, что Todd-odd может быть реализовано с помощью меньшего числа этапов лифтинг-преобразования, чем Todd. Это обусловлено свойствами симметрии произведения Кронекера T R с собой. Сигнальный ориентированный граф преобразования 1400 Todd-odd и листинг 1500 программы его реализации в коде C++ показаны на фиг. 14 и 15 соответственно.
Можно видеть, что только один нетривиальный поворот, реализованный посредством трех этапов нетривиального лифтинг-преобразования, требуется, чтобы реализовать Todd-odd. Этот поворот соответствует безмасштабному одномерному двухточечному преобразованию Адамара.
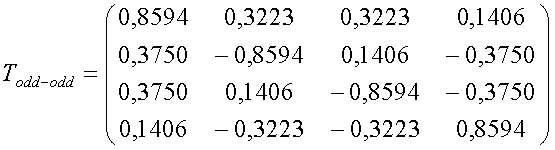
Как и в случае других рассмотренных здесь преобразований, Todd-odd, как представлено в уравнении (13), является инволютивной, хотя и не является точной до бита инверсией себя. Инверсия 1600 без потерь Todd-odd получается посредством реверсирования сигнального ориентированного графа, используемого для прямого преобразования, как показано на фиг. 16.
D. Представление и получение вышеописанных реализаций преобразований 2×2
В приведенных здесь иллюстрациях обратимого безмасштабного двумерного преобразования с помощью этих трех обратимых двумерных преобразований применяются следующие точки. Во-первых, упорядочивание 1700 данных 2×2, приводящее к вышеуказанным сигнальным ориентированным графам и коду C++, выполняется так, как показано на фиг. 17. Точки пространственной области показаны слева, а соответствующие точки частотной области - справа. Цветовое кодирование с помощью четырех уровней серого, чтобы указывать четыре точки данных, введено здесь, чтобы облегчить описание обратимого безмасштабного двумерного преобразования, которое следует далее.
Часто двухточечные преобразования или повороты задаются как следующая операция:
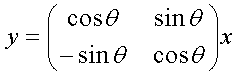
вместо инволютивной формы
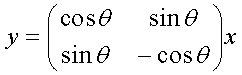
Эти две формы по сути идентичны, поскольку они отличаются только в знаке второго коэффициента преобразования. Здесь используется второе представление (15), хотя все рассмотрение в данном документе в равной степени применимо к первой форме (14).
Структура базовых преобразований 2×2, TH, Todd и Todd-odd, заданных выше, составляется посредством отмечания того, что каждое двухточечное преобразование является поворотом. Дополнительно произведение Кронекера двух двухточечных поворотов задается следующим образом:
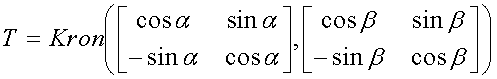
Затем мы задаем оператор H следующим образом:
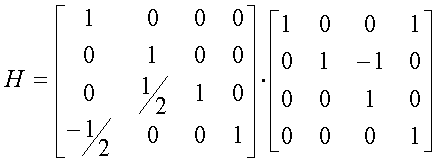
H представляет ненормированную операцию двойной "бабочки" и может быть эффективно реализован с помощью лифтинг-преобразования.
Выполняется следующая факторизация:
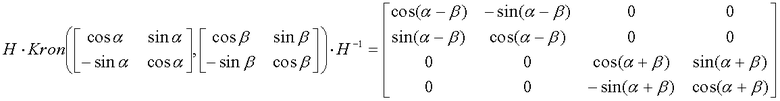
На ее основе произведение Кронекера типа Т может быть реализовано как каскад из 3 стадий.
A. Операция двойной "бабочки", заданная оператором H с помощью этапов лифтинг-преобразования.
B. Двухточечные повороты между первой парой компонентов и между второй парой компонентов.
C. Обращение двойной "бабочки", выполненной на этапе A.
Для специального случая TH предусмотрено даже более простое разложение, которое показано в качестве сигнального ориентированного графа 800 на фиг. 8 и описано выше. Для других случаев (к примеру, Todd и Todd-odd) результирующая структура может быть обобщена как ориентированный граф 2500, показанный на фиг. 25.
Если посмотреть на три сигнальных ориентированных графа преобразований, описанных выше (а также их инверсий), можно заметить фундаментальную схожесть в их структуре. Первая стадия преобразования - это операция лифтинг-преобразования между коэффициентами a-d и b-c. Также последняя стадия - это процесс обратного лифтинг-преобразования (опуская знак и перемены коэффициентов). Соответственно первая стадия обратного преобразования - это операция лифтинг-преобразования между A и D, а также между B и C, с обратной операцией на последней стадии. Этапы лифтинг-преобразования между диагональными элементами - это отличительный признак объединенного двумерного преобразования 2×2, представленного здесь.
В следующем разделе обсуждается составление безмасштабного преобразования без потерь, которое аппроксимирует DCT/IDCT 4×4. Хотя примерный вариант осуществления преобразования показан в этом подробном техническом описании, аналогичная процедура с дополнительным определением других элементарных обратимых основанных на лифтинг-преобразовании преобразований 2×2 может быть использована, чтобы сгенерировать варианты осуществления обратимого преобразования с большим числом измерений с требуемыми свойствами.
E. Безмасштабное преобразование без потерь
Четырехточечное DCT может быть уменьшено до последовательности четырех операций "бабочки", как показано на сигнальном ориентированном графе по фиг. 3. Первая стадия состоит из двух "бабочек", выполняющих двухточечные операции Адамара над входными данными (т.е. одно двухточечное преобразование Адамара с индексами 0 и 3 входных данных; и второе с индексами 1 и 2 входных данных). Вторая стадия содержит двухточечную операцию Адамара над низкочастотными результатами первой стадии, чтобы сгенерировать четные частотные компоненты (индексы 0 и 2), и двухточечное вращение на π/8, чтобы сгенерировать нечетные частотные компоненты (индексы 1 и 3).
В двух измерениях DCT может быть реализован раздельно: вертикальное одномерное четырехточечное DCT каждого столбца входных данных 4×4, за которым следует горизонтальное одномерное четырехточечное DCT строк (или наоборот). Это изображено как раздельная реализация 100 DCT на фиг. 18. Альтернативно, две описанные выше стадии одномерного DCT могут чередоваться между вертикальным и горизонтальным, используя теорию уравнения (5), как показано в качестве реализации 1900 чередующегося DCT на фиг. 19.
Более того, при следовании вышеуказанному подходу соответствующие горизонтальные и вертикальные стадии могут быть дополнительно объединены. Например, первая стадия - это двухточечное преобразование Адамара в отношении "внутренних" и "внешних" входных элементов. Горизонтальная и вертикальная стадии могут быть объединены вместе в 4 применениях двумерного преобразования Адамара 2×2 в отношении 16 элементов входных данных, причем каждое преобразование применяется к симметричному набору входных точек. Также горизонтальная и вертикальная стадии второго этапа могут быть объединены в преобразование Адамара 2×2 и три преобразования 2×2, два из которых являются транспонированием. Заметим, что последние три преобразования 2×2 на самом деле являются двумерными переотображениями Todd и Todd-odd, заданных ранее.
Более конкретно, обратимое безмасштабное двумерное преобразование 650 (фиг. 6) реализуется посредством перегруппировки операций преобразования в схему преобразований Адамара 2×2, Todd и Todd-odd. Две стадии этого преобразования 650 выполняются, как показано на фиг. 20 и 21 соответственно. Каждая стадия состоит из четырех преобразований 2×2, которые могут быть выполнены в произвольной последовательности или параллельно в рамках стадии.
Для обратного двумерного преобразования 750 (фиг. 7) стадии реверсируются надлежащим образом, и этапы в рамках каждой стадии преобразования используют инверсию этапов процесса прямого преобразования. Как указывалось ранее, обратимое преобразование Адамара 2×2 T H является собственной инверсией, в смысле побитовой точности или без потерь. Поэтому вторая стадия обратного преобразования Фотона - это просто первая стадия прямого преобразования Фотона, как показано на фиг. 20. Первая стадия 2200 обратного преобразования Фотона изображена на фиг. 22. Четыре этапа в рамках этой стадии (которые, как и для случая прямого преобразования, могут быть исполнены в произвольном порядке или параллельно) применяют инверсии T H, Todd и Todd-odd, как задано ранее, и переотображаются обратно в двумерное пространство 2×2.
После выполнения этапов прямого усовершенствованного двумерного преобразования, показанных на фиг. 20 и 21, получившиеся коэффициенты преобразования упорядочиваются, как показано на фиг. 23. То же упорядочивание 2300 предполагается для коэффициентов, инверсно преобразованных с помощью этапов на фиг. 22 и 20, в этом порядке.
Вышеописанная усовершенствованная реализация прямого двумерного преобразования 650 состоит из пяти применений T H, двух применений Todd и одного применения Todd-odd к каждому блоку 4×4. То же число применений этих преобразований вовлечено в реализацию обратного двумерного преобразования 750. Следовательно, общее число этапов нетривиального лифтинг-преобразования равно 5×0+2×6+1×3 = 15 для каждого блока, чтобы реализовать прямое или обратное двумерное преобразования без потерь. Это около 1 нетривиального этапа на пиксель. Нетривиальный этап - это операция формы (3 × x + r) >> k, где x - это операнд, r и k - это ограничения, определяющие округление и битовый сдвиг, k равно 2, 3 или 4. Также предусмотрено 17 одноместных сдвигов вправо (т.е. x >> 1) на блок. Сложения, вычитания и отрицания не учитываются в данном обзоре.
Для сравнения рассмотрим раздельную реализацию 1800 двумерного DCT, проиллюстрированную на фиг. 18. Допустим, что каждое четырехточечное DCT реализуется с помощью трех двухточечных нормированных операций Адамара, как показано на фиг. 3, и поворот на π/8 реализован с помощью трех этапов нетривиального лифтинг-преобразования. Общее число операций нетривиального лифтинг-преобразования на блок 4×4 для прямого или обратного преобразования составляет 2×4×3 = 24. Общее число одноместных сдвигов вправо также составляет 24. Эти числа примерно на 50% выше, чем в усовершенствованных реализациях прямого преобразования 650 и обратного преобразования 750, не учитывая тот факт, что результирующее преобразование генерирует базисные функции с нормами в диапазоне от 1/4 до 2 (или до 4, если исключаются базисные функции иррационального диапазона). Наоборот, все базисные функции усовершенствованного преобразования 650 являются единичными нормами.
F. Усовершенствованное преобразование для цветового пространства 4:2:0
В одной примерной реализации кодера 600 (фиг. 6) и декодера 700 (фиг. 7) цветовое пространство YUV 4:2:0 используется, чтобы представлять цвет пикселей в изображении (или видеокадре). В данном примере кодека макроблок в цветовом пространстве YUV 4:2:0 задается как мозаика 16×16 пикселей в канале сигнала яркости (Y) и мозаика 8×8 в каналах сигналов цветности (U и V). Они дополнительно делятся на блоки 4×4, которые кодируются с преобразованием, используя вышеописанное преобразование 650. Преобразование 650 4×4 применяется к DC коэффициентам каналов сигнала яркости. Тем не менее, только выборки 2×2 цветности доступны в макроблоке. Примерный кодек затем применяет TH, которым, как описано выше, является обратимое безмасштабное преобразование Адамара 2×2, к значениям цветности постоянного тока в каждом макроблоке. Таким образом, структура макроблока формата примерного кодека сохраняется, и дополнительные преобразования не должны быть введены в кодеке для обработки формата 4:2:0.
G. Минимизация ошибок округления
Ошибки округления появляются в этапах лифтинг-преобразования преобразований TH, Todd и Todd-odd, которые влекут за собой битовый сдвиг вправо. Эти ошибки округления имеют известное смещение и могут нарастать в ходе преобразования. Например, известно, что этап формы x+ = (y >> 1) приводит к смещению на -1/4 в значении x по сравнению с его математическим эквивалентом x:= x + y/2. Это обусловлено тем, что (y >> 1) - это деление на 2 с округлением в меньшую сторону, которое является точным, если y - четное число, и смещается на 1/2, если y - нечетное число. С вероятностной точки зрения, оно смещается на -1/4. Ошибок округления нельзя избежать в преобразованиях целое-в-целое, задействующих лифтинг-преобразование, но желательно минимизировать смещение в системе в целом.
Формулировки T H, Todd и Todd-odd, показанные выше как фрагменты кода C++, добавляют переменные коэффициенты в операнды, которые делятся или битово сдвигаются вправо. Эти коэффициенты выбираются таким образом, чтобы минимизировать смещение. В частности, можно показать, что смещение в четырех коэффициентах преобразования после операции первой стадии T H (к несмещенному вводу) с помощью листинга 900 кода C++ на фиг. 9 составляет [1/4 -1/4 -1/4 -1/4]. Применение на второй стадии T H в усовершенствованном двумерном преобразовании 650 (фиг. 6) оперирует с DC значениями первой стадии, т.е. с коэффициентами, которые уже смещены на 1/4. Результат операции на второй стадии генерирует смещение в [3/4 -1/4 -1/4 -1/4]. Поскольку первый коэффициент - это DC постоянного тока, он, как ожидается, будет иметь большое значение, и относительно высокое смещение в 3/4 не влияет на эффективность кодирования.
Этапы нетривиального лифтинг-преобразования в Todd и Todd-odd предоставляют свободу выбирать коэффициенты округления для минимизации смещения при преобразовании. Листинг 1500 кода C++ (фиг. 15) для Todd-odd показывает, что иногда нецентральные правила округления (например, a+ = (3 b + 5) >> 3) приводят к меньшему общему смещению, особенно в тех случаях, когда входные данные смещены сами. Для этапов усовершенствованного двумерного преобразования Todd и Todd-odd все входы смещены на -1/4.
В типичном случае задание кодека ограничено заданием декодера потока битов. Исключение из этого правила делается для кодеков без потерь, поскольку кодер и декодер должны точно соответствовать друг другу для того, чтобы входные данные были восстановлены без потерь. В случае кодека с переключением между зажимами “с потерями” и “без потерь” это задается и на стороне кодера, и на стороне декодера. Тем не менее, когда с кодером осуществляются действия только в режиме “с потерями”, некоторые сокращения или улучшения могут быть допустимы, которые обеспечивают лучшую производительность (в показателях искажения в зависимости от скорости передачи или показателя вычислительных циклов), чем базовая производительность, заданная в спецификации кодека.
Одно средство повышения производительности кодера относится к смещению коэффициента преобразования. Можно уменьшить эффект смещения в некоторых вариантах осуществления кодера 600/декодера 700 посредством выполнения следующей процедуры для каждого блока 4×4.
1. Увеличить размер блока 4×4 посредством умножения на m = 2 k (в типичном случае хорошо подходит m = 4).
2. Выполнить усовершенствованное двумерное преобразование 650 над блоком.
3. Квантовать блок с помощью квантователя, который в m раз превышает исходный требуемый параметр квантования (например, использовать коэффициент квантования (QP) в 32, если требуемое значение QP равно 8, а m = 4 на этапе 1).
На стороне декодера 700 изменений нет, хотя более оптимальные значения PSNR возможны при той скорости передачи битов. Разумеется, это не подходит для кодирования без потерь.
3. Вычислительная среда
Вышеописанный кодек с усовершенствованным обратимым безмасштабным двумерным преобразованием может быть применен в любом из множества устройств, в котором выполняется обработка цифровых мультимедийных сигналов, в том числе (помимо других примеров) на вычислительных машинах (компьютерах); на оборудовании для записи, передачи и приема изображений и видео; на портативных видеопроигрывателях; в устройствах видеоконференц-связи и т.д. Методики кодирования цифрового мультимедиа могут быть реализованы в аппаратной схемотехнике, а также в программном обеспечении обработки цифрового мультимедиа, исполняемом на вычислительной машине или в другой вычислительной среде, такой как показана на фиг. 24.
Фиг. 24 иллюстрирует обобщенный пример подходящей вычислительной среды 2400, в которой могут быть реализованы описанные варианты осуществления. Не подразумевается, что вычислительная среда 2400 налагает какое-либо ограничение на область использования или функциональность изобретения, поскольку настоящее изобретение может быть реализовано в различных вычислительных средах общего или специального назначения.
Согласно фиг. 24 вычислительная среда 2400 включает в себя, по меньшей мере, один модуль 2410 обработки данных и память 2420. На фиг. 24 эта наиболее общая конфигурация 2430 показана пунктирной линией. Модуль 2410 обработки данных исполняет машиноисполняемые инструкции и может быть реальным или виртуальным процессором. В многопроцессорной системе несколько модулей обработки данных исполняют машиноисполняемые инструкции, чтобы повысить вычислительную мощность. Памятью 2420 может быть энергозависимая память (к примеру, регистры, кэш, ОЗУ), энергонезависимая память (к примеру, ПЗУ, электрически стираемое программируемое ПЗУ (ЭСППЗУ), флэш-память и т.д.) или какое-либо их сочетание. Память 2420 сохраняет программное обеспечение 2480, реализующее описанный кодер/декодер и преобразования.
Вычислительная среда может иметь дополнительные признаки. Например, вычислительная среда 2400 включает в себя хранилище 2440 данных, устройства 2450 ввода, одно или более устройств 2460 вывода и одно или более подключений 2470 связи. Механизм межкомпонентного соединения (не показан), такой как шина, контроллер или сеть соединяет между собой компоненты вычислительной среды 2400. В типичном случае программное обеспечение операционной системы (не показано) предоставляет рабочую среду для другого программного обеспечения, исполняемого в вычислительной среде 2400, и координирует действия компонентов вычислительной среды 2400.
Хранилище 2440 данных может быть съемным или стационарным и включает в себя магнитные диски, магнитные ленты или кассеты, CD-ROM, CD-RW, DVD или любой другой носитель, который может быть использован, чтобы сохранять информацию, и к которому можно осуществлять доступ в рамках вычислительной среды 2400. Хранилище 2440 данных сохраняет инструкции для программного обеспечения 2480, реализующие кодек с усовершенствованным SDLT.
Устройством(ами) 2450 ввода может быть устройство сенсорного ввода, такое как клавиатура, мышь, перо или шаровой манипулятор, устройство голосового ввода, устройство сканирования или другое устройство, которое обеспечивает ввод в вычислительную среду 2400. Для аудиоустройством(ами) 2450 ввода может быть звуковая плата или аналогичное устройство, которое принимает ввод звука в аналоговой или цифровой форме, либо устройство считывания CD-ROM, которое предоставляет аудиовыборки вычислительной среде.
Устройствами 2460 вывода может быть дисплей, принтер, динамик, устройство записи CD-RW или другое устройство, которое предоставляет вывод из вычислительной среды 2400.
Коммутационные соединения 2470 обеспечивают обмен данными по среде обмена данными с другой вычислительной объектной сущностью. Среда обмена данными передает информацию, такую как машиноисполняемые инструкции, сжатую аудио- и видеоинформацию или другие данные в модулированном информационном сигнале. Модулированный информационный сигнал - это сигнал, одна или более характеристик которого установлены или изменены таким образом, чтобы кодировать информацию в этом сигнале. В качестве примера, а не ограничения, среда обмена данными включает в себя проводные или беспроводные методики, реализованные с помощью электрического, оптического, радиочастотного, инфракрасного, акустического или другого носителя.
Методики обработки цифрового мультимедиа в данном документе могут быть описаны в общем контексте машиночитаемых носителей. Машиночитаемые носители - это любые доступные носители, к которым можно осуществлять доступ в вычислительной среде. В качестве примера, а не ограничения, в вычислительной среде 2400 машиночитаемые носители включают в себя память 2420, хранилище 2440 данных, среды обмена данными и сочетания любого из вышеуказанного.
Методики обработки цифрового мультимедиа в данном документе могут быть описаны в общем контексте машиноисполняемых инструкций, таких как включенные в программные модули, исполняемые в вычислительной среде на целевом реальном или виртуальном процессоре. В общем, программные модули включают в себя процедуры, программы, библиотеки, объекты, классы, компоненты, структуры данных и т.д., которые выполняют конкретные задачи или реализуют определенные абстрактные типы данных. Функциональные возможности программных модулей могут быть сочетаемы или разделены между программными модулями, как требуется в различных вариантах осуществления. Машиноисполняемые инструкции для программных модулей могут быть исполняемы в локальной или распределенной вычислительной среде.
Для целей представления подробное описание использует такие термины, как "определить", "сгенерировать", "настроить" и "применить", чтобы описывать операции вычислительной машины в вычислительной среде. Эти термины являются высокоуровневыми абстракциями для операций, выполняемых вычислительной машиной, и их не следует путать с действиями, выполняемыми человеком. Фактические операции вычислительной машины, соответствующие этим терминам, различаются в зависимости от реализации.
Принимая во внимание множество возможных вариантов осуществления, к которым могут быть применены принципы нашего изобретения, мы заявляем в изобретении все такие варианты осуществления, которые могут подпадать под объем, определяемый нижеследующей формулой изобретения и ее эквивалентами.



Изобретение относится к блочному основанному на преобразовании сжатию цифрового мультимедиа. Технический результат заключается в снижении вычислительной сложности пары раздельного двумерного преобразования и его инверсии, используемой в системе кодера/декодера цифрового мультимедиа. Для этого реализованы способ обработки двумерных цифровых мультимедийных данных, способ выполнения инверсии двумерного преобразования, кодер и декодер системы сжатия с потерями/без потерь. Двумерное преобразование и его инверсия имеют реализацию в качестве последовательности этапов лифтинг-преобразования. Эта пара преобразования имеет свойства энергетического сжатия и также выполняется без потерь, и является безмасштабной. Операции преобразования реорганизованы в каскад элементарных преобразований, включающих в себя преобразование Адамара 2×2 и преобразования 2×2, содержащие повороты с лифтинг-преобразованием. Эти элементарные преобразования имеют реализации в качестве последовательности операций лифтинг-преобразования. 4 н. и 16 з.п. ф-лы, 25 ил.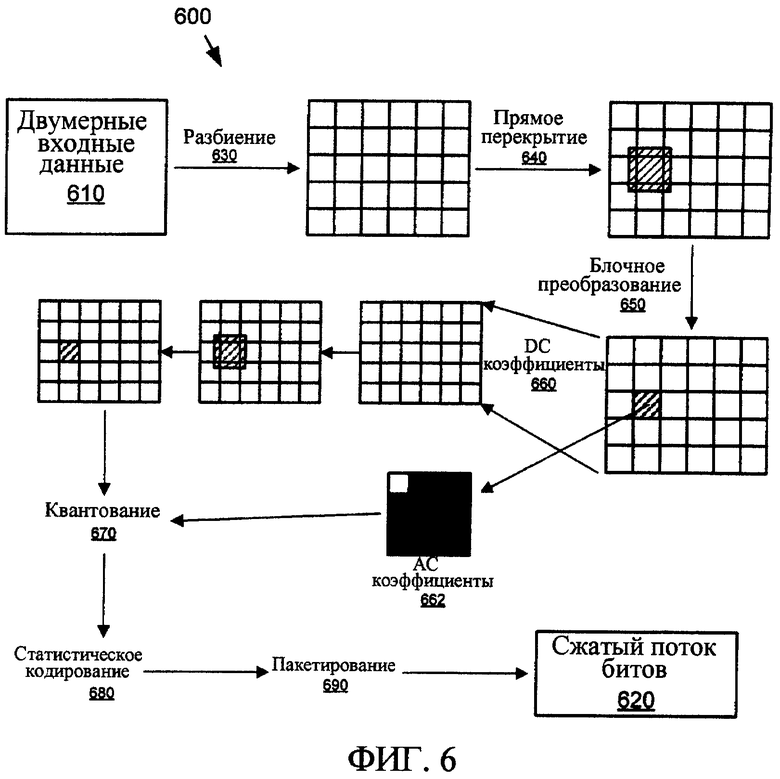
1. Способ обработки двумерных цифровых мультимедийных данных, содержащий этапы, на которых
принимают ввод двумерных цифровых мультимедийных данных;
выполняют в отношении этих цифровых мультимедийных данных кодирование или декодирование с блочным основывающимся на преобразовании сжатием данных, используя обратимое безмасштабное двумерное блочное преобразование, заданное как одномерное преобразование, применяемое горизонтально и вертикально к двумерному блоку упомянутых цифровых мультимедийных данных, причем это преобразование двумерного блока упомянутых цифровых мультимедийных данных осуществляется посредством того, что на каждой из двух или более стадий, чередующих операции из горизонтальных и вертикальных одномерных преобразований, применяют эти операции на соответствующей стадии, реорганизованные как набор элементарных преобразований, реализованных в качестве этапов лифтинг-преобразования, к независимым поднаборам значений в двумерном блоке; и
выводят кодированные или декодированные цифровые мультимедийные данные.
2. Способ по п.1, дополнительно содержащий на первой из упомянутых стадий этап, на котором применяют преобразование Адамара 2×2 к независимым поднаборам из четырех значений в двумерном блоке значений.
3. Способ по п.2, в котором поднаборы из четырех значений содержат:
группу из четырех значений по углам двумерного блока;
группу из четырех значений в центре двумерного блока;
группу из четырех значений по центрам горизонтальных краев двумерного блока и
группу из четырех значений по центрам вертикальных краев двумерного блока.
4. Способ по п.1, дополнительно содержащий на второй из упомянутых стадий этап, на котором применяют набор преобразований к независимым поднаборам из четырех значений в двумерном блоке значений, причем по меньшей мере одно из этого набора преобразований реализовано в форме каскада из трех стадий, содержащего:
операцию двойной "бабочки", заданную оператором Н с помощью этапов лифтинг-преобразования, где
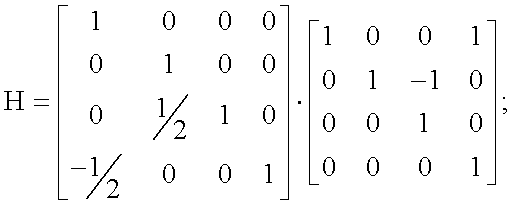
двухточечные повороты между первой парой значений компонентов и между второй парой значений компонентов соответственно; и
обращение операции двойной "бабочки".
5. Способ по п.1, дополнительно содержащий на второй из упомянутых стадий этап, на котором применяют набор преобразований к независимым поднаборам из четырех значений в двумерном блоке значений, причем этот набор преобразований включает в себя преобразование Адамара 2×2, нечетное преобразование поворота 2×2, полученное как произведение Кронекера двухточечного преобразования Адамара и двухточечной матрицы поворота, и нечетное-нечетное преобразование поворота 2×2, полученное как произведение Кронекера двухточечных матриц поворота.
6. Способ по п.1, содержащий уменьшение смещения по ошибкам округления, при этом способ дополнительно содержит этап, на котором для операции "бабочки", задействующей деление или битовый сдвиг вправо, добавляют варьирующийся коэффициент к операндам, делимым или сдвигаемым побитово вправо, перед соответствующей операцией "бабочки".
7. Способ по п.1, содержащий уменьшение смещения по ошибкам округления для сжатия с потерями, при этом способ дополнительно содержит этапы, на которых
до преобразования масштабируют двумерный блок посредством умножения на коэффициент;
выполняют преобразование и
квантуют получившиеся в результате коэффициенты преобразования с помощью квантователя, равного требуемому квантователю, умноженному на упомянутый коэффициент.
8. Способ выполнения инверсии обработки двумерных цифровых мультимедийных данных, содержащий этапы, на которых
принимают ввод кодированных цифровых мультимедийных данных;
выполняют в отношении кодированных цифровых мультимедийных данных блочное основывающееся на преобразовании восстановление данных, используя обратимое безмасштабное двумерное обратное блочное преобразование, заданное как одномерное обратное преобразование, применяемое горизонтально и вертикально к двумерному блоку кодированных цифровых мультимедийных данных, причем это обратное преобразование двумерного блока кодированных цифровых мультимедийных данных осуществляется посредством того, что на каждой из двух или более стадий, чередующих операции из горизонтальных и вертикальных одномерных обратных преобразований, применяют эти операции на соответствующей стадии, реорганизованные как набор элементарных преобразований, реализованных в качестве этапов лифтинг-преобразования, к независимым поднаборам значений в двумерном блоке; и
выводят восстановленные двумерные цифровые мультимедийные данные.
9. Способ по п.8, дополнительно содержащий на первой из упомянутых стадий этап, на котором применяют набор преобразований к независимым поднаборам из четырех значений в двумерном блоке значений, причем этот набор преобразований включает в себя преобразование Адамара 2×2, нечетное преобразование поворота 2×2, полученное как произведение Кронекера двухточечного преобразования Адамара и двухточечной матрицы поворота, и нечетное-нечетное преобразование поворота 2×2, полученное как произведение Кронекера двухточечных матриц поворота.
10. Способ по п.9, в котором поднаборы из четырех значений содержат группы из четырех значений вверху слева, вверху справа, внизу слева и внизу справа в двумерном блоке.
11. Способ по п.9, в котором двумерное преобразование Адамара 2×2, нечетное преобразование поворота 2×2 и нечетное-нечетное преобразование поворота 2×2 задаются следующими уравнениями, аппроксимированными до четырех десятичных знаков:
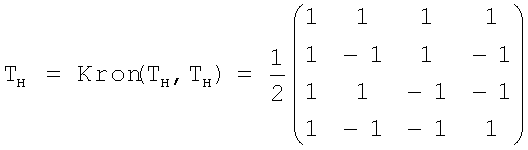 ,
,
 и
и
 .
.
12. Способ по п.8, дополнительно содержащий на второй из упомянутых стадий этап, на котором применяют преобразование Адамара 2×2 к независимым поднаборам из четырех значений в двумерном блоке значений.
13. Кодер системы сжатия с потерями/без потерь для выполнения сжатия с потерями/без потерь двумерных цифровых мультимедийных данных с помощью блочного основанного на преобразовании кодирования, использующего обратимое безмасштабное двумерное преобразование, заданное как четырехточечное преобразование, применяемое вертикально и горизонтально к двумерным блокам цифровых мультимедийных данных, при этом кодер содержит
буферное запоминающее устройство для буферизации двумерных цифровых мультимедийных данных, которые должны быть закодированы;
процессор для применения упомянутого преобразования к двумерным блокам цифровых мультимедийных данных посредством, на каждой из двух или более стадий, чередующих операции из горизонтального и вертикального одномерного четырехточечного преобразования, применения этих операций на соответствующей стадии, реорганизованных как набор элементарных преобразований 2×2, реализованных в качестве этапов лифтинг-преобразования, к независимым поднаборам из четырех значений в двумерном блоке,
при этом процессор дополнительно выполнен с возможностью статистического кодирования коэффициентов преобразования, полученных упомянутым преобразованием двумерного блока.
14. Кодер по п.13, в котором элементарные преобразования содержат преобразование Адамара 2×2, нечетное преобразование поворота 2×2, полученное как произведение Кронекера двухточечного преобразования Адамара и двухточечной матрицы поворота, и нечетное-нечетное преобразование поворота 2×2, полученное как произведение Кронекера двухточечных матриц поворота.
15. Кодер по п.13, в котором процессор на первой стадии применяет преобразование Адамара 2×2 к поднаборам из четырех значений соответствующего цифрового мультимедийного блока, включающего в себя наборы из четырех значений по углам, в центре, верхнем/нижнем краях и левом/правом краях цифрового мультимедийного блока.
16. Кодер по п.13, в котором процессор на второй стадии применяет преобразование Адамара 2×2 к поднабору из четырех значений вверху слева соответствующего цифрового мультимедийного блока, преобразование Адамара 2×2, нечетное преобразование поворота 2×2, полученное как произведение Кронекера двухточечного преобразования Адамара 2×2 и двухточечной матрицы поворота, к поднаборам из четырех значений вверху справа и внизу слева соответствующего цифрового мультимедийного блока, и нечетное-нечетное преобразование поворота 2×2, полученное как произведение Кронекера двухточечной матрицы поворота с самой собой, к поднабору из четырех значений внизу справа соответствующего цифрового мультимедийного блока.
17. Декодер системы сжатия с потерями/без потерь для выполнения восстановления с потерями/без потерь сжатых двумерных цифровых мультимедийных данных с помощью блочного основанного на преобразовании декодирования, использующего инверсию обратимого безмасштабного двумерного преобразования, при этом декодер содержит буферное запоминающее устройство для буферизации коэффициентов преобразования блоков сжатых двумерных цифровых мультимедийных данных; и
процессор для статистического декодирования коэффициентов преобразования упомянутых блоков и для применения обратного преобразования к двумерному блоку цифровых мультимедийных данных посредством, на каждой из двух или более стадий, чередующих операции из горизонтального и вертикального одномерного четырехточечного обратного преобразования, применения этих операций на соответствующей стадии, реорганизованных как набор элементарных преобразований 2×2, реализованных в качестве этапов лифтинг-преобразования, к независимым поднаборам из четырех значений в двумерном блоке.
18. Декодер по п.17, в котором элементарные преобразования содержат преобразование Адамара 2×2, нечетное преобразование поворота 2×2, полученное как произведение Кронекера двухточечного преобразования Адамара и двухточечной матрицы поворота, и нечетное-нечетное преобразование поворота 2×2, полученное как произведение Кронекера двухточечных матриц поворота.
19. Декодер по п.18, в котором процессор на первой стадии применяет преобразование Адамара 2×2 к поднабору из четырех значений вверху слева соответствующего цифрового мультимедийного блока, преобразование Адамара 2×2, нечетное преобразование поворота 2×2, полученное как произведение Кронекера двухточечного преобразования Адамара и двухточечной матрицы поворота, к поднаборам из четырех значений вверху справа и внизу слева соответствующего цифрового мультимедийного блока, и нечетное-нечетное преобразование поворота 2×2, полученное как произведение Кронекера двухточечных матриц поворота, к поднабору из четырех значений внизу справа соответствующего цифрового мультимедийного блока.
20. Декодер по п.18, в котором процессор на второй стадии применяет преобразование Адамара 2×2 к поднаборам из четырех значений соответствующего цифрового мультимедийного блока, включающего в себя наборы из четырех значений по углам, в центре, верхнем/нижнем краях и левом/правом краях цифрового мультимедийного блока.
| М | |||
| FERRETTI, D.RIZZO, "A Parallel Architecture for the 2-D Discrete Wavelet Transform with Integer Lifting Scheme", Journal of VLSI Signal Processing 28, 2001, реферат; главы 1-3 | |||
| ЯКОВЛЕВ А.Н | |||
| "Введение в вейвлет-преобразования" | |||
| Министерство Образования Российской Федерации Новосибирский Государственный Технический Университет, Новосибирск, 2003; |
Авторы
Даты
2011-03-10—Публикация
2005-11-17—Подача