Описание
Уровень техники
Настоящее изобретение относится к области способов оценивания нефтяных и газовых подземных пластов, а более конкретно к способам и устройствам для определения коллекторских свойств подземных пластов с использованием количественных диагностических способов испытания кандидата на повторный разрыв пласта.
Нефтяные и газовые углеводороды могут занимать поровые пространства в подземных пластах, таких как, например, песчаниковые подземные пласты. Поровые пространства часто являются сообщающимися и имеют определенную проницаемость, которая представляет собой меру способности породы пропускать поток флюида. В случае, если проницаемость вблизи ствола скважины является низкой, или в случае, когда произошло нарушение эксплуатационных качеств в области вблизи ствола скважины, для повышения добычи из ствола скважины могут быть выполнены операции по гидравлическому разрыву пласта.
Гидравлический разрыв пласта представляет собой процесс, при котором флюид под высоким давлением нагнетают в пласт для образования и/или удлинения трещин, которые проникают в пласт. Эти трещины могут создавать каналы притока флюидов в скважину, повышающие краткосрочную продуктивность скважины. Расклинивающие агенты различных видов, химические или физические, часто используют для поддержания трещин открытыми и для предотвращения смыкания трещин после того, как давление разрыва сбрасывают.
При гидравлическом разрыве пласта можно столкнуться с различными проблемами во время операций разрыва, приводящими к менее чем оптимальному гидравлическому разрыву пласта. В соответствии с этим после гидравлического разрыва пласта может быть желательным оценивание эффективности гидравлического разрыва пласта, выполняемое сразу, или получение исходных данных о коллекторских свойствах для более позднего сравнения и оценивания. Одним примером проблемы, с которой время от времени сталкиваются при гидравлическом разрыве пласта, являются пропущенные слои. А именно, во время первоначального заканчивания нефтяные или газовые скважины могут содержать слои, пропущенные при гидравлическом разрыве специально или случайно.
Успех гидравлического разрыва пласта часто зависит от свойств скважины-кандидата, выбранной для воздействия на пласт. Выбор хорошего кандидата для интенсификации притока может привести к успеху, тогда как выбор плохого кандидата может привести к экономической неэффективности. Чтобы выбрать наилучшего кандидата для интенсификации притока или повторной интенсификации потока, необходимо учесть много параметров. Некоторые важные параметры для гидравлического разрыва пласта включают в себя проницаемость пласта, распределение механических напряжений в пласте, вязкость пластового флюида, коэффициент нарушения коллекторских свойств пласта и давление в коллекторе. Были разработаны различные способы для определения свойств пласта и тем самым для оценивания эффективности выполненной ранее обработки пласта с целью интенсификации притока или осуществленных воздействий на пласт.
Известные способы, предназначенные для идентификации в недостаточной степени функционирующих скважин и для повторного заканчивания пропущенных слоев, большей частью являются безуспешными, отчасти потому, что для способов характерна тенденция к чрезмерному упрощению сложной проблемы многочисленных слоев, и потому, что в них основное внимание обращается на характеристики скважин, дающих смесь продукции из двух или более горизонтов, и на возможность повторного возбуждения скважины без основательного исследования свойств слоев и возможности повторного заканчивания слоев. Сложность многослойной среды возрастает по мере увеличения числа слоев с различными свойствами. Слои с различными свойствами пор, давлениями гидравлического разрыва пласта и проницаемостями могут сосуществовать в одной и той же группе слоев. Значительный недостаток исследования свойств слоев заключается в отсутствии диагностического контроля экономической эффективности при определении проницаемости слоев, давления и количественного оценивания эффективности выполненной ранее обработки пласта для интенсификации притока или осуществленных воздействий на пласт.
Этим известным способам часто присущи разнообразные недостатки, включая отсутствие точности и/или неэффективность вычислительного метода, приводящая к способам, которые требуют слишком больших затрат времени. Кроме того, известные способы часто не имеют точного средства для количественного определения гидропроводности пласта.
Результаты геофизических исследований в эксплуатационной скважине после гидравлического разрыва, изображения гидравлического разрыва пласта вблизи ствола скважины, полученные с помощью радиоактивных индикаторов, и изображения в дальнем поле микросейсмических трещин, все они, позволяют считать, что от около 10% до около 40% слоев, намеченных для заканчивания во время работ по первичному гидравлическому разрыву пласта, могут быть пропущены или интенсифицированы неэффективно при использовании схем гидравлического разрыва пласта на ограниченной части продуктивного интервала.
Количественное оценивание пропущенных слоев обычно сопряжено с трудностью, отчасти потому, что получают изображения очень небольшого количества заканчиваемых скважин. Следовательно, пропущенные или неэффективно интенсифицированные слои не могут быть легко идентифицированы и должны прогнозироваться на основании анализа потока скважины, дающей смесь продукции из двух или более горизонтов, каротажа в эксплуатационной скважине или обычного исследования переходного процесса изменения давления в отдельных слоях.
В качестве одного примера известный способ описан в публикации 2002/0096324 патентной заявки США (Poe), в которой рассмотрен способ идентификации в недостаточной степени функционирующих или плохо функционирующих продуктивных слоев с целью повторной обработки или повторной интенсификации притока. Однако в этом способе используют анализ данных о добыче из притока к продуктивной скважине для вывода заключения о свойстве слоев, а не используют методику непосредственных измерений. Результатом этого ограничения может быть плохая точность, и кроме того, необходимо осуществлять распределение суммарной добычи из скважины по каждому слою на основании диаграмм каротажа в эксплуатационной скважине, получаемых на протяжении периода эксплуатации скважины, которые могут иметься или могут не иметься.
Другие способы оценивания эффективности ранее выполненных работ по гидравлическому разрыву пласта включают в себя обычное исследование переходного процесса изменения давления, которое включает в себя исследование депрессии, восстановления давления, спада давления после нагнетания. Эти способы могут быть использованы для идентификации существующей трещины, сохраняющей остаточную ширину, являющейся результатом ранее выполненной операции по гидравлическому разрыву пласта или осуществленных воздействий на пласт, но для известных способов могут требоваться сутки добычи и контроль давления для каждого, взятого в отдельности слоя. Вследствие этого в случае ствола скважины, имеющего многочисленные продуктивные слои, для оценивания всех слоев может потребоваться испытание отдельных слоев в течение срока, составляющего от недель до месяцев. Для многих скважин возможная отдача не оправдывает затрат этого вида.
Делались попытки проведения диагностического испытания в скважинах с многочисленными слоями, имеющими низкую проницаемость. Один пример такого способа раскрыт в Hopkins C.W., et al., “The use of injection/falloff tests and pressure buildup tests to evaluate fracture geometry and post-stimulation well performance in the Devonian shales”, paper SPE 23433, 22-25 (1991). Согласно этому способу описаны несколько диагностических методик, использованных для скважины в девонском сланце с целью выявления присутствия уже существующей трещины (трещин) в многочисленных целевых слоях на протяжении интервала, составлявшего 727 футов. Диагностические испытания включают в себя испытания изоляции потоков, исследования сообщений в стволе скважины, исследования спада давления после нагнетания азота и обычные исследования депрессии и восстановления давления.
Несмотря на то, что этот диагностический способ позволяет оценивать некоторые коллекторские свойства, он, однако, является затратным и занимающим много времени, даже в случае относительно простого случая, когда имеются только четыре слоя. Многие кандидаты на повторный разрыв пласта из числа скважин газовой залежи с низкой проницаемостью содержат расположенные друг над другом линзовидные песчаные пласты с числом слоев от 20 до 40, которые должны быть оценены своевременно и с наименьшими затратами.
В другом способе используют квазиколичественный способ интерпретации исследования переходного процесса изменения давления, раскрытый в Huang H., et al., “A short shut-in time testing method for determining stimulation effectiveness in low permeability gas reservoirs”, GASTIPS, 6, №4, 28 (Fall 2000). Этот «упрощенный способ интерпретации исследования при остановке скважины» предназначен для получения данных относительно только эффективности уже существующей трещины. Для получения верхнего и нижнего пределов проницаемости и эффективной полудлины трещины в способе используют опорные точки типовой кривой с логарифмическим масштабом по обеим осям (точки окончания заполнения нефтью ствола скважины, начала псевдолинейного потока, окончания псевдолинейного потока и начала псевдорадиального потока) и известные соотношения между давлением и свойствами системы в этих точках.
В другом способе для коллекторов с низкой проницаемостью используют испытания закачиванием азота в качестве диагностического испытания до разрыва пласта, раскрытые в Jochen J.E., et al., “Quantifying layered reservoir properties with a novel permeability test”, SPE 25864, 12-14 (1993). В соответствии с этим способом описано испытание нагнетанием азота в виде кратковременного нагнетания небольшого объема азота при более низком давлении, чем давление инициирования и распространения трещины, с последующим длительным периодом спада давления. В отличие от исследования спада давления после нагнетания азота, который использовали Hopkins и соавторы, результаты испытания закачиванием азотом анализируют, используя типовые кривые испытания закачиванием и сопоставляя динамику процесса нагнетания и спада давления с помощью конечно-разностного имитатора коллектора.
Аналогичным образом, как раскрыто в Craig D.P., et al., “Permeability, pore pressure and leakoff-type distribution in rocky mountain basins”, SPE Production & Facilities, 48 (February 2005), исследования некоторых видов по спаду давления после нагнетания в трещину регулярно проводят с 1998 г в качестве способа диагностики до разрыва пласта с целью оценивания проницаемости пласта и среднего давления в коллекторе. Эти исследования спада давления после нагнетания в трещину, которые по существу представляют собой гидравлический мини-разрыв пласта и в которых коллекторские свойства интерпретируют на основании спада давления, отличаются от испытаний закачиванием азота тем, что давление во время нагнетания больше, чем давление инициирования и распространения трещины. При исследованиях спада давления после нагнетания в трещину обычно необходимы низкий расход и нагнетание небольшого объема обработанной воды с последующим продолжительным периодом остановки скважины. Проницаемость относительно подвижного пластового флюида и среднее давление в коллекторе могут быть интерпретированы на основании снижения давления. Однако при исследовании спада давления после нагнетания в трещину может оказаться невозможным с достаточной точностью осуществить оценку кандидатов на повторный разрыв пласта, поскольку в соответствующей известной теории не учитываются уже существующие трещины.
Поэтому известные способы для оценивания свойств пласта имеют много недостатков, включая отсутствие возможности количественно определить гидропроводность коллектора, отсутствие экономической эффективности, вычислительную неэффективность и/или отсутствие точности. Даже среди способов, разработанных для того, чтобы количественно определять гидропроводность коллектора, такие способы могут быть практически нецелесообразными для оценивания пластов, имеющих многочисленные слои, такие как, например, расположенные друг над другом линзовидные коллекторы с низкой проницаемостью.
Сущность изобретения
Настоящее изобретение относится к области способов оценивания нефтяных и газовых подземных пластов, а более конкретно, к способам и устройствам для определения коллекторских свойств подземных пластов путем использования количественных диагностических способов испытания кандидата на повторный разрыв пласта.
Согласно некоторым осуществлениям способ определения гидропроводности коллектора по меньшей мере одного слоя подземного пласта, имеющего уже существующие трещины, имеющие пластовый флюид, содержит этапы, на которых: (а) изолируют по меньшей мере один слой подземного пласта, подлежащего испытанию; (b) вводят нагнетаемый флюид в по меньшей мере один слой подземного пласта при давлении нагнетания, превышающем давление гидравлического разрыва подземного пласта, в течение периода нагнетания; (с) перекрывают ствол скважины в течение периода остановки скважины; (d) измеряют данные спада давления со стороны подземного пласта в течение периода нагнетания и в течение последующего периода остановки скважины; и (е) определяют количественно гидропроводность коллектора по меньшей мере одного слоя подземного пласта, анализируя данные спада давления с помощью количественной диагностической модели кандидата на повторный разрыв пласта.
Согласно некоторым осуществлениям система для определения гидропроводности коллектора по меньшей мере одного слоя подземного пласта путем использования данных спада давления при переменном расходе со стороны по меньшей мере одного слоя подземного пласта, измеряемых в течение периода нагнетания и в течение последующего периода остановки скважины, содержит множество датчиков давления для измерения данных спада давления; и процессор, функционирующий для преобразования данных спада давления с целью получения эквивалентных давлений при постоянном расходе и с целью определения количественно гидропроводности коллектора по меньшей мере одного слоя подземного пласта путем анализа спада давления при переменном расходе с использованием анализа типовой кривой в соответствии с количественной диагностической моделью кандидата на повторный разрыв пласта.
Согласно некоторым осуществлениям компьютерная программа, сохраняемая на материальном носителе данных, для осуществления анализа по меньшей мере одного свойства в скважинных условиях содержит исполняемые команды, которые побуждают компьютер к определению количественно гидропроводности коллектора по меньшей мере одного слоя подземного пласта путем анализа данных спада давления при переменном расходе с помощью количественной диагностической модели кандидата на повторный разрыв пласта.
Признаки и преимущества настоящего изобретения должны быть понятными для специалистов в данной области техники. Хотя специалистами в данной области техники могут быть сделаны многочисленные изменения, такие изменения находятся в рамках сущности изобретения.
Краткое описание чертежей
Этими чертежами иллюстрируются конкретные аспекты некоторых осуществлений настоящего изобретения, и они не должны использоваться для ограничения или определения изобретения.
На чертежах:
фигура 1 - блок-схема последовательности операций, иллюстрирующая одно осуществление способа количественного определения гидропроводности коллектора;
фигура 2 - блок-схема последовательности операций, иллюстрирующая одно осуществление способа количественного определения гидропроводности коллектора;
фигура 3 - блок-схема последовательности операций, иллюстрирующая одно осуществление способа количественного определения гидропроводности коллектора;
фигура 4 - вид трещины с бесконечной высокой удельной проводимостью под произвольным углом относительно оси x D;
фигура 5 - график с логарифмическим масштабом по обеим осям зависимости безразмерного давления от безразмерного времени для крестовой трещины с бесконечной высокой удельной проводимостью, при этом δ L={0, 1/4, 1/2 и 1};
фигура 6 - вид трещины с конечной удельной проводимостью под произвольным углом относительно оси x D;
фигура 7 - иллюстрация дискретизации крестовой трещины;
фигура 8 - график с логарифмическим масштабом по обеим осям зависимости безразмерного давления от безразмерного времени для крестовой трещины с конечной удельной проводимостью, при этом δ L=1 и δ C=1;
фигура 9 - график с логарифмическим масштабом по обеим осям зависимости безразмерного давления от безразмерного времени для трещин с конечной удельной проводимостью, при этом δ L=1, δ C=1, пересекающихся под углами π/2, π/4 и π/8;
фигура 10 - пример результата исследования спада давления после нагнетания в трещину в отсутствие уже существующего гидравлического разрыва пласта;
фигура 11 - пример сопоставления с типовой кривой для исследования спада давления после нагнетания в трещину в отсутствие уже существующего гидравлического разрыва пласта;
фигура 12 - пример результата диагностического испытания кандидата на повторный разрыв пласта при наличии уже существующего гидравлического разрыва пласта; и
фигура 13 - пример графика с логарифмическим масштабом по обеим осям результатов диагностического испытания кандидата на повторный разрыв пласта при наличии поврежденного уже существующего гидравлического разрыва пласта.
Описание предпочтительных осуществлений
Настоящее изобретение относится к области способов оценивания нефтяных и газовых подземных пластов, а более конкретно, к способам и устройствам для определения коллекторских свойств подземных пластов путем использования количественных диагностических способов испытания кандидата на повторный разрыв пласта.
Способы настоящего изобретения могут быть полезными для оценивания свойств пласта путем использования количественных диагностических способов испытания кандидата на повторный разрыв пласта, в которых можно использовать нагнетаемые флюиды при давлениях, превышающих давление инициирования и распространения трещины. В частности, способы настоящей заявки могут быть использованы для оценивания свойств пласта, таких как, например, эффективная полудлина уже существующей трещины, удельная проводимость уже существующей трещины, гидропроводность коллектора и среднее давление в коллекторе. Кроме того, способы настоящей заявки могут быть использованы для определения, является ли уже существующая трещина поврежденной. Среди прочего, настоящее изобретение может быть полезным для определения на основании оцененных свойств пласта эффективности выполненного ранее гидравлического разрыва пласта, чтобы определить, требуется ли повторное воздействие на пласт вследствие менее чем оптимального результата гидравлического разрыва пласта. В соответствии с этим способы настоящего изобретения могут быть использованы для получения методики, предназначенной для определения, является ли желательным повторное воздействие на пласт и когда оно является желательным, путем количественного применения диагностического способа исследования спада давления после нагнетания в трещину кандидата на повторный разрыв пласта.
В большинстве случаев способы настоящей заявки позволяют осуществлять относительно быстрое определение эффективности выполненной ранее обработки или обработок пласта для интенсификации притока или воздействия на пласт путем нагнетания флюида в пласт при давлении нагнетания, превышающем давление разрыва пласта, и регистрации данных спада давления. Данные спада давления могут быть проанализированы для определения некоторых свойств пласта, включая, если желательно, гидропроводность пласта.
Согласно некоторым осуществлениям способ определения гидропроводности коллектора по меньшей мере одного слоя подземного пласта, имеющего уже существующие трещины, имеющие пластовый флюид, содержит этапы, на которых: (а) изолируют по меньшей мере один слой подземного пласта, подлежащего исследованию; (b) вводят нагнетаемый флюид в по меньшей мере один слой подземного пласта при давлении нагнетания, превышающем давление гидравлического разрыва подземного пласта, в течение периода нагнетания; (с) перекрывают ствол скважины в течение периода остановки скважины; (d) измеряют данные спада давления со стороны подземного пласта в течение периода нагнетания и в течение последующего периода остановки скважины; и (е) определяют количественно гидропроводность коллектора по меньшей мере одного слоя подземного пласта, анализируя данные спада давления с помощью количественной диагностической модели кандидата на повторный разрыв пласта.
Термин «диагностическое испытание кандидата на повторный разрыв пласта», используемый в настоящей заявке, относится к вычислительным оценкам, рассмотренным ниже в Разделах I и II, используемым для оценивания некоторых коллекторских свойств пласта, включая гидропроводность слоя или многочисленных слоев пласта. Испытание показывает, что существующая трещина, сохраняющая остаточную ширину, имеет соответствующую упругоемкость, а новая искусственно образованная трещина создает дополнительную упругоемкость. Следовательно, при исследовании спада давления после нагнетания в трещину в слое с уже существующей трещиной будет наблюдаться характеристика изменяющейся упругоемкости в течение периода спада давления и будет наблюдаться изменение упругоемкости при закрытии гидравлического разрыва пласта. В сущности, при испытании искусственно создают трещину, чтобы быстро идентифицировать уже существующую трещину, сохраняющую остаточную ширину.
Способы и модели настоящей заявки являются обобщениями идей Craig D.P. и частично основаны на этих идеях, изложенных в диссертации “Analytical modeling of a fracture-injection/falloff sequence and the development of refracture-candidate diagnostic test”, PhD dissertation, Texas A&M Univ., Колледж-Стейшен, Техас (2005), которая полностью включена в настоящую заявку посредством ссылки, и идей заявки №10/813698 на патент США, поданной 3 марта 2004 г под названием “Methods and apparatus for detecting fracture with significant residual width from previous treatments”, которая полностью включена в настоящую заявку посредством ссылки.
На фигуре 1 показан пример осуществления количественного диагностического способа испытания кандидата на повторный разрыв пласта, реализующего некоторые аспекты количественной диагностической модели кандидата на повторный разрыв пласта. Для определения гидропроводности коллектора по меньшей мере одного слоя подземного пласта способ 100 обычно начинают на этапе 105. На этапе 110 изолируют по меньшей мере один слой подземного пласта. Для испытания способами настоящего изобретения в течение этапа изоляции слоев предпочтительно каждый подземный слой изолировать индивидуально, по одному. Несколько слоев могут быть испытаны одновременно, но при таком объединении слоев в оценки гидропроводности может вноситься дополнительная вычислительная неопределенность.
Нагнетаемый флюид вводят (этап 120) в по меньшей мере один слой подземного пласта при давлении нагнетания, превышающем давление разрыва пласта, в течение периода нагнетания. Нагнетаемый флюид может быть жидкостью, газом или смесью их. В некоторых примерах осуществлений объем нагнетаемого флюида, вводимого в подземный слой, может быть приблизительно эквивалентен объему порового пространства набивки из расклинивающего агента для существующей трещины, если известно или предполагается, что она существует. Предпочтительно ограничивать введение нагнетаемого флюида относительно коротким периодом времени по сравнению со временем реакции коллектора, которое для конкретных пластов может быть в пределах от нескольких секунд до минут. В более предпочтительных осуществлениях при типичных применениях введение нагнетаемого флюида может быть ограничено временем, меньшим, чем около 5 мин. В случае пластов, имеющих уже существующие трещины, нагнетаемый флюид предпочтительно вводить таким образом, чтобы создавалось изменение объема существующих и создаваемых трещин, то есть по меньшей мере приблизительно удвоенного оцененного объема поровых пространств набивки из расклинивающего агента. После введения нагнетаемого флюида ствол скважины может быть перекрыт на период времени от нескольких минут до нескольких дней, что зависит от отрезка времени, на котором по данным спада давления обнаруживают приближение падающего давления к давлению в коллекторе.
В течение периода нагнетания и в течение последующего периода остановки скважины измеряют (этап 140) данные спада давления со стороны подземного пласта. Данные спада давления могут быть измерены датчиком давления или множеством датчиков давления. После введения нагнетаемого флюида ствол скважины может быть перекрыт на период времени от около нескольких часов до около нескольких дней, что зависит от отрезка времени, на котором по данным спада давления обнаруживают приближение падающего давления к давлению в коллекторе. Затем согласно этапу 150 данные спада могут быть проанализированы для определения гидропроводности коллектора подземного пласта в соответствии с количественной диагностической моделью кандидата на повторный разрыв пласта, рассмотренной более подробно ниже в Разделах I и II. Способ 100 заканчивают на этапе 225.
На фигуре 2 показан пример реализации количественного определения гидропроводности коллектора (показанной этапом 150 способа 100). В частности, способ 200 начинают на этапе 205. Этап 210 представляет собой этап преобразования данных спада давления при переменном расходе в эквивалентные давления при постоянном расходе и использования анализа типовой кривой для сопоставления эквивалентных давлений при постоянном расходе с типовой кривой. Этап 220 представляет собой этап определения количественно гидропроводности коллектора по меньшей мере одного слоя подземного пласта путем анализа эквивалентных давлений при постоянном расходе с помощью количественной диагностической модели кандидата на повторный разрыв пласта. Способ 200 заканчивают на этапе 225.
Один или несколько способов настоящего изобретения можно реализовать посредством системы обработки информации. Для целей этого раскрытия система обработки информации может включать в себя любое инструментальное средство или совокупность инструментальных средств, способных осуществлять вычисление, классификацию, обработку, передачу, прием, считывание, инициирование, переключение, сохранение, отображение, обнаружение, измерение, регистрацию, воспроизведение, контроль или использование информации любого вида, интеллектуальной, или данных для коммерческой деятельности, науки, контроля или других целей. Например, системой обработки информации может быть персональный компьютер, сетевое устройство хранения данных или любое другое подходящее устройство, и они могут быть различными по размеру, форме, характеристикам, функциональной возможности и цене. Система обработки информации может включать в себя оперативное запоминающее устройство (ОЗУ), один или несколько ресурсов для обработки информации, таких, как центральный процессор (ЦП или процессор) или аппаратные или программные логические схемы управления, постоянное запоминающее устройство и/или энергонезависимое запоминающее устройство другого вида. Дополнительные компоненты системы обработки информации могут включать в себя один или несколько дисковых накопителей, один или несколько сетевых портов для связи с внешними устройствами, а также различные устройства ввода и вывода, такие, как клавиатура, мышь и телевизионный дисплей. Система обработки информации также может включать в себя одну или несколько шин, функционирующих для передачи сообщений между различными аппаратными компонентами.
I. Количественная диагностическая модель испытания кандидата на повторный разрыв пласта
Диагностическая модель испытания кандидата на повторный разрыв пласта представляет собой расширение теоретической модели нагнетания в трещину/спада давления с помощью решений для переходного процесса изменения давления в многочисленных произвольно ориентированных трещинах с бесконечно высокой или конечной удельной проводимостью, используемых для адаптации модели. Теоретическая модель нагнетания в трещину/спада давления представлена в заявке Реестр HES 2005-IP-018458U1 патентного поверенного под названием “Methods and apparatus for determining reservoir properties of subterranean formations”, поданной одновременно с настоящей заявкой, при этом раскрытие указанной заявки полностью включено в настоящую заявку посредством ссылки.
Испытанием выявляется, что существующая трещина, сохраняющая остаточную ширину, имеет соответствующую упругоемкость, а новая, искусственно образованная трещина создает дополнительную упругоемкость. Следовательно, исследованием спада давления после нагнетания в трещину в слое с уже существующей трещиной будет выявляться изменяющаяся упругоемкость во время спада давления и будет наблюдаться изменение упругоемкости при закрытии гидравлического разрыва. В сущности, при испытании искусственно создают трещину, чтобы быстро идентифицировать уже существующую трещину, сохраняющую остаточную ширину.
Рассмотрим уже существующую трещину, которая расширяется во время выполнения последовательности из нагнетания в трещину и спада давления, но при этом полудлина трещины остается неизменной. При постоянной полудлине трещины во время нагнетания и спаде давления до закрытия трещины изменения объема трещины являются функцией ширины трещины, а коэффициент упругоемкости до закрытия трещины эквивалентен коэффициенту упругоемкости расширяющейся трещины и записывается в виде
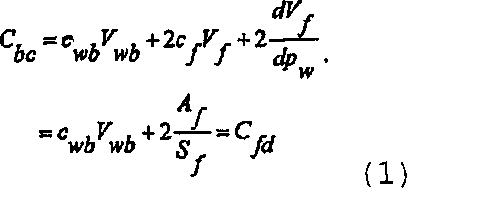
(Система условных обозначений, используемая повсюду в этом описании, охарактеризована ниже в Разделе VI),
где S f является жесткостью трещины, описанной в диссертации Craig D.P., “Analytical modeling of a fracture-injection/falloff sequence and the development of a refracture-candidate diagnostic test”, PhD dissertation, Texas A&M Univ., Колледж-Стейшен, Техас (2005). В случае эквивалентности упругоемкости до закрытия трещины и упругоемкости расширенной трещины дифференцирование, аналогичное показанному ниже в Разделе III, приводит к решению для безразмерного давления, записываемому как
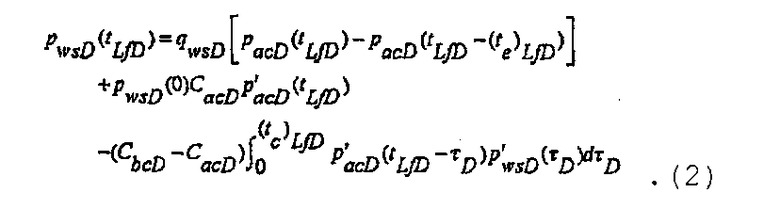
В качестве альтернативы во время нагнетания вторичная трещина может быть инициирована в плоскости, отличающейся от плоскости первичной трещины. В случае образования вторичной трещины и в предположении, что объем первичной трещины остается постоянным, коэффициент упругоемкости распространяющейся трещины записывается в виде
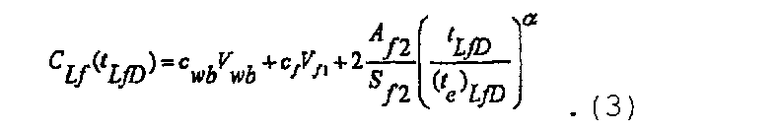
Коэффициент упругоемкости до закрытия трещины может быть определен как

а коэффициент упругоемкости после закрытия трещины может быть записан в виде
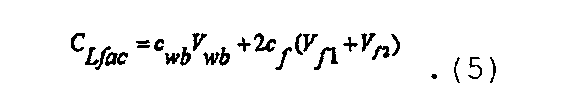
При новых формулировках коэффициента упругоемкости решение для последовательности из нагнетания в трещину и спада давления в случае уже существующей трещины и распространяющейся вторичной трещины записывается как

Отвечающие предельному случаю решения для единственной расширенной трещины идентичны отвечающим предельному случаю решениям для спада давления после нагнетания в трещину (уравнения 19 и 20 в одновременно рассматриваемой заявке на патент США, регистрационный номер … [Реестр № HES 2005-IP-018458U1 патентного поверенного]), когда (te)LfD☐t LfD. При распространении вторичной трещины удовлетворяющее предельному случаю решение до закрытия трещины для (te)LfD□tLfD<(tc)LfD может быть записано в виде

где p LfbcD является решением для безразмерного давления при депрессии с постоянным расходом в скважине, выдающей продукт из многочисленных трещин с постоянной упругоемкостью до закрытия трещин, которое в области Лапласа может быть записано как
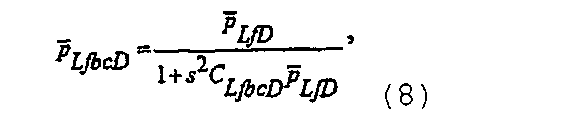
и при этом 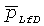 представляет собой решение в области Лапласа для коллектора в случае добычи из многочисленных произвольно ориентированных трещин с конечной или бесконечно высокой удельной проводимостью. Новые решения для многочисленных трещин получены ниже в Разделе IV для случая произвольно ориентированных трещин с бесконечно высокой удельной проводимостью и в Разделе V для случая произвольно ориентированных трещин с конечной удельной проводимостью. В новых решениях для многочисленных трещин учитываются изменяющаяся полудлина трещин, изменяющаяся удельная проводимость и изменяющийся угол расхождения между трещинами.
представляет собой решение в области Лапласа для коллектора в случае добычи из многочисленных произвольно ориентированных трещин с конечной или бесконечно высокой удельной проводимостью. Новые решения для многочисленных трещин получены ниже в Разделе IV для случая произвольно ориентированных трещин с бесконечно высокой удельной проводимостью и в Разделе V для случая произвольно ориентированных трещин с конечной удельной проводимостью. В новых решениях для многочисленных трещин учитываются изменяющаяся полудлина трещин, изменяющаяся удельная проводимость и изменяющийся угол расхождения между трещинами.
При наличии распространения вторичной трещины удовлетворяющее предельному случаю решение после закрытия трещины, когда tLfD□(tc)LfD□(te)LfD, записывается в виде
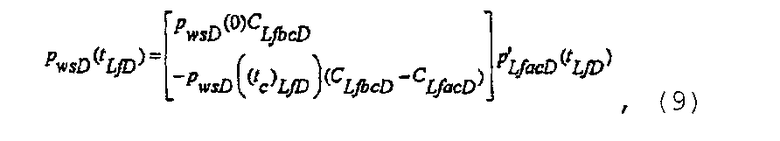
где p LfacD является решением для безразмерного давления при депрессии с постоянным расходом в скважине, выдающей продукт из многочисленных трещин с постоянной упругоемкостью после закрытия трещин, которое в области Лапласа может быть записано как
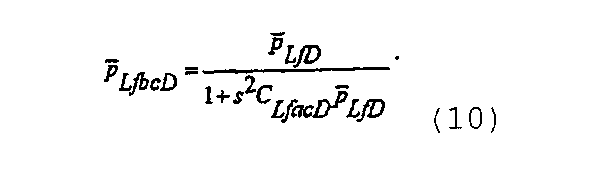
Удовлетворяющие предельному случаю решения представляют собой решения для испытания закачиванием, и это позволяет предположить, что результаты диагностического испытания кандидата на повторный разрыв пласта можно анализировать как результаты испытания закачиванием при условии, что время нагнетания меньше по сравнению с реакцией коллектора.
Следовательно, согласно некоторым осуществлениям при испытании кандидата на повторный разрыв пласта можно использовать следующее:
- Изоляцию слоя, подлежащего испытанию.
- Нагнетание жидкости или газа при давлении, превышающем давление инициирования и распространения трещины. Согласно некоторым осуществлениям нагнетаемый объем может быть приблизительно эквивалентен объему порового пространства набивки из расклинивающего агента в существующей трещине, если известно или предполагается, что она существует. Согласно некоторым осуществлениям время нагнетания может быть ограничено несколькими минутами.
- Остановку скважины и регистрацию данных спада давления. Согласно некоторым осуществлениям период измерения может составлять несколько часов.
Для качественной интерпретации можно использовать следующие этапы, к которым относятся:
- Идентификация закрытия гидравлического разрыва во время спада давления путем использования способов, таких как способы раскрытые в Craig D.P., et al., “Permeability, pore pressure, and leakoff-type distribution in rocky mountain basins”, SPE Production & Facilities, 48 (February 2005).
- Момент времени в конце закачивания, t ne, становится нулевым моментом отсчета времени, ∆t=0. Вычисление момента остановки скважины относительно окончания закачивания в виде
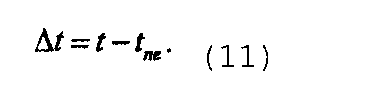
В некоторых случаях t ne является очень малым по сравнению с t, и ∆t=t. Специалисту в данной области техники, имеющему выгоду от этого раскрытия, должно быть понятно, что t ne можно приравнять к нулю, принять приблизительно равным нулю, с тем, чтобы аппроксимировать ∆t. Поэтому член ∆t, используемый в настоящей заявке, охватывает реализации, когда t ne предполагается равным нулю или приблизительно равным нулю. В случае нагнетания слабо сжимаемого флюида в коллектор, содержащий сжимаемый флюид, или нагнетания сжимаемого флюида в коллектор, содержащий сжимаемый флюид, используют свойства сжимаемого пластового флюида и вычисляют скорректированное время в виде

где псевдовремя может быть определено как
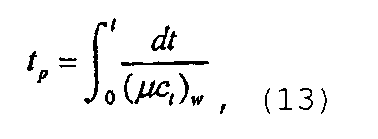
а скорректированное время или нормированное псевдовремя может быть определено как
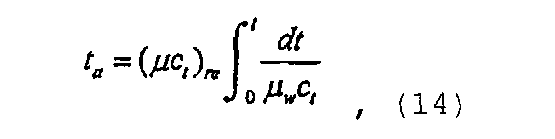
где нижний индекс “re” обозначает произвольное исходное условие, выбранное для удобства.
- Перепад давления в случае нагнетания слабосжимаемого флюида в коллектор, содержащий слабосжимаемый флюид, может быть вычислен как
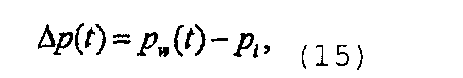
или в случае нагнетания слабосжимаемого флюида в коллектор, содержащий сжимаемый флюид, или нагнетания сжимаемого флюида в коллектор, содержащий сжимаемый флюид, используют свойства сжимаемого флюида коллектора и вычисляют скорректированный перепад псевдодавления как

где
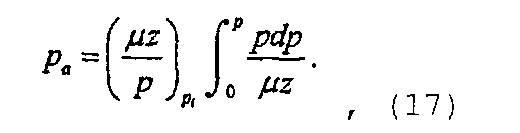
при этом псевдодавление может быть определено как
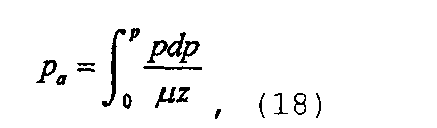
а скорректированное псевдодавление или нормированное псевдодавление может быть определено как

где нижний индекс “re” обозначает произвольное исходное условие, выбранное для удобства.
Исходные условия при определениях скорректированного псевдодавления и скорректированного псевдовремени являются произвольными, и различные формы решения могут быть получены путем простой замены нормирующих исходных условий.
- Вычисление функции построения кривой производной давления в виде
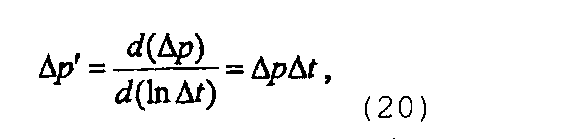
или

- Преобразование зарегистрированных данных спада давления при переменном расходе в эквивалентное давление, как если бы расход был постоянным, путем интегрирования перепада давления по времени, что для слабосжимаемого флюида может быть записано в виде
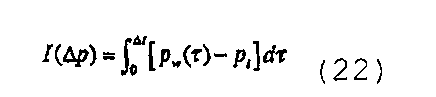
или для слабосжимаемого флюида, нагнетаемого в коллектор, содержащий сжимаемый флюид, или для нагнетания сжимаемого флюида в коллектор, содержащий сжимаемый флюид, функция построения кривой давления может быть вычислена как
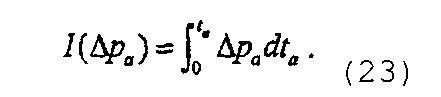
- Вычисление функции построения кривой производной давления в виде
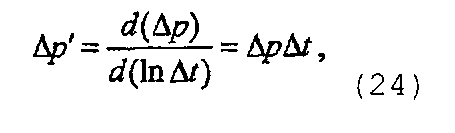
или
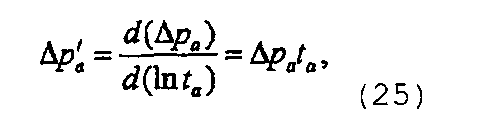
- Построение графика с логарифмическим масштабом по обеим осям, I(∆p) от ∆t или I(∆p a) от t a.
- Построение графика с логарифмическим масштабом по обеим осям, 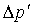 от Δt или
от Δt или 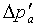 от t
a.
от t
a.
- Исследование поведения упругоемкости до и после закрытия трещины.
II. Анализ и интерпретация данных в общих чертах
Изменение значения упругоемкости при закрытии трещины наводит на мысль о существовании трещины, сохраняющей остаточную ширину. Когда упругоемкость снижается, существующая трещина является неповрежденной. В противоположность этому поврежденная трещина или трещина, проявляющая скин-эффект забившейся трещины, свидетельствует об очевидном повышении коэффициента упругоемкости.
При количественной диагностической интерпретации кандидата на повторный разрыв пласта используют сопоставление с типовой кривой или, если обнаруживают псевдорадиальный поток, то используют анализ после закрытия трещины, предложенный в Gu H., et al., “Formation permeability determination using impulse-fracture injection”, SPE 25425 (1993), или в Abousleiman Y., Cheng A.H-D. and Gu H., “Formation permeability determination by micro of mini-hydraulic fracturing”, J. of Energy Resources Technology, 116, №6, 104 (June 1994). Анализ после закрытия трещины является предпочтительным, поскольку для вычисления гидропроводности не требуется знать полудлину трещины. Однако имеется весьма малая вероятность, что псевдорадиальный поток будет наблюдаться во время относительно непродолжительного спада давления, и сопоставление с типовой кривой может быть необходимым. На основании точки сопоставления давления на типовой кривой при постоянном расходе, при постоянной упругоемкости до закрытия трещины, гидропроводность может быть вычислена на промысловых установках как
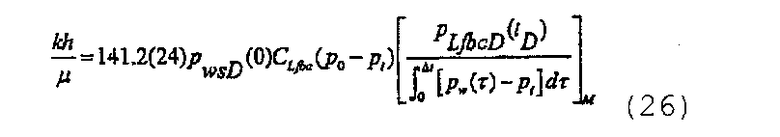
или на основании точки сопоставления давления после закрытия трещины путем использования типовой кривой изменяющейся упругоемкости
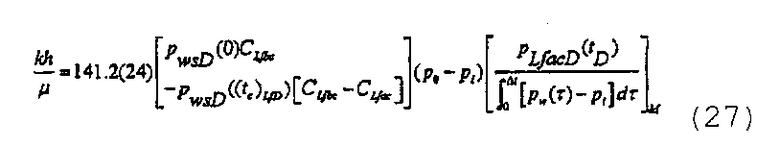
Количественной интерпретации присущи два ограничения. Во-первых, для точных вычислений эквивалентного давления при постоянном расходе и производной давления, уравнения 22-25, должно быть известно среднее давление в коллекторе. Во-вторых, для вычисления гидропроводности необходимы полудлины первичной и вторичной трещин. В предположении, что полудлина вторичной трещины может быть оценена путем построения изображения или аналитическими способами, предложенными в Valk P.P. and Economides M.J., “Fluid-leakoff delineation in high permeability fracturing”, SPE Production & Facilities, 117 (May 1999), полудлину первичной трещины вычисляют на основании сопоставления с типовой кривой, L f1=L f2/δ L. При известности полудлин обеих трещин коэффициенты упругоемкости до и после закрытия трещины могут быть вычислены в соответствии с диссертацией Craig D.P., “Analytical modeling of a fracture-injection/falloff sequence and the development of a refracture-candidate diagnostic test”, PhD dissertation, Texas A&M Univ., Колледж-Стейшен, Техас (2005), и оценена гидропроводность.
III. Теоретическая модель А - Решение для нагнетания в трещину/спада давления в коллекторе в отсутствие уже существующей трещины
Предположим, что слабосжимаемым флюидом заполняют ствол скважины и трещину, и его нагнетают с постоянным расходом при давлении, достаточном для создания нового гидравлического разрыва или расширения существующей трещины. Баланс масс во время нагнетания в трещину может быть записан в виде
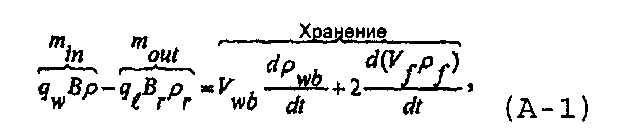
где 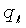 представляет собой расход флюида, протекающего в коллектор из трещины,
представляет собой расход флюида, протекающего в коллектор из трещины, 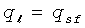 , а V
f является объемом трещины.
, а V
f является объемом трещины.
В предположении постоянной плотности, ρ=ρ wb=ρ f=ρ r, и постоянного объемного коэффициента пласта, B=B r, уравнение материального баланса может быть записано в виде
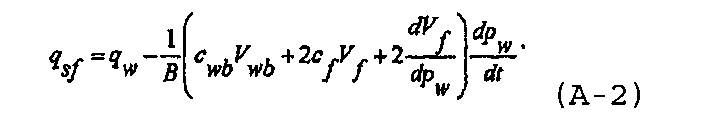
Во время нагнетания с постоянным расходом в случае изменения длины и ширины трещины объем трещины может быть записан как
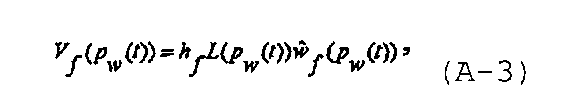
а коэффициент упругоемкости распространяющейся трещины может быть записан в виде
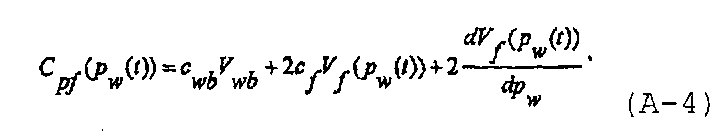
Безразмерное давление в стволе скважины для случая спада давления после нагнетания в трещину может быть записано как
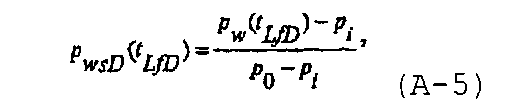
где p i представляет собой исходное давление в коллекторе, а p 0 является произвольным опорным давлением. В нулевой момент времени давление в стволе скважины повышают до давления p w0 «открытия», которое обычно задают равным p 0, и безразмерное давление в стволе скважины в нулевой момент времени может быть записано в виде
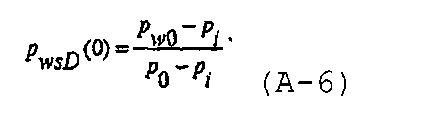
Зададим безразмерное время как
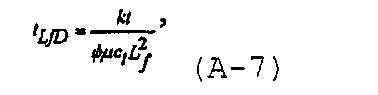
где L f является полудлиной трещины в конце закачивания. Безразмерный расход из коллектора может быть определен как
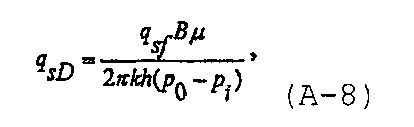
а безразмерный расход из скважины может быть определен как
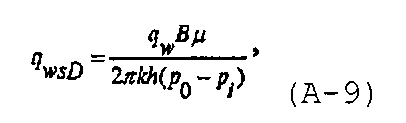
где q w является расходом при нагнетании в скважину.
При наличии безразмерных переменных уравнение материального баланса для распространяющейся трещины во время нагнетания может быть записано в виде
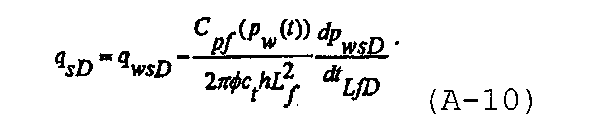
Безразмерный коэффициент упругоемкости трещины зададим как
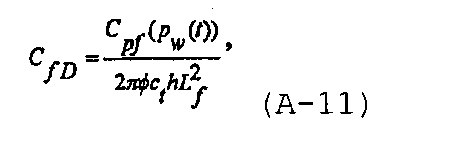
и уравнение безразмерного материального баланса во время нагнетания при давлении, достаточном для создания и увеличения протяженности гидравлического разрыва, может быть записано в виде
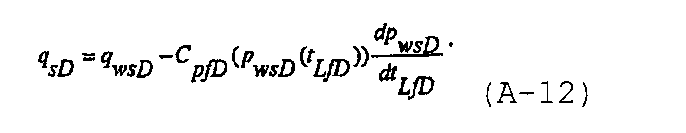
Используя способ Correa и Ramey, раскрытый в Correa A.C. and Ramey H.J., Jr., “Combined effects of shut-in and production: Solution with a new inner boundary condition”, SPE 15579 (1986), и Correa A.C. and Ramey H.J., Jr., “A method for pressure buildup analysis of drillstem tests”, SPE 16802 (1987), уравнение материального баланса, применимое во все моменты времени для последовательности из нагнетания в трещину и спада давления совместно с созданием и увеличением протяженности трещины и при постоянной упругоемкости после закрытия трещины, можно записать в виде
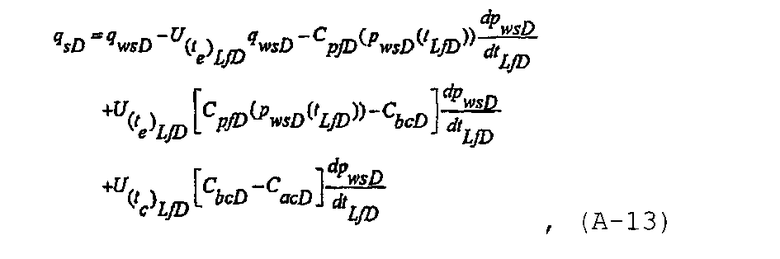
где единичная ступенчатая функция определяется как
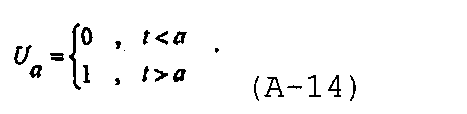
После разложения и упрощения преобразование Лапласа уравнения материального баланса для нагнетания с созданием и увеличением протяженности трещины записывается как
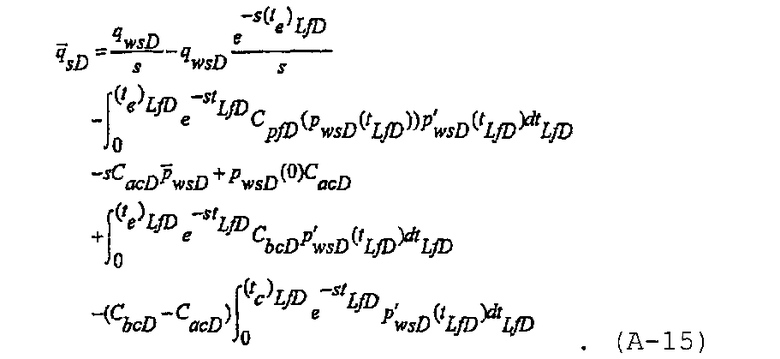
При увеличении полудлины трещины во время нагнетания может потребоваться решение для безразмерного давления как в случае распространяющейся трещины, так и трещины с фиксированной полудлиной. Решение для безразмерного давления может быть получено путем интегрирования решения для линейного источника, которое может быть записано в виде
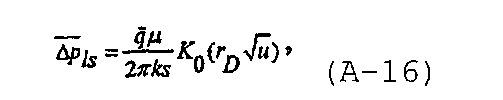
интегрированием от 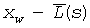 до
до 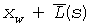 по
по  , где u=sf(s) и f(s)=1 для коллектора с единообразной пористостью. В данном случае предполагается, что полудлина трещины может быть записана как функция только переменной s Лапласа. В функции безразмерных переменных
, где u=sf(s) и f(s)=1 для коллектора с единообразной пористостью. В данном случае предполагается, что полудлина трещины может быть записана как функция только переменной s Лапласа. В функции безразмерных переменных 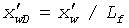 и
и 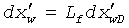 решение для линейного источника интегрируют от
решение для линейного источника интегрируют от 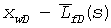 до
до 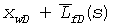 , что может быть записано как
, что может быть записано как
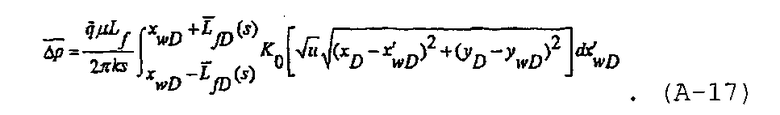
В предположении, что центр скважины находится в начале координат, x wD=y wD=0,
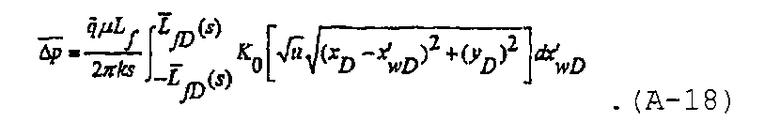
В области Лапласа в предположении постоянного потока расход может быть записан в виде
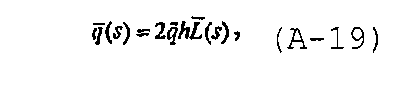
а решение для плоского источника может быть записано в безразмерных членах как
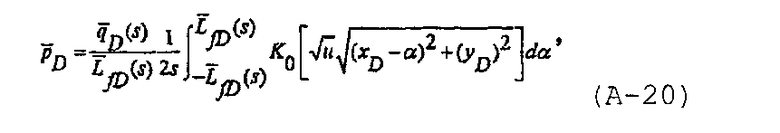
где
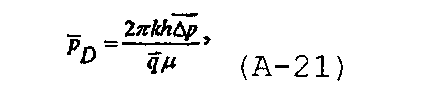

и, задав суммарный расход в виде 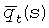 , безразмерный расход можно записать как
, безразмерный расход можно записать как
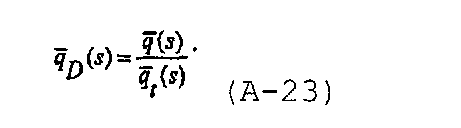
Можно предположить, что суммарный расход возрастает пропорционально с увеличением полудлины трещины, так что 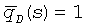 . Решение оценивают в плоскости трещины, и после упрощения интеграла с использованием тождества Ozkan и Raghanan, раскрытого в Ozkan E. and Raghanan R., “New solutions for well-test-analysis problems: Part 2 - Computational considerations and applications”, SPEFE, 369 (September 1991), решение в области Лапласа для безразмерного потока при изменяющейся полудлине трещины может быть записано в виде
. Решение оценивают в плоскости трещины, и после упрощения интеграла с использованием тождества Ozkan и Raghanan, раскрытого в Ozkan E. and Raghanan R., “New solutions for well-test-analysis problems: Part 2 - Computational considerations and applications”, SPEFE, 369 (September 1991), решение в области Лапласа для безразмерного потока при изменяющейся полудлине трещины может быть записано в виде

а решение для бесконечно высокой удельной проводимости может быть получено путем оценивания решения для однородного потока при  , и оно может быть записано как
, и оно может быть записано как
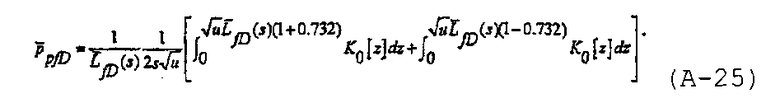
Во время распространения трещины безразмерная полудлина трещины в области Лапласа изменяется от 0 до 1, и, используя приближение степенной модели, представленное в Nolte K.G., “Determination of fracture parameters from fracturing pressure decline”, SPE 8341 (1979), безразмерную полудлину трещины в области Лапласа можно записать в виде
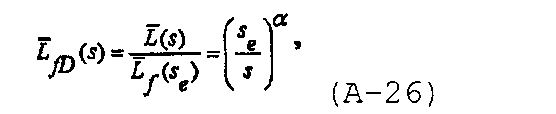
где s e является переменной области Лапласа в конце закачивания. В области Лапласа безразмерная полудлина трещины может быть записана для случая распространения и закрытия трещины как
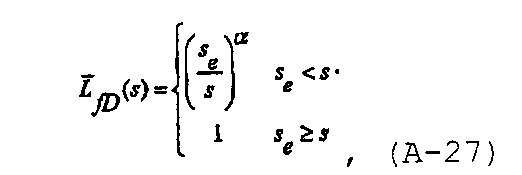
где показатель степенной модели находится в пределах от α=1/2 в случае низкоэффективной (высокое давление разрыва до протекания флюида) трещины до α=1 в случае высокоэффективной (низкое давление разрыва до протекания флюида) трещины.
В течение периода до закрытия трещины и после закрытия трещины, когда полудлина трещины является неизменной, решение в области Лапласа для безразмерного давления в коллекторе для случая трещины с бесконечно высокой удельной проводимостью может быть записано в виде

Может быть осуществлена суперпозиция двух различных моделей коллектора, одной для распространяющейся трещины и одной для трещины с фиксированной длиной, чтобы получить решение для безразмерного давления в стволе скважины согласно записи интегралов суперпозиции (Дюамеля) в виде
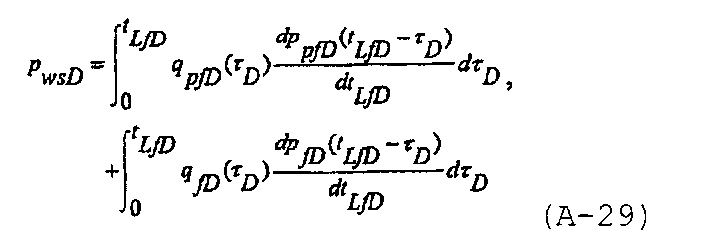
где q pfD(t LfD) представляет собой безразмерный расход в случае модели распространяющейся трещины, а q fD(t LfD) представляет собой безразмерный расход в случае модели трещины с фиксированной полудлиной, используемой в течение периода до закрытия трещины и спада давления после закрытия трещины. Исходное состояние в трещине и коллекторе представляет собой постоянное исходное давление, p D(t LfD)=p pfD(t LfD)=p fD(t LfD)=0, и с учетом исходного состояния преобразование Лапласа относительно интеграла суперпозиции (Дюамеля) записывается как
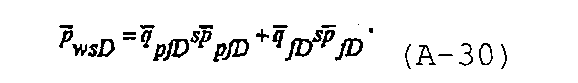
В области Лапласа уравнение безразмерного материального баланса может быть разделено на часть, относящуюся к нагнетанию, и часть, относящуюся к спаду давления, согласно записи в виде

при этом безразмерный расход из коллектора во время распространения трещины может быть записан как
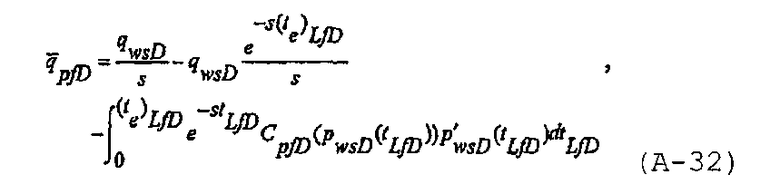
а безразмерный расход через трещину до закрытия трещины и после закрытия трещины может быть записан в виде
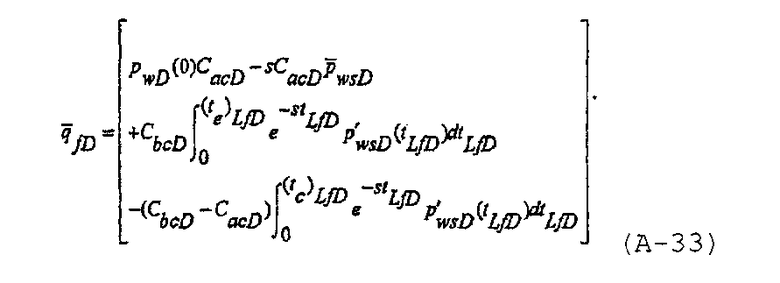
При использовании принципа суперпозиции для получения решения необходимо, чтобы зависящий от давления безразмерный коэффициент упругоемкости распространяющейся трещины был записан как функция только времени. Допустим, что распространение трещины моделируется степенной моделью и записывается как
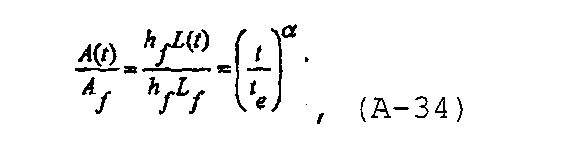
Объем трещины как функции времени может быть записан в виде
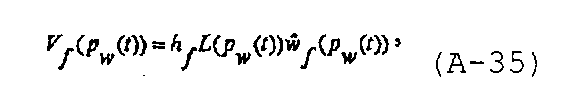
используя степенную модель, его также можно записать как
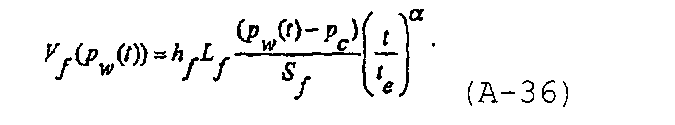
Производная объема трещины по давлению в стволе скважины может быть записана в виде
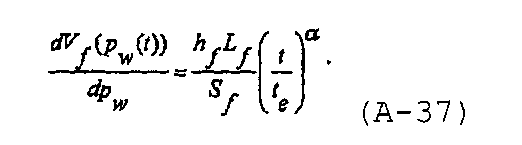
Напомним, что коэффициент упругоемкости распространяющейся трещины может быть записан как
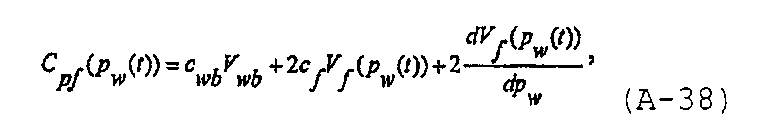
при этом с учетом степенной модели распространения трещины он может быть записан в виде
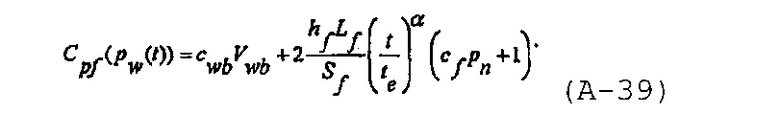
Как отмечено в Hagoort J., “Waterflood-induced hydraulic fracturing”, PhD Thesis, Delft Tech. Univ. (1981), Koning E.J.L. and Niko H., “Fractured water-injection wells: A pressure falloff test for determining fracturing dimensions”, SPE 14458 (1985), Koning E.J.L., “Waterflooding under fracturing conditions”, PhD Thesis, Delft Technical University (1988), van den Hoek P.J., “Pressure transient analysis in fractured produced water injection wells”, SPE 77946 (2002), и van den Hoek P.J., “A novel methodology to derive the dimensions and degree of containment of waterflood-induced fractures from pressure transient analysis”, SPE 84289 (2003), c f p n(t)□ 1, и коэффициент упругоемкости распространяющейся трещины может быть записан как
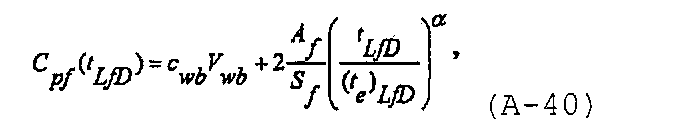
при этом он не является функцией давления и позволяет использовать принцип суперпозиции для получения решения.
Объединение уравнений материального баланса и интегралов суперпозиции (Дюамеля) приводит к

и после обращения во временную область решение для спада давления после нагнетания в трещину применительно к случаю распространяющейся трещины, постоянной упругоемкости до закрытия трещины и постоянной упругоемкости после закрытия трещины может быть записано в виде

Отвечающие предельному случаю решения могут быть получены с учетом интегрального члена, содержащего упругоемкость распространяющейся трещины. Когда tLfD□(t e)LfD, производная решения для распространяющейся трещины может быть записана как
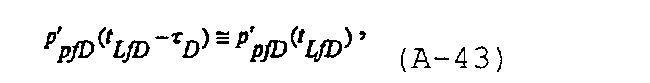
и производная решения для трещины также может быть аппроксимирована в виде
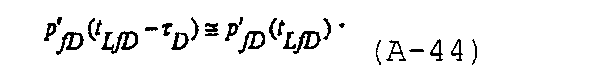
Из формулировки безразмерного решения для распространяющейся трещины следует, что, когда t
LfD>(t
e)LfD, решения для распространяющейся трещины и для трещины являются одинаковыми, и отсюда  . Следовательно, при tLfD□(te)LfD решение для безразмерного давления в стволе скважины может быть записано как
. Следовательно, при tLfD□(te)LfD решение для безразмерного давления в стволе скважины может быть записано как
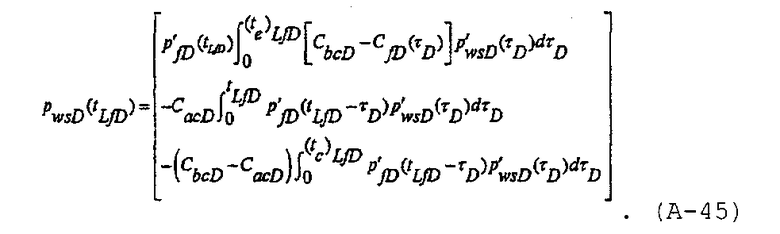
Коэффициент упругоемкости до закрытия трещины по определению всегда больше, чем коэффициент упругоемкости распространяющейся трещины, и разность двух коэффициентов не может быть равна нулю, если только моментально не образуется трещина половинной длины. Однако разность является относительно небольшой по сравнению с C bcD или C acD, и когда безразмерное время нагнетания является небольшим и t LfD>(t e)LfD, интегральный член, содержащий коэффициент упругоемкости распространяющейся трещины, становится пренебрежимо малым.
Поэтому при небольшом безразмерном времени нагнетания и (te)LfD□tLfD<(tc)LfD отвечающее предельному случаю решение для безразмерного давления в стволе скважины до закрытия трещины может быть записано в виде

и оно может быть упрощено в области Лапласа и обращено обратно во временную область для получения отвечающего предельному случаю решения для безразмерного давления в стволе скважины до закрытия трещины, записываемого в виде
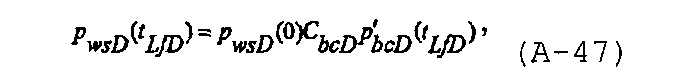
которое является решением для испытания закачиванием в случае скважины с гидравлическим разрывом, с постоянной упругоемкостью до закрытия трещины.
Когда безразмерное время нагнетания является небольшим, и tLfD□(tc)LfD□(te)LfD, производная решения для трещины может быть аппроксимирована как
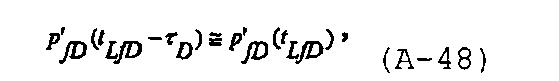
а при tLfD□(tc)LfD и 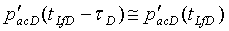 решение для безразмерного давления в стволе скважины можно записать в виде
решение для безразмерного давления в стволе скважины можно записать в виде
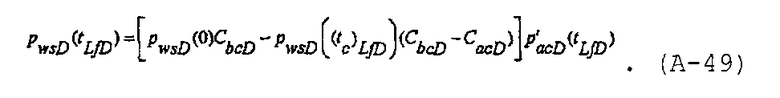
IV. Теоретическая модель В - Аналитическое решение для переходного процесса изменения давления в случае скважины, имеющей многочисленные вертикальные трещины с бесконечно высокой удельной проводимостью в бесконечном плитчатом коллекторе
На фигуре 4 вертикальная трещина показана под произвольным углом θ относительно оси x D. Как предложено в Craig D.P., “Analytical modeling of a fracture-injection/falloff sequence and the development of a refracture-candidate diagnostic test”, PhD Dissertation, Texas A&M Univ., Колледж-Стейшен, Техас (2005), в предположении изотропного коллектора решение В области Лапласа для плоского источника с однородным потоком может быть записано в виде

где безразмерные переменные определяются как


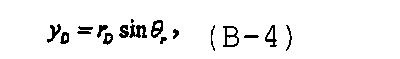
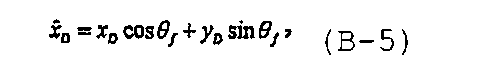
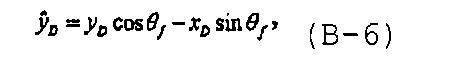
а θ f является углом между трещиной и осью x D, (r D,θ r) представляют собой полярные координаты точки (x D,y D), а (α,θ f) являются полярными координатами точки вдоль трещины, что раскрыто в Ozkan E., Yildiz T. and Kuchuk F.J., “Transient pressure behavior of duallateral wells”, SPE 38760 (1997). Объединение уравнений с (В-3) по (В-6) приводит к

и
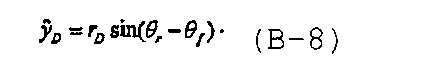
Следовательно, решение в области Лапласа для плоского источника для случая трещины, повернутой на угол θ f от точки (r D,θ r), может быть записано в виде
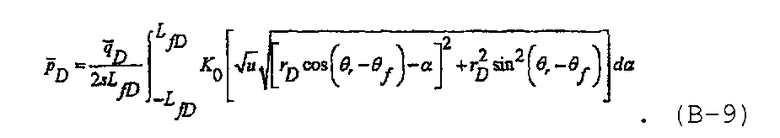
В случае скважины, имеющей n f трещин, сообщающихся в стволе скважины, суммарный расход из скважины в предположении, что вся добыча осуществляется через трещины, может быть записан как
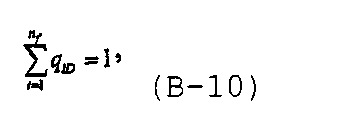
где q iD является безразмерным расходом через i-тую трещину, определяемым как
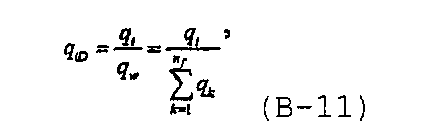
а q i является расходом через i-тую трещину.
Как раскрыто в Raghavan R., Chen C-C. and Agarwal B., “An analysis of horizontal wells intercepted by multiple fractures”, SPEJ 235 (September 1997), решение для безразмерного давления получают в результате суперпозиции всех трещин и записывают, используя интеграл суперпозиции (Дюамеля) в виде
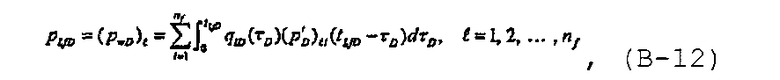
где в производной давления учитываются воздействия трещины i на трещину 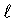 .
.
Преобразование Лапласа относительно уравнения безразмерного расхода может быть записано как

а при начальном условии p D(t LfD=0)=0 преобразование Лапласа относительно решения для безразмерного давления может быть записано в виде
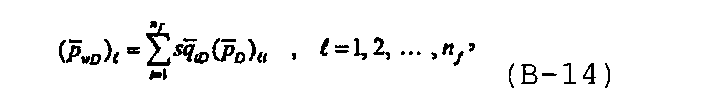
где 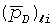 является решением в области Лапласа для однородного потока в случае единственной трещины, записываемым с учетом воздействий многочисленных трещин как
является решением в области Лапласа для однородного потока в случае единственной трещины, записываемым с учетом воздействий многочисленных трещин как
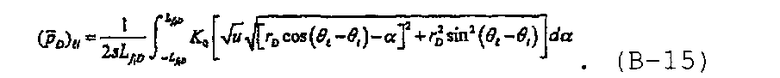
Теперь решение в области Лапласа для многочисленных трещин при однородном потоке может быть записано в виде
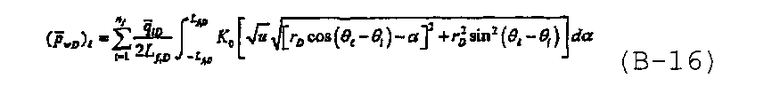
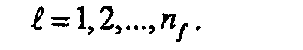
В области Лапласа может быть получено полуаналитическое решение для многочисленных произвольно ориентированных трещин с бесконечно высокой удельной проводимостью. Если поток не является однородным вдоль трещины (трещин), решение можно записать, используя суперпозицию, при которой учитываются воздействия многочисленных трещин, в виде
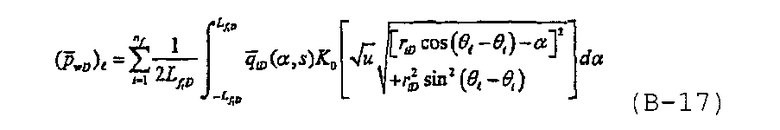
где 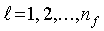 . Если точка (r
iD,θ
i) сводится к точке вдоль оси i-ой трещины, то ось координат и ось трещины совпадают и уравнение (В-7) приводится к
. Если точка (r
iD,θ
i) сводится к точке вдоль оси i-ой трещины, то ось координат и ось трещины совпадают и уравнение (В-7) приводится к
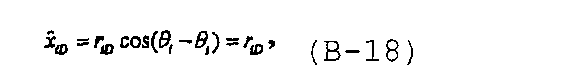
и решение для многочисленных трещин может быть записано как
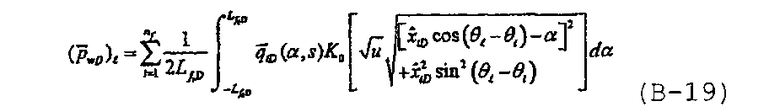
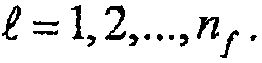
В предположении, что каждая трещина является однородной и симметричной, то есть 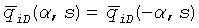 , решение для многочисленных трещин с бесконечно высокой удельной проводимостью в случае изотропного коллектора может быть записано в виде
, решение для многочисленных трещин с бесконечно высокой удельной проводимостью в случае изотропного коллектора может быть записано в виде
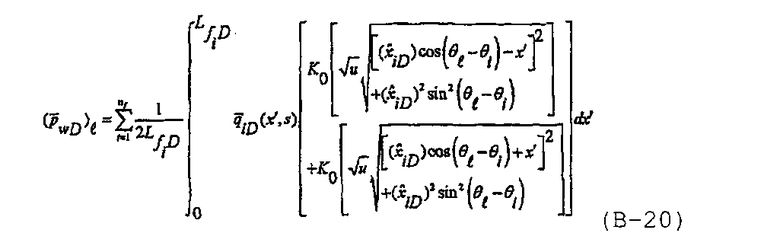
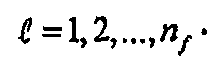
Полуаналитическое решение вместо решения для многочисленных трещин с бесконечно высокой удельной проводимостью получают, разделяя каждую трещину на n
fs равных сегментов длиной 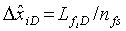 и предполагая, что поток является постоянным в каждом сегменте. Хотя число сегментов в каждой трещине является одинаковым, длина сегмента может быть особой для каждой трещины,
и предполагая, что поток является постоянным в каждом сегменте. Хотя число сегментов в каждой трещине является одинаковым, длина сегмента может быть особой для каждой трещины,  . В случае дискретизации решение в области Лапласа для многочисленных трещин с бесконечно высокой удельной проводимостью при изотропном резервуаре может быть записано как
. В случае дискретизации решение в области Лапласа для многочисленных трещин с бесконечно высокой удельной проводимостью при изотропном резервуаре может быть записано как
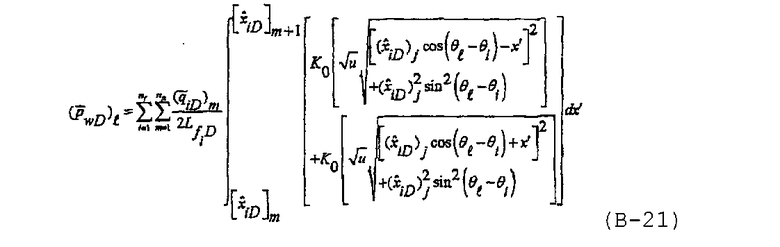
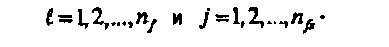
Решение для многочисленных трещин с бесконечно высокой удельной проводимостью с учетом анизотропии проницаемости в бесконечном плитчатом коллекторе получают, задавая безразмерные переменные расстояния, предложенные в Ozkan E. and Raghavan R., “New solutions for well-test-analysis problems: Part 1 - Analytical considerations”, SPEFE, 359 (September 1991), в виде
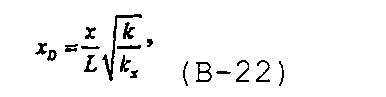
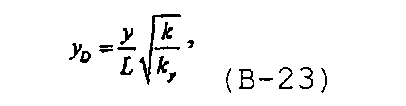
и
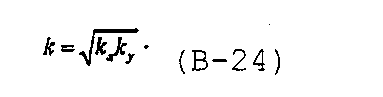
Безразмерные переменные изменяют масштаб анизотропного коллектора с преобразованием в эквивалентную изотропную систему. В результате изменения масштаба изменяются безразмерные полудлины трещин, и они должны быть повторно определены, как предложено в Spivey J.P. and Lee W.J., “Estimating the pressure-transient response for a horizontal or a hydraulically fractured well at an arbitrary orientation in an anisotropic reservoir”, SPE Reservoir Eval. & Eng. (October 1999), в виде
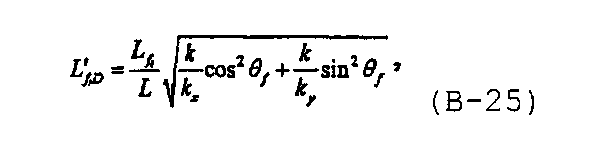
при этом угол трещины относительно оси x D с измененным масштабом может быть записан как
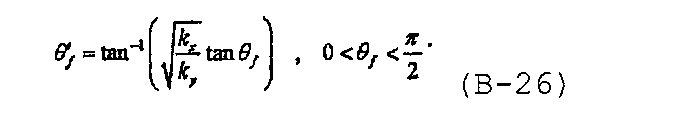
Когда θ
f=0 или θ
f=π/2, масштаб угла не изменяется, и 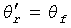 .
.
При наличии повторно определенных безразмерных переменных решение для многочисленных трещин с бесконечно высокой удельной проводимостью с учетом анизотропии проницаемости может быть записано в виде
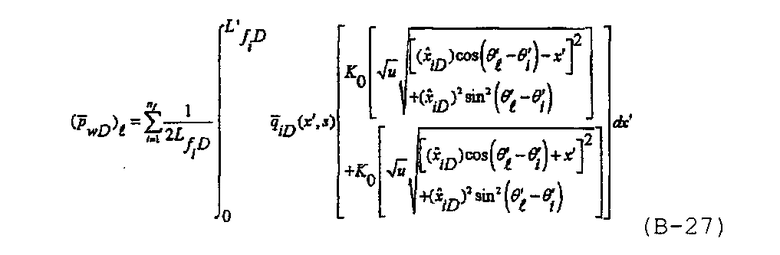
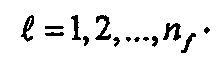
где угол θ' определен в эквивалентном изотропном коллекторе с измененным масштабом и связан с анизотропным коллектором формулой
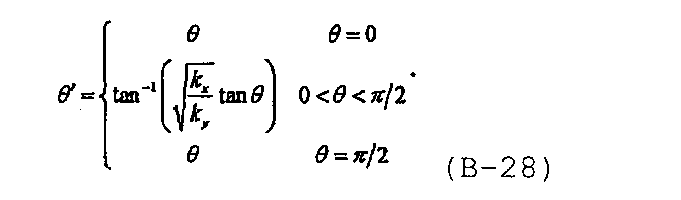
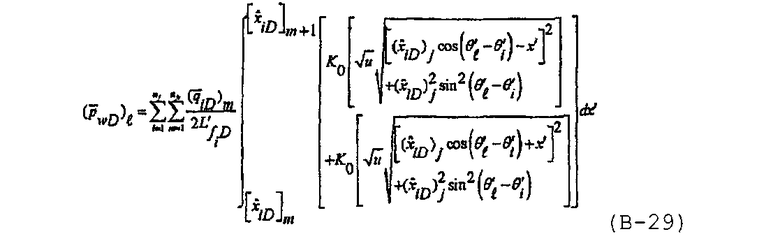
Полуаналитическое решение в области Лапласа для многочисленных произвольно ориентированных трещин с бесконечно высокой удельной проводимостью может быть записано как
 ,
,
при этом в области Лапласа суммарный безразмерный расход определяется по формуле

а уравнение, относящееся к безразмерному давлению в стволе скважины, для каждой трещины записывается как
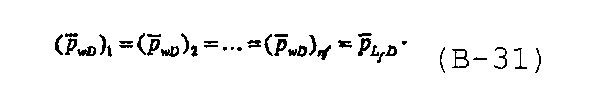
Для каждой трещины, разделенной на n fs сегментов одинаковой длины с однородным потоком, уравнениями с (В-29) по (В-31) описывается система (n f n fs+2) уравнений с (n f n fs+2) неизвестными. Для решения системы уравнений необходимо записать уравнение для каждого сегмента трещины, что показано ниже в Разделе V для многочисленных трещин с конечной удельной проводимостью. Систему уравнений решают в области Лапласа и обращают во временную область, чтобы получить безразмерное давление, используя алгоритм Стефеста, предложенный в Stehfest H., “Numerical inversion of Laplace transforms”, Communications of the ACM, 13, № 1, 47-49 (January 1970).
На фигуре 5 показаны график с логарифмическим масштабом по обеим осям, иллюстрирующий зависимость безразмерного давления от безразмерного времени для простой трещины с бесконечно высокой удельной проводимостью, и график произведения (1+δ
L) и безразмерного давления для крестовой щели с бесконечно высокой удельной проводимостью, где угол между щелями равен π/2. На фигуре 5 вставкой графически иллюстрируется крестовая трещина с полудлиной 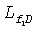 первичной трещины, а полудлина вторичной трещины определяется отношением полудлин вторичной трещины и первичной трещины,
первичной трещины, а полудлина вторичной трещины определяется отношением полудлин вторичной трещины и первичной трещины,  при этом δ
L=1 на фигуре 5. На фигуре 5 показано, что в очень ранние моменты безразмерного времени все кривые совмещаются, но поскольку эффекты взаимодействия наблюдаются в крестовых трещинах, решения для простой трещины и крестовых трещин расходятся.
при этом δ
L=1 на фигуре 5. На фигуре 5 показано, что в очень ранние моменты безразмерного времени все кривые совмещаются, но поскольку эффекты взаимодействия наблюдаются в крестовых трещинах, решения для простой трещины и крестовых трещин расходятся.
V. Теоретическая модель С - Аналитическое решение для переходного процесса изменения давления в случае скважины, имеющей многочисленные вертикальные трещины с конечной удельной проводимостью в бесконечном плитчатом коллекторе
Чтобы получить решение для многочисленных вертикальных трещин с конечной удельной проводимостью, необходимо записать общее решение для вертикальной трещины с конечной удельной проводимостью, находящейся под любым произвольным углом θ относительно оси x D. Затем точное решение следует из полуаналитических решений для конечной удельной проводимости, предложенных в Cinco-L., H., Samaniego-V., F. and Dominguez-A., F., “Transient pressure behavior for a well with a finite-conductivity vertical fracture”, SPEJ, 253 (August 1978), и для случая дуальной пористости, предложенных в Cinco-Ley H. and Samaniego-V., F., “Transient pressure analysis: Finite conductivity fracture case versus damage fracture case”, SPE 10179 (1981). На фигуре 6 показана в изотропном коллекторе вертикальная трещина с конечной удельной проводимостью под углом θ относительно оси x D.
Чтобы получить решение для конечной удельной проводимости, необходимо связать коллектор и компоненты потока через трещину, а при получении решения предположить, что
- трещина моделируется как однородная плитчатая пористая среда и имеет полудлину L f, трещины, ширину w f трещины и полностью проходит сквозь всю толщу h коллектора;
- флюид втекает в трещину вдоль длины трещины, и поток не поступает через концы трещины;
- поток флюида в трещине является несжимаемым и установившимся вследствие ограниченного объема порового пространства трещины по сравнению с коллектором;
- центральная ось трещины совмещена с осью 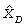 , которая повернута на угол θ от оси x
D.
, которая повернута на угол θ от оси x
D.
В статье Cinco-L., H., Samaniego-V., F. and Dominguez-A., F., “Transient pressure behavior for a well with a finite-conductivity vertical fracture”, SPEJ, 253 (August 1978), показано, что в области Лапласа распределение давлений в трещине с конечной удельной проводимостью может быть записано как

где  является общим решением для коллектора, а безразмерная удельная проводимость трещины определяется как
является общим решением для коллектора, а безразмерная удельная проводимость трещины определяется как
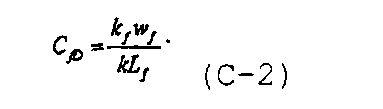
При наличии приведенных выше в Разделе IV определений решение в области Лапласа для многочисленных произвольно ориентированных трещин с конечной удельной проводимостью применительно к единственной трещине, предложенное в Craig D.P., “Analytical modeling of a fracture-injection/falloff sequence and the development of a refracture-candidate diagnostic test”, PhD dissertation, Texas A&M Univ., Колледж-Стейшен, Техас (2005), записывается в виде
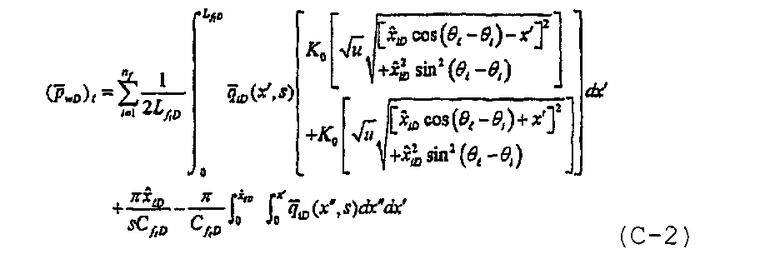
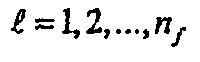 .
.
Полуаналитическое решение вместо решения для многочисленных трещин с конечной удельной проводимостью может быть получено при дискретизации компонента коллектора, описанной выше в Разделе IV, и трещины. Как показано в Cinco-Ley H. and Samaniego-V., F., “Transient pressure analysis: Finite conductivity fracture case versus damage fracture case”, SPE 10179 (1981), компонент потока трещины, который может быть записан в виде
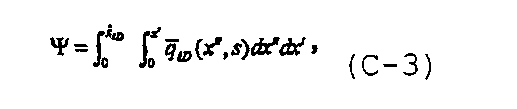
можно аппроксимировать формулой
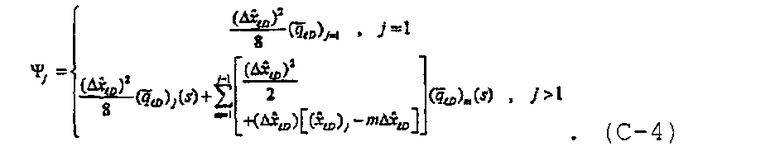
При объединении компонентов коллектора и потока трещины, и с учетом анизотропии, полуаналитическое решение для многочисленных трещин с конечной удельной проводимостью может быть записано как
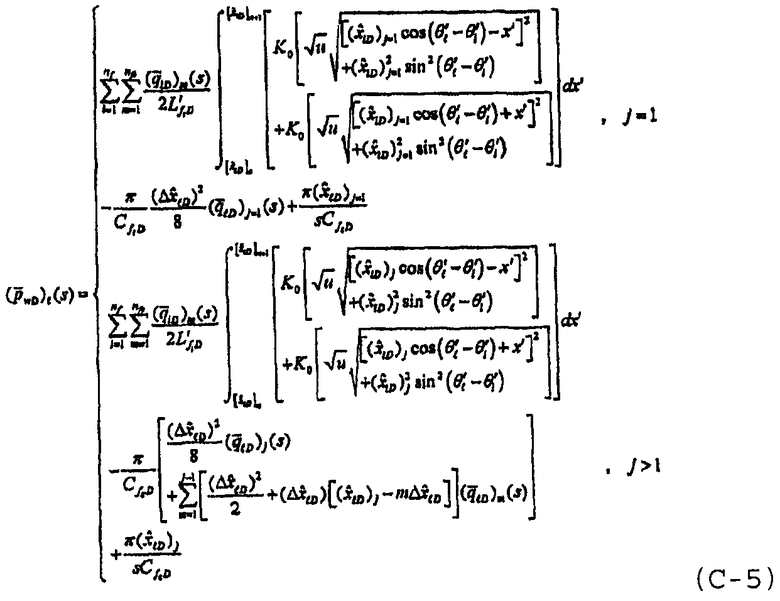
при j=1,2,…,n
fs и  , и наличии безразмерного суммарного расхода, определяемого в области Лапласа формулой
, и наличии безразмерного суммарного расхода, определяемого в области Лапласа формулой

а уравнение, относящееся к безразмерному давлению в стволе скважины, записывается для каждой трещины как
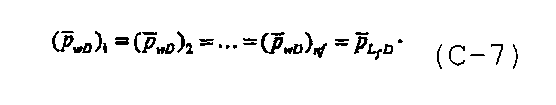
Для каждой трещины, разделенной на n fs сегментов одинаковой длины с однородным потоком, уравнениями с (С-5) по (С-7) описывается система (n f n fs+2) уравнений и (n f n fs+2) неизвестных. Для решения системы уравнений необходимо записать уравнение для каждого сегмента трещины. Для примера рассмотрим дискретизированную крестовую трещину, при этом, как показано на фигуре 7, каждое крыло трещины разделено на три сегмента.
Определим следующие переменные подстановки как
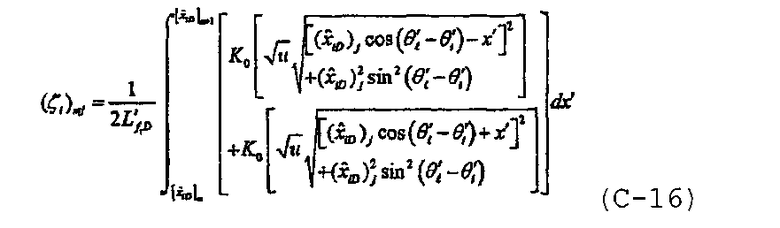
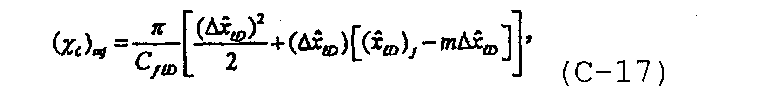
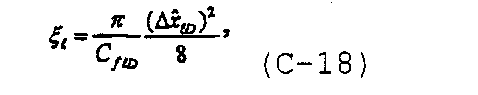
и
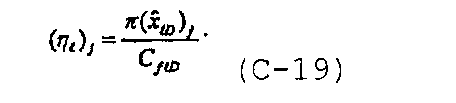
В случае крестовой трещины в анизотропном коллекторе, показанной на фигуре 7, первичная трещина ориентирована под углом 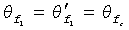 , а вторичная трещина ориентирована под углом
, а вторичная трещина ориентирована под углом 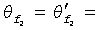 π/2. Пусть опорная длина задана как
π/2. Пусть опорная длина задана как 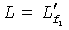 и пусть длина вторичной трещины задана как
и пусть длина вторичной трещины задана как 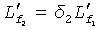 . Следовательно, безразмерные полудлины трещин определяются как
. Следовательно, безразмерные полудлины трещин определяются как 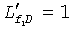 и
и 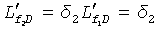 .
.
Положим j=1, и тогда уравнение безразмерного давления для первичной трещины после приведения подобных членов может быть записано в виде

Для j=2 уравнение безразмерного давления может быть записано как
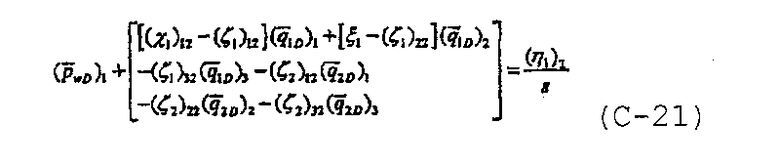
и для j=3 уравнение безразмерного давления может быть записано в виде

Уравнение безразмерного давления для вторичной трещины может быть записано для случая j=1 в виде
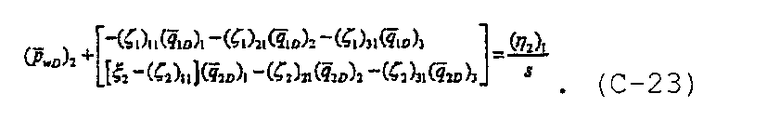
При j=2 уравнение безразмерного давления для вторичной трещины может быть записано как

и при j=3 уравнение безразмерного давления может быть записано в виде
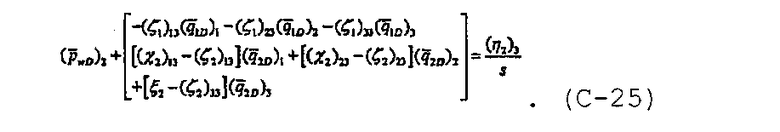
При наличии разложенного в ряд уравнения расхода и записанного в виде
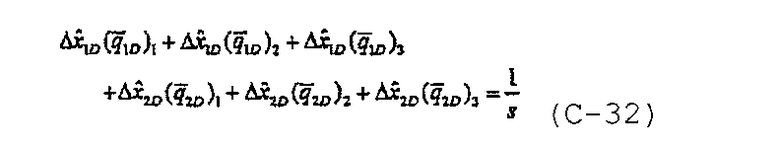
и с учетом  линейная система уравнений также может быть записана в матричной форме
линейная система уравнений также может быть записана в матричной форме
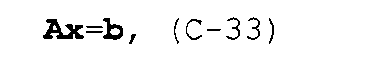
где
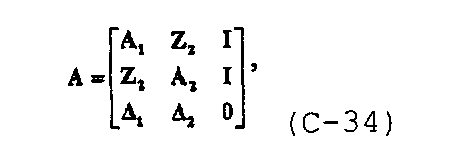
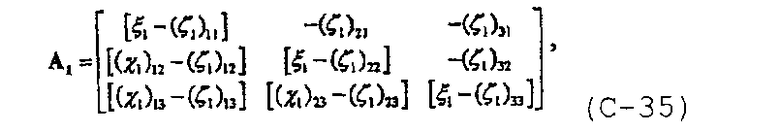
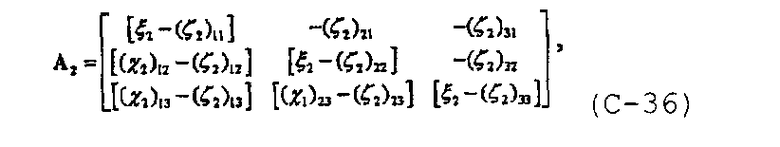

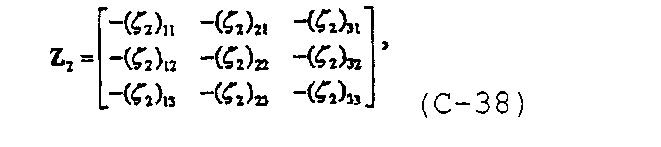
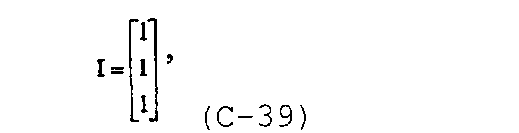
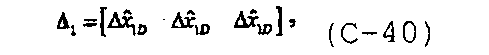
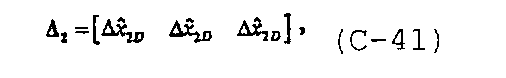

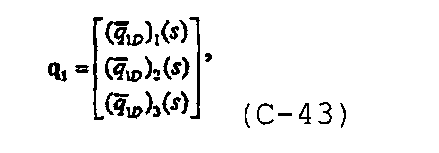

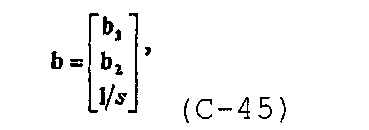
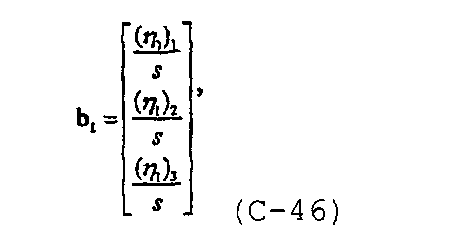
и
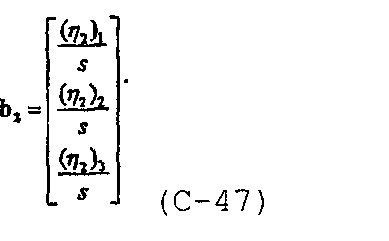
В диссертации Craig D.P., “Analytical modeling of a fracture-injection/falloff sequence and the development of a refracture-candidate diagnostic test”, PhD dissertation, Texas A&M Univ., Колледж-Стейшен, Техас (2005), показано, что для n f трещин с n fs сегментами система уравнений также может быть записана в общей форме.
На фигуре 8 представлен график с логарифмическим масштабом по обеим осям зависимости безразмерного давления и производной безразмерного давления от безразмерного времени для крестовой трещины, при этом угол между трещинами составляет π/2. На фигуре 8 δ L=1, а вставкой графически иллюстрируется крестовая трещина с удельной проводимостью C f1D первичной трещины, а удельная проводимость вторичной трещины определяется отношением удельных проводимостей вторичной и первичной трещин, δ C=C f2D=C f1D, при этом δ С=1 на фигуре 8.
В дополнение к тому, что каждая трещина может иметь особую полудлину и удельную проводимость, в решении для многочисленных трещин также допускается произвольный угол между трещинами. На фигуре 9 показаны типовые кривые при постоянном расходе для случая равных полудлин δ L=1 первичной и вторичной трещин и равных удельных проводимостей δ С=1 первичной и вторичной трещин, при этом C f1D=100π. Как видно из типовых кривых для θ f2=π/2, π/4 и π/8, типовыми кривыми иллюстрируются влияния уменьшения угла между трещинами.
VI. Система условных обозначений, используемых в настоящей заявке, относящаяся к следующим терминам:
А - площадь трещины во время распространения, L2, м2
A f - площадь трещины, L2, м2
A ij - элемент матрицы, безразмерный
В - объемный коэффициент пласта, безразмерный
c f - сжимаемость флюида в трещине, Lt2/m, Па-1
c t - полная сжимаемость, Lt2/m, Па-1
c wb - сжимаемость флюида в стволе скважины, Lt2/m, Па-1
С - упругоемкость ствола скважины, L4t2/m, м3/Па
C f - удельная проводимость трещины, m3, м3
C ac - упругоемкость после закрытия трещины, L4t2/m, м3/Па
C bc - упругоемкость до закрытия трещины, L4t2/m, м3/Па
C pf - упругоемкость распространяющейся трещины, L4t2/m, м3/Па
C fbc - упругоемкость трещины до закрытия, L4t2/m, м3/Па
C pLf - упругоемкость распространяющейся трещины при наличии многочисленных трещин, L4t2/m, м3/Па
C Lfac - упругоемкость многочисленных трещин после закрытия, L4t2/m, м3/Па
C Lfbc - упругоемкость многочисленных трещин до закрытия, L4t2/m, м3/Па
h - высота, L, м
h f - высота щели, L, м
I - интегральная функция, m/Lt, Па·с
k - проницаемость, L2, м2
k x - проницаемость по направлению x, L2, м2
k y - проницаемость по направлению y, L2, м2
K 0 - модифицированная функция Бесселя второго рода (нулевого порядка), безразмерная
L - полудлина распространяющейся трещины, L, м
L f - полудлина трещины, L, м
n f - число трещин, безразмерное
n fs - число сегментов трещины, безразмерное
p 0 - давление в стволе скважины в нулевой момент времени, m/Lt2, Па
p c - давление при закрытии трещины, m/Lt2, Па
p f - давление в коллекторе при добыче из единственной трещины, m/Lt2, Па
p i - среднее давление в коллекторе, m/Lt2, Па
p n - полезное давление в трещине, m/Lt2, Па
p w - давление в стволе скважины, m/Lt2, Па
p ac - давление в коллекторе при постоянной упругоемкости после закрытия трещины, m/Lt2, Па
p Lf - давление в коллекторе при добыче из многочисленных трещин, m/Lt2, Па
p pf - давление в коллекторе при наличии распространяющейся трещины, m/Lt2, Па
p wc - давление в стволе скважины при постоянном расходе, m/Lt2, Па
p ws - давление в стволе скважины при изменяющемся расходе, m/Lt2, Па
p fac - давление в трещине при постоянной упругоемкости трещины после закрытия, m/Lt2, Па
p pLf - давление в коллекторе при наличии распространяющейся вторичной трещины, m/Lt2, Па
p Lfac - давление в коллекторе при добыче из многочисленных трещин и постоянной упругоемкости после закрытия трещин, m/Lt2, Па
p Lfbc - давление в коллекторе при добыче из многочисленных трещин и постоянной упругоемкости до закрытия трещин, m/Lt2, Па
q - расход из коллектора, L3/t, м3/с
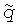 - поток с поверхности трещины, L3/t, м3/с
- поток с поверхности трещины, L3/t, м3/с
q w - расход через ствол скважины, L3/t, м3/с
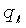 - расход флюида при протечке, L3/t, м3/с
- расход флюида при протечке, L3/t, м3/с
q s - расход из коллектора, L3/t, м3/с
q t - суммарный расход, L3/t, м3/с
q f - расход через трещину, L3/t, м3/с
q pf - расход через распространяющуюся трещину, L3/t, м3/с
q sf - расход со вскрытой поверхности забоя и стенок скважины в песчаном пласте, L3/t, м3/с
q ws - переменный расход через ствол скважины, L3/t, м3/с
r - радиус, L, м
s - переменная преобразования Лапласа, безразмерная
s e - переменная преобразования Лапласа в конце нагнетания, безразмерная
S f - жесткость трещины, m/L2t2, Па/м
S fs - скин-эффект на поверхности трещины, безразмерный
(S fs)ch - скин-эффект закупоренной трещины, безразмерный
t - время, t, с
t e - момент времени в конце нагнетания, t, с
t c - момент времени при закрытии гидравлического разрыва, t, с
t LfD - безразмерное время, безразмерная величина
u - переменная подстановки, безразмерная
U a - единичная ступенчатая функция, безразмерная
V f - объем трещины, L3, м3
V fr - остаточный объем трещины, L3, м3
V w - объем ствола скважины, L3, м3
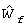 - средняя ширина трещины, L, м
- средняя ширина трещины, L, м
x - координата точки вдоль оси x, L, м
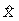 - координата точки вдоль оси
- координата точки вдоль оси 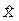 , L, м
, L, м
x w - положение ствола скважины вдоль оси x, L, м
y - координата точки вдоль оси y, L, м
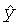 - координата точки вдоль оси
- координата точки вдоль оси 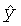 , L, м
, L, м
y w - положение ствола скважины вдоль оси y, L, м
α - показатель роста трещины, безразмерный
δ L - отношение полудлин вторичной и первичной трещин, безразмерное
Δ - разность, безразмерная
ζ - переменная подстановки, безразмерная
η - переменная подстановки, безразмерная
θ r - опорный угол, в радианах
θ f - угол трещины, в радианах
µ - вязкость, m/Lt, Па·с
ξ - переменная подстановки, безразмерная
ρ - плотность, m/L3, кг/м3
τ - переменная подстановки, безразмерная
φ - пористость, безразмерная
χ - переменная подстановки, безразмерная
ψ - переменная подстановки, безразмерная
Нижние индексы
D - безразмерный
i - индекс трещины, безразмерный
j - индекс сегмента, безразмерный
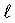 - индекс трещины, безразмерный
- индекс трещины, безразмерный
m - индекс сегмента, безразмерный
t - индекс времени, безразмерный
Для содействия лучшему пониманию настоящего изобретения приводятся нижеследующие примеры конкретных аспектов некоторых осуществлений. Никоим образом нижеследующие примеры не должны толковаться как ограничивающие или определяющие объем изобретения.
Примеры
Эксплуатационный пример
Результаты исследования спада давления после нагнетания в трещину в слое в отсутствие уже существующей трещины показаны на фигуре 10, которая содержит график зависимости расхода при нагнетании и забойного давления от времени. В течение 5,3 мин осуществлялось нагнетание воды в количестве 17,7 баррелей, обработанной 2%-ным KCl, за которым следовал период остановки скважины на 16 ч. На фигуре 11 представлен график эквивалентного давления при постоянном расходе и производной давления, построенный в значениях скорректированных псевдопеременных при использовании таких способов, какие раскрыты в Craig D.P., “Analytical modeling of a fracture-injection/falloff sequence and the development of a refracture-candidate diagnostic test”, PhD dissertation, Texas A&M Univ., Колледж-Стейшен, Техас (2005), в виде наложенной типовой кривой депрессии при постоянном расходе для скважины с добычей через вертикальную трещину с бесконечно высокой удельной проводимостью и постоянной упругоемкостью. Полудлина трещины, оцененная на основании анализа Nolte-Shlyapobersky, раскрытого в Correa A.C. and Ramey H.J., Jr., “Combined effects of shut-in and production: Solution with a new inner boundary condition”, SPE 15579 (1986), составляла 127 футов, а проницаемость на основании сопоставления с типовой кривой составляла 0,827 мД, что хорошо совпадает с проницаемостью 0,522 мД, оцененной на основании последующего сопоставления с типовой кривой испытания скважины при повышении давления.
Результаты диагностического испытания кандидата на повторный разрыв пласта с уже существующей трещиной показаны на фигуре 12, которая содержит график зависимости расхода при нагнетании и забойного давления от времени. До испытания слой был интенсифицирован гидравлическим разрывом пласта посредством проппанта 20/40 в количестве 250000 фунтов, но спустя 7 дней добыча из слоя была ниже ожидаемых результатов, и было использовано диагностическое испытание. В течение 18,5 мин осуществлялось нагнетание воды в количестве 75,8 баррелей, обработанной 2%-ным KCl, за которым следовал период остановки скважины на 4 ч. На фигуре 13 представлен график зависимости эквивалентного давления при постоянном расходе и производной давления от времени остановки скважины, построенный в значениях скорректированных псевдопеременных при использовании таких способов, какие раскрыты в Craig D.P., “Analytical modeling of a fracture-injection/falloff sequence and the development of a refracture-candidate diagnostic test”, PhD dissertation, Texas A&M Univ., Колледж-Стейшен, Техас (2005), и показана характеристическая реакция поврежденной трещины в случае скин-эффекта закупоренной скважины. Следует отметить, что переход от первой линии единичного наклона ко второй линии единичного наклона начинается при закрытии гидравлического разрыва. Следовательно, диагностическое испытание кандидата на повторный разрыв пласта качественно указывает на поврежденную уже существующую трещину, сохраняющую остаточную ширину. Поскольку данные не детализировались после прекращения действия упругоемкости, количественный анализ не является возможным.
Таким образом, приведенные выше результаты свидетельствуют, среди прочего, о том, что:
- При диагностическом испытании кандидата на повторный разрыв пласта в изолированном слое можно использовать жидкость или газ, нагнетаемый в небольшом объеме при низком расходе и давлении, превышающем давление инициирования и распространения трещины, с последующим продолжительным периодом остановки скважины.
- При условии, что время нагнетания меньше по сравнению с реакцией коллектора, результаты диагностики кандидата на повторный разрыв пласта можно анализировать как результаты испытания закачиванием.
- Изменение упругоемкости при закрытии трещины качественно может указывать на наличие уже существующей трещины. Видимое повышение упругоемкости может указывать на то, что уже существующая трещина повреждается.
- Количественный анализ типовой кривой с использованием решений для депрессии при постоянном расходе и изменяющейся упругоемкости в случае коллектора, выдающего продукт через многочисленные произвольно ориентированные трещины с бесконечно высокой или с конечной удельной проводимостью, может быть использован для оценивания полудлины (полудлин) трещин и гидропроводности коллектора пласта.
Следовательно, настоящее изобретение хорошо приспособлено для получения конечных результатов и достижения указанных преимуществ, а также тех, которые присущи ему. Хотя специалистами в данной области техники могут быть сделаны многочисленные изменения, такие изменения находятся в рамках сущности этого изобретения, определяемой прилагаемой формулой изобретения. Термины в формуле изобретения являются очевидными, без труда понимаемыми, не считая других, точно и ясно определенных заявителем.

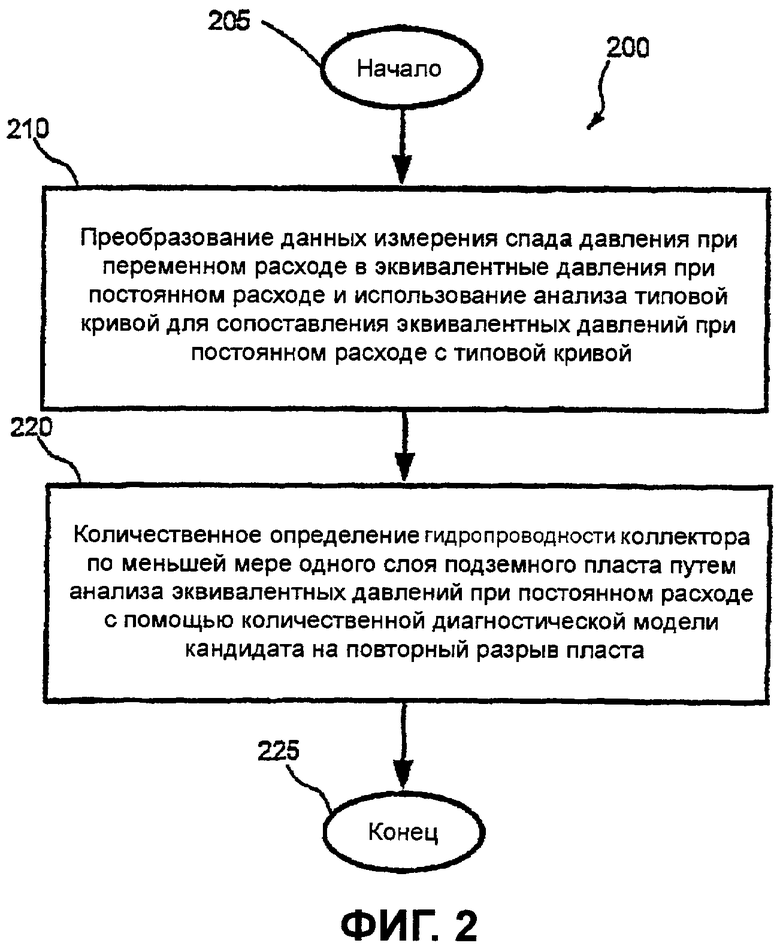
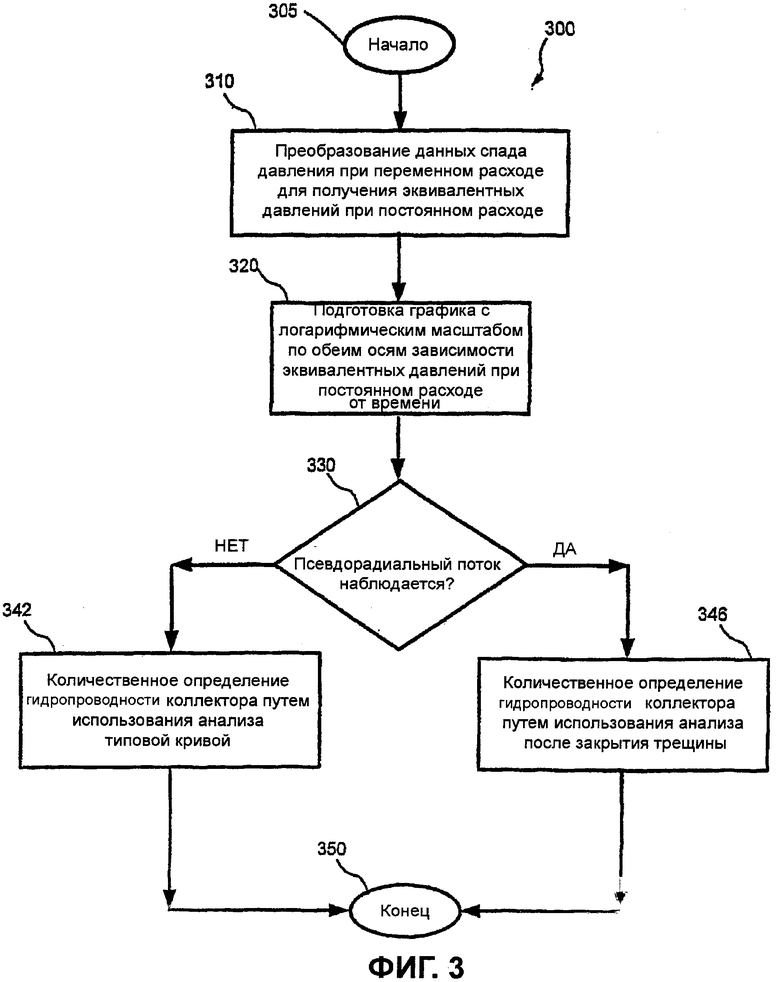
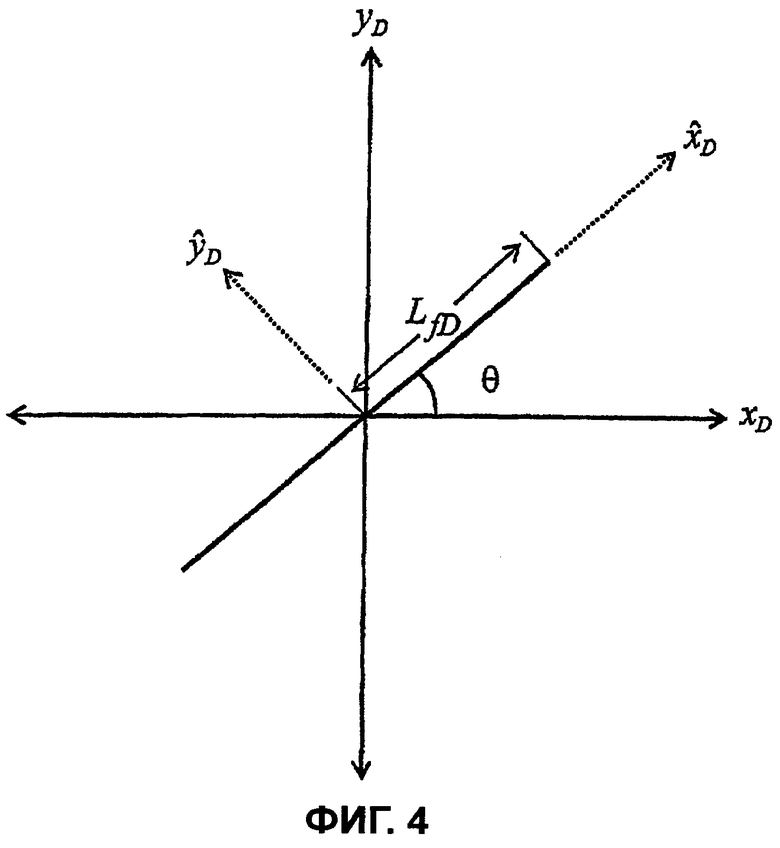
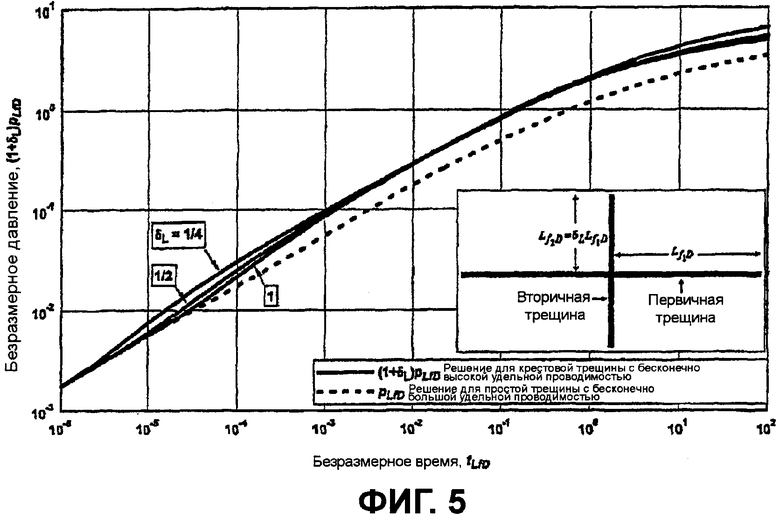

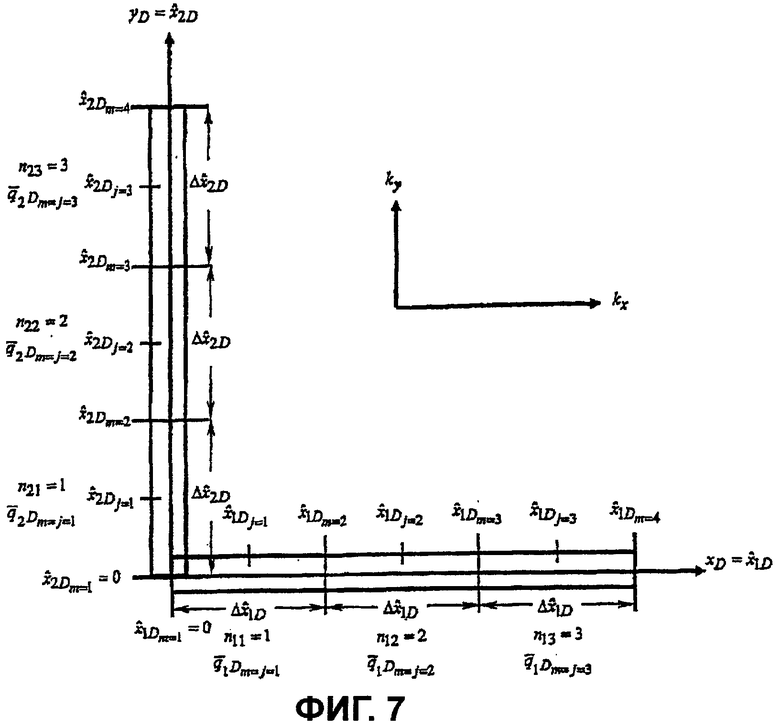
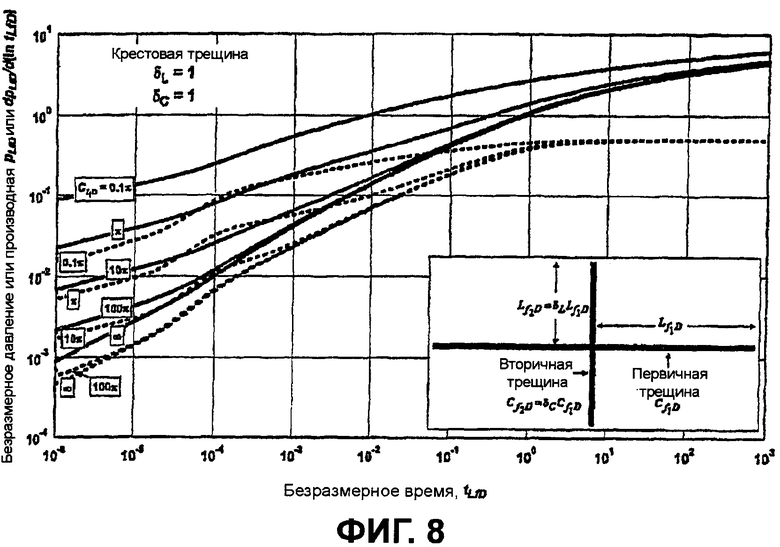
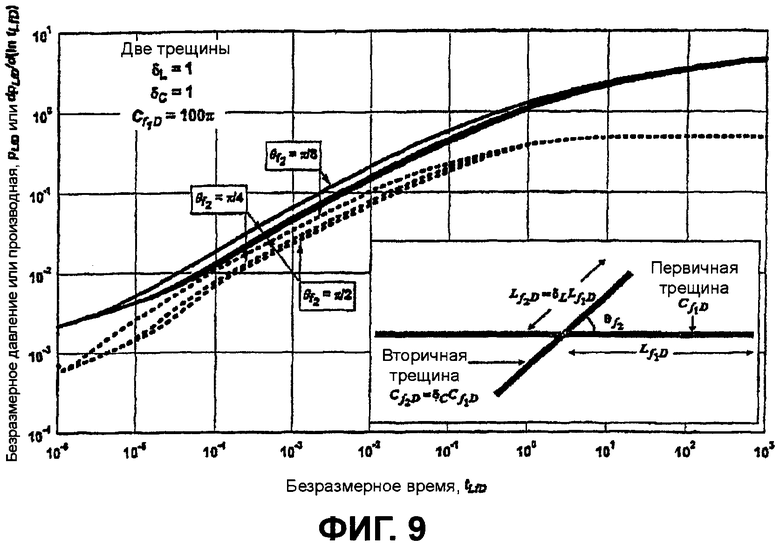
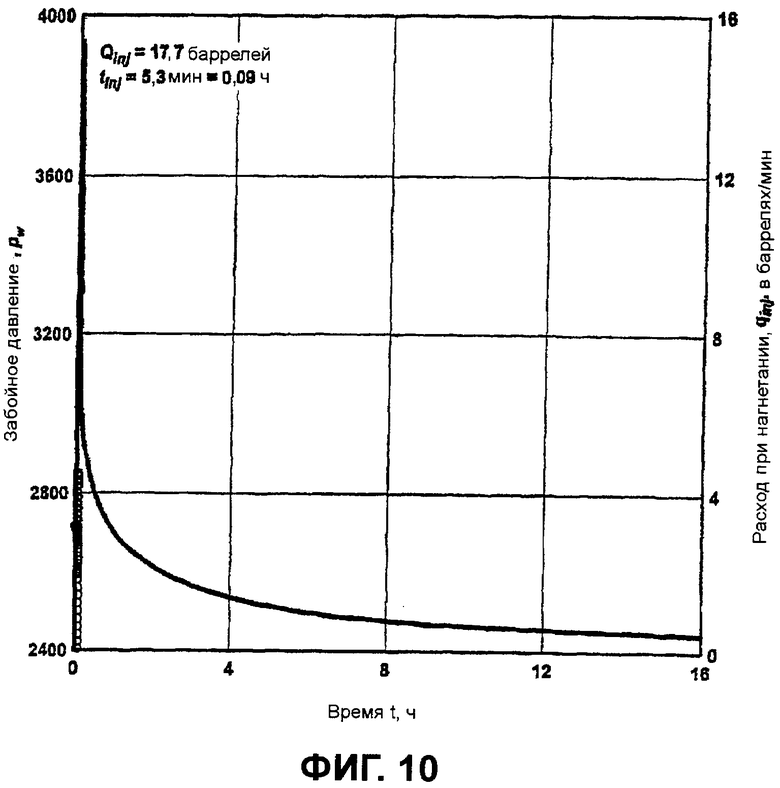
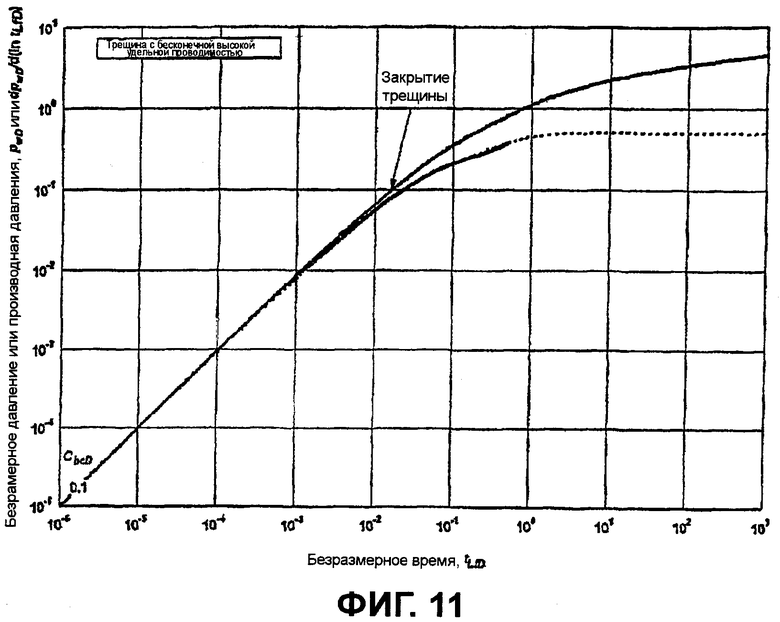
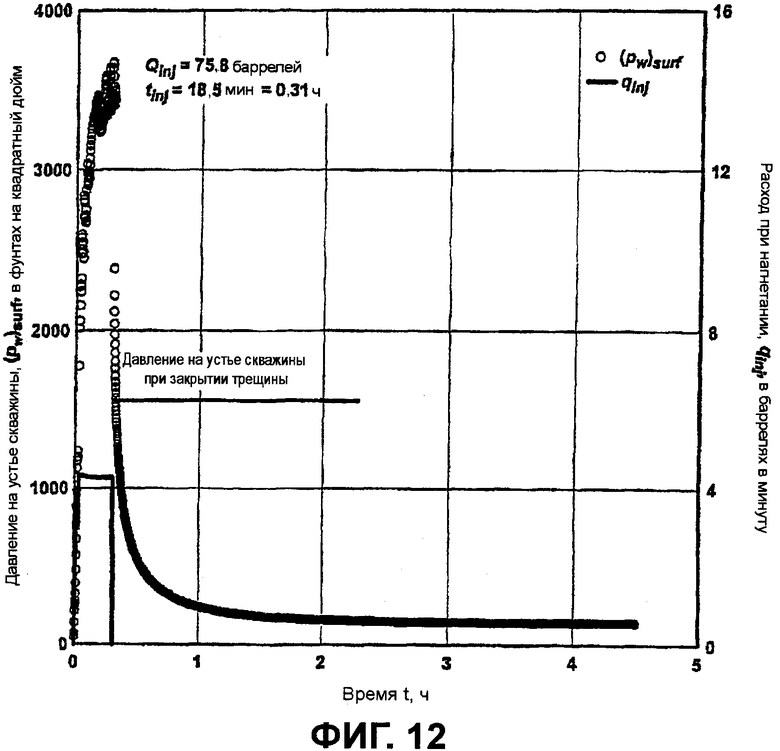
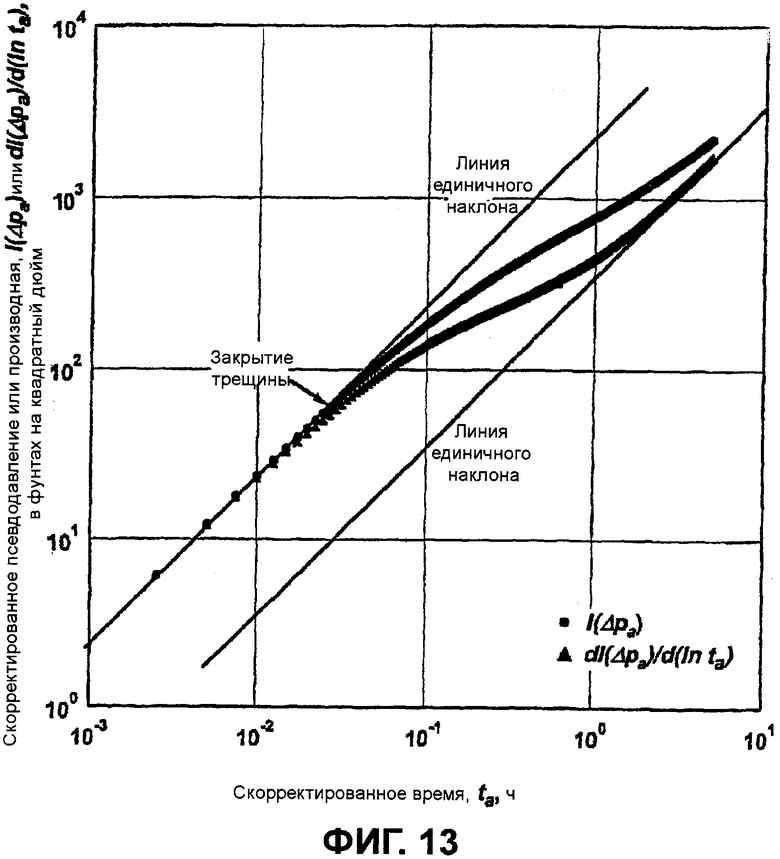
Группа изобретений относится к области исследования подземных нефтяных и газовых пластов, более конкретно для определения коллекторских свойств - гидропроводности коллекторов и средних пластовых давлений пласта путем использования количественных диагностических способов испытания кандидата на повторный разрыв пласта. Техническим результатом является повышение точности определения свойств пласта. Для этого изолируют слой подземного пласта. Вводят нагнетаемый флюид в подземный пласт при давлении нагнетания, превышающем давление гидравлического разрыва пласта. Перекрывают ствол скважины в течение периода остановки скважины. Измеряют данные спада давления со стороны подземного пласта в течение периода нагнетания и в течение периода остановки скважины. Определяют гидропроводность слоя подземного пласта, анализируя данные спада давления с помощью количественной диагностической модели кандидата на повторный разрыв пласта. Количественно определяют гидропроводность на промысловых установках по точке сопоставления до закрытия трещины или по точке сопоставления после закрытия трещины по математическим зависимостям. При этом нагнетаемый флюид является сжимаемым, и коллектор содержит слабо сжимаемый или сжимаемый флюид. 2 н. и 12 з.п. ф-лы, 13 ил.
1. Способ определения гидропроводности коллектора по меньшей мере одного слоя подземного пласта, имеющего уже существующие трещины, имеющие пластовый флюид, содержащий этапы, на которых
(a) изолируют по меньшей мере один слой подземного пласта, подлежащего испытанию,
(b) вводят нагнетаемый флюид в по меньшей мере один слой подземного пласта при давлении нагнетания, превышающем давление гидравлического разрыва подземного пласта, в течение периода нагнетания,
(c) перекрывают ствол скважины в течение периода остановки скважины,
(d) измеряют данные спада давления со стороны подземного пласта в течение периода нагнетания и в течение последующего периода остановки скважины и
е) определяют количественно гидропроводность по меньшей мере одного слоя подземного пласта, анализируя данные спада давления с помощью количественной диагностической модели кандидата на повторный разрыв пласта,
причем нагнетаемый флюид является сжимаемым, и коллектор содержит слабо сжимаемый или сжимаемый флюид, и при этом гидропроводность коллектора определяют количественно на промысловых установках по точке сопоставления до закрытия трещины как
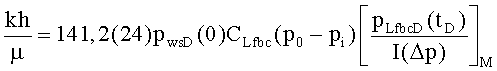
или по точке сопоставления после закрытия трещины как
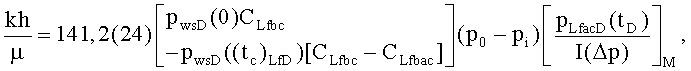
где k - проницаемость, L2, м2,
h - высота, L, м,
µ - вязкость, m/Lt, Па·с,
pwsD(0) - безразмерное давление в стволе скважины в нулевой момент времени,
CLfbc - упругоемкость многочисленных трещин до закрытия, L4t2/m, м3/Па,
р0 - давление в стволе скважины в нулевой момент времени, m/Lt2, Па,
pi - начальное давление в момент t=tne времени, m/Lt2, Па,
pLfbcD(tD) - безразмерное давление в коллекторе при добыче из многочисленных трещин и постоянной упругоемкостью до закрытия трещин в момент безразмерного времени,
I(Δp) - функция разности давлений,
М - индекс сегмента,
pwsD(tc)LfD - безразмерное давление в стволе скважины в момент безразмерного времени закрытия гидравлического разрыва,
CLfac - упругоемкость многочисленных трещин после закрытия, L4t2/m, м3/Па,
PLfacD(tD) - безразмерное давление в коллекторе при добыче из многочисленных трещин с постоянной упругоемкостью после закрытия трещин в момент безразмерного времени.
2. Способ определения гидропроводности коллектора по меньшей мере одного слоя подземного пласта, имеющего уже существующие трещины, имеющие пластовый флюид, содержащий этапы, на которых
(а) изолируют по меньшей мере один слой подземного пласта, подлежащего испытанию,
(b) вводят нагнетаемый флюид в по меньшей мере один слой подземного пласта при давлении нагнетания, превышающем давление гидравлического разрыва подземного пласта, в течение периода нагнетания,
(c) перекрывают ствол скважины в течение периода остановки скважины,
(d) измеряют данные спада давления со стороны подземного пласта в течение периода нагнетания и в течение последующего периода остановки скважины и
(e) определяют количественно гидропроводность по меньшей мере одного слоя подземного пласта, анализируя данные спада давления с помощью количественной диагностической модели кандидата на повторный разрыв пласта,
причем нагнетаемый флюид является сжимаемым и содержит подходящие добавки для совместимости с подземным пластом, и коллектор содержит слабо сжимаемый или сжимаемый флюид, и при этом гидропроводность коллектора определяют количественно на промысловых установках по точке сопоставления до закрытия трещины как
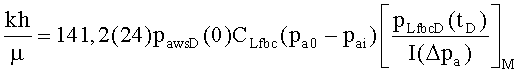
или по точке сопоставления после закрытия трещины как
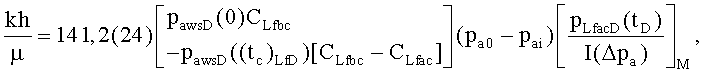
где k - проницаемость, L2, м2,
h - высота, L, м,
µ - вязкость, m/Lt, Па·с,
pawsD(0) - скорректированное безразмерное давление в стволе скважины в нулевой момент времени,
CLfbc - упругоемкость многочисленных трещин до закрытия, L4t2/m3, м3/Па,
pa0 - скорректированное давление в стволе скважины в нулевой момент времени, m/Lt2, Па,
pai - скорректированное давление в момент t=tne времени, m/Lt2, Па,
pLfbcD(tD) - безразмерное давление в коллекторе при добыче из многочисленных трещин и постоянной упругоемкостью до закрытия трещин в момент безразмерного времени,
I(Δра) - скорректированная функция разности давлений,
М - индекс сегмента,
pawsD(tc)LfD - скорректированное безразмерное давление в стволе скважины в момент безразмерного времени закрытия гидравлического разрыва,
CLfac - упругоемкость многочисленных трещин после закрытия, L4t2/m, м3/Па,
PLfacD(tD) - безразмерное давление в коллекторе при добыче из многочисленных трещин с постоянной упругоемкостью после закрытия трещин в момент безразмерного времени.
3. Способ по п.1 или 2, в котором этап (е) осуществляют, преобразуя данные спада давления в эквивалентные давления при постоянном расходе и используя анализ типовой кривой для сопоставления эквивалентных давлений при постоянном расходе с типовой кривой, чтобы определить количественно гидропроводность коллектора.
4. Способ по п.1 или 2, в котором этап (е) осуществляют,
преобразуя данные спада давления, чтобы получить эквивалентные давления при постоянном расходе,
подготавливая график с логарифмическим масштабом по обеим осям зависимости эквивалентных давлений при постоянном расходе от времени, и
определяя количественно гидропроводность коллектора по меньшей мере одного слоя подземного пласта путем анализа данных спада давления при переменном расходе, используя анализ типовой кривой согласно количественной диагностической модели кандидата на повторный разрыв пласта.
5. Способ по п.3, в котором пластовый флюид является сжимаемым, и в котором преобразование данных спада давления основано на свойствах сжимаемого пластового флюида в коллекторе, при этом на этапе преобразования
определяют момент времени остановки скважины относительно конца периода нагнетания,
определяют скорректированное время и
определяют скорректированный перепад псевдодавления.
6. Способ по п.5, в котором на этапе преобразования
определяют момент времени остановки скважины относительно окончания нагнетания: Δt=t-tne,
определяют скорректированное время 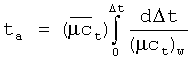 и
и
определяют скорректированный перепад давления
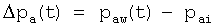 , где
, где 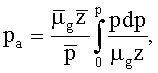
при этом
tne - момент времени в конце периода нагнетания, t, с,
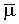 - вязкость пластового флюида при среднем давлении в коллекторе, m/Lt, Па·с,
- вязкость пластового флюида при среднем давлении в коллекторе, m/Lt, Па·с,
(µct)w - произведение вязкости и сжимаемости скважинного флюида в момент t времени,
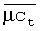 - произведение вязкости и сжимаемости скважинного флюида при среднем давлении,
- произведение вязкости и сжимаемости скважинного флюида при среднем давлении,
ра - псевдодавление m/Lt2, Па,
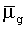 - вязкость газа при среднем давлении в коллекторе, m/Lt, Па·с,
- вязкость газа при среднем давлении в коллекторе, m/Lt, Па·с,
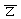 - фактический коэффициент сжимаемости газа при среднем давлении,
- фактический коэффициент сжимаемости газа при среднем давлении,
p - давление, m/Lt2, Па,
p - среднее давление в коллекторе, m/Lt2, Па,
paw(t) - скорректированное давление в момент t времени, m/Lt2, Па,
pai - скорректированное давление в момент t=tne времени, m/Lt2, Па,
ct - полная сжимаемость, Lt2/m, Па-1,
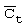 - полная сжимаемость при среднем давлении в коллекторе, Lt2/m, Па-1, и
- полная сжимаемость при среднем давлении в коллекторе, Lt2/m, Па-1, и
µg - вязкость газа, m/Lt, Па·с,
z - фактический коэффициент сжимаемости газа.
7. Способ по п.6, дополнительно содержащий этап, на котором подготавливают график с логарифмическим масштабом по обеим осям зависимости функции давления от времени I(Δpa)=f(ta),
где 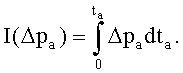
8. Способ по п.6, дополнительно содержащий этап, на котором подготавливают график с логарифмическим масштабом по обеим осям зависимости функции производной давления от времени 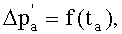
где 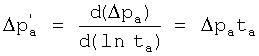 .
.
9. Способ по п.3, в котором пластовый флюид является слабо сжимаемым, и в котором преобразование данных спада давления основано на свойствах слабо сжимаемого пластового флюида в коллекторе, при этом на этапе преобразования
определяют момент времени остановки скважины относительно конца периода нагнетания Δt=t-tne и
определяют перепад давления Δp(t)=pw(t)-pi,
при этом
tne - момент времени в конце периода нагнетания, t, с,
pw(t) - давление в момент t времени, m/Lt2, Па, и
pi - начальное давление в момент t=tne времени, m/Lt2, Па.
10. Способ по п.9, в котором на этапе преобразования определяют момент времени остановки скважины относительно окончания нагнетания Δt=t-tne и
определяют перепад давления Δp(t)=pw(t)-pi,
где tne - момент времени в конце периода нагнетания, t, с,
pw(t) - давление в момент t времени, m/Lt2, Па и
pi - начальное давление в момент t=tne времени, m/Lt2, Па.
11. Способ по п.9, дополнительно содержащий этап, на котором строят график с логарифмическим масштабом по обеим осям зависимости функции давления от времени I(Δp)=f(Δt).
12. Способ по п.10, где 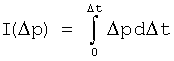 или
или 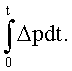
13. Способ по п.9, дополнительно содержащий этап, на котором строят график с логарифмическим масштабом по обеим осям зависимости функций производных давления от времени Δp'=f(Δt).
14. Способ по п.13, где 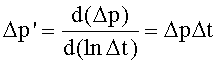 или
или 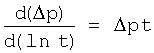 .
.
| US 2005222852 A1, 06.10.2005 | |||
| СПОСОБ ОПРЕДЕЛЕНИЯ ХАРАКТЕРИСТИК СКВАЖИНЫ, ПРИЗАБОЙНОЙ ЗОНЫ И ПЛАСТА | 2001 |
|
RU2189443C1 |
| СПОСОБ РАЗРАБОТКИ НЕФТЯНОЙ ЗАЛЕЖИ С ПРИМЕНЕНИЕМ ЭМУЛЬСИОННОЙ КОМПОЗИЦИИ | 2001 |
|
RU2185500C1 |
| СПОСОБ ИНТЕНСИФИКАЦИИ ПРИТОКА УГЛЕВОДОРОДОВ ИЗ СКВАЖИН С АНОМАЛЬНО ВЫСОКИМИ ПЛАСТОВЫМИ ДАВЛЕНИЯМИ | 2006 |
|
RU2316646C2 |
| СПОСОБ ЭКСПЛУАТАЦИИ СКВАЖИНЫ | 1999 |
|
RU2151856C1 |
| СПОСОБ ОДНОВРЕМЕННО-РАЗДЕЛЬНОЙ РАЗРАБОТКИ НЕСКОЛЬКИХ ЭКСПЛУАТАЦИОННЫХ ОБЪЕКТОВ И СКВАЖИННАЯ УСТАНОВКА ДЛЯ ЕГО РЕАЛИЗАЦИИ | 2001 |
|
RU2211311C2 |
| US 5303582 A, 19.04.1994 | |||
| US 2002096324 A1, 25.07.2002. | |||
Авторы
Даты
2011-04-27—Публикация
2006-10-02—Подача