Предшествующий уровень техники
Настоящее изобретение относится к области методик оценок подземных формаций нефти и газа, а более конкретно, к способам и системам определения свойств пластов подземных формаций с использованием способов исследования гидроразрыва/падающего давления.
Углеводороды нефти и газа могут занимать пространство пор в подземных формациях, таких, например, как песчаниковые формации. Пространства пор часто взаимосвязаны и имеют определенную проницаемость, которая представляет собой способность породы к прохождению потока текучей среды. Оценка свойств пласта подземных формаций является желательной для определения того, является ли гарантированной обработка с целью интенсификации, и/или того, какой тип обработки с целью интенсификации является гарантированным. Например, оценка проводимости пласта или множества пластов в подземной формации может давать ценную информацию относительно того, является ли подземный пласт или пласты желательными кандидатами на обработку посредством гидроразрыва. В дополнение к этому может быть желательным установление базовых свойств пласта подземных формаций, с которыми в дальнейшем будут делаться сравнения. Таким образом, более поздние измерения в течение срока службы скважины свойств пласта, таких как проводимость или эффективность интенсификации, могут сравниваться с начальными базовыми измерениями.
Выбор хорошего кандидата на интенсификацию может привести к успеху, в то время как выбор плохого кандидата может привести к экономической неудаче. Для выбора наилучшего кандидата на интенсификацию или повторную интенсификацию существует множество параметров, которые должны рассматриваться. Некоторые важные параметры для гидравлического разрыва включают в себя проницаемость формации, распределение напряжений на месте, вязкость текучей среды в пласте, скин-фактор, проводимость и давление в пласте.
Существует множество обычных способов для оценки свойств пласта подземных формаций, но, как будет показано, эти обычные способы имеют множество недостатков, включая отсутствие желаемой точности и/или неэффективность способа, что приводит к созданию способов, которые могут потребовать слишком большого времени.
Обычные способы, исследование с переменным давлением, которые включают в себя исследования понижения давления, повышения или гидроразрыва/падающего давления, представляют собой обычные способы оценки свойств пласта перед его обработкой посредством интенсификации. Однако эти способы, чтобы они были точными, требуют длительных времен исследования. Например, свойства пласта, интерпретируемые из обычного исследования с восстановлением давления, как правило, требуют длительного периода понижения давления с последующим периодом восстановления давления с такой же или большей продолжительностью, при этом общее время исследования для одного пласта растягивается на несколько дней. В дополнение к этому обычное исследование с переменным давлением в формации с низкой проницаемостью может потребовать небольшой обработки для разрывов или образования разломов перед исследованием для обеспечения хорошего сообщения между скважиной и формацией. Как следствие, в скважине, содержащей множество продуктивных пластов, могут потребоваться недели или месяцы исследования изолированного пласта для оценки всех пластов. Для многих скважин, в особенности для скважин с низкой проницаемостью формаций, потенциальная прибыль не позволяет этот тип инвестиций.
Другой способ оценки формации использует исследования с помощью слоя азота в качестве диагностического исследования перед разрывами в пластах с низкой проницаемостью, как описано в Jochen J.E. et al., Quantifying Layered Reservoir Properties With a Novel Permeability Test, SPE 25864 (1993). Этот способ описывает исследование с нагнетанием азота в качестве короткого импульса нагнетаемого азота с малым объемом при давлении, меньшем, чем давление инициирования и распространения разрыва, с последующим продолжительным периодом падающего давления. Исследования с помощью слоя азота анализируются с использованием теоретических кривых исследования с помощью слоя и посредством последовательного согласования нагнетания и падения давления с моделированием пласта с помощью конечных разностей.
Обычные методики анализа гидроразрыва/падающего давления - давления до закрытия - переходного процесса, как описано в Mayerhofer and Economides, Permeability Estimation From Fracture Calibration Treatments, SPE 26039 (1993), и анализ после схлопывания, как описано в Gu H. et al., Formation Permeability Determination Using Impulse-Fracture Injection, SPE 25425 (1993), делают возможными количественный анализ только конкретных и малых частей уменьшения давления в последовательности гидроразрыва/падающего давления. Данные до закрытия, которое может продолжаться от нескольких секунд до нескольких часов, могут анализироваться на проницаемость и устойчивость к поверхностному растрескиванию, а данные после закрытия могут анализироваться на проводимость пласта и среднее давление в пласте при условии, что наблюдается псевдорадиальный поток. В пластах с низкой проницаемостью или когда в течение нагнетания создается относительно длинный разрыв, продолжительный период закрывания составляет часы или, возможно, дни - как правило, требуется для наблюдения псевдорадиального потока. Количественная оценка проводимости из данных падающего давления до образования псевдорадиального потока после закрытия, которая представляет собой главную часть регистрируемого уменьшения давления, является невозможной с помощью существующих теоретических моделей предельных случаев, поскольку существующие модели предельных случаев применимы только к падению давления до закрытия и к падению давления после закрытия, что включает в себя режим псевдорадиального потока.
Таким образом, обычные способы оценки свойств формации имеют разнообразные недостатки, включающие отсутствие способности количественного определения проводимости пласта, отсутствие экономической эффективности, вычислительную неэффективность и/или отсутствие точности. Даже среди способов, разработанных для количественного определения проводимости пласта, такие способы могут быть непрактичными для оценки формаций, имеющих множество пластов, таких, например, как пакетированные линзовидные пласты с низкой проницаемостью.
Сущность изобретения
Настоящее изобретение относится к области методик оценки подземных формаций нефти и газа, а более конкретно, к способам и системам определения свойств пласта подземных формаций с использованием способов исследования гидроразрыва/падающего давления.
Пример способа определения проводимости, по меньшей мере, одного пласта подземной формации, содержащей текучую среду, включает в себя следующие стадии: (a) изолирование, по меньшей мере, одного пласта подземной формации, который должен исследоваться; (б) нагнетание жидкости в, по меньшей мере, один пласт подземной формации при давлении нагнетания, превышающем давление разрыва подземной формации в течение периода нагнетания; (в) закрытие скважины в течение периода закрытия; (г) измерение данных падающего давления от подземной формации в течение периода нагнетания и в течение последующего периода закрытия; (д) количественное определение проводимости, по меньшей мере, одного пласта подземной формации посредством анализа данных о падении давления с помощью модели исследования гидроразрыва/падающего давления.
Пример системы для определения проводимости, по меньшей мере, одного пласта подземной формации посредством использования данных для падающего давления с переменной скоростью, по меньшей мере, от одного пласта подземной формации, измеренных в течение периода нагнетания и в течение последующего периода закрытия, включает в себя множество датчиков давления для измерения данных по падению давления и процессор, предназначенный для преобразования данных по падению давления с получением эквивалентных давлений для постоянной скорости и для количественного определения проводимости, по меньшей мере, одного пласта подземной формации посредством анализа данных по падению давления для переменной скорости с использованием анализа теоретической кривой в соответствии с моделью исследования гидроразрыва/падающего давления.
Пример компьютерной программы, хранимой на материальной среде для хранения данных, для анализа, по меньшей мере, одного свойства скважины содержит исполняемые инструкции, которые заставляют компьютер количественно определять проводимость, по меньшей мере, из одного пласта подземной формации посредством анализа данных по падению давления с переменной скоростью с помощью модели исследования гидроразрыва/падающего давления.
Особенности и преимущества настоящего изобретения будут ясны специалистам в данной области. Хотя специалистами в данной области могут быть выполнены многочисленные изменения, такие изменения находятся в объеме настоящего изобретения.
Краткое описание чертежей
Чертежи иллюстрируют определенные аспекты некоторых вариантов осуществления настоящего изобретения и не должны использоваться для ограничения или определения настоящего изобретения.
Фигура 1 представляет блок-схему одного из вариантов осуществления способа количественного определения проводимости пласта.
Фигура 2 представляет собой блок-схему одного из вариантов осуществления способа количественного определения проводимости пласта.
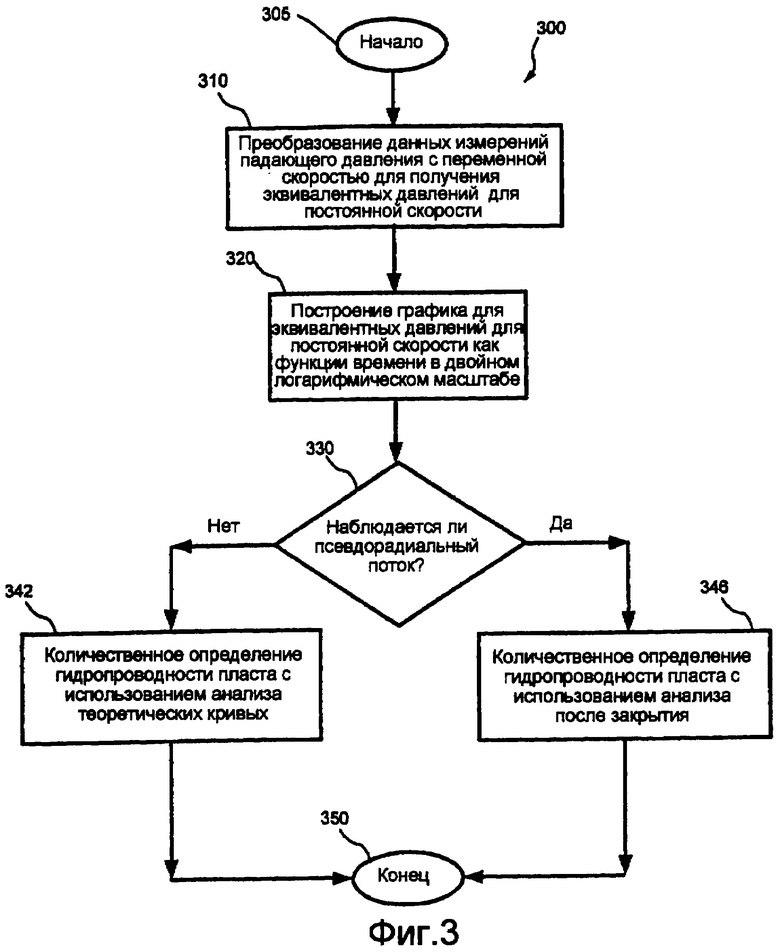
Фигура 3 представляет собой блок-схему одного из вариантов осуществления способа количественного определения проводимости пласта.
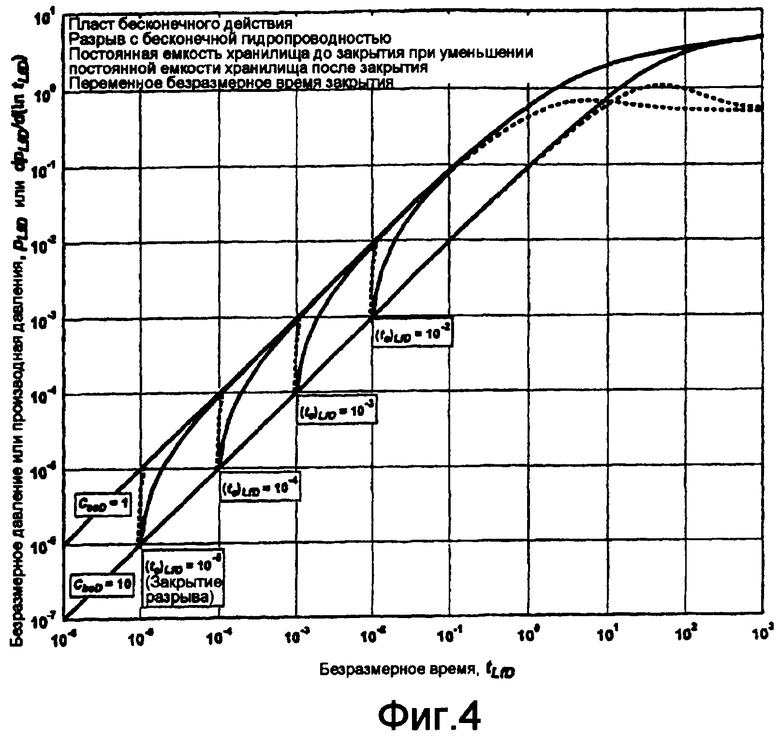
Фигура 4 показывает график безразмерного давления и производной давления как функции безразмерного времени и иллюстрирует случай, который демонстрирует постоянную емкость хранилища до закрытия, C bcD = 10, и постоянную емкость хранилища после закрытия, C acD = 1, при переменном безразмерном времени закрытия.
Фигура 5 представляет график в двойном логарифмическом масштабе безразмерного давления и производной давления как функции безразмерного времени без скин-эффекта с поверхностными разрывами,  =0, но с переменным скин-эффектом с закрытыми разрывами, (
=0, но с переменным скин-эффектом с закрытыми разрывами, ( )ch = {0,05, 1, 5}.
)ch = {0,05, 1, 5}.
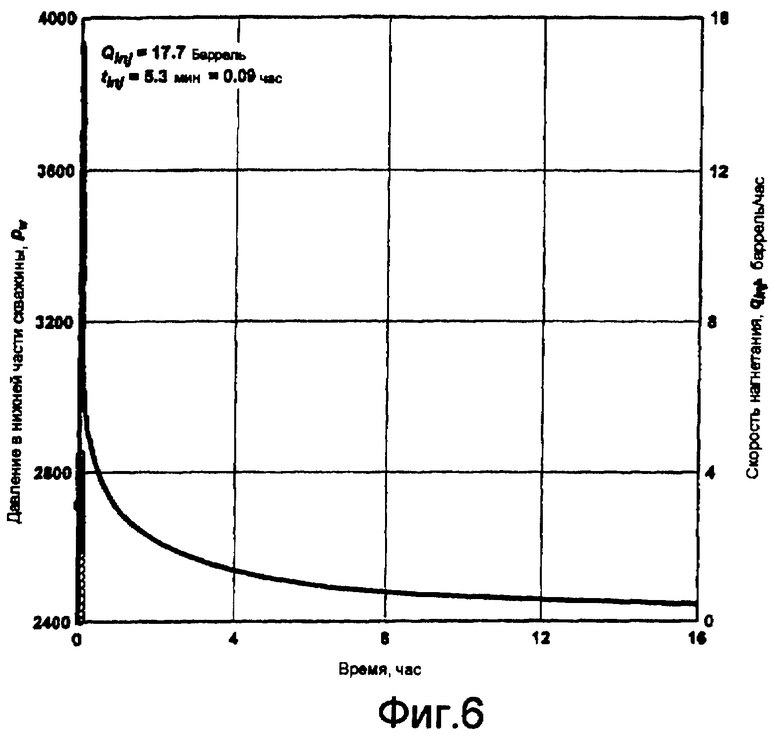
Фигура 6 показывает пример исследования гидроразрыва/падающего давления без существующего ранее гидравлического разрыва.
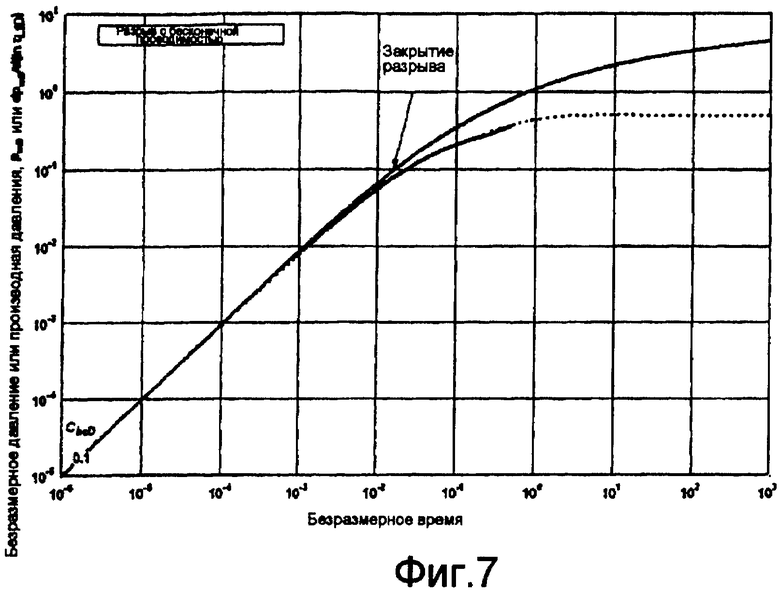
Фигура 7 показывает пример согласования типа кривой для исследования гидроразрыва/падающего давления без существующего ранее гидравлического разрыва.
Описание предпочтительных вариантов осуществления
Настоящее изобретение относится к области методик оценки подземных формаций нефти и газа, а более конкретно, к способам и системам определения свойств пласта подземных формаций с использованием способов исследования гидроразрыва/падающего давления.
Способы по настоящему изобретению могут быть пригодными для оценки свойств формации посредством использования способов гидроразрыва/падающего давления, при которых нагнетаются текучие среды при давлениях, превышающих давление инициирования и распространения разрывов в формации. В частности, способы, приводимые здесь, могут использоваться для оценки свойств формации, таких, например, как проводимость пласта и среднее давление пласта. Из оцениваемых свойств формации способы по настоящему изобретению могут быть пригодными, среди прочих вещей, для оценки формации в качестве кандидата на начальную обработку с целью разрыва и/или для установления базовых свойств пласта, с которыми впоследствии может осуществляться сравнение.
В определенных вариантах осуществления способ определения проводимости, по меньшей мере, одного пласта подземной формации, содержащей текучую среду, включает в себя следующие стадии: (a) изолирования, по меньшей мере, одного пласта подземной формации, которая должна исследоваться; (б) нагнетания жидкости в, по меньшей мере, один пласт подземной формации при давлении нагнетания, превышающем давление разрыва подземной формации в течение периода нагнетания; (в) закрытие скважины в течение периода закрытия; (г) измерение данных по падению давления от подземной формации, в течение периода нагнетания и в течение последующего периода закрытия; (д) количественное определение проводимости, по меньшей мере, одного пласта подземной формации посредством анализа данных по падению давления с помощью модели исследования гидроразрыва/падающего давления.
Термин "модель исследования гидроразрыва/падающего давления", как здесь используется, относится к вычислительным оценкам, используемым для оценки свойств пласта и/или проводимости пласта или множества пластов формации. Способы и теоретическая модель, на которой основываются вычислительные оценки, показаны ниже в Секциях II и III. Это исследование учитывает, что новый индуцированный разрыв создает дополнительный доступный объем в формации. Как следствие, исследование гидроразрыва/падающего давления в пласте может демонстрировать переменную емкость хранилища в течение падения давления, и может наблюдаться изменение емкости хранилища при гидравлическом закрытии разрыва. В сущности, исследование индуцирует разрыв для быстрого определения определенных свойств пласта.
Более конкретно, способы, приводимые здесь, могут использовать нагнетание жидкости или газа во временных рамках, которые являются относительно короткими по сравнению с откликом пласта, что делает возможным анализ исследования гидроразрыва/падающего давления посредством преобразования данных по падению давления с переменной скоростью в эквивалентные давления для постоянной скорости и построение графиков теоретических кривых в двойном логарифмическом масштабе для постоянной скорости. Анализ теоретических кривых делает возможной графическую идентификацию режимов потока - емкости хранилища: псевдолинейного потока, псевдорадиального потока, и анализ делает возможным согласование теоретических кривых для определения проводимости пласта. Как следствие, по существу все данные по падению давления, которые могут быть измерены - от периода до закрытия до периода после закрытия - в течение исследования гидроразрыва/падающего давления, могут использоваться для оценки свойств формации, таких как проводимость пласта.
Способы и модели здесь представляют собой расширения и частично основываются на концепциях Craig D.P., Analytical Modeling of a Fracture-Injection/Falloff Sequence and the Development of a Refracture-Candidate Diagnostic Test, PhD dissertation, Texas A&M Univ., College Station, Texas (2005), которая включена в данное описание путем ссылки, и заявки на патент США № 10/813698, зарегистрированной 3 марта 2004 года, озаглавленной "Methods and Apparatus for Detecting Fracture with Significant Residual Width from Previous Treatments", которая также включена в данное описание путем ссылки.
Фигура 1 показывает вариант осуществления способа исследования гидроразрыва/падающего давления, воплощающего определенные аспекты модели гидроразрыва/падающего давления. Способ 100 начинается со стадии 105 определения проводимости, по меньшей мере, одного пласта подземной формации. По меньшей мере, один пласт подземной формации изолируется на стадии 110. В течение стадии изолирования пласта каждый из подземных пластов предпочтительно индивидуально изолируется по одному для исследования посредством способов по настоящему изобретению. Множество пластов может исследоваться одновременно, но такое группирование пластов может вводить дополнительную вычислительную неопределенность в оценки проводимости.
Нагнетаемая жидкость вводится в, по меньшей мере, один пласт подземной формации при давлении нагнетания, превышающем давление разрыва, в течение периода нагнетания на стадии 120. В определенных вариантах осуществления нагнетание жидкости ограничивается относительно коротким периодом времени по сравнению со временем отклика пласта, которое в конкретных формациях может находиться в пределах от нескольких секунд примерно до 10 минут. В предпочтительных вариантах осуществления нагнетание жидкости может ограничиваться менее примерно чем 5 минутами. В определенных вариантах осуществления время нагнетания может ограничиваться до нескольких минут. После нагнетания жидкости на стадии 130 скважина может включаться в течение периода времени примерно от нескольких часов до нескольких дней, который в некоторых вариантах осуществления может зависеть от продолжительности времени для данных по падению давления, чтобы продемонстрировать падение давления до давления пласта.
На стадии 140 данные по падению давления измеряют от подземной формации в течение периода нагнетания и в течение последующего периода закрывания. Данные по падению давления могут измеряться с помощью датчика давления или множества датчиков давления. На стадии 150 данные по падению давления могут затем анализироваться для определения проводимости пласта подземной формации в соответствии с моделью гидроразрыва/падающего давления, как показано более подробно ниже, в Секциях II и III.
Фигура 2 показывает пример осуществления количественного определения проводимости пласта (изображенный на стадии 150 Способа 100). В частности, способ 200 начинается на стадии 205. Стадия 210 включает в себя стадию преобразования данных по падению давления с переменной скоростью в эквивалентные давления для постоянной скорости и использования анализа теоретических кривых для согласования эквивалентных давлений для постоянной скорости на теоретической кривой. Стадия 220 включает в себя стадию количественного определения проводимости пласта, по меньшей мере, из одного пласта подземной формации посредством анализа эквивалентных давлений для постоянной скорости с помощью модели исследования гидроразрыва/падающего давления. Способ 200 заканчивается на стадии 225.
Фигура 3 показывает пример осуществления определения проводимости пласта. Способ 300 начинается на стадии 305. Измеренные данные по падению давления преобразуются для получения эквивалентных давлений для постоянной скорости на стадии 310. График в двойном логарифмическом масштабе получают из эквивалентных давлений для постоянной скорости как функции времени на стадии 320. Если псевдорадиальный поток не наблюдается, анализ теоретических кривых может использоваться для количественного определения проводимости пласта в соответствии с моделью исследования гидроразрыва/падающего давления на стадии 342. Если наблюдается псевдорадиальный поток, анализ после закрытия может использоваться для количественного определения проводимости пласта на стадии 346. Эти общие стадии объясняются более подробно ниже, в Секциях II и III. Способ 300 заканчивается на стадии 350.
Один или несколько способов по настоящему изобретению могут осуществляться с помощью системы обработки информации. Для целей настоящего описания система обработки информации может включать в себя любой инструментарий или набор инструментариев, работающий для вычисления, классификации, обработки, передачи, приема, извлечения, создания, переключения, хранения, отображения, демонстрации, детектирования, регистрации, воспроизведения, преобразования и использования любой формы информации, интеллекта или данных для целей бизнеса, науки, контроля или других целей. Например, система обработки информации может представлять собой персональный компьютер, сетевое устройство для хранения данных или любое другое соответствующее устройство и может изменяться по размеру, форме, рабочим характеристикам, функциональности и цене. Система обработки информации может содержать оперативную память, один или несколько ресурсов обработки, такой как центральный узел процессора или аппаратную или программную управляющую логику, постоянное запоминающее устройство и/или другие типы нестираемой памяти. Дополнительные компоненты системы обработки информации могут включать в себя один или несколько дисководов, один или несколько сетевых портов для сообщения с внешними устройствами, такими как различные устройства ввода и вывода, такие как клавиатура, мышка и видеодисплей. Система обработки информации может также включать в себя одну или несколько шин, работающих для передачи сообщений между различными аппаратными компонентами.
I. Анализ и интерпретация данных в целом
Количественная интерпретация может использовать следующие далее стадии в определенных вариантах осуществления.
Идентификация гидравлического закрытия разрыва во время падения давления с использованием таких, например, способов, как те, которые описаны в Craig D.P. et al., Permeability, Pore Pressure, and Leakoff-Type Distributions in Rocky Mountain Basins, SPE PRODUCTION & FACILITIES, 48 (February 2005).
Момент времени при окончании понижения давления, t ne , становится эталонным нулевым временем, Δt = 0. Вычисление времени закрывания по отношению к концу понижения давления как
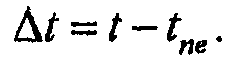 (1)
(1)
В некоторых случаях t ne является очень малым по отношению к t и Δt = t. Как увидит специалист в данной области с помощью настоящего описания, t ne может считаться нулем или приблизительно нулем для приблизительного определения Δt. Таким образом, термин Δt, как здесь используется, включает в себя осуществления, где t ne считается равным нулю или приблизительно равным нулю. Для нагнетания слабо сжимаемой текучей среды в пласт, содержащий сжимаемую текучую среду, или нагнетания сжимаемой текучей среды в пласт, содержащий сжимаемую текучую среду, использование свойств сжимаемой текучей среды в пласте и вычисление установленного времени как
 (2)
(2)
где псевдовремя определяется как
 (3)
(3)
и установленное время или нормированное псевдовремя определяется по формуле:
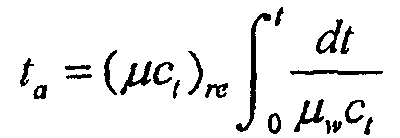 (4)
(4)
где нижний индекс 're' относится к произвольным эталонным условиям, выбранным из соображений удобства.
Разность давлений для нагнетания слабо сжимаемой текучей среды в пласт, содержащий слабо сжимаемую текучую среду, может вычисляться по формуле:
 (5)
(5)
или разность давлений для нагнетания слабо сжимаемой текучей среды в пласт, содержащий сжимаемую текучую среду, или нагнетания сжимаемой текучей среды в пласт, содержащий сжимаемую текучую среду, использование свойств сжимаемой текучей среды пласта и вычисление установленной разности псевдодавлений по формуле:
 (6)
(6)
где
 (7)
(7)
где псевдодавление может определяться по формуле:
 (8)
(8)
и установленное псевдодавление или нормированное псевдодавление может определяться по формуле:
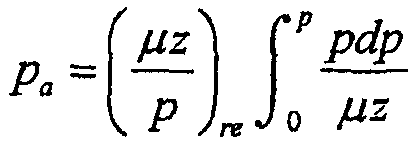 (9)
(9)
где нижний индекс 're' относится к произвольным эталонным условиям, выбранным из соображений удобства.
Эталонные условия в определениях установленного псевдодавления и установленного псевдовремени являются произвольными, и различные формы решения могут быть получены посредством простого изменения нормировочных эталонных условий.
Вычисление производной давления как функции для построения графика по формуле
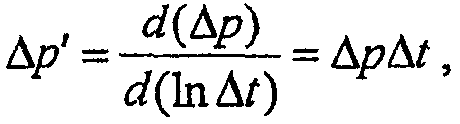 (10)
(10)
или
 (11)
(11)
Преобразование зарегистрированных данных по падению давления с переменной скоростью в эквивалентное давление, когда скорости постоянны, посредством интегрирования разности давлений по времени, что для слабо сжимаемой текучей среды может быть выражено формулой:
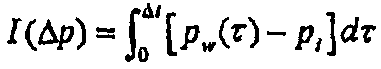 (12)
(12)
или для слабо сжимаемой текучей среды, нагнетаемой в пласт, содержащий сжимаемую текучую среду, или для нагнетания сжимаемой текучей среды в пласт, содержащий сжимаемую текучую среду, давление как функция для построения графика может вычисляться по формуле
 (13)
(13)
вычисление производной давления как функции для построения графика по формуле
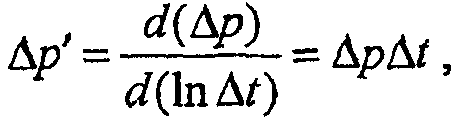 (14)
(14)
или
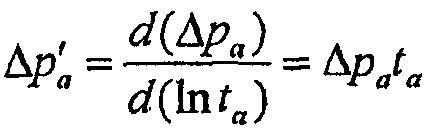 (15)
(15)
Построение графика в двойном логарифмическом масштабе зависимости I(Δp) от Δt или I(Δp a ) от t a.
Построение графика в двойном логарифмическом масштабе зависимости Δp' от Δt или Δp a ' от t a.
Исследование поведения емкости хранилища до и после закрытия.
Количественная диагностическая интерпретация кандидатов на повторное трещинообразование требует согласования теоретических кривых или, если наблюдается псевдорадиальный поток, анализа после закрытия. Анализ после закрытия может осуществляться такими способами, как описано в Gu H. et al., Formation Permeability Using Impulse-Fracture Injection, SPE 25425 (1993), или Abousleiman Y., Cheng A. H-D. and Gu H., Formation Permeability Determination by Micro or Mini-Hydraulic Fracturing, J. OF ENERGY RESOURCES TECHNOLOGY, 116, №6, 104 (June 1994). Анализ после закрытия является предпочтительным, поскольку он не требует знания половинной длины разрывов для вычисления проводимости. Однако вероятность наблюдения псевдорадиального потока в течение относительно короткого падения давления является малой, и может быть необходимым согласование теоретических кривых. От точки согласования давления на теоретической кривой для постоянной скорости с постоянной емкостью хранилища до закрытия проводимости могут быть вычислены в полевых устройствах по формуле:
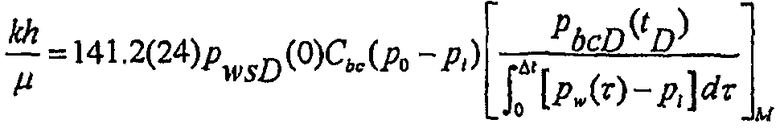 (16)
(16)
или от точки согласования давления после закрытия с использованием теоретической кривой для хранилища с переменной емкостью по формуле:
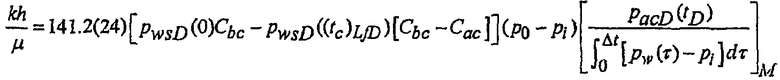 (17)
(17)
Количественная интерпретация имеет два ограничения. Во-первых, для точного вычисления эквивалентного давления и производной давления для постоянной скорости должно быть известно среднее давление пласта, формулы 12 и 15. Во-вторых, для вычисления проводимости требуется половинная длина разрыва. Половинная длина разрыва может оцениваться посредством обработки изображений или аналитических способов, и коэффициенты емкости хранилища до закрытия и после закрытия могут вычисляться с помощью таких способов, как те, которые описаны в Craig D.P., Analytical Modeling of Fracture-Injection/Falloff Sequence and the Development of a Refracture-Candidate Diagnostic Test, PhD dissertation, Texas A&M Univ., College Station, Texas (2005), и оцениваться проводимость.
II. Модель исследования гидроразрыва/падающего давления
Исследование гидроразрыва/падающего давления использует короткое нагнетание при давлении, достаточном для гидравлического возникновения и распространения разрывов, с последующим продолжительным периодом закрывания. В течение периода закрывания индуцируемый разрыв закрывается, что разделяет данные по падению давления на части до закрытия и после закрытия. Отдельные теоретические описания данных до закрытия и после закрытия представляются, как описано в Mayerhofer M.J. and Economides M.J., Permeability Estimation From Fracture Calibration Treatments, SPE 26039 (1993), Mayerhofer M.J., Ehlig-Economides C.A. и Economides M.J., Pressure-Transient Analysis of Fracture-Calibration Tests, JPT, 229 (March 1995), Gu H. et al., Formation Permeability Determination Using Impulse-Fracture Injection, SPE 25425 (1993), and Abousleiman Y., Cheng A. H-D., and Gu H., Formation Permeability Determination by Micro- or Mini-Hydraulic Fracturing, J. OF ENERGY RESOURCES TECHNOLOGY 116, №6, 104 (June 1994).
Mayerhofer and Economides и Mayerhofer et al. разработали анализ переходного давления до закрытия, в то время как Gu et al. и Abousleiman et al. представили теорию анализа после закрытия. С помощью анализа до закрытия и после закрытия могут количественно анализироваться только конкретные и малые части понижения давления в течение последовательности исследований гидроразрыва/падающего давления.
Данные до закрытия, которое может продолжаться в течение от нескольких секунд до нескольких часов, могут анализироваться на проницаемость и устойчивость к поверхностному разрыву, и данные после закрытия могут анализироваться на проводимость пласта и среднее давление пласта при условии наблюдения псевдорадиального потока. Однако при низкой проницаемости пласта или когда в течение нагнетания создается относительно длинный разрыв, как правило, требуется продолжительный период закрывания - часы или, возможно, дни, для наблюдения псевдорадиального потока. Количественная оценка проводимости из данных по падению давления после закрытия до установления псевдорадиального потока, которые представляют собой подавляющее большинство регистрируемого понижения давления, с помощью существующих теоретических моделей является невозможной.
Однофазная теоретическая модель гидроразрыва/падающего давления, принимающая во внимание создание разрывов, закрытие разрывов и диффузию после закрытия, представлена ниже в Секции III. Модель учитывает распространение разрывов как зависимую от времени емкость хранилища, и решение относительно безразмерного давления при гидроразрыве/падающем давлении для случая с распространением разрывов, постоянной емкостью хранилища до закрытия и постоянной емкостью хранилища после закрытия записывается как
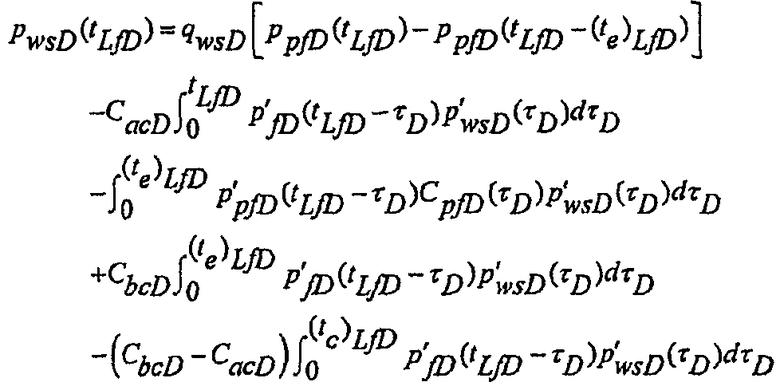
где c bcD представляет собой безразмерную емкость хранилища до закрытия, c acD представляет собой безразмерную емкость хранилища после закрытия и c pfD представляет собой безразмерный коэффициент емкости хранилища при распространении разрывов.
Два решения для предельных случаев также приводятся ниже в Секции III для короткого безразмерного времени нагнетания, 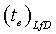 . Решение для предельного случая до закрытия, где
. Решение для предельного случая до закрытия, где  и
и  представляет собой безразмерное время при закрытии, определяется по формуле:
представляет собой безразмерное время при закрытии, определяется по формуле:
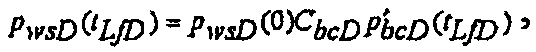 (19)
(19)
и представляет собой решение для исследования с помощью водяной пробки для скважины с гидравлическим разрывом с постоянной емкостью хранилища до закрытия. Решение для предельного случая после закрытия, где  определяется по формуле
определяется по формуле
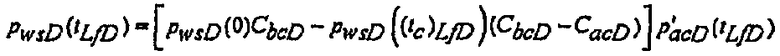 (20)
(20)
и представляет собой решение для исследования с помощью водяной пробки, но включает в себя переменную емкость хранилища.
Как представленные однофазные решения для предельного случая, так и другие решения, представленные в Craig D.P., Analytical Modeling of Fracture-Injection/Falloff Sequence and the Development of a Refracture-Candidate Diagnostic Test, PhD dissertation, Texas A&M Univ., College Station, Texas (2005), иллюстрируют, что исследование гидроразрыва/падающего давления может анализироваться как исследование с помощью водяной пробки, когда время нагнетания является коротким по отношению к отклику пласта.
При исследовании воздействия распространения разрывов на данные по нагнетанию/падению давления, Larsen L. and Bratvold R.B., Effects of Propagating Fractures on Pressure-Transient Injection and Falloff Data, SPE 20580 (1990), также продемонстрировали, что, когда свойства текучих сред фильтрата и пласта различаются, однофазная модель переходного давления является пригодной для использования, если глубина проникновения фильтрата является малой. Таким образом, для последовательности гидроразрыва/падающего давления с разрывом, создаваемым в течение короткого периода нагнетания, данные по падению давления могут анализироваться как исследование с помощью водяной пробки с использованием однофазного решения для переходного давления в форме теоретических кривых для постоянной скорости понижения давления с переменной емкостью хранилища.
Анализ теоретических кривых последовательностей гидроразрыва/падающего давления использует преобразование давления, зарегистрированного в течение периода падающего давления с переменной скоростью, для получения эквивалентного давления "для постоянной скорости", как описано в Peres A.M.M. et al., A New General Pressure-Analysis Procedure for Slug Tests, SPE FORMATION EVALUATION, 292 (December 1993). Согласование теоретических кривых с использованием новых теоретических кривых для переменной емкости хранилища, для постоянной скорости может затем использоваться для оценки проводимости и для идентификации периодов протекания, для специализированного анализа с использованием существующих способов до закрытия и после закрытия, как представлено в Craig D.P., Analytical Modeling of a Fracture-Injection/Falloff Sequence and the Development of Refracture-Candidate Diagnostic Test, PhD dissertation, Texas A&M Univ., College Station, Texas (2005).
С использованием способа вычислений, аналогичного тому, который показан ниже, в Секции III, Craig получил решение для безразмерного давления, для скважины в бесконечном плоском пласте с открытым разрывом, поддерживаемым начальным давлением пласта, который закрывается в течение понижения давления с постоянной скоростью, при постоянной емкости хранилища до закрытия и после закрытия, которое определяется формулой:
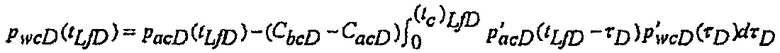 (21)
(21)
где p wcD означает, что решение для давления относится к постоянной скорости, и p acD представляет собой решение для безразмерного давления, для понижения давления с постоянной скоростью, при постоянной емкости хранилища после закрытия, которое записывается в терминах преобразования Лапласа следующей формулой:
 (22)
(22)
и  представляет собой решение в терминах преобразования Лапласа для пласта, производимого из одного вертикального разрыва с бесконечной или конечной проводимостью.
представляет собой решение в терминах преобразования Лапласа для пласта, производимого из одного вертикального разрыва с бесконечной или конечной проводимостью.
Фигура 4 показывает график безразмерного давления и производной давления как функции безразмерного времени и иллюстрирует случай, который демонстрирует постоянную емкость хранилища до закрытия, C bcD = 10, и постоянную емкость хранилища после закрытия, C acD = 1, с переменным безразмерным временем закрытия.
Объем разрыва перед закрытием больше, чем остаточный объем разрыва после закрытия, 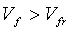 , и изменение объема разрыва по отношению к давлению является положительным. Таким образом, емкость хранилища до закрытия, когда разрыв является открытым и закрывается, больше, чем емкость хранилища после закрытия, что определяется формулой:
, и изменение объема разрыва по отношению к давлению является положительным. Таким образом, емкость хранилища до закрытия, когда разрыв является открытым и закрывается, больше, чем емкость хранилища после закрытия, что определяется формулой:
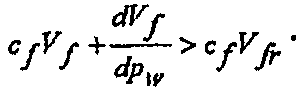 (23)
(23)
Как следствие, понижение емкости хранилища, как показано на Фигуре 4, должно ожидаться в течение понижения давления с постоянной скоростью, с закрытием разрывов, как продемонстрировано для закрытия индуцируемых заводнением разрывов в течение периода падающего давления Koning E.J.L. and Niko H., Fractured Water-Injection Wells: A Pressure Falloff Test for Determining Fracturing Dimensions, SPE 14458 (1985), Koning E.J.L., Waterflooding Under Fracturing Conditions, PhD Thesis, Delft Technical University (1988), van den Hoek P.J., Pressure Transient Analysis in Fractured Produced Water Injection Wells, SPE 77946 (2002), and van den Hoek P.J., A Novel Methodology td Derive Dimensions and Degree of Containment of Waterflood-Induced Fractures From Pressure Transient Analysis, SPE 84289 (2003).
В определенных случаях емкость хранилища, как может показаться, увеличивается в течение понижения давления при постоянной скорости с закрытием разрывов. Модель скважин при переменной емкости хранилища для пластов с природными разрывами ограниченной протяженности в сообщении со скважиной описывается в Spivey J.P. и Lee W.J., Variable Wellbore Storage Models for Dual-Volume Wellbore, SPE 56615 (1999). Модель с переменной емкостью хранилища включает в себя коэффициент емкости хранилища, природные разрывы и поверхностные природные разрывы, осуществляющие сообщение с пластом, и коэффициент емкости хранилища скважины и скин-слоя после завершения скважины, осуществляющего сообщение между природными разрывами и скважиной. Модель Spivey и Lee с радиальной геометрией, с природными разрывами ограниченной протяженности в сообщении со скважиной демонстрирует, что емкость хранилища может, как кажется, увеличиваться, когда значение призабойной зоны после завершения скважины больше нуля.
Концепция Spivey and Lee может быть расширена на понижение давления с постоянной скоростью для скважины с вертикальным гидравлическим разрывом посредством закрывания в него поверхностных разрывов и скин-эффекта закрытых разрывов, как описывается в Cinco-Ley H. and Samaniego-V. F., Transient Pressure Analysis: Finite Conductivity Fracture Case Versus Damage Fracture Case, SPE 10179 (1981). Проблема формулируется посредством рассмотрения сначала только емкости хранилища скважины и записи уравнения для безразмерного материального баланса следующим образом:
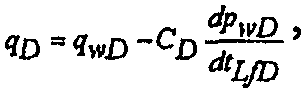 (24)
(24)
где c D представляет собой безразмерный коэффициент емкости хранилища для скважины, определяемый по формуле
 (25)
(25)
Уравнение безразмерного материального баланса объединяется с интегралом Дюгамеля в терминах преобразования Лапласа, и решение для скважины записывается формулой:
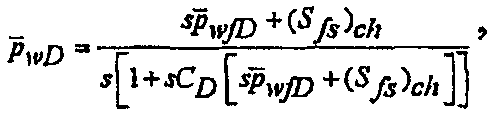 (26)
(26)
где 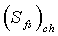 представляет собой скин-эффект закрытых разрывов и
представляет собой скин-эффект закрытых разрывов и  представляет собой решение для безразмерного давления в терминах преобразования Лапласа в разрыве вне скважины.
представляет собой решение для безразмерного давления в терминах преобразования Лапласа в разрыве вне скважины.
Перед закрытием разрыва безразмерное давление в нем вне скважины представляет собой просто функцию емкости хранилища до закрытия разрыва и скин-эффекта с поверхностными разрывами, 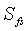 и может быть записано в терминах преобразования Лапласа в виде формулы:
и может быть записано в терминах преобразования Лапласа в виде формулы:
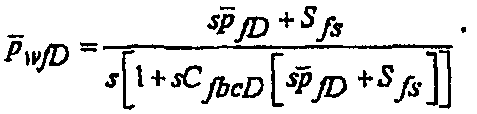 (27)
(27)
где безразмерная емкость хранилища до закрытия разрыва определяется по формуле:
 (28)
(28)
и коэффициент емкости хранилища до закрытия разрыва определяется по формуле:
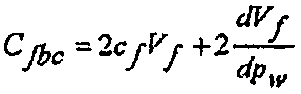 (29)
(29)
Безразмерное давление в скважине перед закрытием, учитывающее скин-эффект с поверхностными разрывами, емкость хранилища до закрытия, скин-эффект с закрытыми разрывами и емкость хранилища скважины, получают посредством численного обратного преобразования Лапласа для решения, представленного уравнениями 26 и 27.
После закрытия разрыва решение вне скважины, учитывающее переменную емкость хранилища с разрывами, является аналогичным решению для безразмерного давления для скважины в бесконечном плоском пласте с открытым разрывом, поддерживаемым посредством начального давления пласта, который закрывается в течение понижения давления, при постоянной емкости хранилища, до закрытия и после закрытия. Решение может быть записано в виде формулы:
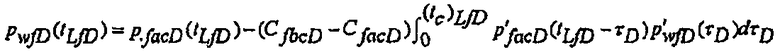 (30)
(30)
где безразмерная емкость хранилища после закрытия разрыва определяется по формуле:
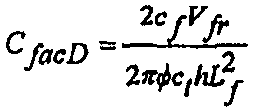 (31)
(31)
и 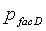 представляет собой решение для безразмерного давления в разрыве, для постоянной скорости понижения давления при постоянной емкости хранилища, которое записывается в терминах преобразования Лапласа в виде формулы:
представляет собой решение для безразмерного давления в разрыве, для постоянной скорости понижения давления при постоянной емкости хранилища, которое записывается в терминах преобразования Лапласа в виде формулы:
 (32)
(32)
После закрытия разрыва решение для безразмерного давления в скважине получается посредством оценки дискретизированного решения во временной области для безразмерного давления вне скважины и в разрыве в каждый момент времени 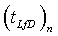 . ДЛЯ известного безразмерного давления во временной области в разрыве вне скважины решение в терминах преобразования Лапласа, которое записывается в виде формулы:
. ДЛЯ известного безразмерного давления во временной области в разрыве вне скважины решение в терминах преобразования Лапласа, которое записывается в виде формулы:
 (33)
(33)
может оцениваться численно и объединяться с решением в терминах преобразования Лапласа для скважины, уравнение 26, и численно преобразовываться обратно во временной области, как описывается в Craig D.P., Analytical Modeling of a Fracture-Injection/Falloff Sequence and the Development of Refracture-Candidate Diagnostic Test, PhD dissertation, Texas A&M Univ., College Station, Texas (2005).
Фигура 5 представляет график безразмерного давления и производной давления в двойном логарифмическом масштабе как функции безразмерного времени без скин-эффекта с поверхностными разрывами,  = 0, но с переменным скин-эффектом с закрытыми разрывами,
= 0, но с переменным скин-эффектом с закрытыми разрывами, 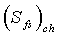 ={0,05, 1, 5}. Фигура 5 демонстрирует, что емкость хранилища, как кажется, повышается в течение понижения давления с постоянной скоростью в скважине с закрытием разрывов и скин-эффектом с закрытыми разрывами.
={0,05, 1, 5}. Фигура 5 демонстрирует, что емкость хранилища, как кажется, повышается в течение понижения давления с постоянной скоростью в скважине с закрытием разрывов и скин-эффектом с закрытыми разрывами.
III. Теоретическая модель A - Решение для нагнетательного разрыва/падающего давления в пласте без существующего ранее разрыва
Предположим, что слабо сжимаемая текучая среда заполняет скважину и разрыв и нагнетается при постоянной скорости и при давлении, достаточном для создания нового гидравлического разрыва или расширения существующего разрыва. В качестве термина, используемого здесь, термин сжимаемая текучая среда относится к газам, в то время как термин слабо сжимаемая текучая среда относится к жидкостям. Массовый баланс в течение осуществления гидроразрыва может быть определен по формуле:
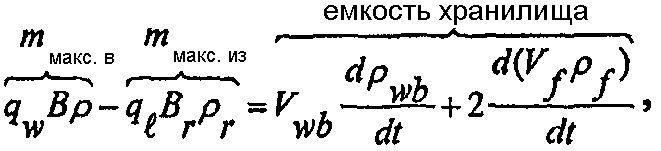 (А-1)
(А-1)
где  представляет собой скорость утечки текучей среды в пласт из разрыва,
представляет собой скорость утечки текучей среды в пласт из разрыва, 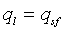 , и
, и 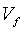 представляет собой объем разрыва.
представляет собой объем разрыва.
Уравнение материального баланса может быть записано в предположении постоянной плотности, 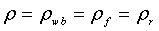 , и постоянного объемного коэффициента формации, B = B
r
, в виде формулы:
, и постоянного объемного коэффициента формации, B = B
r
, в виде формулы:
 (А-2)
(А-2)
В течение нагнетания с постоянной скоростью, с изменением длины и ширины разрыва объем разрыва может быть определен по формуле:
 (А-3)
(А-3)
и коэффициент емкости хранилища распространяющегося разрыва может быть определен по формуле:
 (А-4)
(А-4)
Безразмерное давление в скважине для гидроразрыва/падающего давления может быть определено по формуле:
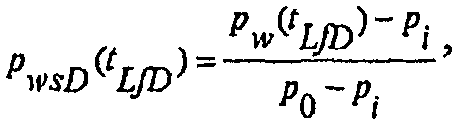 (А-5)
(А-5)
где p i представляет собой начальное давление в пласте и p 0 представляет собой произвольное эталонное давление. В момент времени ноль давление в скважине повышается до "открывающего давления" давления p w0, которое, как правило, устанавливается равным p 0, и безразмерное давление в скважине в момент времени ноль может быть определено по формуле:
 (А-6)
(А-6)
Безразмерное время определено по формуле:
 (А-7)
(А-7)
где  представляет собой половинную длину разрыва в конце понижения давления. Безразмерная скорость потока для пласта может определяться по формуле:
представляет собой половинную длину разрыва в конце понижения давления. Безразмерная скорость потока для пласта может определяться по формуле:
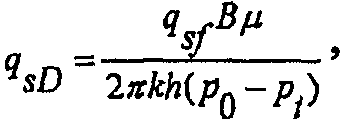 (А-8)
(А-8)
и безразмерная скорость потока для скважины может определяться по формуле:
 (А-9)
(А-9)
где q w представляет собой скорость нагнетания для скважины.
С безразмерными переменными уравнение материального баланса для распространяющегося разрыва в течение нагнетания может иметь следующий вид:
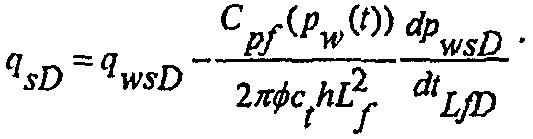 (А-10)
(А-10)
Безразмерный коэффициент емкости хранилища разрыва определен по формуле:
 (А-11)
(А-11)
и безразмерное уравнение материального баланса в течение нагнетания при давлении, достаточном образования и расширения гидравлического разрыва, может быть выражено в следующем виде:
 (А-12)
(А-12)
С использованием техники Correa and Ramey, как описывается в Correa A.C. and Ramey H.J., Jr., Combined Effects of Shut-In and Production: Solution With a New Inner Boundary Condition, SPE 15579 (1986) and Correa A.C. and Ramey H.J., Jr., A Method for Pressure Buildup Analysis of Drillstem Tests, SPE 16802 (1987), уравнение материального баланса, верное при всех временах для последовательности гидроразрыва/падающего давления с образованием и расширением разрывов и при постоянной емкости хранилища после закрытия, может быть определено следующим образом:
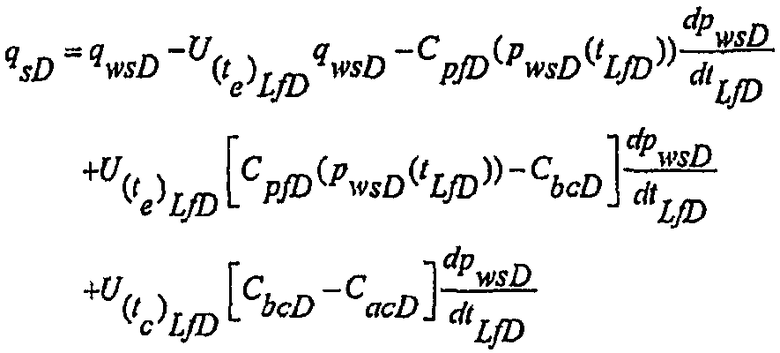 (А-13)
(А-13)
где единичная ступенчатая функция определяется по формуле:
 (А-14)
(А-14)
Преобразование Лапласа уравнения материального баланса для нагнетания с образованием и расширением разрывов после раскрытия скобок и упрощения имеет следующий вид:
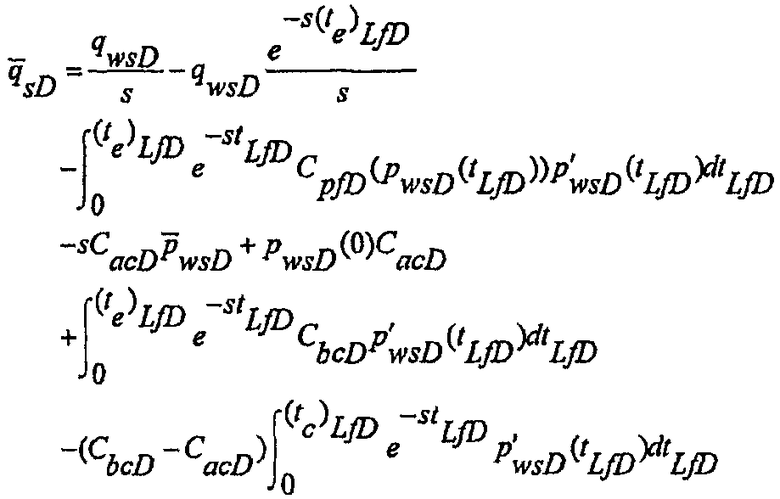 (А-15)
(А-15)
Для половинной длины разрыва, увеличивающейся в течение нагнетания, решение для безразмерного давления может потребоваться как для распространения, так и для фиксированной половинной длины разрыва. Решение для безразмерного давления может быть получено посредством интегрирования решения с линейным источником и записано в следующем виде:
 (А-16)
(А-16)
От  до
до  , по
, по 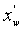 , где
, где  и
и  , для пласта с однородной пористостью. Здесь предполагается, что половинная длина разрыва может быть записана как функция параметра преобразования Лапласа, s, и только. В терминах безразмерных переменных
, для пласта с однородной пористостью. Здесь предполагается, что половинная длина разрыва может быть записана как функция параметра преобразования Лапласа, s, и только. В терминах безразмерных переменных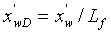 и
и  решение для линейного источника интегрируется от
решение для линейного источника интегрируется от 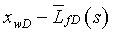 до
до 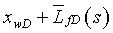 , что может быть записано следующей формулой:
, что может быть записано следующей формулой:
 (А-17)
(А-17)
Считая, что центр скважины находится в начале координат, при ,
,
 (А-18)
(А-18)
Предполагая постоянный поток массы, скорость потока в терминах преобразования Лапласа может быть записана в виде формулы:
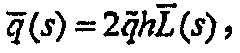 (А-19)
(А-19)
и решение с плоским источником может быть записано в безразмерных терминах в виде формулы:
 (А-20)
(А-20)
где
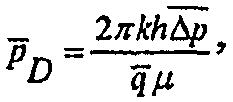 (А-21)
(А-21)
 (А-22)
(А-22)
и определяя общую скорость потока как  , безразмерная скорость потока может быть записана в виде формулы:
, безразмерная скорость потока может быть записана в виде формулы:
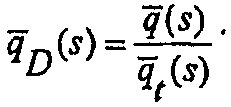 (А-23)
(А-23)
Можно предположить, что общая скорость потока увеличивается пропорционально увеличению половинной длины разрыва, так что  . Решение оценивается в плоскости разрыва, и после упрощения интеграла с использованием равенства Ozkan и Raghavan, как описано в Ozkan E. and Raghavan R., New Solutions for Well-Test-Analysis Problems: Part 2-Computational Considerations and Applications, SPEFE, 369 (September 1991), безразмерное решение с однородным потоком массы в терминах преобразования Лапласа для переменной половинной длины разрывов может быть записано в виде формулы:
. Решение оценивается в плоскости разрыва, и после упрощения интеграла с использованием равенства Ozkan и Raghavan, как описано в Ozkan E. and Raghavan R., New Solutions for Well-Test-Analysis Problems: Part 2-Computational Considerations and Applications, SPEFE, 369 (September 1991), безразмерное решение с однородным потоком массы в терминах преобразования Лапласа для переменной половинной длины разрывов может быть записано в виде формулы:
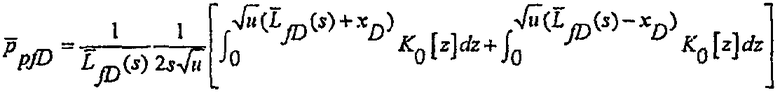 (24)
(24)
и решение с бесконечной проводимостью может быть получено посредством оценки решения с однородным потоком массы при  и может быть записано в виде формулы:
и может быть записано в виде формулы:
 (А-25)
(А-25)
Безразмерная половинная длина разрыва в терминах преобразования Лапласа изменяется в пределах между 0 и 1 в течение распространения разрыва и с использованием модели со степенной аппроксимацией, как показано в Nolte K.G., Determination of Fracture Parameters From Fracturing Pressure Decline, SPE 8341 (1979), безразмерная половинная длина разрыва в терминах преобразования Лапласа может быть записана в виде формулы:
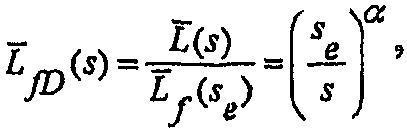 (А-26)
(А-26)
где s e представляет собой параметр преобразования Лапласа в момент окончания понижения давления. Безразмерная половинная длина разрыва в терминах преобразования Лапласа в течение распространения и закрытия разрыва может быть записана в виде формулы:
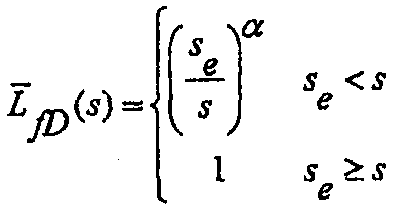 (А-27)
(А-27)
где показатель степени степенной модели находится в пределах от α = 1/2 для низкой эффективности (высокой протечки) трещин до α = 1 для высокой эффективности (низкой протечки) разрывов.
В течение периода до закрытия и после закрытия разрыва, когда половинная длина разрыва является неизменной, решение для безразмерного давления пласта, для разрыва с бесконечной проводимостью в терминах преобразования Лапласа может быть записано в виде формулы:
 (А-28)
(А-28)
Две различные модели пласта, одна для распространения разрыва и одна для разрыва с фиксированной длиной, могут использоваться вместе для получения решения для безразмерного давления в скважине посредством записи интегралов Дюгамеля в виде формулы:
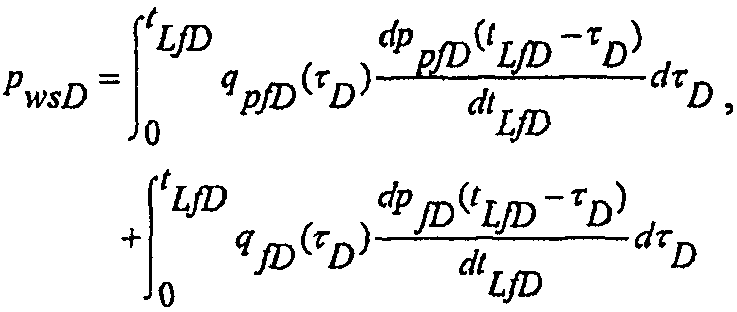 (А-29)
(А-29)
где  представляет собой безразмерную скорость потока для модели распространения разрыва и
представляет собой безразмерную скорость потока для модели распространения разрыва и 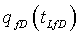 представляет собой безразмерную скорость потока для модели с фиксированной половинной длиной разрыва, которые используются в течение периода до закрытия и падения давления после закрытия. Начальное условие в разрыве и в пласте представляет собой постоянное начальное давление,
представляет собой безразмерную скорость потока для модели с фиксированной половинной длиной разрыва, которые используются в течение периода до закрытия и падения давления после закрытия. Начальное условие в разрыве и в пласте представляет собой постоянное начальное давление, 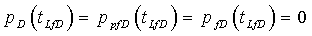 , и с начальным условием, преобразование Лапласа интеграла Дюгамеля записывается в виде формулы:
, и с начальным условием, преобразование Лапласа интеграла Дюгамеля записывается в виде формулы:
 (А-30)
(А-30)
Безразмерное уравнение материального баланса в терминах преобразования Лапласа может быть разделено на части нагнетания и падения давления, если записать его в виде формулы:
 (А-31)
(А-31)
где безразмерная скорость потока в пласте в течение распространения трещины может быть записана в виде формулы:
 (А-32)
(А-32)
и безразмерная скорость потока до закрытия и после закрытия разрыва может быть записана в виде формулы:
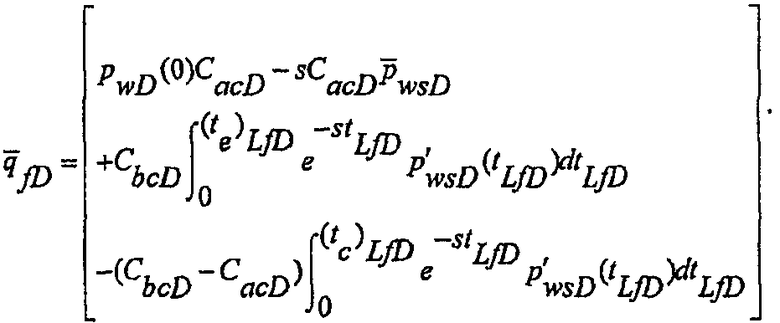 (А-33)
(А-33)
При использовании принципа суперпозиции для получения решения требуется, чтобы зависящий от давления безразмерный коэффициент емкости хранилища для распространяющегося разрыва был записан как функция только одного лишь времени. Путь распространения разрыва может моделироваться с помощью степенной модели и записывается в виде формулы:
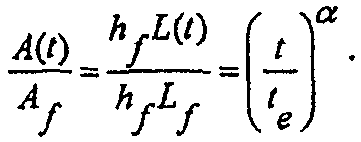 (А-34)
(А-34)
Объем разрыва как функция времени может быть определен по формуле:
 (А-35)
(А-35)
что при использовании степенной модели может также быть записано в виде формулы:
 (А-36)
(А-36)
Производная от объема разрыва по давлению в скважине может быть определена по формуле:
 (А-37)
(А-37)
Напомним, что коэффициент емкости хранилища для распространяющегося разрыва может быть определен по формуле:
 (А-38)
(А-38)
что с помощью включенной сюда степенной модели распространения трещины может быть записано в следующем виде:
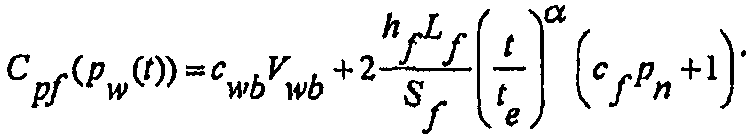 (А-39)
(А-39)
Как отмечают Hagoort J., Waterflood-induced hydraulic fracturing, PhD Thesis, Delft Tech. Univ. (1981), Koning E.J.L. and Niko H., Fractured Water-Injection Wells: A Pressure Falloff Test for Determining Fracturing Dimensions, SPE 14458 (1985), Koning E.J.L., Waterflooding Under Fracturing Conditions, PhD Thesis, Delft Technical University (1988), van den Hoek P.J., Pressure Transient Analysis in Fractured Produced Water Injection Wells, SPE 77946 (2002), и van den Hoek P.J., A Novel Methodology to Derive the Dimensions and Degree of Containment of Waterflood-Induced Fractures From Pressure Transient Analysis, SPE 84289 (2003), 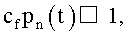 и коэффициент емкости хранилища для распространяющихся разрывов может быть определен по формуле:
и коэффициент емкости хранилища для распространяющихся разрывов может быть определен по формуле:
 (А-40)
(А-40)
Он не является функцией давления и дает возможность использовать принцип суперпозиции для получения решения.
Объединение уравнения материального баланса и интегралов Дюгамеля приведет к следующему:
 (А-41)
(А-41)
и после обратного преобразования к временной переменной, решение для гидроразрыва/падающего давления, для случая распространяющегося разрыва, постоянной емкости хранилища до закрытия и постоянной емкости хранилища после закрытия может быть записано в виде:
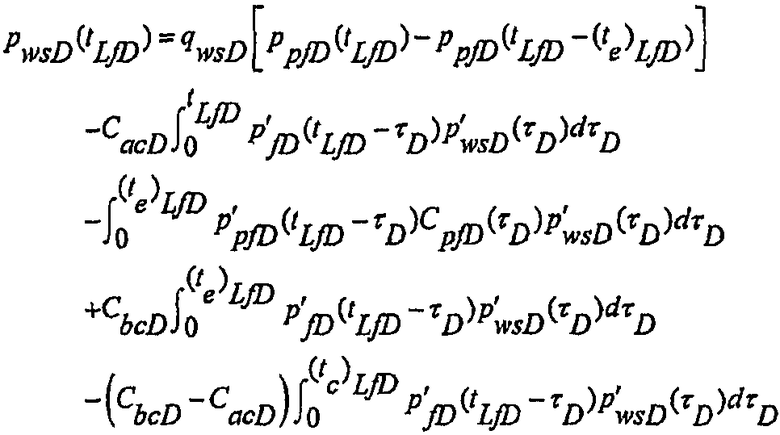 (А-42)
(А-42)
Решения для предельного случая могут быть получены посредством рассмотрения члена в интеграле, содержащего емкость хранилища для распространяющегося разрыва. Когда 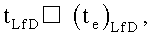 решение для производной для распространяющегося разрыва может быть записано в виде формулы:
решение для производной для распространяющегося разрыва может быть записано в виде формулы:
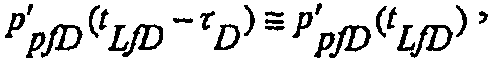 (А-43)
(А-43)
и решение для производной для разрыва может также быть аппроксимировано в виде формулы:
 (А-44)
(А-44)
Определение безразмерного решения для распространяющегося разрыва утверждает, что, когда 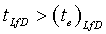 , решения для распространяющегося разрыва и разрыва равны и
, решения для распространяющегося разрыва и разрыва равны и 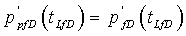 . Как следствие, для
. Как следствие, для  решение для безразмерного давления в скважине может быть определено в виде:
решение для безразмерного давления в скважине может быть определено в виде:
 (А-45)
(А-45)
Коэффициент емкости хранилища до закрытия по определению всегда больше, чем коэффициент емкости для распространяющегося разрыва, и разность двух коэффициентов не может быть равна нулю, если только половинная длина разрыва не создается мгновенно. Однако разность является также относительно малой, если сравнивать с C
bcD или C
acD, и когда безразмерное время нагнетания является коротким и  , член в интеграле, содержащий коэффициент емкости хранилища для распространяющегося разрыва, становится пренебрежимо малым.
, член в интеграле, содержащий коэффициент емкости хранилища для распространяющегося разрыва, становится пренебрежимо малым.
Таким образом, для короткого безразмерного времени нагнетания и  для предельного случая до закрытия решение для безразмерного давление в скважине может быть записано в виде формулы:
для предельного случая до закрытия решение для безразмерного давление в скважине может быть записано в виде формулы:
 (А-46)
(А-46)
что может быть упрощено в терминах преобразования Лапласа и преобразовано обратно к временной переменной для получения решения для безразмерного давления в скважине до закрытия для предельного случая, определенного по формуле:
 (А-47)
(А-47)
которое представляет собой решение для исследования с помощью пласта для подвергающейся гидроразрыву скважины с постоянной емкостью хранилища до закрытия.
Когда безразмерное время нагнетания является коротким и  производная от решения в разрыве может быть аппроксимирована по формуле:
производная от решения в разрыве может быть аппроксимирована по формуле:
 (А-48)
(А-48)
и при  и
и  решение для безразмерного давления в скважине может записано в виде:
решение для безразмерного давления в скважине может записано в виде:
 (А-49)
(А-49)
что представляет собой решение для исследования с помощью водяной пробки с переменной емкостью хранилища.
IV. Обозначения
Обозначения, используемые в описании, относятся к следующим терминам:
A = площадь разрыва в течение распространения, L2, m2
 = площадь разрыва, L2, м2
= площадь разрыва, L2, м2
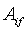 = матричный элемент, безразмерный
= матричный элемент, безразмерный
B = объемный коэффициент формации, безразмерный
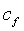 = сжимаемость текучей среды в разрыве, Lt2/м, Па-1
= сжимаемость текучей среды в разрыве, Lt2/м, Па-1
c t = общая сжимаемость, Lt2/м, Па-1
c wb = сжимаемость текучей среды в скважине, Lt2/м, Па-1
C = емкость хранилища скважины, L4t2/м, м3/Па
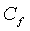 = проводимость разрыва, м3, м3
= проводимость разрыва, м3, м3
C ac = емкость хранилища после закрытия, L4t2/м, м3/Па
C bc = емкость хранилища до закрытия, L4t2/м, м3/Па
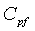 = емкость хранилища для распространяющегося разрыва, L4t2/м, м3/Па
= емкость хранилища для распространяющегося разрыва, L4t2/м, м3/Па
 = емкость хранилища для разрыва до закрытия, L4t2/м, м3/Па
= емкость хранилища для разрыва до закрытия, L4t2/м, м3/Па
 = емкость хранилища для распространяющегося разрыва для множества разрывов, L4t2/м, м3/Па
= емкость хранилища для распространяющегося разрыва для множества разрывов, L4t2/м, м3/Па
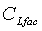 = емкость хранилища после закрытия для множества разрывов, L4t2/м, м3/Па
= емкость хранилища после закрытия для множества разрывов, L4t2/м, м3/Па
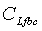 = емкость хранилища до закрытия для множества разрывов, L4t2/м, м3/Па
= емкость хранилища до закрытия для множества разрывов, L4t2/м, м3/Па
h = высота, L, м
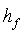 = высота разрыва, L, м
= высота разрыва, L, м
I = интеграл, м/Lt, Па·сек
k = проницаемость, L2, м2
k x = проницаемость в направлении x, L2, м2
k y = проницаемость в направлении y, L2, м2
K 0 = модифицированная функция Бесселя второго рода (нулевого порядка), безразмерная
L = половинная длина распространяющегося разрыва, L, м
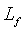 = половинная длина разрыва, L, м
= половинная длина разрыва, L, м
 = количество разрывов, безразмерное
= количество разрывов, безразмерное
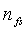 = количество сегментов разрывов, безразмерное
= количество сегментов разрывов, безразмерное
p 0 = давление в скважине в момент времени ноль, м/Lt2, Па
p c = давление закрытия в разрыве, м/Lt2, Па
 = давление в пласте с выходом от отдельного разрыва, м/Lt2, Па
= давление в пласте с выходом от отдельного разрыва, м/Lt2, Па
 = среднее давление в пласте, м/Lt2, Па
= среднее давление в пласте, м/Lt2, Па
p n = общее давление для разрывов, м/Lt2, Па
p w = давление в скважине, м/Lt2, Па
p ac = давление в пласте с постоянной емкостью хранилища после закрытия, м/Lt2, Па
 = давление пласта с выходом от множества разрывов, м/Lt2, Па
= давление пласта с выходом от множества разрывов, м/Lt2, Па
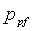 = давление в пласте с распространяющимися разрывами, м/Lt2, Па
= давление в пласте с распространяющимися разрывами, м/Lt2, Па
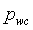 = давление в скважине с постоянной скоростью потока, м/Lt2, Па
= давление в скважине с постоянной скоростью потока, м/Lt2, Па
 = давление в скважине с переменной скоростью потока, м/Lt2, Па
= давление в скважине с переменной скоростью потока, м/Lt2, Па
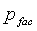 = давление в разрыве с постоянной емкостью хранилища после закрытия разрывов, м/Lt2, Па
= давление в разрыве с постоянной емкостью хранилища после закрытия разрывов, м/Lt2, Па
 = давление в пласте с распространяющимися вторичными разрывами, м/Lt2, Па
= давление в пласте с распространяющимися вторичными разрывами, м/Lt2, Па
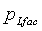 = давление в пласте с выходом от множества разрывов и с постоянной емкостью хранилища после закрытия, м/Lt2, Па
= давление в пласте с выходом от множества разрывов и с постоянной емкостью хранилища после закрытия, м/Lt2, Па
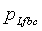 = давление в пласте с выходом от множества разрывов и с постоянной емкостью хранилища до закрытия, м/Lt2, Па,
= давление в пласте с выходом от множества разрывов и с постоянной емкостью хранилища до закрытия, м/Lt2, Па,
q = скорость потока в пласте, L3/t, м3/s
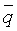 = поток массы для поверхностных разрывов, L3/t, м3/s
= поток массы для поверхностных разрывов, L3/t, м3/s
q w = скорость потока в скважине, L3/t, м3/s
q t = скорость протечки текучей среды, L3/t, м3/s
q s = скорость потока в пласте, L3/t, м3/s
q t = общая скорость потока, L3/t, м3/s
q f = скорость потока в разрыве, L3/t, м3/s
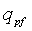 = скорость потока в распространяющемся разрыве, L3/t, м3/s
= скорость потока в распространяющемся разрыве, L3/t, м3/s
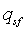 = скорость потока на вскрытой поверхности, L3/t, м3/s
= скорость потока на вскрытой поверхности, L3/t, м3/s
q ws = переменная скорость потока в скважине, L3/t, м3/s
r = радиус, L, м
s = параметр преобразования Лапласа, безразмерный
s e - параметр преобразования Лапласа в конце нагнетания, безразмерный
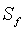 = жесткость разрыва, м/L2t2, Па/м
= жесткость разрыва, м/L2t2, Па/м
 = скин-эффект с поверхностными разрывами, безразмерный
= скин-эффект с поверхностными разрывами, безразмерный
 = скин-эффект с закрытыми разрывами, безразмерный
= скин-эффект с закрытыми разрывами, безразмерный
t = время, t, сек
t e = время в конце нагнетания, t, сек
t c = время при гидравлическом закрытии разрыва, t, сек
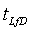 = безразмерное время, безразмерное
= безразмерное время, безразмерное
u = переменная подстановки, безразмерная
U a = единичная ступенчатая функция, безразмерная
 = объем разрыва, L3, м3
= объем разрыва, L3, м3
 = объем остаточного разрыва, L3, м3
= объем остаточного разрыва, L3, м3
V w = объем скважины, L, м
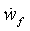 = средняя ширина разрыва, L, м
= средняя ширина разрыва, L, м
 = координата точки вдоль оси x, L, м
= координата точки вдоль оси x, L, м
 = координата точки вдоль оси
= координата точки вдоль оси  , L, м
, L, м
 = положение в скважине вдоль оси x, L, м
= положение в скважине вдоль оси x, L, м
 = координата точки вдоль оси
= координата точки вдоль оси  , L, м
, L, м
 = координата точки вдоль оси
= координата точки вдоль оси  , L, м
, L, м
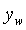 = положение в скважине вдоль оси
= положение в скважине вдоль оси  , L, м
, L, м
α = степенной показатель роста разрыва, безразмерный
δL = отношение вторичной половинной длины разрыва к первичной, безразмерное
Δ = разность, безразмерная
ζ = переменная подстановки, безразмерная
η = переменная подстановки, безразмерная
θ r = эталонный угол, радианы
 = угол трещины, радианы
= угол трещины, радианы
µ = вязкость, м/Lt, Па·сек
ξ = переменная подстановки, безразмерная
ρ = плотность, м/L3, кг/м3
τ = переменная подстановки, безразмерная
φ = пористость, безразмерная
X = переменная подстановки, безразмерная
ψ = переменная подстановки, безразмерная
Нижние индексы
D = безразмерный
i = индекс разрыва, безразмерный
j = индекс сегмента, безразмерный
J = индекс разрыва, безразмерный
m = индекс сегмента, безразмерный
n = индекс момента времени, безразмерный
Для облегчения лучшего понимания настоящего изобретения приводится следующий пример вариантов осуществления изобретения, которые не должны рассматриваться в качестве ограничивающих или определяющих рамки настоящего изобретения.
Пример
Исследования давления при гидроразрыве/падении давления в пласте без существующих ранее разрывов показано на Фигуре 6, которая иллюстрирует график зависимости скорости нагнетания и скважинного давления от времени: осуществлялось 5,3-минутное нагнетание 17,7 барреля воды, обработанной 2% KCl, после чего следовал 16-часовой период закрытия.
Фигура 7 иллюстрирует график эквивалентного давления при постоянной скорости и производной давления, построенные в терминах установленных псевдопеременных с использованием способов, таких как те, которые описаны в Craig D.P., Analytical Modeling of Fracture-Injection / Falloff Sequence and the Development of a Refracture-Candidate Diagnostic Test, PhD dissertation, Texas A&M Univ., College Station, Texas (2005), обсуждающей теоретические кривые для постоянной скорости понижения давления, для скважины, добывающей из вертикального разрыва с бесконечной проводимостью, с постоянной емкостью хранилища. Половинная длина разрыва согласно оценкам составляет 127 фут, с использованием анализа Nolte-Shlyapobersky, как описано в Valko P.P. and Economides M.J., Fluid-Leakoff Delineation in High Permeability Fractiring, SPE PRODUCTION AND FACILITIES (MAY 1986), и проницаемость по согласованию теоретических кривых составляет 0,827 миллидарси, что находится в разумном согласии с проницаемостью 0,522 миллидарси, оцененной по последующему согласованию теоретических кривых для исследования с восстановлением давления.
Таким образом, приведенные выше результаты показывают следующее.
Диагностическое исследование изолированного пласта - кандидата на повторный разрыв может потребовать нагнетания жидкости или газа в малом объеме с низкой скоростью при давлении, превышающем давление создания разрыва пласта и давление распространения разрыва, с последующим продолжительным периодом закрывания.
При условии, что время нагнетания является коротким по отношению к отклику пласта, последовательность гидроразрыва/падающего давления может анализироваться как исследование с помощью водяной пробки.
Количественный анализ теоретических кривых с использованием решения для постоянной скорости понижения давления для пласта, с выходом от разрыва с бесконечной или конечной проводимостью может использоваться для оценки проводимости пласта формации.
В связи с вышеизложенным настоящее изобретение является хорошо адаптированным для получения рассмотренных результатов и преимуществ, а также тех, которые являются присущими ему здесь. Хотя специалистом в данной области могут быть проделаны многочисленные изменения, такие изменения охватываются объемом настоящего изобретения, как определено в прилагаемой формуле изобретения. Термины в формуле изобретения имеют их прямое, обычное значение, если только заявитель четко не определяет иного.



Предложены способы и системы для оценки подземных формаций нефти и газа. А именно, для определения проводимости пластов и средних давлений формации с использованием способов исследования гидроразрыва/падающего давления. Техническим результатом является повышение точности определения свойств пластов. Для этого изолируют, по меньшей мере, один исследуемый пласт подземной формации. Нагнетают жидкость в, по меньшей мере, один пласт подземной формации при давлении нагнетания, превышающем давление разрыва подземной формации в течение периода нагнетания. Закрывают скважину в течение периода закрывания. Измеряют данные по падению давления от подземной формации, в течение периода нагнетания и в течение последующего периода закрытия. Количественно определяют проводимость, по меньшей мере, одного пласта подземной формации посредством анализа данных по падению давления с помощью модели исследования гидроразрыва/падающего давления. При этом пластовая текучая среда является слабо сжимаемой или сжимаемой. Проводимость пласта количественно определяют от точки согласования до закрытия разрыва или от точки согласования после закрытия разрыва по математическим зависимостям. 3 н. и 13 з.п. ф-лы, 7 ил.
1. Способ определения проводимости, по меньшей мере, одного пласта подземной формации, содержащего пластовую текучую среду, включающий в себя следующие стадии:
(а) изолирование, по меньшей мере, одного исследуемого пласта подземной формации;
(б) нагнетание жидкости в, по меньшей мере, один пласт подземной формации при давлении нагнетания, превышающем давление разрыва подземной формации в течение периода нагнетания;
(в) закрытие скважины в течение периода закрывания;
(г) измерение данных по падению давления от подземной формации в течение периода нагнетания и в течение последующего периода закрытия;
(д) количественное определение проводимости, по меньшей мере, одного пласта подземной формации посредством анализа данных по падению давления с помощью модели исследования гидроразрыва/падающего давления,
при этом пластовая текучая среда является слабо сжимаемой и проводимость пласта количественно определяется в полевых устройствах от точки согласования до закрытия разрыва по формуле
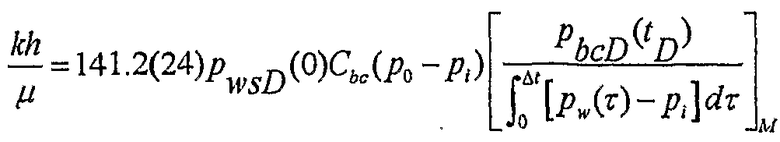
или от точки согласования после закрытия разрыва:
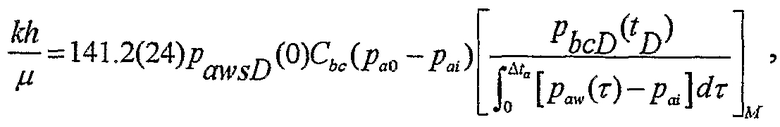
где k - проницаемость, L2;
h - высота, L;
µ - вязкость, м/Lt;
pwsD(0) - безразмерное давление в скважине в момент времени ноль;
pawsD(0) - установленное безразмерное давление в скважине в момент времени ноль;
Сbс - емкость хранилища до закрытия, l4t2/м;
p0 - давление в скважине в момент времени ноль, м/Lt2;
pi представляет собой начальное давление в момент времени t=tne, м/Lt2;
ра0 - установленное давление в скважине в момент времени ноль, м/Lt2;
pai представляет собой установленное давление в момент времени t=tne, м/Lt2;
рbсD(tD) - безразмерное давление в пласте с постоянной емкостью хранилища до закрытия в момент безразмерного времени;
pw - давление в скважине, м/Lt2;
paw - установленное давление в скважине, м/Lt2;
τ - безразмерная переменная подстановки;
М - безразмерный индекс сегмента.
2. Способ определения проводимости, по меньшей мере, одного пласта подземной формации, содержащего пластовую текучую среду, включающий в себя следующие стадии:
(а) изолирование, по меньшей мере, одного исследуемого пласта подземной формации;
(б) нагнетание жидкости в, по меньшей мере, один пласт подземной формации при давлении нагнетания, превышающем давление разрыва подземной формации в течение периода нагнетания;
(в) закрытие скважины в течение периода закрывания;
(г) измерение данных по падению давления от подземной формации в течение периода нагнетания и в течение последующего периода закрытия;
(д) количественное определение проводимости, по меньшей мере, одного пласта подземной формации посредством анализа данных по падению давления с помощью модели исследования гидроразрыва/падающего давления,
при этом пластовая текучая среда является сжимаемой и проводимость пласта количественно определяется в полевых устройствах от точки согласования до закрытия разрыва по формуле
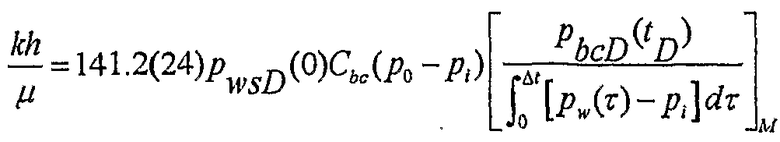
или от точки согласования после закрытия разрыва:
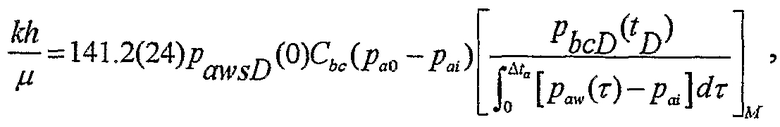
где k - проницаемость, L2;
h - высота, L;
µ - вязкость, м/Lt;
pwsD(0) - безразмерное давление в скважине в момент времени ноль;
pawsD(0) - установленное безразмерное давление в скважине в момент времени ноль;
Сbс - емкость хранилища до закрытия, L4t2/м;
p0 - давление в скважине в момент времени ноль, м/Lt2;
pi представляет собой начальное давление в момент времени t=tne, м/Lt2;
ра0 - установленное давление в скважине в момент времени ноль, м/Lt2;
pai представляет собой установленное давление в момент времени t=tne, м/Lt2;
pbcD(tD) - безразмерное давление в пласте с постоянной емкостью хранилища до закрытия в момент безразмерного времени;
pw - давление в скважине, м/Lt2;
paw - установленное давление в скважине, м/Lt2;
τ - безразмерная переменная подстановки;
М - безразмерный индекс сегмента.
3. Способ по п.1, в котором стадия (д) осуществляется посредством преобразования данных по падению давления в эквивалентные давления для постоянных скоростей и с использованием анализа теоретических кривых для согласования эквивалентных давлений для постоянных скоростей с теоретическими кривыми для количественного определения проводимости пласта.
4. Способ по п.2, в котором стадия (д) осуществляется посредством преобразования данных по падению давления в эквивалентные давления для постоянных скоростей и с использованием анализа теоретических кривых для согласования эквивалентных давлений для постоянных скоростей с теоретическими кривыми для количественного определения проводимости пласта.
5. Способ по п.1 или 2, в котором стадия (д) осуществляется посредством преобразования данных по падению давления для получения эквивалентного давления для постоянной скорости, построения графика для эквивалентного давления для постоянной скорости в двойном логарифмическом масштабе как функции времени и количественного определения проводимости, по меньшей мере, одного пласта подземных формаций посредством анализа данных по падению давления для переменной скорости с использованием анализа теоретических кривых в соответствии с моделью исследования гидроразрыва/падающего давления.
6. Способ по п.4, в котором пластовая текучая среда является сжимаемой и преобразование данных по падению давления основывается на свойствах сжимаемой пластовой текучей среды и стадия преобразования включает в себя определение времени закрывания по отношению к концу периода нагнетания, определение установленного времени и определение установленной разности псевдодавлений.
7. Способ по п.6, в котором стадия преобразования включает в себя определение времени закрывания по отношению к концу периода нагнетания по следующей формуле:
Δt=t-tne;
определение установленного времени по следующей формуле:

и
определение установленной разности псевдодавлений по следующей формуле:
Δpa(t)=paw(t)-pai,
где

где tne представляет собой момент времени при окончании периода нагнетания, t;
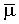 представляет собой вязкость пластовой текучей среды при среднем давлении в пласте, м/Lt;
представляет собой вязкость пластовой текучей среды при среднем давлении в пласте, м/Lt;
(µct)w представляет собой произведение вязкости на сжимаемость текучей среды в скважине в момент времени t;
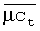 представляет собой произведение вязкости на сжимаемость текучей среды в скважине при среднем давлении в пласте;
представляет собой произведение вязкости на сжимаемость текучей среды в скважине при среднем давлении в пласте;
ра представляет собой установленное давление, м/Lt2,
р представляет собой давление, м/Lt2;
 представляет собой среднее давление в пласте, м/Lt2;
представляет собой среднее давление в пласте, м/Lt2;
paw(t) представляет собой установленное давление в момент времени t, м/Lt2;
pai представляет собой установленное давление в момент времени t=tne, м/Lt2;
ct представляет собой общую сжимаемость, Lt2/м;
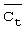 представляет собой общую сжимаемость при среднем давлении в пласте, Lt2/м;
представляет собой общую сжимаемость при среднем давлении в пласте, Lt2/м;
z представляет собой фактор отклонения для реального газа;
 представляет собой фактор отклонения для реального газа при среднем давлении в пласте;
представляет собой фактор отклонения для реального газа при среднем давлении в пласте;
µg - вязкость газа, м/Lt;
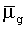 - вязкость газа при среднем давлении в пласте, м/Lt.
- вязкость газа при среднем давлении в пласте, м/Lt.
8. Способ по п.7, дополнительно включающий в себя стадию построения графика давления как функции времени в двойном логарифмическом масштабе, как функции: I(Δpa)=f(ta),
где 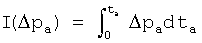 .
.
9. Способ по п.7, дополнительно включающий в себя стадию построения графика функции производной давления как функции времени в двойном логарифмическом масштабе: Δра'=f(ta),
где 
10. Способ по п.3, в котором пластовая текучая среда является слабо сжимаемой и преобразование данных по падению давления с переменной скоростью основываются на свойствах слабо сжимаемой пластовой текучей среды и стадия преобразования включает в себя определение времени закрытия по отношению к моменту окончания периода нагнетания и определение разности давлений.
11. Способ по п.10, в котором стадия преобразования включает в себя определение времени закрытия по отношению к моменту окончания периода нагнетания по формуле Δt=t-tne;
определение разности давлений по формуле
Δp(t)=pw(t)-pi,
где tne представляет собой время в конце периода нагнетания, t;
pw(t) представляет собой давление в момент времени t, м/Lt2; и
pi представляет собой начальное давление в момент времени t=tne, М/Lt2.
12. Способ по п.10, дополнительно включающий в себя стадию построения графика функции давления как функции времени в двойном логарифмическом масштабе: I(Δp)=f(Δt).
13. Способ по п.12, в котором

14. Способ по п.10, дополнительно включающий в себя стадию построения графика функции производной давления как функции времени в двойном логарифмическом масштабе: Δр'=f(Δt).
15. Способ по п.13, в котором

16. Компьютерно-читаемый носитель данных, содержащий программный код, выполняемый на компьютере для осуществления способа по любому из пп.1-15.
| US 2005222852 A1, 06.10.2005 | |||
| СПОСОБ ОПРЕДЕЛЕНИЯ ХАРАКТЕРИСТИК СКВАЖИНЫ, ПРИЗАБОЙНОЙ ЗОНЫ И ПЛАСТА | 2001 |
|
RU2189443C1 |
| СПОСОБ РАЗРАБОТКИ НЕФТЯНОЙ ЗАЛЕЖИ С ПРИМЕНЕНИЕМ ЭМУЛЬСИОННОЙ КОМПОЗИЦИИ | 2001 |
|
RU2185500C1 |
| СПОСОБ ИНТЕНСИФИКАЦИИ ПРИТОКА УГЛЕВОДОРОДОВ ИЗ СКВАЖИН С АНОМАЛЬНО ВЫСОКИМИ ПЛАСТОВЫМИ ДАВЛЕНИЯМИ | 2006 |
|
RU2316646C2 |
| СПОСОБ ЭКСПЛУАТАЦИИ СКВАЖИНЫ | 1999 |
|
RU2151856C1 |
| СПОСОБ ОДНОВРЕМЕННО-РАЗДЕЛЬНОЙ РАЗРАБОТКИ НЕСКОЛЬКИХ ЭКСПЛУАТАЦИОННЫХ ОБЪЕКТОВ И СКВАЖИННАЯ УСТАНОВКА ДЛЯ ЕГО РЕАЛИЗАЦИИ | 2001 |
|
RU2211311C2 |
| US 5303582 A, 19.04.1994. | |||
Авторы
Даты
2011-10-27—Публикация
2006-10-02—Подача