Область техники
Настоящее изобретение относится к способам расчета продуктивности горизонтальных скважин в залежах сланцевого газа при гидроразрыве, применяемым в области разработки нефтяных и газовых месторождений, и, в частности, оно относится к способу расчета продуктивности горизонтальных скважин в залежах сланцевого газа при гидроразрыве в условиях нестационарной диффузии.
Предпосылки изобретения
В связи с тем, что противоречия, касающиеся потребления энергии в Китае, усиливаются с каждым днем, сланцевый газ в качестве эффективного дополнения к нетрадиционным ресурсам нефти и газа привлекает к себе большое внимание, а также стал ключевым звеном в добыче и накоплении природного газа в Китае. Сланцевый газ характеризуется разными условиями залегания в коллекторе, и его механизм миграции является сложным и обычно включает несколько механизмов миграции, таких как адсорбция, десорбция, диффузия, просачивание и т. п., но при этом традиционная теория просачивания не подходит в случае залежей сланцевого газа, а правильное и четкое понимание закономерностей просачивания в залежах сланцевого газа, а также правильное представление механизма миграции сланцевого газа имеют большое значение при руководстве разработкой залежей сланцевого газа. Сланцевый газ в матрице мигрирует в систему естественных трещин за счет диффузии. Диффузия делится на квазистационарную и нестационарную диффузию, однако в реальном процессе разработки залежей газа квазистационарная диффузия практически отсутствует. Миграция газа из матрицы в естественные трещины больше соответствует нестационарной диффузии. Благодаря таким характеристикам сланцев, как низкая пористость, сверхнизкая проницаемость и т. п., способ многоступенчатого гидроразрыва пласта в горизонтальной скважине стал общепринятой мерой для увеличения производства, и точный прогноз производительности горизонтальной скважины в залежи сланцевого газа после гидроразрыва является ключевым в оценке эффективности операции по гидроразрыву пласта и в том, будет ли разработка залежей сланцевого газа успешной; к способам создания моделей продуктивности залежей сланцевого газа относятся аналитические способы, способы численного моделирования и полуаналитические способы. В способах численного моделирования в основном используются компьютерные программы для нахождения примерных решений, но такие особенности, как большое число требующихся в начале параметров залежей газа, длительное время итерирования для нахождения решения, высокие требования к аппаратному обеспечению и т. п., ограничивают их применение. Аналитические способы упрощают реальную ситуацию: используют очень абстрактные и идеализированные физические модели, решения которых непосредственно находят с помощью разных математических методов, при этом достоверность прогнозирования продуктивности в основном зависит от степени точности физической модели и ограничивающих условий больше. Полуаналитические способы основаны на аналитических способах: исходя из основного механизма просачивания в залежах сланцевого газа, создают точную математическую модель и получают решение точечного источника посредством теории функций точечного источника, а затем рассматривают сложную форму трещин, полученных при гидроразрыве. Точная модель производства создается на основании распространения трещин от гидроразрыва. Эта идея простая и интуитивно понятная, а также характеризуется высокой эксплуатационной пригодностью, и можно получить точные результаты прогнозирования.
Таким образом, необходимый сегодня способ прогнозирования продуктивности горизонтальных скважин в залежах сланцевого газа при гидроразрыве должен иметь следующие характеристики: (1) для динамического прогнозирования добычи на ранних этапах требуется небольшое количество параметров и результаты расчета являются точными; (2) ввиду сложного механизма просачивания в залежах сланцевого газа точное прогнозирование ранней добычи осуществляется в условиях нестационарной диффузии.
Суть изобретения
Задачей настоящего изобретения является создание способа расчета продуктивности горизонтальных скважин в залежах сланцевого газа при гидроразрыве в условиях нестационарной диффузии, который является надежным и простым в применении и посредством которого на основании заданных параметров коллектора сланцевого газа и параметров трещин от гидроразрыва может быть осуществлено точное прогнозирование продуктивности горизонтальных скважин в залежах сланцевого газа при гидроразрыве в условиях нестационарной диффузии.
Для решения вышеуказанной технической задачи в настоящем изобретении используется следующее техническое решение.
Залежь сланцевого газа рассматривается как двойная система с тяжелой средой, которая в основном содержит систему матрицы сланцев и систему естественных трещин, при этом просачивание сланцевого газа в коллекторе происходит в два этапа: на первом этапе газ после десорбции в коллекторе сланцевого газа переходит в систему естественных трещин за счет нестационарной диффузии; на втором этапе происходит процесс, при котором газ из естественных трещин попадает в трещины от гидроразрыва и по трещинам от гидроразрыва течет в ствол скважины с выведением на поверхность.
Способ расчета продуктивности горизонтальных скважин в залежах сланцевого газа при гидроразрыве в условиях нестационарной диффузии, включающий следующие этапы, на которых:
(1) собирают параметры гидроразрыва, полученные в результате операции по гидроразрыву пласта, включающие расстояние между трещинами от гидроразрыва, длину трещин, азимутальный угол и количество трещин; рассчитывают коэффициент упругоемкости залежи сланцевого газа ω, коэффициент протекания между порами в условиях нестационарной диффузии λ, модуль безразмерной проницаемости γD, коэффициент адсорбции/десорбции сланцевого газа σ и ограниченную пропускную способность трещин от гидроразрыва СFD;
(2) на основании сочетания собранных параметров гидроразрыва определяют положение трещин от гидроразрыва в прямоугольной системе координат; выделяют трещины от гидроразрыва и определяют координаты микроэлементов всех трещин, а затем на основании теории функции точечного источника и принципа суперпозиции для перепадов давления находят давление на конце каждой трещины от гидроразрыва;
(3) на основании принципа эквивалентной площади создают модель просачивания сквозь трещины от гидроразрыва с получением давления для каждой трещины от гидроразрыва в стволе горизонтальной скважины;
(4) рассчитывают продуктивность горизонтальной скважины в залежах сланцевого газа при гидроразрыве в условиях нестационарной диффузии.
Параметры, рассчитанные на этапе (1), включают коэффициент упругоемкости залежи сланцевого газа ω, коэффициент протекания между порами в условиях нестационарной диффузии λ, модуль безразмерной проницаемости γD, коэффициент адсорбции/десорбции сланцевого газа σ и ограниченную пропускную способность трещин от гидроразрыва СFD, при этом процесс их расчета следующий.
Поры матрицы и естественные трещины, которые развиваются в коллекторе сланцевого газа, являются основными пространствами для накопления сланцевого газа в коллекторе; чтобы описать величину упругоемкости матрицы и естественных трещин, определяют коэффициент упругоемкости залежи сланцевого газа ω, который рассчитывают следующим образом (李晓平.地下油气渗流力学[M].北京:石油工业出版社, 2007:153):
 ,
,
где 
ki – коэффициент начальной проницаемости системы естественных трещин, м2;
μi – начальная вязкость газа, Па•с;
ϕ – пористость системы естественных трещин, безразмерная величина;
Cgi – коэффициент начального сжатия газа, Па-1;
h – толщина залежи сланцевого газа, м;
qsc – начальная продуктивность скважины сланцевого газа, м3/с.
Газ из системы матрицы сланцев мигрирует в систему естественных трещин за счет квазистационарной диффузии, и для характеристики особенности миграции на этом этапе определяют коэффициент протекания между порами в условиях диффузии λ, который рассчитывают следующим образом (李晓平.地下油气渗流力学[M].北京:石油工业出版社, 2007:154):
 ,
,
где 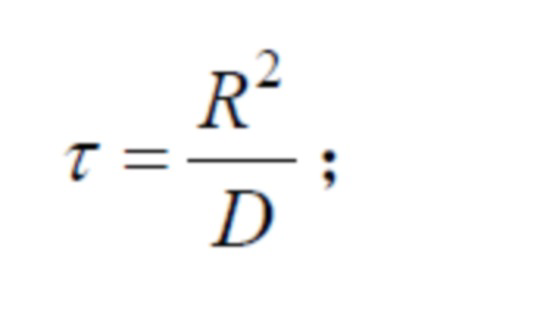
Lref – исходная длина, при этом согласно настоящему изобретению выбирают радиус ствола горизонтальной скважины, м;
D – коэффициент диффузии, м2/с;
R – радиус сферической части матрицы сланцев, м.
В залежи сланцевого газа образуется большое количество естественных трещин; когда давление в коллекторе снижается, возникают эффекты, связанные с чувствительностью к напряжениям, поэтому для характеристики чувствительности к напряжениям определяют модуль безразмерной проницаемости γD, который рассчитывают следующим образом (Liu M, Xiao C, Wang Y, et al. Sensitivity analysis of geometry for mutli-stage fractured horizontal wells with consideration of finite-conductivity fractures in shale gas reservoirs [J]. Journal of Natural Gas Science & Engineering, 2015, 22: 182-195):
 ,
,
где ;
;
Z – коэффициент отклонения газа, безразмерная величина;
μ – вязкость газа, Па•с;
T – температура коллектора сланцевого газа, К;
psc – давление в стандартных условиях (установленное значение для нефтяной отрасли Китая составляет 0,101325 МПа), Па;
Tsc – температура в стандартных условиях (температура в стандартных условиях, установленная для нефтяной отрасли Китая составляет 293 К), К;
γ – коэффициент чувствительности к напряжениям, Па-1;
p – давление системы естественных трещин, Па.
4) Пористая поверхность залежи сланцевого газа содержит большое количество адсорбированного газа, и адсорбция газа после десорбции оказывает большое влияние на его миграцию в залежи сланцевого газа, поэтому для характеристики адсорбционной способности залежи сланцевого газа вводят коэффициент адсорбции/десорбции σ, который рассчитывают следующим образом:
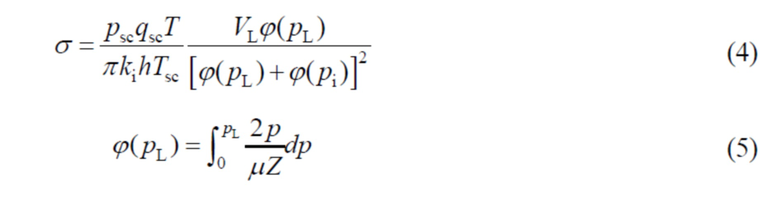
 ,
,
где φ(pL) – ленгмюровское псевдодавление, Па/с;
φ(pi) – начальное псевдодавление залежи сланцевого газа, Па/с;
pL – ленгмюровское давление сланцевого газа, Па;
VL – ленгмюровский объем сланцевого газа, см3/м3;
pi – начальное давление залежи сланцевого газа, Па.
Ленгмюровское давление pL и ленгмюровский объем VL в формулах (4)–(6) являются параметрами, характеризующими адсорбционно-десорбционную характеристику сланцевого газа (Langmuir I. The adsorption of gases on plane surfaces of glass, mica and platinum [J]. Journal of Chemical Physics, 2015, 40(12):1361–1403), и ленгмюровское псевдодавление определяют на основании псевдодавления для преобразования PL в псевдодавление.
5) Трещины от гидроразрыва, образующиеся в результате гидроразрыва, обладают ограниченной пропускной способностью; пропускную способность трещин от гидроразрыва CFD рассчитывают следующим образом:
 ,
,
где kF – коэффициент проницаемости трещин от гидроразрыва, м2;
wF – ширина трещин от гидроразрыва, м;
CFD – пропускная способность трещин от гидроразрыва, безразмерная величина.
Процесс на этапе (2) заключается в следующем: на основании параметров гидроразрыва в случае представления распределения положений трещин от гидроразрыва в плоской прямоугольной системе координат каждую трещину от гидроразрыва делят на определенное количество микроэлементов и после выделения устанавливают координаты микроэлементов каждой трещины от гидроразрыва и концов каждой трещины от гидроразрыва.
Координаты центра микроэлементов трещин от гидроразрыва
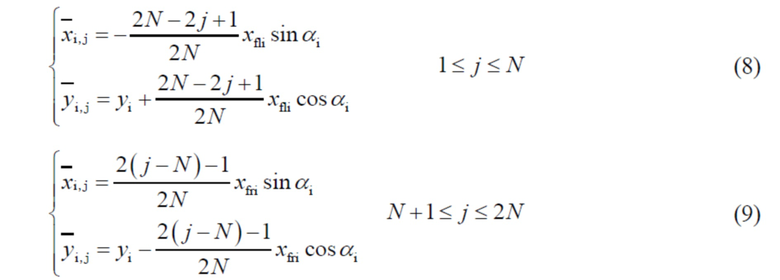 .
.
Координаты узловых точек микроэлементов трещин от гидроразрыва
 .
.
Координаты концов трещин от гидроразрыва являются координатами узловых точек микроэлементов на концах двух крыльев трещин от гидроразрыва, то есть j = 1 или 2N.
При этом:
 i,j – горизонтальная координата центра j-го микроэлемента i-й трещины от гидроразрыва, м;
i,j – горизонтальная координата центра j-го микроэлемента i-й трещины от гидроразрыва, м;
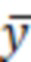 i,j – вертикальная координата центра j-го микроэлемента i-й трещины от гидроразрыва, м;
i,j – вертикальная координата центра j-го микроэлемента i-й трещины от гидроразрыва, м;
xi,j – горизонтальная координата узловой точки j-го микроэлемента i-й трещины от гидроразрыва, м;
yi,j – вертикальная координата узловой точки j-го микроэлемента i-й трещины от гидроразрыва, м;
yi – вертикальная координата пересечения i-й трещины от гидроразрыва со стволом горизонтальной скважины, м;
xfli – длина трещины на левом крыле i-й трещины от гидроразрыва, м;
xfri – длина трещины на правом крыле i-й трещины от гидроразрыва, м;
N – число дискретных микроэлементов на одном крыле трещины от гидроразрыва;
αi – угол между i-й трещиной от гидроразрыва и осью y, градусы.
Потом на основании теории функции точечного источника и принципа суперпозиции для перепадов давления, с помощью преобразования Лапласа получают формулу расчета давления на конце m-й трещины от гидроразрыва (孔祥言.高等渗流力学[M].合肥:中国科学技术大学出版社,1999:171-172;张建国,杜殿发,侯健,等.油气层渗流力学[M].东营:中国石油大学出版社,2009:79-84):
 ,
,
где x, y – горизонтальная и вертикальная координаты некоторой точки в пласте, м;
xi,j,xi,j+1 – горизонтальная координата узловой точки j-го микроэлемента i-й трещины от гидроразрыва, м;
yi – значение координаты точки пересечения i-й трещины от гидроразрыва с осью y, м;
ym – значение координаты точки пересечения m-й трещины от гидроразрыва с осью y, м;
xw,yw – горизонтальная и вертикальная координаты центра микроэлемента трещины от гидроразрыва, м;
xwDi – переменная интегрирования, безразмерная величина;
xflm – длина трещины на левом крыле m-й трещины от гидроразрыва, м;
RD – расстояние от центра микроэлемента некоторой трещины до некоторой точки пласта, безразмерная величина;
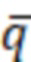 flD – безразмерный дебит i-й трещины, безразмерная величина;
flD – безразмерный дебит i-й трещины, безразмерная величина;
s – переменная Лапласа, безразмерная величина;
αm – угол между m-й трещиной от гидроразрыва и осью y, °;
M – количество трещин от гидроразрыва, образовавшихся в результате гидроразрыва в горизонтальной скважине в залежи сланцевого газа;
K0 – модифицированная функция Бесселя второго рода нулевого порядка.
Процесс на этапе (3) является следующим:
Сначала на основании принципа эквивалентной площади создают модель просачивания сквозь трещины от гидроразрыва и получают формулу просачивания газа в виде плоскорадиального потока в трещинах от гидроразрыва (Mukherjee H, Economides M J. A parametric comparison of horizontal and vertical well performance [J]. SPE Formation Evaluation, 1991, 6(2):209-216):
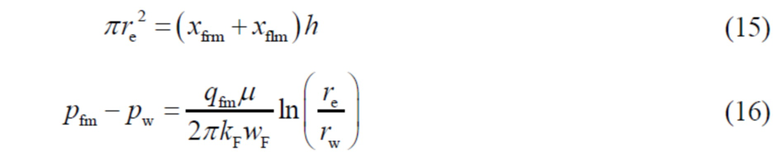 .
.
На основании формул (15) и (16) можно получить:
 ,
,
где re – радиус питания после перехода в плоскорадиальный поток, м;
rw – радиус ствола горизонтальной скважины, м;
xflm – длина трещины на левом крыле m-й трещины от гидроразрыва, м;
xfrm – длина трещины на правом крыле m-й трещины от гидроразрыва, м;
pfm – давление на конце m-й трещины от гидроразрыва, Па;
pw – давление в стволе горизонтальной скважины, Па;
qfm – дебит m-й трещины от гидроразрыва, м3/с.
Принимая во внимание ограниченную пропускную способность трещин от гидроразрыва, с помощью методов преобразования Лапласа и преобразования возмущений можно получить модель просачивания сквозь трещины от гидроразрыва в пространстве Лапласа (孔祥言.高等渗流力学[M].合肥:中国科学技术大学出版社,1999:202-206; Pedrosa O A. Pressure Transient Response in Stress-Sensitive Formations [J]. SPE California Regional Meeting, 1986) и получить формулу расчета давления в m-й трещине от гидроразрыва в стволе горизонтальной скважины:
 ,
,
где ;
;
xfrm – длина трещины на правом крыле m-й трещины от гидроразрыва, м;
 fmD – давление, возникающее на конце m-й трещины от гидроразрыва, безразмерная величина;
fmD – давление, возникающее на конце m-й трещины от гидроразрыва, безразмерная величина;
 wmD – давление в m-й трещине от гидроразрыва в стволе горизонтальной скважины, безразмерная величина;
wmD – давление в m-й трещине от гидроразрыва в стволе горизонтальной скважины, безразмерная величина;
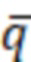 fmD – безразмерный дебит m-й трещины от гидроразрыва.
fmD – безразмерный дебит m-й трещины от гидроразрыва.
Подставляют формулу расчета давления на конце m-й трещины от гидроразрыва и получают выражение для давления в m-й трещине от гидроразрыва в стволе горизонтальной скважины:
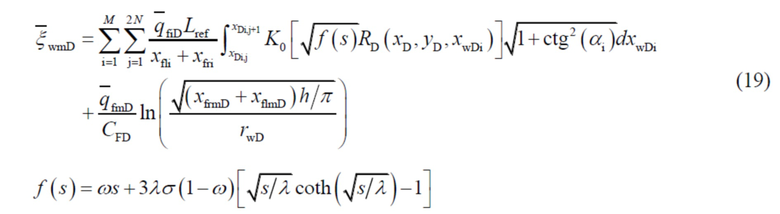 .
.
Этап (4) состоит в следующем:
1) на основании допущения, что просачивание в стволе горизонтальной скважины не испытывает сопротивления, то есть давление  wmD в m-й трещине от гидроразрыва в стволе горизонтальной скважины равно забойному давлению
wmD в m-й трещине от гидроразрыва в стволе горизонтальной скважины равно забойному давлению  wD, полученная на этапе (3) формула расчета давления в трещинах от гидроразрыва в стволе горизонтальной скважины содержит безразмерный дебит
wD, полученная на этапе (3) формула расчета давления в трещинах от гидроразрыва в стволе горизонтальной скважины содержит безразмерный дебит 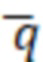 fmD m-й трещины от гидроразрыва и забойное давление
fmD m-й трещины от гидроразрыва и забойное давление 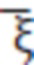 wD; тогда на основании ограничительных условий для дебита и того, что m=1, 2, 3, ..., М, можно получить систему уравнений, состоящую из M+1 уравнений, содержащих
wD; тогда на основании ограничительных условий для дебита и того, что m=1, 2, 3, ..., М, можно получить систему уравнений, состоящую из M+1 уравнений, содержащих f1D,
f1D,  f2D,
f2D,  f3D,...,
f3D,..., 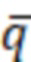 fMD,
fMD,  wd; подставляют параметры, рассчитанные на этапе (1), решают и получают забойное давление
wd; подставляют параметры, рассчитанные на этапе (1), решают и получают забойное давление  wD при постоянном дебите скважины сланцевого газа;
wD при постоянном дебите скважины сланцевого газа;
2) На основании отношения преобразования между забойным давлением  wD при постоянном дебите скважины сланцевого газа и дебитом газовой скважины при постоянном забойном давлении
wD при постоянном дебите скважины сланцевого газа и дебитом газовой скважины при постоянном забойном давлении  D в пространстве Лапласа можно получить безразмерный дебит
D в пространстве Лапласа можно получить безразмерный дебит  D скважины сланцевого газа при постоянном забойном давлении в пространстве Лапласа; тогда на основании численного обращения и определения безразмерного дебита получают дебит
D скважины сланцевого газа при постоянном забойном давлении в пространстве Лапласа; тогда на основании численного обращения и определения безразмерного дебита получают дебит  скважины сланцевого газа в реальном пространстве, то есть продуктивность горизонтальной скважины в залежи сланцевого газа при гидроразрыве в условиях нестационарной диффузии.
скважины сланцевого газа в реальном пространстве, то есть продуктивность горизонтальной скважины в залежи сланцевого газа при гидроразрыве в условиях нестационарной диффузии.
Конкретный процесс является следующим:
На основании того, что формула (19) содержит как безразмерный дебит  fmD m-й трещины от гидроразрыва, так и забойное давление
fmD m-й трещины от гидроразрыва, так и забойное давление 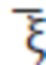 wD и m=1, 2, 3..., М, можно получить М уравнений в общем случае с М+1 неизвестных величин, в том числе
wD и m=1, 2, 3..., М, можно получить М уравнений в общем случае с М+1 неизвестных величин, в том числе 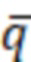 f1D,
f1D, 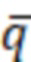 f2D,
f2D,  f3D ,...,
f3D ,...,  fMD и
fMD и  wd;
wd;
тогда на основании ограничительных условий для дебита:
 , –
, –
можно получить систему уравнений из М+1 уравнений, при этом формальное представление посредством матрицы следующее:
 ,
,
где m=1, 2, 3, ..., M; i=1, 2, 3, ..., M.
С помощью метода Гаусса (李庆扬,王能超,易大义.数值分析(第5版)[M].清华大学出版社,北京:2008) решают систему матричных уравнений (21), и можно получить забойное давление 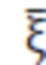 wd при постоянном дебите скважины сланцевого газа.
wd при постоянном дебите скважины сланцевого газа.
На основании отношения преобразования между забойным давлением 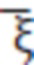 wD при постоянном дебите скважины сланцевого газа и дебитом
wD при постоянном дебите скважины сланцевого газа и дебитом  D газовой скважины при постоянном забойном давлении в пространстве Лапласа (Van Everdingen A F, Hurst W. The application of the Laplace transformation to flow problems in reservoirs [J]. Journal of Petroleum Technology, 1949, 1 (12): 305-324) получают безразмерный дебит qD в скважине сланцевого газа при постоянном забойном давлении в пространстве Лапласа
D газовой скважины при постоянном забойном давлении в пространстве Лапласа (Van Everdingen A F, Hurst W. The application of the Laplace transformation to flow problems in reservoirs [J]. Journal of Petroleum Technology, 1949, 1 (12): 305-324) получают безразмерный дебит qD в скважине сланцевого газа при постоянном забойном давлении в пространстве Лапласа
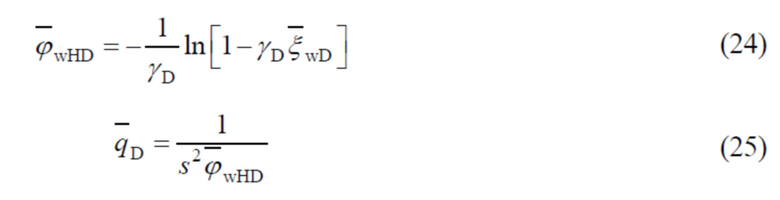 ,
,
На основании численного обращения (同登科,陈钦雷.关于Laplace数值反演Stehfest方法的一点注记[J].石油学报,2001,22(6):91-92) получают безразмерный дебит qD скважины сланцевого газа в реальном пространстве; наконец, на основании определения безразмерного дебита рассчитывают дебит q скважины сланцевого газа, то есть продуктивность горизонтальной скважины в залежи сланцевого газа при гидроразрыве в условиях нестационарной диффузии:
 ,
,
Формул, используемых в настоящем изобретении, сравнительно много, и их последовательное перечисление может показаться громоздким, поэтому, чтобы обеспечить простоту и понятность описания настоящего изобретения, здесь перечислены только те формулы и параметры расчета, которые необходимы при расчете продуктивности, тогда как формулы и параметры расчета, которые здесь не приведены, изложены в соответствующих документах, на которые делается ссылка.
По сравнению с аналогами, известными из предшествующего уровня техники, полезные эффекты настоящего изобретения следующие:
(1) В представленном способе учитывается фактический механизм миграции в залежах сланцевого газа, используется перетекание в естественные трещины в условиях нестационарной диффузии и учитываются эффекты чувствительности к напряжениям естественных трещин; на основании принципа эквивалентности площадей создают модель просачивания сквозь трещины от гидроразрыва с учетом ограниченной пропускной способности; с помощью методов, основанных на функциях точечного источника, и принципа суперпозиции для перепадов давления находят выражение для давления в трещинах от гидроразрыва в стволе горизонтальной скважины; затем путем решения системы матричных уравнений получают забойное давление в пространстве Лапласа; наконец, на основании отношения преобразования получают продуктивность скважины сланцевого газа. Способ характеризуется ясностью подхода для нахождения продуктивности и простотой в применении.
(2) Сравнение факторов в модели, созданной согласно представленному способу, является всеобъемлющим, скорость решения высокая, на ранних этапах нет необходимости в большом количестве параметров коллектора и точность расчетов высокая.
Описание прилагаемых графических материалов
На фиг. 1 представлено схематическое изображение дискретной модели трещин в горизонтальной скважине при многоступенчатом гидроразрыве в залежи сланцевого газа.
На фиг. 2 представлена схема корреляции кривой снижения фактической продуктивности некоторой скважины сланцевого газа за 600 дней и кривой продуктивности, полученной расчетами.
Конкретные способы осуществления
Ниже настоящее изобретение описано с помощью прилагаемых графических материалов и фактических данных с площадки.
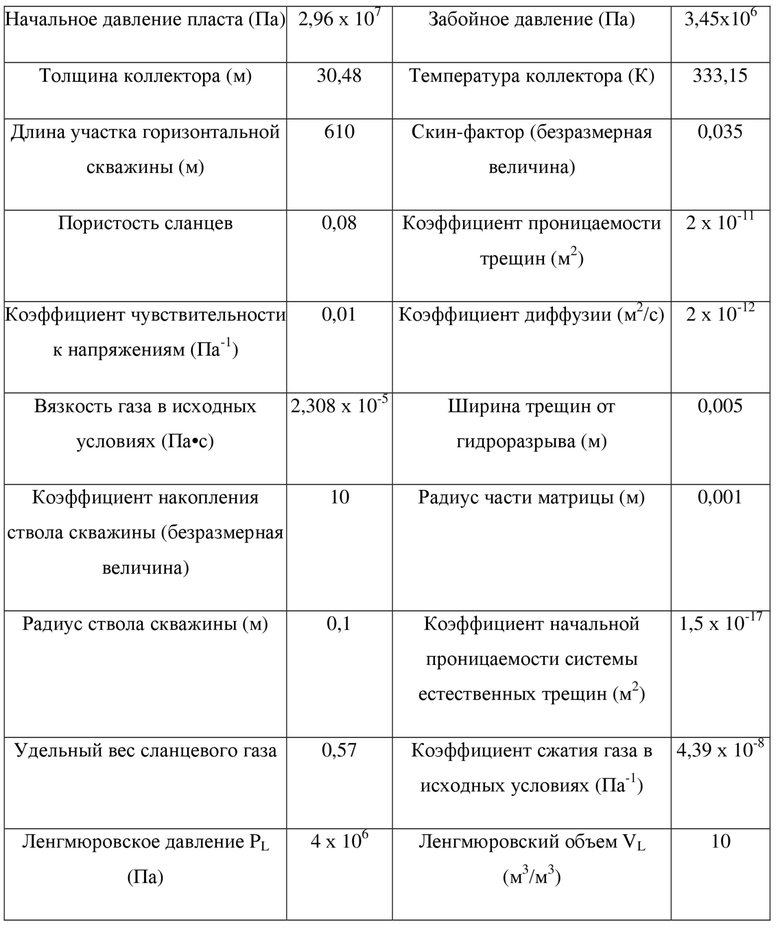
В качестве примера взята некоторая скважина сланцевого газа; толщина коллектора сланцевого газа скважины составляет 30 м, средняя пористость коллектора сланцевого газа составляет 0,08, коэффициент проницаемости матрицы сланцев составляет 2,5 × 10-9 мД, а проницаемость системы естественных трещин составляет 0,015 мД; можно понять, что эта залежь сланцевого газа является коллектором со сверхнизкой проницаемостью и низкой пористостью, и для создания потока промышленного газа необходимо провести операцию по гидроразрыву пласта. Конкретные параметры залежи сланцевого газа приведены в таблице 1.
Таблица 1. Основные параметры некоторой скважины сланцевого газа
Способ расчета продуктивности горизонтальных скважин в залежах сланцевого газа при гидроразрыве в условиях нестационарной диффузии, включающий следующие этапы, на которых:
этап 1: рассчитывают такие промежуточные параметры, как коэффициент упругоемкости ω, коэффициент протекания между порами в условиях нестационарной диффузии λ, модуль безразмерной проницаемости γD, коэффициент адсорбции/десорбции сланцевого газа σ и пропускная способность трещин СFD, для удобства решений последующих уравнений;
этап 2: на основании параметров гидроразрыва в случае представления распределения положений трещин от гидроразрыва в плоской прямоугольной системе координат каждую трещину от гидроразрыва делят на определенное количество микроэлементов (как показано на фиг. 1), затем на основании формул (8)–(9) после выделения устанавливают координаты микроэлементов каждой трещины от гидроразрыва и концов каждой трещины от гидроразрыва, после чего получают выражение для давления, возникающего на конце каждой трещины от гидроразрыва при образовании всех трещин от гидроразрыва;
этап 3: на основании давления на конце каждой трещины от гидроразрыва получают выражение для давления в трещинах от гидроразрыва в стволе горизонтальной скважины;
этап 4: из сочетания формул (12) и (18) можно получить давление во всех трещинах от гидроразрыва в стволе горизонтальной скважины в залежи сланцевого газа; на основании ограничительных условий для дебита с помощью метода Гаусса можно решить систему матричных уравнений (21) и получить забойное давление ξwD при постоянном дебите скважины сланцевого газа; затем на основании формулы (25) вычисляют и получают безразмерный дебит в пространстве Лапласа при постоянном забойном давлении в скважине сланцевого газа; наконец, на основании определения (26) безразмерного потока можно получить дебит скважины сланцевого газа.
Из фиг. 2 понятно, что продуктивность скважины сланцевого газа, полученная расчетом согласно представленному способу, может соответствовать фактической кривой продуктивности, при этом погрешность относительно небольшая, что указывает на то, что способ расчета продуктивности горизонтальных скважин в залежах сланцевого газа при гидроразрыве в условиях нестационарной диффузии, представленный согласно настоящему изобретению, является по сути подходящим, и также можно непосредственно предсказывать тенденцию к снижению продуктивности скважины сланцевого газа на более поздних этапах, управлять оптимизацией параметров горизонтальных скважин при гидроразрыве и оценивать эффективность операции по гидроразрыву пласта.
| название | год | авторы | номер документа |
|---|---|---|---|
| СПОСОБ РАСЧЕТА ОБЪЕМА ОБРАТНОГО ПОТОКА ЖИДКОСТИ ДЛЯ ГИДРОРАЗРЫВА ПЛАСТА ПРИ ГИДРОРАЗРЫВЕ В ГОРИЗОНТАЛЬНЫХ СКВАЖИНАХ В ЗАЛЕЖАХ ГАЗА ТРЕЩИНОВАТЫХ ПЕСЧАНИКОВ | 2019 |
|
RU2723769C1 |
| Способ и система моделирования трещин гидроразрыва пласта бесконечно-конечной проводимости и поперечно-продольного расположения относительно горизонтального ствола скважины | 2020 |
|
RU2745142C1 |
| Способ исследования скважин при стационарных и не стационарных режимах работы | 2020 |
|
RU2752885C1 |
| СПОСОБ ДОБЫЧИ СЛАНЦЕВОГО ГАЗА | 2012 |
|
RU2503799C2 |
| СПОСОБ ОПРЕДЕЛЕНИЯ ВРЕМЕНИ ВЫДЕРЖКИ СКВАЖИНЫ ПОСЛЕ ГИДРОРАЗРЫВА С ИСПОЛЬЗОВАНИЕМ РАСПРОСТРАНЕНИЯ ПОЛЗУЧЕСТИ ТРЕЩИН ГИДРОРАЗРЫВА | 2021 |
|
RU2787144C2 |
| СПОСОБ ВЫБОРА СИСТЕМЫ РАЗРАБОТКИ МЕСТОРОЖДЕНИЯ | 2018 |
|
RU2692369C1 |
| СПОСОБ РАЗРАБОТКИ НЕФТЯНОЙ ЗАЛЕЖИ | 2012 |
|
RU2514046C1 |
| СПОСОБ РЕАЛИЗАЦИИ ВЕРТИКАЛЬНОГО ЗАВОДНЕНИЯ НЕФТЯНОЙ ЗАЛЕЖИ | 2007 |
|
RU2342523C2 |
| СПОСОБ РАЗРАБОТКИ НИЗКОПРОНИЦАЕМЫХ НЕФТЕГАЗОВЫХ ПЛАСТОВ | 2015 |
|
RU2579039C1 |
| СПОСОБ РАЗРАБОТКИ СЛАНЦЕВЫХ НЕФТЕГАЗОНОСНЫХ ЗАЛЕЖЕЙ И ТЕХНОЛОГИЧЕСКИЙ КОМПЛЕКС ОБОРУДОВАНИЯ ДЛЯ ЕГО ОСУЩЕСТВЛЕНИЯ | 2014 |
|
RU2547847C1 |

Изобретение относится к способу расчета продуктивности горизонтальных скважин в залежах сланцевого газа при гидроразрыве в условиях нестационарной диффузии. Способ включающий этапы, на которых: собирают параметры гидроразрыва, полученные в результате операции по гидроразрыву пласта, и рассчитывают коэффициент упругоемкости залежи сланцевого газа, коэффициент протекания между порами в условиях нестационарной диффузии, модуль безразмерной проницаемости, коэффициент адсорбции/десорбции сланцевого газа и ограниченную пропускную способность трещин от гидроразрыва. Определяют положение трещин от гидроразрыва в прямоугольной системе координат; выделяют трещины от гидроразрыва и определяют координаты микроэлементов всех трещин; на основании теории функции точечного источника и принципа суперпозиции для перепадов давления находят давление на конце каждой трещины от гидроразрыва. На основании принципа эквивалентной площади создают модель просачивания сквозь трещины от гидроразрыва с получением давления для каждой трещины от гидроразрыва в стволе горизонтальной скважины. Рассчитывают продуктивность горизонтальной скважины в залежах сланцевого газа при гидроразрыве в условиях нестационарной диффузии. Настоящее изобретение является надежным и простым в применении, при этом на основании заданных параметров коллектора сланцевого газа и параметров трещин от гидроразрыва можно точно прогнозировать продуктивность горизонтальных скважин в залежах сланцевого газа при гидроразрыве в условиях нестационарной диффузии. 1 з.п. ф-лы, 2 ил., 1 табл.
1. Способ расчета продуктивности горизонтальных скважин в залежах сланцевого газа при гидроразрыве в условиях нестационарной диффузии, включающий следующие этапы, на которых:
(1) собирают параметры гидроразрыва, полученные в результате операции по гидроразрыву пласта, включающие расстояние между трещинами от гидроразрыва, длину трещин, азимутальный угол и количество трещин; рассчитывают коэффициент упругоемкости залежи сланцевого газа ω, коэффициент протекания между порами в условиях нестационарной диффузии λ, модуль безразмерной проницаемости γD, коэффициент адсорбции/десорбции сланцевого газа σ и ограниченную пропускную способность трещин от гидроразрыва CFD;
(2) определяют положение трещин от гидроразрыва в прямоугольной системе координат; выделяют трещины от гидроразрыва и определяют координаты микроэлементов всех трещин; на основании теории функции точечного источника и принципа суперпозиции для перепадов давления находят давление на конце каждой трещины от гидроразрыва;
(3) на основании принципа эквивалентной площади создают модель просачивания сквозь трещины от гидроразрыва с получением давления для каждой трещины от гидроразрыва в стволе горизонтальной скважины;
(4) рассчитывают продуктивность горизонтальной скважины в залежах сланцевого газа при гидроразрыве в условиях нестационарной диффузии;
отличающийся тем, что
процесс на этапе (2) состоит в следующем: на основании параметров гидроразрыва в случае представления распределения положений трещин от гидроразрыва в плоской прямоугольной системе координат каждую трещину от гидроразрыва делят на определенное количество микроэлементов и после выделения устанавливают координаты микроэлементов каждой трещины от гидроразрыва и концов каждой трещины от гидроразрыва:
координаты центра микроэлементов трещин от гидроразрыва
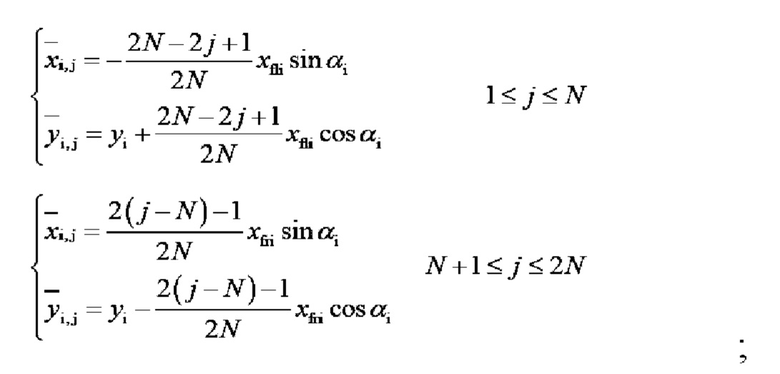
координаты узловых точек микроэлементов трещин от гидроразрыва

при этом координаты концов трещин от гидроразрыва являются координатами узловых точек микроэлементов на концах двух крыльев трещин от гидроразрыва, то есть j=1 или 2N;
где  - горизонтальная координата центра j-го микроэлемента i-й трещины от гидроразрыва, м;
- горизонтальная координата центра j-го микроэлемента i-й трещины от гидроразрыва, м;
 - вертикальная координата центра j-го микроэлемента i-й трещины от гидроразрыва, м;
- вертикальная координата центра j-го микроэлемента i-й трещины от гидроразрыва, м;
xi,j - горизонтальная координата узловой точки j-го микроэлемента i-й трещины от гидроразрыва, м;
yi,j - вертикальная координата узловой точки j-го микроэлемента i-й трещины от гидроразрыва, м;
yi - вертикальная координата пересечения i-й трещины от гидроразрыва со стволом горизонтальной скважины, м;
xfli - длина трещины на левом крыле i-й трещины от гидроразрыва, м;
xfri - длина трещины на правом крыле i-й трещины от гидроразрыва, м;
N - число дискретных микроэлементов на одном крыле трещины от гидроразрыва;
αi - угол между i-й трещиной от гидроразрыва и осью у, градусы;
потом на основании теории функции точечного источника и принципа суперпозиции для перепадов давления с помощью преобразования Лапласа получают формулу расчета давления на конце m-й трещины от гидроразрыва:

х, у - горизонтальная и вертикальная координаты некоторой точки в пласте, м;
xi,j, xi,j+1 - горизонтальная координата узловой точки j-го микроэлемента i-й трещины от гидроразрыва, м;
уi - значение координаты точки пересечения i-й трещины от гидроразрыва с осью у, м;
уm - значение координаты точки пересечения m-й трещины от гидроразрыва с осью у, м;
xw, yw - горизонтальная и вертикальная координаты центра микроэлемента трещины от гидроразрыва, м;
xwDi - переменная интегрирования, безразмерная величина;
Xflm - длина трещины на левом крыле m-й трещины от гидроразрыва, м;
RD - расстояние от центра микроэлемента некоторой трещины до некоторой точки пласта, безразмерная величина;
 - безразмерный дебит i-й трещины, безразмерная величина;
- безразмерный дебит i-й трещины, безразмерная величина;
s - переменная Лапласа, безразмерная величина;
αm - угол между m-й трещиной от гидроразрыва и осью у, °;
М - количество трещин от гидроразрыва, образовавшихся в результате гидроразрыва в горизонтальной скважине в залежи сланцевого газа;
К0 - модифицированная функция Бесселя второго рода нулевого порядка;
Lref - исходная длина, при этом выбирают радиус ствола горизонтальной скважины, м;
при этом процесс на этапе (3) состоит в следующем:
сначала на основании принципа эквивалентной площади создают модель просачивания сквозь трещины от гидроразрыва и получают формулу просачивания газа в виде плоскорадиального потока в трещинах от гидроразрыва:

где rе - радиус питания после перехода в плоскорадиальный поток, м;
rw - радиус ствола горизонтальной скважины, м;
xflm - длина трещины на левом крыле m-й трещины от гидроразрыва, м;
xfrm - длина трещины на правом крыле m-й трещины от гидроразрыва, м;
рfm - давление на конце m-й трещины от гидроразрыва, Па;
pw - давление в стволе горизонтальной скважины, Па;
qfm - дебит m-й трещины от гидроразрыва, м3/с;
h - толщина залежи сланцевого газа, м;
μ - вязкость газа, Па⋅с;
kF - коэффициент проницаемости трещин от гидроразрыва, м2;
wF - ширина трещин от гидроразрыва, м;
принимая во внимание ограниченную пропускную способность трещин от гидроразрыва, получают модель просачивания сквозь трещины от гидроразрыва в пространстве Лапласа и получают формулу расчета давления в m-й трещине от гидроразрыва в стволе горизонтальной скважины:
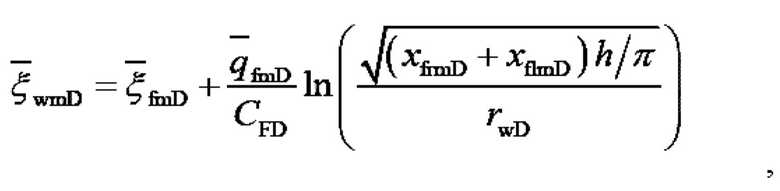
где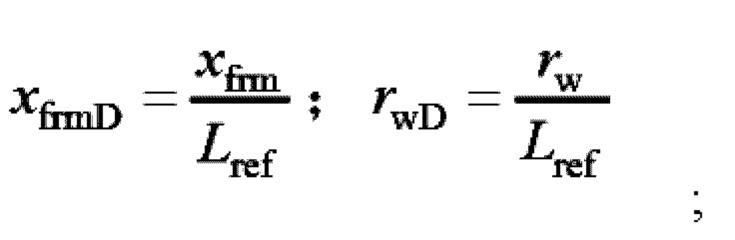
xfrm - длина трещины на правом крыле m-й трещины от гидроразрыва, м;
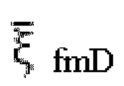 - давление, возникающее на конце m-й трещины от гидроразрыва, безразмерная величина;
- давление, возникающее на конце m-й трещины от гидроразрыва, безразмерная величина;
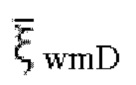 - давление в m-й трещине от гидроразрыва в стволе горизонтальной скважины, безразмерная величина;
- давление в m-й трещине от гидроразрыва в стволе горизонтальной скважины, безразмерная величина;
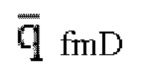 - безразмерный дебит m-й трещины от гидроразрыва, безразмерная величина;
- безразмерный дебит m-й трещины от гидроразрыва, безразмерная величина;
затем подставляют формулу расчета давления на конце m-й трещины от гидроразрыва и получают выражение для давления в m-й трещине от гидроразрыва в стволе горизонтальной скважины:
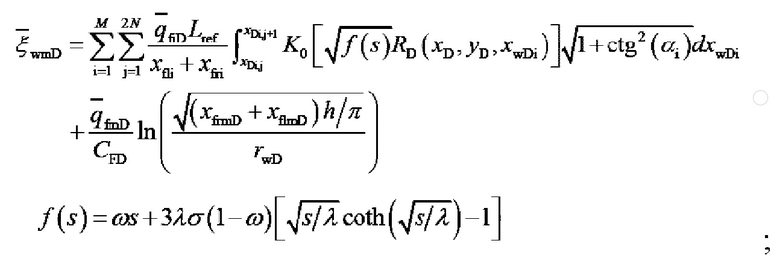
при этом этап (4) состоит в следующем:
1) на основании допущения, что просачивание в стволе горизонтальной скважины не испытывает сопротивления и давление  в m-й трещине от гидроразрыва в стволе горизонтальной скважины равно забойному давлению
в m-й трещине от гидроразрыва в стволе горизонтальной скважины равно забойному давлению 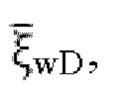 формула расчета давления в трещинах от гидроразрыва в стволе горизонтальной скважины содержит безразмерный дебит
формула расчета давления в трещинах от гидроразрыва в стволе горизонтальной скважины содержит безразмерный дебит  m-й трещины от гидроразрыва и забойное давление
m-й трещины от гидроразрыва и забойное давление  на основании ограничительных условий для дебита и того, что m=1, 2, 3,…, М, получают систему уравнений, состоящую из М+1 уравнений, содержащих
на основании ограничительных условий для дебита и того, что m=1, 2, 3,…, М, получают систему уравнений, состоящую из М+1 уравнений, содержащих  и получают забойное давление
и получают забойное давление 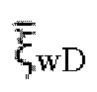 при постоянном дебите скважины сланцевого газа;
при постоянном дебите скважины сланцевого газа;
2) на основании отношения преобразования между забойным давлением 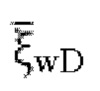 при постоянном дебите скважины сланцевого газа и дебитом
при постоянном дебите скважины сланцевого газа и дебитом  газовой скважины в пространстве Лапласа получают безразмерный дебит
газовой скважины в пространстве Лапласа получают безразмерный дебит 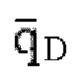 скважины сланцевого газа в пространстве Лапласа, после чего получают дебит q скважины сланцевого газа в реальном пространстве, то есть продуктивность горизонтальной скважины в залежи сланцевого газа при гидроразрыве в условиях нестационарной диффузии.
скважины сланцевого газа в пространстве Лапласа, после чего получают дебит q скважины сланцевого газа в реальном пространстве, то есть продуктивность горизонтальной скважины в залежи сланцевого газа при гидроразрыве в условиях нестационарной диффузии.
2. Способ по п. 1, отличающийся тем, что ограничительные условия для дебита состоят в следующем:

на основании забойного давления 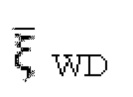 при постоянном дебите скважины сланцевого газа по следующей формуле получают безразмерный дебит
при постоянном дебите скважины сланцевого газа по следующей формуле получают безразмерный дебит 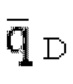 скважины сланцевого газа в пространстве Лапласа:
скважины сланцевого газа в пространстве Лапласа:

с помощью численного обращения получают безразмерный дебит qD скважины сланцевого газа в реальном пространстве и по следующей формуле рассчитывают дебит q скважины сланцевого газа, то есть продуктивность горизонтальной скважины в залежи сланцевого газа при гидроразрыве в условиях нестационарной диффузии:

где qsc - начальная продуктивность скважины сланцевого газа, м3/с.
| СПОСОБЫ И СИСТЕМЫ ДЛЯ ОПРЕДЕЛЕНИЯ СВОЙСТВ ПЛАСТОВ ПОДЗЕМНЫХ ФОРМАЦИЙ | 2006 |
|
RU2432462C2 |
| CN 108240214 A, 03.07.2018 | |||
| CN 107066674 A, 18.08.2017 | |||
| CN 106351651 A, 25.01.2017 | |||
| Иктисанов В.А | |||
| Особенности фильтрации жидкости к скважинам с горизонтальныи окончанием | |||
| Горизонтальные скважины и ГРП в повышении эффективности разработки нефтяных месторождений: Материалы научно-практической конференции | |||
| Казань, | |||
Авторы
Даты
2020-09-24—Публикация
2019-10-04—Подача