Изобретение относится к области электросвязи, а именно к методам передачи видеоизображений по цифровым каналам связи, преимущественно низкоскоростным.
Известны способы кодирования видеоизображений на основе статистического кодирования и кодирования с предсказанием, см., например, книгу: У.Претт. Цифровая обработка изображений. Часть 2. - М.: Мир, 1982, с.641-688. В данных способах кодируют изображения с поэлементной обработкой, когда непрерывный видеосигнал преобразуется в последовательность квантованных отсчетов и затем представляется кодовыми словами в виде нулей и единиц.
Известны также способы кодирования на основе преобразования (см., например, книгу: Н.Ахмед, К.Р.Рао. Ортогональные преобразования при обработке цифровых сигналов. - М.: Радио и связь, 1980, с.192-201; М. Леонард. Схема реализующая алгоритм сжатия изображений неподвижных объектов // Электроника. 1991. №10. С.20-24), включающие выполнение трех операций: сначала изображение подвергается двумерному ортогональному преобразованию, полученные в результате коэффициенты преобразования квантуются и в дальнейшем кодируются для передачи по каналу связи.
Недостатком перечисленных выше способов-аналогов является относительно высокая скорость передачи сообщений при заданном качестве их восстановления на приеме.
Наиболее близким по своей технической сущности к заявленному способу является способ сжатия и восстановления речевых сообщений, описанный в патенте РФ №2226043, МПК7 H04N 7/30 от 20.03.04 г.
Известный способ-прототип заключается в том, что предварительно идентично на передающей стороне и на приемной стороне генерируют случайную квадратную матрицу размером m×m элементов. Генерируют случайные прямоугольные матрицы из единичных и нулевых элементов размером N×m и m×N элементов, преобразуют случайные прямоугольные матрицы размером N×m и m×N элементов путем деления элементов каждой строки случайной прямоугольной матрицы размером N×m элементов на сумму единиц соответствующей строки и деления элементов каждого столбца случайной прямоугольной матрицы размером m×N элементов на сумму единиц соответствующего столбца. Вычисляют матрицу размером N×N элементов путем последовательного перемножения полученной после преобразования прямоугольной матрицы размером N×m элементов, случайной квадратной матрицы размером m×m элементов и полученной после преобразования прямоугольной матрицы размером m×N элементов. Последовательно инвертируют каждый элемент случайных прямоугольных матриц размером N×m и m×N элементов. Затем повторно преобразуют случайные прямоугольные матрицы размером N×m и m×N элементов и повторно вычисляют матрицу размером N×N элементов путем последовательного перемножения полученной после преобразования прямоугольной матрицы размером N×m элементов, случайной квадратной матрицы размером m×m элементов и полученной после преобразования прямоугольной матрицы размером m×N элементов. Вычитают сумму квадратов разности от аналогичной суммы, полученной на предыдущем шаге, и, в случае положительной разности, сохраняют инвертированное значение элемента, а в противном случае - выполняют его повторную инверсию. Передают множество нулевых и единичных элементов прямоугольных матриц размером N×m и m×N элементов по каналу связи, принимают множество нулевых и единичных элементов прямоугольных матриц размером N×m и m×N элементов из канала связи и преобразуют их путем деления элементов каждой строки прямоугольной матрицы размером N×m элементов на сумму единиц соответствующей строки и деления элементов каждого столбца прямоугольной матрицы размером m×N элементов на сумму единиц соответствующего столбца. Каждый элемент случайной квадратной матрицы размером m×m элементов принадлежит диапазону -500÷+500. В качестве сообщения, подлежащего сжатию и восстановлению, используют неподвижное полутоновое видеоизображение, из которого формируют матрицу квантованных отсчетов неподвижного полутонового видеоизображения размером М×М элементов, присвоив каждому ее элемент S(x,y), где x=1,2,…,M; y=1,2,…,M, квантованное значение соответствующего пиксела неподвижного полутонового видеоизображения. Преобразуют матрицу квантованных отсчетов неподвижного полутонового видеоизображения размером М×М элементов к цифровому виду, при этом предварительно формируют матрицу коэффициентов двумерного дискретного косинусного преобразования (ДДКП) размером М×М элементов путем перемножения матрицы дискретного косинусного преобразования (ДКП) размером М×М элементов на матрицу квантованных отсчетов неподвижного полутонового видеоизображения размером М×М элементов и на транспонированную матрицу дискретного косинусного преобразования размером М×М элементов. Формируют матрицу коэффициентов ДДКП размером N×N элементов на основании выражения A(i,j)=L(i,j), где i=1,2,…,N, j=1,2,…,N, L(i,j) - i-й, j-й элемент матрицы коэффициентов ДДКП размером М×М элементов, A(i,j) - i-й, j-й элемент матрицы коэффициентов ДДКП размером N×N элементов, причем выбирают N≤M. На передающей и приемной сторонах идентично формируют нормировочную матрицу размером N×N элементов, элементы которой С(i,j) вычисляют по формуле
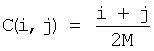 .
.
Затем формируют матрицу нормированных коэффициентов ДДКП размером N×N элементов, путем умножения каждого коэффициента A(i,j) на соответствующий ему элемент нормировочной матрицы размером N×N элементов. После вычисления матрицы размером N×N элементов рассчитывают сумму квадратов разностей между элементами матрицы размером N×N элементов и соответствующими им элементами матрицы нормированных коэффициентов ДДКП размером N×N элементов, а после повторного вычисления матрицы размером N×N элементов повторно рассчитывают сумму квадратов разностей между элементами матрицы размером N×N элементов и элементами матрицы нормированных коэффициентов ДДКП размером N×N элементов. После преобразования на приемной стороне прямоугольных матриц размером N×m и m×N элементов формируют матрицу восстановленных нормированных коэффициентов ДДКП размером N×N элементов путем последовательного перемножения полученной после преобразования прямоугольной матрицы размером N×m, случайной квадратной матрицы размером m×m элементов и полученной после преобразования прямоугольной матрицы размером m×N элементов. Затем формируют матрицу восстановленных коэффициентов ДДКП размером N×N элементов путем деления значения каждого i-го, j-го элемента матрицы восстановленных нормированных коэффициентов ДДКП размером N×N элементов на соответствующий элемент нормировочной матрицы размером N×N элементов. Формируют матрицу восстановленных коэффициентов ДДКП размером М×М элементов, путем присвоения значения каждого i-го, j-го элемента матрицы восстановленных коэффициентов ДДКП размером N×N элементов каждому i-му, j-му элементу матрицы восстановленных коэффициентов ДДКП размером М×М элементов, а в качестве остальных элементов записывают нули. Формируют матрицу восстановленных квантованных отсчетов неподвижного полутонового видеоизображения путем перемножения транспонированной матрицы ДКП размером М×М элементов на матрицу восстановленных коэффициентов ДДКП размером М×М элементов и на матрицу ДКП размером М×М элементов. Представляют матрицу восстановленных квантованных отсчетов неподвижного полутонового видеоизображения размером М×М элементов в виде неподвижного полутонового видеоизображения, присвоив каждому пикселю неподвижного полутонового видеоизображения значение соответствующего элемента матрицы восстановленных квантованных отсчетов неподвижного полутонового видеоизображения размером М×М элементов.
При использовании способа-прототипа без ухудшения качества восстановления сообщений обеспечивается сжатие исходных изображений до величины, при которой возможна передача неподвижных полутоновых изображений по цифровым каналам связи со скоростью 256÷512 кбит/с.
Недостатком этого способа-прототипа является относительно низкое качество восстановленных видеоизображений при использовании каналов связи с ограниченной пропускной способностью. Это объясняется тем, что в способе-прототипе матрицу восстановленных квантованных отсчетов неподвижного полутонового видеоизображения размером М×М элементов вычисляют путем выполнения обратного двумерного дискретного косинусного преобразования над матрицей восстановленных коэффициентов дискретного косинусного преобразования размером М×М элементов. Причем N×N элементов данной матрицы (N≤M), занимающих ее верхний левый квадрант, формируют на основе принятого из канала связи цифрового потока, а остальные элементы считают равными нулю.
При этом делается допущение о том, что N×N элементов матрицы ДДКП содержат наиболее значимые (максимальные по абсолютному значению) коэффициенты. Такое построение декодера привод к тому, что для увеличения коэффициента сжатия необходимо уменьшать параметр N, что приводит к увеличению числа нулевых коэффициентов матрицы ДДКП. С другой стороны, уменьшение значения N приводит к тому, что к нулевому значению приравниваются в том числе и значимые коэффициенты ДДКП. Это, в свою очередь, приводит к снижению качества восстанавливаемых изображений. Таким образом, фиксированная конфигурация ненулевых коэффициентов ДДКП в виде верхнего левого квадранта размером N×N элементов приводит либо к низкому коэффициенту сжатия при хорошем качестве восстановленных изображений, либо к их низкому качеству при относительно высоком коэффициенте сжатия.
Целью изобретения является разработка способа сжатия и восстановления сообщений, обеспечивающего повышение качества восстановленных видеоизображений при использовании низкоскоростных каналов связи.
Поставленная цель достигается тем, что в известном способе сжатия и восстановления сообщений, заключающемся в том, что неподвижное видеоизображение преобразуют в цифровую форму, для чего формируют матрицу квантованных отсчетов неподвижного видеоизображения, вычисляют ее частотные коэффициенты (матрицу спектра изображения) путем выполнения операции двумерного дискретного косинусного преобразования, квантуют частотные коэффициенты, значения которых превышают заданный уровень и передают их по каналу связи, по принятым частотным коэффициентам восстанавливают матрицу квантованных отсчетов неподвижного изображения. В представленном способе после формирования матрицы квантованных отсчетов по значениям ее элементов вычисляют коэффициенты двумерного линейного предсказания ax1, ax2,…,axp и ay1, ay2,…,ayp, где p - глубина предсказания. Затем квантуют их и передают в канал связи, по значениям квантованных коэффициентов двумерного линейного предсказания формируют огибающую частотных коэффициентов. По сформированной огибающей определяют координаты частотных коэффициентов в порядке убывания их абсолютных значений, затем значения частотных коэффициентов, соответствующих найденным координатам, квантуют и последовательно передают в канал связи, причем число Kots подлежащих передаче коэффициентов задают предварительно в зависимости от требуемого качества восстановления изображения. После приема коэффициентов двумерного линейного предсказания и частотных коэффициентов, по коэффициентам двумерного линейного предсказания формируют на приемной стороне огибающую частотных коэффициентов, так же как на передающей стороне, по которой присваивают принятым частотным коэффициентам координаты в структуре матрицы спектра изображения, а вместо недостающих частотных коэффициентов в структуре матрицы оставляют нулевые значения. После чего восстанавливают изображение путем перемножения транспонированной матрицы дискретно-косинусного преобразования на матрицу восстановленных коэффициентов двумерного дискретно-косинусного преобразования и на матрицу дискретно-косинусного преобразования. Представляют матрицу восстановленных квантованных отсчетов неподвижного полутонового видеоизображения в виде неподвижного полутонового видеоизображения, присвоив каждому пикселю неподвижного полутонового видеоизображения значение соответствующего элемента матрицы восстановленных квантованных отсчетов неподвижного полутонового видеоизображения.
Благодаря новой совокупности существенных признаков, за счет вычисления огибающей частотных коэффициентов неподвижного полутонового изображения и вычисления коэффициентов двумерного линейного предсказания матрицы спектра этого изображения, обеспечивается существенное сокращение объема цифрового потока на выходе кодера. Для уменьшения цифрового представления видеоизображения кодируют и передают не все спектральные коэффициенты, а только Kots спектральных коэффициентов из области спектра с максимальной энергией.
Таким образом, отличие предлагаемого способа сжатия от способа-прототипа состоит в том, что область значимых коэффициентов спектра не является фиксированной, а определяется для каждого сжимаемого сообщения путем вычисления огибающей спектра на основе коэффициентов двумерного линейного предсказания.
Это позволяет повысить качество восстановленных видеоизображений при использовании каналов связи с ограниченной пропускной способностью.
Заявленный способ поясняется чертежами:
- Фиг.1 - Формирование матрицы квантованных отсчетов;
- Фиг.2 - Спектральное представление коэффициентов преобразования;
- Фиг.3 - Представление i-го, j-го элемента значения яркости i-го, j-го пикселя исходного изображения как линейной комбинации предшествующих отсчетов;
- Фиг.4 - Формирование матриц Dy;
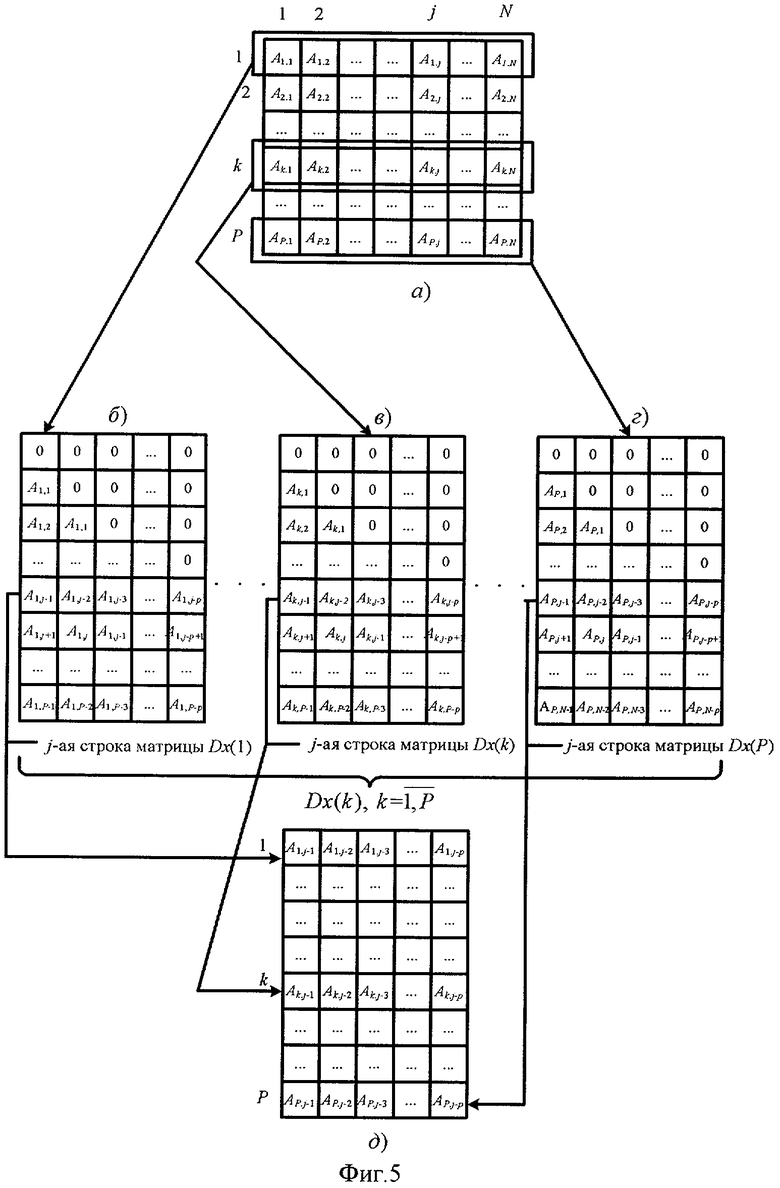
- Фиг.5 - Формирование матриц Dx и М(j);
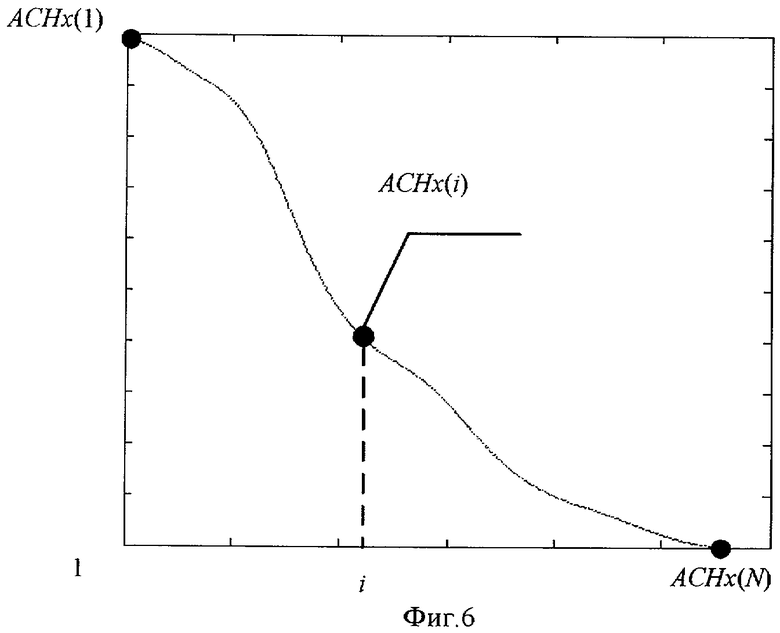
- Фиг.6 - Вычисление огибающей по строкам ACHx(i), 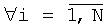 ;
;
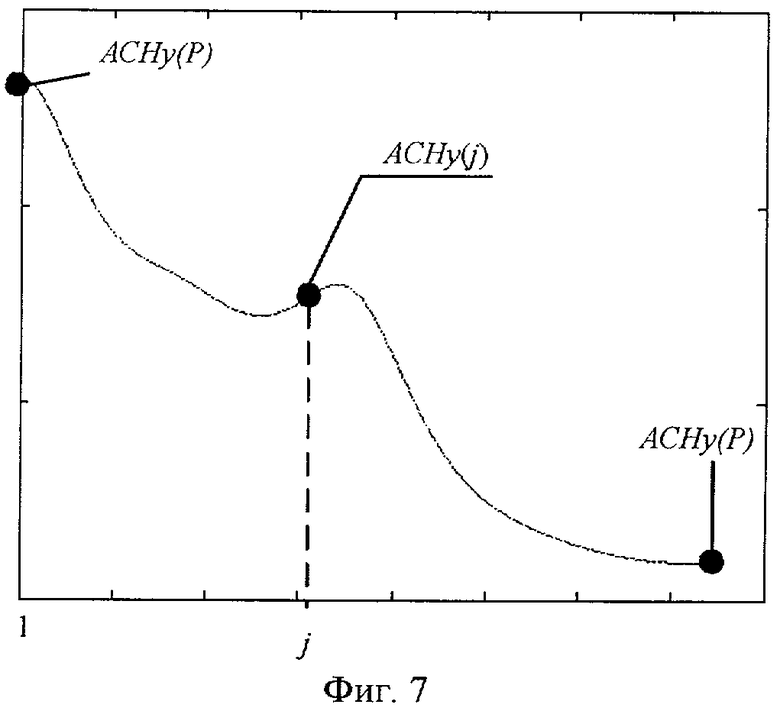
- Фиг.7 - Вычисление огибающей по столбцам ACHy(j), 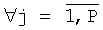 ;
;
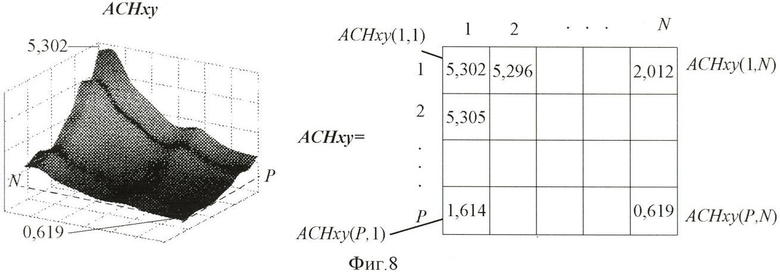
- Фиг.8 - Расчет огибающей коэффициентов ДДКП;
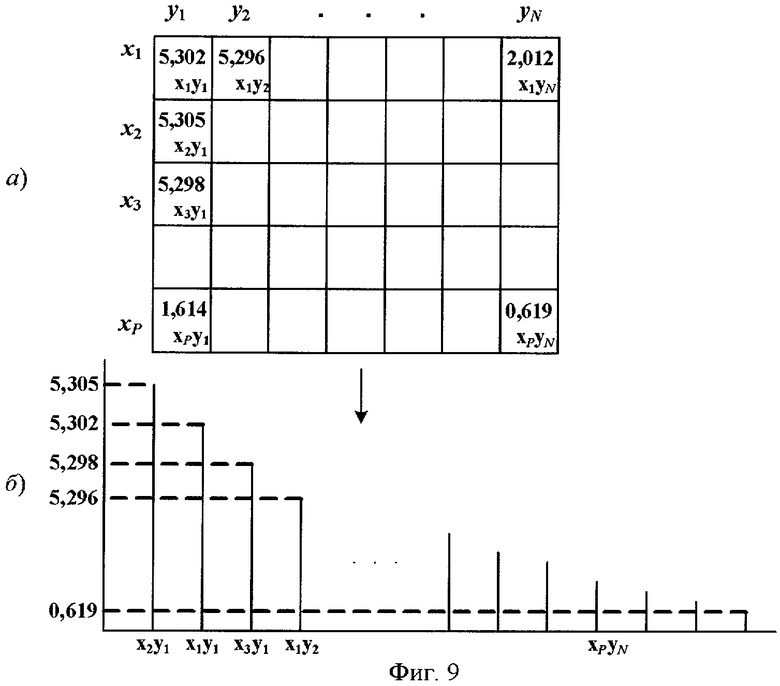
- Фиг.9 - Ранжирование элементов матрицы огибающей коэффициентов ДДКП в порядке убывания значений;
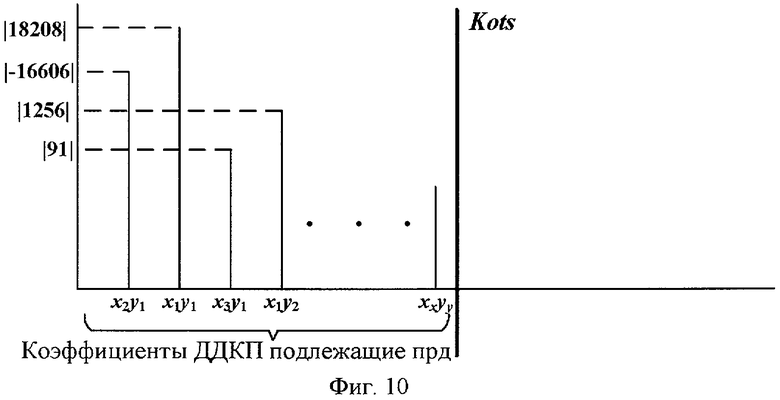
- Фиг.10 - Формирование последовательности частотных коэффициентов подлежащих передаче по каналу связи;
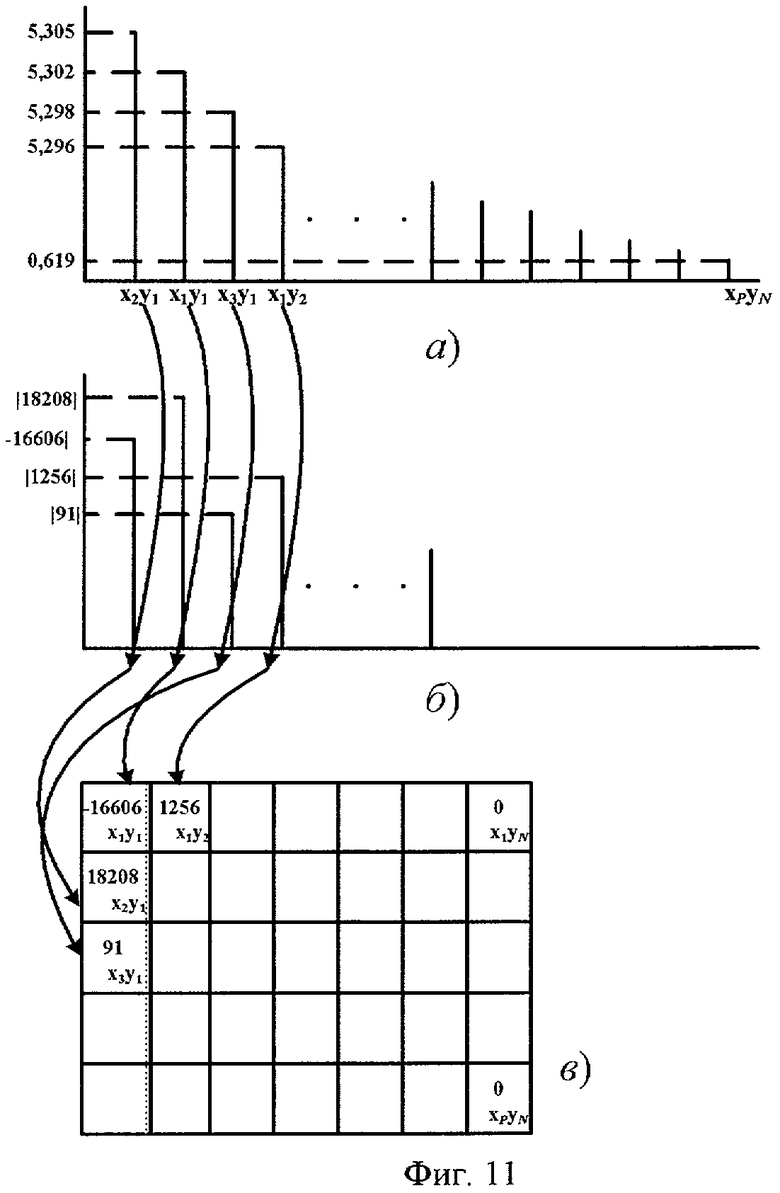
- Фиг.11 - Восстановление матрицы ДДКП на приемной стороне;
- Фиг.12 - Сжатие и восстановление видеоизображения.
Возможность реализации заявленного способа сжатия и восстановления сообщений объясняется следующим. При необходимости передачи по каналу связи сообщения, для передачи которого в условиях ограничения скорости предоставляемого канала связи требуется недопустимо большой временной интервал, используют различные приемы сокращения объема цифрового представления передаваемого сообщения.
Например (см. книгу: У.Претт. Цифровая обработка изображений. Часть 1. - М.: Мир, 1982, с.96-118), кодируемое сообщение представляют в виде произведения матрицы опорных векторов на матрицу коэффициентов разложения. Для этой цели используют один из известных приемов: дискретное косинусное преобразование, быстрое преобразование Фурье, преобразование Карунена-Лоэва, Вейвлет-преобразование и другие. При этом по каналу связи достаточно передать только коэффициенты разложения в предположении, что на приемной стороне для восстановления сообщения будут использоваться аналогичные (как и на передаче) опорные вектора.
Такой прием обуславливает некоторое снижение объема информации, необходимого для передачи по каналу связи, и одновременное достижение требуемого качества восстановленных сообщений.
Таким образом, при некотором ухудшении качества передаваемой информации обеспечивают снижение объема информации, необходимого для передачи. В то же время объем передаваемой информации о матрице опорных векторов и матрице коэффициентов разложения все еще велик, что не соответствует требованиям к современным каналам связи при сохранении требуемого качества. В предлагаемом способе решается задача снижения объема передаваемой информации при одновременном сохранении требуемого качества.
Предлагаемый способ включает проведение следующих действий.
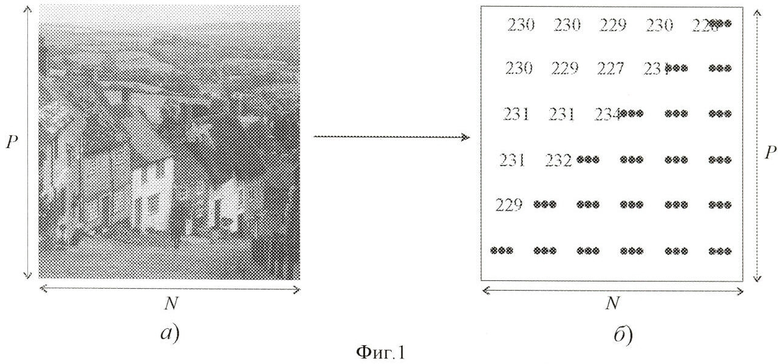
В качестве сообщения, подлежащего сжатию и восстановлению, далее рассматривается неподвижное полутоновое видеоизображение (см. фиг.1а), из которого формируют матрицу квантованных отсчетов неподвижного полутонового видеоизображения размером P×N элементов, присвоив каждому ее элементу A(i,j), где i=1,2,…,Р; j=1,2,…,N, квантованное значение соответствующего пикселя неподвижного полутонового видеоизображения (см. фиг.1б и фиг.12 (1)).
С целью уменьшения объема информации, передаваемой по каналу связи, используют дискретное косинусное преобразование, описанное, например, в кн.: Н.Ахмед, К.Р.Рао. Ортогональные преобразования при обработке цифровых сигналов. - М.: Связь, 1980, с.156-159.
Матрицу коэффициентов ДДКП размером PxN элементов формируют на основании выражения 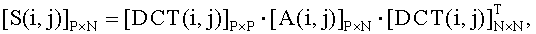 где
где 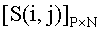 - матрица коэффициентов ДДКП размером P×N элементов,
- матрица коэффициентов ДДКП размером P×N элементов,  - матрица квантованных отсчетов неподвижного полутонового видеоизображения размером P×N элементов,
- матрица квантованных отсчетов неподвижного полутонового видеоизображения размером P×N элементов, 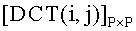 - матрица прямого ДКП, размером Р×Р элементов;
- матрица прямого ДКП, размером Р×Р элементов; 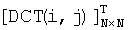 - матрица обратного ДКП, размером N×N элементов (см. фиг.12 (2)).
- матрица обратного ДКП, размером N×N элементов (см. фиг.12 (2)).
Наиболее информативными, с точки зрения качества восстановления передаваемого видеоизображения (см. фиг.2а) являются коэффициенты ДДКП с максимальной энергией, располагающиеся, как правило, в левом верхнем квадранте матрицы коэффициентов ДДКП размером P×N элементов. Однако, как показывают исследования, местоположение значимых коэффициентов для различных изображений может быть различным (см. фиг.2б).
Для определения местоположения значимых коэффициентов находят огибающую коэффициентов ДДКП. С этой целью вычисляют коэффициенты двумерного линейного предсказания ax1, ax2,…,axp и ay1, ay2,…,ayp,, где p - глубина предсказания (см. фиг.12 (3)). Величину p выбирают в пределах от 8 до 12. Такой диапазон выбора количества вычисляемых коэффициентов линейного предсказания связан с тем, что при p меньше 8 на приемной стороне не удастся с необходимой точностью аппроксимировать огибающую спектра видеоизображения, увеличение же значения параметра p больше 12 не дает какого-либо значительного повышения точности аппроксимации. Для вычисления коэффициентов двумерного линейного предсказания, как и в случае вычисления коэффициентов одномерного линейного предсказания, необходимо решить задачу минимизации среднеквадратической ошибки между исходным и предсказанным сообщениями, относительно этих коэффициентов (см., например, книги: Дж.Д.Маркел, А.Х.Грей. Линейное предсказание речи. - М.: Связь, 1980, с.13-23; А.А.Устинов, А.А.Рощин, Д.А.Бардюков. Параметрическое кодирование речи с линейным предсказанием. - СПб.: ВАС, 2008, с.30-32).
Поясним особенности вычисления коэффициентов двумерного линейного предсказания.
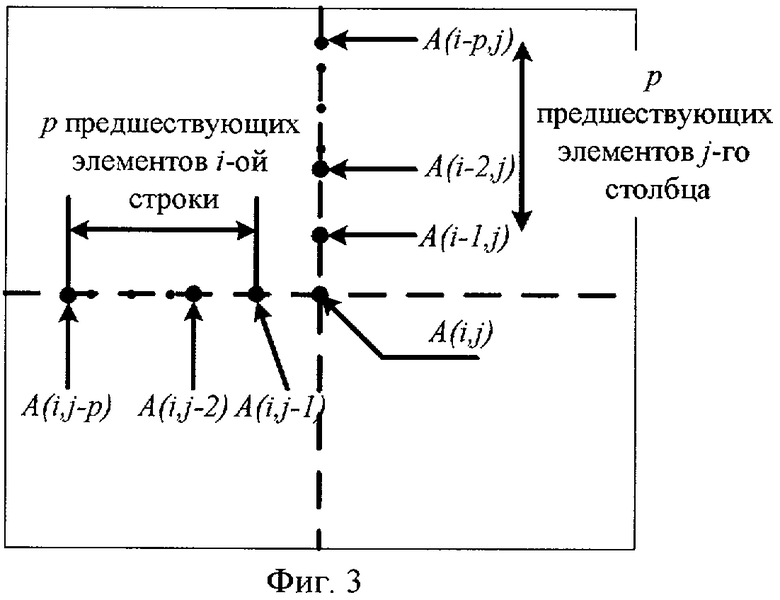
Пусть A(i,j) - i-й, j-й элемент значения яркости i-го, j-го пикселя исходного изображения, тогда предсказанное значение i-го, j-го элемента изображения
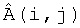 можно определить как линейную комбинацию p предшествующих элементов i-й строки и p предшествующих элементов j-го столбца (см. фиг.3):
можно определить как линейную комбинацию p предшествующих элементов i-й строки и p предшествующих элементов j-го столбца (см. фиг.3):
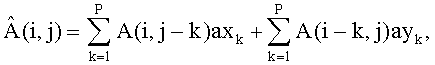
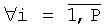 ,
, 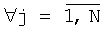 .
.
Для всех элементов j-го столбца исходного изображения данное выражение можно записать в матричной форме в виде:
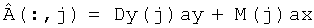 ,
,
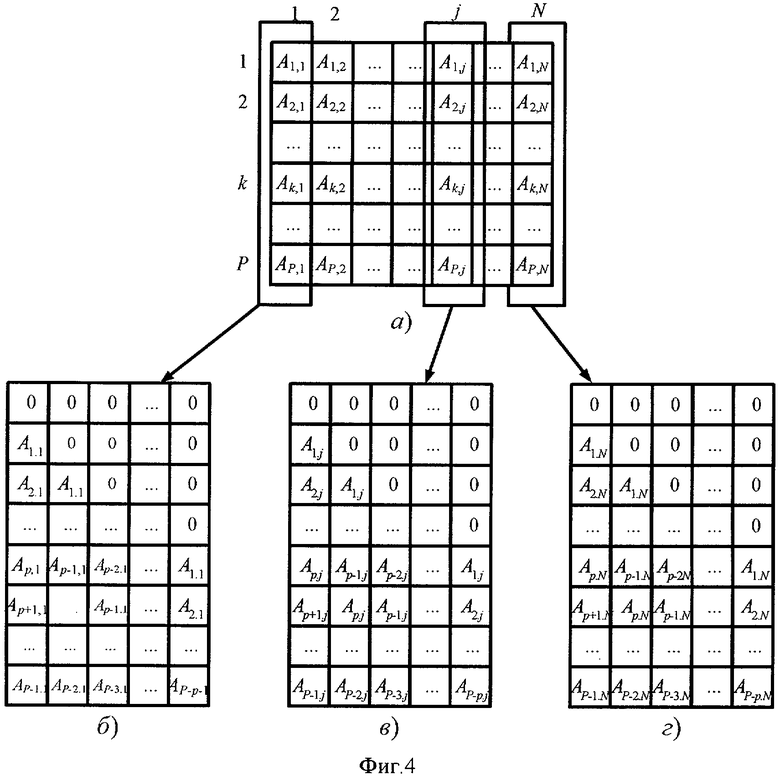
где Dy(j) - матрица размером P×p, составленная из элементов j-го столбца изображения (см. фиг 4а), имеющая вид (см. фиг.4в):
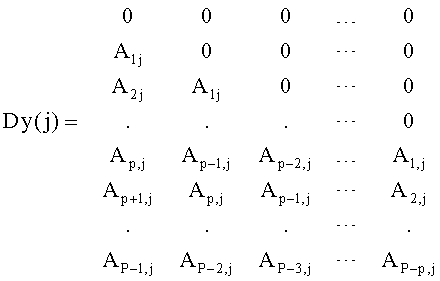
M(j)- матрица размером Р×р элементов (см. фиг.5д), состоящая из j-x строк матриц Dx(k), 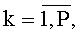 имеющих вид (см. фиг.5б, в, г):
имеющих вид (см. фиг.5б, в, г):
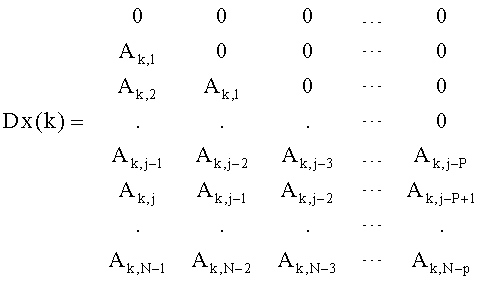
С учетом найденного выражения для j-го предсказанного столбца задачу поиска коэффициентов предсказания в виде векторов ax и ay можно записать в виде:
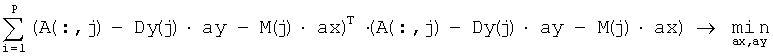
Решение данной задачи приведено в приложении. После вычисления коэффициентов двумерного линейного предсказания ax и ay их преобразуют в вид, пригодный для квантования, квантуют и передают в канал связи, по значениям квантованных коэффициентов двумерного линейного предсказания вычисляют двумерную огибающую коэффициентов ДДКП.
Как было отмечено выше, непосредственно коэффициенты предсказания не квантуются. Это объясняется их высокой чувствительностью к влиянию ошибок цифрового канала связи и отсутствием четких диапазонов динамического изменения, что, в свою очередь, затрудняет процесс их квантования. Поэтому перед квантованием введен промежуточный этап, заключающийся в преобразовании коэффициентов предсказания в набор линейных спектральных частот (ЛСЧ) (см., например, книгу: А.А.Устинов, А.А.Рощин, Д.А.Бардюков. Параметрическое кодирование речи с линейным предсказанием. - СПб.: ВАС, 2008, с.37 -43).
Для вычисления двумерной огибающей коэффициентов ДДКП определяют элементы (см. фиг.6 и 7 соответственно):
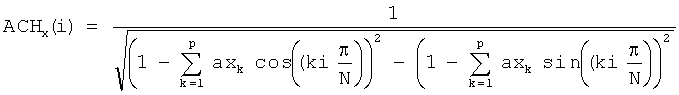 ,
,
 ,
,
где P и N - размеры матрицы изображения, 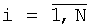 ,
, 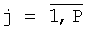 , ax и ау - значения вычисленных 2p коэффициентов двумерного линейного предсказания. На основе найденных элементов ACHx(i),
, ax и ау - значения вычисленных 2p коэффициентов двумерного линейного предсказания. На основе найденных элементов ACHx(i), 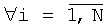 и ACHy(j),
и ACHy(j), 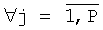 вычисляют элементы двумерной огибающей коэффициентов ДДКП в соответствии с выражением (см. фиг.8 и фиг.12(4)):
вычисляют элементы двумерной огибающей коэффициентов ДДКП в соответствии с выражением (см. фиг.8 и фиг.12(4)):
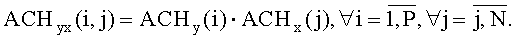
Ранжируют элементы матрицы огибающей частотных коэффициентов (см. фиг.9а) в порядке убывания их значений (см. фиг.9б). По сформированной огибающей (см. фиг.8) определяют координаты частотных коэффициентов в порядке убывания их абсолютных значений. Затем значения частотных коэффициентов, соответствующих найденным координатам, квантуют и последовательно передают в канал связи, причем число Kots подлежащих передаче коэффициентов, задают предварительно в зависимости от требуемого качества восстановления изображения (см. фиг.10 и фиг.12(5)).
После приема коэффициентов двумерного линейного предсказания и частотных коэффициентов (см. фиг.12 (7)), по коэффициентам двумерного линейного предсказания формируют на приемной стороне огибающую частотных коэффициентов (см. фиг.12 (8)), так же как на передающей стороне (см. фиг.8). По сформированной огибающей (см. фиг.11а) присваивают принятым частотным коэффициентам (см. фиг.11б) координаты в структуре матрицы спектра изображения, а вместо недостающих частотных коэффициентов в структуре матрицы оставляют нулевые значения (см. фиг.11в и фиг.12 (10)).
Далее формируют матрицу восстановленных квантованных отсчетов неподвижного полутонового видеоизображения (см. фиг.12 (11)) путем перемножения транспонированной матрицы ДКП размером Р×Р элементов на матрицу восстановленных коэффициентов ДДКП размером P×N элементов и на матрицу ДКП размером N×N элементов, т.е. на основании формулы:
 ,
,
где 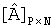 - матрица восстановленных квантованных отсчетов неподвижного полутонового видеоизображения размером P×N элементов.
- матрица восстановленных квантованных отсчетов неподвижного полутонового видеоизображения размером P×N элементов.
На последнем этапе представляют матрицу 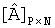 в виде неподвижного полутонового видеоизображения, присвоив каждому пикселю неподвижного полутонового видеоизображения значение соответствующего элемента матрицы
в виде неподвижного полутонового видеоизображения, присвоив каждому пикселю неподвижного полутонового видеоизображения значение соответствующего элемента матрицы 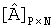 .
.
В целом процесс сжатия и восстановления неподвижного полутонового видеоизображения можно представить в виде схемы (см. фиг.12).
1 - матрица квантованных отсчетов неподвижного полутонового видеоизображения;
2 - матрица частотных коэффициентов неподвижного полутонового видеоизображения;
3 - коэффициенты двумерного линейного предсказания матрицы неподвижного полутонового видеоизображения 1;
4 - огибающая частотных коэффициентов неподвижного полутонового видеоизображения;
5 - последовательность частотных коэффициентов неподвижного полутонового видеоизображения, подлежащая передаче;
6 - цифровой канал связи;
7 - восстановленные коэффициенты двумерного линейного предсказания матрицы неподвижного полутонового видеоизображения 1;
8 - огибающая частотных коэффициентов неподвижного полутонового видеоизображения, сформированная на основе 7;
9 - последовательность принятых частотных коэффициентов неподвижного полутонового видеоизображения;
10 - восстановленная матрица частотных коэффициентов неподвижного полутонового видеоизображения;
11 - восстановленная матрица квантованных отсчетов неподвижного полутонового видеоизображения.
Для оценки возможности достижения сформулированного технического результата при использовании заявленного способа сжатия и восстановления сообщений было проведено имитационное моделирование на ПЭВМ. В предлагаемом способе высокая степень сжатия исходного сообщения достигнута за счет того, что для формирования на приемной стороне неподвижного полутонового видеоизображения в цифровой канал связи необходимо передать 2p коэффициентов двумерного линейного предсказания и Kots коэффициентов ДДКП.
Практические исследования показывают, что при оставлении 1/16 спектральных коэффициентов двумерного дискретно-косинусного преобразования от общего количества коэффициентов матрицы коэффициентов двумерного дискретно-косинусного преобразования размером 512×512 элементов пиковое отношение сигнал/шум для исходного и восстановленного видеоизображения составляет порядка 40 дБ.
При P и N равными 512 коэффициент сжатия при качестве 40 дБ соответствует 50 раз. Исследования показывают, что при сжатии исходного изображения в соответствии со способом-прототипом при сжатии в 50 раз пиковое соотношение сигнал/шум для восстановленного изображения соответствует 31 дБ.
Приложение
Задача поиска коэффициентов линейного предсказания ax и ay сводится к решению выражения (1):
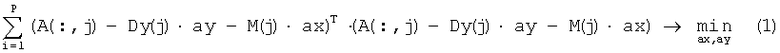
где Dy(j) - матрица размером Р×р, составленная из элементов j-го столбца изображения, имеющая вид (см. фиг.5):
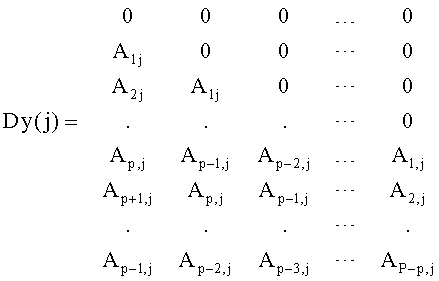
M(j) - матрица размером Р×p элементов, состоящая из j-строк матриц Dx(k), 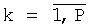 , имеющей вид (см. фиг.6):
, имеющей вид (см. фиг.6):

Для вычисления ax найдем производную целевой функции (1) относительно данного вектора и приравняем ее к нулю:
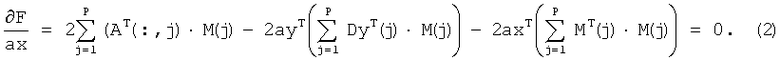
Вектор коэффициентов линейного предсказания ах определим путем решения уравнения (2):
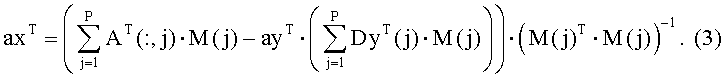
Для сокращения громоздкости дальнейших расчетов введем следующие обозначения:
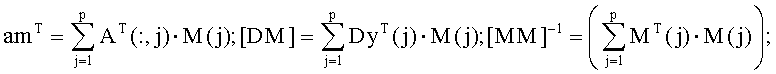
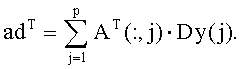
Перепишем выражение (3) с вновь введенными обозначениями:
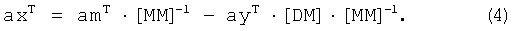
Для нахождения ау подставим выражение (4) в выражение целевой функции:
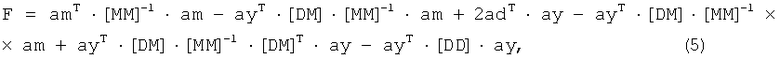
где 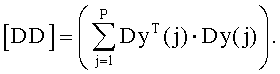
Найдем производную целевой функции (5) по ay и приравняем ее к нулю:
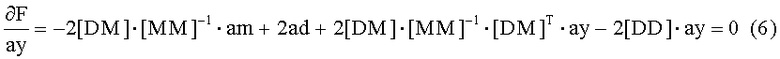
Решая уравнение (6) относительно ay, получим:
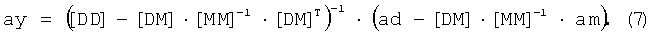
Таким образом, результатом последовательного решения уравнений (6) и (2) являются коэффициенты линейного предсказания ay и ax.
| название | год | авторы | номер документа |
|---|---|---|---|
| СПОСОБ СЖАТИЯ И ВОССТАНОВЛЕНИЯ ПОДВИЖНЫХ ЦВЕТНЫХ ВИДЕОИЗОБРАЖЕНИЙ | 2010 |
|
RU2434358C1 |
| СПОСОБ СЖАТИЯ И ВОССТАНОВЛЕНИЯ СООБЩЕНИЙ | 2005 |
|
RU2288547C1 |
| СПОСОБ СЖАТИЯ И ВОССТАНОВЛЕНИЯ СООБЩЕНИЙ | 2003 |
|
RU2246798C1 |
| СПОСОБ СЖАТИЯ И ВОССТАНОВЛЕНИЯ СООБЩЕНИЙ | 2002 |
|
RU2226043C1 |
| СПОСОБ СЖАТИЯ И ВОССТАНОВЛЕНИЯ СООБЩЕНИЙ | 2004 |
|
RU2261532C1 |
| СПОСОБ СЖАТИЯ И ВОССТАНОВЛЕНИЯ СООБЩЕНИЙ | 2007 |
|
RU2374785C2 |
| СПОСОБ БИОМЕТРИЧЕСКОЙ АУТЕНТИФИКАЦИИ ПО ПОЧЕРКУ В КОМПЬЮТЕРИЗИРОВАННОЙ СИСТЕМЕ КОНТРОЛЯ ДОСТУПА | 2011 |
|
RU2469397C1 |
| СПОСОБ ИЗМЕРЕНИЙ И ОБРАБОТКИ НАЧАЛЬНЫХ НЕПРАВИЛЬНОСТЕЙ ФОРМЫ ТОНКОСТЕННЫХ ЦИЛИНДРИЧЕСКИХ ОБОЛОЧЕК | 2015 |
|
RU2605642C1 |
| СПОСОБ СТАТИСТИЧЕСКОГО ПРИЕМОЧНОГО КОНТРОЛЯ КРУПНОГАБАРИТНЫХ ЦИЛИНДРИЧЕСКИХ ОБОЛОЧЕК ТОПЛИВНЫХ БАКОВ РАКЕТ | 2015 |
|
RU2583421C1 |
| Способ построения системы диаграммообразования приемной цифровой антенной решетки | 2021 |
|
RU2774214C1 |

Изобретение относится к области электросвязи, и, в частности, к способам передачи видеоизображений по цифровым каналам связи, преимущественно по низкоскоростным. Техническим результатом является обеспечение сжатия и восстановления неподвижных полутоновых изображений при уменьшении скорости передачи информации с сохранением заданного качества восстановления. Указанный технический результат достигается тем, что на передающей стороне вычисляют матрицу частотных коэффициентов видеоизображения путем выполнения операции двумерного косинусного преобразования. Затем вычисляют 2р коэффициентов двумерного линейного предсказания (КДЛП) матрицы квантованных отсчетов неподвижного полутонового изображения и передают их в цифровой канал связи. По квантованным значениям КДЛП формируют огибающую частотных коэффициентов, по которой определяют координаты частотных коэффициентов в порядке убывания их абсолютных значений. Затем значения частотных коэффициентов, соответствующих найденным координатам, квантуют и передают в канал связи. При восстановлении сообщений на основе принятых из канала связи КДЛП формируют огибающую частотных коэффициентов, по которой присваивают принятым частотным коэффициентам координаты в структуре их матрицы и восстанавливают видеоизображение путем выполнения операции обратного двумерного дискретного косинусного преобразования над восстановленной матрицей частотных коэффициентов. 3 з.п ф-лы, 12 ил.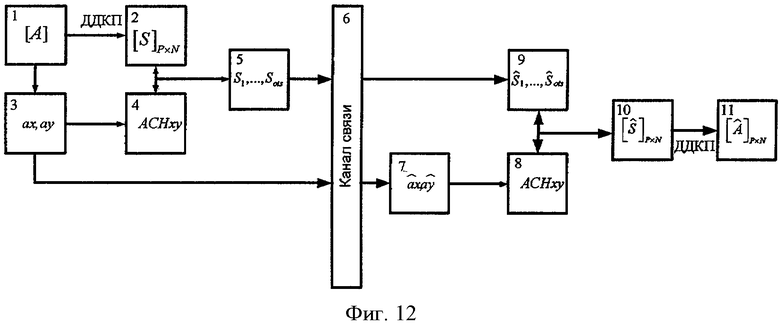
1. Способ сжатия и восстановления неподвижных полутоновых видеоизображений, заключающийся в том, что неподвижное видеоизображение преобразуют в цифровую форму, для чего формируют матрицу квантованных отсчетов неподвижного видеоизображения, вычисляют ее частотные коэффициенты (матрицу спектра изображения) путем выполнения операции двумерного дискретного косинусного преобразования, квантуют частотные коэффициенты значения которых превышают заданный уровень и передают их по каналу связи, по принятым частотным коэффициентам восстанавливают матрицу квантованных отсчетов неподвижного изображения, отличающийся тем, что после формирования матрицы квантованных отсчетов по значениям ее элементов вычисляют 2р коэффициентов двумерного линейного предсказания ах1, ах2, …, ахр и ay1, ау2, …, аур, где p - глубина предсказания, затем квантуют их и передают в канал связи, по значениям квантованных коэффициентов двумерного линейного предсказания формируют огибающую частотных коэффициентов, по которой определяют координаты частотных коэффициентов в порядке убывания их абсолютных значений, затем значения частотных коэффициентов, соответствующих найденным координатам, квантуют и последовательно передают в канал связи, причем число Kots подлежащих передаче коэффициентов, задают предварительно в зависимости от требуемого качества восстановления изображения, после приема коэффициентов двумерного линейного предсказания и частотных коэффициентов, по коэффициентам двумерного линейного предсказания формируют на приемной стороне огибающую частотных коэффициентов, по которой присваивают принятым частотным коэффициентам координаты в структуре матрицы спектра изображения, после чего восстанавливают изображение путем выполнения обратного двумерного дискретного косинусного преобразования над восстановленной матрицей спектра изображения, а вместо недостающих частотных коэффициентов в структуре матрицы оставляют нулевые значения.
2. Способ по п.1, отличающийся тем, что коэффициенты двумерного линейного предсказания вычисляют путем решения задачи минимизации среднеквадратической ошибки между матрицами исходного и предсказанного изображения, относительно коэффициентов двумерного линейного предсказания ах1, ах2, …, ахр и ау1, ау2, … аур, а их число р выбирают в интервале р=8÷12.
3. Способ по п.1, отличающийся тем, что огибающую частотных коэффициентов формируют путем последовательного вычисления огибающей по строкам ACHx (i) и столбцам ACHy (j) матрицы частотных коэффициентов по формулам:
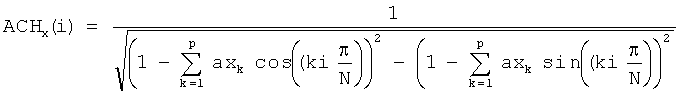 ,
,
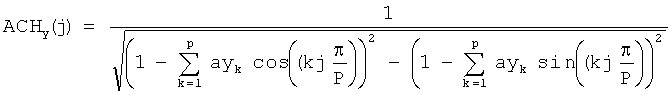 ,
,
где P и N размеры матрицы изображения, i=1,N, j=1,P, ax и ay значения вычисленных 2p коэффициентов двумерного линейного предсказания, а полную огибающую частотных коэффициентов рассчитывают как векторное произведение:
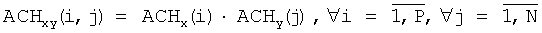 .
.
4. Способ по п.1, отличающийся тем, что значение Kots выбирают в соответствии с необходимым качеством восстанавливаемого изображения.
| СПОСОБ СЖАТИЯ И ВОССТАНОВЛЕНИЯ СООБЩЕНИЙ | 2002 |
|
RU2226043C1 |
| СПОСОБ СЖАТИЯ И ВОССТАНОВЛЕНИЯ СООБЩЕНИЙ | 2005 |
|
RU2288547C1 |
| СПОСОБ СЖАТИЯ И ВОССТАНОВЛЕНИЯ СООБЩЕНИЙ | 2007 |
|
RU2374785C2 |
| СПОСОБ И УСТРОЙСТВО ДЛЯ КОДИРОВАНИЯ ИЗОБРАЖЕНИЯ | 1994 |
|
RU2127962C1 |
| EP 1422664 A2, 26.05.2004 | |||
| US 2002150157 A1, 17.10.2002 | |||
| US 5287200 A, 15.02.1994 | |||
| CHUNG-YEN LU, KUEI-ANN WEN, On the Design of Selective Coefficient DCT Module, IEEE TRANSACTIONS ON CIRCUITS AND SYSTEMS FOR VIDEO TECHNOLOGY, vol.8, №2, April 1998. | |||
Авторы
Даты
2011-05-20—Публикация
2010-01-25—Подача