Изобретение относится к способу и устройству для определения мгновенного массового потока при пульсирующих течениях.
Из документа Uchida S., 1956, “The Pulsating Viscous Flow Superposed on the Steady Laminar Motion of Incompressible Fluid in a Circular Pipe”, J. Appl. Mat. Phys. (ZAMP), vol. 7, pp. 403-422, известно аналитическое решение для любых пульсирующих течений.
В документе Durst et al., “Measurement of Instantaneous Flow Rates in Periodically Operating Injection Systems”, Experiments in Fluids 20 (1996), pp. 178-188, показано, что аналитическое решение, предложенное Uchida, может быть применено для измерения скорости пульсирующего течения на оси трубы посредством лазерной доплеровской анемометрии (LDA). Основанный на этих знаниях способ измерения описан также, например, в документе US 6510842 В2. Также способы, основанные на принципе LDA, в общем случае, имеют недостатки во многих аспектах. Аналитическое решение содержит функции Бесселя, решение которых на практике требует высоких вычислительных затрат. Поэтому непрерывное измерение периодического пульсирующего течения невозможно. Предоставление устройства для осуществления LDA связано с высокими затратами. Помимо этого, подобное устройство является чувствительным, особенно чувствительным к колебаниям, и не пригодно для управления или регулирования, например, устройства впрыска в автомобилях.
В документе Ray S., et al., 2005, “Mass Flow Rate Controlled Fully Developed Laminar Pulsating Pipe Flows”, Journal of Fluids Engineering, vol., 127, pp.1-13, описано другое аналитическое решение с применением безразмерных чисел. Тем самым можно избежать требующего затрат решения функций Бесселя.
Задачей изобретения является устранение недостатков, свойственных уровню техники. В частности, должны быть предложены способ и устройство, с помощью которых можно определить мгновенный массовый поток периодически пульсирующих течений с улучшенным разрешением по времени. Согласно другой цели изобретения способ должен иметь возможность осуществления максимально надежным и экономичным устройством. В частности, должно быть возможным непрерывное измерение периодически осциллирующих течений, как, например, в устройствах впрыска для автомобилей.
Указанная задача решается признаками пунктов 1 и 11 формулы изобретения. Предпочтительные варианты выполнения изобретения характеризуются признаками пунктов 2-10 и 12-24 формулы изобретения.
Согласно изобретению, предусмотрен способ для определения мгновенной скорости массового потока течения флюида, пульсирующего периодически с частотой f, со следующими этапами:
а) определение градиента давления, существующего в потоке в течение периода,
b) вычисление гармонической амплитуды градиента давления посредством преобразования Фурье,
с) преобразование частоты f и времени t в безразмерные числа F и τ, и
d) определение скорости массового потока с применением таблицы, из которой для каждого безразмерного числа F частоты f можно извлечь, по меньшей мере, одно соответствующее значение, описывающее скорость массового потока и/или разность фаз.
Предложенный способ обеспечивает возможность быстрого и точного определения мгновенной скорости массового потока флюида или жидкости. Предложенный способ позволяет определять мгновенную скорость массового потока с чрезвычайно высоким разрешением по времени. В частности, можно измерять массовый поток топлива в устройствах впрыска автомобилей при каждом процессе впрыска с высокой точностью. Это обеспечивает возможность прецизионного управления процессом впрыска. Тем самым можно улучшить коэффициент полезного действия двигателя и избежать нежелательного неполного сгорания топлива. Предложенный способ также обеспечивает возможность, в частности, точного управления процессами многократного впрыска во время такта. Вышеназванные преимущества обеспечиваются, в частности, посредством предложенного измерения градиента давления и вычислительных этапов, выполняемых с высоким быстродействием современными вычислителями с применением таблиц. Предложенное измерение градиента давления обеспечивает возможность - в противоположность известным из уровня техники оптическим методам - непрерывного определения мгновенной скорости массового потока флюида во время одного и того же периода.
Согласно предпочтительному выполнению этапы (а)-(d) повторяются для каждого периода. Это обеспечивает возможность особенно точного воспроизведения мгновенной скорости массового потока и, тем самым, быстрого управления управляющими элементами для управления потоком жидкости на основе измеренных значений. Предпочтительным образом, в течение одного периода определяется, по меньшей мере, 500, предпочтительно, по меньшей мере, 1000 значений мгновенной скорости массового потока. Это обеспечивает возможность, в частности, при разработке форсунок или вентилей определение временных характеристик скорости массового потока в течение периода. Тем самым можно подобные элементы направления течения или управляющие элементы оптимизировать в отношении скорости массового потока при пульсирующих течениях.
Согласно предпочтительному варианту выполнения мгновенная скорость массового потока 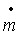 определяется из произведения безразмерной скорости массового потока
определяется из произведения безразмерной скорости массового потока 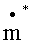 и средней скорости массового потока
и средней скорости массового потока 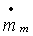 , а именно:
, а именно:
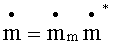
причем для безразмерной скорости 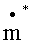 массового потока справедливо равенство:
массового потока справедливо равенство:
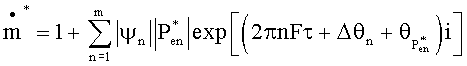
а для средней скорости 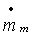 массового потока справедливо равенство:
массового потока справедливо равенство:
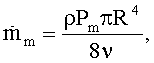
где Pm - средний градиент давления, R - радиус трубы, ρ - плотность и ν - вязкость.
При этом предпочтительным образом в предложенной согласно изобретению таблице для каждого безразмерного числа F частоты сохраняется точно одно значение 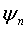 и точно одно значение
и точно одно значение 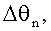 и безразмерная скорость массового потока определяется тем, что из таблицы для каждого предварительно заданного безразмерного числа F частоты извлекаются значения
и безразмерная скорость массового потока определяется тем, что из таблицы для каждого предварительно заданного безразмерного числа F частоты извлекаются значения 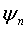 и
и 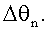 Это обеспечивает возможность особенно быстрого вычисления мгновенной скорости массового потока.
Это обеспечивает возможность особенно быстрого вычисления мгновенной скорости массового потока.
Согласно другому особенно предпочтительному выполнению измеряется температура флюида. Из температуры может определяться кинематическая вязкость флюида. Это обеспечивает возможность особенно точного вычисления мгновенной скорости массового потока и при изменяющихся температурах флюида. Предпочтительный способ обладает универсальностью.
Согласно другому особенно предпочтительному варианту выполнения сначала для кинематической вязкости принимается значение вязкости, а затем точно рассчитывается. Для этого кинематическая вязкость может вычисляться из функции скорости массового потока m в момент времени t=0 по принятым и итерационно изменяемым значениям вязкости. Кинематическая вязкость может в этом случае определяться, например, из смены знака скорости массового потока m в функции. При вышеуказанном выполнении кинематическая вязкость флюида определяется, таким образом, путем использования дополнительно доступной информации во время восстановления переходного расхода. В частности, для этого может использоваться информация о том, что расход перед отпиранием запорного элемента на выходе трубопровода потока (в типовом случае, клапана впрыска для двигателей внутреннего сгорания) вынужденным образом должен равняться нулю. Так как значение кинематической вязкости вызывает сдвиг восстанавливаемого периодического хода массового потока, восстановленный массовый поток от нуля вычисляется только тогда, когда принятое значение вязкости также является корректным. Тем самым можно разработать простой численный способ, посредством которого вязкость параметрически изменяется, и восстановленный расход в опорный момент времени, в который он известен (например, нуль при закрытом клапане), сравнивается с известным значением. Посредством последующей интерполяции может определяться значение вязкости, которое приводит к корректному восстановленному значению расхода в опорный момент времени. Это значение вязкости соответствует фактически существующей кинематической вязкости флюида на участке измерения.
Вышеописанный способ можно применять также для того, чтобы определять кинематическую вязкость флюидов.
Представленное устройство может, наряду с определением характеристики расхода, также определять и выдавать вязкость флюида.
В качестве альтернативы, при известном флюиде и известной зависимости кинематической вязкости от температуры может также определяться температура.
Согласно изобретению предложено устройство для определения мгновенной скорости массового потока, периодически пульсирующего с частотой f течения флюида, содержащее
аа) средство определения давления для определения градиента давления, существующего в потоке в течение периода,
bb) вычислитель, связанный со средством для определения давления, включающий в себя
bb1) средство вычисления гармонической амплитуды градиента давления посредством преобразования Фурье,
bb2) средство для преобразования частоты f и времени t в безразмерные числа F, τ, и
bb3) средство для определения скорости массового потока с применением таблицы, из которой для каждого безразмерного числа F частоты f, можно извлечь, по меньшей мере, одно соответствующее значение, описывающее скорость массового потока и/или разность фаз.
Предложенное устройство является надежным и обеспечивает возможность быстрого и точного измерения мгновенной скорости массового потока. Оно не подвержено воздействию помех и может, по сравнению с уровнем техники, изготавливаться с пониженными затратами.
Согласно предпочтительному варианту осуществления предусмотрено пусковое устройство для запуска последовательности вычислений, включающей в себя этапы (bb1)-(bb3). Предпочтительным образом также предусмотрен управляемый пусковым устройством элемент управления течением, предпочтительно клапан. Это обеспечивает особенно простое выполнение устройства. Тем самым одновременно гарантируется, что, например, частота моментов времени запуска последовательности вычислений коррелирована с моментами времени отпирания и запирания клапана.
Согласно другому варианту выполнения изобретения средство определения давления содержит усилитель с подключенным аналого-цифровым преобразователем. Это обеспечивает возможность цифровой последующей обработки измеренных сигналов.
Средство определения давления может включать в себя дифференциальный датчик давления. Дифференциальный датчик давления имеет предпочтительным образом динамический диапазон, по меньшей мере, 1:1000. Альтернативным образом, средство определения давления может также включать в себя два разнесенных друг от друга в направлении потока, предпочтительно пьезоэлектрических или пьезорезистивных датчика давления и средство для определения дифференциального давления. В этом случае датчики давления предпочтительным образом имеют динамический диапазон, по меньшей мере, 1:10000, предпочтительно, по меньшей мере, 1:80000, особенно предпочтительно 1:100000 или более. С помощью предложенного дифференциального датчика или датчика давления можно измерять мгновенную скорость массового потока и пульсирующих течений, находящихся под высоким давлением. Тем самым обеспечивается разрешение дифференциальных давлений в диапазоне от 1 до 100 Па. При применении предложенного средства определения давления, в частности, в устройствах впрыска для двигателей, турбин, горелок и т.п. обеспечивается возможность определения мгновенной скорости массового потока.
Согласно другому предпочтительному выполнению предусмотрено устройство измерения температуры для измерения температуры текучего флюида. При этом речь может идти, например, о термоэлементе или подобном средстве.
Предпочтительным образом вычислитель также включает в себя средство для вычисления кинематической вязкости. Вычисление кинематической вязкости может осуществляться согласно вышеописанному способу на основе принятой кинематической вязкости. В качестве альтернативы этому вычисление кинематической вязкости может также осуществляться на основе измеренных значений температуры. Тем самым можно избежать ошибок, обусловленных изменением температуры флюида. Определение мгновенной скорости массового потока является особенно точным.
Согласно другому варианту выполнения предусмотрено, что средство определения давления и, при необходимости, устройство измерения температуры приводится в контакт с флюидом в трубе. Труба может представлять собой трубопровод между источником давления, например насосом впрыска, и форсункой впрыска.
Средство определения давления и, при необходимости, устройство измерения температуры целесообразно размещены ниже по потоку от источника давления, предусмотренного на одном конце трубы. Ниже по потоку от средства определения давления и, при необходимости, устройства измерения температуры целесообразно предусмотрен элемент управления потоком. Элемент управления потоком может, например, подключаться к форсунке. Предложенное устройство пригодно, в частности, для точного управления массовым потоком в устройствах впрыска.
Ниже со ссылками на чертежи более подробно объяснены теоретические основы соответствующего изобретению способа, а также примеры осуществления. На чертежах показано следующее:
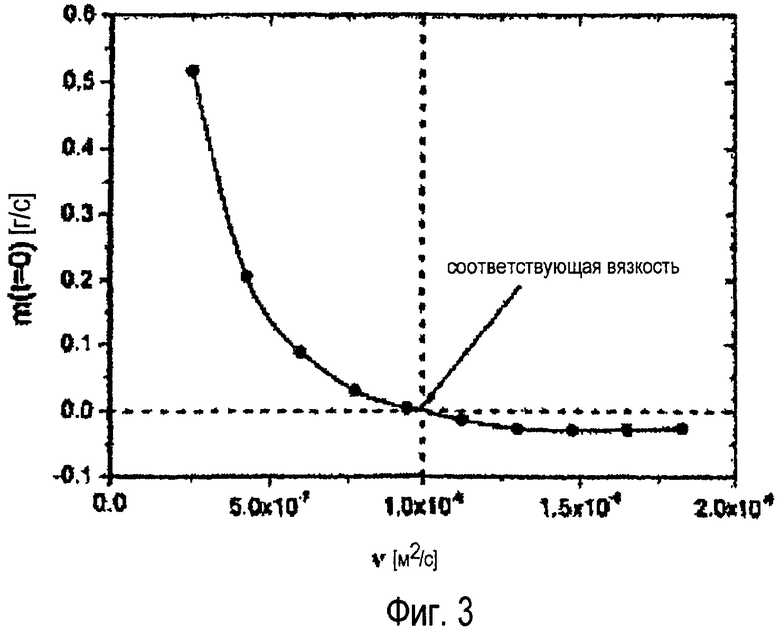
фиг.1 - нормированное отношение амплитуд и разность фаз между осцилляциями массового потока и градиента давления как функция безразмерной частоты,
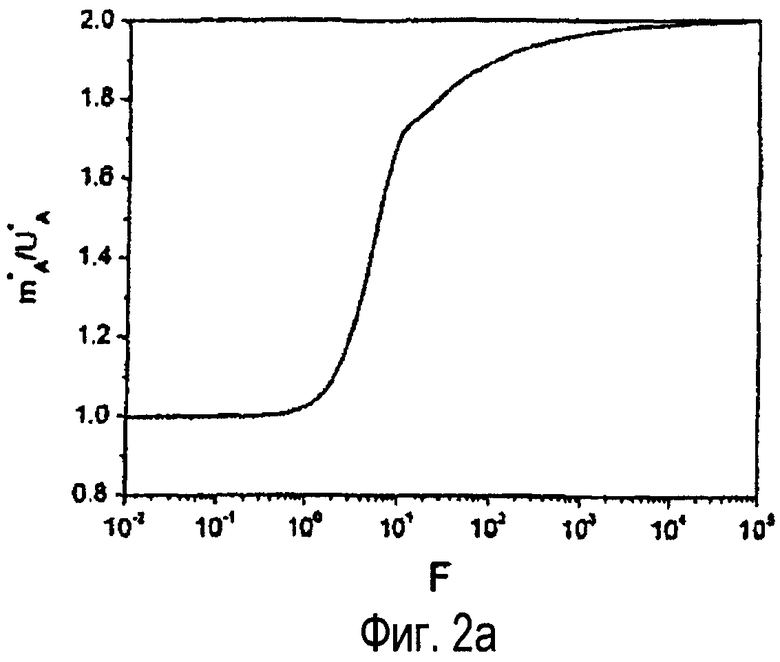
фиг.2а - амплитудная характеристика по отношению к безразмерной частоте,
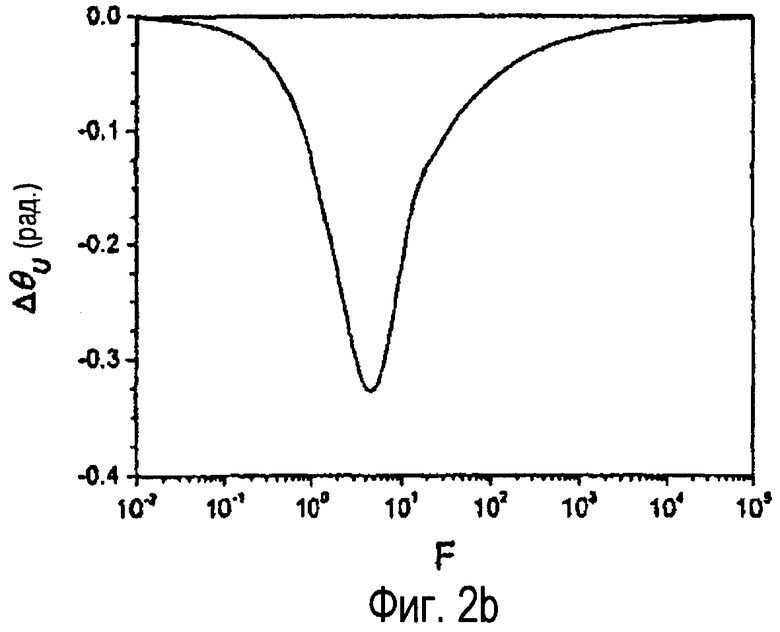
фиг.2b - сдвиг фазы по отношению к безразмерной частоте,
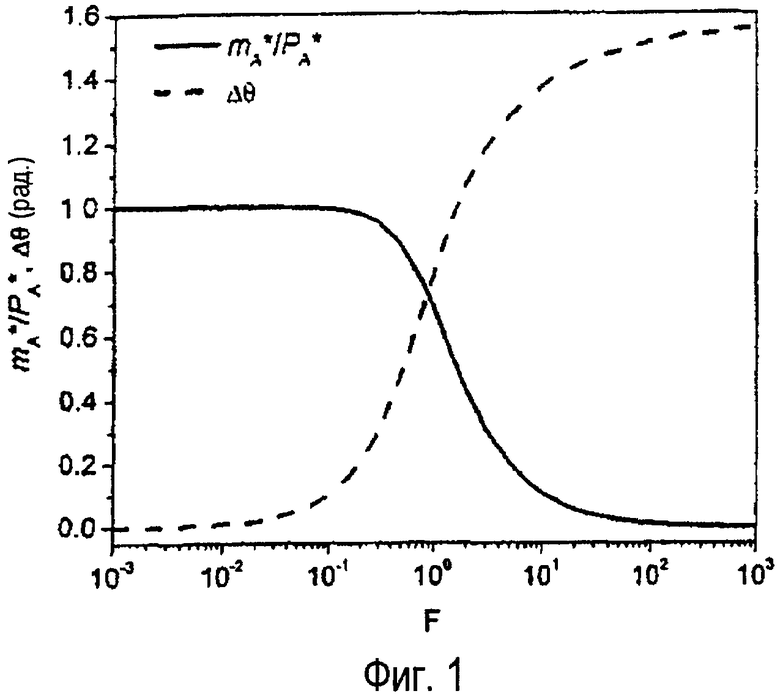
фиг.3 - скорость массового потока к моменту времени t=0 для принятых значений кинематической вязкости υ,
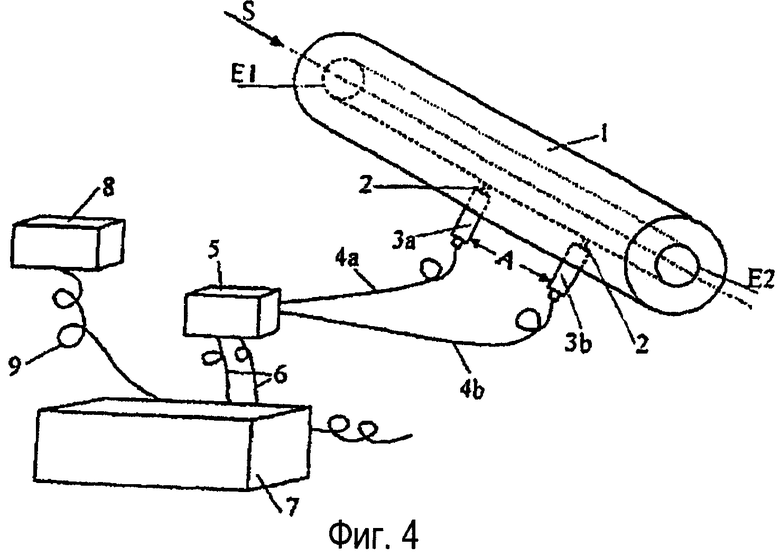
фиг.4 - схематичное представление измерительного устройства,
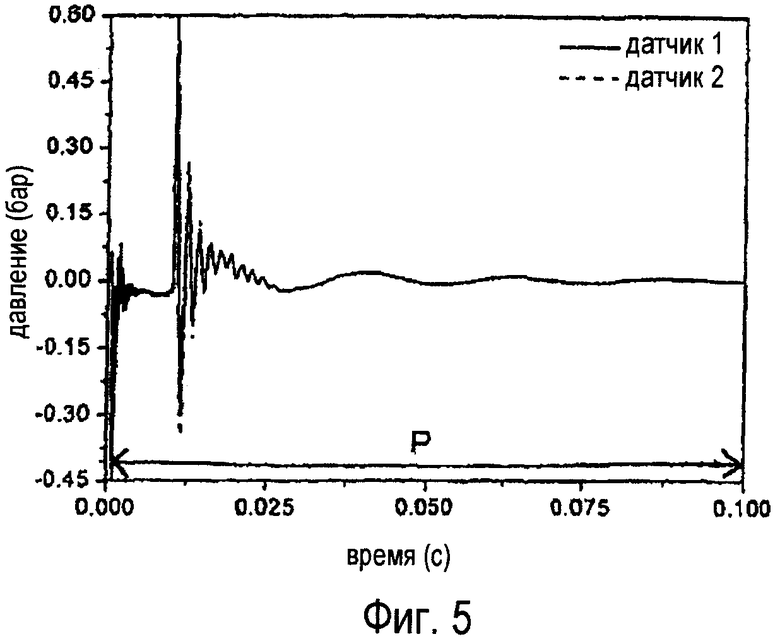
фиг.5 - характеристика давления для одного периода, измеренная на датчиках по фиг.3,
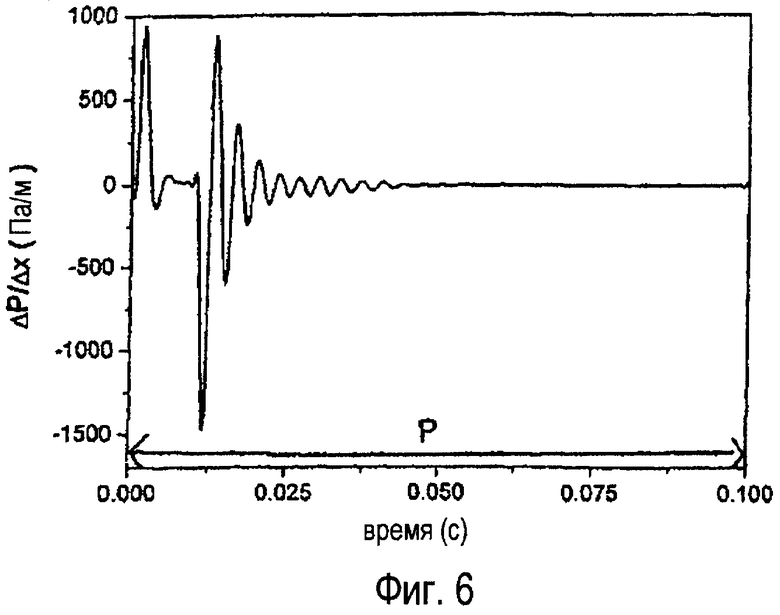
фиг.6 - градиент давления по времени, вычисленный на основе характеристики давления согласно фиг.4,
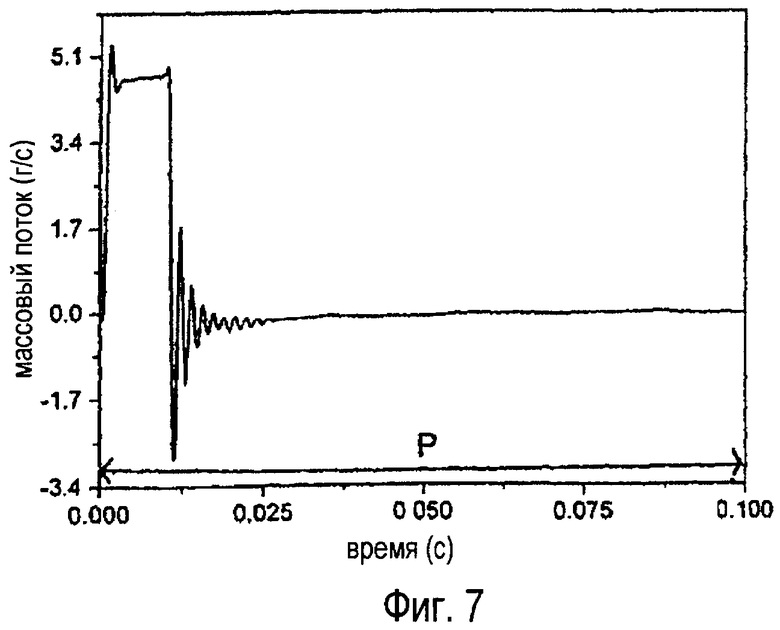
фиг.7 - скорость массового потока по времени, вычисленная на основе градиента давления согласно фиг.5, и
фиг.8 - диаграмма процесса с существенными этапами вычисления.
В последующем изложении сначала более подробно объясняются теоретические основы заявленного способа.
Выведенное в работе Lambossy P. (1952), Oscillations forcées d'un liquide incompressible et visqueux dans un tube rigide et horizontal. Calcul de la force frottement, Helv. Physica Acta 25, 371-386) уравнение для поля скоростей гармонически осциллирующего, ламинарного, полностью установившегося течения в трубе может быть расширено для любого изменяющегося во времени градиента давления, что можно выразить следующим рядом Фурье:
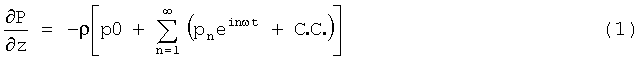
Причем С.С. обозначает комплексно сопряженный аргумент. Ламинарное течение в трубе можно описать с помощью упрощенной формы уравнений Навье-Стокса:
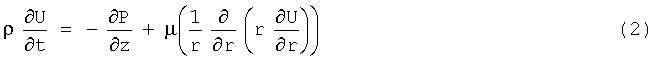
Путем подстановки градиента давления 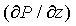 из уравнения (1) в уравнение (2) получаем парциальное дифференциальное уравнение, которое описывает поле скоростей. Линейность этого уравнения позволяет результирующее поле скоростей вычислить посредством суперпозиции уравнений Lambossy как решение для гармонического случая, которые вводятся в сумму всех n членов градиента давления:
из уравнения (1) в уравнение (2) получаем парциальное дифференциальное уравнение, которое описывает поле скоростей. Линейность этого уравнения позволяет результирующее поле скоростей вычислить посредством суперпозиции уравнений Lambossy как решение для гармонического случая, которые вводятся в сумму всех n членов градиента давления:
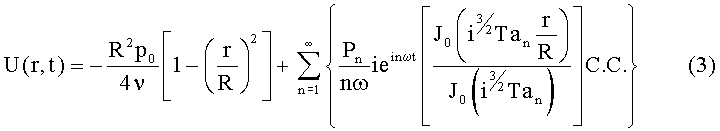
Это уравнение содержит число Тейлора Tan n-ой гармонической осцилляции, за счет чего для каждой частичной частоты определяется получаемый профиль скорости. Число Тейлора Tan определяется следующим образом:

Градиент давления пульсирующего течения можно выразить в следующей обобщенной форме как ряд Фурье:
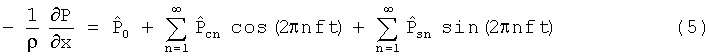
и в безразмерной форме и введением комплексного градиента давления:
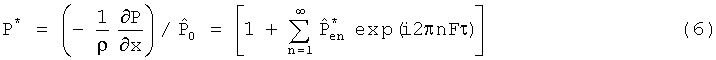
Соответствующее переходное поле скорости в соответствии с решением Lambossy из уравнения (3) в комплексной форме имеет вид:
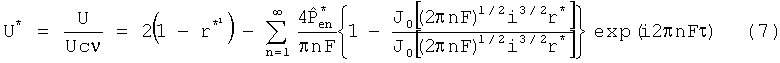
причем осуществляется следующая нормировка:
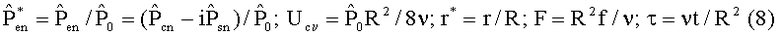
Массовый поток можно вычислить в безразмерной комплексной форме:
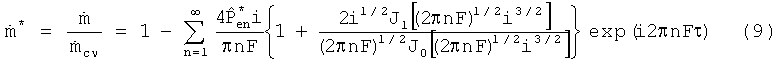
Нормированный массовый поток состоит из стационарной составляющей и суммы гармонических составляющих:

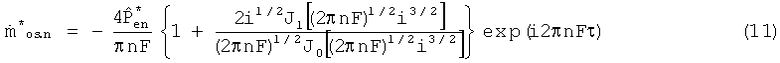
Путем ввода комплексной переменной ψ, которая зависит только от безразмерной частоты F:
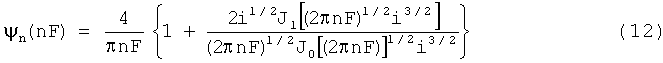
n-ая гармоника осциллирующей составляющей массового потока может быть выражена следующим образом:
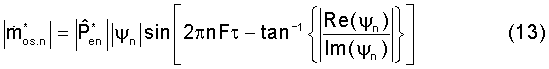
Тогда полный нормированный массовый поток можно выразить следующим образом:
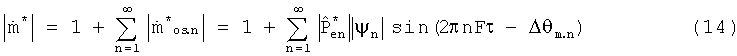
Если градиент давления измеряется и, за счет преобразования Фурье, известны гармонические коэффициенты в следующей форме:
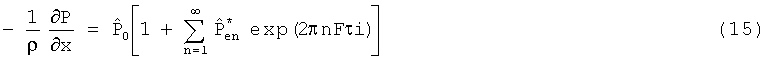
то можно вычислить массовый поток в следующем виде:
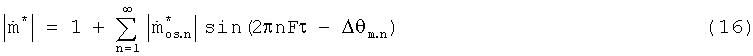
причем
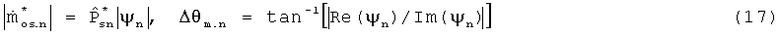
Для нормировки необходимы значения, измеренные на периоде:
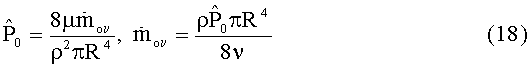
Из приведенного выше обсуждения следует, что для измерения каждой n-ой гармоники осциллирующей составляющей массового потока должны быть известны только безразмерное отношение амплитуд 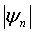 , а также разность фаз
, а также разность фаз 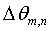 между осцилляциями массового потока и градиента давления, которые являются функцией безразмерной частоты F. Зависимость безразмерного отношения амплитуд и разности фаз от безразмерной частоты должна определяться лишь однократно и сохраняться. Определенная таким образом функция может в форме некоторой таблицы, например «таблицы преобразования», применяться для быстрого вычисления переходных массовых потоков любого пульсирующего, ламинарного, полностью созданного течения в трубе, если измеряется переходный процесс градиента давления. Кроме того, можно установить, что для определения переходного массового потока из характеристики градиента давления должна быть известна только кинематическая вязкость υ, в то время как плотность при вычислениях может быть сокращена и требуется только для последующего вычисления объемного потока.
между осцилляциями массового потока и градиента давления, которые являются функцией безразмерной частоты F. Зависимость безразмерного отношения амплитуд и разности фаз от безразмерной частоты должна определяться лишь однократно и сохраняться. Определенная таким образом функция может в форме некоторой таблицы, например «таблицы преобразования», применяться для быстрого вычисления переходных массовых потоков любого пульсирующего, ламинарного, полностью созданного течения в трубе, если измеряется переходный процесс градиента давления. Кроме того, можно установить, что для определения переходного массового потока из характеристики градиента давления должна быть известна только кинематическая вязкость υ, в то время как плотность при вычислениях может быть сокращена и требуется только для последующего вычисления объемного потока.
На фиг.1 показано нормированное отношение амплитуд и разность фаз между осцилляциями массового потока и осцилляциями градиента давления как функция безразмерной частоты.
Подобным образом, также в безразмерной форме может использоваться измерение скорости в определенном радиальном положении для определения переходного расхода:
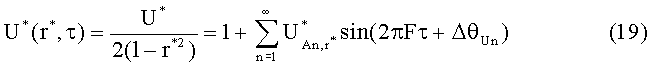
Для каждой n-ой гармонической составляющей безразмерного массового потока может определяться отношение амплитуд между нормированными осцилляциями скорости к осцилляциям массового потока:

а также разность фаз 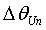 между осцилляциями скорости к осцилляциям массового потока. Нормировка скорости может осуществляться по средней скорости:
между осцилляциями скорости к осцилляциям массового потока. Нормировка скорости может осуществляться по средней скорости:

Для каждого радиального положения измерения скорости получаем другую функцию отношения амплитуд и разности фаз в зависимости от безразмерной частоты. Фиг.2а и 2b показывают в зависимости от безразмерной частоты ход отношения амплитуд и сдвига фазы для осевого положения трубы.
В последующем описании более подробно поясняется конкретный, предпочтительно реализованный с помощью компьютера, пример вычисления мгновенной скорости массового потока.
1А. Проводятся измерения давления одновременно двумя датчиками давления, которые размещены в двух точках вдоль трубы. Для единственного периода впрыска получаем:

где t - время и Р - давление.
2А. Вычисление градиента давления 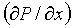 для t=const. При известном расстоянии
для t=const. При известном расстоянии 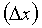 между точками измерения давления:
между точками измерения давления:

3А. Вычисление среднего градиента давления 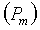 для единственного периода впрыска
для единственного периода впрыска 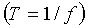 , где Т - период и f - частота впрыска, причем эти значения известны из управляющего сигнала клапана впрыска.
, где Т - период и f - частота впрыска, причем эти значения известны из управляющего сигнала клапана впрыска.
4А. Вычисление безразмерного градиента давления путем деления градиента давления на средний градиент давления с безразмерным временем τ и безразмерной частотой F, определяемыми следующим образом:
- безразмерный градиент давления
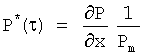
- безразмерное время
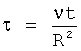
- безразмерная частота F
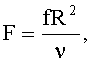
где R - радиус трубы и υ - кинематическая вязкость флюида.
5А. Быстрое преобразование Фурье для безразмерного градиента давления для вычисления безразмерных амплитуд 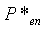 :
:
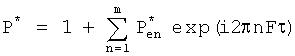
При этом n - индекс суммирования, 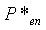 - безразмерная комплексная амплитуда давления составляющей n-го ряда Фурье и m - общее число Фурье-составляющих для хорошего согласования между измеренными градиентами давления и их Фурье-приближением.
- безразмерная комплексная амплитуда давления составляющей n-го ряда Фурье и m - общее число Фурье-составляющих для хорошего согласования между измеренными градиентами давления и их Фурье-приближением.
6А. Вычисление безразмерной скорости массового потока согласно
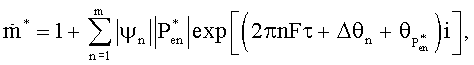
где 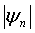 - коэффициент амплитуды безразмерной скорости массового потока,
- коэффициент амплитуды безразмерной скорости массового потока, 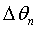 - сдвиг фаз между градиентом давления и скоростью массового потока и
- сдвиг фаз между градиентом давления и скоростью массового потока и 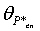 - фаза комплексной безразмерной амплитуды давления. Вычисление неизвестной в приведенном выше уравнении безразмерной скорости массового потока может быть проведено следующим образом:
- фаза комплексной безразмерной амплитуды давления. Вычисление неизвестной в приведенном выше уравнении безразмерной скорости массового потока может быть проведено следующим образом:
а. Считывание значений коэффициентов 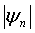 амплитуды безразмерной скорости массового потока и разности фаз
амплитуды безразмерной скорости массового потока и разности фаз 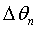 для каждой Фурье-составляющей nF из таблицы преобразования от n=1 до n=m согласно
для каждой Фурье-составляющей nF из таблицы преобразования от n=1 до n=m согласно
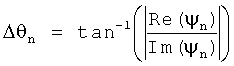
Подходящая таблица преобразования может быть сформирована, например, следующим образом:
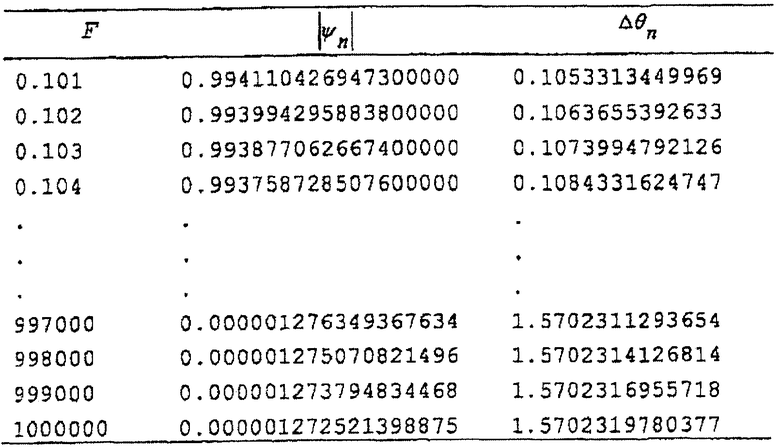
b. Вычисление 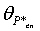 из известного
из известного 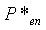 для каждой Фурье-составляющей nF из таблицы преобразования от n=1 до n=m согласно
для каждой Фурье-составляющей nF из таблицы преобразования от n=1 до n=m согласно
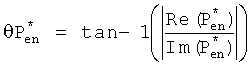
7А. Вычисление средней скорости массового потока 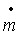 , которая вычисляется из среднего градиента давления
, которая вычисляется из среднего градиента давления 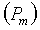 согласно
согласно
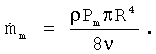
8А. Преобразование безразмерной скорости массового потока 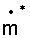 в безразмерную скорость массового потока
в безразмерную скорость массового потока 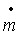 путем перемножения на среднюю скорость массового потока согласно
путем перемножения на среднюю скорость массового потока согласно
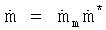
На основе приведенного выше способа вычислений можно точно вычислить кинематическую вязкость, например, согласно следующим этапам:
1В. Вычисление градиента давления согласно этапам 1А-3А.
2В. Подстановка принятого значения для кинематической вязкости υ. Такое значение при известном флюиде может приниматься как хорошее приближение.
3В. Вычисление скорости массового потока согласно этапам 4А-8А.
4В. Определение значения скорости массового потока в нулевой момент времени  (t=0) вместе с принятым значением кинематической вязкости υ. Определение может осуществляться посредством сохранения в вычислителе процесса.
(t=0) вместе с принятым значением кинематической вязкости υ. Определение может осуществляться посредством сохранения в вычислителе процесса.
5В. Повторение этапов 2В-4В с измененными значениями для кинематической вязкости до тех пор, пока знак в значении  (t=0) не изменится.
(t=0) не изменится.
6В. Нахождение кинематической вязкости υ посредством интерполяции значений, определенных на этапе 4В. На фиг. 3 представлена скорость массового потока к моменту времени t=0 в зависимости от принятых значений кинематической вязкости υ. Из изменения знака для скорости массового потока можно точно определить кинематическую вязкость.
Резюмируя, можно сделать вывод, что посредством приведенной выше аналитической обработки можно создать способ оценки, который может использовать однократно вычисленные безразмерные разность фаз и отношения амплитуд как функцию безразмерной частоты в форме «таблицы преобразования» и обеспечивает возможность получения зависимых от времени расходов, например, через клапаны впрыска, практически «в реальном времени».
Расход можно реконструировать либо путем измерения переходного градиента давления, либо также характеристики изменения скорости в любом стационарном радиальном положении. В первом случае массовый поток восстанавливается непосредственно, в то время как во втором случае сначала может восстанавливаться объемный поток и при известной плотности флюида также массовый поток.
Вместо градиента давления на этапе (а) может также измеряться характеристика изменения скорости в течение одного периода. Это может следовать посредством обычного способа по принципу LDA.
На фиг.4 схематично показана существенная часть устройства, пригодного для осуществления способа. Труба 1 имеет в своей оболочке два отверстия 2, которые предусмотрены в направлении S течения на расстоянии А друг от друга. Ссылочной позицией Е1 обозначен первый конец, а ссылочной позицией Е2 обозначен второй конец трубы 1. Отверстия 2 плотно закрыты закрепленными в них пьезоэлектрическими датчиками 3а, 3b давления. Датчики 3а, 3b давления имеют предпочтительно динамический диапазон 1:100000. Они подключены посредством первого кабеля 4а, 4b к усилителю 5, посредством которого сигналы заряда, сформированные датчиками 3а, 3b давления, усиливаются и затем преобразуются в цифровую форму аналого-цифровым преобразователем (не показан).
Усилитель 5 посредством второго кабеля 6 связан с вычислителем процесса, например компьютером 7. Ссылочной позицией 8 обозначено устройство управления или пусковое устройство, которое третьим кабелем 9 также связано с компьютером 7. Устройство 8 управления может также быть связано с клапаном (не показан), посредством которого второй конец Е2 трубы 1 может периодически открываться и закрываться.
На фиг. 5 показаны в зависимости от времени сигналы давления, выработанные датчиками 3а, 3b давления в течение периода Р. Сигналы давления показывают в течение периода Р (едва различимую) разницу.
На фиг. 6 показан график зависимости от времени дифференциального градиента давления.
На фиг. 7 показана скорость массового потока в зависимости от времени, определенная способом, соответствующим изобретению, для одного периода Р.
На фиг.8 еще раз представлены существенные этапы способа, соответствующего изобретению. Измерение разности давлений может выполняться, например, посредством двух датчиков 3а, 3b давления. Из измеренных значений давления можно определить дифференциальное давление. Но также возможно вместо двух датчиков 3а, 3b давления применять дифференциальный датчик давления для измерения дифференциального давления.
На следующем этапе с помощью вычислений из дифференциального давления определяется градиент давления. С применением градиента давления затем на основе вышеописанной теории производится вычисление скорости массового потока с применением «таблицы преобразования». При этом следует сослаться, в частности, на уравнения (6)-(18). Вычисление требует относительно низких вычислительных затрат и может с помощью вычислителя 7 процесса проводиться настолько быстро, что возможно непрерывное измерение мгновенного массового потока пульсирующей текущей жидкости.
Перечень ссылочных позиций
1 - труба
2 - отверстие
3а 3b - датчик давления
4а, 4b - первый кабель
5 - усилитель
6 - второй кабель
7 - компьютер
8 - пусковое устройство
9 - третий кабель
А - расстояние
Е1 - первый конец
Е2 - второй конец
Т - период
S - направление течения
С помощью двух пьезоэлектрических датчиков давления измеряют дифференциальное давление в потоке. Определяют градиент давления, существующий в потоке в течение одного периода (Р). Вычисляют гармоническую амплитуду градиента давления посредством преобразования Фурье. Преобразуют частоту f и время t в безразмерные числа F, τ, и определяют массовый расход потока с помощью таблицы преобразования, устанавливающей соответствие между величиной F и значениями ψn и Δθn, характеризующими массовый расход потока, где ψn - коэффициент амплитуды безразмерного массового расхода, Δθn - разность фаз между осцилляциями градиента давления и массового расхода для n-ой гармонической составляющей массового расхода, путем считывания из упомянутой таблицы для каждого числа F частоты f соответствующих значений ψn, Δθn, описывающих мгновенный массовый расход потока для полученного градиента давления. Изобретение повышает точность определения массового расхода за счет обеспечения непрерывного измерения с высоким временным разрешением при помощи надежного и экономичного устройства, содержащего средство для определения градиента давления и компьютер. 2 н. и 22 з.п. ф-лы, 8 ил., 1 табл.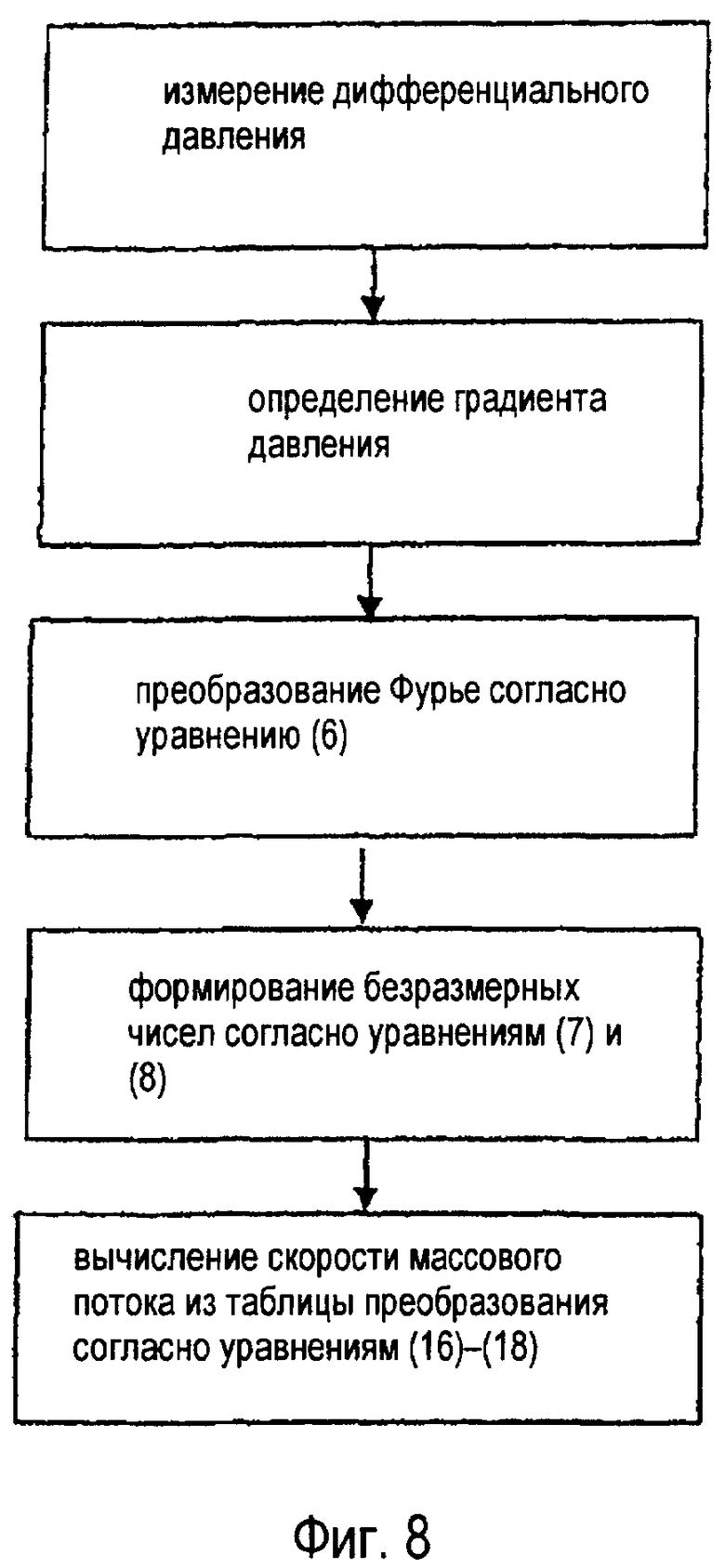
1. Способ для определения мгновенного массового расхода потока флюида, пульсирующего периодически с частотой f, содержащий следующие этапы:
a) измеряют давление с помощью двух датчиков (3а, 3b) давления, разнесенных друг от друга в направлении потока,
b) определяют градиент давления, существующий в потоке в течение одного периода (Р),
c) вычисляют гармоническую амплитуду градиента давления посредством преобразования Фурье,
d) преобразуют частоту f и время t в безразмерные числа F, τ, и
e) определяют массовый расход потока с применением таблицы преобразования, устанавливающей соответствие между безразмерной величиной F и значениями ψn и Δθn, характеризующими массовый расход потока, где ψn - коэффициент амплитуды безразмерного массового расхода потока, Δθn - разность фаз между осцилляциями градиента давления и массового расхода потока для n-й гармонической составляющей массового расхода потока, путем считывания из упомянутой таблицы для каждого безразмерного числа F частоты f соответствующих значений ψn, Δθn, описывающих мгновенный массовый расход потока для упомянутого определенного градиента давления.
2. Способ по п.1, в котором этапы (а)-(е) повторяются для каждого периода (Р).
3. Способ по п.1, в котором в течение одного периода (Р) определяется, по меньшей мере, 500, предпочтительно, по меньшей мере, 1000 значений мгновенного массового расхода потока.
4. Способ по п.1, в котором мгновенный массовый расход потока m определяется из произведения безразмерного массового расхода потока n и среднего массового расхода потока mm, а именно:
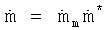
причем для безразмерного массового расхода потока справедливо равенство:
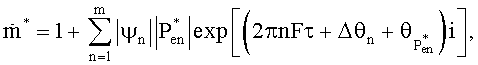
где n - индекс суммирования, 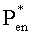 - безразмерная комплексная амплитуда давления n-й составляющей ряда Фурье и m - общее число Фурье-составляющих и
- безразмерная комплексная амплитуда давления n-й составляющей ряда Фурье и m - общее число Фурье-составляющих и 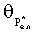 - фаза комплексной безразмерной амплитуды давления;
- фаза комплексной безразмерной амплитуды давления;
а для среднего массового расхода потока справедливо равенство:
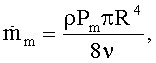
где Рm - средний градиент давления, R - радиус трубы и ν - вязкость.
5. Способ по п.4, в котором в таблице для каждого безразмерного числа F частоты сохраняется точно одно значение ψn и точно одно значение Δθn, и безразмерный массовый расход потока определяется считыванием из таблицы для каждого предварительно заданного безразмерного числа F частоты значений ψn и Δθn.
6. Способ по п.1, в котором измеряют температуру флюида.
7. Способ по п.6, в котором из температуры определяют кинематическую вязкость флюида.
8. Способ по п.7, в котором сначала для кинематической вязкости принимают значение вязкости, а затем его точно рассчитывают.
9. Способ по п.1, в котором кинематическую вязкость вычисляют из функции массового расхода потока m в момент времени t=0 по принятым и итерационно изменяемым значениям вязкости.
10. Способ по п. 9, в котором кинематическую вязкость определяют из смены знака массового расхода потока m в функции.
11. Устройство для определения мгновенного массового расхода потока флюида, периодически пульсирующего с частотой f, содержащее
аа) средство (3а, 3b) определения давления для определения градиента давления, существующего в потоке в течение периода (Р),
bb) компьютер (7), связанный со средством (3а, 3b) определения давления, содержащий
bb1) средство вычисления гармонической амплитуды градиента давления посредством преобразования Фурье,
bb2) средство для преобразования частоты f и времени t в безразмерные числа F, τ, и
bb3) средство для определения массового расхода потока с применением таблицы преобразования, устанавливающей соответствие между безразмерной величиной F и значениями ψn и Δθn, характеризующими массовый расход потока, где ψn - коэффициент амплитуды безразмерного массового расхода потока, Δθn - разность фаз между осцилляциями градиента давления и массового расхода потока для n-й гармонической составляющей массового расхода потока, путем считывания из упомянутой таблицы для каждого безразмерного числа F частоты f соответствующих значений ψn, Δθn, описывающих мгновенный массовый расход потока для упомянутого определенного градиента давления.
12. Устройство по п.11, содержащее пусковое устройство (8) для запуска последовательности вычислений, включающей в себя этапы (bb1)-(bb3).
13. Устройство по п.12, содержащее элемент управления потоком, предпочтительно клапан, управляемый пусковым устройством (8).
14. Устройство по п.11, в котором средство (3а, 3b) измерения давления содержит усилитель (5) с подключенным за ним аналого-цифровым преобразователем.
15. Устройство по п.11, в котором средство (3а, 3b) измерения давления включает в себя дифференциальный датчик давления.
16. Устройство по п.15, в котором дифференциальный датчик давления имеет динамический диапазон, по меньшей мере, 1:1000.
17. Устройство по п.11, в котором средство (3а, 3b) измерения давления включает в себя два разнесенных друг от друга в направлении потока, предпочтительно пьезоэлектрических или пьезорезистивных датчика (3а, 3b) давления и средство для определения дифференциального давления.
18. Устройство по п.17, в котором датчики (3а, 3b) давления имеют динамический диапазон, по меньшей мере, 1:10000, предпочтительно, по меньшей мере, 1:100000.
19. Устройство по п.11, в котором предусмотрено устройство измерения температуры для измерения температуры флюида.
20. Устройство по п.11, в котором компьютер (7) также содержит средство для вычисления кинематической вязкости.
21. Устройство по п.20, в котором вычисление кинематической вязкости осуществляется на основе измеренных значений температуры.
22. Устройство по п.19, в котором средство (3а, 3b) измерения давления и устройство измерения температуры приведены в контакт с флюидом в трубе (1).
23. Устройство по п.19, в котором средство (3а, 3b) измерения давления и устройство измерения температуры размещены ниже по потоку от источника давления, предусмотренного на одном конце (Е1) трубы (1).
24. Устройство по п.19, содержащее элемент управления потоком, размещенный ниже по потоку от средства (3а, 3b) измерения давления и устройства измерения температуры.
| Journal of fluids engineering, 2005 - 05, vol | |||
| Способ получения морфия из опия | 1922 |
|
SU127A1 |
| RU 2002132839 A, 10.06.2004 | |||
| US 6439592 В1, 26.02.2002 | |||
| Способ обработки целлюлозных материалов, с целью тонкого измельчения или переведения в коллоидальный раствор | 1923 |
|
SU2005A1 |
| US 6510842 B2, 28.01.2003. | |||
Авторы
Даты
2011-06-20—Публикация
2006-06-16—Подача