Предлагаемое изобретение относится к средствам отображения информации (СОИ), значительную область применения которых представляют матричные и сегментные знакосинтезирующие индикаторы (ЗСИ).
Индикатор матричный с регулируемой эквивалентной площадью различения знаков может найти применение во всех средствах отображения информации, в которых требуется улучшение восприятия цифровых знаков.
Наибольший информационный объем в различных устройствах вычислительной и измерительной техники приходится на отображение семипозиционных десятичных цифр.
К недостаткам начертания семипозиционных цифровых знаков следует отнести большое число позиционных элементов, входящих в цифровой формат, из которого формируются десятичные знаки, неравномерность распределения позиционных элементов в знаках, невысокая разрешающая способность знаков по ширине и высоте их; неравномерность энергопотребления при формировании знаков. В итоге: невысокое восприятие знаков и невысокая скорость опознания их.
Стремление достигнуть улучшения различения цифровых знаков изменением их начертания и уменьшением габаритного размера цифрового формата (снижением числа точечных элементов в нем) приведет к непривычности начертания знаков.
Непривычность начертания знаков при этом должна быть оправдана наилучшими эргономическими параметрами восприятия их - наибольшей разрешающей способностью как по высоте, так и по ширине знака.
Целью предлагаемого изобретения является:
1. уменьшение габаритного размера цифрового формата знаков по высоте;
2. улучшение параметрических характеристик цифровых знаков: увеличение разрешающей способности по высоте и ширине их;
3. уменьшение неравномерности по числу точечных элементов в знаках;
4. уменьшение неравномерности энергопотребления в знаках;
5. увеличение динамического диапазона изменения величины эквивалентной площади различения.
Указанная цель достигается тем, что на информационном поле индикатора формируются цифровые знаки, начертание которых обеспечивает наибольшую разрешающую способность их восприятия.
Важным требованием к индикатору является обеспечение возможности восприятия отображаемой цифровой информации с заданных расстояний наблюдения. Исходя из этих требований, устанавливаются требования к параметрам ЗСИ: расстояние наблюдения, угловой размер знака, линейный размер знака по высоте /1 - стр.98/.
Для правильного выбора линейных размеров цифровых знаков (высоты, ширины, толщины контура знака) необходимо знать угловой размер знака, определяемый остротой зрения. Угловой размер знака - это угол между двумя лучами, направленными от глаза к крайним точкам (линиям) знака
α=2arctg(h/2L), или h=2Ltgα/2, L=h/2tgα/2, где h - линейный размер знака по высоте; L - расстояние от глаза до знака; α - угловой размер знака или угол зрения, под которым виден знак /2 - стр.115/.
Исходя из расстояния наблюдения L, устанавливаемого опытным путем, и оптимального значения углового размера знака, находят высоту знака h. Зная высоту знака, можно вычислить его ширину, толщину контура знака, а также расстояние между знаками. Ширина знака должна составлять (3/5)h, толщина контура знака - (1/8)h, а расстояние между знаками - 1/2 ширины знака /2 - стр.116/.
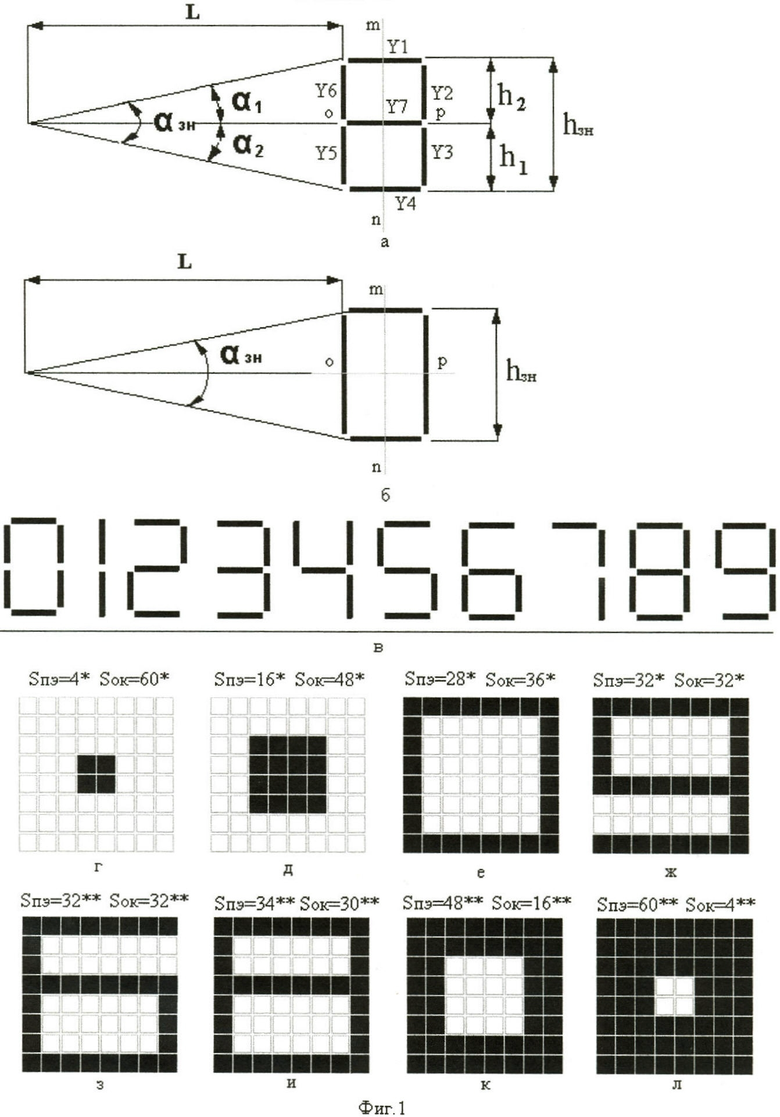
Однако для количественной оценки восприятия отображаемой цифровой информации недостаточно этих величин, найденных опытным путем. Так, например, восприятие различных знаков одного и того же семисегментного формата индикатора будут различны при одном и том же расстоянии наблюдения и при одном и том же угловом размере их. Цифры 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 (фиг.1в) различаются числом и расположением сегментов, различной величиной площади, занимаемой высветившимися позиционными элементами знака, и величиной площади («окном»), расположенной между этими позиционными элементами, различной разрешающей способностью. Разрешающая способность знака оценивается по возможности различения оператором двух воспроизводимых линий, находящихся на некотором расстоянии друг от друга /2 - стр.115/.
Так, например, при рассмотрении начертания цифр семисегментного формата индикатора следует заметить, что при одной и той же высоте отображаемых знаков и их углового размера по высоте дальность наблюдения по формуле одна и та же (L=h/2tgα/2). Но нельзя сказать, чтобы восприятие любого семисегментного знака с одного и того же расстояния было одним и тем же. Если сравнить начертания цифровых знаков 8 (фиг.1а) и 0 (фиг.1б), то окажется, что дальность расстояния при рассмотрении цифры 0 можно увеличить. Эффективный угловой размер по высоте цифры 0 в два раза больше или иначе, больше у нее разрешающая способность по высоте /3/ вследствие отсутствия среднего сегмента в начертании этой цифры. Цифра 7 имеет наибольшую разрешающую способность вследствие того, что в ее начертании присутствуют всего лишь два сегмента (горизонтальный и вертикальный) и кроме этих сегментов нет других вертикальных или горизонтальных сегментов, находящихся на некотором расстоянии от них, ухудшающих различение оператором этого знака. Другие знаки семисегментного формата (кроме цифры 1 и 7) имеют в своем начертании или по два вертикальных, или по три горизонтальных сегмента, ухудшающих восприятие их.
Под восприятием понимают процесс целостного отражения предметов, возникающий при непосредственном воздействии физических раздражителей (стимулов) на рецепторные поверхности органов чувств. Этот многоуровневый процесс, заканчивающийся формированием чувственного образа, включает следующие стадии: обнаружение, различение, идентификация, опознание /4 - стр.46/.
Обнаружение - стадия восприятия, на которой оператор выделяет объект из фона. При этом устанавливается лишь наличие сигнала в поле зрения без оценки его формы и признаков /4 - стр.46/.
Для количественной оценки восприятия знаков на стадии обнаружения без оценки его формы и признаков воспользуемся габаритными размерами информационного поля матричного индикатора (8×8=64 мм2) типа КИПГО2А-8×8Л /5 - стр.353/ без учета расстояния между точечными элементами. Матричный метод отображения, для удобства вычислений позволит наглядно, не проставляя размеров на фигурах, определить:
1. габаритные размеры знаков по ширине (Lзн) и высоте (hзн);
2. площадь, занимаемую знаком (Sзн);
3. площадь, занимаемую позиционными элементами отображения знака (Sпэ);
4. площадь, расположенную между этими позиционными элементами отображения (площадь «окна» - Sок);
5. толщину контура знака (s).
Габаритные размеры элемента излучения информационного поля матрицы на любой фигуре материалов заявки принимаем размером 1×1 мм2.
Придавая площади, занимаемой позиционными элементами отображения знака (Sпэ), значения от 0 до 64 мм2 (при отображении знаков используется все информационное поле индикатора КИПГО2А-8×8Л) дискретно через 2 мм2, можно проследить зависимость отношения площади позиционных элементов к площади «окна» (Sпэ/Sок) от площади позиционных элементов (Sпэ). Можно проследить и обратную зависимость - отношение площади «окна» к площади позиционных элементов (Sок/Sпэ) от площади позиционных элементов (Sпэ). Площадь, занимаемую «окном» (Sок), вычисляем по формуле Sок=Sзн-Sпэ, где Sзн - площадь знака, равная 64 мм2 (Sзн=Sпэ+Sок), занимающая все информационное поле индикатора. На фиг.1г-фиг.1л отображено заполнение информационного поля произвольными фигурами с определенной площадью, кратной 2 мм2, позиционных элементов.
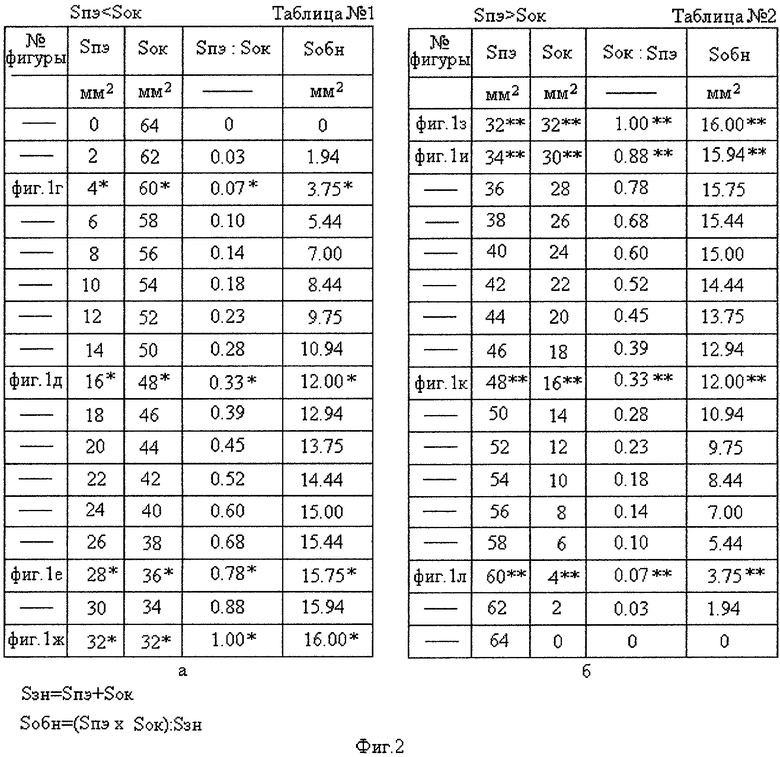
Для каждой пары величин Sпэ и Sок, при постоянной площади знака (Sзн=Sпэ+Sок), находим отношение Sпэ/Sок (при условии Sпэ<Sок) и все цифровые данные заносим в таблицу №1 (фиг.2а).
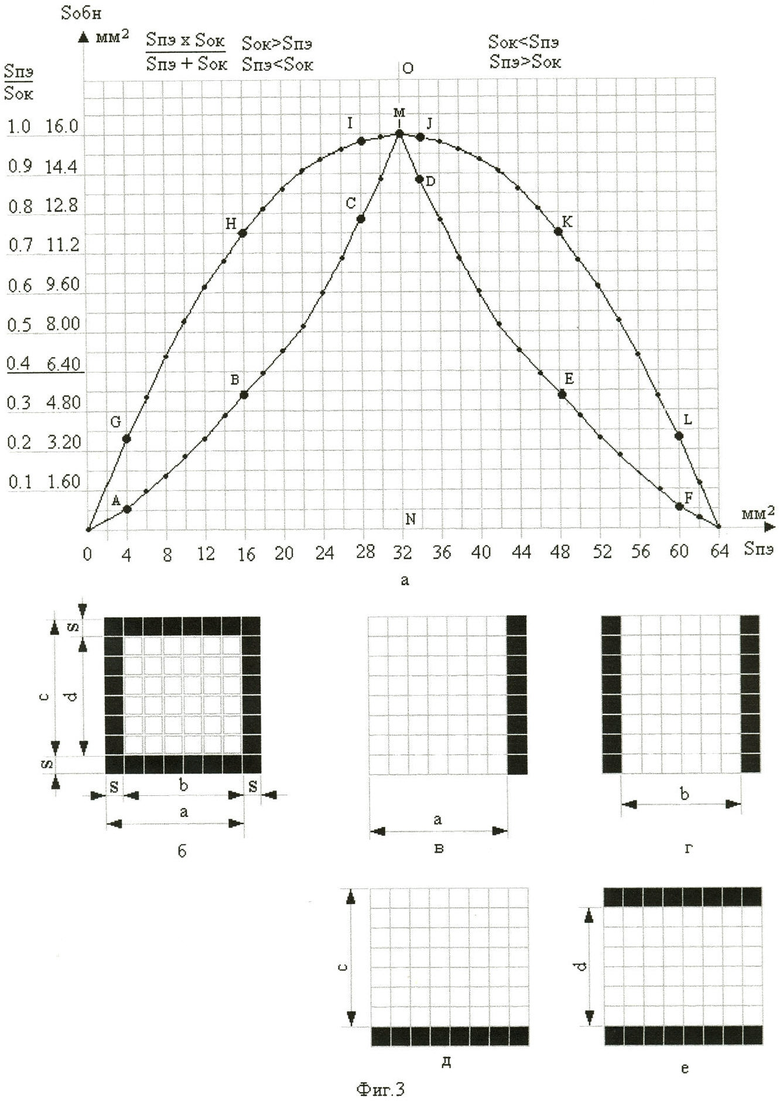
По данным таблицы №1 построен возрастающий участок АВСМ (Sпэ=0-32 мм2) кривой (от нуля до точки М) зависимости отношения Sпэ/Sок (фиг.3a) от площади позиционных элементов отображения знака (Sпэ). Точки А, В, С, М кривой соответствуют значениям величин площади позиционных элементов, отображенных на фиг.1г-фиг.1ж соответственно. В таблице №1 эти точки отмечены «звездочками». Максимальное значение величины отношения Sпэ/Sок равно 1 (точка М, фиг.1ж), достигаемое при равенстве площади позиционных элементов и площади «окна» (Sпэ=Sок=32 мм2). Величина отношения Sпэ/Sок характеризует возможность обнаружения знака без оценки его формы. И чем больше эта величина (при Sпэ<Sок), тем возможность обнаружения знака выше. На возрастающем участке кривой ABCMDEF (фиг.3а) возможность обнаружения знака увеличивается (фиг.1г-фиг.1ж), когда меньшая площадь позиционных элементов (Sпэ=0-32 мм2) выделяется на фоне большей площади «окна» (Sок=64 мм2 - 32 мм2).
В точке М кривой величина отношения Sпэ/Sок (при Sпэ<Sок) равна обратной величине этого отношения (фиг.1з) Sок/Sпэ (при Sпэ>Sок), которая также характеризует возможность обнаружения знака. В этой точке возможность обнаружения знака максимальна (Sпэ=Sок).
Для построения убывающего участка кривой (фиг.3а), для каждой пары величин Sпэ и Sок (Sпэ>Sок), находим отношение Sок/Sпэ (при Sок<Sпэ) и все цифровые данные заносим в таблицу №2 (фиг.2б). По данным таблицы №2 построен убывающий участок MDEF кривой (от точки М вправо до 0) зависимости отношения Sок/Sпэ от площади позиционных элементов отображения знака (Sпэ). Точки М, D, Е, F кривой соответствуют значениям величин площади позиционных элементов, отображенных на фиг.1з-фиг.1л соответственно. В таблице №2 эти точки отмечены двумя звездочками.
На убывающем участке кривой ABCMDEF (от точки М вправо до 0) возможность обнаружения знака уменьшается (фиг.1з-фиг.1л) при уменьшении площади «окна» (Sок=32 мм2 - 0). Все более выявляется площадь «окна» на фоне большей площади позиционных элементов (Sпэ=32 мм2 - 64 мм2).
Кривая ABCMDEF, состоящая из возрастающего и убывающего участков, характеризует возможность обнаружения знака в зависимости от соотношений:
1. площади позиционных элементов к площади «окна» (Sпэ/Sок) на возрастающем участке кривой при Sпэ<Sок от 0 до 1 (увеличивается возможность обнаружения знака);
2. площади «окна» к площади позиционных элементов (Sок/Sпэ) на убывающем участке кривой при Sок<Sпэ от 1 до 0 (уменьшается возможность обнаружения знака).
Симметричная форма двух участков общей кривой относительно прямой (OMN), проходящей через точку М перпендикулярно оси абсцисс подтверждает равнозначность величин Sпэ/Sок и Sок/Sпэ по возможности обнаружения знака, расположенные по разные стороны от оси симметрии.
Максимальной возможностью обнаружения знака (точка М на кривой) является условие, при котором площадь позиционных элементов равна площади «окна» (Sпэ=Sок). И, следовательно, отношение площади позиционных элементов (Sпэ) к площади «окна» (Sок) равно 1 (Sпэ/Soк=1) или, что тоже самое, равно 1 отношение площади «окна» к площади позиционных элементов (Sок/Sпэ=1).
Только при достижении равенства значений величин площади «окна» и площади позиционных элементов (Sпэ=Sок) возможность обнаружения знака максимальна (Sпэ/Sок=1).
Точка М (фиг.3а), в которой соблюдено условие равенства площади позиционных элементов и площади «окна» (Sпэ=Sок=32 мм2), отображена результатами вычислений (Sпэ/Sок и Sок/Sпэ), относящихся к фиг.1ж и фиг.1з. В двух таблицах №1 и №2 (фиг.2а, фиг.2б) эти результаты отмечены одной и двумя «звездочками» соответственно.
Подобным же образом построена кривая GHIMJKL (фиг.3а). Для построения этой кривой выбран другой метод, который отличается тем, что функция, равная произведению аргументов (Sпэ×Sок), деленному на сумму этих аргументов (Sпэ+Sок), выражена величиной с размерностью площади (мм2). Т.е. числовые значения функции показывают не просто возможность обнаружения знака в относительных величинах, а показывают величину эквивалентной площади обнаружения (Sобн) знака в каждой точке кривой. Кривая GHIMJKL, отображающая функцию Sобн=(Sпэ×Sок):(Sпэ+Sок) в зависимости от величины Sпэ соответствует в каждой точке конкретному габаритному размеру знака (формату матрицы 8×8), в пределах которого изменяется и площадь позиционных элементов, и площадь» окна» (Sзн=Sпэ+Sок).
Максимум кривой GHIMJKL в точке М совпадает с максимумом кривой ABCMDEF в той же точке М при выбранном масштабе по оси ординат. В этой точке при равенстве площади позиционных элементов отображения знака и площади «окна» (Sпэ=Sок=32 мм2) достигается максимальная возможность обнаружения знака (Sпэ/Sок=Sок/Sпэ=1). Причем максимальная возможность обнаружения знака подтверждается конкретной, имеющей размерность (мм2), величиной - эквивалентной площадью обнаружения знака (Sобн).
Результаты вычислений для эквивалентной площади обнаружения знака
Sобн=(Sпэ×Sок):(Sпэ+Sок),
по которым построена кривая GHIMJKL, записаны в таблицу №1 и таблицу №2 (фиг.2а, фиг.2б). На кривой увеличенными точками G, Н, I и J, К, L показаны результаты вычислений, относящиеся к фиг.1г-фиг.1ж и фиг.1з-фиг.1л соответственно, а в таблице №1 и таблице №2 эти результаты вычислений выделены одной и двумя «звездочками».
В таблице №1 результаты вычислений отображают величину эквивалентной площади обнаружения (Sобн) знака, занимаемую позиционными элементами отображения знака (фиг.1г-фиг.1ж) на фоне площади «окна» при Sпэ<Sок.
В таблице №2 результаты вычислений отображают величину эквивалентной площади обнаружения (Sобн) знака (фиг.1з-фиг.1л), занимаемую площадью «окна» на фоне позиционных элементов при Sок<Sпэ.
Точка М, в которой соблюдено условие равенства величины площади позиционных элементов и величины площади «окна» (Sпэ=Sок=32 мм2), отображена результатами вычислений эквивалентной площади обнаружения знака, относящихся к фиг.1ж и фиг.1з. В двух таблицах №1 и №2 (фиг.2а, фиг.2б) эти результаты отмечены одной и двумя «звездочками» соответственно.
Кривая GHIMJKL характеризует изменение величины эквивалентной площади обнаружения знака в зависимости от соотношений:
1. площади позиционных элементов к площади «окна» (Sпэ<Sок);
2. площади «окна» к площади позиционных элементов (Sок<Sпэ).
В первом случае величина эквивалентной площади обнаружения знака увеличивается (фиг.1г-фиг.1ж) при увеличении площади позиционных элементов на возрастающем участке GHIM кривой (Sпэ<Sок) от нуля до точки М (фактически обнаруживается в поле зрения величина эквивалентной площади позиционных элементов на фоне площади «окна»).
Во втором случае величина эквивалентной площади обнаружения знака уменьшается (фиг.1з-фиг.1л) при увеличении площади позиционных элементов на убывающем участке кривой MJKL (Sок<Sпэ), начиная с точки М (фактически обнаруживается в поле зрения величина эквивалентной площади «окна» на фоне большей площади позиционных элементов).
Максимальная величина эквивалентной площади обнаружения при постоянной площади формата индикатора достигается при равенстве площади позиционных элементов и площади «окна» (Sпэ=Sок=32 мм2). При других соотношениях величин площади позиционных элементов и площади «окна» величина эквивалентной площади обнаружения знака будет меньше.
На фиг.1 л, например, видно, что величина площади «окна» равна 4 мм2 (4 точечных элемента матрицы), величина площади позиционных элементов равна 60 мм2, а величина эквивалентной площади обнаружения (Sобн) знака, определяемая формулой, показывает 3.75 мм2.
При Sок<Sпэ фактически обнаруживается в поле зрения величина эквивалентной площади «окна» на фоне площади позиционных элементов. Несоответствие величины площади «окна», представленной на фиг.1 л (Sок=4 мм2), с результатом вычислений по формуле (Sобн=3.75 мм2) объясняется относительностью восприятия малой величины площади «окна» на ограниченной площади позиционных элементов отображения знака.
Так, например, если сохранить величину площади «окна» Sок, равной 4 мм2 и увеличить площадь позиционных элементов знака Sпэ, скажем, в 10 раз (Sпэ=600 мм2), увеличив при этом габаритный размер знака, то результат вычисления эквивалентной площади обнаружения знака приблизится к указанной на фиг.1 л величине площади «окна», равной 4 мм2:
Sобн=(Sпэ×Sок)/(Sпэ+Sок)=(600×4):(600+4)=3.97 мм2.
Точно также, если на фиг.1г величина площади позиционных элементов знака равна 4 мм2 (4 точечных элемента матрицы), а величина площади «окна» равна Sок=60 мм2, величина эквивалентной площади обнаружения знака будет меньше (Sобн=3.75 мм2) величины площади позиционных элементов (Sпэ=4 мм2).
При увеличении площади «окна», при постоянной площади позиционных элементов, например, до 600 мм2, увеличив при этом габаритный размер знака, величина эквивалентной площади обнаружения знака также увеличится, приближаясь к величине площади позиционных элементов, отображенной на фиг.1г:
Sобн=(Sпэ×Sок)/(Sпэ+Sок)=(4×600):(4+600)=3.97 мм2.
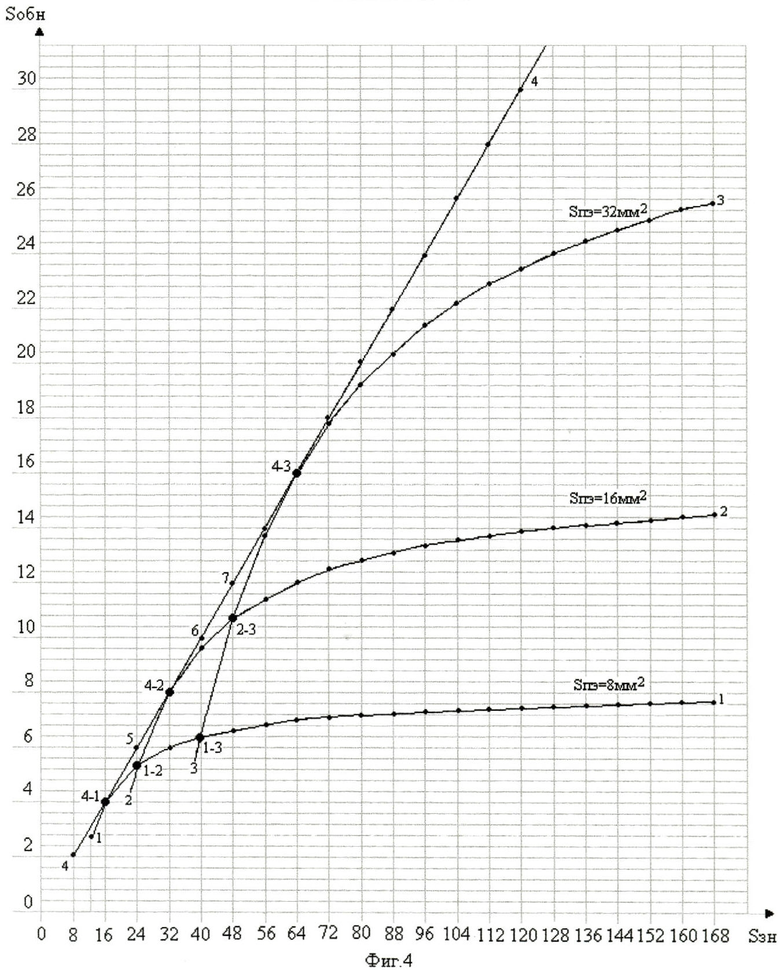
Проследить зависимость величины эквивалентной площади обнаружения (Sобн) от величины площади знака(Sзн=Sпэ+Sок) при постоянной величине площади позиционных элементов с изменением величины площади «окна» можно с помощью графика (фиг.4).
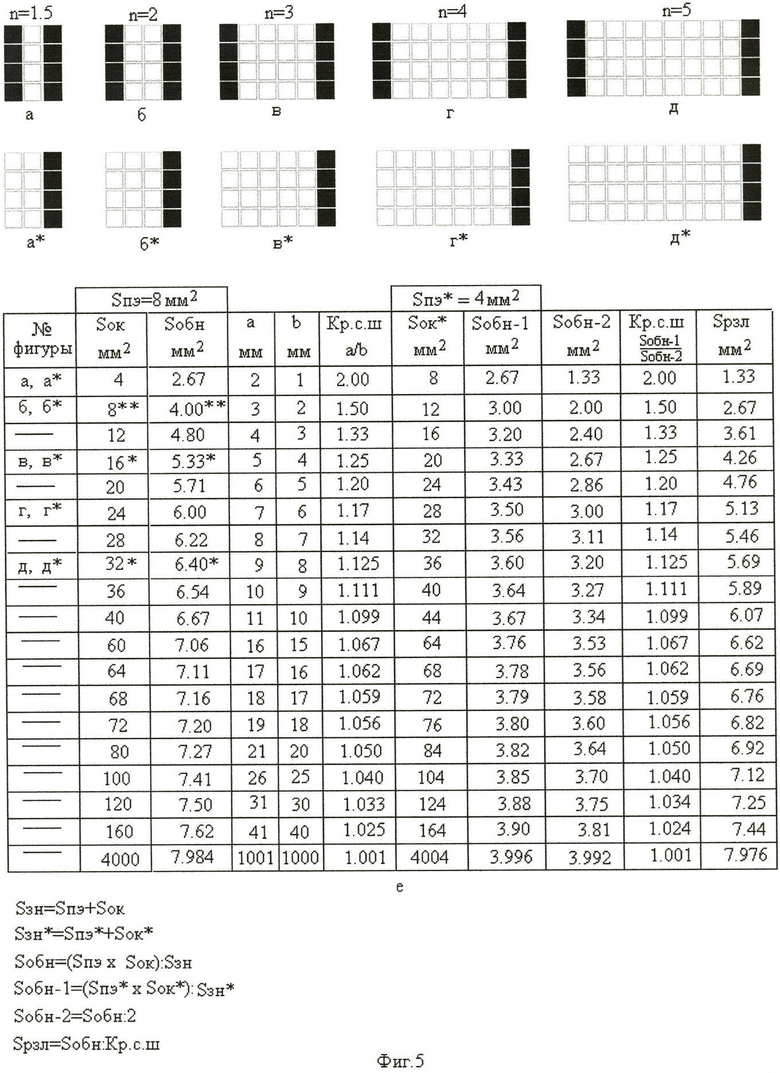
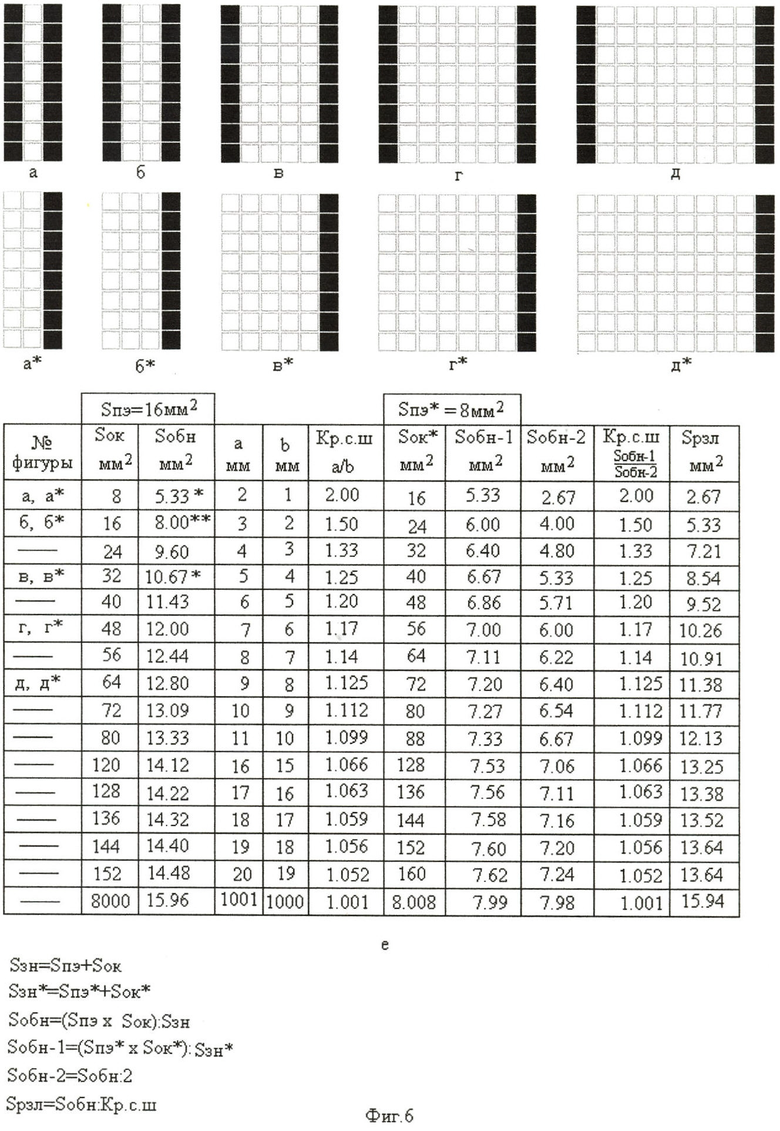
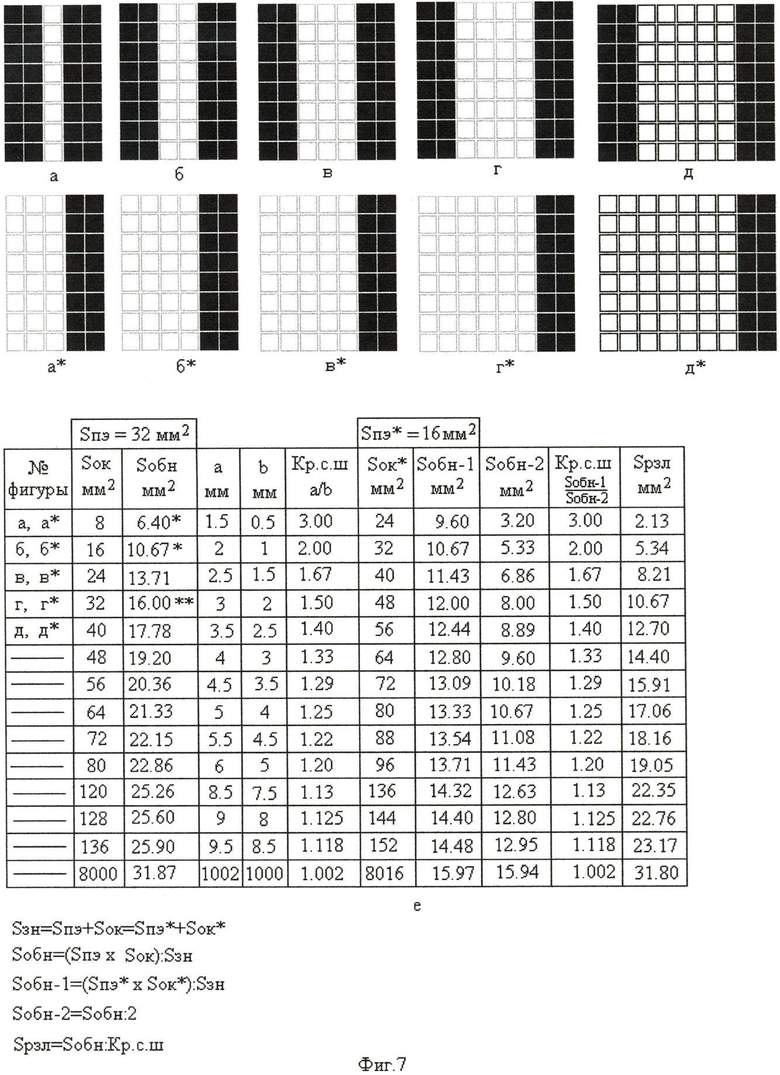
Три кривые 1-1, 2-2, 3-3 построены по данным таблиц (фиг.5е, фиг.6е, фиг.7е соответственно). Величина площади «окна» (Sок) и величина эквивалентной площади обнаружения знака Sобн=(Sпэ×Sок):(Sпэ+Sок) занесены во 2 и в 3 колонки этих таблиц, при постоянной площади позиционных элементов (Sпэ=8 мм2, Sпэ=16 мм2, Sпэ=32 мм2, соответственно для фиг.5е, фиг.6е, фиг.7е). В первой колонке этих таблиц указаны номера фигур (а, б, в, г, д - без «звездочек»), по которым производился расчет величины эквивалентной площади обнаружения знака (Sобн).
Величина эквивалентной площади обнаружения знака (Sобн) с увеличением площади «окна» стремится к величине площади позиционных элементов. При достаточно большой величине площади «окна» (фиг.5е - 4000 мм2, фиг.6е - 8000 мм2, фиг.7е - 8000 мм2) величина эквивалентной площади обнаружения (Sобн=7.99 мм2, Sобн=15,96 мм2 и Sобн=31.87 мм2 соответственно) вплотную приближается к величине площади позиционных элементов (Sобн=8.00 мм2, Sобн=16.00 мм2 и Sобн=32.00 мм2).
Точка пересечения (1-2) кривой 1-1 и кривой 2-2 (фиг.4) показывает, что величина эквивалентной площади обнаружения (Sобн=5.33 мм2) при одной и той же величине площади знака (Sзн=24 мм2) одна и та же (фиг.5е и фиг.6е). Но величина площади позиционных элементов у знака на фиг.6б (Sпэ=16 мм2, Sок=8 мм2) в два раза больше, чем у знака на фиг.5в (Sпэ=8 мм2, Sок=16 мм2).
Увеличенная площадь позиционных элементов в сравнении с величиной площади «окна» (при Sпэ>Sок) у знака на фиг.6а не дала преимущества в величине эквивалентной площади обнаружения перед знаком на фиг.5в, со значительно меньшей величиной площади позиционных элементов.
Точка (2-3) пересечения кривой 3-3 с кривой 2-2 показывает (фиг.4), что эквивалентная площадь обнаружения (Sобн=10.67 мм2) при одной и той же площади знака (Sзн=48 мм2) одна и та же (фиг.6е и фиг.7е). Но площадь позиционных элементов у знака на фиг.7в (Sпэ=32 мм2, Sок=16 мм2) в два раза больше чем у знака на фиг.6д (Sпэ=16 мм2, Sок=16 мм2).
Увеличенная площадь позиционных элементов в сравнении с величиной площади «окна» (при Sпэ>Sок) у знака на фиг.7в не дала преимущества в величине эквивалентной площади обнаружения со значительно меньшей величиной площади позиционных элементов у знака на фиг.6д.
Точка (1-3) пересечения кривой 3-3 с кривой 1-1 показывает (фиг.4), что эквивалентная площадь обнаружения (Sобн=6.40 мм2) при одной и той же площади знака (Sзн=40 мм2) одна и та же (фиг.5е и фиг.7е), но площадь позиционных элементов у знака на фиг.7а (Sпэ=32 мм2, Sок=8 мм2) в четыре раза больше чем у знака на фиг.5д (Sпэ=8 мм2, Sок=16 мм2).
Увеличенная площадь позиционных элементов в сравнении с площадью «окна» (при Sпэ>Sок) у знака на фиг.7а не дала преимущества в величине эквивалентной площади обнаружения перед знаком на фиг.5д, со значительно меньшей площадью позиционных элементов.
Зависимость величины эквивалентной площади обнаружения (Sобн) от величины площади (Sзн) знака (фиг.4), величина площади позиционных элементов соответствующего знака в которых равна площади «окна» (Sпэ=Sок), показывает прямая 4-4, касательная к каждой из кривых (1-1, 2-2, 3-3) в точках (4-1,4-2,4-3 соответственно). Этим точкам соответствует знаки (фиг.5б - Sпэ=8 мм2, Sок=8 мм2, Sобн=4 мм2; фиг.6б - Sпэ=16 мм2, Sок=16 мм2, Sобн=8 мм2 и фиг.7г - Sпэ=32 мм2, Sок=32 мм2, Sобн=16 мм2), величина площади позиционных элементов которых равна величине площади «окна».
График зависимости величины эквивалентной площади обнаружения (Sобн) от величины площади знака (Sзн), построенный по результатам таблиц (фиг.5е, фиг.6е, фиг.7е - кривая 1-1, кривая 2-2 и кривая 3-3 соответственно), показан на фиг.4. Из этого графика видно, что при увеличении площади «окна» и постоянной площади позиционных элементов (Sпэ=8 мм2 - кривая 1-1, Sпэ=16 мм2 - кривая 2-2, Sпэ=32 мм2 - кривая 3-3) величина эквивалентной площади обнаружения знака (Sобн) приближается к величине площади позиционных элементов (Sпэ).
Использовать практически увеличение площади знака до такой величины, чтобы величина эквивалентной площади обнаружения (Sобн) знака достигла величины площади позиционных элементов (Sпэ), не имеет смысла из-за значительного увеличения габаритного размера знака индикатора.
Оптимальной характеристикой при выборе величины площади позиционных элементов (Sпэ) отображения и равной ей величине площади «окна» (Sок) при заданном габаритном размере знака (Sзн) является прямая, касательная одновременно к кривой 1-1, кривой 2-2 и кривой 3-3. Эта прямая касается каждой кривой в тех точках ее, в которых соблюдается равенство Sпэ=Sок=Sзн/2 для данного габаритного размера знака (Sзн=Sпэ+Sок). Так, например, по точкам прямой 5, 6 и 7, площадь знака в которых равна соответственно 24 мм2, 40 мм2 и 48 мм2, оптимальной величиной площади позиционных элементов будут 12 мм2, 20 мм2 и 24 мм2 соответственно. Величина эквивалентной площади обнаружения каждого знака будет при этом равна 6 мм2, 10 мм2 и 12 мм2 (фиг.4).
Величина эквивалентной площади обнаружения знака в этих точках равна Sобн=(Sпэ×Sок): (Sпэ+Sок)=Sзн/4. И при увеличении площади позиционных элементов по отношению к величине площади «окна», т.е. при Sпэ>Sок, при рассматриваемом габаритном размере знака, не приведет к увеличению величины эквивалентной площади обнаружения, т.е. не приводит к улучшению возможности его обнаружения. Только при равенстве величины площади позиционных элементов и величины площади «окна» достигается максимальная величина эквивалентной площади обнаружения (Sобн) знака и максимальная возможность его (Sпэ/Sок=Sок/Sпэ=1) обнаружения (точка М на кривой ABMCD и на кривой EFMGH - фиг.3а).
Различение - стадия восприятия, на которой оператор способен выделить детали, позиционные элементы отображения знака /4 - стр.46/. Способность средств отображения информации воспроизводить мелкие детали характеризуется их разрешающей способностью. Разрешающая способность это одна из параметрических характеристик индикатора, определяемая особенностью восприятия зрительной информации человеком - оператором. Разрешающая способность определяется как максимальное число отдельных участков на единицу длины или поверхности индикатора, имеющих достаточный для их восприятия контраст. Количественно она оценивается числом пар оптических линий («линия-промежуток»), приходящихся на 1 мм или 1 см, или минимально возможной шириной линий на экране /4 - стр.21/.
Разрешающую способность индикаторов можно оценивать по возможности различения оператором двух воспроизводимых световых точек или линий, находящихся на некотором расстоянии друг от друга. При низкой разрешающей способности оператор принимает две точки (линии) за одну, а при высокой разрешающей способности две очень близкие точки (линии) воспринимаются как отдельные. Повышать разрешающую способность можно до определенного предела, свыше которого изображение не будет восприниматься глазом /2 - стр.115/.
Чем меньше расстояние между параллельно расположенными позиционными элементами отображения в знаке, тем меньше разрешающая способность знака, тем хуже возможность различения его.
Разрешающая способность по ширине знака (n) на фиг.5а-фиг.5д, определяемая числом пар «линия-промежуток» (ширину «промежутка» выбираем равной ширине линии или равной толщине контура знака), возрастает от 1.5 до 5. Увеличивается возможность различения знака с возрастанием разрешающей способности. Увеличивается эквивалентная площадь различения знака. Но количественно оценить влияние увеличения разрешающей способности на увеличение эквивалентной площади различения знака по величине числа «пар-промежуток» на этих фигурах нельзя. Можно сказать только, что разрешающая способность знака по ширине у фиг.5д больше разрешающей способности знака по ширине у фиг.5а.
Чтобы количественно оценить влияние разрешающей способности знака на величину эквивалентной площади при различении его, необходимо связать величины, отображающие разрешающую способность знака по ширине с эквивалентной площадью обнаружения его.
Для этого необходимо ввести коэффициент разрешающей способности по ширине (Кр.с.ш) знака. И с помощью этого коэффициента вычислить эквивалентную площадь различения знака (Sрзл) по формуле:
Sрзл=Sобн:Кр.с.ш
Величина коэффициента разрешающей способности уменьшает возможность восприятия знака и скорость его опознания.
Для определения коэффициента разрешающей способности знака (фиг.3б) по ширине (Кр.с.ш) удобнее разрешающую способность его выразить не числом пар «линия-промежуток», а толщиной вертикального позиционного элемента отображения знака (s).
С помощью толщины контура знака измеряем промежуток (а) между одной вертикальной линией знака до границы ширины знака (фиг.3в) и промежуток (b) между противоположными вертикальными линиями знака (фиг.3г). Т.е. измеряется толщиной контура знака (фиг.3б) расстояние от одного вертикального позиционного элемента отображения до границы (фиг.3в) ширины знака (а) и измеряется расстояние промежутка (b) между двумя вертикальными позиционными элементами (ширина «окна») знака (фиг.3г).
Рассматривается возможность различения одного (фиг.3в) вертикального позиционного элемента в одном случае и возможность различения каждого позиционного элемента отображения (фиг.3г), во втором случае, при одной и той же ширине знака. Частное от деления, a/b (безразмерное число) можно характеризовать как относительную величину разрешающей способности знака или величину коэффициента разрешающей способности знака по ширине (Кр.с.ш=a/b). Чем больше эта величина (Кр.с.ш=a/b), тем ниже разрешающая способность по ширине знака.
Т.е. величина этого отношения (a/b>1) уменьшает возможность различения каждого из двух позиционных элементов отображения (фиг.3г) по отношению к возможности различения лишь одного позиционного элемента отображения при отсутствии второго позиционного элемента отображения (фиг.3в), при одной и той же ширине знака.
Определим величины коэффициентов разрешающей способности (Кр.с.ш=a/b) по ширине знака, состоящего из двух вертикальных позиционных элементов, расположенных на одном расстоянии друг от друга (фиг.6а), и двух вертикальных позиционных элементов, расположенных на другом расстоянии друг от друга (фиг.6д). Величины а и b (фиг.6а и фиг.6д), измеренные числом толщины позиционного элемента, определяют значения коэффициентов разрешающей способности по ширине. Отношения а/b (Кр.с.ш=a/b) будут соответственно равны Кр.с.ш=2/1=2 (фиг.6е, 1 строка) и Кр.с.ш=9/8=1.125 (фиг.6е, 8 строка).
Для подтверждения правильности расчета коэффициента (Кр.с.ш) разрешающей способности того и другого знака (фиг.6а, фиг.6д) проверяем его другой формулой, используемой для определения величины эквивалентной площади обнаружения знака:
Sобн=(Sпэ×Sок):(Sпэ+Sок)
Определяется величина эквивалентной площади обнаружения одного вертикального позиционного элемента при двух (Sобн-2) вертикальных (фиг.6а, фиг.6д), расположенных параллельно на некотором расстоянии друг от друга позиционных элементов отображения, на занимаемой ими площади (Sпэ+Sок), по формуле:
Sобн-2=(Sпэ×Sок):(Sпэ+Sок):2 или Sобн-2=Sобн/2 (фиг.6е - колонки 2, 3 и 9 таблицы).
Определяется величина эквивалентной площади обнаружения одного вертикального позиционного элемента при одном (Sобн-1) вертикальном (фиг.6а*, фиг.6д*) позиционном элементе отображения, расположенном (фиг.6е - колонки 7 и 8 таблицы) на той же площади (Sзн*=Sзн) по формуле:
Sобн-1=(Sпэ*×Sок*):(Sпэ*+Sок*)
Величина эквивалентной площади обнаружения (Sобн-1) одного позиционного элемента, расположенного на ограниченном (Sзн) пространстве (фиг.6а*, фиг.6д*) больше величины эквивалентной площади обнаружения (Sобн-2) этого же позиционного элемента на том же ограниченном пространстве (Sзн) при расположении второго позиционного элемента на некотором расстоянии от него (фиг.6а, фиг.6д).
Величина отношения Sобн-1/Sобн-2 определяет коэффициент разрешающей способности (фиг.6е - 10 колонка таблицы), при вертикально расположенных позиционных элементах, по ширине знака (Кр.с.ш=Sобн-1/Sобн-2). Для фиг.6а и фиг.6д коэффициенты разрешающей способности, определяемые по различным методам расчета (Кр.с.ш=a/b или Кр.с.ш=Sобн-1/Sобн-2) в точности совпадают (коэффициент Кр.с.ш для фиг.6а равен Кр.с.ш=a/b=2:1=2, или Кр.с.ш=Sобн-1/Sобн-2=5.33 мм2:2.67 мм2=2, строка 1 таблицы, а для фиг.6д коэффициент Кр.с.ш=a/b=9:8=1.125 или Кр.с.ш=Sобн-1/Sобн-2=7.20 мм2:6.40 мм2=1.125, строка 8 таблицы - фиг.6е).
Коэффициент разрешающей способности Кр.с.ш=(Sобн-1)/(Sобн-2) показывает уменьшение эквивалентной площади обнаружения одного из двух (Sобн-2) позиционных элементов отображения (фиг.6а) по отношению к эквивалентной площади обнаружения одного (Sобн-1) при одном отображенном позиционном элементе (фиг.6а*), расположенном на той же площади. Чем больше величина этого отношения, тем меньше эквивалентная площадь различения (Sрзл) знака (Sрзл=Sобн/Кр.с.ш). Для фиг.6а эквивалентная площадь обнаружения знака (Sобн=5.33 мм2) в два раза больше эквивалентной площади различения знака (Sрзл=Sобн/Кр.с.ш=5.33 мм2:2=2.67 мм2).
Возможность различения знака, выраженная эквивалентной площадью различения (Sрзл) с учетом коэффициента разрешающей способности по ширине (Sрзл=Sобн/Кр.с.ш) при сравнении фигур (фиг.6а и фиг.6д), показана в таблице (фиг.6е - строки 1 и 8 сверху). На фиг.5, фиг.6, фиг.7 представлены примеры фигур с различной разрешающей способностью по ширине знака и результаты величин коэффициентов разрешающей способности, занесенных в таблицы.
Из этих таблиц видно, что чем больше разрешающая способность знака, чем дальше отстоят друг от друга позиционные элементы отображения, тем меньше коэффициент разрешающей способности. Величина эквивалентной площади различения (Spзл) каждого знака меньше эквивалентной площади обнаружения этого же знака на коэффициент разрешающей способности знака (Sрзл=Sобн/Кр.с.зн). Коэффициент разрешающей способности стремится к 1 при достаточно большом расстоянии между позиционными элементами знака (фиг.5е, фиг.6е, фиг.7е - нижние строки таблиц).
В этом случае величина эквивалентной площади различения знака стремится к величине эквивалентной площади обнаружения знака (позиционные элементы знака не оказывают никакого влияния друг на друга).
Точно также определяется коэффициент разрешающей способности (Кр.с.в=c/d) по высоте знака (фиг.3д, фиг.3е).
При определении величины коэффициента разрешающей способности по высоте знака, имеющего один горизонтальный позиционный элемент (фиг.3д), измеряется расстояние толщиной этого позиционного элемента до границы высоты знака (с) и измеряется расстояние (d) промежутка (фиг.3е) между двумя горизонтальными позиционными элементами, расположенными по границе высоты знака.
Частное от деления, c/d (безразмерное число) можно характеризовать как относительную величину разрешающей способности знака или величину коэффициента разрешающей способности знака по высоте (Кр.с.в=c/d). Чем больше эта величина (Кр.с.в=c/d), тем ниже разрешающая способность по высоте знака.
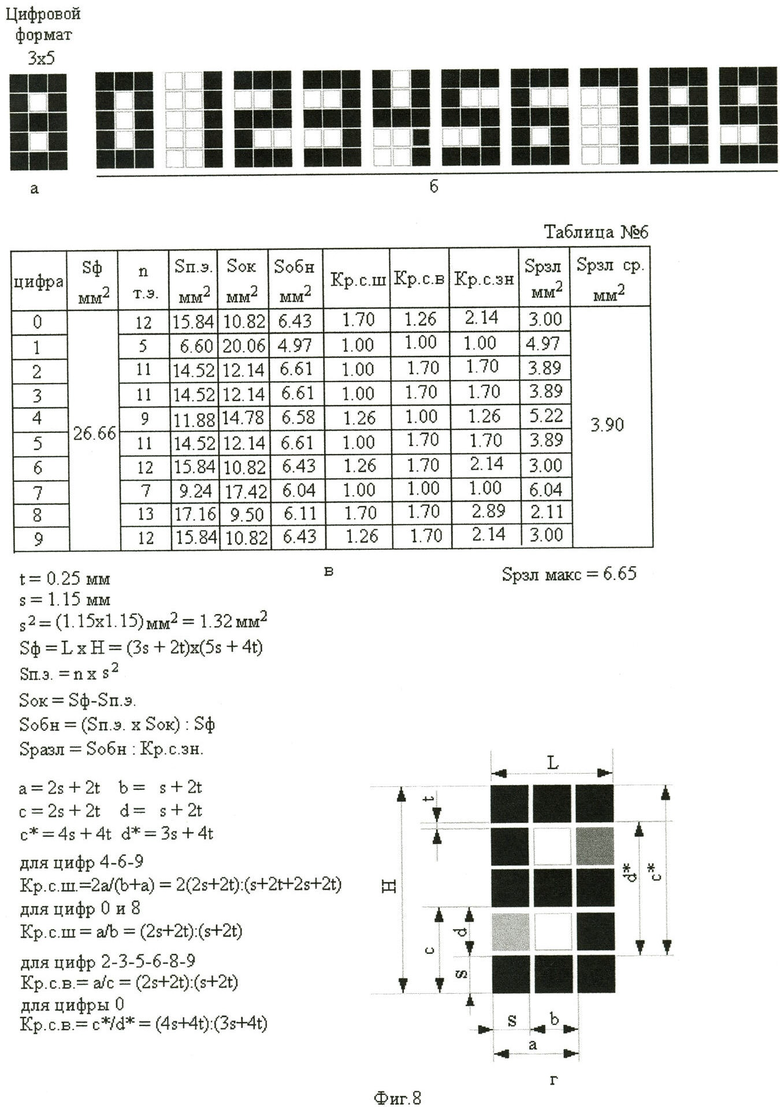
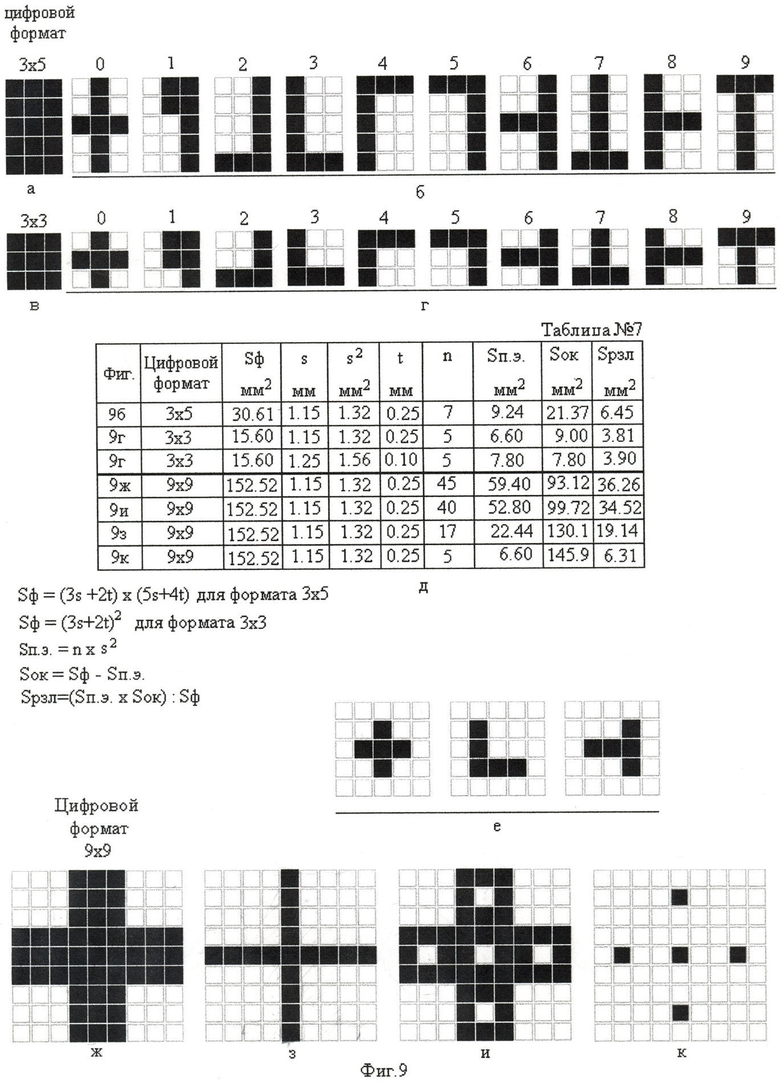
В качестве прототипа выбираем матричный электролюминесцентный индикатор МЭЛ-1 с видом матрицы 27×160 /5 - стр.382/. При формировании 7-позиционных цифр на лицевой стороне матричного индикатора воспользуемся наименьшим цифровым семипозиционным форматом с числом точечных элементов его, равным 3х5 (фиг.8а). Начертания семипозиционных знаков (фиг.8б) соответствуют рис.8.1. /1 - стр.91, 5 строка сверху/ или на рис.8.2. /1 - стр.98, 3 строка сверху/. Такие цифры на матричном поле индикатора при их отображении не имеют отклонения от вертикали.
Для каждого отображаемого знака цифрового формата 3×5 определяем и заносим в таблицу №6 (фиг.8в)
1. n - число точечных элементов по ширине и высоте знака соответственно;
2. Площадь формата знака на 3×5 точечных элементов, с учетом промежутка между ними (t=0.25 мм), при ширине и высоте точечного элемента s=1.15 мм, равна:
Sф=(3s+2t)×(5s+4t)=(1.15×3+0.25×2)×(1.15×5+0.25×4)=26.66 мм2;
3. Площадь высветившихся позиционных элементов знака (Sпэ): Sпэ=n×s2;
4. площадь «окна» (Sок), равной площади формата знака (Sф) за вычетом площади (Sпэ) позиционных элементов знака (Sок=Sф-Sпэ);
5. величину эквивалентной площади обнаружения по формуле:
Sобн=(Sпэ×Sок):(Sпэ+Sок);
6. величины коэффициентов разрешающей способности по ширине для знаков 0 и 8 (линейный размер точечного элемента s=1.15 мм, расстояние между точечными элементами t=0.25 мм) равны: Кр.с.ш=a/b, где а=2s+2t, и b=s+2t (фиг.8г).
Кр.с.ш=a/b-(2s+2t):(s+2t)=(2×1.15+2×0.25):(1.15+2×0.25)=2.80:1.65-1.70 (фиг.8в -10 и 2 строки снизу, колонка 7);
7. величины коэффициентов разрешающей способности по ширине знака для цифр 1, 2, 3, 5 и 7 (фиг.8а и фиг.8б), у которых второй вертикальный позиционный элемент отсутствует, относительно которого измеряется расстояние b, и формула будет выглядеть так: Кр.с.ш=a/b=а/а=1, при b=а.
В этом случае измеряется расстояние (а) от одного позиционного элемента до границы знака (фиг.8г) и измеряется то же расстояние от одного позиционного элемента также до границы знака (b=а) при отсутствии второго позиционного элемента.
Отсутствие второго позиционного элемента знака эквивалентно расположению второго позиционного элемента на достаточно большом расстоянии, не оказывающем влияние на различение первого позиционного элемента. И коэффициент разрешающей способности в этом случае будет равен Кр.с.ш=1;
8. величины коэффициентов разрешающей способности по ширине знака для цифр 4, 9 и 6, у которых отсутствует точечный элемент слева в нижней половине (цифры 4 и 9) знака и справа в верхней половине (цифра 6) знака (фиг.8г - слабо затемненные точечные элементы);
для цифр 4 и 9:
а. измеряется суммарное расстояние (а+а) от правого нижнего (второй снизу) точечного элемента и от правого верхнего (второй сверху) точечного элемента до границ знака в нижней и верхней половинах его;
б. измеряется суммарное расстояние (а+b) от правого нижнего (второй снизу) точечного элемента до границы знака (а), при отсутствии точечного элемента слева в нижней половине (второго снизу) знака, и от правого верхнего точечного элемента до верхнего (второго сверху) точечного элемента (b) слева в верхней половине знака, при его наличии.
Коэффициент разрешающей способности по ширине знака вычисляется по формуле:
Кр.с.ш=(a+a):(b+a), где а=2s+2t, и b=s+2t
Kp.c.ш=2(2s+2t):(s+2t+2s+2t)=2(2×1.15+2×0.25):(1.15+2×0.25+2×1.15+2×0.25)=5.6:4.45=1.26 (фиг.8в - 6 и 1 строки снизу соответственно, колонка 7).
Такая же величина коэффициента разрешающей способности по ширине знака (Кр.с.ш=1.26) будет равна и для цифры 6 (фиг.8г - 4 строка снизу, колонка 7);
9. величины коэффициентов разрешающей способности по высоте для знаков 2, 3, 5, 6, 8 и 9 (фиг.8г): Кр.с.в=c/d, где с=2s+2t, и d=s+2t
Kp.c.в=(2s+2t):(s+2t)=(2×1.15+2×0.25):(1.15+2×0.025)=2.80:1.65=1.70
(фиг.9б - 8, 7, 5, 4, 2, 1 строки снизу соответственно, колонка 8);
10. величину коэффициента разрешающей способности по высоте для знака 0:
Кр.с.в=c*/d*, где с*=4s+4t, и d*-=3s+4t (фиг.8г)
Kp.c.в=(4s+4t):(3s+4t)=(4×1.15+4×0.25):(3×1.15+4×0.25)=5.6:4.45=1.26 (фиг.8в - 10 строка снизу, колонка 8);
11. величины коэффициентов разрешающей способности по высоте для знаков 4 и 7:
Кр.с.в=c/d=1 (при d=c);
12. величину коэффициентов разрешающей способности по высоте для знака 1:
Кр.с.в=1 (у этого знака нет горизонтального позиционного элемента);
13. величины коэффициентов разрешающей способности каждого знака (фиг.8в, колонка 9).
Величина коэффициента разрешающей способности знака равна произведению величины коэффициента разрешающей способности по ширине знака на величину коэффициента разрешающей способности по высоте знака:
Кр.с.зн=Кр.с.ш×Кр.с.в;
14. величину эквивалентной площади (Sрзл=Sобн/Кр.с.зн) различения знака (фиг.8в, колонка 10). Величина эквивалентной площади различения знака (Sрзл) меньше величины эквивалентной площади обнаружения знака (Sобн) на величину коэффициента разрешающей способности знака (Кр.с.зн).
Чем больше величина коэффициента разрешающей способности знака, тем значительнее уменьшается величина эквивалентной площади различения знака по сравнению с величиной эквивалентной площади обнаружения его. При величине эквивалентной площади обнаружения знака (цифра 8), равной 6.11 мм2, величина эквивалентной площади различения уменьшилась почти в 3 раза до 2.11 мм2 (при Кр.с.зн=2.89).
Из таблицы №6 (фиг.8в) видно, что величина эквивалентной площади различения (Sрзл) у большинства семипозиционных знаков меньше чем величина эквивалентной площади обнаружения (Sобн) на величину коэффициента разрешающей способности знака. И только у цифр 1 и 7, у которых коэффициент разрешающей способности знака равен 1, величина эквивалентной площади различения равна величине эквивалентной площади обнаружения (Sобн=Sрзл).
Невозможно при начертании 7-позиционных знаков устранить влияние коэффициента разрешающей способности знака на величину эквивалентной площади различения. При уменьшении величины коэффициента разрешающей способности величина эквивалентной площади обнаружения знака стремится к величине эквивалентной площади различения его. Но для уменьшения величины коэффициента разрешающей способности при формировании таких знаков необходимо увеличивать площадь «окна» между позиционными элементами. Увеличение площади «окна» приводит к увеличению формата знака.
Чтобы у каждого десятичного знака величина эквивалентной площади обнаружения (Sобн) была бы равна величине эквивалентной площади различения (Sрзл) без увеличения площади «окна», необходимо изменить начертание знаков.
Начертание контура любого десятичного знака, состоящего из точечных элементов, должно быть представлено не более чем из одной горизонтальной и одной вертикальной линии. Сокращение отображаемых линий в знаках до минимально возможного числа (подобно цифрам 1 и 7 при семипозиционном начертании - фиг.8б) приведет к улучшению их различения. Величина эквивалентной площади различения таких цифр будет равна величине эквивалентной площади обнаружения их (фиг.8в, 3 и 9 строки таблицы №6). Скорость опознания знака должна увеличиться.
Величина площади «окна» (не зачерненные точечные элементы) семипозиционного (фиг.8а) цифрового формата 3×5 является одной из составляющих частей общей площади «окна» (Sок) любого десятичного знака (обозначим ее Sок-ф). Не зачерненные точечные элементы цифрового формата осуществляют основную функцию площади «окна»: возможность различения позиционных элементов знака как по высоте, так и по ширине знака. Площадь «окна» цифрового формата (Sок-ф) разграничивает точечные элементы семипозиционного знака, расположенные по разные стороны ее. Без нее отображение семипозиционных знаков невозможно (Фиг.8а). Но именно эта часть общей площади «окна» (Sок-ф), расположенная внутри знаков, ухудшает различение их при уменьшении габаритных размеров точечных элементов и цифрового формата в целом. И чем меньше величина этой площади, чем меньше цифровой формат знаков, тем больше величина коэффициента разрешающей способности знака (Кр.с.зн). Но исключить эту часть общей площади «окна» (Sок-ф) из семипозиционного формата нельзя. Величина этой части общей площади «окна» цифрового формата (Sок-ф) из не высветившихся точечных элементов, как величина неуправляемая (пассивная) при формировании знаков, остается постоянной во всех отображаемых знаках. На эти не зачерненные точечные элементы цифрового формата при формировании десятичных знаков смена сигнала управления с гашения на высвечивание и с высвечивания на гашение не поступает.
При уменьшении величины этой площади с уменьшением габаритных размеров формата противоположно расположенные позиционные элементы знака сближаются. Увеличивается коэффициент разрешающей способности, уменьшается величина эквивалентной площади различения, восприятие знака ухудшается.
Вторая составляющая часть общей площади «окна» (Sок) образуется при формировании знака из не высветившихся точечных элементов (Sн.т.э) контура семипозиционного формата. Эта активная, управляемая часть (Sн.т.э), общей площади «окна» (Sок), каждый точечный элемент которой может быть высвечен или погашен при формировании знака из контура семипозиционного формата, в зависимости от начертания знака. При поступлении сигнала управления на высвечивание некоторой части точечных элементов семипозиционного формата формируется площадь контура знака из высветившихся точечных элементов (Sв.т.э или Sпэ - площадь позиционных элементов знака). Одновременно, из другой, оставшейся части точечных элементов цифрового формата, при поступлении сигнала управления на гашение формируется площадь «окна» из не высветившихся точечных элементов (Sн.т.э). Эта составляющая часть (Sн.т.э) общей площади «окна» (Sок) изменяет свою величину с переходом от формирования одного знака к другому в зависимости от начертания знака.
Третьей составляющей частью общей площади «окна» (Sок) является сумма площадей промежутков между точечными элементами (Sпр). Она остается постоянной и неуправляемой величиной общей площади «окна».
Таким образом, величина общей площади «окна» при формировании знака будет равна:
Sок=Sок-ф+Sн.т.э+Sпр
Для построения нового цифрового алфавита, у всех знаков которого величина эквивалентной площади обнаружения была бы равна величине эквивалентной площади различения, необходимо, прежде всего, избавиться от пассивной площади «окна» (Sок-ф) наименьшего цифрового семипозиционного формата 3×5 (не зачерненные точечные элементы - фиг.8а), расположенного внутри семипозиционного формата. Для этого на эти пассивные точечные элементы будем подавать сигналы управления на высвечивание или на гашение в зависимости от начертания того или иного знака. При смене сигнала управления (с гашения на высвечивание или с высвечивания на гашение) при формировании знаков каждый из этих точечных элементов (теперь активно управляемых) будет входить либо в площадь контура знака из высветившихся точечных элементов (Sв.т.э или Sпэ), либо в площадь «окна» из не высветившихся точечных элементов (Sн.т.э).
В этом случае величина общей площади «окна» будет состоять из величины не высветившихся точечных элементов (Sн.т.э) и из величины площади промежутков между точечными элементами (Sпр). Величина пассивной площади «окна» семипозиционного цифрового формата (Sок-ф) при формировании новых знаков заменена на эквивалентную ей активную (управляемую) величину площади «окна» из не высветившихся точечных элементов (Sн.т.э). При этом цифровой формат 3×5 (фиг.8а) принимает вид матрицы 3×5 (фиг.9а). В новом цифровом формате увеличено число активно управляемых точечных элементов с 13 до 15. Увеличение числа активных точечных элементов в цифровом формате 3×5 до формата матрицы вида 3×5 увеличило число возможных цифровых знаков, позволило создать новый цифровой алфавит десятичных чисел (фиг.9б).
В соответствии с начертанием десятичных знаков (фиг.9б), цифровым форматом которых является матрица вида 3×5, в которой все точечные элементы активны, в процессе формирования от одного знака к другому знаку на каждый точечный элемент матрицы вида 3×5 поступают сигналы управления на высвечивание и на гашение.
Контур любого десятичного знака состоит не более чем из одной вертикальной и одной горизонтальной линии из высветившихся точечных элементов. Коэффициент разрешающей способности знака у всех десятичных цифр при их начертании наименьший. У всех цифровых знаков одна и та же величина площади контура знака из высветившихся точечных элементов (Sв.т.э или Sпэ) с одним и тем же их числом, равным 7. Величина площади «окна» (Sок=Sпр+Sн.т.э), равная сумме величин площадей промежутков между точечными элементами (Sпр) и величины площади «окна» из одного и того же числа не высветившихся точечных элементов (Sн.т.э), у всех знаков одна и та же. Или площадь «окна» равна разности между величиной площади цифрового формата (Sф) и величиной площади контура знака (Sв.т.э или Sпэ) из высветившихся точечных элементов (Sок=Sф-Sпэ).
На фиг.9д, 6 строка снизу таблицы №7, приведены расчетные величины необходимых параметров цифровых знаков. Величина эквивалентной площади различения десятичных знаков (от 0 до 9) равна величине эквивалентной площади их обнаружения (Sрзл=Sобн=6.45 мм2) и в 1.7 раза превышает среднюю величину эквивалентной площади различения (Sрзл ср.=3.90 мм2) семипозиционных знаков того же формата (фиг.8в, таблица №6).
Перейти от матрицы вида 3×5 (фиг.9а) к наименьшей по числу точечных элементов матрице вида 3×3 (фиг.9в) при отображении новых цифровых знаков (фиг.9г) не вызывает никаких осложнений. Все точечные элементы матрицы вида 3×3 активно участвуют в формировании контура знака из высветившихся точечных элементов (Sв.т.э. или Sпэ) и площади «окна» из не высветившихся точечных элементов (Sн.т.э). Сигналы управления на высвечивание и на гашение в процессе формирования десятичных знаков поступают на все точечные элементы матрицы вида 3×3 (цифрового формата 3×3) в зависимости от их начертания. Формат матрицы вида 3×5 уменьшен до формата 3×3, т.е. уменьшен по высоте в 1.7 раза. Если средняя величина эквивалентной площади различения на цифру (Sрзл ср.) при формировании семипозиционных знаков и цифровом формате 3×5 равна 3.90 мм2 (фиг.8в), то средняя величина эквивалентной площади различения на цифру у цифрового алфавита с постоянным числом точечных элементов в знаке при цифровом формате 3×3 почти такая же и равна 3.80 мм2 (фиг.9д, таблица №7, 6 строка снизу, колонка 10). Причем эта величина (Sрзл=3.81 мм2) постоянна при начертании каждой цифры, имеющей постоянное число (n=5) точечных элементов в любом десятичном знаке. Постоянное число точечных в знаках при данном формате уменьшает неравномерность яркости свечения знаков и неравномерность энергопотребления в знаках, тогда как при начертании семипозиционных цифр эта величина (Sрзл ср.) находится в границах 2.11 мм2 - 6.04 мм2 (фиг. 8в, таблица №:6, столбец 10). Одни знаки различимы хорошо (цифра 1 и 7), а другие совсем плохо (цифра 8, 9, 6 и 0). Величина эквивалентной площади различения у них колеблется от 2.11 мм2 до 3.00 мм2. Опознать такие цифры уже затруднительно.
Величину эквивалентной площади различения новых десятичных цифр от 0 до 9 с постоянным числом точечных элементов в знаках можно увеличить до максимального значения (Sрзл=Sф:4=15.60:4=3.90 мм2). Для этого необходимо уменьшить величину промежутка (t) между точечными элементами до 0.10 мм и увеличить формат точечного элемента до 1.25×1.25 мм2, сохранив габаритный размер (Sф=15.60 мм2) цифрового формата (фиг.9д, таблица №7, 5 строка снизу, колонка 10).
При этом величина площади позиционных элементов (Sпэ) равна площади «окна» (Sок).
Если некоторые начертания семипозиционных знаков (фиг.8б - цифры 0, 6, 9) и позволяют достигнуть почти максимальной величины эквивалентной площади обнаружения их (Sобн=6.43 мм2 и почти равна значению Sф : 4=26.6:4=6.65 мм2), то из-за коэффициента разрешающей способности у этих знаков величина эквивалентной площади различения (Sрзл=3.00 мм2) у них значительно ниже максимальной для рассматриваемого формата (фиг.8в, таблица №6 - 10, 4 и 1 строки снизу соответственно).
При уменьшении промежутка между точечными элементами в семипозиционном формате величина эквивалентной площади различения знаков еще более уменьшится из-за увеличения коэффициента разрешающей способности их.
Таким образом, при изменении привычного семипозиционного начертания десятичных знаков (фиг.8б), при котором площадь «окна» знака (Sок-ф + Sн.т.э) ограничена позиционными элементами (особенно явно это видно у цифры 8) и расположена внутри знака, при начертании новых знаков площадь «окна» (Sн.т.э) из не высветившихся точечных элементов расположена (особенно явно это видно у новой цифры 0) по отношению к вертикальной и горизонтальной линиям контура знака (фиг.9г) снаружи знака. При формировании любого другого десятичного знака нового алфавита площадь «окна» из не высветившихся точечных элементов (Sн.т.э) не ограничена с двух сторон вертикальными или горизонтальными линиями контура знака, т.е. не расположена между ними. Она расположена снаружи контура знака, а контур знака расположен внутри площади «окна» из не высветившихся точечных элементов (Sн.т.э).
Это хорошо видно, если сформировать знаки на информационном поле большего формата, чем их формат (фиг.9е). В этом случае площадь «окна» не влияет на величину коэффициента разрешающей способности знака.
Обычно при масштабировании семипозиционных знаков, с переходом, например, от цифрового формата 3×5 (фиг.8а) к цифровому формату 5×7 (фиг.10и), увеличивается ширина и высота цифрового формата. Толщина контура знака (s) при формировании знаков не изменяется. При этом величина средней эквивалентной площади различения при формировании знаков увеличивается менее чем в три раза (при увеличенной площади цифрового формата и уменьшенным коэффициентом разрешающей способности знаков) с 3.90 мм2 до 10.48 мм2 (фиг.8в, таблица №6 и фиг.10л, таблица №8 соответственно).
Габаритные размеры информационного поля индикатора МЭЛ-1 (27×160) позволяют увеличить динамический диапазон изменения величины эквивалентной площади различения при формировании новых знаков:
1. за счет использования наименьшего цифрового формата 3×3;
2. за счет наименьшего коэффициента разрешающей способности при начертании новых знаков;
3. за счет толщины контура знака.
Величина эквивалентной площади различения знаков при масштабировании их с переходом от цифрового формата 3×3 (фиг.9в) к цифровому формату 9×9 (фиг.9ж) увеличивается пропорционально увеличению числа точечных элементов по высоте и по ширине цифрового формата и пропорционально увеличению толщины контура знака, равной ширине предыдущего цифрового формата 3×3. При таком масштабировании ширина и высота каждого позиционного элемента цифрового формата 9×9 равна ширине и высоте цифрового формата 3×3. Величина эквивалентной площади различения (Sрзл) увеличилась более чем в 9 раз (с 3.81 мм2 до 36.26 мм2) пропорционально увеличению габаритного размера цифрового формата и пропорционально толщине контура знака (фиг.9г, фиг.9ж, фиг.9д, таблица №7, строки 6 и 4 снизу соответственно, колонка 10).
Величина эквивалентной площади различения знаков при масштабировании их с переходом от цифрового формата 3×3 (фиг.9г - цифра 0) к цифровому формату 9×9 (фиг.9з) без изменения контура знака увеличивается только пропорционально увеличению числа точечных элементов по высоте и по ширине цифрового формата. Величина эквивалентной площади различения (Sрзл) увеличилась в этом случае только в 5 раз (с 3.81 мм2 до 19.14 мм2 - фиг.9г, фиг.9з, фиг.9д, таблица №7, строки 6 и 2 снизу соответственно, колонка 10).
Формирование любого десятичного знака с увеличенной толщиной контура его позволяет выявлять децимальную точку на знаке погашением точечного элемента, расположенного в центре каждого позиционного элемента его (фиг.9и). Величина эквивалентной площади различения знака в этом случае уменьшается с 36.26 мм2 до 34.52 мм2 (фиг.9д, 4 и 3 строки соответственно, колонка 10, таблицы №7). При формировании многозначного числа децимальная точка выявляется на последнем знаке целого числа, после которого формируется дробная его часть.
Для увеличения диапазона изменения величины эквивалентной площади различения знака можно воспользоваться формированием знака с помощью одного лишь точечного элемента, расположенного в центре каждого позиционного элемента знака (фиг.9к, фиг.9д, таблица №7, 1 строка снизу). Величина эквивалентной площади различения знака значительно уменьшена (Sрзл=6.31 мм2). Диапазон изменения величины эквивалентной площади различения знака увеличен.
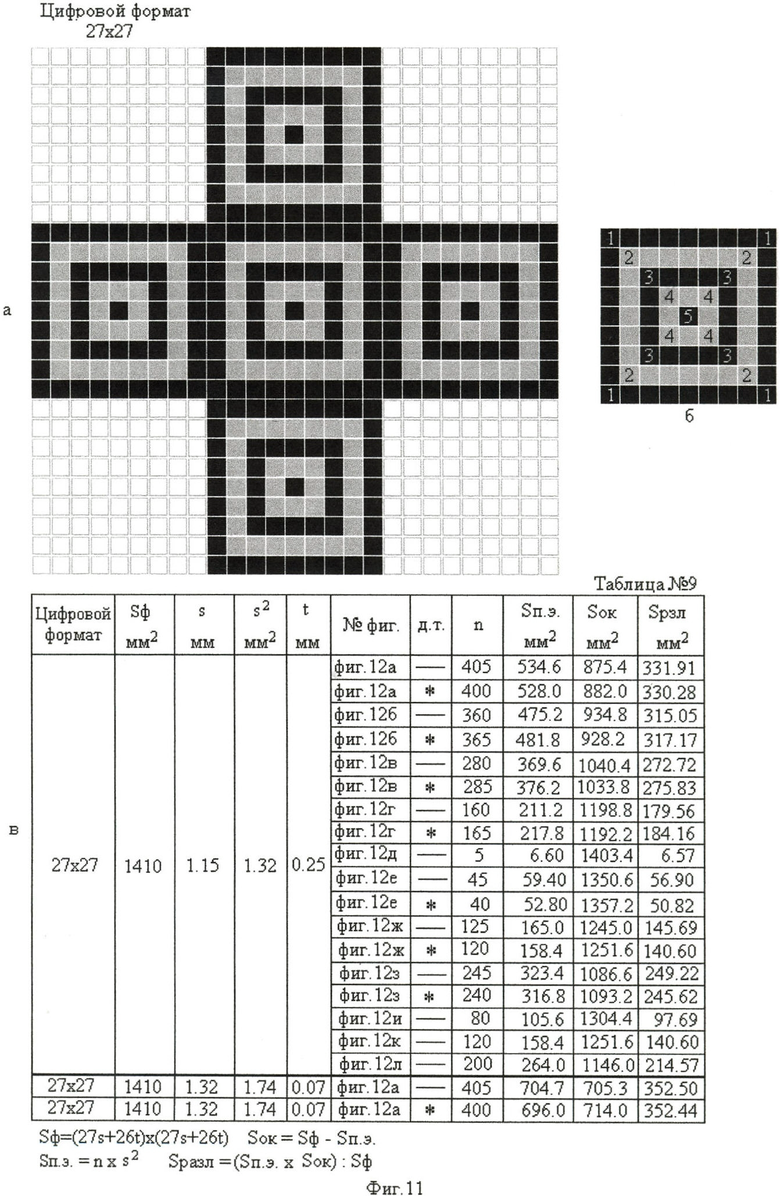
Величина эквивалентной площади различения (Sрзл) знаков при масштабировании их с переходом от цифрового формата 9×9 (фиг.9ж) к цифровому формату 27×27 (фиг.11а), с одновременным увеличением толщины контура знака, равной цифровому формату (9×9), возрастает более чем в 9 раз (с 36.26 мм2 до 331.91 мм2 - фиг.9д, таблица №7, строка 4 снизу, колонка 10 и фиг.11в, таблица №9, 20 строка снизу, колонка 11 соответственно). Число всех высветившихся точечных элементов при формировании 5 позиционных элементов любого десятичного знака (фиг.11а) равно: n=9×9×5=405 (9×9=81 - фиг.12а для одного позиционного элемента). Увеличение эквивалентной площади различения пропорционально увеличению габаритного размера цифрового формата и пропорционально толщине контура знака. Величина эквивалентной площади различения знака максимальна при всех высветившихся точечных элементах его. Причем для каждого десятичного знака от 0 до 9, при использовании конкретного цифрового формата, величина эквивалентной площади различения одна и та же.
Изменяя число высветившихся точечных элементов знака, можно регулировать величину эквивалентной площади различения его в широких пределах. Для этого представляем формат (9×9) каждого позиционного элемента знака, содержащий набор из пяти (1-5) независимо управляемых контуров форматов (фиг.11б), составляющих его площадь. Толщина контура любого формата (1-5) соответствует одному точечному элементу. Число точечных элементов (n) в контуре каждого из таких форматов соответственно (фиг.11б) равно:
1. n=32 - в контуре первого формата 9×9;
2. n=24 - в контуре второго формата 7×7;
3. n=16 - в контуре третьего формата 5×5;
4. n=8 - в контуре четвертого формата 3×3;
5. n=1 - в контуре пятого формата 1×1.
Таким образом, при формировании знака независимо управляемые контуры форматов высвечиваются или погашаются в различных комбинациях, изменяя толщину и габаритный размер формата позиционного элемента, и величину эквивалентной площади различения знака (фиг.12).
При не высвечивании, например, только контура 5-го формата 1×1 (фиг.12а), расположенного в центре каждого позиционного элемента (слабо зачерненный точечный элемент) число точечных элементов знака на пяти позиционных элементах его уменьшится на 5 (1×5). Величина эквивалентной площади различения при числе точечных элементов (n=400) в знаке уменьшится (фиг.11в, таблица №9, 19 строка снизу).
Уменьшение величины эквивалентной площади различения знака выявится в виде не высветившегося точечного элемента на каждом позиционном элементе. Этот не высветившийся точечный элемент на фоне остальных высветившихся элементов (фиг.12а) можно использовать как децимальную точку при формировании знака.
При не высвечивании одновременно контуров 5-го и 4-го форматов в центре каждого позиционного элемента (фиг.12б) число точечных элементов знака на пяти позиционных элементах его уменьшится на 45 (n=9×5) с 400 до 365. Величина эквивалентной площади различения знака уменьшится (фиг. 11в, таблица №9, 18 строка снизу). Точечный элемент (слабо затемненный) при формировании знака без децимальной точки не высвечивается.
При формировании знака с децимальной точкой этот точечный элемент высветится на всех пяти позиционных элементах знака (фиг.12б). Величина эквивалентной площади различения знака увеличится (фиг.11в, таблица №9, 17 строка снизу). Увеличение эквивалентной площади различения знака при высвечивании точечного элемента 5-го формата на фоне не высветившихся точечных элементов контура 4-го формата, расположенных в непосредственной близости от него, можно использовать как децимальную точку при формировании знака.
Таким образом, децимальную точку на каждом позиционном элементе знака можно выявить как погашением точечного элемента контура, состоящего из одного точечного элемента 5-го формата (фиг.12а, фиг.12е-2з), расположенного в центре каждого позиционного элемента знака, так и его высвечиванием (фиг.12б-фиг.12г, фиг 12. и - фиг.12л). Это зависит от того, высвечены точечные элементы контура 4-го формата, расположенные в непосредственной близости от него, или они погашены.
На фиг.12 представлены варианты (фиг.12а-фиг.12л) на примере одного из пяти позиционных элементов знака, формируемых при изменении числа высветившихся точечных элементов, изменяющих величину эквивалентной площади различения знака. При формировании знака независимо управляемые контуры форматов, из которых состоит каждый позиционный элемент его, высвечиваются или погашаются в различных комбинациях, изменяя толщину и габаритный размер позиционного элемента, и величину эквивалентной площади различения знака. Кодирование пространственной ориентацией /5 - стр.62/ или кодирование утолщением и габаритным размером каждого позиционного элемента знака приводит к заметному отличию одного варианта визуального отображения цифровых знаков от другого варианта. Все необходимые формулы для расчета параметров знака приведены на фиг.11. Исходные данные и результаты вычислений в соответствии с фиг.12а-фиг.12л занесены в таблицу №9, фиг.11в для цифровых знаков от 0 до 9.
Величина эквивалентной площади различения знака изменяется в пределах от Sрзл=331.91 мм2 (фиг.12а-фиг.11в, таблица №9, строка 20 снизу) до Sрзл=56.90 мм2 (фиг.12е-фиг.11в, таблица №9, строка 11 снизу).
На фиг.12д показан пример возможности формирования знака с наименьшей величиной эквивалентной площади различения (Sрзл=6.57 мм2 - фиг.12д, фиг.11в, таблица №9, 12 строка снизу) знака, когда на каждом позиционном элементе знака высвечивается один лишь точечный элемент в центре его.
С уменьшением промежутка между точечными элементами индикатора до t=0.07 мм и одновременным увеличением линейного размера точечного элемента до s=1.32 мм, при сохранении габаритного размера цифрового формата Sф=1410 мм2 можно достичь максимального значения величины эквивалентной площади различения знака, когда на каждом позиционном элементе знака высвечиваются все точечные элементы.
Максимальное значение величины эквивалентной площади различения определяется по формуле: Sрзл макс=Sф:4=1410 мм2:4=352.50 мм2 (фиг.11в, таблица №9, 2 строка снизу) и определено на основании формул, представленных на фиг.11. При выявлении децимальной точки, погашением точечного элемента в центре каждого позиционного элемента знака, величина эквивалентной площади уменьшается (фиг.11в, таблица №9, 1 строка снизу).
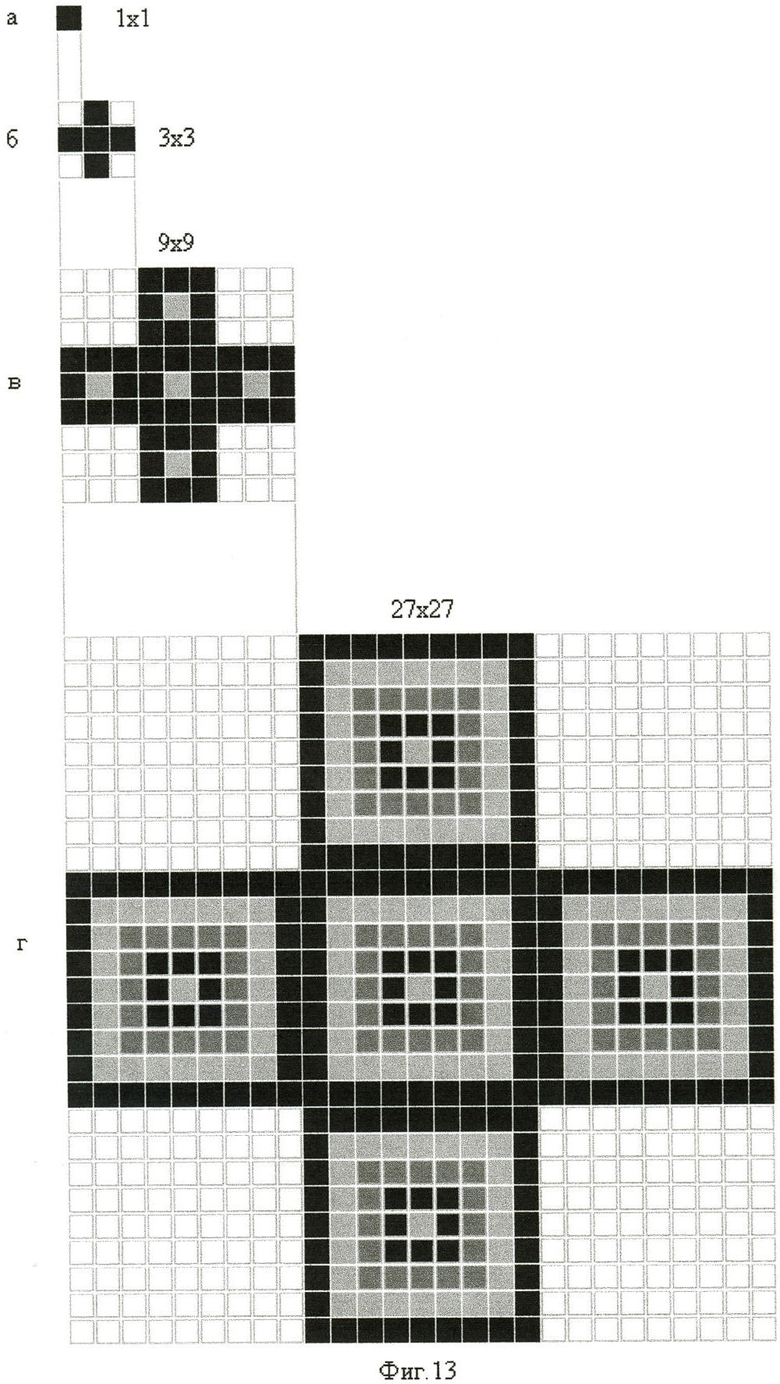
Наглядная демонстрация формирования знаков при масштабировании их в сторону увеличения в пределах заданного цифрового формата, допускаемого форматом информационного поля индикатора, показана на фиг.13. Ширина и высота позиционного элемента каждого последующего по величине габаритного размера цифрового формата последовательно увеличивается пропорционально ширине и высоте цифрового формата предыдущего по величине габаритного размера цифрового формата.
Величина эквивалентной площади различения знаков также увеличивается пропорционально увеличению габаритного размера цифрового формата и толщине контура знака, равной ширине предыдущего по величине габаритного размера цифрового формата.
С возрастанием цифрового формата возрастают его функциональные возможности. Если при наименьшем цифровом формате 1×1 (фиг.13а) возможно сформировать только два знака: соответствующие двум числам 0 и 1 (не высвечивается или высвечивается точечный элемент), то на цифровом формате 3×3 (фиг.13б) формируются уже десять цифровых знаков, соответствующих числам от 0 до 9. Децимальная точка формируется рядом со знаком. Величина эквивалентной площади различения каждого десятичного знака равна Sрзл=3.81 мм2.
На цифровом формате 9×9 (фиг.13в) формируются десять цифровых знаков, соответствующих числам от 0 до 9, с возможностью формирования децимальной точки, выявляемой погашением точечного элемента, расположенного в центре каждого позиционного элемента знака.
На цифровом формате 27×27 (фиг.11а) формируются цифровые знаки:
1. в режиме (фиг.12а), в котором используются все точечные элементы каждого из пяти позиционных элементов (n=9×9×5=405) при формировании каждого из десяти цифровых знаков, соответствующих числам от 0 до 9, и децимальная точка, выявляемая погашением точечного элемента, расположенного в центре каждого позиционного элемента знака (фиг.12а). В этом режиме, без отображения децимальной точки, величина эквивалентной площади различения знака максимальна;
2. в режиме (фиг.12б-фиг.12л), в котором при формировании десяти цифровых знаков, соответствующих числам от 0 до 9, погашаются или высвечиваются в различной комбинации контуры форматов (1-5) каждого позиционного элемента знака. Формирование знаков с изменяющимся числом точечных элементов в знаках (с изменяющейся величиной эквивалентной площади различения их) преследует следующие цели: 1. экономию энергопотребления; 2. слежение за изменением измеряемого параметра объекта за пределы рабочего режима (в системах автоматического регулирования). На контролируемом объекте может создаваться аварийная ситуация либо при увеличении, либо при уменьшении измеряемой величины параметра объекта.
Источники информации
1. Н.И.Вуколов, А.Н.Михайлов. Знакосинтезирующие индикаторы. Справочник. М.: Радио и связь, 1987.
2. Печников А.В., Сидоренко Г.В., Федорова С.А. Средства передачи и отображения информации. М.: Радио и связь, 1991.
3. Патент №2037886 на изобретение «Устройство для индикации» выдан 19 июня 1995 года. Приоритет изобретения 19 февраля 1992 года. Заявка №5037630. Автор Патраль А.В.
4. Алиев Т.М., Вигдоров Д.И. Кривошеев В.П. Системы отображения информации. М.: Высшая школа, 1988.
5. Б.Л. Лисицын. Отечественные приборы индикации и их зарубежные аналоги. М.: Радио и связь, 1993.

Изобретение относится к средствам отображения цифровой информации. Технический результат заключается в уменьшении неравномерности энергопотребления от знака к знаку за счет обеспечения равной величины площади высветившихся точечных элементов знака. В матричном индикаторе позиционные элементы цифрового формата распределены на контуры форматов 9×9, 7×7, 5×5, 3×3, 1×1, высвечивание или погашение которых вызывают изменение числа точечных элементов в них, сохраняя при форматировании цифровых знаков от 0 до 9 постоянство числа точечных элементов в них, соответствующее измененному числу высвеченных точечных элементов в контурах форматов, а децимальная точка выявляется на знаке либо погашением, либо высвечиванием контура формата 1×1 в зависимости от того, высвечен или погашен он при формировании знаков. 13 ил.
Индикатор матричный с регулируемой эквивалентной площадью различения цифровых знаков, оформленный в металлостеклянный корпус с четырьмя розетками типа РП15-50ГВ, расположенными с обратной стороны корпуса, на лицевой стороне которого расположена электролюминесцентная матрица вида 27×160 с габаритными размерами элементов отображения 1,32×1,32 мм и расстояниями между ними 0,07 мм, предназначен для отображения информации в виде букв, символов, графиков, семипозиционных и цифровых знаков от 0 до 9 с постоянным числом точечных элементов в них в формате 27×27 и децимальной точки, отличающийся тем, что позиционные элементы цифрового формата распределены на контуры форматов 9×9, 7×7, 5×5, 3×3, 1×1, высвечивание или погашение которых вызывают изменение числа точечных элементов в них, сохраняя при форматировании цифровых знаков от 0 до 9 постоянство числа точечных элементов в них, соответствующие измененному числу высвеченных точечных элементов в контурах форматов, а децимальная точка выявляется на знаке либо погашением, либо высвечиванием контура формата 1×1 в зависимости от того высвечен или погашен он при формирование знаков.
| ИНДИКАТОР ЦИФРОВОЙ СЕГМЕНТНЫЙ С МАСШТАБИРОВАНИЕМ ЗНАКА | 2005 |
|
RU2302042C1 |
| US 6055461, 25.04.2000 | |||
| JP 56044887 A, 24.04.1981 | |||
| JP 56043577 A, 22.04.1981 | |||
| ЛИСИЦЫН Б.Л | |||
| Отечественные приборы индикации и их зарубежные аналоги | |||
| - М.: Радио и связь, 1993, с.382-384, 305-307 | |||
| ЕРМАКОВ О.Н | |||
| Полупроводниковые знакосинтезирующие индикаторы, Радио и связь, 1993, с.21. | |||
Авторы
Даты
2011-06-27—Публикация
2009-02-24—Подача