Предлагаемое изобретение относится к средствам отображения информации (СОИ), значительную область применения которых представляют устройства для индикации.
Устройство для индикации с наилучшей идентификацией знаков может найти применение во всех средствах отображения информации, в которых требуется уменьшение габаритных размеров цифровых знаков индикатора без ухудшения восприятия их и повышенное обеспечение помехозащищенности знаков при их формировании.
Устройства для индикации с применением матричных и сегментных индикаторов позволяют в синтезированном виде высветить сложную информацию в виде букв русского и латинского алфавита, символов и цифровых знаков от 0 до 9. И наибольший объем информации в различных устройствах вычислительной и измерительной техники приходится на цифровую индикацию.
Недостаток устройств индикации с применением сегментных и матричных индикаторов при формировании цифровых знаков заключается в неодинаковом и большом числе визуально воспринимаемых элементов отображения. Это приводит к неодинаковой разрешающей способности начертания знаков при их формировании, к неодинаковому восприятию их на стадиях обнаружения, различения и идентификации. К тому же в устройствах для индикации с применением семисегментных и матричных индикаторов, особенно с небольшим числом элементов отображения в знаках, невысокая помехозащищенность их. Стремление достигнуть наилучшего восприятия знаков при итаблица х формировании, приводит к непривычности начертания знаков, которое должно быть оправдано целью предлагаемого изобретения.
Целью предлагаемого изобретения является:
1) уменьшение габаритных размеров знаков;
2) улучшение параметрических характеристик цифровых знаков:
а) увеличение разрешающей способности знаков;
б) улучшение восприятия знаков на стадиях обнаружения, различения и идентификации;
3) повышение помехозащищенности цифровых знаков при их формировании;
4) увеличение информационной емкости индикатора.
Указанная цель достигается формированием на информационном поле индикатора цифровых знаков, кодированных формой и пространственной ориентацией их.
Уменьшение цифрового формата знака в устройстве для индикации с наилучшей идентификацией знаков можно продемонстрировать, взяв для сравнения формирование знаков на матричном индикаторе КИПГО2А-8×8Л с видом матрицы 8×8 /1 - стр.353/ цифровых знаков на основе арабского алфавита в наименьшем формате их 3×5 (фиг.1а, фиг.1б).
Для каждого отображаемого знака (фиг.1б) цифрового формата с видом матрицы 3×5 (фиг.1а) определяем и заносим в таблицу №1 (фиг.1в):
1) величину площади высветившихся (позиционных) элементов отображения в знаке (Sпэ), равную величине площади (s×s) одного элемента отображения, умноженной на количество элементов отображения (n) в сформированном знаке (Sп.э.=s2×n). Величина площади элемента отображения данного индикатора (для простоты начертания и расчета элемент отображения принят квадратным со сторонами, равными диаметру его /1 - стр.355/) равна:
s2=(s×s)=0.95 мм × 0.95 мм=0.9025 мм2;
2) величину площади цифрового формата (Sф), равную (фиг.1г)
Sф=L×Н=(3s+2t)×(5s+4t),
где L=(3s+2t) - ширина цифрового формата, Н=(5s+4t) - высота цифрового формата;
s - ширина (высота) элемента отображения (0.95 мм);
t - промежуток между элементами отображения, равный 0.3 мм как по ширине, так и по высоте знака;
Sф=(3s+2t)×(5s+4t)=(0.95×3+0.3×2)×(0.95×5+0.3×4)=20.53 мм2;
3) величину площади «окна» (Sок), равную величине площади цифрового формата (знака) (Sф) за вычетом величины площади позиционных (высветившихся) элементов отображения знака (Sп.э.):
Sок=Sф-Sп.э.
Обнаружение - стадия восприятия, на которой оператор выделяет объект из фона. При этом устанавливается лишь наличие сигнала в поле зрения без оценки его формы и признаков /2 - стр.46/. На первой стадии восприятия знака, при обнаружении, оператор выделяет общую площадь, занимаемую элементами отображения на фоне площади «окна» его;
4) величину эквивалентной площади обнаружения (Sобн) знака, определяемую по формуле /3/:
Sобн=(Sпэ×Sок):(Sпэ+Sок).
Способность средств отображения информации воспроизводить мелкие детали характеризуется их разрешающей способностью.
Разрешающую способность начертания знаков индикатора можно оценивать по возможности различения оператором двух воспроизводимых световых точек или линий, находящихся на некотором расстоянии друг от друга. При низкой разрешающей способности оператор принимает две точки (линии) за одну, а при высокой разрешающей способности две очень близкие точки (линии) воспринимаются как отдельные. Повышать разрешающую способность начертания знаков можно до определенного предела, свыше которого изображение не будет восприниматься глазом /4 - стр.115/;
5) величины коэффициентов разрешающей способности знаков (фиг.1г):
а. величину коэффициента разрешающей способности по ширине для знаков 0 и 8, равную:
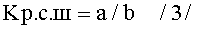 ,
,
где а=2s+2t и b=s+2t (фиг.1г) - линейный размер точечного элемента s=0.95 мм, расстояние между элементами отображения t=0.3 мм
Kр.с.ш.=a/b=(2s+2t):(s+2t)=(2×0.95+2×0.3):(0.95+2×0.3)=2.50:1.55=1.61 (фиг.1в, таблица №1, 10 и 2 строки снизу, колонка 7);
б) величину коэффициентов разрешающей способности по ширине знака для цифр 1, 2, 3, 5 и 7 (фиг.1б). У этих знаков отсутствуют элементы отображения (эти элементы отображения на фиг.1г, например, для цифры 3 осветлены), относительно которых определяется коэффициент разрешающей способности по ширине знака (Kр.с.ш=a/b).
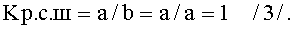
В этом случае измеряется расстояние (а) от элемента отображения, расположенного справа (например, второй снизу), до границы знака (фиг.1 г) и измеряется то же расстояние от этого же элемента отображения также до границы знака (b=a), при отсутствии второго элемента отображения, расположенного слева (второй снизу) в начертании знака. Отсутствие второго элемента отображения, расположенного слева (второй снизу) в начертании знака, эквивалентно расположению второго элемента отображения, расположенного слева (второй снизу) на достаточно большом расстоянии, не оказывающем влияние на различение элемента отображения, расположенного справа (второй снизу). И коэффициент разрешающей способности в этом случае будет равен Kр.с.ш=1;
в) величину коэффициентов разрешающей способности по ширине знака для цифр 4, 9 и 6, у которых отсутствует элемент отображения расположенный, слева в нижней половине (цифры 4 и 9) знака и расположенный справа в верхней половине (цифра 6) знака (фиг.1 г); для цифр 4 и 9 /3/:
во-первых, измеряется суммарное расстояние (a+a) от элемента отображения, расположенного справа (второй снизу), и от элемента отображения, расположенного справа (второй сверху) в начертании знака, до границ знака в нижней и верхней половинах его;
во-вторых, измеряется суммарное расстояние (a+b) от элемента отображения, расположенного справа (второй снизу), до границы знака (а), при отсутствии элемента отображения, расположенного слева в нижней половине (второй снизу) знака, и от элемента отображения, расположенного справа (второй сверху), до элемента отображения (b), расположенного слева (второй сверху), при его наличии.
Коэффициент разрешающей способности по ширине знака вычисляется по формуле /3/:
Kр.с.ш=(a+a):(b+a), где а=2s+2t и b=s+2t
Kр.c.ш=2(2s+2t):(s+2t+2s+2t)=2(2×0.95+2×0.3):(0.95+2×0.3+2×0.95+2×0.3)=5.00:4.05=1.23 (фиг.1в, таблица №1, 6 и 1 строки снизу, соответственно, колонка 7).
Подобным же образом определяется величина коэффициента разрешающей способности по ширине знака для цифры 6, ее величина также будет равна (Kр.с.ш.=1.23 - фиг.1в, таблица №1, 4 строка снизу, колонка 7);
г) величину коэффициентов разрешающей способности по высоте для знаков 2, 3, 5, 6, 8 и 9 (фиг.1б) определяем по формуле: 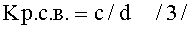 ,
,
где с=2s+2t и d=s+2t (фиг.1г).
Kр.c.в=(2s+2t):(s+2t)=(2×0.95+2×0.3):(0.95+2×0.3)=2.50:1.55=1.61 (фиг.1в, таблица №1, 8, 7, 5, 4, 2, 1 строки снизу, колонка 8);
д) величину коэффициента разрешающей способности по высоте для знака 0:
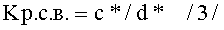 .
.
где с*=4s+4t и d*=3s+4t (фиг.1 г).
Kр.c.в=(4s+4t):(3s+4t)=(4×0.95+4×0.3):(3×0.95+4×0.3)=5.00:4.05=1.23 (фиг.1в, таблица №1,10 строка снизу, колонка 8);
е) величину коэффициентов разрешающей способности по высоте для знаков 4 и 7:
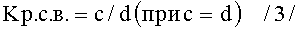 ;
;
ж) величину коэффициентов разрешающей способности по высоте для знака 1 /3/:
Kр.с.в=1 (у этого знака нет горизонтально расположенных элементов отображения).
Величина коэффициента разрешающей способности знака равна произведению величины коэффициента разрешающей способности по ширине знака на величину коэффициента разрешающей способности по высоте знака:
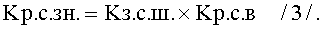
Величины коэффициентов разрешающей способности знака занесены в таблицу №1 (фиг.1в, колонка 9).
Различение - стадия восприятия, на которой оператор способен выделить детали, высветившиеся элементы отображения знака /2 - стр.46/ на фоне площади «окна» знака;
6) величину эквивалентной площади различения (Sрзл) знака (фиг.1в, таблица №1, колонка 10).
Чтобы количественно оценить величину эквивалентной площади различения знака, необходимо связать величину эквивалентной площадью обнаружения знака и разрешающую способность его. Величина эквивалентной площади различения знака (Sрзл) равна частному от деления величины эквивалентной площади обнаружения знака на величину коэффициента разрешающей способности его по формуле:
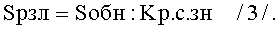
Величина эквивалентной площади различения знака (Sрзл) меньше величины эквивалентной площади обнаружения его (Sобн) на величину коэффициента разрешающей способности знака (Kр.с.зн).
Средняя величина эквивалентной площади различения на знак при начертании знаков на основе матричного цифрового формата 3×5 равна 3.11 мм2:
Sрзл.ср.=3.11 мм2.
Идентификация - стадия восприятия /2, стр.46/, на которой оператор отождествляет объект с эталоном, хранящимся в памяти (или отождествляет два одновременно воспринимаемых объекта);
7) величину эквивалентной площади идентификации (Sидн) знака (фиг.1в, таблица №1, колонка 12).
Величина эквивалентной площади идентификации знака равна частному от деления величины эквивалентной площади различения знака на величину коэффициента идентификации его (Kидн):
Sидн=Sрзл/Kидн.
Определение коэффициента идентификации знака.
При отображении привычных цифровых знаков на основе арабского алфавита используется цифровой формат, представленный цифрой 8 в формате матрицы вида 3×5 (фиг.1а). Изменение общего для всех знаков замкнутого контура цифрового формата за счет погашения соответствующих элементов отображения его, образуется ряд цифровых знаков (0, 1, 2, 3, 4, 5, 6, 7 и 9) с разомкнутым в разных местах контуром цифры 8 (фиг.1б).
Замкнутый контур цифрового формата, представленный цифрой, 8 всякий раз разрывается при формировании этих знаков. А при идентификации того или иного высвеченного цифрового знака необходимо визуально различить изменение в различных по расположению местах замкнутого контура и соотносить это изменение с тем или иным знаком. Это вызывает трудности восприятия знаков на стадии идентификации, увеличивает время ее.
Кроме того, у цифровых знаков на основе арабского алфавита с видом матрицы 3×5 неодинаковая величина площади высветившихся элементов отображения, неодинаковая величина коэффициента разрешающей способности, неодинаковое количество высветившихся элементов отображения (фиг.1б, фиг.1в, таблица №1).
Различие величины площади высветившихся элементов отображения в знаках при изменяющейся величине площади «окна» в них не позволяет получить одинаковую и максимальную величину эквивалентной площади обнаружения в знаках. Постоянная площадь «окна» цифрового формата с видом матрицы 3×5 (фиг.1а), представленная двумя точечными элементами (светлый фон), разделяющая по вертикали и по горизонтали линии контура знака приводит к увеличению коэффициента разрешающей способности знака при его начертании, к затруднению восприятия знака на стадии различения. Различие величины коэффициента разрешающей способности у знаков (Kр.с.зн), определяемой начертаниями их, не позволяет получить одинаковую, а тем более, максимальную величину эквивалентной площади различения знака у цифр такого алфавита. А изменяющееся число высветившихся элементов отображения в контурах знаков цифрового формата затрудняет получить одинаковую и максимальную величину эквивалентной площади идентификации знака (фиг.1в, таблица №1).
Величина коэффициента идентификации знака определяет число визуально отличительных признаков при начертании его. При формировании цифровых знаков визуально отличительными признаками их являются элементы отображения (их число и расположение). Однако, идентифицировать знаки, формируемые на матричных индикаторах с большим числом элементов отображения затруднительно. Идентифицировать с большой достоверностью знаки можно по совокупному числу элементов отображения, приходящихся на горизонтальные и вертикальные линии при их начертании.
Так, например, цифра 1, представленная при формировании ее одной вертикальной линией из элементов отображения, легко идентифицируется при формировании знака и без подсчета числа высветившихся элементов отображения, вследствие привычности ее начертания. В этом случае величина коэффициента идентификации знака равна не 5 (по числу отличительных признаков, равных числу элементов отображения), а по совокупному числу элементов отображения, представляющих одну вертикальную линию (Kидн=1). При идентификации, например, цифры 9, представленной тремя горизонтальными и двумя вертикальными (справа из пяти элементов отображения и слева из трех элементов отображения) линиями из элементов отображения, величина коэффициента идентификации будет равен 5 (по числу отличительных признаков при начертании знака), вследствие привычности начертания знака.
Для каждого из цифровых знаков величина коэффициента идентификации (Kидн) и величина эквивалентной площади идентификации (Sидн) сведены в таблицу №1, колонки 11 и 12 (фиг.1в), соответственно. Средняя величина эквивалентной площади идентификации на знак у знаков формата с видом матрицы 3х5 равна 1.10 мм2 (и никак не больше того); Sидн=1.10 мм2.
Для улучшения восприятия знаков на стадии идентификации, для уменьшения коэффициента идентификации их, необходимо уменьшать число визуально отличительных признаков при начертании их.
Такие цифровые знаки с постоянным числом высветившихся элементов отображения и с коэффициентом разрешающей способности, равным 1 (Kр.с.зн.=1), представлены на фиг.2 в формате 5×7 /3, фиг.11/.
Параметры знаков при их формировании с постоянным числом высветившихся точечных элементов в них в формате 5×7 показаны на фиг.2 /3, фиг.11м/, без учета промежутков между элементами отображения:
а. число (n) высветившихся (позиционных) элементов отображения в знаке равно 11;
б. коэффициент разрешающей способности знака минимален и равен 1 (Kр.с.зн.=1);
в. величина высветившихся (позиционных) элементов отображения (Sп.э.) равна 11 мм2, при размере элемента отображения 1.0 мм × 1.0 мм (Sп.э.=11 мм2);
г.величина площади «окна» знака (Sок) из невысветившихся элементов отображения равна 24 мм2 (Sок=24 мм2);
д. величина эквивалентной площади различения (Sрзл) знака равна величине эквивалентной площади обнаружения (Sобн) его и равна
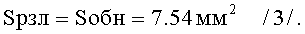
Равенство величин эквивалентной площади обнаружения и эквивалентной площади различения (Sобн=Sрзл) показывает, что две стадии восприятия знака - обнаружение и различение сливаются в одну стадию, на которой оператор выделяет элементы знака. Время опознания знака уменьшается.
Число визуально отличительных признаков при начертании этих знаков, содержащих только по одной горизонтальной и одной вертикальной линии, равно 2, т.е. величина коэффициента идентификации при их начертании равна 2 (Kидн=2).
Величина эквивалентной площади идентификации знака будет равна:
Sидн=Sрзл: Kидн=7.54 мм2:2=3.77 мм2, при цифровом формате с видом матрицы 5×7.
Перейти от цифрового формата с видом матрицы 5×7 (фиг.2) к цифровому формату с видом матрицы 3×3 (фиг.1е) с уменьшенным числом элементов отображения при формировании цифровых знаков на информационном поле матричного индикатора КИПГ02А-8×8Л с видом матрицы 8×8 не вызывает никаких осложнений. Сигналы управления на высвечивание и на гашение в процессе формирования цифровых знаков поступают на все элементы отображения матрицы вида 3×3 (цифрового формата 3×3). Из высветившихся (позиционных) элементов отображения формируется величина площади (Sп.э.) контура знака, а из оставшихся невысветившихся элементов отображения формируется величина площади (Sок) «окна» его. Величина площади цифрового формата равна:
Sф=(3s+2t)×(3s+2t)=(0.95×3+0.3×2)×(0.95×3+0.3×2)=11.90 мм2,
где s=0.95 мм -линейный размер элемента отображения по горизонтали и вертикали.
Величина площади пяти высветившихся элементов (Sп.э.) равна:
Sп.э.=5(s×s)=4.5 мм2 (фиг.1ж, таблица №2, строка 2 снизу).
Величина площади «окна» равна разности между величиной площади цифрового формата (Sф) и величиной площади контура знака (Sп.э.=45 мм2) из высветившихся элементов отображения (Sок=Sф-Sп.э.=7.40 мм2).
Величина эквивалентной площади обнаружения знака равна:
Sобн=(Sпэ×Sок):(Sпэ+Sок)=(4.5 мм2 × 7.4 мм2): 11.90 мм2=2.80 мм2.
При формировании цифрового знака площадь «окна» (Sок) из невысветившихся точечных элементов не ограничена с двух сторон вертикальными или горизонтальными линиями контура знака из элементов отображения его, т.е. не расположена между ними.
Это хорошо видно, если расположить цифровой формата с видом матрицы 3×3 на формате матричного индикатора с большей по величине матрицей, например, вида 5×5 (фиг.1д). Площадь «окна» знака расположена снаружи контура знака, а контур знака расположен внутри площади «окна» его из невысветившихся элементов отображения.
В этом случае величина площади «окна» не влияет на величину коэффициента разрешающей способности знака /3/.
Величина эквивалентной площади различения (Sрзл) равна при этом величине эквивалентной площади обнаружения знака (Sобн) его, т.к. коэффициент разрешающей способности знаков (Kр.с.зн) при их начертании наименьший и равен 1 (Sрзл=Sобн/Kр.с.зн=Sобн). Уменьшение величины коэффициента разрешающей способности знака до минимального значения привело к увеличению эквивалентной площади различения знака и скорости его восприятия на стадии различения /3/.
У всех знаков цифрового алфавита с постоянным числом точечных элементов в них (фиг.1ж, таблица №2, строка 2 снизу):
а) величина эквивалентной площади обнаружения (Sобн=2.80 мм2) одна и та же;
б) коэффициент разрешающей способности знаков при их начертании равен 1 (Kр.с.зн.=1);
в) величина эквивалентной площади различения (Sрзл=2.80 мм2) одна и та же и равна величине эквивалентной площади обнаружения знака (Sрзл=Sобн: Kр.с.зн=Sобн).
Знаки цифрового алфавита представлены незамкнутым контуром из элементов отображения, воспроизводящих горизонтальные и вертикальные линии его.
Величина эквивалентной площади идентификации знака при его начертании определяется как частное от деления величины эквивалентной площади различения знака на коэффициент идентификации его (Kидн=2) или на число визуально отличительных признаков при начертании знака (фиг.1ж, таблица №2, колонка 10, строка 2 снизу):
Sидн.=Sрзл./ Кидн.ср.=2.80 мм2: 2=1.40 мм2.
Если величина эквивалентной площади различения знака равна величине эквивалентной площади обнаружения его, то величина эквивалентной площади идентификации значительно ниже этих величин.
В то же время, средняя величина эквивалентной площади идентификации на знак у меньшего цифрового формата с видом матрицы 3×3 (фиг.1ж, таблица №2, колонка 10, строка 2 снизу), равная 1.40 мм2 (Sидн.ср.=1.40 мм2) для цифровых знаков с постоянным числом высветившихся элементов отображения в них, оказалась выше средней величины эквивалентной площади идентификации на знак у цифрового формата, вдвое большего по высоте, с видом матрицы 3×5 на основе арабского цифрового алфавита, равной 1.10 мм2 (фиг.1в, таблица №1, колонка 13).
Начертания цифровых знаков с постоянным числом высветившихся элементов отображения позволяют еще увеличить эквивалентную площадь различения их без изменения габаритного размера формата матрицы вида 3×3 изменением величины промежутка между элементами отображения. При этом можно достичь равенства величин площади высветившихся (позиционных) элементов отображения знака (Sп.э) и площади «окна» (Sок) его (Sп.э.=Sок).
Так, например, при уменьшении величины промежутка (t) между элементами отображения до 0.09 мм (t=0,09 мм), при сохранении того же габаритного размера цифрового формата (Sф=11.90 мм2) возрастает величина площади элемента отображения с 0.90 мм2 (при размере элемента отображения 0.95 мм × 0.95 мм) до 1.19 мм2 (при размере элемента отображения 1.09 мм × 1.09 мм). Величина площади позиционных (высветившихся) элементов отображения (Sп.э.) равна величине площади высветившегося одного элемента отображения (S п.э.-1), умноженной на число (n) элементов отображения в знаке:
Sп.э.=Sп.э.-1×n=1.19 мм2 × 5=5.95 мм2.
Величина площади «окна» знака (Soк) равна величине площади из высветившихся (позиционных) элементов его:
Sп.э.=Sок=5.95 мм2.
Величина эквивалентной площади различения знака (Sрзл) возрастает (фиг.1ж, таблица №2, строка 1 снизу,) до максимального значения при Sп.э.=Sок=Sф:2=5.95 мм2 для данного габаритного размера цифрового формата (Sрзл=Sф:4=11.90 мм2:4=2.975 мм2). Величина эквивалентной площади идентификации знака (Sидн=1.4875 мм2) также увеличилась (фиг.1ж, таблица №2, колонка 10, строка 1 снизу).
При дальнейшем уменьшении цифрового формата с видом матрицы 3×3 до цифрового формата с видом матрицы 2×2 (фиг.3а) изменяется начертание цифровых знаков при их формировании, у которых число элементов отображения в знаках различно. В каждой из двух групп цифровых знаков 0, 5, 6, 7, 8, 9 (фиг.3б, таблица №3, строка 2 снизу) и 1, 2, 3, 4 (фиг.3б, таблица №3, строка 1 снизу), с постоянным числом (2 и 1, соответственно) высветившихся элементов отображения, подсчитаны величины эквивалентной площади обнаружения, различения на знак и средней величины эквивалентной площади идентификации на знак (фиг.3б, таблица №3).
Идентифицировать такие знаки, представленные, например, многозначным числом, затруднительно. Если из цифрового алфавита (фиг.4а) сформируем два многозначных числа (фиг.4б, фиг.4в) с одним и тем же числом элементов отображения в каждом из них, расположенных, например, на одном и том же уровне по высоте, то прочесть их будет затруднительно в связи с поиском места расположения разрядов этого числа. Прочтение многозначных чисел (12212 или 57755) затрудняется тем, что один и тот же по начертанию знак может принимать различное значение в зависимости от того, как оператор определит его место в ряду формируемых чисел. Ему надо научиться определять по расстоянию между разрядами, какой величине соответствует сформированный знак. Время идентификации при формировании таких знаков увеличивается.
Только при начертаниях цифровых знаков 0 и 9 (фиг.4а), время их идентификации может быть уменьшено, поскольку начертания их визуально различны по расположению элементов отображения цифрового формата.
Такое уменьшение цифрового формата и системы отображения визуального кодирования цифровой информации не достигает цели в улучшении восприятия знаков на стадии идентификации. Да и средняя величина эквивалентной площади идентификации на знак при формировании таких знаков незначительна (фиг.3б, таблица №3).
Выбор оптимальной системы визуального кодирования, определяемой уменьшением габаритного размера цифрового формата, без ухудшения восприятия цифровых знаков - основная задача предлагаемого изобретения.
Под визуальным кодированием информации понимают операцию отождествления условных знаков (символов, сигналов) с тем или иным видом информации. Выбор оптимального кода связан с обеспечением максимальной скорости и надежности приема и переработки информации человеком, т.е. с достижением максимальной эффективности выполнения операций зрительного поиска, обнаружения, различения, идентификации и опознания сигналов. Каждый из способов кодирования - это категория кодирования или вид алфавита /2, стр.61/.
Кодирование формой является универсальным средством представления информации благодаря алфавиту различных символов. Лучше различаются и распознаются простые геометрические фигуры, состоящие из небольшого количества элементов /2, стр.61/.
Если же тот же самый по габаритным размерам (4,0 мм2) цифровой формат (фиг.3а) в виде квадрата, представленный матрицей вида 2х2, разделить на четыре элемента отображения не перпендикулярными линиями к сторонам квадрата через центр оси его, а диагоналями этого квадрата, то получим иное расположение такого же количества элементов отображения цифрового формата (фиг.3в).
Параметры знаков такого цифрового формата (фиг.3г, таблица №4), состоящего из четырех элементов отображения, не отличаются от величин параметров знаков (фиг.3б, таблица №3), цифровой формат которых представлен в виде матрицы 2×2 (фиг.3а). Габаритные размеры элементов отображения на фиг.3в равны габаритным размерам элементов отображения на фиг.3а, занимающих одну и ту же величину части площади цифрового формата.
Если из цифрового алфавита (фиг.4 г) сформируем два многозначных числа (фиг.4д, фиг.4е), отображающих, например, два многозначных числа (41141 и 86688, соответственно) с одним и тем же числом элементов отображения в каждом из них, то эти многозначные числа отлично идентифицируются, не требуя дополнительного времени для поиска места расположения разряда. Начертания элементов цифрового формата с габаритным размером 4,0 мм2 (2 мм × 2 мм) при формировании знаков в виде треугольников и их сочетаний визуально ориентированы.
По визуально ориентированным знакам точно идентифицируется их величина в ряду разрядов многозначного числа (фиг.4д, фиг.4е). При формировании знаков облегчается задача идентификации их и повышается скорость восприятия знаков на этой стадии.
Таким образом, наименьшее число элементов отображения (n=4) в цифровом формате (2 мм × 2 мм), при формировании цифровых знаков, необходимо потребовало не только визуального кодирования формой, но и кодирования пространственной ориентации фигур путем их поворота в поле зрения оператора. В этом случае, фигуры, отображающие знаки, легко распознаются друг от друга в цифровом ряду разрядов многозначного числа и быстро и легко идентифицируются. Цифровые знаки при формировании, форматом которых является квадрат, разделенный диагоналями на элементы отображения, представляют начертание фигур в виде единичных или сдвоенных треугольников, в соответствии с числом элементов отображения в них.
При идентификации знаков, визуально кодированных формой и пространственной ориентацией фигур путем их поворота, облегчается работа оператора, который способен определить величину любого многозначного числа по начертаниям фигур, составленных на основании предлагаемого цифрового алфавита.
Элементы отображения цифрового формата в виде треугольников ограничены основаниями сторон квадрата и половинами длин его диагоналей, представляющие равнобедренные стороны их. Однако при формировании того или иного знака, изменение числа высвеченных элементов отображения в нем на единицу при возникновении одиночной ошибки, он может идентифицироваться как другой знак представленного цифрового алфавита. К тому же фигуры, представленные цифрами 1-4 (фиг.3в), имеют величину площади высветившихся (позиционных) элементов отображения (Sп.э.) в два раза меньшую остальных фигур, что сказывается и на величине эквивалентной площади обнаружения (Sобн) знака (фиг.3г, таблица №4, нижняя строка, колонки 2 и 4). Вершины таких равнобедренных треугольников расположены на пересечении диагоналей квадрата.
Наилучшим восприятием знаков на стадии обнаружения обладает цифровой алфавит, все знаки которого при формировании их имеют одинаковую величину площади из высветившихся элементов отображения (Sп.э.) цифрового формата, равную величине площади «окна» (Sок) из невысветившихся элементов отображения его. В этом случае величина площади из высветившихся элементов отображения (Sп.э.) и величина площади «окна» знака (Sок) равны половине величины площади цифрового формата (Sп.э.=Sок=0.5Sф), без учета величины промежутков между элементами отображения. При этом величина эквивалентной площади обнаружения знака (Sобн) достигает максимального значения и равна одной четверти величины площади формата:
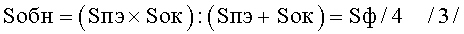
Время восприятия знака на стадии обнаружения уменьшается.
На основании цифровых знаков, представленных на фиг.3в, необходимо построить цифровой алфавит, у которого все цифровые знаки при их формировании удовлетворяли бы условию:
Sп.э.=Sок,
без учета промежутков между элементами отображения, т.е. чтобы величина площади из высветившихся элементов отображения (Sв.э.=Sп.э.) максимально близко приблизилась бы к величине площади из невысветившихся элементов отображения (Sн.в.э.=Sок). Этому условию (фиг.3в) не удовлетворяют только фигуры, представленные цифровыми знаками 1-4. Величина площади из высветившихся элементов отображения (Sв.э.=Sп.э.) у них значительно меньше величины площади «окна» (Sок=Sн.в.э.) из невысветившихся элементов отображения (фиг.3г, таблица №4, нижняя строка, колонки 2 и 3 соответственно), без учета промежутков между элементами отображения.
Чтобы сформировать цифровые знаки 1-4, которые удовлетворяли бы условию: Sп.э.=Sок, необходимо увеличить площади фигур в виде треугольников (фиг.3в -цифровые знаки 1-4), без учета промежутков между ними. Для этого необходимо увеличить высоту каждого из равнобедренных треугольников (цифровые знаки 1-4), оставив без изменения их основания (стороны квадрата).
В таком случае вершина этих равнобедренных треугольников переместится из центра оси симметрии квадрата (фиг.3в - фигуры 1-4) на середину стороны квадрата, противоположной основанию соответствующего треугольника (фиг.3д - фигуры 1-4). Величина площади фигур в виде треугольников увеличится. Это позволило увеличить площадь из высветившихся элементов отображения (Sп.э.) при формировании цифровых знаков (1-4) в виде треугольников в два раза (фиг.3е, фиг.3ж, таблица №5, колонка 6, строка 1 снизу) и приблизить ее к величине площади из невысветившихся элементов отображения (Sок) цифрового формата. Все 10 цифровых знаков имеют величину площади из высветивших элементов отображения (Sп.э.), равную величине площади из невысветившихся элементов отображения (Sок), без учета величины площади промежутков между элементами отображения (Sпр).
Чтобы создать цифровой формат, при управлении элементами отображения которого были бы сформированы десять фигур, представленные на фиг.3д, необходимо на плоскость в виде квадрата, представляющего информационное поле его, нанести:
1) диагонали квадрата, необходимые для формирования цифровых знаков 0 и 5-9 (фиг.3е);
2) контуры четырех фигур, для формирования цифровых знаков 1-4, представляющие их (фиг.3е).
В результате информационное поле цифрового формата в виде квадрата разделилось пересечениями линий, проведенных из углов его к серединам смежных, противоположных этим углам, сторон квадрата, с линиями его диагоналей на 32 элемента отображения (фиг.3е, фиг.5а), из которых можно сформировать 10 цифровых знаков.
Начертание фигуры, отображаемой цифрой 1 (фиг.5б), представляет собой равнобедренный треугольник, основанием которого является нижняя горизонтальная сторона квадрата (IG), а вершина его (В) расположена на середине верхней горизонтальной (АС) стороне его.
Величина площади равнобедренного треугольника IBGI (фиг.5а) из высветившихся элементов отображения (Sпэ.), без учета промежутков между элементами отображения при формировании фигуры, представленной цифрой 1, равна половине величины площади квадрата или половине величины площади цифрового формата (Sпэ.=0.5Sф). Вторая половина величины площади квадрата из невысветившихся элементов отображения состоит из прямоугольных треугольников BCGB и AIBA, суммарная величина площади которых составляет половину величины площади «окна» (Sок), без учета промежутков между элементами отображения.
Начертание фигуры, отображаемой цифрой 2 (фиг.5б), представляет собой равнобедренный треугольник, основанием которого является левая вертикальная сторона квадрата (АI), а вершина его (Е) расположена на середине правой вертикальной (CG) стороне его. Величина площади равнобедренного треугольника АЕIА (фиг.5а) из высветившихся элементов отображения (Sп.э.), без учета промежутков между элементами отображения при формировании фигуры, представленной цифрой 2, равна половине величины площади квадрата или половине величины площади цифрового формата (Sп.э.=0.5 Sф). Вторая половина величины площади квадрата из невысветившихся элементов отображения состоит из прямоугольных треугольников АСЕА и IEGI, суммарная величина площади которых составляет половину величины площади «окна» (Sок), без учета промежутков между элементами отображения.
Начертание фигуры, отображаемой цифрой 3 (фиг.5б), представляет собой равнобедренный треугольник, основанием которого является верхняя горизонтальная сторона квадрата (АС), а вершина его (Н) расположена на середине нижней горизонтальной (IG) стороне его. Величина площади равнобедренного треугольника АСНА (фиг.5а) из высветившихся элементов отображения (Sп.э.), без учета промежутков между элементами отображения при формировании фигуры, представленной цифрой 3, равна половине величины площади квадрата или половине величины площади цифрового формата (Sп.э.=0.5 Sф). Вторая половина величины площади квадрата из невысветившихся элементов отображения состоит из прямоугольных треугольников CGHC и АНIА, суммарная величина площади которых составляет половину величины площади «окна» (Sок), без учета промежутков между элементами отображения.
Начертание фигуры, отображаемой цифрой 4 (фиг.5б), представляет собой равнобедренный треугольник, основанием которого является правая вертикальная сторона квадрата (CG), а вершина его (K) расположена на середине левой вертикальной (IА) стороне его. Величина площади равнобедренного треугольника CGKC (фиг.5а) из высветившихся элементов отображения (Sп.э.), без учета промежутков между элементами отображения при формировании фигуры, представленной цифрой 4, равна половине величины площади квадрата или половине величины площади цифрового формата (Sп.э.=0.5 Sф). Вторая половина величины площади квадрата из невысветившихся элементов отображения состоит из прямоугольных треугольников АСКА и IKGI, суммарная величина площади которых составляет величину площади «окна» (Sок), без учета промежутков между элементами отображения.
Начертание контуров фигур при формировании цифровых знаков от 1 до 4 в виде равнобедренного треугольника (фиг.5а, фиг.5б) имеет основанием ту или иную сторону квадрата, а вершина ее располагается на середине противоположной соответствующей основанию равнобедренного треугольника стороны квадрата. Величина площади из высветившихся элементов отображения (Sп.э.) при формировании цифровых знаков от 1 до 4 в виде равнобедренных треугольников равна половине величины площади цифрового формата или равна величине площади из невысветившихся элементов отображения (Sок), без учета промежутков между элементами отображения (фиг.5б).
Начертание фигуры, отображаемой цифрой 5 (фиг.5в), представляет собой равнобедренный треугольник CGIC, основанием которого является диагональ IC квадрата, соединяющая смежные стороны его CG и GI, исходящие из угла G квадрата (фиг.5а). Величина площади равнобедренного треугольника (CGIC) из высветившихся элементов отображения (Sп.э.), без учета промежутков между элементами отображения (фиг.5а) при формировании фигуры, представленной цифрой 5, равна половине величины площади квадрата или половине величины площади цифрового формата (Sп.э.=0.5 Sф). Вторая половина величины площади квадрата из невысветившихся элементов отображения (Sок), равная величине площади равнобедренного треугольника (СIАС), составляет величину площади «окна» (Sок), без учета промежутков между элементами отображения.
Начертание фигуры, отображаемой цифрой 6 (фиг.5в), представляет собой равнобедренный треугольник IAGI, основанием которого является диагональ AG квадрата, соединяющая концы смежных сторон его IА и IG, исходящие из угла I квадрата (фиг.5а). Величина площади равнобедренного треугольника (AGIA) из высветившихся элементов отображения (Sп.э.), без учета промежутков между элементами отображения (фиг.5а) при формировании фигуры, представленной цифрой 6, равна половине величины площади квадрата или половине величины площади цифрового формата (Sп.э.=0.5 Sф). Вторая половина величины площади квадрата из невысветившихся элементов отображения (Sок), равная величине площади равнобедренного треугольника(АССА), составляет величину площади «окна» (Sок), без учета промежутков между элементами отображения.
Начертание фигуры, отображаемой цифрой 7 (фиг.5в), представляет собой равнобедренный треугольник IАСI, основанием которого является диагональ IC квадрата, соединяющая концы смежных сторон его АI и АС, исходящие из угла А квадрата (фиг.5а). Величина площади равнобедренного треугольника (СIАС) из высветившихся элементов отображения (Sп.э.), без учета промежутков между элементами отображения (фиг.5а) при формировании фигуры, представленной цифрой 7, равна половине величины площади квадрата или половине величины площади цифрового формата (Sп.э.=0.5 Sф). Вторая половина величины площади квадрата из невысветившихся элементов отображения (Sок), равная величине площади равнобедренного треугольника (CGIC), составляет величину площади «окна» (Sок), без учета промежутков между элементами отображения.
Начертание фигуры, отображаемой цифрой 8 (фиг.5в), представляет собой равнобедренный треугольник ACGA, основанием которого является диагональ AG квадрата, соединяющая концы смежных сторон его АС и CG, исходящие из угла С квадрата (фиг.5а). Величина площади равнобедренного треугольника (ACGA) из высветившихся элементов отображения (Sп.э.), без учета промежутков между элементами отображения (фиг.5а) при формировании фигуры, представленной цифрой 8, равна половине величины площади квадрата или половине величины площади цифрового формата (Sп.э.=0.5 Sф). Вторая половина величины площади квадрата из невысветившихся элементов отображения (Sок), равная величине площади равнобедренного треугольника (AIGA), составляет величину площади «окна» (Sок), без учета промежутков между элементами отображения.
Начертания фигур в виде равнобедренных треугольников при формировании знаков, отображаемых цифрами 5-8, образованы теми или иными смежными сторонами квадрата, исходящими из соответствующих углов его, являющиеся сторонами равнобедренных треугольников, а соответствующие им диагонали квадрата, соединяющие противоположные стороны их, являются основаниями того или иного равнобедренного треугольника. Величина площади из высветившихся элементов отображения (Sп.э.), при формировании цифровых знаков от 5 до 8 в виде равнобедренных треугольников, равна величине площади из невысветившихся элементов отображения (Sок), без учета промежутков между элементами отображения (фиг.5б).
Начертание фигуры, отображаемой цифрой 0 (фиг.5 г), представляет собой два равнобедренных треугольника АIОА и COGC, (фиг.5а), основаниями которых являются вертикальные стороны АI и CG квадрата, а полудиагонали его AG и СI представлены равнобедренными сторонами этих треугольников. Величина площади, ограниченной сторонами двух равнобедренных треугольников AGCIA из высветившихся элементов отображения (Sп.э.), без учета промежутков между элементами отображения (фиг.5а) при формировании фигуры, представленной цифрой 0, равна половине величины площади квадрата или половине величины площади цифрового формата (Sп.э.=0.5 Sф).
Вторая половина величины площади квадрата, равная величине площади двух равнобедренных треугольников ACIGA из невысветившихся элементов отображения, составляет величину площади «окна» (Sок), без учета промежутков между элементами отображения (фиг.5а, фиг.5г).
Начертание фигуры, отображаемой цифрой 9 (фиг.5г), представляет собой два равнобедренных треугольника АОСА и IOGI (фиг.5а), основаниями которых являются горизонтальные стороны АС и IG квадрата, а полудиагонали его AG и СI представлены равнобедренными сторонами этих треугольников.
Величина площади, ограниченной сторонами двух равнобедренных треугольников ACIGA из высветившихся элементов отображения (Sп.э.), без учета промежутков между элементами отображения при формировании фигуры, представленной цифрой 9, равна половине величины площади квадрата или половине величины площади цифрового формата (Sп.э.=0.5 Sф). Вторая половина величины площади квадрата, равная величине площади двух равнобедренных треугольников AGCIA из невысветившихся элементов отображения составляет величину площади «окна» (Sок), без учета промежутков между элементами отображения (фиг.5а, фиг.5 г).
Все фигуры (фиг.3е, фиг.5б-фиг.5 г), представляющие знаки цифрового алфавита, при их формировании имеют величину площади из высветившихся элементов отображения (Sв.э.=Sп.э.), равную величине площади из невысветившихся элементов (Sн.в.э.=Sок) отображения, без учета величины промежутка между ними. Коэффициент разрешающей способности знаков равен 1 (Kр.с.зн.=1).
Наилучшим восприятием знака при формировании его на стадии идентификации обладает фигура с сосредоточенными (или сконцентрированными) внутри замкнутого контура ее высветившимися элементами отображения (фиг.4з), без учета величины промежутка между элементами отображения.
Сосредоточение высветившихся элементов отображения (Sп.э.) по площади в замкнутом контуре фигуры, равной величине площади «окна» (Sок) из невысветившихся элементов отображения его, увеличивает эквивалентную площадь обнаружения знака и величину эквивалентной площади различения его (фиг.4з, фиг.3ж, таблица №5, строка 1 снизу). Фигура, представленная тем или иным знаком цифрового алфавита, при формировании визуально воспринимается оператором на стадии идентификации единственным по начертанию замкнутым контуром, который на фоне площади «окна» не вызывает у него сомнений в опознании ее.
Цифровой знак, представленный такой фигурой из высветившихся элементов отображения на фоне площади «окна» из невысветившихся элементов отображения, однозначно идентифицируется по единственному признаку его - замкнутому контуру фигуры с коэффициентом идентификации (Kидн), равным 1 (фиг.4з).
Столь большое различие между замкнутым контуром фигуры, представленной тем или иным знаком при его формировании и всеми другими замкнутыми контурами фигур, обеспечивается избыточностью цифрового формата, представленного тридцатью двумя элементами отображения, позволяет безошибочно идентифицировать его.
Величина эквивалентной площади идентификации такого знака увеличивается до максимального значения. При этом визуальное восприятие знаков (фиг.4з) на стадиях обнаружения, различения и идентификации будет наилучшим, без учета промежутков между элементами отображения, а их величины эквивалентной площади обнаружения, различения и идентификации будут наибольшими и равными (фиг.4з, фиг.2ж, таблица №5, строка 1 снизу).
Sобн=Sрзл=Sидн.
Фигуры при их формировании на основе 32-элементного цифрового формата (фиг.5а) представлены на фиг.3е, фиг.5б, фиг.5в, фиг.5г с учетом промежутка между элементами отображения, а на фиг.4з - без учета промежутков между элементами отображения.
При нанесении светоизлучающего материала на лицевую поверхность цифрового формата, состоящего из 32 элементов отображения, площадь промежутков между этими элементами (Sпр) может составлять значительную величину.
Реально величина площади из высветившихся элементов (Sп.э.) и величина площади из невысветившихся элементов отображения (Sок), участвующих в формулах расчета величин эквивалентных площадей обнаружения и различения знаков, определяются по формулам:
Sп.э.=Sв.э.-Sпр, Sок=Sн.в.э.+Sпр,
где Sпр - величина площади промежутков между элементами отображения.
И чем меньше величина промежутка между элементами отображения, тем ближе величина площади из высветившихся элементов отображения (Sв.э.), увеличиваясь, приближается к величине площади позиционных элементов отображения (Sп.э.), равной половине величины площади цифрового формата. А величина площади из невысветившихся элементов отображения (Sн.в.э.), уменьшаясь, приближается к величине площади «окна» знака (Sок), равной половине величины площади цифрового формата.
Величина площади промежутков между элементами отображения цифрового формата распределяется поровну при формировании знака между высветившимися и невысветившимися элементами отображения. При формировании того или иного знака, за счет распределенной величины площади промежутков (Sпр) между элементами отображения, величина площади из высветившихся элементов отображения (Sв.э.), уменьшится на половину величины площади промежутков (0.5Sпр) между элементами отображения. А величина площади из невысветившихся элементов отображения (Sн.в.э.) увеличится на эту же величину половины площади промежутков между элементами отображения (0.5Sпр.). Т.о., величина площади позиционных элементов (Sп.э.) при формировании знака будет равна разнице между величиной площади высветившихся элементов отображения (Sв.э.) и половиной величины площади промежутков (0.5Sпр.) между ними:
Sп.э.=Sв.э.-0.5Sпр.
На такую же величину (0.5Snp) возрастает площадь «окна» знака, включающая в себя величину площади из невысветившихся элементов отображения (Sн.в.э.) и половину той же величины площади промежутков (0.5Sпр) между элементами отображения:
Sок=Sн.в.э.+0.5Sпр.
Величина площади промежутков между элементами отображения в цифровом формате равна:
Sпр=t × L,
где t - толщина линии промежутков между элементами отображения, а L - суммарная длина линий промежутков между всеми элементами отображения.
Максимальная величина эквивалентной площади обнаружения (Sобн) знака 131 достигается при равенстве величины площади позиционных элементов (Sп.э.=0.5Sф) и величины площади «окна» (Soк=0.5Sф). При этом величина ее определяется по формуле:
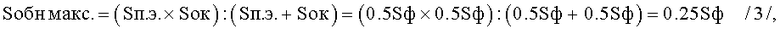
где Sф - величина площади цифрового формата, при Sп.э.=Sок=0.5Sф, при Sпр=0.
Рассчитаем наибольшую величину площади промежутков между элементами отображения (Sпр) цифрового формата, при которой величина эквивалентной площади идентификация знака не должна быть уменьшена, например, до уровня ниже 0.7 от уровня максимальной величины эквивалентной площади идентификации его.
При величине площади цифрового формата (Sф), равной 2 мм × 2 мм=4 мм2 максимальная величина эквивалентной площади обнаружения знака (Sобн), без учета промежутков между элементами отображения, будет равна:
Sобн макс.=(Sп.э.×Sок):(Sп.э.+Sок)=(2.0 мм2 × 2.0 мм2): (2.0 мм2 + 2.0 мм2)=1.00 мм2, при Sп.э.=Sок=0.5Sф=2 мм2 при Sпр=0 (фиг.3ж, таблица №5, колонка 8, строка 1 снизу).
С увеличением толщины (t) линии промежутков между элементами отображения, или с увеличением общей площади промежутков (Sпр), уменьшается величина эквивалентной площади обнаружения знака (Sобн) и, соответственно, уменьшаются величины эквивалентной площади различения (Sрзл) и идентификация (Sидн) их.
Например, при величине общей площади промежутков (Sпр) в цифровом формате (Sф=2×2=4 мм2), равной половине величины площади цифрового формата (Sпр=2 мм2), величина эквивалентной площади обнаружения знака (Sобн) будет равна:
Sобн=(Sп.э.×Sок):(Sп.э.+Sок)={(Sв.э.-0.5Sпр)x(Sн.в.э+Sпр)}:{(Sв.э.-0.5Sпр)+(Sн.в.э+Sпр)}={(2 мм-1 мм)×(2 мм+1 мм)}×{(2 мм-1 мм)+(2 мм+1 мм)}=(1 мм×3 мм):(1 мм+3 мм)=0.75 мм2.
При определении общей площади (Sпр) промежутков между элементами отображения для данного цифрового формата 2 мм×2 мм (фиг.3е) необходимо определить длину (L) контура всех линий промежутков и толщину линии промежутков (t) между элементами отображения (фиг.5а).
Рассчитываем длину (L1) диагонали AG (CI) квадрата формата 2 мм×2 мм. Она равна:
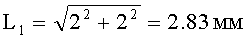 .
.
Таких диагоналей в цифровом формате две: AG и CI (фиг.5а). Суммарная длина их равна:
2L1=5.66 мм.
Рассчитываем диагональ (L2) BG прямоугольника BCGH (1 мм×2 мм). Она равна:
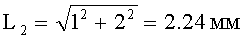 .
.
Таких диагоналей 8 по числу равнобедренных сторон четырех треугольников в цифровом формате, представляющих цифры 1-4. Суммарная их длина равна:
8L2=8×2.24 мм=17.92 мм.
Суммарная длина всех проведенных линий квадрата при определении контуров элементов отображения цифрового формата составляет:
L=2L1+8L2=5.66 мм+17.92 мм=23.58 мм.
Причем приблизительно половина длины этих линий (11.79 мм) высветятся в пределах площади из высветившихся элементов отображения при формировании знака, а вторая половина длины этих линий (11.79 мм) окажется в пределах площади из невысветившихся элементов отображения.
Для габаритного размера формата индикатора 2 мм×2 мм толщину линий промежутков (t), разделяющих элементы отображения, принимаем равными 0.09 мм (фиг.3е, фиг.3ж, таблица №5, колонка 3, строка 3 снизу).
При этом суммарная величина площади всех проведенных промежутков (Sпр) между элементами отображения при формировании знака будет равна:
Sпр=L×t=23.58 мм×0.09 мм=2.12 мм2 (фиг.3ж, таблица №5, колонка 4), причем половина их площади (1.06 мм2) будет расположена среди высветившихся элементов отображения (0.5Sпр=1.06), уменьшая их суммарную величину.
Величина площади позиционного элемента при формировании знака, равная половине величины площади цифрового формата без учета величины площади промежутков между элементами отображения, равна:
Sп.э.=0.5Sф=2 мм2 (фиг.3ж, таблица №5, колонка 6, строка 1 снизу),
а с их учетом (фиг.3е) она равна:
Sп.э.=0.5Sф-0.5Sпр=2 мм2-1.06 мм2=0.94 мм2 (фиг.3ж, таблица №5, колонка 6, строка 3 снизу).
Величина площади «окна» при формировании знака, равная половине величины площади цифрового формата без учета величины площади промежутков между элементами отображения, равна:
Sок=Sф-Sп.э.=4 мм2-2 мм2=2 мм2 (фиг.3ж, таблица №5, колонка 7, строка 1 снизу),
а с их учетом она равна:
Sок=0.5Sф+0.5Sпр=2 мм2+1.06 мм2=3.06 мм2 (фиг.3е, фиг.3ж, таблица №5, колонка 7, строка 3 снизу).
Величина эквивалентной площади обнаружения (Sобн) знака с учетом величины площади промежутков между элементами отображения равна:
Sобн=(Sп.э.×Sок):(Sп.э.+Sок)=(0.94×3.06): (0.94+3.06)=0.72 мм2 (фиг.3ж, таблица №5, колонка 8, строка 3 снизу),
а без их учета
Sобн=(Sn-э.×Sок):(Sп.э.+Sок)=(2×2):(2+2)=1.00 мм2 (фиг.3ж, таблица №5, колонка 8, строка 1 снизу).
Чем меньше суммарная величина площади промежутков между элементами отображения цифрового формата, тем больше величины эквивалентной площади обнаружения, различения и идентификации знака, тем лучше восприятие знака на стадиях обнаружения, различения и идентификации. Причем увеличение площади промежутков между элементами отображения не влечет за собой заметного визуального изменения замкнутого контура фигуры, отображающей знак. Для цифрового формата 2 мм×2 мм толщина линий промежутков (t), разделяющих элементы отображения, равная 0.09 мм, должна быть принята как величина максимальная. При этой толщине линий промежутков (t) между элементами отображения цифрового формата величина эквивалентной площади обнаружения (Sобн) знака будет на уровне 0.72 от ее максимальной величины.
Визуально изменение толщины линий между промежутками между элементами отображения воспринимается как изменение яркости фигуры, отображающей знак (фиг.3е и фиг.4з).
При толщине линий промежутков (t), разделяющих элементы отображения цифрового формата, равной 0.01 мм (фиг.3е, фиг.3ж, таблица №5, колонка 3, строка 2 снизу), суммарная величина площади промежутков между элементами отображения будет равна 0.24 мм2 (фиг.3ж, таблица №5, колонка 4, строка 2 снизу).
Суммарная величина площади между высветившимися элементами отображения будет равна: 0.5Sпр=L×t=11.79 мм×0.01 мм=0.12 мм2.
Величина площади из высветившихся элементов (Sп.э.) при формировании знака, равная половине величины площади цифрового формата с учетом величины площади промежутков между элементами отображения, равна:
Sп.э.=0.5Sф-0.5Sпр=2 мм2-0.12 мм2=1.88 мм2 (фиг.3ж, таблица №5, колонка 6, строка 2 снизу).
Величина площади «окна» (Sок) при формировании знака, равная половине величины площади цифрового формата с учетом величины площади промежутков между элементами отображения, равна:
Sок=Sф-(Sп.э.-0.5Sпр)=4 мм2-2 мм2+0.12 мм2=2.12 мм2 (фиг.3ж, таблица №5, колонка 7, строка 2 снизу).
Величина эквивалентной площади обнаружения знака с учетом величины площади промежутков между элементами отображения при этом будет равна:
Sобн=(Sп.э.×Sок):(Sп.э.+Sок)=(1.88.×2.12): (1.18+2.12)=0.996 мм2 (фиг.3ж, таблица №5, колонка 8, строка 2 снизу).
Величина эквивалентной площади обнаружения знака при толщине линий промежутков (t), разделяющих элементы отображения цифрового формата, равной 0.01 мм, отличается от максимальной ее величины не более чем на 0.5% при габаритных размерах цифрового формата 2×2 мм. Чем меньше толщина линий промежутков (t) между элементами отображения, тем ближе величина площади из высветившихся элементов отображения знака приближается к величине площади «окна» его, тем ближе величина эквивалентной площади обнаружения знака приближается к максимальной величине (Sобн). Таким образом, при формировании цифрового знака величина площади из высветившихся элементов отображения (Sп.э.) приближается к величине площади из невысветившихся элементов отображения (Sок) с уменьшением суммарной величины площади промежутков между элементами отображения. И чем меньше суммарная величина площади промежутков между элементами отображения, тем лучше восприятие знака на стадиях обнаружения, различения и идентификации. А начертания знаков (фиг.4з) соответствуют максимальной величине эквивалентной площади обнаружения, различения и идентификации их.
Для сравнения восприятия цифровых знаков представленных алфавитов на стадиях обнаружения, различения и идентификации необходимо представить параметры их при одной и тоже величине габаритных размеров цифрового формата.
Эти параметры сведены в таблицу №6 (фиг.4и).
Для цифрового формата (фиг1а) с видом матрицы 3×5 (Sф=20.53 мм2) при формировании цифр (фиг.1б) на основе арабского алфавита приведены средние величины параметров на знак (фиг.4и, таблица №6, строка 3 снизу), подсчитанные из результатов таблицы №1 (фиг.1в).
Для цифрового формата с видом матрицы 3×5 (Sф=20.53 мм2) при отображении цифровых знаков с постоянным числом высветившихся элементов отображения (фиг.4ж) всегда можно добиться равенства величины площади из высветившихся элементов отображения знака (Sп.э.), равной величине площади «окна» его (Sп.э.=Sок). И при величине коэффициента разрешающей способности знака при их начертании, равном 1, величины эквивалентной площади обнаружения и различения у них будут равны максимальному для данного формата значению (фиг.4и, таблица №6, строка 2 снизу).
Для цифрового формата с 32 элементами отображения (фиг.4з) при формировании знаков всегда можно добиться соотношения (за счет уменьшения величины промежутка между элементами отображения), при котором величина площади из высветившихся элементов отображения (Sп.э.) будет отличаться от величины площади «окна» (Sок) на очень малую величину.
При этом величину площади из высветившихся элементов отображения (Sп.э.) при формировании знака можно принять равной величине площади «окна» (Sок) его (фиг.4и, таблица №6, строка 1 снизу).
Величина площади цифрового формата, равная 20.53 мм2 (Sф=20.53 мм2) обеспечивается линейными размерами квадрата 4.53 мм×4.53 мм.
Если по средней величине эквивалентной площади обнаружения знака (Sобн) все три цифровых алфавита одинаковы, то средняя величина эквивалентной площади идентификации на знак у алфавита на основе арабских цифровых знаков значительно меньше из-за большой средней величины на знак коэффициента разрешающей способности (Kр.с.зн) и величины коэффициента идентификации (Kидн). А средняя величина эквивалентной площади идентификации на знак оказалась значительно выше у цифрового формата с 32 элементами отображения благодаря наименьшему коэффициенту идентификации на знак.
Начертание знаков на основе цифрового арабского алфавита имеют невысокую помехозащищенность при формировании их и невысокое качество восприятия цифровых знаков. Изменение числа высветившихся элементов отображения при одиночной ошибке (0-1) у семисегментных знаков вызывает отображение вместо одного формируемого знака из представленных ниже пар их другого знака данного алфавита (6а).

При формировании цифровых знаков, если возникла одиночная ошибка (0-1), ее не обнаружить, т.к. вместо знака, например, цифры 8 могут быть, отображены: цифра 9, цифра 6 или цифра 0 (фиг.6а). И наоборот, при возникновении одиночной ошибки (1-0) при формировании цифр 9, 6 или 0 может быть отображена цифра 8.
Точно так же трудно идентифицировать отображаемые знаки: цифру 5 и цифру 9, цифру 5 и цифру 6, цифру 3 и цифру 9, цифру 1 и цифру 7.
Помехоустойчивость таких знаков невелика и определяется кодовым расстоянием (d) по Хэммингу /5, стр.256/.
Кодовое расстояние по Хэммингу между некоторыми знаками при формировании цифр семисегментного формата равно 1 (d=1).
Точно также трудно идентифицировать отображаемые знаки при формировании их на информационном поле матричного индикатора с видом матрицы 3×5 (фиг.1а). При невысвечивании одного элемента отображения в цифровом формате, который представлен цифрой 8, могут быть отображены цифры 0, 6 и 9 (фиг.1б). Или, например, вместо цифры 6 или цифры 9 может быть высвечена цифра 5 при возникновении одиночной ошибки (фиг.1б).
Для того, чтобы можно было обнаружить одиночные ошибки (ошибки, возникающие не более чем в одном из разрядов кода управления цифровым форматом), минимальное кодовое расстояние по Хэммингу, по отношению к отображаемым знакам цифрового алфавита, должно быть не менее 2/5, стр.257/.
Управление 32-элементным цифровым форматом
Устройство для индикации (фиг.6б), содержащее индикатор HG1 для отображения цифровой информации и преобразователь двоично-десятичного кода DD1 в 7-позиционный код (Y1, Y2, Y3, Y4, Y5, Y6, Y7) управления элементами (А, В, С, D, Е, F, G) 7-сегментного индикатора /6 - стр.143, рис.5.19 / выберем в качестве прототипа.
Структурную схему устройства для индикации, содержащую 32-элементный цифровой формат знаков и преобразователь, например, двоично-десятичного кода 8-4-2-1 в 32-позиционный код управления элементами отображения, нетрудно построить.
Принимаем условия при управлении 32 элементами отображения цифрового формата: каждый элемент отображения (обозначен цифрами 1-32) 32-элементного цифрового формата должен светиться, если на некотором входе его устанавливается сигнал с уровнем логического «0», либо не светиться, если на некотором входе его устанавливается уровень логической «1». Погашая и высвечивая соответствующие элементы отображения цифрового формата (фиг.5а) при формировании того или иного цифрового знака, на информационном поле его отображаются десять цифровых знаков (фиг.5б, фиг.5в, фиг.5г). Сигнал, соответствующий определенной позиции 32-позиционного кода на выходных выводах преобразователя двоично-десятичного кода, должен гасить или высвечивать соответствующий элемент цифрового формата.
Построение структурной схемы преобразователя, например, двоично-десятичного кода 8-4-2-1 в 32-позиционный код управления элементами цифрового формата не представляет никаких трудностей. Известны методы построения структурных схем преобразователей из одного двоичного кода в другой с помощью упрощения логических выражений функции Y=f(X).
Метод Квайна для минимизации функций ручным способом оказывается весьма трудоемким, но для сложных функций с большим числом аргументов задача решается с помощью ЭВМ. Метод минимизации функции с помощью карт Вейча обеспечивает простоту получения результата. Он используется при минимизации относительно несложных функций (с числом аргументов до 5) ручным способом. Этот метод требует элементов изобретательности и не может быть использован для решения задачи минимизации с помощью ЭВМ /5-стр.133/. Рассмотрим наиболее простой и демонстративно наглядный цифровой метод /7/ построения преобразователя двоично-десятичного кода 8-4-2-1 в 32-позиционный код управления 32 элементами предлагаемого цифрового формата. Этот метод пригоден как для работы вручную, так и на ЭВМ.
На вход преобразователя кода (DD1) поступают сигналы с выходов двоично-десятичного счетчика /8 - стр.81, рис.39а/, работающего в коде 8-4-2-1 (фиг.6в). Таблица истинности сигналов двоично-десятичного кода 8-4-2-1 с прямых выходов двоично-десятичного счетчика, представленная на фиг.6г, таблица №6 /9 - стр.681/, совмещена с таблицей истинности сигналов двоично-десятичного кода 8-4-2-1 с инверсных выходов двоично-десятичного счетчика. Каждая комбинация входного двоично-десятичного кода 8-4-2-1 рассматривается как двоичное число, равное числу, обозначенному соответствующей ей цифре десятичного кода, которой должна соответствовать строго определенная комбинация сигналов выходного 32-позиционного кода для управления 32 элементами отображения при формировании соответствующих фигур, представленных соответствующими знаками цифрового формата.
Таблица истинности двоично-десятичного 4-разрядного кода 8-4-2-1 (фиг.6г, таблица №7) содержит двоичные кодовые комбинации (сочетания уровней логического «0» и уровней логической «1») аргументов Х и их инверсий 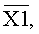 однозначно определяющие каждую цифру (0, 1, 2, 3, 4, 5, 6, 7, 8, 9) десятичного кода. По той же таблице истинности видно, что уровням логической «1» соответствует одна комбинация цифр из десятичного кода того или иного аргумента Х или его инверсии
однозначно определяющие каждую цифру (0, 1, 2, 3, 4, 5, 6, 7, 8, 9) десятичного кода. По той же таблице истинности видно, что уровням логической «1» соответствует одна комбинация цифр из десятичного кода того или иного аргумента Х или его инверсии 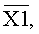 а уровням логического «0» соответствует другая комбинация из оставшихся цифр десятичного кода. Так, например, уровням логической «1» аргумента Х1 соответствует по таблице истинности комбинация из цифр 13579 десятичного кода. Уровням логического «0» того же аргумента Х1 соответствует по таблице истинности (фиг.6г, таблица №7) комбинация из оставшихся цифр 02468 десятичного кода.
а уровням логического «0» соответствует другая комбинация из оставшихся цифр десятичного кода. Так, например, уровням логической «1» аргумента Х1 соответствует по таблице истинности комбинация из цифр 13579 десятичного кода. Уровням логического «0» того же аргумента Х1 соответствует по таблице истинности (фиг.6г, таблица №7) комбинация из оставшихся цифр 02468 десятичного кода.
На фиг.6д (построчная цифровая запись двоично-десятичного кода 8-4-2-1) представлены все значения цифровых комбинаций десятичного кода, соответствующие (уровня логического «0» и уровня логической «1») аргументам Х1, Х2, Х3, Х4 и их инверсиям 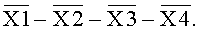 Комбинация цифр десятичного кода, представляющая значение аргумента или его инверсии с уровнем логической «1», обозначается без черточки сверху над ней (например, 13579).
Комбинация цифр десятичного кода, представляющая значение аргумента или его инверсии с уровнем логической «1», обозначается без черточки сверху над ней (например, 13579).
Табличный метод записи истинности двоично-десятичного кода 8-4-2-1 можно дополнить цифрами десятичного кода из построчной цифровой записи двоично-десятичного кода 8-4-2-1 (фиг.7а, таблица №8), указав без черточки сверху над выбранной цифрой уровень логической «1» и с черточкой сверху над цифрой - уровень логического «0». Построчная поразрядная цифровая запись двоично-десятичного кода 8-4-2-1, соответствующая записи этого кода в табличной форме, становится более наглядной (фиг.7б). Каждому разряду двоично-десятичного кода 8-4-2-1 соответствует комбинация цифр десятичного кода как с уровнем логической «1», так и с уровнем логического «0».
На основании представленных фигур, отображающих цифровые знаки из высвеченных и невысвеченных элементов отображения (фиг.5б, фиг.5в, фиг.5г) 32-элементного цифрового формата (фиг.5а), составляем таблицу истинности 32-разрядного позиционного кода управления (фиг.8). Высвечивание элементов отображения цифрового формата при формировании знаков в таблице истинности 32-позиционного кода (уровень логического «0») выделено темным фоном. Гашение элементов отображения цифрового формата при формировании знаков в таблице истинности 32-позиционного кода (уровень логической «1») выделено светлым фоном.
При формировании фигуры (фиг.5а, фиг.5г), представленной цифровым знаком 0, высвечиваются элементы отображения 9-16, 25-32 (фиг.8а - уровень логического «0»), соответствующие цифре 0. Остальные элементы отображения цифрового формата погашены (фиг.8а - уровень логической «1»).
При формировании фигуры (фиг.5а, фиг.5б), представленной цифровым знаком 1, высвечиваются элементы отображения 4-7, 11-13, 17-24, 29, 30, 32 (фиг.8а - уровень логического «0»). Остальные элементы отображения цифрового формата погашены (фиг.8а - уровень логической «1»).
При формировании фигуры (фиг.5а, фиг.5б), представленной цифровым знаком 2, высвечиваются элементы отображения 5, 6, 8, 12-15, 19-21, 25-32 (фиг.8а - уровень логического «0»). Остальные элементы отображения цифрового формата погашены (фиг.8а - уровень логической «1»).
При формировании фигуры (фиг.5а, фиг.5б), представленной цифровым знаком 3, высвечиваются элементы отображения 1-8, 13, 14, 16, 20-23, 27-29 (фиг.8а - уровень логического «0»). Остальные элементы отображения цифрового формата погашены (фиг.8а - уровень логической «1»).
При формировании фигуры (фиг.5а, фиг.5б), представленной цифровым знаком 4, высвечиваются элементы отображения 3-5, 9-16, 21, 22, 24, 28-31 (фиг.8а - уровень логического «0»). Остальные элементы отображения цифрового формата погашены (фиг.8а - уровень логической «1»).
При формировании фигуры (фиг.5а, фиг.5в), представленной цифровым знаком 5, высвечиваются элементы отображения 9-16 и 17-24 (фиг.8а - уровень логического «0»). Остальные элементы отображения цифрового формата погашены (фиг.8а - уровень логической «1»).
При формировании фигуры (фиг.5а, фиг.5в), представленной цифровым знаком 6, высвечиваются элементы отображения 17-24 и 25-32 (фиг.8а - уровень логического «0»). Остальные элементы отображения цифрового формата погашены (фиг.8а - уровень логической «1»).
При формировании фигуры (фиг.5а, фиг.5в), представленной цифровым знаком 7, высвечиваются элементы отображения 1-8 и 25-32 (фиг.8а - уровень логического «0»). Остальные элементы отображения цифрового формата погашены (фиг.8а - уровень логической «1»).
При формировании фигуры (фиг.5а, фиг.5в), представленной цифровым знаком 8, высвечиваются элементы отображения 1-8 и 9-16 (фиг.8а - уровень логического «0»). Остальные элементы отображения цифрового формата погашены (фиг.8а - уровень логической «1»).
При формировании фигуры (фиг.5а, фиг.5 г), представленной цифровым знаком 9, высвечиваются элементы отображения 1-8, 17-24 (фиг.8а - уровень логического «0»). Остальные элементы отображения цифрового формата погашены (фиг.8а - уровень логической «1»).
По гашению и высвечиванию каждого элемента отображения (1-32) цифрового индикатора (фиг.5а, фиг.5б, фиг.5в, фиг.5 г) при формировании соответствующих цифровых знаков от 0 до 9 на основании 32-позиционного кода управления 32 элементами цифрового формата (фиг.8а) составляем построчную цифровую запись его:
Построчная цифровая запись позиций (1-32) 32-позиционного кода управления соответствующими элементами отображения 1-32 цифрового формата индикатора представлена цифрами десятичного кода с уровнем логической «1» без черточки сверху над ними:

Построчная цифровая запись позиций (1-32) 32-позиционного кода управления соответствующими элементами отображения 1-32 цифрового формата индикатора представлена цифрами десятичного кода с уровнем логического «0» с черточкой сверху над ними:
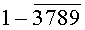
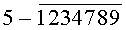
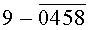
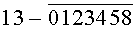
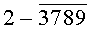
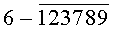
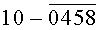
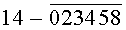
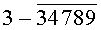
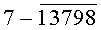
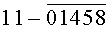
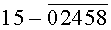
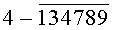
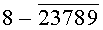
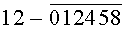
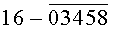
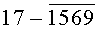
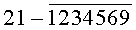
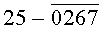
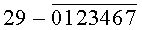
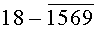
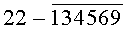
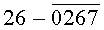
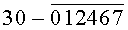
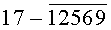
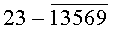
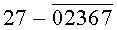
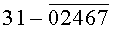
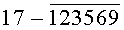
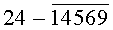
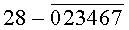
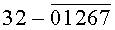
Позиции 32-позиционного кода (1-32) с уровнем логической «1», являющиеся сигналами управления элементами отображения (1-32, соответственно) цифрового формата, с выходных выводов 1-32 преобразователя кода поступают на определенные входы цифрового формата, погашая соответствующие элементы отображения 1-32 его в моменты формирования одноименных цифровых знаков от 0 до 9.
Позиции 32-позиционного кода (1-32) с уровнем логического «0», являющиеся сигналами управления элементами отображения (1-32, соответственно) цифрового формата, с выходных выводов 1-32 преобразователя кода поступают на определенные входы цифрового формата, высвечивая соответствующие элементы отображения 1-32 его в моменты формирования одноименных цифровых знаков от 0 до 9.
Таким образом, на основании таблиц истинности двоично-десятичного кода 8-4-2-1 (фиг.6г, таблица №7) и 32-позиционного кода (фиг.8) и построчной записи их легко построена, применяя цифровой метод /7/, структурная схема преобразователя двоично-десятичного кода 8-4-2-1 в 32-позиционный код (фиг.9, фиг.10, фиг.11).
По сигналам, представленным комбинациями цифр десятичного кода, с уровнем логической «1» и уровнем логического «0» на входах и выходах логических элементов И-НЕ структурной схемы преобразователя кода (фиг.9, фиг.10, фиг.11), легко прослеживается преобразование двоично-десятичного кода 8-4-2-1 в 32-позиционный код управления элементами индикатора.
На выходных выводах 1-32 преобразователя при формировании, например, фигуры, представленной цифрой 1, высвечиваются элементы отображения 4-7, 11-13, 17-24, 29, 30, 32. Остальные элементы отображения цифрового формата погашены.
Для проверки правильности построения структурной схемы преобразователя необходимо убедиться, что при формировании того или иного знака на информационном поле цифрового формата отобразился именно этот знак. Например, при формировании фигуры, представленной цифрой 1 (фиг.5б, фиг.8), необходимо убедиться, что высвечиваются только элементы отображения 4, 5, 6, 7, 11, 12, 13, 17, 18, 19, 20, 21, 22, 23, 24, 29, 30, 32. Остальные элементы цифрового формата должны быть погашены. Для этого убеждаемся, что на выходных выводах структурной схемы преобразователя одноименных с элементами отображения цифрового формата присутствует комбинация цифр десятичного кода, содержащая цифру 1 с уровнем логической «1» (без черточки сверху). Такими одноименными выходными выводами структурной схемы преобразователя будут: 1, 2, 3, 8, 14 (фиг.9), 9, 10, 15, 16 (фиг.10) 25, 26, 27, 28, 31 (фиг.11). Одноименные элементы отображения индикатора, при формировании фигуры, представленной цифрой 1, погашены. Остальные элементы отображения индикатора 4, 5, 6, 7, 11, 12, 13, 17, 18, 19, 20, 21, 22, 23, 24, 29, 30, 32 цифрового формата должны быть высвечены. На выходных выводах структурной схемы преобразователя одноименных с элементами отображения цифрового формата в комбинации цифр десятичного кода отсутствует цифра 1 с уровнем логической «1» (4, 5, 6, 7. 11, 12, 13, 17, 18, 19, 20, 21, 22, 23, 24, 29, 30, 32).
Сравнивая высветившиеся и погашенные элементы отображения при формировании фигуры, представленной цифрой 1 (фиг.5б, фиг.8), видим, что преобразование цифры 1 десятичного кода в отображение фигуры, представленной одноименным цифровым знаком 1, осуществлено правильно.
Помехозащищенность начертания цифровых знаков при их формировании обеспечивается 32-элементным цифровым форматом при управлении его элементами отображения 32-позиционным кодом.
Цифровому формату с большим числом элементов отображения (n=32), при формировании неповторяемых по внешнему очертанию замкнутых контуров фигур, соответствует большое число разрядов позиционного кода управления. Большое число разрядов позиционного кода управления позволяет безошибочно идентифицировать знаки при одиночных ошибках.
Избыточное число элементов отображения цифрового формата позволило создать фигуры, кодированные формой и пространственным расположением, представляющие цифровые знаки, каждый из которых при его формировании не может быть при возникновении одноразовых (или даже двухразовых) помех с уровнем 0-1 или 1-0 принят за другой цифровой знак данного алфавита.
Так, например, между формированием фигуры, представленной цифровым знаком 0, и формированием фигуры, представленной цифровым знаком 1, кодовое расстояние по Хэммингу в разрядах 32-разрядного кода равно 22.
Фигура, представляющая цифровой знак 0 - 11111111000000001111111100000000
Фигура, представляющая цифровой знак 1 - 11100001110001110000000011110010
Между формированием фигуры, представленной цифровым знаком 0, и формированием фигуры, представленной цифровым знаком 2, кодовое расстояние по
Хэммингу в разрядах 32-разрядного кода равно 10.
Фигура, представляющая цифровой знак 0 - 11111111000000001111111100000000
Фигура, представляющая цифровой знак 2 - 11110010111000011100011100000000
Между формированием фигуры, представленной цифровым знаком 1, и формированием фигуры, представленной цифровым знаком 2, кодовое расстояние по Хэммингу в разрядах 32-разрядного кода равно 16.
Фигура, представляющая цифровой знак 1 - 11100001110001110000000011110010
Фигура, представляющая цифровой знак 2 - 11110010111000011100011100000000
Можно убедиться, что кодовое расстояние по Хэммингу между формируемыми знаками цифрового алфавита с постоянной величиной площади высветившихся элементов значительно больше 2, что обеспечивает хорошую помехозащищенность их.
Не повторяющиеся по начертанию замкнутые контуры фигур цифрового алфавита однозначно идентифицируются при возникновении одноразовых помех.
Цифровой знак следует считать помехозащищенным, когда вызванная помехой одиночная ошибка в формировании фигуры, представленной тем или иным знаком, не превращает формируемый знак в другой знак цифрового алфавита. Т.е., замкнутый контур фигуры при формировании того или иного знака при одиночной ошибке нельзя принять за другую фигуру, представленную другим знаком цифрового алфавита. При формировании цифровых знаков на основе 32-элементного цифрового формата одиночная ошибка не исключает идентификацию их. Т.е., цифровой знак при его формировании, представленный той или иной фигурой, в случае одиночной ошибки невозможно нарушить так, чтобы отобразился замкнутый контур фигуры, представленный другим знаком цифрового алфавита. Замкнутый контур фигуры будет идентифицироваться только с тем цифровым знаком, который формируется.
Причем, если одиночная ошибка погашает элемент отображения при формировании знака, не нарушая замкнутость контура его (фиг.12а), то не высвечивание такого элемента отображения на идентификацию знака оказывает только лишь косвенное влияние, уменьшая величину эквивалентной площади обнаружения и, следовательно, уменьшая величины эквивалентной площади различения и идентификации этого знака. Идентифицировать такой знак не представляет затруднений.
В том случае, если одиночная ошибка, погашая элемент отображения, разрывает замкнутый контур фигуры при формировании знака, нарушая непрерывность образующей линии контура его (фиг.126), то незамкнутый контур фигуры оператор мысленно достраивает его до замкнутого контура, отождествляя его с эталоном, хранящимся в памяти. При этом он не принимает его за контур другой какой-либо фигуры данного цифрового алфавита. Незначительное нарушение замкнутого контура знака при возникновении одиночной ошибки не вызовет сомнения оператора в идентификации того знака, который формируется.
Влияние изменения величины промежутка между элементами отображения на изменение восприятия цифрового знака показано на фиг.12в-фиг.12з.
При величине промежутка, визуально не различимого на фигуре, величина эквивалентной площади обнаружения знака максимальна (фиг.12в). Чем меньше величина промежутка между элементами отображения цифрового формата, тем больше величина площади из высветившихся элементов отображения, тем больше величины эквивалентной площади обнаружения, различения и идентификации знака, тем лучше восприятие знака. Увеличение промежутка между элементами отображения сказывается на уменьшении величины эквивалентной площади, обнаружении знака в связи с уменьшением величины площади из высветившихся элементов отображения и увеличении площади «окна» из невысветившихся элементов отображения.
Толщина линии промежутка (фиг.12г, фиг.12д, фиг.12е, фиг.12ж) изменилась в 7 раз (t, 3t, 5t, 7t, соответственно). Но соотношение равенства величин эквивалентной площади обнаружения, различения и идентификации знака остается без изменения
Sобн=Sрзл=Sидн,
при невысвечивании элементов отображения (5, 21, 23), не разрывающих замкнутый контур фигуры цифрового знака, и даже при одновременном невысвечивании одного элемента отображения (13), разрывающего замкнутый контур фигуры при возникновении соответствующих ошибок вида 0-1 (фиг.12з).
Размещение цифрового формата с 32 элементами отображения на лицевой стороне корпуса матричного индикатора типа КИПГО2А-8×8Л /1 - стр.354/ невозможно из-за недостаточности числа (16) выводов для управления элементами отображения, расположенных на обратной стороне корпуса его.
Если же использовать матричный индикатор типа КИПГО3А-8×8К /1 - 356/, габаритные размеры информационного, величина площади корпуса которого в 4 раза больше корпуса матричного индикатора КИПГ02А-8×8Л, то с обратной стороны корпуса индикатора можно разместить в 4 раза большее (16×4) число выводов для управления индикатором.
На лицевой стороне матричного индикатора типа КИПГО3А-8х8К можно разместить в 4 раза большее число (16×16) элементов отображения с теми же габаритными размерами их (0.95×0.95), соответствующие матричному индикатору КИПГО2А-8×8Л, и в четыре раза большее число цифровых форматов, например, с видом матрицы 3х5 (фиг.13а, фиг.13б).
Число фиксированных знакомест или число цифровых форматов с 32 элементами отображения определяется числом имеющихся выводов на корпусе индикатора. При управлении элементами отображения цифровых форматов в мультиплексном режиме, на лицевой стороне корпуса индикатора типа КИПГО3А-8×8К возможно разместить до 25 фиксированных знакомест (цифровых разрядов) с децимальными точками (фиг.13в). Это в три раза больше, чем могло бы быть размещено цифровых разрядов с видом матрицы 3×5 на информационном поле индикатора с видом матрицы 16×16 для отображения цифр на основе арабского алфавита (фиг.13б).
Параметры знаков цифрового формата с 32 элементами отображения при их формировании сведены в таблицу (фиг.13д, таблица №9):
1) величина площади цифрового формата (Sф) равна 3s×3s (фиг.13е), где s - линейный размер элемента отображения, равный 0.95 мм (фиг.13а);
Sф=L×Н=3s×3s=3×0.95×3×0.95=2.85 мм×2.85 мм=8.12 мм2;
2) определяем величину общей площади промежутков (Sпр) между элементами отображения для данного цифрового формата 2.85 мм×2.85 мм:
а) определяем длину (L1) диагонали AG (CI) квадрата (фиг.5а) формата 2.85 мм×2.85 мм
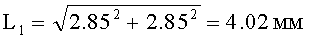
Суммарная величина двух таких диагоналей равна: 2L1=8.04 мм;
б) рассчитываем диагональ (L2) BG прямоугольника BCGH (1.42 мм х 2.85 мм). Она равна:
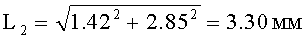
Таких диагоналей 8 по числу равнобедренных сторон четырех треугольников в цифровом формате, представляющих цифры 1-4 (фиг.5а). Суммарная их длина равна:
8L2=8×3.30 мм=26.40 мм;
в) суммарная величина длин всех проведенных линий квадрата при определении контуров элементов отображения цифрового формата составляет:
L=2L1+8L2=8.04 мм+26.40 мм=34.44 мм.
Причем половина длины этих линий (17.22 мм) высветятся в пределах площади из высветившихся элементов отображения при формировании знака, а вторая половина длины этих линий (17.22 мм) окажется в пределах площади из невысветившихся элементов отображения.
Для габаритного размера цифрового формата 2.85 мм×2.85 мм толщину линий промежутков (t), разделяющих элементы отображения, принимаем равными 0.10 мм (фиг.13д, таблица №9, колонка 3, строка 2 снизу).
При этом суммарная величина площади всех проведенных промежутков (Sпр) между элементами отображения при формировании знака будет равна:
Sпр=L×t=34.44 мм×0.1 мм=3.44 мм2 (фиг.13д, таблица №9, колонка 4, строка 2 снизу), причем половина их площади (0.5Sпр.=1.72 мм2) будет расположена среди высветившихся элементов отображения, уменьшая их величину (Sп.э.)
Величина площади позиционного элемента при формировании знака, равная половине величины площади цифрового формата без учета величины площади промежутков между элементами отображения, равна:
Sп.э.=Sф:2=(8.12 мм2:2)=4.06 мм2 (фиг.13д, таблица №9, колонка 7, строка 3 снизу),
а с их учетом она равна:
Sп.э.=0.5Sф-0.5Sпр=4.06 мм2-1.72 мм2=2.34 мм2 (фиг.13д, таблица №9, колонка 7, строка 2 снизу).
Величина площади «окна» при формировании знака, равная половине величины площади цифрового формата без учета величины площади промежутков между элементами отображения, равна:
Sок=0.5Sф=4.06 мм2 (фиг.13д, таблица №9, колонка 7, строка 3 снизу),
а с их учетом она равна:
Sок=0.5Sф+0.5Sпр=4.06 мм2+1.72 мм2=5.78 мм2 (фиг.13д, таблица №9, колонка 8, строка 2 снизу).
Величина эквивалентной площади обнаружения (Sобн) знака с учетом величины площади промежутков между элементами отображения равна:
Sобн=(Sп.э.×Sок):(Sп.э.+Sок)=(2.34.×5.78): (2.34+5.78)=1.38 мм2 (фиг.13д, таблица №9, колонка 9, строка 2 снизу), а без их учета
Sобн=(Sп.э.×Sок):(Sп.э.+Sок)=(4.06×4.06):(4.06+4.06)=2.03 мм2 (фиг.13д, таблица №12, колонка 9, строка 3 снизу).
Sидн=Sрзл=Sобн=2.03 мм2 (фиг.13д, таблица №9, колонки 9-11,строка 3 снизу - без учета величины промежутка между элементами отображения), а с учетом промежутка между элементами отображения (t), равным 0.1 мм, равна: Sидн=Sрзл=Sобн=1.38 мм2 (фиг.13д, таблица №9, колонки 9-11, строка 2 снизу).
Чем больше суммарная величина площади промежутков между элементами отображения цифрового формата, тем меньше величины эквивалентной площади обнаружения, различения и идентификации знака.
С другой стороны, уменьшение величины промежутка (t), разделяющего элементы отображения цифрового формата, улучшает восприятие цифровых знаков, увеличивая эквивалентные площади обнаружения, различения и идентификации их.
Так, например, суммарная величина площади промежутков между высветившимися элементами отображения при t=0.01 мм будет равна:
Sпр=L×t=34.44 мм×0.01 мм=0.34 мм2 (фиг.13д, таблица №9, колонка 4, строка 1 снизу).
Величина площади позиционного элемента при формировании знака, равная половине величины площади цифрового формата с учетом величины площади промежутков между элементами отображения, равна:
Sп.э.=0.5Sф-0.5Sпр=4.06 мм2-0.17 мм2=3.89 мм2 (фиг.13д, таблица №9, колонка 7, строка 1 снизу).
Величина площади «окна» при формировании знака, равная половине величины площади цифрового формата с учетом величины площади промежутков между элементами отображения, равна:
Sок=0.5Sф+0.5Sпр.=4.06 мм2+0.17 мм2=4.23 мм2 (фиг.13д, таблица №9, колонка 8, строка 1 снизу).
Величина эквивалентной площади обнаружения знака с учетом величины площади промежутков между элементами отображения при этом будет равна:
Sобн=(Sп.э.×Sок):(Sп.э.+Sок)=(3.89×4.23): (3.89+4.23)=2.026 мм2 (фиг.13д, таблица №9, колонка 9, строка 1 снизу).
Sидн=Sрзл=Sобн=2.026 мм2 (фиг.13д, таблица №12, колонки 9-11,строка 1 снизу) с учетом промежутка между элементами отображения (t), равным 0.01 мм.
Величина эквивалентной площади обнаружения знака, с величиной площади из высветившихся элементов отображения, равной величине площади из невысветившихся элементов отображения, при толщине линий промежутков (t), разделяющих элементы отображения его, равной 0.01 мм, отличается от возможной максимальной ее величины (фиг.13д, таблица №9, строка 3 снизу) не более чем на 0.4% при габаритных размерах цифрового формата 2.85×2.85 мм. При равенстве величин эквивалентной площади обнаружения, различения и идентификации знака три стадии его восприятия сливаются в одну стадию. Время восприятия знака уменьшается.
Sобн=Sрзл=Sидн (фиг.13г, таблица №9).
Величина эквивалентной площади идентификации такого знака увеличивается до максимального значения, равного величине эквивалентной площади обнаружения знака.
Таким образом, величина эквивалентной площади идентификации цифрового знака (фиг.13д, таблица №9), величина площади из высветившихся элементов отображения которого при формировании его равна величине площади из невысветившихся элементов отображения цифрового формата, без учета промежутков между элементами отображения, превышает среднюю величину эквивалентной площади идентификации знаков на основе арабского алфавита при большей площади их цифрового формата (фиг.1в, таблица №1). А информационная емкость индикатора увеличена в три раза (фиг.13б, фиг.13г).
Сосредоточенные высветившиеся элементы отображения (фиг.13г) при формировании того или иного знака визуально воспринимаются замкнутым контуром фигуры (фиг.3д), заполненной высвеченными элементами отображения. Замкнутый контур фигуры при ее начертании принадлежит только одному из цифрового алфавита знаку его. При формировании знака с величиной площади из высветившихся элементов отображения, равной величине площади из невысветившихся элементов отображения, замкнутый контур фигуры является единственным признаком при идентификации его. Фактически идентифицируется замкнутый контур фигуры, принадлежащий только одному из цифрового алфавита знаку его (фиг.3д), коэффициент идентификации которого равен 1 (Kидн=1). Сконцентрированные элементы отображения, расположенные внутри замкнутого контура фигуры, на фоне площади «окна» из невысветившихся элементов цифрового формата увеличивают эквивалентную площадь обнаружения знака, а следовательно, и эквивалентную площадь различения и идентификации знака. А образующий замкнутый контур фигуры из высвеченных элементов отображения помогает легко идентифицировать представляемый ею цифровой знак.
Распределение пяти цифровых форматов по ширине индикатора:
1) при линейном размере ширины цифрового формата L=3s=2.85 мм (фиг.13е) на долю 5 цифровых форматов из 20 мм индикатора приходится 14.25 мм;
2) оставшиеся 5.75 мм (20.0 мм-14.25 мм=5.75 мм) по ширине информационного поля индикатора приходится на 5 промежутков между цифровыми разрядами;
3) в промежутках между цифровыми разрядами, равных по 1.15 мм, могут быть размещены децимальные точки с линейными размерами, равными 0.75 мм×0.75 мм;
4) расстояние между цифровыми разрядами и децимальной точкой приняты по 0.2 мм
(0.2 мм+0.75 мм+0.2 мм=1.15 мм).
Цифровые знаки с величиной площади из высветившихся элементов отображения, равной величине площади из невысветившихся элементов отображения, без учета расстояния между ними, (фиг.13г) легко запоминаются. Кодированные формой и пространственной ориентации фигуры путем их поворота в поле зрения оператора в ряду разрядов многозначного числа быстро и легко идентифицируются. Визуально идентифицируемая фигура цифрового формата, содержащая высвеченные элементы отображения в единственном из цифрового алфавита замкнутом контуре ее, представленная соответствующим знаком при его формировании, легко опознается.
Цифровые знаки предлагаемого алфавита (фиг.14а), отображающие ряд цифр 1-4 (фиг.14б) и 5-8 (фиг.14в) цифрового формата при их отображении, позволяют оператору лучше воспринимать цифровую информацию. Между измеряемой величиной и цифровым знаком, отображающим эту величину, существует функциональная связь (фиг.14д, таблица №10). Она заключается в том, что большей измеряемой величине соответствует больший угол поворота, кратный 90° по часовой стрелке в ряду групп чисел (1-4, 5-8). Или иначе, начертания цифр, отображающие большую величину числа, повернуты по часовой стрелке на угол, кратный 90° по отношению к начертаниям цифр, отображающим меньшую величину числа (фиг.14б, фиг.14в, таблица №10). Наименьшей величиной числа в ряду цифр 1-4 является цифра 1, а в ряду 5-8 наименьшей величиной числа является цифра 5. Повороту фигуры, представленной тем или иным знаком, на каждые 90° от начальной величины числа (цифра 1 или цифра 5) в соответствующем ряду цифр (1-4 или 5-8) к величине числа прибавляется 1 (фиг.14б или фиг.14в, таблица №10). При повороте на 90° по часовой стрелке фигуры, представленной цифрой 0 (фиг.14 г), будет отображена фигура, представленная цифрой 9.
При идентификации таких знаков облегчается работа оператора, который мнемонически способен определить величину любого многозначного числа, составленного на основании предлагаемого цифрового алфавита.
Пример управления цифровыми форматами индикатора на 25 фиксированных знакомест при измерении 5-х параметров контролируемого объекта на пять разрядов представлен на структурной схеме (фиг.15). Ограниченное число выводов, имеющихся на корпусе индикатора, определяет для управления шестнадцатью 32-элементными цифровыми форматами знаков мультиплексный режим работы его. Для этого все одноименные выводы 1-32 элементов отображения всех 25 фиксированных знакомест соединены параллельно и подключены (фиг.15) к соответствующим выводам формирователя тока (ФТ).
Индикация того или иного из пяти пятиразрядных измеряемых параметров объекта может быть кодирована своим цветом.
Генератор тактирующих импульсов (ГТИ) является синхронизирующим звеном схемы /10 - стр.95/. По его первому тактирующему импульсу срабатывают два устройства - оперативное запоминающее устройство (ОЗУ), хранящее кодовую информацию в виде четырехразрядного двоично-десятичного кода (ДДК) для всех двадцати пяти разрядов, и сканирующее устройство выбора цифрового разряда. ОЗУ (оперативное запоминающее устройство) выдает на информационные входы дешифратора четырехразрядный двоично-десятичный код (ДДК) для цифры первого разряда первого измеряемого параметра объекта. Преобразованная дешифратором информация в виде 32-позиционного кода с выходов (ФТ) формирователя токов (1, 2-31, 32) поступает на соответствующие одноименные элементы отображения всех цифровых форматов (всех разрядов и всех измеряемых параметров объекта). Сканирующее устройство выбора цифрового разряда подключает через формирователь тока У1 общий вывод 33 цифрового формата первого разряда первого измеряемого параметра объекта. При первом тактовом импульсе только первая цифра (первый разряд) первого измеряемого параметра объекта и индицируется. Цикл последовательного управления цифрами первого измеряемого параметра продолжается. По пятому тактовому импульсу ГТИ подключает на информационные входы дешифратора информацию о пятом разряде первого измеряемого параметра объекта, а сканирующее устройство выбора цифрового разряда через формирователь тока цифрового знака подключает (вывод 37) только пятую цифру первого измеряемого параметра.
Если на вход сканирующего устройства выбора цифрового разряда последовательно поступают сигналы управления, определяющие индикацию второго измеряемого параметра объекта, то с поступлением тактовых импульсов через формирователи тока цифрового знака У6-У11, соответственно, подключаются общие выводы 38-42 цифровых форматов первого, второго, третьего, четвертого и пятого разрядов второго измеряемого параметра объекта. Высвечивание цифровых знаков к этому времени уже в соответствии с тактовым импульсом подготовлено входными данными (ОЗУ, ДДК, дешифратором и формирователем тока - ФТ). В такой же последовательности индицируются цифровые знаки при работе схемы при измерении третьего, четвертого и пятого параметра объекта, подключая через формирователи тока цифрового знака (У11-У15, У16-У20, У21-У25, соответственно) последовательно цифры пяти их разрядов (I-V), подключая общие выводы цифровых форматов (43-47, 48-52 и 53-57, соответственно).
При необходимости индикации дробных десятичных значений измеряемых параметров объекта, поступающие на схему управления данные должны содержать информацию о включении децимальной точки (ДТ). Сигнал наличия ДТ дает разрешение на запоминание децимальной точки оперативным запоминающим устройством (ОЗУ ДТ). Все выводы от всех 25 цифровых форматов объединены и подключены к выводу 58.
Децимальная точка выявляется на том знаке и в тот синхронизированный с тактовыми импульсами момент, когда должен высветиться соответствующий знак с децимальной точкой, после которого уже отображается дробная часть числа. Децимальная точка выявляется на соответствующем знаке подключением питания к выводу 58 (вывод с ОЗУ ДТ).
Литература
1. Б.Л.Лисицын. Отечественные приборы индикации и их зарубежные аналоги. М.: «Радио и связь». 1993 г.
2. Алиев Т.М., Вигдоров Д.И. Кривошеев В.П. Системы отображения информации. М.: «Высшая школа». 1988 г.
3. Патент №2338270 на изобретение «Индикатор матричный с наилучшим восприятием цифровых знаков», выдан 19 ноября 2008 года. Приоритет изобретения от 21 мая 2007 года. Автор Патраль А.В.
4. Печников А.В., Сидоренко Г.В., Федорова С.А. Средства передачи и отображения информации. М.: «Радио и связь». 1991 г.
5. Б.А.Калабеков, И.А.Мамзелей. Цифровые устройства микропроцессорные системы. М.: «Радио и связь». 1987 г.
6. Яблонский Ф.М. и Троицкий Ю.В. Средства отображения информации. М.: «Высшая Школа». 1985 г.
7. «Энциклопедический Фонд России»: www.russika.ru - П - Преобразователь кода. Автор Патраль А.В.
8. B.C.Гутников. Интегральная электроника в измерительных приборах. Л.: «Энергия». 1974 г.
9. Справочник по интегральным микросхемам. Под редакцией Тарабрина Б.В. М.: «Энергия». 1980 г.
10. Васерин Н.Н., Дадерко Н.К., Прокофьев Г.А. Применение полупроводниковых индикаторов. Под ред. Е.С.Липина. М.: «Энергоатомиздат». 1991 г.
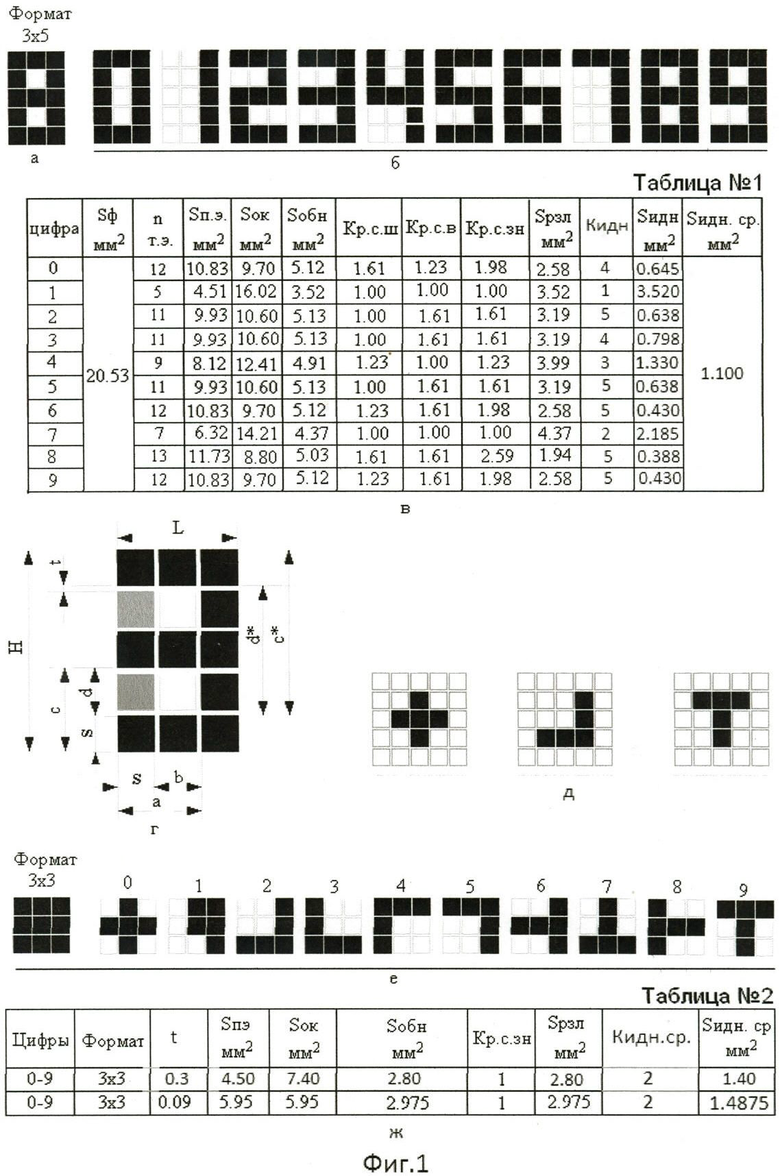
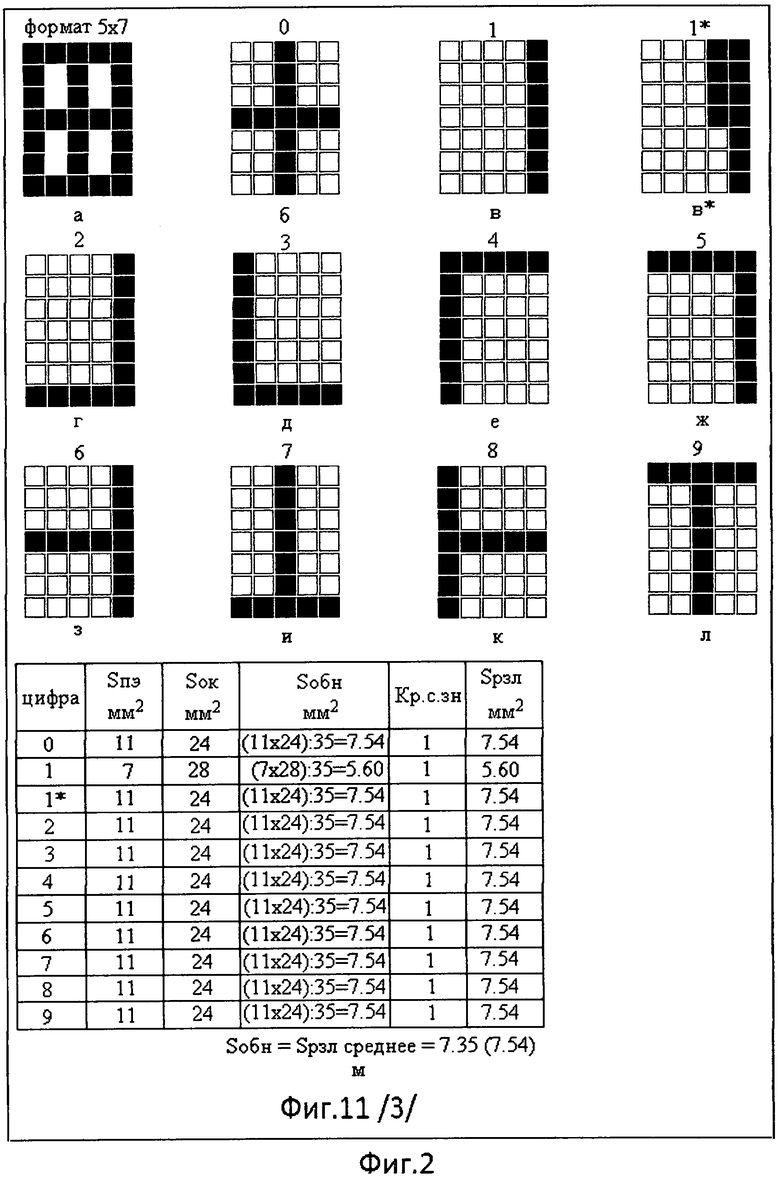
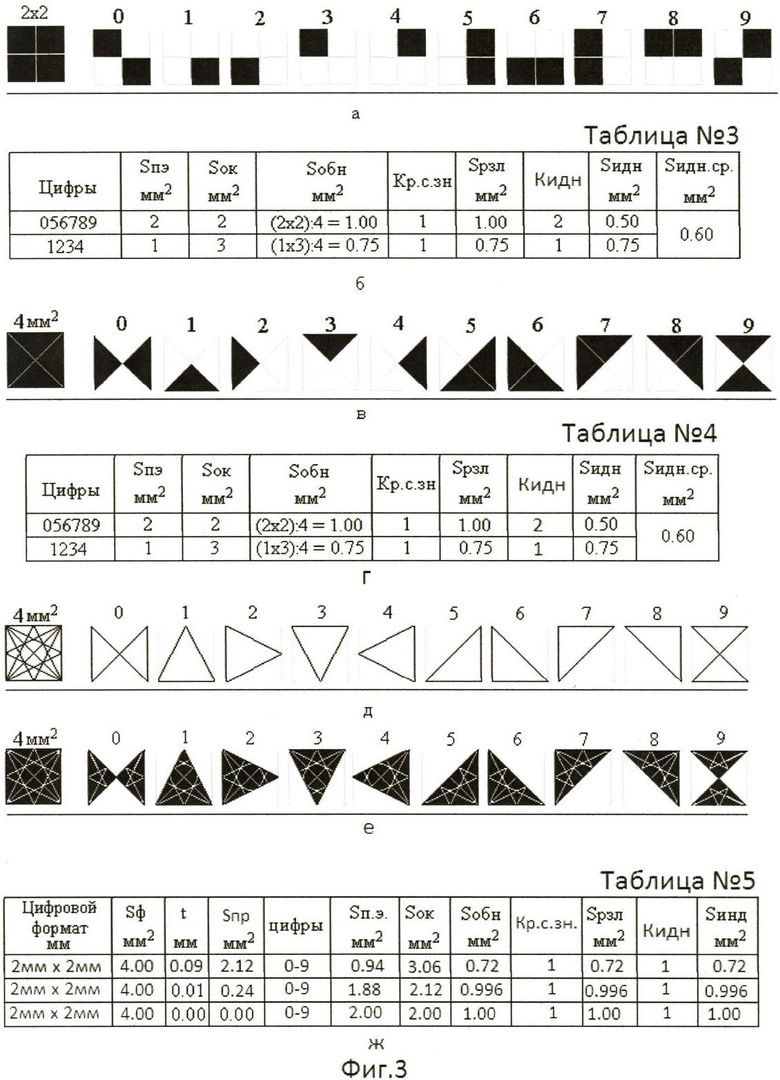

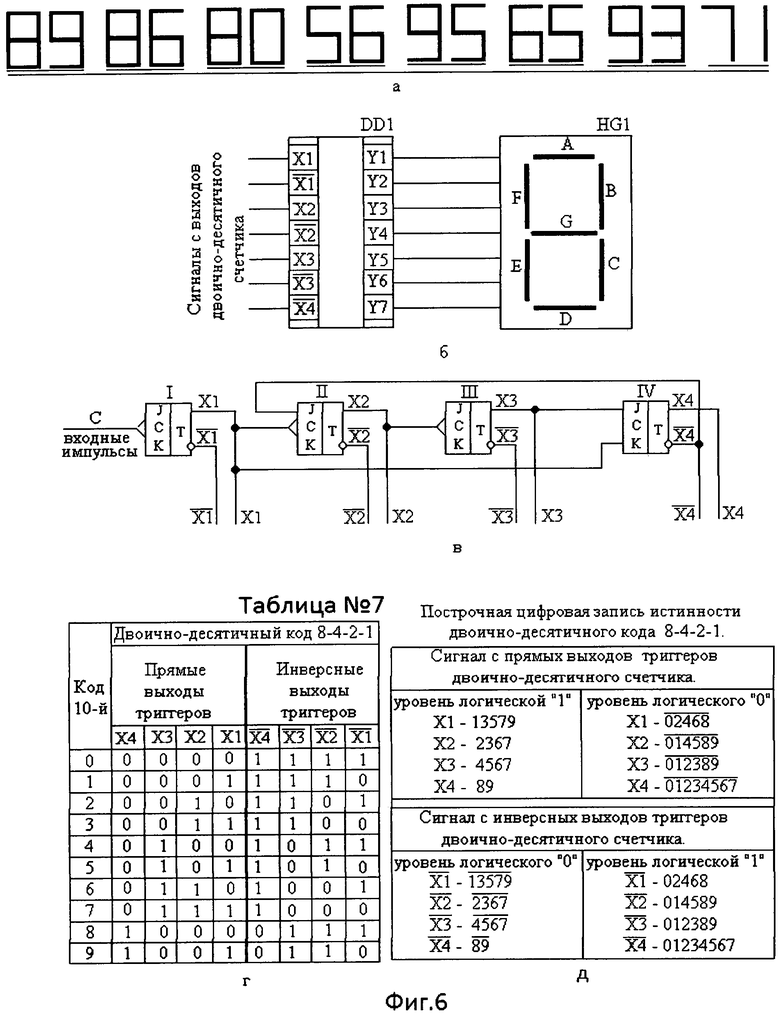
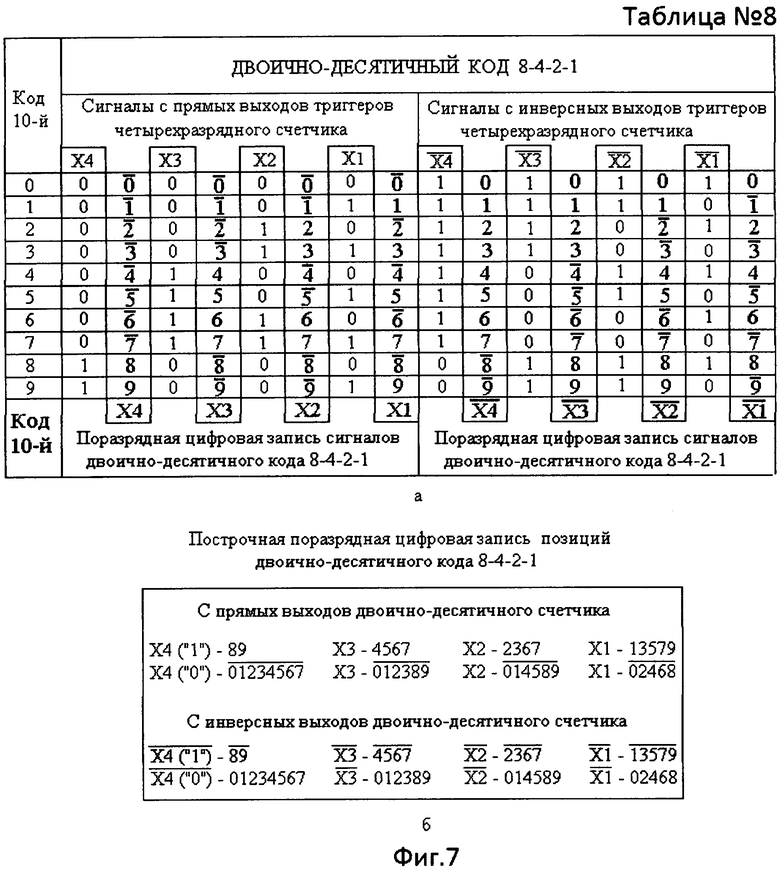
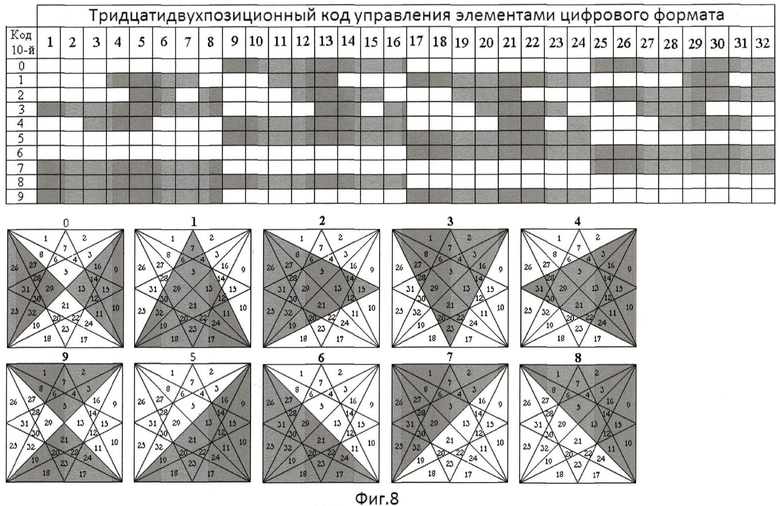
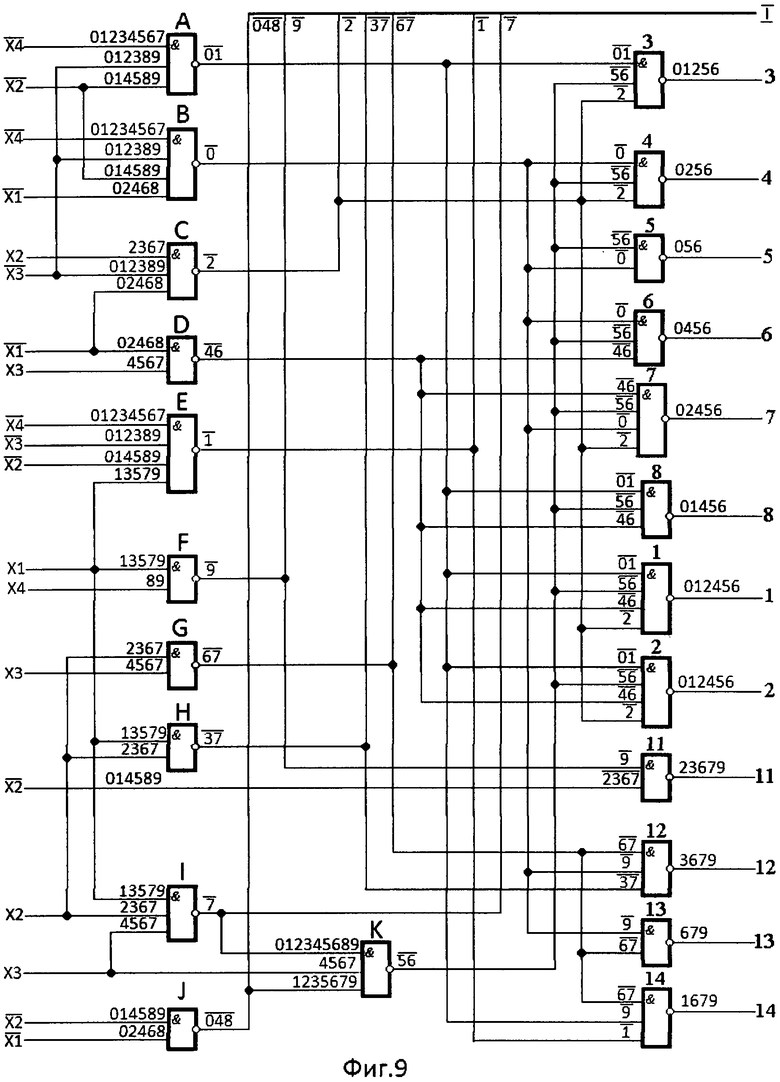
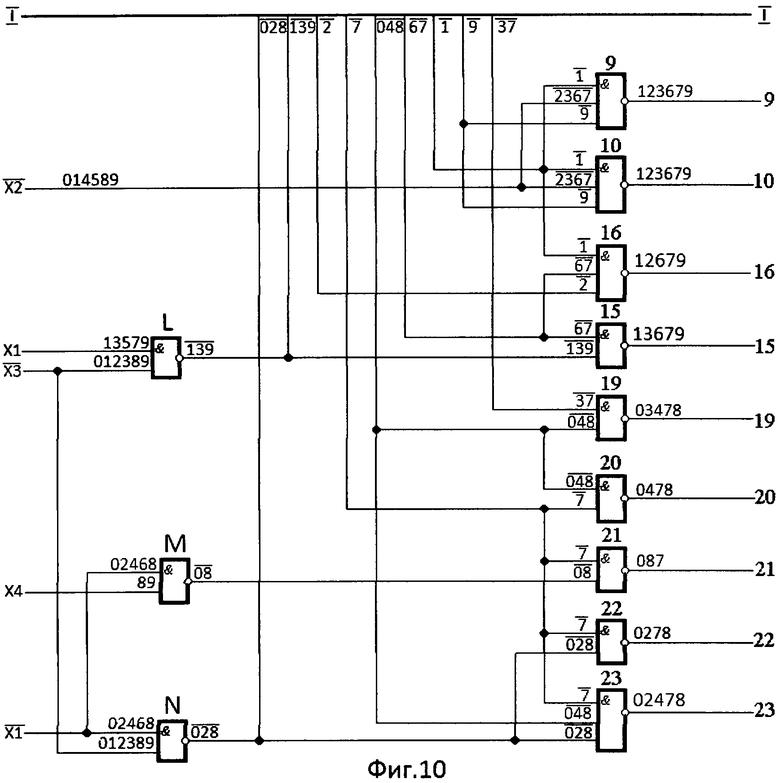
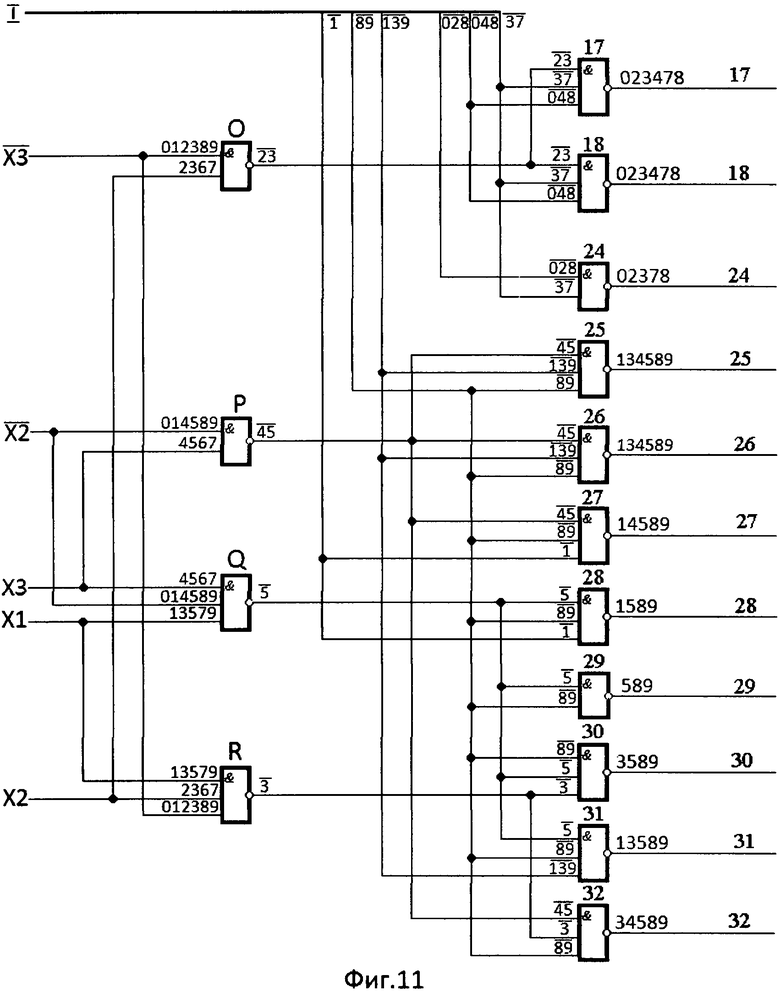
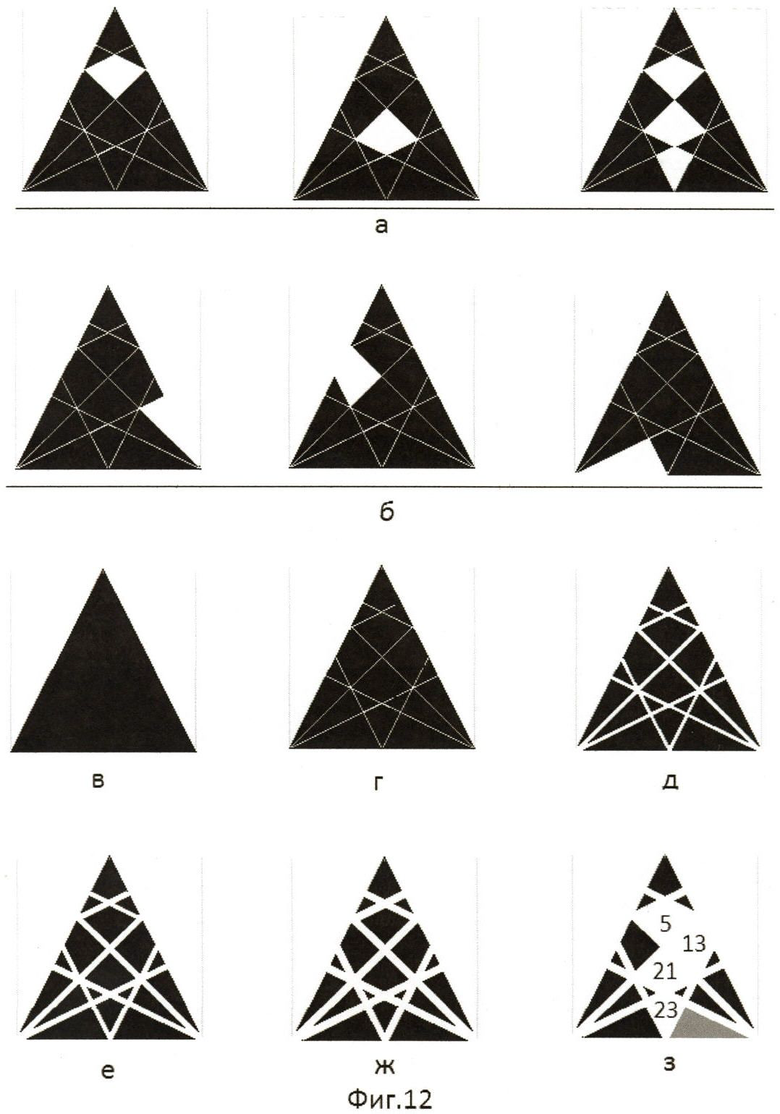
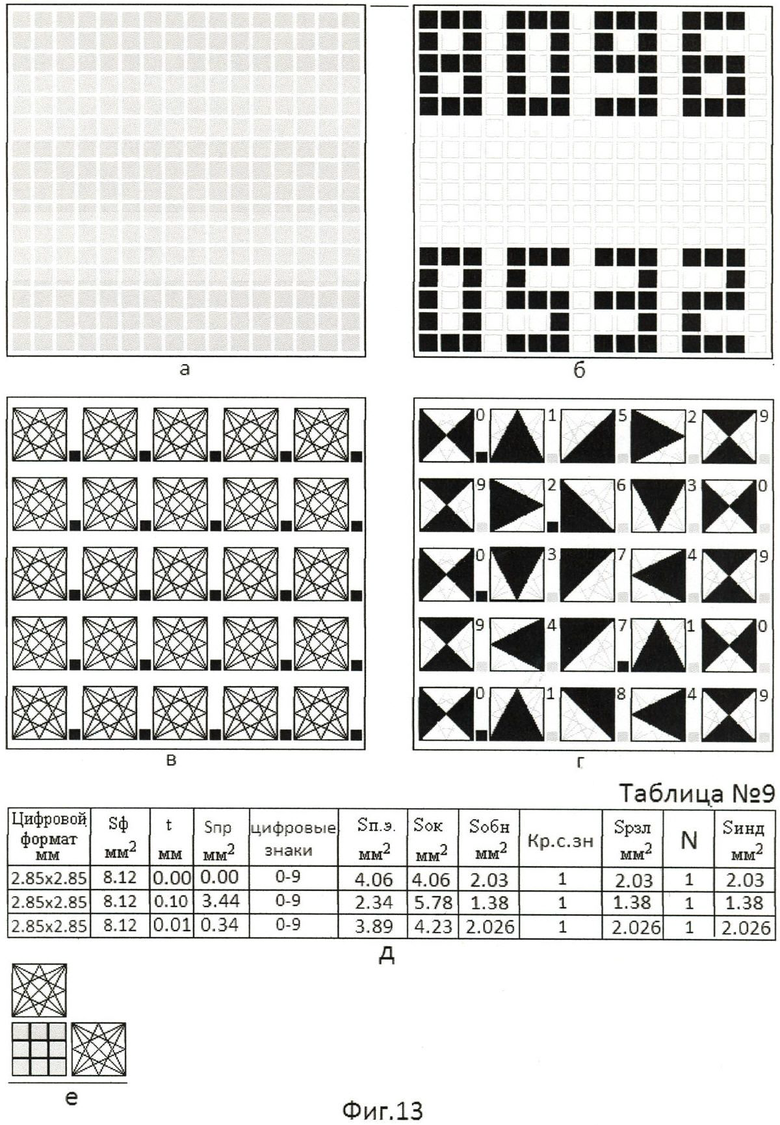
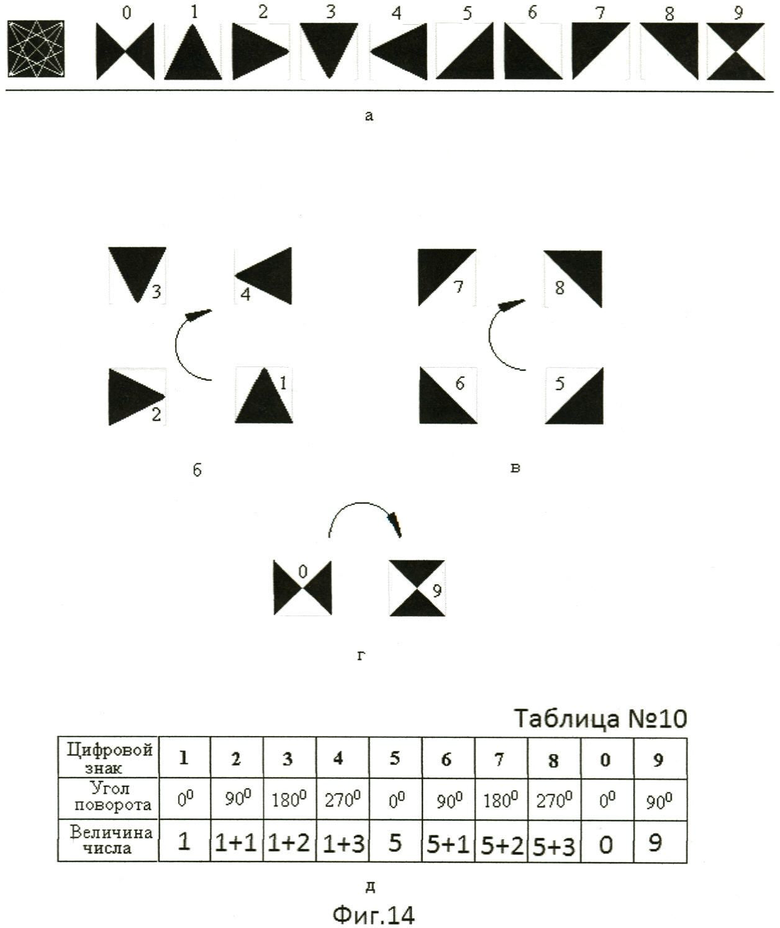
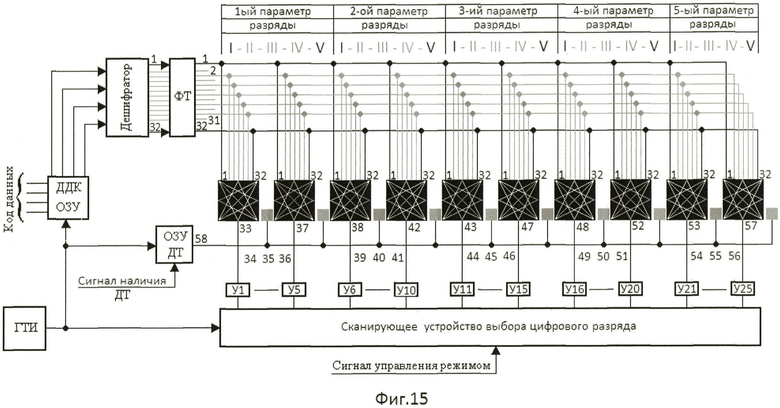
Изобретение относится к средствам отображения цифровой информации. Техническим результатом является увеличение цифрового информационного объема средств отображения информации без ухудшения восприятие цифровых знаков. Для визуального отсчета цифровой информации используется цифровой алфавит, начертание цифровых знаков которого обеспечивается наилучшим восприятием их на стадиях обнаружения, различения и идентификации. Элементы отображения цифрового формата, представляющего знакоместо индикатора, образованы в результате пересечений линий, проведенных из углов квадрата, представляющего информационное поле его, к серединам смежных, противоположных этим углам, сторон квадрата, с линиями его диагоналей, и при формировании знаков величина площади из высветившихся элементов отображения равна величине площади из невысветившихся элементов отображения, без учета величины промежутков между ними. 15 ил.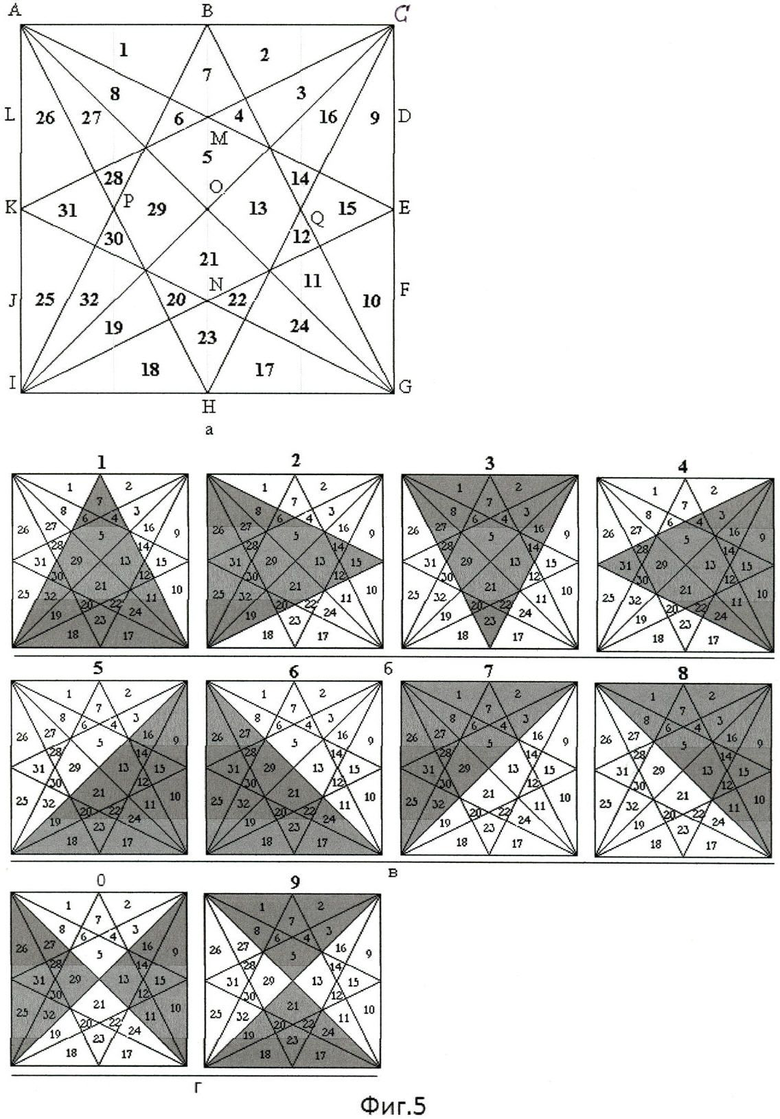
Устройство для индикации с наилучшей идентификацией знаков, содержащее преобразователь двоично-десятичного кода 8-4-2-1 в позиционный код управления элементами индикатора, габаритные размеры информационного поля которого в виде квадрата 20 мм × 20 мм соответствуют индикатору типа КИПГОЗА-8×8К, на лицевой стороне его размещены 25 знакомест, а с обратной стороны корпуса индикатора расположены 64 вывода, предназначено для отображения цифровых знаков от 0 до 9 и децимальной точки в мультиплексном режиме управления, отличающееся тем, что элементы отображения цифрового формата, представляющего знакоместо индикатора, образованы в результате пересечений линий, проведенных из углов квадрата, представляющего информационное поле его, к серединам смежных, противоположных этим углам, сторон квадрата с линиями его диагоналей, и при формировании знаков величина площади из высветившихся элементов отображения равна величине площади из не высветившихся элементов отображения без учета величины промежутков между ними.
| УСТРОЙСТВО ДЛЯ ИНДИКАЦИИ С УВЕЛИЧЕННОЙ ИНФОРМАЦИОННОЙ ЕМКОСТЬЮ | 2003 |
|
RU2249912C2 |
| Рифленый лист | 1987 |
|
SU1431881A1 |
| US 4288792 A1, 08.09.1981 | |||
| ПОРШНЕВОЙ ВАКУУМНЫЙ НАСОС ДВОЙНОГО ДЕЙСТВНЯ | 0 |
|
SU233827A1 |
| ИНДИКАТОР ЦИФРОВОЙ СЕГМЕНТНЫЙ С МАСШТАБИРОВАНИЕМ ЗНАКА | 2005 |
|
RU2302042C1 |
| ИНДИКАТОР ЦИФРОВОЙ СЕГМЕНТНЫЙ УНИВЕРСАЛЬНЫЙ | 2005 |
|
RU2298239C2 |
| УСТРОЙСТВО ДЛЯ ИЗМЕРЕНИЯ И ИНДИКАЦИИ ВЕЛИЧИНЫ УГЛА ПОЛОЖЕНИЯ ВАЛА | 2002 |
|
RU2231215C2 |
| ЕР 1640958 А2, 29.03.2006. | |||
Авторы
Даты
2012-08-27—Публикация
2011-01-12—Подача