Предлагаемое изобретение относится к средствам отображения информации (СОИ), значительную область применения которых представляют знакосинтезирующие индикаторы (ЗСИ).
Индикатор цифровой многоразрядный (3×3) с форматом знаков 2×2 может найти применение во всех средствах отображения информации, в которых требуется улучшение восприятия цифровых знаков с одновременным уменьшением энергетических затрат при их формировании.
Матричные индикаторы позволяют в синтезированном виде высветить сложную информацию в виде знаков, букв русского и латинского алфавита, символов и десятичных цифр от 0 до 9. И на долю цифровой информации приходится наибольший расход энергетических затрат в различных устройствах вычислительной и измерительной техники.
Большой расход электропитания, который является одним из недостатков полупроводниковых ЗСИ [1 - стр.68], в немалой степени объясняется их начертанием с большим числом отображаемых элементов в знаках. К другим недостаткам этого начертания относятся также:
1. большие габаритные размеры индикаторов;
2. невысокая разрешающая способность знаков;
3. большое среднее число точечных элементов на знак;
4. невысокая цифровая информационная емкость индикаторов.
И как результат этих недостатков - невысокое восприятие знаков, выражающееся в затруднении различения между некоторыми семипозиционными знаками и скорости опознания их.
Стремление достигнуть уменьшения энергетических затрат и улучшения восприятия десятичных знаков снижением числа элементов при их формировании приводит к непривычности начертания знаков.
Непривычность начертания знаков при этом должна быть оправдана не только уменьшением энергетических затрат, но и наилучшими эргономическими параметрами восприятия их.
Целью предлагаемого изобретения является:
1. уменьшения цифрового формата знака;
2. уменьшения среднего числа точечных элементов на знак;
3. уменьшение энергопотребления на цифровой знак;
4. улучшение параметрических характеристик цифровых знаков, улучшение их восприятия;
5. увеличение цифровой информационной емкости без увеличения габаритных размеров информационного поля индикаторов.
Указанная цель достигается формированием новых десятичных цифровых знаков на информационном поле индикатора с минимально возможным числом отображаемых элементов в них.
Разрешающую способность индикаторов можно оценивать по возможности различения оператором двух воспроизводимых световых точек или линий, находящихся на некотором расстоянии друг от друга. При низкой разрешающей способности оператор принимает две точки (линии) за одну, а при высокой разрешающей способности две очень близкие точки (линии) воспринимаются как отдельные.
Повышать разрешающую способность можно до определенного предела, свыше которого изображение не будет восприниматься глазом [2 - стр.115].
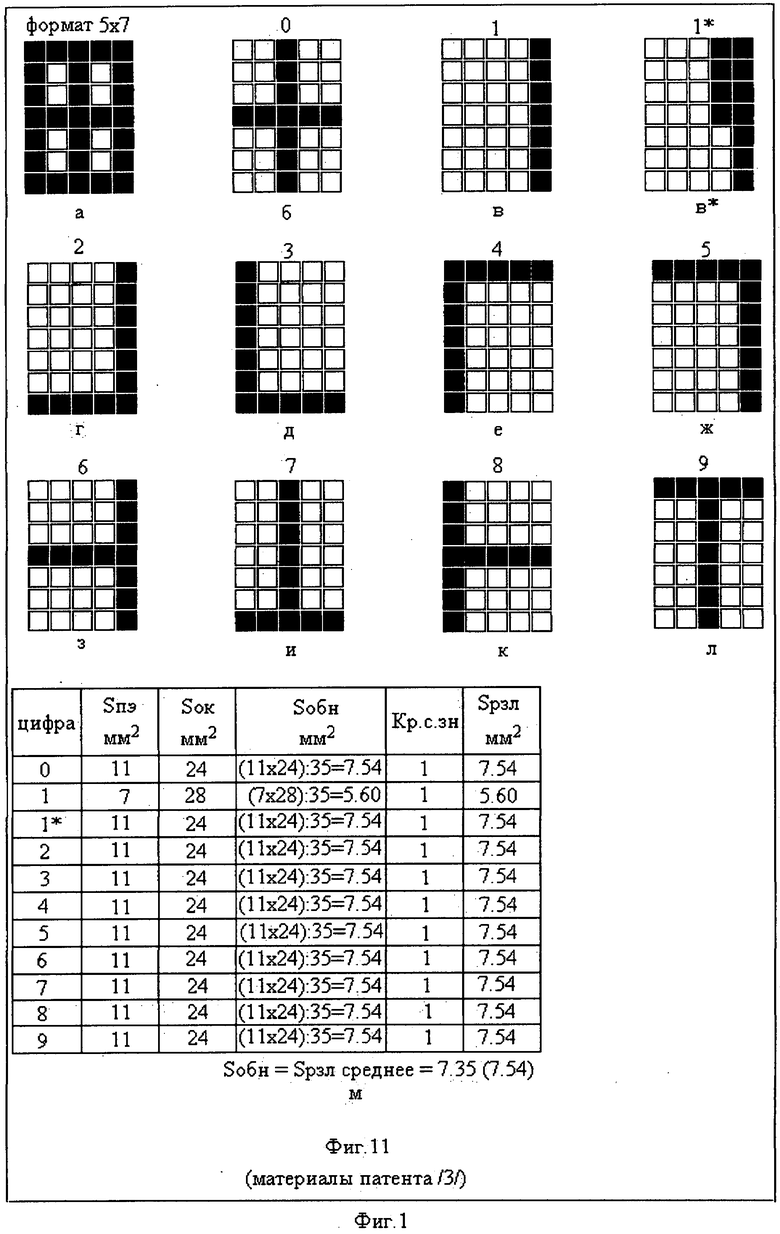
Повышение разрешающей способности до предела осуществлено на матричном индикаторе при формировании цифровых знаков с постоянным числом точечных элементов в них [3, фиг.11 - материалы патента].
Этот матричный индикатор (фиг.1) с наилучшим восприятием цифровых знаков принят в качестве основы для сравнительного анализа параметров новых цифровых знаков на информационном поле предлагаемого индикатора цифрового многоразрядного (3×3) с форматом знаков 2×2.
Под восприятием понимают процесс целостного отражения предметов, возникающий при непосредственном воздействии физических раздражителей (стимулов) на рецепторные поверхности органов чувств. Этот многоуровневый процесс, заканчивающийся формированием чувственного образа, включает следующие стадии: обнаружение, различение, идентификация, опознание [4 - стр.46].
Обнаружение - стадия восприятия, на которой оператор выделяет объект из фона. При этом устанавливается лишь наличие сигнала в поле зрения без оценки его формы и признаков [4 - стр.46].
Величина эквивалентной площади обнаружения знака (Sобн) определяется по формуле [3]:
Sобн=(Sп.э × Sок):(Sп.э+Sок), где
Sп.э - величина площади высветившихся точечных элементов формата знака;
Sок - величина площади невысветившихся точечных элементов формата знака.
Только при равенстве величины площади позиционных элементов (Sп.э) и величины площади «окна» (Sок) знака достигается максимальная величина эквивалентной площади обнаружения (Sобн) знака и максимальная скорость его (при Sп.э=Sок) обнаружения 131, равная одной четверти площади формата знака (Sзн):
Sобн=(Sп.э × Sок):(Sп.э+Sок)=Sзн/4.
Различение - стадия восприятия, на которой оператор способен выделить детали, позиционные элементы отображения знака [4 - стр.46]. Способность средств отображения информации воспроизводить мелкие детали характеризуется их разрешающей способностью.
Чтобы количественно оценить влияние разрешающей способности знака на величину эквивалентной площади при различении его, необходимо связать величины, отображающие разрешающую способность знака по ширине с эквивалентной площадью обнаружения его.
Для этого необходимо ввести коэффициент разрешающей способности (Кр.с.зн) знака. И с помощью этого коэффициента вычислить эквивалентную площадь различения знака (Sрзл) по формуле:
Sрзл=Sобн:Кр.с.зн [3].
Уменьшение величины коэффициента разрешающей способности знака увеличивает эквивалентную площадь различения знака и скорость его опознания.
Чтобы у каждого десятичного знака величина эквивалентной площади обнаружения (Sобн) была равна величине эквивалентной площади различения (Sрзл), необходимо, чтобы разрешающая способность знака была максимальна. Т.е. необходимо, чтобы величина коэффициента разрешающей способности знака (Кр.с.зн) была бы минимально возможной и равна 1 [3].
При формировании знаков (фиг.1, [3, фиг.11м]) цифрового алфавита формата 5×7 число высветившихся точечных элементов в них постоянно (Sп.э=11), коэффициент разрешающей способности любого знака равен 1 (Кр.с.зн=1), размер точечного элемента принят 1.0 мм × 1.0 мм, а промежуток между точечными элементами по контуру знака исключен. Величина эквивалентной площади обнаружения знака (Sобн) равна величине эквивалентной площади различения знака (Sрзл):
Sрзл=Sобн:Кр.с.зн=Sобн [3].
На первой стадии восприятия знака, при обнаружении, оператор выделяет общую площадь, занимаемую позиционными элементами на фоне площади «окна». На второй стадии восприятия знака, при различении, оператор выделяет расположение отдельных позиционных элементов на фоне площади «окна».
Равенство величин эквивалентной площади обнаружения и эквивалентной площади различения (Sобн=Sрзл) показывает, что две стадии восприятия знака - обнаружение и различение - сливаются в одну стадию, на которой оператор выделяет элементы знака. Время опознания знака уменьшается.
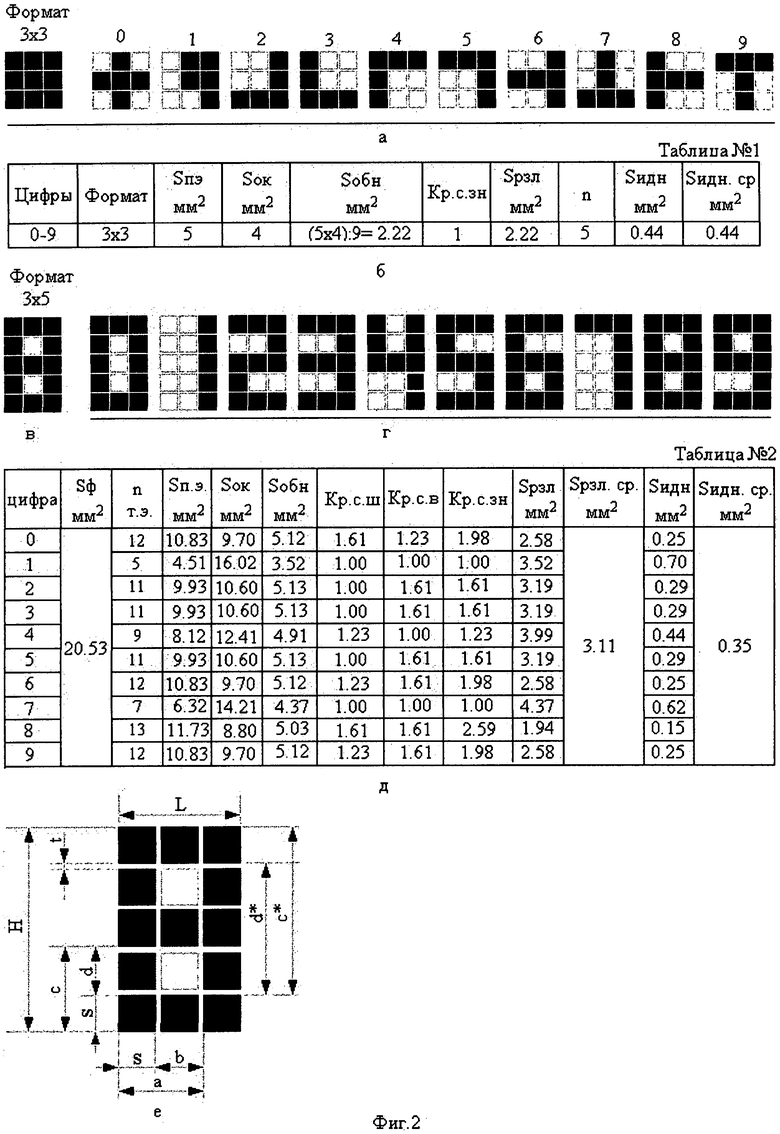
Перейти от формата индикатора с видом матрицы 5×7 (фиг.1, [3, фиг.11м]) к формату индикатора с видом матрицы 3×3 (фиг.2а) с уменьшенным числом точечных элементов при отображении цифровых знаков не вызывает никаких осложнений. Сигналы управления на высвечивание и на гашение в процессе формирования десятичных знаков поступают на все точечные элементы матрицы вида 3×3 (цифрового формата 3×3). Т.е. все точечные элементы матрицы вида 3×3 активно участвуют в процессе формирования контура знака из высветившихся точечных элементов (Sп.э) и площади «окна» из оставшихся невысветившихся точечных элементов (Sок) ее в зависимости от начертания знака. Или точнее, площадь «окна» равна разности между величиной площади цифрового формата (Sф=9 мм2) и величиной площади контура знака (Sв.т.э=Sп.э=5 мм2) из высветившихся точечных элементов (Sок=Sф-Sв.т.э=4 мм2). При формировании любого десятичного знака площадь «окна» из невысветившихся точечных элементов (Sн.т.э) не ограничена с двух сторон вертикальными или горизонтальными линиями контура знака из точечных элементов его, т.е. не расположена между ними. Она расположена снаружи контура знака, а контур знака расположен внутри площади «окна» из невысветившихся точечных элементов (Sн.т.э). В таком случае величина площади «окна» не влияет на величину коэффициента разрешающей способности знака. Величина эквивалентной площади обнаружения знака (Sобн) равна при этом величине эквивалентной площади различения (Sрзл) его, т.к. коэффициент разрешающей способности знаков (Кр.с.зн) при их начертании наименьший и равен 1:
[Sобн=(Sп.э×Sок):Sф=Sрзл].
Уменьшение величины коэффициента разрешающей способности знака увеличивает эквивалентную площадь различения знака и скорость его опознания.
Формат матрицы вида 5×7 уменьшен до формата 3×3, т.е. уменьшено число точечных элементов почти в 4 раза с 35 до 9. Если величина эквивалентной площади различения (Sрзл) знаков у формата 5×7 равна 7.54 мм2 (фиг.1, [3, фиг.11 м]), то величина эквивалентной площади различения (Sрзл) знаков у формата 3×3 уменьшилась менее чем в 3.5 раза и равна 2.22 мм2 (фиг.2б, таблица №1).
Сокращение позиционных (точечных) элементов при формировании любого десятичного знака привело к относительному (по отношению к габаритным размерам цифровых форматов) улучшению возможности его различения.
Если же величину эквивалентной площади различения знака (Sрзл) распределить на величины эквивалентной площади различения каждого точечного элемента, высветившегося при формировании знака, разделив ее на число (n) точечных элементов в знаке, то получится величина эквивалентной площади различения каждого точечного элемента (Sрзл.т.э) знака. При этом каждый точечный элемент в знаке различим, и оператор способен идентифицировать любой высветившийся знак предлагаемого цифрового алфавита.
Величина эквивалентной площади различения каждого точечного элемента знака (Sрзл.т.э) названа величиной эквивалентной площади идентификации знака (Sидн).
Идентификация - стадия восприятия [4, стр.46], на которой оператор отождествляет объект с эталоном, хранящимся в памяти (или отождествляет два одновременно воспринимаемых объекта). Величина эквивалентной площади идентификации (Sидн) каждого знака при его формировании занесена в таблицу №1 (фиг.2б). Она вычисляется по формуле:
Sидн=Sрзл/n или Sидн=Sрзл/Sп.э, где n=Sп.э,
т.к. каждый высветившийся точечный элемент равен 1×1 мм2 (Sидн=0.44 мм2).
Этот наименьший пока формат цифровых знаков (3×3) необходимо сравнить с наименьшим форматом семипозиционных знаков (3×5) по их восприятию на стадии идентификации.
В качестве прототипа выбран матричный индикатор КИПГО2А-8×8Л (корпус типа КИ13-1) с видом матрицы 8×8 [5 - стр.353]. При формировании семипозиционных цифр на лицевой стороне матричного индикатора можно воспользоваться наименьшим цифровым семипозиционным форматом с числом точечных элементов его, равным 3×5 (фиг.2в).
Для каждого отображаемого знака (фиг.2г) формата 3×5 (фиг.2в) определяют [3] и заносят в таблицу №2 (фиг.2д):
1. площадь позиционных элементов знака (Sп.э), равную площади (s×s) точечного элемента, умноженной на количество точечных элементов (n) в данном знаке (Sп.э=s2×n). Площадь точечного элемента данного индикатора равна (для простоты начертания и расчета точечный элемент принят квадратным со сторонами, равными диаметру) [2 - стр.355]:
Sт.э=(s×s)=0.95 мм × 0.95 мм=0.90 мм2;
2. площадь формата знака (фиг.2е), равную Sф=L×Н=(3s+2t)×(5s+4t), где
L=(3s+2t) - ширина формата знака,
Н=(5s+4t) - высота формата знака;
s - ширина (высота) точечного элемента (0.95 мм);
t - промежуток между точечными элементами, равный 0.3 мм как по ширине, так и по высоте знака;
площадь формата знака на 3×5 точечных элементов равна
Sф=(3s+2t)×(5s+4t)=(0.95×3+0.3×2)×(0.95×5+0.3×4)=20.53 мм2;
3. площадь «окна» (Sок), равную площади формата знака (Sф) за вычетом площади (Sп.э) позиционных элементов знака (Soк=Sф-Sп.э);
4. величину эквивалентной площади обнаружения по формуле:
Sобн=(Sп.э × Sок):(Sп.э + Sок);
5. величину коэффициентов разрешающей способности по ширине для знаков (фиг.2 г) 0 и 8 (линейный размер точечного элемента s=0.95 мм, расстояние между точечными элементами t=0.3 мм), равную: Кр.с.ш=а/b, где а=2s+2t и b=s+2t (фиг.2е), или
Кр.с.ш=а/b=(2s+2t):(s+2t)=(2×0.95+2×0.3):(0.95+2×0.3)=2.50:1.55=1.61 (фиг.2д, 10 и 2 строки снизу, колонка 7);
6. величину коэффициентов разрешающей способности по ширине знака для цифр 1, 2, 3, 5 и 7 (фиг.2г). У этих знаков отсутствуют точечные элементы (эти элементы на фиг.2е, например, для цифры 3 осветлены), относительно которых определяется коэффициент разрешающей способности по ширине знака (Кр.с.ш=а/b).
Кр.с.ш=а/b=а/а=1 [3].
В этом случае измеряется расстояние (а) от одного позиционного элемента до границы знака (фиг.2е) и измеряется то же расстояние от одного позиционного элемента также до границы знака (b=а), при отсутствии второго позиционного элемента. Отсутствие второго позиционного элемента знака эквивалентно расположению второго позиционного элемента на достаточно большом расстоянии, не оказывающем влияние на различение первого позиционного элемента. И коэффициент разрешающей способности в этом случае будет равен Кр.с.ш=1;
7. величину коэффициентов разрешающей способности по ширине знака для цифр 4, 9 и 6, у которых отсутствует позиционный элемент слева в нижней половине (цифры 4 и 9) знака и справа в верхней половине (цифра 6) знака (фиг.2г);
для цифр 4 и 9 [3]:
а. измеряется суммарное расстояние (а+а) от правого нижнего (второй снизу) позиционного элемента и от правого верхнего (второй сверху) позиционного элемента до границ знака в нижней и верхней половинах его;
б. измеряется суммарное расстояние (а+b) от правого нижнего (второй снизу) позиционного элемента до границы знака (а), при отсутствии позиционного элемента слева в нижней половине (второго снизу) знака, и от правого верхнего позиционного элемента до верхнего (второго сверху) позиционного элемента (b) слева в верхней половине знака, при его наличии.
Коэффициент разрешающей способности по ширине знака вычисляется по формуле:
Кр.с.ш=(а+а):(b+а), где а=2s+2t и b=s+2t,
Kp.c.ш=2(2s+2t):(s+2t+2s+2t)=2(2×0.95+2×0.3):(0.95+2×0.3+2×0.95+2×0.3)=5.00:4.05=1.23 (фиг.2д - 6 и 1 строки снизу соответственно, колонка 7).
Подобным же образом определяется величина коэффициента разрешающей способности по ширине знака для цифры 6, ее величина также будет равна Кр.с.ш=1.23 (фиг.2д, 4 строка снизу, колонка 7);
8. величину коэффициентов разрешающей способности по высоте для знаков 2, 3, 5, 6, 8 и 9 (фиг.2г) определяют по формуле: Кр.с.в=c/d, где с=2s+2t и d=s+2t (фиг.2е).
Kp.c.в=(2s+2t):(s+2t)=(2×0.95+2×0.3):(0.95+2×0.3)=2.50:1.55=1.61 (фиг.2д - 8, 7, 5,4, 2,1 строки снизу соответственно, колонка 8);
9. величину коэффициента разрешающей способности по высоте для знака 0:
Кр.с.в=c*/d*, где с*=4s+4t и d*=3s+4t (фиг.2е);
Kp.c.в=(4s+4t):(3s+4t)=(4×0.95+4×0.3):(3×0.95+4×0.3)=5.00:4.05=1.23 (фиг.2д - 10 строка снизу, колонка 8);
10. величину коэффициентов разрешающей способности по высоте для знаков 4 и 7:
Кр.с.в=c/d=1 (при d=c);
11. величину коэффициентов разрешающей способности по высоте для знака 1:
Кр.с.в=1 (у этого знака нет горизонтального позиционного элемента);
12. величины коэффициентов разрешающей способности каждого знака (фиг.2д, колонка 9).
Величина коэффициента разрешающей способности знака равна произведению величины коэффициента разрешающей способности по ширине знака на величину коэффициента разрешающей способности по высоте знака:
Кр.с.зн=Кр.с.ш × Кр.с.в [3];
13. величину эквивалентной площади (Sрзл=Sобн/Кр.с.зн) различения знака (фиг.2д, колонка 10). Величина эквивалентной площади различения знака (Sрзл) меньше величины эквивалентной площади обнаружения знака (Sобн) на величину коэффициента разрешающей способности знака (Кр.с.зн).
Средняя величина эквивалентной площади различения на знак у семипозиционных знаков цифрового формата 3×5 равна 3.11 мм2.
Определяют величину эквивалентной площади идентификации (Sидн) каждого знака при его формировании. На примере формирования семипозиционных цифр 0, 6, 8 и 9 формата 3×5 видно, что невозможно эти цифры идентифицировать, если невозможно различить каждый точечный элемент при их отображении. При формировании цифр 0, 6 и 9 их начертания (12 т.э) отличаются от начертания цифры 8 (13 т.э) одним лишь точечным элементом.
Определив величину эквивалентной площади идентификации для каждой цифры по формуле:
Sидн=Sрзл/n или Sидн=Sрзл/Sп.э, где n=Sп.э,
заносят ее в таблицу №2 (фиг.2д, колонка 12).
Средняя величина эквивалентной площади идентификации на знак у семипозиционных цифр оказалась значительно ниже (Sидн.ср.=0.35 мм2), чем у знаков со значительно меньшим цифровым форматом (Sидн.ср.=0.44 мм2), с постоянным и меньшим числом точечных элементов на знак (фиг.2б, таблица №1, колонка 10).
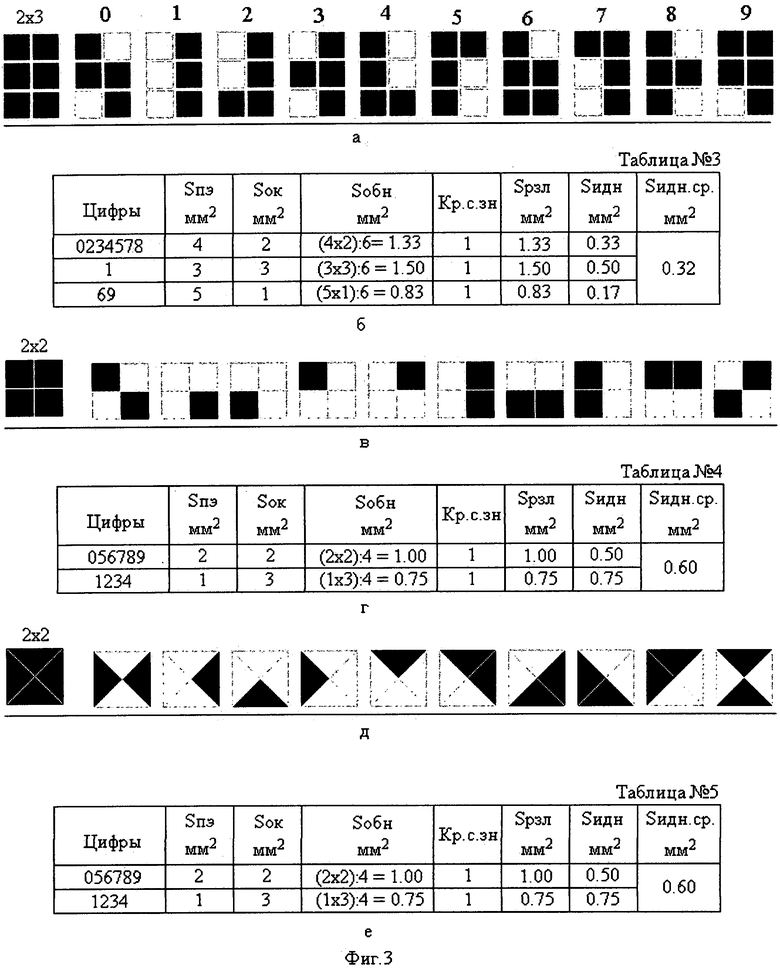
При дальнейшем уменьшении цифрового формата с 3×3 до цифрового формата 2×3 (фиг.3а) изменяется начертание цифр при их формировании, у которых число точечных элементов в каждом знаке различно. В каждой группе знаков, с постоянным числом высветившихся точечных элементов, подсчитаны величины эквивалентной площади: обнаружения, различения и идентификации знака (фиг.3б, таблица №3). В этом случае для сравнения по восприятию цифр на стадии идентификации необходимо определить среднюю величину эквивалентной площади идентификации на знак (Sидн.ср.). Так, если величины эквивалентной площади идентификации на знак равны:
при формировании семи четырехточечных знаков (цифры 0234578), Sидн = 0.33 мм2;
при формировании одного трехточечного знака (цифра 1), Sидн = 0.50 мм2;
при формировании двух пятиточечных знаков (цифры 6 и 9), Sидн = 0.17 мм2,
то средняя величина эквивалентной площади идентификации на знак (Sидн.ср.) равна частному от деления суммарной величины эквивалентной площади идентификации всех знаков на их число:
Sидн.ср.=(0.33 мм2 × 7+0.50 мм2 × 1+0.17 мм2 × 2):10=0.32 мм2.
С уменьшением формата матрицы индикатора уменьшение габаритного размера его происходит быстрее, чем уменьшение средней величины эквивалентной площади идентификации на знак.
При рассмотрении цифрового формата с видом матрицы 2×2 (фиг.3в), когда габаритный размер его уменьшился в 1.5 раза в сравнении с предыдущим цифровым форматом 2×3 (фиг.3а), средняя величина эквивалентной площади на знак идентификации даже увеличилась до 0.60 мм2 (фиг.3г, таблица №4). Она превысила среднюю величину эквивалентной площади идентификации (Sидн=0.35 мм2) семипозиционных знаков цифрового формата 3×5 (фиг.2д, таблица №2), у которых в формируемых знаках значительно больше (от 5 до 13) точечных элементов. Тогда как у цифровых знаков формата 2×2 число точечных элементов в знаке не более двух.
Становится понятно, что чем меньше среднее число высветившихся элементов на знак у данного цифрового алфавита, тем больше величина эквивалентной площади идентификации на знак, тем выше скорость восприятия знака на стадии идентификации.
С уменьшением цифрового формата, когда число высветившихся точечных элементов на знак уменьшилось (фиг.3в), средняя величина эквивалентной площади идентификации на знак даже увеличилась до 0.60 мм2 (фиг.3г, таблица №4). Но идентифицировать такие знаки затруднительно.
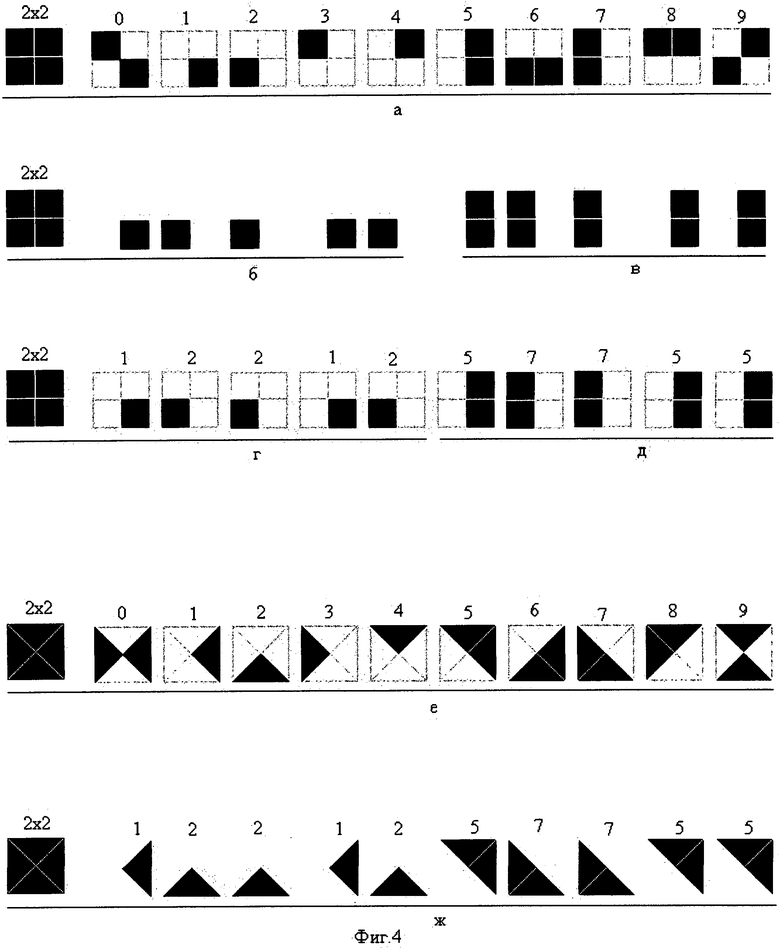
Если из цифрового алфавита (фиг.4а) сформировать, например, два многозначных числа (фиг.4б, фиг.4в) с одним и тем же числом точечных элементов в каждом из них, расположенных на одном и том же уровне по высоте, то прочесть их будет затруднительно в связи с поиском места расположения разрядов этого числа. Прочтение многозначных чисел (12212 или 57755) затрудняется тем, что один и тот же по начертанию знак может принимать различное значение в зависимости от того, как оператор определит его место в ряду формируемых чисел. Его надо научиться определять по расстоянию между разрядами, какой величине соответствует сформированный знак. Время идентификации при формировании таких знаков увеличится, несмотря на сравнительно большую величину эквивалентной площади идентификации на знак. Если же каждый разряд знаков при их формировании сопроводить отображением границ этого цифрового формата (фиг.4г, фиг.4д), то задача идентификации этих многозначных чисел (12212 или 57755) упрощается, сократится время их идентификации. Задача с идентификацией многозначных чисел при начертании знаков в виде единичных элементов отображения (квадрата) или прямоугольника (сдвоенных элементов отображения) осложняется и при других значениях отображаемых многозначных чисел. Таким образом, идентифицировать такие знаки, визуально кодированные формой и пространственным расположением однотипных элементов, затруднительно. Только при начертаниях цифр 0 и 9 время их идентификации может быть уменьшено, поскольку начертания их визуально различны по расположению элементов формата индикатора. Таким образом, формирование визуально не ориентированного знака с уменьшенным числом (2×2) простых (например, в виде квадратов и прямоугольников) элементов в нем затрудняет определение величины многозначного числа. В таком цифровом формате возникает необходимость изменить начертание элементов управления его.
Выбор оптимальной системы визуального кодирования определяется главным образом задачами, которые решает оператор, и спецификой его работы.
Под визуальным кодированием информации понимают операцию отождествления условных знаков (символов, сигналов) с тем или иным видом информации. Выбор оптимального кода связан с обеспечением максимальной скорости и надежности приема и переработки информации человеком, т.е. с достижением максимальной эффективности выполнения операций зрительного поиска, обнаружения, различения, идентификации и опознания сигналов. Каждый из способов кодирования - это категория кодирования или вид алфавита.
Кодирование формой является универсальным средством представления информации благодаря алфавиту различных символов. Лучше различаются и распознаются простые геометрические фигуры, состоящие из небольшого количества элементов.
При использовании в качестве кодовых категорий формы, размера, цвета и пространственной ориентации фигур наименьшую точность имеет идентификация по размеру [4 - стр.61].
Если же тот же самый по габаритным размерам (2×2) цифровой формат (фиг.3в) в виде квадрата разделить на четыре позиционных элемента не перпендикулярными линиями к сторонам квадрата через центр оси его, а диагоналями этого квадрата, то получится иное расположение позиционных элементов (2×2) цифрового формата (фиг.3д).
Параметры знаков такого цифрового формата (фиг.3е, таблица №5), состоящего из четырех (2×2) светоизлучающих диодов, излучающая поверхность которых представляет фигуру в виде равнобедренного треугольника, не отличаются от величин параметров знаков (фиг.3г, таблица №4), формат которых представлен в виде матрицы 2×2. Линейные размеры основания каждого такого треугольника (фиг.3д) равны размерам стороны квадрата цифрового формата с видом матрицы 2×2 (фиг.3в).
При формировании знаков из цифрового алфавита (фиг.4е), отображающих те же два многозначных числа (12212 и 57755), они отлично идентифицируются (Sидн=0.60 мм2, фиг.3е, таблица №5), не требуя дополнительного времени для поиска места расположения разряда (фиг.4ж).
Начертания элементов нового цифрового формата (2×2) при формировании знаков в виде треугольников и их сочетаний визуально ориентированы (фиг.4ж).
По визуально ориентированным знакам, помимо пространственного расположения их, точно идентифицируется их величина в ряду разрядов многозначного числа. При формировании знаков облегчается задача идентификации их и повышается скорость восприятия знаков на этой стадии.
Таким образом, наименьшее число позиционных элементов (2×2) в цифровом формате, при формировании десятичных знаков, необходимо требует не только визуального кодирования формой, но и пространственной ориентации фигур путем их поворота в поле зрения оператора. В этом случае фигуры, отображающие знаки, легко распознаются друг от друга в цифровом ряду разрядов многозначного числа и быстро и легко идентифицируются.
Цифровые знаки при формировании, цифровым форматом (2×2) которых является квадрат, разделенный диагоналями на позиционные элементы, представляют начертание фигур в виде единичных или сдвоенных треугольников. Каждая такая фигура цифрового алфавита, представленная десятичным знаком, формируется ориентированными в пространстве позиционными элементами цифрового формата.
При идентификации таких знаков облегчается работа оператора, который мнемонически способен определить величину любого многозначного числа, составленного на основании предлагаемого цифрового алфавита.
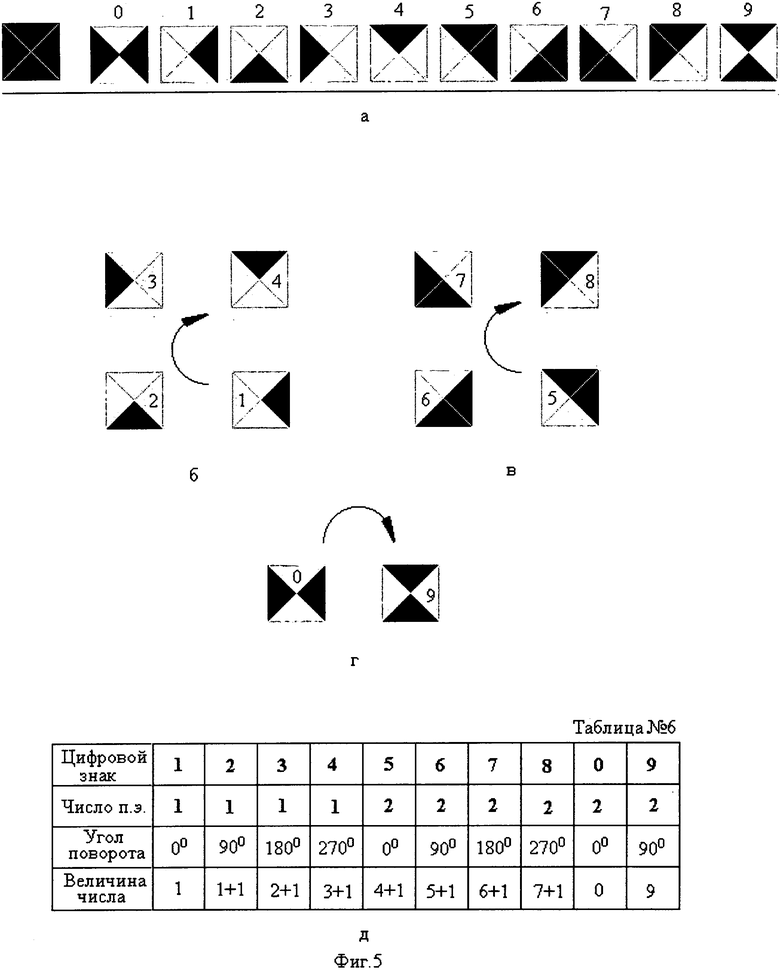
Цифровые знаки предлагаемого алфавита (фиг.5а), отображающие ряд цифр 1-4 (фиг.5б) и 5-8 (фиг.5в) цифрового формата при их формировании, позволяют оператору лучше воспринимать цифровую информацию. Между измеряемой величиной и цифровым знаком, отображающим эту величину, существует функциональная связь (фиг.5д, таблица №5). Она заключается в том, что большей измеряемой величине соответствует большее число высвеченных элементов цифрового формата (сравнение ряда цифр 1-4 и 5-7).
При равном числе высвеченных элементов цифрового формата (ряд цифр 1-4 или ряд цифр 5-7) начертания цифр, отображающие большую величину, повернуты по часовой стрелке на угол, кратный 90°, по отношению к начертаниям цифр, отображающим меньшую величину (фиг.5б, таблица №6). Наименьшей величиной числа в ряду цифр 1-4 является цифра 1, а в ряду 5-8 наименьшей величиной является цифра 5.
Величина числа, отображаемая соответствующей цифрой, складывается как из числа высвеченных элементов формата индикатора, так и угла поворота, на который повернут знак по отношению к наименьшей величине числа в ряду цифр (1-4 или 5-8).
Повороту элемента (элементов) цифрового формата при формировании цифр на каждые 90° от начальной величины числа в ряду цифр (цифра 1 или цифра 5) к величине числа прибавляется 1 (фиг.5д, таблица №6).
Начертания, представляющих цифровые знаки 0 и 9, при их формировании с одинаковым числом высветившихся элементов, отличаются друг от друга также пространственной ориентацией этих фигур путем их поворота на 90°.
Таким образом, при формировании десятичных знаков поступающие сигналы управления на элементы цифрового формата вызывают высвечивание фигур в виде треугольников и комбинаций из них, осуществляя в начертании фигур визуальное изменение пространственной ориентации, путем их поворота (фиг.3д, фиг.5а).
Сокращение позиционных (точечных) элементов в цифровом формате при формировании любого десятичного знака привело к относительному (по отношению к габаритным размерам цифрового формата) увеличению средней эквивалентной площади идентификации на знак.
Средняя величина эквивалентной площади идентификации на знак у семипозиционных цифр формата 3×5 равна всего лишь 0.35 мм2, а у цифрового формата 2×2 с элементами отображения в виде треугольников, при вчетверо меньшей площади цифрового формата, величина эквивалентной площади идентификации равна (Sидн.ср=0.60 мм2).
Если сравнить величину эквивалентной площади идентификации у семипозиционных цифр формата 3×5 (фиг.2д, таблица №2), то окажется, что только цифры 1 и 7 с меньшим числом элементов отображения этого цифрового алфавита имеют примерно такую же по величине эквивалентную площадь идентификации. Большое число точечных элементов в знаках уменьшает величину эквивалентной площади идентификации и увеличивает время их восприятия на стадии идентификации.
Управление цифрового четырехпозиционного формата не представляет никаких трудностей.
Известны методы построения структурных схем преобразователей из одного двоичного кода в другой с помощью упрощения логических выражений функции Y=f(X). Метод Квайна для минимизации функций ручным способом оказывается весьма трудоемким, но для сложных функций с большим числом аргументов задача решается с помощью ЭВМ.
Метод минимизации функции с помощью карт Вейча обеспечивает простоту получения результата. Он используется при минимизации относительно несложных функций (с числом аргументов до 5) ручным способом. Этот метод требует элементов изобретательности и не может быть использован для решения задачи минимизации с помощью ЭВМ [6 - стр.133].
Теперь будет рассмотрен наиболее простой и демонстративно наглядный цифровой метод [7] построения преобразователя двоично-десятичного кода в 4-позиционный код управления элементами 4-позиционного предлагаемого цифрового формата. Этот метод пригоден как для работы вручную, так и на ЭВМ.
Прежде всего составляют таблицу истинности 4-позицинного кода управления элементами цифрового формата.
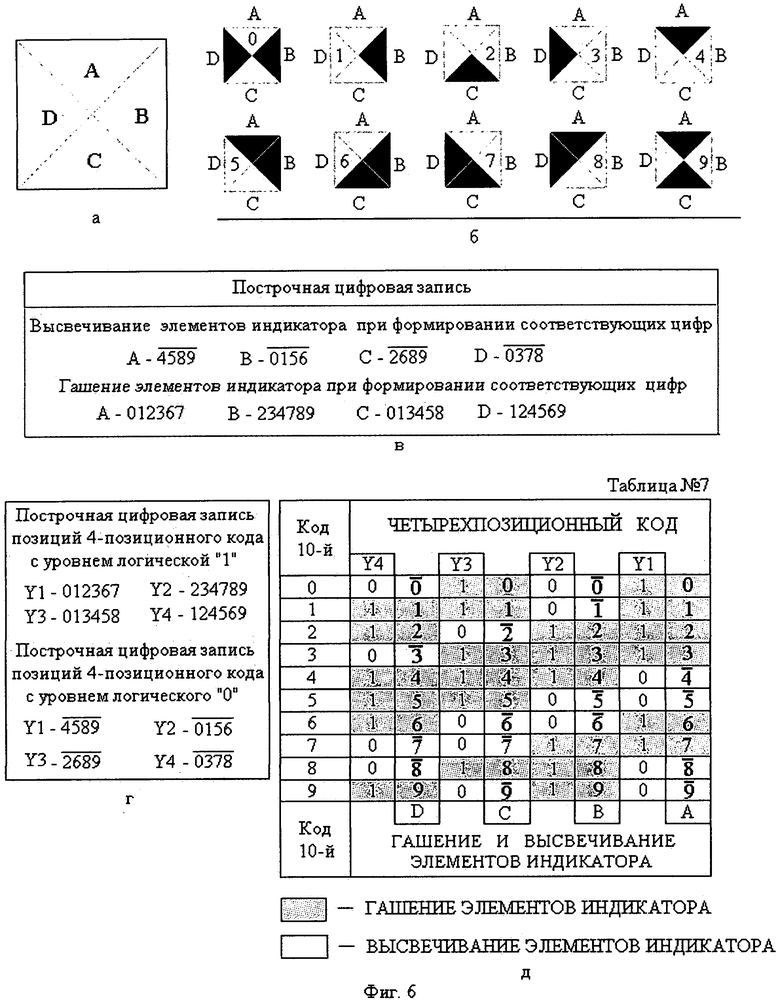
По гашению и высвечиванию каждого элемента (А, В, С, D) цифрового индикатора (фиг.6а) при формировании соответствующих цифр (фиг.6б) составляют построчную цифровую запись их управления (фиг.6в). При поступлении уровня логического «0» на элементы (А, В, С, D) цифрового формата они высвечиваются. Над комбинациями соответствующих цифр, при формировании которых элементы цифрового формата высвечиваются, сверху ставится черточка (фиг.6в). При поступлении уровня логической «1» на элементы (А, В, С, D) цифрового формата они погашаются. Над комбинациями соответствующих цифр, при формировании которых элементы цифрового формата погашаются, черточка сверху не ставится (фиг.6в).
Построчная цифровая запись позиций 4-позиционного кода управления соответствующими элементами цифрового формата записывается аналогично в цифровой форме.
Позиции 4-позиционного кода (Y1, Y2, Y3, Y4) с уровнем логической «1», являющиеся сигналами управления элементами (А, В, С, D соответственно) цифрового формата, погашаются при формировании указанных цифр и записываются комбинациями этих цифр без черточки сверху (фиг.6г).
Позиции 4-позиционного кода (Y1, Y2, Y3, Y4) с уровнем логического «0», являющиеся сигналами управления элементами (А, В, С, D соответственно) цифрового формата, высвечиваются при формировании указанных цифр и записываются комбинациями этих цифр с черточкой сверху (фиг.6г).
На основании построчной цифровой записи позиций (Y1, Y2, Y3, Y4) четырехпозиционного кода с уровнем логической»1» и уровнем логического «0» (фиг.6г) на фиг.6д (таблица №7) представлена таблица истинности этого кода. Эту таблицу истинности добавляют столбцами (А, В, С, D соответственно), указывающим гашение и высвечивание элементов цифрового формата при формировании соответствующих цифр.
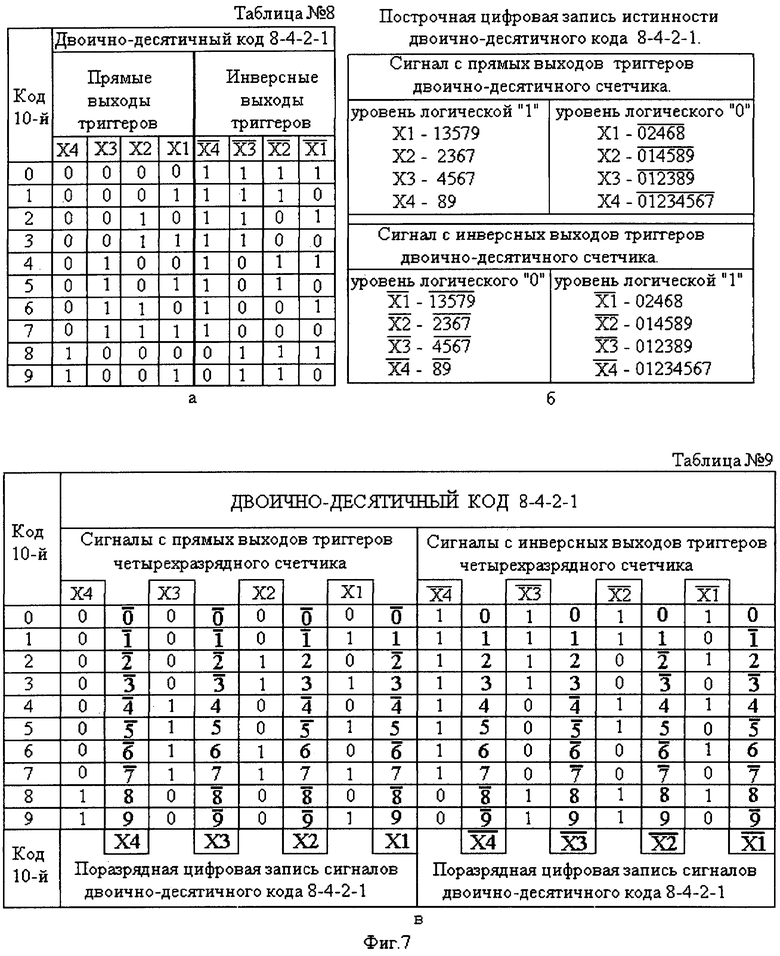
Для построения преобразователя двоично-десятичного кода в 4-позиционный код управления элементами цифрового формата выберают самый распространенный двоично-десятичный код 8-4-2-1 [8 - стр.681]. Таблица истинности двоично-десятичного кода 8-4-2-1 представлена на фиг.7а (таблица №8) как с прямых, так и с инверсных выходов двоично-десятичного счетчика 8-4-2-1.
Каждая комбинация входного двоично-десятичного кода 8-4-2-1 рассматривается как двоичное число, равное числу, обозначенному соответствующей ей десятичной цифрой, которой должна соответствовать строго определенная комбинация сигналов выходного четырехпозиционного кода для управления элементами цифрового формата, соответствующая той же цифре.
Таблица истинности двоично-десятичного 4-разрядного кода 8-4-2-1 (фиг.7а, таблица №8) содержит двоичные кодовые комбинации (сочетания уровней логического «0» и уровней логической «1») аргументов Х и их инверсий 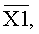 однозначно определяющие каждую цифру (0, 1, 2, 3, 4, 5, 6, 7, 8, 9) десятичного кода.
однозначно определяющие каждую цифру (0, 1, 2, 3, 4, 5, 6, 7, 8, 9) десятичного кода.
По той же таблице истинности видно, что уровням логической «1» соответствует одна комбинация цифр из десятичного кода того или иного аргумента Х или его инверсии 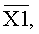 а уровням логического «0» соответствует другая комбинация из оставшихся цифр десятичного кода. Так, например, уровням логической «1» аргумента X1 соответствует по таблице истинности комбинация из цифр 13579 десятичного кода. Уровням логического «0» того же аргумента X1 соответствует по таблице истинности (фиг.7а, таблица №8) комбинация из оставшихся цифр 02468 десятичного кода.
а уровням логического «0» соответствует другая комбинация из оставшихся цифр десятичного кода. Так, например, уровням логической «1» аргумента X1 соответствует по таблице истинности комбинация из цифр 13579 десятичного кода. Уровням логического «0» того же аргумента X1 соответствует по таблице истинности (фиг.7а, таблица №8) комбинация из оставшихся цифр 02468 десятичного кода.
На фиг.7б (построчная цифровая запись двоично-десятичного кода 8-4-2-1) представлены все цифровые комбинации значений (уровня логического «0» и уровня логической «1») аргументов X1, Х2, Х3, Х4 и их инверсий 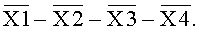
Комбинация цифр, представляющая значение аргумента или его инверсии с уровнем логической «1» для каждой цифры десятичного кода, обозначается без черточки сверху над ней (например, 13579).
Комбинация цифр, представляющая значение аргумента или инверсии его с уровнем логического «0» для каждой цифры десятичного кода, обозначается с черточкой сверху над ней (например, 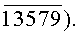
Эти обозначения касаются всех цифровых комбинаций, представляющих значения аргументов и их инверсий с уровнем логической «1» и уровнем логического «0» соответственно, на входах и выходах всех логических элементов И-НЕ структурной схемы преобразователя кода.
Табличный метод записи истинности двоично-десятичного кода 8-4-2-1 можно дополнить цифрами десятичного кода из построчной цифровой записи двоично-десятичного кода 8-4-2-1 (фиг.7в, таблица №9), указав без черточки сверху над выбранной цифрой уровень логической «1» и с черточкой сверху над цифрой - уровень логического «0». При этом построчная поразрядная цифровая запись двоично-десятичного кода 8-4-2-1, соответствующая записи его в табличной форме, становится более наглядной.
Каждому разряду кода 8-4-2-1 соответствует комбинация цифр десятичного кода как с уровнем логической «1», так и с уровнем логического «0».
На основании таблиц истинности 4-рахрядного (фиг.7в, таблица №9) и 4-позиционного кодов (фиг.6д, таблица №7) легко построить, применяя цифровой метод, структурную схему преобразователя двоично-десятичного кода 8-4-2-1 в 4-позиционный код (фиг.8а).
По сигналам, представленным комбинациями цифр десятичного кода, с уровнем логической «1» и уровнем логического «0» на входах и выходах логических элементов И-НЕ структурной схемы преобразователя кода (фиг.8а), прослеживается преобразование 4-разрядного кода 8-4-2-1 в 4-позиционный код управления элементами цифрового формата.
Сигналы гашения и высвечивания с выходных выводов (Yl, Y2, Y3, Y4) преобразователя кода (фиг.8а) с уровнем логической «1» и уровнем логического «0» поступают при формировании знаков на соответствующие элементы (А, В, С, D) цифрового формата (фиг.8б). Элементы цифрового формата погашаются (уровень лог. «1») или высвечиваются (уровень лог. «0») при формировании тех же цифровых знаков (фиг.8в), которые указываются на выходных выводах преобразователя кода (фиг.8а).
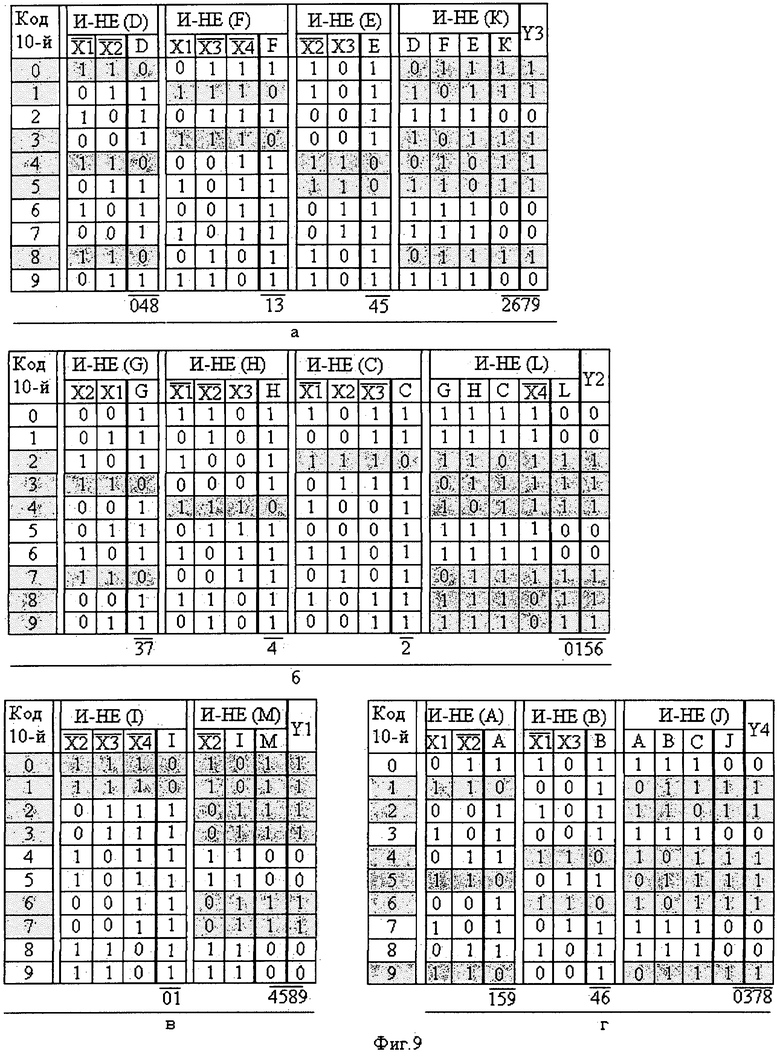
Дополнительно преобразование двоично-десятичного кода 8-4-2-1 в 4-позиционный код управления элементами цифрового формата можно просмотреть по таблицам истинности для всех логических элементов И-НЕ структурной схемы преобразователя (фиг.9).
Прохождение сигналов гашения элементов (А, В, С, D) цифрового формата при формировании тех или иных цифр прослеживается по таблицам истинности затемненными строками их.
На выходных выводах логических элементов И-НЕ (J, К, L, М) показан результат преобразования в виде сигналов с уровнем логической «1» и уровнем логического «0», соответствующих позициям выходного кода (Y4, Y3, Y2, Y1 соответственно) при гашении и высвечивании элементов цифрового формата.
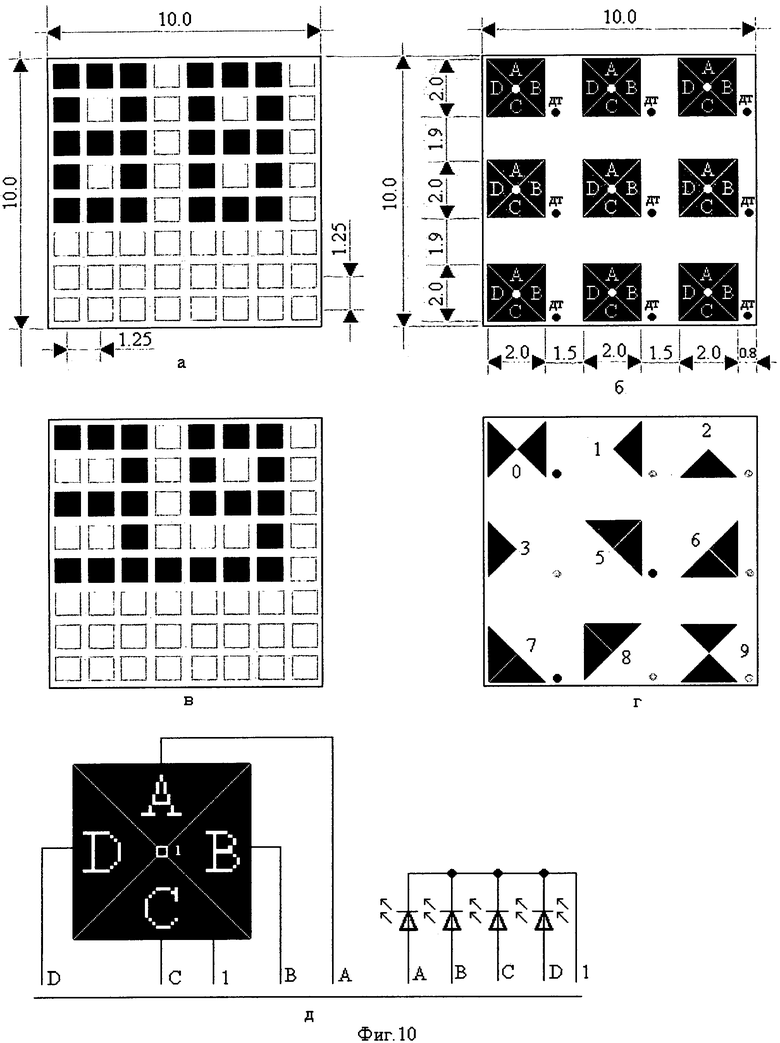
Практическое применение индикатора цифрового многоразрядного (3×3) с форматом знаков 2×2 можно осуществить на базе корпуса типа КИ13-1 матричного индикатора КИПГО2А-8х8Л [5 - стр.353], на лицевой стороне которого расположена матрица вида 8×8 (фиг.10а). Этот матричный индикатор выбран в качестве прототипа, чтобы на сравнении предлагаемого наименьшего цифрового формата и наименьшего семипозиционного формата при формировании тех и других знаков на одном и том же по габаритным размерам информационном поле показать преимущество первого перед вторым.
На информационном поле матричного индикатора КИПГО2А-8х8Л можно отобразить максимально два разряда цифровых знаков формата 3×5 с децимальными точками (фиг.10в).
Используют корпус матричного индикатора типа КИ13-1 с габаритными размерами 10.0×10.0 мм, на лицевую сторону которого наносятся светоизлучающие диоды, распределенные по девяти (3×3) разрядам наименьшего цифрового формата 2×2 (эквивалентного по габаритным размерам матрице вида 2×2) знаков (фиг.10б).
На фиг.10в представлена цифровая информация в виде десятичной дроби - 3,9. Почти все семипозиционные цифры (0, 2, 3, 5, 6, 8, 9) на матричном индикаторе формата 3×5 формируются из 12 точечных элементов плюс-минус один точечный элемент.
Знак, представленный одиннадцатью точечными элементами, распределенными так, что сочетания их могут восприниматься оператором как цифра 3, следует считать идентифицированным. Точно так же знак, представленный двенадцатью точечными элементами, распределенными так, что сочетания их могут восприниматься оператором как цифра 9, следует считать идентифицированным.
При расхождении в начертании знака всего в один точечный элемент, из цифрового формата в 13 элементов отображения, увеличивается время идентификации знака. Или при одинаково большом количестве точечных элементов в знаках, но с различным их расположением при формировании знаков идентификация их по времени будет увеличена. И только тогда, когда расположение всех точечных элементов в знаке не затрудняет их различения (Кр.с.зн=1), число высветившихся элементов в знаке минимально, величина эквивалентной площади идентификации максимальна и максимальна скорость его восприятия. Наиболее быстро отождествляются с эталоном, хранящимся в памяти оператора, цифры 1 и 7 семипозиционного формата 3×5. У них наибольшая величина эквивалентной площади идентификации и меньшее число высветившихся элементов в знаках.
На фиг.10г представлены три трехразрядные цифровые информации с децимальной точкой в виде десятичных дробей - 0.12-35.6-7.89. Каждый разряд многозначного числа представлен одним или двумя элементами цифрового формата. Почти в 6 раз среднее число элементов на знак у такого цифрового алфавита меньше. Наименьшее число элементов наименьшего формата знаков 2×2 при их формировании при наименьшем коэффициенте разрешающей способности знака (Кр.с.зн=1) уменьшает время их восприятия на стадии идентификации. Идентифицировать каждую из цифр (3 и 9) двузначного числа (фиг.10в) значительно труднее, чем любой цифровой знак, например, из трехзначного числа 0.12 (фиг.10г), представленный всего одним или двумя элементами отображения.
Цифровая информационная емкость индикатора цифрового многоразрядного (3×3) с форматом знаков 2×2 увеличилась почти в 5 раз (фиг.10б) с применением того же корпуса типа К13-1.
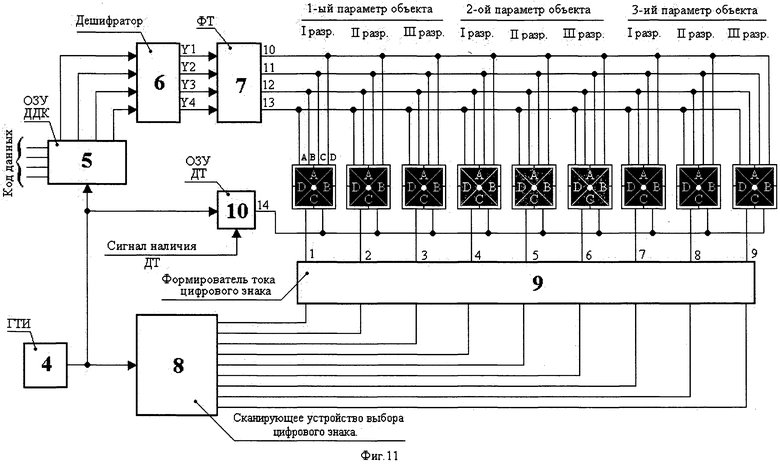
Пример управления индикатора цифрового многоразрядного (3×3) с форматом знаков 2×2 на три разряда и с измерением трех параметров объекта представлен на структурной схеме (фиг.11). Каждый измеряемый параметр объекта из трех разрядов может быть кодирован своим цветом (фиг.10б, фиг.10г). Ограниченное число выводов (16), имеющихся на корпусе КИ13-1, определяет для индикатора с отображением трех трехразрядных цифровых измерений мультиплексный режим управления элементами отображения.
Для этого все одноименные выводы элементов (А, В, С, D) цифрового формата соединены параллельно [9 - стр.95] и подключены к соответствующим выходам (10-13) формирователя (ФТ - 7) тока (фиг.11).
Генератор тактирующих импульсов (ГТИ - 4) является синхронизирующим звеном схемы.
По первому тактирующему импульсу сканирующее устройство выбора цифрового знака (8) подключает через формирователи тока цифрового знака (9) общий вывод 1 первого цифрового формата (1-й разряд, 1-й параметр объекта), подготавливая первую цифру к возможности возбуждения. (Выводы каждого из элементов (А, В, С, D соответственно) и общий вывод 1 от четырех элементов наименьшего формата знаков (2×2) показаны на фиг.10д.) По первому же тактирующему импульсу оперативное запоминающее устройство (ОЗУ - 5), хранящее кодовую информацию в виде четырехразрядного двоично-десятичного кода для всех девяти цифровых форматов, подключает на информационные входы дешифратора (6) четырехразрядный двоично-десятичный код (ДЦК - 5) для индикации цифры первого разряда первого измеряемого параметра объекта. Преобразованная дешифратором (6) информация в виде четырехпозиционного кода (Y1, Y2, Y3, Y4) с выходов (10-13) формирователя токов (ФТ - 7) поступает на соответствующие одноименные элементы всех цифровых форматов всех разрядов и всех измеряемых параметров объектов (фиг.11). Но по первому тактирующему импульсу только первая цифра (1-й разряд, 1-й измеряемый параметр объекта) индицируется.
По второму тактовому импульсу (ГТИ - 4) сканирующее устройство выбора цифрового знака (8) отключает общий вывод 1 первого цифрового формата (1-й разряд, 1-й измеряемый параметр объекта), подключая через формирователи тока цифрового знака (9) общий вывод 2 второго цифрового формата (2-й разряд, 1-й измеряемый параметр объекта), подготавливая вторую цифру к возможности возбуждения. Оперативное запоминающее устройство (ОЗУ - 5) по второму тактовому импульсу (ГТИ - 4) подключает на информационные входы дешифратора (6) четырехразрядный двоично-десятичный код (ДДК - 5) для индикации цифры второго разряда первого измеряемого параметра объекта.
Преобразованная дешифратором (6) информация в виде четырехпозиционного кода (Y1, Y2, Y3, Y4) с выходов (10-13) формирователя токов (ФТ - 7) поступает на соответствующие одноименные элементы всех цифровых форматов всех разрядов и всех измеряемых параметров объектов (фиг.11). Но по второму тактирующему импульсу только вторая цифра (2-й разряд, 1-й измеряемый параметр объекта) индицируется.
Цикл последовательного управления цифрами первого измеряемого параметра продолжается. В такой же последовательности индицируются цифровые знаки при работе схемы при измерении второго и третьего параметров объекта. При необходимости индикации дробных десятичных значений параметров объекта поступающие на схему управления данные должны содержать информацию о включении децимальной точки. Сигнал наличия ДТ дает разрешение на запоминание децимальной точки оперативным запоминающим устройством (ОЗУ ДТ - 10). Все выводы от точечного элемента отображения с индексом дт всех позиционных элементов отображения знака и всех разрядов объединены и подключены к выводу 14. Децимальная точка (вывод 14 - ОЗУ ДТ) высвечивается на том знаке, и в тот синхронизированный с тактовыми импульсами момент, когда должен высветиться соответствующий знак с децимальной точкой, после которого отображается дробная часть числа (фиг.11).
Фиксированные положения цифровых форматов на информационном поле индикатора позволяют индицировать цифровую информацию в 3-цветном отображении (фиг.10б, фиг.11 - 2-й измеряемый параметр объекта выделен светлым фоном): для каждого измеряемого параметра объекта - свой цвет, что может облегчить работу оператора.
ЛИТЕРАТУРА
1. Н.И.Вуколов, А.Н.Михайлов. Знакосинтезирующие индикаторы. Справочник. Москва. «Радио и связь». 1987 г.
2. Печников А.В., Сидоренко Г.В., Федорова С.А. Средства передачи и отображения информации. Москва. «Радио и связь». 1991 г.
3. Патент №2338270 на изобретение «Индикатор матричный с наилучшим восприятием цифровых знаков», выдан 19 ноября 2008 года. Приоритет изобретения от 21 мая 2007 года. Автор Патраль А.В.
4. Алиев Т.М., Вигдоров Д.И., Кривошеев В.П. Системы отображения информации. Москва. «Высшая школа». 1988 г.
5. Б.Л.Лисицын. Отечественные приборы индикации и их зарубежные аналоги. Москва. «Радио и связь». 1993 г.
6. Б.А.Калабеков, И.А.Мамзелей. Цифровые устройства микропроцессорные системы. Москва. «Радио и связь». 1987 г.
7. «Энциклопедический фонд России»: www.russika.ru - П - Преобразователь кода. Автор Патраль А.В.
8. Справочник по интегральным микросхемам. Под редакцией Тарабрина Б.В. Москва. «Энергия». 1980 г.
9. Васерин Н.Н., Дадерко Н.К., Прокофьев Г.А. Применение полупроводниковых индикаторов. Под ред. Е.С.Липина. Москва. «Энергоатомиздат». 1991 г.
Изобретение относится к средствам отображения цифровой информации. Технический результат заключается в улучшении восприятия знаков, увеличении цифрового информационного объема средств отображения информации, за счет использования изобретения в приборах цифрового визуального отсчета измеряемых величин. Для визуального отсчета цифровой информации используется новый десятичный цифровой алфавит, начертание любого цифрового знака которого имеет вид треугольника с поворотом, а наименьшее число высветившихся элементов при формировании знаков уменьшает время восприятия их на стадии идентификации. 11 ил.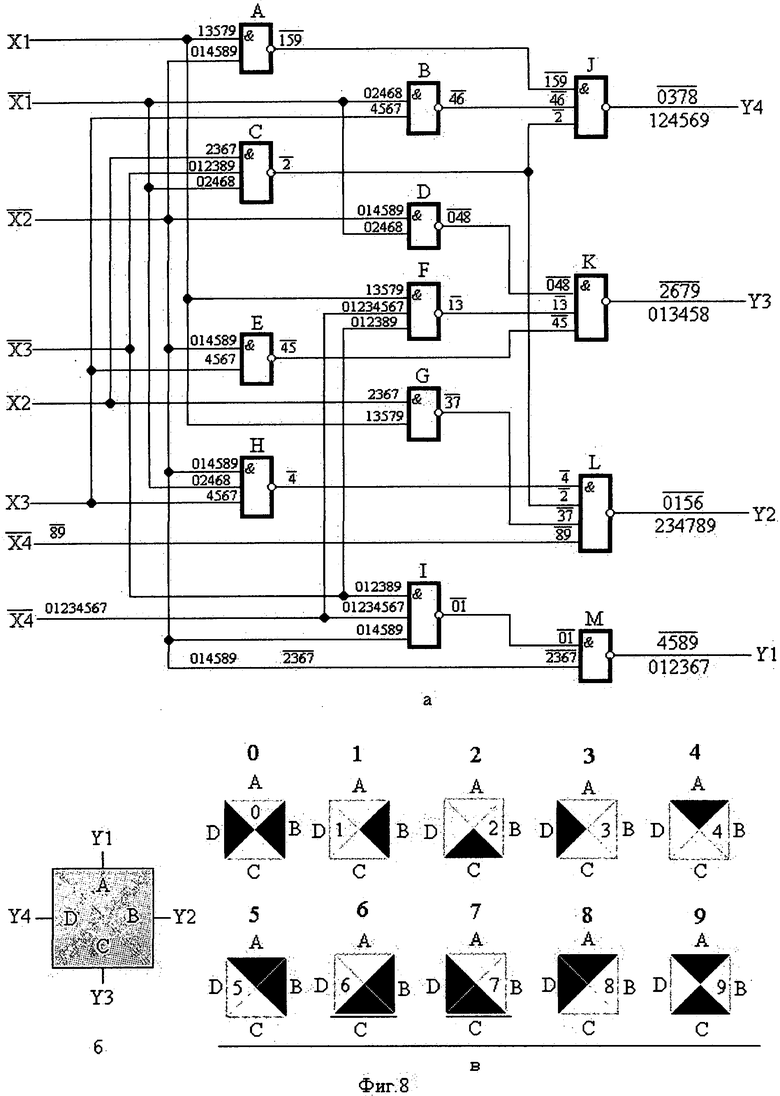
Индикатор цифровой многоразрядный (3×3) с форматом знаков 2×2, оформленный в пластмассовый корпус типа КИ13-1 с выводами (16 шт.), расположенными с обратной стороны корпуса, на лицевой стороне которого расположено информационное поле с числом знакомест 3×3, представленные цифровыми форматами знаков 2×2, предназначен для отображения в мультиплексном режиме управления десятичных чисел от 0 до 9 с децимальными точками, отличающийся тем, что при формировании десятичных знаков высвечиваются фигуры в виде треугольников и комбинациями из них, визуальное изменение пространственной ориентации которых путем поворота этих фигур представляют десятичные цифровые знаки, а наименьшее число высветившихся элементов в них уменьшает время восприятия знаков на стадии идентификации.
| ИНДИКАТОР МАТРИЧНЫЙ С НАИЛУЧШИМ ВОСПРИЯТИЕМ ЦИФРОВЫХ ЗНАКОВ | 2007 |
|
RU2338270C1 |
| ИНДИКАТОР ЦИФРОВОЙ СЕГМЕНТНЫЙ С ПАРАЛЛЕЛЬНЫМ ОТОБРАЖЕНИЕМ ЗНАКОВ | 2005 |
|
RU2311692C2 |
| УСТРОЙСТВО ИНДИКАЦИИ | 2003 |
|
RU2289856C2 |
| US 6055461 A, 25.04.2000. | |||
Авторы
Даты
2011-08-27—Публикация
2010-04-20—Подача