Область техники, к которой относится изобретение
Настоящее изобретение относится к последовательности системы беспроводной связи и, в частности, к способу установки циклического сдвига с учетом характеристик последовательности CAZAC для решения проблемы частотного сдвига.
Уровень техники
Последовательность с постоянной амплитудой и нулевой автокорреляцией (CAZAC-последовательность) представляет собой одну из различных последовательностей, которые интенсивно обсуждались в контексте технологии LTE проекта 3GPP (далее, 3GPP LTE).
Каналы обычно извлекают множество различных идентификаторов (ID) или информации с использованием CAZAC-последовательности, например, каналы синхронизации (например, первичный SCH, вторичный SCH и BCH (широковещательный канал)) для синхронизации нисходящей линии связи, другие каналы синхронизации (например, RACH (канал произвольного доступа)) для синхронизации восходящей линии связи и каналы пилот-сигнала (например, пилот-сигнал данных и пилот-сигнал качества канала). Кроме того, вышеупомянутая CAZAC-последовательность служила для выполнения скремблирования.
К CAZAC-последовательности применяли два типа способов, а именно первый способ изменения корневого индекса на другой корневой индекс и применения измененного корневого индекса и второй способ осуществления циклического сдвига (CS) для последовательности с одним корнем и применения результата CS.
Если текущий корневой индекс изменяют на новый корневой индекс, между текущим корневым индексом и новым корневым индексом возникает слабая взаимная корреляция, однако отсутствуют ограничения на разработку использования последовательностей.
В случае циклического сдвига, взаимная корреляция между текущим корневым индексом и новым корневым индексом равна нулю, и поэтому два корневых индекса используют, когда каждый из корневых индексов нуждается в высоком коэффициенте подавления. В частности, когда в одной соте совместно используются частотно-временные ресурсы и передаются сигналы данных/управления, два вышеупомянутых корневых индекса приспосабливают для различения разных сигналов или устройств UE.
Характерным примером CAZAC-последовательностей является последовательность Задова-Чу (ZC-последовательность), и последовательность Задова-Чу можно описать следующим уравнением 1:
[Уравнение 1]
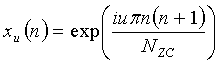 для нечетных Nzc,
для нечетных Nzc,
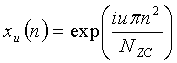 для четных Nzc,
для четных Nzc,
где «n» указывает индекс выборки, «Nzc» обозначает длину ZC-последовательности, и «u» обозначает корневой индекс ZC-последовательности.
Однако если сдвиг в частотной области возникает таким же образом, как в случае, когда CAZAC-последовательность передается с использованием схемы OFDM (мультиплексирования с ортогональным частотным разделением), то возможно чрезмерное ухудшение функциональной характеристики или частоты сигнала ложной тревоги, или пропускной способности.
В частности, если к CAZAC-последовательности применяется циклический сдвиг (CS), то частотный или временной сдвиг возникает чрезмерно, так что сложно различить последовательности.
Сущность изобретения
Техническая задача
Соответственно, настоящее изобретение относится к такому способу установки циклического сдвига (CS) с учетом частотного сдвига, который, по существу, устраняет одну или более проблему, вследствие ограничений и недостатков родственных технических устройств.
Задачей настоящего изобретения является обеспечение способа установки циклического сдвига (CS) для противодействия частотному сдвигу, таким образом, что упомянутый способ может легко предотвращать ухудшение последовательности (например, CAZAC-последовательности) в условиях, когда возникает частотный сдвиг.
Дополнительные преимущества, задачи и признаки изобретения частично изложены ниже в последующем описании и частично станут очевидными специалистам со средним уровнем компетентности в данной области техники после изучения нижеследующего материала или могут быть изучены из практики применения изобретения. Цели и другие преимущества изобретения можно осуществить и выполнить с помощью структуры, частично показанной в приведенном описании и формуле настоящего изобретения, а также на прилагаемых чертежах.
Техническое решение
Для выполнения упомянутых задач и получения других преимуществ и, в соответствии с целью изобретения, как показано и широко поясняется в настоящей заявке, обеспечивается способ выполнения установки циклического сдвига, который следует применять к данной последовательности для противодействия влиянию доплеровской частоты, более высокой, чем предварительно заданная величина. В соответствии с данным способом, выполняются следующие этапы: получают первую переменную (du) циклического сдвига, соответствующую доплеровскому сдвигу разноса одной поднесущей, с использованием корневого индекса (u) данной последовательности; получают вторичные переменные, содержащие число групп (G), содержащихся в данной последовательности, длину каждой группы (S) и число циклических сдвигов на группу (P), с использованием первой переменной (du); и устанавливают циклический сдвиг, который следует применить к данной последовательности, в соответствии с вторичными переменными.
В предпочтительном варианте, вторичные переменные дополнительно содержат некоторое число дополнительных циклических сдвигов, которые применимы к данной последовательности, не на основании группы (R).
В предпочтительном варианте, данная последовательность является последовательностью Задова-Чу (ZC-последовательностью), и первую переменную получают согласно уравнению
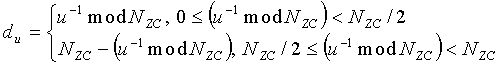
где «u» означает корневой индекс ZC-последовательности, и «NZC» соответствует длине ZC-последовательности.
И, в данном случае, вторичные переменные получают иначе, в зависимости от диапазона первой переменной (du), и диапазон первой переменной разбивают с помощью критерия, соответствующего 1/3 от длины данной последовательности (Nzc/3).
И, если диапазон первой переменной (du) составляет Ncs≤du<(Nzc/3), то вторичные переменные можно получить согласно уравнениям
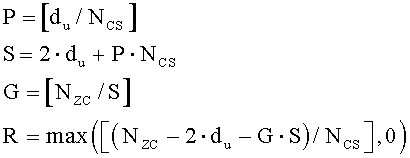
где «NCS» является предварительно заданным параметром циклического сдвига, «P» соответствует числу циклических сдвигов на группу, «S» соответствует длине каждой группы, «G» соответствует числу групп, и «R» соответствует числу дополнительных циклических сдвигов.
С другой стороны, если диапазон первой переменной (du) составляет (Nzc/3)≤du≤(Nzc-Ncs)/2, то вторичные переменные можно получить согласно уравнениям
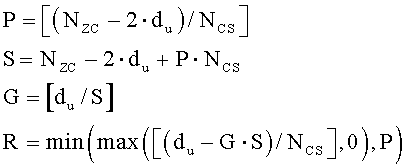
где «NCS» является предварительно заданным параметром циклического сдвига, «P» соответствует числу циклических сдвигов на группу, «S» соответствует длине каждой группы, «G» соответствует числу групп, и «R» соответствует числу дополнительных циклических сдвигов.
И, в предпочтительном варианте, упомянутая установка циклического сдвига (C ν) выполняется в соответствии с уравнением вида
C ν=S·[ν/P]+(ν mod P)·N CS, ν=0,1,…,(P·G+R-1).
И данная последовательность может служить для генерации преамбулы произвольного доступа.
В соответствии с другим аспектом настоящего изобретения предлагается способ настройки циклического сдвига, который следует применять к данной последовательности, при этом способ содержит следующие этапы: определяют, следует ли установить циклический сдвиг в соответствии с ограниченными наборами, ограниченными вследствие доплеровского сдвига; и устанавливают циклический сдвиг, который следует применять к данной последовательности, с учетом циклического сдвига, соответствующего доплеровскому сдвигу разноса одной поднесущей, если определяют, что циклический сдвиг следует устанавливать в соответствии с ограниченными наборами.
В предпочтительном варианте, когда определяют, что циклический сдвиг следует установить в соответствии с ограниченными наборами, упомянутая установка циклического сдвига, который следует применять к данной последовательности, содержит следующие этапы: получают первую переменную (du), указывающую циклический сдвиг, соответствующий доплеровскому сдвигу разноса одной поднесущей, с использованием корневого индекса (u) данной последовательности; получают вторичные переменные, содержащие число групп (G), содержащихся в данной последовательности, длину каждой группы (S), число циклических сдвигов на группу (P), с использованием первой переменной (du), и число дополнительных циклических сдвигов, которые применимы к данной последовательности, не на основании группы (R); и устанавливают циклический сдвиг, который следует применить к данной последовательности, в соответствии с вторичными переменными.
В предпочтительном варианте, данная последовательность является последовательностью Задова-Чу (ZC-последовательностью), и первую переменную получают согласно уравнению
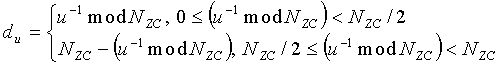 ,
,
где «u» означает корневой индекс ZC-последовательности, и «NZC» соответствует длине ZC-последовательности.
И вторичные переменные можно получить иначе, в зависимости от диапазона первой переменной (du), и диапазон первой переменной разбивают с помощью критерия, соответствующего 1/3 от длины данной последовательности (Nzc/3).
В данном случае, если диапазон первой переменной (du) составляет Ncs≤du<(Nzc/3), то вторичные переменные получают согласно уравнениям
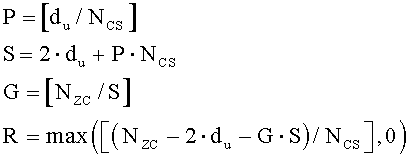
где «NCS» является предварительно заданным параметром циклического сдвига, «P» соответствует числу циклических сдвигов на группу, «S» соответствует длине каждой группы, «G» соответствует числу групп, и «R» соответствует числу дополнительных циклических сдвигов.
С другой стороны, если диапазон первой переменной (du) составляет (Nzc/3)≤du≤(Nzc-Ncs)/2, то вторичные переменные можно получить согласно уравнениям
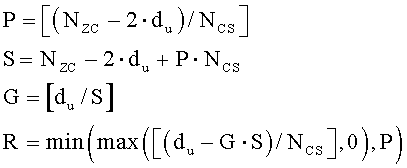
где «NCS» является предварительно заданным параметром циклического сдвига, «P» соответствует числу циклических сдвигов на группу, «S» соответствует длине каждой группы, «G» соответствует числу групп, и «R» соответствует числу дополнительных циклических сдвигов.
И, в предпочтительном варианте, циклический сдвиг (С ν) выполняется согласно следующему уравнению,
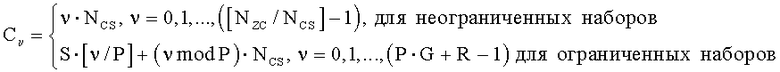
И данная последовательность может служить для генерации преамбулы произвольного доступа.
В соответствии с другим аспектом настоящего изобретения предлагается способ настройки циклического сдвига, который следует применять к данной последовательности, при этом способ содержит следующие этапы: (a) получают переменную du из уравнения
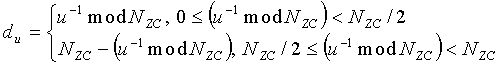 ,
,
где «u» означает корневой индекс данной последовательности, и «NZC» соответствует длине данной последовательности; (b) получают переменные G, S, P и R из уравнений
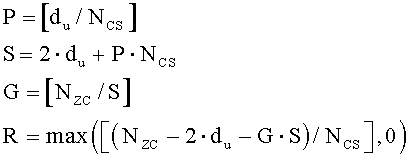
когда диапазон первой переменной (du) составляет Ncs≤du<(Nzc/3), и переменные G, S, P и R получают из уравнений
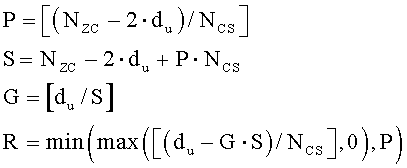
когда диапазон первой переменной (du) составляет (Nzc/3)≤du≤(Nzc-Ncs)/2,
где «NCS» является предварительно заданным параметром циклического сдвига; (c) устанавливают циклический сдвиг (С ν) согласно уравнению
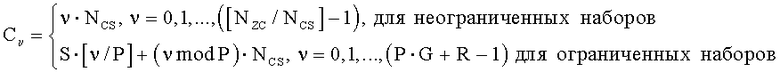
в котором ограниченные наборы являются наборами циклических сдвигов, ограниченными вследствие доплеровского сдвига, и неограниченные наборы являются наборами циклических сдвигов, не ограниченными вследствие доплеровского сдвига.
В соответствии с другим аспектом настоящего изобретения предлагается способ передачи преамбулы произвольного доступа с использованием циклического сдвига, при этом способ содержит следующие этапы: получают корневой индекс (u) последовательности преамбулы произвольного доступа из системной информации; устанавливают циклический сдвиг, который следует применить к данной последовательности, причем при упомянутой установке, когда определяют, что циклический сдвиг следует устанавливать в соответствии с ограниченными наборами, ограниченными вследствие доплеровского сдвига, циклический сдвиг, который следует применить к данной последовательности, устанавливают с учетом циклического сдвига, соответствующего доплеровскому сдвигу разноса одной поднесущей; генерируют последовательность в соответствии с корневым индексом (u), с установленным циклическим сдвигом; и передают последовательность с циклическим сдвигом в качестве преамбулы произвольного доступа.
В предпочтительном варианте, когда определяют, что циклический сдвиг следует устанавливать в соответствии с ограниченными наборами, упомянутая установка циклического сдвига, который следует применить к данной последовательности, содержит следующие этапы: получают первую переменную (du), указывающую циклический сдвиг, соответствующий доплеровскому сдвигу разноса одной поднесущей, с использованием корневого индекса (u) данной последовательности; получают вторичные переменные, содержащие число групп (G), содержащихся в данной последовательности, длину каждой группы (S), число циклических сдвигов на группу (P), с использованием первой переменной (du), и число дополнительных циклических сдвигов, которые применимы к данной последовательности, не на основе группы (R); и устанавливают циклический сдвиг, который следует применить к последовательности, в соответствии с вторичными переменными.
В предпочтительном варианте, в котором данная последовательность является последовательностью Задова-Чу (ZC-последовательностью), и первую переменную получают согласно уравнению
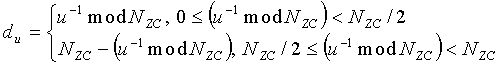
где «u» означает корневой индекс ZC-последовательности, и «NZC» соответствует длине ZC-последовательности.
В предпочтительном варианте вторичные переменные получают иначе, в зависимости от диапазона первой переменной (du), и диапазон первой переменной разбивают с помощью критерия, соответствующего 1/3 от длины данной последовательности (Nzc/3).
В частности, если диапазон первой переменной (du) составляет Ncs≤du<(Nzc/3), то вторичные переменные можно получить согласно уравнениям
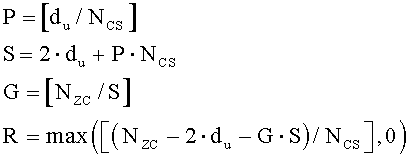
где «NCS» является предварительно заданным параметром циклического сдвига, «P» соответствует числу циклических сдвигов на группу, «S» соответствует длине каждой группы, «G» соответствует числу групп, и «R» соответствует числу дополнительных циклических сдвигов.
С другой стороны, если диапазон первой переменной (du) составляет (Nzc/3)≤du≤(Nzc-Ncs)/2, то вторичные переменные можно получить согласно уравнениям
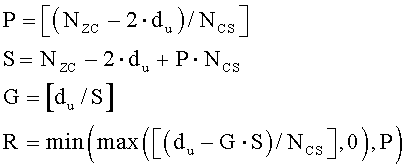
где «NCS» является предварительно заданным параметром циклического сдвига, «P» соответствует числу циклических сдвигов на группу, «S» соответствует длине каждой группы, «G» соответствует числу групп, и «R» соответствует числу дополнительных циклических сдвигов.
И, в предпочтительном варианте, циклический сдвиг (С ν) выполняется согласно следующему уравнению
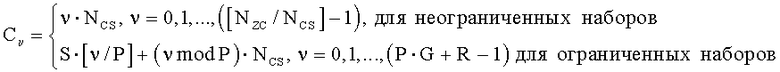
Следует понимать, что как вышеприведенное общее описание, так и последующее подробное описание служат для примера и пояснения и предназначены для обеспечения дополнительного пояснения заявленного изобретения.
Технический результат
Настоящее изобретение позволяет легко устанавливать интервал циклического сдвига (CS) в конкретном месте, без наложения, с учетом отклика канала принимаемой (Rx) последовательности и ложного положения данной принимаемой (Rx) последовательности, хотя принимаемый (Rx) сигнал сдвинут на величину частотного сдвига независимо от категорий области, генерирующей последовательность, так что можно значительно уменьшить число ошибок обнаружения и частоты ложных тревог.
И, если соте с частотным сдвигом, превосходящим предварительно заданный уровень, назначается последовательность циклического сдвига (CS), то настоящее изобретение позволяет свести к минимуму влияние частотного сдвига на соту со значительной подвижностью абонентов.
Описание чертежей
Сопроводительные чертежи, которые включены для обеспечения более глубокого понимания изобретения, иллюстрируют варианты осуществления изобретения и, вместе с описанием, служат для объяснения принципов изобретения.
На чертежах:
Фиг. 1 - концептуальная схема, изображающая влияние частотного сдвига, вызываемого формированием импульсов в частотной области, когда последовательность отображается в поднесущую, в соответствии с настоящим изобретением;
Фиг. 2 - концептуальная схема, изображающая разные ситуации частотного сдвига, существующие во множестве сот, в соответствии с настоящим изобретением;
Фиг. 3 - концептуальная схема, представляющая способ назначения последовательности, когда последовательность является CAZAC-последовательностью, в соответствии с настоящим изобретением;
Фиг. 4 - концептуальная схема, изображающая ложные составляющие, которые возникают в отклике канала в частотной области принимаемой последовательности вследствие частотного сдвига, в соответствии с настоящим изобретением;
Фиг. 5 - концептуальная схема, представляющая способ установки нового блока применения циклического сдвига (CS) путем введения дополнительного запасного поля в старый блок применения CS, в соответствии с настоящим изобретением;
Фиг. 6 и 7 - концептуальные схемы, изображающие примеры применения дополнительного запасного поля, показанного на фиг. 5, в условиях, когда индекс последовательности имеет небольшое значение, в соответствии с настоящим изобретением;
Фиг. 8 и 9 - концептуальная схема, изображающая примерные дополнительные запасные поля, показанные на фиг. 5, в условиях, когда индекс последовательности имеет большое значение, в соответствии с настоящим изобретением;
Фиг. 10 - пример единственной группы, состоящей из P наборов циклических сдвигов, в соответствии с настоящим изобретением;
Фиг. 11 - концептуальная схема, представляющая способ установки группы применения циклических сдвигов и интервала применения циклического сдвига для каждой группы в соответствии с настоящим изобретением;
Фиг. 12 показывает положения, где импульсы возникают вследствие взаимных помех, когда CAZAC-индекс содержится в интервале N/3 - N/2 в соответствии с настоящим изобретением;
Фиг. 13 - блок-схема последовательности операций, изображающая получение ограниченного набора циклических сдвигов в соответствии с одним вариантом осуществления настоящего изобретения;
Фиг. 14 - концептуальная схема, представляющая способ установки переменной (du) циклического сдвига, соответствующего доплеровскому сдвигу, связанному с разносом 1 поднесущей, когда устанавливается ограниченный набор циклических сдвигов в соответствии с настоящим изобретением;
Фиг. 15 - концептуальная схема, представляющая особый случай, в котором переменная (du) меньше, чем основной блок NCS, к которому применяется циклический сдвиг (CS), в соответствии с настоящим изобретением;
Фиг. 16 - концептуальная схема, представляющая способ вычисления переменной, устанавливающей циклический сдвиг в интервале NCS≤du<(NZC/3), в соответствии с настоящим изобретением;
Фиг. 17 - концептуальная схема, представляющая способ вычисления переменной, устанавливающей циклический сдвиг в интервале (NZC/3)≤du<(NZC-NCS)/2, в соответствии с настоящим изобретением;
Фиг. 18 и 19 - концептуальные схемы, представляющие способ сокращения числа последовательностей преамбул с ZCZ из-за ложного отклика в случае, когда Nzc=839, Ncs=100 и du=155, в соответствии с настоящим изобретением;
Фиг. 20 - концептуальная схема, показывающая коэффициент увеличения доступного ограниченного циклического сдвига после того, как снято ограничение начального положения циклического сдвига в случае Nzc=839, в соответствии с настоящим изобретением;
Фиг. 21 - концептуальная схема, изображающая примерный циклический сдвиг в случае, когда Nzc=839, Ncs=40 и du=150, в соответствии с одним вариантом осуществления настоящего изобретения;
Фиг. 22 - концептуальная схема, изображающая примерный циклический сдвиг в случае, когда Nzc=839, Ncs=40 и du=399, в соответствии с одним вариантом осуществления настоящего изобретения;
Фиг. 23 - концептуальная схема, изображающая примерный циклический сдвиг в случае, когда Nzc=839, Ncs=40 и du=150, в соответствии с другим вариантом осуществления настоящего изобретения; и
Фиг. 24 - концептуальная схема, изображающая примерный циклический сдвиг в случае, когда Nzc=839, Ncs=40 и du=399, в соответствии с другим вариантом осуществления настоящего изобретения.
Вариант осуществления изобретения
Ниже приведены подробные ссылки на предпочтительные варианты осуществления настоящего изобретения, примеры которого показаны на сопроводительных чертежах. В дальнейшем, где можно, одинаковые цифровые позиции служат на всех чертежах для обозначения одинаковых или похожих частей.
Перед описанием настоящего изобретения следует понять, что большинство терминов, описанных в настоящем изобретении, соответствуют общим терминам, широко известным в данной области техники, но некоторые термины выбраны автором настоящей заявки по мере необходимости и поясняются в дальнейшем в последующем описании настоящего изобретения. Поэтому целесообразно, чтобы термины, введенные автором настоящей заявки, понимались на основе их смыслового значения в настоящем изобретении.
Для удобства описания и облегчения понимания настоящего изобретения общие структуры и устройства, широко известные в данной области техники, в дальнейшем, не упоминаются или обозначаются блок-схемами или схемами последовательностей операций. По возможности, одинаковые цифровые позиции служат на всех чертежах для обозначения одинаковых или похожих частей.
Настоящее изобретение обеспечивает способ установки циклического сдвига (CS) для противодействия частотному сдвигу, так что упомянутый способ может легко предотвращать ухудшение характеристик последовательности (например, CAZAC-последовательности). С упомянутой целью, настоящее изобретение предлагает способ применения циклического сдвига к CAZAC-последовательности и влияние частотного сдвига CAZAC-последовательности.
Циклический сдвиг можно применить к CAZAC-последовательности в соответствии с двумя схемами, а именно, первой схемой для выполнения циклического сдвига на последовательности и способом для умножения экспоненциальной функции других участков на последовательность во временной или частотной области и выполнения циклического сдвига на результате умножения.
Циклический сдвиг «d» применяется к индексу «k» по частоте в частотной области. Если индекс последовательности равен M, и последовательность длины N представлена в виде c(k; d, M, N), то способ выполнения циклического сдвига на последовательности можно представить следующим уравнением 2:
[Уравнение 2]
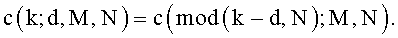
Где «d» означает величину циклического сдвига, и «mod» означает модулярный оператор.
Способ применения циклического сдвига умножением экспоненциальной функции на последовательность можно выразить следующим уравнением 3:
[Уравнение 3]
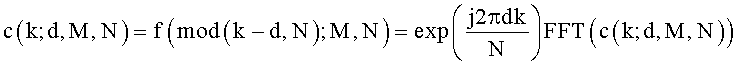
Тем временем, хотя каждое из вышеприведенных уравнений 2 и 3 показывает примерный циклический сдвиг, примененный в частотной области, циклический сдвиг можно применить к последовательности во временной области с индексом «n» выборки во временной области. В данном случае, пример применения циклического сдвига можно представить следующим уравнением 4:
[Уравнение 4]
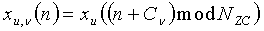 ,
,
где «Cν» означает степень циклического сдвига, «n» означает индекс выборки, «NZC» означает длину ZC-последовательности, и «u» означает корневой индекс ZC-последовательности.
CAZAC-последовательности можно отличать одну от другой при условии, что используются разные корневые индексы, но следует отметить, что CAZAC-последовательности различаются по взаимной корреляции.
Однако в случае, по меньшей мере, двух CAZAC-последовательностей, связанных с циклическим сдвигом, значение взаимной корреляции между CAZAC-последовательностями равно нулю, так как вышеупомянутые CAZAC-последовательности используют, когда требуется высокий коэффициент подавления для двух CAZAC-последовательностей.
В частности, CAZAC-последовательности, связанные с циклическим сдвигом, совместно используют частотно-временные ресурсы в пределах одной соты, так что их можно использовать для различения разных сигналов/устройств UE во время передачи данных/сигналов управления.
Однако если частотный сдвиг в частотной области происходит таким же образом, как в случае, в котором CAZAC-последовательность передается с использованием схемы OFDM, то, в рамках настоящего изобретения, можно столкнуться с чрезмерным ухудшением функциональной характеристики и частоты сигнала ложной тревоги.
В нижеследующем описании предлагается пример, в котором последовательность передается в частотной области, и другой пример, в котором последовательность передается с использованием схемы OFDM.
На фиг. 1 представлена концептуальная схема, изображающая влияние частотного сдвига, вызываемого формированием импульсов в частотной области, когда последовательность отображается в поднесущую, в соответствии с настоящим изобретением.
Как показано на фиг. 1, каждый из отсчетов последовательности отображается в поднесущую. Если принимающая станция выполняет выборку сигнала вследствие частотного сдвига, как обозначено местом «помехи», то сигналы соседних поднесущих смешиваются в пределах одного отсчета. Другими словами, если функция формирования импульсов имеет вид p(x), то отклик произвольной поднесущей можно представить следующим уравнением 5:
[Уравнение 5]
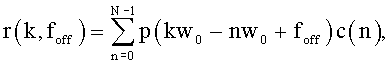
где «r(k, foff)» означает частную характеристику в режиме приема (Rx) в месте k-той поднесущей, если частотный сдвиг равен foff, «c(n)» означает CAZAC-последовательность, отображенную в поднесущую пользовательским оборудованием (UE), «p(f)» означает функцию формирования импульсов в частотной области, и ω 0 характеризует разнос поднесущей.
В случае foff=0, вышеприведенное уравнение 5 дает только значение c(k). Иначе, в случае foff≠0 сигнал соседней поднесущей может поступать в принимающую станцию так, что в приемной станции ухудшаются функциональные характеристики. Вследствие ухудшения функциональных характеристик, вызываемого частотным сдвигом, вероятность встречи ошибки обнаружения в принимающей станции повышается, и в принимающей станции может неизбежно возрастать частота ложных тревог и/или пропуска обнаружения.
В частности, в том случае, если циклический сдвиг применяется во временной области, и CAZAC-последовательность передается в частотной области, то различные последовательности различить невозможно. И вышеупомянутая проблема может возникать в ситуации, даже когда CAZAC-последовательность передается во временной области как временной сдвиг.
Иначе говоря, если возникает частотный или временной сдвиг, то способы применения циклического сдвига неизбежно должны претерпевать ухудшение функциональных характеристик. Кроме того, влияние частотного сдвига равным образом применимо к конкретному случаю, в котором циклический сдвиг применяется во временной области, как выражено уравнением 4.
Поэтому существует настоятельная необходимость в разработке новой технологии для предотвращения ухудшения функциональной характеристики последовательности (т.е. CAZAC-последовательности) в условиях, когда происходит частотный сдвиг.
В частности, в случае применения циклического сдвига к CAZAC-последовательности, возникает чрезмерный частотный или временной сдвиг, так что, в рамках настоящего изобретения, сталкиваются с затруднением различения последовательностей, когда частотный или временной сдвиг занимает, по меньшей мере, половину разноса одной поднесущей.
Однако величина частотного сдвига и величина доплеровского сдвига могут быть разными в отдельных сотах сотовой системы мобильной связи.
Поэтому, в соответствии с одним вариантом осуществления, настоящее изобретение обеспечивает разные способы установки циклического сдвига (CS) согласно величине частотных сдвигов отдельных сот, и далее приведено подробное описание упомянутых способов.
На фиг. 2 представлена концептуальная схема, изображающая разные ситуации частотного сдвига, существующие во множестве сот, в соответствии с настоящим изобретением.
Как показано на фиг. 2, настоящее изобретение позволяет определять, что конкретная сота, содержащая много устройств UE с большой подвижностью, в сотовой системе мобильной связи, содержащей много сот, характеризуется большим частотным сдвигом. Устройство UE, находящееся в пределах соты, охватывающей жилые районы, с очень высокой вероятностью может быть низкоскоростным устройством UE, так что частотный сдвиг в пределах соты может быть небольшим.
На фиг. 2 более подробно показаны соты A и B, прилегающие к высокоскоростной железной дороге, и сота C, удаленная от высокоскоростной железной дороги.
В случае с сотами A и B, прилегающими к высокоскоростной железной дороге, очень высока вероятность, что в соответствующей соте находится множество высокоскоростных устройств UE, так что настоящее изобретение дает преимущество в том, что можно назначать последовательность, которая является очень устойчивой к частотному сдвигу.
Например, в случае с сотой C около жилого района, удаленного от высокоскоростной железной дороги, вероятность пребывания высокоскоростного устройства UE в соответствующей соте относительно низка, что устраняет необходимость назначения исключительно такой последовательности, которая очень устойчива к частотному сдвигу.
В случае доступной последовательности (например, CAZAC-последовательности), первые последовательности, вызванные корневыми индексами отдельных последовательностей, и вторые последовательности, вызванные циклическим сдвигом, примененным к первым последовательностям, могут обладать разными характеристиками частотного сдвига.
Поэтому настоящее изобретение устанавливает ограниченный случай и неограниченный случай и обеспечивает способы установки циклического сдвига для отдельных случаев.
Ограниченный случай означает, что влияние доплеровского сдвига выше, чем предварительно заданная пороговая величина, так что при установке интервала применения циклического сдвига (CS) возникает неожидаемое ограничение.
Неограниченный случай означает, что влияние доплеровского сдвига равно или меньше, чем предварительно заданная пороговая величина, так что ограничения при установке интервала применения CS не существует.
Ниже приведено подробное описание способа установки циклического сдвига.
На фиг. 3 представлена концептуальная схема, изображающая способ назначения последовательности, когда последовательность является CAZAC-последовательностью, в соответствии с настоящим изобретением.
CAZAC-последовательность может содержать корневую последовательность каждой корневой CAZAC-последовательности и последовательность с нулевой зоной корреляции (ZCZ-последовательность), к которым применяют разные циклические сдвиги (именуемые также круговыми сдвигами).
Кроме того, на фиг. 3 показана корневая последовательность для каждого корневого индекса в Nt корневых индексах и набор ZCZ-последовательности, в котором L циклических сдвигов применены к каждой корневой последовательности.
В данном случае, ZCZ указывает интервал применения циклического сдвига, к которому применяется циклический сдвиг (CS), чтобы узел B мог различать сигналы RACH.
Между тем, если CAZAC-последовательность используют, когда имеет место частотный сдвиг, то в рамках настоящего изобретения возможны сложности различения ZCZ-последовательности при частотном сдвиге. Поэтому настоящее изобретение позволяет определять, что ZCZ-последовательность не используют в предварительно заданной соте с частотным сдвигом, превосходящим предварительно заданный уровень.
При этом выбор порогового значения, применяемого для принятия решения о величине частотного сдвига каждой соты, можно сделать правильно в зависимости от числа доступных последовательностей соответствующей системы и величины частотного сдвига каждой соты.
Если определено, что в соте имеет место частотный сдвиг, превосходящий предварительно заданный уровень, то вероятность нахождения высокоскоростного устройства UE в данной соте является очень высокой, как показано для соты A или B.
Однако если определено, что ZCZ-последовательность не используется в соте с частотным сдвигом, превосходящим предварительно заданный уровень, то возможно наличие только индексов Nt, основанных на CAZAC-индексах, так что число доступных последовательностей становится меньше.
Если коэффициент повторного использования последовательности становится меньше, то последовательности следует назначать в соответствии с планированием сот. Однако данное назначение, основанное на планировании сот, может неожиданно повысить сложность процесса назначения последовательностей отдельным сотам, так что другое решение может потребоваться дополнительно в условиях, когда число доступных последовательностей составляет проблему.
Кроме того, в случае использования только Nt последовательностей и не использования ZCZ-последовательности может возникать проблема оценки двухсторонней задержки или односторонней задержки, в то время как характеристика обнаружения последовательности улучшается. То есть, может возникать проблема опознавания позиции корреляционного пика, изменяющегося вследствие двухсторонней задержки или односторонней задержки, и позиции корреляционного пика, изменяющегося вследствие частотного сдвига. Поэтому для устранения упомянутой проблемы, возможно, дополнительно потребуется другое решение.
Между тем, вышеупомянутая проблема сложности различения ZCZ-последовательностей из-за частотного сдвига ужесточается в условиях, когда CAZAC-индекс является очень большим или не является очень малым.
При более подробном рассмотрении, если «k» означает индекс в частотной области, «N» означает длину CAZAC-последовательности, «M» означает CAZAC-последовательность, и передаваемый (Tx) сигнал представляется как «c(k, N, M)», то принимаемый (Rx) сигнал можно представить следующим уравнением 6:
[Уравнение 6]
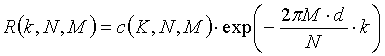 ,
,
где «d» означает величину задержки в частотной области, вызванной частотным сдвигом.
Как можно видеть из уравнения 6, если CAZAC-индекс «M» имеет очень малое значение, или если CAZAC-индекс «M» имеет максимальное значение из всех индексов Nt последовательностей, то влияние экспоненциальной функции, обусловленное частотным сдвигом, постепенно уменьшается, так что фактор влияния частотного сдвига на Rx-сигнал постепенно ослабевает.
Если CAZAC-последовательность назначается соте с частотным сдвигом больше предварительно заданного уровня, то настоящее изобретение позволяет назначать только корневую последовательность. В случае использования CAZAC-последовательности с ZCZ из-за недостаточного числа корневых последовательностей, настоящее изобретение допускает использование в CAZAC-последовательности особой последовательности, которая находится в исходном предварительно заданном диапазоне или последнем предварительно заданном диапазоне, из полных индексов. При этом следует отметить, что термин «предварительно заданный диапазон» можно установить различными способами в зависимости от характеристик обнаружения системы.
В случае сравнения вышеупомянутого способа с другим способом, позволяющим не использовать ZCZ-последовательность в соте с большим частотным сдвигом, вышеупомянутый способ повышает категории или типы доступных последовательностей, что почти устраняет необходимость выполнения планирования сот.
При более подробном рассмотрении, если число полных CAZAC-последовательностей равно Nt, как показано на фиг. 3, то последовательность для использования в соте с большим частотным сдвигом можно задать CAZAC-индексами 0, 1, 2, Nt-2, Nt-1 и Nt.
Между тем, в случае использования CAZAC-последовательности для соты с частотным сдвигом, превосходящим предварительно заданный уровень, отсутствует необходимость использования только таких индексов, которые отличаются от вышеупомянутых CAZAC-индексов 0, 1, 2, Nt-1, Nt-2 и Nt. Чтобы ослабить взаимные помехи между вышеупомянутой CAZAC-последовательностью и другой последовательностью, используемой для соты с большим частотным сдвигом, настоящее изобретение позволяет не использовать индекс последовательности, запрошенный для соты с большим частотным сдвигом, при необходимости, в результате чего обеспечивается высокая эффективность.
При этом в случае использования ZCZ-последовательности для обеспечения определенного числа доступных последовательностей в соте с большим частотным сдвигом и/или для обеспечения выполнения оценки временной задержки, имеющей место в канале, настоящее изобретение устанавливает интервал циклического сдвига в ограниченном случае с учетом ложной частоты (т.е. доплеровского сдвига), вызванной частотным сдвигом. В результате, настоящее изобретение предотвращает ухудшение функциональной характеристики, вызываемое частотным сдвигом, и ниже приведено соответствующее подробное описание.
Если принято решение, что частотный сдвиг имеет место, то частотную характеристику Rx-сигнала может представить вышеприведенным уравнением 6.
Между тем, уравнение 6 показывает, что значение сигнала передается из всех соседних поднесущих вследствие частотного сдвига. Однако, в действительности, конкретная составляющая, оказывающая сильное влияние на отклик канала Rx-сигнала, может быть задана части, находящейся по обеим сторонам соответствующей поднесущей, при этом часть получает сигнал соседней поднесущей.
Поэтому, для случая только первого порядка, уравнение 6 можно представить тремя членами, как показано в нижеследующем уравнении 7:
[Уравнение 7]
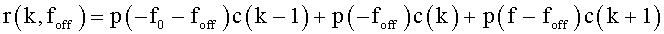
Между тем, принимающая станция вводит число, комплексно сопряженное c(n), в Rx-сигнал, и результат введения можно представить нижеследующим уравнением 8:
[Уравнение 8]
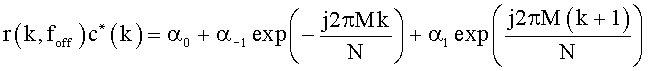
Функцию формирования импульсов, выраженную уравнением 7, несложно выразить функцией приподнятого косинуса или sinc-функцией.
Для удобства описания, функцию формирования импульсов представляют постоянными с помощью постоянных α 0, α --1 и α 1.
Как показывает уравнение 8, отклик канала Rx-сигнала наблюдается в трех точках, т.е. «t» означает намеченную позицию во временной области, «t-M» означает позицию, сдвинутую влево, и «t+M» означает позицию, сдвинутую вправо. Очевидно, что отклик канала, сгенерированный в позиции, сдвинутой на M с учетом сдвига вправо-влево, соответствует ложной составляющей Rx-сигнала, т.е. составляющей доплеровского сдвига разноса 1 поднесущей.
Вышеописанное явление, при котором в отклике канала появляется ложная составляющая вследствие частотного сдвига, показано на фиг. 4.
На фиг. 4 представлена концептуальная схема, изображающая ложные составляющие, которые появляются в отклике канала во временной области принимаемой последовательности вследствие частотного сдвига, в соответствии с настоящим изобретением.
Если циклический сдвиг применяется к последовательности, используемой в конкретной соте с частотным сдвигом, превосходящим предварительно заданный уровень, то отдельный отклик канала появляется в намеченной позиции в отклике Rx-канала соответствующей последовательности, и две дополнительных ложных составляющих могут появиться в отклике Rx-канала соответствующей последовательности в соответствии с доплеровским сдвигом разноса 1 поднесущей.
Поэтому, если интервал применения CS установлен независимо от намеченной позиции и позиций ложных составляющих, то из-за вызванного задержкой расширения канала и задержки распространения сигнала происходит непредвиденное наложение отклика канала и ложной составляющей Rx-последовательности, так что может произойти искажающее наложение намеченной позиции и позиции ложной составляющей для разных последовательностей, использующих CS.
Соответственно, если принимается решение в пользу ограниченного случая, когда в CAZAC-последовательности назначается интервал применения CS, то настоящее изобретение учитывает ложную составляющую, сгенерированную в отклике канала, таким образом, что устанавливает интервал применения CS в течение конкретного периода, в пределах которого отклик канала Rx-последовательности не совмещается с ложной составляющей в вышеупомянутом отклике канала.
На фиг. 4 изображен примерный случай, в котором образуется ложная составляющая со смещением M (где M=индекс последовательности), когда CAZAC-последовательность генерируется в частотной области. Однако если CAZAC-последовательность генерируется во временной области, то позицию генерации ложной составляющей, обусловленной доплеровским сдвигом разноса 1 поднесущей, можно определять разными способами.
Ниже приведено подробное описание всех случаев применения CS, используемых для отдельных областей. Для удобства описания и более глубокого понимания настоящего изобретения на фиг. 5-11 принято, что циклический сдвиг установлен равным T0.
На фиг. 5 показана концептуальная схема, представляющая способ установки нового блока применения циклического сдвига (CS) путем введения дополнительного запасного поля в старый блок применения CS, в соответствии с настоящим изобретением.
В соответствии с настоящим изобретением, циклически сдвинутая преамбула генерируется по схеме, учитывающей составляющую RACH. Однако в среде, в которой присутствует частотный сдвиг, связанный с OFDM, принимающая станция в соответствии с настоящим изобретением вполне может ошибочно принять нормальную последовательность за другую последовательность.
Чтобы исключить возникновение вышеупомянутой проблемы, в настоящем изобретении предусмотрена возможность применения дополнительного запасного поля на циклический сдвиг, как показано на фиг. 5.
Как показано на фиг. 5, вызванное задержкой расширение характеризует вызванное задержкой расширение канала, и двухсторонняя задержка (RTD) характеризует время распространения сигнала на физическом пути между абонентским пользовательским устройством (устройством UE) и узлом B. В случае применения дополнительного запасного поля на циклический сдвиг, настоящее изобретение обеспечивает настройку размера запасного поля для каждой последовательности sequence, так что можно ослабить влияние частотного сдвига, когда используется последовательность.
В случае исполнения частотного сдвига с использованием дополнительного запасного поля, выбор блока циклического сдвига определяется функцией CAZAC-последовательности. Иначе говоря, в связи с CAZAC-последовательностью «M», блок циклического сдвига представлен следующим уравнением 9:
[Уравнение 9]
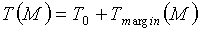 ,
,
где T0 означает обычный блок циклического сдвига, не зависящий от индекса последовательности, и Tmargin(M) означает дополнительное запасное поле, используемое, когда индекс последовательности равен M. Данное запасное поле можно выбрать другими способами в зависимости от применений последовательности и циклического сдвига.
Поэтому, хотя целесообразно, чтобы блок циклического сдвига составлял, по меньшей мере, 2M, данное дополнительное запасное поле можно заменять другим запасным полем в зависимости от участка применения CS. Вышеупомянутая ситуация показана на фиг. 6 и 7.
На фиг. 6 и 7 представлены концептуальные схемы, изображающие примеры применения дополнительного запасного поля, показанного на фиг. 5, в условиях, когда индекс последовательности имеет небольшое значение, в соответствии с настоящим изобретением.
При этом, как показано на фиг. 6, интервал M, обусловленный частотным сдвигом, меньше, чем интервал T0 циклического сдвига. Даже при использовании такого диапазона можно устранить проблему наложения с другими последовательностями. Однако может возникать проблема оценки информации по временной задержке передаваемой последовательности. Поэтому, в одном варианте осуществления настоящего изобретения, целесообразно не использовать такой диапазон, когда интервал M, обусловленный частотным сдвигом, меньше, чем интервал T0 циклического сдвига. Однако может существовать система, использующая такой диапазон в зависимости от требований системы.
Косо заштрихованная часть фиг. 6 и 7 показывает возможность циклического сдвига.
Если сигнал, не испытывающий влияния частотного сдвига, находится в позиции «t», то импульс, затронутый частотным сдвигом, может появляться в одной точке слева и может появляться в одной точке справа. Если сигнал содержит T0 как основной блок циклического сдвига, то Tmargin(M) можно установить равным 2M.
Дополнительное запасное поле применяется ко всем индексам, так что настоящее изобретение позволяет задать циклический сдвиг, обладающий высокой устойчивостью к частотным/временным сдвигам.
Однако чем больше индекс последовательности, тем больше значение Tmargin(M). В результате, число доступных циклических сдвигов сводится к «1». Для предотвращения сокращения числа циклических сдвигов, настоящее изобретение предлагает подробное описание случая с большим CAZAC-индексом.
На фиг. 8 и 9 представлена концептуальная схема, изображающая примерные дополнительные запасные поля, показанные на фиг. 5, в условиях, когда индекс последовательности имеет большое значение, в соответствии в настоящим изобретением.
На фиг. 8 показан случай, когда CAZAC-индекс «M» составляет 2T0-3T0, и на фиг. 9 показан случай, когда CAZAC-индекс «M» составляет 2T0-4T0. Хотя в случае, показанном на фиг. 8, учитывается основной блок циклического сдвига, в промежуточное пространство можно дополнительно вводить набор циклических сдвигов, обозначенный косо заштрихованной частью. Случай на фиг. 9 характеризуется более широким пространством, и поэтому в данное более широкое пространство можно ввести, по меньшей мере, два циклических сдвига.
На фиг. 10 показан пример единственной группы, состоящей из P наборов циклических сдвигов, в соответствии с настоящим изобретением. Как показано на фиг. 10, если, в порядке обобщения вышеприведенного пояснения, слоты, обозначенные косо заштрихованными частями, задаются в диапазоне 3M, в котором импульсами создается блок, и диапазон M равен PT0~(P+1)T0, то можно видеть, что создается P наборов циклических сдвигов.
Для удобства описания, блок 3M или 2M+PT0 далее именуется группой циклических сдвигов. Конкретная последовательность, к которой применяется циклический сдвиг, содержит предварительно заданное число групп циклических сдвигов. К каждой группе циклических сдвигов можно применить предварительно заданное число циклических сдвигов, так что к составляющей циклического сдвига, обусловленной доплеровским сдвигом, можно применить предварительно заданное число циклических сдвигов.
На фиг. 11 представлена концептуальная схема, изображающая способ установки группы применения циклических сдвигов и интервала применения циклического сдвига для каждой группы в соответствии с настоящим изобретением.
Как показано на фиг. 11, блоки групп циклических сдвигов можно задавать на полных последовательностях, и каждую группу циклических сдвигов можно задавать, как показано на фиг. 10. При условии, что число групп циклических сдвигов равно G, и число циклических сдвигов для каждой группы равно P, суммарное число доступных циклических сдвигов равно P*G. Как показано на фиг. 11, в соответствии с одним вариантом осуществления настоящего изобретения принято, что последовательность разбита на группы, и каждая группа производит поиск ограниченного доступного циклического сдвига в каждой группе.
В случае применения вышеупомянутой схемы, все доступные циклические сдвиги определяются в диапазоне индексов, в котором число групп циклических сдвигов равно «1». Если длина последовательности равна N, то данный диапазон, имеющий длину N последовательности, соответствует индексам, изменяющимся в диапазоне от 1-N/3 до 2N/3-N-1. В таком случае, k-тый индекс содержит ту же группу циклических сдвигов, что (N-k)-тый индекс, и набор циклических сдвигов.
На фиг. 12 показаны места, где импульсы возникают вследствие взаимной помехи, когда CAZAC-индекс содержится в интервале N/3-N/2 в соответствии с настоящим изобретением.
Одиночный прямоугольник на фиг. 12 обозначает блок циклического сдвига. Если CAZAC-индекс больше, чем «N/3», то все последовательные позиции циклических сдвигов (т.е. позиции циклических сдвигов, заданные посредством T0) использовать невозможно, и их можно использовать в соответствии с предварительно заданными правилами.
Ниже приведено описание способа установки ограниченного набора циклических сдвигов в соответствии с одним вариантом осуществления настоящего изобретения.
На фиг. 13 представлена блок-схема последовательности операций, изображающая получение ограниченного набора циклических сдвигов в соответствии с одним вариантом осуществления настоящего изобретения.
Как показано на фиг. 13, если ограниченный набор циклических сдвигов устанавливается в соте с частотным сдвигом, превосходящим предварительно заданную пороговую величину, то настоящее изобретение обеспечивает способ установки циклического сдвига с учетом наложения ложных составляющих, чтобы исключить искажающее наложение искомого отклика канала и ложных составляющих.
С этой целью, как показано на этапе S1301 на фиг. 13, настоящее изобретение обеспечивает расстояние «du» между откликом, сгенерированным доплеровским сдвигом, и искомым откликом канала с использованием данного корневого индекса «u» последовательности. При этом упомянутое расстояние соответствует циклическому сдвигу, сгенерированному доплеровским сдвигом, соответствующим разносу 1 поднесущей.
В дальнейшем приведено подробное описание переменной «du».
На фиг. 14 представлена концептуальная схема, показывающая способ установки переменной (du) циклического сдвига, соответствующего доплеровскому сдвигу, сопоставляемому разносом 1 поднесущей, когда устанавливается ограниченный набор циклических сдвигов в соответствии с настоящим изобретением.
Как показано на фиг. 14(a), если влияние доплеровской частоты отсутствует, то пик, сгенерированный операцией корреляции в принимающей станции, присутствует в позиции, обозначенной «1401». Вследствие вызванного задержкой расширения и двухсторонней задержки (RTD), позиция пика в принимающей станции оказывается в блоке NCS (1402) циклического сдвига, применяемого в качестве блока циклического сдвига, по существу, выбираемого системой.
Между тем, в случае присутствия доплеровской частоты, соответствующей разносу 1 поднесущей, позиция пика, вызываемого операцией корреляции в принимающей станции, выбирается в соответствии с индексами последовательностей.
В соответствии с настоящим изобретением, расстояние между позицией пика, основанной на доплеровском сдвиге, соответствующем разносу Δf 1 поднесущей, и идеальной позицией пика называется «du».
Другими словами, на фиг. 14(b) показан сдвиг отклика канала в принимающей станции, вызванный доплеровской частотой -Δf. На фиг. 14(c) показан сдвиг отклика канала в принимающей станции, вызванный доплеровской частотой +Δf. С учетом вышеупомянутого явления, значение «du» можно считать циклическим сдвигом, вызванным доплеровским сдвигом.
Если ограниченный циклический сдвиг устанавливается с учетом циклического сдвига, соответствующего доплеровскому сдвигу разноса 1 поднесущей, то настоящее изобретение обеспечивает контроль за устанавливаемым ограниченным циклическим сдвигом для исключения его частичного совпадения с перемещением отклика канала, вызванным доплеровским сдвигом.
Настоящее изобретение исключает зарезервированные участки, обозначенные как «зарезервированные» на фиг. 14(b) и 14 (c), из установленного интервала циклического сдвига, так что можно предотвратить путаницу между откликами канала, даже при возникновении относительно большого доплеровского сдвига.
Как показано выше на фиг. 13, по настоящему изобретению, получение вторичных переменных осуществляется на этапе S1302 с использованием переменной «du», полученной на вышеупомянутом этапе S1301. А именно, согласно настоящему изобретению определяются число (G) групп циклических сдвигов, число (P) циклических сдвигов, применимых к каждой группе, и длина (S) каждой группы из текущих последовательностей (например, ZC-последовательностей).
Вышеупомянутые вторичные переменные следует устанавливать различным образом, в соответствии с индексами последовательностей, так как длина группы заменяется на другую в соответствии с индексами последовательностей. И переменная «du» зависит от индекса последовательности, так что настоящее изобретение обеспечивает способ определения вторичных переменных в соответствии с диапазоном переменной «du».
Кроме того, в соответствии с настоящим изобретением можно применять не только вышеописанный групповой циклический сдвиг, но также дополнительный циклический сдвиг, использующий особый участок, который не содержится в группе циклических сдвигов в пределах диапазона последовательности, и подробное описание упомянутого циклического сдвига приведено в дальнейшем.
Затем, на этапе S1303, согласно настоящему изобретению устанавливается циклический сдвиг с помощью вторичных переменных, полученных на этапе S1302.
Подробное описание математической взаимосвязи между переменными для применения циклического сдвига приведено ниже.
Ограниченный циклический сдвиг предложен в соответствии с настоящим изобретением, чтобы не допускать порождения сильного эффекта воздействия доплеровской частоты.
В дальнейшем будет приведено подробное описание другого смещения «Coff» циклического сдвига, отличного от переменной «du».
Значение «Coff» указывает величину смещения, создаваемого доплеровским сдвигом.
Если величина смещения, создаваемого доплеровским сдвигом, меньше, чем половина диапазона данной последовательности, то данная величина смещения может иметь такое же значение, как переменная du. В ином случае, если степень смещения, создаваемого доплеровским сдвигом, равна или больше половины диапазона данной последовательности, то результирующая величина, получаемая, когда значение «Coff» вычитают из полной длины последовательности, соответствует переменной du.
Значение «Coff» зависит от корневого индекса используемой последовательности. Преамбулу можно генерировать либо во временной области, либо в частотной области. Взаимосвязь между значениями «Coff» и «u» зависит от области, генерирующей преамбулу.
Если ZC-последовательность генерируется в частотной области, и циклический сдвиг применяется во временной области, то настоящее изобретение позволяет вывести значение «Coff» с использованием нижеследующего способа, и в дальнейшем будет приведено его подробное описание.
В качестве допущения принято, что энергия сигнала передается из значения, переносимого из соседней поднесущей, соответствующей доплеровской частоте. Предполагается также, что перенос из соседней несущей происходит только в позицию поднесущей, отстоящую от текущей поднесущей на одно пустое место, и такой случай именуют случаем первого порядка. В данном случае, Rx-сигнал на конкретной поднесущей суммируется из трех членов, показанных в уравнении 10:
[Уравнение 10]
s(n)=p(-foff)c(n)+p(-w0-foff)c(n-1)+p(w0-foff)c(n+1),
где функцию формирования импульсов «p(f)» можно выразить функцией приподнятого косинуса или sinc-функцией. Для удобства описания, если установить постоянные c0, c-1 и c1, то значение s(n) можно выразить в виде s(n)=c0c(n)+c-1c(n-1)+c1c(n+1). Для удобства описания, если сопряженную последовательность умножить на полученное значение s(n), то можно получить нижеследующее уравнение 11:
[Уравнение 11]
s(n)c*(n)=c*(n)(c0c(n)+c-1c(n-1)+c1c(n+1))=с0+c-1c(n-1)c*(n)+c1c(n+1)c*(n)
Если, в уравнении 11, «c(n)=x(n)» выражается через CAZAC-последовательность, то c(n-1)c * (n) можно выразить с помощью нижеследующего уравнения 12:
[Уравнение 12]
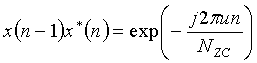 .
.
В данном случае, «u» означает корневой индекс, и «Nzc» означает длину последовательности.
Если уравнение 12 применить к уравнению 11, то можно заметить, что «s(n)» состоит из трех сигналов. Первый член значения «s(n)» означает простую постоянную составляющую, второй член характеризует комплексную экспоненциальную волну с частотой u/Nzc, и третий член характеризует комплексную экспоненциальную волну с частотой -u/Nzc. Поэтому значение «Coff» можно представить следующим уравнением 13:
[Уравнение 13]
Coff,u=u
Наоборот, если ZC-последовательность генерируется от временной области, и циклический сдвиг генерируется от частотной области, то значение «Coff» можно вычислить следующим способом.
Если преамбула RACH, принятая без частотного сдвига, установлена равной r(n), то сигнал RACH, принимаемый с частотным сдвигом, можно представить следующим уравнением 14:
[Уравнение 14]
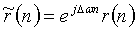 .
.
Где Δω равно Δω=2πΔf/f S, и Δf означает частотный сдвиг в герцах (Гц), и fS означает частоту выборки преамбулы RACH.
Автокорреляцию значения 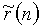 можно вычислить с использованием уравнения «r(n)=xu(n)», в котором «u» указывает индекс ZC-последовательности.
можно вычислить с использованием уравнения «r(n)=xu(n)», в котором «u» указывает индекс ZC-последовательности.
[Уравнение 15]
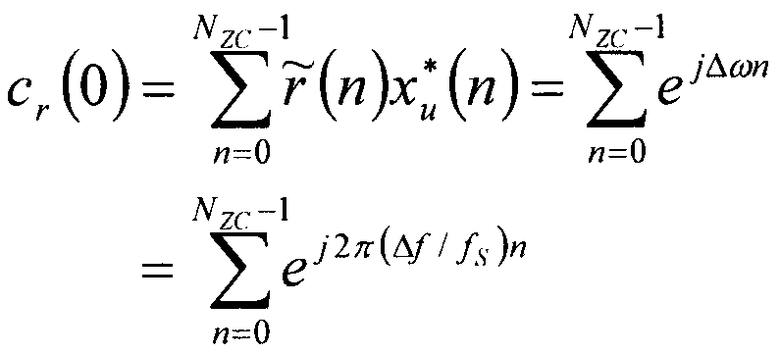
Если, в уравнении 15, «Coff,u» характеризует запасное поле частотного сдвига, то автокорреляцию 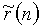 можно вычислить с использованием
можно вычислить с использованием
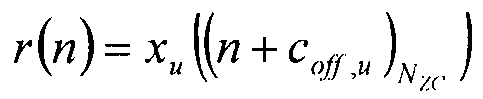
в следующем уравнении 16:
[Уравнение 16]
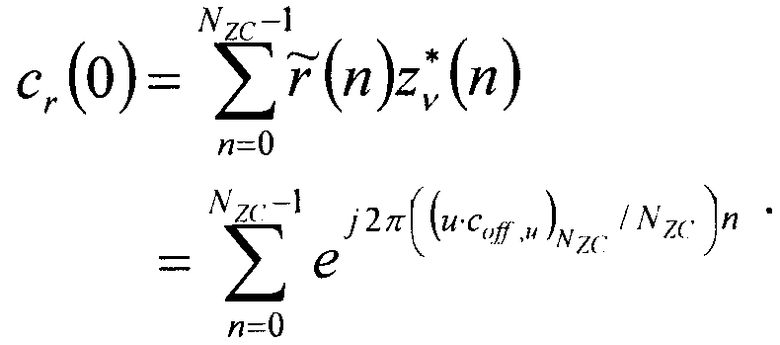
В уравнении 16, «( )Nzc» означает модулярную операцию относительно значения «Nzc». Если Coff,u'=u*Coff,u является корневым индексом, связанным со сдвигами при выборке, и γ означает показатель повторной выборки, представляющий собой ответ на временной сдвиг, то значение Coff,u' можно представить выражением
C off,u '=(γ-1)N ZC.
С использованием уравнений 15 и 16, значение γ можно представить выражением
γ=1+Δf/f S.
Позицию отклика канала называют главным лепестком, и позицию отклика ложной составляющей канала, испытывающего влияние (+/-) доплеровской частоты, называют боковым лепестком.
Для уточнения, главный лепесток показывает позицию при сдвиге, равном 0, и соответствует нормальной позиции отклика канала в отсутствие влияния доплеровской частоты.
Положительный (+) боковой лепесток показывает позицию, обусловленную положительным (+) сдвигом, и соответствует ложной позиции отклика под влиянием положительной (+) доплеровской частоты. Отрицательный (-) боковой лепесток показывает позицию, обусловленную отрицательным (-) сдвигом, и соответствует ложной позиции отклика под влиянием отрицательной (-) доплеровской частоты.
Как можно видеть из уравнения 16, главный лепесток автокорреляционного пика возникает в позиции с координатой Coff,u=0 или Coff,u'=0. Согласно вышеупомянутому уравнению 16, пара боковых лепестков возникает согласно условию, выраженному нижеследующим уравнением 17:
[Уравнение 17]
(u*Coff,u)Nzc=-1
Поэтому результат «u*Coff,u-m*Nzc» равен «-1», как следует из
«Coff,u=(m*Nzc-1)/u». В данном случае, «m» означает наименьшее целое число, способное обеспечить, чтобы значение Coff,u было целым числом. Например, если длина ZC-последовательности равна 839 и корневой индекс равен 300, то значение «m» устанавливают равным 59, и значение Coff,u устанавливается 165.
В случае использования ZC-последовательности во временной области, значение Coff можно задавать с помощью нижеследующего уравнения 18:
[Уравнение 18]
Coff,u=(Nzcm-1)/u
В уравнении 18, «m» означает наименьшее положительное число, способное обеспечить, чтобы значение Coff,u было целым числом, и «Nzc» означает длину ZC-последовательности.
Все индексы «u» являются взаимно простыми числами со значением Nzc. Поэтому существует положительное целое число (uinv=1/u), способное удовлетворить уравнению (u*uinv=1 mod Nzc). Следовательно, значение Coff,u можно удобно представить с помощью нижеследующего уравнения 19:
[Уравнение 19]
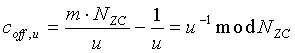 .
.
В уравнении 19, отрицательный знак (-) противоположен положительному знаку
(+), так что данное уравнение можно представить в виде нижеследующего уравнения 20:
[Уравнение 20]
Coff,u=(1/u)mod Nzc.
Вкратце, если CAZAC-последовательность используют в частотной области, то индекс «u» CAZAC-последовательности становится равным «Coff», без какого-либо изменения. Если CAZAC-последовательность используют во временной области, то с индексом «u» CAZAC-последовательности выполняется операция «(1/u) mod Nzc», чтобы можно было получить значение Coff.
В том случае, если ZC-последовательность используют в частотной или временной области, и используют особенность сопряжения между Coff и ZC-последовательностями, то расстояние «du» между главным лепестком и боковым лепестком можно выразить нижеследующим уравнением 21:
[Уравнение 21]
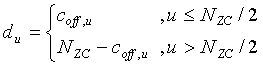 .
.
Настоящее изобретение обеспечивает ряд различных способов установки ограниченных циклических сдвигов, например, первый способ установки ограниченного циклического сдвига без использования фиксированной позиции циклического сдвига, и второй способ установки ограниченного циклического сдвига с использованием фиксированной позиции циклического сдвига.
Первый способ соответствует ограниченному циклическому сдвигу без учета предварительно заданной позиции сдвига. Второй способ соответствует ограниченному циклическому сдвигу с учетом предварительно заданной позиции сдвига.
Что касается первого способа, то существует ряд различных способов, а именно, способ непосредственного использования значения сдвига Va-того ограниченного циклического сдвига, и способ установки интервала циклического сдвига с использованием значения «Cva» сдвига. А именно, циклически сдвинутая последовательность становится последовательностью xu,v(n)=xu((n+CVa) mod Nzc), как показано в уравнении 4.
Что касается первого способа, то существует ряд различных способов, использующих десятичную дробь «Va» для использования в циклическом сдвиге, например, способ установки интервала циклического сдвига посредством вычисления десятичной дроби «Va» индекса сдвига.
Иначе говоря, если длину циклического сдвига установить равной Ncs, то получают циклически сдвинутый индекс «xu,Va(n)=xu((n+round(vaNCS)) mod Nzc)». В данном случае, оператор «round» означает функцию округления.
Что касается второго способа, то существует ряд различных способов, использующих целое число «Va» для использования в циклическом сдвиге, например, способ установки интервала циклического сдвига посредством вычисления целого числа «Va» индекса сдвига. А именно, циклически сдвинутая последовательность приобретает вид xu,Va(n)=xu((n+vaNCS) mod NZC).
При этом если циклический сдвиг осуществляют на число, кратное Ncs, то преамбулы произвольного доступа, каждая из которых содержит участок с нулевой зоной корреляции (ZCZ), не имеющий корреляционной связи в u-той корневой ZC-последовательности, определяются уравнением xu,v(n)=xu((n+vNCS) mod NZC). Данное определение пригодно для соты с небольшой/средней подвижностью абонентов, в которой отсутствует проблема сильного частотного сдвига. Однако если ограниченный циклический сдвиг применяют в соте с большой подвижностью абонентов, то вышеприведенное определение не пригодно для соты с большой подвижностью абонентов. В частности, доступное значение «v» ограничено, и число доступных преамбул с ZCZ сокращается до 1/3 от числа преамбул с ZCZ в общем случае.
Ниже приведено подробное описание вариантов осуществления, соответствующих вышеупомянутым случаям.
Наилучший вариант осуществления изобретения
Данный вариант осуществления настоящего изобретения относится к способу установки ограниченного циклического сдвига с учетом влияния только доплеровского сдвига, без использования фиксированной позиции циклического сдвига.
Настоящее изобретение предполагает, что преамбула генерируется с использованием ZC-последовательности в виде CAZAC-последовательности.
Значение «du» в нижеследующем уравнении 22 отражает особый случай, в котором ZC-последовательность генерируется в частотной области.
[Уравнение 22]
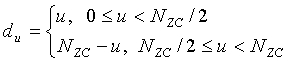 .
.
В случае генерации ZC-последовательности во временной области, значение «du» можно представить с помощью нижеследующего уравнения 23:
[Уравнение 23]
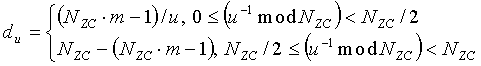
В уравнении 23, «m» означает наименьшее положительное число, способное обеспечить, чтобы значение «du» было целым числом, и Nzc означает длину ZC-последовательности. Уравнение 23 можно также представить в виде нижеследующего уравнения 24:
[Уравнение 24]
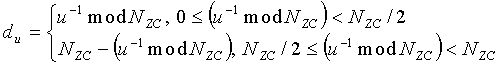
Поэтому, v-тый циклический сдвиг u-того корневого индекса можно задать в виде xu,v(n)=xu((n+Cv) mod NZC). При этом если выбран общий циклический сдвиг, то значение Cv можно представить в виде Cv=v*NCS. Если выбран ограниченный циклический сдвиг, то значение Cv можно получить из уравнения 25.
[Уравнение 25]
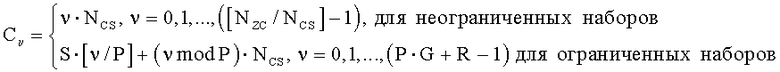
Если выбран ограниченный циклический сдвиг без предварительно заданной позиции сдвига, то данный случай считается первым случаем (случай 1), и его подробное описание приведено ниже.
Корень ZC-последовательности с номером u и v-тая преамбула произвольного доступа, из которых каждый(ая) имеет нулевую зону корреляции, задаются выражением «xu,v(n)=xu((n+Cv) mod NZC)».
В данном случае, «Cv» указано в вышеприведенном уравнении 25.
Другими словами, в случае неограниченных наборов, испытывающих небольшое воздействие доплеровского сдвига, настоящее изобретение позволяет устанавливать циклический сдвиг, соответствующий целому кратному от Ncs, равному основному блоку циклического сдвига.
Однако в случае неограниченных наборов, испытывающих меньшее воздействие доплеровского сдвига, можно устанавливать циклический сдвиг, соответствующий целому кратному от Ncs.
В соответствии с фиг. 13, в случае ограниченных наборов, испытывающих сильное воздействие доплеровского сдвига, можно установить число (G) групп циклических сдвигов, число (P) циклических сдвигов, применимых к каждой группе циклических сдвигов, и число (R) дополнительных циклических сдвигов.
Способ вычисления каждой вторичной переменной можно выбирать по-разному, согласно диапазону «du», как ранее указано на фиг. 13.
На интервале Ncs≤du<(Nzc/3), отделяющем ложную составляющую, число циклических сдвигов на одну группу задается выражением 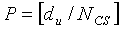 , и существует G (
, и существует G (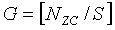 ) групп, каждая из которых имеет длину
) групп, каждая из которых имеет длину 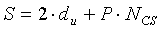 , и число ограниченных дополнительных циклических сдвигов задается выражением
, и число ограниченных дополнительных циклических сдвигов задается выражением 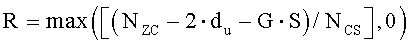
На интервале (Ncs/3)≤du≤(Nzc-Ncs)/2, отделяющем ложную составляющую, число циклических сдвигов на одну группу задается выражением 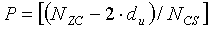 , и существует G (
, и существует G (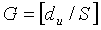 ) групп, каждая из которых имеет длину
) групп, каждая из которых имеет длину 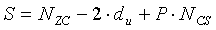 , и число ограниченных дополнительных циклических сдвигов задается выражением
, и число ограниченных дополнительных циклических сдвигов задается выражением 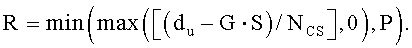
Ниже приведено подробное описание принципов вычисления вышеупомянутых вторичных переменных.
(1) d u <N CS
На фиг. 15 приведена концептуальная схема, представляющая особый случай, в котором переменная (du) меньше, чем основной блок NCS, к которому применяется циклический сдвиг (CS), в соответствии с настоящим изобретением.
Блок (NCS) циклического сдвига разработан с учетом вызванного задержкой расширения и RTD (двухсторонней задержки), которые могут формироваться в канале. Поэтому, если du меньше, чем NCS, то пик, обусловленный расширением, вызванным задержкой, и/или RTD, в пределах диапазона NCS может частично совпадать с другим пиком, вызванным доплеровским сдвигом, как показано на фиг. 15. Поэтому при установке ограниченного циклического сдвига данный вариант осуществления не предусматривает установки циклического сдвига для случая, в котором значение du меньше, чем значение NCS.
(2) N CS ≤d u <(N ZC /3)
На фиг. 16 приведена концептуальная схема, представляющая способ вычисления переменной, устанавливающей циклический сдвиг в интервале NCS≤du<(NZC/3), в соответствии с настоящим изобретением.
Как показано на фиг. 16, участок циклического сдвига, порождаемый доплеровской частотой, находится в интервале NCS≤du<(NZC/3). В частности, участок циклического сдвига появляется в диапазоне длины последовательности, расположенном на обеих сторонах намеченного циклического сдвига.
В соответствии с данным вариантом осуществления, участки циклического сдвига, вызываемые доплеровской частотой на обеих сторонах циклического сдвига, можно сгруппировать в одну группу. Кроме того, в настоящем изобретении определяется, сколько значений Ncs можно использовать без частичного совмещения с другими значениями в пределах диапазона «du». Число ограниченных циклических сдвигов, доступных для каждой группы, можно установить равным P. А именно, значение P можно вычислить с помощью нижеследующего 26:
[Уравнение 26]
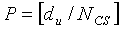
Расстояние между конкретным откликом 1601 канала и ложной составляющей 1601a, обусловленной доплеровским сдвигом, обозначено «du». Расстояние между конкретным откликом 1601 канала и другой ложной составляющей 1601a, обусловленной доплеровским сдвигом, обозначено «du».
Если к каждой группе применяется P циклических сдвигов, то ложные составляющие, сгенерированные на левом участке на основе отклика 1601 канала, содержатся в диапазоне du, а другие ложные составляющие, сгенерированные на правом участке на основе отклика 1601 канала, могут находиться снаружи диапазона du.
При этом в случае учета всех операций установки ложных составляющих из P откликов канала, сгенерированных на правом участке, соответствующая длина определяется выражением P·NCS (1602).
Поэтому длина (S) одного циклического сдвига может быть равна сумме длины «du» и длины «P·NCS», и выражается нижеследующим уравнением 27:
[Уравнение 27]
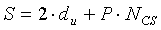
При этом число групп циклических сдвигов в полных последовательностях можно вычислить делением полной длины (NZC) последовательности на длину (S) группы и можно выразить нижеследующим уравнением 28:
[Уравнение 28]
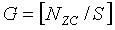
При этом, как показано на фиг. 16, можно оставить конкретный участок 1603 с длиной, меньшей, чем длина (S) группы. Длина участка «1603» соответствует «NZC-G·S», где NZC означает длину полной последовательности, G означает число групп, и S означает длину группы.
Если NZC-G·S-2du больше, чем NCS, то дополнительный циклический сдвиг можно также применить к вышеупомянутому участку 1603, и его подробное изображение приведено на фиг. 16, но как для участка «1604». Поэтому в том случае, если число циклических сдвигов, которые не основаны на группе циклического сдвига, равно R, значение R можно выразить нижеследующим уравнением 29:
[Уравнение 29]
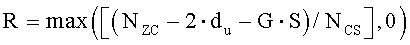
(3) (N ZC /3) ≤ d u < (N ZC - N CS )/2
На фиг. 17 приведена концептуальная схема, представляющая способ вычисления переменной, устанавливающей циклический сдвиг в интервале (NZC/3)≤du<(NZC-NCS)/2, в соответствии с настоящим изобретением.
На участке (NZC/3)≤du, в отличие от вышеописанного случая (2) (т.е. вышеупомянутого случая (2) NCS≤du<(NZC/3)), позиции отклика канала и ложных составляющих, обусловленных доплеровским сдвигом, выходят за полную длину NZC последовательности, так что ложная составляющая может возникать между откликом канала в идеальном случае и диапазоном du.
Например, при пике, находящемся в позиции «1701» на фиг. 17, ложные составляющие могут возникать в позициях 1701a и 1701b посредством (+/-) доплеровского сдвига. Поэтому число циклических сдвигов, применимых к одной группе циклических сдвигов, в данном случае (3), задается участком «NZC-2du» (1702), находящимся в центре фиг. 17, так что число P ограниченных циклических сдвигов, применимых к каждой группе, можно вычислить из нижеследующего уравнения 30:
[Уравнение 30]
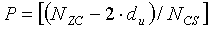
В данном случае (3) длину S каждой группы циклических сдвигов можно выразить с помощью нижеследующего уравнения 31:
[Уравнение 31]
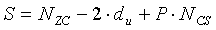
Переменная S равна сумме длины участка (NZC-2du) 1702, и длина участка 1703 соответствует длине «P·NCS». Длина «P·NCS» может изменяться при изменении числа циклических сдвигов, применимых к каждой фактической группе, находящейся с правой стороны.
При этом в вышеупомянутом случае (3) определяется число групп циклических сдвигов в данной ZC-последовательности путем учета того, сколько длин (S, где S = длина конкретной группы) будет допускаться в диапазоне du (1704), тогда как в вышеупомянутом случае (2) определялось число групп циклических сдвигов в подобной данной ZC-последовательности путем учета того, сколько длин (S) будет допускаться на длине Nzc полной последовательности.
Пространство между конкретным откликом канала и двумя ложными составляющими для данного отклика канала превосходит диапазон полной последовательности, так что настоящее изобретение обеспечивает контроль за тем, чтобы отдельные ложные составляющие не совмещались между собой в пределах диапазона du. Число групп циклического сдвига можно выразить нижеследующим уравнением 32:
[Уравнение 32]
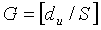
И, наконец, группа циклического сдвига устанавливается в диапазоне du (1704), как описано выше, и можно оставлять участок 1705, имеющий длину, короче длины группы циклического сдвига. Упомянутая длина участка 1705 соответствует «du-G·S». Если длина участка 1705 больше, чем NCS, то к данной длине можно применить дополнительный циклический сдвиг.
Поэтому число R дополнительных циклических сдвигов можно представить выражением 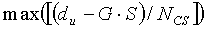 .
.
Если длина (S) каждой группы циклических сдвигов больше, чем «P», то дополнительные циклические сдвиги, соответствующие числу, большему, чем «P», могут частично совмещаться с участком (+/-) ложной составляющей на правом участке. Поэтому настоящий вариант осуществления может указывать число R дополнительных циклических сдвигов, как показано в нижеследующем уравнении 33:
[Уравнение 33]
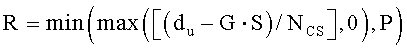
(4) (N ZC -N CS )/2≤d u
Как показано на фиг. 17, участок Nzc-2du (1702), находящийся в центральной части, должен превосходить NCS, чтобы циклический сдвиг можно было применять к каждой группе. А именно, данное требование можно представить в виде NZC-2du>NCS.
Если вышеупомянутое требование формулируется отличающимися способами на основе значения du, то можно заметить, что должно удовлетворяться уравнение
NZC-NCS>2du (т.е. (NZC-NCS)/2>du). Поэтому настоящий вариант осуществления не устанавливает ограниченного циклического сдвига в диапазоне (NZC-NCS)/2>du.
Ниже, на основании вышеприведенного пояснения для отдельных интервалов, приведено подробное описание только ограниченного набора, содержащегося в уравнении 25. Во-первых, ограниченный набор согласно уравнению 25 можно представить с помощью нижеследующего уравнения 34
[Уравнение 34]
C ν=S·[ν/P]+(ν mod P)·N CS, ν=0,1,…,(P·G+R-1).
Ниже приведено описание отдельных членов, используемых при упомянутом циклическом сдвиге.
В уравнении 34, S·[ν/P] указывает начальную точку каждой группы циклических сдвигов. Если значение ν меньше, чем число P циклических сдвигов для каждой группы, то S·[ν/P] означает «0». Если значение ν больше, чем число P циклических сдвигов для каждой группы, но меньше, чем «2P», то S·[ν/P] означает «S», что соответствует длине одной группы циклических сдвигов.
Если значение ν больше, чем «2P», но меньше, чем «3P», то S·[ν/P] означает «2S», что соответствует длине двух групп циклических сдвигов.
Член (ν mod P)·N CS указывает позицию циклического сдвига, применяемого к каждой группе (или позицию дополнительного циклического сдвига). Другими словами, значение ν сдвигается в другую позицию на предварительно заданное расстояние NCS интервалами P раз.
Значение ν в уравнении 34 (или уравнении 25, содержащем уравнение 34) не проводит различия между группами или составляющими групп и характеризует общее число циклических сдвигов. В результате, общее число циклических сдвигов можно представить выражением P·G+R.
Видоизмененные примеры
Ниже приведено описание ряда различных видоизмененных примеров, применимых в настоящем изобретении.
Хотя вышеупомянутый наилучший вариант осуществления относится к особому случаю, в котором отсутствует ограничение, касающееся начальной точки циклического сдвига, настоящее изобретение применимо не только к вышеупомянутому случаю, но также к другим ограниченным случаям.
Ниже приведено описание не только вышеупомянутого наилучшего варианта осуществления, но также всех вариантов осуществления, допускающих их применение, в общем, в соответствии с настоящим изобретением.
Позиция, в которой возникает ложная составляющая вследствие (+) доплеровской частоты, обозначается позицией «+сдвиг», и позиция, в которой возникает ложная составляющая вследствие (-) доплеровской частоты, обозначается позицией «-сдвиг».
На фиг. 18 и 19 приведены концептуальные схемы, представляющие способ сокращения числа последовательностей преамбул с ZCZ из-за ложного отклика в случае, когда Nzc=839, Ncs=100 и du=155, в соответствии с настоящим изобретением.
Циклический сдвиг, показанный на фиг. 18, может начинаться в любой позиции. Циклический сдвиг, показанный на фиг. 19, может выполняться только в позиции, кратной NCS. Значение NCS на фиг. 18 равно этому же значению на фиг. 19, однако начальные позиции отдельных циклических сдвигов на фиг. 18 и 19 различаются.
В заключение, случай на фиг. 18 может создать намного больше циклических сдвигов, чем в случае на фиг. 19. Точнее, случай на фиг. 18 устраняет ограничение на начальную позицию циклического сдвига, так что в данном случае возможно получение дополнительного ограниченного циклического сдвига.
На фиг. 20 представлена концептуальная схема, показывающая коэффициент увеличения доступного ограниченного циклического сдвига после того, как снято ограничение начального положения циклического сдвига в случае Nzc=839, в соответствии с настоящим изобретением.
Устранение ограничения на начало циклического сдвига не может увеличить сложность аппаратного обеспечения.
Поэтому предпочтителен ограниченный циклический сдвиг без учета предварительно заданной позиции сдвига, и вышеупомянутый наилучший вариант осуществления создан на основе вышеупомянутого допущения.
Однако настоящее изобретение применимо также к ограниченному циклическому сдвигу с предварительно заданной позицией сдвига, и поэтому в нижеследующем описании представлено два вышеупомянутых случая.
Во-первых, ниже будет описан случай ограниченного циклического сдвига (т.е. случай 1), не учитывающий предварительно заданной позиции сдвига.
Уравнение 21 указывает расстояние, отделяющее ложную составляющую, независимо от области генерации преамбулы. Число доступных ограниченных циклических сдвигов на одну корневую ZC-последовательность определяется по-разному, в соответствии с корневым индексом и значением NCS, так что для применения в разных диапазонах расстояний, отделяющих ложные составляющие, требуются разные уравнения.
В частности, существуют два диапазона расстояний, отделяющих ложные составляющие, в которых отсутствует разделение ложных откликов. Диапазон, в котором можно использовать ограниченный циклический сдвиг, устанавливается в виде NCS≤du≤(NZC-NCS)/2. В этом диапазоне диапазон циклических сдвигов и два диапазона ложных составляющих не имеют частичных совмещений между собой.
В данном случае, если преамбула генерируется в частотной области, то значение «du» устанавливается равным «u», т.е. du=u. Если преамбула генерируется во временной области, то значение «du» устанавливается равным «1/u mod Nzc», т.е. du=1/u mod Nzc. Число ограниченных циклических сдвигов может быть представлено нижеследующим уравнением 35:
[Уравнение 35]
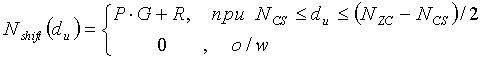
В уравнении 35, «P» означает число ограниченных циклических сдвигов на одну группу, «G» означает число групп, сгенерированных в одной последовательности преамбулы, и «R» означает число ограниченных дополнительных циклических сдвигов, которые не основаны на дополнительной группе.
Доступный диапазон ограниченного циклического сдвига определяется выражением NCS≤du≤(NZC-NCS)/2. Этот интервал «NCS≤du≤(NZC-NCS)/2» можно разбить на интервалы «NCS≤du<(NZC/3)» и «(NZC/3)≤du≤(NZC-NCS)/2» на основе Nzc/3.
Причина, по которой диапазон расстояний, отделяющих ложную составляющую, разбивают на «NCS≤du<(NZC/3)» и «(NZC/3)≤du≤(NZC-NCS)/2», на основе Nzc/3, поясняется ранее в тексте.
Поэтому NCS≤du≤(NZC-NCS)/2 выбирается по-разному, исходя из «Nzc/3». Описание диапазона NCS≤du<(NZC/3) и диапазона (NZC/3)≤du≤(NZC-NCS)/2 приведено ниже.
Если начальная позиция первой группы назначена «0», то диапазон Va-того ограниченного циклического сдвига определяется как [CVa, start, CVa, end] из уравнений 36 и 37.
[Уравнение 36]
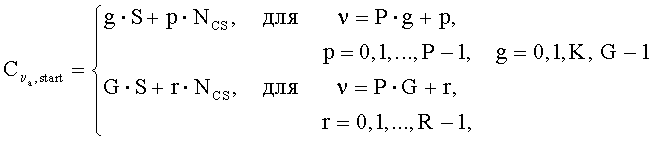
[Уравнение 37 ]
CVa, end=CVa, start+Ncs-1
Ложная составляющая возникает в позициях, указываемых нижеследующими уравнениями 38 и 39:
[Уравнение 38]
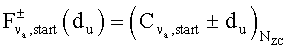
[Уравнение 39]
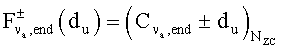
В уравнении 39, член «()Nzc» означает модулярную операцию.
Во-первых, диапазон NCS≤du<(NZC/3) расстояний, отделяющих ложные составляющие, (т.е. диапазон 1 расстояний, отделяющих ложные составляющие) содержит число 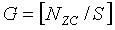 групп. Каждая группа содержит число
групп. Каждая группа содержит число 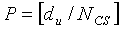 ограниченных циклических сдвигов. Длина каждой группы имеет значение
ограниченных циклических сдвигов. Длина каждой группы имеет значение 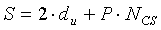 . Если доступный дополнительный циклический сдвиг является положительным (+) числом, то значение R определяется выражением
. Если доступный дополнительный циклический сдвиг является положительным (+) числом, то значение R определяется выражением 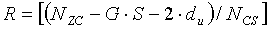 .
.
На фиг. 21 представлена концептуальная схема, изображающая примерный циклический сдвиг в случае, когда Nzc=839, Ncs=40 и du=150, в соответствии с одним вариантом осуществления настоящего изобретения. Каждая группа содержит три циклических сдвига, и два дополнительных циклических сдвига существуют в остальных диапазонах. В данном примере, общее число ограниченных циклических сдвигов равно «5».
В одном варианте осуществления настоящего изобретения, в уравнения 36 и 37 подставляется число вычисленных групп, число ограниченных циклических сдвигов на одну группу и длина группы, и затем устанавливается интервал применения циклических сдвигов с учетом вышеупомянутых параметров.
Затем, в диапазоне (NZC/3)≤du≤(NZC-NCS)/2 расстояний, отделяющих ложные составляющие, (т.е. в диапазоне 2 расстояний, отделяющих ложные составляющие) число доступных циклических сдвигов на одну группу определяется из выражения 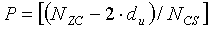 , длина каждой группы определяется из выражения
, длина каждой группы определяется из выражения 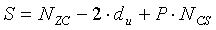 , и существует G групп (где
, и существует G групп (где 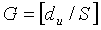 ).
).
Дополнительный циклический сдвиг выбирается из центральной части и остаточной части правой стороны. В данном случае, число выбранных циклических сдвигов должно быть наименьшим числом циклических сдвигов. А именно, если значение R является положительным числом, то число дополнительных циклических сдвигов определяется выражением 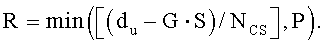 Начальная позиция Va-того ограниченного циклического сдвига вычисляется подстановкой вышеупомянутых параметров в уравнения 36 и 37.
Начальная позиция Va-того ограниченного циклического сдвига вычисляется подстановкой вышеупомянутых параметров в уравнения 36 и 37.
На фиг. 22 представлена концептуальная схема, изображающая примерный циклический сдвиг в случае, когда Nzc=839, Ncs=40 и du=399, в соответствии с одним вариантом осуществления настоящего изобретения.
В наличии имеются четыре группы, каждая из которых содержит один циклический сдвиг и один дополнительный циклический сдвиг. В данном примере, общее число циклических сдвигов равно 5.
В соответствии с данным вариантом осуществления настоящего изобретения, число вычисленных групп, число ограниченных циклических сдвигов на одну группу и длина группы подставляются в уравнения 36 и 37, и затем, с учетом вышеупомянутых параметров, устанавливается интервал применения циклических сдвигов.
На самом деле, знак (=) равенства между двумя диапазонами расстояний, отделяющих ложные составляющие, может не иметь значения или может иметь сравнительно малое значение. Например, в случае использования ZC-последовательности, имеющей длину 839, значение (Nzc/3) равно 279,67 (т.е. (Nzc/3)=279,67), и поэтому полученные разбиением диапазоны Ncs≤du<(Nzc/3) и (Nzc/3)≤du≤(Nzc-Ncs)/2 могут давать такие же результаты, как полученные разбиением диапазоны Ncs≤du≤(Nzc/3) и (Nzc/3)<du≤(Nzc-Ncs)/2.
Далее приведено описание ограниченного циклического сдвига (т.е. случая 2), учитывающего предварительно заданную позицию сдвига.
Способ генерации ограниченного циклического сдвига с использованием предварительно заданной позиции сдвига изменяется на другой способ. Каждый диапазон расстояний, отделяющих ложные составляющие, содержит не только G групп, каждая из которых содержит P циклических сдвигов, но также первый дополнительный циклический сдвиг из R1 групп.
В случае использования предварительно заданной позиции сдвига, настоящее изобретение содержит особый дополнительный циклический сдвиг, иной, чем в другом случае, в котором не существует предварительно заданной позиции сдвига на участке диапазонов 2 расстояний, отделяющих ложные составляющие.
На участке диапазонов 2 расстояний, отделяющих ложные составляющие, главная область образуется, как правило, на передних отсчетах последовательности, и области ложных составляющих образуются, как правило, на задних отсчетах последовательности. Однако в соответствии со случаем 2, главная область образуется на задних отсчетах последовательности, и области ложных составляющих образуются на передних отсчетах последовательности.
Второй дополнительный циклический сдвиг обозначается через R2. Второй дополнительный циклический сдвиг не образуется в диапазоне 1 расстояний, отделяющих ложные составляющие. Общее число ограниченных циклических сдвигов можно представить с помощью нижеследующего уравнения 40:
[Уравнение 40]
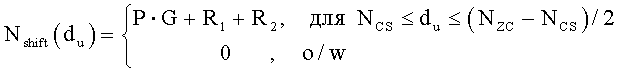
В том случае, если начальной позицией первой группы является «0», Va-тый ограниченный циклический сдвиг задается в интервале [CVa, start, CVa, end], определяемом из уравнений 41 и 42:
[Уравнение 41]
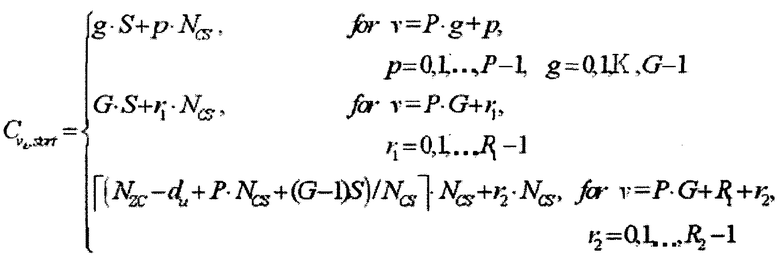
[Уравнение 42]
CVa, end=CVa, start+Ncs-1.
Сопутствующая ложная составляющая образуется в позициях, задаваемых нижеследующими уравнениями 43 и 44:
[Уравнение 43]
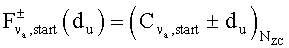
[Уравнение 44]
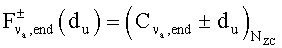
В уравнениях 43 и 44, член «()Nzc» означает модулярную операцию.
В диапазоне NCS≤du<(NZC/3) расстояний, отделяющих ложные составляющие, (т.е. в диапазоне 1 расстояний, отделяющих ложные составляющие) существует G групп (где 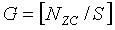 ), P ограниченных циклических сдвигов (где
), P ограниченных циклических сдвигов (где 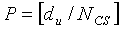 ), и длина каждой группы имеет значение
), и длина каждой группы имеет значение 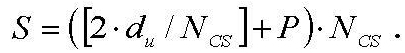 Если значение R1 является положительным (+) числом, то число первых дополнительных циклических сдвигов определяется выражением
Если значение R1 является положительным (+) числом, то число первых дополнительных циклических сдвигов определяется выражением 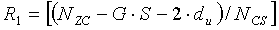 .
.
На фиг. 23 представлена концептуальная схема, изображающая примерный циклический сдвиг в случае, когда Nzc=839, Ncs=40 и du=150, в соответствии с другим вариантом осуществления настоящего изобретения. На фиг. 23 каждая группа содержит три циклических сдвига и два циклических сдвига. В данном примере общее число ограниченных циклических сдвигов равно «5».
В соответствии с данным вариантом осуществления настоящего изобретения, число вычисленных групп, число ограниченных циклических сдвигов на одну группу и длина группы подставляются в уравнения 41 и 42, и затем, с учетом вышеупомянутых параметров, устанавливается интервал применения циклических сдвигов.
Затем, в диапазоне (NZC/3)≤du≤(NZC-NCS)/2 расстояний, отделяющих ложные составляющие, (т.е. в диапазоне 2 расстояний, отделяющих ложные составляющие) число доступных циклических сдвигов на одну группу определяется из выражения 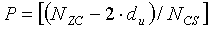 , длина каждой группы определяется из выражения
, длина каждой группы определяется из выражения 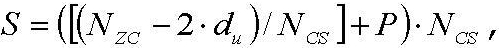 и существует G групп (где
и существует G групп (где 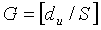 ).
).
Первый дополнительный циклический сдвиг вычисляют таким же способом, как для диапазона 1 расстояний, отделяющих ложные составляющие. Если значение R1 является положительным числом, то число первых дополнительных циклических сдвигов определяется выражением 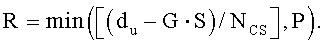
Если значение R1 равно «0» (т.е. R1=0), то следует определить наличие или отсутствие второго дополнительного циклического сдвига. Форма второго дополнительного циклического сдвига противоположна форме обычного циклического сдвига, как показано на последнем циклическом сдвиге, изображенном на фиг. 23.
В настоящем изобретении выполняется определение, является ли диапазон ложных составляющих для второго дополнительного циклического сдвига доступным диапазоном (т.е. 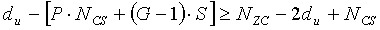 ), и выполняется определение, доступен ли интервал циклического сдвига (т.е.
), и выполняется определение, доступен ли интервал циклического сдвига (т.е. 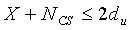 ).
).
На фиг. 24 представлена концептуальная диаграмма, изображающая примерный циклический сдвиг в случае, когда Nzc=839, Ncs=40 и du=399, в соответствии с другим вариантом осуществления настоящего изобретения. На фиг. 24 каждая группа содержит три циклических сдвига и не содержит первого дополнительного циклического сдвига (т.е. содержит нулевой первый дополнительный циклический сдвиг). И каждая группа дополнительно содержит один дополнительный циклический сдвиг, в котором относительная позиция главной области противоположна относительной позиции области ложных составляющих. Указанный второй дополнительный циклический сдвиг не создается, когда фиксированная позиция циклического сдвига не применяется, как показано на фиг. 22. В данном примере, число всех ограниченных циклических сдвигов равно «4».
В соответствии с данным вариантом осуществления изобретения, число вычисленных групп, число ограниченных циклических сдвигов на одну группу и длина группы подставляются в уравнения 41 и 42, и затем, с учетом вышеупомянутых параметров, устанавливается интервал применения циклических сдвигов.
В соответствии с другим вариантом осуществления, особая система с фиксированным циклическим сдвигом может определять циклический сдвиг в соответствии со следующим способом.
Сначала полный диапазон последовательности разбивается по значениям циклического сдвига.
Затем, по настоящему изобретение, выполняется поиск диапазона
(±u или ±(m*Nzc-1)/u), в котором взаимные помехи, вызываемые частотным сдвигом, образуются в первом диапазоне (т.е. n=1). В данном случае существует множество диапазонов, в каждом из которых возникают взаимные помехи.
Например, в случае учета только первой взаимной помехи, максимальное число диапазонов генерации взаимных помех можно установить равным «4».
Затем, если первый диапазон не имеет частичного совмещения со всеми диапазонами взаимных помех, вызванных частотным сдвигом, то первый диапазон устанавливается равным доступному диапазону, и остальные диапазоны, вызванные частотным сдвигом, устанавливаются равными ограниченному диапазону (именуемому также запрещенным диапазоном).
Согласно настоящему изобретению выполняется переход к следующему диапазону (т.е. n=n+1) и повторный поиск диапазона, в котором генерируются взаимные помехи из-за частотного сдвига.
Хотя в настоящем изобретении выполняется поиск диапазона генерации взаимных помех в n-ном диапазоне, если диапазон контроля, несколько диапазонов, вызванных частотным сдвигом, предварительно созданный доступный диапазон и предварительно установленные запретные диапазоны не имеют частичного совмещения между собой, то по настоящему изобретению определяется, что текущий диапазон является доступным диапазоном, и определяется, что несколько вышеупомянутых диапазонов, вызванных частотным сдвигом и соответствующих текущему диапазону, являются запрещенными диапазонами. Если вышеупомянутый процесс повторяется до достижения последнего диапазона, то настоящее изобретение позволяет определить циклический сдвиг в системе, включая фиксированный циклический сдвиг.
В соответствии с еще одним вариантом осуществления настоящего изобретения, вышеупомянутый установленный интервал применения циклических сдвигов можно применять в системе мобильной связи только в соте с большой подвижностью абонентов, включая несколько сот.
В данном случае, настоящее изобретение позволяет определять, характеризуется ли соответствующая сота большой подвижностью абонентов, путем определения, превосходит ли частотный сдвиг, связанный с сотой, предварительно заданный уровень, после получения информации о соте. В данном случае, предварительно заданный уровень указывает величину частотного сдвига, которую может легко выбирать или изменять специалистами в данной области техники.
В предпочтительном варианте настоящее изобретение позволяет контролировать узел B или устройство UE, чтобы определять, является ли соответствующая сота сотой с большой подвижностью абонентов. Однако устройству UE сложно оценивать величину частотного сдвига каждого из остальных устройств UE, находящихся в соте. Поэтому более предпочтителен вариант, когда узел B определяет, является ли соответствующая сота сотой с большой подвижностью абонентов, путем оценки нескольких устройств UE соты и широковещательно передает полученный сигнал по широковещательному каналу.
Между тем, если установлено, что соответствующая сота не имеет признаков соты с высокой подвижностью абонентов, то настоящее изобретение допускает включение процесса для назначения последовательности, не назначаемой соты с большой подвижностью абонентов.
Ниже в описании показано, что уравнения преобразовываются в другие уравнения с такими же исходными условиями, как в наилучшем варианте осуществления, и далее приведено подробное описание таких преобразований.
В связи наилучшим вариантом осуществления, вышеупомянутые уравнения можно также выразить следующим образом.
Если 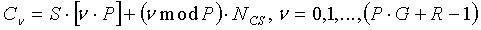 и
и 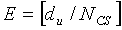 ,
, 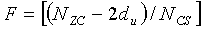 в диапазоне NCS≤du≤(NZC/3) расстояний, отделяющих ложные составляющие, то значения P и G выражаются в виде P=E,
в диапазоне NCS≤du≤(NZC/3) расстояний, отделяющих ложные составляющие, то значения P и G выражаются в виде P=E, 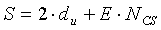 ,
, 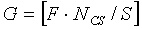 .
.
Если 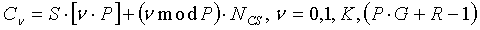 и
и 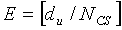 ,
, 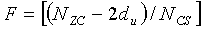 в диапазоне (Nzc/3)≤du≤(Nzc-Ncs)/2 расстояний, отделяющих ложные составляющие, то значения P, S, G и R выражаются в виде P=F,
в диапазоне (Nzc/3)≤du≤(Nzc-Ncs)/2 расстояний, отделяющих ложные составляющие, то значения P, S, G и R выражаются в виде P=F, 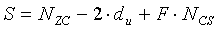 ,
, 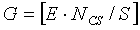 ,
, 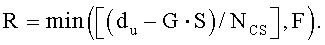
Далее в описании поясняется случай ограниченного циклического сдвига с учетом предварительно заданной позиции сдвига (случай 2) и с использованием других уравнений.
Корневая ZC-последовательность с номером u, содержащая область нулевой корреляции, т.е. v-тая преамбула произвольного доступа, определяется выражением xu,v(n)=xu((n+Cv) mod NZC). В данном случае, значение Cv задается уравнением 45:
[Уравнение 45]
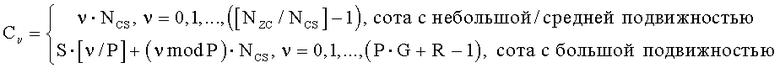
при этом, 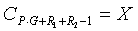 , если R
2=1, для соты с большой мобильностью.
, если R
2=1, для соты с большой мобильностью.
В данном случае, параметры соты с большой мобильностью абонентов можно определить, исходя из следующего пояснения.
А именно, в диапазоне Ncs≤du<(Nzc/3) ложных составляющих, значение P определяется выражением 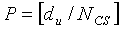 , значение S определяется выражением
, значение S определяется выражением 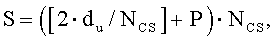 и значение G определяется выражением
и значение G определяется выражением 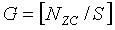 . Первый дополнительный циклический сдвиг R1 определяется выражением
. Первый дополнительный циклический сдвиг R1 определяется выражением 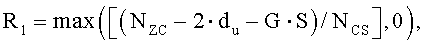 и второй дополнительный циклический сдвиг R2 определяется как R2=0.
и второй дополнительный циклический сдвиг R2 определяется как R2=0.
В диапазоне (Nzc/3)≤du<(Nzc-Ncs)/2 ложных составляющих, значение P определяется выражением 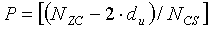 , значение S определяется выражением
, значение S определяется выражением 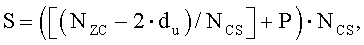 и значение G определяется выражением
и значение G определяется выражением 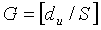 . Первый дополнительный циклический сдвиг определяется выражением
. Первый дополнительный циклический сдвиг определяется выражением 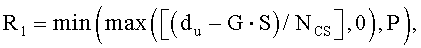 второй дополнительный циклический сдвиг R2 определяется как R2=1 в случае R1=0 и «X-Ncs<2du». В данном случае, значение X определяется выражением
второй дополнительный циклический сдвиг R2 определяется как R2=1 в случае R1=0 и «X-Ncs<2du». В данном случае, значение X определяется выражением 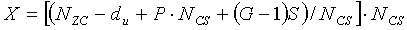 .
.
В случае ограниченного циклического сдвига xu,v(n)=xu((n+Cv) mod NZC), способ непосредственного использования величины сдвига для ν-того ограниченного циклического сдвига описан выше. Кроме данного способа, можно воспользоваться другим способом применения значение Va для Va-того ограниченного циклического сдвига так, чтобы ограниченный циклический сдвиг можно было применить в настоящем изобретении. При более подробном рассмотрении видно, что аналогичный циклический сдвиг можно создать с использованием уравнения xu,Va(n)=xu((n+round(vaNCS)) mod NZC).
В случае создания циклического сдвига с использованием вышеупомянутого способа принципиальная идея эквивалентна идеям, лежащим в основе вышеупомянутых способов. Однако к упомянутым способам применяются отличающиеся уравнения.
Ниже, с использованием других уравнений, приведено описание случая (случая 1) ограниченного циклического сдвига без учета предварительно задаваемой позиции сдвига.
Индекс (ν) для циклического сдвига представляется следующим уравнением 46:
[Уравнение 46]
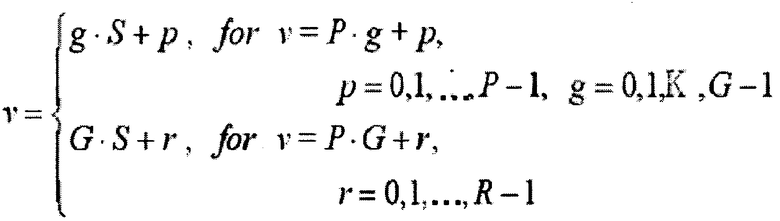
В диапазоне Ncs≤du<(Nzc/3) ложных составляющих, значение P определяется выражением 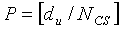 , значение S определяется выражением
, значение S определяется выражением 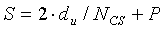 , и значение G определяется выражением
, и значение G определяется выражением 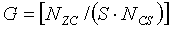 , и дополнительный циклический сдвиг R определяется выражением
, и дополнительный циклический сдвиг R определяется выражением 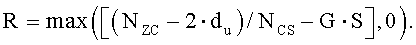
В диапазоне (Nzc/3)≤du<(Nzc-Ncs)/2 ложных составляющих, значение P определяется выражением 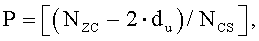 значение S определяется выражением
значение S определяется выражением 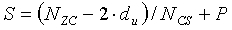 , значение G определяется выражением
, значение G определяется выражением 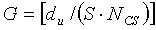 , и значение R определяется выражением
, и значение R определяется выражением 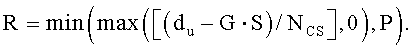
Если принять 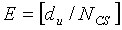 ,
, 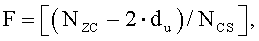 то вышеприведенное выражение можно представить другими способами. Точнее, в диапазоне Ncs≤du<(Nzc/3) ложных составляющих, значение P определяется выражением P=E, значение S определяется выражением
то вышеприведенное выражение можно представить другими способами. Точнее, в диапазоне Ncs≤du<(Nzc/3) ложных составляющих, значение P определяется выражением P=E, значение S определяется выражением 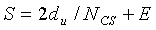 , значение G определяется выражением
, значение G определяется выражением 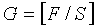 , и значение R определяется выражением
, и значение R определяется выражением 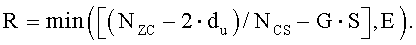
В диапазоне (Nzc/3)≤du≤(Nzc-Ncs)/2 ложных составляющих, значение P определяется выражением P=F, значение S определяется выражением 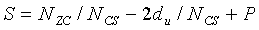 , значение G определяется выражением
, значение G определяется выражением 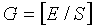 , и значение R определяется выражением
, и значение R определяется выражением 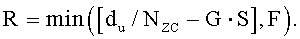
Далее, с использованием других уравнений, приведено описание случая (случая 2) ограниченного циклического сдвига с учетом предварительно заданной позиции сдвига.
Индекс (ν) для циклического сдвига представляется следующим уравнением 47:
[Уравнение 47]
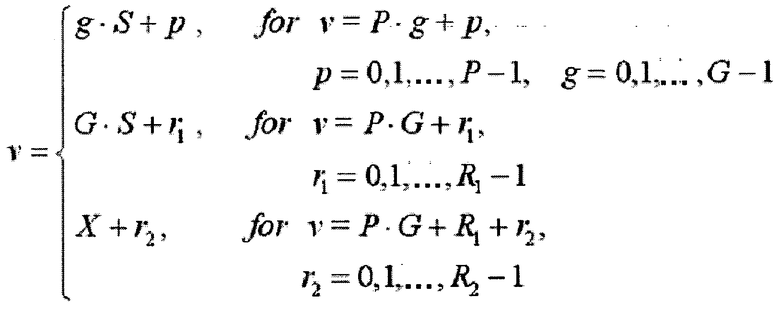
В диапазоне Ncs≤du<(Nzc/3) ложных составляющих, значение P определяется выражением 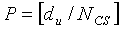 , значение S определяется выражением
, значение S определяется выражением 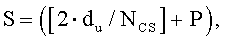 и значение G определяется выражением
и значение G определяется выражением 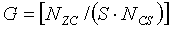 , и дополнительный ограниченный циклический сдвиг R1 определяется выражением
, и дополнительный ограниченный циклический сдвиг R1 определяется выражением 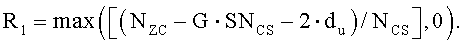
В диапазоне (Nzc/3)≤du<(Nzc-Ncs)/2 ложных составляющих, значение P определяется выражением 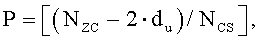 значение S определяется выражением
значение S определяется выражением 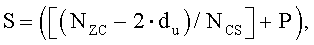 значение G определяется выражением
значение G определяется выражением 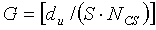 , и значение R1 определяется выражением
, и значение R1 определяется выражением 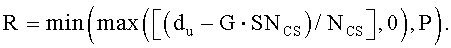
Если R1=0 и 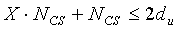 , то значение R2 можно представить как R2=1. В данном случае, значение X определяется выражением
, то значение R2 можно представить как R2=1. В данном случае, значение X определяется выражением 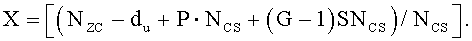
Если принять 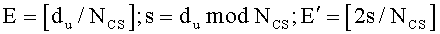 и
и 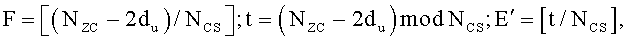 то в диапазоне Ncs≤du<(Nzc/3) ложных составляющих значение P определяется выражением P=E, значение S определяется выражением S=2F+F', значение G определяется выражением
то в диапазоне Ncs≤du<(Nzc/3) ложных составляющих значение P определяется выражением P=E, значение S определяется выражением S=2F+F', значение G определяется выражением 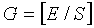 , и значение R2 определяется выражением
, и значение R2 определяется выражением 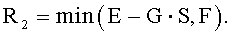
Если R1=0 и 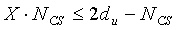 , то значение R2 можно представить как R2=1. В данном случае, значение X определяется выражением
, то значение R2 можно представить как R2=1. В данном случае, значение X определяется выражением 
Как описано выше, в соответствии с вышеупомянутыми вариантами осуществления, в случае реализации циклически сдвинутой последовательности с использованием CAZAC-последовательности, настоящее изобретение позволяет задать набор циклических сдвигов, допускающий устранение неопределенности сдвига, вызываемой частотным или временным сдвигом.
Кроме того, при оценке несинхронизированного канала, частотный сдвиг или временной сдвиг не настраивается по этому несинхронизированному каналу, так что настоящее изобретение позволяет повысить мощность данного канала.
В зависимости от действия фильтра формирования импульсов, настоящее изобретение позволяет задавать набор циклических сдвигов, в котором учитываются взаимные помехи первого порядка, взаимные помехи второго порядка и взаимные помехи более высокого порядка.
Следует отметить, что термины, применяемые в настоящем изобретении, в большинстве своем определены с учетом функций настоящего изобретения и могут быть определены иначе, в зависимости от намерения специалистов в данной области техники или обычного практического применения. Поэтому, целесообразно, чтобы вышеупомянутые термины понимались с учетом всего содержания описания настоящего изобретения.
Специалистам в данной области техники должно быть очевидно, что в настоящее изобретение можно вносить различные модификации и изменения, не выходящие за пределы сущности или объема изобретения. Следовательно, предполагается, что настоящее изобретение охватывает модификации и изменения настоящего изобретения, при условии, что они находятся в пределах объема притязаний прилагаемой формулы изобретения и ее эквивалентов.
Промышленная применимость
Как очевидно из вышеприведенного описания, настоящее изобретение позволяет легко устанавливать интервал циклических сдвигов (CS) в конкретном месте, не содержащем перекрытий, путем учета отклика канала для принятой (Rx) последовательности и местоположения ложных составляющих данной принятой (Rx) последовательности, даже если принимаемый (Rx) сигнал сдвигается из-за расширения, вызванного задержкой в канале, или задержки распространения, независимо от категорий области генерации последовательности, так что можно легко сократить число ошибок обнаружения и частоту сигнала ложной тревоги.
И, если последовательность циклического сдвига (CS) назначается соте с частотным сдвигом, превосходящим предварительно заданный уровень, то настоящее изобретение позволяет свести к минимуму влияние частотного сдвига на соту со значительной подвижностью абонентов.
Настоящее изобретение относится к первому способу назначения последовательности каждой соте с учетом характеристик CAZAC-последовательности и второму способу установки циклического сдвига, который должен применяться к первому способу. Поэтому настоящее изобретение применимо в беспроводной системе связи (например, устройстве UE и узле B).
Хотя, для наглядности представлено описание предпочтительных вариантов осуществления настоящего изобретения, специалистам в данной области техники будет очевидна возможность создания различных модификаций и внесения дополнений и замен, без выхода за пределы объема и сущности изобретения, определяемых в прилагаемой формуле изобретения.
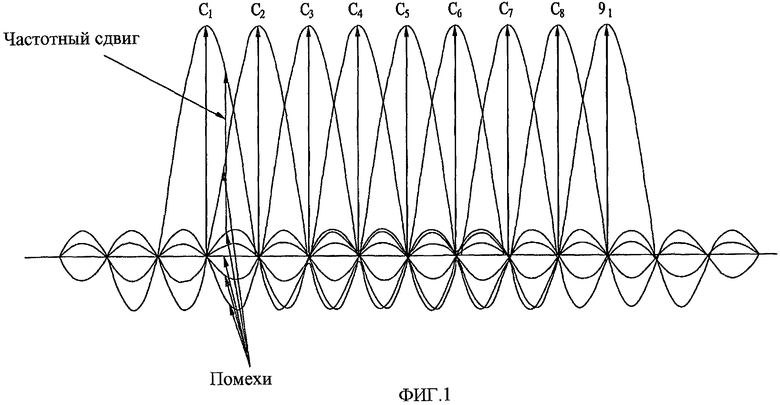
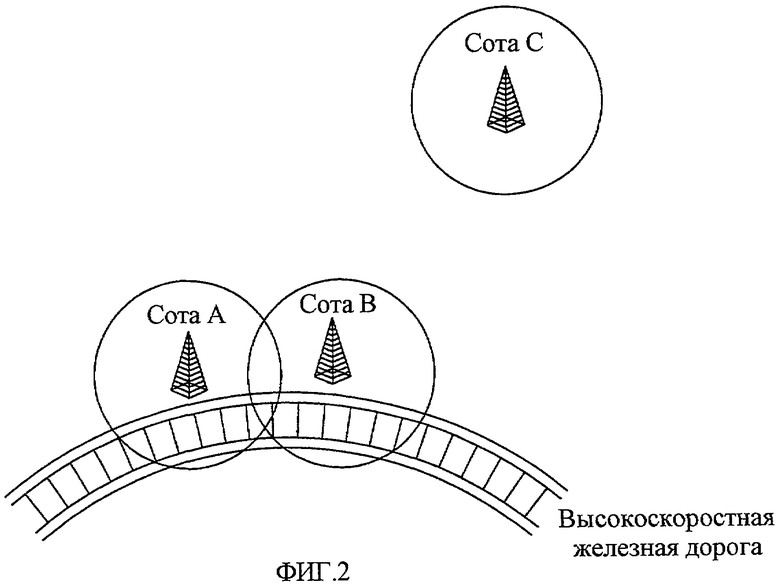
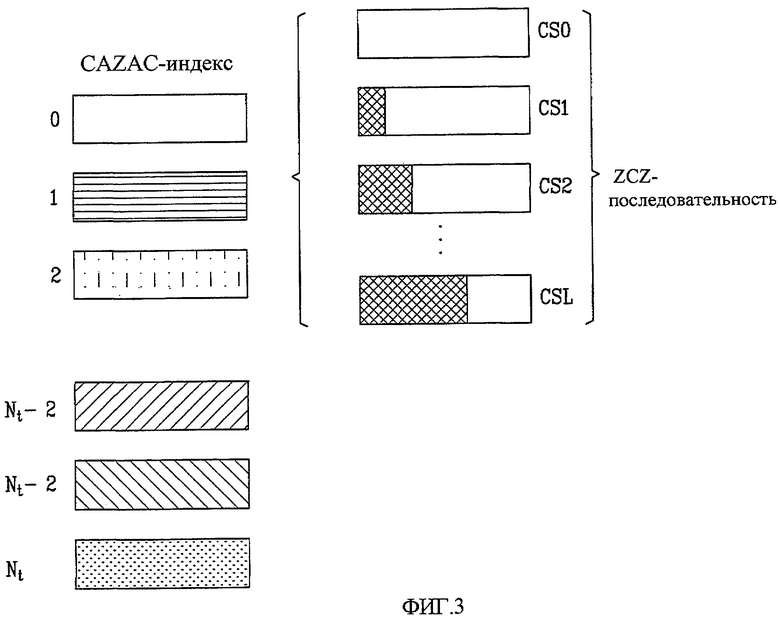
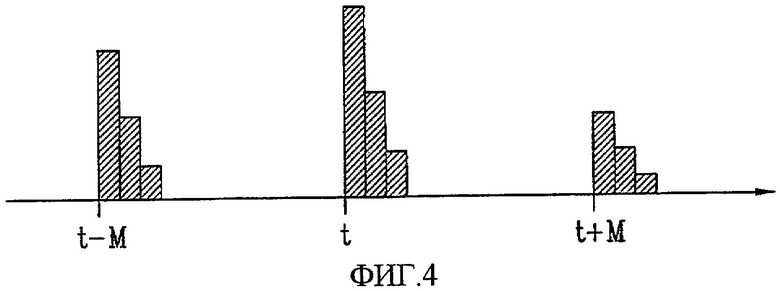
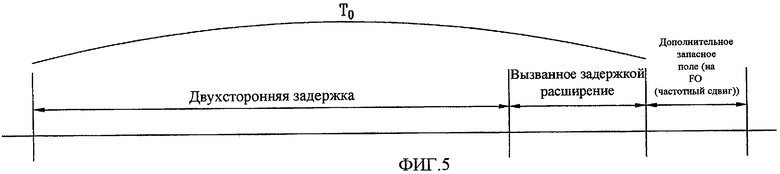
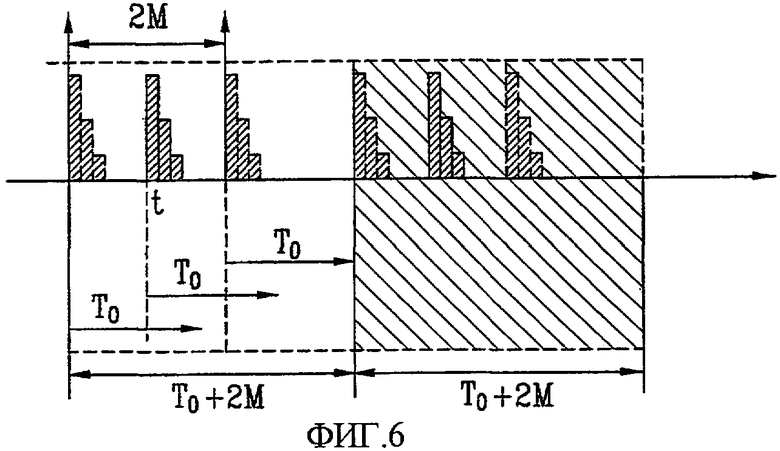
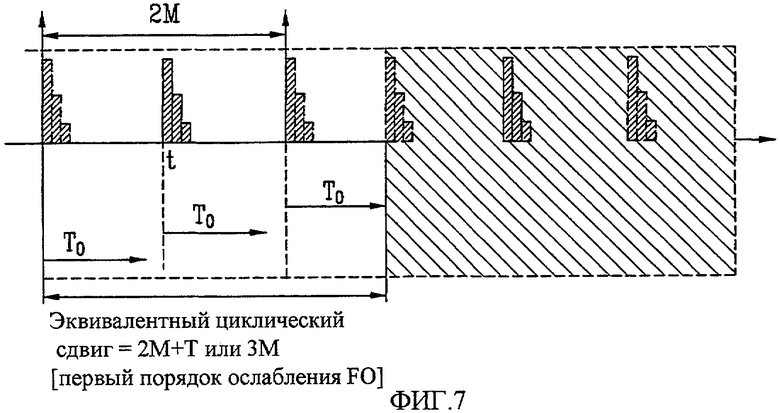
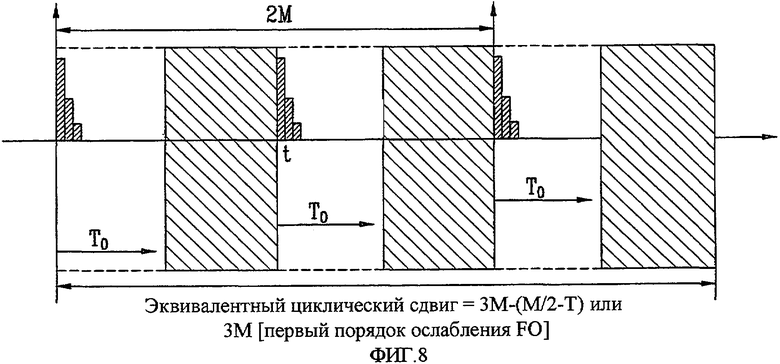
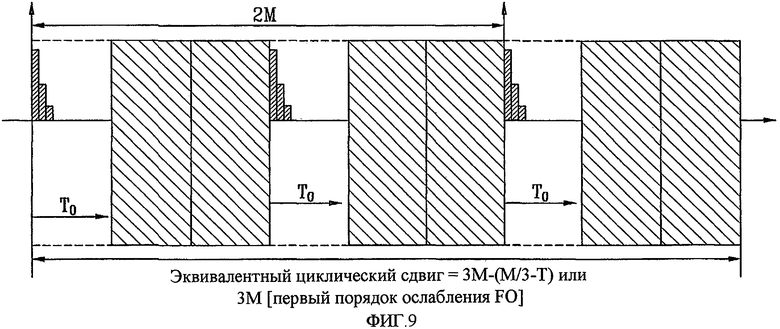
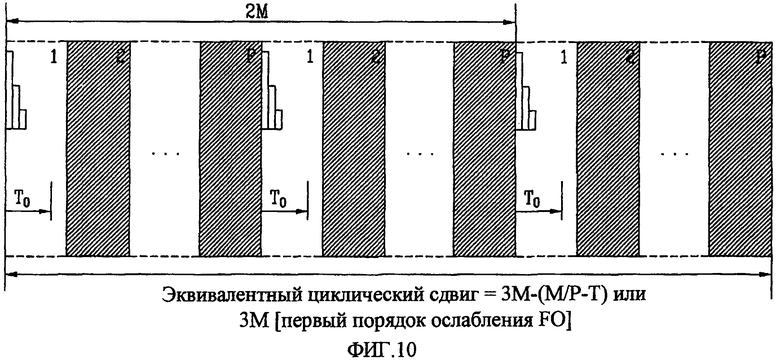


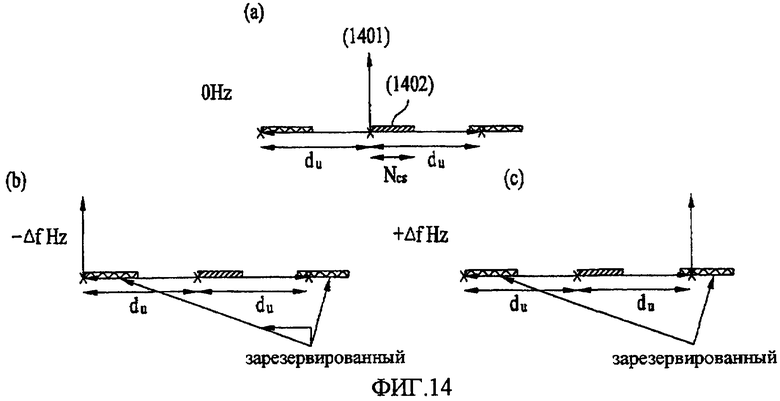
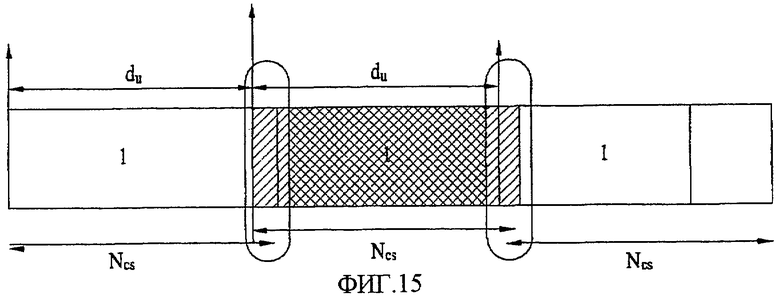
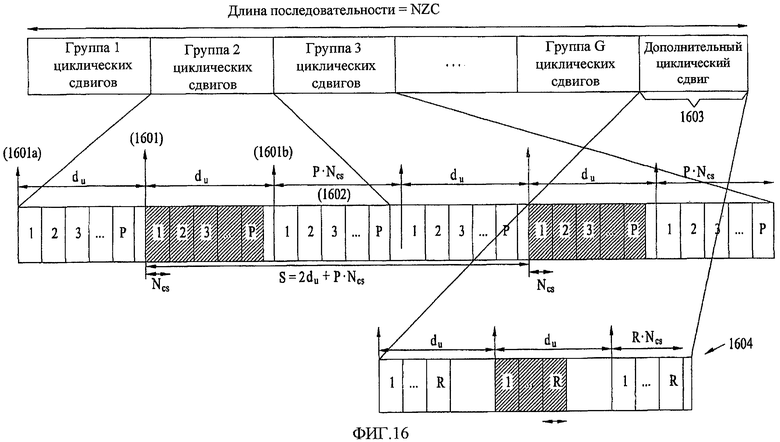
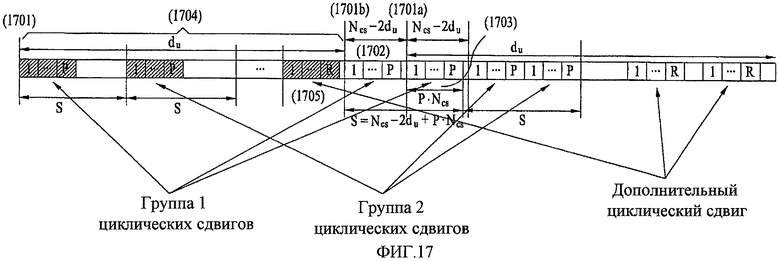
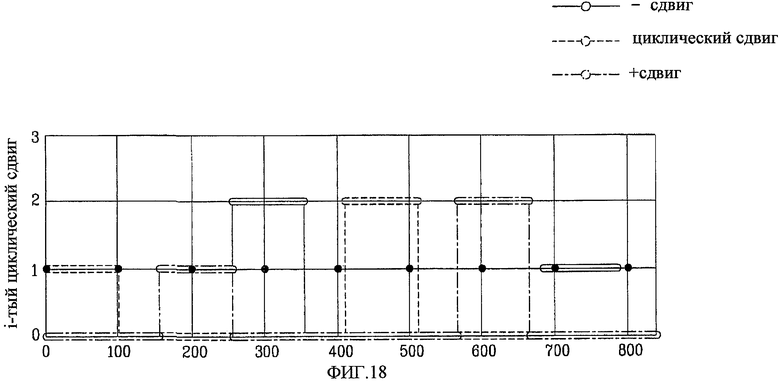
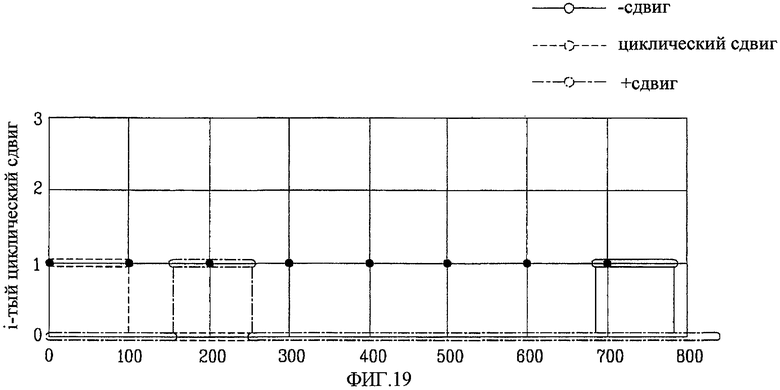
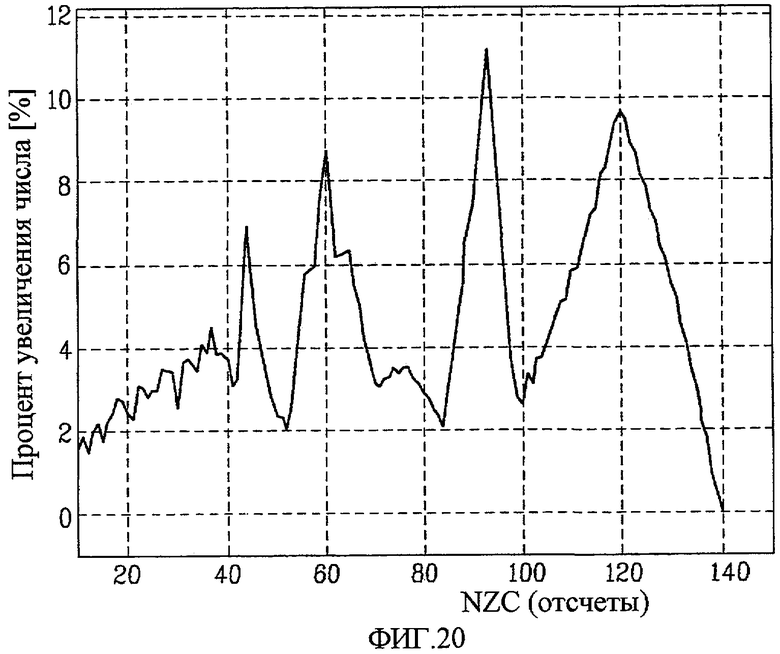
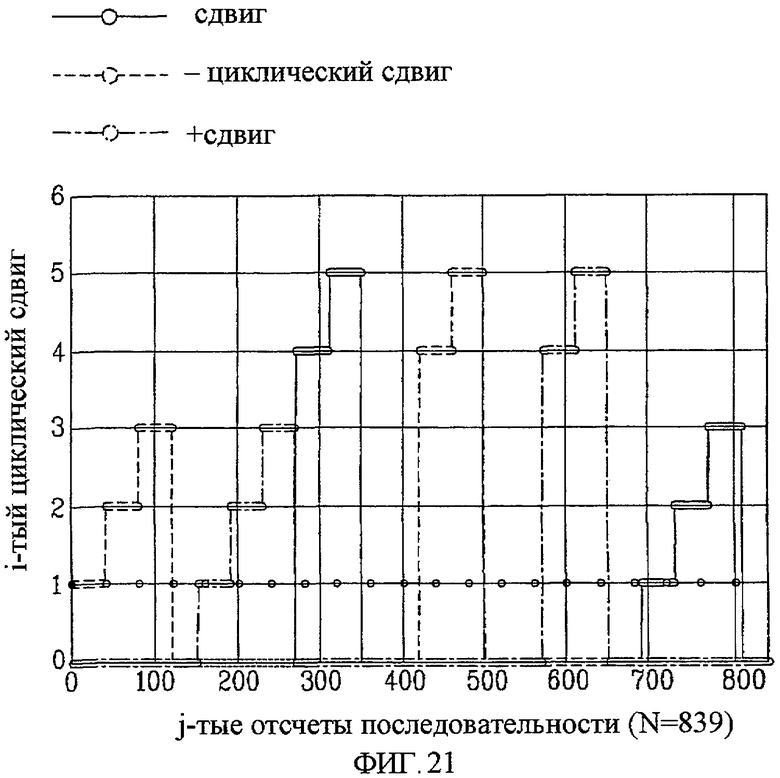
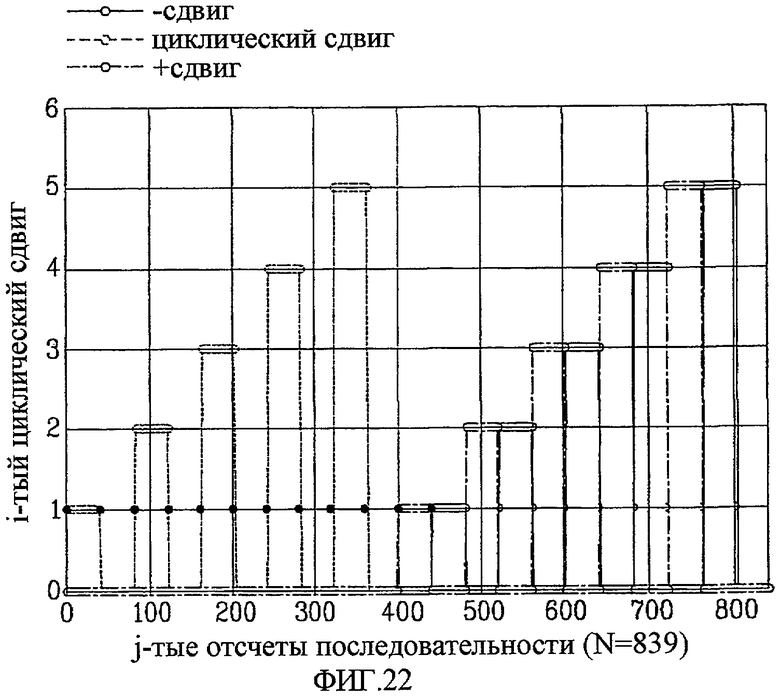
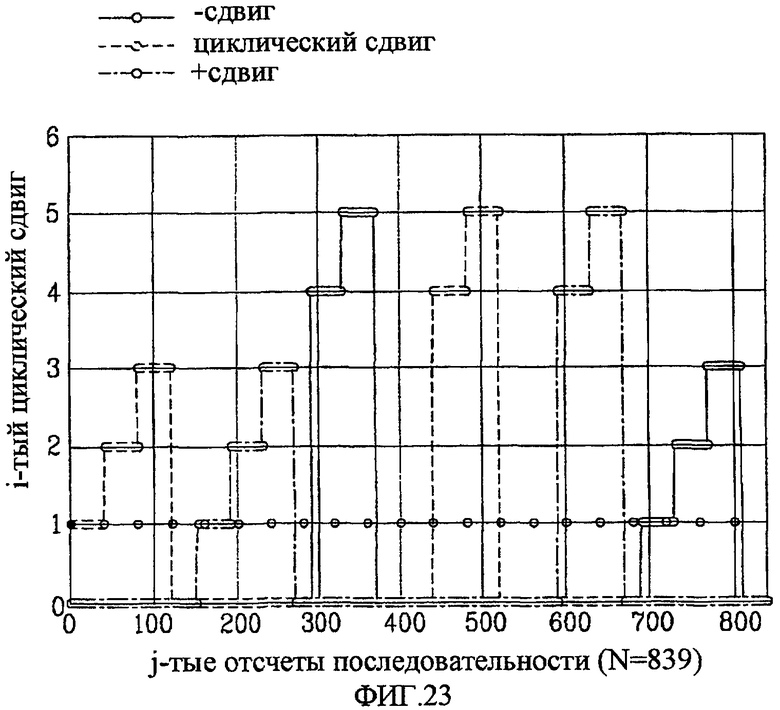
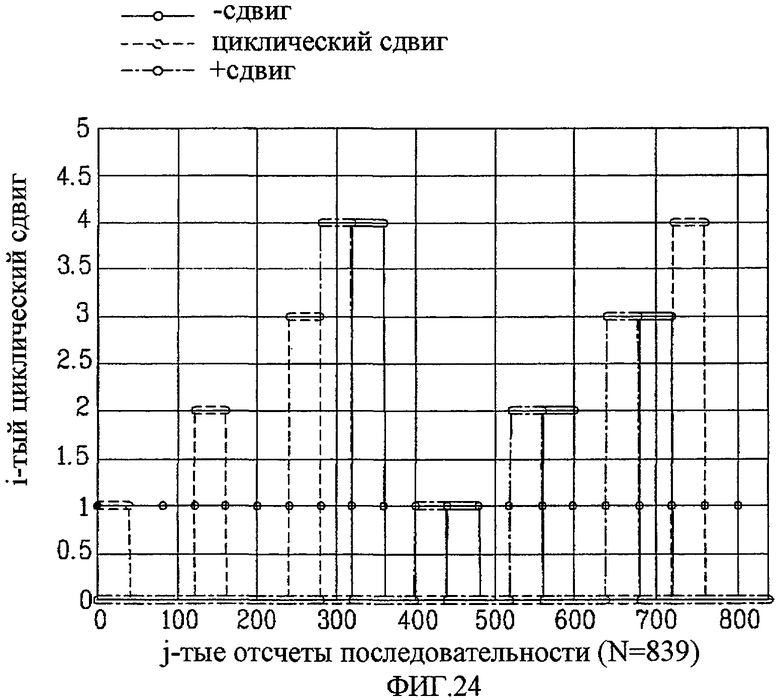
Изобретение относится к беспроводной связи, в частности к способам установки циклического сдвига с учетом характеристик последовательности CAZAC. Достигаемый технический результат - повышение пропускной способности. Способ заключается в том, что получают первую переменную (du) циклического сдвига, соответствующую доплеровскому сдвигу разноса одной поднесущей, с использованием корневого индекса (u) данной последовательности; получают вторичные переменные с использованием первой переменной (du), причем вторичные переменные содержат число групп (G), сформированных посредством группирования данной последовательности, длину каждой группы (S) и число применимых величин циклических сдвигов (Р) для каждой группы; и устанавливают величину циклического сдвига, который следует применить к данной последовательности, в соответствии с вторичными переменными. 4 н. и 20 з.п. ф-лы, 24 ил.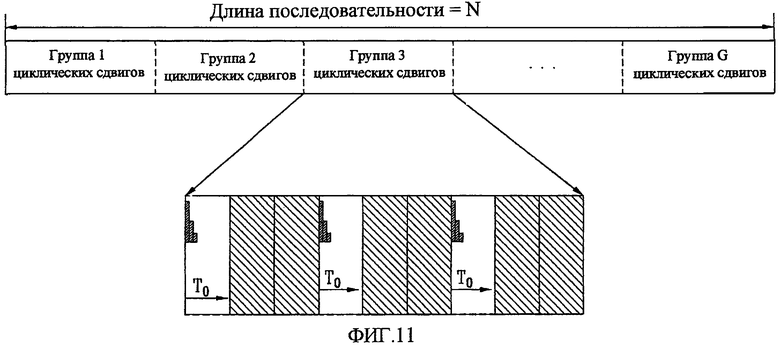
1. Способ настройки циклического сдвига, который следует применять к данной последовательности для противодействия влиянию высокой доплеровской частоты, более высокой, чем предварительно заданная величина, содержащий этапы на которых:
получают первую переменную (du) циклического сдвига, соответствующую доплеровскому сдвигу разноса одной поднесущей, с использованием корневого индекса (u) данной последовательности;
получают вторичные переменные с использованием первой переменной (du), причем вторичные переменные содержат число групп (G), сформированных посредством группирования данной последовательности, длину каждой группы (S) и число применимых величин циклических сдвигов (Р) для каждой группы; и устанавливают величину циклического сдвига, который следует применить к данной последовательности в соответствии с вторичными переменными.
2. Способ по п.1, в котором вторичные переменные дополнительно содержат некоторое число дополнительных циклических сдвигов, которые применимы к данной последовательности, не на основании группы (R).
3. Способ по п.1 или 2, в котором данная последовательность является последовательностью Задова-Чу (ZC) и
первую переменную получают согласно уравнению
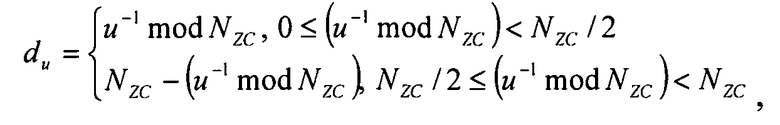
где «u» указывает корневой индекс ZC-последовательности и «NZC» соответствует длине ZC-последовательности.
4. Способ по п.3, в котором вторичные переменные получают иначе в соответствии с диапазоном первой переменной (du) и диапазон первой переменной разбивают с помощью критерия, соответствующего 1/3 длины данной последовательности (NZC/3).
5. Способ по п.4, в котором:
если диапазон первой переменной (du) составляет NCS≤du<(NZC/3), то вторичные переменные получают из уравнений
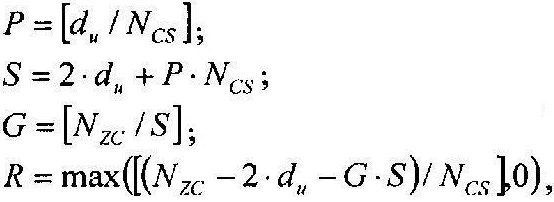
где «NCS» является предварительно заданным параметром циклического сдвига, «Р» соответствует числу циклических сдвигов на группу, «S» соответствует длине каждой группы, «G» соответствует числу групп и «R» соответствует числу дополнительных циклических сдвигов.
6. Способ по п.4, в котором:
если диапазон первой переменной (du) составляет (NZC/3)≤du≤(NZC-NCS)/2, то вторичные переменные получают из уравнений
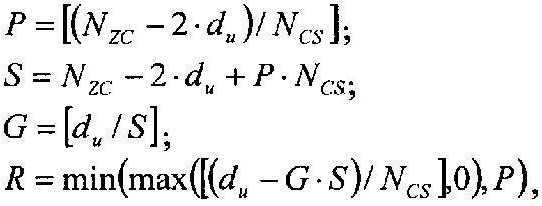
где «NCS» является предварительно заданным параметром циклического сдвига, «Р» соответствует числу циклических сдвигов на группу, «S» соответствует длине каждой группы, «G» соответствует числу групп и «R» соответствует числу дополнительных циклических сдвигов.
7. Способ по п.5 или 6, в котором упомянутая установка циклического сдвига (Сν) выполняется в соответствии с уравнением вида
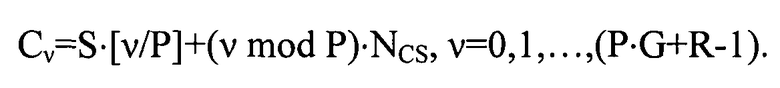
8. Способ по п.1, в котором данная последовательность предназначена для генерации преамбулы произвольного доступа.
9. Способ настройки циклического сдвига, который следует применять к данной последовательности, содержащий этапы, на которых:
определяют, следует ли устанавливать циклический сдвиг в соответствии с ограниченными наборами, ограниченными вследствие доплеровского сдвига; и
устанавливают циклический сдвиг, который следует применять к данной последовательности, с учетом циклического сдвига, соответствующего доплеровскому сдвигу разноса одной поднесущей, когда определяют, что циклический сдвиг следует установить в соответствии с ограниченными наборами.
10. Способ по п.9, в котором:
когда определяют, что циклический сдвиг следует установить в соответствии с ограниченными наборами, упомянутая установка циклического сдвига, который следует применять к данной последовательности, содержит этапы, на которых:
получают первую переменную (du), показывающую циклический сдвиг, соответствующий доплеровскому сдвигу разноса одной поднесущей, с использованием корневого индекса (u) данной последовательности;
получают вторичные переменные, содержащие число групп (G), содержащихся в данной последовательности, длину (S) каждой группы, число (Р) циклических сдвигов на группу, с использованием первой переменной (du), и число дополнительных циклических сдвигов, которые применимы к данной последовательности, не на основании группы (R); и устанавливают циклический сдвиг, который следует применить к данной последовательности в соответствии с вторичными переменными.
11. Способ по п.10, в котором данная последовательность является последовательностью Задова-Чу (ZC) и первую переменную получают из уравнения
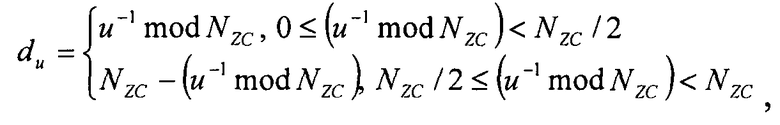
где «u» указывает корневой индекс ZC-последовательности и «NZC» соответствует длине ZC-последовательности.
12. Способ по п.11, в котором вторичные переменные получают иначе, в соответствии с диапазоном первой переменной (du) и диапазон первой переменной разбивают с помощью критерия, соответствующего 1/3 длины данной последовательности (NZC/3).
13. Способ по п.12, в котором:
если диапазон первой переменной (du) составляет Ncs≤du<(Nzc/3), то вторичные переменные получают согласно уравнениям
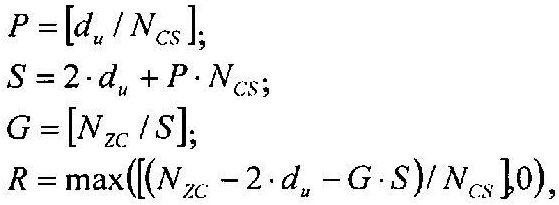
где «NCS» является предварительно заданным параметром циклического сдвига, «Р» соответствует числу циклических сдвигов на группу, «S» соответствует длине каждой группы, «G» соответствует числу групп и «R» соответствует числу дополнительных циклических сдвигов.
14. Способ по п.12, в котором:
если диапазон первой переменной (du) составляет (NZC/3)≤du≤(NZC-NCS)/2, то вторичные переменные получают из уравнений
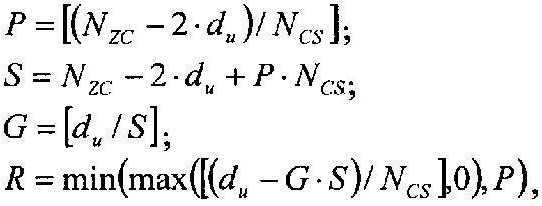
где «NCS» является предварительно заданным параметром циклического сдвига, «Р» соответствует числу циклических сдвигов на группу, «S» соответствует длине каждой группы, «G» соответствует числу групп и «R» соответствует числу дополнительных циклических сдвигов.
15. Способ по п.13 или 14, в котором циклический сдвиг (Сν) выполняется согласно следующему уравнению:
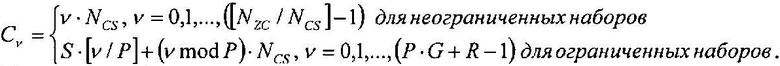
16. Способ по п.9, в котором данная последовательность предназначена для генерации преамбулы произвольного доступа.
17. Способ передачи преамбулы произвольного доступа посредством настройки циклического сдвига, который следует применять к данной последовательности в передатчике, содержащий этапы, на которых:
(а) получают переменную du из уравнения
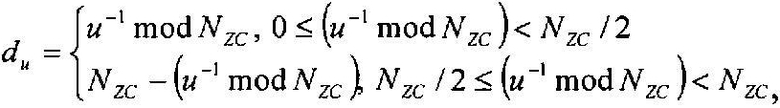
где «u» указывает корневой индекс данной последовательности и «NZC» соответствует длине данной последовательности; (b) получают переменные G, S, Р и R из уравнений
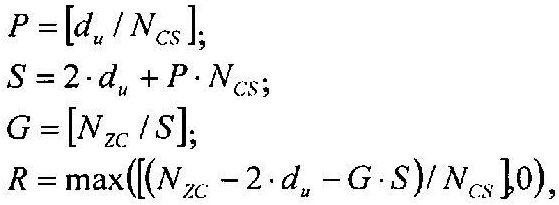
когда диапазон первой переменной (du) составляет NCS**du<(NZC/3), и переменные G, S, Р и R получают из уравнений
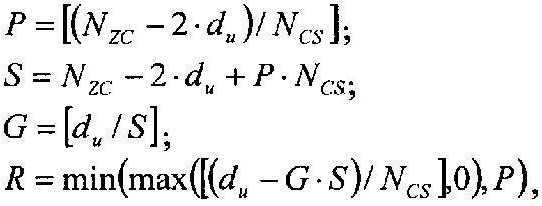
когда диапазон первой переменной (du) составляет (NZC/3)≤du≤(NZC-NCS)/2, причем «NCS» является предварительно заданным параметром циклического сдвига;
(с) устанавливают циклический сдвиг (С**) согласно уравнению
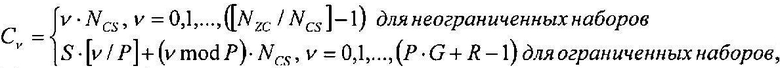
причем ограниченные наборы являются наборами циклических сдвигов, ограниченными вследствие доплеровского сдвига, а неограниченные наборы являются наборами циклических сдвигов, не ограниченными вследствие доплеровского сдвига; и
(d) передают преамбулу произвольного доступа в приемник посредством использования установленного циклического сдвига.
18. Способ передачи преамбулы произвольного доступа с использованием циклического сдвига, содержащий этапы, на которых:
получают корневой индекс (u) последовательности для преамбулы произвольного доступа из системной информации;
устанавливают циклический сдвиг, который следует применить к последовательности, причем циклический сдвиг, который следует применить к последовательности, устанавливают с учетом циклического сдвига, соответствующего доплеровскому сдвигу разноса одной поднесущей, когда определяют, что циклический сдвиг следует установить в соответствии с ограниченными наборами, ограниченными вследствие доплеровского сдвига;
генерируют последовательность в соответствии с корневым индексом (u) с установленным циклическим сдвигом и
передают последовательность с циклическим сдвигом в качестве преамбулы произвольного доступа.
19. Способ по п.18, в котором:
когда определяют, что циклический сдвиг следует устанавливать в соответствии с ограниченными наборами, упомянутая установка циклического сдвига, который следует применить к последовательности, содержит этапы, на которых:
получают первую переменную (du), указывающую циклический сдвиг, соответствующий доплеровскому сдвигу разноса одной поднесущей, с использованием корневого индекса (u) данной последовательности;
получают вторичные переменные, содержащие число групп (G), содержащихся в последовательности, длину (S) каждой группы, число (Р) циклических сдвигов на группу с использованием первой переменной (du) и число дополнительных циклических сдвигов, которые применимы к последовательности, не на основе группы (R); и устанавливают циклический сдвиг, который следует применить к последовательности, в соответствии с вторичными переменными.
20. Способ по п.19, в котором данная последовательность является последовательностью Задова-Чу (ZC) и первую переменную получают согласно уравнению
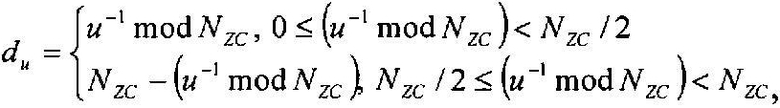
где «u» указывает корневой индекс ZC-последовательности и «NZC» соответствует длине ZC-последовательности.
21. Способ по п.20, в котором вторичные переменные получают иначе, в соответствии с диапазоном первой переменной (du) и диапазон первой переменной разбивают с помощью критерия, соответствующего 1/3 длины данной последовательности (NZC/3).
22. Способ по п.21, в котором:
если диапазон первой переменной (du) составляет NCS≤du<(NZC/3), то вторичные переменные получают из уравнений
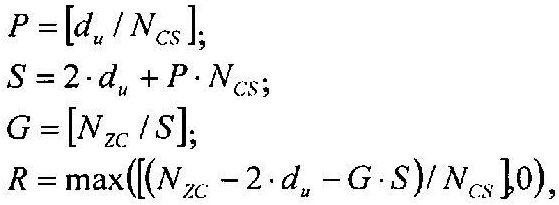
где «NCS» является предварительно заданным параметром циклического сдвига, «Р» соответствует числу циклических сдвигов на группу, «S» соответствует длине каждой группы, «G» соответствует числу групп и «R» соответствует числу дополнительных циклических сдвигов.
23. Способ по п.21, в котором:
если диапазон первой переменной (du) составляет (NZC/3)≤du≤(NZC-NCS)/2, то вторичные переменные получают из уравнений
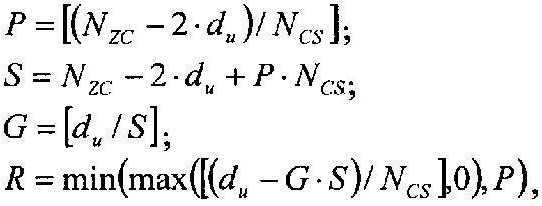
где «NCS» является предварительно заданным параметром циклического сдвига, «Р» соответствует числу циклических сдвигов на группу, «S» соответствует длине каждой группы, «G» соответствует числу групп и «R» соответствует числу дополнительных циклических сдвигов.
24. Способ по п.22 или 23, в котором циклический сдвиг (Сν) выполняется согласно следующему уравнению
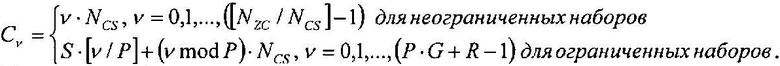
| LG ELECTRONICS: "RACH Design under Frequency Offset", 3GPP TSG-RAN WG1, R1- 063162, 06.11.2006 | |||
| ЩИТОВОЙ ДЛЯ ВОДОЕМОВ ЗАТВОР | 1922 |
|
SU2000A1 |
| СПОСОБ И УСТРОЙСТВО ДЛЯ ПОИСКА ДЛЯ ЭСТАФЕТНОЙ ПЕРЕДАЧИ ОБСЛУЖИВАНИЯ В СЛУЧАЕ ШИРОКОПОЛОСНОГО МНОЖЕСТВЕННОГО ДОСТУПА С КОДОВЫМ РАЗДЕЛЕНИЕМ КАНАЛОВ (ШМДКР) | 2002 |
|
RU2290757C2 |
Авторы
Даты
2011-11-20—Публикация
2008-01-04—Подача