Область техники
Настоящее изобретение относится к способу генерации опорной сигнальной последовательности и, в частности, к способу группирования последовательностей, имеющих переменную длину, соответствующую одному или нескольким размерам блока ресурсов, способу генерации опорной сигнальной последовательности и способу генерации опорной сигнальной последовательности с использованием последовательности Задова-Чу (ZC).
Уровень техники
Нижеследующее объяснение рассматривается, в основном, применительно к системе 3GPP LTE, но настоящее изобретение не ограничивается этой системой, и иллюстративная система 3GPP LTE предназначена лишь для того, чтобы специалист в данной области техники мог понять настоящее изобретение.
Существует много последовательностей, используемых для передачи сигнала, но в системе 3GPP LTE (3rd Generation Partnership Project Long Term Evolution) последовательность CAZAC (Constant Amplitude Zero Auto-Correlation, постоянная амплитуда, нулевая автокорреляция) образует базовую последовательность для передачи сигналов. Последовательность CAZAC можно использовать на различных каналах для извлечения ID или информации управления, например каналах восходящей/нисходящей линии связи (SCH), включающих в себя P-SCH (первичный SCH) и S-SCH (вторичный SCH), пилот-канал для передачи опорного сигнала. Кроме того, последовательность CAZAC можно использовать при скремблировании.
В качестве последовательностей CAZAC, в основном, используется два типа последовательностей CAZAC, т.е. последовательность CAZAC GCL и последовательность CAZAC Задова-Чу. Два типа последовательностей CAZAC связаны друг с другом отношением комплексного сопряжения. Таким образом, последовательность CAZAC GCL можно получить путем вычисления комплексно сопряженной последовательности CAZAC Задова-Чу. Последовательность CAZAC Задова-Чу задается следующим образом.
[Уравнение 1]
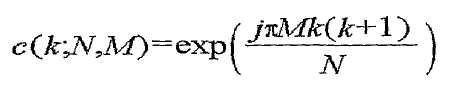 (для нечетных N)
(для нечетных N)
[Уравнение 2]
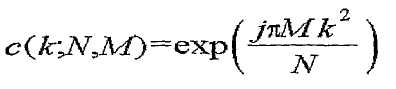 (для четных N),
(для четных N),
где k представляет индекс компонента последовательности, N представляет длину генерируемой последовательности CAZAC и M представляет ID последовательности или индекс последовательности.
Когда последовательность CAZAC Задова-Чу, заданная Уравнениями 1 и 2, и последовательность CAZAC GCL, которая получена комплексным сопряжением последовательности CAZAC Задова-Чу, представлены посредством c(k;N,M), эти последовательности могут иметь следующие три признака.
[Уравнение 3]
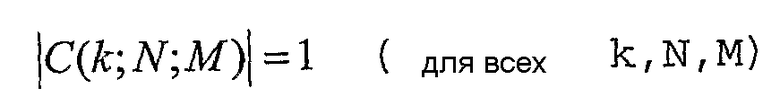
[Уравнение 4]
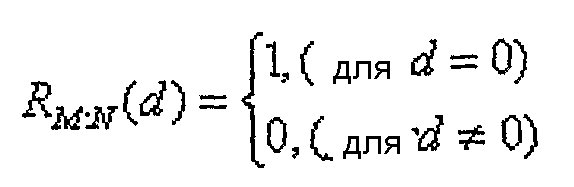
[Уравнение 5]
RM1,M2;N(d)=p (для всех M1, M2 и N)
Уравнение 3 означает, что последовательность CAZAC всегда имеет размер 1, и Уравнение 4 указывает, что автокорреляционная функция последовательности CAZAC выражается дельта-функцией. В этом случае автокорреляция основана на круговой корреляции. Кроме того, Уравнение 5 указывает, что взаимная корреляция всегда является постоянной.
Из этих двух видов последовательности CAZAC нижеследующее объяснение, в основном, сосредоточено на последовательности Задова-Чу (далее "последовательности ZC").
В системе 3GPP LTE, использующей эту последовательность ZC в качестве опорной сигнальной последовательности, длина последовательности ZC должна быть равна размеру блока ресурсов. Кроме того, можно использовать не только последовательность длиной в один размер блока ресурсов, но и опорную сигнальную последовательность, имеющую длину, соответствующую нескольким размерам блока ресурсов.
В односотовой среде опорные сигналы передаются методом локального FDM (мультиплексирования с частотным разделением) для мультиплексирования сигналов от нескольких экземпляров пользовательского оборудования (UE). Однако в многосотовой среде опорные сигналы передаются дополнительным методом CDM (мультиплексирования с кодовым разделением) для различения сигналов от сигналов соседних сот. При этом мультиплексировании можно использовать два метода. Один является методом CDM с использованием последовательностей ZC, имеющих разные индексы корня, а другой является методом CDM с использованием последовательностей ZC, имеющих один и тот же индекс (M) корня, но по-разному примененный циклический сдвиг.
Когда длина опорных сигналов, использующих эти разновидности последовательностей ZC, одинакова, значения взаимной корреляции в обоих случаях невелики. Однако, если бы опорные сигналы, имеющие другую длину, приходили как помеха от соседних сот и передавались с использованием того же частотного диапазона или перекрывающегося частотного диапазона, значение взаимной корреляции было бы значительным.
Раскрытие изобретения
Задача изобретения
Соответственно, настоящее изобретение призвано обеспечивать способ генерации опорной сигнальной последовательности, который минимизирует помеху, обусловленную сигналами, имеющими другую длину, поступающими из соседних сот.
Для этого способа настоящее изобретение также обеспечивает способ эффективного группирования последовательностей, согласно которому каждая из групп состоит из последовательностей, имеющих высокое значение взаимной корреляции, и поддерживает последовательности переменной длины для использования в качестве опорных сигналов.
Кроме того, настоящее изобретение обеспечивает способ генерации опорной сигнальной последовательности на основе вышеописанного группирования.
Решение задач
Для решения этих задач и достижения других преимуществ и согласно цели изобретения, реализованной и широко описанной здесь, предусмотрен способ группирования последовательностей, имеющих переменную длину, соответствующую одному или нескольким размерам блока ресурсов. Согласно одному варианту осуществления способ содержит этапы, на которых группируют последовательности в группы так, чтобы каждая из групп содержала, по меньшей мере, одну последовательность каждой длины, причем сгруппированная последовательность является базовой последовательностью, которая используется для применения циклического сдвига, соответствующего переменному значению циклического сдвига, и базовая последовательность с циклическим сдвигом используется в качестве опорной сигнальной последовательности.
Предпочтительно, количество групп равно 30.
Кроме того, группирование можно осуществлять так, чтобы каждая из групп содержала одну базовую последовательность каждой длины, соответствующей от 1 до 5 размерам блока ресурсов, и две базовые последовательности каждой длины, соответствующей 6 или более размерам блока ресурсов.
Предпочтительно, базовая последовательность, имеющая длину, соответствующую 3 или более размерам блока ресурсов, задается с использованием последовательности Задова-Чу (ZC), и базовая последовательность, имеющая длину, соответствующую 1 или 2 размерам блока ресурсов, задается с использованием последовательности, отличной от последовательности ZC.
В другом аспекте настоящего изобретения предусмотрен способ генерации опорной сигнальной последовательности. В одном варианте осуществления этого аспекта способ содержит этапы, на которых задают одну или несколько базовых последовательностей, имеющих переменную длину, соответствующую одному или нескольким размерам блока ресурсов; и применяют циклический сдвиг, соответствующий переменному значению циклического сдвига, к заданной базовой последовательности, причем базовые последовательности делятся на группы и каждая из групп содержит, по меньшей мере, одну базовую последовательность каждой длины.
В этом случае базовую последовательность можно задать посредством циклического расширения последовательности ZC, имеющей длину (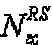 ), заданную наибольшим простым числом, которое меньше размера соответствующей опорной сигнальной последовательности. Кроме того, базовую последовательность можно задать усечением последовательности ZC, имеющей длину (
), заданную наибольшим простым числом, которое меньше размера соответствующей опорной сигнальной последовательности. Кроме того, базовую последовательность можно задать усечением последовательности ZC, имеющей длину (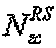 ), заданную наименьшим простым числом, которое больше размера соответствующей опорной сигнальной последовательности. Кроме того, в этом варианте осуществления, предпочтительно, количество групп равно 30.
), заданную наименьшим простым числом, которое больше размера соответствующей опорной сигнальной последовательности. Кроме того, в этом варианте осуществления, предпочтительно, количество групп равно 30.
Кроме того, каждая из групп может содержать одну базовую последовательность каждой длины, соответствующую от 1 до 5 размерам блока ресурсов, и две базовые последовательности каждой длины, соответствующей 6 или более размерам блока ресурсов.
Кроме того, базовую последовательность, имеющую длину, соответствующую 3 или более размерам блока ресурсов, можно задать с использованием последовательности Задова-Чу (ZC) с конкретным индексом (q) последовательности ZC, и базовую последовательность, имеющую длину, соответствующую 1 или 2 размерам блока ресурсов, можно задать с использованием последовательности, отличной от последовательности ZC.
Кроме того, предпочтительно, конкретный индекс (q) последовательности ZC является функцией индекса (u) группы и индекса номера базовой последовательности (v) в группе.
Кроме того, заданную базовую последовательность с циклическим сдвигом можно использовать для опорной сигнальной последовательности восходящей линии связи.
Кроме того, согласно вышеописанным вариантам осуществления размер блока ресурсов может соответствовать размеру 12 поднесущих в частотной области.
В другом аспекте настоящего изобретения предусмотрен способ генерации опорной сигнальной последовательности с использованием последовательности Задова-Чу (ZC). В одном варианте осуществления этого аспекта способ содержит этапы, на которых задают конкретную базовую последовательность с использованием q-й корневой последовательности ZC, причем базовые последовательности делятся на группы, и "q" является функцией индекса (u) группы и индекса (v) номера базовой последовательности в группе; и применяют циклический сдвиг, соответствующий переменному значению циклического сдвига, к заданной базовой последовательности для генерации опорной сигнальной последовательности.
В одном случае, конкретный индекс (q) последовательности ZC можно определить одним из уравнений,
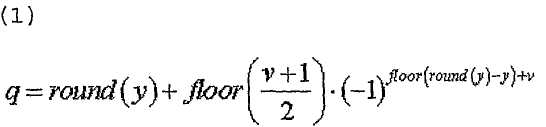
где 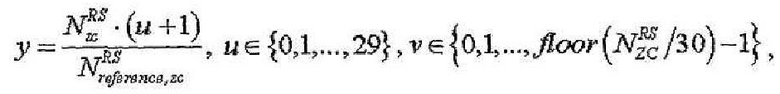
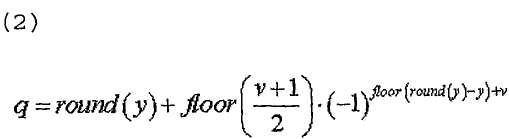
где 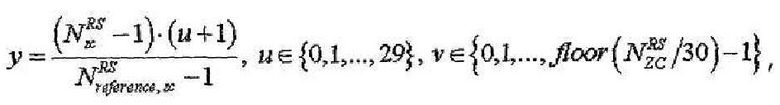 или
или
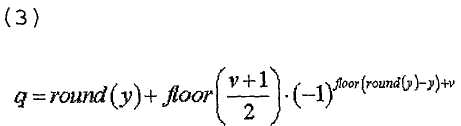
где 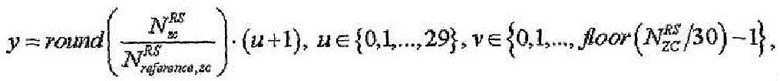
где 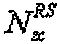 - длина, заданная наибольшим простым числом, которое меньше размера соответствующей опорной сигнальной последовательности,
- длина, заданная наибольшим простым числом, которое меньше размера соответствующей опорной сигнальной последовательности, 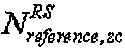 - размер соответствующей опорной сигнальной последовательности, "round(z)" является функцией округления до ближайшего целого числа, ближайшего к z, и "floor(z)" является функцией, возвращающей наибольшее целое число, не превышающее z. Однако
- размер соответствующей опорной сигнальной последовательности, "round(z)" является функцией округления до ближайшего целого числа, ближайшего к z, и "floor(z)" является функцией, возвращающей наибольшее целое число, не превышающее z. Однако 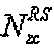 может быть длиной, заданной наименьшим простым числом, которое больше соответствующей опорной сигнальной последовательности согласно другому варианту осуществления этого изобретения.
может быть длиной, заданной наименьшим простым числом, которое больше соответствующей опорной сигнальной последовательности согласно другому варианту осуществления этого изобретения.
В другом случае, конкретный индекс (q) последовательности ZC можно определить одним из уравнений,
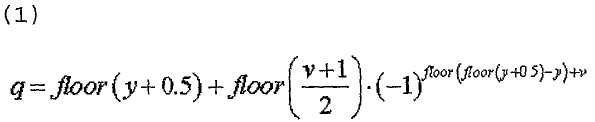
где 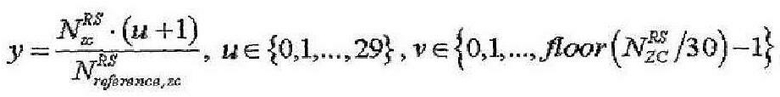
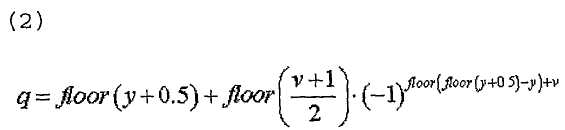
где 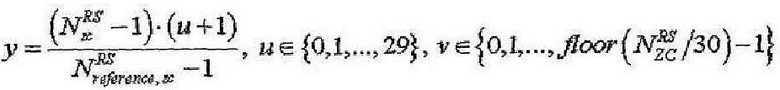 или
или
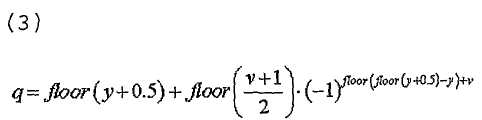
где 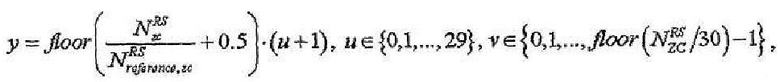
где 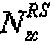 - длина, заданная наибольшим простым числом, которое меньше размера соответствующей опорной сигнальной последовательности,
- длина, заданная наибольшим простым числом, которое меньше размера соответствующей опорной сигнальной последовательности, 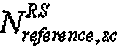 - размер соответствующей опорной сигнальной последовательности, "round(z)" является функцией округления до ближайшего целого числа, ближайшего к z, и "floor(z)" является функцией, возвращающей наибольшее целое число, не превышающее z. Однако
- размер соответствующей опорной сигнальной последовательности, "round(z)" является функцией округления до ближайшего целого числа, ближайшего к z, и "floor(z)" является функцией, возвращающей наибольшее целое число, не превышающее z. Однако 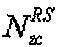 может быть длиной, заданной наименьшим простым числом, которое больше соответствующей опорной сигнальной последовательности, согласно другому варианту осуществления этого изобретения.
может быть длиной, заданной наименьшим простым числом, которое больше соответствующей опорной сигнальной последовательности, согласно другому варианту осуществления этого изобретения.
В одном конкретном варианте осуществления этого изобретения максимальное количество индексов (v) номера базовой последовательности в каждой группе можно задать равным 2, и затем конкретный индекс (q) последовательности ZC можно определить одним из уравнений,
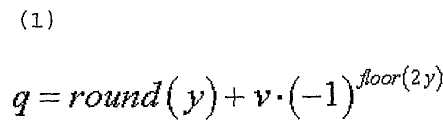
где 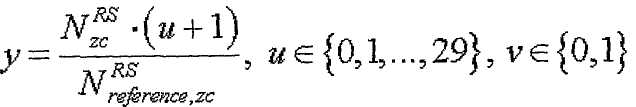
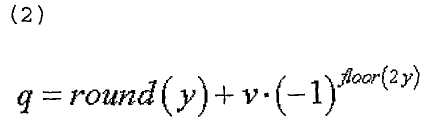
где 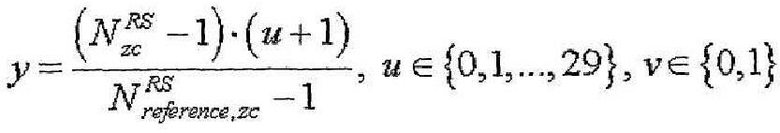 или
или
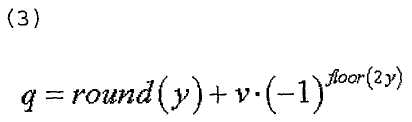
где 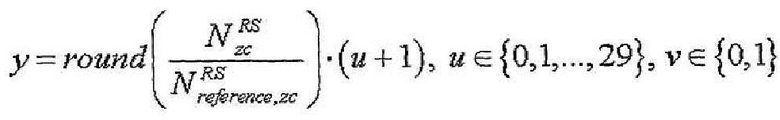
или одним из уравнений,
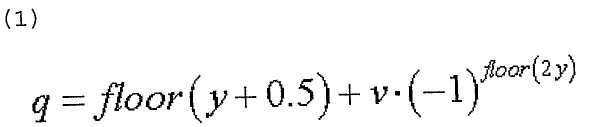
где 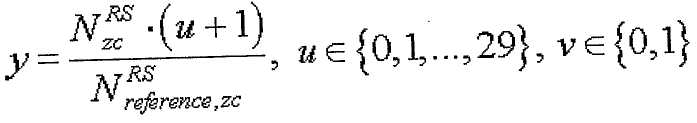
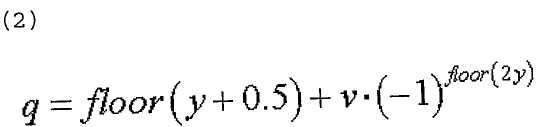
где 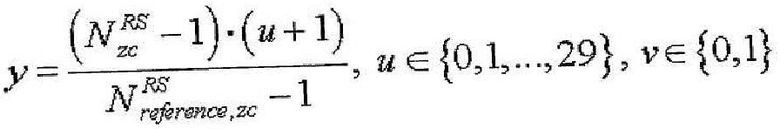 или
или
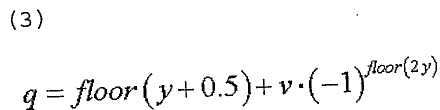
где 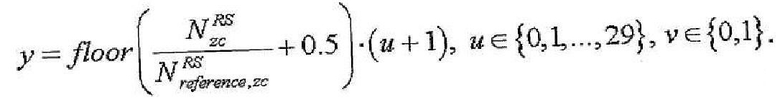
Предпочтительно, 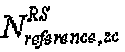 можно задать равным 31 или 37, но для
можно задать равным 31 или 37, но для 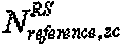 можно задать и другие значения.
можно задать и другие значения.
Преимущества изобретения
Согласно этим вариантам осуществления этого изобретения, поскольку базовая последовательность для применения циклического сдвига группируется и каждая группа содержит, по меньшей мере, одну базовую последовательность каждой длины, UE может использовать последовательности разной длины в качестве опорной сигнальной последовательности, когда конкретная группа выделяется одной соте или Node B.
Кроме того, поскольку каждая группа содержит базовые последовательности, имеющие высокую взаимную корреляцию, если каждая группа выделяется одной соте или Node B, межсотовую помеху можно минимизировать.
Описание чертежей
Фиг. 1 - обобщенная схема, поясняющая метод генерации усеченной последовательности.
Фиг. 2 - обобщенная схема, поясняющая метод генерации с использованием заполняющей части.
Фиг. 3-5 - обобщенные схемы группирования последовательностей согласно одному варианту осуществления этого изобретения.
Осуществление изобретения
Далее, предпочтительные варианты осуществления настоящего изобретения будут подробно описаны со ссылкой на прилагаемые чертежи. Следует понимать, что подробное описание, которое будет раскрыто совместно с прилагаемыми чертежами, призвано описывать иллюстративные варианты осуществления настоящего изобретения и не призвано описывать уникальный вариант осуществления, который может выполнять настоящее изобретение.
Далее, подробное описание включает в себя некоторые детали, позволяющие полностью понять настоящее изобретение. Однако специалисту в данной области техники очевидно, что настоящее изобретение можно осуществлять без указанных деталей. Во избежание неоднозначности концепции настоящего изобретения известные в технике конструкции и устройства будут опущены или будут показаны в виде блок-схемы на основании основных функций каждой конструкции или устройства. Кроме того, по мере возможности, одни и те же позиции будут использоваться в чертежах и описании изобретения для обозначения одинаковых или сходных деталей.
Как указано выше, настоящее изобретение призвано обеспечивать способ генерации опорной сигнальной последовательности, который минимизирует помеху, обусловленную сигналами, имеющими другую длину, поступающими из соседних сот.
Для этого рассмотрим длину последовательности CAZAC.
В настоящее время в системе 3GPP LTE размер блока ресурсов (RB) для передачи любой разновидности символа OFDM, включая символ опорного сигнала, соответствует размеру 12 поднесущих. Потому, когда ZC генерируется для опорной сигнальной последовательности восходящей линии связи, размер последовательности ZC будет соответствовать размеру 12 поднесущих.
В случае последовательности CAZAC количество индексов (M) последовательностей CAZAC которые можно отличать друг от друга, определяется количеством взаимно простых чисел, взаимно простых с длиной (N) последовательности. Поэтому при генерации последовательности ZC длиной 12 количество последовательностей ZC, имеющих разные индексы последовательности, равно 4. Однако, если последовательность ZC генерируется на основании длины, равной простому числу (N), количество последовательностей ZC, имеющих разные индексы последовательности, может быть равно N-1, что максимизирует количество последовательностей ZC. Таким образом обеспечены различные способы генерации последовательности CAZAC на основании длины, равной простому числу.
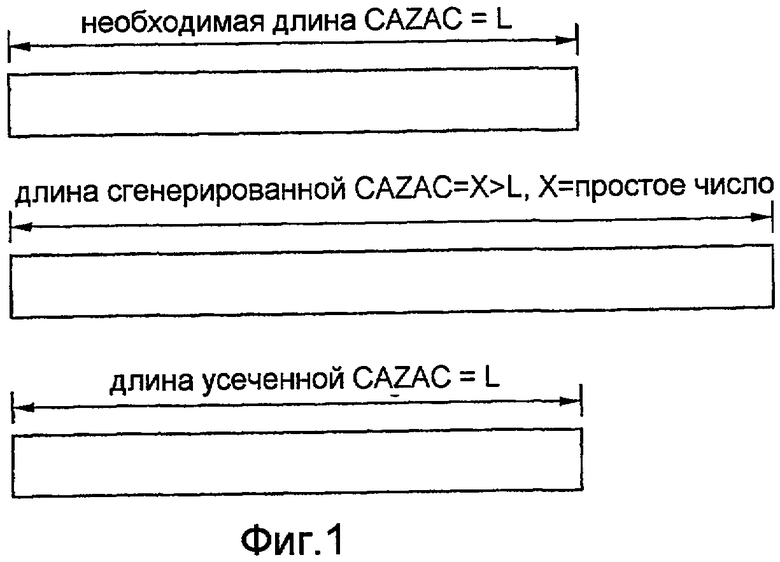
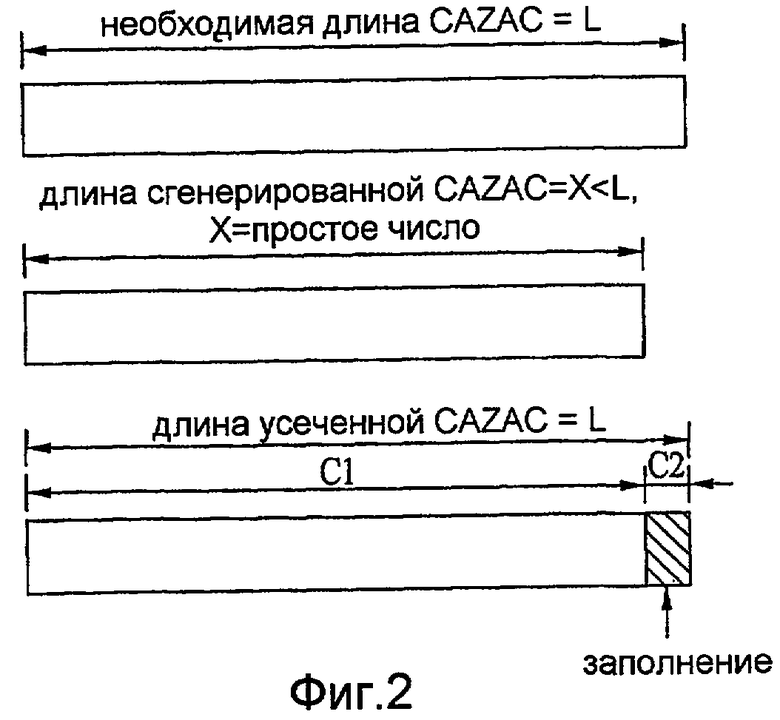
Сначала опишем метод генерации усеченной последовательности.
На фиг. 1 показана обобщенная схема, поясняющая метод генерации усеченной последовательности.
Согласно фиг. 1, когда необходимая длина последовательности CAZAC равна "L", генерируется последовательность CAZAC, имеющая длину, равную простому числу "X" (где X>L). Кроме того, сгенерированная последовательность CAZAC GCL, имеющая длину "X", усекается до длины "L", т.е. часть последовательности, имеющая длину "X-L", отсекается.
Согласно этому способу количество последовательностей CAZAC достигает максимума. Но поскольку часть сгенерированной последовательности отсекается, свойства авто/кросс-корреляции последовательности CAZAC, определяемые уравнениями 4 и 5, несколько ухудшаются. Кроме того, при исключении последовательностей, имеющих низкие корреляционные свойства, фактическое количество последовательностей уменьшается. Кроме того, вследствие усечения хорошее свойство PAPR последовательности CAZAC также может ухудшаться.
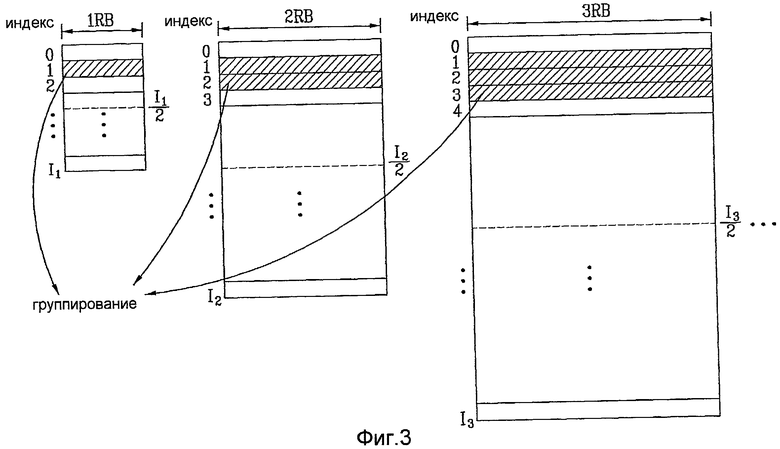
Таким образом представлен другой тип способов генерации последовательности CAZAC на основании длины, равной простому числу. Один из этих способов предусматривает генерацию последовательности CAZAC, имеющей длину, равную простому числу "X" (где X<L), и добавление компонентов, имеющих длину "L-X" к сгенерированной последовательности CAZAC GCL. Эти компоненты, добавляемые к сгенерированной последовательности, можно называть заполняющей частью, поэтому этот способ можно называть методом генерации с использованием заполняющей части.
На фиг. 2 показана обобщенная схема, поясняющая метод генерации с использованием заполняющей части.
Согласно фиг. 2, когда необходимая длина последовательности CAZAC равна "L", генерируется последовательность CAZAC длиной "X", которая является максимальным простым числом, меньшим "L". Заполняющая часть, имеющая длину "L-X", добавляется к сгенерированной последовательности.
Согласно одному способу для такого рода способов заполняющая часть может состоять из нулей. Согласно этому способу количество последовательностей CAZAC можно максимизировать. Кроме того, свойства авто/кросс-корреляции последовательности CAZAC можно поддерживать, когда различение между последовательностями осуществляется в отношении длины "C1", показанной на фиг. 2.
Предпочтительно, заполняющая часть может быть циклическим расширением последовательности CAZAC. Таким образом, заполняющую часть (C2) можно генерировать путем циклического копирования первой части сгенерированной последовательности CAZAC GCL и добавления к сгенерированной последовательности. Благодаря этому результирующая последовательность может иметь хорошие свойства авто/кросс-корреляции, даже когда различение последовательностей производится в отношении полной длины последовательности (L). Поэтому этот способ имеет дополнительное преимущество над вышеописанным способом, использующим заполняющую часть, состоящую из нулей.
Настоящее изобретение для генерации опорной сигнальной последовательности с использованием последовательности CAZAC, в основном, основано на методе генерации с использованием заполняющей части, генерируемой посредством вышеописанного циклического расширения. Однако ограничиваться этим методом генерации не обязательно, т.е. настоящее изобретение может быть основано на методе генерации усеченной последовательности и методе генерации с использованием заполняющей части, состоящей из нулей.
На этом основании рассмотрим межсотовую помеху, обусловленную использованием последовательностей, имеющих разную длину.
Когда последовательность CAZAC используется в качестве опорной сигнальной последовательности, межсотовая помеха пропорциональна значению взаимной корреляции между двумя последовательностями. Таким образом, в нижеследующих примерах значение взаимной корреляции, обусловленной перекрытием между исходным опорным сигналом, переданным посредством определенной области ресурсов, и входящими последовательностями, поступающими из соседних сот, длина которых отличается от длины исходного опорного сигнала, и переданными посредством той же области ресурсов, рассматривается в отношении индекса последовательностей ZC.
В частности, в нижеследующих примерах рассматриваются последовательности, имеющие длину 1 RB, 2 RB и 3 RB. Предположим, что последовательности, имеющие длину 1 RB и 2 RB, генерируются посредством циклического расширения последовательности ZC, имеющей длину, заданную наибольшим простым числом, которое меньше соответствующего размера блока ресурсов. Кроме того, предположим, что последовательность, имеющая длину 3 RB, генерируется методом генерации усеченной последовательности. Таким образом можно генерировать последовательности, имеющие соответствующий размер блока ресурсов, на основании длины, равной простому числу, одним из 3 вышеупомянутых методов генерации.
Сначала рассмотрим случай, когда последовательность, имеющая длину 1 RB, и последовательность, имеющая длину 2 RB, перекрываются в одной и той же области ресурсов. Последовательность, имеющую длину 1 RB, и последовательность, имеющую длину 2 RB, можно выразить следующим образом.
[Уравнение 6]
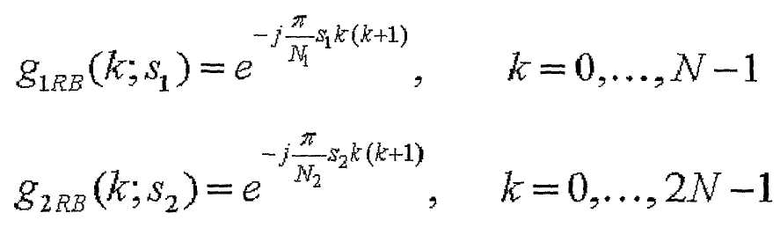
Здесь s1 и s2 обозначают индексы, являющиеся взаимно простыми, с длиной последовательности (N или 2N). В этом примере для последовательностей, имеющих длину 1 RB и длину 2 RB, генерируются с использованием метода циклического расширения, s1 может быть равен 1, 2, …, 10, и s2 может быть равен 1, 2, …, 22. N1 может быть равно 11, и N2 может быть равно 23.
На этом основании значение взаимной корреляции (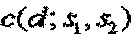 ), генерируемое, когда последовательность длиной 1 RB перекрывается с последовательностью длиной 2 RB в области первых 12 поднесущих последовательности длиной 2 RB, можно выразить следующим образом.
), генерируемое, когда последовательность длиной 1 RB перекрывается с последовательностью длиной 2 RB в области первых 12 поднесущих последовательности длиной 2 RB, можно выразить следующим образом.
[Уравнение 7]
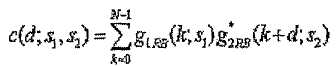
Для d=0,
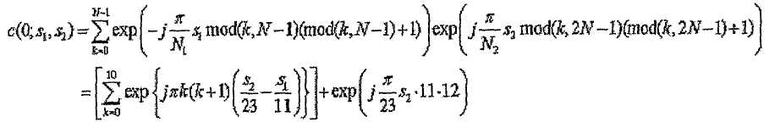
Из уравнения 7 следует, что, если комбинация индексов последовательности (s1 и s2) удовлетворяет условию, что выражение 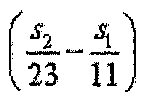 приближается к нулю, последовательности, указанные этими индексами последовательности, дают высокую взаимную корреляцию.
приближается к нулю, последовательности, указанные этими индексами последовательности, дают высокую взаимную корреляцию.
Таким образом, один вариант осуществления настоящего изобретения предусматривает осуществление группирования последовательностей в группы так, чтобы последовательности, содержащиеся в каждой группе, имели высокую взаимную корреляцию друг с другом. Если рассматривать последовательность длиной 1 RB и последовательность длиной 2 RB, предусмотрено группирование комбинации индексов последовательности, которая удовлетворяет условию, что выражение 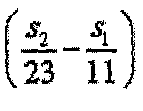 приближается к нулю.
приближается к нулю.
Однако для определения более общего условия для группирования последовательностей, рассмотрим некоторые другие примеры.
Когда последовательность длиной 1 RB перекрывается в области последних 12 поднесущих последовательности длиной 2 RB, значение взаимной корреляции 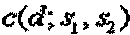 двух последовательностей можно выразить следующим образом.
двух последовательностей можно выразить следующим образом.
[Уравнение 8]

Для d=0
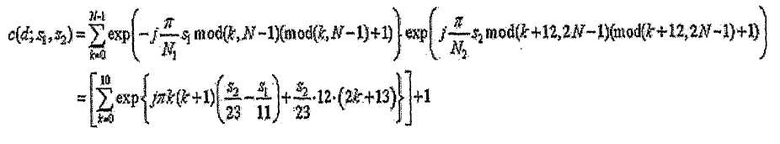
Согласно уравнению 8 также можно заключить, что, если комбинация индексов последовательности (s1 и s2) удовлетворяет условию, что выражение 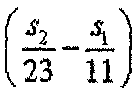
приближается к нулю, последовательности, указанные этими индексами последовательности, дают высокую взаимную корреляцию. Поэтому, если рассматривать последовательность длиной 1 RB и последовательность длиной 2 RB, позиция, где происходит перекрывание, не изменяет условие группирования.
Теперь рассмотрим случай, когда последовательность длиной 1 RB и последовательность длиной 3 RB перекрываются в одной и той же области ресурсов.
Прежде всего, последовательность длиной 1 RB и последовательность длиной 3 RB можно выразить следующим образом.
[Уравнение 9]
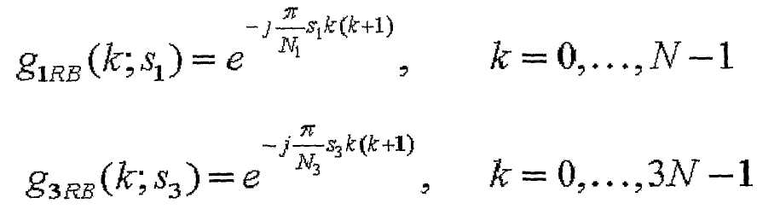
Здесь s1 и s3 обозначают индексы, являющиеся взаимно простыми с длиной последовательности (N или 3N). В этом примере, когда последовательности длиной 1 RB генерируются с использованием метода циклического расширения и последовательность длиной 3 RB генерируется с использованием метода генерации усеченной последовательности, s1 может быть равен 1, 2, …, 10, и s2 может быть равен 1, 2, …, 36. N1 может быть равно 11, и N2 может быть равно 37.
На этом основании, если последовательность длиной 1 RB перекрывается в области первых 12 поднесущих последовательности длиной 3 RB, значение взаимной корреляции между двумя последовательностями можно выразить следующим образом.
[Уравнение 10]
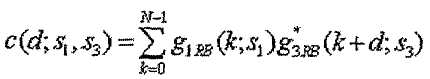
Для d=0,
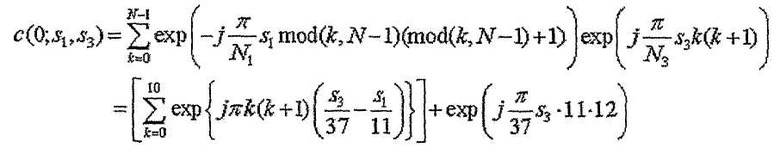
Из уравнения 10 следует, что, если комбинация индексов последовательности (s1 и s3) удовлетворяет условию, что выражение 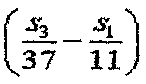 приближается к нулю, последовательности, указанные этими индексами последовательности, дают высокую взаимную корреляцию. Таким образом, если рассматривать последовательность длиной 1 RB и последовательность длиной 3 RB, предусмотрено группирование комбинации индексов последовательности, которая удовлетворяет условию, что выражение
приближается к нулю, последовательности, указанные этими индексами последовательности, дают высокую взаимную корреляцию. Таким образом, если рассматривать последовательность длиной 1 RB и последовательность длиной 3 RB, предусмотрено группирование комбинации индексов последовательности, которая удовлетворяет условию, что выражение 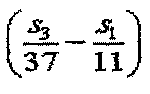 приближается к нулю.
приближается к нулю.
Чтобы подтвердить соотношение в позиции, где происходит перекрывание, рассмотрим случай, когда последовательность длиной 1 RB перекрывается в области вторых 12 поднесущих последовательности длиной 3 RB. В этом случае значение взаимной корреляции между этими двумя последовательностями можно выразить следующим образом.
[Уравнение 11]
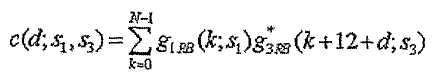
Для d=0,
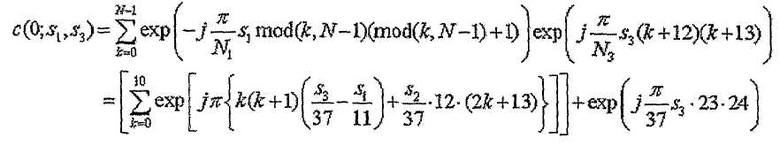
Когда последовательность длиной 1 RB перекрывается в области последних 12 поднесущих последовательности длиной 3 RB, значение взаимной корреляции можно выразить следующим образом.
[Уравнение 12]
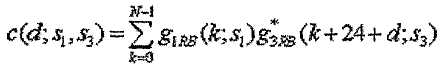
Для d=0,
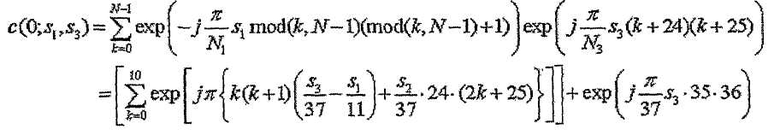
Согласно уравнениям 11 и 12 также можно заключить, что, если комбинация индексов последовательности (s1 и s3) удовлетворяет условию, что выражение 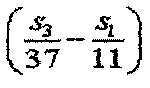 приближается к нулю, последовательности, указанные этими индексами последовательности, дают высокую взаимную корреляцию. Поэтому, если рассматривать последовательность длиной 1 RB и последовательность длиной 3 RB, позиция, где происходит перекрывание, не изменяет условие группирования.
приближается к нулю, последовательности, указанные этими индексами последовательности, дают высокую взаимную корреляцию. Поэтому, если рассматривать последовательность длиной 1 RB и последовательность длиной 3 RB, позиция, где происходит перекрывание, не изменяет условие группирования.
Согласно вышеприведенным примерам данный вариант осуществления предусматривает осуществление группирования последовательностей так, чтобы два индекса последовательности из всех индексов последовательности, сгруппированных в одну и ту же группу, удовлетворяли условию, что выражение (s2/N2 - s1/N1) приближается к нулю, если рассматривать две последовательности, имеющие длину N1 и N2. Здесь N1 и N2 могут быть максимальными взаимно простыми числами, которые меньше результирующей опорной сигнальной последовательности. Кроме того, s1 и s2 обозначают индексы корня последовательностей ZC и их можно выбирать в диапазонах 1~(N1-1) и 1~(N2-1) соответственно.
На основании этой концепции рассмотрим более общий метод группирования с учетом последовательностей разной длины.
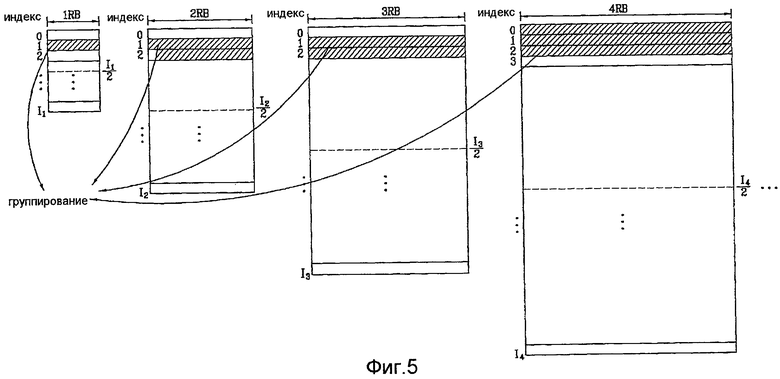
На фиг. 3-5 показаны обобщенные схемы группирования последовательностей согласно одному варианту осуществления этого изобретения.
Согласно этому варианту осуществления из последовательностей разной длины, например 1 RB, 2 RB, 3 RB …, как показано на фиг. 3, последовательности, индексы которых удовлетворяют вышеупомянутому условию высокой взаимной корреляции, можно группировать в одну и ту же группу. Каждую из групп последовательностей можно выделять одной и той же соте или Node B.
В общем случае, FDM осуществляется для каждой соты или Node B, что позволяет минимизировать помеху, обусловленную использованием последовательностей, имеющих разную длину, одной соты или Node B. Таким образом, выделяя последовательности, имеющие высокую взаимную корреляцию, одной и той же соте или Node B, можно минимизировать межсотовую помеху, обусловленную использованием последовательностей разной длины.
Еще один вариант осуществления этого изобретения предусматривает осуществление группирования так, чтобы каждая из групп содержала, по меньшей мере, одну последовательность каждой длины. Таким образом, выделение группы последовательностей одной и той же соте или Node B позволяет UE, находящемуся в этой соте или Node B, использовать опорные сигнальные последовательности различной длины. Однако конкретный метод группирования можно задавать по-разному.
Во-первых, количество последовательностей, выделенных одной группе, может быть пропорционально количеству RB, которое соответствует длине опорной сигнальной последовательности. Согласно фиг. 3 одна последовательность для последовательности длиной 1 RB, две последовательности для последовательности длиной 2 RB, 3 последовательности для последовательности длиной 3 RB и т.д. группируются.
Во-вторых, количество последовательностей, выделенных одной группе, может быть постоянным числом. Согласно фиг. 4 одна последовательность для последовательности каждой длины группируется в одну и ту же группу.
Данный вариант осуществления может предусматривать осуществление группирования так, чтобы количество последовательностей, выделенных одной группе, не было ни пропорциональным длине последовательности, ни постоянным. На фиг. 5 показан пример группирования последовательностей так, чтобы одна последовательность для последовательности длиной 1 RB, 2 последовательности для последовательности длиной 2 RB, 2 последовательности для последовательности длиной 3 RB и 3 последовательности для последовательности длиной 4 RB и т.д. группировались в одну группу.
Аналогично вышеописанному, если каждая группа содержит, по меньшей мере, одну последовательность каждой длины, можно задать максимальное количество последовательностей на группу. Когда максимальное количество последовательностей на группу задано, способ выбора индекса корня последовательности ZC с учетом предельного количества последовательностей можно задать следующим образом.
Если для каждой длины последовательности выбрана одна последовательность и если одна конкретная последовательность с индексом s1 и длиной N1 уже выбрана для этой группы, можно выбирать одну последовательность (имеющую индекс s2) для каждой длины, индекс которой делает выражение (s2/N2-s1/N1) ближайшим к нулю, где N2 - длина последовательности, соответствующая рассматриваемой длине. Если же для каждой определенной длины последовательности выбрано 2 последовательности и если одна конкретная последовательность с индексом s1 и длиной N1 уже выбрана для этой группы, можно выбирать две последовательности для этой длины, чтобы выражение (s2/N2-s1/N1) стремилось к нулю. Это можно дополнительно обобщить до максимального количества последовательностей "x" для каждой длины.
Еще один метод группирования можно задать следующим образом. Если для каждой длины последовательности выбрана одна последовательность и если одна конкретная последовательность с индексом s1 и длиной N1 уже выбрана для этой группы, сначала выбираем определенное число (y) последовательностей из последовательностей, для которых выражение (s2/N2-s1/N1) приближается к определенному значению, и затем выбираем одну последовательность из y последовательностей, которая имеет высокую взаимную корреляцию с последовательностью, имеющей индекс s1. Если же для каждой определенной длины последовательности выбрано 2 последовательности и если одна конкретная последовательность с индексом s1 и длиной N1 уже выбрана для этой группы, сначала выбираем определенное число (y) последовательностей из последовательностей, для которых выражение (s2/N2-s1/N1) приближается к определенному значению, и затем выбираем две последовательности из y последовательностей, которые имеют высокую взаимную корреляцию с последовательностью, имеющей индекс s1. Это можно дополнительно обобщить до максимального количества последовательностей «x» для каждой длины.
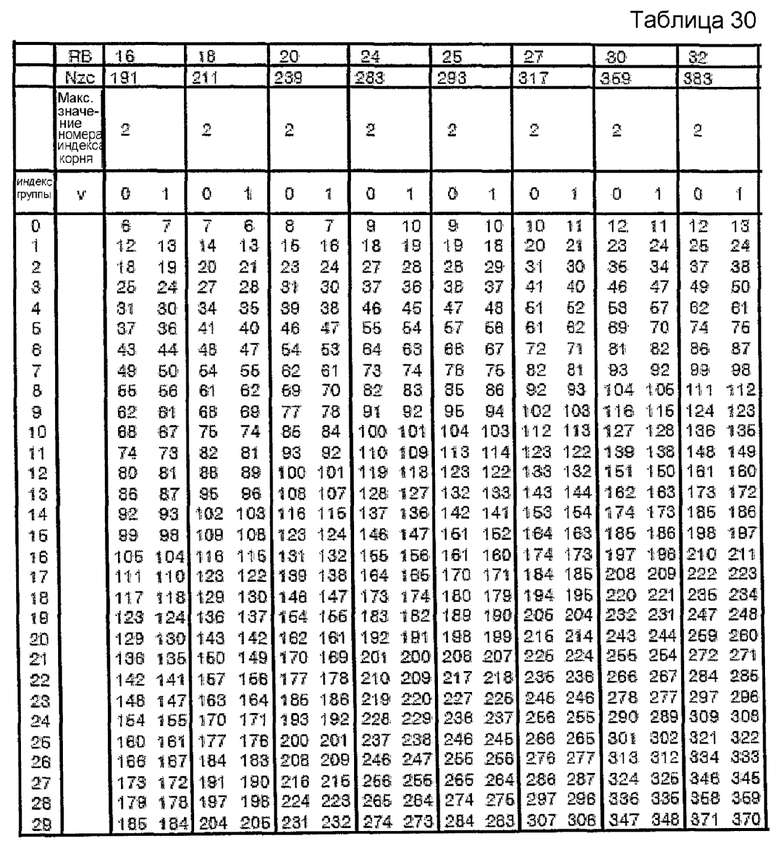
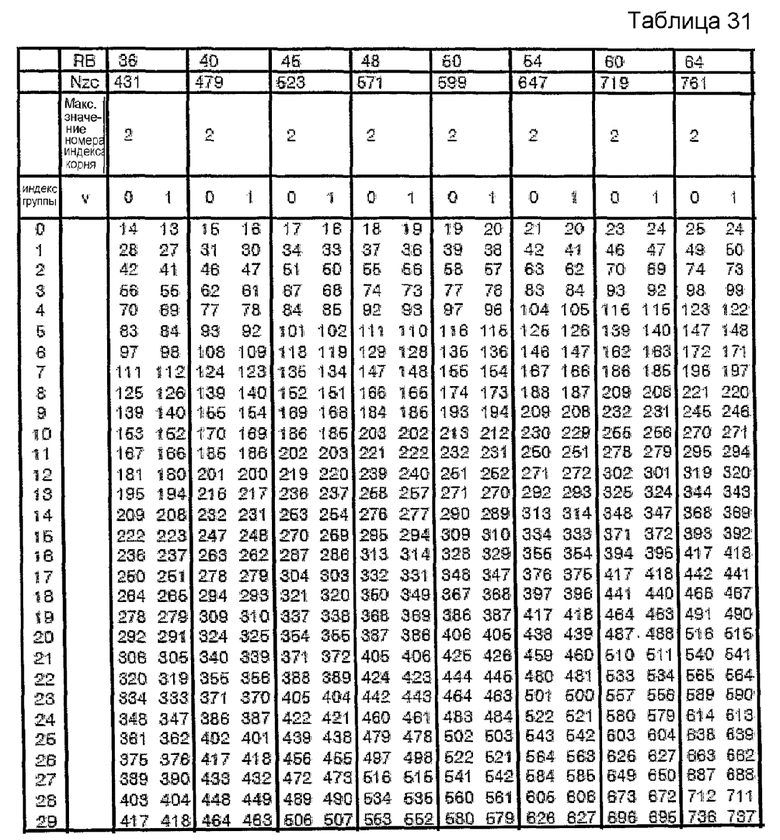
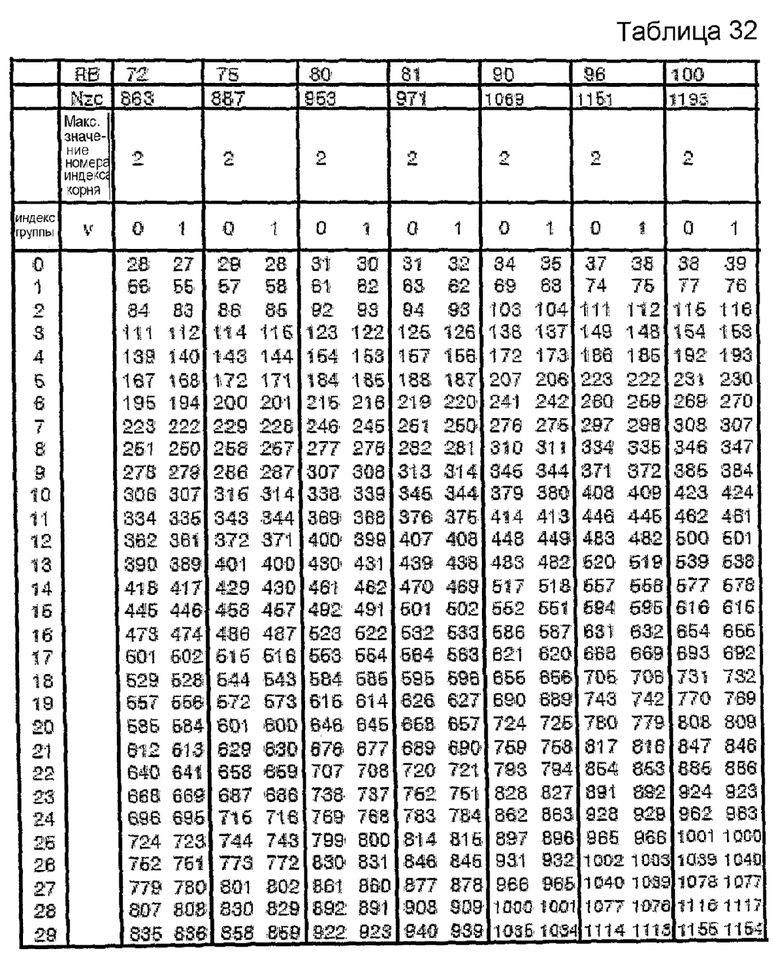
В вышеприведенных примерах сначала выбирают одну конкретную последовательность с индексом s1 и длиной N1, которая становится опорой для выбора остальных последовательностей. Эту опорную последовательность можно задать как последовательность длиной 1 RB, последовательность длиной 2 RB, последовательность длиной 3 RB и т.д. Однако в нижеследующем объяснении предположим, что опорная последовательность представляет собой последовательность длиной 3 RB. Поскольку количество индексов последовательности для длины 3 RB равно 30, количество групп для группирования последовательностей согласно этому варианту осуществления изобретения может быть равно 30.
В случае, когда количество индексов корня для последовательности длиной 3 RB равно 30, количество индексов корня, выбранное для определенной группы, можно определить следующим образом.
[Уравнение 13]
round (количество индексов корня для последовательности определенной длины/30)
Здесь "round(z)" является функцией округления до ближайшего целого числа, ближайшего к z.
Согласно уравнению 13 для длины 3 RB и 4 RB можно выбирать 1 последовательность. Для длины 5 RB~6 RB можно выбирать 2 последовательности. Кроме того, для длины свыше 6 RB можно выбирать 3 или более последовательностей соответственно. Кроме того, согласно одному варианту осуществления этого изобретения последовательность длиной меньше 3 длин RB можно задавать по-разному без использования последовательности ZC. Благодаря этому количество последовательностей, выбранных для длины 1 RB и длины 2 RB, можно задать равным 1.
В итоге, согласно этому варианту осуществления количество последовательностей на группу можно задать следующим образом.
[Уравнение 14]
{1RB, 2RB, 3RB, 4RB, 5RB, 6RB, 8RB, 9RB, 10RB, 12RB, 15RB, 16RB, 18RB, 20RB, 24RB, 25RB, …}={1, 1, 1, 1, 2, 2, 3, 3, 4, 5, 6, 6, 7, 8, 9, 9, …}
На этом основании в нижеследующих таблицах 1-5 показан пример группирования последовательностей, при котором каждая группа содержит количество последовательностей согласно уравнению 14, и последовательности, выбранные для каждой группы, удовлетворяют вышеупомянутому условию высокой взаимной корреляции.
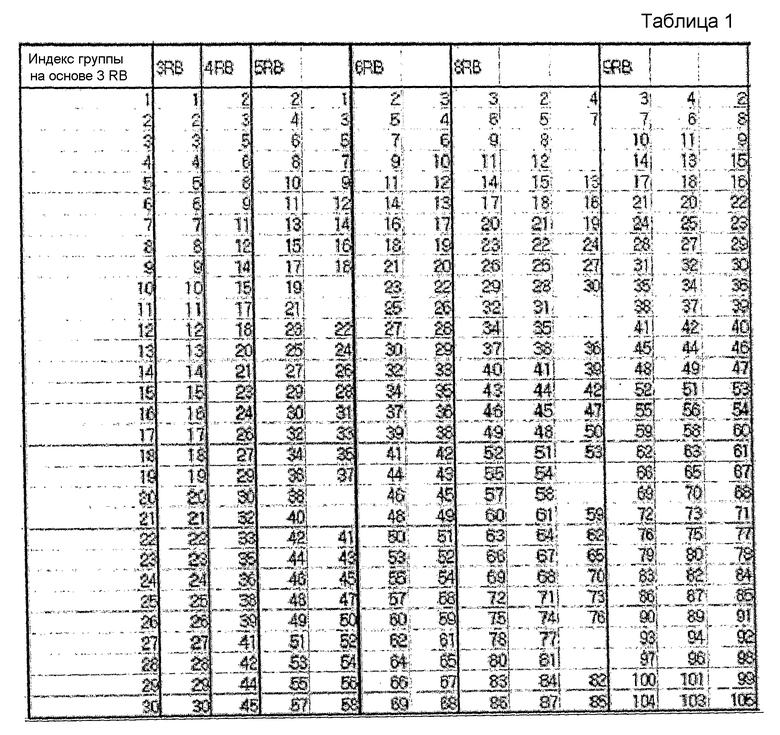
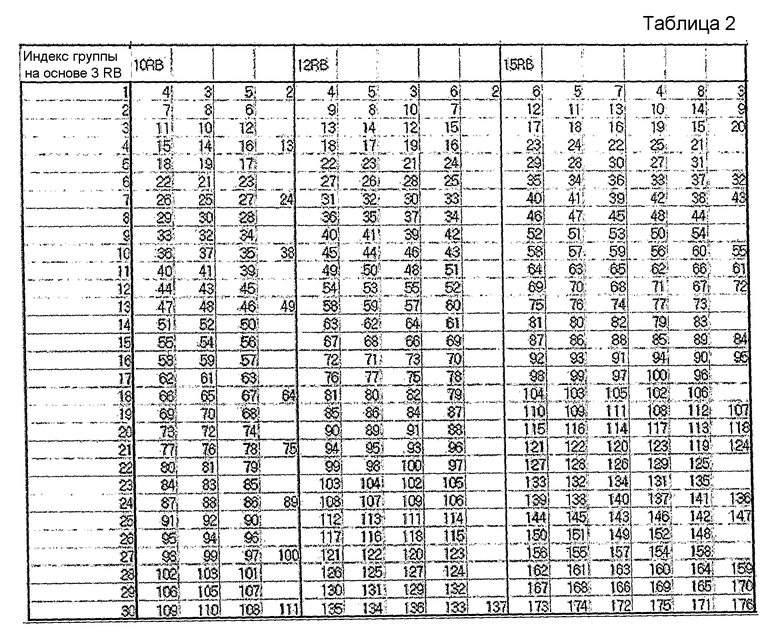
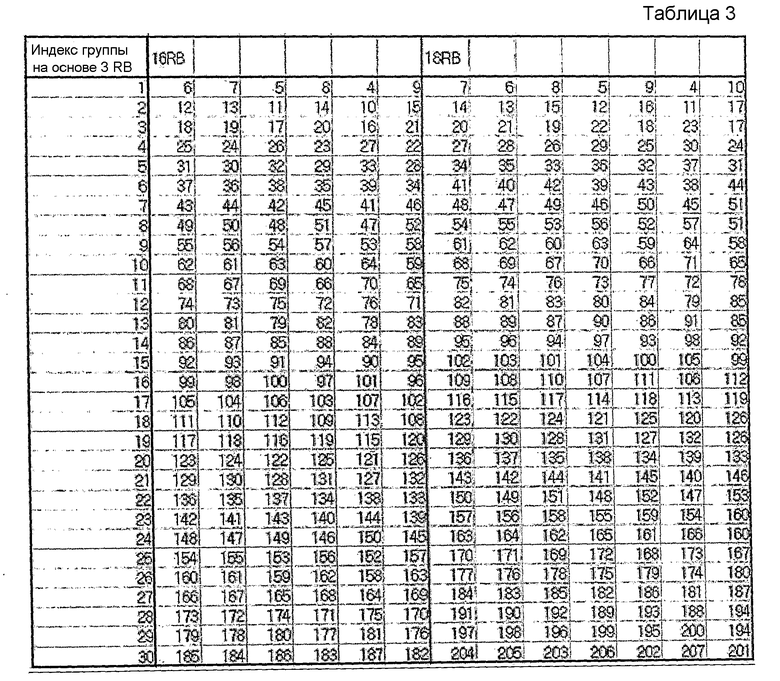
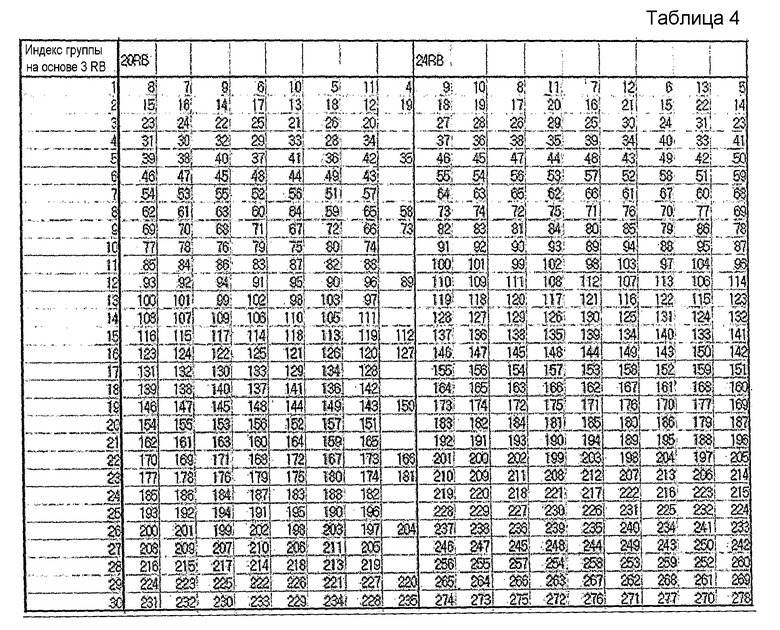
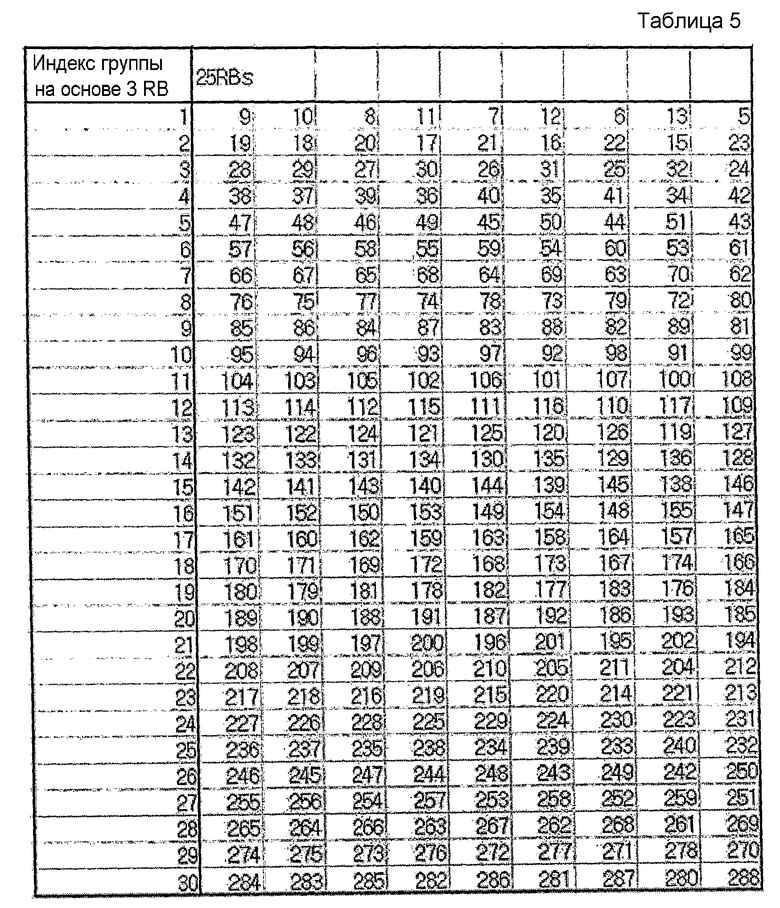
В таблицах 1-5 последовательности длиной 1 RB и 2 RB не показаны, поскольку последовательности длиной 1 RB и 2 RB задаются иначе.
В другом примере в случае, когда количество индексов корня для последовательности длиной 3 RB равно 30, количество индексов корня, выбранное для определенной группы, можно определить следующим образом.
[Уравнение 15]
floor (количество индексов корня для последовательности определенной длины/30)
Здесь floor(z) является функцией, возвращающей наибольшее целое число, не превышающее z.
Согласно уравнению 15 для длины 3~5 RB можно выбирать 1 последовательность. Для длины 6~8 RB можно выбирать 2 последовательности. Кроме того, для длины свыше 9 длин RB можно выбирать 3 или более последовательностей соответственно. Кроме того, согласно одному варианту осуществления этого изобретения последовательность длиной меньше 3 длин RB можно задавать по-разному без использования последовательности ZC. Благодаря этому количество последовательностей, выбранных для длины 1 RB и длины 2 RB, можно задать равным 1.
В итоге, согласно этому варианту осуществления количество последовательностей на группу можно задать следующим образом.
[Уравнение 16]
{1RB, 2RB, 3RB, 4RB, 5RB, 6RB, 8RB, 9RB, 10RB, 12RB, 15RB, 16RB, 18RB, 20RB, 24RB, 25RB, …}={1, 1, 1, 1, 1, 2, 2, 3, 3, 4, 5, 6, 7, 7, 9, 9, …}
На этом основании в нижеследующих таблицах 6-8 показан пример группирования последовательностей, при котором каждая группа содержит количество последовательностей согласно уравнению 16, и последовательности, выбранные для каждой группы, удовлетворяют вышеупомянутому условию высокой взаимной корреляции.
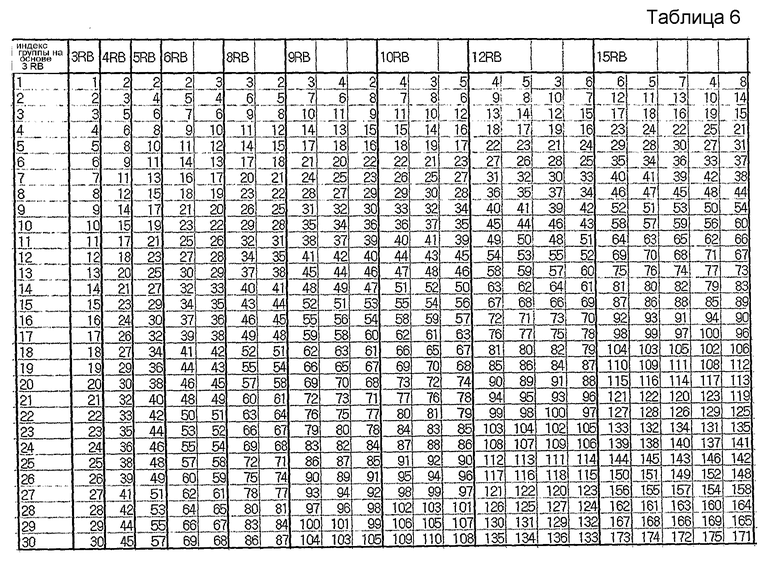
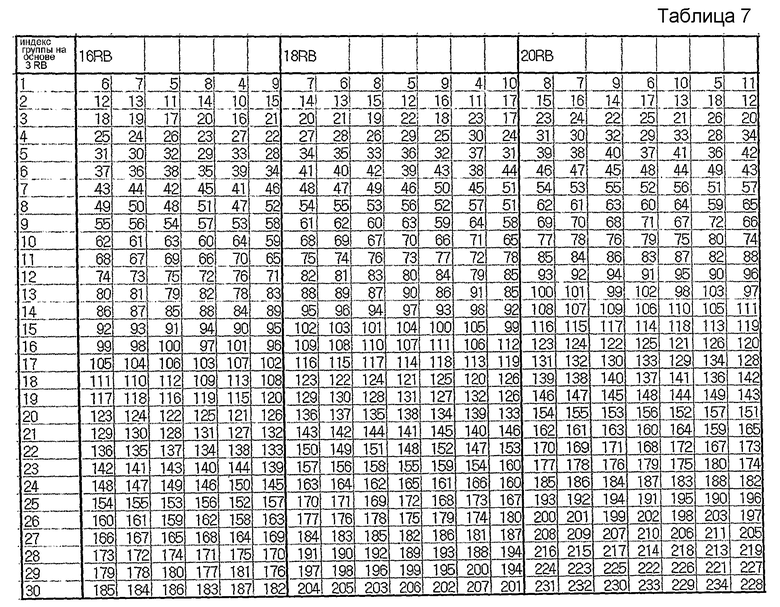
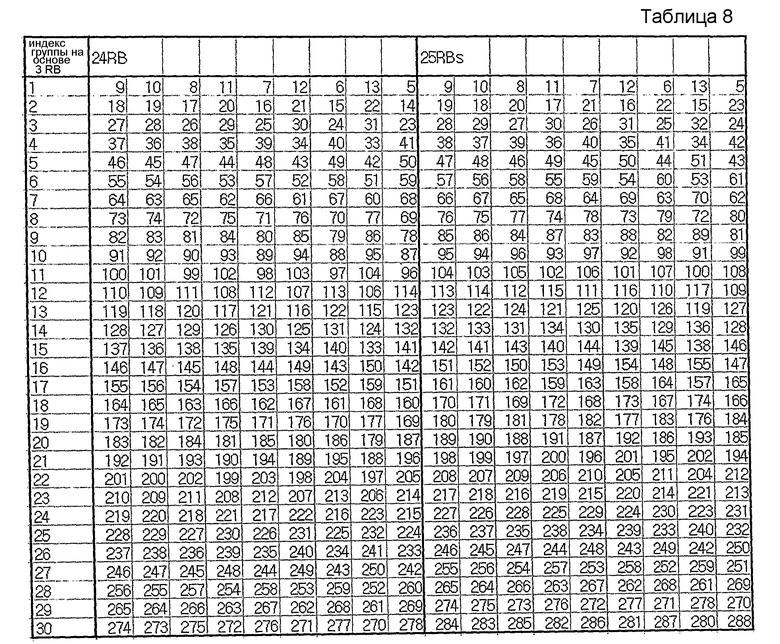
Наподобие таблиц 1-5 в таблицах 6-8 последовательности длиной 1 RB и 2 RB не показаны, поскольку последовательности длиной 1 RB и 2 RB задаются иначе.
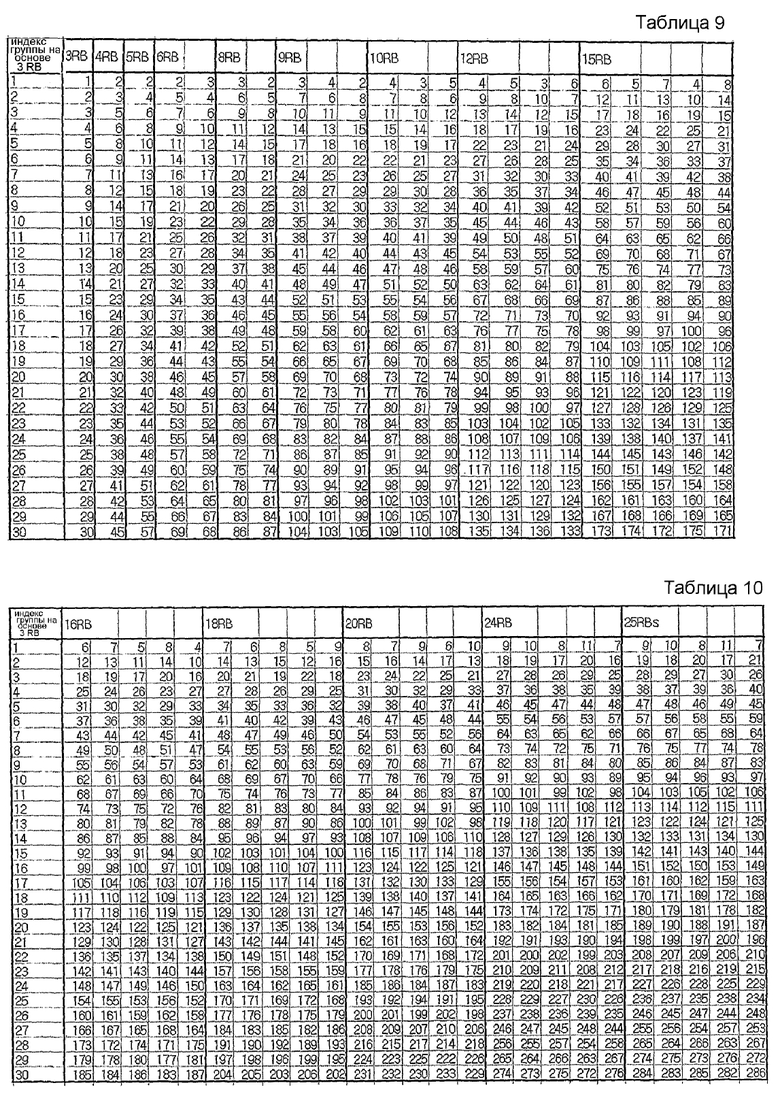
В еще одном варианте осуществления этого изобретения максимальное количество последовательностей на каждую группу можно заранее определить по различным причинам. В нижеследующих таблицах 9 и 10 показан пример случая, когда максимальное количество последовательностей на группу ограничено 5 последовательностями.
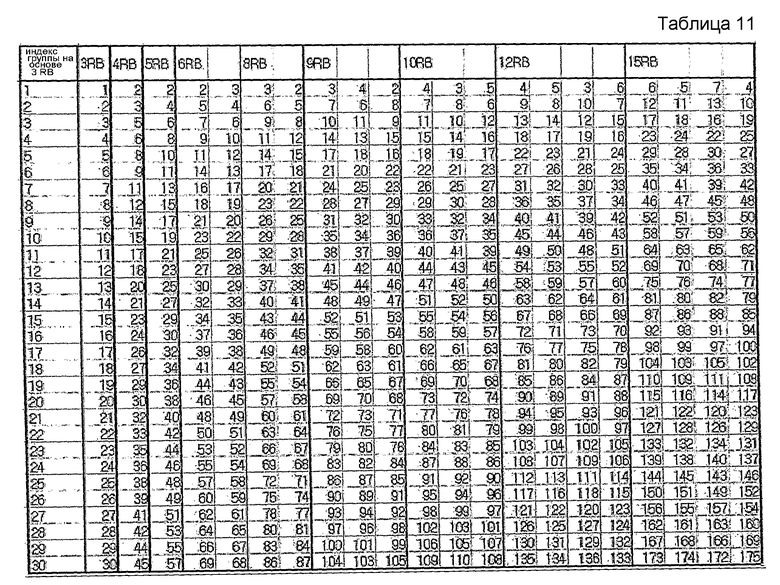
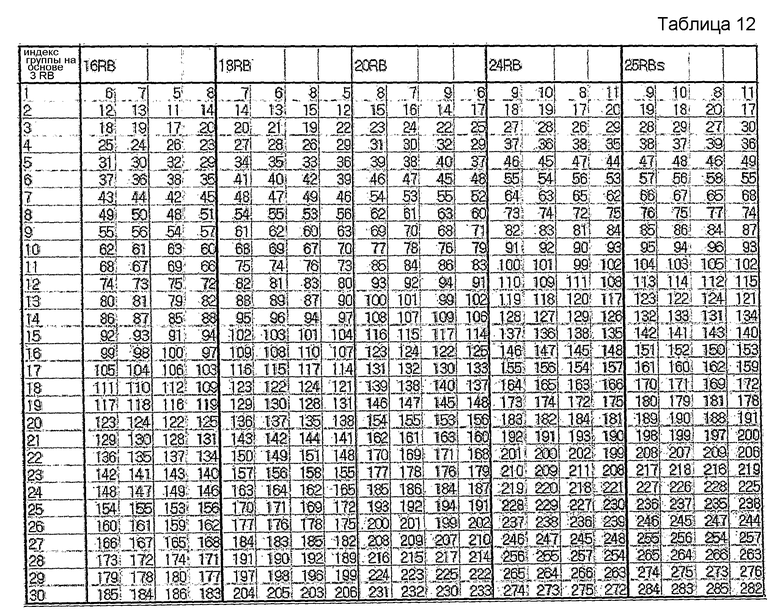
В другом примере, максимальное количество последовательностей можно заранее определить равным 4. Этот случай показан в нижеследующих таблицах 11 и 12.
В другом примере максимальное количество последовательностей можно заранее определить равным 3. Этот случай показан в нижеследующих таблицах 13 и 14.
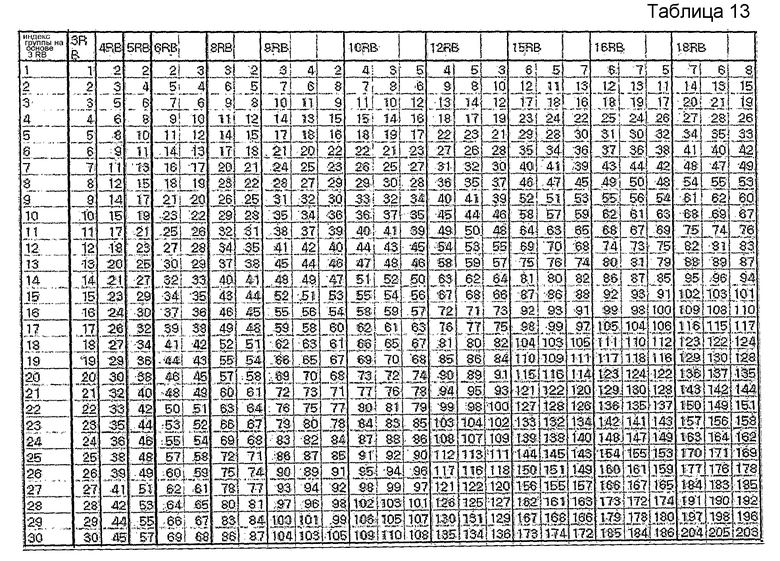
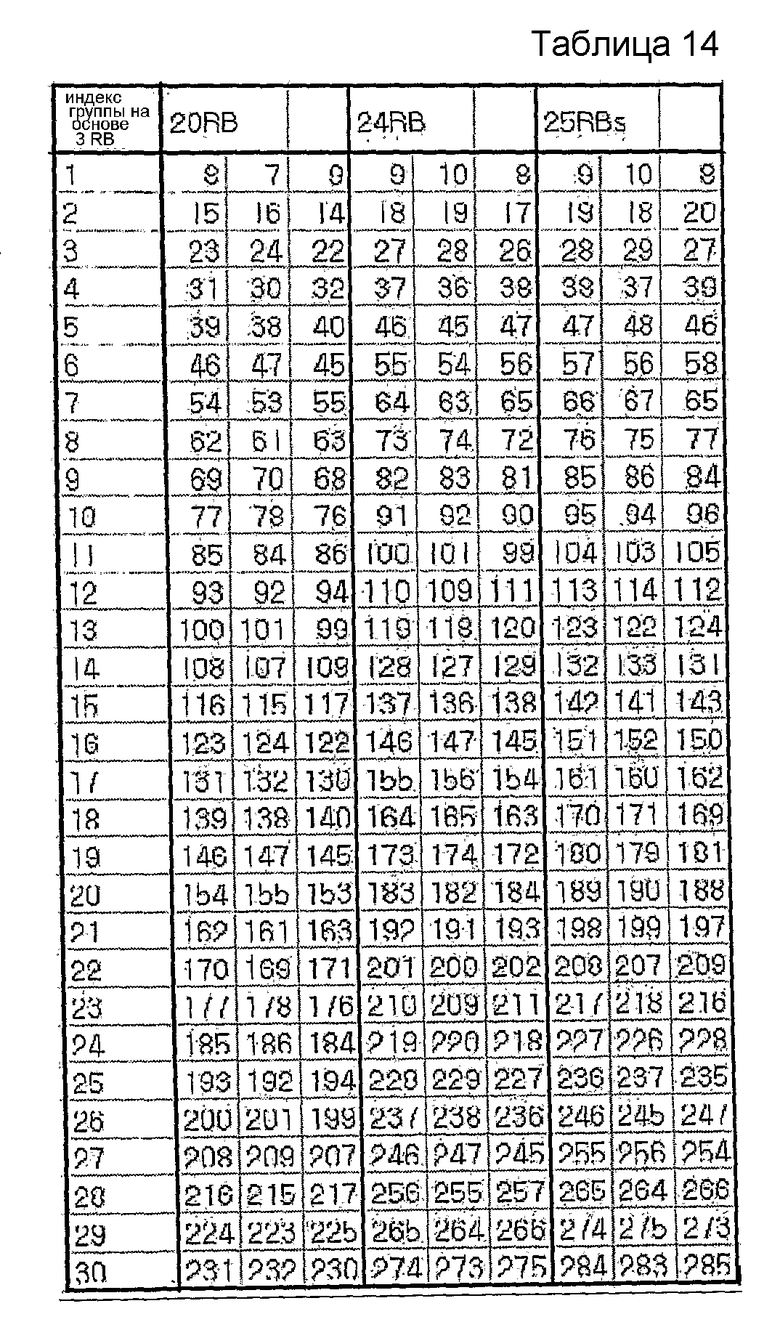
В другом примере максимальное количество последовательностей можно заранее определить равным 2. Этот случай показан в нижеследующих таблицах 15 и 16.
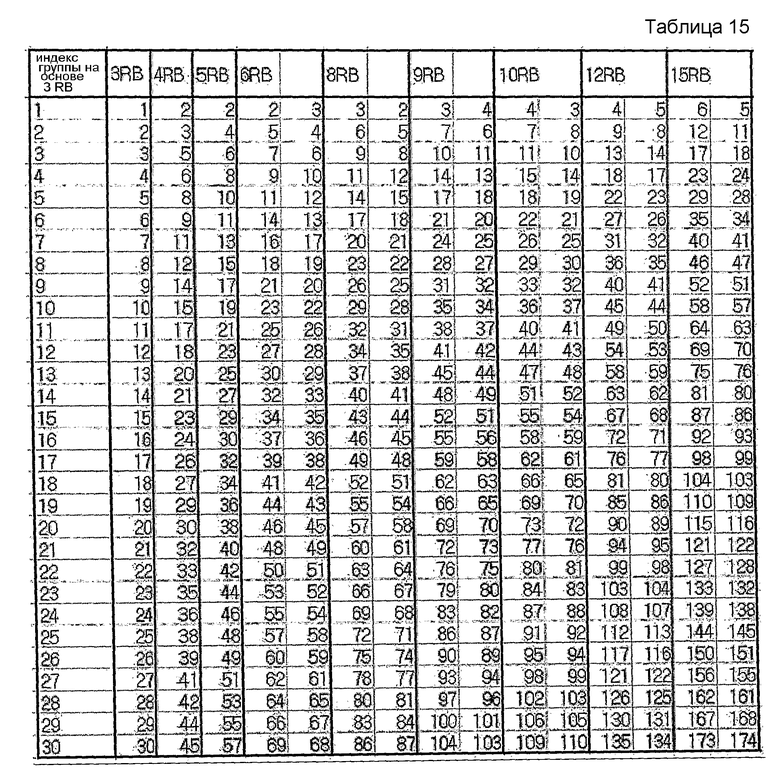
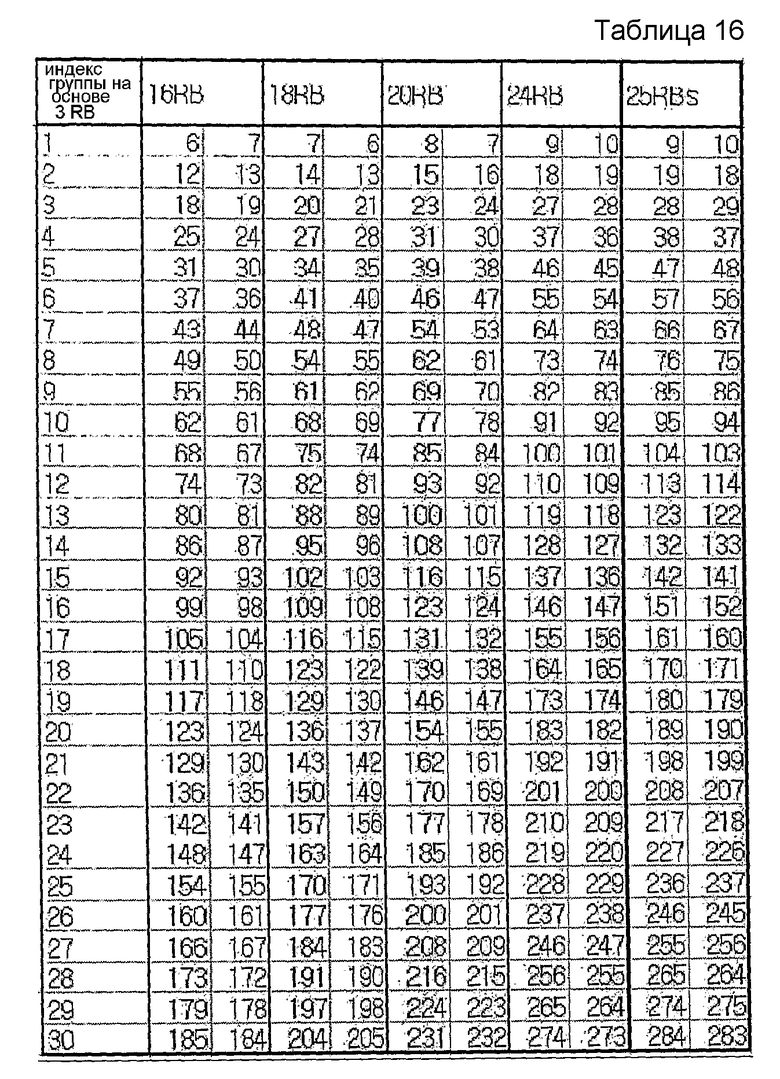
В другом примере максимальное количество последовательностей можно заранее определить равным 1. Этот случай показан в нижеследующей таблице 17.
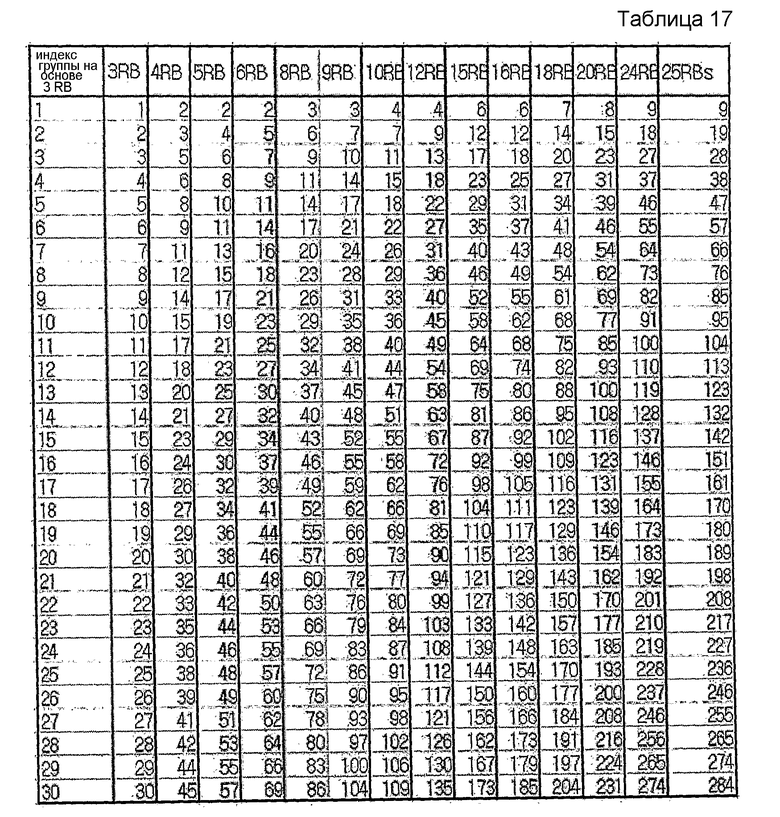
С учетом сложности конфигурации и гибкости поддержки возможности UE использовать опорную сигнальную последовательность переменной длины один вариант осуществления этого изобретения предусматривает осуществление группирования так, чтобы каждая из групп содержала одну базовую последовательность каждой длины, соответствующей длине от 1 до 5 RB, и две базовые последовательности каждой длины, соответствующей длине 6 RB или более. Это соответствует таблицам 15 и 16.
Здесь базовая последовательность - это последовательность ZC, указанная индексом корня, которая используется для применения циклического сдвига, соответствующего различным значениям циклического сдвига. Базовую последовательность с циклическим сдвигом можно использовать в качестве опорной сигнальной последовательности.
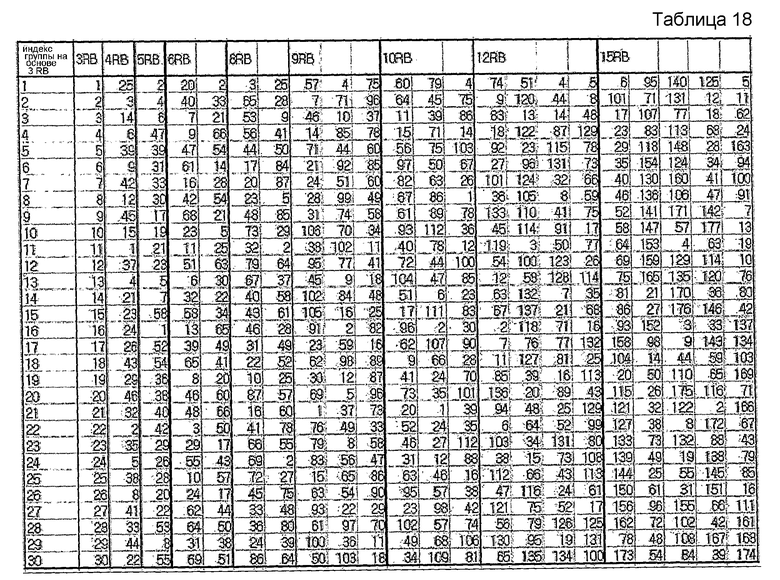
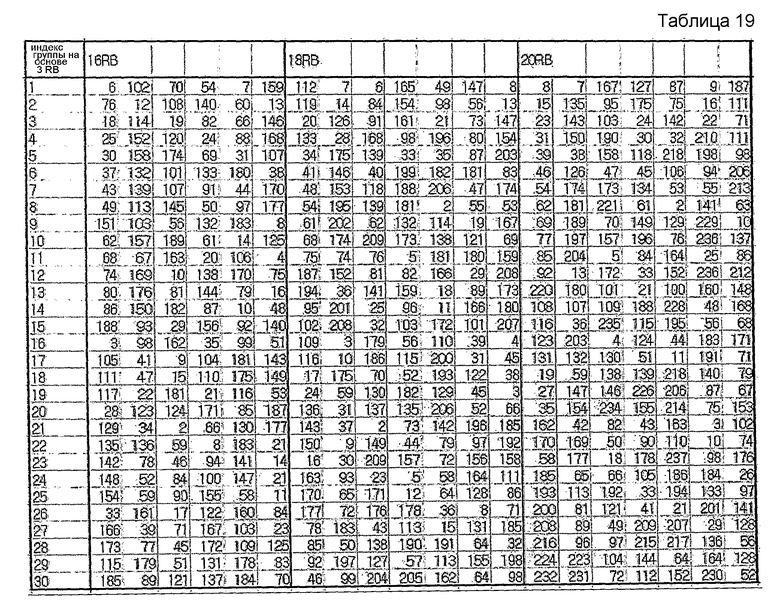
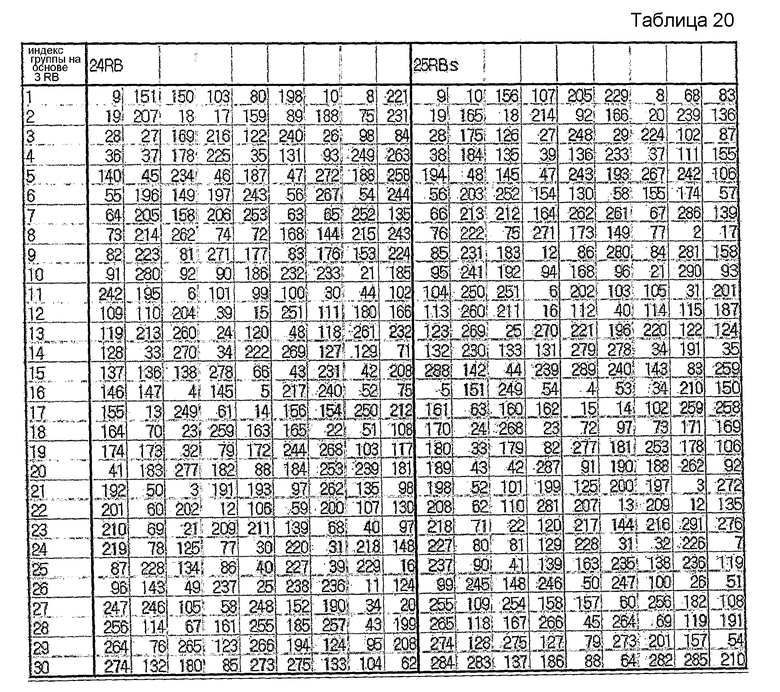
В вышеприведенных таблицах 1-17 отражен случай выбора индекса(ов) корня с использованием выражения (s1/N1-s2/N2). Однако в еще одном варианте осуществления этого изобретения индекс(ы) корня можно выбирать путем вычисления фактического значения взаимной корреляции. Нижеследующие таблицы 18-0 соответствуют таблицам 6-8, но индексы корня выбираются путем вычисления фактического значения взаимной корреляции.
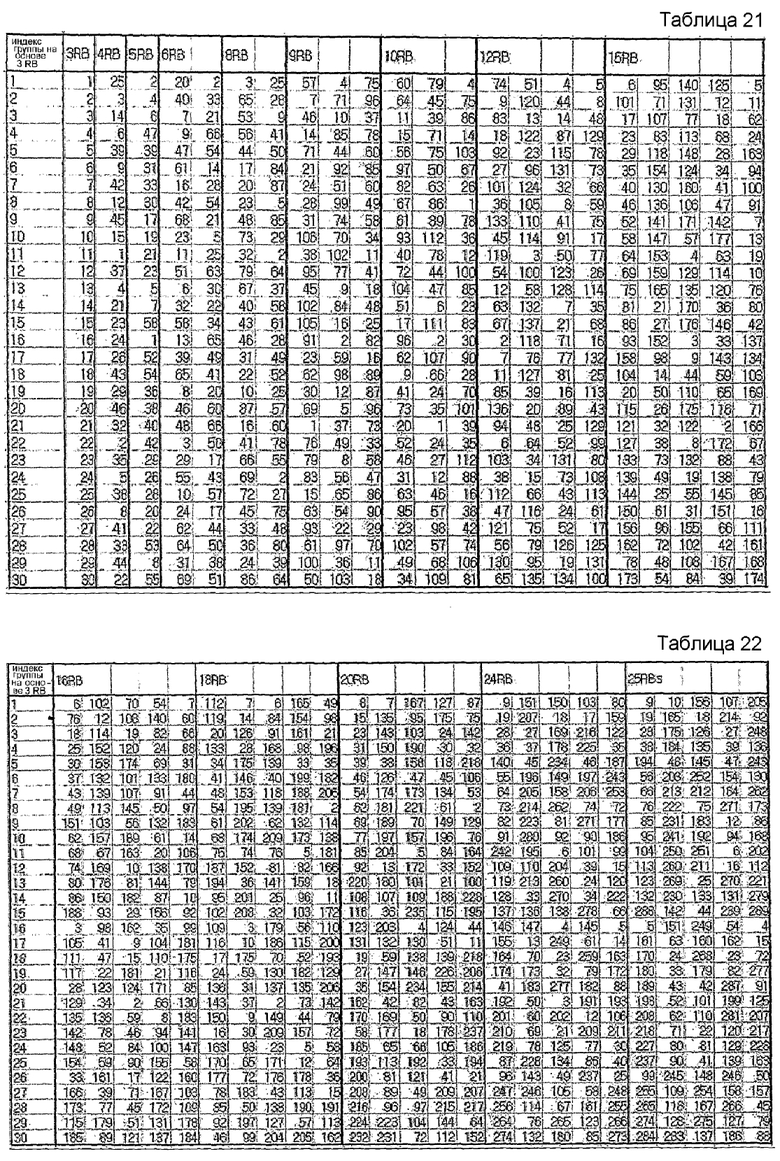
В этом случае, если максимальное количество последовательностей на каждую группу заранее определено равным 5, группирование можно осуществлять согласно нижеследующим таблицам 21 и 22. В таблицах 21 и 22 также отражен случай выбора базовых последовательностей путем вычисления фактической взаимной корреляции.
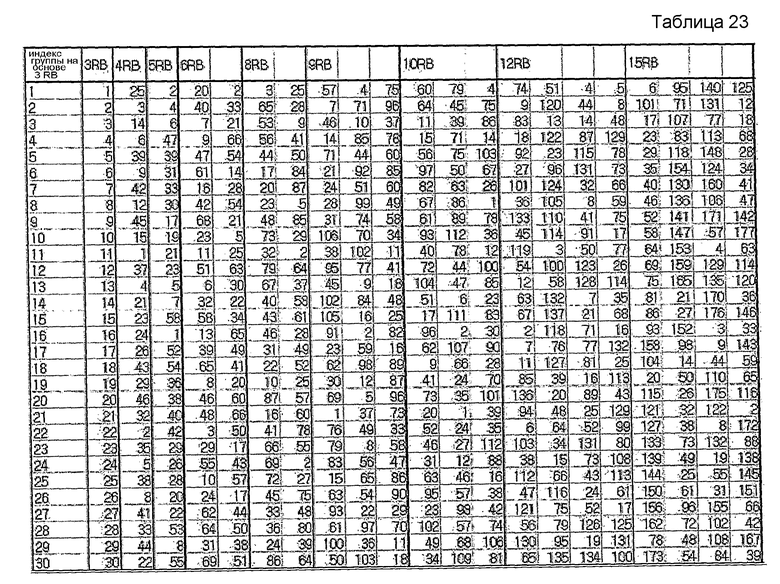
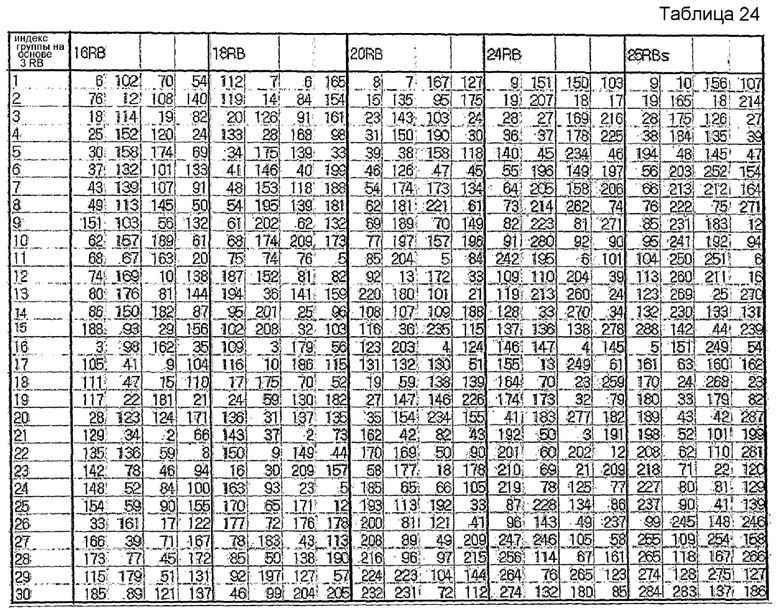
В другом примере, если максимальное количество последовательностей на каждую группу заранее определено равным 4, группирование можно осуществлять согласно нижеследующим таблицам 23 и 24. В таблицах 23 и 24 также отражен случай выбора базовых последовательностей путем вычисления фактической взаимной корреляции.
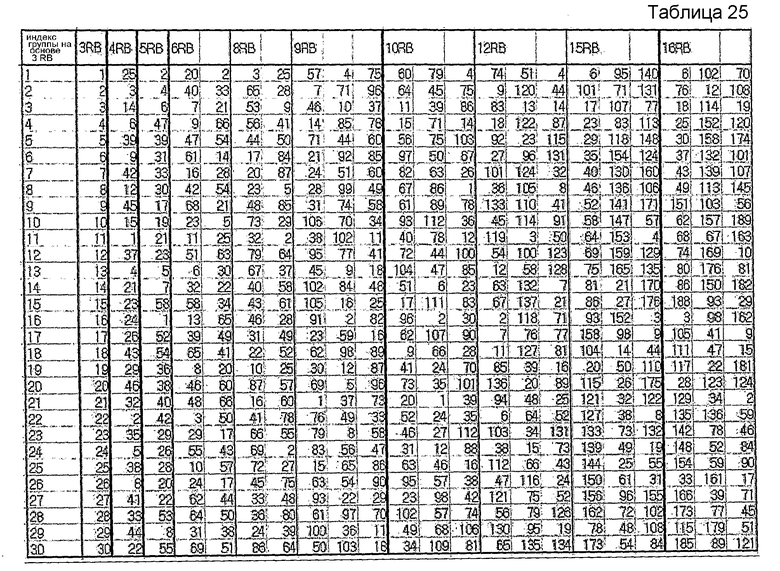
В другом примере, если максимальное количество последовательностей на каждую группу заранее определено равным 3, группирование можно осуществлять согласно нижеследующим таблицам 25 и 26. В таблицах 25 и 26 также отражен случай выбора базовых последовательностей путем вычисления фактической взаимной корреляции.
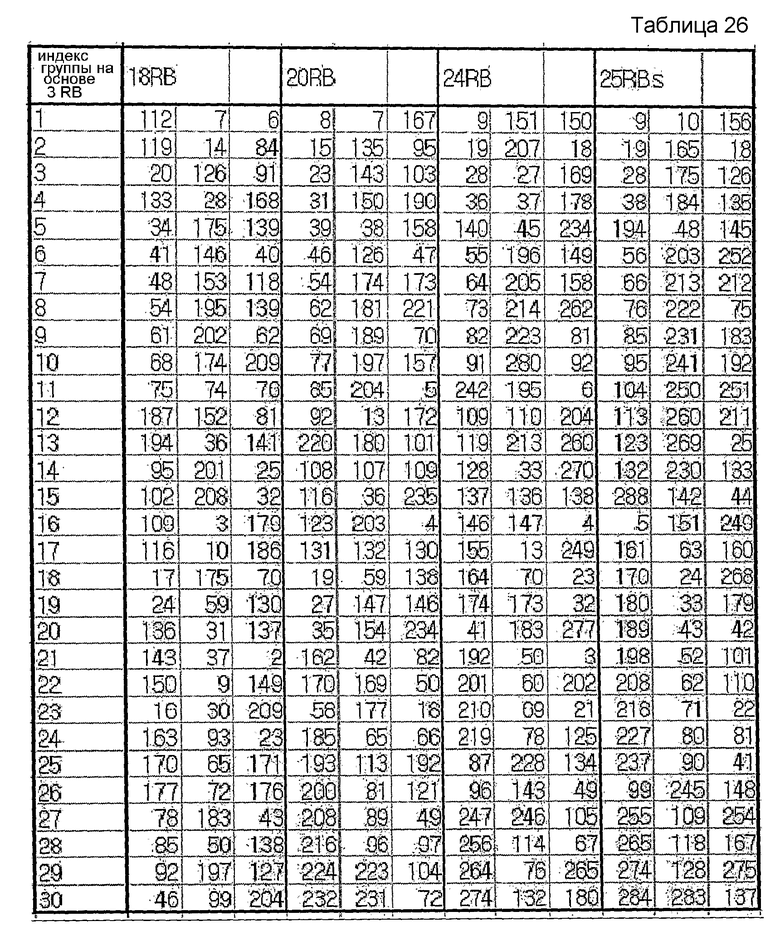
В другом примере, если максимальное количество последовательностей на каждую группу заранее определено равным 2, группирование можно осуществлять согласно нижеследующей таблице 27. В таблице 27 также отражен случай выбора базовых последовательностей путем вычисления фактической взаимной корреляции.
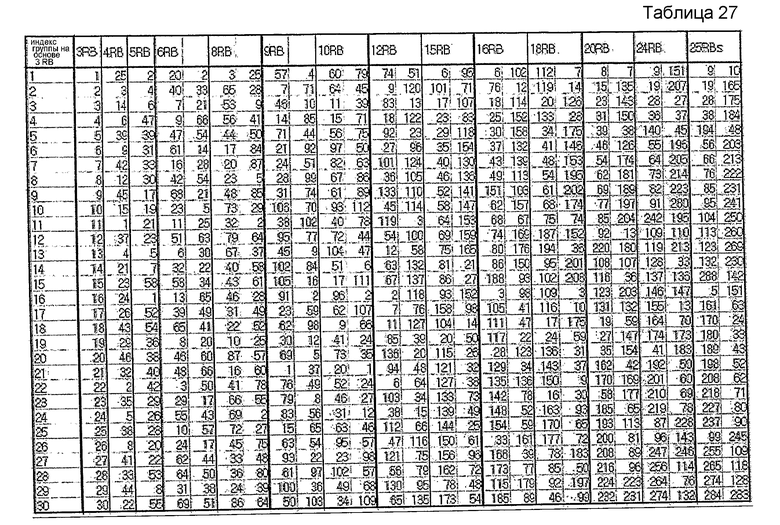
В другом примере, если максимальное количество последовательностей на каждую группу заранее определено равным 1, группирование можно осуществлять согласно нижеследующей таблице 28. В таблице 28 также отражен случай выбора базовых последовательностей путем вычисления фактической взаимной корреляции.
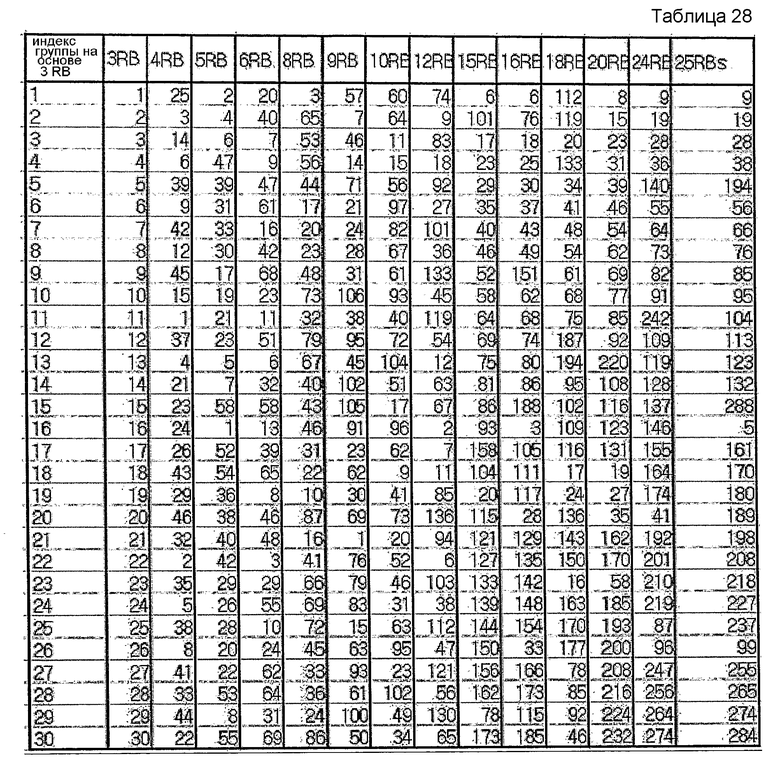
Для вышеописанных случаев таблицы можно реорганизовать согласно выделенному количеству последовательностей для каждой группы и каждой длины.
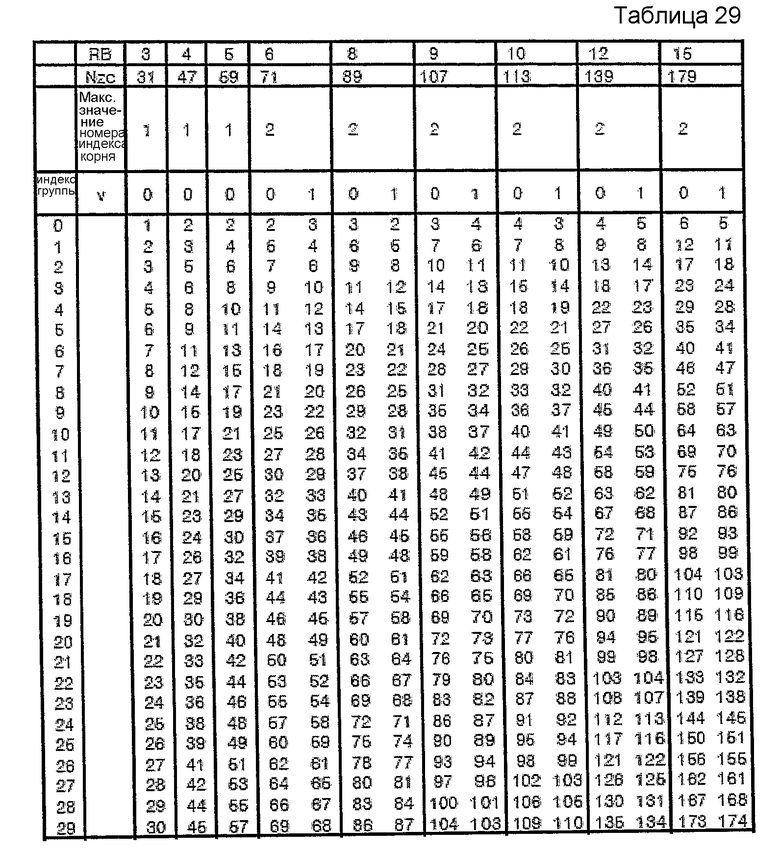
Для другого примера этого изобретения вышеприведенные таблицы можно распространить до длины 100 RB, и нижеследующие таблицы показывают этот пример. В этом примере максимальное значение номера индекса (v) корня для длины 5 RB или меньше задано равным 1, и максимальное значение номера (v) индекса корня для длины, превышающей 5 RB, задано равным 2.
На основании этих концепций настоящее изобретение обеспечивает следующий способ генерации опорной сигнальной последовательности с использованием последовательности ZC.
Для генерации опорной сигнальной последовательности один вариант осуществления настоящего изобретения задает конкретную базовую последовательность для применения циклического сдвига. В этом варианте осуществления базовая последовательность задается с использованием последовательности ZC с определенным индексом корня (далее “q”). Конкретная базовая последовательность выбирается из групп базовых последовательностей, и каждая группа базовых последовательностей содержит базовые последовательности, имеющие высокую взаимную корреляцию, как указано выше. Поэтому, если нужно выбрать конкретную базовую последовательность с индексом "q", "q" следует выбирать с учетом индекса группы (далее "u") и индекса номера базовой последовательности в каждой группе (далее “v”). Таким образом, "q" должен быть функцией "u" и "v".
После выбора конкретной базовой последовательности с индексом корня "q" к выбранной базовой последовательности можно применять циклический сдвиг, соответствующий различным значениям циклического сдвига.
Если рассматривать соотношение между "q", "u" и “v” более конкретно, "q" можно получить согласно следующим уравнениям. Следующие уравнения 17 и 18 позволяют выбрать индекс "q", отвечающий условию, что выражение (s1/N1-s2/N2) приближается к нулю.
[Уравнение 17]
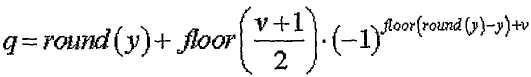
где 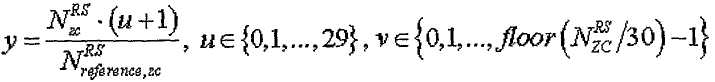
[Уравнение 18]
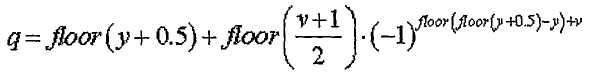
где 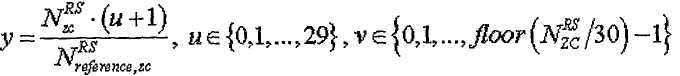
Здесь 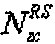 - длина генерации корневой последовательности ZC, используемой при генерации q-й корневой последовательности ZC, и
- длина генерации корневой последовательности ZC, используемой при генерации q-й корневой последовательности ZC, и 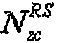 задается наибольшим простым числом, которое меньше размера соответствующей опорной сигнальной последовательности. Таким образом, базовая последовательность генерируется методом циклического расширения.
задается наибольшим простым числом, которое меньше размера соответствующей опорной сигнальной последовательности. Таким образом, базовая последовательность генерируется методом циклического расширения.
Кроме того, 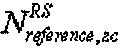 - это длина, заданная наибольшим простым числом, которое меньше размера опорной последовательности, например длины 3 RB. Если группирование основано на длине 3 RB, то
- это длина, заданная наибольшим простым числом, которое меньше размера опорной последовательности, например длины 3 RB. Если группирование основано на длине 3 RB, то 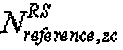 равно 31. "round(z)" является функцией округления до ближайшего целого числа, ближайшего к z, и "floor(z)" является функцией, возвращающей наибольшее целое число, не превышающее z.
равно 31. "round(z)" является функцией округления до ближайшего целого числа, ближайшего к z, и "floor(z)" является функцией, возвращающей наибольшее целое число, не превышающее z.
Согласно другому варианту осуществления этого изобретения, если последовательность ZC генерируется методом усечения, то 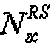 можно задать наименьшим простым числом, которое больше размера соответствующей опорной сигнальной последовательности. В этом случае
можно задать наименьшим простым числом, которое больше размера соответствующей опорной сигнальной последовательности. В этом случае 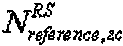 может представлять собой длину, заданную наименьшим простым числом, которое больше размера опорной последовательности, например длины 3 RB. Если группирование основано на длине 3 RB, то
может представлять собой длину, заданную наименьшим простым числом, которое больше размера опорной последовательности, например длины 3 RB. Если группирование основано на длине 3 RB, то 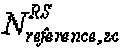 может быть равно 37.
может быть равно 37.
Согласно уравнениям 17 и 18 "m"-й элемент "q"-й последовательности ZC (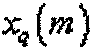 ) можно выразить следующим образом.
) можно выразить следующим образом.
[Уравнение 19]
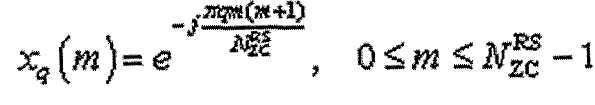
Поскольку "round(y)" и "floor(y+0.5)" фактически эквивалентны, уравнения 17 и 18 имеют один и тот же смысл. В уравнениях 17 и 18 выражение 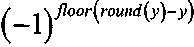 означает, что если "y" имеет значение 0.5 или более в своем десятичном разряде,
означает, что если "y" имеет значение 0.5 или более в своем десятичном разряде, 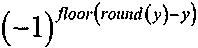
можно вычислить как "1", и если "y" имеет значение меньше 0.5 в своем десятичном разряде, 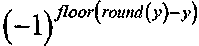 можно вычислить как "-1". Поэтому
можно вычислить как "-1". Поэтому 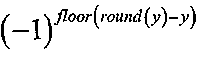
можно заменить 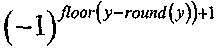 или любыми другими эквивалентными выражениями, имеющими один и тот же смысл.
или любыми другими эквивалентными выражениями, имеющими один и тот же смысл.
В вышеприведенных примерах, когда группирование осуществляется для длины свыше 3 RB на основании длины 3 RB и при генерации последовательности ZC на основании метода циклического расширения, 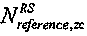 может быть равно 31. Кроме того, при генерации последовательности ZC методом усечения
может быть равно 31. Кроме того, при генерации последовательности ZC методом усечения 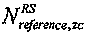 может быть равно 37. Когда группирование осуществляется для длины свыше 4 RB на основании длины 4 RB и при генерации последовательности ZC на основании метода циклического расширения,
может быть равно 37. Когда группирование осуществляется для длины свыше 4 RB на основании длины 4 RB и при генерации последовательности ZC на основании метода циклического расширения, 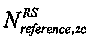 может быть равно 47. Кроме того, при генерации последовательности ZC методом усечения,
может быть равно 47. Кроме того, при генерации последовательности ZC методом усечения, 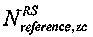 может быть равно 49. Это можно легко применить к группированию на основании другой длины.
может быть равно 49. Это можно легко применить к группированию на основании другой длины.
Вышеприведенные таблицы можно получить из уравнений 17 и 18. Нижеследующие примеры демонстрируют выбор индекса корня согласно уравнениям 17 и 18.
Сначала, если Nreference,zc=31, способ выбора первой группы ("u"=0), когда 1)Nzc=47, 2)Nzc=71, 3)Nzc=211, осуществляется следующим образом. В нижеследующих примерах используется уравнение 18.
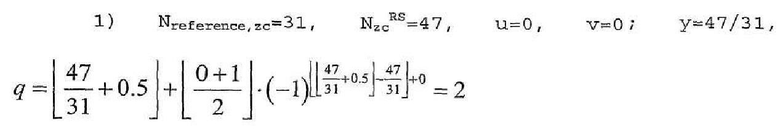
Поэтому для длины 4 RB количество первых базовых последовательностей (v=0) в первой группе (u=0) равно 2 (q=2).
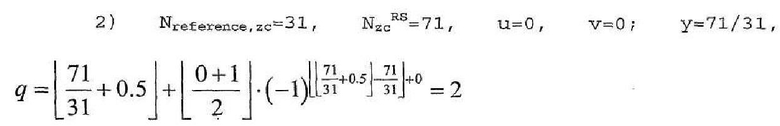
Поэтому для длины 6 RB количество первых базовых последовательностей (v=0) в первой группе (u=0) равно 2 (q=2).
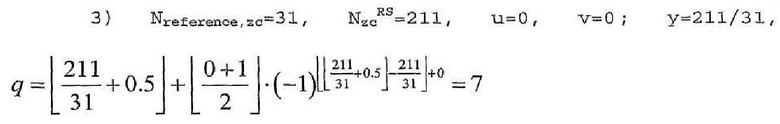
Поэтому для длины 18 RB количество первых базовых последовательностей (v=0) в первой группе (u=0) равно 7 (q=7).
Для вышеописанных случаев выбранные индексы (q) корня соответствуют данным в таблицах 6-8, которые генерируются на основании длины 3 RB.
В другом примере, если Nreference,zc=47 (на основании длины 4 RB), способ выбора второй группы (u=1), когда 1)Nzc=59, 2)Nzc=107, 3)Nzc=139 осуществляется следующим образом. В нижеследующих примерах используется уравнение 18.
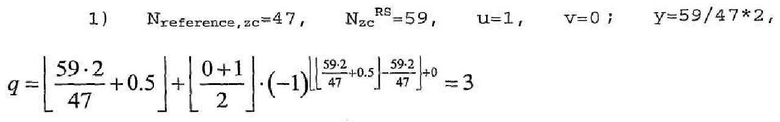
Поэтому для длины 5 RB количество первых базовых последовательностей (v=0) во второй группе (u=1) равно 3 (q=3).
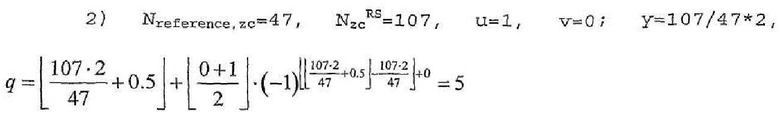
Поэтому для длины 9 RB количество первых базовых последовательностей (v=0) во второй группе (u=1) равно 5 (q=5).
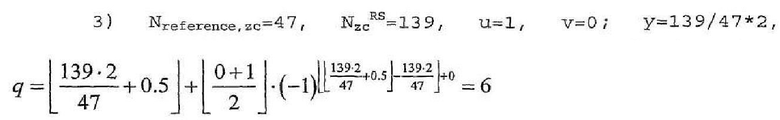
Поэтому для длины 12 RB количество первых базовых последовательностей (v=0) во второй группе (u=1) равно 6 (q=6).
В еще одном варианте осуществления настоящего изобретения уравнения 17 и 18 можно заменить следующим образом.
[Уравнение 20]
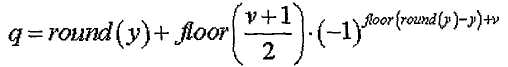
где 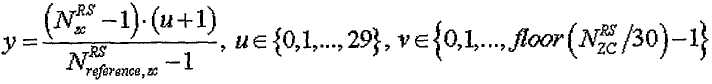
[Уравнение 21]
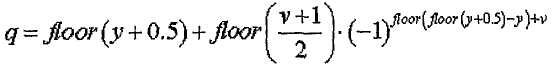
где 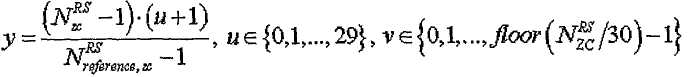
Поскольку «round(y)» и «floor(y+0.5)» фактически эквивалентны, уравнения 20 и 21 имеют один и тот же смысл.
В еще одном варианте осуществления настоящего изобретения уравнения 17 и 18 можно заменить следующим образом.
[Уравнение 22]
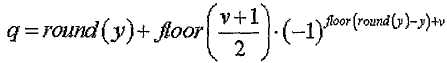
где 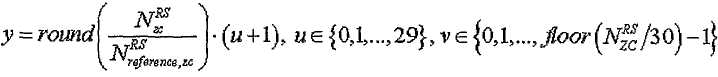
[Уравнение 23]
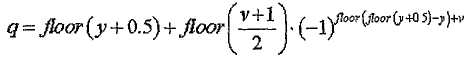
где 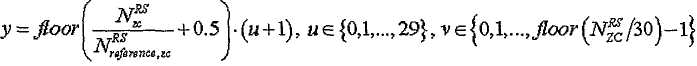
Эти уравнения соответствуют различным методам группирования, объясненным в связи с вышеприведенными таблицами.
Если максимальное количество последовательностей, которые можно сгруппировать в одну группу, заранее определено равным 2, уравнения 17-18, 20-21 и 22-23 можно упростить следующим образом соответственно.
[Уравнение 24]
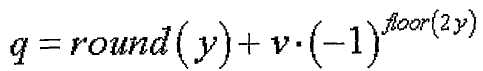
где 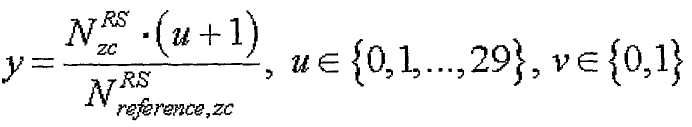
[Уравнение 25]
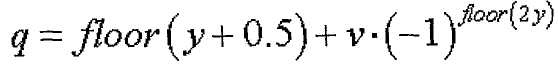
где 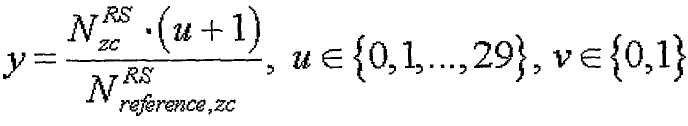
[Уравнение 26]
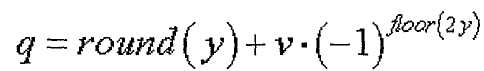
где 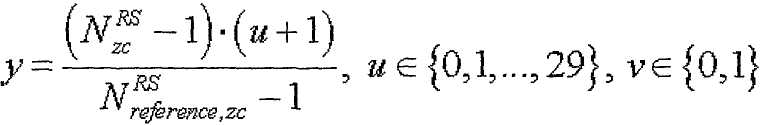
[Уравнение 27]
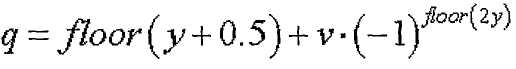
где 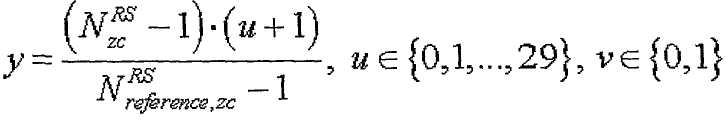
[Уравнение 28]
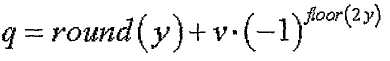
где 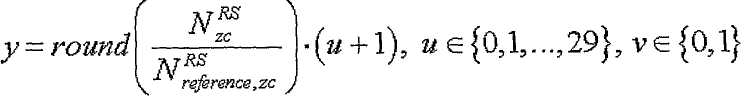
[Уравнение 29]
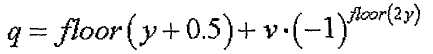
где 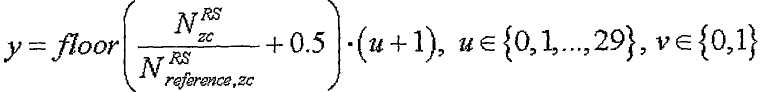
Уравнения 17-18, 20-21 и 22-23 позволяют выбирать индекс корня ZC, отвечающий условию, что выражение (s1/N1-s2/N2) приближается к нулю. Уравнения 24-29 позволяют выбирать индекс корня ZC, когда максимальное количество последовательностей каждой длины на группу ограничено 2.
Однако, если обобщить эти уравнения так, чтобы выражение (s1/N1-s2/N2) приближалось к конкретному значению (T), можно получить следующие уравнения. В этом случае значение "T" может быть равно 0, 1/2, -1/2, 1/3, -1/3. Однако значение "T" может иметь другое значение.
В следующих уравнениях уравнения 30 и 31 позволяют выбирать индекс корня ZC, когда максимальное количество последовательностей каждой длины на группу может иметь максимальное значение. Уравнения 32 и 33 позволяют выбирать индекс корня ZC, когда максимальное количество последовательностей каждой длины на группу ограничено 2.
[Уравнение 30]
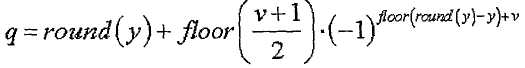
где 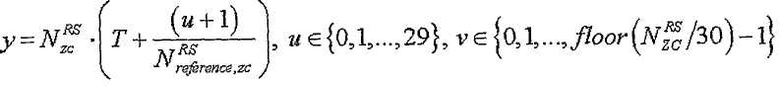
[Уравнение 31]
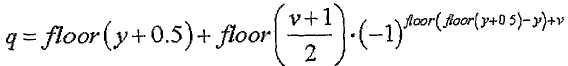
где 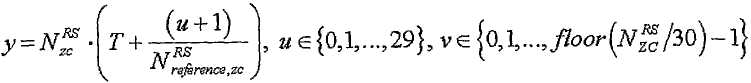
[Уравнение 32]
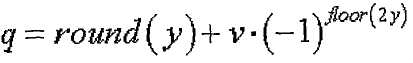
где 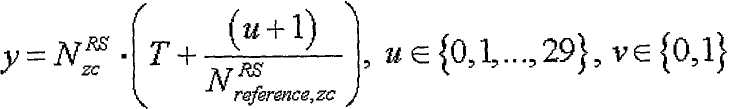
[Уравнение 33]
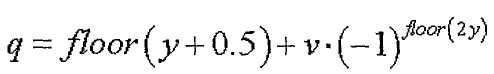
где 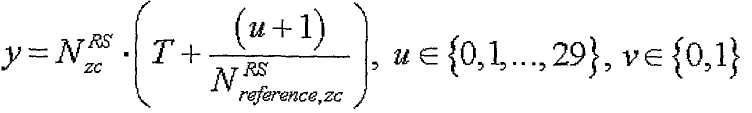
Специалистам в данной области техники очевидно, что настоящее изобретение можно реализовать в других конкретных формах, не выходя за рамки сущности и отличительных признаков изобретения. Таким образом, вышеописанные варианты осуществления следует рассматривать во всех отношениях как иллюстративные, но не ограничительные. Объем изобретения должен определяться разумной интерпретацией формулы изобретения, и все изменения, укладывающиеся в эквивалентный объем изобретения, должны быть включены в объем изобретения.
Промышленное применение
Согласно вариантам осуществления настоящего изобретения можно минимизировать межсотовую помеху, обусловленную использованием последовательностей переменной длины. Если каждая сгруппированная базовая последовательность выделяется конкретной соте или Node B, UE может использовать последовательность переменной длины в качестве опорного сигнала.
Эти способы пригодны для использования в системе 3GPP LTE (3rd Generation Partnership Project Long Term Evolution). Однако специалисту в данной области техники очевидно, что эти способы можно применять к любой системе беспроводной связи, использующей последовательности разной длины в качестве опорных сигнальных последовательностей.
Изобретение относится к области передачи сигналов с использованием генерации опорной сигнальной последовательности и с использованием группирования последовательностей. Достигаемый технический результат - минимизация помехи, обусловленной сигналами, имеющими другую длину, поступающими из соседних сот. Согласно этому способу получают одну или несколько базовых последовательностей, имеющих переменную длину, применяют циклический сдвиг, соответствующий переменному значению циклического сдвига, к одной или нескольким базовым последовательностям для генерации опорной сигнальной последовательности, передают опорную сигнальную последовательность на принимающую сторону. 2 н. и 14 з.п. ф-лы, 5 ил., 32 табл.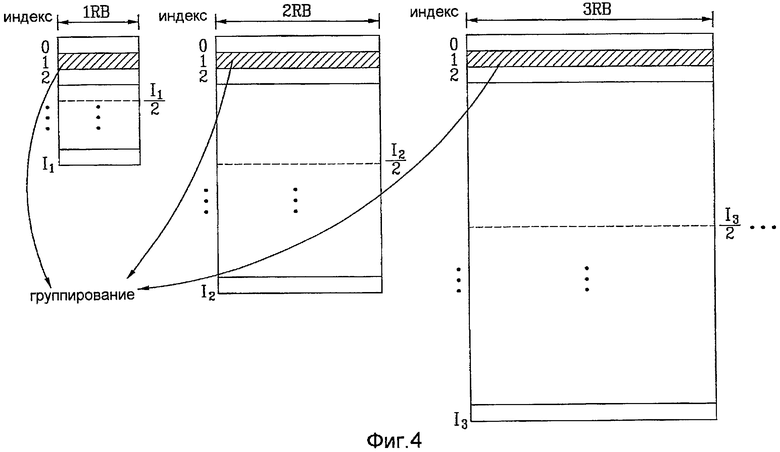
1. Способ передачи опорной сигнальной последовательности на передающей стороне, способ содержит этапы, на которых получают одну или несколько базовых последовательностей, имеющих переменную длину, соответствующую одному или нескольким размерам блока ресурсов, применяют циклический сдвиг, соответствующий переменному значению циклического сдвига, к одной или нескольким базовым последовательностям для генерации опорной сигнальной последовательности, и передают опорную сигнальную последовательность на принимающую сторону, причем базовые последовательности получаются из совокупности базовых последовательностей, разделенной на группы последовательностей, и каждая группа последовательностей содержит, по меньшей мере, одну базовую последовательность каждой длины.
2. Способ по п.1, в котором размер блока ресурсов соответствует размеру 12 поднесущих в частотной области.
3. Способ по п.1, в котором одну или несколько базовых последовательностей получают посредством циклического расширения последовательности ZC, имеющей длину 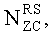 заданную наибольшим простым числом, которое меньше соответствующей длины опорной сигнальной последовательности.
заданную наибольшим простым числом, которое меньше соответствующей длины опорной сигнальной последовательности.
4. Способ по п.1, в котором одна или несколько базовых последовательностей получаются путем усечения последовательности ZC, имеющей длину 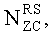 заданную наименьшим простым числом, которое больше соответствующей длины опорной сигнальной последовательности.
заданную наименьшим простым числом, которое больше соответствующей длины опорной сигнальной последовательности.
5. Способ по п.1, в котором количество групп последовательностей равно 30.
6. Способ по п.5, в котором каждая из групп последовательностей содержит одну базовую последовательность каждой длины, соответствующей от 1 до 5 размерам блока ресурсов, и две базовые последовательности каждой длины, соответствующей 6 или более размерам блока ресурсов.
7. Способ по п.6, в котором базовую последовательность, имеющую длину, соответствующую 3 или более размерам блока ресурсов, получают с использованием последовательности Задова-Чу (ZC) с конкретным индексом q последовательности ZC, и в котором базовую последовательность, имеющую длину, соответствующую 1 или 2 размерам блока ресурсов, получают с использованием другой последовательности, отличной от последовательности ZC.
8. Способ по п.7, в котором заданный индекс q последовательности ZC является функцией индекса u группы и индекса v номера базовой последовательности в группе.
9. Способ передачи опорной сигнальной последовательности с использованием последовательности Задова-Чу (Zadoff-Chu(ZC)) на передающей стороне, способ содержит этапы, на которых получают базовую последовательность с использованием q-й корневой последовательности ZC из совокупности базовых последовательностей, причем совокупность базовых последовательностей делится на группы, и q является функцией индекса u группы последовательностей и индекса v номера базовой последовательности в группе последовательностей;
применяют циклический сдвиг, соответствующий переменному значению циклического сдвига, к полученной базовой последовательности для генерации опорной сигнальной последовательности и передают опорную сигнальную последовательность на принимающую сторону.
10. Способ по п.9, в котором число u равно 30 и число v задают на основании длины базовой последовательности.
11. Способ по п.9, в котором заданный индекс q последовательности ZC определяется согласно
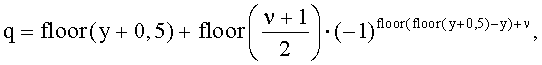
где
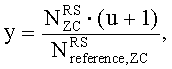 u∈{0,1,…,29},
u∈{0,1,…,29}, 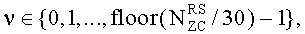
где 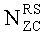 - длина генерации корневой последовательности ZC, используемой при генерации q-й корневой последовательности ZC,
- длина генерации корневой последовательности ZC, используемой при генерации q-й корневой последовательности ZC, 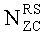 задается наибольшим простым числом, которое меньше длины полученной базовой последовательности,
задается наибольшим простым числом, которое меньше длины полученной базовой последовательности, 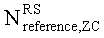 - заданное опорное простое число, и floor(z) является функцией, возвращающей наибольшее целое число, не превышающее z.
- заданное опорное простое число, и floor(z) является функцией, возвращающей наибольшее целое число, не превышающее z.
12. Способ по п.9, в котором конкретный индекс q последовательности ZC определяется согласно
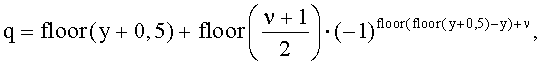
где
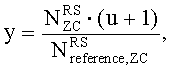 u∈{0,1,…,29},
u∈{0,1,…,29}, 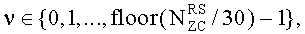
где 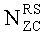 - длина генерации корневой последовательности ZC, используемой при генерации q-й корневой последовательности ZC,
- длина генерации корневой последовательности ZC, используемой при генерации q-й корневой последовательности ZC, 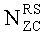 задается наименьшим простым числом, которое больше длины полученной базовой последовательности,
задается наименьшим простым числом, которое больше длины полученной базовой последовательности, 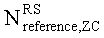 - заданное опорное простое число, и floor(z) является функцией, возвращающей наибольшее целое число, не превышающее z.
- заданное опорное простое число, и floor(z) является функцией, возвращающей наибольшее целое число, не превышающее z.
13. Способ по п.9, в котором максимальное количество базовых последовательностей в каждой группе последовательностей равно 2 и в котором индекс q последовательности ZC определяется согласно
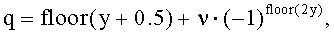
где
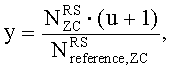 u∈{0,1,…,29}, ν∈{0,1},
u∈{0,1,…,29}, ν∈{0,1},
где 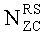 - длина генерации корневой последовательности ZC, используемой при генерации q-й корневой последовательности ZC,
- длина генерации корневой последовательности ZC, используемой при генерации q-й корневой последовательности ZC, 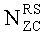 задается наибольшим простым числом, которое меньше длины полученной базовой последовательности,
задается наибольшим простым числом, которое меньше длины полученной базовой последовательности, 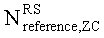 - заданное опорное простое число, и floor(z) является функцией, возвращающей наибольшее целое число, не превышающее z.
- заданное опорное простое число, и floor(z) является функцией, возвращающей наибольшее целое число, не превышающее z.
14. Способ по п.9, в котором максимальное количество базовых последовательностей в каждой группе последовательностей равно 2 и
в котором заданный индекс q последовательности ZC определяется согласно
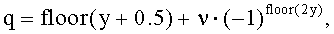
где
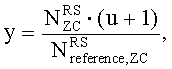 u∈{0,1,…,29}, ν∈{0,1}
u∈{0,1,…,29}, ν∈{0,1}
где 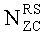 - длина генерации корневой последовательности ZC, используемой при генерации q-й корневой последовательности ZC,
- длина генерации корневой последовательности ZC, используемой при генерации q-й корневой последовательности ZC, 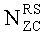 задается наименьшим простым числом, которое больше длины полученной базовой последовательности,
задается наименьшим простым числом, которое больше длины полученной базовой последовательности, 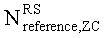 - заданное опорное простое число, и floor(z) является функцией, возвращающей наибольшее целое число, не превышающее z.
- заданное опорное простое число, и floor(z) является функцией, возвращающей наибольшее целое число, не превышающее z.
15. Способ по п.11 или 13, в котором заданное опорное простое число равно 31.
16. Способ по п.12 или 14, в котором заданное опорное простое число равно 37.
| Способ обработки целлюлозных материалов, с целью тонкого измельчения или переведения в коллоидальный раствор | 1923 |
|
SU2005A1 |
| СПОСОБ И УСТРОЙСТВО УПРАВЛЕНИЯ ПЕРЕДАЧЕЙ ПАКЕТОВ ДАННЫХ В КАНАЛЕ СВЯЗИ ОБЩЕГО ПОЛЬЗОВАНИЯ | 1998 |
|
RU2137312C1 |
| СПОСОБ ПЕРЕДАЧИ ДАННЫХ С КОММУТАЦИЕЙ ПАКЕТОВ | 1998 |
|
RU2195789C2 |
| US 5430774 A, 04.07.1995 | |||
| US 6115354 A, 05.09.2000. | |||
Авторы
Даты
2011-05-20—Публикация
2008-02-01—Подача