За последнее десятилетие растущая потребность в электронных официальных и финансовых операциях, использование приложений цифровых подписей и требования к секретности информации обусловили большее внимание к генераторам случайных чисел (ГСЧ). В этом отношении ГСЧ, которые в прошлом обычно использовались для криптографии в военных целях, в настоящее время играют важную роль в разработке оборудования обычной цифровой связи.
Почти все криптографические системы требуют непредсказуемых значений; поэтому одним из основных компонентов криптографических механизмов является ГСЧ. Генерация пар открытых/секретных ключей для асимметричных алгоритмов и ключей для симметричных и гибридных криптографических систем требует случайных чисел. Одноразовый блокнот, вызовы, нонцесы, байты, заполняющие блок, и маскирующие значения созданы с использованием генераторов истинно случайных чисел (ГИСЧ) [1]. Генераторы псевдослучайных чисел (ГПСЧ) генерируют биты детерминированным образом. Для того чтобы оказаться генерированными ГИСЧ, псевдослучайные последовательности должны засеваться из более короткой, истинно случайной последовательности [2]. Кроме того, ГСЧ используются во многих областях, включая метод Монте-Карло, компьютерное моделирование, статистическая выборка, методы стохастической оптимизации, нанесение «водяных знаков» для аутентификации изображений, порядок аутентификации между двумя узлами криптографического оборудования и хеширование начальных значений криптографического модуля, который реализует алгоритм.
Даже если конструкция ГСЧ известна, какое-либо эффективное предсказание относительно выхода сделать невозможно. Для того чтобы отвечать требованиям секретности одноразового блокнота, генерации ключей и любых иных криптографических приложений, ГИСЧ должен иметь следующие свойства: выходной поток битов ГИСЧ должен отвечать всем статистическим критериям случайности; следующий случайный бит должен быть непредсказуемым [3]; должна быть исключена возможность воспроизведения одного и того же выходного потока битов [4]. Наилучшим способом генерации действительно случайных чисел является использование естественной случайности реального мира путем отыскания случайного события, которое случается регулярно [4]. Примеры такого события, которое можно использовать, включают время, прошедшее в течение периода радиоактивного распада, тепловой и дробовой шум, джиттер («дрожание») генератора и количество заряда полупроводникового конденсатора [2].
В научно-технической литературе описываются несколько конструкций ГСЧ; однако для генерации случайных чисел упоминаются, в основном, четыре разных способа: усиление источника шума [5, 6], дискретизация с использованием двух генераторов с джиттером [1, 7-9], хаотические отображения с дискретным временем [10-14] и хаотические генераторы с непрерывным временем [15, 18]. Несмотря на тот факт, что использование хаотических отображений с дискретным временем при реализации ГСЧ некоторое время уже хорошо известно, лишь совсем недавно было показано, что для реализации ГИСЧ можно использовать и хаотические генераторы с непрерывным временем. Следуя в этом направлении, мы исследовали эффективность предлагаемых новшеств при генерации случайных двоичных данных из хаотических генераторов с непрерывным временем.
Скорости передачи в битах ГСЧ, которые обычно можно найти в литературе и серийно выпускаемых изделиях, стали недостаточными из-за возросших скоростей передачи данных оборудованием цифровой связи. По сравнению с ГСЧ, основанными на хаотических отображениях с дискретным временем, усилении источника шума и дискретизации с использованием двух генераторов с джиттером, оказывается, что ГСЧ, основанные на хаотических генераторах с непрерывным временем, могут обеспечивать намного более высокие и постоянные скорости передачи данных без последующей обработки с менее сложными интегральными схемами. В заключение, можно сделать вывод, что хаотические генераторы с непрерывным временем можно интегрировать в сегодняшний процесс в ГГц-диапазоне, и что использование хаоса с непрерывным временем с предложенными новшествами является очень перспективным для генерации случайных чисел с очень высокой производительностью.
Для обеспечения совместимости с другими элементами системы предпочтительно использовать хаотические генераторы, которые можно интегрировать на силиконе. Предпринят ряд попыток внедрить хаотические генераторы с дискретным, а также непрерывным временем на базе КМОП-технологии. В большинстве этих попыток полученные в результате схемы были сложными и занимали большую площадь силикона. В хаотических генераторах с дискретным временем обычно используются методы переключения конденсаторов или тока. Использование умножителя в дополнение ко многим конденсаторам и операционным усилителям приводит к большой схеме. По сравнению с ГСЧ, основанных на источниках хаоса с дискретным временем, оказывается, что ГСЧ, основанные на источниках хаоса с непрерывным временем, могут обеспечивать намного более высокие скорости передачи данных с менее сложными и менее шумными интегральными схемами, особенно из-за отсутствия последующих стадий выборки и запоминания.
В способе усиления источника шума, показанном на фиг.1, используется широкополосный усилитель с высоким коэффициентом усиления для обработки белого шума, имеющего малое напряжение переменного тока. Этот шум необходимо усилить до уровня, на котором для него можно точно установить порог без смещения тактируемым компаратором. Это наиболее распространенный способ генерации случайных чисел для однокристальных решений и решений на уровне плат.
В низковольтных КМОП ИС широкополосный белый шум создают два разных механизма шума: дробовой шум (генерируемый потоком тока через p-n-переход) и тепловой шум (генерируемый случайным движением электронов в резисторе). Шум лавинного умножения - это не практичный выбор для источника шума из-за обычного высокого пробивного напряжения (>6 В постоянного тока) стабилитронов, изготовленных по КМОП-технологии на монолитных подложках. Как показано на фиг.1, интегральная топология источника шума использует в качестве генератора теплового шума большой резистор. Резисторы легко изготавливаются из поликремния или диффузионных слоев и не требуют тока смещения для генерации шума, как в случае полупроводниковых переходов. Кроме того, поликремниевый резистор имеет низкий индекс фликер-шума (обычно -30 дБ), обеспечивая низкие уровни шума 1/f.
Если принять шум 1/f пренебрежимо малым, напряжение теплового шума резистора-источника RSrc будет 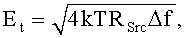 где k - постоянная Больцмана, Т - абсолютная температура, RSrc - сопротивление и Δf - ширина полосы шумов. Ширина полосы шумов для Et обычно ограничивается фильтром нижних частот первого порядка, образованным RSrc и эквивалентной входной емкостью усилителя CAmp. При условии, что ширина полосы частот -3 дБ усилителя больше ширины полосы шумов, общее эквивалентное напряжение шума Eni из-за Et на входе усилителя будет
где k - постоянная Больцмана, Т - абсолютная температура, RSrc - сопротивление и Δf - ширина полосы шумов. Ширина полосы шумов для Et обычно ограничивается фильтром нижних частот первого порядка, образованным RSrc и эквивалентной входной емкостью усилителя CAmp. При условии, что ширина полосы частот -3 дБ усилителя больше ширины полосы шумов, общее эквивалентное напряжение шума Eni из-за Et на входе усилителя будет 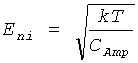 , где есть теоретический предел для теплового шума, генерируемого резистором, шунтированным конденсатором. Амплитуду напряжения теплового шума в полосе частот шириной 1 Гц можно повысить путем увеличения значения RSrc, но за счет уменьшения ширины полосы теплового шума, так что при данной CAmp Eni будет оставаться постоянным.
, где есть теоретический предел для теплового шума, генерируемого резистором, шунтированным конденсатором. Амплитуду напряжения теплового шума в полосе частот шириной 1 Гц можно повысить путем увеличения значения RSrc, но за счет уменьшения ширины полосы теплового шума, так что при данной CAmp Eni будет оставаться постоянным.
В способе дискретизации с использованием двух генераторов с джиттером используется случайный источник, полученный из двух генераторов в режиме свободной генерации - одного быстрого и другого более медленного. Опубликованные конструкции ГСЧ с использованием этого способа свидетельствуют о том, что типичные уровни джиттера генератора не являются почти достаточными для получения статистической случайности. Поэтому источник шума используется для модуляции частоты более медленного генератора, а быстрый генератор дискретизируется нарастающим фронтом модулированного шумом более медленного генератора. Дрейф между двумя генераторами служит источником случайных двоичных знаков. Подобно способу усиления источника шума, шум необходимо усилить до уровня, на котором его можно использовать для модуляции частоты более медленного генератора. Частота более медленного генератора, которая определяет скорость передачи данных, ограничивается, в основном, шириной полосы частот шумового сигнала, используемого для модуляции, причем основной причиной этого ограничения является ширина полосы частот усилителя.
В предлагаемом новшестве сигнал хаотического генератора величиной порядка нескольких вольт с номинальной средней (центральной) частотой в ГГц-диапазоне был преобразован в двоичные последовательности непосредственно компаратором без использования усилителя, причем теоретический предел для скорости передачи данных определяется номинальной средней (центральной) частотой хаотического генератора, что дает в результате скорость порядка нескольких Гбит/с. Такие высокие скорости передачи данных могут обеспечить привлекательность ГСЧ с непрерывным временем по сравнению с ГСЧ, основанными на других способах. В качестве ядра предлагаемой конструкции ГСЧ может использоваться как автономный, так и неавтономный хаотический генератор, причем случайные данные можно получать из одномерного сечения или путем периодической дискретизации (выборки) одного из состояния хаотической системы.
При сравнении предлагаемого новшества с прежней конструкцией ГСЧ, основанной на хаотическом генераторе с непрерывным временем, приведенном в работе [15], предлагаемое новшество, как показала численная проверка, обеспечивает скорости в 7 раз выше. Кроме того, примерная последовательность битов, приведенная на сайте http://www.esat.kuleuven.ac.be/~mey/Ds2RbG/Ds2RbG.html, не выдерживает тесты на блочную частоту, последовательностей и приближенной энтропии полного тестового набора Национального института стандартов и технологий (США). Кроме того, контур компенсации сдвига, который был использован в предлагаемом новшестве для максимального повышения статистического качества выходной последовательности и обеспечения робастности к колебаниям параметров и атакам, неосуществим для предыдущей конструкции, приведенной в работе [15], по той причине, что полученная последовательность битов может пройти полный набор тестов Diehard (набор статистических тестов для измерения качества набора случайных чисел, разработаны Джорджем Марсальей (George Marsaglia)) благодаря фон-неймановской обработке.
Вначале мы выполнили числовую проверку, что потоки битов, генерированные предложенным новшеством, проходят четыре основных теста случайных чисел из тестового набора FIPS-140-2 [16]. Внешняя помеха - это одна из основных проблем при разработке ГСЧ, поскольку сигналы помехи и случайные сигналы имеют сравнимые уровни. Для того чтобы решить эту проблему и обеспечить робастность к колебаниям параметров и атакам, направленным на взлом, мы предложили контуры компенсации сдвига и частотной коррекции, которые повышают статистическое качество генерируемых последовательностей битов. Кроме того, мы экспериментально проверили, что двоичные данные, полученные из предлагаемых новшеств, проходят тесты полного набора тестов Национального института стандартов и технологий (США) для измерения качества набора случайных чисел [17].
Из-за своей крайней чувствительности к начальным условиям и имея положительную экспоненту Ляпунова и шумоподобный энергетический спектр, хаотические системы допускают их использование для генерации случайных чисел. Для того чтобы получить случайные двоичные данные из хаотической системы с непрерывным временем, мы предложили интересный способ, основанный на генерации необратимых двоичных данных из сигнала данного хаотического генератора. Следует отметить, что основной характеристикой для генерации псевдослучайных чисел является необратимость [19]. В предложенном новшестве для получения случайных битов из автономного или неавтономного хаотического генератора мы использовали следующее:
1. Выборки состояния x1 из одномерного сечения, полученные при переходе из другого состояния (х2, x3, … или xn), определенного как x2..n(t)=x2..n(0) c dx2..n/dt>0 или dx2..n/dt<0.
2. Периодические выборки состояния x1, х2, … или xn, полученные на нарастающих фронтах внешнего периодического импульсного сигнала, то есть в моменты времени t, удовлетворяющие условию ωtmod2π=0, где ω - частота импульсного сигнала.
В случае использования неавтономного хаотического генератора в качестве ядра предлагаемой конструкции ГСЧ:
3. Для получения случайных битов использовалось также одномерное сечение состояния x1, полученное на нарастающих фронтах внешнего периодического импульсного сигнала (в моменты времени t, удовлетворяющие условию ωtmod2π=t0, где ω - частота импульсного сигнала и 0<t0<1), используемого для возбуждения неавтономного хаотического генератора.
В определенных выше сечениях х1, x2, … или xn - это нормализованные величины хаотического генератора, используемого в качестве ядра предлагаемого ГСЧ. Следует отметить, что хотя n-мерные траектории в плоскости х1-х2-…-xn являются обратимыми, можно получить и необратимое сечение, учитывая значения, соответствующие лишь одному из состояний, скажем, х1.
Вначале мы численно сгенерировали х1 и исследовали распределение выбранных значений для определения соответствующих сечений, где распределение выглядит как случайный сигнал. Хотя мы не смогли найти сечений, значения х1 которых имеет единственное нормальное или X2 распределение [2] для отличного набора параметров, мы определили различные сечения, где распределение x1 имеет по меньшей мере две области. Для соответствующего набора параметров распределение состояния x1 в определенных выше сечениях выглядит, как показано на фиг.2.
Распределение х1, имеющее две области, навело нас на мысль генерировать случайные двоичные данные из областных значений x1 для областных порогов. Следуя в этом направлении, мы сгенерировали двоичные данные S(top)i и S(bottom)i из одномерных сечений по формуле (1):
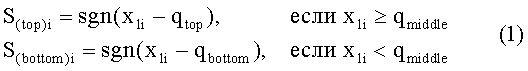
где sgn(.) - знаковая функция, x1i - значения x1, полученные из одного из определенных выше сечений, qtop и qbottom - пороги для верхнего и нижнего распределений соответственно и qmiddle - граница между распределениями. Для того чтобы смочь выбрать пороги подходящим образом, мы исследовали верхнее и нижнее распределения, как показано на фиг.2, а затем qtop и qbottom были определены как медианы верхнего и нижнего распределений соответственно.
Генерация двоичной последовательности, получаемой таким образом, не настолько зависит от значения qmiddle, поскольку для этого граничного значения плотность распределения х минимальна. Однако для пороговых значений (qtop, qbottom) плотность распределения х максимальна, так что полученная двоичная последовательность может быть смещенной. Для того чтобы удалить неизвестное смещение в этой последовательности, можно использовать хорошо известный метод выравнивания фон Неймана [20]. Этот метод заключается в преобразовании пары битов 01 в выход 0, 10 - в выход 1, и в исключении пар битов 00 и 11. Однако этот метод снижает производительность, поскольку генерирует приблизительно 1 бит из 4 битов.
Для того чтобы устранить это смещение, чтобы не снизить производительность, вместо фон-неймановской обработки был использован другой метод - операция ⊗ (исключающее ИЛИ). Потенциальной проблемой, связанной с методом исключающее ИЛИ, является то, что малое количество корреляции между входными битами придадут выходу значительное смещение [4]. Коэффициенты корреляции генерированных двоичных последовательностей Stop и Sbottom, полученных из определенных выше сечений, рассчитаны очень близкими 0, и установлено, что генерированные двоичные последовательности являются независимыми. Это, собственно, и ожидалось, поскольку хаотические системы характеризуются тем, что имеют положительную экспоненту Ляпунова [21], и автокорреляция хаотического временного ряда резко исчезает. В соответствии с этим результатом, мы сгенерировали новые двоичные данные S(xor)i, используя приведенную формулу (2):
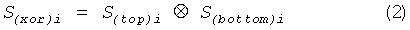
Среднее значение ψ двоичной последовательности Sxor, полученной таким образом, можно рассчитать по приведенной формуле (3):
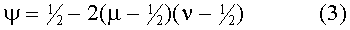
где среднее значение Stop=µ, а среднее значение Sbottom=ν. Таким образом, если µ и ν близки ½, то ψ очень близко ½. Как результат, мы численно проверили, что последовательность битов Sxor, которая была получена из различных сечений, определенных выше для соответствующих пороговых значений, по методике, приведенной в формуле (2), прошла тесты из тестового набора Федерального стандарта по обработке информации (США) FIPS-140-2 без фон-неймановской обработки. Мы назвали генерацию случайных чисел по вышеупомянутой методике «областной ГСЧ».
Из-за отсутствия доступа к подходящему производственному оборудованию мы решили изготовить предложенные новшества, используя дискретные компоненты, чтобы продемонстрировать осуществимость этих схем. Кроме того, мы экспериментально сгенерировали потоки битов.
При областной ГСЧ для того, чтобы получить необратимое сечение, была использована только одна переменная х1, и напряжение ν1, соответствующее переменной х1, было преобразовано в двоичные последовательности. Для того чтобы получить случайные биты из автономного или неавтономного хаотического генератора путем использования периодических выборок х1, была использована схема, показанная на фиг.3. Выходной поток битов компараторов дискретировался и запоминался в двоичном формате на нарастающем фронте внешнего периодического генератора прямоугольных импульсов νp(t) для получения значений ν1 в сечении, определенном как ωtmod2π=0.
Для того чтобы реализовать методику, в которой использовались выборки х1 из одномерного сечения автономного или неавтономного хаотического генератора, полученного при переходе из другого состояния (х2, x3, … или xn), определенного как x2..n(t)=x2..n(0) с dx2..n/dt>0 или dx2..n/dt<0, выходной поток битов компараторов ν1 дискретировался и запоминался в двоичном формате на нарастающем или заднем фронтах компаратора другого состояния ν2…n с использованием схемы, приведенной на фиг.4.
В предлагаемом новшестве для генерации случайных битов можно использовать и одномерное сечение х1 из неавтономного хаотического генератора, полученное в моменты времени t, удовлетворяющие условию ωtmod2π=t0. Для того чтобы получить значения х1 в определенном сечении, выходной поток битов компараторов дискретировался и запоминался в двоичном формате после логического элемента задержки в откорректированный момент времени внутри периода последовательности внешних периодических импульсов νp(t), которая использовалась и для возбуждения неавтономного хаотического генератора. Схема реализации представлена на фиг.5.
В приведенных выше схемах областной генерации случайных чисел компараторы были реализованы на чипах LM211, а для реализации порогов в формуле (1) были использованы уровни напряжения Vtop, Vmiddle и Vbottom соответственно. Vtop и Vbottom были генерированы двумя 12-битовыми цифроаналоговыми преобразователями (ЦАП) напряжения. Каждый ЦАП можно настраивать с шагами 0,5859375 мВ, а опорное напряжение ЦАП равно 2,4 В. При реализации формула (1) и формула (2) преобразуются в следующее:
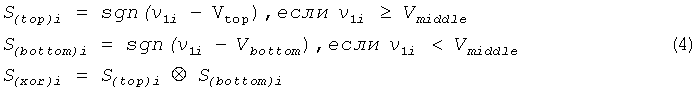
Для загрузки двоичных данных в компьютер были разработаны аппаратные средства на основе матрицы логических элементов с эксплуатационным программированием, имеющие интерфейс периферийных устройств. В матрице логических элементов с эксплуатационным программированием были реализованы компенсация сдвига для порогов Vtop и Vbottom, частотная коррекция; логический элемент задержки и операция «исключающее ИЛИ». После компенсации сдвига и частотной коррекции и операции «исключающее ИЛИ», случайные числа - кандидаты загружались в компьютер через интерфейс периферийных устройств. Максимальная скорость хранения данных наших аппаратных средств на основе матрицы логических элементов с эксплуатационным программированием равна 62 Мбит/сек.
Мы экспериментально определили, что для соответствующего набора параметров и при отрегулированных задержках дискретизации есть различные сечения, где распределение ν1 имеет две области, которое выглядит подобно тому, как показано на фиг.2.
Для того чтобы смочь определить начальные значения порогов подходящим образом, подобно генерации численных битов, были исследованы верхнее и нижнее распределения. Затем были определены начальные значения Vtop и Vbottom как медианы верхнего и нижнего распределений соответственно. Частота дискретизации для ν1 была определена путем деления частоты νp(t) или выхода компаратора ν2…n на значение предварительного делителя частоты в матрице логических элементов с эксплуатационным программированием. Для определения начального значения предварительного делителя частоты подходящим образом, наблюдался частотный спектр ν1, который выглядит, как показано на фиг.6. Как показано на этой фигуре, хаотический сигнал ν1 имеет шумоподобный энергетический спектр. Средняя (центральная) частота хаотического генератора показана сплошным маркером. До пунктирного маркера, в области, в которой энергетический спектр является плоским, хаотический сигнал ν1 содержит все частоты в равных количествах, и спектральная плотность мощности находится в своем максимуме. Следовательно, без потери общности, ν1(t) и ν1(t+t0) можно рассматривать как некоррелированные для всех t0, не равных 0, и ν1 можно дискретизировать до частоты дискретизации fsampling, показанной пунктирным маркером как источник случайных сигналов. Наконец, начальное значение предварительного делителя частоты было определено путем деления частоты νp(t) или выхода компаратора ν2…n на fsampling.
Компенсации сдвига для порогов Vtop и Vbottom были осуществлены путем реализации однобитового теста из тестового набора Федерального стандарта по обработке информации (США) FIPS-140-2 [16] для двоичных последовательностей Stop и Sbottom. Для каждой последовательности были получены потоки битов длиной 20000 битов; если число нулей >10275, то соответствующий порог снижался, а если число нулей <9725, то соответствующий порог повышался. Контур частотных коррекций был осуществлен путем реализации теста последовательностей из тестового набора Федерального стандарта по обработке информации (США) FIPS-140-2 для двоичной последовательности Sxor. Если 3 потока битов Sxor длиной 20000 битов, которые были получены последовательно, не проходили тест последовательностей, что указывало на дискретизацию ν1 с запасом по частоте, то частота дискретизации ν1 снижалась путем повышения значения предварительного делителя частоты. При необходимости в этом, частота дискретизации могла повышаться извне через интерфейс периферийных устройств.
После того как значения предварительного делителя частоты и порогов стали стабильными, из определенных выше сечений с использованием схем, приведенных на фиг.3, фиг.4 и фиг.5, был получен поток битов длиной не менее 500 Мбит, который был подвергнут полному тестовому набору Национального института стандартов и технологий (США). Как результат, мы экспериментально проверили, что последовательность битов Sxor прошла тесты из тестового набора для измерения качества набора случайных чисел без фон-неймановской обработки. Значения Р были однородными, и доля проходящих последовательностей была большей минимальной степени прохождения для каждого статистического теста.
Скорость передачи данных Sxor эффективно становится равной (fsampling/2) из-за деления ν1 на две области согласно распределению. Скорость передачи данных Sxor можно рассчитать как fxor≈0,05/τ, где τ - постоянная времени для хаотического генератора. Мы можем заключить, что хаотические генераторы могут легко интегрироваться в сегодняшний процесс с номинальной средней (центральной) частотой в ГГц-диапазоне. Следует, однако, отметить, что в научно-технической литературе сообщается о хаотических схемах, действующих на значительно более высоких частотах. Например, в работе [18] представлены результаты тактового моделирования варианта хаотического генератора, выполненного на биполярном плоскостном транзисторе, работающего на частоте 5,3 ГГц. Итак, все это указывает на то, что использование хаоса с непрерывным временем является очень перспективным в генерации случайных чисел с очень высокой производительностью. Как результат, предлагаемый способ является также усиленной архитектурой, в которую добавлены контуры компенсации сдвига и частотной коррекции для максимального повышения статистического качества выходной последовательности и обеспечения робастности к внешней помехе, колебаниям параметров и атакам, направленным на взлом.
ПРОМЫШЛЕННАЯ ПРИМЕНИМОСТЬ
2. ГЕНЕРАТОР СЛУЧАЙНЫХ ЧИСЕЛ С КОМПЕНСАЦИЕЙ СДВИГА И ЧАСТОТНОЙ КОРРЕКЦИЕЙ, ОСНОВАННЫЙ НА АВТОНОМНОМ ХАОТИЧЕСКОМ ГЕНЕРАТОРЕ, ДЛЯ ПРИМЕНЕНИЯ В КРИПТОГРАФИИ
В предлагаемой конструкции мы получили случайные данные путем периодической дискретизации одного из состояний хаотической системы и численно проверили, что потоки битов, генерированные предлагаемым ГСЧ, проходят четыре основных теста случайных чисел из тестового набора Федерального стандарта по обработке информации (США) FIPS-140-2. Внешняя помеха - это одна из основных проблем при разработке ГСЧ, поскольку сигналы помехи и случайные сигналы имеют сравнимые уровни. Для того чтобы решить эту проблему и обеспечить робастность к колебаниям параметров и атакам, направленным на взлом, мы предложили контуры компенсации сдвига и частотной коррекции, которые повышают статистическое качество генерируемых последовательностей битов. Кроме того, мы экспериментально проверили, что двоичные данные, полученные из хаотического генератора, проходят тесты полного набора тестов Национального института стандартов и технологий (США) для измерения качества набора случайных чисел.
3. АВТОНОМНЫЙ ХАОТИЧЕСКИЙ ГЕНЕРАТОР
Автономный хаотический генератор, используемый как ядро ГСЧ, был предложен в работе [18]. Хаотический генератор на МОП-структурах представлен на фиг.7 и построен по схеме классического синусоидального генератора с перекрестными связями с добавлением звена RC3 и каскада дифференциальной пары (М3-М4). Пары транзисторов M9-M8 и М10-М11 используются для реализации простых токовых зеркал с коэффициентом усиления по току в схеме с общим эмиттером k. Принимая, что С1=С2=С3=С, обычный анализ схемы дает следующую формулу (5):
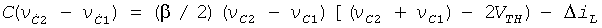
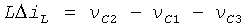
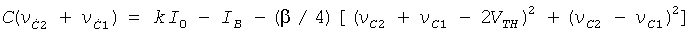
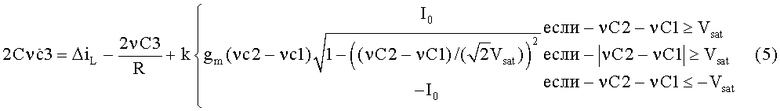
где ΔiL=iL-iR (дифференциальный ток дросселей), 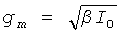 ,
, 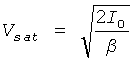 , β=µnCox(W/L)1,2; VTH - пороговое напряжение n-канальной МОП-структуры, µn - подвижность электронов, Сох - емкость оксида МОП-структуры и W/L - отношение ширины канала к его длине для пары транзисторов М1-М2.
, β=µnCox(W/L)1,2; VTH - пороговое напряжение n-канальной МОП-структуры, µn - подвижность электронов, Сох - емкость оксида МОП-структуры и W/L - отношение ширины канала к его длине для пары транзисторов М1-М2.
Используя нормализованные величины: 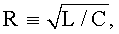 x1=(νC2-νC1)/2Vref, х2=(νC2+νC1)/2Vref, y=ΔiLR/2Vref, z=νC3/2Vref, tn=t/RC, и принимая Vref=VTH, уравнения системы в формуле (5) преобразуются следующим образом:
x1=(νC2-νC1)/2Vref, х2=(νC2+νC1)/2Vref, y=ΔiLR/2Vref, z=νC3/2Vref, tn=t/RC, и принимая Vref=VTH, уравнения системы в формуле (5) преобразуются следующим образом:
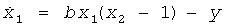
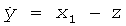
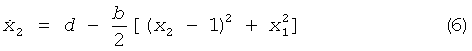
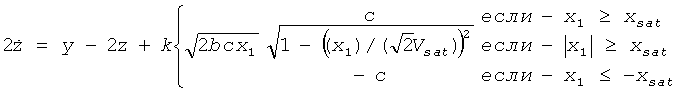
где b=βRVTH, c=I0R/2VTH, d=(kI0-IB)R/2VTH и 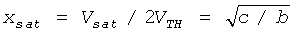 .
.
Уравнения в формуле (6) генерируют хаос для отличного набора параметров. Например, хаотический аттрактор, показанный на фиг.8, получен из численного анализа системы при b=0,9, с=0,15, d=0,7 и k=8 с использованием алгоритма 4-го порядка Рунге-Кутта с адаптивным размером шага.
Использованный хаотический генератор обладает некоторыми значительными преимуществами над существующими генераторами. Для обеспечения требуемой нелинейности в схеме используется дифференциальная пара, которая благодаря своим высоким характеристикам ИС является наиболее широко используемым аналоговым компоновочным блоком. Кроме того, хаотический генератор уравновешен; следовательно, он обеспечивает лучшее подавление помех по питанию и помехоустойчивость.
4. МОДЕЛИРОВАНИЕ СХЕМЫ
Для того чтобы продемонстрировать способность высокочастотной работы хаотического генератора на МОП-структурах, была разработана компоновка схемы, приведенной на фиг.7, с использованием Cadence, а схема была смоделирована с использованием программы SPICE (программы моделирования с ориентацией на интегральные схемы) (уровень 3) с параметрами модели 1,5 мкм КМОП-технологии. Схема была смещена с источником питания ±2,5 В. Значения пассивных компонентов были следующими: L=4,7 мкГн, С=4,7 пФ 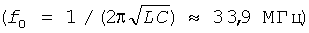 , R=1000 Ом, и токи смещения были I0=240 мкА, IB=100 мкА соответственно. Наблюдавшееся фазовое пространство, соответствующее зависимости между νC2-νC1 и νC3, показано на фиг.9.
, R=1000 Ом, и токи смещения были I0=240 мкА, IB=100 мкА соответственно. Наблюдавшееся фазовое пространство, соответствующее зависимости между νC2-νC1 и νC3, показано на фиг.9.
Понятно, что этот вариант хаотического генератора на МОП-структурах требует внешних дросселей (по отношению к чипу). Пытаться уменьшить величины дросселей, одновременно поддерживая функциональность, было невозможным без повышения напряжений питания, токов смещения и отношения ширины канала к его длине для транзисторов. Однако подобный хаотический аттрактор был получен и путем моделирования с использованием программы SPICE с L=20 нГн, С=0,3 пФ, (f0≈2 ГГц), R=258 Ом и с параметрами модели 0,35 мкм биполярной КМОП-технологии, причем напряжения питания были ±2,5 В, а токи смещения были I0=1300 мкА, IB=400 мкА. Наконец, схема хаотического генератора очень подходит для монолитного исполнения и способна работать на очень высоких частотах.
5. ГЕНЕРАЦИЯ СЛУЧАЙНЫХ ЧИСЕЛ
Из-за своей крайней чувствительности к начальным условиям и имея положительную экспоненту Ляпунова и шумоподобный энергетический спектр, хаотические системы допускают их использование для генерации случайных чисел. Для того чтобы получить случайные двоичные данные из хаотической системы с непрерывным временем, мы предложили интересный способ, основанный на генерации необратимых двоичных данных из сигнала данного хаотического генератора. Следует отметить, что основной характеристикой для генерации псевдослучайных чисел является необратимость.
Для получения случайных двоичных битов из хаотического генератора мы использовали выборки состояния x1 системы в формуле (6), полученные на нарастающих фронтах внешнего периодического импульсного сигнала, то есть в моменты времени t, удовлетворяющие условию ωtmod2π=0, где ω - частота импульсного сигнала. Следует отметить, что хотя 4-мерные траектории в плоскости x1-y-х2-z являются обратимыми, можно получить и необратимое сечение, учитывая значения, соответствующие лишь одному из состояний, скажем, х1.
Вначале мы исследовали распределение периодически выбранных значений х1 для определения соответствующих сечений, где распределение выглядит как случайный сигнал. Хотя мы не смогли найти сечений, значения x1 которых имеют единственное нормальное или X2 распределение для отличного набора параметров, приведенного в формуле (6), мы определили различные сечения, где распределение x1 имеет, по меньшей мере, две области. При b=0,9, с=0,15, d=0,7 и k=8 распределение состояния x1 в определенных выше сечениях показано на фиг.10.
Распределение х1, имеющее две области, навело нас на мысль генерировать случайные двоичные данные из областных значений x1 для областных порогов. Следуя в этом направлении, мы сгенерировали двоичные данные S(top)i и S(bottom)i из одномерного сечения по формуле (7):
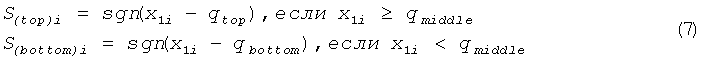
где sgn(.) - знаковая функция, x1i - значения х1 в одномерном сечении, полученные для ωtmod2π=0, qtop и qbottom - пороги для верхнего и нижнего распределений соответственно и qmiddle - граница между распределениями. Для того чтобы смочь выбрать пороги подходящим образом, мы исследовали верхнее и нижнее распределения, как показано на фиг.10, а затем qtop и qbottom были определены как медианы верхнего и нижнего распределений, которые были 0,70569678515 и -0,7932956192 соответственно, когда qmiddle была определена как 0.
Генерация двоичной последовательности, получаемой таким образом, не настолько зависит от значения qmiddle, поскольку для этого граничного значения плотность распределения х минимальна. Однако для пороговых значений (qtop, qbottom) плотность распределения х максимальна, так что полученная двоичная последовательность может быть смещенной. Для того чтобы удалить неизвестное смещение в этой последовательности, можно использовать хорошо известный метод выравнивания фон Неймана. Этот метод заключается в преобразовании пары битов 01 в выход 0, 10 - в выход 1, и в исключении пар битов 00 и 11. Однако этот метод снижает производительность, поскольку генерирует приблизительно 1 бит из 4 битов.
Для того чтобы устранить это смещение и не снизить при этом производительность, вместо фон-неймановской обработки был использован другой метод - операция ⊗ (исключающее ИЛИ). Потенциальной проблемой, связанной с методом исключающее ИЛИ, является то, что малое количество корреляции между входными битами придадут выходу значительное смещение. Коэффициент корреляции генерированных двоичных последовательностей Stop и Sbottom длиной 196 кбит рассчитан равным 0,00446, и установлено, что генерированные двоичные последовательности являются независимыми. Это, собственно, и ожидалось, поскольку хаотические системы характеризуются тем, что имеют положительную экспоненту Ляпунова, и автокорреляция хаотического временного ряда резко исчезает. В соответствии с этим результатом, мы сгенерировали новые двоичные данные S(xor)i, используя приведенную формулу (8):
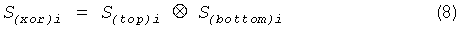
Среднее значение ψ двоичной последовательности Sxor, полученной таким образом, можно рассчитать по приведенной формуле (9):
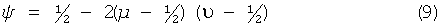
где среднее значение Stop=µ, а среднее значение Sbottom=ν. Таким образом, если µ и ν близки ½, то ψ очень близко ½. Как результат, мы численно проверили, что последовательность битов Sxor, которая была получена из различных сечений, определенных выше для соответствующих пороговых значений, по методике, приведенной в формуле (8), прошла тесты из тестового набора Федерального стандарта по обработке информации (США) FIP S-140-2 без фон-неймановской обработки. Мы назвали генерацию случайных чисел по вышеупомянутой методике «областной ГСЧ».
6. ЭКСПЕРИМЕНТАЛЬНАЯ ПРОВЕРКА И РЕАЛИЗАЦИЯ АППАРАТНЫХ СРЕДСТВ ГСЧ
Из-за отсутствия доступа к подходящему производственному оборудованию мы решили изготовить предложенные новшества, используя дискретные компоненты, чтобы продемонстрировать осуществимость этих схем. Для фиг.7 значения пассивных компонентов были следующими: L=9 мГн, С=10 нФ, R=1000 Ом, IB=100 мкА и I0=250 мкА. МОП-транзисторы и источники тока, которые были реализованы с использованием простых токовых зеркал на основе матриц КМОП-транзисторов LM4007. k был задан равным 8 путем регулирования отношения резисторов нагрузки токовых зеркал. Средняя (центральная) рабочая частота хаотического генератора - 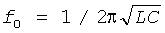 - была отрегулирована до низкого значения частоты 16,77 кГц во избежание влияния на схему паразитических емкостей. Схема была смещена с источником питания ±5 В, и наблюдавшийся аттрактор показан на фиг.11. В порядке, описанном в разделе 5, мы сгенерировали случайные биты по областям путем периодической дискретизации одного из состояний хаотического генератора.
- была отрегулирована до низкого значения частоты 16,77 кГц во избежание влияния на схему паразитических емкостей. Схема была смещена с источником питания ±5 В, и наблюдавшийся аттрактор показан на фиг.11. В порядке, описанном в разделе 5, мы сгенерировали случайные биты по областям путем периодической дискретизации одного из состояний хаотического генератора.
6.1 ОБЛАСТНАЯ ГСЧ
При областной ГСЧ для того, чтобы получить необратимое сечение, была использована только одна переменная х1, и напряжение ν1=νC2-νC1, соответствующее переменной х1, было преобразовано в двоичные последовательности. Для того чтобы реализовать эту методику, была использована схема, показанная на фиг.18. В этой схеме компараторы были реализованы на чипах LM211, а для реализации порогов в формуле (7) были использованы уровни напряжения Vtop, Vmiddle и Vbottom соответственно. Vtop и Vbottom были генерированы двумя 12-битовыми цифроаналоговыми преобразователями (ЦАП) напряжения. Каждый ЦАП можно настраивать с шагами 0,5859375 мВ, а опорное напряжение ЦАП равно 2,4 В. При реализации формула (7) и формула (8) преобразуются в следующее:
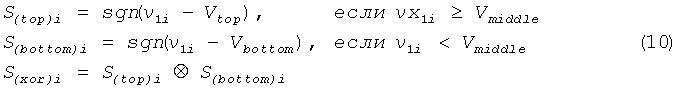
Для загрузки двоичных данных в компьютер были разработаны аппаратные средства на основе матрицы логических элементов с эксплуатационным программированием, имеющие интерфейс периферийных устройств. Для получения значений х в сечении, определенном как tmod2π=0, выходной поток битов компараторов дискретировался и запоминался в двоичном формате на нарастающем фронте внешнего периодического генератора прямоугольных импульсов νp(t). В матрице логических элементов с эксплуатационным программированием были реализованы компенсация сдвига для порогов Vtop и Vbottom и операция «исключающее ИЛИ». После компенсации сдвига и частотной коррекции и операции «исключающее ИЛИ», случайные числа - кандидаты загружались в компьютер через интерфейс периферийных устройств. Максимальная скорость хранения данных наших аппаратных средств на основе матрицы логических элементов с эксплуатационным программированием равна 62 Мбит/сек.
По методике, описанной в разделе 5, мы исследовали распределение ν1. Как результат, распределение ν1, полученное на нарастающем фронте νp(t), показано на фиг.12.
Для того чтобы смочь определить начальные значения порогов подходящим образом, подобно генерации численных битов, были исследованы верхнее и нижнее распределения. Затем были определены начальные значения Vtop и Vbottom как медианы верхнего и нижнего распределений, которые были 1,114 В и -1,122 В соответственно, а Vmiddle была определена как 0 мВ. Частота дискретизации для v1 была определена путем деления частоты νp(t) на значение предварительного делителя частоты в матрице логических элементов с эксплуатационным программированием. Для определения начального значения предварительного делителя частоты подходящим образом, наблюдался частотный спектр ν1, приведенный на фиг.13. Как показано на этой фигуре, хаотический сигнал ν1 имеет шумоподобный энергетический спектр. Средняя (центральная) частота хаотического генератора показана сплошным маркером, установленным на 17 кГц. До пунктирного маркера, установленного на 4 кГц, в области, в которой энергетический спектр является плоским, хаотический сигнал ν1 содержит все частоты в равных количествах, и спектральная плотность мощности находится в своем максимуме. Следовательно, без потери общности, ν1(t) и ν1(t+t0) можно рассматривать как некоррелированные для всех t0, не равных 0, и ν1 можно дискретизировать до 4 кГц, показанной как источник случайных сигналов. Наконец, начальное значение предварительного делителя частоты было определено равным 6, а частота νp(t) была 24 кГц.
Компенсации сдвига для порогов Vtop и Vbottom были осуществлены путем реализации однобитового теста из тестового набора Федерального стандарта по обработке информации (США) FIPS-140-2 для двоичных последовательностей Stop и Sbottom. Для каждой последовательности были получены потоки битов длиной 20000 битов; если число нулей >10275, то соответствующий порог снижался, а если число нулей <9725, то соответствующий порог повышался. Контур частотных коррекций был осуществлен путем реализации теста последовательностей из тестового набора Федерального стандарта по обработке информации (США) FIPS-140-2 для двоичной последовательности Sxor. Если 3 потока битов Sxor длиной 20000 битов, которые были получены последовательно, не проходили тест последовательностей, что указывало на дискретизацию ν1 с запасом по частоте, то частота дискретизации ν1 снижалась путем повышения значения предварительного делителя частоты. При необходимости в этом, частота дискретизации могла повышаться извне через интерфейс периферийных устройств.
После того как значения предварительного делителя частоты и порогов стали стабильными, был получен поток битов длиной 503 Мбит, который был подвергнут полному тестовому набору Национального института стандартов и технологий (США). Как результат, мы экспериментально проверили, что последовательность битов Sxor прошла тесты из тестового набора Национального института стандартов и технологий (США) для измерения качества набора случайных чисел без фон-неймановской обработки. Результаты для однородности значений Р и доли проходящих последовательностей схемы областной ГСЧ приведены в таблице 1. При объеме выборки 503×1 Мбит минимальная степень прохождения для каждого статистического теста за исключением теста на случайное отклонение (вариант) составляет приблизительно 0,976691.
Когда средняя (центральная) частота хаотического генератора была 16,77 кГц, значения предварительного делителя частоты стали стабильными при 7, и скорость передачи данных Sxor эффективно становится равной (24 кГц/7/2) 1714 бит/сек из-за деления ν1 на две области согласно распределению. Максимальную скорость передачи данных Sxor можно рассчитать как 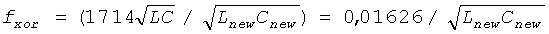 (new - нов.). В разделе 4 мы представили результаты моделирования схемы, которое приводит к средней (центральной) частоте работы, равной (f0≈33,9 МГц). Учитывая, что схема была реализована с параметрами модели 0,35 мкм биполярной КМОП-технологии, как приведено в разделе 4 (f0≈2 ГГц), мы можем заключить, что хаотические генераторы могут легко интегрироваться в сегодняшний процесс с номинальной средней (центральной) частотой в ГГц-диапазоне. Следует, однако, отметить, что в научно-технической литературе сообщается о хаотических схемах, действующих на намного более высоких частотах. Например, в работе [18] представлены результаты тактового моделирования варианта хаотического генератора, выполненного на биполярном плоскостном транзисторе, работающего на частоте 5,3 ГГц. Итак, все это указывает на то, что использование хаоса с непрерывным временем является очень перспективным в генерации случайных чисел с очень высокой производительностью, порядка сотен Мбит/сек.
(new - нов.). В разделе 4 мы представили результаты моделирования схемы, которое приводит к средней (центральной) частоте работы, равной (f0≈33,9 МГц). Учитывая, что схема была реализована с параметрами модели 0,35 мкм биполярной КМОП-технологии, как приведено в разделе 4 (f0≈2 ГГц), мы можем заключить, что хаотические генераторы могут легко интегрироваться в сегодняшний процесс с номинальной средней (центральной) частотой в ГГц-диапазоне. Следует, однако, отметить, что в научно-технической литературе сообщается о хаотических схемах, действующих на намного более высоких частотах. Например, в работе [18] представлены результаты тактового моделирования варианта хаотического генератора, выполненного на биполярном плоскостном транзисторе, работающего на частоте 5,3 ГГц. Итак, все это указывает на то, что использование хаоса с непрерывным временем является очень перспективным в генерации случайных чисел с очень высокой производительностью, порядка сотен Мбит/сек.
7. КОМПЕНСИРОВАННЫЙ ГЕНЕРАТОР СЛУЧАЙНЫХ ЧИСЕЛ НА ОСНОВЕ ДВУХВИТКОВОГО АТТРАКТОРА
В предложенной конструкции мы вначале получили случайные данные путем периодической дискретизации одного из состояний хаотической системы и численно проверили, что потоки битов, генерированные предложенным ГСЧ, проходят четыре основных теста случайных чисел из тестового набора Федерального стандарта по обработке информации (США) FIPS-140-2. Внешняя помеха - это одна из основных проблем при разработке ГСЧ, поскольку сигналы помехи и случайные сигналы имеют сравнимые уровни. Для того чтобы решить эту проблему и обеспечить робастность к колебаниям параметров и атакам, направленным на взлом, мы предложили контуры компенсации сдвига и частотной коррекции, которые повышают статистическое качество генерируемых последовательностей битов. Наконец, мы экспериментально проверили, что двоичные данные, полученные из предлагаемой схемы, проходят тесты полного набора тестов Национального института стандартов и технологий (США) для измерения качества набора случайных чисел без последующей обработки.
8. ДВУХВИТКОВЫЙ АТТРАКТОР
Двухвитковый аттрактор, используемый как ядро ГСЧ, получен из простой модели, приведенной в работе [22], выраженной формулой (11). Следует отметить, что при замене нелинейности непрерывной нелинейностью система «количественно подобна» генератору Чуа (Chua).
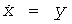

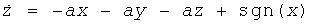
где sgn(.) - знаковая функция. Уравнения в формуле (11) генерируют хаос для отличного набора параметров. Например, хаотический аттрактор, показанный на фиг.14, получен из численного анализа системы при a=0,666… с использованием алгоритма 4-го порядка Рунге-Кутта с адаптивным размером шага.
9. ГЕНЕРАЦИЯ СЛУЧАЙНЫХ БИТОВ
Для того чтобы получить случайные двоичные данные из хаотической системы с непрерывным временем, мы предложили интересный способ, основанный на генерации необратимых двоичных данных из сигнала данной хаотической системы. Следует отметить, что основной характеристикой для генерации псевдослучайных чисел является необратимость.
Для получения случайных битов из хаотического аттрактора мы использовали выборки состояния х системы в формуле (11), полученные на нарастающих фронтах внешнего периодического импульсного сигнала, то есть в моменты времени t, удовлетворяющие условию ωtmod2π=0, где ω - частота импульсного сигнала. Следует отметить, что хотя 3-мерные траектории в плоскости х-y-z являются обратимыми, можно получить и необратимое сечение, учитывая значения, соответствующие лишь одному из состояний, скажем, х.
Вначале мы исследовали распределение периодически выбранных значений х для определения соответствующих сечений, где распределение выглядит как случайный сигнал. Хотя мы не смогли найти сечений, значения х которых имеют единственное нормальное или X2 распределение для разных значений а в формуле (11), мы определили различные сечения, где распределение х имеет по меньшей мере две области. При а=0,666… распределение состояния х в определенном выше сечении показано на фиг.15.
Распределение х, имеющее две области, навело нас на мысль генерировать случайные двоичные данные из областных значений х для областных порогов. Следуя в этом направлении, мы сгенерировали двоичные данные S(top)i и S(bottom)i из одномерного сечения по формуле (12):
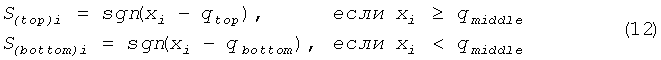
где x1 - значения х в одномерном сечении, полученные для ½tmod2π=0 (ω=1/2), qtop и qbottom - пороги для верхнего и нижнего распределений соответственно, и qmiddle - граница между распределениями. Для того чтобы смочь выбрать пороги подходящим образом, мы исследовали верхнее и нижнее распределения, как показано на фиг.15, а затем qtop и qbottom были определены как медианы верхнего и нижнего распределений, которые были 0,9656158849 и -0,9640518966 соответственно, когда qmiddle была определена как 0.
Генерация двоичной последовательности, получаемой таким образом, не настолько зависит от значения qmiddle, поскольку для этого граничного значения плотность распределения х минимальна. Однако для пороговых значений (qtop, qbottom) плотность распределения х максимальна, так что полученная двоичная последовательность может быть смещенной. Для того чтобы удалить неизвестное смещение в этой последовательности, можно использовать хорошо известный метод выравнивания фон Неймана. Этот метод заключается в преобразовании пары битов 01 в выход 0, 10 - в выход 1, и в исключении пар битов 00 и 11. Однако этот метод снижает производительность, поскольку генерирует приблизительно 1 бит из 4 битов.
Для того чтобы устранить это смещение и не снизить при этом производительность, вместо фон-неймановской обработки был использован другой метод - операция ⊗ (исключающее ИЛИ). Потенциальной проблемой, связанной с методом исключающее ИЛИ, является то, что малое количество корреляции между входными битами придадут выходу значительное смещение. Коэффициент корреляции генерированных двоичных последовательностей Stop и Sbottom длиной 152 кбит рассчитан равным 0,00018, и установлено, что генерированные двоичные последовательности являются независимыми. Это, собственно, и ожидалось, поскольку хаотические системы характеризуются тем, что имеют положительную экспоненту Ляпунова, и автокорреляция хаотического временного ряда резко исчезает. В соответствии с этим результатом, мы сгенерировали новые двоичные данные S(xor)i, используя приведенную формулу (13):
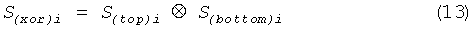
Среднее значение ψ двоичной последовательности Sxor, полученной таким образом, можно рассчитать по приведенной формуле (14):
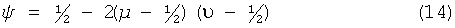
где среднее значение Stop=µ, а среднее значение Sbottom=ν. Таким образом, если µ и ν близки ½, то ψ очень близко ½. Как результат, мы численно проверили, что последовательность битов Sxor, которая была получена из различных сечений, определенных выше для соответствующих пороговых значений, в соответствии с методикой, приведенной в формуле (13), прошла тесты из тестового набора Федерального стандарта по обработке информации (США) FIPS-140-2 без фон-неймановской обработки. Мы назвали генерацию случайных чисел по вышеупомянутой методике «областной ГСЧ».
10. РЕАЛИЗАЦИЯ АППАРАТНЫХ СРЕДСТВ ГСЧ
Из-за отсутствия доступа к подходящему производственному оборудованию мы решили изготовить предложенную схему, используя дискретные компоненты, чтобы продемонстрировать осуществимость схемы.
10.1. ЭКСПЕРИМЕНТАЛЬНАЯ ПРОВЕРКА ХАОТИЧЕСКОГО ГЕНЕРАТОРА
Схема цепи, реализующая двухвитковый аттрактор, приведена на фиг.16. В качестве высокоскоростного операционного усилителя используется усилитель AD844, а для реализации необходимой нелинейности - компаратор напряжений LM211. Значения пассивных компонентов были взяты следующими: R1=R2=aR3=R=10 кОм, R3=15 кОм при a=0,666…, C17=C18=C19=C=2,2 нФ и RK=100 кОм.
Следовательно, средняя (центральная) рабочая частота хаотического генератора f0=1/2πτ, соответствующая постоянной времени τ, где τ=RC, была отрегулирована до низкого значения частоты 7,234 кГц во избежание влияния на схему паразитических емкостей. Схема была смещена источником питания ±5 В, и наблюдавшийся аттрактор показан на фиг.17.
10.2 ОБЛАСТНАЯ ГСЧ
При областной ГСЧ напряжение ν1, соответствующее переменной х, было преобразовано в двоичные последовательности по методике, описанной в разделе 9. Для того чтобы реализовать эту методику, была использована схема, показанная на фиг.18. В этой схеме компараторы были реализованы на чипах LM211, а для реализации порогов в формуле (12) были использованы уровни напряжения Vtop, Vmiddle и Vbottom соответственно. Vtop и Vbottom были генерированы двумя 12-битовыми цифроаналоговыми преобразователями (ЦАП) напряжения. Каждый ЦАП можно настраивать с шагами 0,5859375 мВ, а опорное напряжение ЦАП равно 2,4 В.
Для загрузки двоичных данных в компьютер были разработаны аппаратные средства на основе матрицы логических элементов с эксплуатационным программированием, имеющие интерфейс периферийных устройств. Для получения значений х в сечении, определенном как ωtmod2π=0, выходной поток битов компараторов дискретировался и запоминался в двоичном формате на нарастающем фронте внешнего периодического генератора прямоугольных импульсов νp(t). В матрице логических элементов с эксплуатационным программированием были реализованы компенсация сдвига для порогов Vtop и Vbottom и операция «исключающее ИЛИ». После компенсации сдвига и частотной коррекции и операции «исключающее ИЛИ», случайные числа - кандидаты загружались в компьютер через интерфейс периферийных устройств. Максимальная скорость хранения данных наших аппаратных средств на основе матрицы логических элементов с эксплуатационным программированием равна 62 Мбит/сек.
10.3 КОМПЕНСАЦИЯ СДВИГА И ЧАСТОТНАЯ КОРРЕКЦИЯ
По методике, описанной в разделе 9, мы исследовали распределение ν1. Как результат, распределение ν1, полученное на нарастающем фронте νp(t), показано на фиг.19.
Для того чтобы смочь определить начальные значения порогов подходящим образом, подобно генерации численных битов, были исследованы верхнее и нижнее распределения. Затем были определены начальные значения Vtop и Vbottom как медианы верхнего и нижнего распределений, которые были 470 мВ и -470 мВ соответственно, а Vmiddle была определена как 0 мВ. Частота дискретизации для ν1 была определена путем деления частоты νp(t) на значение предварительного делителя частоты в матрице логических элементов с эксплуатационным программированием.
Для определения начального значения предварительного делителя частоты подходящим образом, наблюдался частотный спектр ν1, приведенный на фиг.20. Как показано на фиг.20, хаотический сигнал ν1 имеет шумоподобный энергетический спектр. Средняя (центральная) частота хаотического генератора показана сплошным маркером, установленным на 7,234 кГц. До пунктирного маркера, установленного на 1,55 кГц, в области, в которой энергетический спектр является плоским, хаотический сигнал ν1 содержит все частоты в равных количествах, и спектральная плотность мощности находится в своем максимуме. Следовательно, без потери общности, ν1(t) и ν1(t+t0) можно рассматривать как некоррелированные для всех t0, не равных 0, и ν1 можно дискретизировать до 1,55 кГц как источника случайных сигналов. Наконец, начальное значение предварительного делителя частоты было определено равным 3, а частота νp(t) была 4,65 кГц.
Компенсации сдвига для порогов Vtop и Vbottom были осуществлены путем реализации однобитового теста из тестового набора Федерального стандарта по обработке информации (США) FIPS-140-2 для двоичных последовательностей Stop и Sbottom. Для каждой последовательности были получены потоки битов длиной 20000 битов; если число нулей >10275, то соответствующий порог снижался, а если число нулей <9725, то соответствующий порог повышался.
Контур частотных коррекций был осуществлен путем реализации теста последовательностей из тестового набора Федерального стандарта по обработке информации (США) FIPS-140-2 для двоичной последовательности Sxor. Если 3 потока битов Sxor длиной 20000 битов, которые были получены последовательно, не проходили тест последовательностей, что указывало на дискретизацию ν1 с запасом по частоте, то частота дискретизации ν1 снижалась путем повышения значения предварительного делителя частоты. Значение предварительного делителя частоты, начальное значение которого было определено как 3, стало стабильным при 4. При необходимости в этом, частота дискретизации могла повышаться извне через интерфейс периферийных устройств. Эффект компенсации сдвига для Vtop, аналогичный эффекту компенсации сдвига для Vbottom, показан на фиг.21; несмотря на тот факт, что начальное значение порога не было задано подходящим образом, среднее значение потока битов длиной 20000 битов было достигнуто и стало стабильным при 1/2 путем компенсации.
10.4 РЕЗУЛЬТАТЫ ТЕСТОВ
После того как значения предварительного делителя частоты и порогов стали стабильными, был получен поток битов длиной 223 Мбит, который был подвергнут полному тестовому набору Национального института стандартов и технологий (США). Как результат, мы экспериментально проверили, что последовательность битов Sxor прошла тесты из тестового набора Национального института стандартов и технологий (США) для измерения качества набора случайных чисел без фон-неймановской обработки. Результаты для однородности значений Р и доли проходящих последовательностей схемы областной ГСЧ приведены в таблице 2, где значение Р (0 ≤ значение Р ≤ 1) - вещественное число, оценивающее вероятность того, что идеальный ГСЧ выдаст последовательность, менее случайную, чем данная последовательность. При объеме выборки 223×1 Мбит минимальная степень прохождения для каждого статистического теста за исключением теста на случайное отклонение (вариант) составляет приблизительно 0,970011.
Когда средняя (центральная) частота хаотического генератора была 7,234 кГц, скорость передачи данных Sxor эффективно становится равной ((4,65 кГц/4)/2) 581 бит/сек (делитель 4) из-за деления ν1 на две области согласно распределению. Скорость передачи данных последовательности битов Sxor можно обобщить как Sxor=581 τ/τnew=0,012782/τnew, где τnew=RnewCnew (new - нов.). В работе [22] представлена чиповая реализация двухвитковой системы с Rnew=28,5 кОм и Cnew=15 пФ, что приводит к средней (центральной) частоте работы f=1/2πτnew=500 кГц. Учитывая, что схема в работе [22] была реализована на относительно медленной 1,2 мкм КМОП-технологии, мы можем заключить, что эта схема может легко интегрироваться в сегодняшний процесс при связи 10 МГц и может генерировать поток битов, близкий к Мбит/сек. Следует, однако, отметить, что в научно-технической литературе сообщается о хаотических схемах, действующих на намного более высоких частотах. Например, в работе [18] представлены результаты тактового моделирования хаотической схемы, работающей на частоте 5,3 ГГц.
При сравнении нашей конструкции областной ГСЧ с предыдущей конструкцией, приведенной в работе [15], мы экспериментально проверили, что для такого же хаотического генератора скорость передачи данных способа ГСЧ, приведенного в работе [15], составляла 385 бит/сек. Кроме того, последовательность битов, полученная способом ГСЧ, приведенным в работе [15], может пройти полный набор тестов Diehard только с фон-неймановской обработкой.
Как результат предлагаемых конструкций, компенсированные генераторы случайных чисел, основанные на неавтономном хаотическом генераторе и двухвитковом аттракторе, являются усиленными архитектурами, в которые добавлены контуры компенсации сдвига и частотной коррекции для максимального повышения статистического качества выходных последовательностей и обеспечения робастности к внешней помехе, колебаниям параметров и атакам, направленным на взлом.
11. ГЕНЕРАТОР СЛУЧАЙНЫХ ЧИСЕЛ НА ОСНОВЕ ДВУХВИТКОВОГО АТТРАКТОРА
В предложенном генераторе случайных чисел мы получили случайные данные из сечения Пуанкаре хаотической системы и численно проверили, что потоки битов, генерированные предложенным генератором случайных чисел, проходят четыре основных теста случайных чисел из тестового набора Федерального стандарта по обработке информации (США) FIPS-140-2. Кроме того, мы экспериментально проверили, что двоичные данные, полученные из предлагаемой схемы, проходят тесты полного набора тестов Национального института стандартов и технологий (США) для измерения качества набора случайных чисел.
12. ДВУХВИТКОВЫЙ АТТРАКТОР
Двухвитковый аттрактор, используемый как ядро ГСЧ, получен из простой модели, приведенной в работе [22], выраженной формулой (15). Следует отметить, что при замене нелинейности непрерывной нелинейностью система «количественно подобна» генератору Чуа (Chua).
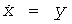

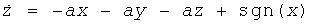
Уравнения в формуле (15) генерируют хаос для отличного набора параметров. Например, хаотический аттрактор, показанный на фиг.22, получен из численного анализа системы при а=0,666 с использованием алгоритма 4-го порядка Рунге-Кутта с адаптивным размером шага.
13. ГЕНЕРАЦИЯ СЛУЧАЙНЫХ БИТОВ
Для того чтобы получить случайные двоичные данные из хаотической системы с непрерывным временем, мы предложили интересный способ, основанный на генерации необратимых двоичных данных из сигнала данной хаотической системы. Следует отметить, что основной характеристикой для генерации псевдослучайных чисел является необратимость.
Для получения случайных битов из хаотического аттрактора мы использовали сечение Пуанкаре, определенное как z(t)=0 системы в формуле (15). Следует отметить, что хотя 2-мерное сечение Пуанкаре в плоскости х-y является обратимым, можно получить и необратимое сечение, учитывая значения, соответствующие лишь одному из состояний, скажем, х.
Вначале мы исследовали распределение периодически выбранных значений х в сечении Пуанкаре, определенном как z(t)=zn при dz/dt>0, где zn изменяется от zmin до zmax, чтобы определить подходящие сечения, где распределение выглядит как случайный сигнал. Хотя мы не смогли найти сечений Пуанкаре, значения х которых имеют единственное нормальное или X2 распределение для разных значений z0, мы определили различные сечения Пуанкаре, где распределение х имеет по меньшей мере две области. Для этой хаотической системы значения состояния х в вышеопределенном сечении Пуанкаре для z(t)=0 и ее распределения показаны на фиг.23 и фиг.24 соответственно.
Распределение х, имеющее две области, навело нас на мысль генерировать случайные двоичные данные из областных значений х для областных порогов. Следуя в этом направлении, мы сгенерировали двоичные данные S(top)i и S(bottom)i из сечения Пуанкаре по формуле (16):
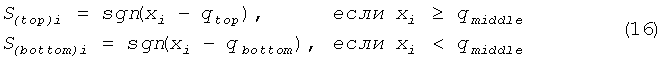
где sgn(.) - знаковая функция, xi - значения х в сечении Пуанкаре, qtop и qbottom - пороги для верхнего и нижнего распределений соответственно и qmiddle - граница между распределениями. Для того чтобы смочь выбрать пороги подходящим образом, мы исследовали верхнее и нижнее распределения, как показано на фиг.24, а затем qtop и qbottom были определены как медианы верхнего и нижнего распределений, которые были 0,8158 и -1,0169 соответственно, когда qmiddle была определена как 0.
Генерация двоичной последовательности, получаемой таким образом, не настолько зависит от значения qmiddle, поскольку для этого граничного значения плотность распределения х минимальна. Однако для пороговых значений (qtop, qbottom) плотность распределения х максимальна, так что полученная двоичная последовательность может быть смещенной. Для того чтобы удалить неизвестное смещение в этой последовательности, можно использовать хорошо известный метод выравнивания фон Неймана. Этот метод заключается в преобразовании пары битов 01 в выход 0, 10 - в выход 1, и в исключении пар битов 00 и 11. Однако этот метод снижает производительность, поскольку генерирует приблизительно 1 бит из 4 битов.
Для того чтобы устранить это смещение и не снизить при этом производительность, вместо фон-неймановской обработки мы использовали другой метод - операция ⊗ (исключающее ИЛИ). Потенциальной проблемой, связанной с методом исключающее ИЛИ, является то, что малое количество корреляции между входными битами придадут выходу значительное смещение. Мы рассчитали коэффициент корреляции генерированных двоичных последовательностей Stop и Sbottom длиной 32000 равным примерно 0,00087 и определили, что генерированные двоичные последовательности являются независимыми. В соответствии с этим результатом, мы сгенерировали новые двоичные данные S(xor)i, используя приведенную формулу (17):
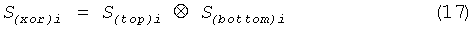
Среднее значение ψ двоичной последовательности Sxor, полученной таким образом, можно рассчитать по приведенной формуле (18):
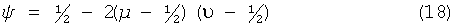
где среднее значение Stop=µ, а среднее значение Sbottom=ν. Таким образом, если µ и ν близки ½, то ψ очень близко ½. Как результат, мы численно проверили, что последовательность битов Sxor, которая была получена для соответствующих пороговых значений, в соответствии с методикой, приведенной в формуле (17), прошла тесты из тестового набора Федерального стандарта по обработке информации (США) FIPS-140-2 без фон-неймановской обработки. Мы назвали генерацию случайных чисел по вышеупомянутой методике «областной ГСЧ».
14. РЕАЛИЗАЦИЯ АППАРАТНЫХ СРЕДСТВ ГСЧ
Из-за отсутствия доступа к подходящему производственному оборудованию мы решили изготовить предложенную схему, используя дискретные компоненты, чтобы продемонстрировать осуществимость схемы.
Схема была смещена источником питания ±5 В. Схема цепи, реализующая двухвитковый аттрактор, приведена на фиг.25. В качестве высокоскоростного операционного усилителя используется усилитель AD844, а для реализации необходимой нелинейности - компаратор напряжений LM211. Значения пассивных компонентов были взяты следующими: R1=R2=aR3=R=10 кОм, R3=15 кОм при а=0,666…, C17=C18=C19=С=2,2 нФ и RK=100 кОм.
Следовательно, средняя (центральная) рабочая частота хаотического генератора f=1/2πτ, соответствующая постоянной времени τ, где τ=RC, была отрегулирована до низкого значения частоты 7,234 кГц во избежание влияния на схему паразитических емкостей. Наблюдавшийся аттрактор показан на фиг.26.
14.1 ОБЛАСТНАЯ ГСЧ
При областной ГСЧ для того, чтобы получить необратимое отображение, использовались только переменные х сечения Пуанкаре. Напряжение ν1, соответствующее переменной х, было преобразовано в двоичные последовательности по методике, описанной в разделе 13. Для того чтобы реализовать эту методику, была использована схема, показанная на фиг.27. В этой схеме компараторы были реализованы на чипах LM211, а для реализации порогов в формуле (16) были использованы уровни напряжения Vtop, Vmiddle и Vbottom соответственно. При реализации формула (16) и формула (17) преобразуются в следующее:

Для загрузки двоичных данных в компьютер были разработаны аппаратные средства на основе матрицы логических элементов с эксплуатационным программированием, имеющие интерфейс периферийных устройств. Для получения значений х в сечении Пуанкаре, определенном как z(t)=0, при dz/dt>0, напряжение ν3, соответствующее переменной z, сравнивалось с 0 В, а на нарастающем фронте этого компаратора дискретировался и запоминался в двоичном формате выходной поток битов других компараторов. В матрице логических элементов с эксплуатационным программированием была реализована операция «исключающее ИЛИ» для последовательности Sxor, и после операции «исключающее ИЛИ», случайные числа - кандидаты загружались в компьютер через интерфейс периферийных устройств. Максимальная скорость хранения данных наших аппаратных средств на основе матрицы логических элементов с эксплуатационным программированием равна 62 Мбит/сек.
По методике, описанной в разделе 13, мы исследовали распределение ν1. Как результат, снимок экрана осциллографа, на котором показано распределение ν1, полученное при ν3(t)=0, при dν3/dt>0, приведен на фиг.28.
Для того чтобы смочь определить пороги подходящим образом, подобно генерации численных битов, мы исследовали верхнее и нижнее распределения. Затем были определены начальные значения Vtop и Vbottom как медианы верхнего и нижнего распределений, которые были 524 мВ и -417 мВ соответственно, а Vmiddle была определена как 0 мВ.
Затем из схемы областной ГСЧ для данных соответствующих пороговых значений был получен поток битов Sxor длиной 105 Мбит. Полученные биты были подвергнуты полному тестовому набору Национального института стандартов и технологий (США) и не прошли тест последовательностей, тест самой длинной последовательности и тест приближенной энтропии. Это указало нам на дискретизацию ν1 с запасом по частоте. Затем, с целью улучшить результаты, мы получили вторую последовательность битов путем реализации счетчика в матрице логических элементов с эксплуатационным программированием. Выходной поток битов других компараторов ν1 дискретный на вторых нарастающих фронтах компаратора ν3.
Как результат, мы экспериментально проверили, что последовательность битов Sxor, генерированная на вторых нарастающих фронтах, прошла тесты полного набора тестов Национального института стандартов и технологий (США) для измерения качества набора случайных чисел без фон-неймановской обработки для данных соответствующих пороговых значений с допуском ±2 мВ.
Результаты тестов для доли прохождения схемы областной ГСЧ приведены в таблице 3. Если основная частота хаотического генератора равна 7,234 кГц, скорость передачи данных последовательности битов Sxor, генерированной на вторых нарастающих фронтах, эффективно становится равной 1820 бит/сек. Скорость передачи данных последовательности битов Sxor можно обобщить как Sxor=1820τ/τnew=0,04004/τnew, где τnew=RnewCnew (new - нов.). В работе [22] представлена чиповая реализация двухвитковой системы со средней (центральной) частотой работы f=1/2πτnew=500 кГц. Учитывая, что схема в работе [22] была реализована на относительно медленной 1,2 мкм КМОП-технологии, мы можем заключить, что эта схема может легко интегрироваться в сегодняшний процесс при связи 10 МГц и может генерировать поток битов порядка нескольких Мбит/сек. Следует, однако, отметить, что в научно-технической литературе сообщается о хаотических схемах, действующих на намного более высоких частотах. Например, в работе [18] представлены результаты тактового моделирования хаотической схемы, работающей на частоте 5,3 ГГц.
При сравнении нашей конструкции областной ГСЧ с предыдущей конструкцией, приведенной в работе [15], мы экспериментально проверили, что для такого же хаотического генератора скорость передачи данных способа ГСЧ, приведенного в работе [15], составляла 1634 бит за 100000 единиц нормализованного времени, а скорость передачи данных областной последовательности Sxor составляла 7719 бит за 100000 единиц нормализованного времени. Кроме того, последовательность битов, полученная способом ГСЧ, приведенным в работе [15], может пройти полный набор тестов Diehard только с фон-неймановской обработкой, и примерная последовательность битов, приведенная на сайте http://www.esat.kuleuven.ac.be/~mey/Ds2RbG/Ds2RbG.html, не выдерживает тесты на блочную частоту, последовательностей и приближенной энтропии полного тестового набора Национального института стандартов и технологий (США).
В заключение, мы экспериментально проверили, что если основная частота хаотического генератора равна 7,234 кГц и без фон-неймановской обработки, скорость передачи данных областной последовательности битов Sxor равна 1820 бит/сек. Учитывая, что в качестве ядра предлагаемой ГСЧ в ИС используется хаотический генератор с непрерывным временем с основной частотой, например, 40 МГц, скорости передачи данных областной ГСЧ можно, вероятно, повысить до 10 Мбит/сек. В заключение, мы можем прийти к выводу, что использование хаоса с непрерывным временем с предложенными новшествами является очень перспективным для генерации случайных чисел с очень высокими и постоянными скоростями передачи данных без последующей обработки.
15. ГЕНЕРАТОРЫ СЛУЧАЙНЫХ ЧИСЕЛ, ОСНОВАННЫЕ НА ХАОСЕ С НЕПРЕРЫВНЫМ ВРЕМЕНЕМ
Несмотря на тот факт, что использование хаотических отображений с дискретным временем при реализации ГСЧ некоторое время уже хорошо известно, лишь совсем недавно было показано, что для реализации ГИСЧ можно использовать и хаотические генераторы с непрерывным временем. Следуя в этом направлении, мы исследовали эффективность предлагаемых хаотических генераторов в качестве ядра ГСЧ.
Хотя в научно-технической литературе описаны много хаотических генераторов, лишь немногие из них разработаны с уделением внимания вопросам высокоэффективной ИС, таким, как низкое потребление энергии, высокочастотная работа, способность работать при низких уровнях напряжения. В этой работе мы представляем простые неавтономные хаотические генераторы, которые подходят для реализации высокоэффективной ИС.
Вначале мы получили случайные данные из одномерного стробоскопического отображения Пуанкаре предлагаемых хаотических систем и численно проверили, что после разделения отображения на области в соответствии с распределением, потоки битов, генерированные ГСЧ, построенным на предлагаемых схемах, прошли четыре основных теста случайных чисел из тестового набора Федерального стандарта по обработке информации (США) FIPS-140-2. Кроме того, мы экспериментально проверили, что двоичные данные, полученные из хаотических схем, проходят тесты полного набора тестов Национального института стандартов и технологий (США) для измерения качества набора случайных чисел.
16. ПРЕДЛАГАЕМЫЕ ГЕНЕРАТОРЫ
Предлагаемый биполярный хаотический генератор представлен на фиг.29. Если паразитические емкости, возникающие между коллекторами биполярных транзисторов и землей, обозначить Ср, обычный анализ схемы дает следующие уравнения состояния:
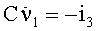
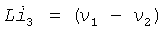
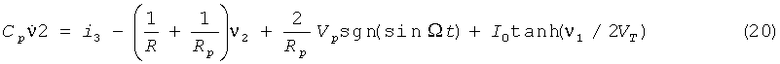
где i3=iR-iL и νp(t) - внешняя периодическая последовательность импульсов, определенная как νp(t)=sgn(sinΩt), и VT - тепловое напряжение (VT=kT/q), при комнатной температуре, равное 25,8 мВ.
Используя нормализованные величины: 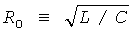 , х=ν1/Vs, y=i3R0/Vs, z=ν2/Vs, с0=I0R0/Vs, α=R0/Rp, β=R0/R,
, х=ν1/Vs, y=i3R0/Vs, z=ν2/Vs, с0=I0R0/Vs, α=R0/Rp, β=R0/R, 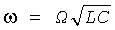 и принимая Vp=0,5Vs=VT и tn=t/RC, где Vs - произвольное напряжение масштабирования, уравнения системы в формуле (20) преобразуются следующим образом:
и принимая Vp=0,5Vs=VT и tn=t/RC, где Vs - произвольное напряжение масштабирования, уравнения системы в формуле (20) преобразуются следующим образом:
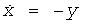
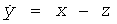
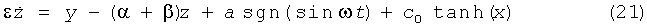
Уравнения в формуле (21) генерируют хаос для отличного набора параметров. Например, хаотический аттрактор, показанный на фиг.30, получен из численного анализа системы при c0=25, α=4, β=12, ω=0,27, ε=0,3 с использованием алгоритма 4-го порядка Рунге-Кутта с адаптивным размером шага.
Предлагаемый хаотический генератор на КМОП-структурах представлен на фиг.31. Пары транзисторов T3-Т4 и T5-T6 используются для реализации простых токовых зеркал, где отношения токов зеркал обозначены как К. Если паразитические емкости, возникающие между затворами пары транзисторов Т1-T2 и землей, обозначить Cp, обычный анализ схемы дает следующие уравнения (22):
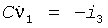
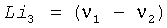
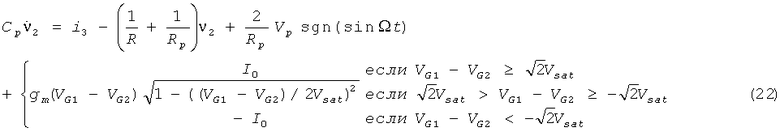
где i3=iR-iL, νp(t)=sgn(sinΩt), 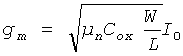 ,
, 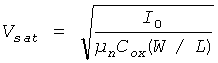 и W/L -отношение ширины канала к его длине для пары транзисторов T1-Т2.
и W/L -отношение ширины канала к его длине для пары транзисторов T1-Т2.
Используя нормализованные величины: 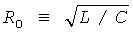 , х=νG1/Vs, y=i3R0/Vs, z=νG2/Vs, с0=2I0R0/Vs, α=R0/Rp, β=R0/R, b0=R0βVs/2,
, х=νG1/Vs, y=i3R0/Vs, z=νG2/Vs, с0=2I0R0/Vs, α=R0/Rp, β=R0/R, b0=R0βVs/2, 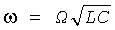 и принимая Vp=0,5Vs и tn=t/RC, где Vs - произвольное напряжение масштабирования, уравнения системы в формуле (22) преобразуются следующим образом:
и принимая Vp=0,5Vs и tn=t/RC, где Vs - произвольное напряжение масштабирования, уравнения системы в формуле (22) преобразуются следующим образом:
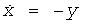
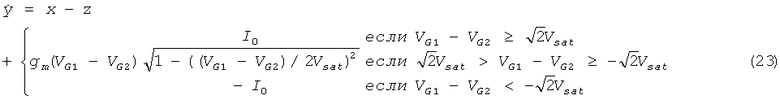
Уравнения в формуле (23) генерируют хаос для отличного набора параметров. Например, хаотический аттрактор, показанный на фиг.32, получен из численного анализа системы при c0=1,5, α=2,67, β=3,38, ω=0,33, b0=0,9, ε=0,1 с использованием алгоритма 4-го порядка Рунге-Кутта с адаптивным размером шага.
Предлагаемые хаотические генераторы обладают некоторыми значительными преимуществами над существующими генераторами. Для обеспечения требуемой нелинейности в обеих схемах используется дифференциальная пара, которая благодаря своим высоким характеристикам ИС является наиболее широко используемым аналоговым компоновочным блоком. Резисторы, используемые в этих схемах, имеют очень малые величины и поэтому могут эффективно реализовываться в ИС. Кроме того, предлагаемые хаотические генераторы уравновешены; следовательно, они обеспечивают лучшее подавление помех по питанию и помехоустойчивость. Наконец, внешним источником, используемым для возбуждения схем, является периодическая последовательность импульсов, которую можно точно и легко реализовать, используя синхронизирующий сигнал, уже имеющийся в чипе.
17. МЕХАНИЗМ ГЕНЕРАЦИИ ХАОСА
Известно, что для показа наличия подков в почти гамильтоновых принудительных плоских диссипативных системах можно использовать условия Мельникова. Согласно теореме Смэйла-Биркхоффа, для данной плоской возмущенной нелинейной системы вида
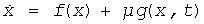 ,
,
где f и g - плавные функции, и g является периодической во времени с периодом Tγ, если выполнены следующие условия:
1. При µ=0 система является гамильтоновой и имеет гомоклиническую орбиту, проходящую через седлообразную критическую точку.
2. При µ=0 система имеет одно семейство параметров периодических орбит θγ(t) с периодом Tγ, на внутренней части гомоклинической орбиты с ∂θγ(0)/∂γ≠0
3. При t0∈[0,T] функция Мельникова
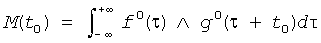
имеет простые нули,
то система имеет хаотические движения и подковы.
Легко проверить, что при ε=0 (паразитические емкости приняты пренебрежимо малыми) систему в формуле (21) можно записать в следующем виде:
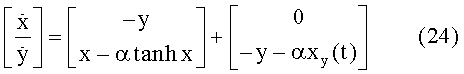
где xp(t)=sgn(sin(ωt)), a=с0/(α+β) и µ=1/(α+β). В этом случае можно легко проверить, что невозмущенная система, получаемая при µ=0, имеет седлообразную критическую точку в источнике при α>1. Кроме того, невозмущенная система является гамильтоновой и имеет гомоклиническую орбиту, проходящую через критическую точку. После замены неплавной функции xp(t)=sgn(sin(ωt)) ее плавной аппроксимацией xp(t)=tanh(10sin(ωt)) мы численно рассчитали функцию Мельникова, приведенную в формуле (25):
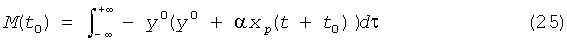
на гомоклинической орбите формулы (24), показанной в правом верхнем углу на фиг.33. Как показано на фиг.33, мы проверили, что при t0∈[0,T] функция Мельникова имеет простые нули, и система по формуле (24) имеет хаотические движения и подковы. Результаты численного анализа системы показывают, что при ненулевых и малых значениях ε система остается хаотической. Например, наибольшая экспонента Ляпунова системы определена равной 0,9 при ε=0,27.
18. ГЕНЕРАЦИЯ СЛУЧАЙНЫХ БИТОВ
Для того чтобы получить случайные двоичные данные из автономной хаотической системы, предложен интересный способ, основанный на генерации необратимых двоичных данных из сигнала данной хаотической системы. Следует отметить, что основной характеристикой для генерации псевдослучайных чисел является необратимость.
Для получения случайных битов из предлагаемых хаотических аттракторов мы использовали стробоскопические отображения Пуанкаре хаотических систем по формулам (21) и (23). Следует отметить, что хотя 2-мерное сечение Пуанкаре в плоскости х-y является обратимым, можно получить и необратимое отображение, учитывая значения, соответствующие лишь одному из состояний, скажем, х.
Вначале мы исследовали распределение значений х в отображении Пуанкаре на протяжении одного периода внешнего периодического импульсного сигнала, чтобы определить подходящие отображения, где распределения выглядят как случайные сигналы. Хотя мы не смогли найти отображений, значения х которых имеют единственное нормальное или X2 распределение, мы определили подходящие сечения Пуанкаре, где распределение х имеет по меньшей мере две области. Для этой биполярной системы отображение Пуанкаре при ωtmod2π=0,30 и соответствующее распределение показаны на фиг.34 и фиг.35 соответственно. Подобно биполярной системе, отображение Пуанкаре при ωtmod2π=0,55 и соответствующее распределение показаны на фиг.36 и фиг.37 соответственно для КМОП-системы.
Распределение х, имеющее две области, навело нас на мысль генерировать случайные двоичные данные из областных значений х для областных порогов. Следуя в этом направлении, мы сгенерировали двоичные данные S(top)i и S(bottom)i из сечения Пуанкаре по формуле (26):
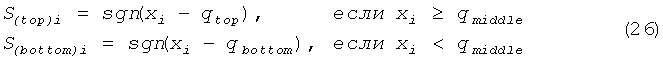
где sgn(.) - знаковая функция, xi - значения х в сечении Пуанкаре, qtop и qbottom - пороги для верхнего и нижнего распределений соответственно и qmiddle - граница между распределениями. Для того чтобы смочь выбрать пороги подходящим образом, мы исследовали верхнее и нижнее распределения, как показано на фиг.35 и фиг.37. Затем для биполярной системы qtop и qbottom были определены как медианы верхнего и нижнего распределений, которые были -0,593 и -2,183 соответственно, когда qmiddle была определена как -1,394. Подобно биполярной системе, для КМОП-системы qtop и qbottom были определены как медианы верхнего и нижнего распределений, которые были 0,549 и -1,576 соответственно, когда, qmiddle была определена как -0,610.
Генерация двоичной последовательности, получаемой таким образом, не настолько зависит от значения qmiddle, поскольку для этого граничного значения плотность распределения х минимальна. Однако для пороговых значений (qtop, qbottom) плотность распределения х максимальна, так что полученная двоичная последовательность может быть смещенной. Для того чтобы удалить неизвестное смещение в этой последовательности, можно использовать хорошо известный метод выравнивания фон Неймана. Этот метод заключается в преобразовании пары битов 01 в выход 0, 10 - в выход 1 и в исключении пар битов 00 и 11.
По вышеупомянутой методике были получены последовательности битов (Stop и Sbottom) длиной 240000 как для биполярной, так и КМОП-системы, которые были подвергнуты четырем тестам (однобитовый, покер, последовательностей и длинной последовательности) из тестового набора Федерального стандарта по обработке информации (США) FIPS-140-2. Мы проверили, что эти последовательности битов проходят эти тесты при данных пороговых значениях с допуском ±0,03.
Для того чтобы устранить это смещение, вместо фон-неймановской обработки мы использовали и другой метод - операция ⊗ (исключающее ИЛИ). Потенциальной проблемой, связанной с методом исключающее ИЛИ, является то, что малое количество корреляции между входными битами придадут выходу значительное смещение. Мы рассчитали коэффициент корреляции генерированных двоичных последовательностей Stop и Sbottom длиной 32000 равным примерно 0,00011 и определили, что генерированные двоичные последовательности являются независимыми. В соответствии с этим результатом, мы сгенерировали новые двоичные данные S(xor)i, используя приведенную формулу (27):
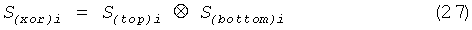
Среднее значение ψ двоичной последовательности Sxor, полученной таким образом, можно рассчитать по приведенной формуле (28):
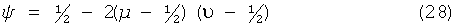
где среднее значение Stop=µ, а среднее значение Sbottom=ν. Таким образом, если µ и ν близки ½, то ψ очень близко ½. Как результат, мы численно проверили, что как для биполярной, так и КМОП-системы последовательности битов Sxor, которые были получены для соответствующих пороговых значений, в соответствии с методикой, приведенной в формуле (27), прошли тесты из тестового набора Федерального стандарта по обработке информации (США) FIPS-140-2 без фон-неймановской обработки. Мы назвали генерацию случайных чисел (Stop, Sbottom, Sxor) по вышеупомянутой методике «областной ГСЧ».
19. ЭКСПЕРИМЕНТАЛЬНАЯ ПРОВЕРКА
Из-за отсутствия доступа к подходящему производственному оборудованию мы решили изготовить предлагаемые схемы хаотического генератора, используя дискретные компоненты, чтобы продемонстрировать осуществимость этих схем. Как биполярная, так и КМОП-схема были смещены источником питания ±5 В, а внешний сигнал νp(t) генерировался генератором прямоугольных импульсов.
Значения пассивных компонентов биполярного генератора были следующими: L=10 мГн, С=10 нФ, R=180 Ом, Rp=120 Ом и I0=1,2 мА. На фиг.29 биполярные транзисторы и источник тока, обозначенный I0 и реализованный с использованием простого токового зеркала, были реализованы на матрицах n-p-n-транзисторов и p-n-p-транзисторов СА3046 и СА3096. Амплитуда νp(t) была 26 мВ. Мы экспериментально проверили, что предлагаемая биполярная схема имеет хаотические движения при следующих значениях частоты νp(t): 5,95 кГц, 6,23 кГц, 7,12 кГц, 13,03 кГц, 14,48 кГц, 14,91 кГц, 17,07 кГц, 17,23 кГц, 18,08 кГц.
Значения пассивных компонентов генератора на КМОП-структурах были следующими: L=10 мГн, С=10 нФ, R=340 Ом, Rp=430 Ом и I0=0,5 мА. На фиг.31 КМОП-транзисторы и источник тока, обозначенный I0 и реализованный с использованием простого токового зеркала, были реализованы на матрицах КМОП-транзисторов LM4007. Амплитуда νp(t) была 383 мВ. Мы экспериментально проверили, что предлагаемая схема на КМОП-структурах имеет хаотические движения при следующих значениях частоты νp(t): 5,95 кГц, 10 кГц, 11,1 кГц, 12,6 кГц.
Для биполярного генератора и генератора на КМОП-структурах частота νp(t) была отрегулирована до низкого значения частоты 5,95 кГц во избежание влияния на схемы паразитических емкостей. Наблюдавшиеся аттракторы показаны на фиг.38 и фиг.39 для биполярного генератора и генератора на КМОП-структурах соответственно.
20. РЕАЛИЗАЦИЯ АППАРАТНЫХ СРЕДСТВ ГСЧ
Мы сгенерировали случайные биты по областям из стробоскопических отображений Пуанкаре предлагаемых хаотических генераторов.
20.1 ОБЛАСТНАЯ ГСЧ
При областной ГСЧ для того, чтобы получить необратимое отображение, использовались только переменные х сечения Пуанкаре. Напряжение ν1, соответствующее переменной х, было преобразовано в двоичные последовательности по методике, описанной в разделе 18. Для того чтобы реализовать эту методику, была использована схема, показанная на фиг.40. В этой схеме компараторы были реализованы на чипах LM311, а для реализации порогов в формуле (26) были использованы уровни напряжения Vtop, Vmiddle и Vbottom соответственно. При реализации формула (26) и формула (27) преобразуются в следующее:

Для загрузки двоичных данных в компьютер были разработаны аппаратные средства на основе матрицы логических элементов с эксплуатационным программированием, имеющие интерфейс периферийных устройств. В установленный момент времени в течение периода внешней периодической последовательности импульсов νp(t) выходной поток битов компараторов дискретировался и запоминался в двоичном формате. В матрице логических элементов с эксплуатационным программированием были реализованы также фон-неймановская обработка для Stop и Sbottom и операция «исключающее ИЛИ» для последовательности Sxor. После фон-неймановской обработки и операции «исключающее ИЛИ», случайные числа - кандидаты загружались в компьютер через интерфейс периферийных устройств. Максимальная скорость хранения данных наших аппаратных средств на основе матрицы логических элементов с эксплуатационным программированием равна 62 Мбит/сек.
По методике, описанной в разделе 18, мы исследовали распределение ν1 в течение одного периода νp(t). Как результат, распределение ν1, полученное через 46 мкс после нарастающих фронтов νp(t), для биполярной схемы и распределение ν1, полученное за 35 мкс до нарастающих фронтов νp(t), для схемы на КМОП-структурах, показаны на фиг.41 и фиг.42 соответственно.
Для того чтобы смочь определить пороги подходящим образом, подобно генерации численных битов, мы исследовали верхнее и нижнее распределения биполярной схемы и схемы на КМОП-структурах. Затем для биполярной системы Vtop и Vbottom были определены как медианы верхнего и нижнего распределений, которые были 103 мВ и -287 мВ соответственно, а Vmiddle было определено как -107 мВ. Подобно биполярной схеме, для схемы на КМОП-структурах Vtop и Vbottom были определены как медианы верхнего и нижнего распределений, которые были 999 мВ и -217 мВ соответственно, а Vmiddle было определено как 560 мВ.
Затем при данных соответствующих пороговых значениях из биполярной хаотической схемы и хаотической схемы на КМОП-структурах были получены потоки битов Stop, Sbottom и Sxor длиной 2 Гбит. Полученные биты были подвергнуты полному тестовому набору Национального института стандартов и технологий (США). Как результат, мы экспериментально проверили, что последовательности битов Stop и Sbottom, полученные таким образом, проходят тесты полного тестового набора Национального института стандартов и технологий (США) после фон-неймановской обработки, и что последовательность битов Sxor, генерированная последовательностями битов Stop и Sbottom, проходит тесты полного тестового набора Национального института стандартов и технологий (США) без фон-неймановской обработки. Результаты тестов, относящиеся к степеням прохождения хаотической схемы на КМОП-структурах, приведены в таблице 4.
Принимая, что верхнее и нижнее распределения имеют приблизительно одинаковую плотность, скорости передачи битов последовательностей Stop и Sbottom равны половине внешней периодической последовательности импульсов. Как объяснялось в разделе 18, фон-неймановская обработка генерирует примерно 1 бит из 4. При частоте νp(t) 5,95 кГц скорости передачи данных последовательностей Stop и Sbottom снижаются до (5,95 кГц /2/4) 743 бит/сек, а скорость передачи данных последовательности Sxor эффективно становится равной (5,95 кГц/2) 2975 бит/сек.
Выше представлены два хаотических генератора с непрерывным временем - биполярный и на КМОП-структурах, приемлемые для реализации на ИС, и ГИСЧ, основанные на этих генераторах. Численные и экспериментальные результаты, представленные в этом разделе, не только подтверждают технико-экономическую осуществимость предлагаемых схем, но и стимулируют их использование в качестве ядра ГИСЧ на высокоэффективных ИС. В заключение, мы экспериментально проверили, что если частоту внешнего периодического импульсного сигнала установить равной 5,95 кГц, скорости передачи данных областных последовательностей и выходной последовательности Sxor равны 743 бит/сек после фон-неймановской обработки и 2975 бит/сек без фон-неймановской обработки соответственно.



ПОЯСНЕНИЯ К ЧЕРТЕЖАМ
Фиг.1. Метод усиления источника шума.
Фиг.2. Распределение х1.
Фиг.3. Областная генерация случайных чисел путем использования периодических выборок.
Фиг.4. Областная генерация случайных чисел из одномерного сечения, полученного при переходах из других состояний.
Фиг.5. Областная генерация случайных чисел из одномерного сечения неавтономного хаотического генератора, полученного на нарастающем фронте νp(t).
Фиг.6. Частотный спектр ν1.
Фиг.7. Автономный хаотический генератор на МОП-структурах.
Фиг.8. Результаты численного анализа хаотического генератора.
Фиг.9. Хаотический аттрактор из моделирования послекомпоновочной схемы.
Фиг.10. Гистограмма x1, полученная при ωtmod2π=0.
Фиг.11. Экспериментальные результаты хаотического генератора.
Фиг.12. Гистограмма ν1, полученная на нарастающем фронте νp(t).
Фиг.13. Частотный спектр ν1.
Фиг.14. Результаты численного анализа хаотического генератора.
Фиг.15. Гистограмма х, полученная при ωtmod2π=0 (ω=1=2).
Фиг.16. Реализация схемы двухвиткового аттрактора.
Фиг.17. Экспериментальные результаты хаотического генератора.
Фиг.18. Областная генерация случайных чисел с использованием хаотического генератора.
Фиг.19. Гистограмма ν1, полученная на нарастающем фронте νp(t).
Фиг.20. Частотный спектр ν1.
Фиг.21. Эффект компенсации сдвига для Vtop.
Фиг.22. Результаты численного анализа хаотического генератора.
Фиг.23. Сечение Пуанкаре для хаотической системы, определенной как z(t)=0.
Фиг.24. Гистограмма х, полученная при z(t)=0.
Фиг.25. Реализация схемы двухвиткового аттрактора.
Фиг.26. Экспериментальные результаты хаотического генератора.
Фиг.27. Областная генерация случайных чисел с использованием хаотического генератора.
Фиг.28. Гистограмма v1, полученная при ν3(t)=0 при dν3/dt>0.
Фиг.29. Предлагаемый биполярный генератор.
Фиг.30. Результаты численного анализа биполярного генератора.
Фиг.31. Предлагаемый генератор на КМОП-структурах.
Фиг.32. Результаты численного анализа генератора на КМОП-структурах.
Фиг.33. Нули функции Мельникова, рассчитанные на гомоклинической орбите, показанной в верхнем правом углу.
Фиг.34. Отображение Пуанкаре биполярной системы при ωtmod2π=0,30.
Фиг.35. Гистограмма х, полученная из биполярной системы при ωtmod2π=0,30.
Фиг.36. Отображение Пуанкаре КМОП-системы при ωtmod2π=0,55.
Фиг.37. Гистограмма х, полученная из КМОП-системы при ωtmod2π=0,55.
Фиг.38. Экспериментальные результаты биполярного хаотического генератора.
Фиг.39. Экспериментальные результаты хаотического генератора на КМОП-структурах.
Фиг.40. Областная генерация случайных чисел с использованием одного лишь предлагаемого хаотического генератора.
Фиг.41. Гистограмма ν1, полученная через 46 мкс после нарастающих фронтов νp(t), для биполярной схемы.
Фиг.42. Гистограмма ν1, полученная за 35 мкс до нарастающих фронтов νp(t), для схемы на КМОП-структурах.
| название | год | авторы | номер документа |
|---|---|---|---|
| СПОСОБ ЗАЩИТЫ ГЕНЕРАТОРА СЛУЧАЙНЫХ ЧИСЕЛ (ГСЧ) ОТ ВМЕШАТЕЛЬСТВ В ФИЗИЧЕСКИЙ ПРОЦЕСС ГЕНЕРАЦИИ | 2019 |
|
RU2719558C1 |
| ВЫСОКОСКОРОСТНОЙ КВАНТОВЫЙ ГЕНЕРАТОР СЛУЧАЙНЫХ ЧИСЕЛ НА ПЕРЕКЛЮЧЕНИИ ПОЛЯРИЗАЦИИ В ПОЛУПРОВОДНИКОВОМ ЛАЗЕРЕ С ВЕРТИКАЛЬНЫМ РЕЗОНАТОРОМ (ВАРИАНТЫ) И СПОСОБ ФОРМИРОВАНИЯ СЛУЧАЙНОЙ ЧИСЛОВОЙ ПОСЛЕДОВАТЕЛЬНОСТИ С ЕГО ПОМОЩЬЮ | 2022 |
|
RU2788400C1 |
| ГЕНЕРАТОР ИСТИННО СЛУЧАЙНЫХ ЧИСЕЛ | 2020 |
|
RU2741865C1 |
| СПОСОБ ГЕНЕРАЦИИ ПАРАЛЛЕЛЬНЫХ ПОТОКОВ ПСЕВДОСЛУЧАЙНЫХ ЧИСЕЛ И УСТРОЙСТВА ДЛЯ ЕГО ОСУЩЕСТВЛЕНИЯ (2 ВАРИАНТА) | 2012 |
|
RU2556430C2 |
| УСТОЙЧИВЫЙ К АТАКАМ КВАНТОВЫЙ ГЕНЕРАТОР СЛУЧАЙНЫХ ЧИСЕЛ НА ИНТЕРФЕРЕНЦИИ ЛАЗЕРНЫХ ИМПУЛЬСОВ СО СЛУЧАЙНОЙ ФАЗОЙ И СПОСОБ ЕГО ПРИМЕНЕНИЯ | 2019 |
|
RU2721585C1 |
| СПОСОБ ШИФРОВАНИЯ ИНФОРМАЦИИ, ПРЕДСТАВЛЕННОЙ ДВОИЧНЫМ КОДОМ | 2014 |
|
RU2581772C2 |
| Способ генерации случайных чисел для систем квантового распределения ключей на запутанных состояниях | 2023 |
|
RU2820799C1 |
| ВЫСОКОСКОРОСТНОЙ КВАНТОВЫЙ ГЕНЕРАТОР СЛУЧАЙНЫХ ЧИСЕЛ НА ИНТЕРФЕРЕНЦИИ ЛАЗЕРНЫХ ИМПУЛЬСОВ С ИСПОЛЬЗОВАНИЕМ МНОГОКАНАЛЬНОГО АНАЛОГО-ЦИФРОВОГО ПРЕОБРАЗОВАТЕЛЯ И СПОСОБ ФОРМИРОВАНИЯ СЛУЧАЙНОЙ ЧИСЛОВОЙ ПОСЛЕДОВАТЕЛЬНОСТИ С ЕГО ПОМОЩЬЮ | 2020 |
|
RU2758889C1 |
| Способ выбора шумовых диодов с использованием измерительного устройства для генератора случайных чисел | 2017 |
|
RU2642351C1 |
| СПОСОБ ПЕРЕДАЧИ СООБЩЕНИЙ В СИСТЕМЕ МНОГОПОЛЬЗОВАТЕЛЬСКОЙ СВЯЗИ | 2004 |
|
RU2273100C1 |
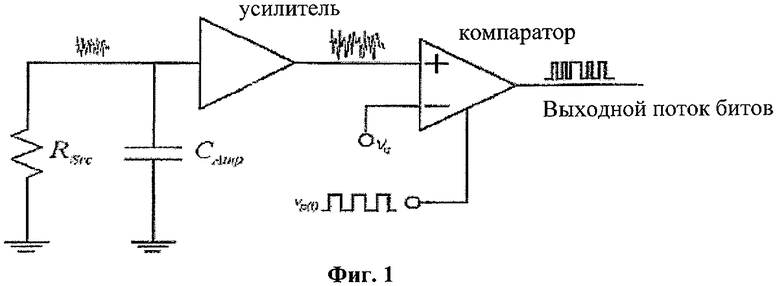
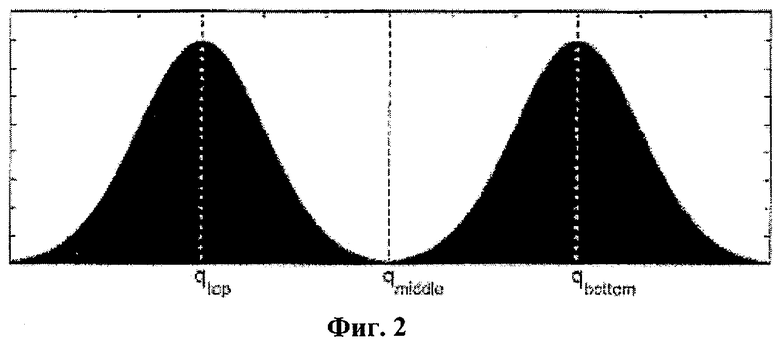
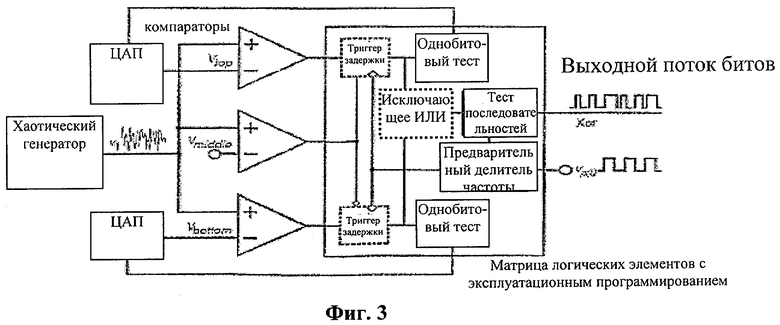
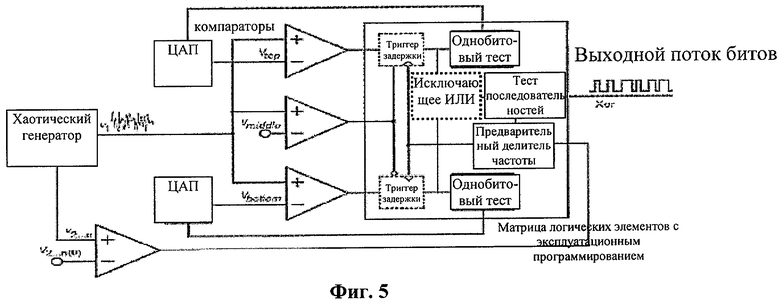
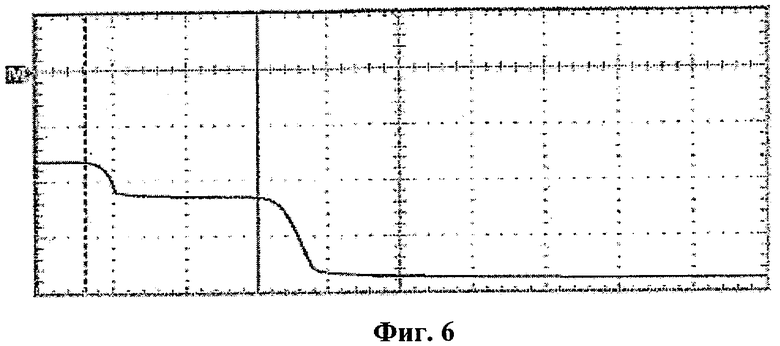
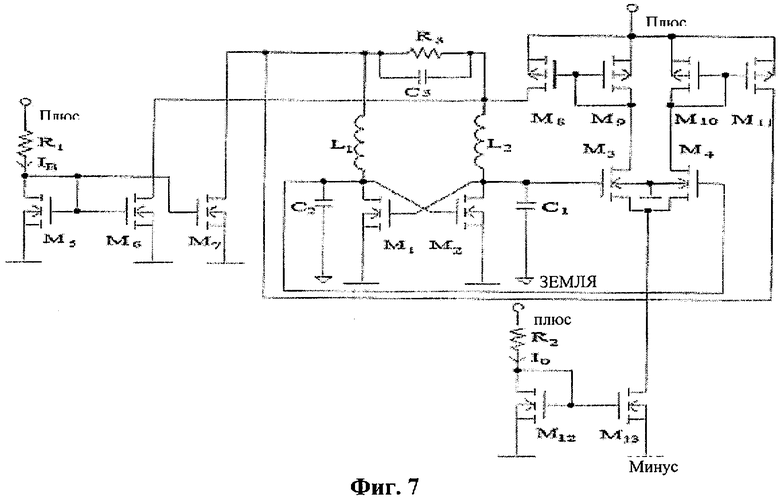
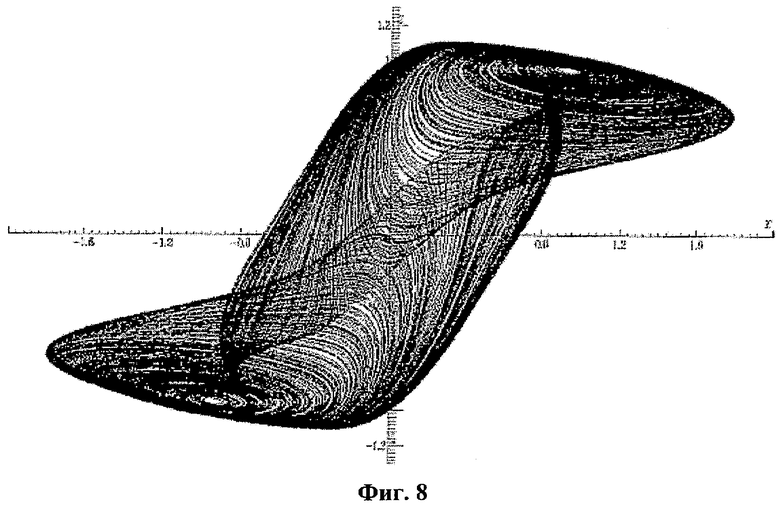
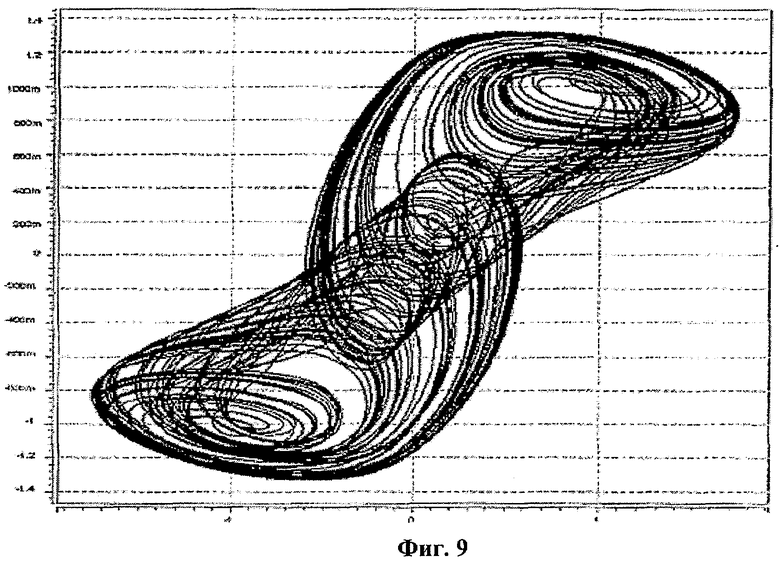
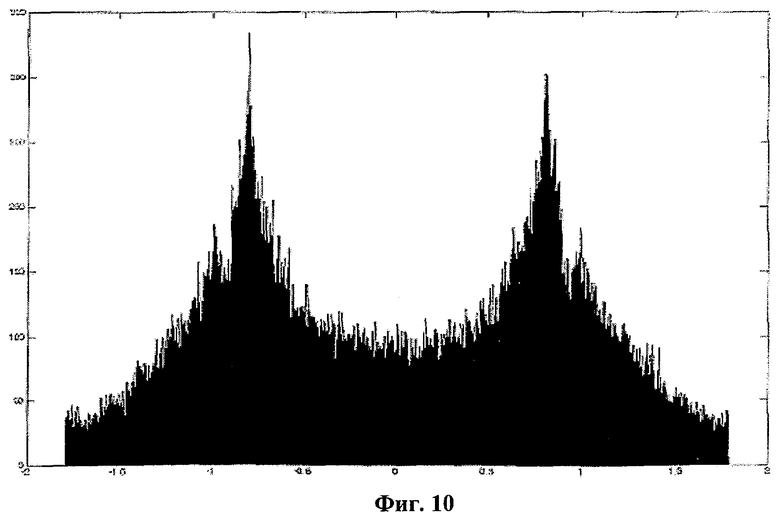

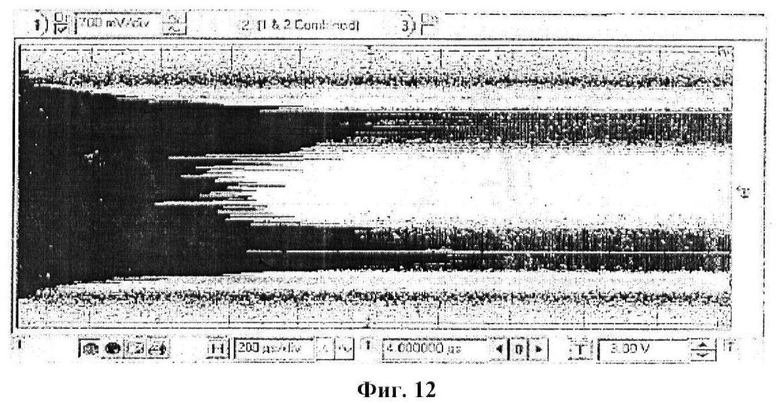
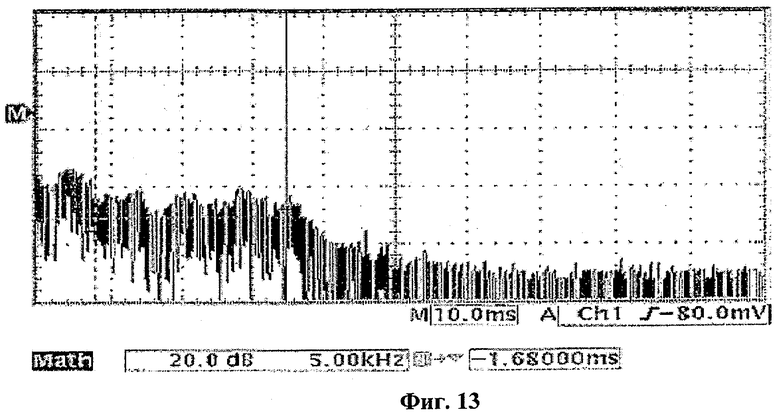
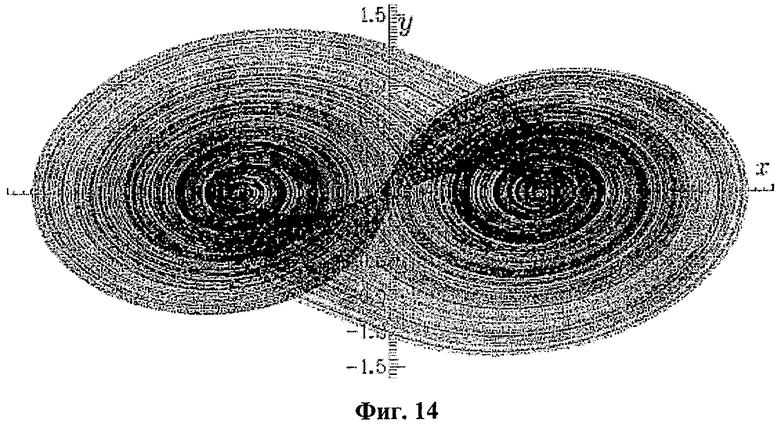
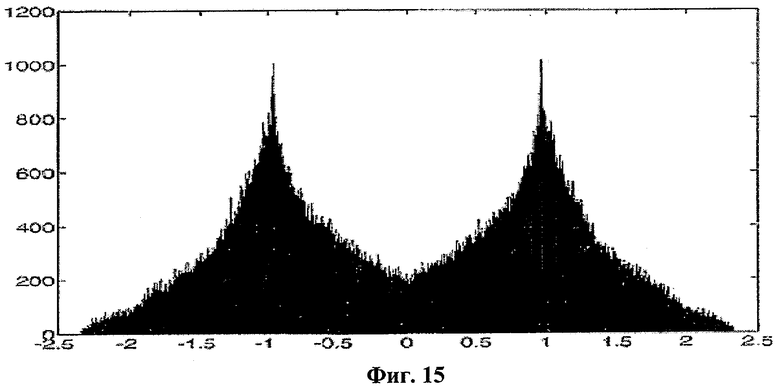
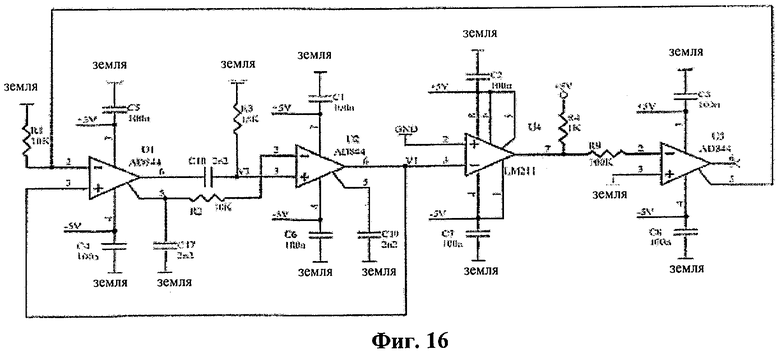
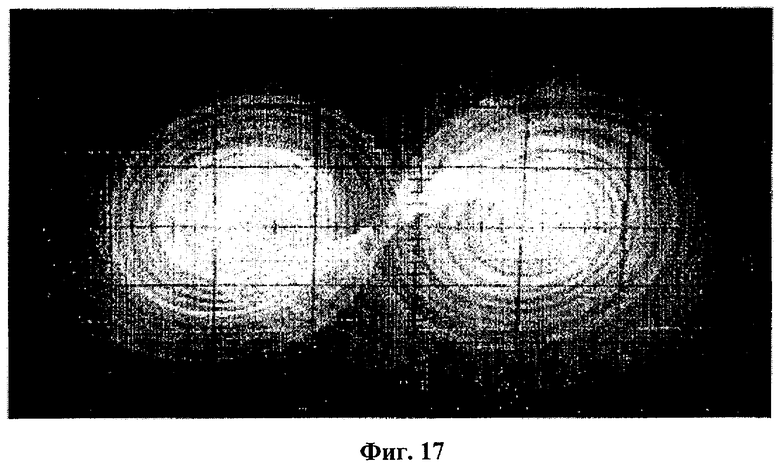
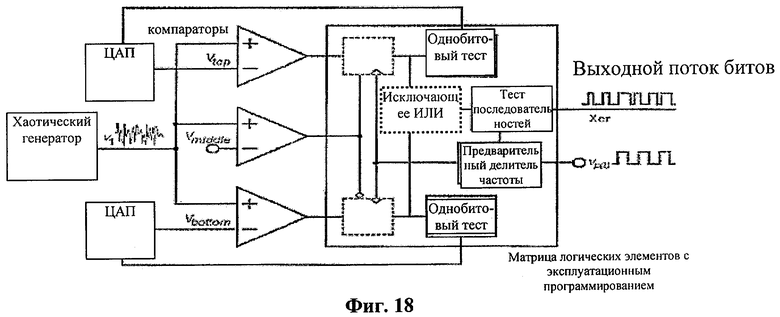
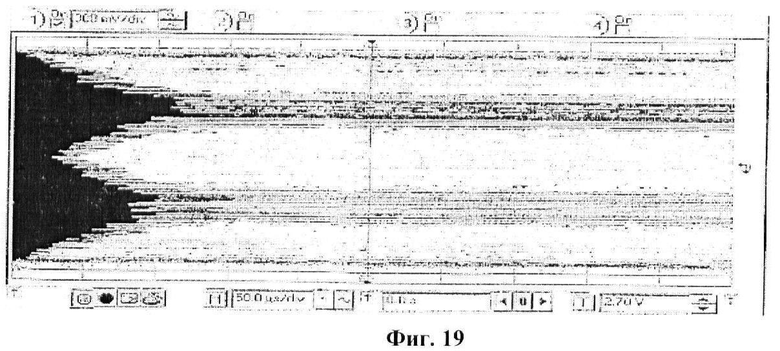
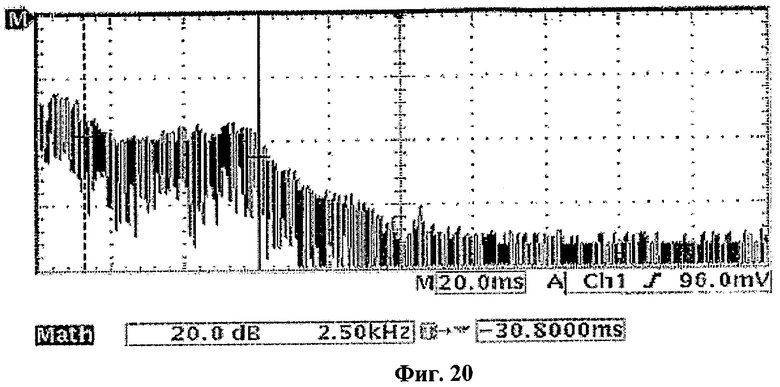
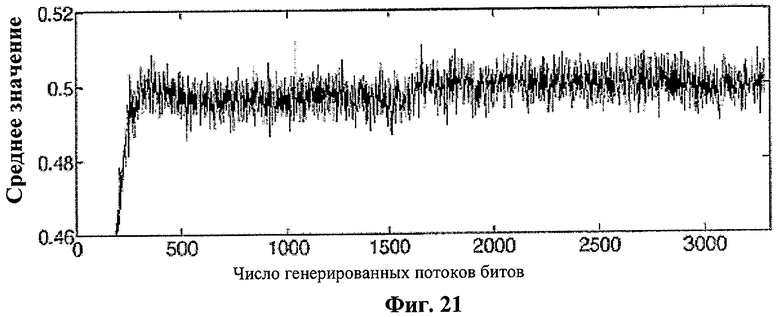
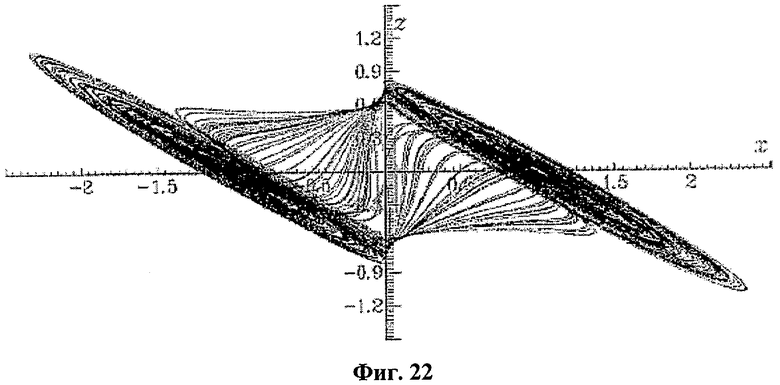
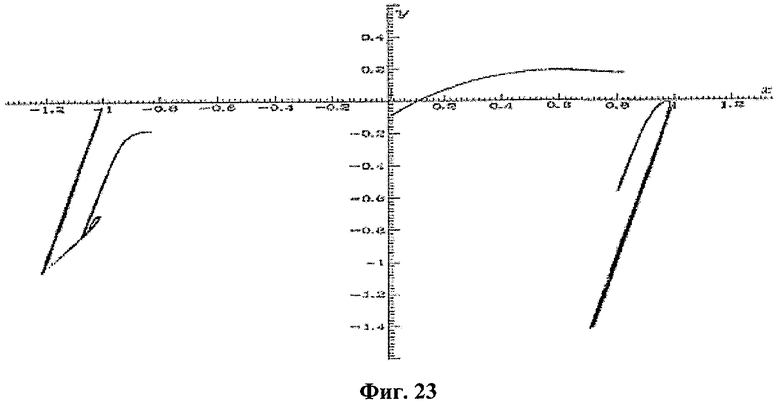
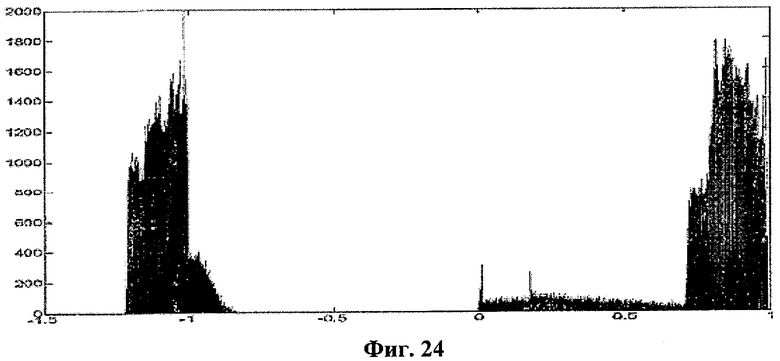
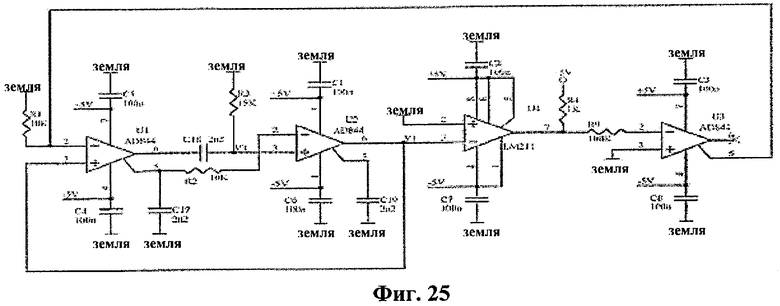

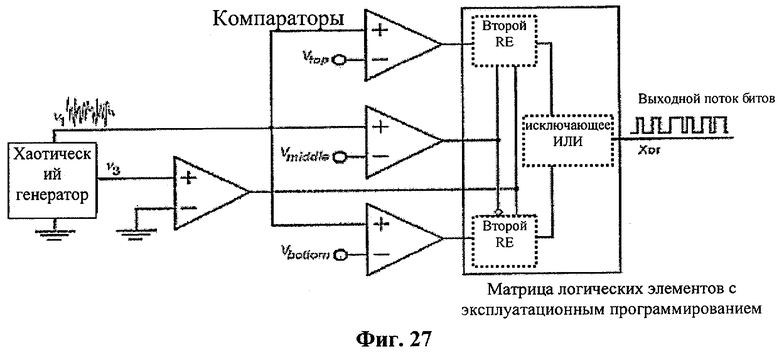

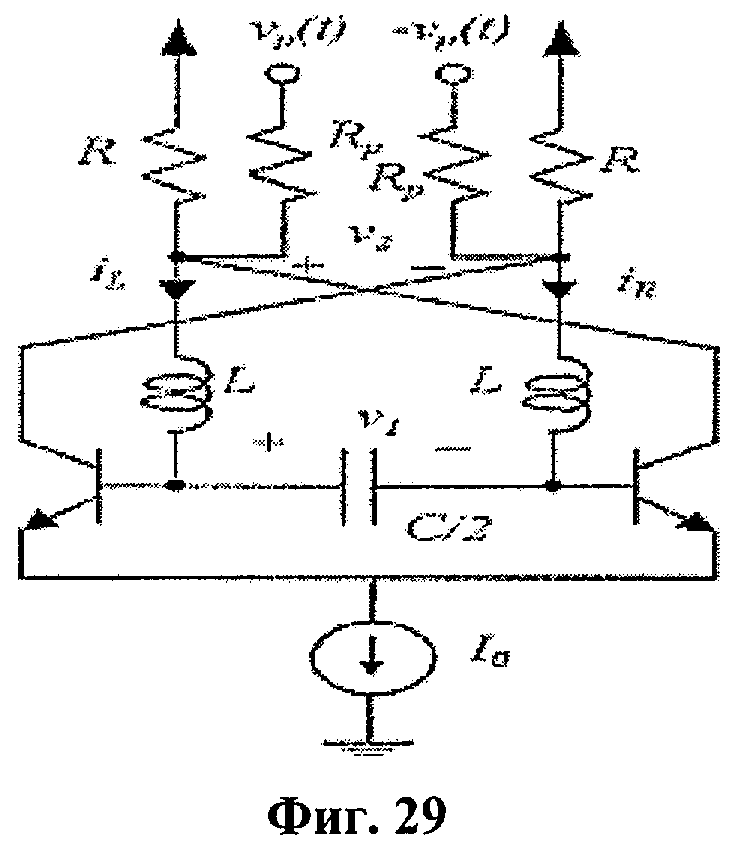
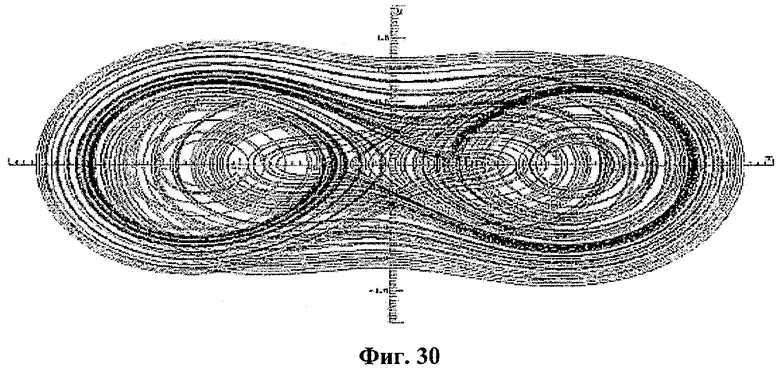
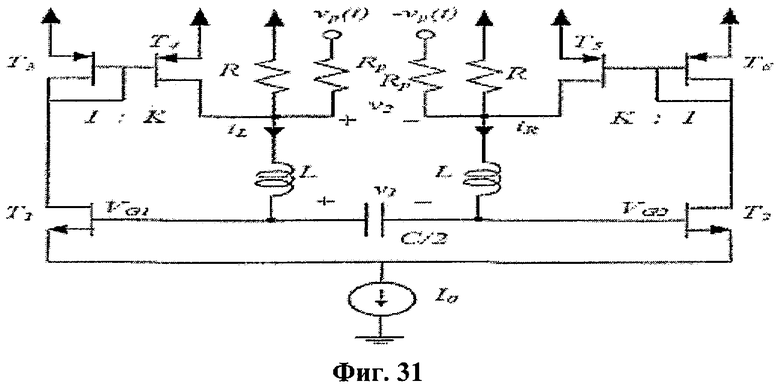
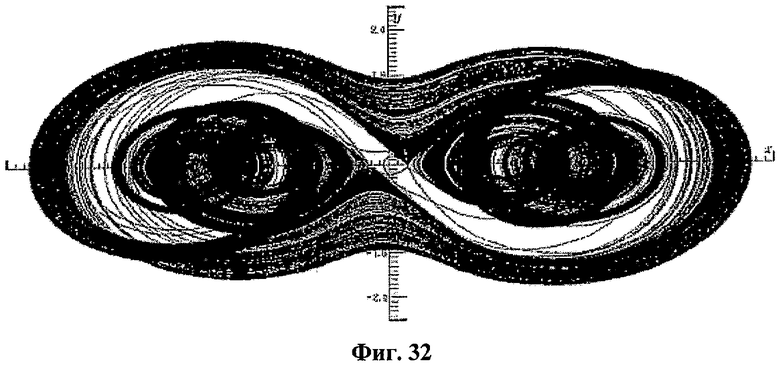
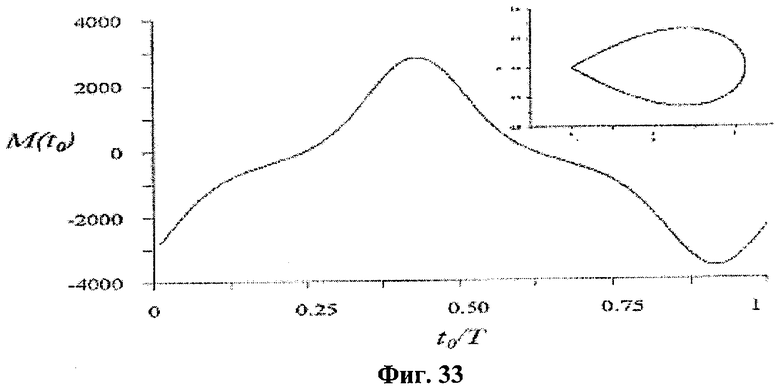

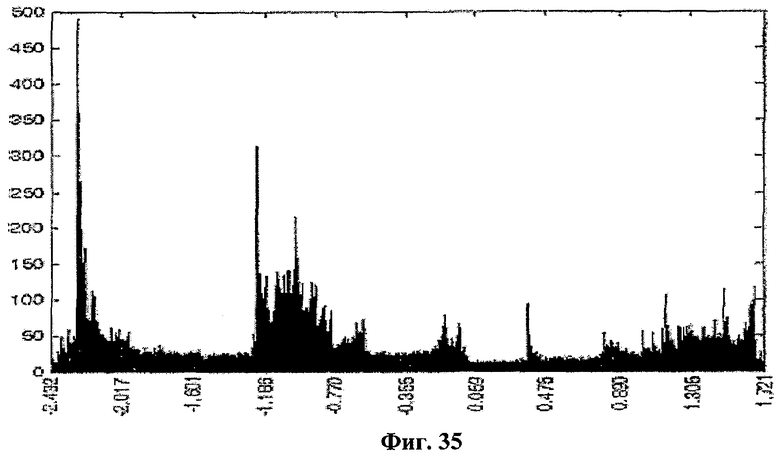
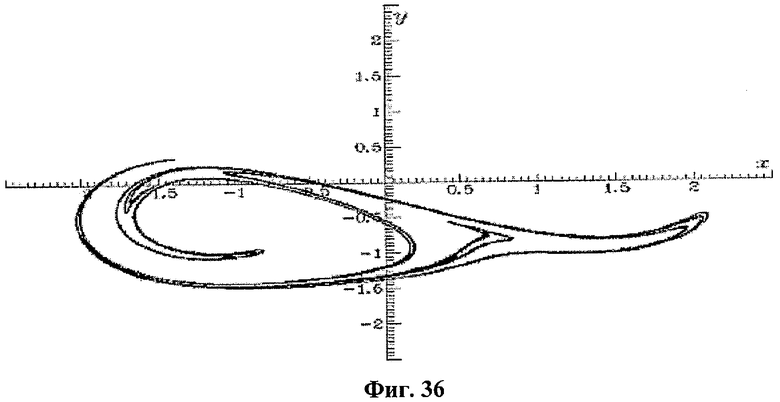
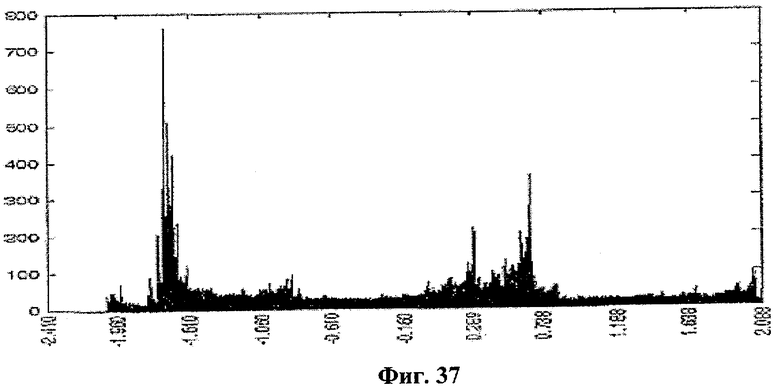
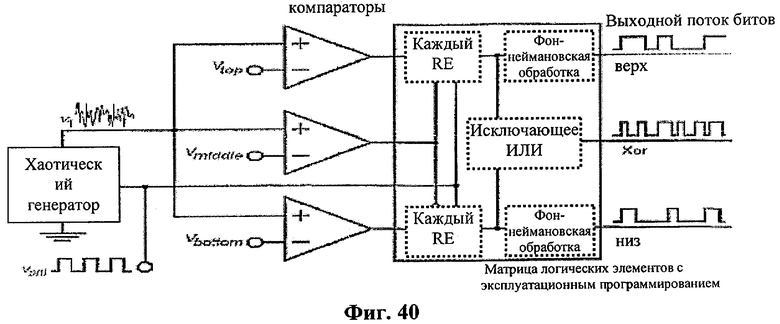
Изобретения относятся к области цифровой связи и могут быть использованы для генерации случайных чисел. Техническим результатом является увеличение производительности, повышение статистического качества выходной последовательности, обеспечение робастности к колебаниям параметров и внешним воздействиям, повышение скорости передачи данных без последующей обработки. В одном из вариантов изобретения устройство содержит три компаратора, хаотический генератор, триггеры задержки, цифроаналоговые преобразователи, делитель частоты, элемент «Исключающее ИЛИ», блоки однобитного теста и теста последовательностей. 5 н. и 12 з.п. ф-лы, 42 ил., 4 табл.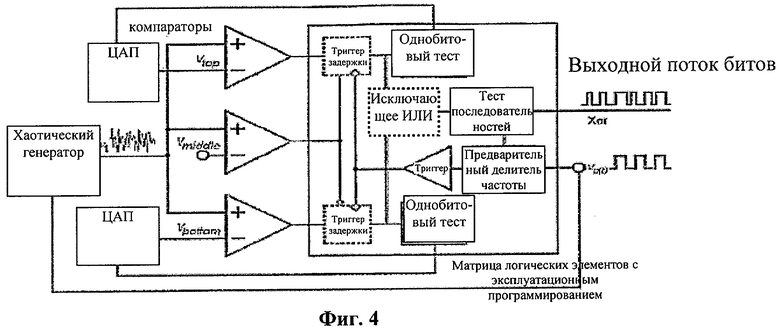
1. Способ генерации случайных битов, который основывают на хаотическом генераторе с непрерывным временем и на генерации необратимых случайных битов по областям в соответствии с распределением из одного из состояний, соответствующего одному из сигналов хаотического генератора, включающий следующие стадии:
а. стадию, на которой определяют необратимые подходящие сечения, где распределение выборок имеет две области, учитывая выборки, принадлежащие лишь одному из состояний, скажем, х1, которое соответствует v1, путем
i. определения подходящего набора параметров нормализованных величин, где выборки состояний x1 из одномерного сечения, которое получают при переходе из другого состояния (х2, х3, ... или xn), определенного как x2...n(t)=x2...n(0) с dx2...n/dt>0 или dx2...n/dt<0, имеют две области, или
ii. подгонки подходящих значений х2…n(0), которые соответствуют v2…n(0), где выборки состояний x1 из одномерного сечения, которое получают при переходе из другого состояния (х2, х3, ... или xn), определенного как x2...n(t)=x2...n(0) с dx2...n/dt>0 или dx2...n/dt<0, имеют две области, или
iii. определения подходящего набора параметров нормализованных величин, где периодические выборки состояния х1, которое получают на нарастающем или заднем фронтах внешнего периодического импульсного сигнала, то есть в моменты времени t, удовлетворяющие условию ωtmod2π=t0 (ω - частота импульсного сигнала), имеют две области, или
iv. подгонки подходящего t0, где периодические выборки состояния х1, которое получают на нарастающем или заднем фронтах внешнего периодического импульсного сигнала, то есть в моменты времени t, удовлетворяющие условию ωtmod2π=t0 (ω - частота импульсного сигнала), имеют две области, или
v. определения подходящего набора параметров нормализованных величин, где выборки состояний x1 из одномерного сечения, которое получают на нарастающем или заднем фронтах периодического импульсного сигнала (в моменты времени t, удовлетворяющие условию ωtmod2π=t0, где ω - частота импульсного сигнала, и 0≤t0≤1), который используют для возбуждения неавтономного хаотического генератора, имеют две области, или
vi. подгонки подходящего t0, где выборки состояний x1 из одномерного сечения, которое получают на нарастающем или заднем фронтах внешнего периодического импульсного сигнала (в моменты времени t, удовлетворяющие условию ωtmod2π=t0, где ω - частота импульсного сигнала, и 0≤t0≤1), который используют для возбуждения неавтономного хаотического генератора, имеют две области;
b. стадию, на которой генерируют случайные двоичные последовательности S(top)i и S(bottom)i из областных значений x1i,
которые получают из подходящего сечения по п.1а для областных порогов по следующей формуле:
S(top)i=sgn(x1i-qtop), если x1i≥qmiddle
S(bottom)i=sgn(x1i-qbottom), если xli<qmiddle,
где sgn(.) - знаковая функция, qtop и qbottom - пороги для верхнего и нижнего распределений соответственно, начальные значения которых являются медианами, и qmiddle - граница между распределениями;
c. стадию, на которой осуществляют компенсации сдвига для порогов qtop и qbottom по п.1b путем реализации однобитового теста;
d. стадию, на которой осуществляют частотную корректировку для частоты дискретизации x1 путем реализации теста последовательностей во избежание дискретизации x1 с запасом по частоте;
e. стадию, на которой генерируют двоичные данные S(xor)i, используя двоичные последовательности S(top)i и S(bottom)i по п.1b по следующей формуле:
S(xor)i=S(top)i(Exor)S(bottom)i,
где операцию исключающее ИЛИ (Exor) используют, чтобы устранить смещение, чтобы не снизить производительность.
2. Способ по п.1, в котором используемое состояние x1 может быть и другим состоянием х2, х3, ... или xn.
3. Способ по п.1, в котором однобитовый тест представляет собой однобитовый тест, выбранный из набора статистических тестов FIPS-140-1, FIPS-140-2 или NIST 800-22.
4. Способ по п.1, в котором тест последовательностей представляет собой тест последовательностей, выбранный из набора статистических тестов FIPS-140-1, FIPS-140-2 или NIST 800-22.
5. Способ генерации случайных битов (S(xor)i) по областям в соответствии с распределением, который основывают на автономном хаотическом генераторе с непрерывным временем, включающий следующие стадии:
а. стадию, на которой определяют необратимые подходящие сечения, где распределение выборок имеет две области, учитывая выборки, принадлежащие лишь одному из состояний, скажем х1, которое соответствует v1, путем
i. определения подходящего набора параметров нормализованных величин, где выборки состояний x1 из одномерного сечения, которое получают при переходе из другого состояния (х2, х3, ... или xn), определенного как x2...n(t)=x2...n(0) с dx2...n/dt>0 или dx2...n/dt<0, имеют две области, или
ii. подгонки подходящих значений х2…n(0), которые соответствуют v2...n(0), где выборки состояний x1 из одномерного сечения, которое получают при переходе из другого состояния (х2, х3, ... или xn), определенного как x2...n(t)=x2...n(0) с dx2...n/dt>0 или dx2...n/dt<0, имеют две области, или
iii. определения подходящего набора параметров нормализованных величин, где периодические выборки состояния х1, х2 ... или xn, которое получают на нарастающем или заднем фронтах внешнего периодического импульсного сигнала, то есть в моменты времени t, удовлетворяющие условию ωtmod2π=t0 (ω - частота импульсного сигнала), имеют две области, или
iv. подгонки подходящего t0, где периодические выборки состояния х1, х2 ... или xn, которое получают на нарастающем или заднем фронтах внешнего периодического импульсного сигнала, то есть в моменты времени t, удовлетворяющие условию ωtmod2π=t0 (ω - частота импульсного сигнала), имеют две области;
b. стадию, на которой генерируют случайные двоичные последовательности S(top)i и S(bottom)i из областных значений x1i, которые получают из подходящего сечения по п.5а для областных порогов по следующей формуле:
S(top)i=sgn(x1i-qtop), если x1i≥qmiddle
S(bottom)i=sgn(x1i-qbottom), если x1i<qmiddle,
где sgn(.) - знаковая функция, qtop и qbottom - пороги для верхнего и нижнего распределений соответственно, начальные значения которых являются медианами, и qmiddle - граница между распределениями;
c. стадию, на которой осуществляют компенсации сдвига для порогов qtop и qbottom по п.5b путем реализации однобитового теста;
d. стадию, на которой осуществляют частотную корректировку для частоты дискретизации x1 путем реализации теста последовательностей во избежание дискретизации x1 с запасом по частоте;
e. стадию, на которой генерируют двоичные данные S(xor)i, используя двоичные последовательности S(top)i и S(bottom)i по п.5b по следующей формуле:
S(xor)i=S(top)i(Exor)S(bottom)i,
где операцию исключающее ИЛИ (Exor) используют, чтобы устранить смещение, чтобы не снизить производительность.
6. Способ по п.5, в котором используемое состояние х1, упомянутое в пп.1 и 2, может быть и другим состоянием х2, х3, … или xn.
7. Способ по п.5, в котором однобитовый тест представляет собой однобитовый тест, выбранный из набора статистических тестов FIPS-140-1, FIPS-140-2 или NIST 800-22.
8. Способ по п.5, в котором тест последовательностей представляет собой тест последовательностей, выбранный из набора статистических тестов FIPS-140-1, FIPS-140-2 или NIST 800-22.
9. Устройство для генерации необратимых случайных битов по областям в соответствии с распределением, основанное на автономном или неавтономном хаотическом генераторе с непрерывным временем, состоящее из:
a. трех компараторов для генерации областных двоичных последовательностей S(top)i и S(bottom)i с использованием порогов Vtop, Vbottom и Vmiddle из сигнала хаотического генератора с непрерывным временем v1, который соответствует х1, которое имеет две области;
b. генератора периодических импульсных сигналов и двух триггеров задержки (D-триггер) для периодической дискретизации областных двоичных последовательностей S(top)i и S(bottom)i;
c. двух блоков однобитового теста (однобитовый тест) и двух цифроаналоговых преобразователей (ЦАП) для генерации и компенсации порогов Vtop и Vbottom, соответствующих qtop и qbottom используемым для верхнего и нижнего распределений соответственно;
d. блока теста последовательностей (тест последовательностей) и блока предварительного делителя частоты (делитель частоты) для коррекции частоты дискретизации v1, которая соответствует х1;
е. логического элемента исключающее ИЛИ (XOR) для устранения смещения и генерации случайных двоичных данных S(xor)i с использованием двоичных последовательностей S(top)i и S(bottom)i.
10. Устройство по п.9, в котором однобитовый тест представляет собой однобитовый тест, выбранный из набора статистических тестов FIPS-140-1, FIPS-140-2 или NIST 800-22.
11. Устройство по п.9, в котором тест последовательностей представляет собой тест последовательностей, выбранный из набора статистических тестов FIPS-140-1, FIPS-140-2 или NIST 800-22.
12. Устройство для генерации случайных битов по областям в соответствии с распределением, основанное на автономном или неавтономном хаотическом генераторе с непрерывным временем, состоящее из:
a. трех компараторов для генерации областных двоичных последовательностей S(top)i и S(bottom)i с использованием порогов Vtop, Vbottom и Vmiddle из сигнала хаотического генератора с непрерывным временем v1, который соответствует х1, которое имеет две области;
b. двух триггеров задержки (D-триггер) и еще одного компаратора для дискретизации областных двоичных последовательностей S(top)i и S(bottom)i из одномерного сечения v1, который соответствует х1, полученному при переходе состояния другого сигнала (v2, v3, ... или vn), который соответствует другому состоянию (х2, х3, ... или xn), определенному как v2...n(t)=v2…n(0), которое соответствует x2...n(t)=x2...n(0) с dx2...n/dt>0 или dx2...n/dt<0;
c. двух блоков однобитового теста (однобитовый тест) и двух цифроаналоговых преобразователей (ЦАП) для генерации и компенсации порогов Vtop и Vbottom, соответствующих qtop и qbottom, используемым для верхнего и нижнего распределений соответственно;
d. блока теста последовательностей (тест последовательностей) и блока предварительного делителя частоты (делитель частоты) для коррекции частоты дискретизации v1, которая соответствует x1;
e. логического элемента исключающее ИЛИ (XOR) для устранения смещения и генерации случайных двоичных данных S(xor)i с использованием двоичных последовательностей S(top)i и S(bottom)i.
13. Устройство по п.12, в котором однобитовый тест представляет собой однобитовый тест, выбранный из набора статистических тестов FIPS-140-1, FIPS-140-2 или NIST 800-22.
14. Устройство по п.12, в котором тест последовательностей представляет собой тест последовательностей, выбранный из набора статистических тестов FIPS-140-1, FIPS-140-2 или NIST 800-22.
15. Устройство для генерации необратимых случайных битов по областям в соответствии с распределением, основанное на неавтономном хаотическом генераторе с непрерывным временем, состоящее из:
a. трех компараторов для генерации областных двоичных последовательностей S(top)i и S(bottom)i с использованием порогов Vtop, Vbottom и Vmiddle из сигнала неавтономного хаотического генератора v1, который соответствует х1, которое имеет две области;
b. генератора периодических импульсных сигналов (vp(t)), который используется для возбуждения неавтономного хаотического генератора; блока задержки (задержка) для настройки соответствующего t0; и двух триггеров задержки (D-триггер) для дискретизации областных двоичных последовательностей S(top)i и S(bottom)i;
c. двух блоков однобитового теста (однобитовый тест) и двух цифроаналоговых преобразователей (ЦАП) для генерации и компенсации порогов Vtop и Vbottom, соответствующих qtop и qbottom, используемым для верхнего и нижнего распределений соответственно;
d. блока теста последовательностей (тест последовательностей) и блока предварительного делителя частоты (делитель частоты) для коррекции частоты дискретизации v1, которая соответствует x1;
e. логического элемента исключающее ИЛИ (XOR) для устранения смещения и генерации случайных двоичных данных S(xor)i с использованием двоичных последовательностей S(top)i и S(bottom)i.
16. Устройство по п.15, в котором однобитовый тест представляет собой однобитовый тест, выбранный из набора статистических тестов FIPS-140-1, FIPS-140-2 или NIST 800-22.
17. Устройство по п.15, в котором тест последовательностей представляет собой тест последовательностей, выбранный из набора статистических тестов FIPS-140-1, FIPS-140-2 или NIST 800-22.
| JP 2006139756 А, 01.06.2006 | |||
| JP 2001209314 А, 03.08.2001 | |||
| US 2006155551 А1, 13.07.2006 | |||
| ГЕНЕРАТОР СЛУЧАЙНЫХ ЧИСЕЛ | 1997 |
|
RU2122232C1 |
Авторы
Даты
2012-01-20—Публикация
2006-08-03—Подача