ОБЛАСТЬ ТЕХНИКИ
Настоящее изобретение относится к области генераторов случайных чисел (ГСЧ), в частности к квантовому ГСЧ, основанному на интерференции лазерных импульсов со случайной фазой.
ПРЕДШЕСТВУЮЩИЙ УРОВЕНЬ ТЕХНИКИ
Случайные числа являются важной частью всех современных криптографических систем и их повседневных приложений, таких как мобильная связь, безналичные платежи, электронная почта, интернет-банкинг, криптовалюта, сети блокчейн и т.д. В подавляющем большинстве случаев для этих приложений используются компьютерные алгоритмы генерации случайных чисел. Поскольку такие алгоритмы по своей природе являются детерминированными, результирующие битовые последовательности не являются действительно случайными и поэтому потенциально уязвимы для различных атак. Появление квантовых компьютеров может сделать криптографические системы, основанные на псевдослучайности, совершенно беззащитными; поэтому сегодня большое внимание уделяется системам квантового распределения ключа (КРК) или «квантовой криптографии», где истинно-случайные числа занимают особое место.
Для получения истинно случайных чисел вместо компьютерного алгоритма используют некоторый физический источник энтропии. Физические генераторы случайных чисел (ГСЧ) можно разделить на две большие группы: 1) ГСЧ, использующие классический шум в качестве источника энтропии, и 2) ГСЧ, основанные на измерении некоторой квантовой величины. В первом случае непредсказуемость физической величины связана с огромным количеством параметров физической системы и их сложной зависимостью от внешних условий. В случае квантовых ГСЧ непредсказуемость физической величины основана на вероятностной природе квантовых явлений. Таким образом, разница между классическими и квантовыми ГСЧ заключается в том, что первые являются принципиально детерминированными (задание достаточного количества начальных условий и знание достаточно полной физической модели процесса позволит предсказать – по крайней мере в принципе – поведение системы), тогда как вторые являются принципиально недетерминированными в силу законов квантовой механики.
За последние десятилетия были предложены многочисленные схемы квантовых ГСЧ, основанные на различных квантовых эффектах [1]; однако большинство современных квантовые ГСЧ используют различные методы квантовой оптики. Действительно, излучение полупроводниковых лазерных диодов является очень удобным источником квантовой случайности. Кроме того, оптические ГСЧ могут обеспечивать очень высокие скорости генерации случайных битов. Фактически, в настоящее время значительные исследовательские усилия сосредоточены на увеличении скорости генерации случайных бит путем улучшения существующих оптических схем и/или создания новых алгоритмов постобработки.
В ряде оптических ГСЧ в качестве источника энтропии используется фазовый шум лазерного излучения. Такие квантовые ГСЧ можно разделить на две группы, характеризующиеся непрерывным [2-4] и импульсным [5, 6] режимами работы лазера. Схемы, использующие непрерывное лазерное излучение, демонстрируют более медленную генерацию случайных чисел, чем квантовые ГСЧ, использующие интерференцию импульсов, поэтому последние, по мнению изобретателей, являются более перспективными, в особенности для приложений, где требуется высокая скорость передачи данных, в частности для КРК.
Схема оптического ГСЧ, использующая интерференцию лазерных импульсов была впервые предложена M. Jofre et al. [5]. Непрерывная последовательность импульсов заводилась в интерферометр Маха-Цендера, плечи в котором были подобраны таким образом, чтобы время задержки в длинном плече было кратно периоду следования импульсов, так что на выходе из интерферометра первый лазерный импульс последовательности встречался, например, с третьим, второй – с четвертым и т.д. Важное условие работы такой схемы состоит в том, что инжекционный ток должен переходить при модуляции через порог генерации, т.е. после каждого импульса лазер должен переводиться в режим усиления спонтанного излучения (УСИ). Поскольку в режиме УСИ переходы в подавляющем большинстве являются спонтанными, любые корреляции фазы электромагнитного поля очень быстро разрушаются. В результате каждый новый лазерный импульс появляется со случайной фазой. C. Abellán. показал, что даже при частоте повторения импульсов более 5 ГГц фазы последующих лазерных импульсов от лазера с распределенной обратной связью (РОС) действительно случайны. Такая высокая частота повторения импульсов позволила достичь скорости передачи до 42 Гбит / с [6].
Большинство предлагаемых реализаций, известных изобретателям, требуют дорогостоящих волоконно-оптических компонентов с сохранением поляризации (англ. polarization maintaining – PM) и быстрых аналого-цифровых преобразователей (АЦП). Кроме того, «сырые» случайные последовательности подвергаются сложным процедурам извлечения случайности, которые также требуют довольно дорогих компонентов, таких как программируемые логические интегральные схемы (ПЛИС) и/или программируемые пользователем вентильные матрицы (ППВМ). Поэтому представляется существенным при проектировании квантового ГСЧ учитывать экономический фактор. В этом контексте имеется несколько способов снизить цену конечного продукта: 1) модифицировать оптическую схему, чтобы избавиться от дорогих компонентов, 2) исключить использование дорогостоящего АЦП, 3) упростить постобработку «сырых» случайных последовательностей.
Однако гораздо более важное требование, которое имеет решающее значение для криптографических приложений, заключается в том, что квантовый ГСЧ должен быть устойчивым к различным атакам противника. Под атакой здесь подразумевается не криптоаналитический алгоритм (по определению, любой квантовый ГСЧ неуязвим для такого рода атак), а некоторое физическое воздействие, которое может незаметно для пользователя перевести ГСЧ в такой режим работы, при котором выходные последовательности бит не являются в действительности случайными. Таким образом, квантовый ГСЧ должен быть не только быстрым и недорогим, но и устойчивым к атакам.
СУЩНОСТЬ ИЗОБРЕТЕНИЯ
Технический результат заключается в создании высокоскоростного, устойчивого к атакам квантового генератора случайных чисел, который, по существу, устраняет недостатки, присущие аналогам существующего уровня техники.
Система генерации случайных чисел включает в себя драйвер лазерных импульсов; лазерный диод, излучающий лазерные импульсы; интерферометр Майкельсона, образованный волоконно-оптическим разветвителем, соединенным с первым зеркалом Фарадея через одномодовое волокно длины 
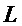
Блок КС может включать в себя, например, компаратор или аналого-цифровой преобразователь, объединенный со схемой выборки и хранения. Длина линии задержки интерферометра 

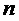

Способ генерации случайных чисел в сочетании с процедурой, обеспечивающей устойчивость к атакам, включает в себя управление лазерным диодом для излучения лазерных импульсов; преобразование фазового шума лазерного излучения в амплитудную модуляцию с помощью интерферометра; детектирование лазерных импульсов, выходящих из интерферометра с использованием фотоприемника; оцифровка выходного сигнала с фотоприемника с использованием цифрового преобразователя; вычисление плотности вероятности сигнала с фотоприемника; определение параметра 
Дополнительные особенности и преимущества изобретения будут изложены в последующем описании и частично будут очевидны или могут быть изучены при практическом использовании изобретения. Преимущества изобретения будут реализованы и достигнуты устройством изобретения, изложенном в письменном описании и формуле изобретения, а также на прилагаемых чертежах.
Следует понимать, что как предшествующее общее описание, так и последующее подробное описание являются примерными и пояснительными и предназначены для обеспечения дальнейшего объяснения заявленного изобретения.
КРАТКОЕ ОПИСАНИЕ ЧЕРТЕЖЕЙ
Прилагаемые чертежи, которые включены в данное описание для обеспечения дополнительного понимания изобретения и составляют его часть, иллюстрируют варианты реализации изобретения и вместе с описанием служат для пояснения принципов изобретения.
На чертежах:
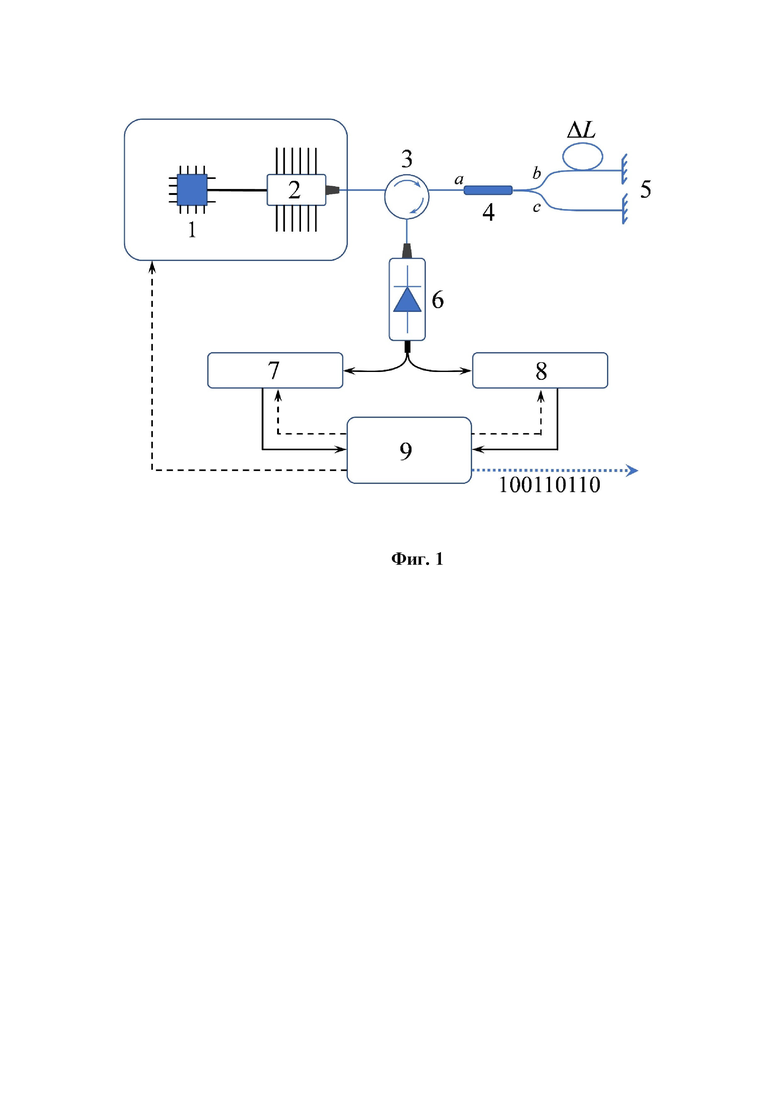
Цифровые обозначения: 1 – драйвер импульсов; 2 – лазерный диод; 3 – оптический циркулятор; 4 – оптический разветвитель; 5 – зеркала Фарадея; 6 –фотоприемник; 7 – цифровой преобразователь; 8 – блок контроля статистики; 9 – вычислительный блок; 10 – аналоговый вход, 11 – сигнал управления, 12 – аналоговый выход, 13 – АЦП.
На Фиг. 1 показана принципиальная схема квантового ГСЧ. 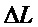
На Фиг. 2 показана схема волоконного интерферометра Маха-Цендера (а) и Майкельсона (б). 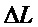
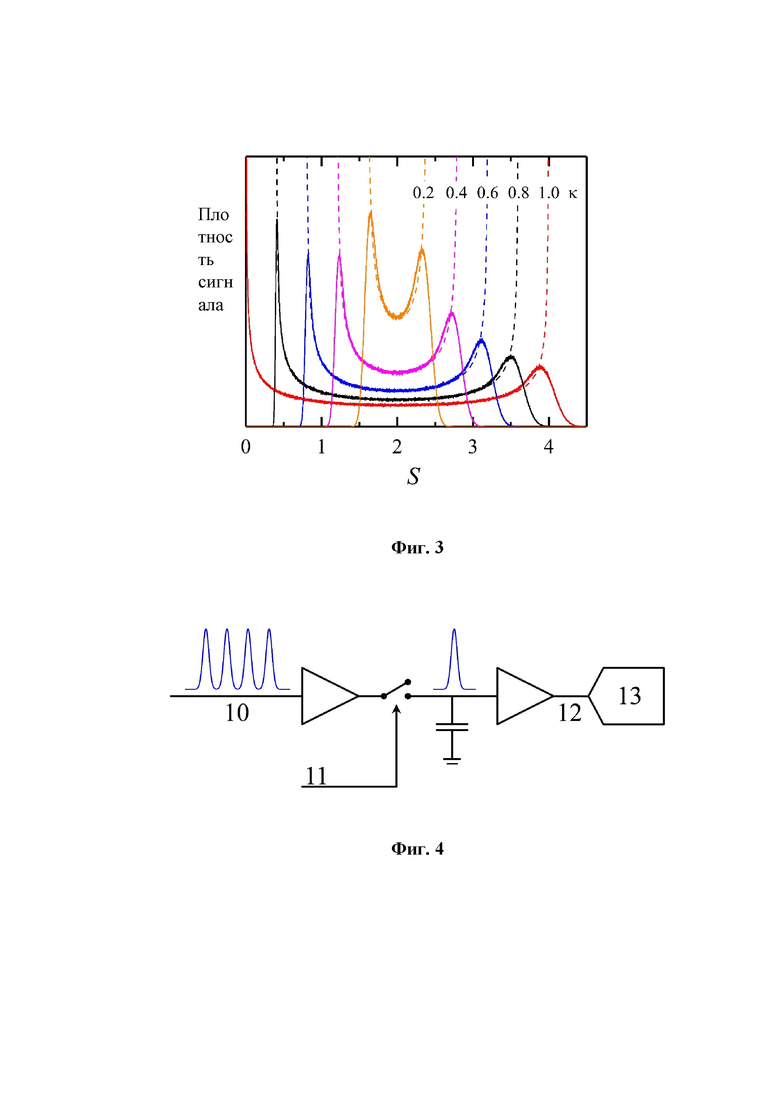
На Фиг. 3 показаны результаты моделирования методом Монте-Карло распределений плотности сигнала, соответствующих интерференции лазерных импульсов со случайной фазой.
На Фиг. 4 показан вариант осуществления блока контроля статистики на основе низкоскоростного АЦП, включающего в себя схему быстрой выборки и хранения.
На Фиг. 5 показана блок-схема, объясняющая алгоритм работы квантового генератора случайных чисел.
ОСУЩЕСТВЛЕНИЕ ИЗОБРЕТЕНИЯ
Теперь будет сделано подробное описание предпочтительных вариантов реализации настоящего изобретения, примеры которых проиллюстрированы на прилагаемых чертежах.
Изобретение реализует извлечение случайных бит из фазы лазерных импульсов и позволяет «на лету» проверять сигнал на наличие возможного вмешательства противника. Квантовый ГСЧ разработан таким образом, чтобы быть простым и недорогим, и представляет собой оптимальное решение для коммерческого производства. Ниже, в первом подразделе, мы подробно рассмотрим оптическую схему с уравнениями, объясняющими наш выбор типа интерферометра. Во втором подразделе мы рассмотрим вопрос, связанный с плотностью распределения случайного сигнала, измерение которой позволяет реализовать эффективную защиту от возможных физических атак. Наконец, в последнем подразделе мы опишем процедуру, которая делает квантовый ГСЧ устойчивым к атакам и обеспечивает его самонастройку.
Оптическая схема
Принципиальная схема предлагаемого квантового ГСЧ показана на Фиг. 1. Источником энтропии квантового ГСЧ является случайная фаза излучения полупроводникового лазера, которая преобразуется в амплитудную модуляцию посредством интерференции лазерных импульсов в интерферометре. Лазер модулируется драйвером импульсов через порог генерации, и непрерывная последовательность импульсов приходит на интерферометр Майкельсона, где время задержки длинного плеча выбирается кратным периоду повторения импульсов. Затем фотодиод детектирует интерференцию двух импульсов, излучаемых лазером в разные моменты времени и, таким образом, имеющих случайные фазы.
Интерференция двух лазерных импульсов может быть представлена как интерференция двух коротких пучков, имеющих колоколообразный временной профиль. Для простоты предположим, что вблизи входа фотоприемника амплитуда электромагнитного поля одиночного импульса определяется гауссовой функцией времени:
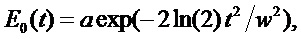
где 
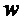

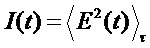


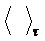
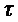




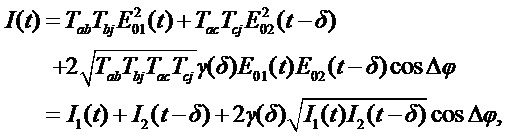
где 

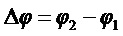
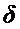


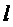
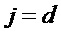



Здесь 
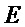
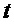
Следует отметить, что фаза отдельного импульса в месте схождения интерферирующих пучков может быть записана как 

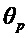




где 
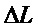

Интегральный сигнал, вызванный попаданием импульса на фотоприемник, определим следующим образом:

где произведена нормировка сигнала на импульс единичной амплитуды. Подставляя (2) в (5), получим:
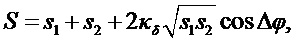
где 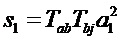

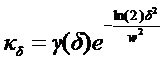
определяет видность интерферометра, причем 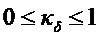
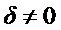

До этого момента считалось, что интерферирующие пучки являются плоскополяризованными, причем плоскость поляризации сохраняется на всем пути распространения импульса по оптоволокну. Такое предположение оправдано лишь в том случае, если в системе используется оптоволокно с сохранением поляризации. Если же используется стандартное одномодовое волокно, то следует учитывать поляризационную модовую дисперсию (ПМД), т.е. принимать во внимание наведенное двулучепреломление. Последнее приводит к тому, что излучение импульса при распространении по волокну перестает быть линейно поляризованным, а приобретает эллиптическую поляризацию.
Рассмотрим кратко интерференцию двух монохроматических пучков с произвольной поляризацией. Пусть имеются две монохроматические волны, распространяющиеся вдоль оси 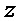

где 




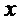
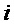
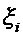
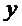
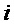
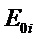
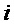



Отсюда следует, что амплитуда результирующей волны равна

Если 





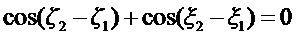
Покажем теперь, как будет влиять ПМД на интерференцию лазерных импульсов. Будем считать, что на выходе из лазера все импульсы поляризованы одинаково, в одной и той же плоскости, и отличаются только фазой начальных колебаний, т.е. для двух различных импульсов:

Дальнейшее рассмотрение будет зависеть от типа интерференционной схемы. Рассмотрим сначала интерферометр Маха-Цендера. Наведенное двулучепреломление приводит к тому, что 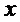



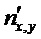
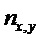


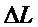

Подставляя (12) в (10), получаем для суммы косинусов:
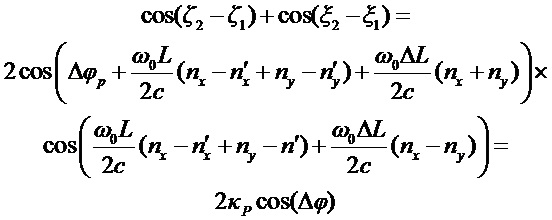
где

и где был введен коэффициент
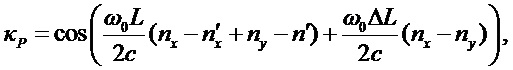
определяющий видность интерферометра, связанную с несовпадением поляризаций интерферирующих импульсов (назовем эту величину поляризационной видностью). Если эффект наведенного двулучепреломления в обоих плечах интерферометра примерно одинаков, т. е. можно положить 
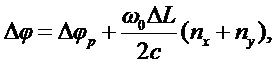
а коэффициент 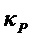

где 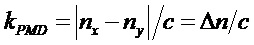




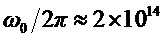

т. е. 



Аналогичный результат получается и для интерферометра Майкельсона с обычными зеркалами. Однако, при использовании зеркал Фарадея вектора обоих поляризационных компонент, 
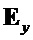

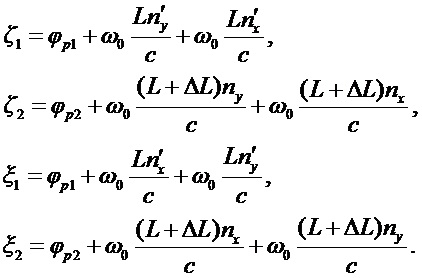
Действительно, из (19) видно, что 
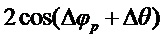

Можно сделать вывод, что использование оптоволокна без сохранения поляризации в случае с интерферометром Маха-Цендера является нежелательным из-за значительного влияния эффекта ПМД. Поэтому, чтобы избежать использования дорогого волокна с сохранением поляризации, следует использовать интерферометр Майкельсона с зеркалами Фарадея.
Плотность вероятности случайного сигнала
С экспериментальной точки зрения, источником энтропии в рассматриваемом квантовом ГСЧ является случайный сигнал 
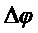
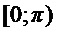




где значения случайных величин 
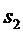


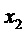


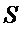
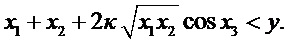
Плотность распределения 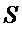


Форма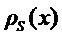


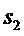
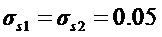

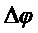
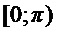
Пунктирные линии на Фиг. 3 соответствуют функции

которая представляет собой распределение плотности сигнала

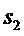

Разность между асимптотами функции

и далее будем для простоты считать эту величину шириной распределения.
Так как изменение 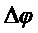
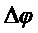


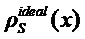
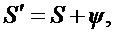
где 
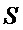
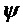
Устойчивость к атакам
Как отмечалось выше, источник случайности является совершенно непредсказуемым, только если он имеет квантовую природу. Классический шум, в свою очередь, является не только принципиально детерминированным, но, что более важно, может подвергаться внешнему воздействию со стороны противника. Таким образом, при строгом подходе для получения истинно-случайной последовательности бит следует использовать лишь квантовую составляющую сигнала. Однако разделить классические и квантовые шумы невозможно, поскольку генерация электрических импульсов, а также детектирование оптического сигнала осуществляется с использованием классических устройств. Поэтому следует каким-то образом оценить соотношение 
При этом, если классическими флуктуациями нельзя пренебречь, то следует учитывать возможное влияние противника, который потенциально имеет доступ к классическому шуму и, таким образом, может поставить под угрозу квантовый ГСЧ, введя корреляции в его выходные данные. Соотношение 
Отношение квантового шума к классическому шуму было оценено рядом авторов для различных квантовых ГСЧ [4, 7-9]. В их работах предполагалось, что шумовой сигнал от фотоприемника содержит классический и квантовый вклады в мультипликативной форме. При таком предположении значение 

Процедуру извлечения случайности можно рассматривать как сжатие необработанной 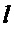

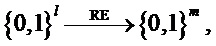
где можно ввести (обычный) коэффициент сжатия 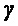

Коэффициент 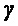
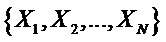

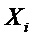


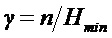
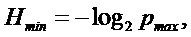
где 
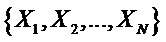
Коэффициент сжатия зависит от того, как оцифровывается сигнал с фотоприемника. При использовании АЦП следует учитывать, что сигнал будет с большей вероятностью попадать в ячейки, соответствующие большей вероятности, то есть оцифровка сигнала с неравномерным распределением плотности автоматически приводит к неоднородной случайной последовательности. Напротив, при оцифровке сигнала с помощью компаратора следует просто подобрать такое пороговое напряжение, чтобы число нулей и единиц в выходной последовательности было одинаковым. Действительно, принимая во внимание истинную случайность фазы 
Следует отметить, что при такой реализации только один бит извлекается на одну выборку, то есть частота генерации случайных бит ограничена частотой повторения лазерных импульсов. Несмотря на это ограничение, использование компаратора представляется очень выгодным, так как 1) он позволяет избежать дорогостоящих АЦП и 2) позволяет извлекать случайные биты без необходимости их обработки и, следовательно, без уменьшения потерь (при условии, что классический шум мал).
Коэффициент сжатия 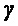

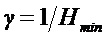

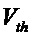
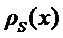
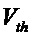

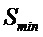
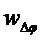
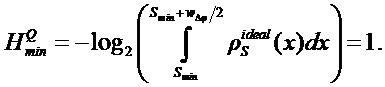
Далее необходимо отметить, что распределение плотности сигнала 

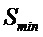
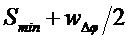

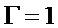
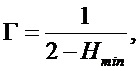
где

и где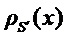
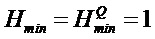
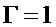
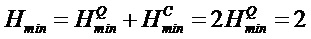
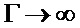
Этот подход может быть легко распространен на случай использования АЦП. Для этого отметим сначала, что распределение плотности 

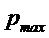
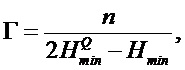
где 

с размером ячейки 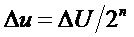

Поскольку значение эффективного коэффициента сжатия отражает вклад от классических флуктуаций, знание 



В первом варианте осуществления изобретения блок КС представляет собой просто высокоскоростной компаратор. В этом случае профиль распределения плотности восстанавливается с использованием развертки порогового напряжения. Для каждого значения 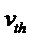
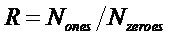
Далее в тексте описания во избежание путаницы, верхний регистр будет использоваться для обозначения порогового напряжения основного компаратора - 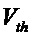
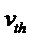



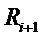


где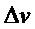
Во втором варианте осуществления можно использовать схему выборки и хранения в комбинации с относительно низкоскоростным АЦП (см. Фиг. 4), скорость работы которого ограничена несколькими миллионами сэмплов в секунду, то есть намного ниже, чем частота повторения импульсов. Отметим, что поскольку мы сознательно избегаем использования высокоскоростного АЦП, заменяя его компаратором и снижая тем самым цену конечного продукта, применение сверхскоростного (и дорогого) АЦП в данном случае представляется нецелесообразным. Роль схемы выборки и хранения на Фиг. 4 сводится к регулярной выборке одного импульса из длинной последовательности импульсов. Для этого управляющий сигнал на Фиг. 4 открывает конденсатор в момент времени, соответствующий приходу импульса, и затем быстро закрывает его на длительное время, устраняя, таким образом, дальнейшие изменения во входном сигнале. Такое «разрежение» позволяет накапливать статистику быстро меняющегося сигнала с фотодетектора медленным АЦП, т. е. позволяет находить
Наконец, рассмотрим осуществление защиты от внешних атак на целостность/достоверность формируемой случайной последовательности. В зависимости от того, как это будет выполнено, может быть предложено два подхода для реализации защиты от атак и, следовательно, два варианта реализации цифрового преобразователя.
Первый вариант предполагает использование одного высокоскоростного компаратора, пороговое напряжение для которого рассчитывается с использованием ранее найденного экспериментального распределения плотности 
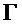
Во втором варианте осуществления можно использовать пару компараторов, пороговые напряжения которых установлены 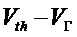



Затем сигналы от двух компараторов 

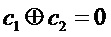
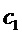
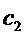
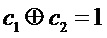
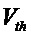
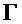

Следует отметить, что вариант осуществления схемы с двумя компараторами концептуально аналогичен случаю, когда ненадежные биты отбрасываются посредством процедуры извлечения случайности. Фактически, отбрасывая сигнал, попадающий в диапазон от 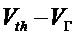

Суммируя вышеизложенное, на Фиг. 5 представлен с помощью упрощенной блок-схемы рабочий цикл квантового ГСЧ. В указанной на Фиг. 5 схеме блок КС реализован с помощью компаратора с разверткой порогового напряжения, а цифровой преобразователь реализован в виде пары компараторов. Сначала мы предполагаем, что лазер непрерывно генерирует короткие импульсы с заданной частотой повторения. Алгоритм работы квантового ГСЧ начинается с расчета 
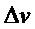
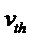









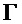
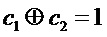
Таким образом, после описания предпочтительного варианта реализации схемы специалистам в данной области должно быть очевидно, что были достигнуты определенные преимущества описанного способа и устройства.
Следует также понимать, что различные модификации, адаптации и их альтернативные варианты осуществления могут быть выполнены в пределах объема и сущности настоящего изобретения. Изобретение определяется формулой изобретения.
Источники информации
[1] M. Herrero-Collantes and J. C. Garcia-Escartin, “Quantum random number generators,” Rev. Mod. Phys., vol. 89, p. 015004, 2017.
[2] H. Guo, W. Tang, Y. Liu, and W. Wei, “Truly random number generation based on measurement of phase noise of a laser,” Phys. Rev. E, vol. 81, p. 051137, 2010.
[3] B. Qi, Y.-M. Chi, H.-K. Lo, and L. Qian, “High-speed quantum random number generation by measuring phase noise of a single-mode laser,” Opt. Lett., vol. 35, pp. 312-314, 2010.
[4] F. Xu, B. Qi, X. Ma, H. Xu, H. Zheng, and H.-K. Lo, “Ultrafast quantum random number generation based on quantum phase fluctuations,” Opt. Express, vol. 20, pp. 12366-12377, 2012.
[5] M. Jofre, M. Curty, F. Steinlechner, G. Anzolin, J. P. Torres, M. W. Mitchell, and V. Pruneri, “True random numbers from amplified quantum vacuum,” Opt. Express, vol. 19, pp. 20665-20672, 2011.
[6] C. Abellán, W. Amaya, M. Jofre, M. Curty, A. Acín, J. Capmany, V. Pruneri, and M. W. Mitchell, “Ultra-fast quantum randomness generation by accelerated phase diffusion in a pulsed laser diode,” Opt. Express, vol. 22, pp. 1645-1654, 2014.
[7] C. Gabriel, C. Wittmann, D. Sych, R. Dong, W. Mauerer, U. L. Andersen, C. Marquardt, and G. Leuchs, “A generator for unique quantum random numbers based on vacuum states,” Nat. Photonics, vol. 4, p. 711, 2010.
[8] X. Ma, F. Xu, H. Xu, X. Tan, B. Qi, and H.-K. Lo, “Postprocessing for quantum random-number generators: Entropy evaluation and randomness extraction,” Phys. Rev. A, vol. 87, p. 062327, 2013.
[9] F. Raffaelli, P. Sibson, J. E. Kennard, D. H. Mahler, M. G. Thompson, and J. C. F. Matthews, “Generation of random numbers by measuring phase fluctuations from a laser diode with a silicon-on-insulator chip,” Opt. Express, vol. 26, pp. 19730-19741, 2018.
| название | год | авторы | номер документа |
|---|---|---|---|
| ВЫСОКОСКОРОСТНОЙ КВАНТОВЫЙ ГЕНЕРАТОР СЛУЧАЙНЫХ ЧИСЕЛ НА ИНТЕРФЕРЕНЦИИ ЛАЗЕРНЫХ ИМПУЛЬСОВ С ИСПОЛЬЗОВАНИЕМ МНОГОКАНАЛЬНОГО АНАЛОГО-ЦИФРОВОГО ПРЕОБРАЗОВАТЕЛЯ И СПОСОБ ФОРМИРОВАНИЯ СЛУЧАЙНОЙ ЧИСЛОВОЙ ПОСЛЕДОВАТЕЛЬНОСТИ С ЕГО ПОМОЩЬЮ | 2020 |
|
RU2758889C1 |
| ВЫСОКОСКОРОСТНОЙ КВАНТОВЫЙ ГЕНЕРАТОР СЛУЧАЙНЫХ ЧИСЕЛ НА ПЕРЕКЛЮЧЕНИИ ПОЛЯРИЗАЦИИ В ПОЛУПРОВОДНИКОВОМ ЛАЗЕРЕ С ВЕРТИКАЛЬНЫМ РЕЗОНАТОРОМ (ВАРИАНТЫ) И СПОСОБ ФОРМИРОВАНИЯ СЛУЧАЙНОЙ ЧИСЛОВОЙ ПОСЛЕДОВАТЕЛЬНОСТИ С ЕГО ПОМОЩЬЮ | 2022 |
|
RU2788400C1 |
| АМПЛИТУДНО-ФАЗОВЫЙ МОДУЛЯТОР НА ПОЛУПРОВОДНИКОВЫХ ЛАЗЕРАХ С ОПТИЧЕСКОЙ ИНЖЕКЦИЕЙ И СПОСОБ ЕГО ПРИМЕНЕНИЯ ДЛЯ КВАНТОВОГО РАСПРЕДЕЛЕНИЯ КЛЮЧЕЙ | 2021 |
|
RU2813164C1 |
| Система квантового распределения ключей с недоверенным центральным узлом и способ приготовления квантовых состояний для протокола квантового распределения ключей с недоверенным центральным узлом | 2024 |
|
RU2834620C1 |
| УЧЕБНАЯ УСТАНОВКА ДЛЯ ВЫПОЛНЕНИЯ ЭКСПЕРИМЕНТОВ ПО КВАНТОВОЙ ОПТИКЕ ДЛЯ ЦЕЛЕЙ ИЗУЧЕНИЯ ПРОТОКОЛОВ КВАНТОВОЙ КРИПТОГРАФИИ | 2019 |
|
RU2722133C1 |
| ДВУХПРОХОДНАЯ СИСТЕМА ФАЗОВОЙ МОДУЛЯЦИИ ДЛЯ КВАНТОВОГО РАСПРЕДЕЛЕНИЯ КЛЮЧЕЙ | 2022 |
|
RU2776030C1 |
| Способ управления интерференционной картиной в однопроходной системе квантовой криптографии | 2017 |
|
RU2665249C1 |
| Волоконно-оптическая система и способ квантового распределения ключей с недоверенным центральным узлом | 2024 |
|
RU2835156C1 |
| Способ обнаружения атаки с ослеплением детекторов в системах квантовой криптографии с поляризационным кодированием | 2021 |
|
RU2783977C1 |
| Устройство определения степени и места возмущения зонной волоконно-оптической системы охраны объектов | 2022 |
|
RU2836460C2 |


Система генерации случайных чисел включает в себя драйвер импульсов; лазерный диод, излучающий лазерные импульсы; волоконно-оптический несбалансированный интерферометр, преобразующий фазовый шум лазерного излучения в амплитудную модуляцию; оптический циркулятор или изолятор, использующийся для предотвращения нежелательной обратной связи в резонатор лазера; фотоприемник, детектирующий лазерные импульсы на выходе из интерферометра; цифровой преобразователь, оцифровывающий выходные данные с фотоприемника; блок контроля статистики, использующийся для расчета плотности вероятности выходного сигнала фотодетектора и определения параметра Г, связанный с отношением классического шума к квантовому и позволяющий оценить квантовую составляющую случайных изменений сигнала и обеспечивать устойчивость системы к атакам; и вычислительный блок, принимающий оцифрованный сигнал с цифрового преобразователя и выводящий истинно-случайную последовательность бит. Технический результат – упрощение конструкции с сохранением защиты от атак. 2 н. и 13 з.п. ф-лы, 5 ил.
1. Квантовый генератор случайных чисел (ГСЧ), включающий в себя:
лазерный диод, приводимый в действие драйвером импульсов;
волоконно-оптический несбалансированный интерферометр, преобразующий фазовый шум лазерного излучения в амплитудную модуляцию;
фотоприемник, выполняющий детектирование лазерных импульсов на выходе из интерферометра;
цифровой преобразователь, выполняющий оцифровку выходных данных с фотоприемника;
блок контроля статистики, осуществляющий вычисление плотности вероятности сигнала с фотоприемника;
и
вычислительный блок, обеспечивающий получение оцифрованного выходного сигнала от цифрового преобразователя и выдачи истинной случайной битовой последовательности.
2. Генератор по п.1, отличающийся тем, что блок контроля статистики включает в себя компаратор.
3. Генератор по п.1, отличающийся тем, что блок контроля статистики включает в себя аналого-цифровой преобразователь, объединенный со схемой выборки и хранения.
4. Генератор по п.1, отличающийся тем, что цифровой преобразователь включает в себя один высокоскоростной компаратор.
5. Генератор по п.1, отличающийся тем, что цифровой преобразователь включает в себя пару высокоскоростных компараторов.
6. Генератор по п.1, отличающийся тем, что волоконно-оптический интерферометр представляет собой интерферометр Майкельсона, построенный из волоконно-оптических компонентов, не поддерживающих поляризацию.
7. Генератор по п.1, отличающийся тем, что линия задержки интерферометра 
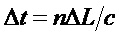

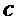
8. Генератор по п.1, отличающийся тем, что дополнительно содержит циркулятор, предотвращающий обратную связь с лазерным диодом.
9. Способ генерации истинно случайных чисел с помощью квантового ГСЧ по любому из пп. 1-8, включающий в себя:
управление лазерным диодом для излучения лазерных импульсов;
преобразование фазового шума лазерного излучения в амплитудную модуляцию с использованием интерферометра;
детектирование лазерных импульсов на выходе из интерферометра с использованием фотоприемника;
оцифровку выходного сигнала фотоприемника с использованием цифрового преобразователя;
вычисление плотности вероятности сигнала фотоприемника;
определение параметра, который связан с отношением классического шума к квантовому шуму, для оценки квантовой составляющей случайных изменений сигнала;
и
обработку выходных данных от цифрового преобразователя и блока контроля статистики для выполнения самонастройки генератора случайных чисел и обнаружения физических атак.
10. Способ по п.10, отличающийся тем, что блок контроля статистики, предназначенный для вычисления плотности вероятности сигнала фотоприемника, включает в себя компаратор.
11. Способ по п.10, отличающийся тем, что блок контроля статистики, предназначенный для вычисления плотности вероятности сигнала фотоприемника, включает в себя аналого-цифровой преобразователь, объединенный со схемой выборки и хранения.
12. Способ по п.10, отличающийся тем, что цифровой преобразователь включает в себя один высокоскоростной компаратор.
13. Способ по п.10, отличающийся тем, что цифровой преобразователь включает в себя пару высокоскоростных компараторов.
14. Способ по п.10, отличающийся тем, что волоконно-оптический интерферометр представляет собой интерферометр Майкельсона, построенный из волоконно-оптических компонентов, не поддерживающих поляризацию.
15. Способ по п.10, отличающийся тем, что линия задержки интерферометра 
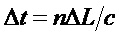

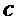
| US 2013036145 A1, 07.02.2013 | |||
| CN 109240645 A, 18.01.2019 | |||
| US 2015331672 A1, 19.11.2015 | |||
| WO 9966641 A1, 23.12.1999. |
Авторы
Даты
2020-05-20—Публикация
2019-07-31—Подача