ОБЛАСТЬ ТЕХНИКИ
[0001] Настоящее техническое решение относится к области генераторов случайных чисел (ГСЧ), в частности к квантовым ГСЧ (КГСЧ), основанных на интерференции лазерных импульсов со случайной фазой, применяемых для формирования случайной числовой последовательности.
ПРЕДШЕСТВУЮЩИЙ УРОВЕНЬ ТЕХНИКИ
[0002] Особое место среди физических ГСЧ занимают КГСЧ, основанные на оцифровке шумов из квантового источника энтропии. Последние два десятилетия было продемонстрировано огромное множество разнообразных квантовых ГСЧ, в которых использовались различные квантовые эффекты [1]. В этом перечне наиболее удобными и относительно дешевыми являются КГСЧ, основанные на различных эффектах квантовой оптики, т.е. использующие в качестве источника квантовой случайности лазерное излучение.
[0003] Оптические КГСЧ, использующие в качестве источника энтропии фазовый шум лазерного излучения можно условно разделить на два типа, характеризующиеся непрерывным [10, 11, 13] и импульсным [12, 14] режимами работы лазера. В обеих схемах в качестве источника энтропии использовались случайные изменения фазы лазерного излучения, вызванные спонтанными переходами, однако между ними существует ряд отличий.
[0004] В режиме непрерывной генерации фаза излучения меняется относительно медленно, поскольку подавляющее большинство переходов являются вынужденными, поэтому квантовые ГСЧ, работающие на этом принципе, не обладают большими скоростями генерации случайных бит. Другой особенностью таких ГСЧ является тот факт, что ширина квантовых шумов обратно пропорциональна интенсивности лазерного излучения [15], поэтому приемлемое соотношение квантового шума к классическому накладывает ограничение на выходную оптическую мощность.
[0005] В работе [12] была предложена альтернативная схема, в которой использовалась интерференция коротких лазерных импульсов, излучаемых полупроводниковым лазером в режиме переключения усиления. При таком режиме работы каждый новый лазерный импульс появляется со случайной фазой, поэтому результат интерференции (интенсивность импульса) будет совершенно случаен. В работе [14] было показано, что «хорошая» случайность сохраняется даже при частоте следования импульсов одночастотного лазера более 5 ГГц фаза успевает «расплыться» настолько, что в интервале [0, π) ее распределение можно считать равномерным. Более того, в отличие от схемы с непрерывной генерацией, схема с интерференцией импульсов не накладывает ограничений на выходную оптическую мощность.
[0006] Таким образом, квантовые ГСЧ на интерференции лазерных импульсов являются очень эффективными с точки зрения скорости генерации случайных бит и перспективными с точки зрения простоты их реализации и дешевизны. Важными недостатками существующих решений, однако, по-прежнему остаются корректность оценки вкладов классических и квантовых шумов, а также влияние несовершенства лазерных импульсов (джиттера, чирпа) на интерференцию и, соответственно, на качество оцифрованной случайности. Очень важным также остается требование повышения скорости генерации случайных бит без существенного увеличения стоимости продукта.
СУЩНОСТЬ ИЗОБРЕТЕНИЯ
[0007] Заявленное изобретение направлено на решение технической проблемы, присущей известным подходам из уровня техники.
[0008] Технический результат заключается в повышении качества случайности оцифрованной числовой последовательности за счет детального анализа вклада классических шумов и строгого определения квантового фактора сжатия, позволяющего достоверно оценить соотношения классического и квантового шумов.
[0009] Непрерывное измерение квантового фактора сжатия обеспечивает устойчивость работы квантового ГСЧ к изменению классических шумов (автонастройку) и, соответственно, обеспечивает устойчивость к возможным атакам.
[0010] Другим техническим результатом является повышение скорости генерации случайных чисел за счет распараллеливания оцифровки случайного интерференционного сигнала между разными ядрами (каналами) аналого-цифрового преобразователя. [ООП] Заявленный технический результат достигается за счет квантового генератора случайных чисел (КГСЧ) на интерференции лазерных импульсов, содержащего: высокоскоростной лазерный драйвер, обеспечивающий управление полупроводниковым лазером, работающим в режиме переключения усиления, который посылает импульсы в волоконный интерферометр Майкельсона; интерферометр Майкельсона, построенный из волоконного светоделителя, двух зеркал Фарадея и линии задержки, длина которой подобрана таким образом, чтобы на выходе из интерферометра происходила интерференция импульсов, испущенных лазером в разные моменты времени;
фотоприемник, обеспечивающий прием результатов интерференции, представляющих собой последовательность оптических импульсов случайной интенсивности;
аналого-цифровой преобразователь (АЦП), обеспечивающий оцифровку импульсов с фотоприемника;
вычислительный блок, связанный с АЦП и осуществляющий постобработку сырой случайной последовательности, а также позволяющий определять статистические свойства интерференции в виде плотности распределения интерференционного сигнала, на основании которой вычисляется квантовый фактор сжатия ГADC, характеризующий вклад классических шумов;
хеширование накопленной выборки случайных бит на основании значения ГADC, причем хеширование и выдача случайных бит происходят параллельно с анализом плотности распределения и вычислением значения ГADC.
[0012] В одном из частных примеров реализации квантового генератора АЦП выполнен многоканальным, причем времена защелкивания каналов АЦП устанавливаются таким образом, чтобы соответствующие отсчеты срабатывали на разных импульсах.
[0013] В другом частном примере реализации квантового генератора случайных чисел дополнительно содержится волоконный оптический полосовой фильтр, обеспечивающий улучшение спектрального соответствия между интерферирующими импульсами на пути их следования от лазера к интерферометру.
[0014] В другом частном примере реализации квантового генератора случайных чисел дополнительно содержится волоконный оптический изолятор или оптический циркулятор, связанный с оптическим полосовым фильтром и препятствующий попаданию отраженных оптических сигналов в лазерный драйвер.
[0015] Заявленный технический результат также достигается за счет осуществления способа формирования случайной числовой последовательности с помощью КГСЧ, при этом способ реализует этапы, на которых:
осуществляется накопление статистики в виде плотности распределения интерференционного сигнала;
осуществляется анализ плотности распределения интерференционного сигнала; вычисляется квантовый фактор сжатия Г, характеризующий вклад классических шумов (кроме вклада АЦП);
вычисляется фактор сжатия ГADC (учитывающий неравномерность и классические шумы, вносимые самим АЦП) на основании накопленной статистики и вычисленного фактора сжатия Г;
осуществляется хеширование накопленной выборки случайных бит на основании значения ГADC
осуществляется преобразование и выдача случайных бит в заданном формате;
причем хеширование и выдача случайных бит происходят параллельно с анализом плотности распределения и вычислением значения квантового фактора сжатия ГADC.
[0016] В одном из частных примеров осуществления способа фактор сжатия ГADC определяется по формуле  где величина
где величина 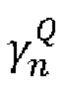 является промежуточным фактором сжатия, связанным с неравномерностью плотности распределения, а величина γENOB - фактор сжатия, связанный с классическими шумами внутри АЦП.
является промежуточным фактором сжатия, связанным с неравномерностью плотности распределения, а величина γENOB - фактор сжатия, связанный с классическими шумами внутри АЦП.
[0017] В другом частном примере осуществления способа формат выдачи случайных бит зависит от типа интерфейса, подключенного к КГСЧ.
[0018] Дополнительные особенности и преимущества заявленного решения будут изложены в последующем описании и частично будут очевидны или могут быть изучены при практическом его использовании. Преимущества настоящего решения реализуются и достигаются с помощью заявленного устройства и способа, и будут подробно раскрыты далее в настоящих материалах заявки.
КРАТКОЕ ОПИСАНИЕ ЧЕРТЕЖЕЙ
[0019] Прилагаемые чертежи, которые включены в данное описание для обеспечения дополнительного понимания сущности заявленного решения и составляют его часть, иллюстрирующую варианты реализации и вместе с описанием служат для пояснения принципов осуществления и работы заявленного решения.
На чертежах:
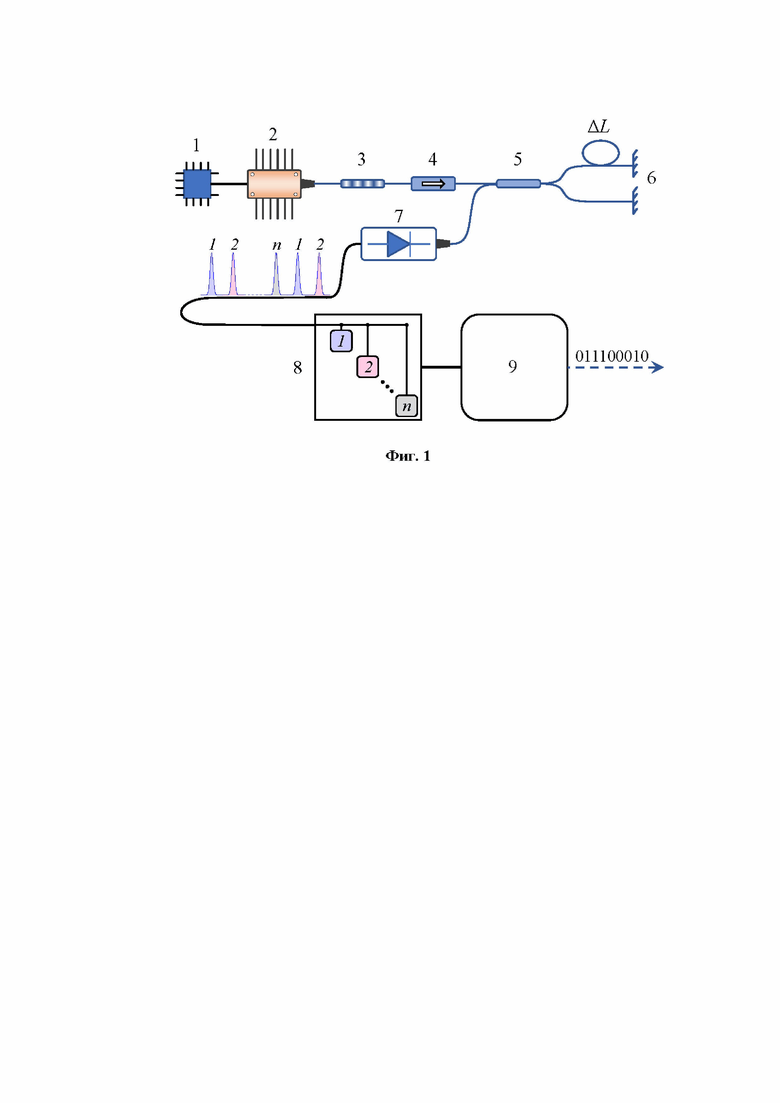
цифровые обозначения: 1 - лазерный драйвер; 2 - полупроводниковый лазер; 3 - волоконный оптический полосовой фильтр; 4 - волоконный оптический изолятор; 5 - волоконный светоделитель; 6 - зеркала Фарадея; 7 - фотоприемник; 8 - n-канальный АЦП; 9 - вычислительный блок; 10 - ядра каналов аналого-цифрового преобразователя (АЦП); 11 - импульсы случайной амплитуды.
[0020] На Фиг. 1 показана схема высокоскоростного КГСЧ.
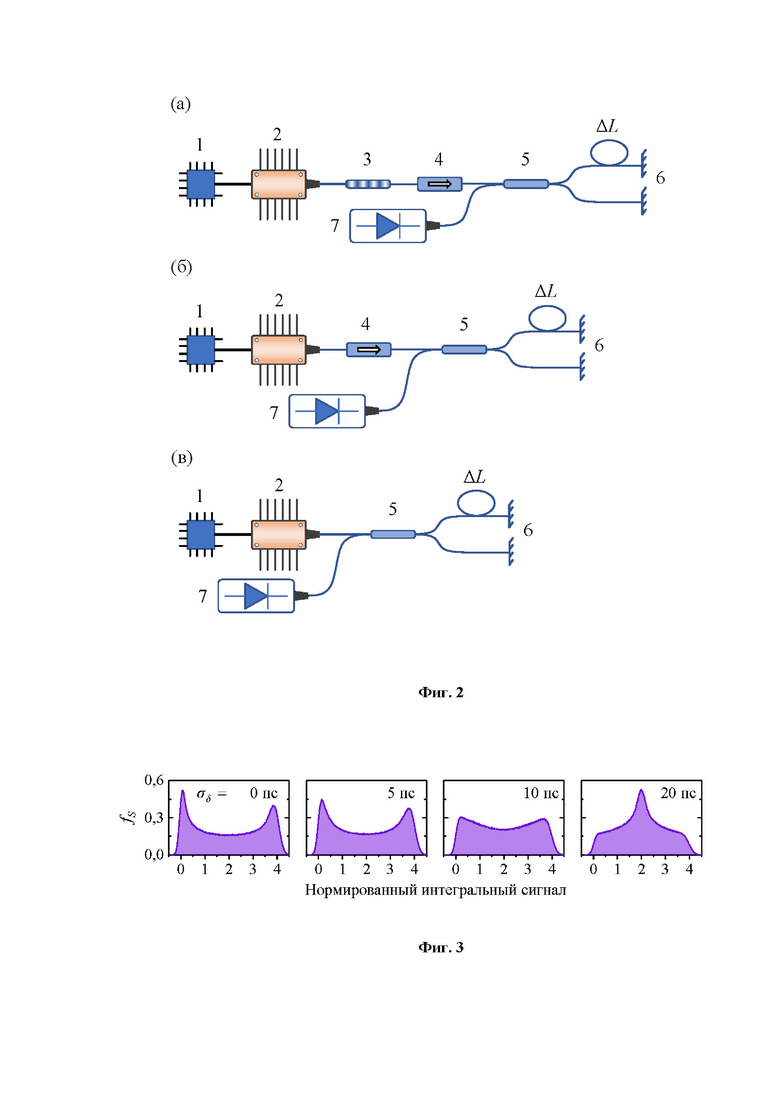
[0021] На Фиг. 2 показана реализация оптического узла КГСЧ: (а) с полосовым фильтром и изолятором (для работы на частоте следования импульсов свыше 1 ГГц); (б) упрощенная схема без полосового фильтра (для работы на частоте следования импульсов ниже 1 ГГц); (в) упрощенная схема без полосового фильтра и оптического изолятора.
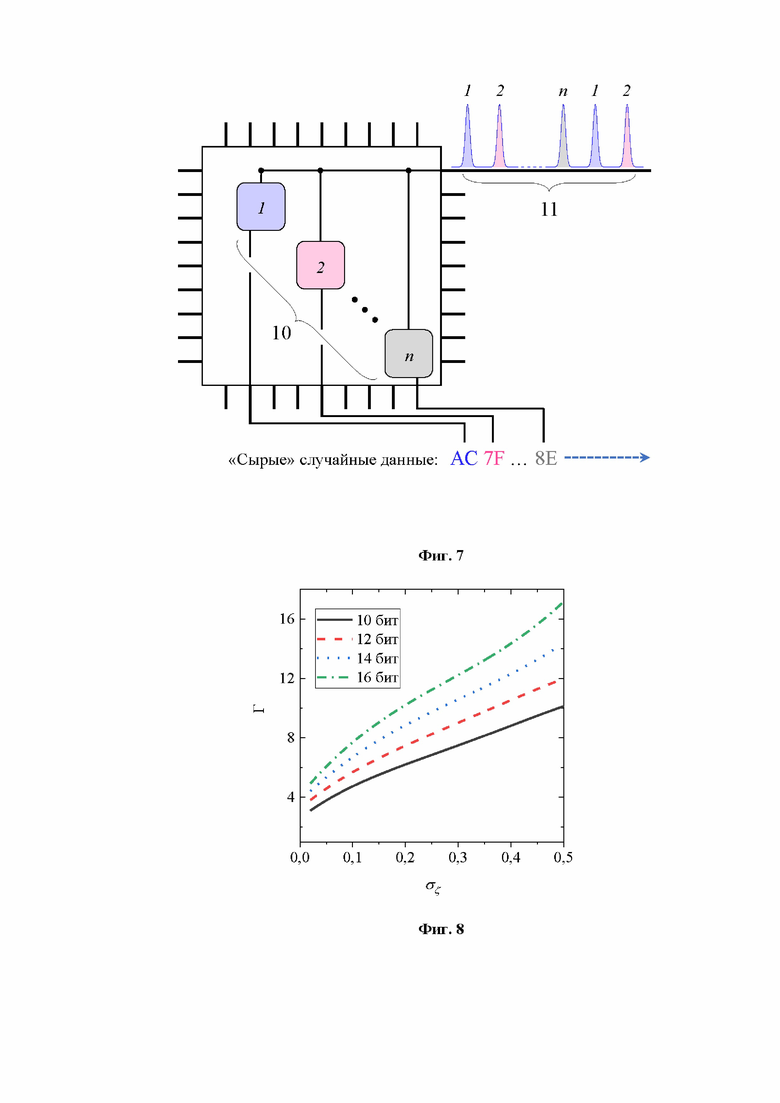
[0022] На Фиг. 3 показаны симуляции Монте-Карло плотности распределения интерференционного сигнала S, задаваемого формулой (1). Значения среднеквадратичного отклонения джиттера указаны на соответствующих симуляциях.
[0023] На Фиг. 4 показаны теоретические зависимости формы лазерного импульса и плотности распределения интерференционного сигнала от величины аналоговой полосы АЦП. Отсчет, по которому «набиралась статистика», обозначен синим кружком. Частота следования лазерных импульсов полагалась равной 2.5 ГГц.
[0024] На Фиг. 5 показаны: (а) спектры лазера, работающего в режиме переключения усиления: синяя пунктирная линия без фильтрации; красная сплошная линия после «обрезания» полосовым оптическим фильтром; (б) плотности распределения интерференционного сигнала, соответствующие площади под импульсом: синие ромбы без фильтрации; красные кружки - с фильтрацией.
[0025] На Фиг. 6 показаны теоретические зависимости формы лазерного импульса и плотности распределения интерференционного сигнала от величины аналоговой полосы АЦП. Отсчет, по которому «набиралась статистика», обозначен синим кружком. Частота следования лазерных импульсов полагалась равной 500 МГц.
[0026] На Фиг. 7 показана условная схема оцифровки импульсов, поступающих с фотоприемника на n-канальный АЦП.
[0027] На Фиг. 8 показаны зависимости квантового фактора сжатия, определяемого формулой (12) от величины гауссова шума на фотоприемнике при использовании АЦП различной разрядности.
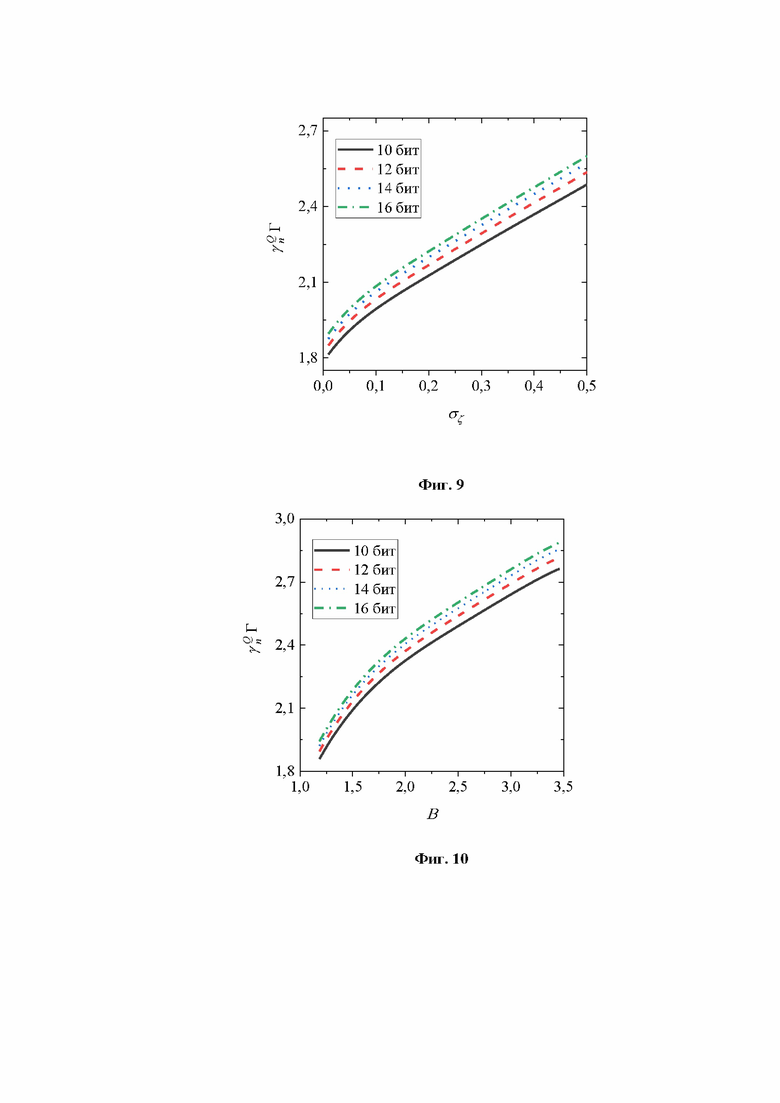
[0028] На Фиг. 9 показана зависимость величины 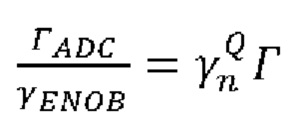 от гауссова шума на фотоприемнике для АЦП различной разрядности.
от гауссова шума на фотоприемнике для АЦП различной разрядности.
[0029] На Фиг. 10 показаны зависимости величины 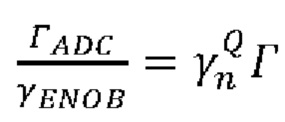 от коэффициента уширения плотности распределения В для АЦП различной разрядности.
от коэффициента уширения плотности распределения В для АЦП различной разрядности.
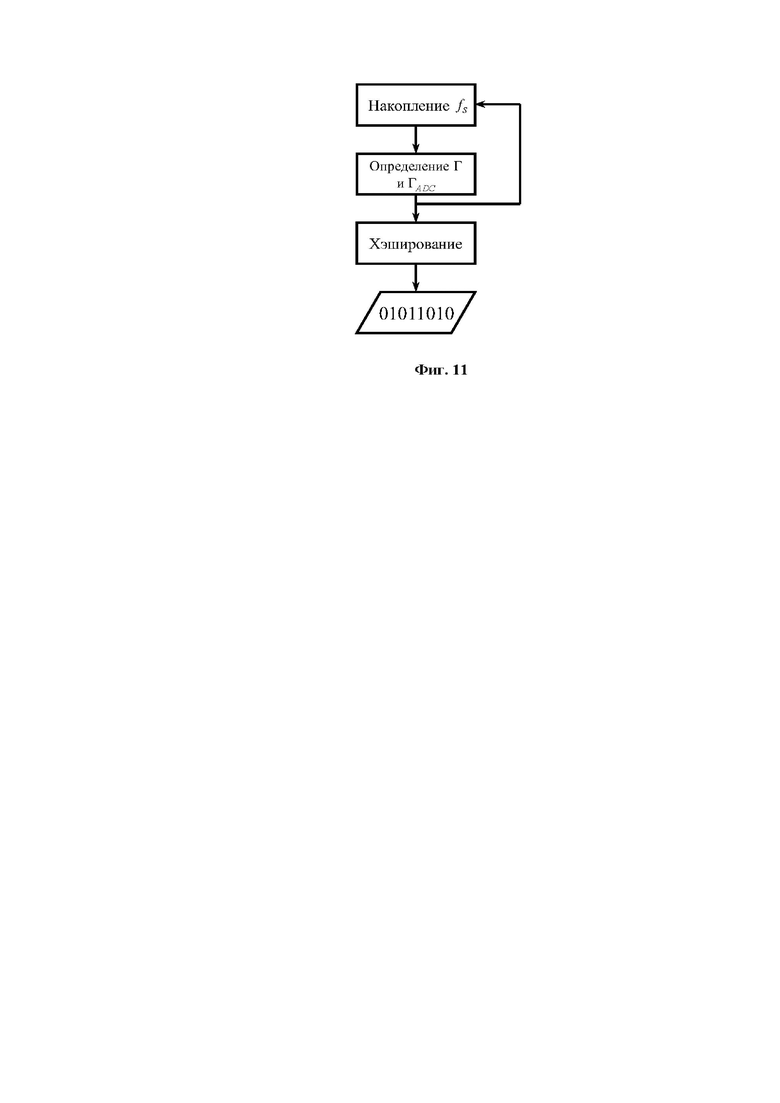
[0030] На Фиг. 11 показана блок-схема осуществления алгоритма работы квантового генератора случайных чисел.
ОСУЩЕСТВЛЕНИЕ ИЗОБРЕТЕНИЯ
[0031] На Фиг. 1 приведена схема высокоскоростного КГСЧ, включающая в себя высокоскоростной лазерный драйвер (1), который управляет полупроводниковым лазером (2), работающим в режиме переключения усиления, который посылает импульсы на волоконный интерферометр Майкельсона, построенный из зеркал Фарадея (6), волоконного светоделителя (5) и линии задержки ΔL, которая подобрана таким образом, что на выходе из интерферометра интерферируют импульсы, испущенные лазером в разные моменты времени.
[0032] Для обеспечения спектрального соответствия между интерферирующими импульсами на пути их следования от лазера к интерферометру может дополнительно устанавливаться волоконный полосовой оптический фильтр (3), за которым следует оптический изолятор (4), препятствующий попаданию отраженных оптических сигналов в лазер (возможно также использование оптического циркулятора).
[0033] Результат интерференции представляет собой последовательность оптических импульсов случайной интенсивности, которые детектируются фотоприемником (7). Детектированные импульсы затем поступают в n-канальный аналого-цифровой преобразователь (8). Времена защелкивания каналов АЦП устанавливаются таким образом, чтобы соответствующие отсчеты срабатывали на разных импульсах. Такой способ оцифровки позволяет использовать относительно медленные ядра АЦП с сохранением высоких скоростей генерации случайных бит. Результаты оцифровки затем направляются на постобработку в вычислительный блок (9).
[0034] В вычислительном блоке накапливается статистика поступающих оцифрованных импульсов, по которой восстанавливается плотность распределения интерференционного сигнала. С использованием найденной плотности распределения определяется квантовый фактор сжатия ГADC, характеризующий вклад классических шумов. Согласно значению ГADC производится хеширование накопленной выборки случайных бит. Анализ плотности распределения и вычисление значения квантового фактора сжатия ГADC происходят параллельно с хешированием и выдачей случайных бит, что обеспечивает устойчивость работы квантового ГСЧ к изменению классических шумов (автонастройку) и, соответственно, обеспечивает устойчивость к возможным атакам.
[0035] Далее будет дано детальное описание осуществления работы КГСЧ и соответствующего способа формирования случайной последовательности бит.
[0036] Генерация квантовой энтропии.
[0037] Генерация квантовой энтропии в рассматриваемом решении с помощью КГСЧ основана на интерференции лазерных импульсов, испускаемых полупроводниковым лазером, работающим в режиме переключения усиления.
[0038] Схемы реализации оптического узла КГСЧ показаны на Фиг. 2 (а, б, в). Полупроводниковый лазер (2), управляемый высокочастотным драйвером (1), испускает короткие импульсы, которые заводятся в волоконный несбалансированный интерферометр Майкельсона, построенный из волоконного светоделителя 50:50 (5), линии задержки длиной ΔL и двух зеркал Фарадея (6). Длина линии задержки ΔL и частота следования лазерных импульсов подобраны таким образом, чтобы на выходе из светоделителя интерферировали импульсы, испущенные лазером в разные моменты времени.
[0039] На Фиг. 2 (а) между интерферометром и лазером помещен полосовой фильтр (3), который не использовался ранее при построении оптических КГСЧ, но который является принципиально важным компонентом на частоте следования лазерных импульсов свыше 2 ГГц. На более низких частотах следования импульсов, однако, использование фильтра (3) не является обязательным, поэтому схема, изображенная на Фиг. 2 (б) и Фиг. 2 (в) является «низкочастотной».
[0040] Поскольку каждый оптический импульс, выходящий из лазера, работающего в режиме переключения усиления, имеет случайную фазу, результат интерференции является совершенно случайным. Случайность интерференции в данном случае связана с процессом фазовой диффузии, которая, в свою очередь, обусловлена вкладом спонтанного излучения, точнее усилением спонтанного излучения (УСИ). Хорошо известно, что спонтанные переходы индуцируются нулевыми колебаниями электромагнитного поля [18, 19]. Таким образом, УСИ можно рассматривать как усиление флуктуаций вакуума, шум которого обычно считается совершенно белым, некоррелированным и широкополосным.
[0041] Несмотря на простоту реализации, интерференция лазерных импульсов имеет ряд особенностей, которые отрицательно сказываются на видности интерференционной картины и могут существенно влиять на форму плотности распределения случайного интерференционного сигнала. Это особенно справедливо в отношении стандартных телекоммуникационных лазеров. Наиболее важными особенностями таких лазеров являются неизбежная модуляция (чирп) лазерной частоты при прямой модуляции током и значительные флуктуации времени излучения импульса (джиттер).
[0042] Можно показать [20-22], что при интерференции лазерных импульсов гауссовой формы (и имеющих, соответственно, линейный чирп) результат интерференции в терминах интегрального сигнала, вызванного попаданием импульса на фотоприемник, может быть записан в виде:
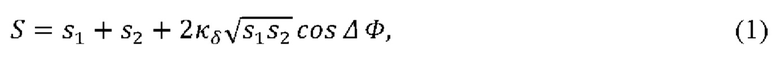
где s1 и s2 - интегральные (нормированные) сигналы, соответствующие выходам с разных плеч интерферометра, ΔФ - разность фаз интерферирующих импульсов, а коэффициент

определяет видность интерференции, причем 0 ≤ κδ ≤ 1; здесь w - среднеквадратичная ширина импульса (ширина импульса на половине высоты его временного профиля равна, соответственно,  α - коэффициент уширения линии (так называемый фактор Генри [15]), а δ - неточность перекрытия интерферирующих импульсов.
α - коэффициент уширения линии (так называемый фактор Генри [15]), а δ - неточность перекрытия интерферирующих импульсов.
[0043] Следует иметь в виду, что помимо случайных изменений разности фаз ΔΦ, приводящих к случайным изменениям интерференционного сигнала, в реальном приборе необходимо учитывать также флуктуации выходной лазерной мощности (флуктуации величин s1 и s2), а также случайные изменения времени испускания лазерных импульсов (джиттер). Из формул (1) и (2) видно, что из-за джиттера (флуктуаций δ) видность становится случайной величиной, так что плотность распределения интегрального сигнала S будет существенно зависеть от плотности распределения δ, т.е. от величины джиттера. Причем зависимость от джиттера будет проявляться сильнее при наличии чирпа, который, согласно формуле (2), увеличивает вклад джиттер в 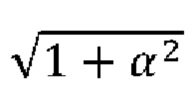 раз.
раз.
[0044] Функцию распределения случайного сигнала S можно определить следующим образом:
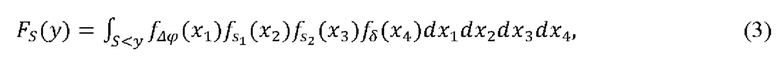
где значения случайных величин ΔΦ, sl, s2 и δ обозначены через х1, х2, x3 и х4, соответственно, и где предполагается, что флуктуации этих величин независимы, так что результирующая плотность распределения представляет собой произведение соответствующих функций плотности распределения:  Область интегрирования определяется неравенством
Область интегрирования определяется неравенством 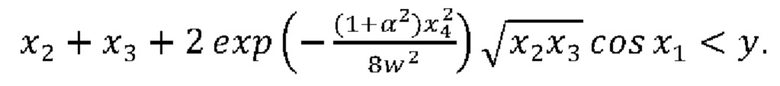
Результирующая функция плотности распределения интерференционного сигнала определяется производной от функции распределения: 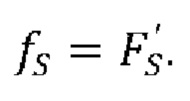 К сожалению, интеграл в формуле (3) не может быть посчитан аналитически, поэтому для нахождения ƒS обычно используются симуляции методом Монте-Карло.
К сожалению, интеграл в формуле (3) не может быть посчитан аналитически, поэтому для нахождения ƒS обычно используются симуляции методом Монте-Карло.
[0045] В реальном устройстве плотность распределения интерференционного сигнала дополнительно «уширена» из-за шумов фотоприемника. Чтобы это учесть, интерференционный сигнал можно записать в следующем виде:

где ζ - классический гауссов шум фотоприемника.
[0046] Плотности распределения случайного интерференционного сигнала S, посчитанные с помощью формулы (1) методом Монте-Карло, показаны на Фиг. 3. В симуляциях для определения видности применялась формула (2), где использовались значения w=50 пс и α=6. Флуктуации величин sl, s2 задавались гауссовой плотностью распределения со средними значениями 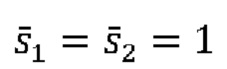 и среднеквадратичными отклонениями
и среднеквадратичными отклонениями 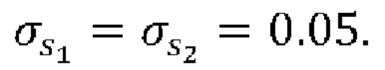 Джиттер тоже задается гауссовой случайной величиной со среднеквадратичным отклонением σδ, пробегающим значения 0, 5, 10 и 20 пс (см Фиг. 3). Шум фотоприемника задается гауссовой случайной величиной σζ = 0.1. Из симуляций видно, что джиттер существенно меняет вид плотности распределения случайного интерференционного сигнала.
Джиттер тоже задается гауссовой случайной величиной со среднеквадратичным отклонением σδ, пробегающим значения 0, 5, 10 и 20 пс (см Фиг. 3). Шум фотоприемника задается гауссовой случайной величиной σζ = 0.1. Из симуляций видно, что джиттер существенно меняет вид плотности распределения случайного интерференционного сигнала.
[0047] Важно подчеркнуть, что формула (1) с видностью, определяемой формулой (2), справедлива только в случае импульсов гауссовой формы. Более того, данное выражение выведено для интегрального сигнала, т.е. для площади под временным профилем импульса. В общем же случае интерференция чирпированного импульса зависит от времени t, т.е. от выбранной точки на временном профиле импульса; кроме того, отклонение формы импульса от гауссовой кривой, например, из-за наличия релаксационных пичков, приведет к значительно более сложной зависимости интерференционного сигнала от разности фаз между импульсами, чем формула (1). Тем не менее, результаты, показанные на Фиг. 3, качественно останутся сходными.
[0048] Оцифровка случайного сигнала
[0049] С экспериментальной точки зрения, оцифровка сигнала не предполагает интегрирования по временному профилю импульса, однако из-за джиттера защелка аналого-цифрового преобразователя (АЦП) для разных импульсов трейна будет срабатывать в разных точках временного профиля импульса, что при получении статистических характеристик, например, плотности распределения интерференционного сигнала, будет соответствовать интегрированию некоторой части импульса, причем эффект такого «неявного интегрирования» будет усиливаться конечностью аналоговой полосы АЦП, приводящей к уширению импульса. Такое уширение будет в каком-то смысле соответствовать увеличению «области интегрирования» [21].
[0050] На Фиг. 4 показаны теоретические плотности распределения случайного интерференционного сигнала, полученные в результате «сбора статистики» не по площади импульса, а в фиксированной точке на профиле лазерного импульса. При расчетах частота следования импульсов предположительно равна 2.5 ГГц. Показаны результаты, соответствующие двум различным значениям джиттера (0 и 10 пс) и трем различным значениям аналоговой полосы пропускания АЦП. Для симуляции полосы пропускания АЦП использовался фильтр Баттерворта 2-го порядка. Лазерные импульсы, точнее их форма с учетом полосы пропускания АЦП, показаны слева от соответствующих плотностей распределения. Предполагается, что полоса пропускания фотоприемника существенно выше, чем полоса АЦП (можно считать ее бесконечной). Выбранная точка, по которой «набиралась статистика», показана синим кружком на импульсе.
[0051] Из Фиг. 4 видно, что плотность распределения остается практически неизменной для разных полос пропускания в отсутствие джиттера. Однако при наличии джиттера форма плотности распределения существенно зависит от полосы пропускания АЦП. Изменение плотности распределения, показанное на Фиг. 4 означает, что к случайности, обусловленной флуктуациями фазы электромагнитного поля, «примешивается» дополнительная случайность, связанная с джиттером, который имеет классическую природу. Другими словами, квантовая случайность оказывается «загрязнена» классическими флуктуациями, которые необходимо «отфильтровать».
[0052] Как уже было сказано выше, влияние джиттера усиливается при наличии частотной модуляции (чирпа), следовательно, совместное влияние чирпа и джиттера на плотность распределения интерференционного сигнала может быть уменьшено с помощью спектральной фильтрации. При фильтрации той части спектра, которая связана с чирпом, можно улучшить статистику интерференции импульсов, как это показано на Фиг. 5.
[0053] Слева, на Фиг. 5 (а), показаны экспериментально полученные спектры лазера, работающего в режиме переключения усиления: синяя пунктирная линия соответствует спектру, полученному без фильтрации, а красная сплошная линия соответствует результату «обрезания» спектра полосовым оптическим фильтром. Видно, что спектр без фильтрации содержит широкое высокочастотное плечо, которое связано с частотной модуляцией (чирпом) лазерного импульса. На Фиг. 5 (б) показаны соответствующие (с фильтрацией и без нее) экспериментальные плотности распределения интерференционного сигнала. Видно, что плотность распределения, полученная с полосовым фильтром, имеет два выраженных максимума, соответствующих конструктивной и деструктивной интерференции, как в модели, показанной на Фиг. 4 при нулевом джиттере.
[0054] Таким образом, на высоких частотах (более 1 ГГц) следования лазерных импульсов (и имеющих, соответственно, небольшую длительность) полосовой оптический фильтр на Фиг. 2 имеет принципиальное значение: с его помощью улучшается спектральное согласование импульсов, что, в свою очередь, улучшает их интерференцию и уменьшает вклад классических шумов, обусловленных джиттером, в случайность интерференционного сигнала.
[0055] Важно отметить, что при уменьшении частоты следования импульсов эффекта «загрязнения» квантовых шумов джиттером можно избежать и без использования полосового фильтра, если генерировать более длинные лазерные импульсы. Если период следования лазерных импульсов равен, например, 2 не (частота следования 500 МГц), то не составит труда генерировать лазерные импульсы шириной порядка 1 нс. Поскольку после начала генерации переходные процессы заканчиваются на временах порядка 200-250 пс, то большая часть импульса будет соответствовать квазистационарному режиму работы лазера. В этом случае вторая половина импульса не будет иметь частотной модуляции (чирпа), а, следовательно, джиттер не будет оказывать существенного влияния на интерференцию.
[0056] Для демонстрации данного эффекта, на Фиг. 6 приведены зависимости плотности распределения случайного интерференционного сигнала, аналогичные тем, что показаны на Фиг. 4, но для значительно более длинных лазерных импульсов, в предположении, что частота их следования равна 500 МГц. Из Фиг. 6 видно, что джиттер не оказывает существенного влияния на плотность распределения, если отсчет, используемый для накопления статистики (синий кружок на временном профиле импульса на Фиг. 6), выбран достаточно далеко от начала импульса. Причем это справедливо даже для АЦП с небольшой (~1 ГГц) аналоговой полосой. Таким образом, при использовании достаточно длинных импульсов (соответственно, на невысоких частотах следования лазерных импульсов) можно упростить оптическую схему, убрав из нее оптический полосовой фильтр, как это сделано на Фиг. 2 (б), без потери требуемой функциональности.
[0057] Необходимо отметить, что, несмотря на отраженное излучение, направляющееся из интерферометра Майкельсона обратно в лазер, из оптической схемы можно убрать изолятор, как это сделано на Фиг. 2 (в). Оптическая схема без изолятора (4) была проверена экспериментально, и было показано, что существенного влияния на случайность фазы между интерферирующими импульсами это не оказывает (по крайней мере, при невысокой частоте следования лазерных импульсов). Дело в том, что фазовая диффузия в режиме переключения усиления на относительно низких частотах лазерной генерации (менее 1 ГГц) оказывается очень эффективной, и для того чтобы стабилизировать фазу между импульсами (т.е. приостановить фазовую диффузию) или хотя бы внести заметные корреляции, необходима оптическая инжекция значительной мощности [23].
[0058] Это показывает, что отраженной мощности, приходящей обратно из интерферометра Майкельсона, оказывается недостаточно для внесения существенных корреляций, так что в этом случае в оптическом изоляторе (4) нет необходимости. Кроме того, следует иметь в виду, что некоторые производители полупроводниковых лазеров помещают в корпус оптический изолятор, что автоматически избавляет от необходимости использовать его в оптической схеме.
[0059] Далее интерферирующие оптические импульсы, преобразованные фотоприемником (7) в электрические сигналы, оцифровываются для последующего извлечения случайности. Как представлено на симуляциях, показанных на Фиг. 4 и Фиг. 6, для извлечения случайности нет необходимости оцифровывать весь импульс, а достаточно лишь получить один отсчет в правильно выбранной точке на временном профиле импульса. Это существенно упрощает задачу и, что важно, значительно снижает требования к частоте выборки АЦП (8). Таким образом, для оцифровки случайного сигнала, получающегося в результате интерференции лазерных импульсов, можно использовать относительно медленные (а следовательно недорогостоящие) АЦП (8), имеющие скорость выборки в несколько сотен мегасэмплов в секунду. При этом, как продемонстрировано на Фиг.6, такому АЦП (8) достаточно иметь аналоговую полосу порядка 1 ГГц.
[0060] На Фиг. 7 показана условная схема оцифровки импульсов, поступающих с фотоприемника (7) на n-канальный АЦП (8), для случая, когда частота следования лазерных импульсов превышает частоту выборки АЦП (8). В этом случае времена защелкивания каналов АЦП (8) можно установить таким образом, чтобы соответствующие отсчеты срабатывали на разных импульсах, т.е. чтобы k-й канал оцифровывал только импульсы с номерами k + mn, где n - количество каналов, k = 1, 2, …, n, а m - целочисленный счетчик. Результаты оцифровки затем направляются на постобработку. Здесь важно отметить, что поскольку каждый импульс независим от других, то сериализация полученных данных (если она необходима) может быть реализована любым удобным способом, и нет необходимости упорядочивать сэмплы в соответствии с тем, в каком порядке приходят импульсы на АЦП (8).
[0061] Определение квантового фактора сжатия.
[0062] Последовательность бит, получаемая непосредственно в результате оцифровки случайного физического сигнала, еще не является истинно случайной (для более строгого определения истинной случайности в контексте КГСЧ см. [24]). Это следует уже из того факта, что плотность распределения случайного сигнала обычно не является равномерной, что, естественно, влечет за собой неравномерность битовой последовательности. Физический источник случайности с неравномерной плотностью распределения измеряемого сигнала иногда называют слабым источником энтропии, обычно подразумевая под этим криптографическую «слабость» получаемого с его помощью секретного ключа. Сырые случайные последовательности, полученные от слабых источников энтропии, непригодны для большинства криптографических приложений.
[0063] Таким образом, сырая случайная последовательность должна быть подвержена математической обработке, в результате которой она становится почти равномерной. Используемые для этого алгоритмы называются процедурами извлечения случайности или экстракторами случайности. Экстрактор случайности можно определить как функцию, которая принимает на вход бинарную последовательность длины N и возвращает последовательность длины М, причем, как правило, Μ<Ν, т.е. процедура извлечения случайности как бы сжимает сырую последовательность, делая ее более случайной. Величину 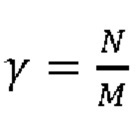 называют иногда фактором сжатия.
называют иногда фактором сжатия.
[0064] Экстрактор случайности можно формально записать как отображение {0,1}N → {0,1}M, где обозначение {0,1}N,M соответствует множеству элементарных исходов, представляющих собой бинарные вектор длины N и М, соответственно. Очевидно, чем сильнее распределение случайных бит отличается от равномерного и чем больше корреляций присутствует в случайной последовательности, тем больше должен быть фактор сжатия, и, следовательно, тем меньше случайности можно извлечь из сырой последовательности. Обычно в процедурах извлечения случайности фактор сжатия γ оценивается через мин-энтропию H∞, приходящуюся на один элемент (т.е. на одно слово) «сырой» случайной последовательности. Таким образом, идеальный экстрактор случайности, примененный к неоднородной случайной последовательности {Х1, Х2, …, XN} с N>>1, где каждое Xi является n-битным словом, может обеспечить ΝΗ∞ почти равномерно распределенных бит [25], т.е. необработанная последовательность будет уменьшена таким экстрактором в у раз, причем

мин-энтропия в формуле (5) определяется как H∞ = -log2 pmax, где pmax - наибольшая вероятность выбрать некоторый случайный элемент из последовательности {Х1, Х2, …, XN}. Если случайный сигнал оцифровывается с помощью АЦП, то n в формуле (5) соответствует разрядности АЦП в битах, тогда как pmax соответствует вероятности наиболее вероятного бина.
[0065] В случае КГСЧ проблема извлечения случайности выходит за рамки данного выше определения. Действительно, классическая процедура извлечения случайности сводится, в сущности, к устранению неравномерности распределения бит в сырой последовательности. Если же стоит задача извлечения квантовой случайности, то следует принимать во внимание не только неравномерность распределения, но и неизбежный вклад классических шумов, примешиваемых к сигналу, получаемому от источника квантовой энтропии.
[0066] Необходимость фильтрации классических шумов обусловлена тем, что Ева (он англ. eavesdropper подслушиватель) может контролировать классические шумы в системе с КГСЧ. Следовательно, Ева может получить часть информации о сырой последовательности случайных бит. Можно, например, представить ситуацию, когда квантовое устройство подключено к внешнему источнику питания, флуктуации напряжения которого составляют 1% от номинального значения. Вполне может оказаться, что источником этих флуктуаций является Ева, которая в этом случае совершенно точно знает истинное значение напряжения в каждый момент времени, а значит, может потенциально получить какую-то часть информации о сырой последовательности. Поэтому необходимо каким-то образом отделить квантовую составляющую сигнала от классической, т.е. отфильтровать классический шум.
[0067] Очевидно, что сделать это непосредственно на физическом уровне чрезвычайно трудно, поскольку измерительные приборы (фотоприемник, АЦП), в той или иной степени, являются приборами классическими. Поэтому обычно принято считать, что наличие классической составляющей эквивалентно присутствию скрытых корреляций, которые можно устранить, пропустив сырую последовательность через экстрактор случайности.
[0068] Следовательно, фактор сжатия теперь должен быть выбран таким, чтобы после процедуры извлечения случайности была устранена не только неравномерность сырой последовательности, но и предполагаемые скрытые корреляции. Очевидно, эту задачу нельзя решить одними только математическими методами, созданными для работы с бинарными последовательностями. Действительно, глядя на случайные последовательности бит, невозможно определить, какой источник энтропии использовался для их получения: квантовый, классический, или псевдослучайный. Поэтому в процедуре извлечения случайности в КГСЧ должна быть заложена конкретная физическая модель источника энтропии. Чтобы отличать квантовый фактор сжатия от определенного выше фактора γ, будем обозначать его Г [24]. Из сказанного очевидно, что Г ≥ γ, причем равенство может быть достигнуто только в отсутствие классических шумов.
[0069] В работе [24] использование квантового фактора сжатия было подробно рассмотрено для случая оцифровки случайного сигнала компаратором. В этом случае Г можно определить следующим образом:

где мин-энтропия определяется как
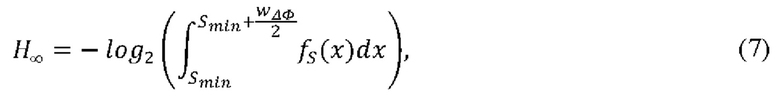
где, как и выше, ƒS(x) - экспериментальная плотность распределения интерференционного сигнала, зависящая в общем случае от флуктуаций выходной мощности лазера, джиттера, шумов фотоприемника и пр. В формуле (7) Smin и wΔФ входят в определение идеальной (квантовой) плотности распределений 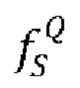 интерференционного сигнала S (формула (1)) в предположении отсутствия иных шумов кроме флуктуаций ΔΦ:
интерференционного сигнала S (формула (1)) в предположении отсутствия иных шумов кроме флуктуаций ΔΦ:
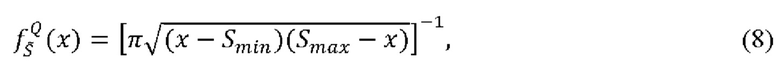
где
а wΔФ = Smax - Smin.
[0070] В работе [24] формула (6) была обобщена на случай АЦП следующим образом:

где

А  определяется таким же образом, но с
определяется таким же образом, но с 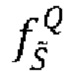 под знаком интеграла. В формуле (11) ΔU - диапазон входных напряжений АЦП, а n - его разрядность. Физический смысл формулы (10) аналогичен смыслу формулы (6): как только вероятность попадания сигнала в бин в окрестности Smin уменьшится из-за вклада классических шумов в 2 раза, мы перестаем доверять оцифрованному шуму. Такой подход соответствует чрезвычайно жесткому ограничению на наличие классических шумов. Так, с использованием формул (1), (10) и (11) можно показать, что уже для 10-битного АЦП квантовый фактор сжатия Г, определяемый формулой (10), устремляется к бесконечности уже при относительных шумах фотоприемника σζ ~0.3% и флуктуациях выходной мощности лазера с
под знаком интеграла. В формуле (11) ΔU - диапазон входных напряжений АЦП, а n - его разрядность. Физический смысл формулы (10) аналогичен смыслу формулы (6): как только вероятность попадания сигнала в бин в окрестности Smin уменьшится из-за вклада классических шумов в 2 раза, мы перестаем доверять оцифрованному шуму. Такой подход соответствует чрезвычайно жесткому ограничению на наличие классических шумов. Так, с использованием формул (1), (10) и (11) можно показать, что уже для 10-битного АЦП квантовый фактор сжатия Г, определяемый формулой (10), устремляется к бесконечности уже при относительных шумах фотоприемника σζ ~0.3% и флуктуациях выходной мощности лазера с  . Для АЦП с большей разрядностью квантовый фактор сжатия из формулы (10) растет еще быстрее с увеличением классических шумов. Таким образом, формула (10) вряд ли может быть использована для оценки квантового фактора сжатия в реальных системах, где уровень шумов обычно существенно больше 0.3%.
. Для АЦП с большей разрядностью квантовый фактор сжатия из формулы (10) растет еще быстрее с увеличением классических шумов. Таким образом, формула (10) вряд ли может быть использована для оценки квантового фактора сжатия в реальных системах, где уровень шумов обычно существенно больше 0.3%.
[0071] Альтернативное определение квантового фактора сжатия для АЦП было дано в [20]:

Физический смысл данной формулы несколько иной: мы перестаем доверять оцифрованному случайному сигналу не тогда, когда вероятность попадания сигнала в бин рядом с Smin уменьшается в два раза, а когда соответствующая мин-энтропия увеличивается в два раза (т.е. становится равной 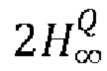 ). Такое условие соответствует менее жесткому ограничению на наличие классических шумов.
). Такое условие соответствует менее жесткому ограничению на наличие классических шумов.
[0072] На Фиг. 8 показаны теоретические зависимости фактора Г, определяемого формулой (12), от величины шумов на фотоприемнике σζ. В представленных симуляциях среднеквадратичное отклонение относительных флуктуаций выходной мощности лазера  устанавливалось равным 0.05. Из Фиг. 8 видно, что при использовании формулы (12) квантовый фактор сжатия Г все еще имеет очень большие значения, из-за которых преимущество АЦП (получение нескольких бит при оцифровке одного лазерного импульса) почти полностью нивелируется на этапе постобработки.
устанавливалось равным 0.05. Из Фиг. 8 видно, что при использовании формулы (12) квантовый фактор сжатия Г все еще имеет очень большие значения, из-за которых преимущество АЦП (получение нескольких бит при оцифровке одного лазерного импульса) почти полностью нивелируется на этапе постобработки.
[0073] Здесь следует подчеркнуть, что формулы (10) и (12) не имеют строгого математического доказательства и, в сущности, являются лишь попыткой обобщить результат, записанный в формуле (6), на случай АЦП. Точкой соприкосновения этих двух различных обобщений является, собственно, формула (6): действительно, из формул (10) и (12) видно, что обе они сводятся к формуле (6) для n=1. В настоящем решении предлагается другой, более строгий, подход для оценки квантового фактора сжатия, в котором Г определяется как произведение нескольких сомножителей (промежуточных факторов сжатия), каждый из которых соответствует вкладу одного из трех эффектов: 1) неравномерности плотности распределения случайного сигнала, 2) внутренним шумам АЦП, которые задаются параметром ΕΝΟΒ (эффективное число бит - effective number of bits), 3) шумам фотоприемника и лазера.
[0074] Промежуточный фактор сжатия, связанный с неравномерностью плотности распределения, будет обозначаться как 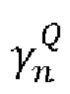 и определяться аналогично формуле (5):
и определяться аналогично формуле (5):

Где 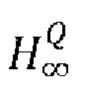 определяется формулой (11), но с плотностью
определяется формулой (11), но с плотностью 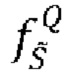 под знаком интеграла, которая, в свою очередь, определяется формулой (8). Произведя вычисления, находим:
под знаком интеграла, которая, в свою очередь, определяется формулой (8). Произведя вычисления, находим:
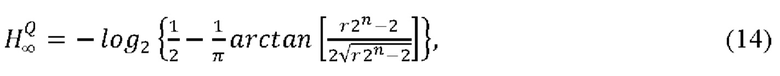
где 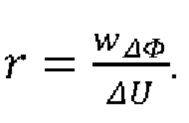 Будем дальше считать, что сигнал с фото приемника усилен таким образом, что диапазон его изменений примерно совпадает с диапазонов входных напряжений АЦП, так что можно считать, что wΔФ ≈ ΔU, т.е. r ≈ 1.
Будем дальше считать, что сигнал с фото приемника усилен таким образом, что диапазон его изменений примерно совпадает с диапазонов входных напряжений АЦП, так что можно считать, что wΔФ ≈ ΔU, т.е. r ≈ 1.
[0075] Следующий фактор сжатия будет обозначен как γENOB и определяться по формуле:

где параметр ΕΝΟΒ обозначает эффективное число бит. Значение, задаваемое параметром ΕΝΟΒ, соответствует той части оцифрованного сигнала, которая гарантированно не «загрязнена» шумами и искажениями, обусловленными несовершенством внутренних компонентов АЦП. Таким образом, γΕΝOΒ можно рассматривать как фактор сжатия, связанный с классическими шумами внутри самого АЦП. Обычно, значение ΕΝΟΒ указано в спецификациях конкретной микросхемы и зависит от разрядности АЦП, а также от величины параметра SINAD (Signal-to-Noise-and-Distortion ratio) [26]:

[0076] Наконец, для определения вклада шумов фотоприемника и лазера необходимо отметить, что эти шумы не должны зависеть от способа оцифровки, поэтому в качестве соотношения между вкладами квантового и классического шумов, точнее той части классического шума, которая связана с несовершенствами лазера и фотоприемника, можно использовать фактор Г, найденный для компаратора, и определяемый формулами (6) и (7). Таким образом, квантовый фактор сжатия для АЦП запишется в следующем виде:

Зависимости величины  от гауссова классического шума на фотоприемнике показаны на Фиг. 9. Как и выше, среднеквадратичное отклонение относительных флуктуаций выходной мощности лазера устанавливалось равным 0.05 для указанных примеров.
от гауссова классического шума на фотоприемнике показаны на Фиг. 9. Как и выше, среднеквадратичное отклонение относительных флуктуаций выходной мощности лазера устанавливалось равным 0.05 для указанных примеров.
[0077] Необходимо учесть, что вклад классических флуктуаций со стороны фотоприемника и лазера КГСЧ не всегда удобно измерять непосредственно, особенно, когда необходимо оценивать вклад этих шумов «на лету» (в процессе работы ГСЧ), поэтому представляется предпочтительным оценивать этот вклад по форме плотности распределения, точнее по отклонению плотности распределения реального сигнала с фотоприемника от идеальной (квантовой) плотности распределения, задаваемой формулой (8).
[0078] В работе [24] было показано, что достаточно эффективно такое сравнение можно осуществлять путем определения величины В, равной отношению полной ширины экспериментальной плотности распределения к «расстоянию» между ее максимумами. На Фиг. 10 показаны зависимости величины 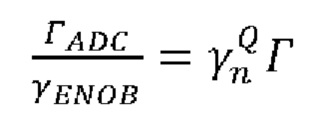 от коэффициента В в предположении, что среднеквадратичное отклонение относительных флуктуаций выходной мощности лазера фиксировано и равно 5%.
от коэффициента В в предположении, что среднеквадратичное отклонение относительных флуктуаций выходной мощности лазера фиксировано и равно 5%.
[0079] Таким образом, для определения полного квантового фактора сжатия ГADC, необходимо измерить отношение ширины экспериментальной плотности распределения к «расстоянию» между ее максимумами (найти коэффициент В), затем определить соответствующее значение величины 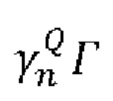 по соответствующему графику на Фиг. 10 и умножить γENOB. Характерные значения γENOB обычно находятся в диапазоне 1.5-1.8, так что даже при значительных шумах в фотоприемнике и лазере значение ГАDС не будет существенно превышать 4.
по соответствующему графику на Фиг. 10 и умножить γENOB. Характерные значения γENOB обычно находятся в диапазоне 1.5-1.8, так что даже при значительных шумах в фотоприемнике и лазере значение ГАDС не будет существенно превышать 4.
[0080] Постобработка.
[0081] В качестве экстрактора случайности для ГСЧ (в том числе для КГСЧ) обычно применяют так называемые экстракторы с «зерном», которые помимо случайной величины принимают на вход «зерно» (относительно короткую случайную последовательность) от сильного источника энтропии. Для реализации экстрактора с «зерном» обычно используют так называемые 2-универсальные хэш-функции, эффективность которых гарантируется леммой остаточных хэшей (leftover hash lemma). Согласно данной лемме, если для случайной величины, определенной на множестве {0,1}n, выполнено неравенство H∞≥k, то отображение {0,1}n → {0,1}m задаваемое 2-универсальным классом хэш-функций, является (k, ε) - экстрактором с «зерном» при условии, что 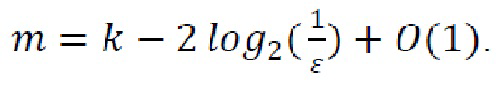 Малый параметр ε выполняет роль параметра «ошибки», задающего статистическое расстояние между равномерным распределением и результирующим распределением бинарной последовательности, полученной после процедуры извлечения случайности.
Малый параметр ε выполняет роль параметра «ошибки», задающего статистическое расстояние между равномерным распределением и результирующим распределением бинарной последовательности, полученной после процедуры извлечения случайности.
[0082] Легко найти связь между параметром ε и факторами сжатия, определенными ранее. Действительно, согласно данному выше определению квантового фактора сжатия для АЦП ГADC, длина бинарной последовательности после процедуры извлечения случайности должны быть равна 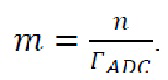 Приравнивая это к длине последовательности, задаваемой леммой остаточных хэшей, получаем
Приравнивая это к длине последовательности, задаваемой леммой остаточных хэшей, получаем

где, согласно формуле (13), первое слагаемое в правой части данного равенства равно 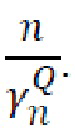
Решая это уравнение относительно ε, определяем:

где

Из формулы (20) видно, что 0<R<0,5: очевидно также, что параметр ошибки ε тем меньше, чем больше длина n входной последовательности.
[0083] Распространенной реализацией хеширования является умножение входных данных (представленных в виде бинарного вектора) на случайную бинарную матрицу [27]. В качестве случайных булевых матриц можно без потери общности использовать так называемые матрицы Теплица. Этот подход является одним из возможных для осуществления заявленного технического решения. Матрицы Теплица являются диагонально-постоянными, т.е. 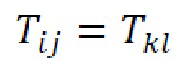 при
при 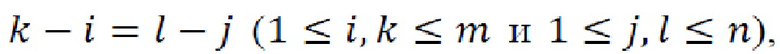 и для построения матрицы необходимо задать только первую строку и первый столбец, а следовательно для описания матрицы m×n требуется всего m+n-1 бит, что существенно экономит длину зерна.
и для построения матрицы необходимо задать только первую строку и первый столбец, а следовательно для описания матрицы m×n требуется всего m+n-1 бит, что существенно экономит длину зерна.
[0084] Для рассматриваемого в настоящем техническом решении КГСЧ алгоритм хеширования матрицами Теплица разбивается на три простых этапа:
1) Для «сырой» бинарной последовательности длины n определяется длина выходной последовательности по формуле: 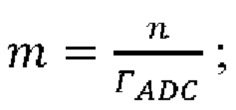
2) Построить матрицу Теплица, используя «зерно» длиной m+n-1;
3)Получить результирующую случайную последовательность в результате перемножения матрицы Теплица с сырой последовательностью.
[0083] Из соображений криптографической стойкости параметр малости обычно выбирают равным ε ~ 2-100 ~ 10-30. Согласно формуле (19), длина сырой случайной последовательности, подаваемой на вход экстрактора случайности, должна быть тогда 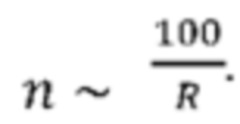 Например, для R=0.25 и ГАDС=4, матрица Теплица будет иметь размер 100×400.
Например, для R=0.25 и ГАDС=4, матрица Теплица будет иметь размер 100×400.
Такие большие матрицы требуют довольно много вычислительных ресурсов, поэтому для ускорения вычислений в качестве вычислительного блока (9) на Фиг. 1 можно, например, использовать программируемые логические интегральные схемы (ПЛИС) или интегральные схемы специального назначения (ASIC), которые позволяют естественным образом осуществить распараллеливание. Кроме того, в целях оптимизации удобно разбить большую матрицу Теплица на блоки (подматрицы) меньшего размера, что позволяет более эффективно использовать ограниченные ресурсы ПЛИС [28].
[0084] На Фиг. 11 представлена обобщенная блок-схема работы способа с помощью КГСЧ, работа которого в деталях была раскрыта в настоящих материалах заявки. В вычислительном блоке (9) КГСЧ происходят следующие операции. Прежде всего, в нем накапливается статистика поступающих оцифрованных импульсов, по которой восстанавливается плотность распределения интерференционного сигнала ƒS. С использованием найденной плотности распределения и графика, показанного на Фиг. 9, определяется квантовый фактор сжатия ГADC (величины 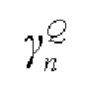 и γENOB, входящие в определение ГADC определяются параметрами АЦП). Согласно значению ГADC производится хеширование накопленной выборки случайных бит. Анализ плотности распределения и вычисление значения квантового фактора сжатия ГADC происходят параллельно с хешированием и выдачей случайных бит, что обеспечивает устойчивость работы КГСЧ к изменению классических шумов (автонастройку) и, соответственно, обеспечивает устойчивость к возможным атакам, а также повышение случайности формируемой случайной последовательности. Наконец, в зависимости от выбранного интерфейса (10G Ethernet, PCIe и пр.), обработанные случайные данные преобразуются в необходимый формат и выдаются потребителю.
и γENOB, входящие в определение ГADC определяются параметрами АЦП). Согласно значению ГADC производится хеширование накопленной выборки случайных бит. Анализ плотности распределения и вычисление значения квантового фактора сжатия ГADC происходят параллельно с хешированием и выдачей случайных бит, что обеспечивает устойчивость работы КГСЧ к изменению классических шумов (автонастройку) и, соответственно, обеспечивает устойчивость к возможным атакам, а также повышение случайности формируемой случайной последовательности. Наконец, в зависимости от выбранного интерфейса (10G Ethernet, PCIe и пр.), обработанные случайные данные преобразуются в необходимый формат и выдаются потребителю.
[0085] В настоящих материалах заявки было представлено предпочтительное раскрытие осуществление заявленного технического решения, которое не должно использоваться как ограничивающее иные, частные воплощения его реализации, которые не выходят за рамки испрашиваемого объема правовой охраны и являются очевидными для специалистов в соответствующей области техники.
Источники информации:
[1] М. Herrero-Collantes and J. С.Garcia-Escartin, "Quantum random number generators," Rev. Mod. Phys., vol. 89, p. 015004, 2017.
[2] T. Jennewein, U. Achleitner, G. Weihs, H. Weinfurter, and A. Zeilinger, "A fast and compact quantum random number generator," Rev. Sci. Instrum., vol. 71, pp. 1675-1680, 2000.
[3] C. Gabriel, C. Wittmann, D. Sych, R. Dong, W. Mauerer, U. L. Andersen, C. Marquardt, and G. Leuchs, "A generator for unique quantum random numbers based on vacuum states," Nat. Photonics, vol. 4, p. 711, 2010.
[4] Y. Shen, L. Tian, and H. Zou, "Practical quantum random number generator based on measuring the shot noise of vacuum states," Phys. Rev. A, vol. 81, p. 063814, 2010.
[5] T. Symul, S. M. Assad, and P. K. Lam, "Real time demonstration of high bitrate quantum random number generation with coherent laser light," Appl. Phys. Lett., vol. 98, p. 231103, 2011.
[6] C. R. S. Williams, J. C. Salevan, X. Li, R. Roy, and Т. E. Murphy, "Fast physical random number generator using amplified spontaneous emission," Opt. Express, vol. 18, pp. 23584-23597, 2010.
[7] A. Argyris, E. Pikasis, S. Deligiannidis, and D. Syvridis, "Sub-Tb/s Physical Random Bit Generators Based on Direct Detection of Amplified Spontaneous Emission Signals," J. Lightwave Technol., vol. 30, pp. 1329-1334, 2012.
[8] P. J. Bustard, D. Moffatt, R. Lausten, G. Wu, I. A. Walmsley, and B. J. Sussman, "Quantum random bit generation using stimulated Raman scattering," Opt. Express, vol. 19, pp. 25173-25180, 2011.
[9] M. J. Collins, A. S. Clark, C. Xiong,  M. J. Steel, and B. J. Eggleton, "Random number generation from spontaneous Raman scattering," Appl. Phys. Lett., vol. 107, p. 141112, 2015.
M. J. Steel, and B. J. Eggleton, "Random number generation from spontaneous Raman scattering," Appl. Phys. Lett., vol. 107, p. 141112, 2015.
[10] Η. Guo, W. Tang, Y. Liu, and W. Wei, "Truly random number generation based on measurement of phase noise of a laser," Phys. Rev. E, vol. 81, p. 051137, 2010.
[11] B. Qi, Y.-M. Chi, H.-K. Lo, and L. Qian, "High-speed quantum random number generation by measuring phase noise of a single-mode laser," Opt. Lett., vol. 35, pp. 312-314, 2010.
[12] M. Jofre, M. Curty, F. Steinlechner, G. Anzolin, J. P. Torres, M. W. Mitchell, and V. Pruneri, "True random numbers from amplified quantum vacuum," Opt. Express, vol. 19, pp. 20665-20672, 2011.
[13] F. Xu, B. Qi, X. Ma, H. Xu, H. Zheng, and H.-K. Lo, "Ultrafast quantum random number generation based on quantum phase fluctuations," Opt. Express, vol. 20, pp. 12366-12377, 2012.
[14] C. Abellan, W. Amaya, M. Jofre, M. Curty, A. Acin, J. Capmany, V. Pruneri, and M. W. Mitchell, "Ultra-fast quantum randomness generation by accelerated phase diffusion in a pulsed laser diode," Opt. Express, vol. 22, pp. 1645-1654, 2014.
[15] C. Henry, "Theory of the linewidth of semiconductor lasers," IEEE J. Quantum. Elect., vol. 18, pp. 259-264, 1982.
[16] G. P. Agrawal, "Effect of gain and index nonlinearities on single-mode dynamics in semiconductor lasers," IEEE J. Quantum. Elect vol. 26, pp. 1901-1909, 1990.
[17] C. Henry, "Phase noise in semiconductor lasers," J. Lightwave Technol., vol. 4, pp. 298-311, 1986.
[18] R. Loudon, "The Quantum Theory of Light", Oxford University, 2000.
[19] R. J. Glauber, "Nobel Lecture: One Hundred Years of Light Quanta," Rev. Mod. Phys., vol. 78, pp. 1267-1278, 2006.
[20] В.Л. Курочкин, P.П. Ермаков, В.В. Заводиленко, А.В. Лосев, А.В. Удальцов, В.В. Шароглазова, Р.А. Шаховой, and Ю.В. Курочкин, "Устойчивый к атакам квантовый генератор случайных чисел на интерференции лазерных импульсов со случайной фазой и способ его применения", patent №2721585 (Российская Федерация), 2020.
[21] R. Shakhovoy, V. Sharoglazova, A. Udaltsov, A. Duplinsky, V. Kurochkin, and Y. Kurochkin, "Influence of chirp, jitter and relaxation oscillations on probabilistic properties of laser pulse interference," submitted.
[22] Z. L. Yuan, M. Lucamarini, J. F. Dynes, B. Frohlich, A. Plews, and A. J. Shields, "Robust random number generation using steady-state emission of gain-switched laser diodes," Appl. Phys. Lett., vol. 104, pp. 261112-261111-261112-261115, 2014.
[23] R. Shakhovoy, M. Puplauskis, V. Sharoglazova, A. Duplinskiy, V. Zavodilenko, A. Losev, and Y. Kurochkin, "Direct phase modulation via optical injection: theoretical study," submitted. 21
[24] R. Shakhovoy, D. Sych, V. Sharoglazova, A. Udaltsov, A. Fedorov, and Y. Kurochkin, "Quantum noise extraction from the interference of laser pulses in optical quantum random number generator," Opt. Express, vol. 28, pp. 6209-6224, 2020.
[25] N. Nisan and A. Ta-Shma, "Extracting Randomness: A Survey and New Constructions," J. Comput. Syst. Sci., vol. 58, pp. 148-173, 1999.
[26] W. Kester (ed.), "Data Conversion Handbook", Elsevier, 2005.
[27] H. Krawczyk, "LFSR-based Hashing and Authentication," proceedings of Advances in Cryptology CRYPTO ’94, Berlin, Heidelberg, 1994.
[28] X. Zhang, Y. Nie, H. Liang, and J. Zhang, "FPGA implementation of Toeplitz hashing extractor for real time post-processing of raw random numbers," proceedings of 2016 IEEE-NPSS Real Time Conference (RT), 2016.
| название | год | авторы | номер документа |
|---|---|---|---|
| УСТОЙЧИВЫЙ К АТАКАМ КВАНТОВЫЙ ГЕНЕРАТОР СЛУЧАЙНЫХ ЧИСЕЛ НА ИНТЕРФЕРЕНЦИИ ЛАЗЕРНЫХ ИМПУЛЬСОВ СО СЛУЧАЙНОЙ ФАЗОЙ И СПОСОБ ЕГО ПРИМЕНЕНИЯ | 2019 |
|
RU2721585C1 |
| ВЫСОКОСКОРОСТНОЙ КВАНТОВЫЙ ГЕНЕРАТОР СЛУЧАЙНЫХ ЧИСЕЛ НА ПЕРЕКЛЮЧЕНИИ ПОЛЯРИЗАЦИИ В ПОЛУПРОВОДНИКОВОМ ЛАЗЕРЕ С ВЕРТИКАЛЬНЫМ РЕЗОНАТОРОМ (ВАРИАНТЫ) И СПОСОБ ФОРМИРОВАНИЯ СЛУЧАЙНОЙ ЧИСЛОВОЙ ПОСЛЕДОВАТЕЛЬНОСТИ С ЕГО ПОМОЩЬЮ | 2022 |
|
RU2788400C1 |
| АМПЛИТУДНО-ФАЗОВЫЙ МОДУЛЯТОР НА ПОЛУПРОВОДНИКОВЫХ ЛАЗЕРАХ С ОПТИЧЕСКОЙ ИНЖЕКЦИЕЙ И СПОСОБ ЕГО ПРИМЕНЕНИЯ ДЛЯ КВАНТОВОГО РАСПРЕДЕЛЕНИЯ КЛЮЧЕЙ | 2021 |
|
RU2813164C1 |
| Система квантового распределения ключей с недоверенным центральным узлом и способ приготовления квантовых состояний для протокола квантового распределения ключей с недоверенным центральным узлом | 2024 |
|
RU2834620C1 |
| КВАНТОВЫЙ ГЕНЕРАТОР СЛУЧАЙНЫХ ЧИСЕЛ | 2015 |
|
RU2613027C1 |
| Способ управления интерференционной картиной в однопроходной системе квантовой криптографии | 2017 |
|
RU2665249C1 |
| ДВУХПРОХОДНАЯ СИСТЕМА ФАЗОВОЙ МОДУЛЯЦИИ ДЛЯ КВАНТОВОГО РАСПРЕДЕЛЕНИЯ КЛЮЧЕЙ | 2022 |
|
RU2776030C1 |
| СПОСОБ ЗАЩИТЫ ГЕНЕРАТОРА СЛУЧАЙНЫХ ЧИСЕЛ (ГСЧ) ОТ ВМЕШАТЕЛЬСТВ В ФИЗИЧЕСКИЙ ПРОЦЕСС ГЕНЕРАЦИИ | 2019 |
|
RU2719558C1 |
| Способ обнаружения атаки с ослеплением детекторов в системах квантовой криптографии с поляризационным кодированием | 2021 |
|
RU2783977C1 |
| СЕТЬ КВАНТОВОГО РАСПРЕДЕЛЕНИЯ КЛЮЧЕЙ | 2015 |
|
RU2621605C2 |


Изобретение относится к области генераторов случайных чисел (ГСЧ), в частности к квантовым ГСЧ (КГСЧ), основанных на интерференции лазерных импульсов со случайной фазой. Технический результат заключается в повышении качества случайности оцифрованной числовой последовательности за счет детального анализа вклада классических шумов и строгого определения квантового фактора сжатия, позволяющего достоверно оценить соотношения классического и квантового шумов. Генератор случайных чисел (КГСЧ) содержит: высокоскоростной лазерный драйвер, интерферометр Майкельсона, два зеркала Фарадея и линии задержки, фотоприемник, аналого-цифровой преобразователь (АЦП), вычислительный блок. 2 н. и 6 з.п. ф-лы, 11 ил.
1. Квантовый генератор случайных чисел (КГСЧ) на интерференции лазерных импульсов, содержащий:
- высокоскоростной лазерный драйвер, обеспечивающий управление полупроводниковым лазером, работающим в режиме переключения усиления, который посылает импульсы в волоконный интерферометр Майкельсона;
- интерферометр Майкельсона, построенный из волоконного светоделителя, двух зеркал Фарадея и линии задержки, длина которой подобрана таким образом, чтобы на выходе из интерферометра происходила интерференция импульсов, испущенных лазером в разные моменты времени;
- фотоприемник, обеспечивающий прием результатов интерференции, представляющих собой последовательность оптических импульсов случайной интенсивности;
- аналого-цифровой преобразователь (АЦП), обеспечивающий оцифровку импульсов с фотоприемника;
- вычислительный блок, связанный с АЦП и осуществляющий
постобработку сырой случайной последовательности, а также позволяющий определять статистические свойства интерференции в виде плотности распределения интерференционного сигнала, на основании которой вычисляется квантовый фактор сжатия ГADC, характеризующий вклад классических шумов;
хеширование накопленной выборки случайных бит на основании значения ГADC,
- причем хеширование и выдача случайных бит происходят параллельно с анализом плотности распределения и вычислением значения ГADC.
2. Квантовый генератор случайных чисел по п. 1, в котором АЦП выполнен многоканальным.
3. Квантовый генератор случайных чисел по п. 2, в котором времена защелкивания каналов АЦП устанавливаются таким образом, чтобы соответствующие отсчеты срабатывали на разных импульсах.
4. Квантовый генератор случайных чисел по п. 1, дополнительно содержащий волоконный оптический полосовой фильтр, обеспечивающий улучшение спектрального соответствия между интерферирующими импульсами на пути их следования от лазера к интерферометру.
5. Квантовый генератор случайных чисел по п. 4, дополнительно содержащий волоконный оптический изолятор или оптический циркулятор, связанный с оптическим полосовым фильтром и препятствующий попаданию отраженных оптических сигналов в лазерный драйвер.
6. Способ формирования случайной числовой последовательности с помощью КГСЧ по любому из пп. 1-5, содержащий этапы, на которых:
- осуществляется накопление статистики в виде плотности распределения интерференционного сигнала;
- осуществляется анализ плотности распределения интерференционного сигнала;
- вычисляется квантовый фактор сжатия Г, характеризующий вклад классических шумов, кроме вклада АЦП;
- вычисляется фактор сжатия ГADC, учитывающий неравномерность и классические шумы, вносимые самим АЦП, на основании накопленной статистики и вычисленного фактора сжатия Г;
- осуществляется хеширование накопленной выборки случайных бит на основании значения ГADC;
- осуществляется преобразование и выдача случайных бит в заданном формате;
причем хеширование и выдача случайных бит происходят параллельно с анализом плотности распределения и вычислением значения квантового фактора сжатия ГADC.
7. Способ по п. 6, в котором фактор сжатия ГADC определяется по формуле 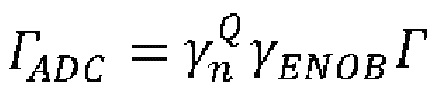 , где величина
, где величина  является промежуточным фактором сжатия, связанным с неравномерностью плотности распределения, а величина γENOB - фактор сжатия, связанный с классическими шумами внутри АЦП.
является промежуточным фактором сжатия, связанным с неравномерностью плотности распределения, а величина γENOB - фактор сжатия, связанный с классическими шумами внутри АЦП.
8. Способ по п. 6, в котором формат выдачи случайных бит зависит от типа интерфейса, подключенного к КГСЧ.
| УСТОЙЧИВЫЙ К АТАКАМ КВАНТОВЫЙ ГЕНЕРАТОР СЛУЧАЙНЫХ ЧИСЕЛ НА ИНТЕРФЕРЕНЦИИ ЛАЗЕРНЫХ ИМПУЛЬСОВ СО СЛУЧАЙНОЙ ФАЗОЙ И СПОСОБ ЕГО ПРИМЕНЕНИЯ | 2019 |
|
RU2721585C1 |
| Многоступенчатая активно-реактивная турбина | 1924 |
|
SU2013A1 |
| ГЕНЕРАТОР ПСЕВДОСЛУЧАЙНОЙ ПОСЛЕДОВАТЕЛЬНОСТИ (ВАРИАНТЫ) | 1999 |
|
RU2163027C2 |
| ГЕНЕРАТОР РАВНОМЕРНО РАСПРЕДЕЛЕННЫХ СЛУЧАЙНЫХ ЧИСЕЛ | 1993 |
|
RU2092892C1 |
Авторы
Даты
2021-11-02—Публикация
2020-12-21—Подача