СПОСОБ УСКОРЕНИЯ МАГНИТНЫХ ДИПОЛЕЙ Российский патент 2014 года по МПК H05H3/00 

Изобретение относится к области ускорительной техники и может быть использовано для решения прикладных задач, в частности для удаления космического мусора и в военном деле.

Область техники

Известен, [1], способ ускорения магнитных диполей одноступенчатым электромагнитным ускорителем. В силу одноступенчатости конечная скорость и, соответственно, энергия ускоренных магнитных диполей в нем мала.

Известен, [2], способ ускорения магнитных диполей, при котором создают, при последовательном выключении токовых витков, в которых предварительно был пропущен ток, движущийся в пространстве токовый импульс. Магнитные диполи, в этом способе, ускоряют с помощью движущегося в пространстве градиента магнитного поля. Использование большого числа витков, в принципе, позволяет достичь большой конечной скорости магнитных диполей.

При протекании электрического тока в витках, магнитных катушках, соленоиде, возникает магнитное поле, которое втягивает магнитный диполь внутрь витка с током. После прохождения магнитным диполем центра витка, градиент магнитного поля меняет знак, из-за чего магнитный диполь начинает ускоряться в обратном направлении, то есть тормозиться. Поэтому, для создания непрерывного ускорения, ток в витке должен быстро обрываться, после прохождения магнитным диполем центра витка.

Этот способ может быть выбран за прототип.

Недостатки прототипа

Однако, несмотря на кажущуюся простоту известного способа, его практическое использование сопряжено с серьезными трудностями.

Из используемых в магнитных диполях ферромагнитных материалах наиболее подходящим является железо, имеющее большой удельный магнитный момент и высокую температуру Кюри. Удельный магнитный момент присущ используемому веществу и увеличен быть не может. Более того, из-за того, что магнитный диполь должен включать в себя также реактивный двигатель с запасом топлива и приборы навигации, то удельный магнитный момент у диполя будет даже меньше, чем у чистого железа. Это не позволяет достичь большой конечной скорости магнитному диполю при таком способе ускорения.

Поясним подробнее. Магнитный момент, приходящийся на одну молекулу в железе, [3], стр.524, составляет величину n_b=2.219 магнетонов Бора. Табличное значение магнетона Бора равно: [3], стр.31, m_b=9.27*10^-21 erg/Gs. Учитывая, что атомная масса железа A_Fe равна: A_Fe=56, найдем, что магнитный момент, приходящийся на один нуклон в железе равен: m_Fe=2*10^-10 eV/(Gs*nucleon) и это значение m_Fe увеличено быть не может.

Вторым принципиальным недостатком прототипа является то, что движение магнитных диполей в нем неустойчиво в продольном направлении. Дело в том, что при притяжении разноименных полюсов магнитов имеет место фазовая неустойчивость.

Так, если, магнитный диполь, немного отстанет от ускоряющего его бегущего токового импульса, то он будет оказываться во все меньшем поле импульса и, в конце концов, навсегда от него отстанет. Если же магнитный диполь излишне приблизится к импульсу тока, то он будет попадать во все большее поле, все сильнее притягиваться к импульсу, в конце концов, его обгонит и развернется на 180 градусов.

Измеряя в процессе ускорения скорость магнитного диполя, можно включить очередную катушку, например, с некоторой задержкой. Но это нельзя сделать, если магнитный диполь уже прилетел, а катушку надо было включить раньше. Это просто говорит о том, что бороться аппаратурными методами с фазовой неустойчивочтивостью достаточно сложно.

С точки зрения взаимного расположения ускоряющего бегущего импульса и магнитного диполя, устойчивым является только случай, когда импульс толкает (а не тянет за собой) магнитный диполь. Это означает, что область фазовой (продольной) устойчивости находится на переднем склоне бегущего импульса.

Действительно, если магнитный диполь начнет опережать импульс и убежит вперед, то он будет попадать во все более слабое поле импульса, меньше ускоряться и, в конце концов, ускоренно бегущий импульс нагонит магнитный диполь. Если же магнитный диполь начнет отставать от импульса, то на его переднем склоне он начнет попадать во все более сильное поле и, в конце концов, вернется к своей фазе на импульсе, фазе, называемой синхронной.

Обе эти причины приводят к тому, что прототип имеет принципиальный недостаток - конечная скорость магнитных диполей в нем мала.

Техническая задача, которую решает данный способ, состоит в устранении указанного недостатка, то есть в увеличении конечной скорости магнитных диполей.

Сущность настоящего изобретения заключается в том, что в способе ускорения магнитных диполей с помощью движущегося в пространстве градиента магнитного поля, создаваемого током, пропускаемым по виткам соленоида, градиент магнитного поля создают последовательным включением токовых витков, при этом ускорение ведут внутри титановой трубки, предотвращающей разворот диполей на 180 градусов в поле бегущего градиента магнитного поля и предотвращающей отклонение диполей от оси ускорения в радиальном направлении.

Связь отличительных признаков с положительным эффектом

Для эффективного ускорения магнитных диполей требуются большие: удельный магнитный момент диполя и градиент ускоряющего магнитного поля. Удельный магнитный момент диполя, по-видимому, может быть увеличен, по сравнению с железом, за счет применения сверхпроводящего токового слоя, расположенного внутри диполя. Градиент магнитного поля, ускоряющий диполь, может быть увеличен за счет использования сверхпроводимости и соленоидов специальной формы. Оба эти пути ведут к увеличению ускоряющей диполь силы: F_z=m*dB_z/dz, где m - удельный магнитный момент диполя, dB_z/dz - градиент магнитного поля.

Предложенный способ можно реализовать с помощью устройства

На Фиг.1 приведена схема устройства. Устройство состоит из пушки 1, где магнитные диполи 2, разгоняются до начальной скорости V_in=1 km/s. Токовыми катушками 3, создающими импульсное магнитное поле, магнитные диполи ускоряют до конечной скорости V_fin=5 km/s. Удерживают магнитные диполи от разворота на 180° и от ухода в радиальном направлении, тем, что ускорение ведут внутри титановой трубки, 4. Выпуск магнитных диполей в атмосферу осуществляется через три буферные полости, представляющие собой отрезки трубы, разделенной торцевыми стенками, в которые встроены импульсные диафрагмы 5. Каждая буферная полость имеет индивидуальную откачку 6.

1. Предварительное ускорение магнитных диполей газодинамическим методом

Начальная, после порохового старта, скорость магнитного диполя может быть оценена из следующих соображений. Тепловая скорость молекул сгоревшего пороха может быть определена из молекулярной массы продуктов горения М и температуры сгоревших продуктов T:

$${\beta }_T={\left(kT/M{c}^2\right)}^{1/2},\left(1\right)$$

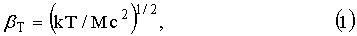
где k=1.38*10^-16 erg/degree - постоянная Больцмана, 1 erg=6.24*10¹¹ eV, М=Nm_n, где m_n - масса нуклона, m_nc²=1 GeV, N - число нуклонов в молекулах продуктов горения, N=100, с=3*10¹⁰ cm/s, скорость света в вакууме, Т=10³ degree. После подстановки численных значений в формулу (1), найдем, что тепловая скорость продуктов горения равна: β_T=3*10^-6. При этом реальная скорость снаряда будет равна: V_sh=1 km/s.

Для достижения этой скорости у снаряда вытянутой, стреловидной формы может потребоваться откачка ствола пушки, то есть удаление газа из ствола при выстреле. Величина противодавления, давления, действующего со стороны воздуха, находящегося в стволе, на снаряд, может быть оценена из формулы:

$$P_{opp}=\rho V_{sh}^2/\mathrm{2,}\left(2\right)$$

где ρ - плотность сжатого воздуха в стволе пушки, ρ=3-4 ρ₀, ρ₀=1.3*10^-3 g/cm³ - плотность воздуха при нормальных условиях. После подстановки численных значений в формулу (2) получим, что величина противодавления может составлять: Р_орр=2.5*10⁷ dn/cm²=25 atm. Таким образом, откачка ствола пушки может быть весьма полезна. В вакууме же должно производиться и магнитодинамическое доускорение снаряда, а выпуск его в атмосферу должен осуществляться через последовательность откачиваемых буферных объемов.

Возможно, впрочем, использование подкалиберного снаряда позволит достичь большей начальной скорости, чем мы предполагаем.

2. Выбор конечной скорости магнитных диполей

Соотношение между скоростью и энергией, приходящейся на нуклон, можно видеть из следующей таблицы.

Таблица 1 Зависимость между скоростью снаряда и энергией, приходящейся на нуклон V_sh, km/s 1 2 3 4 5 ε, eV/nucl. 5*10^-3 2*10^-2 5*10^-2 8*10^-2 0.125

Видно, что конечной скорости магнитного диполя, равной V_{sh fin}=5 km/s, соответствует энергия, приходящаяся на один нуклон в снаряде, порядка W_fin≈0.13 eV/nucleon.

2.1. Подъемная сила

При длине ускорителя L_acc≈300 m его можно располагать только горизонтально, параллельно палубе корабля. Для вывода магнитного диполя за пределы атмосферы можно использовать небольшую асимметрию формы магнитного диполя, такую, чтобы эта форма создавала подъемную силу F_y. Уравнение вертикального движения при этом может быть записано в виде:

$$md{V}_y/dt=C_y{\rho }_0{V}_x^2*S/\mathrm{2,}\left(3\right)$$

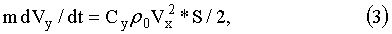
где С_у - аэродинамический коэффициент подъемной силы,

ρ₀=1.3*10^-3 g/cm³ - плотность воздуха у поверхности Земли,

V_x=5 km/s - горизонтальная скорость магнитного диполя, S - поперечное

сечение магнитного диполя.

Выберем диаметр магнитного диполя равным: d_sh=60 mm и массу диполя равной m=2 kg. Потребуем, чтобы за время t_fly=10 s магнитный диполь поднялся на высоту Y>30 km, где сопротивлением воздуха можно пренебречь. Найдем из выражения (3), каким должен быть коэффициент подъемной силы C_y для этого случая:

$$C_y=4mY/\left({\rho }_0{V}_x^2*S*t_{fly}^2\right).\left(4\right)$$

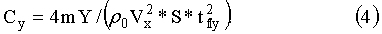
Подставляя цифры в выражение (4): m=2*10³ g, S=28.3 cm², найдем, что коэффициент подъемной силы С_у должен быть равен: C_y≈1.3*10^-2, что, по-видимому, не трудно выполнить небольшим скосом в носовой части магнитного диполя. Такого же порядка должен быть и коэффициент аэродинамического сопротивления C_x.

2.2. Баллистика. Аэродинамическое сопротивление

Рассчитаем движение магнитных диполей, ускоренных электродинамическим способом и выпущенных под углом Θ=0 к горизонту с учетом сопротивления воздуха. Уравнение горизонтального движения магнитных диполей можно записать в виде:

$$md{V}_x/dt=\rho C_{x}S{V}_x^2/\mathrm{2,}\left(5\right)$$

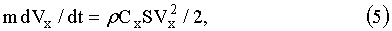
где m - масса магнитного диполя, V_x -скорость, g - 0.01 km/s² - ускорение силы тяжести, 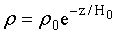$$\rho ={\rho }_0{e}^{-z/H_0}$$ - барометрическая формула изменения плотности атмосферы с высотой, ρ₀=1.3*10^-3 g/cm³ - плотность воздуха у поверхности Земли, Н₀=7 km - значение высоты, на которой плотность падает в е раз.

Аэродинамическим коэффициентом или коэффициентом аэродинамического сопротивления называется безразмерная величина, учитывающая «качество» формы магнитного диполя,

$$C_x=F_x/\left(\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.\right){\rho }_0{V}_x^{2}S.\left(6\right)$$

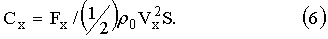
Решение уравнения (5) может быть записано в виде:

$$V\left(t\right)=V_x/[1+\rho C_x{V}_x*S*t/2m].\left(7\right)$$

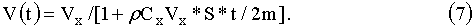
Для того чтобы можно было вычислять изменение скорости магнитных диполей со временем, необходимо найти аэродинамический коэффициент С_х.

2.3. Расчет коэффициента аэродинамического сопротивления магнитных диполей для воздуха

Будем считать, что магнитный диполь имеет форму цилиндрического стержня с конической головной частью. Тогда, при ударе молекулы азота по острому конусу, изменение продольной скорости молекул равно:

$$\Delta V_x=V_x*{\Theta }_t^2/\mathrm{2,}\left(8\right)$$

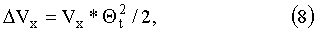
где Θ_t - угол конуса при вершине. Молекулы газа передают магнитному диполю импульс:

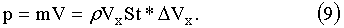
Изменение импульса в единицу времени - сила, сила лобового торможения,

$$F_{x1}=\left(\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.\right)\rho V_{x}S*V_x*{\Theta }_t^2.\left(10\right)$$

Разделив F_x1 на 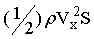$$(\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.)\rho V_x^{2}S$$ , получим коэффициент аэродинамического сопротивления для острого конуса при зеркальном отражении молекул от конуса, (формула Ньютона):

$$C_{xair}={\Theta }_t^2.\left(11\right)$$

Наше рассмотрение соответствует гиперзвуковым скоростям, когда можно пренебречь эффектами, которые возникают при скорости, близкой к скорости звука в невозмущенной среде. Общая эмпирическая формула для коэффициента аэродинамического сопротивления острого конуса приведена в работе, [4], при гиперзвуковых скоростях она переходит в формулу Ньютона.

Пусть длина конусной части магнитного диполя равна: l_cone=60 cm при диаметре снаряда d_sh=60 mm. Это означает, что угол при вершине конуса равен: Θ_t=10^-1 и С_{х air}=10^-2.

2.4. Прохождение магнитных диполей сквозь атмосферу

Составим таблицу, где представим зависимость от времени вертикальной скорости магнитного диполя, его высоты подъема и горизонтальной скорости. Вертикальную скорость будет рассчитывать по формуле:

$$\Delta V_y=C_y\rho V_x^2*S*\Delta t/2m.\left(12\right)$$

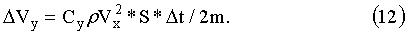
Набор высоты, соответственно:

$$Y=Y_0+V_y^{-}*\Delta t+C_y\rho V_x^2*S_{tr}^{*}{\left(\Delta t\right)}^2/4m,\left(13\right)$$

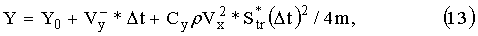
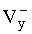
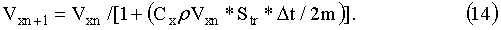
где $$V_y^{-}$$ - средняя вертикальная скорость в промежутке времени Δt. Уменьшение горизонтальной скорости со временем будем описывать формулой (7):

$$V_{xn+1}=V_{xn}/[1+\left(C_x\rho \text{}{V}_{xn}*S_{tr}*\Delta t/2m\right)].\left(14\right)$$

Изменение плотности воздуха с высотой будем учитывать по барометрической формуле ρ=ρ₀*ехр[-y/Н₀], где H₀=7 km. В Таблице 2 приведены параметры полета магнитного диполя в зависимости от времени. Во второй колонке приведена вертикальная скорость магнитного диполя, в третьей - горизонтальная скорость магнитного диполя, в четвертой - набранная высота, которую он будет иметь после соответствующей секунды полета, в пятой - давление атмосферы на этой высоте.

Таблица 2 Параметры полета, для случая С_х, C_y=1.3*10^-2 t, s V_x, km/s V_y, km/s Y, km ρ_air, g/cm³ 0 5 0 0 1.3*10^-3 10 3 3 30 2.6*10^-5

Время подъема до максимальной высоты в этом случае равно: τ_max=V_y/g=300 s, дальность полета $$S=V_x^{*}2{\tau }_{\max }=1800km$$ , максимальная высота подъема: $$Y=V_y^2/2g=450km$$ . Изменяя у снаряда форму конуса в головной части, по-видимому, можно будет переходить от настильной стрельбы к навесной (зенитной) стрельбе.

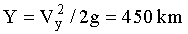
3. Возможность увеличения удельного магнитного момента в магнитном диполе

Удельный магнитный момент диполя может быть увеличен (по сравнению с железом), если внутри диполя поместить сверхпроводящую обмотку из Nb₃Sn и пропустить по ней кольцевой ток.

Рассчитаем, насколько увеличится удельный магнитный момент - магнитный момент, приходящийся на единицу массы магнитного диполя, если в области его цилиндрической части с длиной l_cy1 равной l_cy1=40 cm, поместить сверхпроводящий слой из Nb₃Sn с радиусом r_cy1=3 cm и толщиной 8_cy1=0.2 cm. Будем считать плотность тока в сверхпроводнике равной, [3], стр.312, J_sc=3*10⁵ A/cm². Тогда линейная плотность тока j_sc (A/cm) в таком сверхпроводящем слое будет равна: 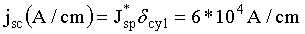$$j_{sc}\left(A/cm\right)=J_{sp}^{*}{\delta }_{cy1}=6*{10}^{4}A/cm$$ . Такая линейная плотность тока создаст на поверхности сверхпроводника напряженность магнитного поля H_sc, равную: H_sc(kGs)=1.226*j (A/cm)≈70 kGs, что не противоречит возможности достижения плотности тока J_sc=3*10⁵ A/cm², [3], стр.312.

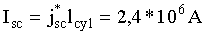
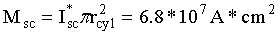
Общий ток, текущий в сверхпроводящем слое I_sc, будет равен: $$I_{sc}=j_{sc}^{*}{l}_{cy1}=\mathrm{2,4}*{10}^{6}A$$ , он приведет к появлению магнитного момента $$M_{sc}=I_{sc}^{*}\pi r_{cy1}^2=6.8*{10}^{7}A*c{m}^2$$ или, в системе СГС, M_sc=6.8*10⁶ erg/Gs.

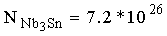
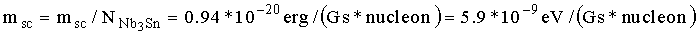
Общая масса сверхпроводящего слоя может быть вычислена исходя из того, что плотность сверхпроводника Nb₃Sn равна ρ_Nb3Sn=8 g/cm³, атомная масса A=400 и в общем объеме сверхпроводника V_sp=150 cm³ содержится $$N_{N{b}_{3}Sn}=7.2*{10}^{26}$$ нуклонов. Удельный магнитный момент, магнитный момент, приходящийся на единицу массы (нуклон), при этом получается равным: $$m_{sc}=m_{sc}/N_{N{b}_{3}Sn}=0.94*{10}^{-20}erg/\left(Gs*nucleon\right)=5.9*{10}^{-9}eV/\left(Gs*nucleon\right)$$ , что примерно 30 раз больше, чем в железе, [3], стр.524.

4. Пути достижения требуемых параметров ускорения

Пусть масса сверхпроводника в магнитном диполе равна $$m_{N{b}_{3}Sn}=1.2kg$$ , масса реактивного двигателя, топлива, приборов навигации и управления пусть так же равна m_Fuel=0.8 kg, тогда удельный магнитный момент в таком магнитном диполе будет равен: m₀=3.5*10^-9 eV/(Gs*nucleon), что, примерно, в 17 раз больше, чем в железе.

Длительность импульса магнитного поля может быть определена из следующих соображений. Чтобы магнитный диполь «помещался» на длине ускоряющего его импульса, замедленная длина волны должна быть порядка: λ_slow=4 m. Временной период соответствующей волны определим из соотношения

$${\lambda }_{slow}=V_{sh}*T_0,\left(15\right)$$

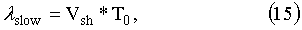
откуда найдем, что Т₀=4 ms и соответствующая этому периоду частота волны равна: f₀=250 Hz. В таком бегущем градиенте магнитного поля и должен ускоряться магнитный диполь.

Выбор диаметра снаряда d_sh=60 mm является компромиссным. С ростом диаметра магнитный момент диполя растет как площадь, то есть пропорционально квадрату диаметра снаряда. Масса сверхпроводника при этом растет как периметр сверхпроводящего слоя, то есть пропорционально диаметру, и удельный магнитный момент - магнитный момент, приходящийся на нуклон, растет пропорционально диаметру снаряда. Однако, увеличение диаметра снаряда, при его разумной длине l_sh~1 m, приводит к тому, что при этом все труднее получить острый конус в головной части цилиндра. Полный угол при вершине конуса равен: Θt⁼d_sh/l_cone и с увеличением диаметра снаряда этот угол становится все больше.

Коэффициент аэродинамического сопротивления острого конуса $$C_x\approx {\Theta }_t^2$$ и этот коэффициент с ростом угла при вершине быстро растет, что приводит к потере скорости снаряда при прохождении атмосферы и делает бессмысленным наращивание скорости снаряда за счет увеличения удельного магнитного момента снаряда, то есть увеличение его диаметра.

Длина ускорения L_acc=3*10² m также не может быть сильно увеличена, так как это затруднит размещение ускорителя на корабле.

5. Выбор толщины стенки ствола пушки Гаусса

Области фазовой устойчивости в азимутально-симметричной волне соответствует область радиальной неустойчивости. Магнитный диполь будет отталкиваться от одноименного полюса, но прежде всего он будет стремиться развернуться на 180° и притянуться к разноименному полюсу.

Предотвратить радиальный уход диполя и его разворот на 180° в поле ускоряющего его импульса можно поместив диполь внутрь титановой трубки, внутренний диаметр которой совпадает с наружным диаметром диполя. Толщина стенки титановой трубки должна быть такова, чтобы внешнее магнитное поле свободно, без искажений проникало внутрь, то есть она должна быть много меньше глубины скин-слоя в титане. При этом изнутри на трубку должно быть нанесено сапфировое или алмазное покрытие, которое будет уменьшать износ внутренней поверхности трубки.

Электрическое сопротивление меди ρ_Cu=1.67*10^-6 Ohm*cm, титана ρ_Ti=55*10^-6 Ohm*cm, [3], стр.305, проводимость σ (размерность σ равна l/s) связана с удельным сопротивлением соотношением: σ=9*10¹¹/ρ и для меди σC_u=5.4*10¹⁷ l/s, для титана σ_Ti=3.23*10¹⁶ l/s. Это позволяет рассчитывать глубину скин-слоя и, тем самым, вычислить возможную толщину стенки трубки, в которой будет ускоряться магнитный диполь.

Найдем толщину скин-слоя для титана для частоты f₀=250 Hz. Она может быть вычислена по формуле:

$${\delta }_{Ti}=c/2\pi {\left(f_0{\sigma }_{Ti}\right)}^{1/2}=1.68cm.\left(16\right)$$

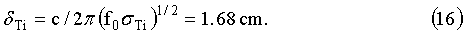
Это означает, что толщина стенки титановой трубки, в которой должен ускоряться магнитный диполь, может быть выбрана равной: Δh_Ti=2 mm.

6. Взаимодействие диполя с градиентом магнитного поля витка с током

Для устойчивого ускорения магнитных диполей нужно «включать» последовательно магнитные катушки, включать по мере того, как продвинется диполь. Магнитное поле витка с током может быть записано в виде, [5]:

$$B_z=I*r_0^2/[2*{\left(r_0^2+z^2\right)}^{3/2}].\left(17\right)$$

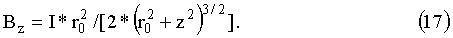
где I₀ - ток в витке, Ампер, r₀ - радиус витка с током, cm, z - расстояние от плоскости витка до точки наблюдения.

В отличие от многосекционной Пушки Гаусса, [2], соответствующую катушку здесь надо «включать» после прохождения магнитным диполем ее центра, а не выключать заранее включенную катушку.

6.1. Структура градиента магнитного поля витка с током

Продифференцируем выражение (17) по z и получим формулу для градиента магнитного поля:

$$d{B}_z/dz=\left(3/2\right)*r_0^2{I}_0^{*}z/{\left(r_0^2+z^2\right)}^{5/2}.\left(18\right)$$

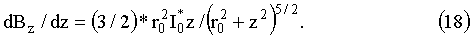
Из этой формулы видно, что градиент поля обращается в нуль в плоскости витка, при z=0.

Будем считать, что на расстоянии, порядка радиуса витка, скорость диполя изменяется незначительно, то есть можно произвести замену переменной z=V_sht. Удельный магнитный момент диполя увеличивается по мере прохождения центром диполя расстояния от плоскости витка по закону:

$$m=2m_0^{*}z/l_{sh},\left(19\right)$$

где m₀=3.5*10^-9 eV/(Gs*nucleon), l_sh - длина диполя. Ток в витке после момента включения пусть нарастает со временем линейно, по закону:

$$I=I_0^{*}4t/T_0,\left(20\right)$$

где Т₀ - временной период замедленной длины волны.

Тогда сила, действующая на диполь, со стороны витка равна:

$$F_z=m_0^{*}\left(z/l_{sh}\right)*\left(3/2\right)*r_0^2*z{I}_0^{*}4\left(t/T_0\right)/{\left(r_0^2+z^2\right)}^{5/2}.\left(21\right)$$

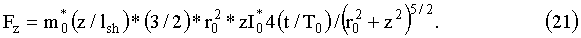
Заменяя t=z/V_sh и интегрируя no z, получим выражение для темпа набора энергии при прохождении магнитным диполем одного витка:

$$\Delta W={\displaystyle \int F_{z}dz={\displaystyle \int m_0^{*}\left(z/l_{sh}\right)*\left(3/2\right)*r_0^2*z{I}_0*4\left(z/V_{sh}{T}_0\right)/{\left(r_0^2+z^2\right)}^{5/2}dz,\left(22\right)}}$$

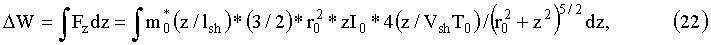
или

$$\Delta W_1=12m_0*\left(r_0^2/l_{sh}\right)*\left(I_0/V_{sh}{T}_o\right){\displaystyle \underset{}{\overset{l_{sh}/2}{\int }}[z^3/{\left(r_0^2+z^2\right)}^{5/2}}]dz.\left(23\right)$$

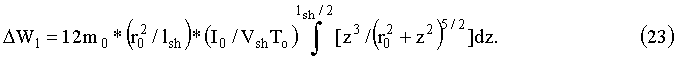
6.2. Переход от одного витка к соленоиду

Интегрирование в формуле (23) надо вести до расстояния, порядка половины длины магнитного диполя: l_sh=l m, такого же порядка должен быть и радиус витка: r₀=lm. После того, как магнитный диполь продвинется на расстояние l_sh/2, его магнитный момент больше не будет нарастать, и магнитный диполь будет просто отталкиваться от витка с током.

Соответствующий набор энергии тогда можно записать в виде:

$$\Delta W_2=6m_0*r_0^2*\left(I_0/V_{sh}{T}_0\right){\displaystyle {\int }_{l_{sh/2}}^{r_0}[z^2/{\left(r_0^2+z^2\right)}^{5/2}]dz.\left(24\right)}$$

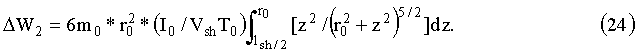
Подставляя численные значения r₀=1 m, l_sh=1 m, вычисляя интегралы и суммируя ΔW₁ и ΔW₂, найдем, что энергия, набранная магнитным диполем при прохождении одного токового витка равна:

$$\Delta W=12m_0*\left(r_0^2/l_{sh}\right)*\left(I_0/V_{sh}{T}_0\right)*5.5*{10}^{-2}.\left(25\right)$$

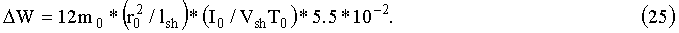
Подставляя в формулу (25) численные значения для начала ускорения и учитывая, что в нашем рассмотрении считается, что на 1 m ускорения приходится 10³ витков, для среднего значения тока ½, то есть умножая AW на 500/m, считая m₀=3.5*10^-9 eV/(Gs*nucleon) и принимая ток в одном витке равным: I₀=150 кА, окончательно получим формулу для темпа набора энергии магнитным диполем:

$$\Delta W=4.33*{10}^{-4}\left(eV/nucleon*m\right).\left(26\right)$$

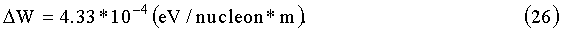
Умножая ΔW=4.33*10^-4 (eV/nucleon*m) на длину ускорения L_acc=300 m, найдем конечную энергию магнитных диполей: W_fin=0.13 eV/nucleon, что соответствует конечной скорости магнитных диполей V_fin=5 km/s.

7. Выпуск магнитных диполей в атмосферу

Магнитные диполи должны ускоряться в довольно глубоком вакууме, P₁≈10^-6 мм рт.ст., в то же время применение их предполагается при нормальных атмосферных условиях: Р₂≈10³ мм рт.ст., так что разница давлений составляет примерно 9 порядков. Для создания такого градиента давления можно использовать несколько буферных полостей, представляющих собой, например, цилиндрические камеры, разделенные торцевыми стенками в которые встроены импульсные диафрагмы. Каждая полость должна иметь индивидуальную вакуумную откачку.

Рассчитаем количество частиц воздуха, которые проникнут в первую, ближайшую к атмосфере, полость. Пусть радиус раскрытия диафрагмы составляет r_0d=10 cm и время, на которое она открывается, составляет t₁=10^-3 s. Тогда линейная скорость движения лепестков ирисовой диафрагмы будет составлять V₁₁=r_0d/t₁=10⁴ cm/s, что не должно представлять большой проблемы для работы механизма. 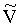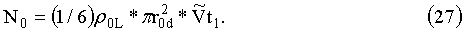Среднюю скорость теплового движения молекул воздуха $$\tilde{V}$$ будем считать примерно равной скорости звука в воздухе: $$\tilde{V}=3*{10}^{4}cm/s$$ . Из всевозможных пространственных ориентаций скорости только 1/6 (1/6 - это одна грань куба) направлена в сторону диафрагмы. Число молекул в сантиметре кубическом воздуха при нормальных условиях, число Лошмидта, равно ρ_0L=2.7*10¹⁹ молекул/cm³. Тогда число молекул, прошедших из атмосферы в первую буферную полость, за время пока диафрагма находится в открытом состоянии, равно:

$$N_0=\left(1/6\right){\rho }_{0L}*\pi r_{0d}^2*\tilde{V}{t}_1.\left(27\right)$$

Подставляя численные значения в формулу (27) найдем, что общее число частиц, прошедших из атмосферы в первую буферную полость равно: N₀=4*10²² частиц. Пусть объем первой полости составляет величину, равную V₀₁=10³ л=10⁶ cm³. Тогда плотность молекул в ней после срабатывания диафрагмы будет равно n₀=4*10¹⁶ молекул/cm³.

Плотность частиц (и давление: р=nkT) в первой буферной полости примерно на 3 порядка меньше плотности частиц в атмосфере при нормальных условиях, так что потребуется, по крайней мере, 3 такие полости для создания соответствующего градиента давления.

Рассмотрим теперь динамику плотности частиц в полости в течение времени между срабатываниями устройства. Пусть полость откачивается через отверстие с площадью S₁=10 cm². Будем считать, что все молекулы, попавшие на эту площадь, удаляются из объема. Будем считать, что время между выстрелами составляет t₂=10^-1 s, то есть частота срабатывания устройства равна F=10 Hz. Уравнение, описывающее уменьшение плотности частиц при откачке, может быть записано в виде:

$$dn=-n*\left(1/6\right)*S_1\tilde{V}t/V_{01}.\left(28\right)$$

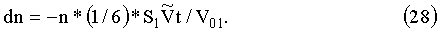
Решение этого уравнения может быть записано в виде:

$$n=n_0*\exp [-*\left(1/6\right)*S_{1}Vt/{\tilde{V}}_{01}],\left(29\right)$$

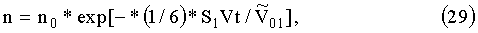
для времени откачки t=t₂ показатель экспоненты примерно равен 5, так что за счет откачки плотность молекул в первой буферной полости уменьшается более чем в 100 раз, n=n₀*7*10^-3, и плотность частиц в первом буферном объеме перед следующим выстрелом будет составлять величину: n₁=4*10¹⁶*7*10^-3=3*10¹⁴ молекул/cm³, на 5 порядков меньше, чем число Лошмидта: ρ_0L=-2.7*10¹⁹ молекул/cm³, соответствующее числу молекул в сантиметре кубическом воздуха при нормальных условиях.

Видно, что перед следующим выстрелом полость можно считать пустой.

Выводы

Максимальная высота подъема магнитных диполей, Y=450 km, получается выше траекторий полета ракет и большей части спутников.

Дальность стрельбы, S_max=1800 km, такова, что с эсминца, расположенного в Аденском заливе, можно простреливать весь залив.

Литература

1. Albert F. Reidl III, "Preliminary Investigation of an Electromagnetic Gun", NWL Technical Not No. TN-E-10/72, July 1972, Naval Weapon Laboratory, Dahlgren VA, 22448.

2. http://ru.wikipedia.org/wiki/IIyniKa Гаусса.

3. Таблицы физических величин. Справочник под ред. И.К.Кикоина, Москва, Атомиздат, 1976.

4. http://www.oocities.org/igor_suslov/AeroSidelnikov.pdf.

5. И.Е.Тамм, Основы теории электричества, ГИТТЛ, Москва, 1954, стр.20.

Изобретение относится к области ускорительной техники и может быть использовано для решения прикладных задач, в частности для удаления космического мусора и в военном деле. Ускорение магнитных диполей в данном способе осуществляют бегущим градиентом магнитного поля, образующегося при последовательном включении токовых витков. Магнитные диполи, содержащие внутри себя сверхпроводящую кольцевую обмотку с током, имеющие коническую головную часть, предварительно ускоряют газодинамическим способом. Внутри магнитных диполей помещают сверхпроводящую Nb₃Sn обмотку и возбуждают в ней кольцевой ток. Разворот диполей на 180 градусов в поле ускоряющего импульса и фокусировку диполей осуществляют тем, что магнитные диполи ускоряют внутри титановой трубки. Магнитные диполи выпускают в атмосферу через три буферные полости, каждая из которых имеет свою индивидуальную откачку. В головной части магнитного диполя делают асимметричный скос, создающий подъемную силу. Техническим результатом является увеличение конечной скорости магнитных диполей. 1 ил., 2 табл.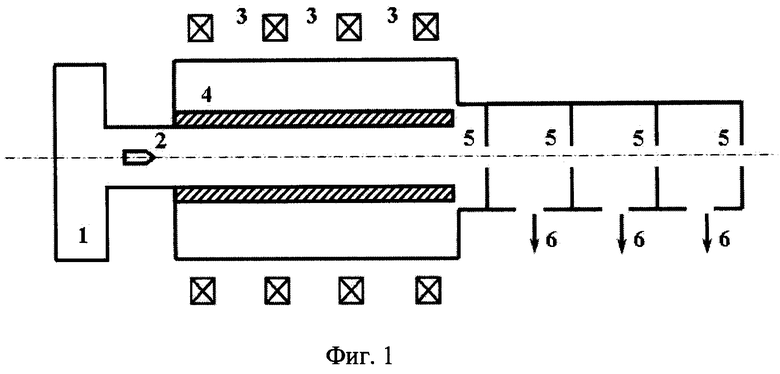

Способ ускорения магнитных диполей с помощью движущегося в пространстве градиента магнитного поля, создаваемого током, пропускаемым по виткам соленоида, отличающийся тем, что градиент магнитного поля создают последовательным включением токовых витков, при этом ускорение ведут внутри титановой трубки, предотвращающей разворот диполей на 180 градусов в поле бегущего градиента магнитного поля и предотвращающей отклонение диполей от оси ускорения в радиальном направлении.