Изобретение относится к области картографии, а именно к составлению приливных карт, полученных при инструментальном определении уровня моря, путем анализа приливных колебаний по временным рядам наблюдений и может быть также использовано при обработке временных рядов наблюдений в гидрометеорологии, а более конкретно относится к способам печатания, размножения, копирования и макетирования, а более конкретно к способам изготовления отдельных видов печатной продукции, например рисунков, а именно к изготовлению географических, морских или синоптических карт - преимущественно к составлению приливных карт.
Известные способы составления приливных карт (Владимиров О.А., Титов В.Б. Опыт расчета котидальных карт с учетом интерференции приливных волн // Труды государственного океанографического института. Вып. 37. Л., Гидрометеоиздат, 1959, с. 155-176 [1], Михайлов В.Д. Оценка качества наблюдений над приливно-отливными течениями для вычисления гармонических постоянных адмиралтейским методом парной обработки // Труды государственного океанографического института. Вып. 37. Л., Гидрометеоиздат, 1959, с. 78-84 [2], Препаленский Ю.В., Ремезова М.В. Приведение уровней моря к единому нулю поста с исключением их вековых изменений // Труды государственного океанографического института. Вып. 37, Л., Гидрометеоиздат, 1959, с. 94-154 [3]) включают определение высоты прилива по вычислениям гармонических постоянных и расчетам амплитуд.
Помимо трудоемкости вычислений, известные способы не обеспечивают необходимую точность, так как порядок вычисляемых амплитуд близок к самой точности вычислений, выполняемых известными способами. Кроме того, ими нельзя пользоваться при вычислении амплитуд для акваторий с явно выраженной конвергенцией энергии приливной волны. Посредством данных способов невозможно вычислить амплитуды на акваториях, где имеет место резкий перепад глубин, а фронт волны подходит к берегу под большим углом. Они не позволяют учесть количественное влияние силы Кориолиса на увеличение амплитуды, что снижает возможность более полного анализа приливов. Аналогичными недостатками обладают и технические решения, приведенные в патентных источниках: SU 98804 А, 01.01.1954 [4], RU 2047221 С1, 27.10.1995 [5].
Известен также способ (Тимонов В.В. О климатическом анализе приливов // Труды государственного океанографического института. Вып. 37, 1959, с. 185-204 [6]), обеспечивающий получение надежных гармонических постоянных с исключением трудоемкой работы по гармоническому анализу с целью выявления недостоверных наблюдений и обеспечивающий наиболее достоверное определение гармонических постоянных без больших затрат времени. Однако из-за того, что масштабы орбит двух смежных или нескольких близких районов с разными глубинами оказываются разными, то при сопоставлении отдельных районов могут появиться дополнительные погрешности, обусловленные тем, что частные результаты из разных сочетаний могут существенно расходиться между собой.
Из известных также технический решений, направленных на сокращение трудоемкости изготовления приливных карт и повышение их достоверности (патенты RU №2254618С1, 20.06.2005 [7], RU №2004134211 А, 10.05.2006 [8], RU №2254618 С1, 20.06.2005 [9], RU №2347067 С1, 20.02.2009 [10], заявки US №2009182516 А1, 16.07.2009 [11], JP №2009002020 А, 08.01.2009 [12]), выявленных недостатков лишен способ составления приливных карт, включающий определение высоты прилива гармонической составляющей волны, ограниченной по контуру акватории, задаваемой амплитудой, углом положения и периодом, и дальнейшую обработку, в котором высоту прилива определяют с учетом угловой скорости гармонической составляющей волны, при этом определяют вещественные плановые координаты точки акватории, направленные на восток и север соответственно, а значения высоты прилива гармонической составляющей волны в фиксированный момент времени определяют через проекцию точки на фазовую окружность, соответствующую данной высоте уровня моря, параметры которой определяют с учетом местоположения внутренних точек акватории и ее контура, а амплитуду колебаний гармонической составляющей волны определяют по значениям высоты прилива в точках с вещественными плановыми координатами для последовательного набора дискретных значений времени, по значению которой определяют время максимального уровня прилива (патент RU №2254618 [7]). Техническим результатом известного способа составления приливных карт является сокращение трудоемкости изготовления приливных карт и повышение их достоверности.
Однако основной технический результат известных способов достигается за счет гармонического анализа исходных данных, сформированных в ряды наблюдений, включающих весь спектр частот фиктивных светил, т.е. оценка гармонических постоянных по таким рядам осуществляется сразу для всего набора частот, что не позволяет разделить приливные колебания от неприливных, снижает устойчивость и точность оценки гармонических постоянных, по которым строятся изолинии.
Кроме того, в последнее время для анализа и визуализации геопространственной информации широкое распространение получили ГИС-технологии.
Для представления пространственной информации средствами ГИС одним из основных способов является способ построения изолиний, при этом для построения изолиний полей различной природы используются разнообразные численные методы пространственной интерполяции (Сантало Л. Интегральная геометрия и геометрические вероятности. - М.: Наука, 1983, 358 с.).
Поскольку различные интерполяционные алгоритмы дают разное положение изолиний, возникает задача оценки их близости. На основе такой оценки можно определить степень сходства различных карт по степени близости положения изолиний на них и повысить достоверность определения возраста прилива.
В настоящее время в океанографической практике пространственную синхронизацию приливных колебаний принято описывать с помощью приливных карт для конкретных акваторий морей. Эти карты строятся для отдельных основных приливных гармоник М2 (главная лунная полусуточная), S2 (главная солнечная полусуточная), К1 (лунно-солнечная суточная), O1 (главная лунная суточная). На приливной карте для конкретной приливной гармоники обычно представлено распределение углов положения гармонических составляющих приливного колебания в условных часах периода данной гармоники и амплитуды гармоники. Приливные карты являются одним из основных инструментов анализа характера пространственного распространения приливных колебаний на открытых акваториях. Они используются в научных и прикладных работах по приливам. Именно на приливных картах отражаются основные географические особенности пространственного распределения приливов, в том числе и амфидромические системы. Одной из наиболее своеобразных особенностей приливных карт является наличие так называемых амфидромических систем с центром в амфидромической точке или амфидромий. Важность знания географического распределения амфидромических точек заключается в том, что амплитуды приливных колебаний при приближении к этим точкам уменьшаются, а в самих точках теоретически равны нулю. В настоящее время само существование и местоположение амфидромической точки на некоторой акватории определяется путем анализа графической структуры приливных карт, точнее - карт изофаз, которые позволяют получить соответствующие возрасты прилива только для тех географических точек, для которых известны гармонические постоянные.
Представление о географической (пространственной) изменчивости в морях времени наступления максимальных вод прилива после сизигий (возраста прилива) получить сложно. Например, можно предположить, что максимальная вода на акватории моря наступает в один и тот же приливной цикл и интервал времени наступления, например максимальной полной воды после любой сизигии постоянный и одинаковый для некоторой географической точки. Однако это не верно. Достаточно взять любые таблицы приливов и соответствующий астрономический ежегодник, чтобы выяснить, что максимальные воды после сизигий в одном и том же географическом пункте наступают через различные интервалы времени. Это объясняется тем, что огибающая амплитуд имеет постоянную не зависящую от времени составляющую, определяемую амплитудами набора гармоник и переменную. При этом частоты гармоник различны. Поэтому разности частот также не равны между собой, и это приводит к смещению момента наступления максимального значения мгновенной амплитуды в последовательные интервалы между сизигиями. При этом огибающая амплитуд имеет основную частоту вблизи максимального значения, и, кроме того, огибающая возмущается колебаниями с высокой частотой. Для некоторых отношений амплитуд могут возникать дополнительные колебания с разными частотами, что дает два максимума у огибающей за период в один лунный месяц и приводит к изменению наступления этих максимумов от месяца к месяцу. При этом изменение фазы приливной гармоники на один градус приводит к смещению максимума почти на один час.
Выявленные особенности временной и пространственной изменчивости возраста прилива и их не учет при океанографическом обеспечении проводки на мелководье плавучих объектов с большой осадкой могут привести к негативным последствиям.
Задача, направленная на устранение указанных недостатков, с одновременным повышением достоверности способа составления приливных карт решена в известном техническом решении (патент RU №2450245 С1, 10.05.2012 [13]), которая достигается за счет того, что в известном способе составления приливных карт, включающем определение высоты прилива по гармонической составляющей волны, ограниченной по контуру акватории, задаваемой амплитудой, углом положения и периодом, и дальнейшую обработку, в котором высоту прилива определяют с учетом угловой скорости гармонической составляющей волны, при этом определяют вещественные плановые координаты точки акватории, направленные на восток и север соответственно, а значения высоты прилива гармонической составляющей волны в фиксированный момент времени определяют через проекцию точки на фазовую окружность, соответствующую данной высоте уровня моря, параметры которой определяют с учетом местоположения внутренних точек акватории и ее контура, а амплитуду колебаний гармонической составляющей волны определяют по значениям высоты прилива в точках с вещественными плановыми координатами для последовательного набора дискретных значений времени, по значению которой определяют время максимального уровня прилива, в котором формирование рядов наблюдений выполняют путем разложения спектра колебаний на непересекающиеся интервалы и декомпозиции исходного ряда на составляющие для каждого интервала частот, декомпозиции исходного ряда подвергают преобразованиям посредством вейвлет Мейера; а оценку гармонических постоянных выполняют для каждого отдельного светила, при этом дополнительно выполняют оценку устойчивости гармонических постоянных, определяют приливные колебания непериодического характера, при построении изолиний определяют меру близости между двумя системами изолиний путем построения метрики Хаусдорфа, определяют временную и пространственную изменчивость возраста прилива между амфидромическими точками изолиний.
Совокупность новых отличительных признаков, заключающихся в том, что формирование рядов наблюдений выполняют путем разложения спектра колебаний на непересекающиеся интервалы и декомпозиции исходного ряда на составляющие для каждого интервала частот, декомпозиции исходного ряда подвергают преобразованиям посредством вейвлет Мейера, а оценку гармонических постоянных выполняют для каждого отдельного светила, при этом дополнительно выполняют оценку устойчивости гармонических постоянных, определяют приливные колебания непериодического характера, при построении изолиний определяют меру близости между двумя системами изолиний путем построения метрики Хаусдорфа, определяют временную и пространственную изменчивость возраста прилива между амфидромическими точками изолиний, что позволяет достичь заявленного технического результата.
Однако в современных условиях, когда активизировался процесс освоения шельфа морей России, стали актуальны задачи обеспечения гидрометеорологической информацией технологической деятельности на море. Важнейшей составляющей этой информации является информация о приливных колебаниях на всем пространстве акватории, на которой осуществляется деятельность, обеспечивающая решение технологических работ.
В этой связи возникает необходимость разработки методов обеспечения информацией о приливах, согласованных по пространству акватории. В настоящее время существующий метод гармонического анализа приливов позволяет формировать данные о приливных колебаниях только локально - точечно. Действительно, получаемые этим методом параметры прилива (к ним относятся число приливных гармоник, частоты и гармонические постоянные) имеют исключительно индивидуальный обособленный характер для каждого пункта акватории. В рамках гармонического анализа приливов гармонические параметры могут принимать любые возможные значения из области возможных значений независимо друг от друга. Технические варианты решения задачи сравнения или согласования гармонических параметров для различных пунктов акватории из известных источников информации не выявлены. Вполне возможно, что такое положение дел вполне удовлетворяет практике предвычисления приливов для отдельных пунктов в виде таблиц приливов. В тоже время, очевидно, что прилив - это пространственное явление, которое охватывает некоторою акваторию и в различных точках этой акватории имеет согласованные между собой приливные колебания. Эта пространственная согласованность прилива должна проявлять себя в каких-либо соотношениях между гармоническими параметрами, определенными для различных точек акватории.
Присущее приливам свойство согласованности приливных колебаний по пространству наиболее явно и полно представляется на приливных картах (Федорова Е.В. Исследование амфидрономических систем на акватории Горла Белого моря и Амурского лимана. - Диссертация на соискание ученой степени к.т.н. - М.: 2003. - 140 с.). Приливные карты свидетельствуют о согласовании приливных колебаний в масштабе всего Мирового океана. Сама возможность построения таких карт является следствием пространственно-временной согласованности приливных колебаний. Приливные карты отражают важнейшее свойство приливов - свойство устойчивости "стационарности" распространения прилива на акватории. Приливные карты указывают на то, что фаза прилива монотонно меняется по пространству акватории, то есть прилив распространяется всегда в одном и том же направлении в локальной окрестности точки акватории, причем таким образом, что разность фаз приливных колебаний между двумя точками акватории постоянна.
Свойство согласованности и стационарности приливных колебаний по пространству было замечено давно и использовалось в навигационной практике. Например, средневековые пираты Северного моря использовали компасы с картушками, на которых по окружности были поставлены отметки направлений на Луну (часовые углы положения Луны на небосводе), при которых в нужных портах побережья наступает полная вода (Cartwright D.E. Tides. A Scientific History. - Cambridge, University Press., 2000. - 292 p.). Очевидно, что на такой картушке разность углов между направлениями на Луну для каких-либо двух портов, например для Северного моря, будет оставаться постоянной. Это отражает факт постоянства разности времени (выраженной в лунных сутках) наступления полных вод в двух портах. Естественно, что это справедливо только для портов, в которых наблюдаются лунные полусуточные приливы.
В известных способах определения уровня моря, основанных на методе гармонического анализа приливов, указанное свойство приливов никаким образом не учитывается. Этот метод позволяет рассчитать набор гармонических постоянных по наблюдениям в некоторой точке акватории, но при этом получаемый набор частот и соответствующие им значения гармонических постоянных никак не связаны с наборами частот и значениями гармонических постоянных в других пунктах акватории.
Задачей предлагаемого технического решения является повышение достоверности при составлении приливных карт за счет пространственного согласования приливных колебаний, измеренных в разных пунктах акватории.
Поставленная задача решается за счет того, что в способе пространственного согласования приливных колебаний при составлении приливных карт, включающем определение высоты прилива по гармонической составляющей волны, ограниченной по контуру акватории, задаваемой амплитудой, углом положения и периодом, и дальнейшую обработку, в котором высоту прилива определяют с учетом угловой скорости гармонической составляющей волны, при этом определяют вещественные плановые координаты точки акватории, направленные на восток и север соответственно, а значения высоты прилива гармонической составляющей волны в фиксированный момент времени определяют через проекцию точки на фазовую окружность, соответствующую данной высоте уровня моря, параметры которой определяют с учетом местоположения внутренних точек акватории и ее контура, а амплитуду колебаний гармонической составляющей волны определяют по значениям высоты прилива в точках с вещественными плановыми координатами для последовательного набора дискретных значений времени, по значению которой определяют время максимального уровня прилива, формирование рядов наблюдений выполняют путем разложения спектра колебаний на непересекающиеся интервалы и декомпозиции исходного ряда на составляющие для каждого интервала частот, декомпозиции исходного ряда подвергают преобразованиям посредством вейвлет Мейера, а оценку гармонических постоянных выполняют для каждого отдельного светила, при этом дополнительно выполняют оценку устойчивости гармонических постоянных, определяют приливные колебания непериодического характера, при построении изолиний определяют меру близости между двумя системами изолиний путем построения метрики Хаусдорфа, определяют временную и пространственную изменчивость возраста прилива между амфидромическими точками изолиний, в отличие от прототипа [13], оценку устойчивости гармонических постоянных выполняют путем районирования приливных колебаний на заданной акватории океана по критерию равенства гармонических параметров, определяемому как разность фаз между двумя приливными колебаниями в двух различных точках акватории.
В части ограничительных признаков способ осуществляется аналогично прототипу [13].
При этом высоту прилива определяют с учетом угловой скорости гармонической составляющей волны. Определяют вещественные плановые координаты точки акватории, направленные на восток и север соответственно. Значения высоты прилива гармонической составляющей волны в фиксированный момент времени определяют через проекцию точки на фазовую окружность, соответствующую данной высоте уровня моря, параметры которой определяют с учетом местоположения внутренних точек акватории и ее контура. Амплитуду колебаний гармонической составляющей волны определяют по значениям высоты прилива в точках с вещественными плановыми координатами для последовательного набора дискретных значений времени, по значению которой определяют время максимального уровня прилива, в котором формирование рядов наблюдений выполняют путем разложения спектра колебаний на непересекающиеся интервалы и декомпозиции исходного ряда на составляющие для каждого интервала частот, а оценку гармонических постоянных выполняют для каждого отдельного светила, при этом дополнительно выполняют оценку устойчивости гармонических постоянных, определяют приливные колебания непериодического характера, при построении изолиний определяют меру близости между двумя системами изолиний, определяют временную и пространственную изменчивость возраста прилива между амфидромическими точками изолиний.
В отличие от прототипа в предлагаемом техническом решении, оценку устойчивости гармонических постоянных выполняют путем районирования приливных колебаний на заданной акватории океана по критерию равенства гармонических параметров.
Покажем на примере, что монотонность распространения фазы прилива вдоль берега нарушается при предвычислении приливов по гармоническим составляющим. Моменты наступления полных (малых) вод в одном пункте могут некоторое время опережать соответствующие моменты наступления полных (малых) вод в соседнем пункте, а затем некоторый период запаздывать. Теоретически разность моментов наступления экстремумов должна иметь всегда один знак.
Положим, что рассматривается односвязная область акватории S, на которой наблюдается один и тот же тип приливных колебаний. Приливные колебания в некоторой точке области S, представленные набором гармонических постоянных, можно записать в виде:

Здесь h(t) - высота прилива в момент времени t, N - число приливных гармоник, aj>0, ωj, gj - амплитуда, частота и начальная фаза, соответственно, j-й приливный гармоники.
Для определенности везде далее будем полагать, что значения амплитуд приливных гармоник попарно различны, и, кроме того, 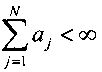 - конечность суммы и
- конечность суммы и 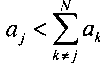 . Последнее условие означает, что любые смежные амплитуды в упорядоченном списке амплитуд имеют один порядок величины. Будем так же предполагать, что индексы j соответствуют значениям амплитуд, расположенных в убывающем порядке, так что максимальной амплитуде соответствует индекс j=1. Будем называть приливную гармонику с индексом j=1 ведущей приливной гармоникой.
. Последнее условие означает, что любые смежные амплитуды в упорядоченном списке амплитуд имеют один порядок величины. Будем так же предполагать, что индексы j соответствуют значениям амплитуд, расположенных в убывающем порядке, так что максимальной амплитуде соответствует индекс j=1. Будем называть приливную гармонику с индексом j=1 ведущей приливной гармоникой.
Каждый элемент суммы в выражении (1) является периодической функцией. Однако сумма периодических функций h(t) является почти периодической функцией. Это значит, что амплитуда и полная фаза являются переменными величинами, зависящими от времени. Это можно прояснить, если воспользоваться представлением (1) в терминах комплексной координаты

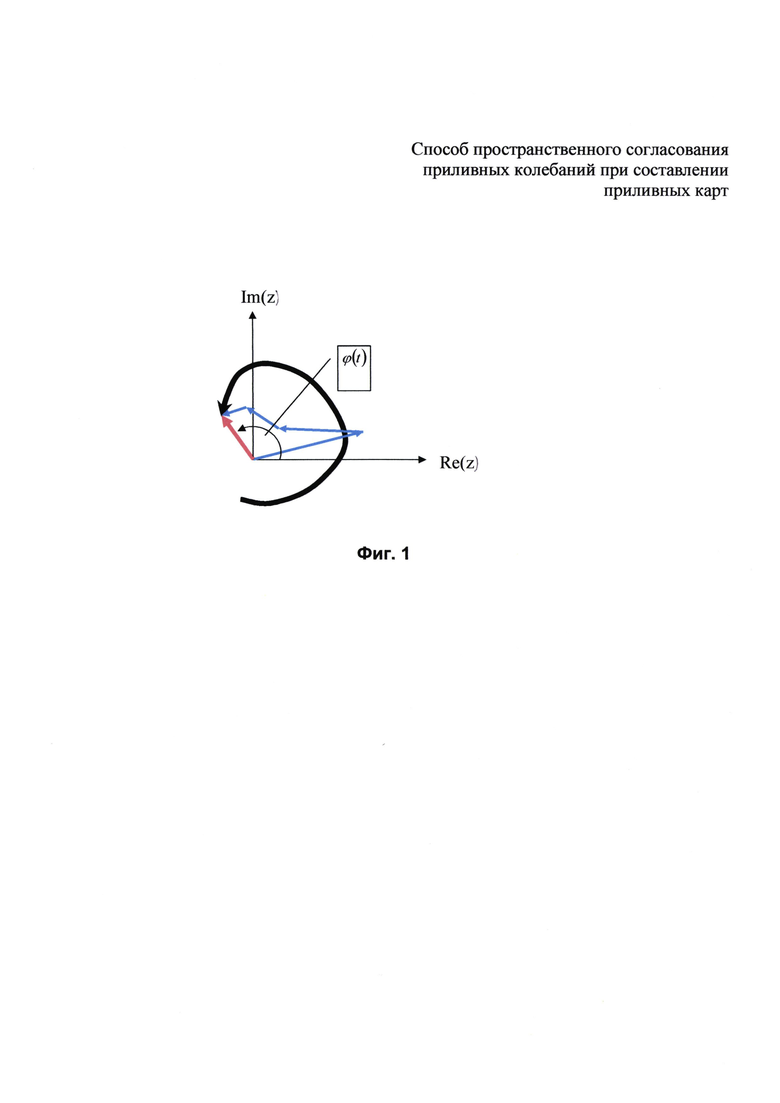
Очевидно, что вектор z(t) зависит от времени и совершает на комплексной плоскости некоторое движение, изменяясь как по модулю, так и по направлению. Выражению (2), в механической интерпретации, соответствует сумма из N равномерно вращающихся с угловыми скоростями ωj векторов плоскости с фиксированными длинами a j. Начальной точкой вектора с индексом j служит конечная точка вектора с индексом j-1. Для первого вектора начальной точкой является нулевая точка координат. Направление вектора z(t) в некоторый момент времени определяет фазу φ(t)=arg(z(t)), которая соответствует фазе прилива в тот момент времени в данной точке акватории.
На фиг. 1 приведен пример эволюции вектора z(t) (поз. 1) при N=4. Вектора (поз. 2), соответствующие приливным гармоникам с длинами aj, вращающихся с угловыми скоростями ωj. Результирующий вектор (поз. 3) суммы приливных гармоник z(t) в момент времени t, имеющий фазу φ(t)=arg(z(t)). Здесь Im(z) и Re(z) - мнимая и действительная части комплексного числа z, соответственно. В таком представлении свойство стационарной синхронизированности и монотонности пространственного распространения фазы прилива по акватории состоит в том, что если в момент времени t0 наблюдается некоторая разность фаз Δφ=φ(t0)-φ′(tQ) для двух различных точек области S, то величина этой разности должна оставаться постоянной и во все другие моменты времени. (Здесь и далее одноименные параметры для точек различаются наличием или отсутствием верхнего штриха). В противном случае, разность фаз прилива Δφ(t) будет зависеть от времени, что может привести даже к смене знака разности фаз, учитывая цикличность значения фазы. В последнем случае на локальном участке области S должна наблюдаться непериодическая реверсивная смена направления распространения фазы прилива. Другими словами разность моментов наступления, например, полных вод, относящихся к одному и тому же приливному циклу, изменит знак для рассматриваемых двух смежных пунктов области S.
Метод гармонического анализа приливов позволяет принимать любые произвольные значения гармоническим параметрам N, a j, gj, а также использовать произвольные конечные наборы приливных частот для различных точек области S. Единственное ограничение на набор частот состоит в том, что множество частот, входящих в ΩN, должно быть некоторым подмножеством бесконечного набора частот Ω∞={n1f1+n2f2+n3f3+n4f4+n5f5+n6f6}, nj=0,±1,±2,… - целые числа, f. - шесть астрономических частот (вращения Земли, изменения долготы Луны, изменения долготы Солнца, изменения долготы перигея Луны, изменения долготы лунного узла, изменения долготы перигея Солнца), то есть ωj∈ΩN⊂Ω∞.
Покажем, что при учете синхронизации в пространственном распределении фаз приливных колебаний в области S необходимо, чтобы выполнялись все без исключения следующие ограничения:
1. Число приливных гармоник N должно быть постоянным для всех точек акватории;
2. Частоты этих приливных гармоник должны быть одними и теми же для всех точек акватории, то есть должен быть постоянным набор частот ΩN;
3. Амплитуды приливных гармоник должны быть подобны для любых двух точек акватории, то есть 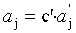
4. В двух различных точках акватории разность между начальной фазой ведущей (максимальной по амплитуде) гармоники и некоторой другой должна быть постоянной, то есть Gk=g1-gk=const, 2≤k≤N.
Докажем необходимость всех этих ограничений. Для этого нужно показать, что если хотя бы одно из этих ограничений не выполняется, то синхронность приливных колебаний в S нарушается. Критерием выполнимости ограничений является постоянство во времени разности фаз между двумя точками акватории. Тогда как свойство синхронизации приливов будет нарушаться, если разность фаз прилива меняется со временем хотя бы для одной пары точек.
Первый шаг состоит в доказательстве справедливости ограничений для суммы двух гармоник N=2, а именно ведущей гармоники с каждой гармоникой из набора. В результате такой процедуры получим N-1 сумму пар гармоник, причем каждая сумма будет представлять собой "почти" гармоническое колебание с медленно меняющейся во времени амплитудой и фазой. Это позволяет применить к двум таким суммам способ доказательства справедливости ограничений, определенный для двух чисто гармонических колебаний. Применяя рекурсивно эту процедуру, будем получать на каждом шаге множество сумм колебаний в количестве, на единицу меньшим, чем на предыдущем шаге. Таким образом, за конечное число шагов мы придем к единственному колебательному процессу со свойствами, известными из построения.
Шаг первый. Следуя Ламбу (Ламб Г. Гидродинамика. Том 1. - Москва-Ижевск: НИЦ «Регулярная и хаотическая динамика», 2003. - 452 с.), запишем явное выражение для суммы двух приливных гармоник с частотами ω1 и ω2, соответствующими амплитудами а1, а2, и начальными фазами g1, g2:

где


Здесь


Пусть справедливы указанные выше ограничения. Тогда для двух точек акватории можно записать гармонические параметры в виде 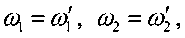 а1=с′а1, а2=с′а2 и начальные фазы g1, g2=g1+G2 и
а1=с′а1, а2=с′а2 и начальные фазы g1, g2=g1+G2 и 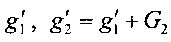 . Подставляя их в выражения (7) и (6) получим
. Подставляя их в выражения (7) и (6) получим
χ(t)=(ω1-ω2)t-G2=χ′ (t)
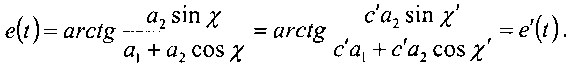
Отсюда разность фаз в этих двух точках будет

то есть при указанных ограничениях разность фаз для двух точек постоянна.
Если хотя бы одно из ограничений не выполняется, то очевидно, что разность фаз будет изменяться во времени. Это следствие того, что фаза суммы приливных гармоник представляет собой фазу ведущей гармоники, возмущенной за счет наличия других гармоник. Эти возмущения довольно сложным образом зависят от частот, амплитуд и начальных фаз. Причем эта зависимость такова, что изменение какого-то типа параметров нельзя компенсировать за счет изменения параметров другого типа, например изменения в частотах нельзя компенсировать за счет изменения амплитуд или начальных фаз.
Таким образом, доказана необходимость указанных ограничений для суммы двух гармоник.
Шаг второй. Пусть N>2. Пусть гармонические параметры заданы для двух различных точек в S и удовлетворяют указанным выше ограничениям. В соответствии с первым этапом получим для каждой точки сумму из двух сложных гармоник: h(t) и h′(t). Очевидно, что разность фаз для каждой такой пары сумм с одинаковыми индексами будет постоянна. Более того, из (8) следует, что для всех пар сумм эта разность равна 
Сумма двух колебаний вида (3) имеет вид, аналогичный (3)-(7), но более громоздкий. Обозначив сумму из двух колебаний вида h(t) (или h′(t)) через s(t), запишем





Пусть для двух точек даны значения вида (9), а именно s(t) и s′(t). Найдем разность фаз между двумя этими колебаниями. По построению разность фаз  , и
, и 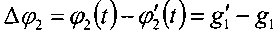 . Подставляя эти выражение (13) получим
. Подставляя эти выражение (13) получим
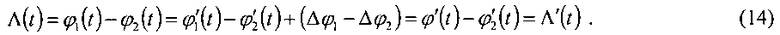
Используя (14) и учитывая, что амплитуды C*(t) и 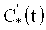
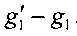 Действительно, имеем
Действительно, имеем

то есть при указанных ограничениях разность фаз колебаний s(t) и s′(t) постоянна.
Если хотя бы одно из ограничений не выполняется, то очевидно, что разность фаз для s(t) и s′ t) будет изменяться во времени.
Таким образом, доказана необходимость указанных ограничений для рекурсивной процедуры определения суммы двух гармоник.
Последующие шаги доказательства сводятся к рекурсивному повторению второго шага. На каждом шаге число колебаний будет уменьшаться на единицу, что в результате приведет к одному колебанию - сумме всех гармоник. При этом на каждом этапе выполнение указанных ограничений будет приводить к постоянству в разности фаз между соответствующими суммами колебаний двух точек.
Следовательно, доказано, что для пространственного согласования приливных колебаний необходимо, чтобы в любой точке акватории S выполнялись одновременно все вышеуказанные четыре условия. В противном случае пространственное распределение фазы прилива во времени должно проявлять хаотическую динамику, что отрицает свойство пространственной синхронности приливов, наблюдаемую в реальности.
Приливные колебания на акватории Мирового океана могут быть районированы по критерию равенства гармонических параметров. Действительно, вследствие указанных ограничений все точки однородного по приливам района акватории должны иметь одни и те же значения гармонических параметров N, ΩN, 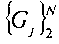 и для всей области можно построить карты распределения с(λ,φ), и g1(λ,φ) где λ и φ - долгота и широта, соответственно. Очевидно, карты распределений с(λ,φ) и g1(λ,φ) представляют собой известные приливные карты для ведущей гармоники. Чаще всего это приливные карты для гармоники М2. Последние всегда служили основой для анализа пространственного распределения приливных колебаний.
и для всей области можно построить карты распределения с(λ,φ), и g1(λ,φ) где λ и φ - долгота и широта, соответственно. Очевидно, карты распределений с(λ,φ) и g1(λ,φ) представляют собой известные приливные карты для ведущей гармоники. Чаще всего это приливные карты для гармоники М2. Последние всегда служили основой для анализа пространственного распределения приливных колебаний.
Способ пространственного согласования приливных колебаний при составлении приливных карт осуществляется следующим образом.
Определяют высоты прилива по гармонической составляющей волны, ограниченной по контуру акватории, задаваемой амплитудой, углом положения и периодом.
При дальнейшей обработке высоту прилива определяют с учетом угловой скорости гармонической составляющей волны.
При этом определяют вещественные плановые координаты точки акватории, направленные на восток и север соответственно, а значения высоты прилива гармонической составляющей волны в фиксированный момент времени определяют через проекцию точки на фазовую окружность, соответствующую данной высоте уровня моря, параметры которой определяют с учетом местоположения внутренних точек акватории и ее контура.
Амплитуду колебаний гармонической составляющей волны определяют по значениям высоты прилива в точках с вещественными плановыми координатами для последовательного набора дискретных значений времени, по значению которой определяют время максимального уровня прилива.
Формирование рядов наблюдений выполняют путем разложения спектра колебаний на непересекающиеся интервалы и декомпозиции исходного ряда на составляющие для каждого интервала частот, декомпозиции исходного ряда подвергают преобразованиям посредством вейвлет Мейера.
Оценку гармонических постоянных выполняют для каждого отдельного светила, при этом дополнительно выполняют оценку устойчивости гармонических постоянных. Определяют приливные колебания непериодического характера, при построении изолиний определяют меру близости между двумя системами изолиний путем построения метрики Хаусдорфа.
Определяют временную и пространственную изменчивость возраста прилива между амфидромическими точками изолиний.
Оценку устойчивости гармонических постоянных выполняют путем районирования приливных колебаний на заданной акватории океана по критерию равенства гармонических параметров, определяемому как разность фаз между двумя приливными колебаниями в двух различных точках акватории.
Измерения уровня моря могут быть выполнены посредством, например, акустического датчика типа «QHR 104» фирмы «VAISALA» (FI) (Ковчин И.С., Степанюк А.И., Ковчин М.И. и др. Измерение волнения и уровня моря с помощью акустических датчиков // Труды VII Российской научно-технической конференции «Навигация, гидрография и океанография: приоритеты развития инновационной морской деятельности», «НГО-2011», 18-20 мая 2011, г. Санкт-Петербург, ОАО «ГНИНГИ», с. 367-377, www.gningi.ru). Графические построения и вычислительные операции реализуются посредством графопостроителя, компьютера со стандартной комплектацией, сканера и монитора.
Источники информации
1. Владимиров О.А., Титов В.Б. Опыт расчета котидальных карт с учетом интерференции приливных волн // Труды государственного океанографического института. Вып. 37. Л.: Гидрометеоиздат. 1959, с. 155-176.
2. Михайлов В.Д. Оценка качества наблюдений над приливно-отливными течениями для вычисления гармонических постоянных адмиралтейским методом парной обработки // Труды государственного океанографического института. Вып. 37. Л.: Гидрометеоиздат. 1959, с. 78-84.
3. Препаленский Ю.В., Ремезова М.В. Приведение уровней моря к единому нулю поста с исключением их вековых изменений // Труды государственного океанографического института. Вып. 37, 1959, с. 94-154.
4. Авторское свидетельство SU 98804 А, 01.01.1954.
5. Патент RU 2047221 С1, 27.10.1995.
6. Тимонов В.В. О климатическом анализе приливов // Труды государственного океанографического института. Вып. 37. 1959, с. 185-204.
7. Патент RU №2254618, 20.06.2005.
8. Патент RU №2004134211 А, 10.05.2006.
9. Патент RU №2254618 С1, 20.06.2005.
10. Патент RU №2347067 С1, 20.02.2009.
11. Заявка US №2009182516 A1, 16.07.2009.
12. Заявка JP №2009002020 А, 08.01.2009.
13. Патент RU №2450245 С1, 10.05.2012.
| название | год | авторы | номер документа |
|---|---|---|---|
| СПОСОБ СОСТАВЛЕНИЯ ПРИЛИВНЫХ КАРТ | 2011 |
|
RU2450245C1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ УРОВНЯ МОРЯ | 2011 |
|
RU2452984C1 |
| СПОСОБ СОСТАВЛЕНИЯ ПРИЛИВНЫХ КАРТ | 2004 |
|
RU2254618C1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ КОЛЕБАНИЯ УРОВНЯ МОРЯ | 2012 |
|
RU2526490C2 |
| СПОСОБ ПРОГНОЗА ШТОРМОВЫХ ПОДЪЕМОВ УРОВНЯ ВОДЫ | 2014 |
|
RU2583063C1 |
| СПОСОБ МОРСКОЙ СЕЙСМИЧЕСКОЙ РАЗВЕДКИ И УСТРОЙСТВО ДЛЯ ЕГО ОСУЩЕСТВЛЕНИЯ | 2008 |
|
RU2388023C1 |
| СПОСОБ РЕГИСТРАЦИИ СЕЙСМИЧЕСКИХ СИГНАЛОВ НА АКВАТОРИИ МОРЯ ПРИ ПОИСКЕ ПОДВОДНЫХ ЗАЛЕЖЕЙ УГЛЕВОДОРОДОВ | 2011 |
|
RU2483330C1 |
| СПОСОБ ОБНАРУЖЕНИЯ ВОЗМОЖНОСТИ НАСТУПЛЕНИЯ КАТАСТРОФИЧЕСКИХ ЯВЛЕНИЙ | 2011 |
|
RU2489736C1 |
| СПОСОБ ПОВЫШЕНИЯ НЕФТЕОТДАЧИ МЕСТОРОЖДЕНИЯ И ДОБЫЧИ НЕФТИ | 2007 |
|
RU2347067C1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ КОЛЕБАНИЯ УРОВНЯ МОРЯ | 2005 |
|
RU2343415C2 |
Изобретение относится к способам составления приливных карт. Сущность: определяют высоту прилива по гармонической составляющей волны, ограниченной по контуру акватории, задаваемой амплитудой, углом положения и периодом. При этом определяют вещественные плановые координаты точки акватории, направленные на восток и север соответственно. Определяют значения высоты прилива гармонической составляющей волны в фиксированный момент времени через проекцию точки на фазовую окружность, соответствующую данной высоте уровня моря. Причем параметры указанной высоты определяют с учетом местоположения внутренних точек акватории и ее контура. Кроме того, определяют амплитуду колебаний гармонической составляющей волны по значениям высоты прилива в точках с вещественными плановыми координатами для последовательного набора дискретных значений времени. По значению амплитуды определяют время максимального уровня прилива. Формируют ряды наблюдений путем разложения спектра колебаний на непересекающиеся интервалы и декомпозиции исходного ряда на составляющие для каждого интервала частот. Декомпозиции исходного ряда подвергают преобразованиям посредством вейвлета Мейера. Оценку гармонических постоянных выполняют для каждого отдельного светила. Дополнительно выполняют оценку устойчивости гармонических постоянных путем районирования приливных колебаний на заданной акватории океана по критерию равенства гармонических параметров. Причем указанный критерий определяют как разность фаз между двумя приливными колебаниями в двух различных точках акватории. Кроме того, определяют приливные колебания непериодического характера. Кроме того, при построении изолиний определяют меру близости между двумя системами изолиний путем построения метрики Хаусдорфа, определяют временную и пространственную изменчивость возраста прилива между амфидромическими точками изолиний. Технический результат: повышение достоверности при составлении приливных карт. 1 ил.
Способ пространственного согласования приливных колебаний при составлении приливных карт, включающий определение высоты прилива по гармонической составляющей волны, ограниченной по контуру акватории, задаваемой амплитудой, углом положения и периодом, и дальнейшую обработку, в котором высоту прилива определяют с учетом угловой скорости гармонической составляющей волны, при этом определяют вещественные плановые координаты точки акватории, направленные на восток и север соответственно, а значения высоты прилива гармонической составляющей волны в фиксированный момент времени определяют через проекцию точки на фазовую окружность, соответствующую данной высоте уровня моря, параметры которой определяют с учетом местоположения внутренних точек акватории и ее контура, а амплитуду колебаний гармонической составляющей волны определяют по значениям высоты прилива в точках с вещественными плановыми координатами для последовательного набора дискретных значений времени, по значению которой определяют время максимального уровня прилива, формирование рядов наблюдений выполняют путем разложения спектра колебаний на непересекающиеся интервалы и декомпозиции исходного ряда на составляющие для каждого интервала частот, декомпозиции исходного ряда подвергают преобразованиям посредством вейвлета Мейера, выполняют оценку гармонических постоянных для каждого отдельного светила, при этом дополнительно выполняют оценку устойчивости гармонических постоянных, определяют приливные колебания непериодического характера, при построении изолиний определяют меру близости между двумя системами изолиний путем построения метрики Хаусдорфа, определяют временную и пространственную изменчивость возраста прилива между амфидромическими точками изолиний, отличающийся тем, что оценку устойчивости гармонических постоянных выполняют путем районирования приливных колебаний на заданной акватории океана по критерию равенства гармонических параметров, определяемому как разность фаз между двумя приливными колебаниями в двух различных точках акватории.
| Жуков Ю.Н | |||
| Ограничения на возможные значения гармонических параметров приливов / Навигация и гидрография, 2014 | |||
| СПОСОБ СОСТАВЛЕНИЯ ПРИЛИВНЫХ КАРТ | 2011 |
|
RU2450245C1 |
| RU 2004134211 А, 10.05.2006. | |||
Авторы
Даты
2016-10-20—Публикация
2015-03-06—Подача