Изобретение относится к области морской гидрологии, а более конкретно к определению приливных колебаний уровня моря.
Известен способ определения колебания уровня моря (патент RU №2343415 С2, 10.01.2009 [1]), в котором технический результат, заключающийся в снижении трудоемкости определения колебания уровня моря с одновременным повышением достоверности определения конечных результатов, достигается тем, что измеряют высоту поверхности уровня моря посредством регистрирующих устройств. Определяют момент верхней кульминации Луны на фиксированном географическом меридиане. Определяют колебания уровня моря путем анализа результатов наблюдений. При этом уровень моря измеряют в различных точках акватории моря, расположенных по возрастанию величины интервала времени между ближайшим предшествующим моментом верхней кульминации Луны и моментом верхней кульминации Луны.
В известном способе определения интервала времени между ближайшим предшествующим моментом времени верхней кульминации Луны и моментом верхней кульминации Луны позволяет определить временной ход приливных колебаний уровня в различных точках акватории моря и получить пространственный ход приливных колебаний на данной акватории на любой астрономический момент времени. Измеренные значения уровня моря в некоторых точках акватории моря, расположенных по возрастанию величины интервала времени, позволяют по изменению фазы прилива определить и временной ход уровня в точке измерения под действием приливных сил. Однако активизация технологического освоения континентального шельфа и прибрежной полосы морей повысила требования к точности и содержанию информации об уровне моря. Данные об уровне моря требуются при планировании и при оперативном обеспечении задач по добыче и транспортировке полезных ископаемых в прибрежных водах северных морей, при проектировании и строительстве портов и технических сооружений. Особую значимость эти данные имеют в задачах океанографического обеспечения так называемых морских операций - особо рискованных работах на море, например буксировка, установка и обеспечение функционирования плавучих буровых вышек.
Буксировку подобных объектов с большой осадкой в морях с приливами планируют на время наступления полной воды прилива с максимальными значениями относительно ближайших по времени. Такие приливы в океанографической практике связываются с явлениями новолуния и полнолуния (сизигиями) и называются сизигийными приливами. Среди серии последовательных сизигийных полных вод встречается вода с максимальной высотой за лунный месяц - период от одного новолуния до непосредственно последующего. Интервал времени от момента наступления новолуния до момента наступления прилива с максимальной полной водой называется возрастом прилива. Этот параметр приливов интересовал мореходов и исследователей со средних веков. Они отмечали, что в различных географических пунктах (портах) океана время наступления максимальной полной воды относительно момента наступления сизигии различно. Это обстоятельство, в частности, Ньютон объясняет особенностями конкретных географических условий формирования прилива в данном месте (Ньютон И. Математические начала натуральной философии. - М.: Издательство ЛКИ. 2008. - 704 с. [17]).
Первоначально, до появления гармонического анализа приливов, понятие возраста прилива относилось к любому типу прилива (полусуточному, суточному и т.д.). С внедрением в практику гармонического анализа приливов единое понятие возраста прилива разделилось. Стали различать возраст прилива или возраст полусуточного прилива, возраст суточного прилива и возраст параллактического прилива. Это условное деление можно объяснить недостаточной эффективностью используемых методов гармонического анализа приливов в начале XX века (Никитин М.В. Гармонический анализ приливов. - Л.: Гидрографическое Управление СССР. Гидрометеорологический отдел, 1925. - 168 с. [18]).
В настоящее время в отечественной и зарубежной практике (Tide and Current Glossary. -NOAA, National Ocean Service, 2000. - 34 p. [19], Вакман Д.Е., Вайнштейн Л.А. Амплитуда, фаза, частота - основные понятия теории колебаний // Успехи физических наук, том 123, вып.4, 1977, с.657-682 [20]) возраст прилива (age of tide=age of phase inequality) количественно выражается в часах среднесолнечного времени. Однако известные математические выражения позволяют получить соответствующие возрасты прилива только для тех географических точек, для которых известны гармонические постоянные. Представление о географической (пространственной) изменчивости в морях времени наступления максимальных вод прилива после сизигий (возраста прилива) на основании этих выражений получить сложно. Например, можно предположить, что максимальная вода на акватории Белого моря наступает в один и тот же приливной цикл. Кроме того, получаемые по известным математическим выражениям значения являются константами, т.е. интервал времени наступления, например, максимальной полной воды после любой сизигии постоянный и одинаковый для некоторой географической точки. Однако - это не верно. Достаточно взять любые таблицы приливов и соответствующий астрономические ежегодник, чтобы выяснить, что максимальные воды после сизигий в одном и том же географическом пункте наступают через различные интервалы времени. Таким образом, можно констатировать, что в настоящее время задача океанографического обеспечения морских операций по проводке объектов с большой осадкой на критических глубинах на акватории с приливами не обеспечена падежной информацией о времени наступления сизигийных приливов. Выявленные недостатки устранены в известном способе определения колебания уровня моря (патент RU №2452984 С1, 10.06.2012 [2].
Известный способ определения колебания уровня моря [2] включает измерение высоты поверхности уровня моря посредством регистрирующих устройств, измерение моментов времени, определение верхней кульминации Луны на фиксированном географическом меридиане, определение колебания уровня моря путем анализа результатов наблюдений по периодическим компонентам во временных рядах результатов наблюдений с определением гармонических постоянных по спектру частот фиктивных светил, при анализе результатов измерений выполняют деление спектра частот на равные временные циклы с последующим их совмещением, в котором гармонические постоянные определяют для отдельного фиктивного светила, временной ход уровня прилива в точке измерения под действием приливных сил определяют по фазовому сдвигу, изменение фазы прилива определяют по измеренным значениям уровня моря в фиксированных точках акватории моря, расположенных по возрастанию величины интервала времени между ближайшим предшествующим моментом времени верхней кульминации Луны и моментом верхней кульминации Луны, в котором пространственную изменчивость времени наступления максимальных вод прилива после сизигий в открытом море определяют по изменению амплитуд гармонической составляющей высоты прилива со временем, при этом преобразования амплитуды, угловой частоты и фазы приливной гармоники по измеренным сигналам осуществляют путем интегрального и линейного преобразования Гильберта.
Известный способ [2] реализуется следующим образом.
Посредством контактных или дистанционных измерителей уровня моря выполняют измерение уровня моря в различных точках акватории моря в различные моменты времени таким образом, чтобы получаемые измерения в каждой точке измерения имели различные значения интервалов времени относительно ближайшего к моменту измерения последнего момента верхней кульминации Луны на фиксированном географическом меридиане.
При этом измеренные значения уровня моря в точках акватории моря, расположенных по возрастанию величины интервала времени между ближайшим предшествующим моментом времени верхней кульминации Луны на фиксированном меридиане и моментом измерения, позволяют установить временной ход уровня под действием приливных сил, что обусловлено тем, что приливные колебания в некоторой точке акватории моря имеют практически постоянный фазовый сдвиг относительно времени верхней кульминации Луны на фиксированном географическом меридиане. Так как сочетания фаз движения Луны вокруг Земли и фаз колебания уровня моря в некоторой точке повторяются с периодом движения Луны вокруг Земли, то измеренные значения уровня моря в некоторой точке акватории моря, расположенные по возрастанию величины интервала времени между ближайшим предшествующим моментом времени верхней кульминации Луны на фиксированном географическом меридиане и моментом измерения, представляют собой изменение фазы прилива, а следовательно, и временной ход уровня в точке измерения под действием приливных сил.
По измеренным приборным значениям уровня моря формируют ряды наблюдений. Определяют значения высоты прилива конкретной гармонической составляющей волны h(t), которая задается амплитудой А, углом положения g (А и g - гармонические постоянные) и периодом Т в соответствии с зависимостью h(t)=Acos(qt-g), где q - угловая скорость гармонической волны за один час среднего времени, t - фиксированный момент времени.
Определяют амплитуды гармонической составляющей высоты прилива. Для анализа гармонических колебаний ось времени разбивается на равные отрезки, которые впоследствии совмещаются друг с другом. В полученном таким образом циклическом времени моменты измерения описывают изменения функции на одном периоде, что обеспечивает связь между временем континентальным (солнечным) и океаническим (приливным) в соответствии с зависимостью x=y-ym, где x - приливное время (число приливных суток от начала приливного года), y - дата солнечного времени (число суток от начала года), уm - число суток между солнечным и приливным временем (число суток от начала года). Вследствие того что периоды системы времени измерения и периоды гармоник колебательного процесса могут быть несоизмеримы, осуществляют преобразование циклического времени в линейное. Далее выполняют дальнейшую обработку с учетом преобразованного времени. Определяют значения высоты прилива h=h(x, y) для последовательного набора дискретных значений времени h=h(x, y, t), например, методом сеток (см., например, Лаврентьев М.А., Шабат Б.В. Методы теории функций переменного. - М-Л.: ГИТТЛ, 1958).
По полученным значениям высоты прилива для последовательного набора дискретных значений времени определяют амплитуды колебаний гармонической составляющей, например, в узлах сетки.
По полученным значениям h=h (x, y, t) определяют время наступления максимального уровня в пунктах измерения.
Известный способ [2] выгодно отличается от известных способов [1], в которых регистрация приливов осуществляется в солнечном (циклическом) времени, что не обеспечивает информативность о повторяемости колебательного процесса, так как приливные колебания, записанные приборами в аномальном для их природы времени, оказываются зашифрованными для непосредственного анализа, что требует выражения результатов наблюдений рядами гармонических колебаний с аппроксимацией артефактов о реальной динамике приливных явлений, что может вносить дополнительные погрешности.
Применение известного способа [2] позволяет при анализе периодической составляющей колебательного процесса использовать множество действительных чисел, в то время как в известных способах, представляющих собой численные расчеты, используются только рациональные числа, что не позволяет определить реальную изменчивость колебательного процесса.
Кроме того, ввиду того что пространственную изменчивость времени наступления максимальных вод прилива после сизигий в открытом море определяют по изменению амплитуд гармонической составляющей высоты прилива со временем, при этом преобразования амплитуды, угловой частоты и фазы приливной гармоники измеренных сигналов осуществляют путем интегрального и линейного преобразований Гильберта, то обеспечивается возможность установления возраста прилива по пространству между стационарными пунктами измерения уровня моря, что существенно повышает океанографическое обеспечение проводки на мелководье плавучих объектов с большой осадкой.
Однако в любых измерениях временных процессов применяют какие-либо часы для хронологической упорядоченности моментов времени. Обычно в качестве часов используют процесс видимого движения Солнца вокруг Земли, а время, определяемое по этим часам, называется среднесолнечным. Точнее, среднее солнечное время - это время, которое определяется изменениями часового угла среднего экваториального Солнца - фиктивной точки, равномерно двигающейся по небесному экватору со средней скоростью движения истинного Солнца по эклиптике и совершающей полный оборот в течение года. Например, в сфере гидрометеорологического обеспечения ВМФ встречается задача, когда в качестве часов используют другой процесс - временной ход приливного уровня. Так, например, изменения приливных течений на некоторой акватории моря синхронизируют с изменениями приливных колебаний уровня моря на одном из береговых постов наблюдения, находящихся в этой акватории. В результате получают карты приливных течений на акватории для каждого водного часа приливных колебаний на береговом посту (Березкин В.А. Динамика моря. - Л., Ленинград, Военно-морская академия им. тов. Ворошилова. Гидрографическое управление главного управления Северного Морского пути при СНК СССР, 1938. - с.516-518. Дуванин А.И. Приливы в море. - Л., ГИМИЗ, 1960. -390 с.).
Осложняющим обстоятельством решения этой задачи является этап вычисления значений водных часов, выраженных в среднесолнечном времени. Это связано с тем, что понятие водного времени, определяемого приливом, является одним из равноправных способов измерения времени на основе какого-либо циклического процесса. Способ по своей сути тождественен измерению общеземных среднесолнечных часов, используемых в обычной жизни. Среднесолнечные часы - это деление интервала времени между двумя смежными кульминациями Солнца (интервал в одни сутки) на равные двадцать четыре интервала. Очевидно, что, основываясь на этой аналогии, сейчас принято рассчитывать водные часы, разбивая интервал времени между моментами наступления двух смежных полных вод на 24 равных интервала для "суточных" приливов, или на 12 равных интервалов для "полусуточных" приливов.
Равномерное деление солнечного суточного периода не правомерно для деления периода прилива. Действительно, длительность среднесолнечного часа определяется величиной угла (фазы) видимого поворота Солнца за 1/24 долю интервала солнечных суток. Угловая скорость видимого движения Солнца по небосклону практически постоянна, следовательно, и длительности интервалов времени соответствующих интервалам среднесолнечных часов практически равны. В градусной мере солнечные сутки равны 360°, а один среднесолнечный час равен времени видимого поворота Солнца на 15°. Однако для временного хода приливов такой равномерной изменчивости в изменении уровня моря не наблюдается. Напротив, временной ход приливных колебаний уровня чрезвычайно переменчив. Это связано с тем, что приливные колебания в большей степени синхронизированы с движением Луны, а не Солнца. Угловое движение Луны вокруг Земли значительно сложнее, менее постоянно, чем движение Солнца. Ответная синхронизация уровня моря на совместное влияние небесных светил и является источником непостоянства изменения фазы прилива, что очевидно должно приводить к непостоянству интервалов времени водных часов.
Дадим формальное обоснование. Любые часы используют цикличность какого-либо процесса, точнее используют изменение фазы Ω(τ) со временем (как общее понятие) τ у некоторого циклического процесса. Чем равномернее изменяется фаза, тем "лучше" часы, наилучшие имеют чисто периодический характер.
В общем смысле фаза Ω(τ) понимается как временная упорядоченная последовательность состояний процесса. В нашем случае удобно представить фазу как угловую меру плоского вращательного движения точки вокруг центра, аналог видимого вращения Солнца вокруг Земли. Математическая запись для плоских координат {x(τ),y(τ)} вращения с единичным радиусом проста:
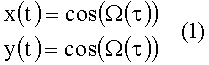
Заметим, что в астрономии фаза Солнца Ω(τ) называется "часовым углом Солнца". Солнечная фаза Ω(τ) изменяется практически равномерно, а как обстоит дело с фазой прилива в среднесолнечном исчислении времени?
Временной ход приливного уровня h(t) в некоторой точке акватории представляется в виде конечной тригонометрической суммы
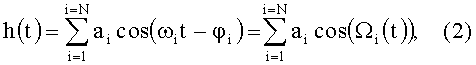
где t - среднесолнечное время, ai, ωi, φi - амплитуда, угловая частота и фаза приливной гармоники i(i=1,…,N). В (2) опущена астрономическая часть фаз для гармоник, чтобы не загромождать формулы элементами, не существенными для рассматриваемой задачи. Выражение (2) содержит частные фазы для отдельных приливных гармоник Ω(τ), а нам нужно получить выражение для одной общей фаза Ω(τ) приливного процесса. Для этой цели воспользуемся представлением приливного хода уровня в виде узкополосного процесса, то есть определим h(t) в виде
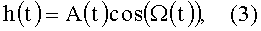
где
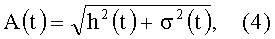
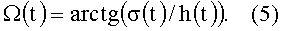
Здесь σ(t) - функция, сопряженная функции h(t), определяется интегральным преобразованием Гильберта
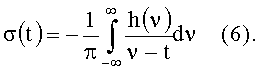
Заметим, что функция h(t) соответствует функции x(t), a σ(t) соответствует y(t) из выражения (1), а выражение (5) определяет искомую фазу прилива.
Явно записать (5) через гармонические постоянные и их частоты практически не возможно вследствие громоздкости получаемого выражения. Однако вполне возможно по предвычисленным значениям приливного уровня вычислить (6), а значит и (5). Задачей предлагаемого технического решения является повышение достоверности определения колебания уровня моря.
Поставленная задача решается за счет того, что в способе определения колебания уровня моря, включающем измерение высоты поверхности уровня моря посредством регистрирующих устройств, измерение моментов времени, определение верхней кульминации Луны на фиксированном географическом меридиане, определение колебания уровня моря путем анализа результатов наблюдений по периодическим компонентам во временных рядах результатов наблюдений с определением гармонических постоянных по спектру частот фиктивных светил, при анализе результатов измерений выполняют деление спектра частот на равные временные циклы с последующим их совмещением, в котором гармонические постоянные определяют для отдельного фиктивного светила, временной ход уровня прилива в точке измерения под действием приливных сил определяют по фазовому сдвигу, изменение фазы прилива определяют по измеренным значениям уровня моря в фиксированных точках акватории моря, расположенных по возрастанию величины интервала времени между ближайшим предшествующим моментом времени верхней кульминации Луны и моментом верхней кульминации Луны, в котором пространственную изменчивость времени наступления максимальных вод прилива после сизигий в открытом море определяют по изменению амплитуд гармонической составляющей высоты прилива со временем, при этом преобразования амплитуды, угловой частоты и фазы приливной гармоники измеренных сигналов осуществляют путем интегрального и линейного преобразований Гильберта, в котором в отличие от аналога и прототипа, определяют значения водных часов, выраженные в среднесолнечном времени, как ближайшие моменты среднесолнечного времени t с фазами прилива, кратным целым значениям 15° для "суточных" приливов (Т=[0,…,24]), или 30° для "полусуточных" приливов (Т=[0,…,12].
Сущность способа поясняется чертежами (фиг.1-3).
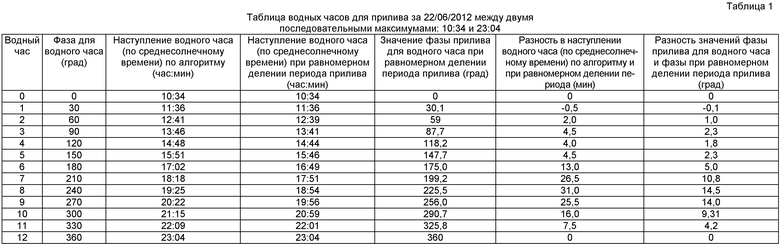
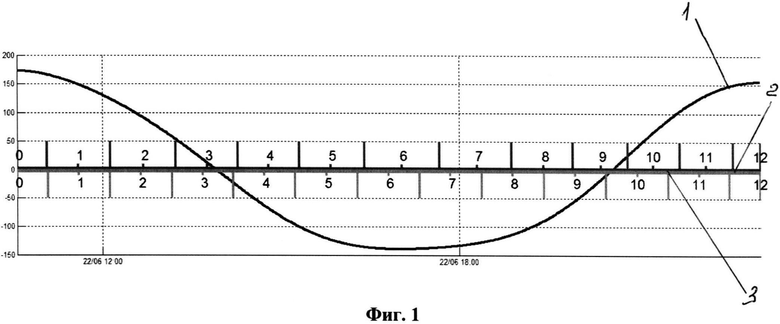
Фиг.1. Пример вычисления водных часов для конкретного периода прилива, где 1 - временной ход приливного уровня моря (в сантиметрах), 2 - границы интервалов водных часов, вычисленных по фазе прилива, 3 - границы интервалов "водных часов", вычисленных равномерным делением периода прилива.
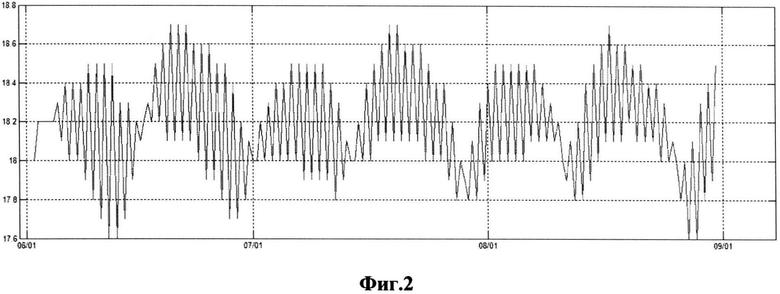
Фиг.2. Временной ход отношения (в процентах) суммы времени ошибочного пересечения интервалов водных часов, вычисленных по алгоритму и равномерным делением интервала, к интервалу периода прилива.
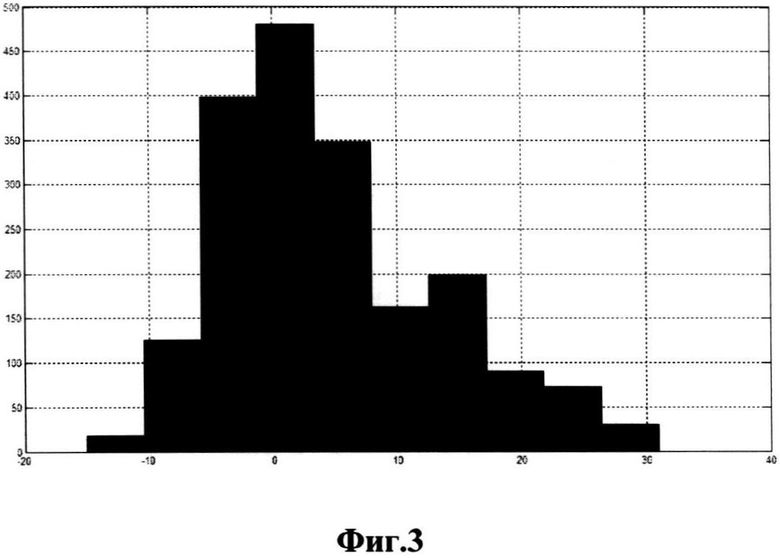
Фиг.3. Гистограмма разности водных часов, вычисленных по фазе прилива и равномерным делением периода (в минутах).
Способ осуществляется следующим образом.
Как и в прототипе [2], посредством контактных или дистанционных измерителей уровня моря выполняют измерение уровня моря в различных точках акватории моря в различные моменты времени таким образом, чтобы получаемые измерения в каждой точке измерения имели различные значения интервалов времени относительно ближайшего к моменту измерения последнего момента верхней кульминации Луны на фиксированном географическом меридиане.
При этом измеренные значения уровня моря в точках акватории моря, расположенных по возрастанию величины интервала времени между ближайшим предшествующим моментом времени верхней кульминации Луны на фиксированном меридиане и моментом измерения, позволяют установить временной ход уровня под действием приливных сил, что обусловлено тем, что приливные колебания в некоторой точке акватории моря имеют практически постоянный фазовый сдвиг относительно времени верхней кульминации Луны на фиксированном географическом меридиане. Так как сочетания фаз движения Луны вокруг Земли и фаз колебания уровня моря в некоторой точке повторяются с периодом движения Луны вокруг Земли, то измеренные значения уровня моря в некоторой точке акватории моря, расположенные по возрастанию величины интервала времени между ближайшим предшествующим моментом времени верхней кульминации Луны на фиксированном географическом меридиане и моментом измерения, представляют собой изменение фазы прилива, а следовательно, и временной ход уровня в точке измерения под действием приливных сил.
По измеренным приборным значениям уровня моря формируют ряды наблюдений. Определяют значения высоты прилива конкретной гармонической составляющей волны h(t), которая задается амплитудой А, углом положения g (А и g - гармонические постоянные) и периодом Т в соответствии с зависимостью h(t)=Acos(qt-g), где q - угловая скорость гармонической волны за один час среднего времени, t - фиксированный момент времени.
Определяют амплитуды гармонической составляющей высоты прилива. Для анализа гармонических колебаний ось времени разбивается на равные отрезки, которые впоследствии совмещаются друг с другом. В полученном таким образом циклическом времени моменты измерения описывают изменения функции на одном периоде, что обеспечивает связь между временем континентальным (солнечным) и океаническим (приливным) в соответствии с зависимостью x=y-ym, где x - приливное время (число приливных суток от начала приливного года), у - дата солнечного времени (число суток от начала года), ym - число суток между солнечным и приливным временем (число суток от начала года). Вследствие того что периоды системы времени измерения и периоды гармоник колебательного процесса могут быть несоизмеримы, осуществляют преобразование циклического времени в линейное. Далее выполняют дальнейшую обработку с учетом преобразованного времени. Определяют значения высоты прилива h=h(x, y) для последовательного набора дискретных значений времени h=h(x, y, t), например, методом сеток (см., например, Лаврентьев М.А., Шабат Б.В. Методы теории функций переменного. - М-Л.: ГИТТЛ, 1958).
По полученным значениям высоты прилива для последовательного набора дискретных значений времени определяют амплитуды колебаний гармонической составляющей, например, в узлах сетки.
По полученным значениям h=h (x, y, t) определяют время наступления максимального уровня в пунктах измерения. Алгоритм вычисления следующий:
Вход: гармонические постоянные для приливного пункта.
Вычислить ежеминутные приливные уровни h(t) по гармоническим постоянным.
Шаг 1. Вычислить преобразование Гильберта σ(t) приливных уровней h(t) по выражению (6).
Шаг 2. Вычислить фазу прилива Ω(t) по выражению (5), используя вычисленные σ(t) и h(t).
Шаг 3. Найти значения t(T) водных часов, выраженные в среднесолнечном времени, как ближайшие моменты среднесолнечного времени t с фазами прилива, кратным целым значениям 15° для "суточных" приливов (T=[0,…,24]), или 30° для "полусуточных" приливов (T=[0,…,12]).
Выход: значения водных часов, выраженные в среднесолнечном времени/(г). На фиг.1-3 приведены результаты такого вычисления для приливных колебаний у острова Сосновца в Белом море, где наблюдается "полусуточный" прилив. Они свидетельствуют о том, что фаза прилива в этом пункте изменчива настолько, что расчет водных часов путем равномерного разбиения приливного периода на 12 водных часов приводит к существенным ошибкам по сравнению с предлагаемым алгоритмом с использованием (6). Предвычисления приливов проведены по гармоникам, заданным в гринвичском часовом поясе на 2012 год (табл.1).
Источники информации
Патент RU №2343415 С2, 10.01.2009.
Патент RU №2452984 С1, 10.06.2012.
| название | год | авторы | номер документа |
|---|---|---|---|
| СПОСОБ ОПРЕДЕЛЕНИЯ УРОВНЯ МОРЯ | 2011 |
|
RU2452984C1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ КОЛЕБАНИЯ УРОВНЯ МОРЯ | 2005 |
|
RU2343415C2 |
| СПОСОБ СОСТАВЛЕНИЯ ПРИЛИВНЫХ КАРТ | 2011 |
|
RU2450245C1 |
| СПОСОБ РЕГИСТРАЦИИ СЕЙСМИЧЕСКИХ СИГНАЛОВ НА АКВАТОРИИ МОРЯ ПРИ ПОИСКЕ ПОДВОДНЫХ ЗАЛЕЖЕЙ УГЛЕВОДОРОДОВ | 2011 |
|
RU2483330C1 |
| СПОСОБ ОБНАРУЖЕНИЯ ВОЗМОЖНОСТИ НАСТУПЛЕНИЯ КАТАСТРОФИЧЕСКИХ ЯВЛЕНИЙ | 2011 |
|
RU2489736C1 |
| СПОСОБ ПОВЫШЕНИЯ НЕФТЕОТДАЧИ МЕСТОРОЖДЕНИЯ И ДОБЫЧИ НЕФТИ | 2007 |
|
RU2347067C1 |
| СПОСОБ МОРСКОЙ СЕЙСМИЧЕСКОЙ РАЗВЕДКИ И УСТРОЙСТВО ДЛЯ ЕГО ОСУЩЕСТВЛЕНИЯ | 2008 |
|
RU2388023C1 |
| СПОСОБ ПОВЫШЕНИЯ НЕФТЕОТДАЧИ МЕСТОРОЖДЕНИЯ | 2012 |
|
RU2492316C1 |
| СПОСОБ ПРОСТРАНСТВЕННОГО СОГЛАСОВАНИЯ ПРИЛИВНЫХ КОЛЕБАНИЙ ПРИ СОСТАВЛЕНИИ ПРИЛИВНЫХ КАРТ | 2015 |
|
RU2599913C2 |
| СПОСОБ ГИДРОМЕТЕОРОЛОГОАКУСТИЧЕСКОГО НАБЛЮДЕНИЯ ЗА АКВАТОРИЕЙ МОРСКОГО ПОЛИГОНА | 2005 |
|
RU2304794C2 |
Изобретение относится к области морской гидрологии и может быть использовано для определения приливных колебаний уровня моря. Сущность: измеряют высоту поверхности уровня моря посредством регистрирующих устройств. Определяют моменты верхней кульминации Луны на фиксированном географическом меридиане. Определяют колебания уровня моря путем анализа результатов наблюдений по периодическим компонентам во временных рядах. При этом определяют гармонические постоянные по спектру частот фиктивных светил. При анализе результатов измерений выполняют деление спектра частот на равные временные циклы с последующим их совмещением, в котором гармонические постоянные определяют для отдельного фиктивного светила. Временной ход уровня прилива в точке измерения под действием приливных сил определяют по фазовому сдвигу. Изменение фазы прилива определяют по измеренным значениям уровня моря в фиксированных точках акватории моря, расположенных по возрастанию величины интервала времени между ближайшим предшествующим моментом времени верхней кульминации Луны и моментом верхней кульминации Луны. Кроме того, по изменению амплитуд гармонической составляющей высоты прилива со временем определяют пространственную изменчивость времени наступления максимальных вод прилива после сизигий в открытом море. При этом преобразования амплитуды, угловой частоты и фазы приливной гармоники сигналов осуществляют посредством интегрального и линейного преобразования Гильберта. Также определяют значения водных часов, выраженные в среднесолнечном времени. Технический результат: повышение достоверности результатов. 1 табл., 3 ил.
Способ определения колебания уровня моря, включающий измерение высоты поверхности уровня моря посредством регистрирующих устройств, измерение моментов времени, определение верхней кульминации Луны на фиксированном географическом меридиане, определение колебания уровня моря путем анализа результатов наблюдений по периодическим компонентам во временных рядах результатов наблюдений с определением гармонических постоянных по спектру частот фиктивных светил, при анализе результатов измерений выполняют деление спектра частот на равные временные циклы с последующим их совмещением, в котором гармонические постоянные определяют для отдельного фиктивного светила, временной ход уровня прилива в точке измерения под действием приливных сил определяют по фазовому сдвигу, изменение фазы прилива определяют по измеренным значениям уровня моря в фиксированных точках акватории моря, расположенных по возрастанию величины интервала времени между ближайшим предшествующим моментом времени верхней кульминации Луны и моментом верхней кульминации Луны, а пространственную изменчивость времени наступления максимальных вод прилива после сизигий в открытом море определяют по изменению амплитуд гармонической составляющей высоты прилива со временем, при этом преобразования амплитуды, угловой частоты и фазы приливной гармоники измеренных сигналов осуществляют путем интегрального и линейного преобразований Гильберта, отличающийся тем, что определяют значения водных часов, выраженные в среднесолнечном времени, как ближайшие моменты среднесолнечного времени t с фазами прилива, кратными целым значениям 15° для "суточных" приливов (T=[0,…,24]) или 30° для "полусуточных" приливов (T=[0,…,12]).
| СПОСОБ ОПРЕДЕЛЕНИЯ УРОВНЯ МОРЯ | 2011 |
|
RU2452984C1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ КОЛЕБАНИЯ УРОВНЯ МОРЯ | 2005 |
|
RU2343415C2 |
| RU 2004134211 A, 10.05.2006 | |||
Авторы
Даты
2014-08-20—Публикация
2012-12-13—Подача