Изобретение относится к текстильной отрасли и может быть использовано для анализа структурных параметров как имеющихся, так и проектируемых образцов тканей.
Переплетение нитей в ткани придает волнистость или извитость основным и уточным нитям.
Известен способ определения извитости (уработки) нити в ткани [ГОСТ ISO 7211-3:1984. Текстиль. Ткани. Структура. Методы анализа. Ч. 3. Определение извитости нити в ткани. - Введ. 15.03.1984.; 8 с.; табл.1], заключающийся в последовательном выполнении следующих операций: формирование лабораторной пробы прямоугольных полосок ткани известной длины; изъятие (удаление) из них нитей; распрямление нитей вручную за счет применения растягивающего усилия по прямой линии без их вытягивания; измерение длины распрямленных нитей с точностью до 1 мм; накопление массива данных; нахождение средней арифметической длины распрямленных нитей; определение разницы между средней длиной выпрямленной нити и расстоянием между ее концами в ткани, выраженной в процентах от последнего.
Однако в нем недостаточна точность и достоверность определения извитости (уработки) нитей в ткани из-за неизбежной субъективной погрешности при принудительном распрямлении вынутых из ткани нитей для ликвидации их волнистости. Кроме того, установленная точность первичных данных (±1 мм) резко влияет на количественную оценку извитости (уработки) нитей в ткани.
За прототип принят способ анализа структуры ткани, в том числе извитости (уработки) нитей в ткани [Патент 2131605 РФ, МПК6 G01N 33/36. Бесконтактный способ анализа структуры ткани / Лустгартен Н.В., Сокова Г.Г., Сергеев А.С.; заявитель и патентообладатель Костромск. госуд. технол. университ. - №98108331/12; заявл. 29.04.1998; опубл. 10.06.1999, - 4 с.: 3 ил.], заключающийся в построении фронтального профиля нити по двум изображениям одного и того же участка ткани, полученным путем фотографирования со смещением аппарата по горизонтали на некоторую величину.
Недостатками прототипа является недостаточная точность и достоверность определения извитости (уработки) нитей ткани из-за неправильного построения профиля нитей в ткани, учета извитости (уработки) нитей только во фронтальной плоскости и невозможность определения извитости (уработки) нитей в однослойных тканях неполотняного переплетения.
Техническим результатом изобретения является повышение точности и достоверности определения извитости (уработки) нитей за счет исключения влияния субъективного фактора, более точного построения профиля нити в ткани, учета извитости (уработки) нитей как во фронтальной, так и в горизонтальной плоскостях, возможность определения извитости (уработки) нитей в однослойных тканях неполотняного переплетения.
Указанный технический результат достигается тем, что в способе, заключающемся в построении фронтального профиля нити по ее изображению, полученному путем фотографирования, согласно изобретению перед фотографированием пробы ткани производят определение линейной плотности основной и уточной пряжи и числа нитей на 10 см ткани по основе и по утку, затем пробу ткани пропитывают клеящим составом, высушивают в расправленном состоянии при нормальных климатических условиях в течение одних суток, производят микросрезы пробы ткани вдоль нитей основы и утка, фотографируют срезы ткани с использованием микроскопа двадцати-двадцатипятикратного увеличения с вебкамерой, на полученных изображениях микросрезов измеряют высоту волны изгиба нити основы hо, диаметры нитей основы и утка в ткани по горизонтальной dог, dуг и вертикальной dов, dув осям, по которым определяют по известным формулам диаметры нитей основы dоп, утка dуп и средний диаметр dср.п нитей на паковках, коэффициент отношения диаметров Kd, коэффициенты смятия нитей основы и утка в ткани по горизонтальной ηог и ηуг, и вертикальной ηов и ηув осям, находят средний расчетный диаметр нитей в ткани dср, определяют коэффициент высоты волны изгиба основы Khо, порядок фазы строения ткани Пф, коэффициент высоты волны изгиба утка Khу и высоту волны изгиба утка hу, находят геометрическую плотность по основе lо и по утку lу в максимально уплотненной ткани; строят переплетение нитей в ткани с раппортами по основе Rо и по утку Rу, при этом переплетение однослойной ткани рассматривают как матрицу A=(ai,j), где i=1,…, Rо - номер основной нити, j=1,…, Rу - номер уточной нити в раппорте переплетения, элементы матрицы a
i,j=1 для основного и a
i,j=0 для уточного перекрытий, для каждой нити находят число пересечек по основе  и по утку
и по утку 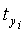 , для каждой нити основы находят максимальную плотность ткани по утку
, для каждой нити основы находят максимальную плотность ткани по утку  , коэффициент наполнения ткани волокнистым материалом по утку
, коэффициент наполнения ткани волокнистым материалом по утку  и фактическую геометрическую плотность ткани по утку:
и фактическую геометрическую плотность ткани по утку:

для каждой нити утка определяют максимальную плотность ткани по основе
Pо max j, коэффициент наполнения ткани волокнистым материалом по основе 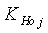 и фактическую геометрическую плотность по основе:
и фактическую геометрическую плотность по основе:
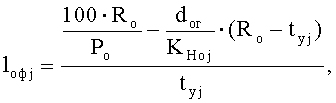
определяют значения больших a 1, a 2 и малых b1, b2 полуосей расчетных эллипсов дуг обхвата основой нижнего и верхнего утков в пересечке:
a1=a2=0,5·dуг+0,5·doв; b1=b2=0,5·dув+0,5·dов,
для каждой основной нити раппорта формируют вектор p коэффициентов полинома четвертой степени:
(b-a)2·z4+2·(b-a)·c·z3+(d2+2·a·(b-a)+c2)·z2+2·a·c·z-d2+a2=0,
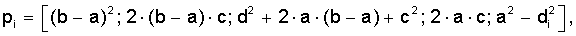
где a, b, c, d - вспомогательные коэффициенты:
a=a1+a2; b=(b1+b2); c=hо-b1-b2 и 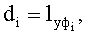
по которому с помощью стандартной функции pp=roots(p) в системе Matlab рассчитывают косинус угла, затем угол наклона прямолинейного участка основы в пересечке к горизонтали β:
βi=arccos(cosβi),
с помощью стандартной функции trapz(y, t) в системе Matlab для каждой основной нити раппорта рассчитывают длины дуг обхвата нитей утка в нижней 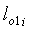 и верхней
и верхней  частях пересечки:
частях пересечки:
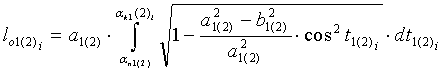
где y - подынтегральное выражение;
 - параметры интегрирования, изменяющиеся в пределах
- параметры интегрирования, изменяющиеся в пределах  ;
;
 ;
;  - углы начала и конца обхватывания расчетных эллипсов утков в нижней и верхней частях пересечки:
- углы начала и конца обхватывания расчетных эллипсов утков в нижней и верхней частях пересечки:
 ;
;  ;
; 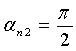 ;
;  ,
,
далее находят их горизонтальные 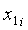 ,
,  и вертикальные
и вертикальные  ,
,  проекции:
проекции:
 ;
;  ;
;  ;
; 
определяют горизонтальную проекцию  и длину
и длину  прямолинейного участка основы в пересечке:
прямолинейного участка основы в пересечке:
 ;
;  ,
,
находят коэффициенты ki и  уравнения прямой, проходящей через прямолинейный участок основы в пересечке:
уравнения прямой, проходящей через прямолинейный участок основы в пересечке:
 ;
;  ,
,
после чего определяют процент извитости (уработки) отдельных нитей основы  во фронтальной плоскости:
во фронтальной плоскости:

аналогичным образом определяют процент извитости (уработки) отдельных нитей утка во фронтальной плоскости:

извитость (уработку) нитей данной системы во фронтальной плоскости находят как среднее значение извитости (уработки) отдельных нитей раппорта:


далее выполняют построение профилей отдельных нитей основы: анализируя матрицу переплетения A=(a i,j), составляют матрицу координат центров уточных нитей вдоль основных нитей O=(oi,j) размером (Rо+1)×(Rу+1), причем для центров первых перекрытий уточных нитей оi,1=0, для центров остальных перекрытий:

находят местоположение верхних и нижних утков, учитывая, что уровень верхних утков расположен на высоте hув, уровень нижних утков находится на расстоянии hун от оси абсцисс:
hув=0,5·(dов+dув); hун=hув-hу,
формируют массивы ординат верхней и нижней частей эллипсообразных сечений утков, находящихся в верхнем и нижнем уровнях:


где t - текущее значение угла поворота радиус-вектора точки эллипса утка, в радианах:
 ,
,
где x - текущее значение горизонтальной проекции радиус-вектора точки эллипса утка:
x=[о(i,j)-0,5·dуг, о(i,j)+0,5·dуг],
далее выстраивают кривую оси волны изгиба нити основы, ее верхней и нижней ветвей, учитывая, что каждая кривая имеет следующие участки: пересечки «слева-направо», пересечки «справа-налево», горизонтальные участки над и под нитями утка, ось волны изгиба i-й основной нити на каждом участке строят по формулам:
- пересечка «слева-направо»:

- пересечка «справа-налево»:

- настил над утками:
 ;
;  ;
;
- настил под утками:
 ;
;  ;
;
выбор соответствующего участка для i-й основной нити производят, анализируя переплетение:

выполняют построение верхней ветви каждой нити основы по формулам:
- пересечка «слева-направо»:

- пересечка «справа-налево»:

- настил над утками:
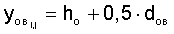 ;
;  ;
;
- настил под утками:

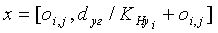 ;
;
где а 1в, a 2в, b1в, b2в - большие и малые полуоси дуг обхвата эллипсов утков в начале и конце пересечки верхней ветви основы определяют по формулам:
а1в=0,5·dуг; b1в=0,5·dув; а2в=0,5·dуг+dов; b2в=0,5·dув+dов;
 ,
,  ,
, 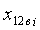 - горизонтальные проекции дуг обхвата расчетных эллипсов утков в начале и конце пересечки и прямолинейного участка верхней ветви основы, определяют по зависимостям:
- горизонтальные проекции дуг обхвата расчетных эллипсов утков в начале и конце пересечки и прямолинейного участка верхней ветви основы, определяют по зависимостям:
 ;
;  ;
; 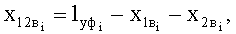
где  - угол обхвата эллипсообразного сечения нити утка верхней ветвью нити основы в начале пересечки:
- угол обхвата эллипсообразного сечения нити утка верхней ветвью нити основы в начале пересечки:
 ;
;
 - угол обхвата эллипсообразного сечения нити утка верхней ветвью нити основы в конце пересечки:
- угол обхвата эллипсообразного сечения нити утка верхней ветвью нити основы в конце пересечки:  ;
;
 - коэффициент угла наклона прямой, проходящей через прямолинейный участок верхней ветви основы:
- коэффициент угла наклона прямой, проходящей через прямолинейный участок верхней ветви основы:
 ,
,
где  - вертикальная проекция нижней дуги верхней ветви основы:
- вертикальная проекция нижней дуги верхней ветви основы:
 ;
;
 - свободный член уравнения прямой, проходящей через прямолинейный участок верхней ветви основы:
- свободный член уравнения прямой, проходящей через прямолинейный участок верхней ветви основы:

где  - вертикальная проекция верхней дуги верхней ветви основы:
- вертикальная проекция верхней дуги верхней ветви основы:
 ;
;
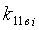 - свободный член уравнения прямой, проходящей через прямолинейный участок верхней ветви основы:
- свободный член уравнения прямой, проходящей через прямолинейный участок верхней ветви основы:
 ,
,
далее выстраивают нижнюю ветвь каждой нити основы по формулам:
- пересечка «слева-направо»:

- пересечка «справа-налево»:

- настил над утками:

 ;
;
- настил под утками:

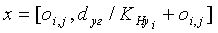 ,
,
где а1н, а2н, b1н, b2н - большие и малые полуоси дуг обхвата расчетных эллипсов утков в начале и конце пересечки нижней ветви основы:
а1н=0,5·dуг+dов; b1н=0,5·dув+dов; а2н=0,5·dуг; b2н=0,5·dув;
 ,
,  ,
,  - горизонтальные проекции дуг обхвата расчетных эллипсов утков в начале и конце пересечки и прямолинейного участка нижней ветви каждой нити основы, определяют по зависимостям:
- горизонтальные проекции дуг обхвата расчетных эллипсов утков в начале и конце пересечки и прямолинейного участка нижней ветви каждой нити основы, определяют по зависимостям:
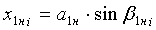 ;
; 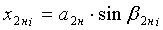 ;
; 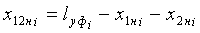 ,
,
где  и
и  - углы обхвата расчетных эллипсов нижней ветвью i-й нити основы в начале и в конце пересечки:
- углы обхвата расчетных эллипсов нижней ветвью i-й нити основы в начале и в конце пересечки:
 ;
; 
 - коэффициент угла наклона прямой, проходящей через прямолинейный участок нижней ветви i-й нити основы:
- коэффициент угла наклона прямой, проходящей через прямолинейный участок нижней ветви i-й нити основы:
 ,
,
где  - свободный член уравнения прямой, проходящей через прямолинейный участок нижней ветви i-й нити основы:
- свободный член уравнения прямой, проходящей через прямолинейный участок нижней ветви i-й нити основы:
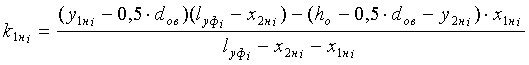 ;
;
 и
и  - вертикальные проекции дуг обхвата расчетных эллипсов утков в начале и конце пересечки нижней ветви каждой нити основы, определяют по зависимостям:
- вертикальные проекции дуг обхвата расчетных эллипсов утков в начале и конце пересечки нижней ветви каждой нити основы, определяют по зависимостям:
 ;
;  ;
;
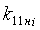 - свободный член уравнения прямой, проходящей через прямолинейный участок нижней ветви i-й нити основы:
- свободный член уравнения прямой, проходящей через прямолинейный участок нижней ветви i-й нити основы:
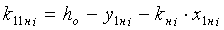 ,
,
далее, анализируя матрицу переплетения А=(аi,j), составляют матрицу координат центров основных нитей вдоль уточных нитей U=(ui,j) размером (Rо+1)×(Rу+1), причем для центров первых перекрытий основных нитей ui,1=0, для центров остальных перекрытий:
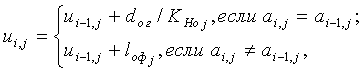
аналогичным образом выполняют построение профилей уточных нитей в последовательности, описанной выше для основных нитей, после чего составляют матрицу координат центров виртуальных уточных нитей вдоль виртуальных основных нитей при отсутствии горизонтальной извитости основных нитей  размером (Rо+1)×(Rу+1), причем для центров первых перекрытий уточных нитей
размером (Rо+1)×(Rу+1), причем для центров первых перекрытий уточных нитей  , для центров остальных перекрытий:
, для центров остальных перекрытий:

далее составляют матрицу координат центров виртуальных основных нитей вдоль виртуальных уточных нитей при отсутствии горизонтальной извитости уточных нитей  размером (Rо+1)×(Rу+1), причем для центров первых перекрытий основных нитей
размером (Rо+1)×(Rу+1), причем для центров первых перекрытий основных нитей  , для центров остальных перекрытий:
, для центров остальных перекрытий:
 ,
,
определяют матрицы отклонений центров уточных и основных нитей образца ткани от центров уточных и основных нитей виртуальной ткани:
DO=О-Овирт.; DU=U-Uвирт.,
просматривая столбцы матриц DO=(dоi,j), формируют одномерный массив максимальных отклонений центров уточных нитей вдоль основных нитей образца ткани Δо длиной Rо+1, просматривая строки матрицы DU=(dуi,j), также формируют одномерный массив максимальных отклонений центров основных нитей вдоль уточных нитей образца ткани Δу длиной Rу+1, после чего производят корректировку матрицы центров уточных нитей вдоль основных нитей О=(оi,j), получают матрицу фактических координат центров уточных нитей вдоль основных нитей  с элементами:
с элементами:
 .
.
Производят корректировку матрицы центров основных нитей вдоль уточных нитей U=(ui,j), получают матрицу фактических координат центров основных нитей вдоль уточных нитей U'=(u'i,j) с элементами:
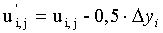 ,
,
далее по координатам матриц  и U'=(u'i,j) выполняют построение горизонтальных проекций осей нитей основы и утка в пределах раппорта переплетения, при отсутствии параллельности горизонтальных проекций осей нитей основы оси ординат определяют извитость (уработку) нитей основы в горизонтальной плоскости:
и U'=(u'i,j) выполняют построение горизонтальных проекций осей нитей основы и утка в пределах раппорта переплетения, при отсутствии параллельности горизонтальных проекций осей нитей основы оси ординат определяют извитость (уработку) нитей основы в горизонтальной плоскости:

в противном случае aгориз.о=0, при отсутствии параллельности горизонтальных проекций нитей утка оси абсцисс определяют извитость (уработку) нитей утка в горизонтальной плоскости:

в противном случае агориз.у=0, далее находят суммарную извитость (уработку) нитей основы и утка:
 ;
; 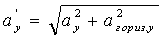 .
.
Указанный технический результат - повышение точности и достоверности определения извитости (уработки) нитей достигается за счет исключения влияния субъективного фактора, так как неизбежная субъективная погрешность при принудительном распрямлении вынутых из ткани нитей для ликвидации их волнистости устраняется. Кроме того, более точно выполняется построение профилей нитей раппорта переплетения в ткани, учитывающее наличие в пересечке нити одной системы нитью другой системы нижней и верхней дуг, огибающих расчетные эллипсообразные сечения нитей первой системы, и прямолинейных отрезков осей нитей второй системы, соединяющих эти дуги, нахождение углов наклона прямолинейных отрезков осей нитей в пересечках, а также прямолинейных участков нитей второй системы в настилах, нахождение фактических координат центров перекрытий основных и уточных нитей и дополнительного учета извитости (уработки) нитей в горизонтальной плоскости, кроме того, появляется возможность определения извитости (уработки) нитей в однослойных тканях любого переплетения.
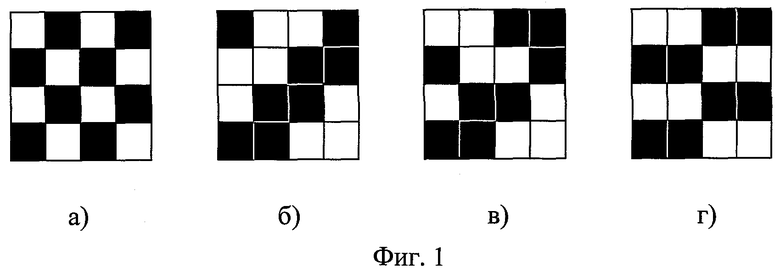
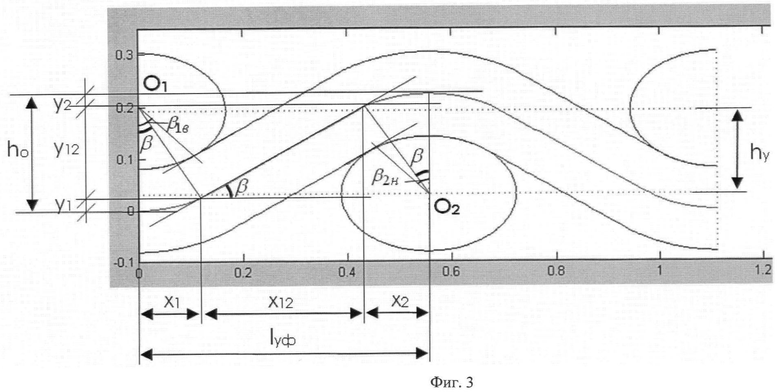
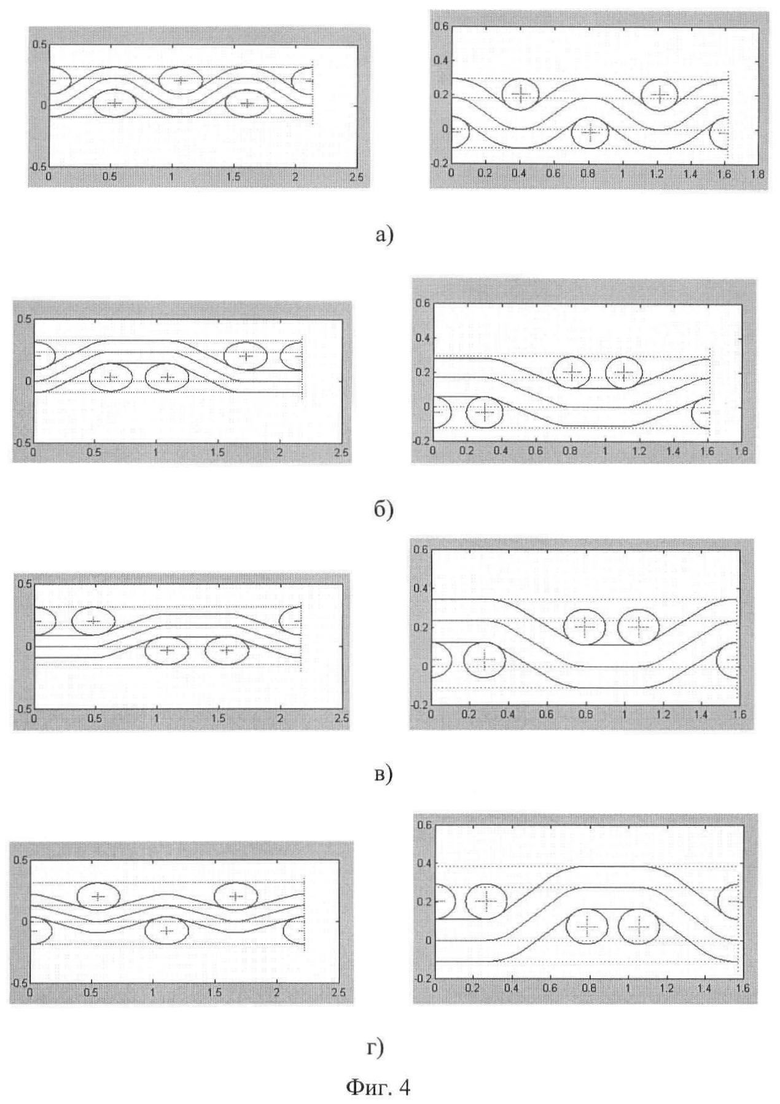
На фиг.1 изображены переплетения образцов ткани: 1-а - полотняного, 1-б - саржи 2/2, 1-в - неправильного усиленного четырехнитного сатина, 1-г - уточного репса 2/2; на фиг.2 - фрагменты микросрезов образцов тканей полотняного переплетения: 2-а - по основе, 2-б - по утку; на фиг.3 представлено строение и расчетные параметры пересечки нити основы; на фиг.4 изображены профили основных и уточных нитей образцов ткани: 4-а - вторых нитей раппорта полотняного переплетения, 4-б - третьих нитей раппорта саржевого переплетения, 4-в - четвертых нитей сатинового переплетения, 4-г - первых нитей репсового переплетения; на фиг.5 представлены горизонтальные проекции осей нитей основы и утка в раппорте переплетения образцов ткани: 5-а - полотняного переплетения, 5-б - саржевого переплетения, 5-в - усиленного сатина, 5-г - репсового переплетения.
Пример практического осуществления способа.
Определяют извитость (уработку) нитей основы и утка в ткани для четырех образцов ткани детского ассортимента, выработанной из хлопчатобумажной пряжи кольцевого способа прядения на базе ткани арт.1670 переплетениями: полотняным, саржей 2/2, усиленным четырехнитным сатином и уточным репсом 2/2, представленными на фиг.1, для наглядности у образца ткани полотняного переплетения рассматривают два раппорта по основе и два раппорта по утку, у уточного репса - два раппорта по утку.
По ГОСТ 6611.1 - 73 «Нити текстильные. Метод определения линейной плотности» определяют линейную плотность нитей основы и утка. Линейная плотность пряжи составила: основы Tо=25 текс, утка Ту=50 текс.
По ГОСТ 3812-72 «Ткани и штучные изделия текстильные. Методы определения плотности по основе и по утку» определяют плотности ткани по основе и по утку, для чего применяют ткацкие лупы, увеличивающие рассматриваемые нити в 4, 5, 7 раз. Через лупу рассматривают участок предварительно расправленной ткани в средней части образца. При этом одна из сторон прорези лупы должна совпадать с направлением подсчитываемых нитей и находиться посередине промежутка между нитями.
Результаты определения плотности образцов ткани по основе и по утку (число нитей на 10 см ткани) приведены в таблице 1.
Подготавливают микросрезы ткани по основе и по утку следующим образом: ткань пропитывают прозрачным клеящим веществом (например, медицинским БФ-6), высушивают в расправленном состоянии в течение 24 часов при относительной влажности воздуха 65±2% и температуре воздуха 20±2°С, затем острым лезвием бритвы срезают образец вдоль нитей основы и вдоль нитей утка, фотографируют срезы с использованием микроскопа двадцатичетырехкратного увеличения с вебкамерой Logitech HD Webkam С510. При использовании микроскопа с менее чем двадцатикратным увеличением возникают трудности с измерением параметров строения микросрезов участков ткани, при более чем двадцатипятикратным увеличением в объектив микроскопа попадает недостаточное количество нитей исследуемого участка ткани. На полученных изображениях микросрезов (фиг.2) измеряют высоту волны изгиба нити основы hо, диаметры нитей основы и утка по горизонтальной dог и dуг и вертикальной dов и dув осям находят по известным формулам диаметры нитей основы dоп, утка dуп, средний диаметр нитей dср.п и коэффициент отношения диаметров нитей на паковках Kd:
 ;
;  ;
;  ;
; 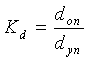 .
.
Находят эмпирические коэффициенты смятия нитей по горизонтальной и вертикальной осям основы ηог, ηов и утка ηуг, ηув:
ηог=dог/dоп; ηов=dов/dоп; ηуг=dуг/dуп; ηув=dув/dуп.
Выполняют проверку, чтобы коэффициенты общего смятия нитей основы τо и утка τу не превышали единицу:
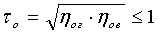 ;
; 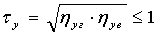 .
.
Диаметры основы и утка на паковках составили: dоп=0,198 мм; dуп=0,279 мм; dср.п=0,239 мм; Kd=0,7097; диаметры нитей в ткани по горизонтальной оси dог=0,214 мм; dуг=0,35 мм, по вертикальной оси doв=0,183 мм; dув=0,222 мм, средний расчетный диаметр нитей в ткани dср=0,203 мм, эмпирические коэффициенты смятия составили ηог=1,082; ηов=0,924; ηуг=1,254; ηув=0,797, коэффициенты общего смятия основы τо=0,9999; утка τу=0,9997.
Из фиг.1 видно, что извитость (уработку) нитей основы и утка первого, второго и четвертого образцов и утка третьего образца можно определять по любой одной нити - все нити раппортов переплетений имеют одинаковое число пересечек; у третьего образца первая и третья нити основы имеют по четыре пересечки, вторая и четвертая - по две, поэтому извитость (уработку) основы для этого образца необходимо рассчитывать как среднее значение извитости (уработки) всех нитей раппорта.
Определяют коэффициент высоты волны изгиба основы Khо, порядок фазы строения ткани Пф, коэффициент высоты волны изгиба утка Khу и высоту волны изгиба утка hу (фиг.3):
 ; Пф=4·Khо+1; Khу=2-Khо; hу=dср·Khу.
; Пф=4·Khо+1; Khу=2-Khо; hу=dср·Khу.
Результаты приведены в таблице 2.
Рассматривают переплетения образцов ткани как матрицы A=(ai,j), где i=1,…, Rо - номер основной нити, j=1,…, Rу - номер уточной нити в раппорте переплетения, элементы матрицы ai,j=1 для основного и ai,j=0 для уточного перекрытий:

Убеждаются в отсутствии единичных или нулевых столбцов и строк матрицы, для каждой нити находят число пересечек по основе  и по утку
и по утку  (таблица 2).
(таблица 2).
Находят геометрическую плотность по основе lо и по утку lу в максимально уплотненной ткани:
 ;
;  ,
,
для каждой нити основы находят максимальную плотность ткани по утку  и коэффициент наполнения ткани волокнистым материалом по утку
и коэффициент наполнения ткани волокнистым материалом по утку  :
:
 ;
;  .
.
Результаты приведены в таблице 3.
Определяют значения больших а1, а2 и малых b1, b2 полуосей расчетных эллипсов дуг обхвата основой нижнего и верхнего утков в пересечке:
а1=а2=0,5·dуг+0,5·dов; b1=b2=0,5·dув+0,5·dов;
а1=а2=0,2665 мм; b1=b2=0,2025 мм.
Находят фактическую геометрическую плотность по основе lоф и по утку lуф (фиг.3):

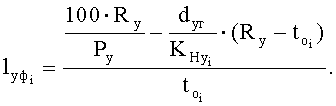
Находят вспомогательные коэффициенты a, b, с, d:
a=a1+а2; b=(b1+b2); c=ho-b1-b2 и  , результаты приведены в таблице 4.
, результаты приведены в таблице 4.
Для каждой основной нити раппорта формируют вектор коэффициентов полинома четвертой степени:
(b-a)2·z4+2·(b-a)·c·z3+(d2+2·a·(b-a)+c2)·z2+2·a·c·z-d2+a2=0,
 :
:
- для основных нитей ткани полотняного переплетения:
 ;
;
- для основных нитей саржи 2/2:

- для основных нитей неправильного усиленного четырехнитного сатина:
- для первой и третьей нитей:
 ;
;
- для второй и четвертой нитей:
 ;
;
- для основных нитей уточного репса 2/2:
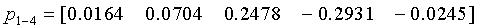 .
.
С помощью стандартной функции pp=roots(p) в системе Matlab рассчитывают косинусы углов наклона прямолинейных участков нитей основы в пересечках к горизонтали, по известным значениям косинусов находят углы β (фиг.3) наклона прямолинейных участков: βi=arccos(cosβi), результаты приведены в таблице 5.
Для каждой основной нити раппорта с помощью стандартной функции trapz(y, t) в системе Matlab рассчитывают длины дуг обхвата нитей утка в нижней  и верхней
и верхней  частях пересечки:
частях пересечки:

где y - подынтегральное выражение;
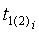 - параметры интегрирования, изменяющиеся в пределах
- параметры интегрирования, изменяющиеся в пределах 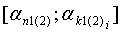 ;
;
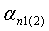 ;
;  - углы начала и конца обхватывания расчетных эллипсов утков в нижней и верхней частях пересечки:
- углы начала и конца обхватывания расчетных эллипсов утков в нижней и верхней частях пересечки:
 ;
;  ;
; 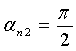 ;
;  .
.
Длины дуг могут быть найдены также вручную известными способами - методом трапеций, методом парабол Симпсона или по «Таблицам неопределенных интегралов» М.Л.Смолянского. Находят горизонтальные  ,
,  и вертикальные
и вертикальные 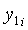 ,
,  (фиг.3) проекции дуг:
(фиг.3) проекции дуг:



 определяют горизонтальные проекции
определяют горизонтальные проекции  (фиг.3) и длины
(фиг.3) и длины  прямолинейных участков нитей основы в пересечках:
прямолинейных участков нитей основы в пересечках:
 ;
; 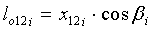 ,
,
находят коэффициенты ki и 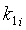 уравнений прямых, проходящих через прямолинейные участки нитей основы в пересечках:
уравнений прямых, проходящих через прямолинейные участки нитей основы в пересечках:
ki=tgβi;  ,
,
после чего определяют процент извитости (уработки) отдельных нитей основы  во фронтальной плоскости:
во фронтальной плоскости:
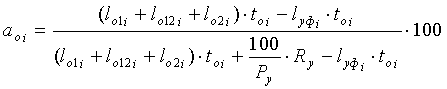
Результаты вычислений приведены в таблице 6.
Извитость (уработку) нитей основы во фронтальной плоскости находят как среднее значение извитости (уработки) отдельных нитей раппорта:

Извитость (уработка) основных нитей во фронтальной плоскости третьего образца составила 3,91%, значения извитости (уработки) основных нитей во фронтальной плоскости остальных образцов приведены в таблице 6.
Аналогичным образом определяют процент извитости (уработки) отдельных нитей утка во фронтальной плоскости. Число пересечек на отдельных уточных нитях у всех переплетений (фиг.1) одинаково, поэтому извитость (уработку) нитей утка во фронтальной плоскости можно определять по любой нити, например, по первой: j=1.
Определяют значения больших a1, а2 и малых b1, b2 полуосей расчетных эллипсов дуг обхвата утком нижней и верхней основ в пересечке:
а1=а2=0,5·dог+0,5·dув; b1=b2=0,5·dов+0,5·dув;
а1=а2=0,2180 мм; b1=b2=0,2025 мм.
Для каждой нити утка определяют максимальную плотность ткани по основе
Po max j и коэффициент наполнения ткани волокнистым материалом по основе  :
:

 .
.
Находят вспомогательные коэффициенты a, b, с, d:
a=a1+a2, b=(b1+b2); 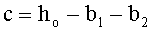 и
и  ,
,
результаты приведены в таблице 7.
Для каждой уточной нити раппорта формируют вектор коэффициентов полинома четвертой степени:
(b-a)2·z4+2·(b-a)·c·z3+(d2+2·a·(b-a)+c2)·z2+2·a·c·z-d2+a2=0,
 :
:
- для ткани полотняного переплетения:
 ;
;
- для ткани с переплетением саржа 2/2:
 ;
;
- для ткани с переплетением неправильный четырехнитный усиленный сатин:
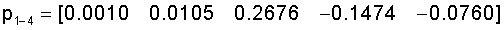 ;
;
- для ткани с переплетением уточный репс 2/2:
 .
.
С помощью стандартной функции pp=roots(p) в системе Matlab рассчитывают косинусы углов наклона прямолинейных участков нитей утка в пересечках к горизонтали, по известным значениям косинусов находят углы наклона прямолинейных участков: βj=arccos(cosβj), результаты приведены в таблице 8.
Для каждой уточной нити раппорта с помощью стандартной функции trapz(y, t) в системе Matlab, рассчитывают длины дуг обхвата нитей основы в нижней 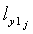 и верхней
и верхней  частях пересечки:
частях пересечки:

где y - подынтегральное выражение;
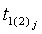 - параметры интегрирования, изменяющиеся в пределах
- параметры интегрирования, изменяющиеся в пределах  ;
;
 ;
;  - углы начала и конца обхватывания расчетных эллипсов основ в нижней и верхней частях пересечки:
- углы начала и конца обхватывания расчетных эллипсов основ в нижней и верхней частях пересечки:
 ;
;  ;
; 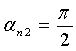 ;
; 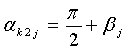 .
.
Находят горизонтальные 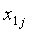 ,
,  и вертикальные
и вертикальные  ,
,  проекции дуг:
проекции дуг:
 ;
; 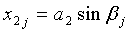 ;
;  ;
;  ,
,
определяют горизонтальные проекции 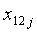 и длины
и длины  прямолинейных участков нитей основы в пересечках:
прямолинейных участков нитей основы в пересечках:
 ;
; 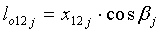 ,
,
находят коэффициенты kj и  уравнений прямых, проходящих через прямолинейные участки нитей утка в пересечках:
уравнений прямых, проходящих через прямолинейные участки нитей утка в пересечках:
kj=tgβj; 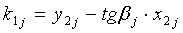 ,
,
после чего определяют процент извитости (уработки) отдельных нитей утка  во фронтальной плоскости:
во фронтальной плоскости:

Результаты вычислений приведены в таблице 9.
Извитость (уработку) нитей утка во фронтальной плоскости находят как среднее значение извитости (уработки) отдельных нитей раппорта:

Извитость (уработка) уточных нитей во фронтальной плоскости приведена в таблице 9.
Анализируя матрицы переплетений А=(ai,j), составляют матрицы координат центров уточных нитей вдоль основных нитей О=(oi,j) размером (Ro+1)×(Ry+1), учитывая, что для центров первых перекрытий уточных нитей oi,1=0, для центров остальных перекрытий:

Получают следующие матрицы координат центров уточных нитей вдоль основных для образцов полотняного, саржевого, сатинового и репсового переплетений:
O=(oi,j):

Находят местоположение верхних и нижних утков, учитывая, что уровень верхних утков расположен на высоте hув, уровень нижних утков находится на расстоянии hун от оси абсцисс:
hув=0,5·(dов+dув); hун=hув-hу,
Результаты представлены в таблице 10.
Формируют массивы ординат верхней и нижней частей эллипсообразных сечений утков, находящихся в верхнем и нижнем уровнях:


где t - текущее значение угла поворота радиус-вектора точки эллипса утка, в радианах:
 ,
,
где x - текущее значение горизонтальной проекции радиус-вектора точки эллипса утка:
x=[o(i,j)-0,5·dуг, o(i,j)+0,5·dуг].
По данным таблиц 2-6 и 8 и матриц переплетений А=(ai,j) в системе Matlab строят (фиг.4) кривые осей волн изгиба нитей основы, учитывая, что каждая кривая имеет следующие участки: пересечки «слева-направо» (участок 1), пересечки «справа-налево» (участок 2), горизонтальные участки над (участок 3) и под (участок 4) нитями утка, ось волны изгиба i-й основной нити на каждом участке строят по формулам:
- пересечка «слева-направо» - участки 1:

- пересечка «справа-налево» - участки 2:

- настил над утками - участки 3:
 ;
;  ;
;
- настил под утками - участки 4:
 ;
;  ;
;
выбор соответствующего участка для i-й основной нити производят, анализируя переплетение:
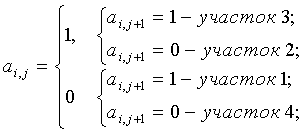
Определяют большие и малые полуоси дуг обхвата эллипсов утков в начале и конце пересечки верхней ветви основы a1в, a2в, b1в, b2в:
а1в=0,5·dуг; b1в=0,5·dув; а2в=0,5·dуг+dов; b2в=0,5·dув+dов;
a1в=0.175 мм; b1в=0,111 мм; a2в=0,358 мм; b2в=0,294 мм.
Находят углы обхвата эллипсообразного сечения нити утка верхней ветвью нити основы в начале и конце пересечки:
 ;
;  ,
,
горизонтальные проекции дуг обхвата расчетных эллипсов утков в начале и конце пересечки и прямолинейного участка верхней ветви основы:
 ;
;  ;
; 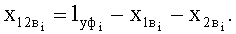
Результаты приведены в таблице 11.

Находят вертикальные проекции нижней и верхней дуг верхней ветви основы:
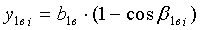 ;
;  ,
,
свободный член уравнения прямой, проходящей через прямолинейный участок верхней ветви основы в пересечке «слева-направо»:
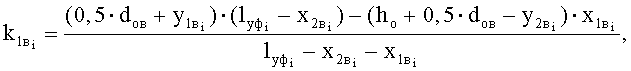
коэффициент угла наклона прямой, проходящей через прямолинейный участок верхней ветви основы в пересечке «слева-направо»:
 ,
,
свободный член уравнения прямой, проходящей через прямолинейный участок верхней ветви основы в пересечке «справа-налево»:

Результаты приведены в таблице 12.
По данным таблиц 11 и 12 выполняют построение верхних ветвей каждой нити основы (фиг.4) по формулам:
- пересечка «слева-направо» - участки 1:

- пересечка «справа-налево» - участки 2:

- настил над утками - участки 3:

 ;
;
- настил под утками - участки 4:


Находят большие и малые полуоси дуг обхвата расчетных эллипсов утков в начале и конце пересечки нижней ветви основы:
а1н=0,5·dуг+dов; b1н=0,5·dув+dов; а2н=0,5·dуг; b2н=0,5·dув;
углы обхвата расчетных эллипсов нижней ветвью каждой нити основы в начале и в конце пересечки:  ;
;  , горизонтальные проекции дуг обхвата расчетных эллипсов утков в начале и конце пересечки и прямолинейного участка нижней ветви каждой нити основы:
, горизонтальные проекции дуг обхвата расчетных эллипсов утков в начале и конце пересечки и прямолинейного участка нижней ветви каждой нити основы:
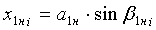 ;
; 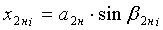 ;
; 
Результаты приведены в таблице 13.


Определяют вертикальные проекции дуг обхвата расчетных эллипсов утков в начале и конце пересечки нижней ветви каждой нити основы:
 ;
;  ;
;
свободный член уравнения прямой, проходящей через прямолинейный участок нижней ветви основы в пересечке «слева-направо»:
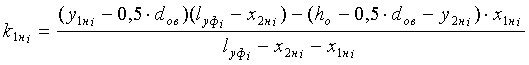 ,
,
коэффициент угла наклона прямой, проходящей через прямолинейный участок нижней ветви нити основы в пересечке «слева-направо»:
 ,
,
и свободный член уравнения прямой, проходящей через прямолинейный участок нижней ветви нити основы в пересечке «справа-налево»:
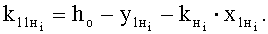
Результаты приведены в таблице 14.
По данным таблиц 13 и 14 выполняют построение нижних ветвей каждой нити основы (фиг.4) по формулам:
- пересечка «слева-направо» - участки 1:

- пересечка «справа-налево» - участки 2:

- настил над утками - участки 3:

 ;
;
- настил под утками - участки 4:

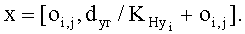
Анализируя матрицу переплетения А=(ai,j), составляют матрицу координат центров основных нитей вдоль уточных нитей U=(ui,j) размером (Rо+1)×(Rу+1), учитывая, что для центров первых перекрытий основных нитей ui,1=0, для центров остальных перекрытий:
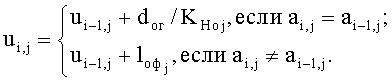
Получают следующие матрицы координат центров основных нитей вдоль уточных для образцов полотняного, саржевого, сатинового и репсового переплетений:
U=(ui,j):

Аналогичным образом выполняют построение профилей уточных нитей (фиг.4) в последовательности, описанной выше для основных нитей.
Составляют матрицу координат центров виртуальных уточных нитей вдоль виртуальных основных нитей при отсутствии горизонтальной извитости основных нитей  размером (Rо+1)×(Rу+1), причем для центров первых перекрытий уточных нитей
размером (Rо+1)×(Rу+1), причем для центров первых перекрытий уточных нитей  , для центров остальных перекрытий:
, для центров остальных перекрытий:

Получают следующие матрицы координат центров виртуальных уточных нитей вдоль виртуальных основных нитей при отсутствии горизонтальной извитости основных нитей для образцов полотняного, саржевого, сатинового и репсового переплетений:
 :
:
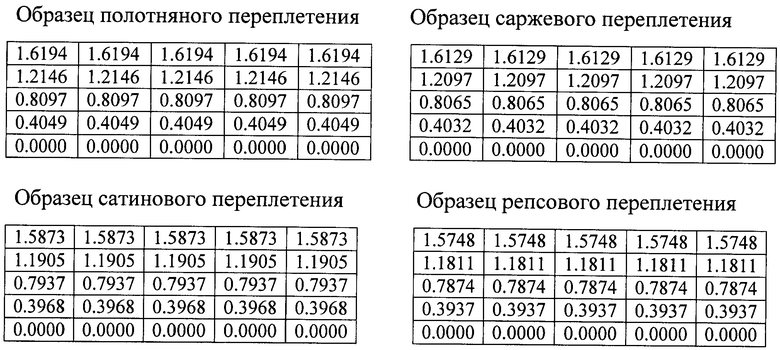
Определяют матрицы отклонений центров уточных нитей образца ткани от центров уточных нитей виртуальной ткани DO=(doi,j):
DO=O-Oвирт..
DO=(doi,j)

Просматривая столбцы матриц DO=(doi,j), формируют одномерный массив максимальных отклонений центров уточных нитей вдоль основных нитей образца ткани Δо длиной Rо+1:
- для основных нитей ткани полотняного переплетения:
 ;
;
- для основных нитей саржи 2/2:
 ;
;
- для основных нитей усиленного сатина:
 ;
;
- для основных нитей уточного репса 2/2:
 .
.
Производят корректировку матриц центров уточных нитей вдоль основных нитей О=(оi,j), получают матрицы фактических координат центров уточных нитей вдоль основных нитей  с элементами:
с элементами:
 .
.
Получают следующие матрицы фактических координат центров уточных нитей вдоль основных для образцов полотняного, саржевого, сатинового и репсового переплетений:
 :
:

Составляют матрицы координат центров виртуальных основных нитей вдоль виртуальных уточных нитей при отсутствии горизонтальной извитости уточных нитей  размером (Rо+1)×(Rу+1), учитывая, что для центров первых перекрытий основных нитей
размером (Rо+1)×(Rу+1), учитывая, что для центров первых перекрытий основных нитей  , для центров остальных перекрытий:
, для центров остальных перекрытий:
 .
.
Получают следующие матрицы координат центров виртуальных основных нитей вдоль виртуальных уточных нитей при отсутствии горизонтальной извитости уточных нитей для образцов полотняного, саржевого, сатинового и репсового переплетений:
 :
:

Определяют матрицы отклонений центров основных нитей образца ткани от центров основных нитей виртуальной ткани DU=(dуi,j):
DU=U-Uвирт.
DU=(dyi,j):
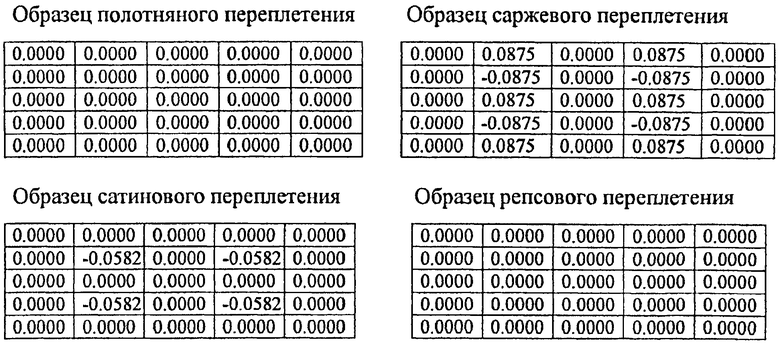
Просматривая строки матриц DU=(dyi,j), формируют одномерный массив максимальных отклонений центров основных нитей вдоль уточных нитей образца ткани Δy длиной Ry+1:
- для уточных нитей ткани полотняного переплетения:
Δy=[0 0 0 0 0];
- для уточных нитей саржи 2/2:
Δy=[0.0875 -0.0875 0.0875 -0.0875 0.0875];
- для уточных нитей усиленного сатина:
Δy=[0 -0.0582 0 -0.0582 0];
- для уточных нитей уточного репса 2/2:
Δy=[0 0 0 0 0].
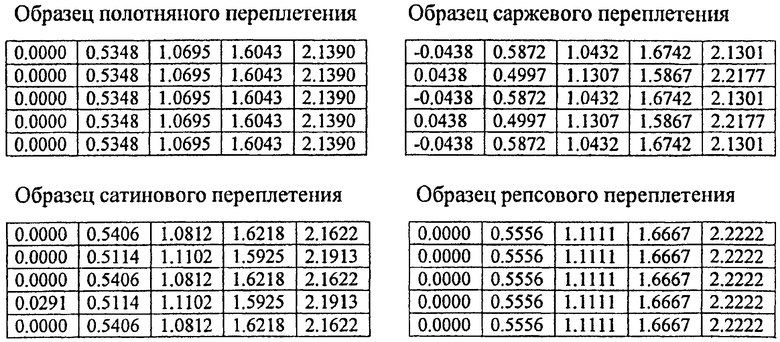
Производят корректировку матриц центров основных нитей вдоль уточных нитей U=(ui,j), получают матрицы фактических координат центров основных нитей вдоль уточных нитей U'=(u'i,j) с элементами:
u'ij=ui,j-0,5·Δyj.
Получают следующие матрицы фактических координат центров основных нитей вдоль уточных для образцов полотняного, саржевого, сатинового и репсового переплетений:
U'=(u'i,j):
По координатам матриц  и U'=(u'i,j) выполняют построение горизонтальных проекций осей нитей основы и утка в пределах раппорта переплетения (фиг.5), при отсутствии параллельности горизонтальных проекций осей нитей основы оси ординат определяют извитость (уработку) нитей основы в горизонтальной плоскости:
и U'=(u'i,j) выполняют построение горизонтальных проекций осей нитей основы и утка в пределах раппорта переплетения (фиг.5), при отсутствии параллельности горизонтальных проекций осей нитей основы оси ординат определяют извитость (уработку) нитей основы в горизонтальной плоскости:

в противном случае агориз.о=0
Получают следующие значения извитости (уработки) нитей основы образцов ткани в горизонтальной плоскости:
- полотняного переплетения: агориз.о=0;
- саржи 2/2: агориз.о=1,72%;
- неправильного четырехнитного сатина: агориз.о=1.25;
- уточного репса 2/2: aгориз.о=0.
При отсутствии параллельности горизонтальных проекций нитей утка оси абсцисс определяют извитость (уработку) нитей утка в горизонтальной плоскости:

в противном случае aгориз.у=0.
Получают следующие значения извитости (уработки) нитей утка образцов ткани в горизонтальной плотности:
- полотняного переплетения: aгориз.у=0;
- саржи 2/2: aгориз.у=2,41%;
- неправильного четырехнитного сатина: aгориз.у=0,3;
- уточного репса 2/2: aгориз.у=0.
Находят суммарную извитость (уработку) нитей основы и утка:
 ;
; 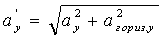 .
.
Полученные значения суммарной извитости (уработки) нитей основы и утка образцов ткани приведены в таблице 15.
ной
| название | год | авторы | номер документа |
|---|---|---|---|
| СПОСОБ ФОРМИРОВАНИЯ ТКАНИ С ПЕРЕМЕННОЙ ПЛОТНОСТЬЮ ПО ОСНОВЕ В ПРОДОЛЬНОМ И ПО УТКУ В ПОПЕРЕЧНОМ НАПРАВЛЕНИЯХ НА ТКАЦКОМ СТАНКЕ | 2000 |
|
RU2187589C2 |
| СПОСОБ ФОРМИРОВАНИЯ ТКАНИ С ПЕРЕМЕННОЙ ПЛОТНОСТЬЮ ПО ОСНОВЕ В ПРОДОЛЬНОМ НАПРАВЛЕНИИ НА ТКАЦКОМ СТАНКЕ | 1995 |
|
RU2127338C1 |
| БИАКСИИЗОТРОПНАЯ ТЕХНИЧЕСКАЯ ТКАНЬ ПОД ЭЛАСТОМЕРНОЕ ПОКРЫТИЕ | 2015 |
|
RU2619922C2 |
| Ткань | 1989 |
|
SU1730245A1 |
| ЯЧЕИСТАЯ ТКАНЬ ПОД ПОЛИМЕРНОЕ ПОКРЫТИЕ | 2002 |
|
RU2233919C2 |
| СПОСОБ ФОРМИРОВАНИЯ ТКАНИ НА ТКАЦКОМ СТАНКЕ | 2002 |
|
RU2213818C1 |
| ТЕХНИЧЕСКАЯ ТКАНЬ ПОД ПОЛИМЕРНОЕ ПОКРЫТИЕ | 2001 |
|
RU2202014C2 |
| РУКАВНАЯ ТКАНЬ ДЛЯ АРМИРОВАНИЯ БЕСКОНЕЧНЫХ ПРИВОДНЫХ РЕМНЕЙ | 2013 |
|
RU2525813C1 |
| Креповая ткань | 1983 |
|
SU1276696A1 |
| Ткань | 2020 |
|
RU2728082C1 |


Изобретение относится к текстильной отрасли и может быть использовано для анализа структурных параметров как имеющихся, так и проектируемых образцов тканей. При осуществлении способа определяют извитость (уработку) нитей основы и утка в ткани как суммарную извитость нитей в вертикальной и горизонтальной плоскостях по высоте волны изгиба основы и диаметрам нитей по горизонтальной и вертикальной осям, полученным по изображениям микросрезов вдоль основы и утка обработанных клеящим веществом участков ткани, предварительно найденным лабораторным путем линейной плотности нитей основы и утка, плотности нитей в ткани по основе и по утку и переплетению нитей в ткани с построением фронтальных профилей нитей раппорта переплетения в ткани, учитывающих наличие в пересечке нити одной системы нитью другой системы нижней и верхней дуг, огибающих расчетные эллипсообразные сечения нитей первой системы, и прямолинейных отрезков осей нитей второй системы, соединяющих эти дуги, нахождения углов наклона прямолинейных отрезков осей нитей в пересечках, а также прямолинейных участков нитей второй системы в настилах, нахождения фактических координат центров перекрытий основных и уточных нитей, построения горизонтальных проекций осей нитей основы и утка и дополнительного учета извитости (уработки) нитей в горизонтальной плоскости. Достигается повышение точности и достоверности определения а также возможность определения извитости (уработки) нитей в однослойных тканях любых переплетений. 15 табл., 5 ил.
Способ определения извитости (уработки) нитей в ткани, заключающийся в построении фронтального профиля нити по ее изображению, полученному путем фотографирования, отличающийся тем, что перед фотографированием пробы ткани производят определение линейной плотности основной и уточной пряжи и числа нитей на 10 см ткани по основе и по утку, затем пробу ткани пропитывают клеящим составом, высушивают в расправленном состоянии при нормальных климатических условиях в течение одних суток, производят микросрезы пробы ткани вдоль нитей основы и утка, фотографируют срезы ткани с использованием микроскопа двадцати-двадцатипятикратного увеличения с вебкамерой, на полученных изображениях микросрезов измеряют высоту волны изгиба нити основы ho, диаметры нитей основы и утка в ткани по горизонтальной dог, dуг и вертикальной dов, dув осям, по которым определяют по известным формулам диаметры нитей основы dоп, утка dуп и средний диаметр dср.п нитей на паковках, коэффициент отношения диаметров Kd, коэффициенты смятия нитей основы и утка в ткани по горизонтальной ηог и ηуг и вертикальной ηов и ηув осям, находят средний расчетный диаметр нитей в ткани dcp, определяют коэффициент высоты волны изгиба основы Kho, порядок фазы строения ткани Пф, коэффициент высоты волны изгиба утка Khy и высоту волны изгиба утка hy, находят геометрическую плотность по основе lo и по утку lу в максимально уплотненной ткани; строят переплетение нитей в ткани с раппортами по основе Ro и по утку Ry, при этом переплетение однослойной ткани рассматривают как матрицу А=(аi,j), где i=1, …, Ro - номер основной нити, j=1, …, Ry - номер уточной нити в раппорте переплетения, элементы матрицы аi,j=1 для основного и аi,j=0 для уточного перекрытий, для каждой нити находят число пересечек по основе  и по
и по  для каждой нити основы находят максимальную плотность ткани по утку
для каждой нити основы находят максимальную плотность ткани по утку  коэффициент наполнения ткани волокнистым материалом по утку
коэффициент наполнения ткани волокнистым материалом по утку  и фактическую геометрическую плотность ткани по утку:
и фактическую геометрическую плотность ткани по утку:

для каждой нити утка определяют максимальную плотность ткани по основе  коэффициент наполнения ткани волокнистым материалом по основе
коэффициент наполнения ткани волокнистым материалом по основе  и фактическую геометрическую плотность по основе:
и фактическую геометрическую плотность по основе:
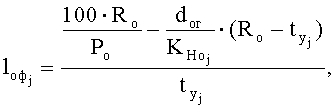
определяют значения больших а1, а2 и малых b1, b2 полуосей расчетных эллипсов дуг обхвата основой нижнего и верхнего утков в пересечке: a1=a2=0,5·dуг+0,5·dов; b1=b2=0,5·dув+0,5·dов,
для каждой основной нити раппорта формируют вектор р коэффициентов полинома четвертой степени:
(b-a)2·z4+2·(b-a)·c·z3+(d2+2·a·(b-a)+c2)·z2+2·a·c·z·d2+a2=0,
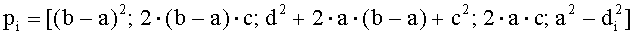
где a, b, c, d - вспомогательные коэффициенты:
a=a1+a2; b=(b1+b2); c=ho-b1-b2 и di=lуфi,
по которому с помощью стандартной функции pp=roots(p) в системе Matlab рассчитывают косинус угла, затем угол наклона прямолинейного участка основы в пересечке к горизонтали β:
по которому с помощью стандартной функции pp=roots(p) в системе Matlab рассчитывают косинус угла, затем угол наклона прямолинейного участка основы в пересечке к горизонтали β:
βi=arccos(cosβi),
с помощью стандартной функции trapz(y,t) в системе Matlab для каждой основной нити раппорта рассчитывают длины дуг обхвата нитей утка в нижней  и верхней
и верхней 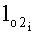 частях пересечки:
частях пересечки:

где у - подынтегральное выражение;
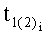 - параметры интегрирования, изменяющиеся в пределах
- параметры интегрирования, изменяющиеся в пределах 
 ;
;  - углы начала и конца обхватывания расчетных эллипсов утков в нижней и верхней частях пересечки:
- углы начала и конца обхватывания расчетных эллипсов утков в нижней и верхней частях пересечки:

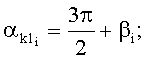

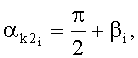
далее находят их горизонтальные 
 и вертикальные
и вертикальные 
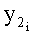 проекции:
проекции:
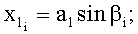

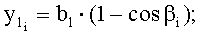

определяют горизонтальную проекцию  и длину
и длину 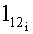 прямолинейного участка основы в пересечке:
прямолинейного участка основы в пересечке:
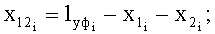

находят коэффициенты ki и 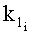 уравнения прямой, проходящей через прямолинейный участок основы в пересечке:
уравнения прямой, проходящей через прямолинейный участок основы в пересечке:

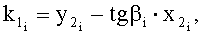
после чего определяют процент извитости (уработки) отдельных нитей основы  а во фронтальной плоскости:
а во фронтальной плоскости:

аналогичным образом определяют процент извитости (уработки) отдельных нитей утка во фронтальной плоскости:
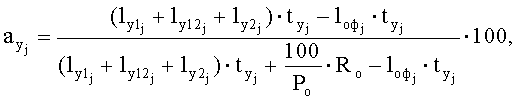
извитость (уработку) нитей данной системы во фронтальной плоскости находят как среднее значение извитости (уработки) отдельных нитей раппорта:


далее выполняют построение профилей отдельных нитей основы: анализируя матрицу переплетения А=(аi,j), составляют матрицу координат центров уточных нитей вдоль основных нитей O=(оi,j) размером (Ro+1)×(Ry+1), причем для центров первых перекрытий уточных нитей oi,j=0, для центров остальных перекрытий:

находят местоположение верхних и нижних утков, учитывая, что уровень верхних утков расположен на высоте hув, уровень нижних утков находится на расстоянии hун от оси абсцисс:


формируют массивы ординат верхней и нижней частей эллипсообразных сечений утков, находящихся в верхнем и нижнем уровнях:
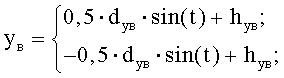

где t - текущее значение угла поворота радиус-вектора точки эллипса утка, в радианах:

где x - текущее значение горизонтальной проекции радиус-вектора точки эллипса утка:

далее выстраивают кривую оси волны изгиба нити основы, ее верхней и нижней ветвей, учитывая, что каждая кривая имеет следующие участки: пересечки «слева-направо», пересечки «справа-налево», горизонтальные участки над и под нитями утка, ось волны изгиба i-й основной нити на каждом участке строят по формулам:
- пересечка «слева-направо»:

- пересечка «справа-налево»:

- настил над утками:
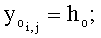

- настил под утками:


выбор соответствующего участка для i-й основной нити производят, анализируя переплетение:

выполняют построение верхней ветви каждой нити основы по формулам:
- пересечка «слева-направо»:
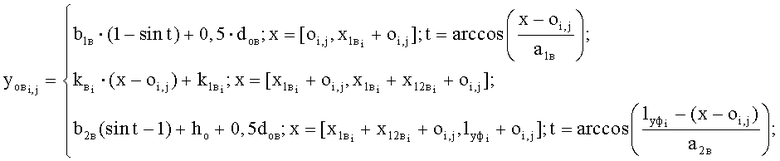
- пересечка «справа-налево»:

- настил над утками:


- настил под утками:


где a1в, а2в, b1в, b2в - большие и малые полуоси дуг обхвата эллипсов утков в начале и конце пересечки верхней ветви основы определяют по формулам:
a1B=0,5·dуг; b1в=0,5·dyв; a2в=0,5·dуг+dов; b2в=0,5·dyв+dов;

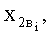
 - горизонтальные проекции дуг обхвата расчетных эллипсов утков в начале и конце пересечки и прямолинейного участка верхней ветви основы, определяют по зависимостям:
- горизонтальные проекции дуг обхвата расчетных эллипсов утков в начале и конце пересечки и прямолинейного участка верхней ветви основы, определяют по зависимостям:


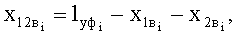
где  - угол обхвата эллипсообразного сечения нити утка верхней ветвью нити основы в начале пересечки:
- угол обхвата эллипсообразного сечения нити утка верхней ветвью нити основы в начале пересечки:

 - обхвата эллипсообразного сечения нити утка верхней ветвью нити основы в конце пересечки:
- обхвата эллипсообразного сечения нити утка верхней ветвью нити основы в конце пересечки: 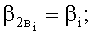
 - коэффициент угла наклона прямой, проходящей через прямолинейный участок верхней ветви основы:
- коэффициент угла наклона прямой, проходящей через прямолинейный участок верхней ветви основы:

где  - вертикальная проекция нижней дуги верхней ветви основы:
- вертикальная проекция нижней дуги верхней ветви основы:

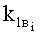 - свободный член уравнения прямой, проходящей через прямолинейный участок верхней ветви основы:
- свободный член уравнения прямой, проходящей через прямолинейный участок верхней ветви основы:

где 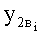 - вертикальная прекция верхней дуги верхней ветви основы:
- вертикальная прекция верхней дуги верхней ветви основы:

 - свободный член уравнения прямой, проходящей через прямолинейный участок верхней ветви основы:
- свободный член уравнения прямой, проходящей через прямолинейный участок верхней ветви основы:

далее выстраивают нижнюю ветвь каждой нити основы по формулам:
- пересечка «слева-направо»:

- пересечка «справа-налево»:

- настил над утками:
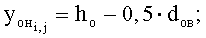

- настил под утками:
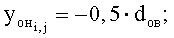

где a1н, а2н, b1н, b2н - большие и малые полуоси дуг обхвата расчетных эллипсов утков в начале и конце пересечки нижней ветви основы: a1н=0,5·dуг+dов; b1н=0,5·dув+dов; a2н=0,5·dуг; b2н=0,5·dув;


 - горизонтальные проекции дуг обхвата расчетных эллипсов утков в начале и конце пересечки и прямолинейного участка нижней ветви каждой нити основы, определяют по зависимостям:
- горизонтальные проекции дуг обхвата расчетных эллипсов утков в начале и конце пересечки и прямолинейного участка нижней ветви каждой нити основы, определяют по зависимостям:
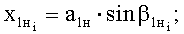
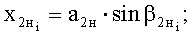

где  и
и  - углы обхвата расчетных эллипсов нижней ветвью i-й нити основы в начале и в конце пересечки:
- углы обхвата расчетных эллипсов нижней ветвью i-й нити основы в начале и в конце пересечки:


 - коэффициент угла наклона прямой, проходящей через прямолинейный участок нижней ветви i-й нити основы:
- коэффициент угла наклона прямой, проходящей через прямолинейный участок нижней ветви i-й нити основы:

где  - свободный член уравнения прямой, проходящей через прямолинейный участок нижней ветви i-й нити основы:
- свободный член уравнения прямой, проходящей через прямолинейный участок нижней ветви i-й нити основы:
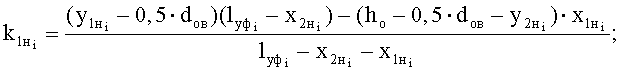
 и
и  вертикальные проекции дуг обхвата расчетных эллипсов утков в начале и конце пересечки нижней ветви каждой нити основы, определяют по зависимостям:
вертикальные проекции дуг обхвата расчетных эллипсов утков в начале и конце пересечки нижней ветви каждой нити основы, определяют по зависимостям:


 - свободный член уравнения прямой, проходящей через прямолинейный участок нижней ветви i-й нити основы:
- свободный член уравнения прямой, проходящей через прямолинейный участок нижней ветви i-й нити основы:
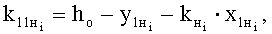
далее, анализируя матрицу переплетения А=(аi,j), составляют матрицу координат центров основных нитей вдоль уточных нитей U=(ui,j) размером (Ro+1)×(Ry+1), причем для центров первых перекрытий основных нитей ui,1=0, для центров остальных перекрытий:

аналогичным образом выполняют построение профилей уточных нитей в последовательности, описанной выше для основных нитей, после чего составляют матрицу координат центров виртуальных уточных нитей вдоль виртуальных основных нитей при отсутствии горизонтальной извитости основных нитей 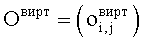 размером (Ro+1)×(Ry+1), причем для центров первых перекрытий уточных нитей
размером (Ro+1)×(Ry+1), причем для центров первых перекрытий уточных нитей 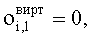 для центров остальных перекрытий:
для центров остальных перекрытий:

далее составляют матрицу координат центров виртуальных основных нитей вдоль виртуальных уточных нитей при отсутствии горизонтальной извитости уточных нитей  размером (Ro+1)×(Ry+1), причем для центров первых перекрытий основных нитей
размером (Ro+1)×(Ry+1), причем для центров первых перекрытий основных нитей  для центров остальных перекрытий:
для центров остальных перекрытий:

определяют матрицы отклонений центров уточных и основных нитей образца ткани от центров уточных и основных нитей виртуальной ткани:
DO=O-Oвирт, DU=U-Uвирт,
просматривая столбцы матриц DO=(doi,j), формируют одномерный массив максимальных отклонений центров уточных нитей вдоль основных нитей образца ткани Δо длиной Ro+1, просматривая строки матрицы DU=(dyi,j), также формируют одномерный массив максимальных отклонений центров основных нитей вдоль уточных нитей образца ткани Δу длиной Ry+1, после чего производят корректировку матрицы центров уточных нитей вдоль основных нитей O=(оi,j), получают матрицу фактических координат центров уточных нитей вдоль основных нитей  с элементами:
с элементами:

производят корректировку матрицы центров основных нитей вдоль уточных нитей U=(ui,j), получают матрицу фактических координат центров основных нитей вдоль уточных нитей U'=(u'i,j) с элементами:

далее по координатам матриц O'=(о'i,j) и U'=(u'i,j) выполняют построение горизонтальных проекций осей нитей основы и утка в пределах раппорта переплетения, при отсутствии параллельности горизонтальных проекций осей нитей основы оси ординат определяют извитость (уработку) нитей основы в горизонтальной плоскости:

в противном случае агориз.o=0, отсутствии параллельности горизонтальных проекций нитей утка оси абсцисс определяют извитость (уработку) нитей утка в горизонтальной плоскости:

в противном случае агориз.у=0, далее находят суммарную извитость (уработку) нитей основы и утка:


| БЕСКОНТАКТНЫЙ СПОСОБ АНАЛИЗА СТРУКТУРЫ ТКАНИ | 1998 |
|
RU2131605C1 |
| 0 |
|
SU386333A1 | |
| СПОСОБ ОПРЕДЕЛЕНИЯ ИЗВИТОСТИ ТЕКСТИЛЬНЫХ НИТЕЙ12 | 0 |
|
SU407224A1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ КООРДИНАТ ТОЧЕК РАЗРЫВА ЭЛЕМЕНТАРНЫХ НИТЕЙ В КОМПЛЕКСНОЙ НИТИ | 2002 |
|
RU2236000C1 |
| Машина для уборки плодов | 1987 |
|
SU1464946A1 |
| Жатка | 1983 |
|
SU1144647A1 |
| КЕРИМОВ С.Г | |||
| Производство технических тканей | |||
| - М.: Легпромбыт-издат., 1994, с.205-206. | |||
Авторы
Даты
2012-12-10—Публикация
2011-06-03—Подача