Изобретение относится к фокусировке когерентного оптического излучения для получения фокусного пятна, ширина которого меньше дифракционного предела в 2D случае (цилиндрическая линза). Данная линза может быть использована в изображающих планарных устройствах, устройствах интегральной оптики, для соединения оптических волноводов, для ввода излучения в фотонно-кристаллические и планарные волноводы и т.д.
Для планарной фокусировки света используются различные типы линз. Самым простым вариантом являются обычные сферические или асферические линзы.
Например, в патенте США US 7408129 B2 от 5.08.2008 (аналог), МПК B23K 26/06, G02B 7/02 используются скрещенные цилиндрические линзы для фокусировки излучения. Излучение от источника вначале фокусируется одной линзой, затем сходящийся пучок фокусируется второй линзой.
Однако с помощью линз из вышеуказанного источника невозможно получить минимальное фокусное пятно в связи с низкой числовой апертурой.
Для достижения острой фокусировки следует использовать линзы с высокой числовой апертурой. Если считать, что фокусное пятно создается только распространяющимися волнами с максимальным наклоном к оптической оси, равным θ, то ширина фокуса по полуспаду интенсивности должна быть равной
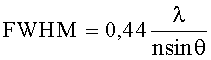 ,
,
где λ - длина волны в вакууме, n - показатель преломления среды, в которой происходит фокусировка света. При числовой апертуре NA=nsinθ, стремящейся к n, ширина фокуса в 2D случае не может быть лучше
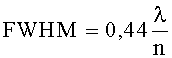
Эту величину можно рассматривать как дифракционный предел в 2D случае. Для уменьшения фокусного пятна меньше дифракционного предела следует фокусировать свет вблизи раздела двух сред, например, материал оптического элемента с показателем преломления n>1 и воздух с показателем преломления 1. Вблизи поверхности раздела сред возбуждаются поверхностные световые волны, конструктивная интерференция которых может приводить к уменьшению фокусного пятна ниже дифракционного предела. Это возможно потому, что поверхностные волны имеют проекцию волнового вектора kx на поперечную координату х, большую, чем волновое число в среде: kx>k0n, где k0=2π/λ - волновое число света в вакууме.
Известно, что градиентные линзы, показатель преломления в которых зависит от координат, могут фокусировать свет вблизи своей поверхности. Наилучшими фокусирующими свойствами обладает градиентная линза, показатель преломления которой описывается выражением:
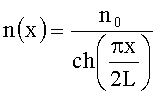
где L - длина линзы, n0 - максимальный показатель преломления на оптической оси, x - поперечная координата (Микаэлян А.Л. Применение свойств среды для фокусирования волн // Доклады академии наук СССР. - 1951. - Вып.81. - С.569-571). Однако для ее изготовления необходимо создать среду, градиентный показатель преломления которой плавно меняется в диапазоне от 1 до n0. На практике это сделать почти невозможно. Обычно используют ступенчатое изменение значения показателя преломления за счет послойного нанесения материалов с различным показателем преломления. Внесение дискретности в изменение показателя преломления отрицательно сказывается на точности изменения показателя преломления, а также на качестве работы линзы. Кроме того, использование материалов с ограниченным набором показателей преломления создает ограничения на расчет (проектирование) такой линзы.
Также для фокусировки когерентного излучения используются дифракционные оптические элементы. Однако в данном случае фокусная плоскость находится за линзой в свободном пространстве, что приводит к увеличению диаметра фокусного пятна.
Наиболее близка к данному изобретению линза-прототип, описанная в статье «Фотонно-кристаллическая линза Микаэляна» Котляра В.В., Триандафилова Я.Р. (Компьютерная оптика. - 2007. - Т.31. - №3. - С.27-31). Данная линза рассчитывается по приведенной выше формуле среднего показателя преломления. Для достижения расчетного среднего показателя преломления в однородном материале линзы создается прямоугольная матрица отверстий размерностью M×N, где М - число отверстий по поперечной оси линзы и N - число отверстий по оптической оси линзы. Центры всех отверстий лежат в узлах прямоугольной сетки размером M×N. Расстояние между центрами d отверстий постоянное и меньше длины волны в среде d<λ/n, где λ - длина волны в вакууме, n - показатель преломления материала линзы. При этом радиусы отверстий рассчитывались по формуле:
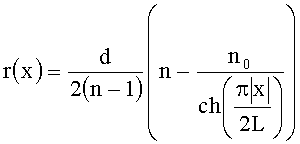
где x - поперечная координата линзы, L - длина линзы вдоль оптической оси z. В работе («Фотонно-кристаллическая линза для сопряжения двух планарных волноводов» / Котляр В.В., Триандафилов Я.Р., Ковалев А.А., Котляр М.И., Волков А.В., Володкин Б.О., Сойфер В.А., О'Фелон Лим, Краусс Томас // Компьютерная оптика, 2008. - Т.32. - №.4. - С.326-336) с помощью моделирования показано, что такая фотонно-кристаллическая линза фокусирует свет в фокусное пятно вблизи своей поверхности с диаметром по полуспаду интенсивности, равным FWHM=0,32λ. Это значение меньше дифракционного предела FWHM=0,44λ, но все-таки достаточно велико, фокусировка света данной фотонно-кристаллической линзой недостаточно острая.
Можно достичь более острой фокусировки света при другой расстановке и расчета диаметра отверстий. Данное изобретение улучшает фокусирующие свойства известной фотонно-кристаллической линзы.
Цель данного изобретения разработать линзу (аналог цилиндрической линзы) для фокусировки плоской световой волны вблизи ее границы с малым фокусным пятном, совмещающую в себе преимущества градиентных линз и возможность простого практического изготовления, не состоящую из набора слоев различных материалов, а также позволяющую сфокусировать свет в пятно меньшего диаметра, чем известные фотонно-кристаллические линзы.
Этого удалось достичь за счет того, что у планарной фотонно-кристаллической микролинзы, имеющей прямоугольную входную апертуру, содержащей отверстия с периодом d поперек и вдоль оптической оси в материале линзы, согласно изобретению четные ряды отверстий, перпендикулярные оптической оси линзы, смещены на d/2 в положительном направлении поперечной оси x, при этом в них со стороны отрицательной части оси x добавлено по одному отверстию для сохранения осевой симметричности расположения отверстий, причем радиус отверстий находится из соотношения
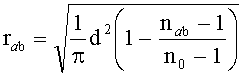
где 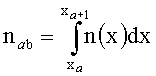
- средний показатель преломления в ячейке с диагональными координатами (xa, yb) и (xa+1, yb+1), xa+1-xa=d, ya+1-ya=d,
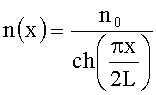
где x - поперечная к оптической оси координата, L - длина линзы, n0 - показатель преломления материала линзы.
Так как при изготовлении линзы по технологии электронной литографии и ионно-химического травления нельзя создать в материале отверстие с очень большим аспектом (отношение глубины цилиндрического отверстия к его диаметру), то существует ограничение по возможному минимальному диаметру отверстия в линзе. Это обстоятельство учитывается при расчете.
Такую планарную линзу можно использовать для фокусировки света в планарный волновод, согласования планарных волноводов, создания изображающих планарных устройств и т.д. Линза рассчитана для телекоммуникационной длины волны света 1,55 мкм и выполнена в кремнии. Показатель преломления кремния для данной длины волны n=3,47. На практике изготовить линзу можно с помощью технологии плазменного или жидкостного травления кремния после нанесения на него маскирующего слоя резиста с отверстиями.
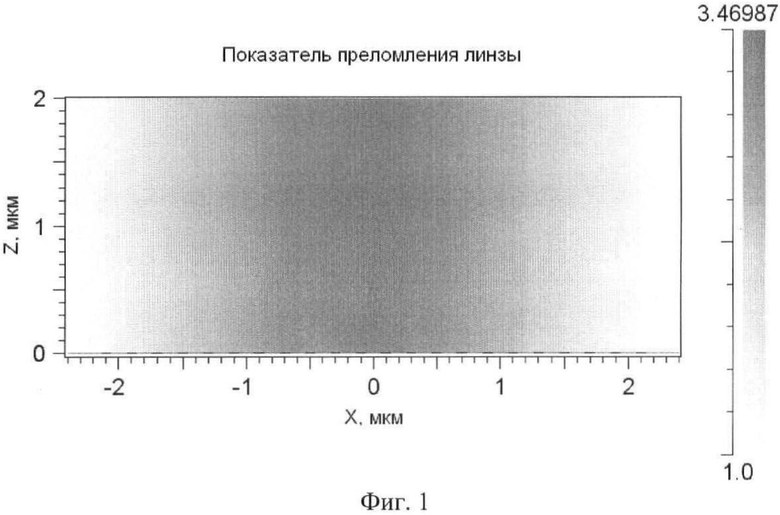
На Фиг.1 приведено (в полутонах) распределение показателя преломления в градиентной гиперболической секансной линзе (аналог) длиной L=2 мкм и шириной 2R=4,8 мкм.
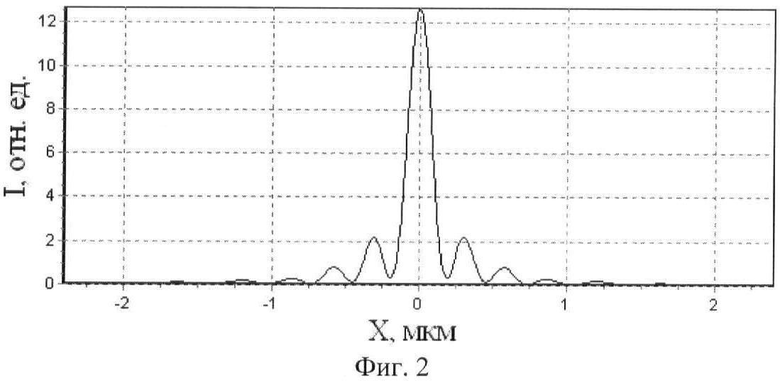
На Фиг.2 приведено распределение интенсивности света в относительных единицах в фокальной плоскости линзы при z=2 мкм.
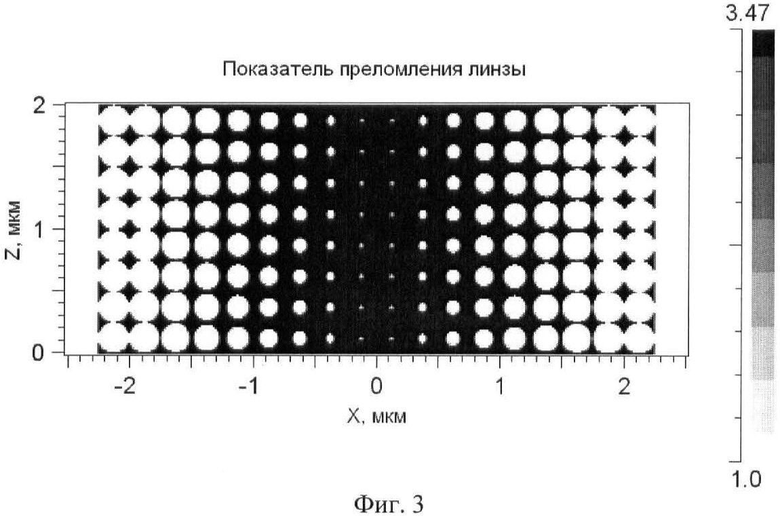
На Фиг.3 приведено распределение показателя преломления в фотонно-кристаллической линзе (прототип) с периодом отверстий d=250 нм.
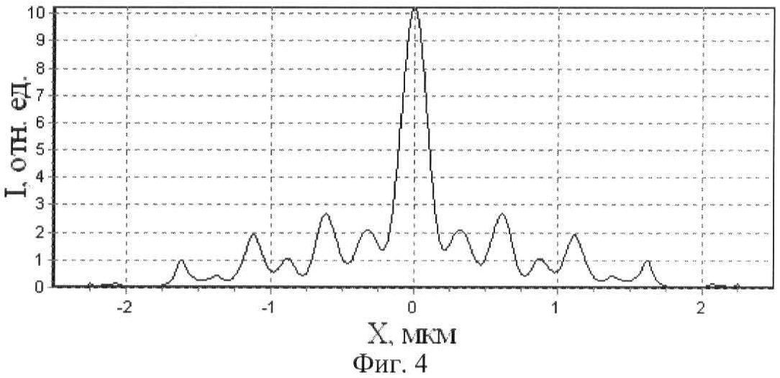
На Фиг.4 приведено распределение интенсивности света в фокальной плоскости фотонно-кристаллической линзы при z=2 мкм.
На Фиг.5 приведено распределение показателя преломления в фотонно-кристаллической линзе с шахматной расстановкой отверстий.
На Фиг.6 приведено распределение интенсивности света в фокальной плоскости фотонно-кристаллической линзы с шахматной расстановкой отверстий.
Для расстановки отверстий в шахматном порядке вся площадь фотонно-кристаллической линзы разбита на М рядов. В первом ряду N отверстий, во 2-м - (N+1) отверстий, в 3-м - N, в 4-м - (N+1) и т.д. Каждое отверстие выполняется в квадратной ячейке. Размер ячейки выбирался из условия возможного размещения в нем отверстия с максимальным диаметром d<λ/n0 и в данном случае был равен 0,25×0,25 мкм.
Обозначим две диагональные координаты произвольной квадратной ячейки как (xa, yb) и (xa+1, yb+1), 1≤a≤N, 1≤b≤M. Средний показатель преломления в ячейке будет равен:
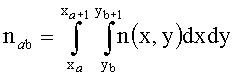
Так как показатель преломления не зависит от координаты у вдоль оптической оси, можно записать:
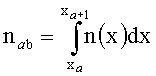
Тогда радиус отверстия с номером (а, b) rab находится по формуле:
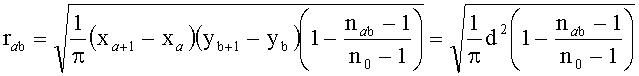
На радиус отверстия накладывается ограничение:
rab<d/2.
В случае получения при расчете радиуса rab более указанных размеров, его размер уменьшается до половины стороны квадратной ячейки размером d. Отверстие располагается по центру ячейки.
На Фиг.1 приведено в градациях серого распределение показателя преломления в градиентной гиперболической секансной линзе (аналог). Видно, что показатель преломления, максимальный по центру, достигающий значения n0=3,47, и спадает к краям до n(R)=1. Ширина микролинзы составляет 2R=4,8 мкм, длина L=2 мкм. Линза рассчитана на длину волны света λ=1,55 мкм.
На Фиг.2 приведено распределение интенсивности I света в относительных единицах в фокальной плоскости линзы, показанной на Фиг.1. Фокальная плоскость расположена на границе линзы при z=2 мкм. Как видно из графика, ширина фокального пятна по полуспаду интенсивности составляет FWHM=0,181 мкм=0,117λ. Дифракционный предел ширины фокусного пятна по полуспаду интенсивности для данного показателя преломления и длины волны составляет
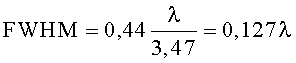
На Фиг.3 приведено распределение показателя преломления в фотонно-кристаллической линзе с расположением отверстий, как в прототипе: центры отверстий находятся в узлах прямоугольной сетки отсчетов. Параметры линзы: максимальный диаметр отверстия равен периоду 0,25 мкм; линза выполнена из 8 рядов и 18 столбцов отверстий в кремнии с показателем преломления n=3,47; ширина и длина линзы те же, что и на Фиг.1.
На Фиг.4 приведено распределение интенсивности света в фокальной плоскости фотонно-кристаллической линзы, показатель преломления которой изображен на Фиг.3. Ширина фокального пятна по полуспаду интенсивности составляет FWHM=0,138λ сразу за линзой.
На Фиг.5 показано распределение показателя преломления в фотонно-кристаллической линзе с расположением отверстий в шахматном порядке. Параметры линзы те же, что и на Фиг.3. Четные ряды линзы имеют по 19 отверстий, нечетные 18.
На Фиг.6 приведено распределение интенсивности света в фокальной плоскости фотонно-кристаллической линзы с расположением отверстий в шахматном порядке (распределение показателя преломления представлено на Фиг.5). Ширина фокального пятна по полуспаду интенсивности составляет FWHM=0,118λ сразу за линзой. Таким образом видно, что данное распределение отверстий имеет преимущество перед распределением отверстий в виде прямоугольной матрицы.
Из приведенного примера видно, что планарная линза с шахматным расположением отверстий формирует более узкое фокусное пятно (при прочих равных условиях), чем планарная фотонно-кристаллическая линза с прямоугольной матрицей отверстий (прототип). Преимущество данной линзы заключается также в простоте и удобстве изготовления с помощью технологий нанолитографии (запись отверстий в маскирующем слое электронного резиста типа ЭРП-40 электронным лучом в электронном микроскопе с литографической приставкой с последующим проявлением резиста и плазмо-химическим травлением подложки) или фотолитографии.
| название | год | авторы | номер документа |
|---|---|---|---|
| ПЛАНАРНАЯ ЦИЛИНДРИЧЕСКАЯ МИКРОЛИНЗА | 2013 |
|
RU2539850C2 |
| ПЛАНАРНАЯ БИНАРНАЯ МИКРОЛИНЗА | 2010 |
|
RU2454760C1 |
| Акустическая линза | 2016 |
|
RU2618600C1 |
| СПОСОБ ПРЯМОЙ ЛАЗЕРНОЙ ЗАПИСИ КИНОФОРМНЫХ ЛИНЗ В ТОЛСТЫХ СЛОЯХ ФОТОЧУВСТВИТЕЛЬНЫХ МАТЕРИАЛОВ ТИПА ФОТОРЕЗИСТОВ (ВАРИАНТЫ) | 2012 |
|
RU2498360C2 |
| Устройство для формирования оптической ловушки с хиральной симметрией | 2021 |
|
RU2781504C1 |
| Мезоразмерная кубоидная пластинчатая линза | 2022 |
|
RU2795677C1 |
| ОПТИЧЕСКИЙ НАКОПИТЕЛЬ ДАННЫХ И СПОСОБЫ ОПТИЧЕСКОЙ ЗАПИСИ И СЧИТЫВАНИЯ | 1996 |
|
RU2146397C1 |
| МНОГОКАНАЛЬНЫЙ КОНФОКАЛЬНЫЙ МИКРОСКОП (ВАРИАНТЫ) | 2014 |
|
RU2574863C1 |
| РАСШИРИТЕЛЬ ПУЧКА | 2000 |
|
RU2183337C2 |
| ДИФРАКЦИОННАЯ ИНТРАОКУЛЯРНАЯ ЛИНЗА | 2000 |
|
RU2186417C2 |
Изобретение относится к фокусировке когерентного оптического излучения для получения фокусного пятна, ширина которого меньше дифракционного предела в 2D случае (цилиндрическая линза). Техническим результатом является фокусировка плоской световой волны вблизи ее границы с малым фокусным пятном. Планарная фотонно-кристаллическая микролинза, имеющая прямоугольную входную апертуру, содержит отверстия с периодом d поперек и вдоль оптической оси в материале линзы. Четные ряды отверстий, перпендикулярные оптической оси линзы, смещены на d/2 в положительном направлении поперечной оси х, при этом в них со стороны отрицательной части оси х добавлено по одному отверстию для сохранения осевой симметричности расположения отверстий, причем радиус отверстий находится из соотношения
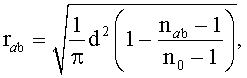
где 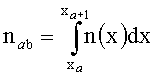
- средний показатель преломления в ячейке с диагональными координатами (xa, yb) и (xa+1, yb+1), xa+1-xa=d, ya+1-ya=d,
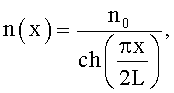
где x - поперечная к оптической оси координата, L - длина линзы, n0 - показатель преломления материала линзы. 6 ил.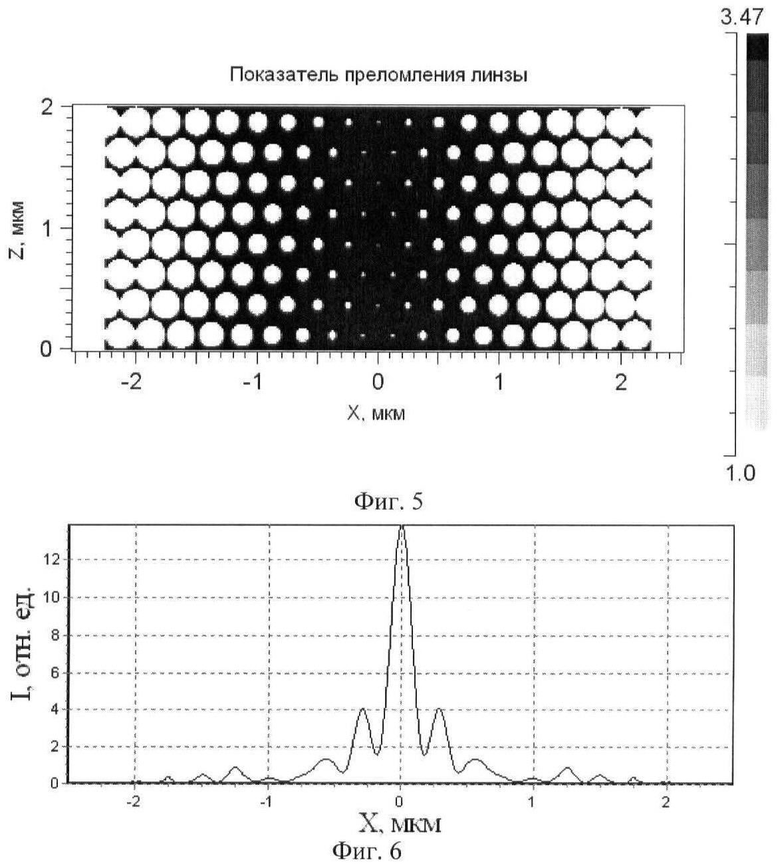
Планарная фотонно-кристаллическая микролинза, имеющая прямоугольную входную апертуру, содержащая отверстия с периодом d поперек и вдоль оптической оси в материале линзы, отличающаяся тем, что четные ряды отверстий, перпендикулярные оптической оси линзы, смещены на d/2 в положительном направлении поперечной оси x, при этом в них со стороны отрицательной части оси x добавлено по одному отверстию для сохранения осевой симметричности расположения отверстий, причем радиус отверстий находится из соотношения
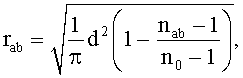
где 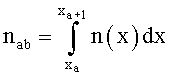 - средний показатель преломления в ячейке с диагональными координатами (xa, yb) и (xa+1, yb+1), xa+1-xa=d, ya+1-ya=d,
- средний показатель преломления в ячейке с диагональными координатами (xa, yb) и (xa+1, yb+1), xa+1-xa=d, ya+1-ya=d, 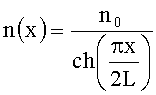 , где x - поперечная к оптической оси координата, L - длина линзы, n0 - показатель преломления материала линзы.
, где x - поперечная к оптической оси координата, L - длина линзы, n0 - показатель преломления материала линзы.
| Планарный акустооптический дискриминатор | 1977 |
|
SU683459A1 |
| СПОСОБ ИЗГОТОВЛЕНИЯ РЕНТГЕНОВСКОЙ ПРЕЛОМЛЯЮЩЕЙ ЛИНЗЫ С ПРОФИЛЕМ ВРАЩЕНИЯ | 2003 |
|
RU2297681C2 |
| РЕКОМБИНАНТНЫЙ ХИМЕРНЫЙ БЕЛОК ANTH1, КОДИРУЮЩАЯ ЕГО НУКЛЕИНОВАЯ КИСЛОТА И ИХ ПРИМЕНЕНИЕ | 2003 |
|
RU2322455C2 |
| Колосоуборка | 1923 |
|
SU2009A1 |
Авторы
Даты
2013-01-20—Публикация
2011-11-17—Подача