Изобретение относится к области криптографии, а именно к формированию ключа шифрования/дешифрования (КлШД), и может быть использовано в качестве отдельного элемента при построении симметричных криптографических систем, предназначенных для передачи шифрованных речевых, звуковых, телевизионных и др. сообщений.
Предлагаемый способ формирования КлШД может использоваться в криптографических системах в случае отсутствия или потери криптосвязности (криптосвязность - наличие у корреспондентов сети связи одинакового КлШД) между корреспондентами сети связи (СС), включающей трех корреспондентов, или установления криптосвязности между новыми корреспондентами СС в условиях ведения нарушителем перехвата информации, передаваемой по открытым каналам связи. Под термином «сеть связи» понимают множество узлов и линий, соединяющих их, причем для любых двух различных узлов существует по крайней мере один соединяющий их путь, как описано, например, в книге Д.Филлипс, А.Гарсиа-Диас, «Методы анализа сетей», М.: Мир, 1984, стр.16.
Известен способ формирования КлШД, описанный в книге У.Диффи «Первые десять лет криптографии с открытым ключом», ТИИЭР, т.76, №5, с.57-58. Известный способ заключается в предварительном распределении между сторонами направления связи (СНС) чисел α и β, где α - простое число и 1≤β≤α-1. Под термином «направление связи» понимают совокупность линий передачи и узлов связи, обеспечивающую связь между двумя пунктами сети, как описано, например, в Национальном стандарте РФ, ГОСТ Р 53111-2008, «Устойчивость функционирования сети связи общего пользования», Москва: Стандартинформ, 2009, стр.7. Передающая сторона направления связи (ПерСНС) и приемная сторона НС (ПрСНС), независимо друг от друга, выбирают случайные соответствующие числа XA и XB, которые хранят в секрете и затем формируют числа на основе XA, α, β на ПерСНС и XB, α, β на ПрСНС. СНС обмениваются полученными цифрами по каналам связи без ошибок. После получения чисел корреспондентов стороны преобразовывают полученные числа с использованием своих секретных чисел в единый КлШД. Способ позволяет шифровать информацию во время каждого сеанса связи на новых КлШД (т.е. исключает хранение ключевой информации на носителях) и сравнительно быстро сформировать КлШД при использовании одного незащищенного канала связи.
Однако известный способ обладает относительно низкой стойкостью КлШД к компрометации (стойкость КлШД к компрометации - способность криптографической системы противостоять попыткам нарушителя получить КлШД, который сформирован и используется законными участниками обмена информацией, при использовании нарушителем информации о КлШД, полученной в результате перехвата, хищения, утраты, разглашения, анализа и т.д.), время действия КлШД ограничено продолжительностью одного сеанса связи или его части, некорректное распределение чисел α и β приводит к невозможности формирования КлШД.
Известен также способ формирования КлШД при использовании квантового канала связи [Патент US №5515438, H04L 9/00 от 07.05.96], который позволяет автоматически сформировать КлШД без дополнительных мер по рассылке (доставке) предварительной последовательности. Известный способ заключается в использовании принципа неопределенности квантовой физики и формирует КлШД посредством передачи фотонов по квантовому каналу. Способ обеспечивает получение КлШД с высокой стойкостью к компрометации, осуществляет гарантированный контроль наличия и степени перехвата КлШД.
Однако реализация известного способа требует высокоточной аппаратуры, что обуславливает высокую стоимость его реализации. Кроме этого, КлШД по данному способу может быть сформирован при использовании волоконно-оптических линий связи ограниченной длины, что существенно ограничивает область применения его на практике.
Наиболее близким по технической сущности к заявляемому способу формирования КлШД является способ формирования КлШД [Патент РФ №2170112 от 20.07.2001].
Способ-прототип включает формирование исходной последовательности (ИП) первым корреспондентом направления связи (НС), кодирование ИП, выделение из кодированной ИП блока проверочных символов, передачу его по прямому каналу связи без ошибок второму корреспонденту НС, формирование декодированной последовательности (ДП) вторым корреспондентом НС, формирование функции хеширования последовательностей первым корреспондентом НС, передачу ее по прямому каналу связи без ошибок второму корреспонденту НС и формирование ключей шифрования/дешифрования первым и вторым корреспондентами НС путем хеширования ИП и ДП по сформированной первым корреспондентом НС функции хеширования последовательностей.
Формирование ИП первым корреспондентом НС заключается в генерировании L раз, где L>104 - выбранная первичная длина ИП, случайного двоичного символа, формировании из него кодового слова путем повторения сгенерированного случайного двоичного символа М раз, где М≥1, и передачи кодового слова по каналу связи с ошибками второму корреспонденту НС, формировании из принятого кодового слова принятого двоичного символа и двоичного символа подтверждения F, передаче двоичного символа подтверждения по обратному каналу без ошибок первому корреспонденту НС, причем при двоичном символе подтверждения F, равном нулю, корреспондентами НС осуществляется стирание сгенерированного случайного двоичного символа и принятого двоичного символа, а при двоичном символе подтверждения F, равном единице, осуществляется запоминание сгенерированного случайного двоичного символа и принятого двоичного символа соответственно первым и вторым корреспондентами НС в качестве i-x элементов, где i=1, 2, 3, …, L-U, исходной и предварительной последовательностей соответственно первого и второго корреспондентов НС, где U - количество стертых символов при формировании исходной и предварительной последовательностей.
Кодирование ИП осуществляется линейным блоковым систематическим двоичным помехоустойчивым (N, K) кодом, порождающая матрица которого имеет размерность K×N, причем N>K. Размеры K и N порождающей матрицы линейного блокового систематического двоичного помехоустойчивого (N, K) кода выбирают K=2m-1-m и N=2m-1, где m≥3. Для кодирования ИП предварительно разделяют на Y подблоков длиной K двоичных символов, где Y=(L-U)/K, затем последовательно начиная с j-го до Y-го из каждого j-го подблока, где j=1, 2, 3, …, Y, формируют j-й кодовый блок длиной N двоичных символов перемножением j-го подблока на порождающую матрицу, затем из j-го кодового блока выделяют j-й подблок проверочных символов длиной N-K двоичных символов, который запоминают в качестве j-го подблока блока проверочных символов кодированной ИП.
Выделение блока проверочных символов ИП заключается в разбиении кодированной ИП на ИП и блок проверочных символов кодированной ИП и выделении последнего.
Передача блока проверочных символов кодированной ИП заключается в передаче его от первого корреспондента НС по прямому каналу связи без ошибок второму корреспонденту НС.
Формирование ДП вторым корреспондентом НС осуществляется следующим образом, предварительную последовательность декодируют линейным блоковым систематическим двоичным помехоустойчивым (N, K) кодом, транспонированная проверочная матрица которого имеет размерность N×(N-K), причем N>K. Размеры K и N проверочной матрицы линейного блокового систематического двоичного помехоустойчивого (N, K) кода выбирают K=2m-1-m и N=2m-1, где m≥3. Для декодирования предварительную последовательность и блок проверочных символов кодированной исходной кодированной последовательности разделяют на Y соответствующих пар декодируемых подблоков и подблоков проверочных символов, где Y=(L-U)/K, причем длины декодируемых подблоков и подблоков проверочных символов выбирают равными соответственно K и N-K двоичных символов, затем формируют Y принятых кодовых блоков длиной N двоичных символов путем конкатенации справа к j-му декодируемому подблоку j-го подблока проверочных символов, где j=1, 2, 3, …, Y, после чего последовательно, начиная с 1-го до Y-го, вычисляют j-й синдром S длиной N-K двоичных символов перемножением j-го принятого кодового блока на транспонированную проверочную матрицу, а по полученному j-му синдрому S исправляют ошибки в j-м декодируемом подблоке, который затем запоминают в качестве j-го подблока декодированной последовательности.
Формирование функции хеширования последовательностей первым корреспондентом НС заключается в формировании двоичной матрицы G размерности (L-U)×T, где Т≥64 - длина формируемого ключа шифрования/дешифрования, причем каждый из элементов двоичной матрицы G генерируют случайным образом.
Передача функции хеширования последовательностей заключается в последовательной передаче, начиная с 1-й по (L-U)-ю строки двоичной матрицы G, от первого корреспондента НС по прямому каналу связи без ошибок второму корреспонденту НС.
Формирование КлШД первым и вторым корреспондентами направления связи заключается в хешировании исходной и декодированной последовательностей по сформированной первым корреспондентом НС функции хеширования последовательностей. Для хеширования последовательностей предварительно на стороне первого корреспондента двоичную матрицу G и ИП, а на стороне второго корреспондента двоичную матрицу G и ДП разделяют на W соответствующих пар подматриц размерности Р×Т, где P=(L-U)/W, и подблоков исходной и декодированной последовательностей длиной Р двоичных символов, затем начиная с 1-го до W-й, вычисляют z-й первичный ключ длины Т двоичных символов, где z=1, 2, 3, …, W, перемножением z-го подблока ИП на z-ю подматрицу Gz на стороне первого корреспондента и z-го подблока ДП на z-ю подматрицу Gz на стороне второго корреспондента, после чего формируют КлШД путем поразрядного суммирования по модулю 2 всех W первичных ключей на сторонах первого и второго корреспондентов направления связи.
Способ-прототип позволяет сформировать КлШД между корреспондентами НС со сравнительно небольшими материальными затратами при большом пространственном разнесении корреспондентов НС.
Недостатком прототипа являются относительно большие временные затраты на формирование КлШД для СС из трех корреспондентов, так как необходимо последовательно формировать КлШД посредством способа-прототипа для каждой пары корреспондентов СС, включающей первого корреспондента, затем выбирать один из сформированных КлШД в качестве КлШД для СС и обеспечивать его получение всеми корреспондентами СС.
Целью заявленного технического решения является разработка способа формирования КлШД, обеспечивающего уменьшение времени формирования КлШД для сети связи, включающей трех корреспондентов.
Поставленная цель достигается тем, что в известном способе формирования ключа шифрования/дешифрования, заключающемся в том, что генерируют случайный двоичный символ на стороне первого корреспондента, формируют из случайного двоичного символа кодовое слово, передают кодовое слово от первого корреспондента второму корреспонденту, формируют принятый двоичный символ, формируют двоичный символ подтверждения, передают двоичный символ подтверждения от второго корреспондента первому, формируют исходную и предварительную последовательности на сторонах первого и второго корреспондентов соответственно, кодируют исходную последовательность, выделяют из кодированной исходной последовательности блок проверочных символов, передают его от первого корреспондента второму, формируют и запоминают декодированную последовательность на стороне второго корреспондента, формируют функцию хеширования на стороне первого корреспондента, передают функцию хеширования от первого корреспондента второму, после чего формируют ключ шифрования/дешифрования из исходной и декодированной последовательностей на сторонах первого и второго корреспондентов соответственно, ключ шифрования/дешифрования формируют одновременно для сети связи, включающей трех корреспондентов. Сформированное первым корреспондентом сети связи кодовое слово одновременно передают по первому и второму каналам связи с независимыми ошибками второму и третьему корреспондентам сети связи соответственно. Передают сформированный вторым корреспондентом сети связи двоичный символ подтверждения F1 по первому обратному и третьему прямому каналам связи без ошибок соответственно первому и третьему корреспондентам сети связи. Передают сформированный третьим корреспондентом сети связи двоичный символ подтверждения F2 по второму обратному и третьему обратному каналам связи без ошибок соответственно первому и второму корреспондентам сети связи. Стирают сгенерированный случайный двоичный символ первого корреспондента сети связи и принятые двоичные символы второго и третьего корреспондентов сети связи при равенстве нулю по крайней мере одного из полученных двоичных символов подтверждения, в противном случае запоминают сгенерированный случайный двоичный символ первого корреспондента сети связи, принятый двоичный символ второго корреспондента сети связи, принятый двоичный символ третьего корреспондента сети связи соответственно в качестве i-x элементов, где i=1, 2, 3, …, L-U, исходной последовательности, первой предварительной последовательности и второй предварительной последовательности, где L>103 - число генераций случайного двоичного символа, U - количество стертых символов при формировании исходной последовательности и предварительных последовательностей. После чего одновременно передают блок проверочных символов кодированной исходной последовательности по первому прямому и второму прямому каналам связи без ошибок соответственно второму и третьему корреспондентам сети связи. После формирования исходной и декодированных последовательностей одновременно передают сформированную первым корреспондентом сети связи функцию хеширования последовательностей по первому прямому и второму прямому каналам связи без ошибок соответственно второму и третьему корреспондентам сети связи. Для формирования кодового слова сгенерированный случайный двоичный символ повторяют М раз, где М≥1. Принятому двоичному символу любого корреспондента сети связи присваивают значение первого двоичного символа принятого кодового слова. Для независимого друг от друга и одновременного формирования двоичного символа подтверждения F1 второго корреспондента или двоичного символа подтверждения F2 третьего корреспондента сети связи первый двоичный символ принятого кодового слова сравнивают с последующими М двоичными символами принятого кодового слова, где M≥1 - число повторений сгенерированного случайного двоичного символа при формировании кодового слова, после чего при наличии М совпадений первого двоичного символа принятого кодового слова с М двоичными символами принятого кодового слова двоичному символу подтверждения F1 второго корреспондента или двоичному символу подтверждения F2 третьего корреспондента присваивают значение единица, а при наличии хотя бы одного несовпадения первого двоичного символа принятого кодового слова с М двоичными символами принятого кодового слова двоичному символу подтверждения F1 второго корреспондента или двоичному символу подтверждения F2 третьего корреспондента присваивают значение ноль. Исходную последовательность кодируют линейным блоковым систематическим двоичным помехоустойчивым (N, K) кодом, где K - длина блока информационных символов и N - длина кодового блока, порождающая матрица которого имеет размерность K×N, причем N>K. При кодировании исходную последовательность предварительно разделяют на Y подблоков длиной К двоичных символов, где Y=(L-U)/K. Затем последовательно начиная с первого до Y-го из каждого j-го подблока, где j=1, 2, 3, …, Y, формируют j-й кодовый блок длиной N двоичных символов перемножением j-го подблока на порождающую матрицу. Из j-го кодового блока выделяют j-й подблок проверочных символов длиной N-K двоичных символов. Запоминают в качестве j-го подблока блока проверочных символов кодированной исходной последовательности. Размеры K и N порождающей матрицы линейного блокового систематического двоичного помехоустойчивого (N, K) кода выбирают K=2m-1-m и N=2m-1, где m≥3. Для формирования первой и второй декодированных последовательностей первую и вторую предварительные последовательности второго и третьего корреспондентов сети связи соответственно независимо и одновременно декодируют линейным блоковым систематическим двоичным помехоустойчивым (N, K) кодом, где K - длина блока информационных символов и N - длина кодового блока, транспонированная проверочная матрица которого имеет размерность N×(N-K), причем N>K. Для одновременного и независимого формирования декодированных последовательностей второго и третьего корреспондентов сети связи предварительные последовательности второго и третьего корреспондентов сети связи и блоки проверочных символов кодированной исходной последовательности разделяют на Y соответствующих пар декодируемых подблоков и подблоков проверочных символов, где Y=(L-U)/K. Длины декодируемых подблоков и подблоков проверочных символов выбирают равными соответственно K и N-K двоичных символов. Затем формируют Y принятых кодовых блоков длиной N двоичных символов путем конкатенации справа к j-му декодируемому подблоку j-го подблока проверочных символов, где j=1, 2, 3, …, Y. Последовательно, начиная с 1-го до Y-го, вычисляют j-й синдром S длиной N-K двоичных символов перемножением j-го принятого кодового блока на транспонированную проверочную матрицу. По полученному j-му синдрому S исправляют ошибки в j-м декодируемом подблоке. Затем запоминают в качестве j-го подблока декодированных последовательностей. Выбирают размеры K и N проверочной матрицы линейного блокового систематического двоичного помехоустойчивого (N, K) кода K=2m-1-m и N=2m-1, где m≥3. Функцию хеширования последовательностей на стороне первого корреспондента сети связи формируют в виде двоичной матрицы G размерности (L-U)×T, где Т≥64 - длина формируемого ключа шифрования/дешифрования, причем каждый из элементов двоичной матрицы G генерируют случайным образом. Функцию хеширования последовательностей, сформированную первым корреспондентом сети связи, одновременно передают последовательно, начиная с первой по (L-U)-ю строки двоичной матрицы G второму и третьему корреспондентам сети связи по первому прямому и второму прямому каналам связи без ошибок соответственно. При одновременном формировании ключа шифрования/дешифрования предварительно двоичную матрицу G и исходную последовательность первого корреспондента сети связи, двоичную матрицу G и первую декодированную последовательность второго корреспондента сети связи, двоичную матрицу G и вторую декодированную последовательность третьего корреспондента сети связи разделяют на W соответствующих пар подматриц размерности Р×Т, где P=(L-U)/W, Т≥64 - длина формируемого ключа шифрования/дешифрования, и соответственно подблоков исходной последовательности, первой декодированной последовательности и второй декодированной последовательности длиной Р двоичных символов соответственно. Затем одновременно начиная с первого до W-й, корреспонденты сети связи вычисляют z-й первичный ключ длины Т двоичных символов, где z=1, 2, 3, …, W, перемножением z-го подблока исходной последовательности первого корреспондента сети связи на z-ю подматрицу Gz, z-го подблока первой декодированной последовательности второго корреспондента сети связи на z-ю подматрицу Gz, z-го подблока второй декодированной последовательности третьего корреспондента сети связи на z-ю подматрицу Gz. После чего одновременно формируют ключ шифрования/дешифрования путем поразрядного суммирования по модулю 2 всех W первичных ключей на сторонах всех корреспондентов сети связи.
Благодаря новой совокупности существенных признаков за счет одновременного формирования КлШД корреспондентами сети связи обеспечивается возможность формирования ключа шифрования/дешифрования для сети связи, включающей трех корреспондентов, и уменьшение временных затрат на формирование КлШД для трех корреспондентов сети связи.
Заявленный способ поясняется фигурами, на которых показаны:
- на фигуре 1 - обобщенная структурная схема сети связи, применяемой в заявленном способе;
- на фигуре 2 - временная диаграмма генерирования случайного двоичного символа на стороне первого корреспондента сети связи;
- на фигуре 3 - временная диаграмма формирования кодового слова на стороне первого корреспондента сети связи;
- на фигуре 4 - временная диаграмма вектора ошибок в первом канале связи с ошибками между первым и вторым корреспондентами сети связи;
- на фигуре 5 - временная диаграмма принятого вторым корреспондентом сети связи кодового слова;
- на фигуре 6 - временная диаграмма формирования вторым корреспондентом сети связи двоичного символа подтверждения F1;
- на фигуре 7 - временная диаграмма формирования вторым корреспондентом сети связи принятого двоичного символа;
- на фигуре 8 - временная диаграмма принятого первым корреспондентом сети связи от второго двоичного символа подтверждения F1;
- на фигуре 9 - временная диаграмма принятого третьим корреспондентом сети связи от второго двоичного символа подтверждения F1;
- на фигуре 10 - временная диаграмма формирования кодового слова на стороне первого корреспондента сети связи (повтор фигуры 3 для показа влияния независимых ошибок во втором канале связи с ошибками между первым и третьим корреспондентами сети связи);
- на фигуре 11 - временная диаграмма вектора ошибок во втором канале связи с ошибками между первым и третьим корреспондентами сети связи;
- на фигуре 12 - временная диаграмма принятого третьим корреспондентом сети связи кодового слова;
- на фигуре 13 - временная диаграмма формирования третьим корреспондентом сети связи двоичного символа подтверждения F2;
- на фигуре 14 - временная диаграмма формирования третьим корреспондентом сети связи принятого двоичного символа;
- на фигуре 15 - временная диаграмма принятого первым корреспондентом сети связи от третьего двоичного символа подтверждения F2;
- на фигуре 16 - временная диаграмма принятого вторым корреспондентом сети связи от третьего двоичного символа подтверждения F2;
- на фигуре 17 - временная диаграмма хранящегося i-го элемента исходной последовательности первого корреспондента сети связи;
- на фигуре 18 - временная диаграмма хранящегося i-го элемента первой предварительной последовательности второго корреспондента сети связи;
- на фигуре 19 - временная диаграмма хранящегося i-го элемента второй предварительной последовательности третьего корреспондента сети связи;
- на фигуре 20 - временная диаграмма сформированной первой предварительной последовательности второго корреспондента сети связи;
- на фигуре 21 - временная диаграмма сформированной второй предварительной последовательности третьего корреспондента сети связи;
- на фигуре 22 - временная диаграмма сформированной исходной последовательности первого корреспондента СС, разделенной на Y подблоков по K символов;
- на фигуре 23 - временная диаграмма выделенного j-го подблока исходной последовательности длиной K двоичных символов;
- на фигуре 24 - временная диаграмма формирования j-го кодового блока длиной N двоичных символов;
- на фигуре 25 - временная диаграмма выделения j-го подблока проверочных символов длиной N-K двоичных символов;
- на фигуре 26 - временная диаграмма формирования блока проверочных символов кодированной ИП из Y подблоков проверочных символов;
- на фигуре 27 - временная диаграмма блока проверочных символов кодированной исходной последовательности, переданного второму и третьему корреспондентам сети связи и разделенного на Y подблоков проверочных символов длиной N-K двоичных символов, и выделение из нее j-го подблока проверочных символов;
- на фигуре 28 - временная диаграмма второй предварительной последовательности третьего корреспондента сети связи, разделенной на Y декодируемых подблоков по K символов, и выделение из нее j-го декодируемого подблока;
- на фигуре 29 - временная диаграмма формирования j-го кодового блока путем конкатенации справа j-го подблока проверочных символов к j-му декодируемому подблоку;
- на фигуре 30 - временная диаграмма вычисления j-го синдрома S длиной N-K двоичных символов и определение местоположения ошибки;
- на фигуре 31 - временная диаграмма исправления ошибки в j-м декодируемом подблоке по полученному j-му синдрому S;
- на фигуре 32 - временная диаграмма формирования второй декодированной последовательности третьего корреспондента СС из Y декодируемых подблоков;
- на фигуре 33 - временная диаграмма блока проверочных символов кодированной исходной последовательности, переданного второму и третьему корреспондентам сети связи и разделенного на Y подблоков проверочных символов длиной N-K двоичных символов, и выделение из нее j-го подблока проверочных символов;
- на фигуре 34 - временная диаграмма первой предварительной последовательности второго корреспондента сети связи, разделенной на Y декодируемых подблоков по K символов, и выделение из нее j-го декодируемого подблока;
- на фигуре 35 - временная диаграмма формирования j-го кодового блока путем конкатенации справа j-го подблока проверочных символов к j-му декодируемому подблоку;
- на фигуре 36 - временная диаграмма вычисления j-го синдрома S длиной N-K двоичных символов;
- на фигуре 37 - временная диаграмма проверки на отсутствие ошибок в j-м декодируемом подблоке по полученному j-му синдрому S;
- на фигуре 38 - временная диаграмма формирования первой декодированной последовательности второго корреспондента сети связи из Y декодируемых подблоков;
- на фигуре 39 - вид сформированной функции хеширования последовательностей;
- на фигуре 40 - временная диаграмма представления функции хеширования в виде последовательности двоичных символов, включающей с первой по (L-U)-ю строки длиной по Т двоичных символов;
- на фигуре 41 - временная диаграмма сформированных исходной последовательности первого корреспондента, первой декодированной последовательности второго корреспондента, второй декодированной последовательности третьего корреспондента сети связи;
- на фигуре 42 - временная диаграмма сформированного ключа шифрования/дешифрования первого, второго и третьего корреспондентов сети связи;
- на фигуре 43 - временная диаграмма формирования КлШД.
На представленных фигурах символом «А» обозначены действия, происходящие на стороне первого корреспондента сети связи, символами «B1» - на стороне второго корреспондента сети связи, символами «В2» - на стороне третьего корреспондента сети связи. Символ «→» обозначает процесс передачи последовательностей двоичных символов по каналам связи между корреспондентами сети связи. На фигурах заштрихованный импульс представляет собой символ «1», а не заштрихованный - символ «0». Знаки «+» и «×» обозначают соответственно сложение и умножение в поле Галуа GF(2). Верхние буквенные индексы обозначают длину последовательности (блока), нижние буквенные индексы обозначают номер элемента в последовательности (блоке).
Реализация заявленного способа заключается в следующем. Современные криптосистемы построены по принципу Керкхоффа, описанного, например, в книге Д.Месси, «Введение в современную криптологию», ТИИЭР т.76, №5, май 1988, с.24, согласно которому полное знание нарушителя включает, кроме информации, полученной с помощью перехвата, полную информацию о порядке взаимодействия корреспондентов СС и процессе формирования КлШД. Формирование общего КлШД можно разделить на три основных этапа.
Первый этап - одновременное формирование исходной (ИП) и предварительных (ПРП) последовательностей. Обеспечение формирования ИП и ПРП производится путем одновременной передачи информации об ИП по первому и второму каналам связи с независимыми ошибками соответственно второму и третьему корреспондентам СС и ее одновременной обработкой всеми корреспондентами СС. Предполагается, что нарушитель знает порядок обработки информации об ИП и перехватывает свою версию информации об ИП, передаваемой первым корреспондентом СС, на выходе независимого канала перехвата и использует ее для формирования своей версии ПРП. Возможность одновременного формирования ключа шифрования/дешифрования для СС, включающей трех корреспондентов, определена построением модели канальной связности корреспондентов, представленной на фиг.1. Уменьшение временных затрат на формирование ключа шифрования/дешифрования достигается одновременным формированием исходной и предварительных последовательностей всех корреспондентов СС.
Второй этап предназначен для обеспечения формирования КлШД с высокой надежностью. Формирование КлШД с высокой надежностью достигается устранением (исправлением) несовпадающих символов (ошибок) в предварительных последовательностях второго и третьего корреспондентов относительно исходной последовательности первого корреспондента СС при использовании корреспондентами дополнительной информации об ИП, переданной по первому и второму прямым каналам связи без ошибок от первого корреспондента второму и третьему корреспондентам СС соответственно. Предполагается, что нарушитель перехватывает дополнительную информацию по каналам перехвата без ошибок и использует ее для устранения несовпадений в своей версии ПРП относительно ИП первого корреспондента. Возможность формирования КлШД для СС из трех корреспондентов и уменьшение времени формирования КлШД в СС достигается одновременной передачей и обработкой дополнительной информации об ИП тремя корреспондентами СС.
Третий этап предназначен для формирования ключа заданной длины с малым количеством информации о ключе, получаемой нарушителем. Обеспечение формирования ключа корреспондентов СС с малым количеством информации о нем у нарушителя обеспечивается путем сжатия последовательностей корреспондентов сети связи, которые получены ими после второго этапа. Предполагается, что нарушителю известен алгоритм сжатия последовательностей. Возможность формирования КлШД для СС из трех корреспондентов и уменьшение временных затрат на формирование КлШД в СС достигается одновременной передачей функции хеширования от первого корреспондента СС по первому прямому и второму прямому каналам связи без ошибок соответственно второму и третьему корреспондентам СС и одновременной обработкой информации в целях формирования КлШД всех корреспондентов СС.
В заявленном способе формирования ключа шифрования/дешифрования для обеспечения возможности формирования КлШД для СС из трех корреспондентов и уменьшения временных затрат на формирование КлШД реализуется следующая последовательность действий.
Предполагается, что нарушитель имеет канал перехвата, с помощью которого он получает информацию о переданных кодовых словах по каналам связи с ошибками для формирования ИП и ПРП корреспондентов СС. Нарушитель может только получать информацию и не может участвовать в информационном обмене. Для обеспечения возможности формирования КлШД для СС из трех корреспондентов и уменьшения временных затрат на формирование КлШД для СС из трех корреспондентов необходимо создание условий, при которых производится одновременное формирование КлШД для СС из трех корреспондентов.
Для создания вышесказанных условий каждый из символов исходной двоичной последовательности, случайно вырабатываемых на стороне первого корреспондента СС (каждый двоичный символ ИП генерируют случайным образом, чтобы обеспечить возможность формирования КлШД для трех корреспондентов СС и уменьшение временных затрат на его формирование), повторяют М раз и одновременно передают второму и третьему корреспондентам сети связи по первому и второму каналам связи с независимыми ошибками соответственно. Второй и третий корреспонденты одновременно принимают каждое из слов кода повторения, если все его элементы или «1» или «0» и выносят решение об информационном символе, соответствующем принятому кодовому слову. В противном случае стирают это кодовое слово. Решение о принятых (стертых) кодовых словах одновременно передают по каналам связи без ошибок всем другим корреспондентам сети. Корреспонденты СС одновременно сохраняют в исходной и предварительных последовательностях символы, которые не были стерты. Нарушитель, также, может удалять символы, которые были стерты корреспондентами СС. Однако символы, сохраняемые нарушителем (т.е. которые соответствуют одновременно сохраненным символам корреспондентов СС), не достаточно надежны, потому что ошибки, возникающие в независимых каналах с ошибками корреспондентов СС, и ошибки, возникающие в канале перехвата, являются независимыми ошибками. Вместо представленного декодирования кодовых слов корреспонденты СС могут одновременно использовать пороговое декодирование. Основное различие при использовании порогового декодирования заключается в том, что корреспонденты СС одновременно принимают каждое из слов кода повторения, не только когда все его элементы или «1» или «0», но и когда число одинаковых двоичных символов в кодовом слове не менее определенного числа (порога). Это приведет, с одной стороны, к уменьшению надежности каждого из одновременно сохраненных символов в предварительных последовательностях (ПРП) на сторонах второго и третьего корреспондентов, с другой стороны корреспонденты СС будут меньше стирать символов ИП (ПРП).
Создание условий, при которых обеспечивается одновременное формирование КлШД для трех корреспондентов СС и уменьшение времени, затрачиваемого на его формирование, реализуется в заявленном способе следующей последовательностью действий по одновременному формированию ИП первого корреспондента СС и предварительных последовательностей второго и третьего корреспондентов СС. Формирование исходной последовательности первого корреспондента СС заключается в следующем. L раз, где L>103, генерируют случайный двоичный символ (см. фиг.2). Известные способы генерирования случайных чисел описаны, например, в книге Д. Кнут «Искусство программирования для ЭВМ», М.: Мир, 1977, т.2, стр.22. Формируют из случайного двоичного символа кодовое слово. Для формирования кодового слова сгенерированный случайный двоичный символ кодируют кодом с М-повторениями (см. фиг.3 и 10), где М≥1. М определяется качеством каналов связи с ошибками. Известные способы кодирования кодом с повторениями описаны, например, в книге Э. Берлекэмп, «Алгебраическая теория кодирования», М.: Мир, 1971, стр.11, однако при одновременном декодировании кодового слова корреспондентами СС используются каналы связи без ошибок, что существенно влияет на увеличение надежности принятых символов. Одновременно передают кодовое слово по первому и второму каналам связи с независимыми ошибками второму и третьему корреспондентам СС соответственно. Временные диаграммы векторов ошибок в каналах связи с независимыми ошибками показаны на фигурах 4 и 11. Под термином «вектор ошибок» понимают поразрядную разность между переданным и принятым кодовыми словами, как описано, например, в книге А. Зюко, Д. Кловский, М. Назаров, Л. Финк «Теория передачи сигналов», М.: Радио и связь, 1986, стр.93. Принятые кодовые слова показаны на фигурах 5 и 12. Известные способы передачи последовательностей по каналам связи с ошибками описаны, например, в книге А. Зюко, Д. Кловский, М. Назаров, Л. Финк, «Теория передачи сигналов», М.: Радио и связь, 1986, стр.11. Второй и третий корреспонденты СС из принятого кодового слова одновременно формируют принятые двоичные символы и двоичные символы подтверждения F1, F2. Принятому двоичному символу на стороне первого и второго корреспондентов СС одновременно присваивают значение первого двоичного символа принятых кодовых слов (см. фиг.7 и 14). Для формирования двоичного символа подтверждения первый двоичный символ принятого кодового слова одновременно сравнивают с последующими М двоичными символами принятого кодового слова. При наличии хотя бы одного несовпадения первого двоичного символа принятого кодового слова с М двоичными символами принятого кодового слова двоичному символу подтверждения присваивают значение «0». При наличии М совпадений первого двоичного символа принятого кодового слова с М двоичными символами принятого кодового слова двоичному символу подтверждения присваивают значение «1», как показано на фигурах 6 и 13. Известные способы сравнения двоичных символов описаны, например, в книге П. Хоровец, У. Хил, «Искусство схемотехники», М.: Мир, т.1, 1983, стр.212. Передают сформированный вторым корреспондентом сети связи двоичный символ подтверждения F1 по первому обратному и третьему прямому каналам связи без ошибок соответственно первому и третьему корреспондентам сети связи, передают сформированный третьим корреспондентом сети связи двоичный символ подтверждения F2 по второму обратному и третьему обратному каналам связи без ошибок соответственно первому и второму корреспондентам сети связи (см. фиг.8, 9, 15 и 16). Известные способы передачи двоичного символа по обратному каналу описаны, например, в книге А. Зюко, Д. Кловский, М. Назаров, Л. Финк «Теория передачи сигналов», М.: Радио и связь, 1986, стр.156. При равенстве нулю по крайней мере одного из полученных двоичных символов подтверждения (F1, F2) сгенерированный случайный двоичный символ первого корреспондента сети связи и принятые двоичные символы второго и третьего корреспондентов сети связи одновременно стирают, в противном случае одновременно запоминают сгенерированный случайный двоичный символ первого корреспондента сети связи, принятый двоичный символ второго корреспондента сети связи, принятый двоичный символ третьего корреспондента сети связи соответственно в качестве i-x элементов, где i=1, 2, 3, …, L-U, исходной последовательности, первой предварительной последовательности и второй предварительной последовательности, где L>103 - число генераций случайного двоичного символа, U - количество одновременно стертых символов при формировании исходной последовательности первого корреспондента сети связи, первой предварительной последовательности второго корреспондента сети связи и второй предварительной последовательности третьего корреспондента сети связи. На фигуре 17 показан i-й элемент исходной последовательности первого корреспондента СС, на фигуре 18 - i-й элемент первой предварительной последовательности второго корреспондента СС, а i-й элемент второй предварительной последовательности третьего корреспондента СС показан на фигуре 19. Известные способы стирания двоичных символов описаны, например, в книге У. Питерсон, Э. Уэлдон «Коды исправляющие ошибки», М.: Мир, 1976, стр.17. Известные способы хранения двоичных символов описаны, например, в книге Л. Мальцев, Э. Фломберг, В. Ямпольский «Основы цифровой техники», М.: Радио и связь, 1986, стр.79. Вид сформированной первой предварительной последовательности показан на фигуре 20, вид сформированной второй предварительной последовательности показан на фигуре 21, а вид сформированной исходной последовательности показан на фигуре 22.
Оценка вероятности ошибок в ПРП корреспондентов СС приведена в Приложении 1.
После применения корреспондентами СС кода с повторениями в ИП первого корреспондента СС и предварительных последовательностях второго и третьего корреспондентов СС остаются несовпадающие символы, что не позволяет корреспондентам СС приступить к непосредственному формированию КлШД. Устранение этих несовпадений может быть реализовано на основе использования помехоустойчивого кодирования. Однако известные помехоустойчивые коды позволяют кодировать последовательности значительно меньшей длины, чем полученная длина ИП (ПРП), равная L-U двоичных символов. Для этого применяют последовательное кодирование, т.е. если длина ИП (ПРП) велика, например 103÷105 двоичных символов, ее разделяют на Y подблоков длиной по K символов, где Y=(L-U)/K.
Каждый подблок длиной по K символов кодируется на стороне первого корреспондента СС линейным систематическим блоковым помехоустойчивым (N, K) двоичным кодом, где K - длина блока информационных символов и N - длина кодового блока. Линейным двоичным кодом называется код, который построен на основе использования линейных операций в поле GF(2), как описано, например, в книге Р. Блейхут «Теория и практика кодов контролирующих ошибки», М.: Мир, 1986, стр.61. Под термином «блоковый код» понимают код, в котором действия производятся над блоками символов, как описано, например, в книге Р. Блейхут «Теория и практика кодов контролирующих ошибки», М.: Мир, 1986, стр.13. Систематическим называется код, в котором кодовое слово начинается с информационных символов, оставшиеся символы кодового слова являются проверочными символами к информационным символам, как описано, например, в книге Р. Блейхут «Теория и практика кодов контролирующих ошибки», М.: Мир, 1986, стр.66. Затем формируемые блоки проверочных символов длиной N-K двоичных символов объединяют в единый блок проверочных символов кодированной ИП длиной Y·(N-K) двоичных символов и одновременно передают его по первому прямому и второму прямому каналам связи без ошибок соответственно второму и третьему корреспондентам СС. Второй и третий корреспонденты СС используют блок проверочных символов кодированной ИП для устранения несовпадений в своих предварительных последовательностях по отношению к ИП и в результате чего получают декодированные последовательности.
Оценка вероятностей ошибочного декодирования предварительных последовательностей корреспондентов сети связи приведена в Приложении 2.
В качестве помехоустойчивых кодов могут использоваться широкий класс кодов Боуза-Чоудхури-Хоквингема, коды Хемминга, Рида-Малера, Рида-Соломона и другие линейные блоковые коды, характеризующиеся своими параметрами N, K, d. В ходе применения корреспондентами СС помехоустойчивого кодирования нарушитель получает дополнительную информацию о КлШД путем перехвата блока проверочных символов кодированной ИП первого корреспондента СС, переданного по первому прямому и второму прямому каналам связи без ошибок соответственно второму и третьему корреспондентам СС. Используя его, нарушитель также исправляет часть несовпадений в своей версии перехваченной ПРП относительно ИП первого корреспондента СС. Это обстоятельство корреспонденты учитывают при формировании из исходной и декодированных последовательностей КлШД для сети связи. Устранение несовпадений (ошибок) в предварительных последовательностях второго и третьего корреспондентов СС реализуется в заявленном способе следующей последовательностью действий. Кодирование исходной последовательности заключается в следующем. Предварительно исходную последовательность разделяют на Y подблоков длиной K двоичных символов, где Y=(L-U)/K, как показано на фиг.22. Известные способы разбиения последовательности на блоки фиксированной длины описаны, например, в книге В. Васильев, В. Свириденко «Системы связи», М.: Высшая школа, 1987, стр.208. Последовательно, начиная с 1-го до Y-го, каждый j-й подблок, где j=1, 2, 3, …, Y, кодируют линейным блоковым систематическим двоичным помехоустойчивым (N, K) кодом (см. фиг.23). Порождающая матрица кода имеет размерность K×N, причем N>K. Размеры K и N порождающей матрицы линейного блочного систематического двоичного помехоустойчивого (N, K) кода выбирают K=2m-1-m и N=2m-1, где m≥3, как описано, например, в книге Р. Блейхут «Теория и практика кодов контролирующих ошибки», М.: Мир, 1986, стр.71. Для кодирования ИП каждый j-й подблок длиной K двоичных символов перемножают на порождающую матрицу кода и получают j-й кодовый блок длиной N двоичных символов, как показано на фиг.24. Известные способы помехоустойчивого кодирования блоков символов описаны, например, в книге Р. Блейхут «Теория и практика кодов контролирующих ошибки», М.: Мир, 1986, стр.63. Из j-го кодового блока выделяют j-й подблок проверочных символов длиной N-K двоичных символов (см. фиг.25). Известные способы выделения блоков фиксированной длины описаны, например, в книге В. Васильев, В. Свириденко «Системы связи», М.: Высшая школа, 1987, стр.208. Запоминают j-й подблок проверочных символов в качестве j-го подблока блока проверочных символов кодированной исходной последовательности. Временная диаграмма формирования блока проверочных символов кодированной ИП показана на фигуре 26. Известные способы хранения последовательности двоичных символов описаны, например, в книге Л. Мальцев, Э. Фломберг, В. Ямпольский «Основы цифровой техники», М.: Радио и связь, 1986, стр.38. Одновременно передают блок проверочных символов кодированной ИП по первому прямому и второму прямому каналам связи без ошибок соответственно второму и третьему корреспондентам СС. Известные способы передачи последовательностей по каналам связи описаны, например, в книге А. Зюко, Д. Кловский, М. Назаров, Л. Финк «Теория передачи сигналов», М.: Радио и связь, 1986, стр.11. Одновременное формирование декодированных последовательностей вторым и третьим корреспондентами СС заключается в следующем. Первую ДП второго корреспондента СС и вторую ДП третьего корреспондента СС одновременно формируют из первой и второй ПРП соответственно. Действия второго и третьего корреспондентов СС по формированию первой и второй ДП соответственно аналогичны и выполняются параллельно, поэтому далее будут показаны действия и их порядок для одного корреспондента СС (для второго корреспондента СС). ПРП и блок проверочных символов кодированной исходной последовательности одновременно разделяют на Y соответствующих пар декодируемых подблоков (см. фиг.28 и 34) и подблоков проверочных символов (см. фиг.27 и 33), где Y=(L-U)/K. Длины декодируемых подблоков и подблоков проверочных символов выбирают равными соответственно K и N-K двоичных символов. Известные способы разбиения последовательности на блоки фиксированной длины описаны, например, в книге В. Васильев, В. Свириденко «Системы связи», М.: Высшая школа, 1987, стр.208. Одновременно формируют Y принятых кодовых блоков длиной N двоичных символов путем конкатенации справа к j-му декодируемому подблоку j-го подблока проверочных символов, где j=1, 2, 3, …, Y, как показано на фиг.29 и 35. Y принятых кодовых блоков одновременно декодируют линейным блоковым систематическим двоичным помехоустойчивым (N, K) кодом (см. фиг.29 и 35). Проверочная матрица кода имеет размерность (N-K)×N, причем N>K. Выбирают размеры K и N проверочной матрицы линейного блокового систематического двоичного помехоустойчивого (N, K) кода K=2m-1-m и N=2m-1, где m≥3, как описано, например, в книге Р. Блейхуг «Теория и практика кодов контролирующих ошибки», М.: Мир, 1986, стр.71. Последовательно, начиная с 1-го до Y-го, вычисляют j-й синдром S длины N-K двоичных символов перемножением j-го принятого кодового блока на транспонированную проверочную матрицу. Временная диаграмма вычисления j-го синдрома S длиной N-K двоичных символов показана на фигурах 30 и 36. По полученному j-му синдрому S исправляют ошибки в j-м декодируемом подблоке (см. фиг.31 и 37). Известные способы синдромного декодирования блоков символов описаны, например, в книге Р. Блейхут «Теория и практика кодов контролирующих ошибки», М.: Мир, 1986, стр.70. Затем j-й декодируемый подблок запоминают в качестве j-го подблока декодированной последовательности, как показано на фиг.32 и 38. Известные способы хранения последовательности двоичных символов описаны, например, в книге Л. Мальцев, Э. Фломберг, В. Ямпольский «Основы цифровой техники», М.: Радио и связь, 1986, стр.38. И получают, таким образом, декодированную последовательность.
После формирования корреспондентами СС тождественных ИП на стороне первого корреспондента СС и ДП на сторонах второго и третьего корреспондентов СС корреспонденты СС должны сформировать КлШД с малым количеством информации нарушителя о КлШД. Для обеспечения малого количества информации нарушителя о КлШД корреспонденты СС используют метод "усиления секретности" последовательностей.
Оценка количества информации Шеннона, получаемого нарушителем о сформированном корреспондентами СС КлШД при использовании метода "усиления секретности", приведено в Приложении 3.
Для обеспечения малой величины информации нарушителя о КлШД в предлагаемом способе формирования КлШД реализуется следующая последовательность действий. Одновременное формирование из ИП и ДП-ей КлШД заключается в следующем. Формируют на стороне первого корреспондента СС функцию хеширования последовательностей в виде двоичной матрицы G размерности (L-U)×T, где Т≥64 - требуемая длина формируемого КлШД. Каждый из элементов двоичной матрицы G генерируют случайным образом (см. фиг.39). Известные способы генерирования случайных чисел описаны, например, в книге Д. Кнут «Искусство программирования для ЭВМ», М.: Мир, 1977, т.2, стр.22. Функцию хеширования последовательностей одновременно передают по первому прямому и второму прямому каналам связи без ошибок соответственно второму и третьему корреспондентам СС, последовательно, начиная с 1-й по (L-U)-ю строки двоичной матрицы G, как показано на фиг.40. Известные способы передачи последовательностей по каналам связи описаны, например, в книге А. Зюко, Д. Кловский, М. Назаров, Л. Финк «Теория передачи сигналов», М.: Радио и связь, 1986, стр.11. КлШД на сторонах первого, второго и третьего корреспондентов СС, одновременно формируют путем хеширования ИП, первой ДП и второй ДП соответственно (см. фиг.41) по сформированной на стороне первого корреспондента сети связи функции хеширования последовательностей, как показано на фиг.42. При формировании КлШД предварительно двоичную матрицу G и ИП первого корреспондента СС, двоичную матрицу G и первую ДП второго корреспондента СС, двоичную матрицу G и вторую ДП третьего корреспондента СС разделяют на W соответствующих пар подматриц размерности Р×Т, где Р=(L-U)/W, и подблоков исходной и декодированных последовательностей длиной Р двоичных символов соответственно. Известные способы разбиения последовательности на блоки фиксированной длины описаны, например, в книге В. Васильев, В. Свириденко «Системы связи», М.: Высшая школа, 1987, стр.208. Затем, начиная с первого до W-й, вычисляют z-й первичный ключ длины Т двоичных символов, где z=1, 2, 3, …, W, перемножением z-го подблока ИП первого корреспондента СС на z-ю подматрицу Gz, z-го подблока первой ДП второго корреспондента СС на z-ю подматрицу Gz, z-го подблока второй ДП третьего корреспондента СС на z-ю подматрицу Gz. После чего формируют КлШД путем поразрядного суммирования по модулю 2 всех W первичных ключей на сторонах всех корреспондентов СС, как показано на фиг.43. Действия по передаче и приему последовательностей по каналам связи с ошибками, прямым и обратным каналам связи без ошибок засинхронизированы. Известные способы синхронизации описаны, например, в книге Е. Мартынов «Синхронизация в системах передачи дискретных сообщений», М.: Связь, 1972, стр.186.
Для подтверждения возможности достижения сформулированного технического результата было проведено аналитическое моделирование, по результатам которого можно сделать вывод о том, что время формирования КлШД для СС посредством предлагаемого способа может быть меньше в 2,29165 раза по сравнению с временем формирования КлШД для СС посредством способа-прототипа. Результаты оценки времени формирования КлШД для СС, включающей трех корреспондентов, приведены в Приложении 4.
Приложение 1.
Оценка вероятности ошибок в предварительных последовательностях корреспондентов сети связи
(В Приложениях 1-4 используются все уловные сокращения, которые использовались в описании изобретения.)
Пусть pm1 - вероятность ошибки на двоичный символ в первом канале связи с ошибками между первым и вторым корреспондентами СС и pm2 - вероятность ошибки на двоичный символ во втором канале связи с ошибками между первым и третьим корреспондентами СС, тогда 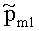 - вероятность ошибки в первой ПРП второго корреспондента СС может быть найдена из выражения:
- вероятность ошибки в первой ПРП второго корреспондента СС может быть найдена из выражения:

Аналогично 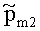 - вероятность ошибки во второй ПРП третьего корреспондента СС, определяется выражением:
- вероятность ошибки во второй ПРП третьего корреспондента СС, определяется выражением:

где pac - вероятность, с которой одновременно принимается блок (длиной М+1 двоичных символов) с М повторениями вторым и третьим корреспондентами, которая определяется с помощью выражения:

где αij - совместная вероятность событий, возникновения ошибки i в первом канале связи с ошибками между первым и вторым корреспондентами СС (наличия ошибки (i=1) или отсутствия ошибки (i=0), причем i∈{0,1}), и возникновения ошибки j во втором канале связи с ошибками между первым и третьим корреспондентами СС (наличия ошибки j=1) или отсутствия ошибки (j=0), причем j∈{0, 1}), при передаче любого символа от первого корреспондента СС по первому и второму каналам связи с независимыми ошибками, где:

Вероятность ошибки в ПРП нарушителя будет зависеть от выбранного им правила приема. Так, если pw - вероятность ошибки на двоичный символ в канале перехвата и нарушитель декодирует по мажоритарному правилу (мажоритарное правило декодирования - правило, когда решение о информационном символе принятого блока кода с повторениями выносится согласно большему количеству одинаковых символов в принятом блоке кода с повторениями), то вероятность ошибки на двоичный символ для принятых информационных символов нарушителя может быть определена из выражения:

Приложение 2
Оценка вероятностей ошибочного декодирования предварительных последовательностей корреспондентов сети связи
Вероятность ошибочного декодирования первой ПРП второго корреспондента СС может быть определена по формуле

где PE01 - вероятность ошибочного декодирования подблока длиной K двоичных символов из первой ПРП второго корреспондента СС, определяемая, как описано, например, в книге Ф. Мак-Вильямс, Н. Слоэн «Теория кодов исправляющих ошибки», М.: Связь, 1979, стр.29,

где 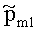 - вероятность ошибки в первой ПРП второго корреспондента СС, полученная из выражения (1.1) Приложения 1, a d - минимальное кодовое расстояние (N, K) кода, которое определяется как минимальное число несовпадающих разрядов в двух любых кодовых словах (N, K) кода, как описано, например, в книге Ф. Мак-Вильямс, Н. Слоэн «Теория кодов исправляющих ошибки», М.: Связь, 1979, стр.20.
- вероятность ошибки в первой ПРП второго корреспондента СС, полученная из выражения (1.1) Приложения 1, a d - минимальное кодовое расстояние (N, K) кода, которое определяется как минимальное число несовпадающих разрядов в двух любых кодовых словах (N, K) кода, как описано, например, в книге Ф. Мак-Вильямс, Н. Слоэн «Теория кодов исправляющих ошибки», М.: Связь, 1979, стр.20.
Вероятность ошибочного декодирования второй ПРП третьего корреспондента СС может быть определена по формуле

PE02 - вероятность ошибочного декодирования подблока длиной K двоичных символов из второй ПРП третьего корреспондента СС, определяется согласно выражению:

где 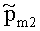 - вероятность ошибки во второй ПРП третьего корреспондента СС, полученная из выражения (1.2) Приложения 1.
- вероятность ошибки во второй ПРП третьего корреспондента СС, полученная из выражения (1.2) Приложения 1.
Приложение 3
Оценка количества информации Шеннона, получаемого нарушителем о сформированном корреспондентами сети связи ключе шифрования/дешифрования при использовании метода «усиления секретности»
Для обеспечения малого количества информации нарушителя о КлШД в предлагаемом способе формирования КлШД используют метод "усиления секретности" последовательностей, основанный на универсальном хешировании, как описано, например, в книге Bennett С., Brassard G., Crepeau С., Maurer U. "Generalized privacy amplification", IEEE Trans. on IT. vol.41, no.6, pp.1915-1923, 1995, стр.1920. Сущность метода «усиления секретности» заключается в следующем. На стороне первого корреспондента СС выбирают случайным образом функцию хеширования из универсального множества функций хеширования. Функцию хеширования передают по первому прямому и второму прямому каналам связи без ошибок соответственно второму и третьему корреспондентам СС. Затем хешируют ИП первого корреспондента СС, первую ДП второго корреспондента СС и вторую ДП третьего корреспондента СС. Результатом хеширования будет сформированный КлШД для сети связи из трех корреспондентов. С вероятностью близкой к единице и равной 1-Рε происходит событие, когда информация нарушителя о КлШД не превысит определенной малой величины Io и с малой вероятностью сбоя Рε возможно событие, при котором информация нарушителя о КлШД будет более Io. ИП длиной L-U двоичных символов отображается при хешировании в последовательность KA длиной Т двоичных символов формируемого КлШД первого корреспондента СС, первая ДП длиной L-U двоичных символов отображается в последовательность K1B длиной Т двоичных символов формируемого КлШД второго корреспондента СС, вторая ДП длиной L-U двоичных символов отображается в последовательность K2B длиной Т двоичных символов формируемого КлШД третьего корреспондента СС. Предполагается, что нарушитель имеет полную информацию о функции хеширования последовательностей корреспондентов СС. Функция хеширования последовательностей должна удовлетворять ряду требований, как описано, например, в книге Ю. Романец, П. Тимофеев, В. Шаньгин «Защита информации в компьютерных системах и сетях», М.: Радио и связь, 1999, с.156:
- функция хеширования должна быть чувствительна к всевозможным изменениям в последовательности, таким как вставки, выбросы, перестановки и т.п.;
- функция хеширования должна обладать свойством необратимости, т.е. задача подбора другой последовательности, которая обладала требуемым значением функции хеширования должна быть вычислительно не разрешима;
- вероятность коллизии, т.е. вероятность события, при котором значения функции хеширования двух различных последовательностей совпадают, должна быть ничтожно мала.
Кроме этого, функция хеширования должна принадлежать универсальному множеству функций хеширования. Универсальное множество функций хеширования определяется следующим образом. Пусть n и r два положительных целых числа, причем n>r. Множество функций G2, отображающих множество двоичных последовательностей длиной n в множество двоичных последовательностей длиной r, называется универсальным, если для любых различных последовательностей x1 и x2 из множества двоичных последовательностей длины n вероятность (коллизии) того, что значение функции хеширования от x1 равно значению функции хеширования от x2(g(x1)=g(x2)), не превосходит 2-r, если функция хеширования g выбирается случайно, в соответствии с равновероятным распределением, из G2, как описано, например, в книге Carter J., Wegman М. "Universal classes of hash functions", Journal of Computer and System Sciences, 1979, Vol.18, pp.143-154, стр.145. Все линейные функции, отображающие множество двоичных последовательностей длиной n в множество двоичных последовательностей длиной r, принадлежат универсальному множеству, как описано, например, в книге Carter J., Wegman M. "Universal classes of hash functions". Journal of Computer and System Sciences, 1979, Vol.18, pp.143-154, стр.150. Линейные функции могут быть описаны двоичными матрицами размерности n×r. Хранение универсального множества G2 функций хеширования последовательностей для ИП, первой и второй ДП (число функций хеширования последовательностей, принадлежащих универсальному множеству G2, велико и составляет величину, равную 2T·(L-U), причем для хранения каждая функция хеширования последовательностей требует T·(L-U) ячеек памяти) труднореализуемо и нецелесообразно. Поэтому случайный равновероятный выбор функции хеширования последовательностей из универсального множества G2 функций хеширования последовательностей на стороне первого корреспондента СС заключается в генерировании случайным образом элементов двоичной матрицы размерности (L-U)×T, которая описывает случайно выбранную функцию хеширования последовательностей из G2. После формирования корреспондентами СС КлШД путем хеширования ИП, первой и второй ДП по случайно выбранной из G2 функции хеширования последовательностей количество информации Шеннона, получаемое нарушителем о КлШД, сформированном корреспондентами СС, не больше чем

где IR - информация Реньи.
Информация Реньи определяется через энтропию Реньи на символ в канале перехвата с вероятностью ошибки на двоичный символ pw, которая характеризует неопределенность нарушителя о КлШД, при знании нарушителем информации, полученной с помощью перехвата, полной информации об алгоритме взаимодействия законных корреспондентов СС и процессе формирования ключа, как описано, например, в книге Bennett С., Brassard G., Crepeau С., Maurer U. "Generalized privacy amplification", IEEE Trans. on IT. vol. 41, no. 6, pp.1915-1923, 1995, стр.1919. Энтропия Реньи равна

Тогда информация Реньи IR, полученная нарушителем при наблюдении последовательностей ПРП длиной L-U символов, определяется выражением
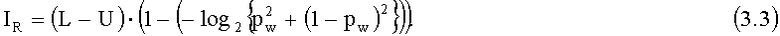
При устранении несовпадений (ошибок) в первой и второй ПРП второго и третьего корреспондентов СС, когда от первого корреспондента передают второму и третьему корреспондентам соответственно по прямым каналам связи без ошибок блок проверочных символов кодированной ИП длиной Y(N-K) двоичных символов, нарушитель получает дополнительную информацию Реньи о КлШД. Дополнительная информация Реньи, полученная нарушителем за счет кодирования ИП IRкод, равна IRкод=Y(N-K), как доказано, например, в лемме 5 работы Maurer U. "Linking Information Reconciliation and Privacy Amplification", J.Cryptology, 1997, no.10, pp.97-110, стр.105. Тогда общее количество информации Реньи, поступающее к нарушителю, равно

В этом случае (3.1) принимает вид:

Количество информации Шеннона, получаемое нарушителем о сформированном корреспондентами СС КлШД, при использовании метода «усиления секретности», больше ограничения Io (определенного в (3.5)) с малой вероятностью сбоя Pε. При использовании корреспондентами кода с повторениями энтропия Реньи и вероятность Рε определяются более сложными соотношениями, описанными, например, в журнале «Проблемы информационной безопасности. Компьютерные системы», СПб, Петровский фонд, №1, 2000 г., стр.18 в статье В. Коржика, В. Яковлева, А. Синюка «Протокол выработки ключа в канале с помехами», причем энтропия Реньи не зависит от выбранного нарушителем правила обработки перехваченных сообщений.
Определение информации Реньи и вероятности Рε при одновременном формировании КлШД для СС требует рассмотрения всех процедур, связанных с одновременной передачей информации по каналам связи с ошибками, к которым относятся: генерирование и передача ИП первого корреспондента СС второму и третьему корреспондентам СС. Для этого каждый из символов исходной двоичной последовательности, случайно вырабатываемых на стороне первого корреспондента СС (каждый двоичный символ ИП генерируют случайным образом, чтобы обеспечить возможность формирования КлШД для трех корреспондентов СС и уменьшение времени его формирования), повторяют М раз и одновременно передают второму и третьему корреспондентам сети связи по первому и второму каналам связи с независимыми ошибками. Второй и третий корреспонденты одновременно принимают каждое из слов кода повторения, если все его элементы или «1» или «0» и выносят решение об информационном символе, соответствующем принятому кодовому слову. В противном случае стирают это кодовое слово. Затем второй и третий корреспонденты одновременно передают решение о принятых (стертых) кодовых словах по каналам связи без ошибок другим корреспондентам сети. Корреспонденты СС одновременно сохраняют в исходной и предварительных последовательностях символы, которые не были стерты. Нарушитель также может удалять символы, которые были стерты корреспондентами СС. Однако символы, сохраняемые нарушителем (т.е. которые одновременно сохранили корреспонденты СС), не достаточно надежны, потому что ошибки, возникающие в каналах связи с ошибками корреспондентов СС, и ошибки, возникающие в канале перехвата, являются независимыми ошибками.
Оценка информации Реньи производится с учетом результатов оценок вероятности ошибок в ПРП корреспондентов СС, приведенных в Приложении 1.
Перепишем выражение (1.3) с учетом (1.4), вынося общие множители за скобки, и получим:
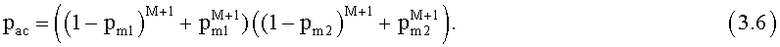
Перепишем (1.1) с учетом (1.4) и (3.6), вынося общие множители за скобки и производя сокращение, и получим:
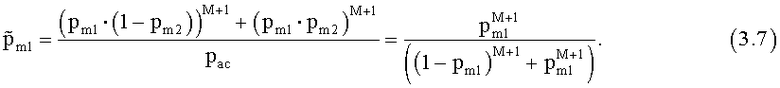
Аналогично перепишем (1.2) с учетом (1.4), (3.6) и получим:

Рассмотрим ситуацию у нарушителя при наблюдении им зашумленной последовательности блоков длиной по М+1 двоичных символов. Обозначим через |z| вес Хемминга (вес Хемминга блока двоичных символов - число не нулевых разрядов в блоке двоичных символов) блока z длиной М+1 двоичных символов, полученного нарушителем. Легко показать, что совместная вероятность событий |z|=d и события, что этот блок принят вторым и третьим корреспондентами, при условии передачи первым корреспондентом СС информационного символа равного 0, равна
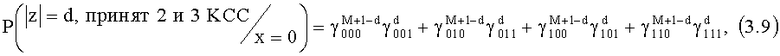
где γijk - совместная вероятность событий, при которых информационный символ x=0, посланный первым корреспондентом СС, получен вторым корреспондентом СС как i, причем i∈{0, 1}, третьим корреспондентом СС как j, причем j∈{0, 1}, и нарушителем как k, причем k∈{0, 1}, где:
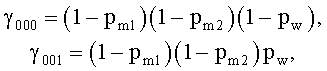

Аналогично для случая, когда х=1, определяем:
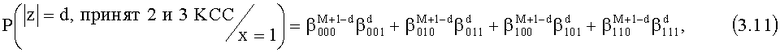
где

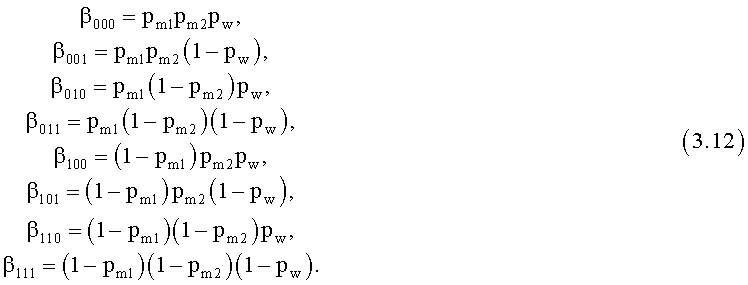
Заменяя (3.10) в (3.9) с учетом (3.6), после выноса общих множителей за скобки и выполнения сокращений получаем вероятность приема нарушителем слова z с весом Хемминга |z|=d при условии, что на вход канала перехвата поступил символ х=0 и второй и третий корреспонденты СС приняли кодовое слово:
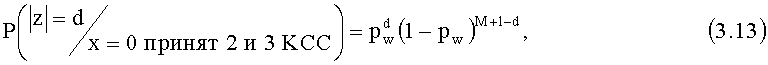
Аналогично, как для (3.13), получаем вероятность приема нарушителем слова z с весом Хемминга |z|=d при условии, что на вход канала перехвата поступил символ х=1 и второй и третий корреспонденты СС приняли кодовое слово:
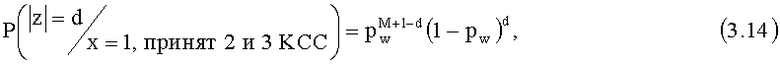
Используя теорему Байеса [как описано, например, в книге Феллер В., "Введение в теорию вероятности и ее приложения", М.: Мир, 1967, 498 с.] и учитывая равномерный закон распределения вероятностей двоичных символов ИП, получаем вероятности передачи символов х=0 при условии, что нарушитель принял блок |z|=d,
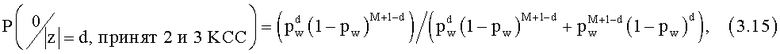
или х=1 при условии, что нарушитель принял блок |z|=d,
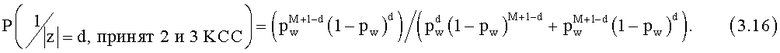
Вероятность приема нарушителем любого блока z веса Хемминга |z|=d
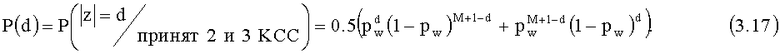
Относительное знание нарушителем ИП длиной L-U представляется его знанием относительно весов Хемминга d1, d2, …, dL-U соответствующих блоков кода с повторениями длиной М+1 символов. Для ПРП нарушителя энтропия Реньи R равна
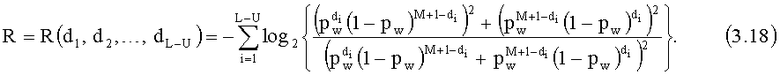
Веса d1, d2, …, dL-U являются случайными величинами и энтропия Реньи, полученная нарушителем, также является случайной величиной. Вероятность Pε - вероятность того, что сумма случайных величин энтропии Реньи символов ИП будет меньше значения (R0-ε)(L-U), где R0 - средняя энтропия Реньи на принятый блок повторения длиной М+1, ε - малая величина, определяющая значение Pε (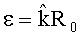 , где
, где 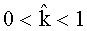 ). Используя границу Чернова [как описано, например, в книге Коржик В.И., Финк Л.М., Щелкунов К.Н. "Расчет помехоустойчивости систем передачи дискретных сообщений". - М.: Радио и связь, 1981. - 231 с.], Рε определяется
). Используя границу Чернова [как описано, например, в книге Коржик В.И., Финк Л.М., Щелкунов К.Н. "Расчет помехоустойчивости систем передачи дискретных сообщений". - М.: Радио и связь, 1981. - 231 с.], Рε определяется
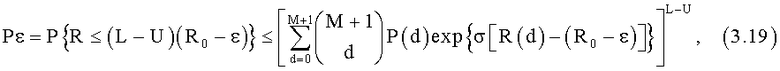
где 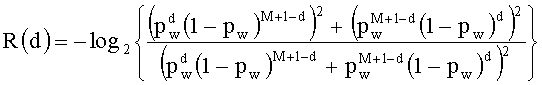
- энтропия Реньи (см. выражение (3.2)) на принятый нарушителем блок кода с повторениями длиной М+1 с весом Хемминга d и P(d) - определяемая согласно выражению (3.17) вероятность приема нарушителем по каналу перехвата блока кода с повторениями длиной М+1 и весом Хемминга d,
R0 определяется

оптимальный параметр σ может быть найден из решения уравнения
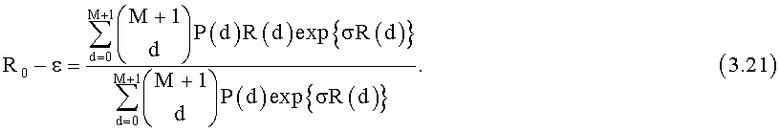
Тогда информация Реньи IR в выражении (3.3) при использовании корреспондентами СС для передачи информации кода с повторениями может быть определена из выражения:

Приложение 4
Оценка времени формирования ключа шифрования/дешифрования для сети связи
Возможность одновременного формирования ключа шифрования/дешифрования для сети связи из трех корреспондентов определена построением модели канальной связности корреспондентов, представленной на фиг.1, особенностью которой является использование для формирования КлШД для СС двух открытых каналов связи с независимыми ошибками. Случайные события возникновения ошибок в каналах связи являются независимыми, как это описано в книге И.Н. Бронштейна, К.А. Семендяева «Справочник по математике для инженеров и учащихся втузов», М.: Наука. Главная редакция физико-математической литературы, 1981, стр.580.
К КлШД для СС целесообразно предъявить ряд требований в условиях минимизации времени его формирования с учетом особенностей его формирования по открытым каналам связи с ошибками.
Требования по достоверности формирования КлШД определяются вероятностью несовпадения сформированных корреспондентами СС КлШД - 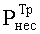 .
.
Требования по безопасности формирования КлШД определяются:
а) требуемой (минимально допустимой) длиной формируемого КлШД - ТTp [двоичных символов];
б) требуемым (максимально допустимым) количеством информации Шеннона, получаемым нарушителем о сформированном КлШД - 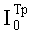 [бит];
[бит];
в) 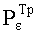 - вероятностью риска, что информация Шеннона о сформированном КлШД превысит
- вероятностью риска, что информация Шеннона о сформированном КлШД превысит 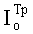 .
.
Время формирования КлШД для СС (Tобщ) определяется временем передачи всей необходимой информации о КлШД СС. При этом сделано предположение, что все задержки по времени, связанные с обработкой информации (генерирование, кодирование, декодирование, сжатие и др.) равны нулю, т.е. выполняются мгновенно. Тогда
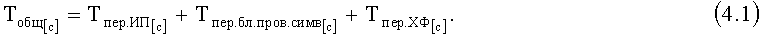
Перепишем (4.1) с учетом заданной технической скорости передачи информации V[дв.c/с] по каналам связи, причем считаем ее одинаковой в любом канале связи, показанном на фиг.1 (с учетом обозначений, принятых в описании изобретения):
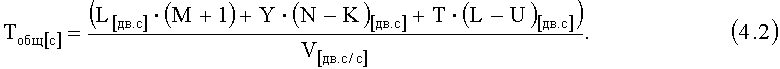
Ввиду того что каждая система передачи информации характеризуется разной V[дв.c/с], предлагается вместо затрачиваемого времени Тобщ[c] использовать обобщенный показатель - общую длину передаваемых последовательностей DLINA, которая из (4.2) определяется согласно выражению
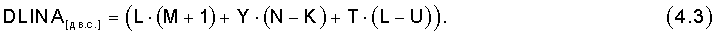
Задача минимизации времени формирования КлШД для СС сводится к подбору параметров процесса формирования КлШД для СС таким образом, чтобы в условиях выполнения требований сформировать КлШД с минимальным параметром DLINA.
Требования к КлШД для СС можно записать в виде

где Pнес - вероятность несовпадения сформированных корреспондентами СС КлШД, которая равна

где PE1 определяется из выражения (2.1), PE2 определяется из выражения (2.3) приложения 2, Io определено в (3.5), а Рε определена в (3.19) Приложения 3.
Зададим требования к КлШД для СС:

Определим общие исходные данные для фиг.1:
1) качество первого канала связи с ошибками - pm1=10-2;
2) качество второго канала связи с ошибками - pm2=2·10-2;
3) качество канала перехвата нарушителя - pw=8·10-2.
Приведем результаты расчета параметров и оценки выполнения требований для условий формирования КлШД для СС с использованием предлагаемого способа формирования КлШД для СС.
Параметры:
L=4400 [дв.с.];
М+1=3 [дв.с.];
U=384 [дв.с.];
N=511 [дв.с.];
K=502 [дв.с.];
Y=8;
ε=7,03·10-3 [бит].
Оценка выполнения требований:
Т=64 [дв.с.];
Рнес=7,35406·10-5;
Io=3,10477·10-11 [бит];
Рε=9,97693·10-6.
Полученная общая длина передаваемых по каналам связи последовательностей равна
DLINA3=2,70296·105 [дв.с.].
Рассмотрим особенности формирования КлШД для СС посредством способа-прототипа. Это становится возможным при реализации следующей последовательности действий, которую назовем методом-прототипом:
1. Посредством способа-прототипа формируется КлШД K1 между первым и вторым корреспондентами СС по каналам связи, как показано на фиг.1.
2. Посредством способа-прототипа формируется КлШД K2 между первым и третьим корреспондентами СС по каналам связи, как показано на фиг.1.
3. Первый корреспондент СС выбирает КлШД K1, сформированный со вторым корреспондентом СС, в качестве КлШД для СС и затем ввиду того, что каналы связи в модели канальной связности, представленной на фиг.1, являются открытыми каналами, первый корреспондент СС шифрует КлШД K1 на КлШД K2 и получает криптограмму С, после чего первый корреспондент СС передает С по каналу связи без ошибок третьему корреспонденту СС.
4. Третий корреспондент СС дешифрует криптограмму С на КлШД K2 и получает КлШД K1. КлШД K1 принимается в качестве КлШД для СС.
Сделано предположение, что первый и третий корреспонденты СС используют безусловно стойкую систему шифрования, которая описана, например, в книге И.Н. Оков «Криптографические системы защиты информации», СПб., ВУС, 2001, стр.78. Использование безусловно стойкой системы шифрования для шифрования КлШД и получение криптограммы C с последующей ее передачей по каналам связи без ошибок (в том числе и к нарушителю) не увеличивает информацию нарушителя о КлШД для СС. Описанный выше порядок и содержание действий по формированию КлШД СС посредством способа-прототипа требует переопределения требований, т.е. переход от общих требований к КлШД для СС к требованиям к парному КлШД, формируемому посредством способа-прототипа.
КлШД для СС не будет достоверен, если хотя бы один из парных КлШД не достоверен. Тогда

где 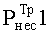 - требуемая величина вероятности несовпадения при формировании парного КлШД методом-прототипом на первом шаге,
- требуемая величина вероятности несовпадения при формировании парного КлШД методом-прототипом на первом шаге, 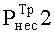 - требуемая величина вероятности несовпадения при формировании парного КлШД на втором шаге метода-прототипа.
- требуемая величина вероятности несовпадения при формировании парного КлШД на втором шаге метода-прототипа.
Пусть 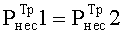 . Тогда перепишем (4.7):
. Тогда перепишем (4.7):

Отсюда

Требование по риску 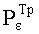 к КлШД для СС не будет выполнено, если будет превышена вероятность риска при формировании хотя бы одного парного ключа по методу-прототипу.
к КлШД для СС не будет выполнено, если будет превышена вероятность риска при формировании хотя бы одного парного ключа по методу-прототипу.

где 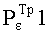 - требуемая величина вероятности риска при формировании парного КлШД на 1 шаге,
- требуемая величина вероятности риска при формировании парного КлШД на 1 шаге, 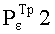 - требуемая величина вероятности риска при формировании парного КлШД на 2 шаге.
- требуемая величина вероятности риска при формировании парного КлШД на 2 шаге.
Пусть 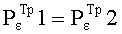 . Тогда перепишем (4.10):
. Тогда перепишем (4.10):

Отсюда

После использования метода-прототипа общая информация Iо нарушителя о формируемом КлШД для СС может быть записана в виде:

где K1 - парный ключ, сформированный на первом шаге метода-прототипа; K2 - парный ключ, сформированный на втором шаге метода-прототипа; f1 - вся информация нарушителя о K1, включая информацию, полученную по каналам связи, и информацию, основанную на знании им всего порядка и содержания обработки информации для получения K1; f2 - вся информация нарушителя о K2, включая информацию, полученную по каналам связи, и информацию, основанную на знании им всего порядка и содержания обработки информации для получения K2.
С учетом особенностей метода-прототипа перепишем (4.13).
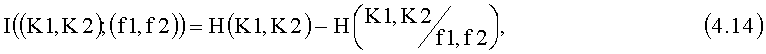
где Н(K1,K2) - энтропия Шеннона ключей K1 и K2, 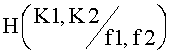 - условная энтропия Шеннона ключей K1 и K2 при условии знания нарушителем информации f1 и f2.
- условная энтропия Шеннона ключей K1 и K2 при условии знания нарушителем информации f1 и f2.
Определимся относительно H(K1,K2). На основании свойства аддитивности энтропии, как показано в книге В.Д. Колесник, Г.Ш. Полтырев «Курс теории информации», М.: Наука. Главная редакция физико-математической литературы, 1982, стр.29, запишем
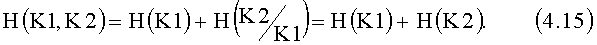
Последнее равенство в (4.15) определяется независимостью событий формирования K1 и K2. Аналогично для 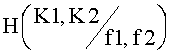 запишем
запишем
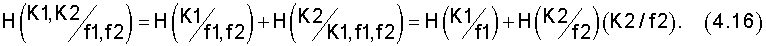
Последнее равенство в (4.16) также определяется независимостью событий формирования K1 и K2.
Перепишем (4.14) с учетом (4.15) и (4.16) и получаем
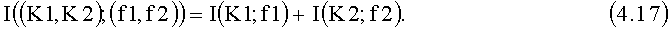
Тогда с учетом (4.17) для 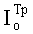 можно записать
можно записать

где  - требуемая величина информации утечки к нарушителю для формируемого парного КлШД K1 на первом шаге;
- требуемая величина информации утечки к нарушителю для формируемого парного КлШД K1 на первом шаге; 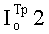 - требуемая величина информации утечки к нарушителю для формируемого парного КлШД K2 на втором шаге.
- требуемая величина информации утечки к нарушителю для формируемого парного КлШД K2 на втором шаге.
Пусть 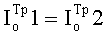 . Тогда
. Тогда

Отсюда

С учетом решения (4.9), (4.12), (4.20) и требований к КлШД СС (4.6) перейдем от требований к КлШД для СС к требованиям к парному КлШД, формируемому с использованием способа-прототипа, используемого в составе метода-прототипа:
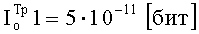
 ;
;
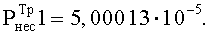
Требование TTp остается без изменений ТTp=64 [дв.с.].
Коррекции подлежит выражение для определения DLINAp - общей длины последовательностей, переданных по каналам связи, при формировании КлШД для СС посредством метода-прототипа.

где DLINA1 - общая длина переданных последовательностей по каналам связи при формировании парного КлШД с использованием способа-прототипа на первом шаге метода-прототипа, которая определяется из выражения (4.3); DLINA2 - общая длина переданных последовательностей по каналам связи при формировании парного КлШД с использованием способа-прототипа на втором шаге метода-прототипа, которая определяется из выражения (4.3); Т - минимально возможная длина передаваемой криптограммы С.
Условие перехода от предлагаемого способа к способу-прототипу заключается в введении предположения о том, что вероятность ошибки в одном из каналов связи с ошибками на фиг.1 равна 0.
Приведем результаты расчета параметров и оценки выполнения измененных требований для формирования парного КлШД с использованием метода-прототипа на каждом его шаге.
Шаг 1. Формирование КлШД K1.
Параметры каналов связи (pm1=10-2, pw=8·10-2).
L=3135 [дв.с.];
М+1=3 [дв.с.];
U=96 [дв.с.];
N=1023 [дв.с.];
K=1013 [дв.с.];
Y=3;
ε=8,3·10-3 [бит].
Оценка выполнения требований метода-прототипа (для первого шага):
Т1=64 [дв.с.];
Рнес1=1,63218·10-6;
Io1=1,97369·10-12 [бит];
Рε1=4,8762·10-6.
Длина передаваемых по каналам связи последовательностей равна
DLINA1=2,70296·105 [дв.с.].
Шаг 2. Формирование КлШД К2.
Параметры каналов связи (pm2=2·10-2, pw=8·10-2).
L=6594 [дв.с.];
М+1=4 [дв.с.];
U=516 [дв.с.];
N=1023 [дв.с.];
K=1013 [дв.с.];
Y=6;
ε=1,06·10-2 [бит].
Оценка выполнения требований метода-прототипа (для второго шага):
Т2=64 [дв.с.];
Рнес2=9,25321·10-8;
Io2=1,78335·10-13 [бит];
Рε2=4,37348·10-6.
Длина передаваемых по каналам связи последовательностей равна
DLINA2=4,15428·105 [дв.с.].
Шаг 3. Оценка длины передаваемой криптограммы С, равной Т [дв.с.].
Общая длина передаваемых по каналам связи последовательностей при формировании КлШД для СС определяется согласно (4.21):
DLINAp=6,19423·105 [дв.с.].
Сравнение длин передаваемых по каналам связи последовательностей DLINA и DLINAp показывает, что DLINAp больше в 2,29165 раза, чем DLINA. Тогда можно сделать вывод о том, что время формирования КлШД для СС посредством предлагаемого способа может быть меньше в 2,29165 раза по сравнению с временем формирования КлШД для СС посредством метода-прототипа с использованием способа-прототипа (при условии одинаковой скорости V[дв.с/с] в любом канале связи, показанном на фиг.1).
| название | год | авторы | номер документа |
|---|---|---|---|
| СПОСОБ ФОРМИРОВАНИЯ КЛЮЧА ШИФРОВАНИЯ / ДЕШИФРОВАНИЯ | 2021 |
|
RU2766319C1 |
| СПОСОБ ФОРМИРОВАНИЯ КЛЮЧЕЙ ШИФРОВАНИЯ/ДЕШИФРОВАНИЯ | 2023 |
|
RU2796051C1 |
| СПОСОБ ФОРМИРОВАНИЯ КЛЮЧА ШИФРОВАНИЯ/ДЕШИФРОВАНИЯ | 2016 |
|
RU2613845C1 |
| СПОСОБ ФОРМИРОВАНИЯ КЛЮЧА ШИФРОВАНИЯ / ДЕШИФРОВАНИЯ | 2021 |
|
RU2774103C1 |
| СПОСОБ ФОРМИРОВАНИЯ КЛЮЧА ШИФРОВАНИЯ / ДЕШИФРОВАНИЯ | 2020 |
|
RU2749016C1 |
| СПОСОБ ФОРМИРОВАНИЯ КЛЮЧА ШИФРОВАНИЯ/ДЕШИФРОВАНИЯ | 2019 |
|
RU2713694C1 |
| СПОСОБ ФОРМИРОВАНИЯ КЛЮЧА ШИФРОВАНИЯ/ДЕШИФРОВАНИЯ | 2000 |
|
RU2171012C1 |
| СПОСОБ ФОРМИРОВАНИЯ КЛЮЧА ШИФРОВАНИЯ/ДЕШИФРОВАНИЯ | 2000 |
|
RU2183051C2 |
| СПОСОБ ФОРМИРОВАНИЯ КЛЮЧА ШИФРОВАНИЯ/ДЕШИФРОВАНИЯ | 2000 |
|
RU2180770C2 |
| СПОСОБ ФОРМИРОВАНИЯ КЛЮЧА ШИФРОВАНИЯ/ДЕШИФРОВАНИЯ | 2000 |
|
RU2180469C2 |
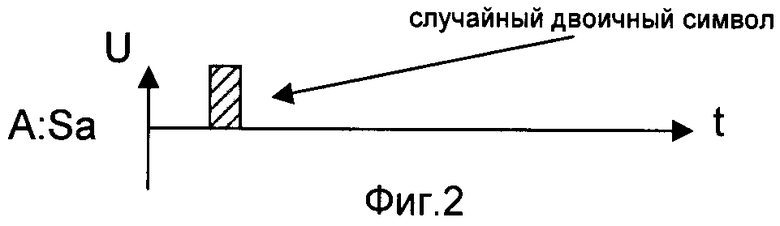
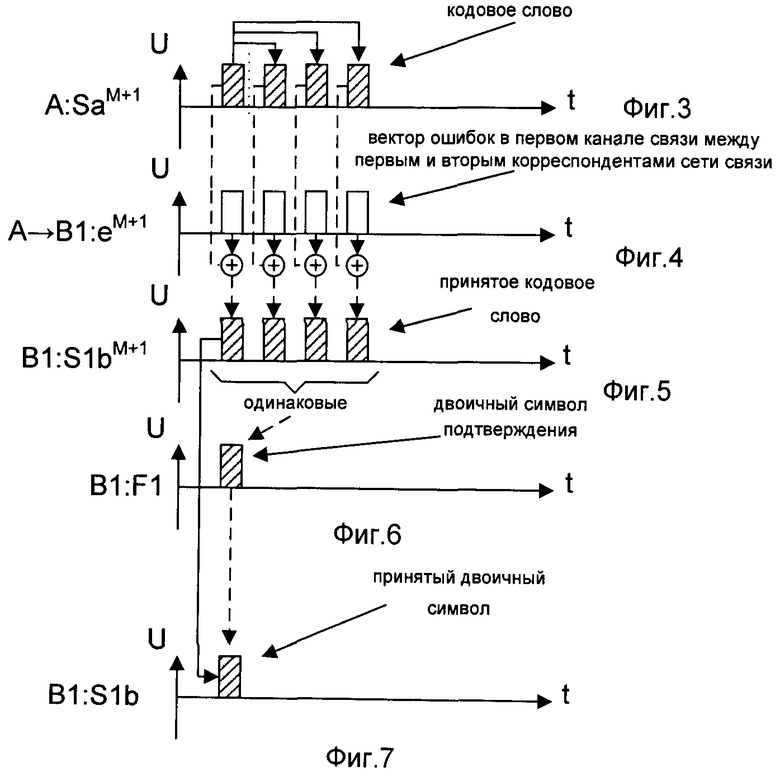
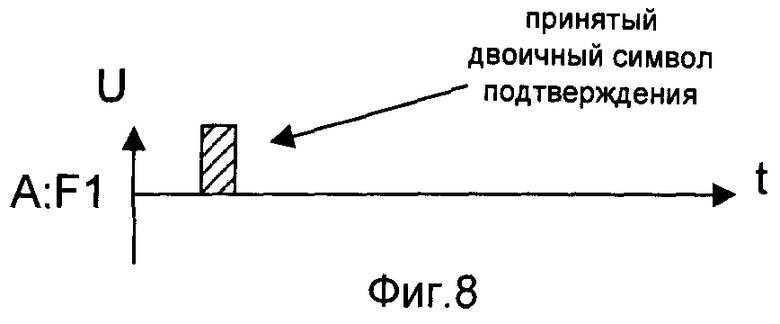
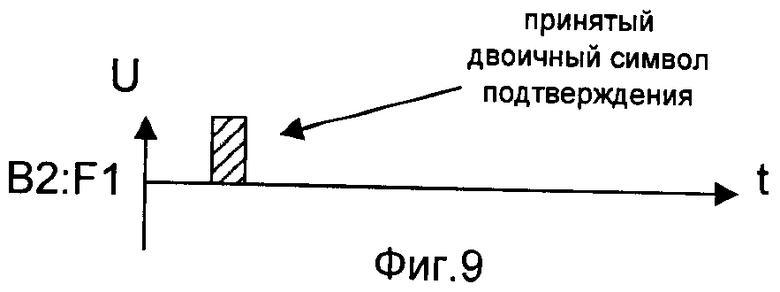
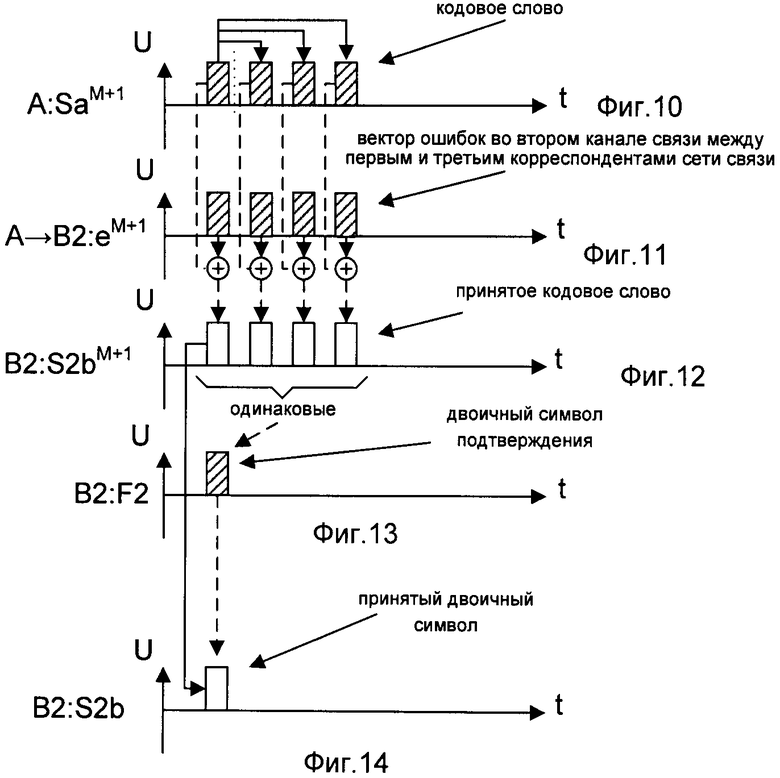
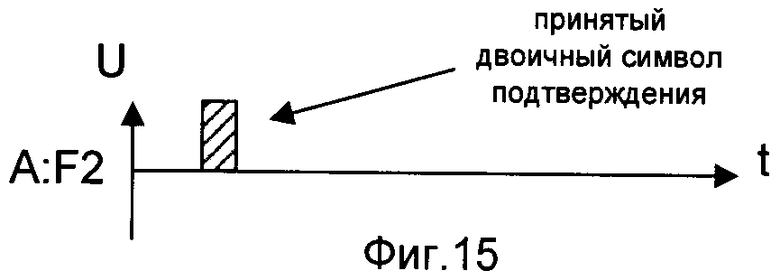
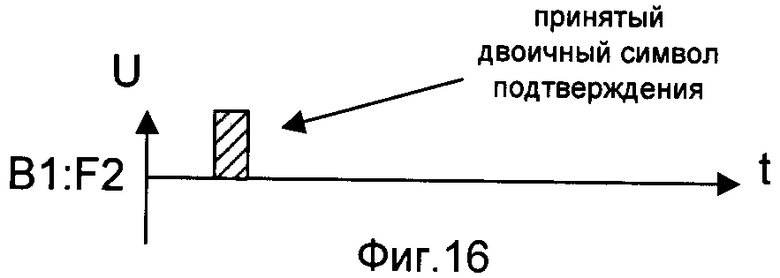
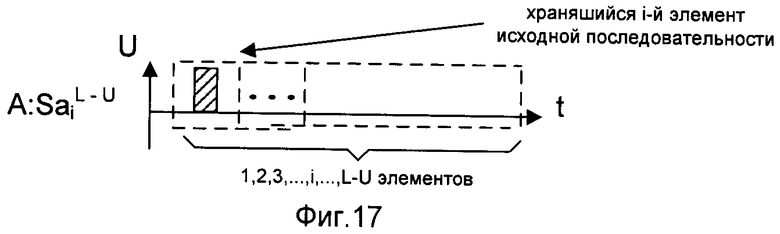
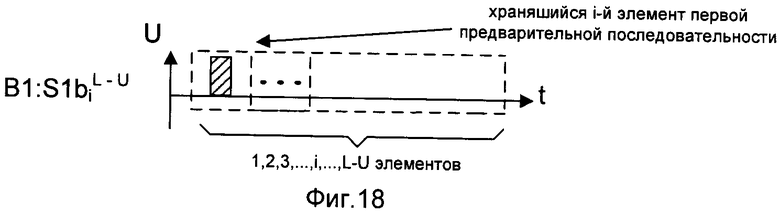
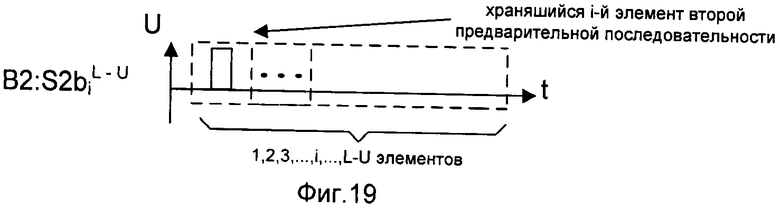
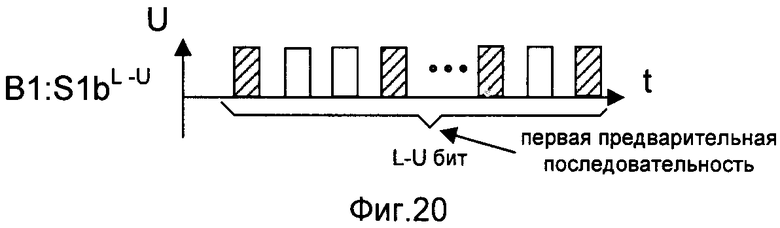

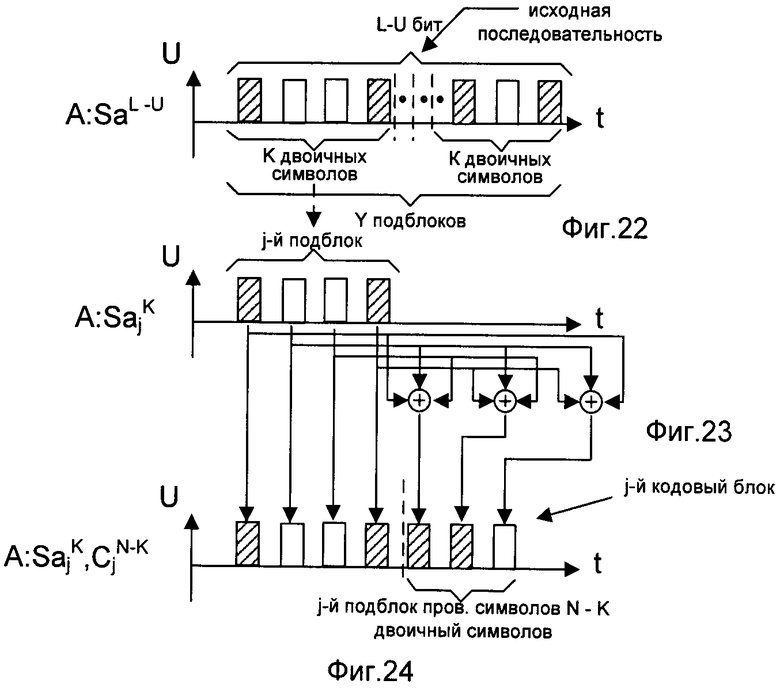
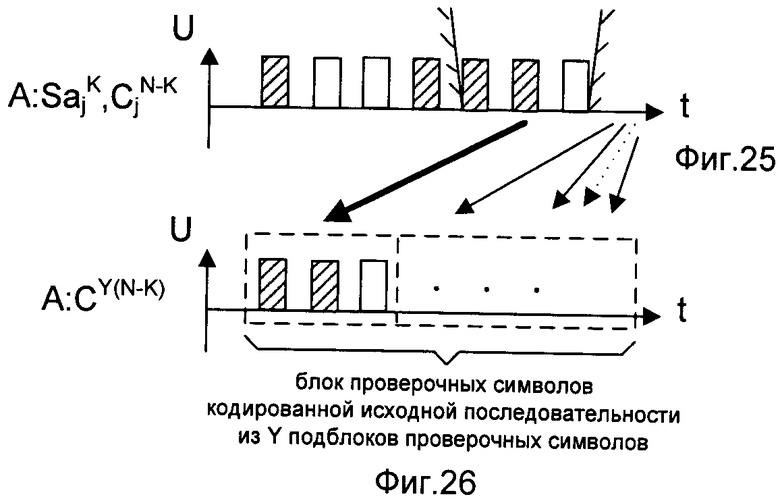
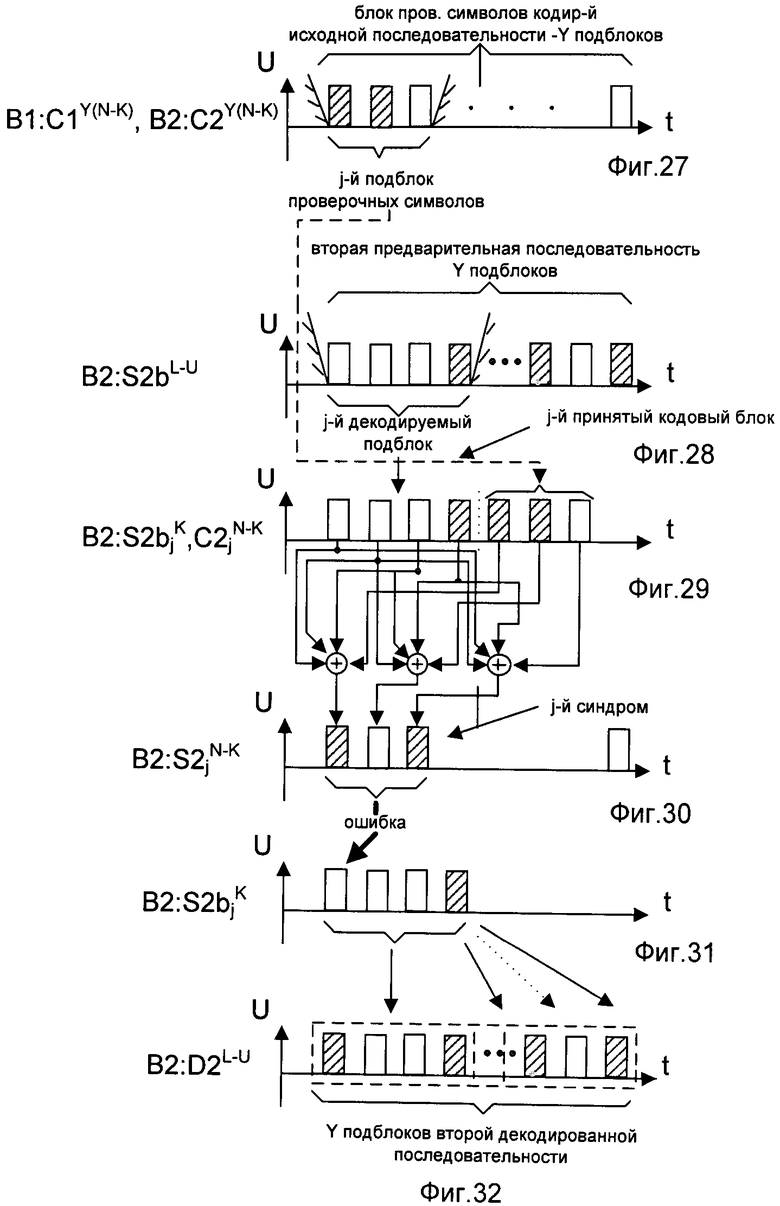
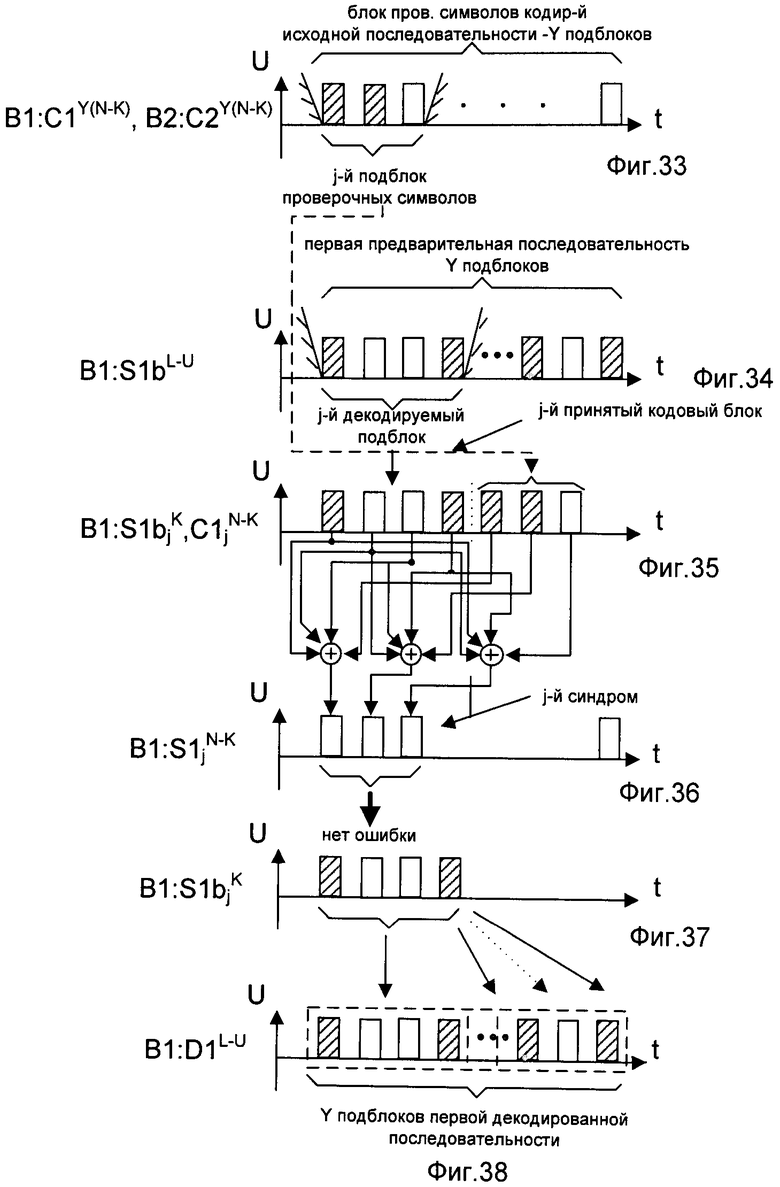
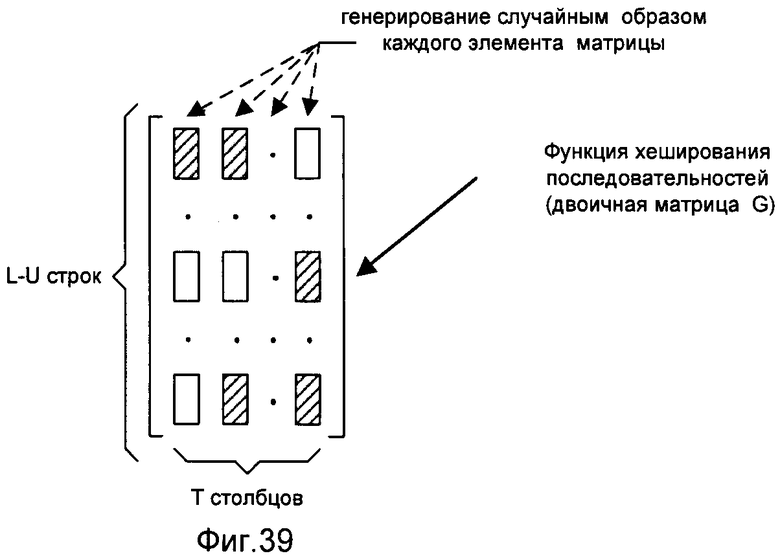
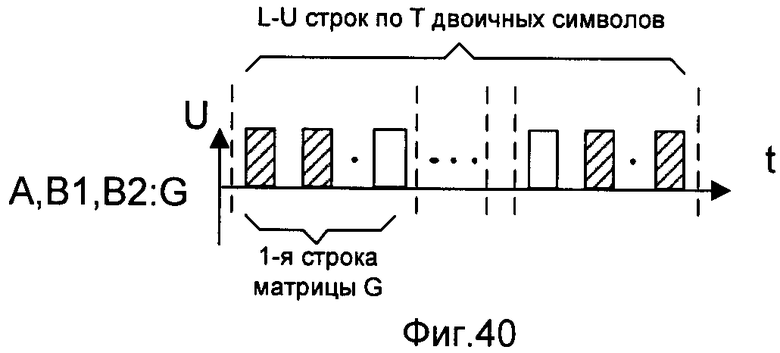
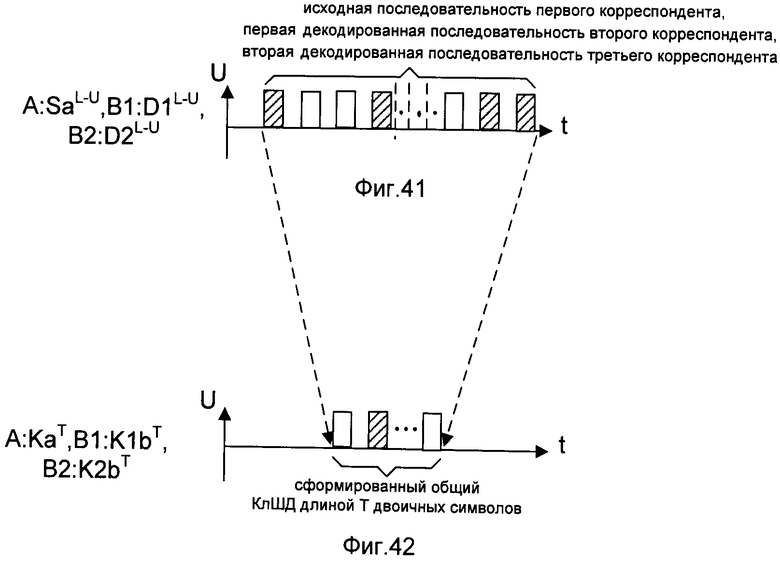
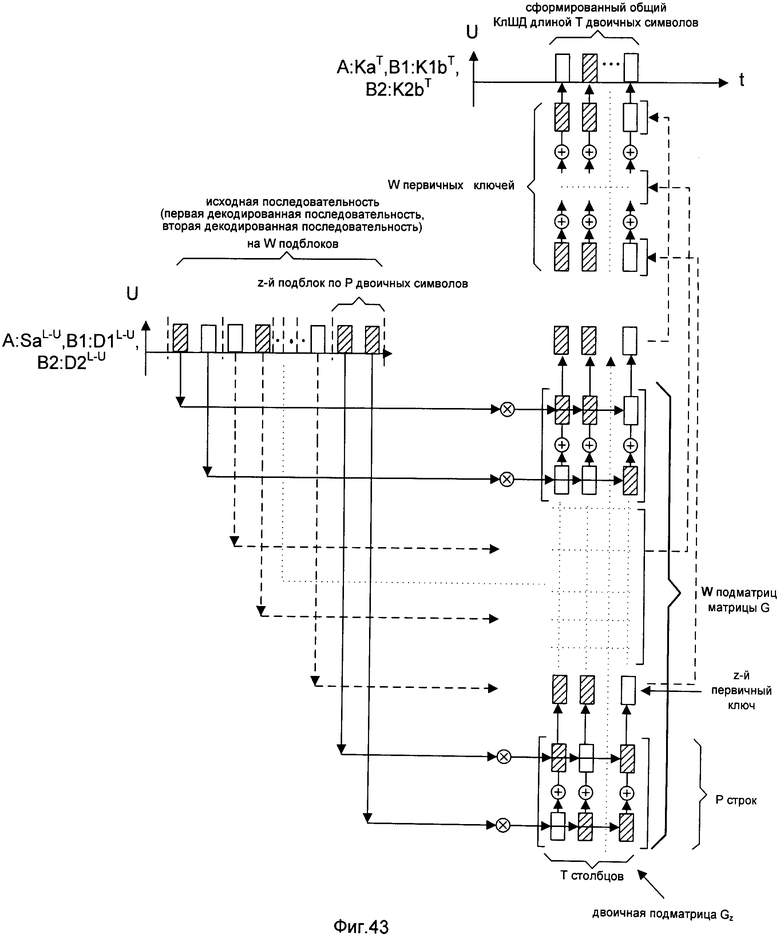
Изобретение относится к передаче данных, а именно к формированию ключа шифрования/дешифрования (K) для передачи данных. Техническим результатом является уменьшение времени формирования K для сети связи, включающей трех корреспондентов. Технический результат достигается тем, что способ формирования K предусматривает одновременное формирование исходной последовательности на стороне 1-го корреспондента сети связи и предварительных последовательностей на сторонах 2-го и 3-го корреспондентов, при этом сформированное 1-м корреспондентом сети связи кодовое слово одновременно передают по каналам связи с независимыми ошибками 2-му и 3-му корреспондентам сети связи соответственно, передают сформированный 2-м корреспондентом сети связи двоичный символ подтверждения по каналам связи без ошибок соответственно 1-му и 3-му корреспондентам сети связи, аналогичным образом передают сформированный 3-м корреспондентом сети связи двоичный символ подтверждения. Затем осуществляется кодирование исходной последовательности, выделение из нее блока проверочных символов, одновременная передача его по прямым каналам связи без ошибок 2-му и 3-му корреспондентам, одновременное формирование декодированных последовательностей 2-м и 3-м корреспондентами и одновременное формирование К всеми корреспондентами сети связи. 10 з.п. ф-лы, 43 ил., 4 прилож.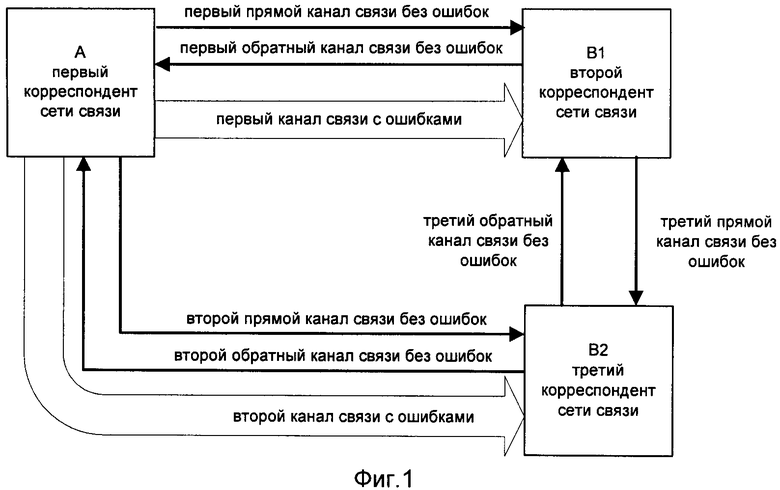
1. Способ формирования ключа шифрования/дешифрования, заключающийся в том, что генерируют случайный двоичный символ на стороне первого корреспондента, формируют из случайного двоичного символа кодовое слово, передают кодовое слово от первого корреспондента второму корреспонденту, формируют принятый двоичный символ, формируют двоичный символ подтверждения, передают двоичный символ подтверждения от второго корреспондента первому, формируют исходную и предварительную последовательности на сторонах первого и второго корреспондентов соответственно, кодируют исходную последовательность, выделяют из кодированной исходной последовательности блок проверочных символов, передают его от первого корреспондента второму, формируют и запоминают декодированную последовательность на стороне второго корреспондента, формируют функцию хеширования на стороне первого корреспондента, передают функцию хеширования от первого корреспондента второму, после чего формируют ключ шифрования/дешифрования из исходной и декодированной последовательностей на сторонах первого и второго корреспондентов соответственно, отличающийся тем, что ключ шифрования/дешифрования формируют одновременно для сети связи, включающей трех корреспондентов, сформированное первым корреспондентом сети связи кодовое слово одновременно передают по первому и второму каналам связи с независимыми ошибками второму и третьему корреспондентам сети связи соответственно, передают сформированный вторым корреспондентом сети связи двоичный символ подтверждения F1 по первому обратному и третьему прямому каналам связи без ошибок соответственно первому и третьему корреспондентам сети связи, передают сформированный третьим корреспондентом сети связи двоичный символ подтверждения F2 по второму обратному и третьему обратному каналам без ошибок первому и второму корреспондентам сети связи, при равенстве нулю, по крайней мере, одного из полученных двоичных символов подтверждения сгенерированный случайный двоичный символ первого корреспондента сети связи и принятые двоичные символы второго и третьего корреспондентов сети связи стирают, в противном случае запоминают сгенерированный случайный двоичный символ первого корреспондента сети связи, принятый двоичный символ второго корреспондента сети связи, принятый двоичный символ третьего корреспондента сети связи соответственно в качестве i-x элементов, где i=1, 2, 3, …, L-U, исходной последовательности, первой предварительной последовательности и второй предварительной последовательности, где L>103 - число генераций случайного двоичного символа; U - количество стертых символов при формировании исходной последовательности и предварительных последовательностей, причем одновременно передают блок проверочных символов кодированной исходной последовательности по первому прямому и второму прямому каналам связи без ошибок соответственно второму и третьему корреспондентам сети связи, после формирования исходной и декодированных последовательностей одновременно передают сформированную первым корреспондентом сети связи функцию хеширования последовательностей по первому прямому и второму прямому каналам связи без ошибок соответственно второму и третьему корреспондентам сети связи.
2. Способ по п.1, отличающийся тем, что для формирования кодового слова сгенерированный случайный двоичный символ повторяют М раз, где М≥1.
3. Способ по п.1, отличающийся тем, что принятому двоичному символу любого корреспондента сети связи присваивают значение первого двоичного символа принятого кодового слова.
4. Способ по п.1, отличающийся тем, что для независимого друг от друга и одновременного формирования двоичного символа подтверждения F1 второго корреспондента сети связи или двоичного символа подтверждения F2 третьего корреспондента сети связи соответственно первый двоичный символ принятого кодового слова сравнивают с последующими М двоичными символами принятого кодового слова, где М≥1 - число повторений сгенерированного случайного двоичного символа при формирования кодового слова, после чего при наличии М совпадений первого двоичного символа принятого кодового слова с М двоичными символами принятого кодового слова двоичному символу подтверждения F1 второго корреспондента или двоичному символу подтверждения F2 третьего корреспондента присваивают значение единица, а при наличии хотя бы одного несовпадения первого двоичного символа принятого кодового слова с М двоичными символами принятого кодового слова двоичному символу подтверждения F1 второго корреспондента или двоичному символу подтверждения F2 третьего корреспондента присваивают значение ноль.
5. Способ по п.1, отличающийся тем, что исходную последовательность кодируют линейным блоковым систематическим двоичным помехоустойчивым (N, K) кодом, где K - длина блока информационных символов, и N - длина кодового блока, порождающая матрица которого имеет размерность K×N, причем N>K, для чего предварительно исходную последовательность разделяют на Y подблоков длиной K двоичных символов, где Y=(L-U)/K, затем последовательно, начиная с первого до Y-го из каждого j-го подблока, где j=1, 2, 3, …, Y, формируют j-й кодовый блок длиной N двоичных символов перемножением j-го подблока на порождающую матрицу, затем из j-го кодового блока выделяют j-й подблок проверочных символов длиной N-K двоичных символов, который запоминают в качестве j-го подблока блока проверочных символов кодированной исходной последовательности.
6. Способ по п.5, отличающийся тем, что размеры K и N порождающей матрицы линейного блокового систематического двоичного помехоустойчивого (N, K) кода выбирают K=2m-1-m и N=2m-1, где m≥3.
7. Способ по п.1, отличающийся тем, что для формирования первой и второй декодированных последовательностей первую и вторую предварительные последовательности второго и третьего корреспондентов сети связи соответственно независимо и одновременно декодируют линейным блоковым систематическим двоичным помехоустойчивым (N, K) кодом, где K - длина блока информационных символов, и N - длина кодового блока, транспонированная проверочная матрица которого имеет размерность N×(N-K), причем N>K, для чего предварительные последовательности и блоки проверочных символов кодированной исходной последовательности разделяют на Y соответствующих пар декодируемых подблоков и подблоков проверочных символов, где Y=(L-U)/K, причем длины декодируемых подблоков и подблоков проверочных символов выбирают равными соответственно K и N-K двоичных символов, затем формируют Y принятых кодовых блоков длиной N двоичных символов путем конкатенации справа к j-му декодируемому подблоку j-го подблока проверочных символов, где j=l, 2, 3, …, Y, затем последовательно, начиная с 1-го до Y-го, вычисляют j-й синдром S длиной N-K двоичных символов перемножением j-го принятого кодового блока на транспонированную проверочную матрицу, а по полученному j-му синдрому S исправляют ошибки в j-м декодируемом подблоке, который затем запоминают в качестве j-го подблока декодированных последовательностей.
8. Способ по п.7, отличающийся тем, что выбирают размеры K и N проверочной матрицы линейного блокового систематического двоичного помехоустойчивого (N, K) кода K=2m-1-m и N=2m-1, где m≥3.
9. Способ по п.1, отличающийся тем, что функцию хеширования последовательностей на стороне первого корреспондента сети связи формируют в виде двоичной матрицы G размерности (L-U)×T, где Т≥64 - длина формируемого ключа шифрования/дешифрования, причем каждый из элементов двоичной матрицы G генерируют случайным образом.
10. Способ по п.1, отличающийся тем, что функцию хеширования последовательностей передают последовательно, начиная с первой по (L-U)-ю строки двоичной матрицы G.
11. Способ по п.1, отличающийся тем, что при одновременном формировании ключа шифрования/дешифрования предварительно двоичную матрицу G и исходную последовательность первого корреспондента сети связи, двоичную матрицу G и первую декодированную последовательность второго корреспондента сети связи, двоичную матрицу G и вторую декодированную последовательность третьего корреспондента сети связи разделяют на W соответствующих пар подматриц размерности Р×Т, где P=(L-U)/W, Т≥64 - длина формируемого ключа шифрования/дешифрования, и соответственно подблоков исходной последовательности, первой декодированной последовательности и второй декодированной последовательности длиной Р двоичных символов соответственно, затем одновременно, начиная с первого до W-й, вычисляют z-й первичный ключ длины Т двоичных символов, где z=1, 2, 3, …, W, перемножением z-го подблока исходной последовательности первого корреспондента сети связи на z-ю подматрицу Gz, z-го подблока первой декодированной последовательности второго корреспондента сети связи на z-ю подматрицу Gz, z-го подблока второй декодированной последовательности третьего корреспондента сети связи на z-ю подматрицу Gz, после чего одновременно формируют ключ шифрования/дешифрования путем поразрядного суммирования по модулю 2 всех W первичных ключей на сторонах всех корреспондентов сети связи.
| RU 2007118781 А, 27.11.2008 | |||
| RU 2004114316 А, 27.10.2005 | |||
| Пломбировальные щипцы | 1923 |
|
SU2006A1 |
| Станок для изготовления деревянных ниточных катушек из цилиндрических, снабженных осевым отверстием, заготовок | 1923 |
|
SU2008A1 |
| Пресс для выдавливания из деревянных дисков заготовок для ниточных катушек | 1923 |
|
SU2007A1 |
| Пресс для выдавливания из деревянных дисков заготовок для ниточных катушек | 1923 |
|
SU2007A1 |
| Способ приготовления лака | 1924 |
|
SU2011A1 |
Авторы
Даты
2013-04-27—Публикация
2012-02-21—Подача