По настоящей заявке на патент испрашивается приоритет по дате подачи предварительной заявки США № 60/816697, поданной 26 июня 2006, предварительной заявки США № 60/841362, поданной 30 августа 2006, предварительной заявки США № 60/847194, поданной 25 сентября 2006, предварительной заявки США № 60/829669, поданной 16 октября 2006, предварительной заявки США № 60/869530, поданной 11 декабря 2006, предварительной заявки США № 60/883932, поданной 8 января 2007, предварительной заявки США № 60/896778, поданной 23 марта 2007, и предварительной заявки США № 60/909335, поданной 30 марта 2007, которые полностью включены в настоящий документ в качестве ссылки.
Область техники, к которой относится изобретение
Это раскрытие относится к компьютерной графике и мультимедиа и, в частности к сжатию графики, изображений и видеоинформации.
Предшествующий уровень техники
Во многих существующих стандартах кодирования видео и изображения используются способы сжатия для обеспечения возможности сохранения или передачи видео и изображений с высоким разрешением как относительно компактных файлов или потоков данных. Такие стандарты кодирования включают в себя стандарт сжатия неподвижного изображения (JPEG), разработанный группой экспертов по видео, международный стандарт сжатия видео- и аудиоданных (MPEG)-1, MPEG-2, часть 2 MPEG-4, H.261, H.263 и другие стандарты кодирования видео или изображения.
Согласно многим из этих стандартов, видеокадры сжимают с использованием "пространственного" кодирования. Эти кадры могут быть исходными кадрами (то есть, i-кадрами) или могут быть остаточными кадрами, сформированными с временным кодированием, которое использует компенсацию движения. Во время пространственного кодирования кадры разбиваются на блоки пикселей равного размера. Например, несжатый кадр может быть разбит на ряд блоков пикселей 8×8. Для каждого блока пикселей, компоненты пикселя разделяются на матрицы значений компонента пикселя. Например, каждый блок пикселей может быть разделен на матрицу значений компонента пикселя Y, матрицу значений компонента пикселя U и матрицу значений компонента пикселя V. В этом примере, значения компонента пикселя Y указывают значения яркости и значения компонентов пикселя U и V представляют значения информации о цвете.
Кроме того, во время пространственного кодирования, к каждой матрице значений компонента пикселя в кодируемом кадре применяется прямое дискретное косинусное преобразование (FDCT). Идеальное одномерное FDCT определяется:
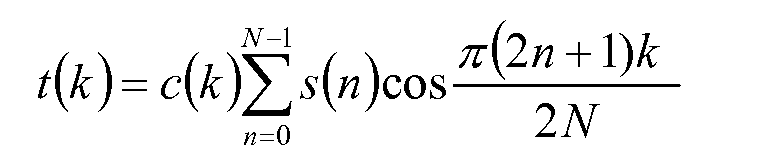
где s - массив N исходных значений, t - массив N преобразованных значений, и коэффициенты c задаются
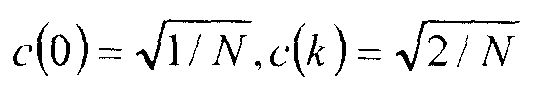
для 1≤k≤N-l.
Идеальное двумерное FDCT определяется формулой:
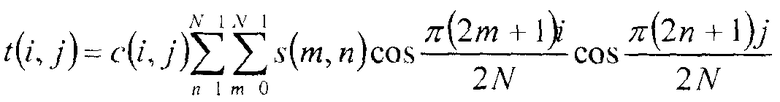
где s - массив N исходных значений, t - массив N преобразованных значений, и c(i,j) задается c(i,j)=c(i)c(j), и причем c(k) определяется, как в одномерном случае.
Матрица коэффициентов формируется при преобразовании блока значений компонента пикселя с использованием FDCT. Далее эту матрицу коэффициентов можно квантовать и кодировать с использованием, например, кодов Хаффмана или арифметических кодов. Битовый поток видео представляет объединенный результат выполнения этого процесса для всех блоков значений цветового компонента в последовательности видеокадров в несжатой последовательности видеокадров.
Несжатый видеокадр может быть получен из битового потока видео с изменением направления этого процесса на обратное. В частности, каждая матрица коэффициентов в битовом потоке восстанавливается из сжатых данных, и восстановленные из сжатых данных значения деквантуются для получения матрицы преобразованных коэффициентов. Далее к каждой матрице преобразованных коэффициентов применяется обратное дискретное косинусное преобразование ("IDCT") для получения матриц значений компонента пикселя. Идеальное одномерное IDCT определяется:
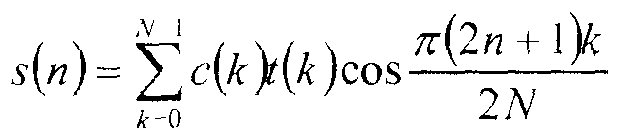
где s - массив N исходных значений, t - массив N преобразованных значений, и коэффициенты c задаются
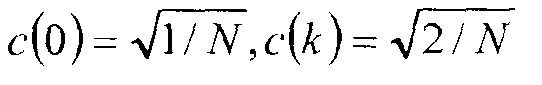
для 1≤k≤N-l.
Идеальное двумерное IDCT определяется формулой:
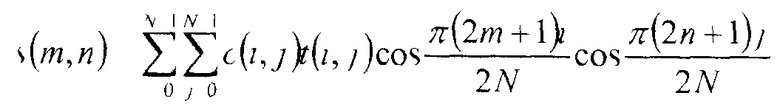
Далее получающиеся в результате матрицы значений компонента пикселя заново собираются в блоки пикселей, и эти блоки пикселей заново собираются для формирования декодированного кадра. Если декодированный кадр является i-кадром, то этот кадр теперь полностью декодирован. Однако если несжатый кадр является прогнозированным или бипрогнозированным кадром, то декодированный кадр является только декодированным остаточным кадром. Законченный кадр формируется с созданием восстановленного кадра с использованием векторов движения, связанных с декодированным кадром, и последующего суммирования восстановленного кадра с декодированным остаточным кадром.
При идеальных обстоятельствах информация не теряется при использовании FDCT для кодирования или IDCT для декодирования блока значений компонента пикселя. Следовательно, при этих идеальных обстоятельствах, декодированная версия видеокадра идентична исходной версии видеокадра. Однако вычисление FDCT или IDCT может быть в вычислительном отношении трудным, потому что вычисление преобразований FDCT и IDCT подразумевает использование вещественных чисел и значительное количество операций умножения. Поэтому вещественные числа, используемые в преобразованиях FDCT и IDCT, часто аппроксимируются с использованием чисел с ограниченной точностью. В результате использования чисел с ограниченной точностью для представления значений вещественных чисел получаются ошибки округления. Кроме того, дополнительные ошибки могут вноситься квантованием и деквантованием.
Ошибки в процессе сжатия и восстановления из сжатых данных могут в результате привести к существенным различиям между исходным несжатым кадром и конечным несжатым кадром. Например, цвета в конечном несжатом кадре могут отличаться от цветов в исходном несжатом кадре. Кроме того, ошибки, вызванные рассогласованием между реализацией преобразований IDCT в кодере и реализацией IDCT в декодере, могут накапливаться во время кодирования и декодирования последовательностей прогнозированных кадров. Эти накопленные ошибки обычно называются "дрейфом IDCT".
Сущность изобретения
Описаны способы аппроксимации вычисления обратного дискретного косинусного преобразования с использованием вычислений с фиксированной запятой. Согласно этим способам, матрицы масштабированных коэффициентов формируются умножением коэффициентов в матрицах закодированных коэффициентов на масштабные множители. Затем, с добавлением значения смещения центра к коэффициенту DC матрицы масштабированных коэффициентов формируются матрицы смещенных коэффициентов. Далее используются арифметические операции с фиксированной запятой для применения преобразования к матрицам смещенных коэффициентов. После этого значения в получающихся в результате матрицах сдвигаются вправо для получения матриц значений компонента пикселя. Матрицы значений компонента пикселя затем объединяются для создания матриц пикселей. Матрицы пикселей, сформированные этими способами, близко напоминают матрицы пикселей, восстановленные из сжатых данных с использованием идеального обратного дискретного косинусного преобразования ("IDCT").
В одном аспекте, способ содержит масштабирование каждого коэффициента в матрице закодированных коэффициентов, 8×8, одним из множителя A, множителя B, множителя C, множителя D, множителя E, множителя F, множителя G, множителя H, множителя I или множителя J для формирования матрицы масштабированных коэффициентов. В этом способе, A=1024, B=1138, C=1730, D=1609, E=1264, F=1922, G=1788, H=2923, I=2718 и J=2528. Способ также содержит использование повторных применений масштабированного одномерного преобразования с фиксированной запятой для преобразования матрицы масштабированных коэффициентов в матрицу преобразованных коэффициентов. Кроме того, способ содержит сдвиг вправо преобразованных коэффициентов в матрице преобразованных коэффициентов для формирования матрицы скорректированных коэффициентов. Каждый скорректированный коэффициент в матрице скорректированных коэффициентов аппроксимирует соответствующее значение в матрице значений, которые можно сформировать с применением идеального двумерного IDCT к матрице закодированных коэффициентов. Кроме того, способ содержит отображение блока пикселей, 8×8. Каждый пиксель в блоке пикселей, 8×8, включает в себя значение компонента пикселя на основе скорректированного коэффициента в матрице скорректированных коэффициентов.
В другом аспекте, устройство содержит модуль масштабирования, который масштабирует каждый коэффициент в матрице закодированных коэффициентов, 8×8, одним из множителя A, множителя B, множителя C, множителя D, множителя E, множителя F, множителя G, множителя H, множителя I или множителя J для формирования матрицы масштабированных коэффициентов, причем A=1024, B=1138, C=1730, D=1609, E=1264, F=1922, G=1788, H=2923, I=2718 и J=2528. Устройство также содержит модуль обратного преобразования, который использует повторные применения масштабированного одномерного преобразования с фиксированной запятой для преобразования матрицы масштабированных коэффициентов в матрицу преобразованных коэффициентов. Кроме того, устройство содержит модуль сдвига вправо, который сдвигает вправо преобразованные коэффициенты в матрице преобразованных коэффициентов для формирования матрицы скорректированных коэффициентов. Каждый скорректированный коэффициент в матрице скорректированных коэффициентов аппроксимирует соответствующее значение в матрице значений, которые можно сформировать с применением идеального двумерного IDCT к матрице закодированных коэффициентов. Устройство также содержит модуль вывода, который выводит блок пикселей, 8×8. Каждый пиксель в блоке пикселей включает в себя значение компонента пикселя на основе скорректированного коэффициента в матрице скорректированных коэффициентов.
В другом аспекте, устройство содержит средство для масштабирования коэффициентов в матрице закодированных коэффициентов, 8×8, одним из множителя A, множителя B, множителя C, множителя D, множителя E, множителя F, множителя G, множителя H, множителя I или множителя J для формирования матрицы масштабированных коэффициентов, причем A=1024, B=1138, C=1730, D=1609, E=1264, F=1922, G=1788, H=2923, I=2718 и J=2528. Кроме того, устройство содержит средство для использования повторных применений масштабированного одномерного преобразования с фиксированной запятой для преобразования матрицы масштабированных коэффициентов в матрицу преобразованных коэффициентов. Кроме того, устройство содержит средство для сдвига вправо преобразованных коэффициентов в матрице преобразованных коэффициентов для формирования матрицы скорректированных коэффициентов. Каждый скорректированный коэффициент в матрице скорректированных коэффициентов аппроксимирует соответствующее значение в матрице значений, которые можно сформировать с применением идеального двумерного IDCT к матрице закодированных коэффициентов. Кроме того, устройство содержит средство для вывода блока пикселей, 8×8. Каждый пиксель в блоке пикселей включает в себя значение компонента пикселя на основе скорректированного коэффициента в матрице скорректированных коэффициентов.
В другом аспекте, изобретение ориентировано на машиночитаемый носитель информации, содержащий команды. Эти команды вызывают масштабирование программируемым процессором каждого коэффициента в матрице закодированных коэффициентов, 8×8, одним из множителя A, множителя B, множителя C, множителя D, множителя E, множителя F, множителя G, множителя H, множителя I или множителя J для формирования матрицы масштабированных коэффициентов, причем A=1024, B=1138, C=1730, D=1609, E=1264, F=1922, G=1788, H=2923, I=2718 и J=2528. Команды также вызывают использование повторных применений масштабированного одномерного преобразования с фиксированной запятой программируемым процессором для преобразования матрицы масштабированных коэффициентов в матрицу преобразованных коэффициентов. Кроме того, команды вызывают сдвиг вправо программируемым процессором преобразованных коэффициентов в матрице преобразованных коэффициентов для формирования матрицы скорректированных коэффициентов. Каждый скорректированный коэффициент в матрице скорректированных коэффициентов аппроксимирует соответствующее значение в матрице значений, которые можно сформировать с применением идеального двумерного IDCT к матрице закодированных коэффициентов. Команды также вызывают вывод программируемым процессором сигналов, которые вызывают отображение устройством отображения блока пикселей, 8×8. Каждый пиксель в блоке пикселей включает в себя значение компонента пикселя на основе скорректированного коэффициента в матрице скорректированных коэффициентов.
В некоторых случаях, машиночитаемый носитель информации может являться частью компьютерного программного продукта, который может быть продан изготовителям и/или использоваться в устройстве кодирования видео. Компьютерный программный продукт может включать в себя машиночитаемый носитель информации и в некоторых случаях может также включать в себя упаковочные материалы.
В нижеследующем описании и прилагаемых чертежах подробно изложены один или несколько примеров. Другие признаки, цели и преимущества изобретения будут очевидны из упомянутых описания и чертежей и из формулы изобретения.
Краткое описание чертежей
Фиг.1 - блок-схема, изображающая иллюстративное устройство, которое кодирует и декодирует файлы мультимедиа.
Фиг.2 - блок-схема, изображающая иллюстративные детали модуля кодирования.
Фиг.3 - блок-схема, изображающая иллюстративные детали модуля декодирования.
Фиг.4 - блок-схема, изображающая иллюстративную работу модуля кодирования.
Фиг.5 - блок-схема, изображающая иллюстративную работу модуля декодирования.
Фиг.6 - блок-схема, изображающая иллюстративные детали модуля обратного дискретного косинусного преобразования ("IDCT").
Фиг.7 - блок-схема, изображающая иллюстративную работу модуля обратного преобразования.
Фиг.8 - блок-схема, изображающая иллюстративные детали модуля прямого дискретного косинусного преобразования ("FDCT").
Фиг.9 - блок-схема, изображающая иллюстративную работу модуля прямого преобразования вектора.
Фиг.10A - блок-схема, изображающая иллюстративное одномерное преобразование.
Фиг.10В - блок-схема, изображающая иллюстративное масштабированное одномерное преобразование.
Фиг.11 - блок-схема, изображающая иллюстративное масштабированное одномерное преобразование, используемое модулем обратного преобразования.
Подробное описание
Фиг.1 является блок-схемой, изображающей иллюстративное устройство 2, которое кодирует и декодирует файлы мультимедиа. Устройство 2 может содержать персональный компьютер, мобильный радиотелефон, сервер, сетевое устройство, компьютер, встроенный в транспортное средство, видеоигровую платформу, переносное видеоигровое устройство, автоматизированное рабочее место, компьютерный киоск, цифровой идентификационный комплект, универсальный компьютер, телевизионную приставку, сетевой телефон, персонального цифрового секретаря, видеоигровую платформу, мобильный медиаплеер, бытовой медиаплеер, цифровой видеопроектор, личный медиаплеер (например, iPod) или другой тип электронного устройства.
Устройство 2 может включать в себя источник 4 мультимедиа для формирования мультимедийных данных. Источник 4 мультимедиа может содержать цифровую видео- или фотокамеру для ввода данных изображения. Источник 4 мультимедиа может быть встроен в устройство 2 или может быть присоединен к устройству 2 как периферийное устройство. Источник 4 мультимедиа может также содержать микрофон для записи аудиоданных. Источник 4 мультимедиа может обеспечивать мультимедийные данные в процессор 6. Процессор 6 может содержать цифровой сигнальный процессор (DSP), микропроцессор или некоторый другой тип интегральной схемы.
Когда процессор 6 принимает мультимедийные данные из источника 4 мультимедиа, модуль 8 кодирования может кодировать мультимедийные данные. Модуль 8 кодирования может содержать программные средства, исполняемые процессором 6. В качестве альтернативы, модуль 8 кодирования может содержать специализированные аппаратные средства в процессоре 6, который кодирует мультимедийные данные. В еще одном альтернативном варианте, модуль 8 кодирования может содержать любую комбинацию программных и аппаратных средств для кодирования мультимедийных данных.
Модуль 8 кодирования может сохранять закодированные мультимедийные данные в репозитории 10 мультимедиа. Репозиторий 10 мультимедиа может содержать флэш-память, оперативное запоминающее устройство, накопитель на жестких дисках или некоторый другой тип энергозависимого или энергонезависимого блока хранения данных.
Модуль 12 декодирования может извлекать закодированные мультимедийные данные из репозитория 10 мультимедиа. Модуль 12 декодирования может содержать программные средства, исполняемые процессором 6. В качестве альтернативы, модуль 12 декодирования может содержать специализированные аппаратные средства в процессоре 6, который декодирует закодированные мультимедийные данные. В еще одном альтернативном варианте, модуль 12 декодирования может содержать комбинацию программных и аппаратных средств, которые совместно функционируют для декодирования закодированных мультимедийных данных.
Блок 14 воспроизведения мультимедиа в устройстве 2 может воспроизводить мультимедийные данные, декодированные модулем 12 декодирования. Например, блок 14 воспроизведения мультимедиа может содержать компьютерный монитор, который воспроизводит мультимедийные данные видео или изображения. В другом примере, блок 14 воспроизведения мультимедиа может содержать устройство вывода аудио (например, динамик), которое воспроизводит звуковые мультимедийные данные аудио. Блок 14 воспроизведения мультимедиа может быть интегрирован в устройство 2 или может быть связан с ним через проводную или беспроводную линию связи как периферийное устройство.
Устройство 2 может также содержать сетевой интерфейс 16. Сетевой интерфейс 16 может обеспечивать связь между устройством 2 и компьютерной сетью через проводную или беспроводную линию связи. Например, сетевой интерфейс 16 может обеспечивать связь между устройством 2 и сетью мобильной радиотелефонной связи. Устройство 2 может принимать файлы мультимедиа через сетевой интерфейс 16. Например, устройство 2 может принимать фотографии, видеоклипы, потоковое видео (например, телевидение, видеоконференцию, кинофильмы), аудиоклипы (например, мелодии для звонка, песни, файлы MP3), потоковое аудио (например, цифровые радиостанции, речевые вызовы и т.д.) через сетевой интерфейс 16. Когда сетевой интерфейс 16 принимает битовый поток видео или файла мультимедиа, сетевой интерфейс 16 может сохранять этот битовый поток видео или файла мультимедиа в репозитории 10 мультимедиа.
Видеосигнал может быть описан в терминах последовательности изображений, которые включают в себя кадры (все изображение), или области (например, изображение, которое содержит или нечетные или четные строки кадра). Кроме того, каждый кадр или область могут включать в себя два или большее количество вырезок или субфрагментов кадра или области. Термин "кадр", используемый в этом документе, или один или в комбинации с другими словами, может относиться к изображению, кадру, области или их слою.
Когда модуль 8 кодирования кодирует последовательность видеокадров, модуль 8 кодирования может начинать с выбора тех видеокадров, которые должны быть "i-кадрами". Например, модуль 8 кодирования может выбирать каждый восьмой кадр как i-кадр. I-кадры являются кадрами, которые не ссылаются на другие кадры. После выбора i-кадров, модуль 8 кодирования использует "пространственное кодирование" для кодирования i-кадров. Кроме того, модуль 8 кодирования может использовать "временное кодирование" для кодирования оставшихся кадров.
Для использования пространственного кодирования для кодирования кадра, модуль 8 кодирования может разбивать данные кадра на блоки пикселей. Например, модуль 8 кодирования может разбивать данные кадра на блоки пикселей, шириной в восемь пикселей и высотой в восемь пикселей (то есть, каждый блок пикселей содержит 64 пикселя). После этого модуль 8 кодирования может разделять значения компонента пикселя из пикселей в каждом блоке пикселей на отдельные матрицы значений компонента пикселя. Значения компонента пикселя одного пикселя являются значениями, которые характеризуют вид пикселя. Например, каждый пиксель может специфицировать значение компонента пикселя Y, значение компонента пикселя Cr и значение компонента пикселя Cb. Значение компонента пикселя Y указывает яркость пикселя, значение компонента пикселя Cr указывает информацию о красном цвете пикселя, и значение компонента пикселя Cb указывает информацию о синем цвете пикселя. В этом примере, когда модуль 8 кодирования разделяет значения компонента пикселя из блока пикселей, модуль 8 кодирования может получать матрицу значений компонента пикселя Y, матрицу значений компонента пикселя Cr и матрицу значений компонента пикселя Cb.
После разделения значений компонентов пикселя в матрицы значений компонента пикселя, со сдвигом влево значений компонента пикселя в матрицах значений компонента пикселя, модуль 8 кодирования формирует матрицы скорректированных коэффициентов. Для каждой матрицы скорректированных коэффициентов, модуль 8 кодирования использует арифметические операции с фиксированной запятой для повторного применения одномерного преобразования к матрице скорректированных коэффициентов, тем самым формируя матрицы преобразованных коэффициентов. Затем модуль 8 кодирования формирует матрицу масштабированных коэффициентов путем масштабирования матрицы преобразованных коэффициентов набором масштабных множителей. Каждый из этих масштабных множителей является целочисленным значением. Масштабные множители были выбраны так, что множители в одномерном преобразовании могут быть аппроксимированы с использованием простых рациональных чисел.
Каждый масштабированный коэффициент в матрице масштабированных коэффициентов аппроксимирует соответствующее значение в матрице значений, которые формируются с применением идеального двумерного прямого дискретного косинусного преобразования ("FDCT") к соответствующей матрице значений цветового компонента. Идеальное одномерное FDCT определяется:
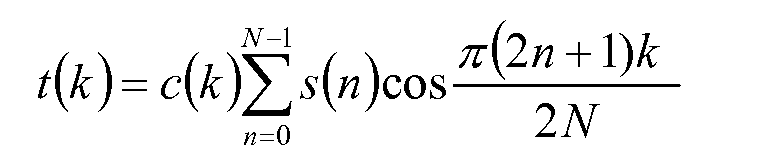
где s - массив N исходных значений, t - массив N преобразованных значений, и коэффициенты c задаются
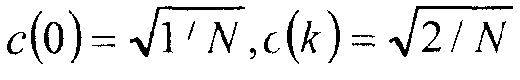
для 1≤k≤N-l.
Идеальное двумерное FDCT определяется формулой:
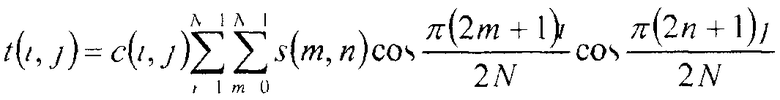
где s - массив N исходных значений, t - массив N преобразованных значений, и c(i,j) задается c(i,j)=c(i)c(j), и причем c(k) определяется, как в одномерном случае.
После получения матрицы масштабированных коэффициентов, модуль 8 кодирования формирует матрицу квантованных коэффициентов путем квантования коэффициентов в матрице масштабированных коэффициентов. Квантование масштабированных коэффициентов может уменьшать количество информации, связанной с высокочастотными коэффициентами в матрице масштабированных коэффициентов. После формирования матрицы квантованных коэффициентов, модуль 8 кодирования может применять схему энтропийного кодирования к матрице квантованных коэффициентов. Например, модуль 8 кодирования может применять схему кодирования методом Хаффмана к квантованным коэффициентам в матрице коэффициентов. Когда модуль 8 кодирования применяет схему энтропийного кодирования к каждой из матриц квантованных коэффициентов, модуль 8 кодирования может выводить закодированные матрицы как часть битового потока видео.
Для использования временного кодирования для кодирования кадра, модуль 8 кодирования может разделять кадр на "макроблоки". В зависимости от используемого стандарта кодирования, эти макроблоки могут иметь фиксированный или переменный размер и могут быть перекрывающимися или неперекрывающимися. Например, каждый макроблок может быть блоком пикселей 16×16. Для каждого макроблока в кадре, модуль 8 кодирования может пытаться идентифицировать исходный макроблок в одном или нескольких опорных кадрах. В зависимости от стандарта кодирования, опорные кадры могут быть i-кадрами, прогнозированными кадрами или бипрогнозированными кадрами. Если модуль 8 кодирования может идентифицировать исходный макроблок в опорном кадре, то модуль 8 кодирования записывает вектор движения для этого макроблока. Вектор движения включает в себя значение x, которое указывает горизонтальное перемещение макроблока относительно идентифицированного исходного макроблока, и значение y, которое указывает вертикальное перемещение макроблока относительно идентифицированного исходного макроблока. Если модуль 8 кодирования не способен идентифицировать исходный макроблок для упомянутого макроблока, то может не потребоваться запись вектора движения модулем 8 кодирования для этого макроблока. Затем, модуль 8 кодирования формирует "восстановленный" кадр. Восстановленный кадр содержит кадр, который получается в результате перемещения макроблоков из опорных кадров согласно записанным векторам движения для текущего кадра. После формирования восстановленного кадра, модуль 8 кодирования вычитает значения компонента пикселя в каждом пикселе восстановленного кадра из соответствующих значений компонента пикселя в соответствующих пикселях текущего кадра, в результате чего получается "остаточный" кадр. После этого модуль 8 кодирования может использовать схему энтропийного кодирования для сжатия векторов движения для макроблоков текущего кадра. Кроме того, модуль 8 кодирования использует описанный выше способ пространственного кодирования для сжатия остаточного кадра.
Модуль 12 декодирования может выполнять процесс, аналогичный процессу модуля 8 кодирования, но в обратном порядке. Например, для выполнения пространственного декодирования, модуль 12 декодирования может применять схему энтропийного декодирования к каждой закодированной матрице квантованных коэффициентов в закодированном битовом потоке видео. После этого модуль 12 декодирования может деквантовать коэффициенты в каждой матрице квантованных коэффициентов, тем самым формируя матрицу деквантованных коэффициентов для каждой матрицы квантованных коэффициентов. Для каждой матрицы квантованных коэффициентов, с масштабированием матрицы квантованных коэффициентов с использованием набора масштабных множителей модуль 12 декодирования формирует матрицу масштабированных коэффициентов. Эти масштабные множители могут быть масштабными множителями, идентичными масштабным множителям, используемым в упомянутом выше пространственном кодировании. После формирования матрицы масштабированных коэффициентов, модуль 12 декодирования использует арифметические операции с фиксированной запятой для повторного применения одномерного преобразования к матрице квантованных коэффициентов, тем самым формируя матрицу преобразованных коэффициентов. Например, модуль 12 декодирования может формировать матрицу промежуточных коэффициентов с применением одномерного преобразования к каждой вектор-строке в матрице масштабированных коэффициентов. В этом примере, модуль 12 декодирования после этого может формировать матрицу преобразованных коэффициентов с применением одномерного преобразования к каждому вектор-столбцу в матрице промежуточных коэффициентов. После формирования матрицы преобразованных коэффициентов, со сдвигом вправо преобразованных коэффициентов в матрице преобразованных коэффициентов модуль 12 декодирования формирует матрицу скорректированных коэффициентов.
Скорректированные коэффициенты в матрице скорректированных коэффициентов аппроксимируют значения, которые формируются с применением идеального двумерного обратного дискретного косинусного преобразования ("IDCT") к матрице деквантованных коэффициентов. Идеальное одномерное IDCT определяется формулой:
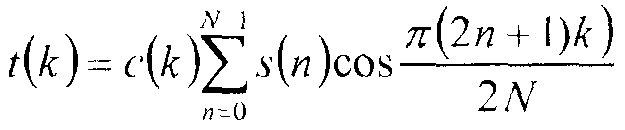
где s - массив N исходных значений, t - массив N преобразованных значений, и коэффициенты c задаются
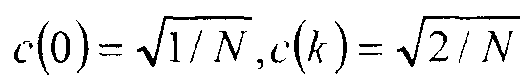
для 1≤k≤N-l.
Идеальное двумерное IDCT определяется формулой:
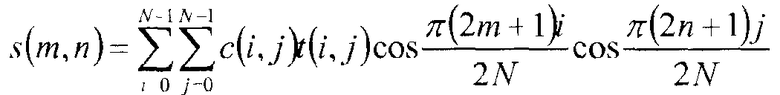
Эти блоки значений компонента пикселя могут затем заново быть собраны в блоки пикселей, и эти блоки пикселей могут заново быть собраны для формирования несжатого видеокадра.
После формирования матрицы скорректированных коэффициентов, модуль 12 декодирования может затем ограничивать скорректированные коэффициенты в матрице скорректированных коэффициентов для обеспечения нахождения скорректированных коэффициентов в пределах диапазона, допустимого для значения компонента пикселя. Модуль 12 декодирования может затем заново собирать матрицы ограниченных коэффициентов в блоки пикселей. После сборки заново блоков значений компонента пикселя в блоки пикселей, со сборкой заново блоков пикселей модуль 12 декодирования может формировать изображение.
Для декодирования прогнозированного кадра, модуль 12 декодирования может использовать способ пространственного декодирования, описанный выше, для декодирования матриц квантованных коэффициентов в остаточном изображении для прогнозированного кадра. Кроме того, модуль 12 декодирования может использовать схему энтропийного декодирования для декодирования векторов движения прогнозированного кадра. Затем, с "перемещением" макроблоков опорных кадров прогнозированного кадра согласно векторам движения модуль 12 декодирования может формировать восстановленный кадр. После формирования восстановленного кадра, модуль 12 декодирования суммирует значения компонента пикселя в каждом пикселе декодированного остаточного кадра с соответствующими значениями компонента пикселя в соответствующих пикселях восстановленного кадра. Результатом этого суммирования является восстановленный прогнозированный кадр.
Способы, описанные в этом раскрытии, могут обеспечить несколько преимуществ. Например, так как в этих способах применяются арифметические операции с фиксированной запятой, то эти способы могут применяться в меньших, менее сложных устройствах, например, мобильных телефонах, персональных цифровых секретарях и личных медиаплеерах. Кроме того, эти способы могут быть применены к форматам, которые включают в себя рекомендации H.261, H.263, H.264, T.81 (JPEG) сектора стандартизации (электросвязи) Международного союза электросвязи (ITU-T), а также форматы мультимедиа Международной организации по стандартизации (ISO)/MEC Группы экспертов по видео (MPEG)-1, MPEG-2 и Части 2 MPEG-4.
Фиг.2 является блок-схемой, изображающей иллюстративные детали модуля 8 кодирования. Модуль 8 кодирования может содержать набор "модулей". Эти модули могут содержать подмножества программных команд модуля 8 кодирования. В качестве альтернативы, эти модули могут содержать программно-аппаратные средства, аппаратные средства, например, одно или несколько специализированных аппаратных средств. В другом альтернативном варианте, эти модули могут содержать программные команды и специализированные аппаратные средства или программно-аппаратные средства.
Как изображено в примере фиг.2, модуль 8 кодирования включает в себя модуль 20 управления кадром, который управляет тем, обрабатывает ли модуль 8 кодирования видеокадр как i-кадр, прогнозированный кадр или бипрогнозированный кадр. Например, когда модуль 8 кодирования принимает видеокадр, модуль 20 управления кадром может устанавливать, указывает ли флажок битового потока, связанный с этим видеокадром, что кадр является i-кадром, прогнозированным кадром или бипрогнозированным кадром. Если модуль 20 управления кадром устанавливает, что флажок битового потока указывает, что кадр является i-кадром, то модуль 20 управления кадром может вызвать обработку видеокадра набором модулей, которые непосредственно выполняют пространственное кодирование видеокадра. С другой стороны, если модуль 20 управления кадром устанавливает, что кадр является прогнозированным кадром или бипрогнозированным кадром, то модуль 20 управления кадром может вызвать обработку видеокадра набором модулей, которые выполняют временное кодирование.
Модуль 8 кодирования включает в себя последовательность модулей для применения пространственного кодирования к видеокадрам. Эти модули включают в себя модуль 22 разделителя на блоки, модуль 24 выделения компонента, модуль 26 прямого преобразования, модуль 28 квантования и модуль 30 энтропийного кодирования. Модуль 22 разделителя на блоки может принимать незакодированные видеокадры из источника 4 мультимедиа, сетевого интерфейса 16 или другого источника. Когда модуль 22 разделителя на блоки принимает незакодированный видеокадр, модуль 22 разделителя на блоки может разделять кадр на блоки пикселей. Модуль 22 разделителя на блоки может предоставить блоки пикселей в модуль 24 выделения компонента.
Когда модуль 24 выделения компонента принимает блоки пикселей, модуль 24 выделения компонента может преобразовывать значения компонента пикселя каждого пикселя в другой цветовой формат. Например, модуль 24 выделения компонента может преобразовывать каждый пиксель из цветового формата "красный-зеленый-синий" (RGB) в цветовой формат YCrCb. После преобразования пикселей в блоке в другой цветовой формат, модуль 24 выделения компонента может разделять значения компонента пикселя из пикселей в блоке на матрицы значений компонента пикселя. Например, модуль 24 выделения компонента может выделять матрицу значений Y, матрицу значений Cr и матрицу значений Cb из одного блока пикселей. Значения Y специфицируют яркость пикселей, значения Cr специфицируют информацию о красном цвете пикселей и значения Cb специфицируют информацию о синем цвете пикселей. После выделения матриц значений компонента пикселя модулем 24 выделения компонента, модуль 24 выделения компонента может предоставить каждую из матриц отдельно в модуль 26 дискретного косинусного преобразования (DCT).
Когда модуль 26 прямого преобразования принимает матрицу значений компонента пикселя, модуль 26 прямого преобразования формирует матрицу масштабированных коэффициентов. Каждый коэффициент в этой матрице масштабированных коэффициентов аппроксимирует коэффициент, который формируется с использованием идеального прямого дискретного косинусного преобразования, для преобразования матрицы значений компонента пикселя.
Модуль 26 прямого преобразования использует арифметические операции с фиксированной запятой для применения одномерного преобразования к матрицам значений компонента пикселя. Использование арифметических операций с фиксированной запятой может быть полезным при некоторых обстоятельствах. Например, малогабаритные устройства, например, мобильные телефоны не могут включать в себя сопроцессор для чисел с плавающей запятой, требуемый для выполнения арифметических операций с плавающей запятой. Модуль 26 прямого преобразования может начинать процесс формирования матрицы масштабированных коэффициентов со сдвига влево каждого из значений компонента пикселя. Например, модуль 26 прямого преобразования может формировать матрицу скорректированных коэффициентов сдвигом влево каждого из значений компонента пикселя на количество битов точности (то есть, количество битов мантиссы) представлений с фиксированной запятой чисел, которые модуль 26 прямого преобразования использует при применении одномерного преобразования плюс количество битов точности, удаленных масштабированием преобразованных коэффициентов, которые получаются в результате применения преобразования. После сдвига влево каждого из значений компонента пикселя, модуль 26 прямого преобразования может выполнять преобразование каждой из вектор-строк матрицы скорректированных коэффициентов. Выполнение дискретного косинусного преобразования каждой из вектор-строк матрицы скорректированных коэффициентов формирует матрицу промежуточных коэффициентов. Затем, модуль 26 прямого преобразования может выполнять преобразование каждого из вектор-столбцов матрицы промежуточных коэффициентов. Выполнение преобразования каждого из вектор-столбцов матрицы промежуточных коэффициентов в результате приводит к матрице преобразованных коэффициентов.
После формирования матрицы преобразованных коэффициентов, модуль 26 прямого преобразования масштабирует преобразованные коэффициенты в различных позициях в матрице преобразованных коэффициентов различными масштабными множителями. Как описано ниже, модуль 12 декодирования может использовать обратные величины этих масштабных множителей при применении обратного преобразования. После окончания модулем 26 прямого преобразования масштабирования преобразованных коэффициентов масштабными множителями, модуль 26 прямого преобразования может выводить получающуюся в результате матрицу масштабированных коэффициентов в модуль 28 квантования.
Когда модуль 28 квантования принимает матрицу коэффициентов из модуля 26 прямого преобразования, модуль 28 квантования 28 может квантовать масштабированные коэффициенты. Модуль 28 квантования может квантовать масштабированные коэффициенты множеством способов, в зависимости от используемого стандарта кодирования. Например, согласно части 2 стандарта MPEG-4, модуль 28 квантования может использовать следующую матрицу квантования для квантования коэффициентов в матрице масштабированных коэффициентов для i-кадра:
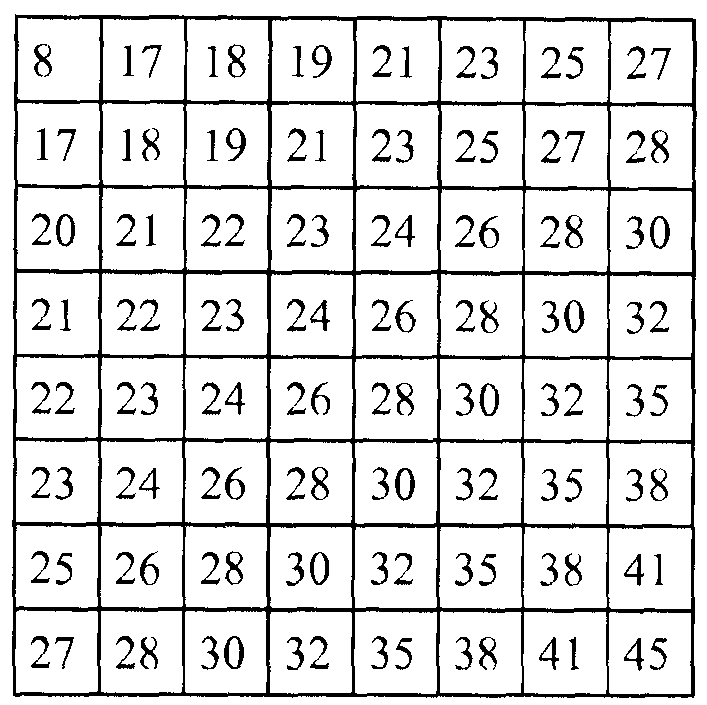
Кроме того, в этом примере, модуль 28 квантования может использовать следующую матрицу квантования для квантования коэффициентов в матрице масштабированных коэффициентов для прогнозированного или бипрогнозированного кадра:
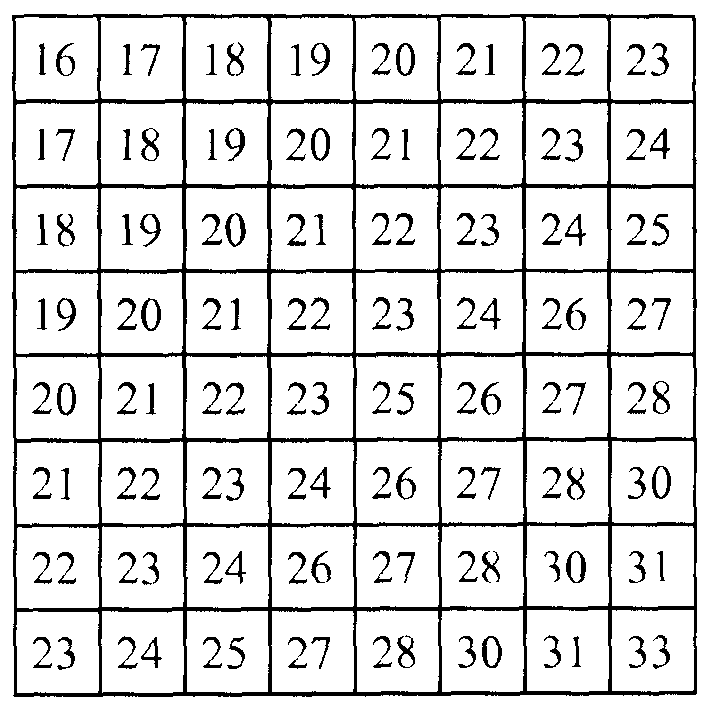
После формирования модулем 28 квантования матрицы квантованных коэффициентов, модуль 30 энтропийного кодирования может сжимать матрицу квантованных коэффициентов с использованием схемы энтропийного кодирования. Для сжатия матрицы квантованных коэффициентов с использованием схемы энтропийного кодирования, модуль 30 энтропийного кодирования может упорядочить квантованные коэффициенты в вектор посредством зигзагообразного шаблона коэффициентов. Другими словами, модуль 30 энтропийного кодирования может упорядочивать все квантованные коэффициенты в двухмерной матрице квантованных коэффициентов в одномерный вектор квантованных коэффициентов в предсказываемом (векторе). После этого модуль 30 энтропийного кодирования может применять схему энтропийного кодирования, например, кодирование методом Хаффмана или арифметическое кодирование, к вектору квантованных коэффициентов.
Модуль 8 кодирования также включает в себя один или несколько модулей для выполнения временного кодирования видеокадров. Как изображено в примере фиг.2, модуль 8 кодирования включает в себя модуль 32 оценки движения, модуль 34 формирования восстановленного кадра и модуль 36 формирования остаточного кадра. Модуль 32 оценки движения пытается идентифицировать исходный макроблок в опорном изображении для каждого макроблока в текущем видеокадре. Модуль 32 оценки движения может пытаться идентифицировать исходный макроблок для макроблока в текущем кадре посредством поиска макроблоков в опорном изображении, которые содержат аналогичные пиксели как макроблок. Модуль 32 оценки движения может вести поиск в областях различных размеров согласно различным стандартам кодирования для идентификации исходного макроблока для макроблока в текущем кадре. Например, модуль 32 оценки движения может вести поиск исходного макроблока в области, которая является пикселями, шириной в 32 пикселя, высотой в 32 пикселя, с текущим макроблоком в центре области поиска. Когда модуль 32 оценки движения идентифицирует исходный макроблок для макроблока в текущем кадре, модуль 32 оценки движения вычисляет вектор движения для этого макроблока в текущем кадре. Вектор движения для макроблока в текущем кадре специфицирует значение x, которое указывает различие в горизонтальной позиции между идентифицированным исходным макроблоком и макроблоком текущего кадра. После того, как модуль 32 оценки движения или вычислил вектор движения или не смог идентифицировать исходный макроблок для каждого макроблока в текущем кадре, модуль 32 оценки движения может предоставить вычисленные векторы движения для текущего кадра в модуль 34 формирования восстановленного кадра.
Модуль 34 формирования восстановленного кадра может использовать векторы движения и опорные кадры для формирования восстановленного кадра. Модуль 34 формирования восстановленного кадра может формировать восстановленный кадр посредством применения векторов движения для каждого макроблока в текущем кадре к исходным макроблокам в опорных кадрах. В действительности, модуль 34 формирования восстановленного кадра создает кадр, в котором макроблоки опорных кадров "перемещены" в позиции, обозначенные соответствующими векторами движения текущего кадра.
Модуль 36 формирования остаточного кадра может формировать остаточный кадр вычитанием значений компонента пикселя в восстановленном кадре из соответствующих значений компонента пикселя в текущем кадре. В общем, остаточный кадр включает в себя меньше информации, чем восстановленный кадр или чем текущий кадр. После формирования остаточного кадра модулем 36 формирования остаточного кадра, модуль 36 формирования остаточного кадра предоставляет остаточный кадр в модуль 22 разделителя на блоки для начала процесса пространственного кодирования остаточного кадра. Кроме того, модуль 32 оценки движения может предоставить векторы движения для текущего кадра в модуль 30 энтропийного кодирования для сжатия векторов движения. После пространственного кодирования остаточного кадра и кодирования векторов движения модулем 30 энтропийного кодирования, модуль 38 вывода потока может форматировать пространственно закодированный остаточный кадр и закодированные векторы движения как часть битового потока видео.
Фиг.3 является блок-схемой, изображающей иллюстративные детали модуля 12 декодирования. Модуль 12 декодирования может содержать модуль 44 энтропийного декодирования, модуль 46 деквантования, модуль 48 обратного преобразования, модуль 50 восстановления пикселя, буфер 51 кадра, модуль 52 объединителя блоков, модуль 53 управления кадром, модуль 54 хранения опорного кадра, модуль 56 формирования восстановленного кадра и модуль 58 формирования прогнозированного кадра. Некоторые или все эти модули могут содержать подмножества программных команд модуля 12 декодирования. В качестве альтернативы, некоторые или все эти модули могут содержать специализированные аппаратные средства или программно-аппаратные средства. В другом варианте, эти модули могут содержать программные команды и специализированные аппаратные средства или программно-аппаратные средства.
Когда модуль 12 декодирования принимает битовый поток, содержащий видеокадр, модуль 44 энтропийного декодирования может применять схему энтропийного декодирования к матрицам квантованных коэффициентов в видеокадре. Битовый поток может включать в себя значение, которое указывает модулю 44 энтропийного декодирования, какую схему энтропийного декодирования применять (к) матрицам квантованных коэффициентов в битовом потоке. Кроме того, модуль 44 энтропийного декодирования может применять идентичную или другую схему энтропийного декодирования для декодирования векторов движения видеокадра.
После применения модулем 44 энтропийного декодирования схемы энтропийного декодирования к матрицам квантованных коэффициентов в видеофайле, модуль 46 деквантования может деквантовать коэффициенты в каждой из матриц квантованных коэффициентов. В зависимости от стандарта кодирования модуль 46 деквантования может деквантовать коэффициенты множеством способов. Например, согласно части 2 стандарта MPEG-4, модуль 46 деквантования может использовать две вышеупомянутые матрицы квантования двумя различными способами. Во-первых, модуль 46 деквантования может использовать эти матрицы квантования для выполнения деквантования в стиле H.263. При деквантовании в стиле H.263, модуль 46 деквантования получает восстановленные коэффициенты F''[v][u] из квантованных значений QF[v][u] следующим образом:
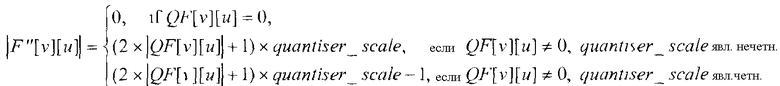
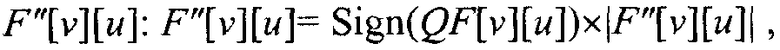
что включает в себя только одно умножение на quantiser_scale, и
во-вторых, модуль 46 деквантования может использовать эти матрицы квантования для выполнения деквантования в стиле MPEG-l/2. При деквантовании в стиле MPEG-1/2, модуль 46 деквантования использует дополнительные весовые матрицы W[w][v][u], где w указывает, какая весовая матрица используется:
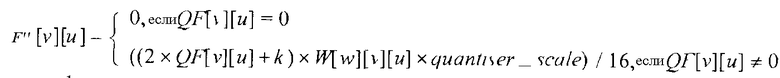
где:

Как описано подробно ниже, модуль 48 обратного преобразования масштабирует каждый из деквантованных коэффициентов конкретными масштабными множителями и добавляет терм смещения центра к коэффициенту DC получающейся в результате матрицы масштабированных коэффициентов. Коэффициент DC является коэффициентом в позиции (0,0) матрицы масштабированных коэффициентов. Затем, модуль 48 обратного преобразования использует повторные применения одномерного преобразования с фиксированной запятой для преобразования матрицы масштабированных коэффициентов в матрицу преобразованных коэффициентов. После преобразования матрицы масштабированных коэффициентов в матрицу преобразованных коэффициентов, модуль 48 обратного преобразования сдвигает вправо каждый преобразованный коэффициент в матрице преобразованных коэффициентов для формирования матрицы скорректированных коэффициентов. Каждый скорректированный коэффициент в матрице скорректированных коэффициентов аппроксимирует соответствующее значение в матрице значений, которые можно сформировать с применением идеального двумерного IDCT к матрице закодированных коэффициентов. Кроме того, модуль 48 обратного преобразования может ограничивать каждый из скорректированных коэффициентов в матрице скорректированных коэффициентов для формирования матрицы ограниченных коэффициентов. Значения ограниченных коэффициентов находятся в пределах диапазонов, соответствующих получающемуся в результате формату значения компонента пикселя. Например, ограниченные коэффициенты могут иметь значения, которые находятся в пределах диапазона [-256, 255]. После ограничения скорректированных коэффициентов модулем 48 обратного преобразования, получающиеся в результате ограниченные значения являются значениями компонента пикселя.
После вывода модулем 48 обратного преобразования матрицы значений компонента пикселя, модуль 50 восстановления пикселя может формировать матрицу пикселей посредством объединения матрицы значений компонента пикселя с матрицами значений компонентов пикселя, связанными с эквивалентными позициями в видеокадре. Например, модуль 50 восстановления пикселя может принимать матрицу значений компонента пикселя Y, матрицу значений компонента пикселя Cb и матрицу значений компонента пикселя Cr из модуля 48 обратного преобразования. Каждая из этих трех матриц может включать в себя компоненты пикселя для одного блока пикселей, 8×8. Каждый из пикселей может включить в себя значение компонента пикселя Y, значение компонента пикселя Cb и значение компонента пикселя Cr. После формирования матрицы пикселей, модуль 50 восстановления пикселя может обеспечивать блок пикселей в модуль 52 объединителя блоков.
Когда модуль 52 объединителя блоков принимает блок пикселей, модуль 52 объединителя блоков может помещать в буфер блок пикселей, пока модуль 52 объединителя блоков не примет некоторые или все блоки пикселей в видеокадре. После приема одного или нескольких блоков пикселей, модуль 52 объединителя блоков может объединять блоки пикселей в видеокадр и может выводить видеокадр в буфер 51 кадра. Видеокадр может быть сохранен в буфере 51 кадра, пока он не будет отображен блоком 51 воспроизведения мультимедиа. Кроме того, модуль 52 объединителя блоков может выводить видеокадр в модуль 54 хранения кадра. Видеокадры в модуле 54 хранения кадра могут использоваться как опорные кадры для восстановления прогнозированных и бипрогнозированных кадров. Кроме того, видеокадры в модуле 54 хранения кадра могут быть остаточными кадрами, которые используются при восстановлении прогнозированных и бипрогнозированных кадров.
Для восстановления прогнозированных или бипрогнозированных кадров, модуль 12 декодирования включает в себя модуль 56 формирования восстановленного кадра. Модуль 56 формирования восстановленного кадра принимает декодированные векторы движения из модуля 44 энтропийного декодирования. Кроме того, модуль 56 формирования восстановленного кадра извлекает опорные кадры для текущего кадра из модуля 54 хранения кадра. После этого модуль 56 формирования восстановленного кадра "перемещает" макроблоки из их позиций в опорных кадрах в позиции, обозначенные векторами движения. Восстановленный кадр получается в результате перемещения макроблоков этим способом. После формирования восстановленного кадра модулем 56 формирования восстановленного кадра, модуль 56 формирования восстановленного кадра предоставляет восстановленный кадр в модуль 58 формирования прогнозированного кадра.
Когда модуль 58 формирования прогнозированного кадра принимает временной кадр, модуль 58 формирования прогнозированного кадра может извлекать из модуля 54 хранения кадра остаточный кадр для текущего кадра. После извлечения остаточного кадра, модуль 58 формирования прогнозированного кадра может суммировать соответствующие значения цветовых компонентов в каждом пикселе остаточного кадра и восстановленного кадра. Восстановленный видеокадр получается в результате этого суммирования. Затем, модуль 58 формирования прогнозированного кадра может выводить этот восстановленный кадр в буфер 51 кадра для конечного отображения в блоке 14 воспроизведения мультимедиа.
Фиг.4 является блок-схемой, изображающей иллюстративную работу модуля 8 кодирования. Хотя работа, описанная в фиг.4, описана в виде последовательности, следует отметить, что эта работа может выполняться конвейерным способом.
Вначале, модуль 8 кодирования принимает последовательность незакодированных видеокадров (60). Например, модуль 8 кодирования может принимать последовательность незакодированных кадров в виде наборов пикселей из источника 4 мультимедиа. Когда модуль 8 кодирования принимает последовательность незакодированных кадров, модуль 20 управления кадром в модуле 8 кодирования может устанавливать, должен ли текущий кадр в последовательности незакодированных кадров быть закодирован как i-кадр или как прогнозированный или бипрогнозированный кадр (62).
Если модуль 20 управления кадром устанавливает, что текущий кадр должен быть закодирован как i-кадр, то модуль 22 разделителя на блоки в модуле 8 кодирования может разделять текущий кадр на блоки пикселей (64). Например, модуль 8 кодирования может разделять текущий кадр на блоки пикселей, 2×2, 4×4 или 8×8.
После разделения текущего кадра на блоки пикселей, модуль 24 выделения компонента может разделять значения компонента пикселя в каждом из блоков пикселей (66). В результате может быть три блока значений компонента пикселя для каждого блока пикселей: блок значений Y, представляющих яркость пикселей, блок значений Cb, представляющих информацию о синем цвете пикселей, и блок значений Cr, представляющих информацию о красном цвете пикселей.
После этого модуль 26 прямого преобразования в модуле 8 кодирования может формировать матрицу масштабированных коэффициентов для каждой из матриц значений компонента пикселя (68). Коэффициенты в этих матрицах масштабированных коэффициентов являются аппроксимациями значений, которые формируются с использованием идеального двумерного прямого дискретного косинусного преобразования соответствующих матриц значений компонента пикселя.
После формирования модулем 26 прямого преобразования матриц масштабированных коэффициентов для каждой из матриц компонентов пикселя, модуль 28 квантования в модуле 8 кодирования может квантовать коэффициенты в каждой из матриц масштабированных коэффициентов (70). После квантования модулем 28 квантования коэффициентов в каждой матрице масштабированных коэффициентов, модуль 30 энтропийного кодирования может выполнять энтропийное кодирование каждой из матриц квантованных коэффициентов (72). Например, модуль 8 кодирования может применять схему кодирования методом Хаффмана или схему арифметического кодирования к каждой матрице квантованных коэффициентов. Энтропийное кодирование дополнительно сжимает данные. Однако процессы энтропийного кодирования в результате не приводят к потере информации. После выполнения энтропийного кодирования каждой матрицы квантованных коэффициентов, модуль 38 вывода потока в модуле 8 кодирования может добавлять закодированные матрицы квантованных коэффициентов в битовый поток для последовательности видеокадров (74). После добавления модулем 38 вывода потока закодированных матриц к битовому потоку, модуль 20 управления кадром может устанавливать, был ли текущий кадр последним видеокадром последовательности кадров (76). Если текущий кадр является последним кадром последовательности кадров ("ДА" 76), то модуль 8 кодирования завершает кодирование последовательности кадров (78). С другой стороны, если текущий кадр не является последним кадром последовательности кадров ("НЕТ" 76), то модуль 8 кодирования может возвращаться к началу цикла и устанавливать, должен ли новый текущий кадр быть закодирован как i-кадр (62).
Если текущий кадр не должен быть закодирован как i-кадр ("НЕТ" 62), то модуль 32 оценки движения в модуле 8 кодирования может разделять текущий кадр на ряд макроблоков (80). Затем, модуль 32 оценки движения может пытаться идентифицировать исходный макроблок в одном или нескольких опорных кадрах для каждого из макроблоков в текущем кадре (82). Модуль 32 оценки движения может далее вычислять вектор движения для каждого из макроблоков в текущем кадре, для которых модуль 32 оценки движения смог идентифицировать исходный макроблок (84). После вычисления векторов движения модулем 32 оценки движения, модуль 34 формирования восстановленного кадра использует векторы движения для формирования восстановленного кадра посредством "перемещения" идентифицированных макроблоков в опорных кадрах в позиции, обозначенные векторами движения (86). Модуль 36 формирования остаточного кадра может далее формировать остаточный кадр для текущего кадра вычитанием значений компонента пикселя в восстановленном кадре из соответствующих значений компонента пикселя в текущем кадре (88). После формирования остаточного кадра модулем 36 формирования остаточного кадра, модуль 30 энтропийного кодирования может использовать схему энтропийного кодирования для кодирования векторов движения для текущего кадра (90). Кроме того, к остаточному кадру может быть применено пространственное кодирование посредством применения этапов с (66) по (74) к остаточному кадру.
Фиг.5 является блок-схемой, изображающей иллюстративную работу модуля 12 декодирования. Хотя работа, описанная в фиг.5, описана в виде последовательности, следует отметить, что эта работа может выполняться конвейерным способом.
Вначале, модуль 12 декодирования принимает закодированный видеокадр (100). После приема закодированного видеокадра, модуль 44 энтропийного декодирования в модуле 12 декодирования может выполнять энтропийное декодирование блоков данных в закодированном кадре (102). Модуль 44 энтропийного декодирования может выполнять энтропийное декодирование, которое эквивалентно энтропийному кодированию, используемому для кодирования кадра. Например, если модуль 8 кодирования использует кодирование методом Хаффмана для кодирования кадра, то модуль 44 энтропийного декодирования использует декодирование методом Хаффмана для декодирования кадра. В результате применения энтропийного декодирования к каждому блоку данных в кадре, модуль 44 энтропийного декодирования формирует набор матриц квантованных коэффициентов.
Затем, модуль 46 деквантования в модуле 12 декодирования может деквантовать коэффициенты в каждой из матриц квантованных коэффициентов (104). После деквантования каждого коэффициента в матрицах квантованных коэффициентов, модуль 48 обратного преобразования в модуле 12 декодирования формирует матрицы значений компонента пикселя (106). Значения компонента пикселя в одной из матриц значений компонента пикселя являются аппроксимациями соответствующих значений, которые формируются посредством преобразования одной из матриц квантованных коэффициентов с использованием идеального двумерного обратного дискретного косинусного преобразования.
После вычисления модулем 48 обратного преобразования матрицы значений компонента пикселя для каждой из матриц коэффициентов, модуль 50 восстановления пикселя в модуле 12 декодирования может объединять соответствующие матрицы значений компонента пикселя для создания блоков пикселей (108). Например, модуль 12 декодирования может объединять блок значений Y со связанным блоком значений Cr и связанным блоком значений Cb для создания блока пикселей YCrCb. После создания блоков пикселей модулем 50 восстановления пикселя, модуль 52 объединителя блоков может заново объединять блоки пикселей в видеокадр (110).
Затем, модуль 53 управления кадром в модуле 12 декодирования может устанавливать, является ли текущий кадр i-кадром (114). Если текущий кадр является i-кадром ("ДА" 114), то модуль 52 объединителя блоков может выводить видеокадр в буфер 51 кадра (114). С другой стороны, если текущий кадр не является i-кадром (то есть, текущий кадр является прогнозированным или бипрогнозированным кадром) ("НЕТ" 114), то модуль 44 энтропийного декодирования использует схему энтропийного декодирования для декодирования векторов движения текущего кадра (116). Затем, модуль 56 формирования восстановленного кадра использует декодированные векторы движения и один или несколько опорных кадров в модуле 54 хранения кадра для формирования восстановленного кадра (118). После этого модуль 58 формирования прогнозированного кадра может использовать восстановленный кадр и кадр, сформированный модулем 52 объединителя блоков, для формирования восстановленного кадра (120).
Фиг.6 является блок-схемой, изображающей иллюстративные детали модуля 48 обратного преобразования. Как изображено в примере фиг.6, модуль 48 обратного преобразования может содержать модуль 140 ввода. Модуль 140 ввода может принимать матрицу коэффициентов из модуля 46 деквантования. Например, модуль 140 ввода может принимать указатель, который указывает положение в модуле памяти устройства 2, где хранится матрица коэффициентов. В качестве альтернативы, модуль 140 ввода может включать в себя внутренние структуры данных, которые хранят матрицу коэффициентов.
Когда модуль 140 ввода принимает матрицу коэффициентов, модуль 140 ввода может предоставить матрицу коэффициентов в модуль 142 масштабирования в модуле 48 обратного преобразования. Модуль 142 масштабирования может выполнять операции, которые формируют значения, аппроксимирующие масштабирование коэффициентов в матрице коэффициентов масштабными множителями в эквивалентных позициях в матрице масштабных множителей. Например, модуль 142 масштабирования может выполнять операции умножения для формирования значений, аппроксимирующих масштабирование коэффициентов в матрице коэффициентов масштабными множителями в эквивалентных позициях в матрице масштабных множителей. В другом примере, модуль 142 масштабирования может выполнять одну или несколько операций сдвига и сложения. Каждый из этих масштабных множителей может быть 8-битовым целочисленным значением. Когда каждый из масштабных множителей является 8-битовым целым числом, динамический диапазон значений, формируемый во время преобразования, уменьшается.
После формирования матрицы масштабированных коэффициентов модулем 142 масштабирования, модуль 144 смещения коэффициента может формировать матрицу смещенных коэффициентов посредством добавления значения смещения центра к коэффициенту DC матрицы масштабированных коэффициентов. Как обсуждалось выше, коэффициент DC матрицы, как правило, находится в верхнем левом углу матрицы. В общем, коэффициент DC представляет среднее значение других коэффициентов в матрице.
Для добавления значения знако-адаптивного смещения к коэффициенту DC в 16-разрядном процессоре, модуль 144 смещения коэффициента может использовать следующую формулу:
DC_coefficient=DC_coefficient+(1<<(P+2)).
В этой формуле, терм (1<<(P+2)) добавлен для обеспечения смещения центра. P - константа, относящаяся к количеству битов мантиссы с фиксированной запятой (то есть, битов справа от символа, отделяющего целую часть числа от дробной), используемых в преобразовании, применяемом модулем 146 обратного преобразования вектора. К P прибавляется число 2, потому что модуль 148 сдвига вправо может сдвигать вправо все коэффициенты на (P+3), где число '3' получается из битов точности, добавляемых выполнением преобразования. Для детального рассмотрения этого момента, если число x сформировано сдвигом влево 1 на (P+2), и число z сформировано сдвигом вправо x на (P+3), то z=1/2. (То есть, 2P+2/2P+3=20/21=1/2). Соответственно, добавление (1<<(P+2)) к коэффициенту DC эквивалентно добавлению (1<<(P+3))/2 к коэффициенту DC.
После формирования матрицы смещенных коэффициентов модулем 144 смещения коэффициента, с применением масштабированного одномерного преобразования с фиксированной запятой к каждой вектор-строке матрицы смещенных коэффициентов модуль 146 обратного преобразования вектора может формировать матрицу промежуточных значений. Затем, модуль 146 обратного преобразования вектора может вычислять матрицу преобразованных коэффициентов с применением масштабированного одномерного преобразования с фиксированной запятой к каждому вектор-столбцу матрицы промежуточных значений. Иллюстративная операция для применения масштабированного одномерного преобразования с фиксированной запятой к вектору масштабированных коэффициентов представлена ниже на фиг.10B.
После формирования матрицы преобразованных коэффициентов модулем 146 обратного преобразования вектора, модуль 148 сдвига вправо может формировать матрицу скорректированных коэффициентов сдвигом вправо каждого из коэффициентов в матрице преобразованных коэффициентов на количество позиций, равное количеству битов, добавленных во время применения преобразования и во время масштабирования. Например, если применение преобразования в результате приводит к дополнительным трем битам и масштабирование коэффициентов добавляет дополнительные десять битов, то модуль 108 сдвига вправо может сдвигать вправо каждый из коэффициентов на тринадцать (3+10) позиций.
После формирования матрицы скорректированных коэффициентов модулем 148 сдвига вправо, модуль 150 ограничения может формировать матрицу ограниченных коэффициентов путем "ограничения" коэффициентов в матрице скорректированных коэффициентов для ограничения коэффициентов максимальным допустимым диапазоном значений компонента пикселя. Например, как правило, значение компонента пикселя может находиться в пределах от -256 до 255. Если матрица скорректированных коэффициентов должна включать в себя коэффициент, равный 270, модуль 150 ограничения ограничивает этот коэффициент максимальным допустимым диапазоном с уменьшением этого коэффициента до 255. После окончания ограничения коэффициентов модулем 150 ограничения, эти коэффициенты могут представлять значения компонента пикселя. Когда модуль 150 ограничения заканчивает ограничение коэффициентов в матрице, модуль 150 ограничения может предоставить матрицу ограниченных коэффициентов в модуль 152 вывода.
Когда модуль 152 вывода принимает матрицу ограниченных коэффициентов (которые теперь являются значениями компонента пикселя), модуль 152 вывода может выводить матрицу значений компонента пикселя в модуль 50 восстановления пикселя.
Фиг.7 является блок-схемой, изображающей иллюстративную работу модуля 34 обратного преобразования. Вначале, модуль 140 ввода принимает матрицу коэффициентов (170). Когда модуль 140 ввода принимает матрицу коэффициентов, модуль 142 масштабирования может масштабировать каждое значение в матрице коэффициентов (172). Например, модуль 142 масштабирования может выполнять операции, в которых каждый коэффициент в матрице коэффициентов умножается на значения в матрице масштабных множителей, которые находятся в эквивалентных позициях.
После масштабирования каждого коэффициента в матрице коэффициентов, модуль 144 смещения коэффициента может добавлять значение смещения центра к коэффициенту DC матрицы коэффициентов (174). После добавления значения смещения к коэффициенту DC матрицы модулем 144 смещения коэффициента, модуль 146 обратного преобразования вектора может устанавливать, меньше ли счетчик строки, чем максимум счетчика строки (176). Вначале, счетчик строки может быть установлен в ноль. Максимум счетчика строки может быть статическим значением, которое равно количеству строк в матрице коэффициентов. Например, если матрица коэффициентов включает в себя восемь строк, то максимум счетчика строки равен восьми.
Если счетчик строки меньше, чем максимум счетчика строки ("ДА" 176), то модуль 146 обратного преобразования вектора может вычислять масштабированное одномерное преобразование с фиксированной запятой вектор-строки матрицы коэффициентов, указываемой счетчиком строки (178). Когда модуль 146 обратного преобразования вектора вычисляет преобразование вектор-строки матрицы коэффициентов, модуль 146 обратного преобразования вектора может заменять исходные коэффициенты в этой вектор-строке коэффициентов вектором промежуточных коэффициентов. После вычисления преобразования вектор-строки матрицы коэффициентов модулем 146 обратного преобразования вектора, модуль 146 обратного преобразования вектора может увеличить счетчик строки (180). После этого модуль 146 обратного преобразования вектора может возвращаться к началу цикла и снова устанавливать, меньше ли счетчик строки, чем максимум счетчика строки (176).
Если счетчик строки не меньше (то есть, больше или равен), чем максимум счетчика строки ("НЕТ" 176), то модуль 146 обратного преобразования вектора может устанавливать, меньше ли счетчик столбца, чем максимум счетчика столбца (182). Вначале, счетчик столбца может быть установлен в ноль. Максимум счетчика столбца может быть статическим значением, которое равно количеству столбцов в матрице коэффициентов. Например, если матрица коэффициентов включает в себя восемь столбцов, то максимум счетчика столбца равен восьми.
Если счетчик столбца меньше, чем максимум счетчика столбца ("ДА" 182), то модуль 146 обратного преобразования вектора может вычислять одномерное преобразование вектор-столбца матрицы промежуточных коэффициентов, указываемого счетчиком столбца (184). Когда модуль 34 обратного преобразования вычисляет преобразование вектор-столбца промежуточных коэффициентов, модуль 34 обратного преобразования заменяет промежуточные коэффициенты в вектор-столбце вектором преобразованных коэффициентов.
После вычисления преобразования вектор-столбца матрицы коэффициентов модулем 146 обратного преобразования вектора, модуль 146 обратного преобразования вектора может увеличить счетчик столбца (186). После этого модуль 146 обратного преобразования вектора может возвращаться к началу цикла и снова устанавливать, меньше ли счетчик столбца, чем максимум счетчика столбца (182).
Если счетчик столбца не меньше (то есть, больше или равен), чем максимум счетчика столбца ("НЕТ" 182), то модуль 148 сдвига вправо может сдвигать вправо каждый из преобразованных коэффициентов в матрице (188). Когда модуль 148 сдвига вправо сдвигает вправо коэффициент, модуль 148 сдвига вправо может сдвигать этот коэффициент вправо на определенное количество позиций. Результатом сдвига вправо каждого из вторых промежуточных коэффициентов в матрице является матрица скорректированных значений. После сдвига вправо каждого из преобразованных коэффициентов модулем 148 сдвига вправо, модуль 150 ограничения может ограничивать скорректированные коэффициенты для обеспечения того, что скорректированные коэффициенты находятся в пределах соответствующего диапазона для значений компонента пикселя (190). Например, модуль 150 ограничения может ограничивать скорректированные коэффициенты для обеспечения того, что скорректированные коэффициенты находятся в пределах диапазона от -256 до 255. Когда модуль 150 ограничения закончит ограничение скорректированных коэффициентов, модуль 152 вывода может выводить получающуюся в результате матрицу значений компонента пикселя (192).
Фиг.8 является блок-схемой, изображающей иллюстративные детали модуля 26 прямого преобразования. Как изображено в примере фиг.8, модуль 26 прямого преобразования содержит модуль 210 ввода, который принимает матрицу значений компонента пикселя из модуля 24 выделения компонента. Когда модуль 210 ввода принимает матрицу значений компонента пикселя, модуль 210 ввода может предоставить матрицу значений компонента пикселя в модуль 212 сдвига влево. Модуль 212 сдвига влево может сдвигать все значения компонента пикселя в матрице значений компонента пикселя влево на количество битов мантиссы, используемых в значениях, которые модуль 214 прямого преобразования вектора использует при выполнении прямого преобразования минус количество битов мантиссы, удаленных при выполнении прямого преобразования. Например, если в значениях при выполнении прямого преобразования используются десять битов мантиссы, и при выполнении прямого дискретного косинусного преобразования три бита мантиссы удаляются, то модуль 212 сдвига влево может сдвигать значения компонента пикселя влево на семь позиций. В другом примере, если в значениях при выполнении прямого преобразования используются три бита мантиссы, и при выполнении прямого преобразования три бита мантиссы удаляются, то модуль 212 сдвига влево может сдвигать значения компонента пикселя влево на ноль позиций.
После сдвига значений компонента пикселя модулем 212 сдвига влево, модуль 214 прямого преобразования вектора может применять прямое преобразование к каждому вектор-столбцу в матрице значений компонента пикселя для формирования матрицы промежуточных значений. Затем, модуль 214 прямого преобразования вектора может применять прямое преобразование к каждой вектор-строке в матрице промежуточных значений для формирования матрицы преобразованных коэффициентов. Когда модуль 214 прямого преобразования вектора применяет прямое преобразование к вектору, модуль 214 прямого преобразования вектора может применять прямое преобразование, описанное в фиг.11, ниже. Отметим, что преобразование, описанное на фиг.11 ниже, является обратным преобразованию, описанному на фиг.10A.
После формирования матрицы преобразованных коэффициентов модулем 214 прямого преобразования вектора, модуль 216 масштабирования может применять масштабные множители к каждому преобразованному коэффициенту в матрице преобразованных коэффициентов. Модуль 216 масштабирования может применять обратные величины масштабных множителей, используемых модулем 142 масштабирования в модуле 48 обратного преобразования. Например, если модуль 142 масштабирования масштабирует коэффициенты сдвигом коэффициентов влево на три позиции, то модуль 216 масштабирования может масштабировать преобразованные значения сдвигом преобразованных значений вправо на три позиции. В другом примере, если модуль 142 масштабирования масштабирует коэффициенты умножением коэффициентов на отдельные масштабные множители в матрице масштабных множителей, то модуль 216 масштабирования может масштабировать преобразованные значения умножением преобразованных значений на масштабные множители в матрице масштабных множителей, и затем сдвигом получающихся в результате значений вправо на некоторую величину. Для уменьшения ошибок округления, модуль 216 масштабирования может добавлять значение смещения центра к каждому из преобразованных значений после умножения преобразованных значений на масштабные множители. Например, модуль 216 масштабирования может использовать следующее уравнение для формирования матрицы масштабированных коэффициентов:
F[v][u]=(F'[v][u]*S[v][u]+(1<<19)-((F'[v][u]>=0)?0:1))>>20
где v=0..7, u=0..7, где S[v][u] - элемент в матрице масштабных множителей, F - матрица масштабированных коэффициентов, и F' - матрица преобразованных коэффициентов.
После формирования матрицы масштабированных коэффициентов модулем 216 масштабирования, модуль 218 вывода может выводить матрицу коэффициентов в модуль 28 квантования.
Фиг.9 является блок-схемой, изображающей иллюстративную работу модуля 26 прямого преобразования. Вначале, модуль 210 ввода принимает матрицу значений компонента пикселя (230). Когда модуль 140 ввода принимает матрицу значений компонента пикселя, модуль 212 сдвига влево может формировать матрицу скорректированных коэффициентов сдвигом (влево) каждого значения в матрице значений компонента пикселя (232). Например, модуль 212 сдвига влево может сдвигать все коэффициенты влево на десять позиций. В этом примере, модуль 212 сдвига влево может сдвигать все коэффициенты вправо на десять позиций, потому что модуль 214 прямого преобразования вектора может использовать арифметические операции с фиксированной запятой, в которых числа закодированы с использованием десяти битов в дробной части. Соответственно, путем сдвига коэффициентов влево на десять позиций, модуль 212 сдвига влево фактически преобразует значения компонента пикселя в числа с фиксированной запятой с десятью битами мантиссы.
После сдвига влево каждого значения компонента пикселя в матрице скорректированных значений, модуль 214 прямого преобразования вектора может устанавливать, меньше ли счетчик столбца, чем максимум счетчика строки (234). Вначале, счетчик столбца может быть установлен в ноль. Максимум счетчика столбца может быть статическим значением, которое равно количеству столбцов в матрице скорректированных коэффициентов. Например, если матрица скорректированных коэффициентов включает в себя восемь столбцов, то максимум счетчика столбца равен восьми.
Если счетчик столбца меньше, чем максимум счетчика столбца ("ДА" 234), то модуль 214 прямого преобразования вектора может вычислять одномерное прямое преобразование вектор-столбца, указываемого счетчиком столбца (236). Когда модуль 214 прямого преобразования вектора вычисляет прямое преобразование вектор-столбца матрицы скорректированных коэффициентов, модуль 214 прямого преобразования вектора заменяет исходные скорректированные коэффициенты в вектор-столбце промежуточными коэффициентами. После вычисления прямого преобразования вектор-столбца матрицы скорректированных коэффициентов модулем 214 прямого преобразования вектора, модуль 214 прямого преобразования вектора может увеличить счетчик столбца (238). После этого модуль 214 прямого преобразования вектора может возвращаться к началу цикла и снова устанавливать, меньше ли счетчик столбца, чем максимум счетчика столбца (234).
Если счетчик столбца не меньше (то есть, больше или равен), чем максимум счетчика столбца ("НЕТ" 234), то модуль 214 прямого преобразования вектора может устанавливать, меньше ли счетчик строки, чем максимум счетчика строки (240). Вначале, счетчик строки может быть установлен в ноль. Максимум счетчика строки может быть статическим значением, которое равно количеству вектор-строк в матрице коэффициентов. Например, если матрица коэффициентов включает в себя восемь строк, то максимум счетчика строки равен восьми.
Если счетчик строки меньше, чем максимум счетчика строки ("ДА" 240), то модуль 214 прямого преобразования вектора может вычислять одномерное дискретное косинусное преобразование вектор-строки, указываемой счетчиком строк (242). Поскольку модуль 214 прямого преобразования вектора уже вычислил прямое преобразование вектор-строк матрицы, то матрица коэффициентов теперь содержит промежуточные коэффициенты. Когда модуль 214 прямого преобразования вектора 214 вычисляет прямое преобразование вектор-строки промежуточных коэффициентов, модуль 214 прямого преобразования вектора заменяет промежуточные коэффициенты в вектор-столбце преобразованными коэффициентами.
После вычисления дискретного косинусного преобразования вектор-строки матрицы коэффициентов модулем 214 прямого преобразования вектора, модуль 214 прямого преобразования вектора может увеличить счетчик строки (244). После этого модуль 214 прямого преобразования вектора может возвращаться к началу цикла и снова устанавливать, меньше ли счетчик строки, чем максимум счетчика строки (240).
Если счетчик строки не меньше (то есть, больше или равен), чем максимум счетчика строки ("НЕТ" 240), то модуль 216 масштабирования может масштабировать каждый преобразованный коэффициент в матрице преобразованных коэффициентов (246). Когда модуль 216 масштабирования масштабирует коэффициент, модуль 216 масштабирования может сдвигать этот коэффициент вправо на определенное количество позиций. После масштабирования каждого из преобразованных коэффициентов модулем 216 масштабирования, модуль 218 вывода может выводить получающуюся в результате матрицу масштабированных коэффициентов (248).
Фиг.10A является блок-схемой, изображающей иллюстративное одномерное преобразование 260. На фиг.10A, значения X0, X1, X2, X3, X4, X5, X6 и X7 представляют входные коэффициенты, и значения x0, x1, x2, x3, x4, x5, x6 и x7 представляют выходные значения преобразования 260. Значение, связанное с линией после кружка с символом "+" внутри, является результатом добавления значений, связанных со стрелками, которые указывают в этот кружок. Значение, связанное с линией после кружка с символом "x" внутри, является результатом умножения коэффициента, помещенного рядом с кружком, и значений, связанных с линиями, которые проходят через кружки. Символ "-" рядом со стрелкой представляет взятие со знаком минус значения, связанного со стрелкой. Например, если значение "10" связано со стрелкой перед символом "-", то со стрелкой после символа "-" связано значение "-10".
Преобразование 260 использует четырнадцать операций умножения на семь специфических иррациональных множителей. Для удобства в этом раскрытии эти специфические иррациональные множители называются α, β, γ, δ, ε, ζ и η. В преобразовании 260, α=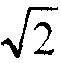 cos(3π/8), β=
cos(3π/8), β=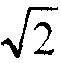 sin(3π/8), γ=cos(π/16), δ=sin(π/16), ε=cos(3π/16), ζ=sin(3π/16) и η=
sin(3π/8), γ=cos(π/16), δ=sin(π/16), ε=cos(3π/16), ζ=sin(3π/16) и η=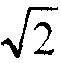 . Отметим, что α, β, γ, δ, ε, ζ и η - все являются иррациональными числами. Поскольку α, β, γ, δ, ε, ζ и η являются иррациональными числами, то для представлений α, β, γ, δ, ε, ζ и η с приемлемой точностью может потребоваться относительно большое количество битов. Следовательно, соблюдение требований типичных стандартов кодирования может быть невозможным при использовании чисел с фиксированной запятой с относительно малым количеством битов мантиссы для вычисления преобразования 260. Кроме того, так как α, β, γ, δ, ε, ζ и η являются иррациональными числами, то может быть невозможным приведение операций умножения на α, β, γ, δ, ε, ζ и η к последовательностям операций сдвига, операций сложения и/или операций вычитания.
. Отметим, что α, β, γ, δ, ε, ζ и η - все являются иррациональными числами. Поскольку α, β, γ, δ, ε, ζ и η являются иррациональными числами, то для представлений α, β, γ, δ, ε, ζ и η с приемлемой точностью может потребоваться относительно большое количество битов. Следовательно, соблюдение требований типичных стандартов кодирования может быть невозможным при использовании чисел с фиксированной запятой с относительно малым количеством битов мантиссы для вычисления преобразования 260. Кроме того, так как α, β, γ, δ, ε, ζ и η являются иррациональными числами, то может быть невозможным приведение операций умножения на α, β, γ, δ, ε, ζ и η к последовательностям операций сдвига, операций сложения и/или операций вычитания.
Фиг.10B является блок-схемой, изображающей иллюстративное одномерное масштабированное преобразование 270. Преобразование 270 является масштабированной версией преобразования 260. В преобразовании 270, значение η было выделено как сомножитель преобразования 260, значение (1/ψ) было выделено как сомножитель значений γ, δ, ε и ζ преобразования 260, и значение (1/φ) было выделено как сомножитель значений α и β преобразования 260. Когда (1/ψ) и (1/φ) выделяются как сомножители этих коэффициентов, следующий вектор представляет значения, на которые умножают X0-X7 перед преобразованием 270:
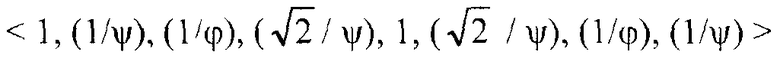
Значения α, β, γ, δ, ε, ζ и η могут изменяться, когда (1/ψ) и (1/φ) выделяются как сомножители α, β, γ, δ, ε и ζ. Для удобства, значения α, β, γ, δ, ε и ζ, после выделения (1/ψ) и (1/φ) как сомножителей, называются α', β', γ', δ', ε' и ζ'. Например, когда ψ=1,352708058 и φ=0,959700091, α'≈133/256, β'≈321/256, γ'≈679/512, δ'≈135/512, ε'≈4605/4096 и ζ'≈1539/2048.
Значения α', β', γ', δ', ε' и ζ' могут быть выбраны различными способами так, чтобы они аппроксимировали произведения α, β, γ, δ, ε и ζ на соответствующие множители ψ или φ. В общем, значения множителей ψ и φ и значения α', β', γ', δ', ε', ζ' могут быть выбраны без изменения всей схемы преобразования 270. Нахождение хороших значений этих множителей может представлять сложную задачу оптимизации, которая может привести к множеству решений с различными оптимальными соотношениями сложности и точности. Например, операции умножения на некоторые значения α', β', γ', δ', ε' и ζ' могут быть более удобными для вычисления, чем другие. Кроме того, значения ψ и φ могут быть важными, потому что они служат базисом для масштабных множителей, и некоторые масштабные множители могут быть более удобными для вычисления, чем другие. Например, операции умножения на первый набор значений для α', β', γ', δ', ε' и ζ' могут аппроксимироваться последовательностями операций сложения и операций сдвига, которые короче последовательностей операций сложения и операций сдвига для другого набора значений для α', β', γ', δ', ε' и ζ'. Например, когда ψ=1,352708058 и φ=0,959700091, γ' может быть аппроксимировано как 679/512. Для аппроксимации умножения на 679/512 могут потребоваться три операции сдвига и три операции сложения. Кроме того, когда ψ=1,1810842 и φ=0,801251953, γ' может быть аппроксимировано как 18981/16384. Для аппроксимации умножения на 18981/16384 могут потребоваться четыре операции сдвига и четыре операции сложения.
Матрица масштабных множителей может быть вычислена умножением транспозиции вектора 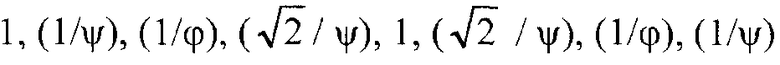 на идентичный вектор. В результате этого получается матрица значений, 8×8:
на идентичный вектор. В результате этого получается матрица значений, 8×8:

В этой матрице масштабных коэффициентов, 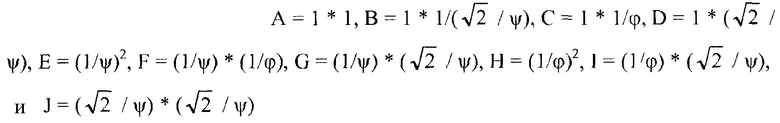 .
.
Так как масштабные множители умножаются на коэффициенты до применения преобразования, масштабные множители A, B, C, D, E, F, G, H, I и J могут быть сдвинуты влево на P позиций, где P - константа согласно количеству битов мантиссы с фиксированной запятой (то есть, битов справа от символа, отделяющего целую часть числа от дробной), используемых в преобразовании. Посредством этого исходные коэффициенты эффективно преобразуются в числа с фиксированной запятой с P битами мантиссы. Другими словами, каждый из коэффициентов в матрице умножается на 2P. Получающиеся в результате значения могут затем быть аппроксимированы целочисленными значениями. Соответственно, A, B, C, D, E, F, G, H, I и J в вышеупомянутой матрице могут быть заменены на 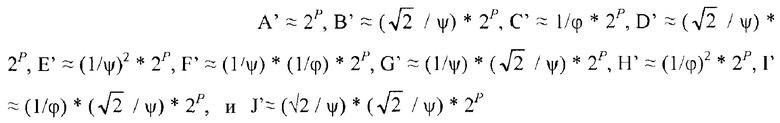
Например, пусть ψ=1,352708058, φ=0,959700091 и P=10. С учетом этих значений ψ, φ и P, можно выбрать масштабные множители A'=1024, B'=757, C'=1067, D'=1071, E'=560, F'=789, G'=792, H'=1112, I'=1116 и J'=1120. Соответственно, в результате может получиться следующая матрица масштабных множителей:
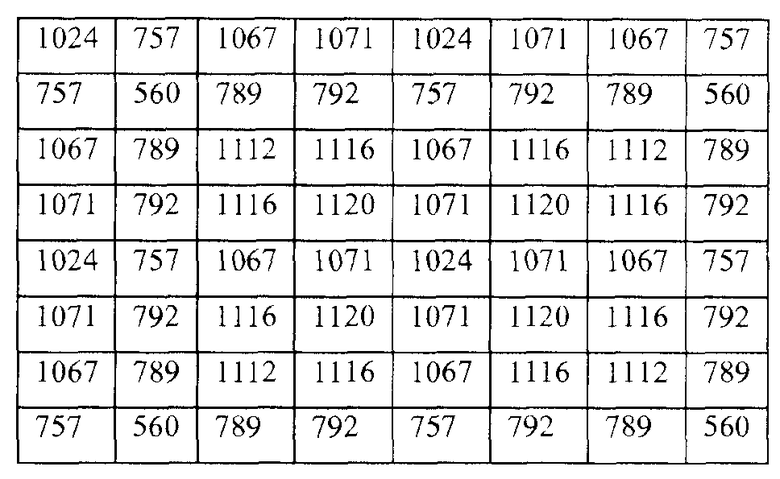
В следующих таблицах суммированы иллюстративные масштабные множители и значения α', β', γ', δ', ε' и ζ', которые могут быть использованы с преобразованием 270.
Таблица 1: Аппроксимации множителей константой, используемые в алгоритме A.
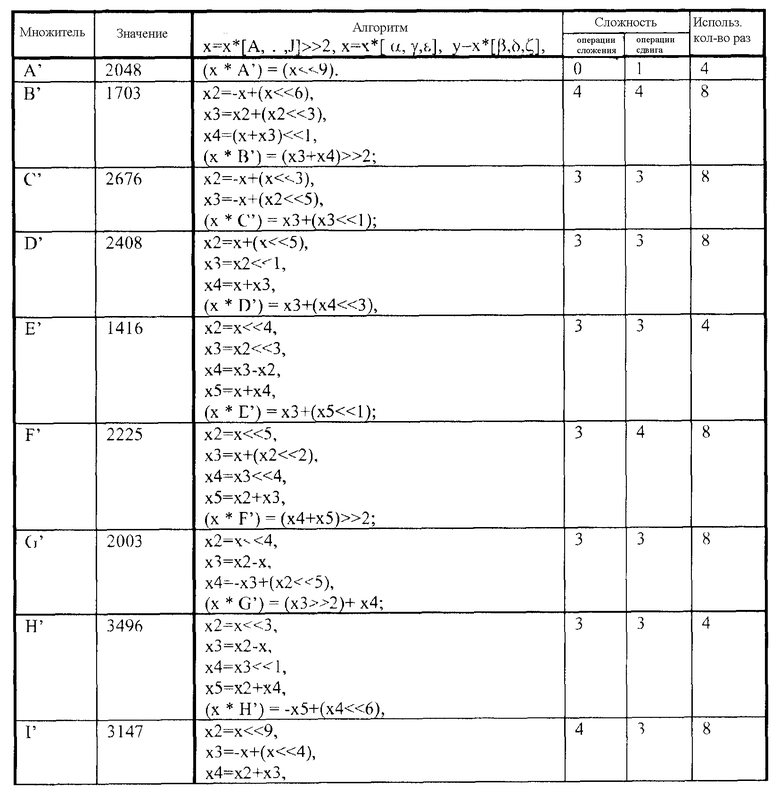
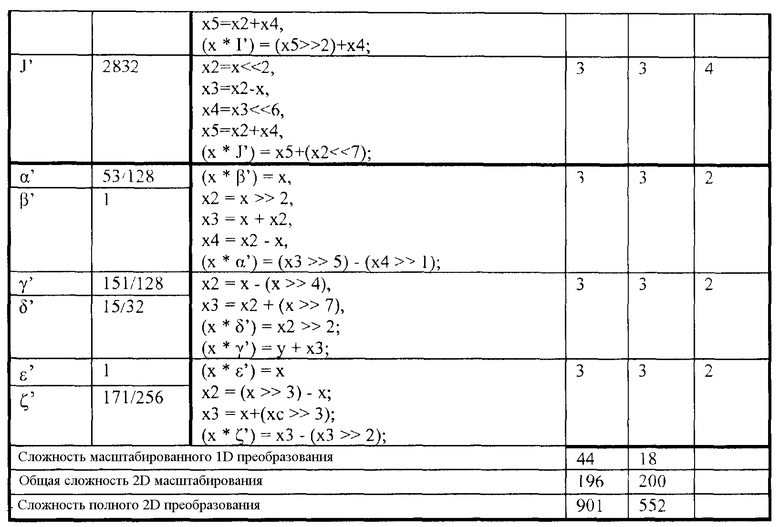
Таблица 2: Аппроксимации множителей константой, используемые в алгоритме B.
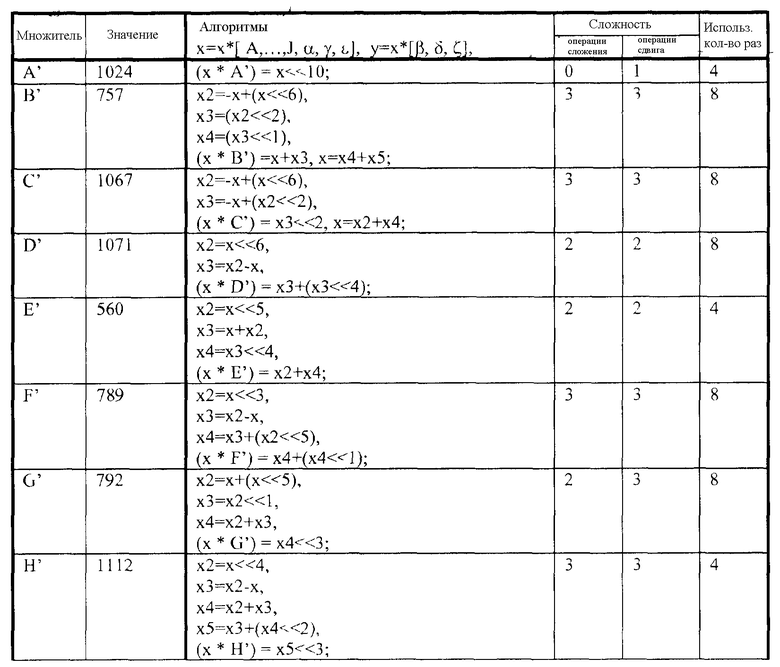
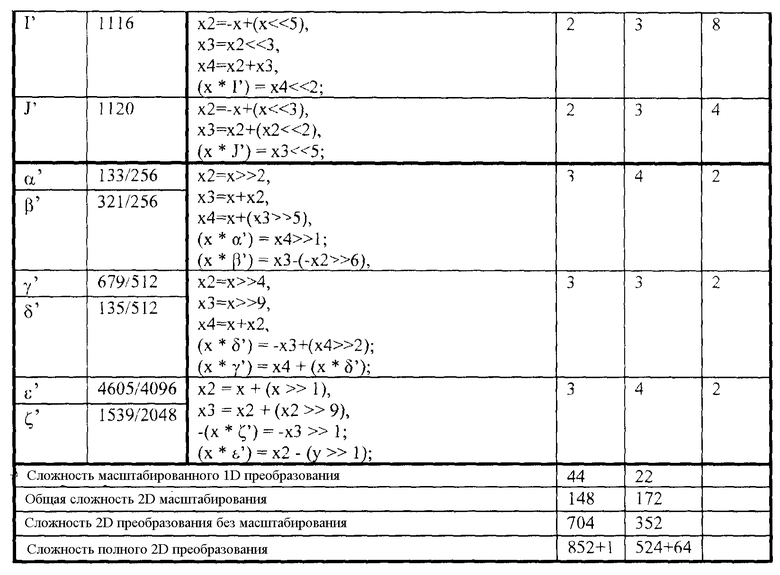
Таблица 3: Аппроксимации множителей константой, используемые в алгоритме C.
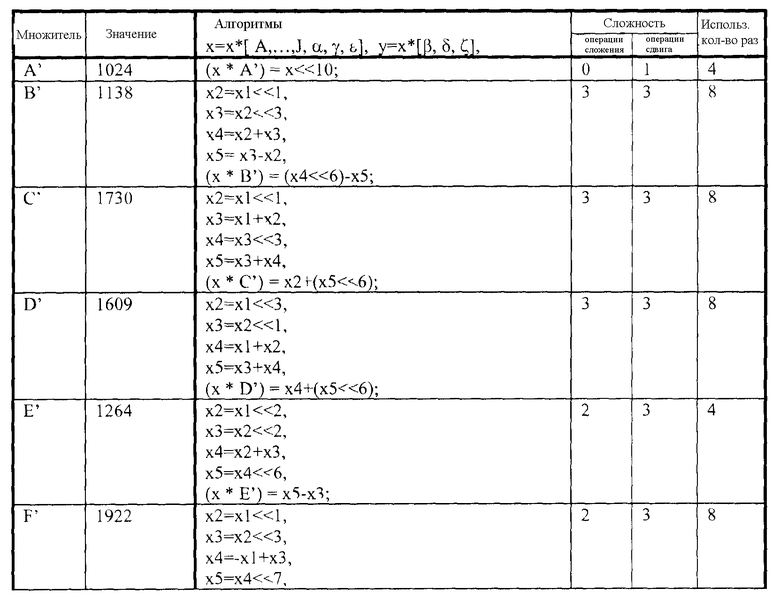
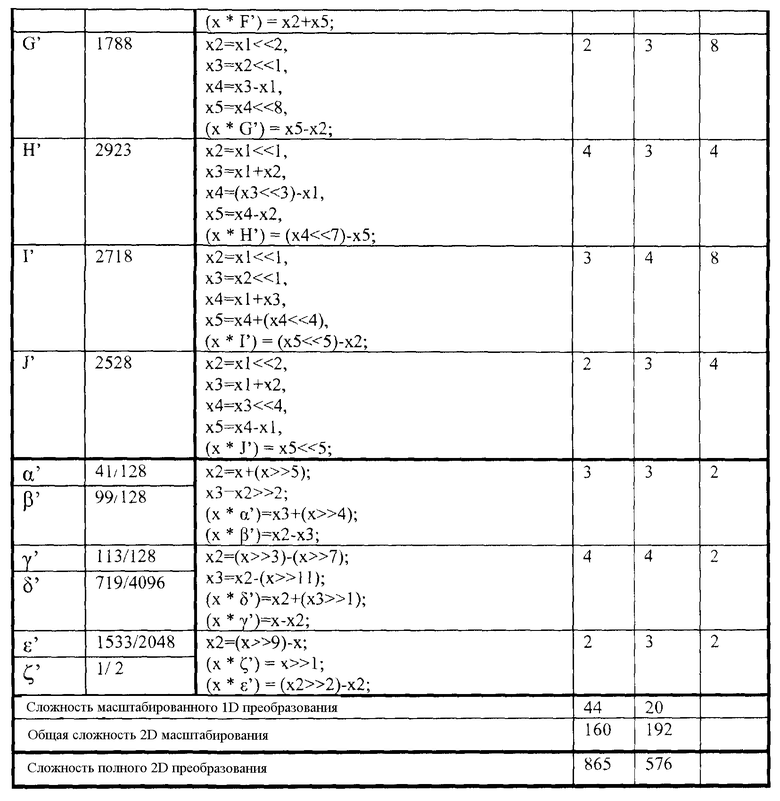
Для иллюстрации того, как модуль 48 IDCT может использовать масштабные множители, постоянные значения и алгоритмы, представленные в вышеупомянутых таблицах, рассмотрим вышеупомянутую таблицу 3. Для применения обратного дискретного косинусного преобразования с использованием значений в таблице 3, модуль 140 ввода в модуле 48 IDCT может принимать матрицу коэффициентов, 8×8. Затем, модуль 142 масштабирования масштабирует коэффициент в позиции [0,0] матрицы множителем A, масштабирует коэффициент в позиции [0,1] матрицы множителем B, масштабирует коэффициент в позиции [0,2] матрицы множителем C, масштабирует коэффициент в позиции [0,3] матрицы множителем D, масштабирует коэффициент в позиции [0,4] матрицы множителем A, масштабирует коэффициент в позиции [0,5] матрицы множителем D, масштабирует коэффициент в позиции [0,6] матрицы множителем C, масштабирует коэффициент в позиции [0,7] матрицы множителем B, масштабирует коэффициент в позиции [1,0] матрицы множителем B, масштабирует коэффициент в позиции [1,1] матрицы множителем E, масштабирует коэффициент в позиции [1,2] матрицы множителем F, масштабирует коэффициент в позиции [1,3] матрицы множителем G, масштабирует коэффициент в позиции [1,4] матрицы множителем B, масштабирует коэффициент в позиции [1,5] матрицы множителем G, масштабирует коэффициент в позиции [1,6] матрицы множителем F, масштабирует коэффициент в позиции [1,7] матрицы множителем E, масштабирует коэффициент в позиции [2,0] матрицы множителем C, масштабирует коэффициент в позиции [2,1] матрицы множителем F, масштабирует коэффициент в позиции [2,2] матрицы множителем H, масштабирует коэффициент в позиции [2,3] матрицы множителем I, масштабирует коэффициент в позиции [2,4] матрицы множителем C, масштабирует коэффициент в позиции [2,5] матрицы множителем I, масштабирует коэффициент в позиции [2,6] матрицы множителем H, масштабирует коэффициент в позиции [2,7] матрицы множителем F, масштабирует коэффициент в позиции [3,0] матрицы множителем D, масштабирует коэффициент в позиции [3,1] матрицы множителем G, масштабирует коэффициент в позиции [3,2] матрицы множителем I, масштабирует коэффициент в позиции [3,3] матрицы множителем J, масштабирует коэффициент в позиции [3,4] матрицы множителем D, масштабирует коэффициент в позиции [3,5] матрицы множителем J, масштабирует коэффициент в позиции [3,6] матрицы множителем I, масштабирует коэффициент в позиции [3,7] матрицы множителем G, масштабирует коэффициент в позиции [4,0] матрицы множителем A, масштабирует коэффициент в позиции [4,1] матрицы множителем B, масштабирует коэффициент в позиции [4,2] матрицы множителем C, масштабирует коэффициент в позиции [4,3] матрицы множителем D, масштабирует коэффициент в позиции [4,4] матрицы множителем A, масштабирует коэффициент в позиции [4,5] матрицы множителем D, масштабирует коэффициент в позиции [4,6] матрицы множителем C, масштабирует коэффициент в позиции [4,7] матрицы множителем B, масштабирует коэффициент в позиции [5,0] матрицы множителем D, масштабирует коэффициент в позиции [5,1] матрицы множителем G, масштабирует коэффициент в позиции [5,2] матрицы множителем I, масштабирует коэффициент в позиции [5,3] матрицы множителем J, масштабирует коэффициент в позиции [5,4] матрицы множителем D, масштабирует коэффициент в позиции [5,5] матрицы множителем J, масштабирует коэффициент в позиции [5,6] матрицы множителем I, масштабирует коэффициент в позиции [5,7] матрицы множителем G, масштабирует коэффициент в позиции [6,0] матрицы множителем C, масштабирует коэффициент в позиции [6,1] матрицы множителем F, масштабирует коэффициент в позиции [6,2] матрицы множителем H, масштабирует коэффициент в позиции [6,3] матрицы множителем I, масштабирует коэффициент в позиции [6,4] матрицы множителем C, масштабирует коэффициент в позиции [6,5] матрицы множителем I, масштабирует коэффициент в позиции [6,6] матрицы множителем H, масштабирует коэффициент в позиции [6,7] матрицы множителем F, масштабирует коэффициент в позиции [7,0] матрицы множителем B, масштабирует коэффициент в позиции [7,1] матрицы множителем E, масштабирует коэффициент в позиции [7,2] матрицы множителем F, масштабирует коэффициент в позиции [7,3] матрицы множителем G, масштабирует коэффициент в позиции [7,4] матрицы множителем B, масштабирует коэффициент в позиции [7,5] матрицы множителем G, масштабирует коэффициент в позиции [7,6] матрицы множителем F и масштабирует коэффициент в позиции [7,7] матрицы множителем E. Когда модуль 142 масштабирования масштабирует эти коэффициенты, модуль 142 масштабирования может использовать значения A=1024, B=1138, C=1730, D=1609, E=1264, F=1922, G=1788, H=2923, I=2718 и J=2528, специфицированные в таблице 6. Эти масштабированные коэффициенты составляют матрицу масштабированных коэффициентов.
После масштабирования коэффициентов модулем 142 масштабирования, модуль 146 обратного преобразования может применять преобразование к каждой вектор-строке матрицы масштабированных коэффициентов для формирования матрицы промежуточных коэффициентов и применять преобразование к каждому вектор-столбцу матрицы промежуточных коэффициентов для формирования матрицы преобразованных коэффициентов. Модуль 146 обратного преобразования может применять преобразование к вектор-строке или вектор-столбцу посредством: вычисления значения x0' суммированием x0 и x4, вычисления значения x4' суммированием x0 и -x4, вычисления значения (x2*α) умножением x2 на значение α, вычисления значения (x6*β) умножением x6 на значение β, вычисления значения (x2*β) умножением x2 на значение β, вычисления значения (x6*α) умножением x6 на значение α, вычисления значения x2' суммированием (x2*α) и -(x6*β), вычисления значения x6' суммированием (x6*α) и (x2*β), вычисления значения x0'' суммированием x0' и x6', вычисления значения x4'' суммированием x4' и x2', вычисления значения x2'' суммированием x4' и -x2', вычисления значения x6'' суммированием x0' и -x6', вычисления значения x7' суммированием x1 и -x7, вычисления значения x1' суммированием x1 и x7, вычисления значения x3' умножением x3 на квадратный корень из двух, вычисления значения x5' умножением x5 на квадратный корень из двух, вычисления значения x7'' суммированием x7' и x5', вычисления значения x3'' суммированием x1' и -x3', вычисления значения x5'' суммированием x7' и -x5', вычисления значения x1'' суммированием x3' и x1', вычисления значения (x7''*ε) умножением x7'' на значение ε, вычисления значения (x7''*ζ) умножением x7'' на значение ζ, вычисления значения (x3''*γ) умножением x3'' на значение γ, вычисления значения (x3''*δ) умножением x3'' на значение δ, вычисления значения (x5''*δ) умножением x5'' на значение δ, вычисления значения (x5''*γ) умножением x5'' на значение γ, вычисления значения (x1''*ε) умножением x1'' на значение ε, вычисления значения x7''' суммированием (x7''*ε) и -(x1''*ζ), вычисления значения x3''' суммированием (x3''*γ) и -(x5''*δ), вычисления значения x5''' суммированием (x5''*γ) и (x3''*δ), вычисления значения x1''' суммированием (x1''*ε) и (x7''*ζ), вычисления значения X0 суммированием x7''' и x0'', вычисления значения X1 суммированием x4'' и x5''', вычисления значения X2 суммированием x2'' и x3''', вычисления значения X3 суммированием x6'' и x7''', вычисления значения X4 суммированием x6'' и -x1''', вычисления значения X5 суммированием x2'' и -x3''', вычисления значения X6 суммированием x4'' и -x5''', вычисления значения X7 суммированием x0'' и -x1''', причем x0, x1, x2, x3, x4, x5, x6, x7 являются коэффициентами в вектор-строке или вектор-столбце, и X1, X2, X3, X4, X5, X6 и X7 являются выходными значениями преобразования. При выполнении этих вычислений, модуль 146 обратного преобразования использует дробные значения α=41/128, β=99/128, γ=1533/2048, δ=1/2, ε=113/128 и ζ=719/4096, умножение на которые вычисляется посредством алгоритма без операций умножения, как указано в таблице 3.
Следующий код содержит иллюстративную реализацию преобразования 270 на языке C:
/* Определение значений масштабных множителей*/
#define A 1024
#define B 1138
#define C 1730
#define D 1609
#define E 1264
#define F 1922
#define G 1788
#define H 2923
#define I 2718
#define J 2528
/* Определение матрицы масштабных множителей */
static int scale [8*8]={
A, B, C, D, A, D, C, B,
B, E, F, G, B, G, F, E,
C, F, H, I, C, I, H, F,
D, G, I, J, D, J, I, G,
A, B, C, D, A, D, C, B,
D, G, I, J, D, J, I, G,
C, F, H, I, C, I, H, F,
B, E, F, G, B, G, F, E
};
void scaled_ld_idct (int *, int *);
void idct (short *P)
{
int block [8*8], block2 [8*8], i;
/* Масштабирование каждого из входных коэффициентов */
for (i=0; i<64; i++)
block[i]=scale[i]*P[i];
/* Добавление смещения к коэффициенту DC */
block[0]+=1<<12;
/* Применение векторного обратного дискретного косинусного преобразования к каждой строке и столбцу блока. */
for (i=0; i<8; i++)
scaled_ld_idct (block + i*8, block2 + i);
for (i=0; i<8; i++)
scaled_ld_idct (block2 + i*8, block + i);
/* Сдвиг вправо каждого из преобразованных коэффициентов */
for (i=0; i<64; i++)
P[i]=block[i]>>13;
}
#define mul_l(y,z)
{
int y2, y3;
y2=(y>>3)-(y>>7);
y3=y2-(y>>11);
z=y2 + (y3>>1);
Y=Y-Y2;
}
#define mul_2(y,z)
{
int y2;
y2=(y>>9)-y;
z=y>>1;
y=(y2>>2)-y2;
}
#define mul_3(y,z)
{
int y2, y3;
y2=y + (y>>5);
y3=y2>>2;
y=y3 + (y>>4);
z=y2-y3;
}
void scaled_ld_idct (int *in, int *out)
{
int x0, xl, x2, x3, x4, x5, x6, x7, xa, xb;
xl=in[l];
x3=in[3];
x5=in[5];
x7=in[7];
xa=xl+x7;
xb=x1-x7;
xl=xa+x3;
x3=xa-x3;
x7=xb+x5;
x5=xb-x5;
mul_l(x3, xa);
mul_l(x5, xb);
x3=x3-xb;
x5=x5 + xa;
mul_2(xl, xa);
mu1_2(x7, xb);
xl=xl+xb;
x7=x7-xa;
x0=in[0];
x2=in[2];
x4=in[4];
x6=in[6];
mul_3(x2, xa);
mul_3(x6, xb);
x2=x2-xb;
x6=x6+xa;
xa=x0+x4;
xb=x0-x4;
x0=xa+x6;
x6=xa-x6;
x4=xb+x2;
x2=xb-x2;
out[0*8]=x0+xl;
out[1*8]=x4+x5;
out[2*8]=x2+x3;
out[3*8]=x6+x7;
out[4*8]=x6-x7;
out[5*8]=x2-x3;
out[6*8]=x4-x5;
out[7*8]=x0-xl;
}
void scaled_ld_fdct (int *, int *);
void fdct (short *P)
{
int block[8*8], block2[8*8], i;
for (i=0; i<64; i++)
block[i]=P[i]<< 7;
for (i=0; i<8; i++)
scaled_ld_fdct (block + i, block2 + i*8);
for (i=0; i<8; i++)
scaled_ld_fdct (block2 + i, block + i*8);
for (i=0; i<64; i++)
P[i]=(block[i]*scale[i]+0x7FFFF-(block[i]>>31))>>20;
}
void scaled_ld_fdct (int *in, int *out)
{
int x0, xl, x2, x3, x4, x5, x6, x7, xa, xb;
x0=in[0*8] + in[7*8];
x1=in[0*8] - in[7*8];
x4=in[l*8] + in[6*8];
x5=in[l*8] - in[6*8];
x2=in[2*8] + in[5*8];
x3=in[2*8] - in[5*8];
x6=in[3*8] + in[4*8];
x7=in[3*8]-in[4*8];
mul_l(x3, xa);
mul_l(x5, xb);
x3=x3+xb;
x5=x5-xa;
mul_2(xl, xa);
mul_2(x7, xb);
xl=xl-xb;
x7=x7+xa;
xa=xl+x3;
x3=xl-x3;
xb=x7+x5;
x5=x7-x5;
xl=xa + xb;
x7=xa-xb;
xa=x0+x6;
x6=x0-x6;
xb=x4+x2;
x2=x4-x2;
x0=xa+xb;
x4=xa-xb;
mul_3(x2, xa);
mul_3(x6, xb);
x2=xb+x2;
x6=x6-xa;
out[0]=x0;
out[1]=xl;
out[2]=x2;
out[3]=x3;
out[4]=x4;
out[5]=x5;
out[6]=x6;
out[7]=x7.
}
Фиг.11 является блок-схемой, изображающей иллюстративное масштабированное преобразование 280, используемое модулем 214 прямого преобразования. На фиг.11, векторы X0, X1, X2, X3, X4, X5, X6 и X7 представляют выходные коэффициенты, и векторы x0, x1, x2, x3, x4, x5, x6 и x7 представляют входные значения. Значение, связанное с линией после кружка с символом "+" внутри, является результатом добавления значений, связанных со стрелками, которые указывают в этот кружок. Значение, связанное с линией после кружка с символом "x" внутри, является результатом умножения коэффициента, помещенного рядом с кружком, на значения, связанные с линиями, которые проходят через кружки. Символ "-" рядом со стрелкой представляет взятие со знаком минус значения, связанного со стрелкой. Например, если значение "10" связано со стрелкой перед символом "-", то со стрелкой после символа "-" связано значение "-10". Кроме того, следует отметить, что описанные выше способы уменьшения ошибки округления, использующие коэффициенты, взятые со знаком минус, и вычитание могут использоваться в алгоритме 190.
В преобразовании 280, выходные значения X0 по X7 умножаются на множители 1, φ, φ, ψ, 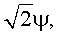
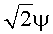
Способы, описанные в этом документе, могут быть реализованы аппаратными средствами, программными средствами, программно-аппаратными средствами или любой их комбинацией. Любые признаки, описанные как модули или компоненты, могут быть реализованы вместе в устройстве логической ИС или отдельно как дискретные, но взаимодействующие логические устройства. Если способы реализованы в программных средствах, то они могут быть реализованы, по меньшей мере, частично машиночитаемым носителем информации, содержащим команды, которые при исполнении выполняют один или несколько способов, описанных выше. Машиночитаемый носитель информации может являться частью компьютерного программного продукта, который может включать в себя компоновочные материалы. Машиночитаемый носитель информации может содержать оперативное запоминающее устройство (RAM), например, синхронную динамическую память (SDRAM), постоянное запоминающее устройство (ROM), энергонезависимое оперативное запоминающее устройство (NVRAM), электрически стираемое программируемое постоянное запоминающее устройство (EEPROM), флэш-память, магнитный или оптический носитель информации и т.п. Упомянутые способы, дополнительно или в качестве альтернативы, могут быть реализованы, по меньшей мере, частично машиночитаемой коммуникационной средой, которая несет или передает код в виде команд или структур данных, и к которым можно получать доступ, читать их и/или исполнять посредством компьютера.
Код может исполняться одним или несколькими процессорами, например, одним или несколькими цифровыми сигнальными процессорами (DSP), универсальными микропроцессорами, специализированными интегральными схемами (ASIC), программируемыми пользователем логическими матрицами (FPGA) или другими эквивалентными интегральными схемами или дискретными логическими схемами. Соответственно, термин "процессор", используемый в данном документе, может относиться к любой из вышеизложенных структур или любой другой структуре, подходящей для реализации способов, описанных в данном документе. Кроме того, в некоторых аспектах, функциональные возможности, описанные в данном документе, могут быть обеспечены в специализированных программных модулях или аппаратных модулях, сконфигурированных для кодирования и декодирования, или встроенных в комбинированный видео кодер-декодер (CODEC).
Были описаны различные варианты осуществления изобретения. Эти и другие варианты осуществления входят в объем следующей формулы изобретения.
| название | год | авторы | номер документа |
|---|---|---|---|
| ЭФФЕКТИВНЫЕ АППРОКСИМАЦИИ С ФИКСИРОВАННОЙ ЗАПЯТОЙ ПРЯМОГО И ОБРАТНОГО ДИСКРЕТНЫХ КОСИНУСНЫХ ПРЕОБРАЗОВАНИЙ | 2007 |
|
RU2417423C2 |
| УМЕНЬШЕНИЕ ОШИБОК ВО ВРЕМЯ ВЫЧИСЛЕНИЯ ОБРАТНОГО ДИСКРЕТНОГО КОСИНУСНОГО ПРЕОБРАЗОВАНИЯ | 2007 |
|
RU2439682C2 |
| СНИЖЕНИЕ ОШИБОК В ХОДЕ ВЫЧИСЛЕНИЯ ОБРАТНОГО ДИСКРЕТНОГО КОСИНУСНОГО ПРЕОБРАЗОВАНИЯ | 2007 |
|
RU2419855C2 |
| ПРЕОБРАЗОВАНИЯ С ОБЩИМИ МНОЖИТЕЛЯМИ | 2007 |
|
RU2429531C2 |
| Декодер кодов Боуза-Чоудхури-Хоквингема | 1990 |
|
SU1783627A1 |
| СПОСОБ ОЦЕНКИ КАЧЕСТВА ЛЬНЯНОЙ ТРЕСТЫ | 2006 |
|
RU2312177C1 |
| СПОСОБ ПРОГНОЗИРОВАНИЯ РАЗВИТИЯ МУЛЬТИФАКТОРНОЙ ПАТОЛОГИИ У ДЕТЕЙ, РОЖДЕННЫХ С ПОМОЩЬЮ ВСПОМОГАТЕЛЬНЫХ РЕПРОДУКТИВНЫХ ТЕХНОЛОГИЙ | 2011 |
|
RU2456911C1 |
| БЫСТРОЕ ВЫЧИСЛЕНИЕ ПРОИЗВЕДЕНИЙ ПОСРЕДСТВОМ ДВОИЧНЫХ ДРОБЕЙ СО ЗНАКОСИММЕТРИЧНЫМИ ОШИБКАМИ ОКРУГЛЕНИЯ | 2008 |
|
RU2468422C2 |
| Способ прогнозирования риска развития преэклампсии | 2016 |
|
RU2642939C1 |
| БЫСТРЫЕ АЛГОРИТМЫ ДЛЯ ВЫЧИСЛЕНИЯ 5-ТОЧЕЧНОГО DCT-II, DCT-IV И DST-IV, И АРХИТЕКТУРЫ | 2008 |
|
RU2464540C2 |
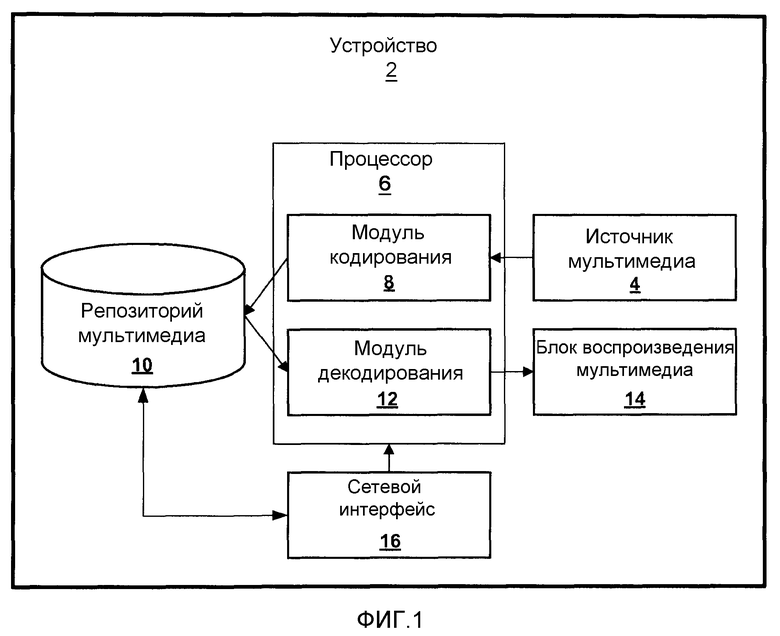
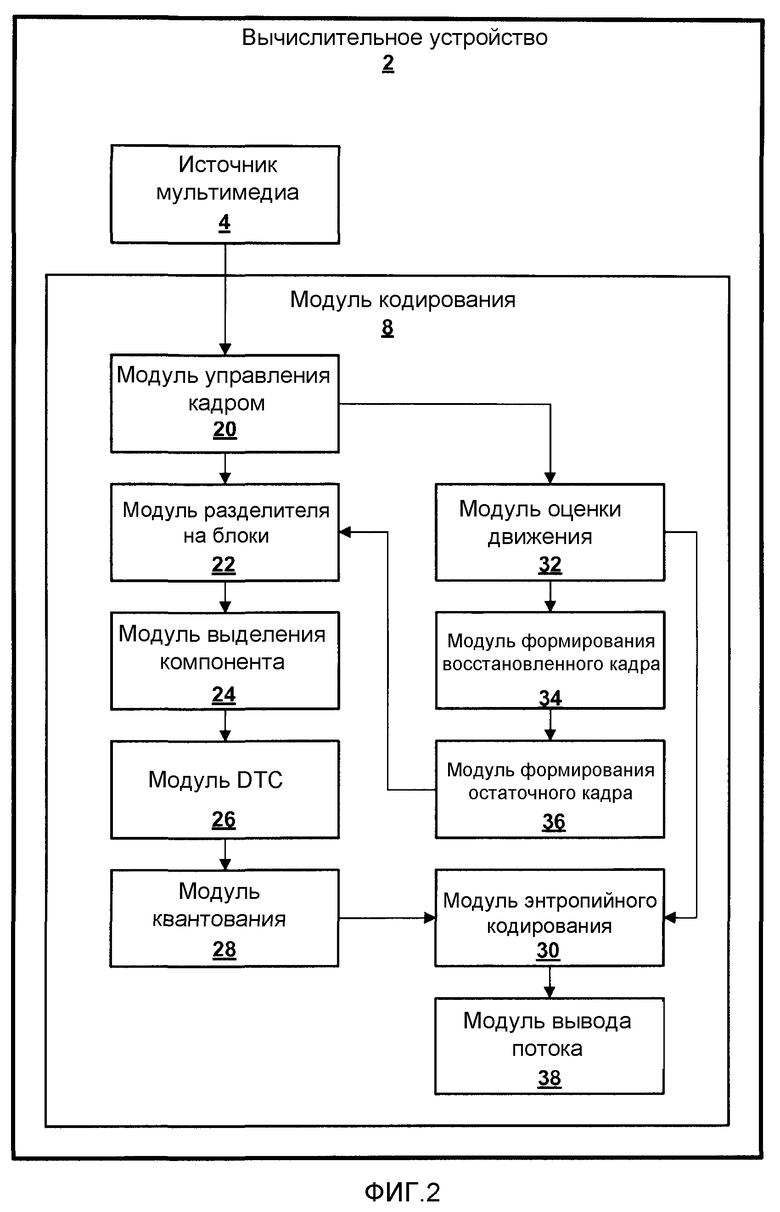
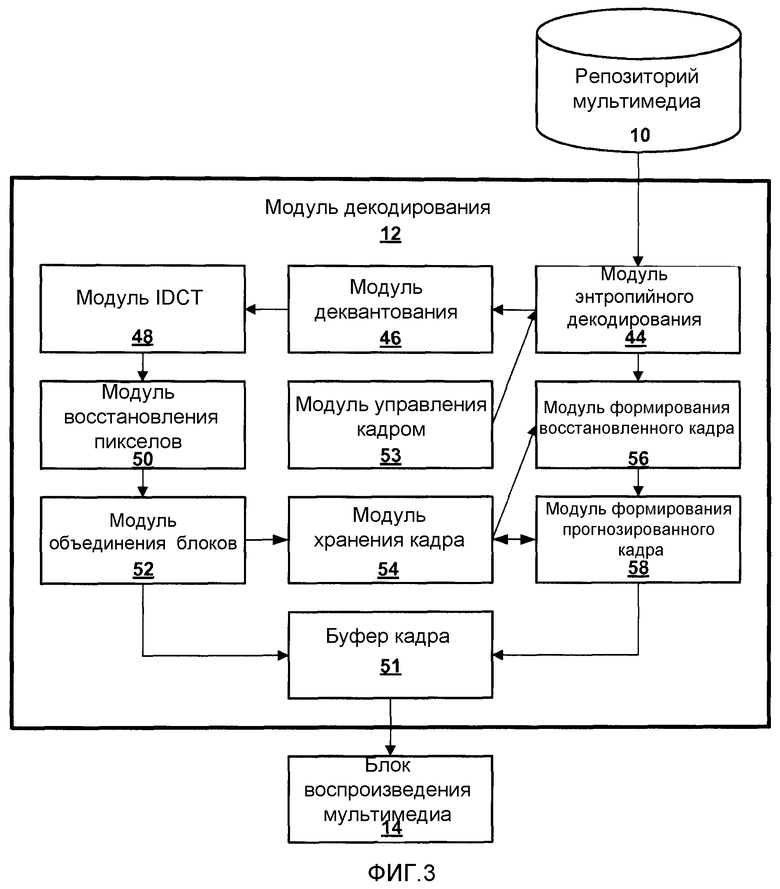
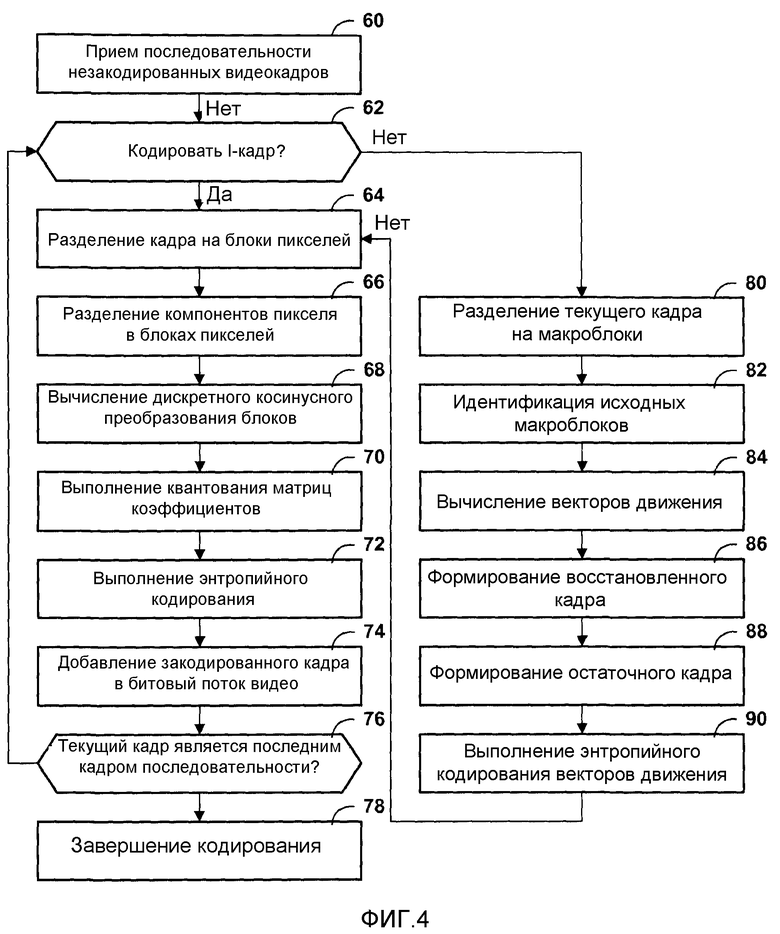
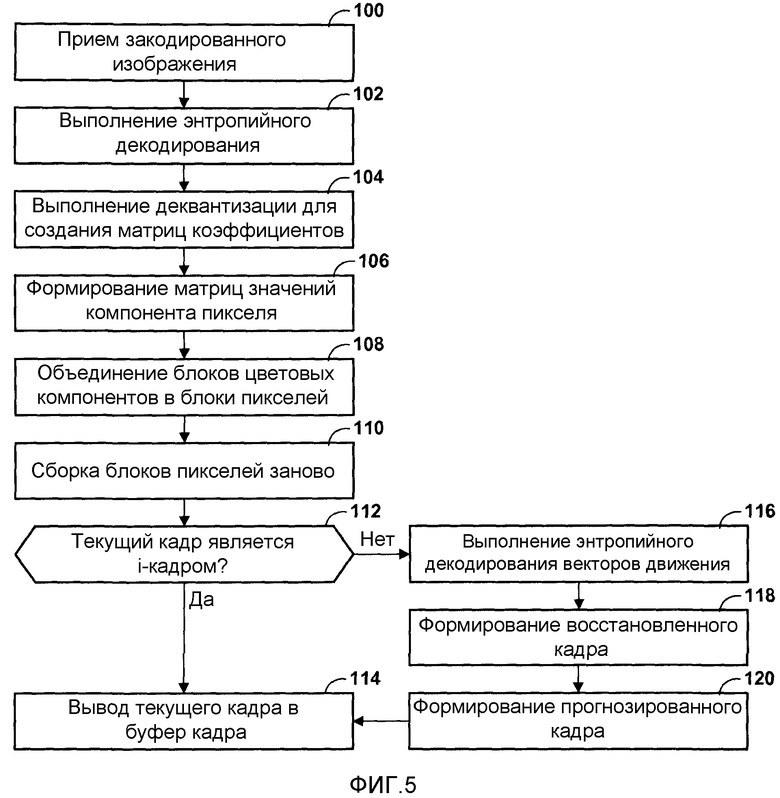
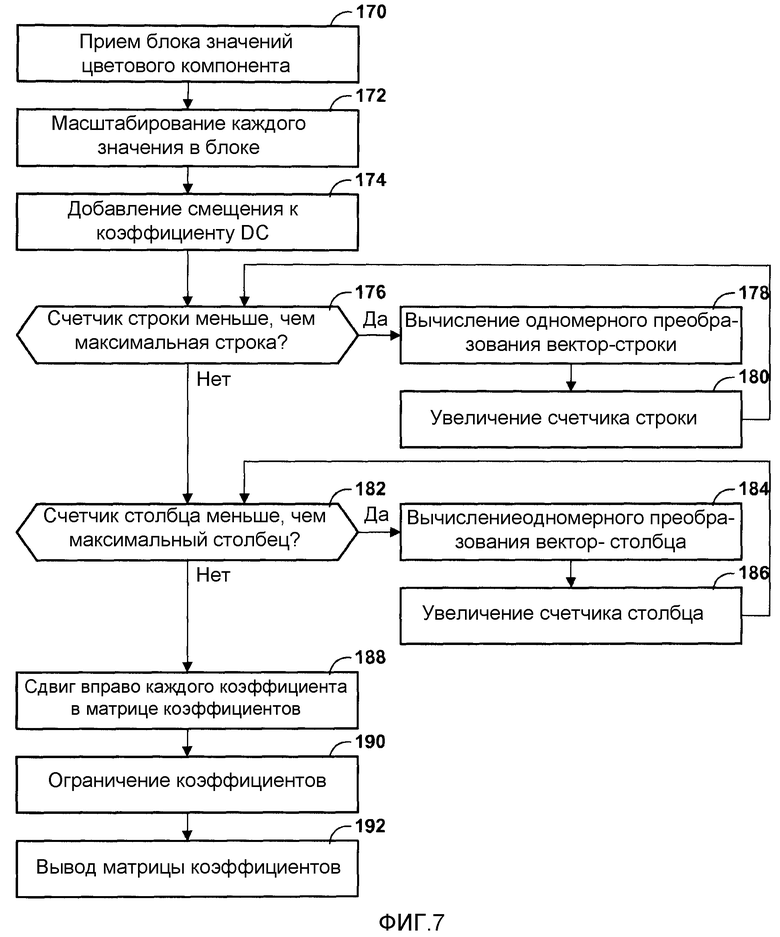
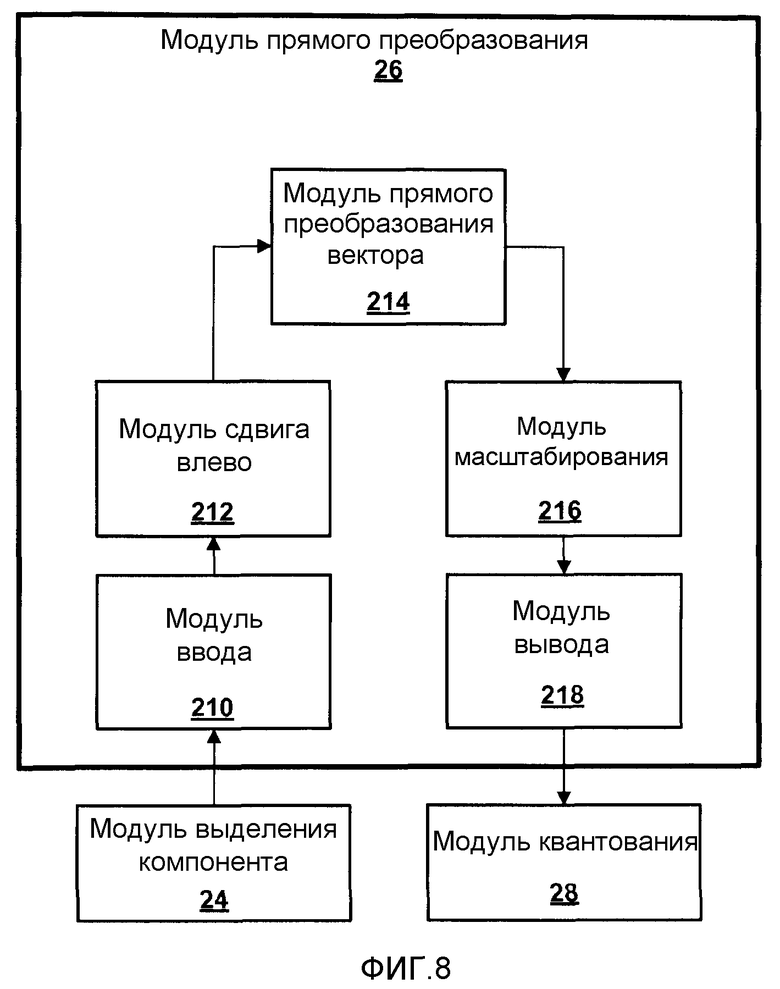
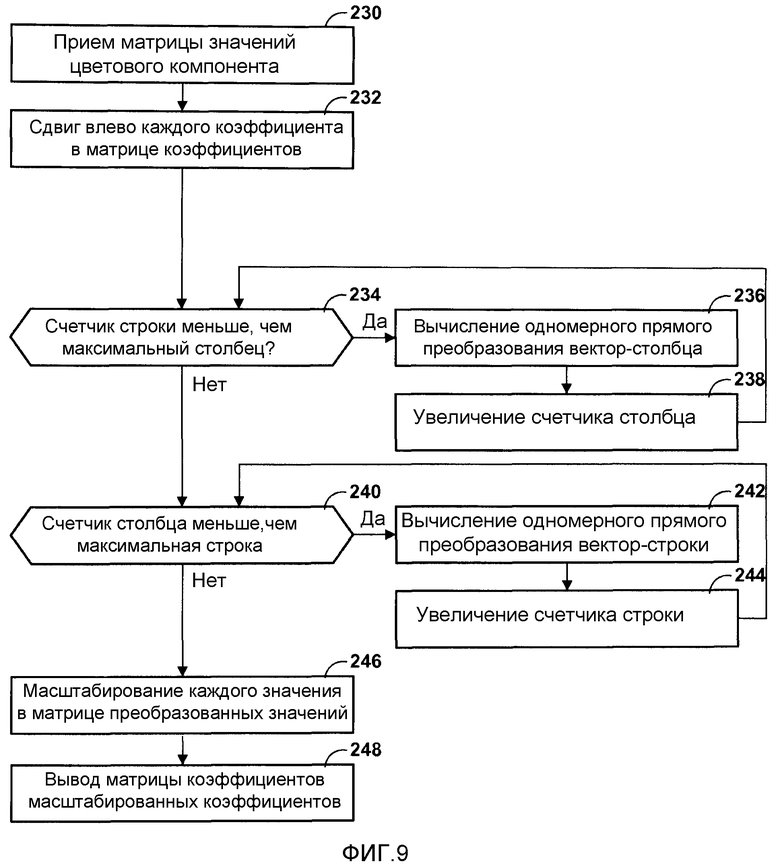
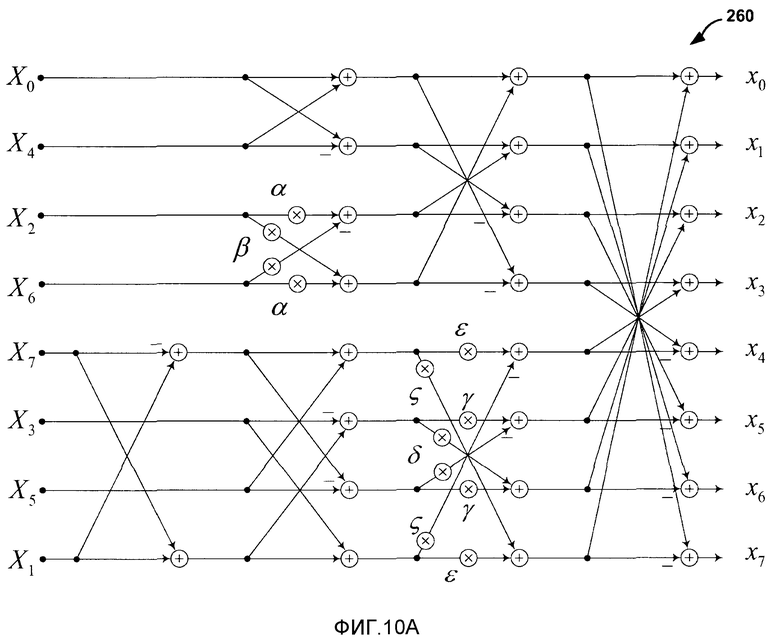
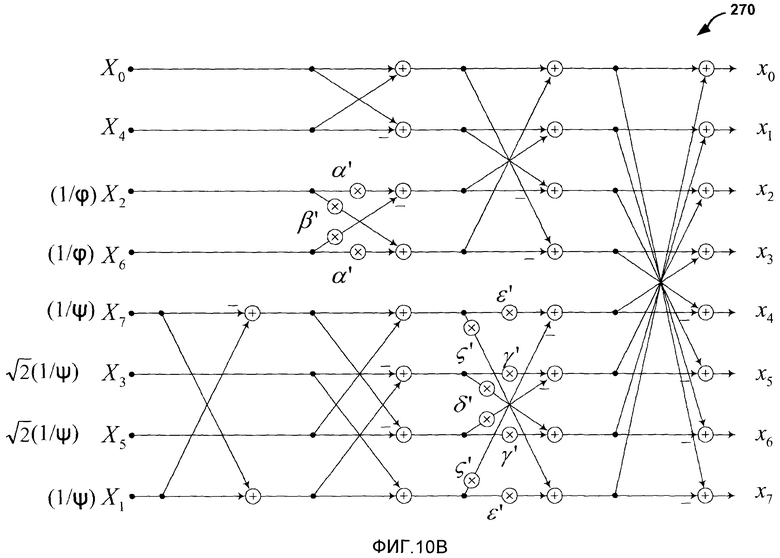
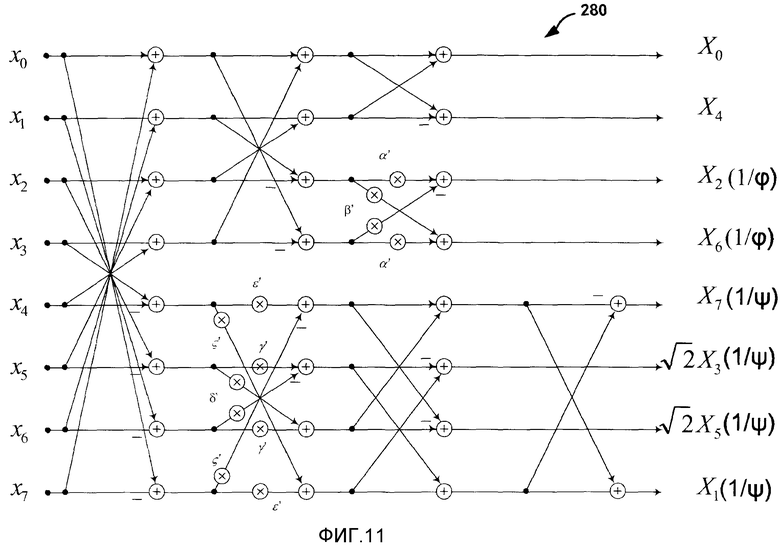
Группа изобретений относится к способу и устройствам для сжатия и отображения изображения. Техническим результатом является исключение ошибок аппроксимации вычисления обратного дискретного косинусного преобразования с использованием вычислений с фиксированной запятой. Способ содержит этапы, на которых масштабируют каждый коэффициент в матрице закодированных коэффициентов с размерами 8×8 одним из множителей для формирования матрицы масштабированных коэффициентов, повторно применяют масштабированные одномерные преобразования с фиксированной точкой для преобразования матрицы масштабированных коэффициентов в матрицу преобразованных коэффициентов, сдвигают вправо преобразованные коэффициенты для формирования матрицы скорректированных коэффициентов, причем каждый скорректированный коэффициент в матрице скорректированных коэффициентов аппроксимирует соответствующее значение в матрице значений, которые можно сформировать с применением идеального двумерного обратного дискретного косинусного преобразования к матрице закодированных коэффициентов, отображают блок пикселей с размерами 8х8, причем каждый пиксель в блоке пикселей включает в себя значение компонента пикселя с учетом скорректированного коэффициента. 4 н. и 23 з.п. ф-лы, 12 ил., 3 табл.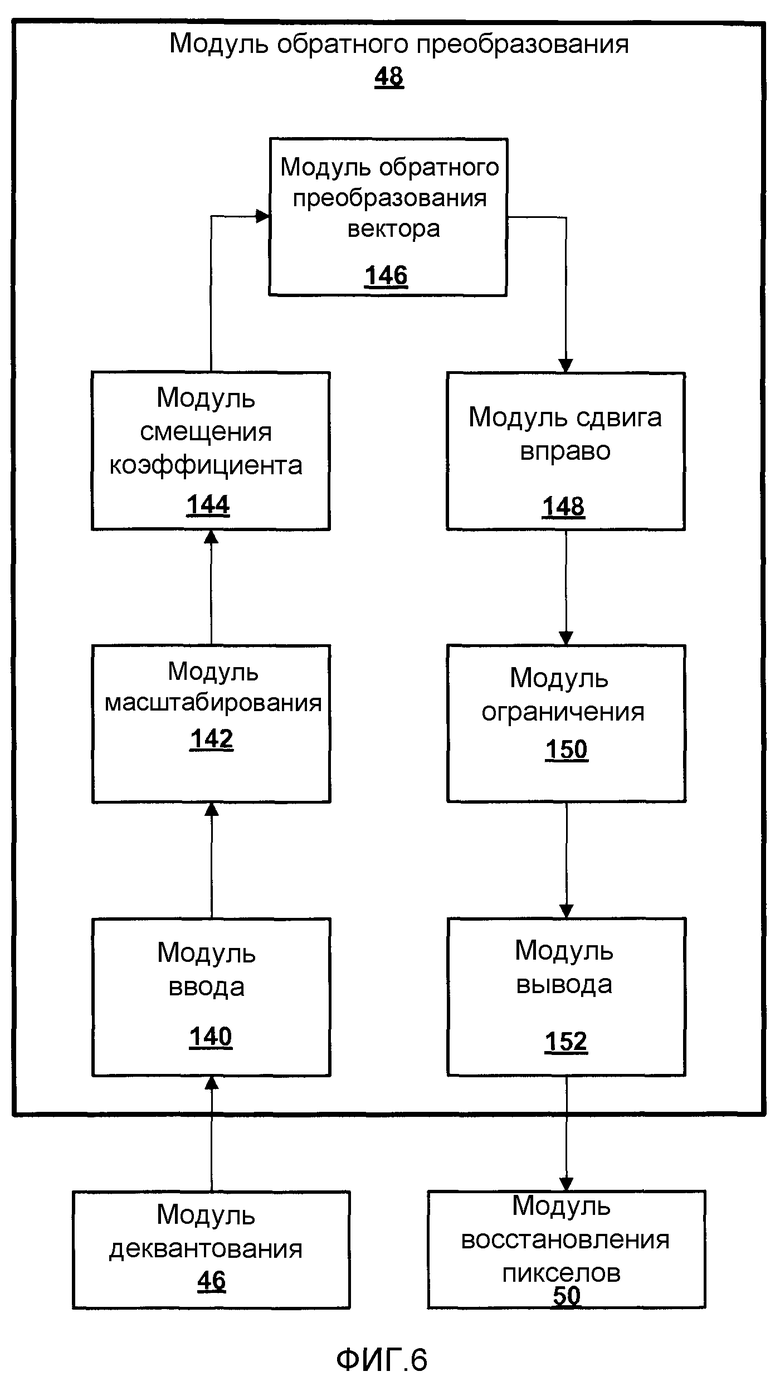
1. Способ сжатия и отображения изображения, причем способ выполняется на компьютере и содержит этапы, на которых:
масштабируют каждый коэффициент в матрице закодированных коэффициентов размером 8×8 одним из множителя A, множителя B, множителя C, множителя D, множителя E, множителя F, множителя G, множителя H, множителя I или множителя J для формирования матрицы масштабированных коэффициентов,
причем A=1024, B=1138, C=1730, D=1609, E=1264, F=1922, G=1788, H=2923, I=2718 и J=2528,
используют повторные применения масштабированного одномерного преобразования с фиксированной запятой для преобразования матрицы масштабированных коэффициентов в матрицу преобразованных коэффициентов,
сдвигают вправо преобразованные коэффициенты в матрице преобразованных коэффициентов для формирования матрицы скорректированных коэффициентов,
причем каждый скорректированный коэффициент в матрице скорректированных коэффициентов аппроксимирует соответствующее значение в матрице значений, которые можно сформировать с применением идеального двумерного обратного дискретного косинусного преобразования ("IDCT") к матрице закодированных коэффициентов,
отображают блок пикселей размером 8×8, причем каждый пиксель в блоке пикселей размером 8×8 включает в себя значение компонента пикселя на основе скорректированного коэффициента в матрице скорректированных коэффициентов,
при этом этап масштабирования коэффициентов в матрице коэффициентов содержит этапы, на которых:
масштабируют коэффициент в позиции [0,0] матрицы закодированных коэффициентов множителем A,
масштабируют коэффициент в позиции [0,1] матрицы закодированных коэффициентов множителем B,
масштабируют коэффициент в позиции [0,2] матрицы закодированных коэффициентов множителем C,
масштабируют коэффициент в позиции [0,3] матрицы закодированных коэффициентов множителем D,
масштабируют коэффициент в позиции [0,4] матрицы закодированных коэффициентов множителем A,
масштабируют коэффициент в позиции [0,5] матрицы закодированных коэффициентов множителем D,
масштабируют коэффициент в позиции [0,6] матрицы закодированных коэффициентов множителем C,
масштабируют коэффициент в позиции [0,7] матрицы закодированных коэффициентов множителем В,
масштабируют коэффициент в позиции [1,0] матрицы закодированных коэффициентов множителем B,
масштабируют коэффициент в позиции [1,1] матрицы закодированных коэффициентов множителем E,
масштабируют коэффициент в позиции [1,2] матрицы закодированных коэффициентов множителем F,
масштабируют коэффициент в позиции [1,3] матрицы закодированных коэффициентов множителем G,
масштабируют коэффициент в позиции [1,4] матрицы закодированных коэффициентов множителем B,
масштабируют коэффициент в позиции [1,5] матрицы закодированных коэффициентов множителем G,
масштабируют коэффициент в позиции [1,6] матрицы закодированных коэффициентов множителем F,
масштабируют коэффициент в позиции [1,7] матрицы закодированных коэффициентов множителем E,
масштабируют коэффициент в позиции [2,0] матрицы закодированных коэффициентов множителем C,
масштабируют коэффициент в позиции [2,1] матрицы закодированных коэффициентов множителем F,
масштабируют коэффициент в позиции [2,2] матрицы закодированных коэффициентов множителем H,
масштабируют коэффициент в позиции [2,3] матрицы закодированных коэффициентов множителем I,
масштабируют коэффициент в позиции [2,4] матрицы закодированных коэффициентов множителем C,
масштабируют коэффициент в позиции [2,5] матрицы закодированных коэффициентов множителем I,
масштабируют коэффициент в позиции [2,6] матрицы закодированных коэффициентов множителем H,
масштабируют коэффициент в позиции [2,7] матрицы закодированных коэффициентов множителем F,
масштабируют коэффициент в позиции [3,0] матрицы закодированных коэффициентов множителем D,
масштабируют коэффициент в позиции [3,1] матрицы закодированных коэффициентов множителем G,
масштабируют коэффициент в позиции [3,2] матрицы закодированных коэффициентов множителем I,
масштабируют коэффициент в позиции [3,3] матрицы закодированных коэффициентов множителем J,
масштабируют коэффициент в позиции [3,4] матрицы закодированных коэффициентов множителем D,
масштабируют коэффициент в позиции [3,5] матрицы закодированных коэффициентов множителем J,
масштабируют коэффициент в позиции [3,6] матрицы закодированных коэффициентов множителем I,
масштабируют коэффициент в позиции [3,7] матрицы закодированных коэффициентов множителем G,
масштабируют коэффициент в позиции [4,0] матрицы закодированных коэффициентов множителем A,
масштабируют коэффициент в позиции [4,1] матрицы закодированных коэффициентов множителем B,
масштабируют коэффициент в позиции [4,2] матрицы закодированных коэффициентов множителем C,
масштабируют коэффициент в позиции [4,3] матрицы закодированных коэффициентов множителем D,
масштабируют коэффициент в позиции [4,4] матрицы закодированных коэффициентов множителем A,
масштабируют коэффициент в позиции [4,5] матрицы закодированных коэффициентов множителем D,
масштабируют коэффициент в позиции [4,6] матрицы закодированных коэффициентов множителем С,
масштабируют коэффициент в позиции [4,7] матрицы закодированных коэффициентов множителем B,
масштабируют коэффициент в позиции [5,0] матрицы закодированных коэффициентов множителем D,
масштабируют коэффициент в позиции [5,1] матрицы закодированных коэффициентов множителем G,
масштабируют коэффициент в позиции [5,2] матрицы закодированных коэффициентов множителем I,
масштабируют коэффициент в позиции [5,3] матрицы закодированных коэффициентов множителем J,
масштабируют коэффициент в позиции [5,4] матрицы закодированных коэффициентов множителем D,
масштабируют коэффициент в позиции [5,5] матрицы закодированных коэффициентов множителем J,
масштабируют коэффициент в позиции [5,6] матрицы закодированных коэффициентов множителем I,
масштабируют коэффициент в позиции [5,7] матрицы закодированных коэффициентов множителем G,
масштабируют коэффициент в позиции [6,0] матрицы закодированных коэффициентов множителем C,
масштабируют коэффициент в позиции [6,1] матрицы закодированных коэффициентов множителем F,
масштабируют коэффициент в позиции [6,2] матрицы закодированных коэффициентов множителем H,
масштабируют коэффициент в позиции [6,3] матрицы закодированных коэффициентов множителем I,
масштабируют коэффициент в позиции [6,4] матрицы закодированных коэффициентов множителем C,
масштабируют коэффициент в позиции [6,5] матрицы закодированных коэффициентов множителем I,
масштабируют коэффициент в позиции [6,6] матрицы закодированных коэффициентов множителем H,
масштабируют коэффициент в позиции [6,7] матрицы закодированных коэффициентов множителем F,
масштабируют коэффициент в позиции [7,0] матрицы закодированных коэффициентов множителем B,
масштабируют коэффициент в позиции [7,1] матрицы закодированных коэффициентов множителем E,
масштабируют коэффициент в позиции [7,2] матрицы закодированных коэффициентов множителем F,
масштабируют коэффициент в позиции [7,3] матрицы закодированных коэффициентов множителем G,
масштабируют коэффициент в позиции [7,4] матрицы закодированных коэффициентов множителем B,
масштабируют коэффициент в позиции [7,5] матрицы закодированных коэффициентов множителем G,
масштабируют коэффициент в позиции [7,6] матрицы закодированных коэффициентов множителем F,
масштабируют коэффициент в позиции [7,7] матрицы закодированных коэффициентов множителем E,
при этом этап применения преобразования или к вектор-строке или к вектор-столбцу содержит этапы, на которых:
вычисляют значение x0' суммированием x0 и x4,
вычисляют значение x4' суммированием x0 и -x4,
вычисляют значение (x2* α) умножением x2 на значение α,
вычисляют значение (x6* β) умножением x6 на значение β,
вычисляют значение (x2* β) умножением x2 на значение β,
вычисляют значение (x6* α) умножением x6 на значение α,
вычисляют значение x2' суммированием (x2* α) и -(x6* β),
вычисляют значение x6' суммированием (x6* α) и (x2* β),
вычисляют значение x0'' суммированием x0' и x6',
вычисляют значение x4'' суммированием x4' и x2',
вычисляют значение x2'' суммированием x4' и -x2',
вычисляют значение x6'' суммированием x0' и -x6',
вычисляют значение x7' суммированием x1 и -x7,
вычисляют значение x1' суммированием x1 и x7,
вычисляют значение x7'' суммированием x7' и x5',
вычисляют значение x3'' суммированием x1' и -x3',
вычисляют значение x5'' суммированием x7' и -x5',
вычисляют значение x1'' суммированием x3' и x1',
вычисляют значение (x7''* ε) умножением x7'' на значение ε,
вычисляют значение (x7''* ζ) умножением x7'' на значение ζ,
вычисляют значение (x3''* γ) умножением x3'' на значение γ,
вычисляют значение (x3''* δ) умножением x3'' на значение δ,
вычисляют значение (x5''* δ) умножением x5'' на значение δ,
вычисляют значение (x5''* γ) умножением x5'' на значение γ,
вычисляют значение (x1''* ζ) умножением x1'' на значение ζ,
вычисляют значение (x1''* ε) умножением x1'' на значение ε,
вычисляют значение x7''' суммированием (x7''* ε) и -(x1''* ζ),
вычисляют значение x3''' суммированием (x3''* γ) и -(x5''* δ),
вычисляют значение x5''' суммированием (x5''* γ) и (x3''* δ),
вычисляют значение x1''' суммированием (x1''* ε) и (x7''* ζ),
вычисляют значение Х0 суммированием x7''' и x0'',
вычисляют значение X1 суммированием x4'' и x5''',
вычисляют значение X2 суммированием x2'' и x3''',
вычисляют значение X3 суммированием x6'' и x7''',
вычисляют значение X4 суммированием x6'' и -x1''',
вычисляют значение X5 суммированием x2'' и -x3''',
вычисляют значение X6 суммированием x4'' и -x5''', и
вычисляют значение X7 суммированием x0'' и -x1''',
причем x0, x1, x2, x3, x4, x5, x6, x7 являются коэффициентами в вектор-строке или вектор-столбце,
причем X1, X2, X3, X4, X5, X6 и X7 являются выходными значениями преобразования, и
причем α=41/128, β=99/128, γ=113/128, δ=719/4096, ε=1533/2048 и ζ=1/2.
2. Способ по п.1, в котором использование повторных применений масштабированного одномерного преобразования с фиксированной запятой заключается в том, что применяют упомянутое преобразование к коэффициентам в одном из векторов-строк или в одном из векторов-столбцов без использования операций умножения или деления.
3. Способ по п.2, в котором вычисление значения (x1* ε) посредством умножения x1 на значение ε и вычисление значения (x1* ζ) посредством умножения x1 на значение ζ заключается в том, что выполняют следующую последовательность арифметических операций:
- вычисляют значение y1, причем y1=(x1>>9)-x1,
- вычисляют значение (x1* ζ) сдвигом вправо x3 на одну позицию, и
- вычисляют значение (x1* ε) вычитанием y1 из (y1>>2); и
при этом вычисление значения (x7*ε) посредством умножения x7 на значение ε и вычисление значения (x7* ζ) посредством умножения x7 на значение ζ заключается в том, что выполняют следующую последовательность арифметических операций:
- вычисляют значение y1', причем y1'=(x7>>9)-x7,
- вычисляют значение (x7* ζ) сдвигом вправо x7 на одну позицию, и
- вычисляют значение (x7* ε) вычитанием y1' из (y1'>>2), и
при этом вычисление значения (x1'' *ε) посредством умножения x1'' на значение ε и вычисление значения (x1''* ζ) посредством умножения x1'' на значение ζ заключается в том, что выполняют следующую последовательность арифметических операций:
- вычисляют значение y1'', причем y1''=(x1''>>9)-x1'',
- вычисляют значение (x1''* ζ) сдвигом вправо x1'' на одну позицию, и
- вычисляют значение (x1''* ε) вычитанием y1'' из (y1''>>2), и
при этом вычисление значения (x7''* ε) посредством умножения x7'' на значение ε и вычисление значения (x7''* ζ) посредством умножения x7'' на значение ζ заключается в том, что выполняют следующую последовательность арифметических операций:
- вычисляют значение y1''', причем y1'''=(x7''>>9)-x7'',
- вычисляют значение (х7''* ζ) сдвигом вправо x7'' на одну позицию, и
- вычисляют значение (x7''* ε) вычитанием y1''' из (y1'''>>2).
4. Способ по п.2, в котором вычисление значения (x3* γ) посредством умножения x3 на значение γ и вычисление значения (x3* δ) посредством умножения x3 на значение δ заключается в том, что выполняют следующую последовательность арифметических операций:
- вычисляют значение y2, причем y2=(x3>>3)-(x3>>7),
- вычисляют значение y3, причем y3=y2-(x3>>11),
- вычисляют значение (x3* δ)=y2+(y3>>1), и
- вычисляют значение (x3* γ) вычитанием y2 из x3, и
при этом вычисление значения (x5* δ) посредством умножения x5 на значение δ и вычисление значения (x5* γ) посредством умножения x5 на значение γ заключается в том, что выполняют следующую последовательность арифметических операций:
- вычисляют значение y2', причем y2'=(x5>>3)-(x5>>7),
- вычисляют значение y3', причем y3'=y2'-(x5>>11),
- вычисляют значение (x5* δ) суммированием y2' и (y3'>>1), и
- вычисляют значение (x5* γ) вычитанием y2' из x5, и
при этом вычисление значения (x3''* γ) посредством умножения x3'' на значение γ и вычисление значения (x3''* δ) посредством умножения x3'' на значение δ заключается в том, что выполняют следующую последовательность арифметических операций:
- вычисляют значение y2'', причем y2''=(x3''>>3)-(x3''>>7),
- вычисляют значение y3", причем y3''=y2''-(x3''>>11),
- вычисляют значение (x3''* δ)=y2''+(γ3''>>1), и
- вычисляют значение (x3''* γ) вычитанием y2'' из x3'', и
при этом вычисление значения (x5''* δ) посредством умножения x5'' на значение δ и вычисление значения (x5''* γ) посредством умножения x5'' на значение γ заключается в том, что выполняют следующую последовательность арифметических операций:
- вычисляют значение y2''', причем y2'''=(x5''>>3)-(x5''>>7),
- вычисляют значение y3''', причем y3'''=y2'''-(x5''>>11),
- вычисляют значение (x5''* δ) суммированием y2''' и (y3'''>>1), и
- вычисляют значение (x5''* γ) вычитанием y2''' из x5''.
5. Способ по п.2, в котором вычисление значения (x2* α) посредством умножения x2 на значение α и вычисление значения (x2* β) посредством умножения x2 на значение β заключается в том, что выполняют следующую последовательность арифметических операций:
- вычисляют значение y1, причем y1=x2+(x2>>5),
- вычисляют значение y2, причем y2=y1>>2,
- вычисляют значение (x2* α) суммированием y2 и (x2>>4), и
- вычисляют значение (x2* β) вычитанием y2 из y1, и
при этом вычисление значения (x6* α) посредством умножения x6 на значение α и вычисление значения (x6* β) посредством умножения x6 на значение β заключается в том, что выполняют следующую последовательность арифметических операций:
- вычисляют значение y1', причем y1'=x2+(x6>>5),
- вычисляют значение y2', причем y2'=y1'>>2,
- вычисляют значение (x6* α) суммированием y2' и (x6>>4), и
- вычисляют значение (x6* β) вычитанием y2' из y1', и
при этом вычисление значения (x2''* α) посредством умножения x2'' на значение α и вычисление значения (x2''* β) посредством умножения x2'' на значение β заключается в том, что выполняют следующую последовательность арифметических операций:
- вычисляют значение y1'', причем y1''=x2''+(x2''>>5),
- вычисляют значение y2'', причем y2''=y1''>>2,
- вычисляют значение (x2''* α) суммированием y2'' и (x2''>>4), и
- вычисляют значение (x2''* β) вычитанием y2'' из y1'', и
при этом вычисление значения (x6''* α) посредством умножения x6'' на значение α и вычисление значения (x6''* β) посредством умножения x6'' на значение β заключается в том, что выполняют следующую последовательность арифметических операций:
- вычисляют значение y1''', причем y1'''=x2+(x6''>>5),
- вычисляют значение y2''', причем y2'''=y1'''>>2,
- вычисляют значение (x6''* α) суммированием y2''' и (x6''>>4), и
- вычисляют значение (x6''* β) вычитанием y2''' из y1'''.
6. Способ по п.5, в котором значения x0, x1, x2, x3, x4, x5, x6, x7, x0', x1', x2', x3', x4', x5', x6', x7', x0'', x1'', x2'', x3'', x4'', x5'', x6'', x7''', x1''', x3''', x5''', x7''', (x2*α), (x6*β), (x2*β), (x6*α), (x7''*ε), (x7''*ζ), (x3''*γ), (x3''*δ), (x5''*δ), (x5''*γ), (x1''*ζ) и (x1''*ε) представлены с использованием чисел с фиксированной запятой, которые включают в себя Р битов в частях мантиссы чисел с фиксированной запятой.
7. Устройство для сжатия и вывода изображения, содержащее:
процессор, запрограммированный для управления,
модуль масштабирования, который масштабирует каждый коэффициент в матрице закодированных коэффициентов размером 8×8 одним из множителя A, множителя B, множителя C, множителя D, множителя E, множителя F, множителя G, множителя H, множителя I или множителя J для формирования матрицы масштабированных коэффициентов,
причем A=1024, B=1138, C=1730, D=1609, E=1264, F=1922, G=1788, H=2923, I=2718 и J=2528,
модуль обратного преобразования, который использует повторные применения масштабированного одномерного преобразования с фиксированной запятой для преобразования матрицы масштабированных коэффициентов в матрицу преобразованных коэффициентов,
модуль сдвига вправо, который сдвигает вправо преобразованные коэффициенты в матрице преобразованных коэффициентов для формирования матрицы скорректированных коэффициентов, причем каждый скорректированный коэффициент в матрице скорректированных коэффициентов аппроксимирует соответствующее значение в матрице значений, которые можно сформировать с применением идеального двумерного обратного дискретного косинусного преобразования ("IDCT") к матрице закодированных коэффициентов, модуль вывода, который выводит блок пикселей размером 8×8, причем каждый пиксель в блоке пикселей размером 8×8 включает в себя значение компонента пикселя на основании скорректированного коэффициента в матрице скорректированных коэффициентов,
при этом модуль обратного преобразования применяет преобразование к вектор-строке или вектор-столбцу посредством:
вычисления значения x0' суммированием x0 и x4,
вычисления значения x4' суммированием x0 и -x4,
вычисления значения (x2* α) умножением x2 на значение α,
вычисления значения (x6* β) умножением x6 на значение β,
вычисления значения (x2* β) умножением x2 на значение β,
вычисления значения (x6* α) умножением x6 на значение α,
вычисления значения x2' суммированием (x2* α) и -(x6* β),
вычисления значения x6' суммированием (x6* α) и (x2* β),
вычисления значения x0'' суммированием x0' и x6',
вычисления значения x4'' суммированием x4' и x2',
вычисления значения x2'' суммированием x4' и -x2',
вычисления значения x6'' суммированием x0' и -x6',
вычисления значения x7' суммированием x1 и -x7,
вычисления значения x1' суммированием x1 и x7,
вычисления значения x7'' суммированием x7' и x5',
вычисления значения x3'' суммированием x1' и -x3',
вычисления значения x5'' суммированием x7' и -x5',
вычисления значения x1'' суммированием x3' и x1',
вычисления значения (x7''* ε) умножением x7'' на значение ε,
вычисления значения (x7''* ζ) умножением x7'' на значение ζ,
вычисления значения (x3''* γ) умножением x3'' на значение γ,
вычисления значения (x3''* δ) умножением x3'' на значение δ,
вычисления значения (x5''* δ) умножением x5'' на значение δ,
вычисления значения (x5''* γ) умножением x5'' на значение γ,
вычисления значения (x1''* ζ) умножением x1'' на значение ζ,
вычисления значения (x1''* ε) умножением x1'' на значение ε,
вычисления значения x7''' суммированием (x7''* ε) и -(x1''* ζ),
вычисления значения x3''' суммированием (x3''* γ) и -(x5''* δ),
вычисления значения x5''' суммированием (x5''* γ) и (x3''* δ),
вычисления значения x1''' суммированием (x1''* ε) и (x7''* ζ),
вычисления значения Х0 суммированием x7''' и x0'',
вычисления значения X1 суммированием x4'' и x5''',
вычисления значения X2 суммированием x2'' и x3''',
вычисления значения X3 суммированием x6'' и x7''',
вычисления значения X4 суммированием x6'' и -x1''',
вычисления значения X5 суммированием x2'' и -x3''',
вычисления значения X6 суммированием x4'' и -x5''', и
вычисления значения X7 суммированием x0'' и -x1''',
причем x0, x1, x2, x3, x4, x5, x6, x7 являются коэффициентами в вектор-строке или вектор-столбце,
причем X1, X2, X3, X4, X5, X6 и X7 являются выходными значениями преобразования, и
причем α=41/128, β=99/128, γ=113/128, δ=719/4096, ε=1533/2048 и ζ=1/2.
8. Устройство по п.7, в котором модуль обратного преобразования применяет преобразование к матрице коэффициентов без использования операций умножения и деления.
9. Устройство по п.8, в котором модуль обратного преобразования вычисляет значение (x1* ε) умножением x1 на значение ε и значение (x1* ζ) умножением x1 на значение ζ посредством выполнения следующей последовательности арифметических операций:
вычисление значения y1, причем y1=(x1>>9)-x1,
вычисление значения (x1* ζ) сдвигом x3 вправо на одну позицию, и
вычисление значения (x1* ε) вычитанием y1 из (y1>>2), и
причем модуль обратного преобразования вычисляет значение (x7* ε) умножением x7 на значение ε и значение (X7* ζ) умножением x7 на значение ζ посредством выполнения следующей последовательности арифметических операций:
вычисление значения y1', причем y1'=(x7>>9)-x7,
вычисление значения (x7* ζ) сдвигом x7 вправо на одну позицию, и
вычисление значения (x7* ε) вычитанием y1' из (y1'>>2), и
причем модуль обратного преобразования вычисляет значение (x1''* ε) умножением x1'' на значение ε и значение (x1''* ζ) умножением x1'' на значение ζ посредством выполнения следующей последовательности арифметических операций:
вычисление значения y1'', причем y1''=(x1''>>9)-x1'',
вычисление значения (x1''* ζ) сдвигом x1'' вправо на одну позицию, и
вычисление значения (x1''* ε) вычитанием y1'' из (y1''>>2), и
причем модуль обратного преобразования вычисляет значение (x7''* ε) умножением x7'' на значение ε и значение (x7''* ζ) умножением x7'' на значение ζ посредством выполнения следующей последовательности арифметических операций:
вычисление значения y1''', причем y1'''=(x7''>>9)-x7'',
вычисление значения (x7''* ζ) сдвигом x7'' вправо на одну позицию, и
вычисление значения (x7''* ε) вычитанием y1''' из (y1'''>>2).
10. Устройство по п.8, в котором модуль обратного преобразования вычисляет значение (x3* γ) умножением x3 на значение γ и значение (x3* δ) умножением x3 на значение δ посредством выполнения следующей последовательности арифметических операций:
вычисление значения y2, причем y2=(x3>>3)-(x3>>7),
вычисление значения y3, причем y3=y2-(x3>>11),
вычисление значения (x3* δ)=y2+*(y3>>1), и
вычисление значения (x3* γ) вычитанием y2 из x3, и
причем модуль обратного преобразования вычисляет значение (x5* δ) умножением x5 на значение δ и значение (x5* γ) умножением x5 на значение γ посредством выполнения следующей последовательности арифметических операций:
вычисление значения y2', причем y2'=(x5>>3)-(x5>>7),
вычисление значения y3', причем y3'=y2'-(x5>>11),
вычисление значения (x5* δ) суммированием y2' и (y3'>>1), и
вычисление значения (x5* γ) вычитанием y2' из x5, и
причем модуль обратного преобразования вычисляет значение (x3''* γ) умножением x3'' на значение γ и значение (x3''* δ) умножением x3'' на значение δ посредством выполнения следующей последовательности арифметических операций:
вычисление значения y2'', причем y2''=(x3''>>3)-(x3''>>7),
вычисление значения y3'', причем y3''=y2''-(x3''>>11),
вычисление значения (x3''*δ)=y2''+(y3''>>1), и
вычисление значения (x3''* γ) вычитанием y2'' из x3'', и
причем модуль обратного преобразования вычисляет значение (x5''* δ) умножением x5'' на значение δ и значение (x5''* γ) умножением x5'' на значение γ посредством выполнения следующей последовательности арифметических операций:
вычисление значения y2''', причем y2'''=(x5''>>3)-(x5''>>7),
вычисление значения y3''', причем y3'''=y2'-(x5''>>11),
вычисление значения (x5''* δ) суммированием y2''' и (y3'''>>1), и
вычисление значения (x5''* γ) вычитанием y2''' из x5''.
11. Устройство по п.8, в котором модуль обратного преобразования вычисляет значение (x2* α) умножением x2 на значение α и значение (x2* β) умножением x2 на значение β посредством выполнения следующей последовательности арифметических операций:
вычисление значения y1, причем y1=x2+(x2>>5),
вычисление значения y2, причем y2=y1>>2,
вычисление значения (x2* α) суммированием y2 и (x2>>4), и
вычисление значения (x2* β) вычитанием y2 из y1, и
причем модуль обратного преобразования вычисляет значение (x6* α) умножением x6 на значение α и значение (x6* β) умножением x6 на значение β посредством выполнения следующей последовательности арифметических операций:
вычисление значения y1', причем y1'=x6+(x6>>5),
вычисление значения y2', причем y2'=y1'>>2,
вычисление значения (x6* α) суммированием y2' и (x6>>4), и
вычисление значения (x6* β) вычитанием y2' из y1', и
причем модуль обратного преобразования вычисляет значение (x2''* α) умножением x2'' на значение α и значение (x2''* β) умножением x2'' на значение β посредством выполнения следующей последовательности арифметических операций:
вычисление значения y1'', причем y1=x2''+(x2''>>5),
вычисление значения y2'', причем y2''=y1''>>2,
вычисление значения (x2''* α) суммированием y2'' и (x2''>>4), и
вычисление значения (x2''* β) вычитанием γ2'' из y1'', и
причем модуль обратного преобразования вычисляет значение (x6''* α) умножением x6'' на значение α и значение (x6''* β) умножением x6'' на значение β посредством выполнения следующей последовательности арифметических операций:
вычисление значения y1''', причем y1'''=x2+(x6''>>5),
вычисление значения y2''', причем y2'''=y1'''>>2,
вычисление значения (x6''* α) суммированием y2''' и (x6''>>4), и
вычисление значения (x6''* β) вычитанием y2''' из y1'''.
12. Устройство по п.7, в котором значения x0, x1, x2, x3, x4, x5, x6, x7, x0', x1', x2', x3', x4', x5', x6', x7', x0'', x1'', x2'', x3'', x4'', x5'', x6'', x7'', x1''', x3''', x5''', x7''', (x2* α), (x6* β), (x2* β), (x6* α), (x7''* ε), (x7''* ζ), (x3''* γ), (x3''* δ), (x5''* δ), (x5''* γ), (x1''* ζ) и (x1''* ε) представлены с помощью чисел с фиксированной точкой, которые включают в себя Р битов в частях мантиссы чисел с фиксированной точкой.
13. Устройство по п.12, в котором Р равно 10.
14. Устройство для сжатия и вывода изображения, содержащее:
средство для масштабирования коэффициентов в матрице закодированных коэффициентов размером 8×8, одним из множителя A, множителя B, множителя C, множителя D, множителя E, множителя F, множителя G, множителя Н, множителя I или множителя J для формирования матрицы масштабированных коэффициентов, причем A=1024, B=1138, C=1730, D=1609, E=1264, F=1922, G=1788, H=2923, I=2718 и J=2528,
средство для использования повторных применений масштабированного одномерного преобразования с фиксированной запятой для преобразования матрицы масштабированных коэффициентов в матрицу преобразованных коэффициентов,
средство для сдвига вправо преобразованных коэффициентов в матрице преобразованных коэффициентов для формирования матрицы скорректированных коэффициентов,
причем каждый скорректированный коэффициент в матрице скорректированных коэффициентов аппроксимирует соответствующее значение в матрице значений, которые можно сформировать с применением идеального двумерного, обратного дискретного косинусного преобразования ("IDCT") к матрице закодированных коэффициентов, и средство для вывода блока пикселей размером 8×8, причем каждый пиксель в блоке пикселей размером 8×8 включает в себя значение компонента пикселя на основании скорректированного коэффициента в матрице скорректированных коэффициентов,
при этом средство для масштабирования коэффициентов содержит:
средство для масштабирования коэффициента в позиции [0,0] матрицы закодированных коэффициентов множителем A,
средство для масштабирования коэффициента в позиции [0,1] матрицы закодированных коэффициентов множителем B,
средство для масштабирования коэффициента в позиции [0,2] матрицы закодированных коэффициентов множителем C,
средство для масштабирования коэффициента в позиции [0,3] матрицы закодированных коэффициентов множителем D,
средство для масштабирования коэффициента в позиции [0,4] матрицы закодированных коэффициентов множителем A,
средство для масштабирования коэффициента в позиции [0,5] матрицы закодированных коэффициентов множителем D,
средство для масштабирования коэффициента в позиции [0,6] матрицы закодированных коэффициентов множителем C,
средство для масштабирования коэффициента в позиции [0,7] матрицы закодированных коэффициентов множителем B,
средство для масштабирования коэффициента в позиции [1,0] матрицы закодированных коэффициентов множителем B,
средство для масштабирования коэффициента в позиции [1,1] матрицы закодированных коэффициентов множителем E,
средство для масштабирования коэффициента в позиции [1,2] матрицы закодированных коэффициентов множителем F,
средство для масштабирования коэффициента в позиции [1,3] матрицы закодированных коэффициентов множителем G,
средство для масштабирования коэффициента в позиции [1,4] матрицы закодированных коэффициентов множителем B,
средство для масштабирования коэффициента в позиции [1,5] матрицы закодированных коэффициентов множителем G,
средство для масштабирования коэффициента в позиции [1,6] матрицы закодированных коэффициентов множителем F,
средство для масштабирования коэффициента в позиции [1,7] матрицы закодированных коэффициентов множителем E,
средство для масштабирования коэффициента в позиции [2,0] матрицы закодированных коэффициентов множителем C,
средство для масштабирования коэффициента в позиции [2,1] матрицы закодированных коэффициентов множителем F,
средство для масштабирования коэффициента в позиции [2,2] матрицы закодированных коэффициентов множителем H,
средство для масштабирования коэффициента в позиции [2,3] матрицы закодированных коэффициентов множителем I,
средство для масштабирования коэффициента в позиции [2,4] матрицы закодированных коэффициентов множителем C,
средство для масштабирования коэффициента в позиции [2,5] матрицы закодированных коэффициентов множителем I,
средство для масштабирования коэффициента в позиции [2,6] матрицы закодированных коэффициентов множителем H,
средство для масштабирования коэффициента в позиции [2,7] матрицы закодированных коэффициентов множителем F,
средство для масштабирования коэффициента в позиции [3,0] матрицы закодированных коэффициентов множителем D,
средство для масштабирования коэффициента в позиции [3,1] матрицы закодированных коэффициентов множителем G,
средство для масштабирования коэффициента в позиции [3,2] матрицы закодированных коэффициентов множителем I,
средство для масштабирования коэффициента в позиции [3,3] матрицы закодированных коэффициентов множителем J,
средство для масштабирования коэффициента в позиции [3,4] матрицы закодированных коэффициентов множителем D,
средство для масштабирования коэффициента в позиции [3,5] матрицы закодированных коэффициентов множителем J,
средство для масштабирования коэффициента в позиции [3,6] матрицы закодированных коэффициентов множителем I,
средство для масштабирования коэффициента в позиции [3,7] матрицы закодированных коэффициентов множителем G,
средство для масштабирования коэффициента в позиции [4,0] матрицы закодированных коэффициентов множителем A,
средство для масштабирования коэффициента в позиции [4,1] матрицы закодированных коэффициентов множителем B,
средство для масштабирования коэффициента в позиции [4,2] матрицы закодированных коэффициентов множителем C,
средство для масштабирования коэффициента в позиции [4,3] матрицы закодированных коэффициентов множителем D,
средство для масштабирования коэффициента в позиции [4,4] матрицы закодированных коэффициентов множителем A,
средство для масштабирования коэффициента в позиции [4,5] матрицы закодированных коэффициентов множителем D,
средство для масштабирования коэффициента в позиции [4,6] матрицы закодированных коэффициентов множителем C,
средство для масштабирования коэффициента в позиции [4,7] матрицы закодированных коэффициентов множителем B,
средство для масштабирования коэффициента в позиции [5,0] матрицы закодированных коэффициентов множителем D,
средство для масштабирования коэффициента в позиции [5,1] матрицы закодированных коэффициентов множителем G,
средство для масштабирования коэффициента в позиции [5,2] матрицы закодированных коэффициентов множителем I,
средство для масштабирования коэффициента в позиции [5,3] матрицы закодированных коэффициентов множителем J,
средство для масштабирования коэффициента в позиции [5,4] матрицы закодированных коэффициентов множителем D,
средство для масштабирования коэффициента в позиции [5,5] матрицы закодированных коэффициентов множителем J,
средство для масштабирования коэффициента в позиции [5,6] матрицы закодированных коэффициентов множителем I,
средство для масштабирования коэффициента в позиции [5,7] матрицы закодированных коэффициентов множителем G,
средство для масштабирования коэффициента в позиции [6,0] матрицы закодированных коэффициентов множителем C,
средство для масштабирования коэффициента в позиции [6,1] матрицы закодированных коэффициентов множителем F,
средство для масштабирования коэффициента в позиции [6,2] матрицы закодированных коэффициентов множителем H,
средство для масштабирования коэффициента в позиции [6,3] матрицы закодированных коэффициентов множителем I,
средство для масштабирования коэффициента в позиции [6,4] матрицы закодированных коэффициентов множителем C,
средство для масштабирования коэффициента в позиции [6,5] матрицы закодированных коэффициентов множителем I,
средство для масштабирования коэффициента в позиции [6,6] матрицы закодированных коэффициентов множителем H,
средство для масштабирования коэффициента в позиции [6,7] матрицы закодированных коэффициентов множителем F,
средство для масштабирования коэффициента в позиции [7,0] матрицы закодированных коэффициентов множителем B,
средство для масштабирования коэффициента в позиции [7,1] матрицы закодированных коэффициентов множителем E,
средство для масштабирования коэффициента в позиции [7,2] матрицы закодированных коэффициентов множителем F,
средство для масштабирования коэффициента в позиции [7,3] матрицы закодированных коэффициентов множителем G,
средство для масштабирования коэффициента в позиции [7,4] матрицы закодированных коэффициентов множителем B,
средство для масштабирования коэффициента в позиции [7,5] матрицы закодированных коэффициентов множителем G,
средство для масштабирования коэффициента в позиции [7,6] матрицы закодированных коэффициентов множителем F, и
средство для масштабирования коэффициента в позиции [7,7] матрицы закодированных коэффициентов множителем E,
при этом средство для применения преобразования содержит:
средство для вычисления значения x0' суммированием x0 и x4,
средство для вычисления значения x4' суммированием x0 и -x4,
средство для вычисления значения (x2* α) умножением x2 на значение α,
средство для вычисления значения (x6* β) умножением x6 на значение β,
средство для вычисления значения (x2* β) умножением x2 на значение β,
средство для вычисления значения (x6* α) умножением x6 на значение α,
средство для вычисления значения x2' суммированием (x2* α) и -(x6* β),
средство для вычисления значения x6' суммированием (x6* α) и (x2* β),
средство для вычисления значения x0'' суммированием x0' и x6',
средство для вычисления значения x4'' суммированием x4' и x2',
средство для вычисления значения x2'' суммированием x4' и -x2',
средство для вычисления значения x6'' суммированием x0' и -x6',
средство для вычисления значения x7' суммированием x1 и -x7,
средство для вычисления значения x1' суммированием x1 и x7,
средство для вычисления значения x7'' суммированием x7' и x5',
средство для вычисления значения x3'' суммированием x1' и -x3',
средство для вычисления значения x5'' суммированием x7' и -x5',
средство для вычисления значения x1'' суммированием x3' и x1',
средство для вычисления значения (x7''* ε) умножением x7'' на значение ε,
средство для вычисления значения (x7''* ζ) умножением x7'' на значение ζ,
средство для вычисления значения (x3''* γ) умножением x3'' на значение γ,
средство для вычисления значения (x3''* δ) умножением x3'' на значение δ,
средство для вычисления значения (x5''* δ) умножением x5'' на значение δ,
средство для вычисления значения (x5''* γ) умножением x5'' на значение γ,
средство для вычисления значения (x1''* ζ) умножением x1'' на значение ζ,
средство для вычисления значения (x1''* ε) умножением x1'' на значение ε,
средство для вычисления значения x7''' суммированием (x7''*ε) и -(x1''*ζ),
средство для вычисления значения x3''' суммированием (x3''*γ) и -(x5''* δ),
средство для вычисления значения x5''' суммированием (x5''* γ) и (x3''* δ),
средство для вычисления значения x1''' суммированием (x1''* ε) и (x7''* ζ),
средство для вычисления значения X0 суммированием x7''' и x0'',
средство для вычисления значения X1 суммированием x4'' и x5''',
средство для вычисления значения X2 суммированием x2'' и x3''',
средство для вычисления значения X3 суммированием x6'' и x7''',
средство для вычисления значения X4 суммированием x6'' и -x1''',
средство для вычисления значения X5 суммированием x2'' и -x3''',
средство для вычисления значения X6 суммированием x4'' и -x5''', и
средство для вычисления значения X7 суммированием x0'' и -x1''',
причем x0, x1, x2, x3, x4, x5, x6, x7 являются коэффициентами в вектор-строке или вектор-столбце,
причем X1, X2, X3, X4, X5, X6 и X7 являются выходными значениями преобразования, и
причем α=41/128, β=99/128, γ=113/128, δ=719/4096, ε=1533/2048 и ζ=1/2.
15. Устройство по п.14, в котором средство для использования повторных применений преобразования применяет преобразование к матрице коэффициентов без использования операций умножения или деления.
16. Устройство по п.15, в котором средство для вычисления значения (x1* ε) умножением x1 на значение ε и средство для вычисления значения (x1* ζ) умножением x1 на значение ζ содержат:
средство для вычисления значения y1, причем y1=(x1>>9)-x1,
средство для вычисления значения (x1* ζ) сдвигом x3 вправо на одну позицию, и
средство для вычисления значения (x1* ε) вычитанием y1 из (y1>>2), и
причем средство для вычисления значения (x7* ε) умножением x7 на значение ε и средство для вычисления значения (x7* ζ) умножением x7 на значение ζ содержат:
средство для вычисления значения y1', причем y1'=(x7>>9)-x7,
средство для вычисления значения (x7* ζ) сдвигом x7 вправо на одну позицию, и
средство для вычисления значения (x7* ε) вычитанием y1' из (y1'>>2), и
причем средство для вычисления значения (x1''* ε) умножением x1'' на значение ε и средство для вычисления значения (x1''* ζ) умножением x1'' на значение ζ содержат:
средство для вычисления значения y1'', причем y1''=(x1''>>9)-x1'',
средство для вычисления значения (x1''* ζ) сдвигом x1'' вправо на одну позицию, и
средство для вычисления значения (x1''* ε) вычитанием y1'' из (y1''>>2), и причем средство для вычисления значения (x7''* ε) умножением x7'' на значение ε и средство для вычисления значения (x7''* ζ) умножением x7'' на значение ζ содержат:
средство для вычисления значения y1''', причем y1'''=(x7''>>9)-x7''',
средство для вычисления значения (x7''* ζ) сдвигом x7'' вправо на одну позицию, и
средство для вычисления значения (x7''* ε) вычитанием y1''' из (y1'''>>2).
17. Устройство по п.15, в котором средство для вычисления значения (x3* γ) умножением x3 на значение γ и средство для вычисления значения (x3* δ) умножением x3 на значение δ содержат:
средство для вычисления значения y2, причем y2=(x3>>3)-(x3>>7),
средство для вычисления значения y3, причем y3=y2-(x3>>11),
средство для вычисления значения (x3* δ)=y2+(y3>>1), и
средство для вычисления значения (x3* γ) вычитанием y2 из x1, и
причем средство для вычисления значения (x5* δ) умножением x5 на значение δ и средство для вычисления значения (x5* γ) умножением x5 на значение γ содержат:
средство для вычисления значения y2', причем y2'=(x5>>3)-(x5>>7),
средство для вычисления значения y3', причем y3'=y2'-(x5>>11),
средство для вычисления значения (x5* δ) суммированием y2' и (y3'>>1), и
средство для вычисления значения (x5* γ) вычитанием y2' из x7, и
причем средство для вычисления значения (x3''* γ) умножением x3'' на значение γ и средство для вычисления значения (x3''* δ) умножением x3'' на значение δ содержат:
средство для вычисления значения y2'', причем y2''=(x1''>>3)-(x1''>>7),
средство для вычисления значения y3'', причем y3''=y2''-(x1''>>11),
средство для вычисления значения (x1''* δ)=y2''+(y3''>>1), и
средство для вычисления значения (x1''* γ) вычитанием y2'' из x1'', и
причем средство для вычисления значения (x5''* δ) умножением x5'' на значение δ и средство для вычисления значения (x5''* γ) умножением x5'' на значение γ содержат:
средство для вычисления значения y2''', причем y2'''=(x5''>>3)-(x5''>>7),
средство для вычисления значения y3''', причем y3'''=y2'''-(x5''>>11),
средство для вычисления значения (x5''* δ) суммированием y2''' и (y3'''>>1), и
средство для вычисления значения (x5''* γ) вычитанием y2''' из x5''.
18. Устройство по п.15, в котором средство для вычисления значения (x2* α) умножением x2 на значение α и средство для вычисления значения (x2* β) умножением x2 на значение β содержат:
средство для вычисления значения y1, причем y1'=x2+(x2>>5),
средство для вычисления значения y2, причем y2=y1>>2,
средство для вычисления значения (x2* α) суммированием y2 и (x2>>4), и
средство для вычисления значения (x2* β) вычитанием y2 из y1, и
причем средство для вычисления значения (x6* α) умножением x6 на значение α и средство для вычисления значения (x6* β) умножением x6 на значение β содержат:
средство для вычисления значения y1', причем y1'=x6+(x6>>5),
средство для вычисления значения y2', причем y2'=y1'>>2,
средство для вычисления значения (x2* α) суммированием y2' и (x6>>4), и
средство для вычисления значения (x2* β) вычитанием y2' из y1', и
причем средство для вычисления значения (x2''* α) умножением x2'' на значение α и средство для вычисления значения (x2''* β) умножением x2'' на значение β содержат:
средство для вычисления значения y1'', причем y1''=x2''+(x2''>>5),
средство для вычисления значения y2'', причем y2''=y1''>>2,
средство для вычисления значения (x2''* α) суммированием y2'' и (x2''>>4), и
средство для вычисления значения (x2''* β) вычитанием y2'' из y1'', и
причем средство для вычисления значения (x6''* α) умножением x6'' на значение α и средство для вычисления значения (x6''* β) умножением x6'' на значение β содержат:
средство для вычисления значения y1''', причем y1'''=x6''+(x6''>>5),
средство для вычисления значения y2''', причем y2'''=y1'''>>2,
средство для вычисления значения (x6''* α) суммированием y2''' и (x6''>>4), и
средство для вычисления значения (x6''* β) вычитанием y2''' из y1'''.
19. Устройство по п.14, в котором значения x0, x1, x2, x3, x4, x5, x6, x7, x0', x1', x2', x3', x4', x5', x6', x7', x0'', x1'', x2'', x3'' x4'', x5'', x6'', x7'', x1''', x3''', x5''', x7''', (x2* α), (x6* β), (x2* β), (x6* α), (x7''* ε), (x7''* ζ), (x3''* γ), (x3''* δ), (x5''* δ), (x5''* γ), (x1''* ζ) и (x1''* ε) представлены с помощью чисел с фиксированной точкой, которые включают в себя Р битов в частях мантиссы чисел с фиксированной точкой.
20. Устройство по п.19, в котором Р равно 10.
21. Машиночитаемый носитель информации, содержащий команды, которые при исполнении побуждают программируемый процессор:
масштабировать каждый коэффициент в матрице закодированных коэффициентов размером 8×8 одним из множителя A, множителя B, множителя C, множителя D, множителя E, множителя F, множителя G, множителя H, множителя I или множителя J для формирования матрицы масштабированных коэффициентов,
причем A=1024, B=1138, C=1730, D=1609, E=1264, F=1922, G=1788, H=2923, I=2718 и J=2528,
использовать повторные применения масштабированного одномерного преобразования с фиксированной точкой для преобразования матрицы масштабированных коэффициентов в матрицу преобразованных коэффициентов,
сдвигать вправо преобразованные коэффициенты в матрице преобразованных коэффициентов для формирования матрицы скорректированных коэффициентов,
причем каждый скорректированный коэффициент в матрице скорректированных коэффициентов аппроксимирует соответствующее значение в матрице значений, которые можно сформировать посредством применения идеального двумерного обратного дискретного косинусного преобразования ("IDCT") к матрице закодированных коэффициентов, и
выводить сигналы, которые побуждают устройство отображения отображать блок пикселей размером 8×8, причем каждый пиксель в блоке пикселей размером 8×8 включает в себя значение компонента пикселя с учетом скорректированного коэффициента в матрице скорректированных коэффициентов,
при этом команды, которые побуждают программируемый процессор масштабировать коэффициенты в матрице коэффициентов, также побуждают программируемый процессор:
масштабировать коэффициент в позиции [0,0] матрицы закодированных коэффициентов множителем A,
масштабировать коэффициент в позиции [0,1] матрицы закодированных коэффициентов множителем B,
масштабировать коэффициент в позиции [0,2] матрицы закодированных коэффициентов множителем C,
масштабировать коэффициент в позиции [0,3] матрицы закодированных коэффициентов множителем D,
масштабировать коэффициент в позиции [0,4] матрицы закодированных коэффициентов множителем A,
масштабировать коэффициент в позиции [0,5] матрицы закодированных коэффициентов множителем D,
масштабировать коэффициент в позиции [0,6] матрицы закодированных коэффициентов множителем C,
масштабировать коэффициент в позиции [0,7] матрицы закодированных коэффициентов множителем B,
масштабировать коэффициент в позиции [1,0] матрицы закодированных коэффициентов множителем B,
масштабировать коэффициент в позиции [1,1] матрицы закодированных коэффициентов множителем E,
масштабировать коэффициент в позиции [1,2] матрицы закодированных коэффициентов множителем F,
масштабировать коэффициент в позиции [1,3] матрицы закодированных коэффициентов множителем G,
масштабировать коэффициент в позиции [1,4] матрицы закодированных коэффициентов множителем B,
масштабировать коэффициент в позиции [1,5] матрицы закодированных коэффициентов множителем G,
масштабировать коэффициент в позиции [1,6] матрицы закодированных коэффициентов множителем F,
масштабировать коэффициент в позиции [1,7] матрицы закодированных коэффициентов множителем E,
масштабировать коэффициент в позиции [2,0] матрицы закодированных коэффициентов множителем C,
масштабировать коэффициент в позиции [2,1] матрицы закодированных коэффициентов множителем F,
масштабировать коэффициент в позиции [2,2] матрицы закодированных коэффициентов множителем H,
масштабировать коэффициент в позиции [2,3] матрицы закодированных коэффициентов множителем I,
масштабировать коэффициент в позиции [2,4] матрицы закодированных коэффициентов множителем C,
масштабировать коэффициент в позиции [2,5] матрицы закодированных коэффициентов множителем I,
масштабировать коэффициент в позиции [2,6] матрицы закодированных коэффициентов множителем H,
масштабировать коэффициент в позиции [2,7] матрицы закодированных коэффициентов множителем F,
масштабировать коэффициент в позиции [3,0] матрицы закодированных коэффициентов множителем D,
масштабировать коэффициент в позиции [3,1] матрицы закодированных коэффициентов множителем G,
масштабировать коэффициент в позиции [3,2] матрицы закодированных коэффициентов множителем I,
масштабировать коэффициент в позиции [3,3] матрицы закодированных коэффициентов множителем J,
масштабировать коэффициент в позиции [3,4] матрицы закодированных коэффициентов множителем D,
масштабировать коэффициент в позиции [3,5] матрицы закодированных коэффициентов множителем J,
масштабировать коэффициент в позиции [3,6] матрицы закодированных коэффициентов множителем I,
масштабировать коэффициент в позиции [3,7] матрицы закодированных коэффициентов множителем G,
масштабировать коэффициент в позиции [4,0] матрицы закодированных коэффициентов множителем A,
масштабировать коэффициент в позиции [4,1] матрицы закодированных коэффициентов множителем B,
масштабировать коэффициент в позиции [4,2] матрицы закодированных коэффициентов множителем C,
масштабировать коэффициент в позиции [4,3] матрицы закодированных коэффициентов множителем D,
масштабировать коэффициент в позиции [4,4] матрицы закодированных коэффициентов множителем A,
масштабировать коэффициент в позиции [4,5] матрицы закодированных коэффициентов множителем D,
масштабировать коэффициент в позиции [4,6] матрицы закодированных коэффициентов множителем C,
масштабировать коэффициент в позиции [4,7] матрицы закодированных коэффициентов множителем В,
масштабировать коэффициент в позиции [5,0] матрицы закодированных коэффициентов множителем D,
масштабировать коэффициент в позиции [5,1] матрицы закодированных коэффициентов множителем G,
масштабировать коэффициент в позиции [5,2] матрицы закодированных коэффициентов множителем I,
масштабировать коэффициент в позиции [5,3] матрицы закодированных коэффициентов множителем J,
масштабировать коэффициент в позиции [5,4] матрицы закодированных коэффициентов множителем D,
масштабировать коэффициент в позиции [5,5] матрицы закодированных коэффициентов множителем J,
масштабировать коэффициент в позиции [5,6] матрицы закодированных коэффициентов множителем I,
масштабировать коэффициент в позиции [5,7] матрицы закодированных коэффициентов множителем G,
масштабировать коэффициент в позиции [6,0] матрицы закодированных коэффициентов множителем C,
масштабировать коэффициент в позиции [6,1] матрицы закодированных коэффициентов множителем F,
масштабировать коэффициент в позиции [6,2] матрицы закодированных коэффициентов множителем H,
масштабировать коэффициент в позиции [6,3] матрицы закодированных коэффициентов множителем I,
масштабировать коэффициент в позиции [6,4] матрицы закодированных коэффициентов множителем C,
масштабировать коэффициент в позиции [6,5] матрицы закодированных коэффициентов множителем I,
масштабировать коэффициент в позиции [6,6] матрицы закодированных коэффициентов множителем H,
масштабировать коэффициент в позиции [6,7] матрицы закодированных коэффициентов множителем F,
масштабировать коэффициент в позиции [7,0] матрицы закодированных коэффициентов множителем B,
масштабировать коэффициент в позиции [7,1] матрицы закодированных коэффициентов множителем E,
масштабировать коэффициент в позиции [7,2] матрицы закодированных коэффициентов множителем F,
масштабировать коэффициент в позиции [7,3] матрицы закодированных коэффициентов множителем G,
масштабировать коэффициент в позиции [7,4] матрицы закодированных коэффициентов множителем B,
масштабировать коэффициент в позиции [7,5] матрицы закодированных коэффициентов множителем G,
масштабировать коэффициент в позиции [7,6] матрицы закодированных коэффициентов множителем F, и
масштабировать коэффициент в позиции [7,7] матрицы закодированных коэффициентов множителем E,
при этом команды, которые побуждают программируемый процессор применять преобразование или к вектор-строке, или к вектор-столбцу, также побуждают программируемый процессор:
вычислять значение x0' суммированием x0 и x4,
вычислять значение x4' суммированием x0 и -x4,
вычислять значение (x2* α) умножением x2 на значение α,
вычислять значение (x6* β) умножением x6 на значение β,
вычислять значение (x2* β) умножением x2 на значение β,
вычислять значение (x6* α) умножением x6 на значение α,
вычислять значение x2' суммированием (x2* α) и -(x6* β),
вычислять значение x6' суммированием (x6* α) и (x2* β),
вычислять значение x0'' суммированием x0' и x6',
вычислять значение x4'' суммированием x4' и x2',
вычислять значение x2'' суммированием x4' и -x2',
вычислять значение x6'' суммированием x0' и -x6',
вычислять значение x7' суммированием x1 и -x7,
вычислять значение x1' суммированием x1 и x7,
вычислять значение x7'' суммированием x7' и x5',
вычислять значение x3'' суммированием x1' и -x3',
вычислять значение x5'' суммированием x7' и -x5',
вычислять значение x1'' суммированием x3' и x1',
вычислять значение (x7''* ε) умножением x7'' на значение ε,
вычислять значение (x7''* ζ) умножением x7'' на значение ζ,
вычислять значение (x3''* γ) умножением x3'' на значение γ,
вычислять значение (x3''* δ) умножением x3'' на значение δ,
вычислять значение (x5''* δ) умножением x5'' на значение δ,
вычислять значение (x5''* γ) умножением x5'' на значение γ,
вычислять значение (x1''* ζ) умножением x1'' на значение ζ,
вычислять значение (x1''* ε) умножением x1'' на значение ε,
вычислять значение x7''' суммированием (x7''* ε) и -(x1''* ζ),
вычислять значение x3''' суммированием (x3''* γ) и -(x5''* δ),
вычислять значение x5''' суммированием (x5''* γ) и (x3''* δ),
вычислять значение x1''' суммированием (x1''* ε) и (x7''* ζ),
вычислять значение X0 суммированием x7''' и x0'',
вычислять значение X1 суммированием x4'' и x5''',
вычислять значение X2 суммированием x2'' и x3''',
вычислять значение X3 суммированием x6'' и x7''',
вычислять значение X4 суммированием x6'' и -x1''',
вычислять значение X5 суммированием x2'' и -x3''',
вычислять значение X6 суммированием x4'' и -x5''', и
вычислять значение X7 суммированием x0'' и -x1''',
причем x0, x1, x2, x3, x4, x5, x6, x7 являются коэффициентами в вектор-строке или вектор-столбце,
причем X1, X2, X3, X4, X5, X6 и X7 являются выходными значениями преобразования, и
причем α=41/128, β=99/128, γ=113/128, δ=719/4096, ε=1533/2048 и ζ=1/2.
22. Машиночитаемый носитель информации по п.21, в котором команды побуждают программируемый процессор применять преобразование посредством побуждения программируемого процессора применять преобразование к коэффициентам в одной из вектор-строк или в одном из вектор-столбцов без использования операций умножения или деления.
23. Машиночитаемый носитель информации по п.22,
в котором команды побуждают программируемый процессор вычислять значение (x1* ε) умножением x1 на значение ε и значение (x1* ζ) умножением x1 на значение ζ посредством побуждения программируемого процессора:
вычислять значение y1, причем y1=(x1>>9)-x1,
вычислять значение (x1* ζ) сдвигом x3 вправо на одну позицию, и
вычислять значение (x1* ε) вычитанием y1 из (y1>>2), и
в котором команды побуждают программируемый процессор вычислять значение (x7* ε) умножением x7 на значение ε и значение (x7* ζ) умножением x7 на значение ζ посредством побуждения программируемого процессора:
вычислять значение y1', причем y1'=(x7>>9)-x7,
вычислять значение (x7* ζ) сдвигом x7 вправо на одну позицию, и
вычислять значение (x7* ε) вычитанием y1' из (y1'>>2), и
причем команды побуждают программируемый процессор вычислять значение (x1''* ε) умножением x1'' на значение ε и значение (x1''* ζ) умножением x1'' на значение ζ посредством побуждения программируемого процессора:
вычислять значение y1'', причем y1''=(x1''>>9)-x1'',
вычислять значение (x1''* ζ) сдвигом x1'' вправо на одну позицию, и
вычислять значение (x1''* ε) вычитанием y1'' из (y1''>>2), и
причем команды побуждают программируемый процессор вычислять значение (x7''* ε) умножением x7'' на значение ε и значение (x7''* ζ) умножением x7'' на значение ζ посредством побуждения программируемого процессора:
вычислять значение y1''', причем y1'''=(x7''>>9)-x7'',
вычислять значение (x7''* ζ) сдвигом x7' вправо на одну позицию, и
вычислять значение (x7''* ε) вычитанием y1''' из (y1'''>>2).
24. Машиночитаемый носитель информации по п.22, в котором команды побуждают программируемый процессор вычислять значение (x3* γ) умножением x3 на значение γ и значение (x3* δ) умножением x3 на значение δ посредством побуждения программируемого процессора:
вычислять значение y2, причем y2=(x3>>3)-(x3>>7),
вычислять значение y3, причем y3=y2-(x3>>11),
вычислять значение (x3* δ)=y2+(y3>>1), и
вычислять значение (x3* γ) вычитанием y2 из x3, и
причем команды побуждают программируемый процессор вычислять значение (x5* δ) умножением x5 на значение δ и значение (x5* γ) умножением x5 на значение γ посредством побуждения программируемого процессора:
вычислять значение y2', причем y2'=(x5>>3)-(x5>>7),
вычислять значение y3', причем y3'=y2'-(x5>>11),
вычислять значение (x5* δ) суммированием y2' и (y3'>>1), и
вычислять значение (x5* γ) вычитанием y2' из x5, и
причем команды побуждают программируемый процессор вычислять значение (x3''* γ) умножением x3'' на значение γ и значение (x3''* δ) умножением x3'' на значение δ посредством побуждения программируемого процессора:
вычислять значение y2'', причем y2''=(x3''>>3)-(x3''>>7),
вычислять значение y3'', причем y3''=y2''-(x3''>>11),
вычислять значение (x3''* δ)=y2''+(y3''>>1), и
вычислять значение (x3''* γ) вычитанием y2'' из x3'', и
причем команды побуждают программируемый процессор вычислять значение (x5''* δ) умножением x5'' на значение δ и значение (x5''* γ) умножением x5'' на значение γ посредством побуждения программируемого процессора:
вычислять значение y2''', причем y2'''=(x5''>>3)-(x5''>>7),
вычислять значение y3''', причем y3'''=y2'''-(x5''>>11),
вычислять значение (x5''* δ) суммированием y2''' и (y3'''>>1), и
вычислять значение (x5''* γ) вычитанием y2''' из x5''.
25. Машиночитаемый носитель информации по п.22, в котором команды побуждают программируемый процессор вычислять значение (x2* α) умножением x2 на значение α и значение (x2* β) умножением x2 на значение β посредством побуждения программируемого процессора:
вычислять значение y1, причем y1=x2+(x2>>5),
вычислять значение y2, причем y2=y1>>2,
вычислять значение (x2* α) суммированием y2 и (x2>>4), и
вычислять значение (x2* β) вычитанием y2 из y1, и
причем команды побуждают программируемый процессор вычислять значение (x6* α) умножением x6 на значение α и значение (x6* β) умножением x6 на значение β посредством побуждения программируемого процессора:
вычислять значение y1', причем y1'=x6+(x6>>5),
вычислять значение y2', причем y2'=y1'>>2,
вычислять значение (x6* α) суммированием y2' и (x6>>4), и
вычислять значение (x6* β) вычитанием y2' из y1', и
причем команды побуждают программируемый процессор вычислять значение (x2''* α) умножением x2'' на значение α и значение (x2''* β) умножением x2'' на значение β посредством побуждения программируемого процессора:
вычислять значение y1'', причем y1''=x2''+(x2''>>5),
вычислять значение y2'', причем y2''=y1''>>2,
вычислять значение (x2''* α) суммированием y2'' и (x2''>>4), и
вычислять значение (x2''* β) вычитанием y2'' из y1'', и
причем команды побуждают программируемый процессор вычислять значение (x6''* α) умножением x6'' на значение α и значение (x6''* β) умножением x6'' на значение β посредством побуждения программируемого процессора:
вычислять значение y1''', причем y1'''=x6''+(x6''>>5),
вычислять значение y2''', причем y2'''=y1'''>>2,
вычислять значение (x6''* α) суммированием y2''' и (x6''>>4), и
вычислять значение (x6''* β) вычитанием y2''' из y1'''.
26. Машиночитаемый носитель информации по п.21, в котором значения x0, x1, x2, x3, x4, x5, x6, x7, x0', x1', x2', x3', x4', x5', x6', x7', x0'', x1'', x2'', x3'', x4'', x5'', x6'', x7'', x1''', x3''', x5''', x7''', (x2* α), (x6* β), (x2* β), (x6* α), (x7''* ε), (x7''* ζ), (x3''* γ), (x3''* δ), (x5''* δ), (x5''* γ), (x1''* ζ) и (x1''* ε) представлены с помощью чисел с фиксированной точкой, которые включают в себя Р битов в частях мантиссы чисел с фиксированной точкой.
27. Машиночитаемый носитель информации по п.26, в котором Р равно 10.
| СЖАТИЕ ИЗОБРАЖЕНИЯ С ИСПОЛЬЗОВАНИЕМ ДИСКРЕТНОГО КОСИНУСНОГО ПРЕОБРАЗОВАНИЯ АДАПТИВНО ОПРЕДЕЛЕННОГО РАЗМЕРА БЛОКА НА ОСНОВАНИИ ДИСПЕРСИИ | 2000 |
|
RU2273112C2 |
| СПОСОБ ПОКАДРОВОГО СЖАТИЯ ИЗОБРАЖЕНИЙ | 1994 |
|
RU2122295C1 |
| Аппарат для очищения воды при помощи химических реактивов | 1917 |
|
SU2A1 |
| US 2006129622 A1, 15.06.2006 | |||
| US 6694342 B1, 17.02.2004 | |||
| US 2003078953 A1, 24.04.2003 | |||
| US 6799192 B1, 28.09.2004. | |||
Авторы
Даты
2013-10-20—Публикация
2007-06-26—Подача