Данная заявка притязает на приоритет предварительной патентной заявки США №60/816,697, поданной 26 июня 2006 г., предварительной патентной заявки США №60/841,362, поданной 30 августа 2006 г., предварительной патентной заявки США №60/847,194, поданной 25 сентября 2006 г., предварительной патентной заявки США №60/829,669, поданной 16 октября 2006 г., и предварительной патентной заявки США №60/869,530, поданной 11 декабря 2006 г., содержание которых, в полном объеме, настоящим включено посредством ссылки.
Область техники
Изобретение относится к компьютерной графике и мультимедиа и, в частности, к сжатию информации графики, изображений и видео.
Уровень техники
Многие существующие стандарты кодирования изображения и видео используют методы сжатия, позволяющие сохранять или передавать изображения и видео высокого разрешения в виде относительно компактных файлов или потоков данных. Такие стандарты кодирования включают в себя Joint Photographic Experts Group (JPEG), Moving Pictures Experts Group (MPEG)-1, MPEG-2, MPEG-4 часть 2, H.261, H.263 и другие стандарты кодирования изображения или видео.
В соответствии со многими из этих стандартов видеокадры сжимаются с использованием “пространственного” кодирования. Эти кадры могут быть исходными кадрами (т.е. i-кадрами) или могут быть остаточными кадрами, генерируемыми в процессе временного кодирования, который использует компенсацию движения. В ходе пространственного кодирования кадры разбиваются на блоки пикселей равного размера. Например, несжатый кадр можно разбить на множество блоков пикселей 8×8. Для каждого блока пикселей компоненты пикселя делятся на матрицы значений компонентов пикселя. Например, каждый блок пикселей можно разделить на матрицу значений компонента Y пикселя, матрицу значений компонента U пикселя и матрицу значений компонента V пикселя. В этом примере значения компонента Y пикселя указывают значения яркости и значения компонентов U и V пикселя представляют значения цветности.
Кроме того, в ходе пространственного кодирования прямое дискретное косинусное преобразование (FDCT) применяется к каждой матрице значений компонентов пикселя в кодируемом кадре. Идеальное одномерное FDCT определяется как
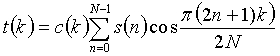 ,
,
где s - это массив из N исходных значений, t - это массив из N преобразованных значений, и коэффициенты c задаются как
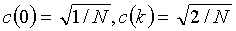
для 1≤k≤N-1.
Идеальное двумерное FDCT определяется по формуле:
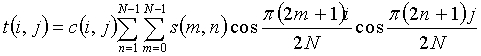 ,
,
где s - это массив из N исходных значений, t - это массив из N преобразованных значений, и c(i,j) задается соотношением c(i,j)=c(i)c(j), где c(k) определяется, как в одномерном случае.
Матрица коэффициентов получается, когда блок значений компонентов пикселя преобразуется с использованием FDCT. Эту матрицу коэффициентов затем можно квантовать и кодировать с использованием, например, кода Хаффмана или арифметического кода. Битовый поток видеосигнала представляет комбинированный результат осуществления этого процесса на всех блоках значений компонентов пикселя в последовательности видеокадров в несжатой последовательности видеокадров.
Несжатый видеокадр можно получить из битового потока видеосигнала, обратив этот процесс. В частности, каждая матрица коэффициентов в битовом потоке распаковывается, и распакованные значения деквантуются для получения матрицы преобразованных коэффициентов. Затем обратное дискретное косинусное преобразование (“IDCT”) применяется к каждой матрице преобразованных коэффициентов для получения матрицы значений компонентов пикселя. Идеальное одномерное IDCT определяется как
 ,
,
где s - это массив из N исходных значений, t - это массив из N преобразованных значений, и коэффициенты c задаются как
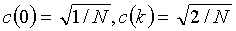
для 1≤k≤N-1.
Идеальное двумерное IDCT определяется по формуле:

Результирующие матрицы значений компонентов пикселя затем повторно собираются в блоки пикселей, и эти блоки пикселей повторно собираются для формирования декодированного кадра. Если декодированный кадр является i-кадром, кадр теперь полностью декодирован. Однако, если несжатый кадр является прогнозирующим или дважды прогнозирующим кадром, декодированный кадр является всего лишь декодированным остаточным кадром. Окончательный кадр генерируется путем построения реконструированного кадра с использованием векторов движения, связанных с декодированным кадром, с последующим прибавлением реконструированного кадра к декодированному остаточному кадру.
В идеальном случае при использовании FDCT для кодирования или IDCT для декодирования блока значений компонентов пикселя информация не теряется. Таким образом, в этом идеальном случае декодированная версия видеокадра идентична исходной версии видеокадра. Однако вычисление FDCT или IDCT может быть вычислительно трудным, поскольку вычисления FDCT и IDCT предусматривают использование действительных чисел и значительного количества операций умножения. По этой причине действительные числа, используемые в FDCT и IDCT, нередко аппроксимируют с использованием чисел с ограниченной точностью. Использование чисел с ограниченной точностью для представления действительных чисел приводит к возникновению ошибок округления. Кроме того, квантование и деквантование могут вносить дополнительные ошибки.
Ошибки в процессе сжатия и распаковки могут приводить к значительным различиям между исходным несжатым кадром и конечным несжатым кадром. Например, цвета в конечном несжатом кадре могут отличаться от цветов в исходном несжатом кадре. Кроме того, ошибки, обусловленные расхождением между реализацией операций IDCT на кодере и реализацией операций IDCT на декодере, могут накапливаться в ходе кодирования и декодирования последовательностей прогнозируемых кадров. Эти накопленные ошибки, в целом, именуются “дрейфом IDCT”.
Сущность изобретения
Описаны методики снижения ошибки округления в ходе вычисления дискретного косинусного преобразования с использованием вычислений с фиксированной запятой. Согласно этим методикам матрица масштабированных коэффициентов вычисляется путем умножения коэффициентов в матрице коэффициентов на масштабные коэффициенты. Затем значение среднего смещения и значение дополнительного смещения суммируются с коэффициентом постоянной составляющей матрицы масштабированных коэффициентов. Затем обратное дискретное косинусное преобразование применяется к результирующей матрице масштабированных коэффициентов. Затем значения в результирующей матрице сдвигаются вправо для получения матрицы значений компонентов пикселя. Описанное здесь сложение значения дополнительного смещения с коэффициентом постоянной составляющей снижает ошибки округления, обусловленные этим правым сдвигом. В результате окончательная версия цифрового медиафайла, который распаковывается с использованием этих методов, становится ближе к исходной версии цифрового медиафайла.
Согласно одному аспекту способ содержит этап, на котором генерируют матрицу смещенных коэффициентов путем сложения одного или нескольких значений смещения с коэффициентом матрицы исходных коэффициентов. Способ также содержит этап, на котором генерируют матрицу преобразованных коэффициентов с использованием арифметики с фиксированной запятой для повторного применения одномерного преобразования к коэффициентам в матрице смещенных коэффициентов. Кроме того, способ содержит этап, на котором генерируют матрицу выходных коэффициентов путем правого сдвига коэффициентов в матрице преобразованных коэффициентов. Коэффициенты в матрице выходных коэффициентов являются аппроксимациями значений, которые были бы получены путем преобразования матрицы исходных коэффициентов с использованием идеального обратного дискретного косинусного преобразования. Способ также содержит этап, на котором предписывают блоку представления медиа выводить слышимые или видимые сигналы на основании матрицы выходных значений. В результате сложения значений смещения с коэффициентом положительные ошибки и отрицательные ошибки оказываются, в среднем, равными по величине и оказываются, в среднем, симметричными относительно нуля. Ошибки представляют разности между значениями, полученными в результате правого сдвига представлений ограниченной точности с фиксированной запятой для коэффициентов в матрице преобразованных коэффициентов на первую величину, и результатами деления коэффициентов в матрице преобразованных коэффициентов на 2 в степени первой величины, безотносительно к точности.
Согласно другому аспекту устройство содержит модуль смещения коэффициентов, который генерирует матрицу смещенных коэффициентов путем сложения одного или нескольких значений смещения с коэффициентом матрицы исходных коэффициентов. Устройство также содержит модуль обратного преобразования, который генерирует матрицу преобразованных коэффициентов с использованием арифметики с фиксированной запятой для повторного применения одномерного преобразования к коэффициентам в матрице смещенных коэффициентов. Кроме того, устройство содержит модуль правого сдвига, который генерирует матрицу выходных коэффициентов путем правого сдвига коэффициентов в матрице преобразованных коэффициентов. Коэффициенты в матрице выходных коэффициентов являются аппроксимациями значений, которые были бы получены путем преобразования матрицы исходных коэффициентов с использованием идеального обратного дискретного косинусного преобразования. Устройство также содержит драйвер представления, который предписывает блоку представления медиа выводить слышимые или видимые сигналы на основании матрицы выходных коэффициентов. В результате сложения значений смещения с коэффициентом положительные ошибки и отрицательные ошибки оказываются, в среднем, равными по величине и оказываются, в среднем, симметричными относительно нуля. Ошибки представляют разности между значениями, полученными в результате правого сдвига представлений ограниченной точности с фиксированной запятой для коэффициентов в матрице преобразованных коэффициентов на первую величину, и результатами деления коэффициентов в матрице преобразованных коэффициентов на 2 в степени первой величины, безотносительно к точности.
Согласно еще одному аспекту устройство содержит средство для генерации матрицы смещенных коэффициентов путем сложения одного или нескольких значений смещения с коэффициентом матрицы исходных коэффициентов. Устройство также содержит средство для генерации матрицы преобразованных коэффициентов с использованием арифметики с фиксированной запятой для повторного применения одномерного преобразования к коэффициентам в матрице смещенных коэффициентов. Кроме того, устройство содержит средство для генерации матрицы выходных коэффициентов путем правого сдвига коэффициентов в матрице преобразованных коэффициентов. Коэффициенты в матрице выходных коэффициентов являются аппроксимациями значений, которые были бы получены путем преобразования матрицы исходных коэффициентов с использованием идеального обратного дискретного косинусного преобразования. Устройство также содержит средство для предписания блоку представления медиа выводить слышимые или видимые сигналы на основании матрицы выходных значений. В результате сложения значений смещения с коэффициентом положительные ошибки и отрицательные ошибки оказываются, в среднем, равными по величине и оказываются, в среднем, симметричными относительно нуля. Ошибки представляют разности между значениями, полученными в результате правого сдвига представлений ограниченной точности с фиксированной запятой для коэффициентов в матрице преобразованных коэффициентов на первую величину, и результатами деления коэффициентов в матрице преобразованных коэффициентов на 2 в степени первой величины, безотносительно к точности.
Согласно еще одному аспекту изобретение предусматривает компьютерно-считываемый носитель, содержащий инструкции. При выполнении инструкции предписывают процессору генерировать матрицу смещенных коэффициентов путем сложения одного или нескольких значений смещения с коэффициентом матрицы исходных коэффициентов. Инструкции также предписывают процессору генерировать матрицу преобразованных коэффициентов с использованием арифметики с фиксированной запятой для повторного применения одномерного преобразования к коэффициентам в матрице смещенных коэффициентов. Кроме того, инструкции предписывают процессору генерировать матрицу выходных коэффициентов путем правого сдвига коэффициентов в матрице преобразованных коэффициентов. Коэффициенты в матрице выходных коэффициентов являются аппроксимациями значений, которые были бы получены путем преобразования матрицы исходных коэффициентов с использованием идеального обратного дискретного косинусного преобразования. Инструкции также предписывают блоку представления медиа выводить слышимые или видимые сигналы на основании матрицы выходных значений. В результате сложения значений смещения с коэффициентом положительные ошибки и отрицательные ошибки оказываются, в среднем, равными по величине и оказываются, в среднем, симметричными относительно нуля. Ошибки представляют разности между значениями, полученными в результате правого сдвига представлений ограниченной точности с фиксированной запятой для коэффициентов в матрице преобразованных коэффициентов на первую величину, и результатами деления коэффициентов в матрице преобразованных коэффициентов на 2 в степени первой величины, безотносительно к точности.
Согласно еще одному аспекту способ содержит этап, на котором генерируют матрицу отрегулированных коэффициентов путем сдвига влево каждого коэффициента в матрице исходных коэффициентов. Способ также содержит этап, на котором генерируют матрицу преобразованных коэффициентов с использованием арифметики с фиксированной запятой для повторного применения одномерного преобразования к коэффициентам в матрице отрегулированных коэффициентов. Кроме того, способ содержит этап, на котором генерируют матрицу масштабированных коэффициентов путем масштабирования каждого коэффициента в матрице преобразованных коэффициентов. Кроме того, способ содержит этап, на котором генерируют матрицу смещенных коэффициентов путем сложения одного или нескольких значений смещения с одним или несколькими коэффициентами в матрице масштабированных коэффициентов. Способ также содержит этап, на котором генерируют матрицу выходных коэффициентов путем правого сдвига коэффициентов в матрице смещенных коэффициентов на первую величину. Матрица исходных коэффициентов представляет медиаданные. Коэффициенты в матрице выходных коэффициентов являются аппроксимациями значений, которые были бы получены путем преобразования матрицы исходных коэффициентов с использованием идеального прямого дискретного косинусного преобразования. В результате сложения значений смещения с коэффициентом положительные ошибки и отрицательные ошибки оказываются, в среднем, равными по величине и оказываются, в среднем, симметричными относительно нуля. Ошибки представляют разности между значениями, полученными в результате правого сдвига представлений ограниченной точности с фиксированной запятой для коэффициентов в матрице смещенных коэффициентов на первую величину, и результатами деления коэффициентов в матрице смещенных коэффициентов на 2 в степени первой величины, безотносительно к точности.
Согласно еще одному аспекту устройство содержит модуль левого сдвига, который генерирует матрицу отрегулированных коэффициентов путем сдвига влево каждого коэффициента в матрице исходных коэффициентов. Устройство также содержит модуль прямого преобразования, который генерирует матрицу преобразованных коэффициентов с использованием арифметики с фиксированной запятой для повторного применения одномерного преобразования к коэффициентам в матрице отрегулированных коэффициентов. Кроме того, устройство содержит модуль масштабирования, который генерирует матрицу масштабированных коэффициентов путем масштабирования каждого коэффициента в матрице преобразованных коэффициентов. Устройство также содержит модуль смещения коэффициентов, который генерирует матрицу смещенных коэффициентов путем сложения одного или нескольких значений смещения с одним или несколькими коэффициентами в матрице масштабированных коэффициентов. Кроме того, устройство содержит модуль правого сдвига, который генерирует матрицу выходных коэффициентов путем правого сдвига коэффициентов в матрице смещенных коэффициентов на первую величину. Матрица исходных коэффициентов представляет медиаданные. Коэффициенты в матрице выходных коэффициентов являются аппроксимациями значений, которые были бы получены путем преобразования матрицы исходных коэффициентов с использованием идеального прямого дискретного косинусного преобразования. В результате сложения значений смещения с коэффициентом положительные ошибки и отрицательные ошибки оказываются, в среднем, равными по величине и оказываются, в среднем, симметричными относительно нуля. Ошибки представляют разности между значениями, полученными в результате правого сдвига представлений ограниченной точности с фиксированной запятой для коэффициентов в матрице смещенных коэффициентов на первую величину, и результатами деления коэффициентов в матрице смещенных коэффициентов на 2 в степени первой величины, безотносительно к точности.
Согласно еще одному аспекту устройство содержит средство для генерации матрицы отрегулированных коэффициентов путем сдвига влево каждого коэффициента в матрице исходных коэффициентов. Устройство также содержит средство для генерации матрицы преобразованных коэффициентов с использованием арифметики с фиксированной запятой для повторного применения одномерного преобразования к коэффициентам в матрице отрегулированных коэффициентов. Кроме того, устройство содержит средство для генерации матрицы масштабированных коэффициентов путем масштабирования каждого коэффициента в матрице преобразованных коэффициентов. Устройство также содержит средство для генерации матрицы смещенных коэффициентов путем сложения одного или нескольких значений смещения с одним или несколькими коэффициентами в матрице масштабированных коэффициентов. Кроме того, устройство содержит средство для генерации матрицы выходных коэффициентов путем правого сдвига коэффициентов в матрице смещенных коэффициентов на первую величину. Матрица исходных коэффициентов представляет медиаданные. Коэффициенты в матрице выходных коэффициентов являются аппроксимациями значений, которые были бы получены путем преобразования матрицы исходных коэффициентов с использованием идеального прямого дискретного косинусного преобразования. В результате сложения значений смещения с коэффициентом положительные ошибки и отрицательные ошибки оказываются, в среднем, равными по величине и оказываются, в среднем, симметричными относительно нуля. Ошибки представляют разности между значениями, полученными в результате правого сдвига представлений ограниченной точности с фиксированной запятой для коэффициентов в матрице смещенных коэффициентов на первую величину, и результатами деления коэффициентов в матрице смещенных коэффициентов на 2 в степени первой величины, безотносительно к точности.
Согласно еще одному аспекту компьютерно-считываемый носитель содержит инструкции. Инструкции предписывают программируемому процессору генерировать матрицу отрегулированных коэффициентов путем сдвига влево каждого коэффициента в матрице исходных коэффициентов. Инструкции также предписывают процессору генерировать матрицу преобразованных коэффициентов с использованием арифметики с фиксированной запятой для повторного применения одномерного преобразования к коэффициентам в матрице отрегулированных коэффициентов. Кроме того, инструкции предписывают процессору генерировать матрицу масштабированных коэффициентов путем масштабирования каждого коэффициента в матрице преобразованных коэффициентов. Кроме того, инструкции предписывают процессору генерировать матрицу смещенных коэффициентов путем сложения одного или нескольких значений смещения с одним или несколькими коэффициентами в матрице масштабированных коэффициентов. Инструкции также предписывают процессору генерировать матрицу выходных коэффициентов путем правого сдвига коэффициентов в матрице смещенных коэффициентов на первую величину. Матрица исходных коэффициентов представляет медиаданные. Коэффициенты в матрице выходных коэффициентов являются аппроксимациями значений, которые были бы получены путем преобразования матрицы исходных коэффициентов с использованием идеального прямого дискретного косинусного преобразования. В результате сложения значений смещения с коэффициентом положительные ошибки и отрицательные ошибки оказываются, в среднем, равными по величине и оказываются, в среднем, симметричными относительно нуля. Ошибки представляют разности между значениями, полученными в результате правого сдвига представлений ограниченной точности с фиксированной запятой для коэффициентов в матрице смещенных коэффициентов на первую величину, и результатами деления коэффициентов в матрице смещенных коэффициентов на 2 в степени первой величины, безотносительно к точности.
В ряде случаев компьютерно-считываемый носитель может составлять часть компьютерного программного продукта, который может продаваться производителям и/или использоваться в устройстве. Компьютерный программный продукт может включать в себя компьютерно-считываемый носитель и в ряде случаев также может включать в себя упаковочные материалы.
Подробное рассмотрение одного или нескольких примеров приведено в прилагаемых чертежах и в нижеследующем описании. Другие признаки, задачи и преимущества изобретения явствуют из описания и чертежей, а также из формулы изобретения.
Краткое описание чертежей
Фиг.1 - блок-схема иллюстративного устройства, которое кодирует и декодирует медиафайлы.
Фиг.2 - подробная блок-схема иллюстративного модуля кодирования.
Фиг.3 - подробная блок-схема иллюстративного модуля декодирования.
Фиг.4 - логическая блок-схема, иллюстрирующая принцип работы модуля кодирования.
Фиг.5 - логическая блок-схема, иллюстрирующая принцип работы модуля декодирования.
Фиг.6 - подробная блок-схема иллюстративного модуля обратного дискретного косинусного преобразования (“IDCT”).
Фиг.7 - логическая блок-схема, иллюстрирующая принцип работы модуля IDCT.
Фиг.8 - подробная блок-схема иллюстративного модуля прямого дискретного косинусного преобразования (“FDCT”).
Фиг.9 - логическая блок-схема, иллюстрирующая принцип работы модуля FDCT.
Фиг.10 - схема первого иллюстративного одномерного преобразования.
Фиг.11 - схема второго иллюстративного одномерного преобразования.
Фиг.12 - схема иллюстративного масштабированного одномерного преобразования, используемого модулем IDCT.
Подробное описание
На фиг.1 показана блок-схема иллюстративного устройства 2, которое кодирует и декодирует медиафайлы. Устройство 2 может содержать персональный компьютер, мобильный радиотелефон, сервер, сетевое устройство, компьютер, встроенный в транспортное средство, платформу для видеоигр, портативное устройство для видеоигр, компьютерную рабочую станцию, компьютерный общественный терминал, цифровой идентификационный комплект, универсальный компьютер, телевизионную приставку, сетевой телефон, карманный персональный компьютер, платформу для видеоигр, мобильный медиаплеер, домашний медиаплеер, цифровой видеопроектор, персональный медиаплеер (например, iPod) или электронное устройство другого типа.
Устройство 2 может включать в себя медиаисточник 4 для генерации медиаданных. Медиаисточник 4 может содержать цифровые видеокамеру или фотоаппарат для захвата данных изображения. Медиаисточник 4 может быть встроен в устройство 2 или может быть подключен к устройству 2 в качестве периферийного устройства. Медиаисточник 4 также может содержать микрофон для записи аудиоданных. Медиаисточник 4 может выдавать медиаданные на процессор 6. Процессор 6 может содержать цифровой сигнальный процессор (“ЦСП”), микропроцессор или интегральную схему другого типа.
Когда процессор 6 принимает медиаданные от медиаисточника 4, модуль 8 кодирования может кодировать медиаданные. Модуль 8 кодирования может содержать программное обеспечение, выполняемое процессором 6. Альтернативно модуль 8 кодирования может содержать специализированное оборудование в процессоре 6, которое кодирует медиаданные. Согласно еще одной альтернативе модуль 8 кодирования может содержать любую комбинацию программного обеспечения и оборудования для кодирования медиаданных.
Модуль 8 кодирования может хранить кодированные медиаданные в медиахранилище 10. Медиахранилище 10 может содержать флэш-память, оперативную память, накопитель на жестких дисках или энергозависимое или энергонезависимое запоминающее устройство другого типа.
Модуль 12 декодирования может извлекать кодированные медиаданные из медиахранилища 10. Модуль 12 декодирования может содержать программное обеспечение, выполняемое процессором 6. Альтернативно модуль 12 декодирования может содержать специализированное аппаратное обеспечение в процессоре 6, которое декодирует кодированные медиаданные. Согласно еще одной альтернативе модуль 12 декодирования может содержать комбинацию программного и аппаратного обеспечения которые совместно декодируют кодированные медиаданные.
Драйвер 13 представления в устройстве 2 предписывает блоку 14 представления медиа представлять медиаданные, декодированные модулем 12 декодирования. Например, блок 14 представления медиа может содержать компьютерный монитор, который представляет медиаданные изображения или видео. В другом примере блок 14 представления медиа может содержать устройство вывода аудио (например, громкоговоритель), которое представляет медиаданные аудио. Блок 14 представления медиа может быть встроен в устройство 2 или может быть подключен посредством проводной или беспроводной линии связи к устройству 2 в качестве периферийного устройства. Драйвер 13 представления может содержать драйвер устройства или другой программный, аппаратный или программно-аппаратный блок или какой-либо другой механизм, который предписывает блоку 14 представления медиа представлять медиаданные.
Устройство 2 также может содержать сетевой интерфейс 16. Сетевой интерфейс 16 может облегчать связь между устройством 2 и компьютерной сетью по проводной или беспроводной линии связи. Например, сетевой интерфейс 16 может облегчать связь между устройством 2 и сетью мобильной телефонной связи. Устройство 2 может принимать медиафайлы через сетевой интерфейс 16. Например, устройство 2 может принимать фотографии, видеозаписи, потоковое видео (например, телевидение, видеоконференции, кинофильмы), аудиозаписи (например, рингтоны, песни, MP3-файлы), потоковое аудио (например, цифровые радиостанции, речевые вызовы и т.д.) через сетевой интерфейс 16. Когда сетевой интерфейс 16 принимает медиафайл или битовый поток видеосигнала, сетевой интерфейс 16 может сохранять медиафайл или битовый поток видеосигнала в медиахранилище 10.
Видеосигнал можно описать как последовательность изображений, которая включает в себя кадры (картинки целиком) или поля (например, картинки, которые содержат нечетные или четные строки кадра). Кроме того, каждый кадр или поле может включать в себя две или более серии последовательных макроблоков или более мелкие части кадра или поля. Здесь термин “кадр”, отдельно или в сочетании с другими словами, может означать изображение, кадр, поле или серию последовательных макроблоков в нем.
Когда модуль 8 кодирования кодирует последовательность видеокадров, модуль 8 кодирования может сначала выбрать некоторые видеокадры как “i-кадры.” Например, модуль 8 кодирования может выбрать каждый восьмой кадр в качестве i-кадра. I-кадры это кадры, которые не имеют отношения к другим кадрам. Выбрав i-кадры, модуль 8 кодирования использует “пространственное кодирование” для кодирования i-кадров. Кроме того, модуль 8 кодирования может использовать “временное кодирование” для кодирования остальных кадров.
Чтобы использовать пространственное кодирование для кодирования кадра, модуль 8 кодирования может разбить данные кадра на блоки пикселей. Например, модуль 8 кодирования может разбить данные кадра на блоки пикселей, которые составляют восемь пикселей в ширину и восемь пикселей в высоту (т.е. каждый блок пикселей содержит 64 пикселя). Затем модуль 8 кодирования может разделить значения компонентов пикселя для пикселей в каждом блоке пикселей на отдельные матрицы значений компонентов пикселя. Значения компонентов пикселя для пикселя - это значения, характеризующие внешний вид пикселя. Например, каждый пиксель может характеризоваться значением компонента Y пикселя, значением компонента Cr пикселя и значением компонента Cb пикселя. Значение компонента Y пикселя указывает яркость пикселя, значение компонента Cr пикселя указывает красную составляющую цветности пикселя, и значение компонента Cb пикселя указывает синюю составляющую цветности пикселя. В этом примере, когда модуль 8 кодирования разделяет значения компонентов пикселя для блока пикселей, модуль 8 кодирования может получить матрицу значений компонента Y пикселя, матрицу значений компонента Cr пикселя и матрицу значений компонента Cb пикселя.
Разделив значения компонентов пикселя на матрицы значений компонентов пикселя, модуль 8 кодирования генерирует матрицу преобразованных коэффициентов для каждой матрицы значений компонентов пикселя. Модуль 8 кодирования может генерировать матрицу преобразованных коэффициентов для матрицы значений компонентов пикселя, сначала сгенерировав матрицу отрегулированных коэффициентов путем сдвига влево значений компонентов пикселя в матрице значений компонентов пикселя. Затем модуль 8 кодирования использует арифметику с фиксированной запятой для повторного применения одномерного преобразования к матрице отрегулированных коэффициентов, тем самым генерируя матрицу коэффициентов. В некоторых реализациях модуль 8 кодирования затем может генерировать матрицу преобразованных коэффициентов путем масштабирования матрицы преобразованных коэффициентов с помощью множества масштабных коэффициентов. Каждый из этих масштабных коэффициентов имеет целочисленное значение. Масштабные коэффициенты выбираются таким образом, чтобы коэффициенты в одномерном преобразовании можно было аппроксимировать с использованием простых рациональных чисел. В реализациях, не предусматривающих использование масштабирования, матрица коэффициентов, генерируемая путем применения преобразования, является матрицей преобразованных коэффициентов.
Каждый коэффициент в матрице преобразованных коэффициентов аппроксимирует соответствующее значение в матрице значений, которые были бы получены путем применения идеального двумерного прямого дискретного косинусного преобразования (“FDCT”) к матрице кодированных коэффициентов. Идеальное одномерное FDCT определяется как
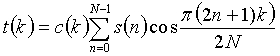 ,
,
где s - это массив из N исходных значений, t - это массив из N преобразованных значений, и коэффициенты c задаются как
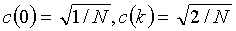
для 1≤k≤N-1.
Идеальное двумерное FDCT определяется по формуле:
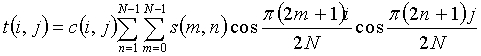 ,
,
где s - это массив из N исходных значений, t - это массив из N преобразованных значений, и c(i,j) задается соотношением c(i,j)=c(i)c(j), где c(k) определяется, как в одномерном случае.
Получив матрицу преобразованных коэффициентов, модуль 8 кодирования генерирует матрицу квантованных коэффициентов путем квантования коэффициентов в матрице преобразованных коэффициентов. Квантование преобразованных коэффициентов может сокращать объем информации, связанной с высокочастотными коэффициентами в матрице преобразованных коэффициентов. После генерации матрицы квантованных коэффициентов модуль 8 кодирования может применять схему энтропийного кодирования к матрице квантованных коэффициентов. Например, модуль 8 кодирования может применять схему кодирования по Хаффману к квантованным коэффициентам в матрице коэффициентов. Когда модуль 8 кодирования применяет схему энтропийного кодирования к каждой из матриц квантованных коэффициентов, модуль 8 кодирования может выводить кодированные матрицы как часть битового потока видеосигнала.
Чтобы использовать временное кодирование для кодирования кадра, модуль 8 кодирования может делить кадр на “макроблоки”. В зависимости от используемого стандарта кодирования эти макроблоки могут иметь фиксированный или переменный размер и могут быть перекрывающимися или неперекрывающимися. Например, каждый макроблок может состоять из 16×16 блоков пикселей. Для каждого макроблока в кадре модуль 8 кодирования может пытаться идентифицировать исходный макроблок в одном или нескольких опорных кадрах. В зависимости от стандарта кодирования опорные кадры могут быть i-кадрами, прогнозирующими кадрами или дважды прогнозирующими кадрами. Если модуль 8 кодирования способен идентифицировать исходный макроблок в опорном кадре, модуль 8 кодирования записывает вектор движения для макроблока. Вектор движения включает в себя значение x, которое указывает горизонтальное перемещение макроблока относительно идентифицированного исходного макроблока, и значение y, которое указывает вертикальное перемещение макроблока относительно идентифицированного исходного макроблока. Если модуль 8 кодирования не способен идентифицировать исходный макроблок для макроблока, модулю 8 кодирования может не требоваться записывать вектор движения для макроблока. Затем модуль 8 кодирования генерирует “реконструированный” кадр. Реконструированный кадр содержит кадр, который мог бы получиться путем перемещения макроблоков из опорных кадров в соответствии с записанными векторами движения для текущего кадра. После генерации реконструированного кадра модуль 8 кодирования вычитает значения компонентов пикселя в каждом пикселе для реконструированного кадра из соответствующих значений компонентов пикселя в соответствующих пикселях текущего кадра, получая “остаточный” кадр. Затем модуль 8 кодирования может использовать схему энтропийного кодирования для сжатия векторов движения для макроблоков текущего кадра. Кроме того, модуль 8 кодирования использует вышеописанный метод пространственного кодирования для сжатия остаточного кадра.
Модуль 12 декодирования может осуществлять процесс, аналогичный осуществляемому модулем 8 кодированию, но в обратной последовательности. Например, для осуществления процесса пространственного декодирования модуль 12 декодирования может применять схему энтропийного декодирования к каждой кодированной матрице квантованных коэффициентов в кодированном битовом потоке видеосигнала. Затем модуль 12 декодирования может деквантовать коэффициенты в каждой матрице квантованных коэффициентов, тем самым генерируя матрицу деквантованных коэффициентов для каждой матрицы квантованных коэффициентов. Для каждой матрицы квантованных коэффициентов модуль 12 декодирования генерирует матрицу масштабированных коэффициентов путем масштабирования матрицы квантованных коэффициентов.
После генерации матрицы масштабированных коэффициентов модуль 12 декодирования генерирует матрицу смещенных коэффициентов путем сложения значения среднего смещения и значения дополнительного смещения с коэффициентом постоянной составляющей матрицы. Коэффициент постоянной составляющей матрицы - это коэффициент, равный среднему значению других коэффициентов в матрице. Обычно коэффициент постоянной составляющей - это коэффициент в верхнем левом углу матрицы. Как описано более подробно ниже, сложение значений смещения с коэффициентом постоянной составляющей может снижать ошибки округления, когда модуль 12 декодирования сдвигает вправо значения, полученные путем применения разложения посредством обратного дискретного косинусного преобразования к каждой/му строке и столбцу матрицы. Эти ошибки округления могут быть обусловлены тем, что эти сдвиги вправо заменяют более вычислительно-трудоемкие операции деления и что операции правого сдвига в арифметике с фиксированной запятой не всегда дают те же результаты, что операции деления.
После генерации матрицы смещенных коэффициентов модулем 12 декодирования модуль 12 декодирования использует арифметику с фиксированной запятой для генерации матрицы преобразованных коэффициентов для матрицы смещенных коэффициентов. Модуль 12 декодирования генерирует матрицу преобразованных коэффициентов путем повторного применения одномерного преобразования к матрице смещенных коэффициентов. Например, модуль 12 декодирования может генерировать матрицу промежуточных коэффициентов путем применения одномерного преобразования к каждому вектору-строке матрицы смещенных коэффициентов. В этом примере модуль 12 декодирования затем может генерировать матрицу преобразованных коэффициентов путем применения одномерного преобразования к каждому вектору-столбцу в матрице промежуточных коэффициентов.
Модуль 12 декодирования может применять это одномерное преобразование с использованием последовательности “операций типа бабочка.” В общем случае “операция типа бабочка” - это операция, в которой первое промежуточное значение получается путем умножения первого входного значения на первую константу, второе промежуточное значение получается путем умножения первого входного значения на вторую константу, третье промежуточное значение получается путем умножения второго входного значения на первую константу, четвертое промежуточное значение получается путем умножения второго входного значения на вторую константу, первое выходное значение получается путем сложения первого промежуточного значения и третьего промежуточного значения, и второе выходное значение получается путем сложения второго промежуточного значения и четвертого промежуточного значения с отрицательным знаком. В операции типа бабочка константы могут быть любыми рациональными или иррациональными числами, включая единицу. Иллюстративные операции типа бабочка показаны в преобразованиях, представленных на фиг.10, 11 и 12.
В системах, где имеется ограниченное количество битов для представления чисел, было бы непрактично осуществлять операции умножения на иррациональные константы в операциях типа бабочка. По этой причине модуль 12 декодирования может аппроксимировать операции умножения на иррациональные константы путем умножения значений на рациональные дроби, аппроксимирующие иррациональные константы. Для эффективного умножения значения на рациональную дробь модуль 12 декодирования может умножать значение на числитель рациональной дроби и затем сдвигать вправо результирующие значения на log2 знаменателя рациональной дроби. Как отмечено выше, операции правого сдвига могут обуславливать ошибки округления, поскольку операции правого сдвига в арифметике с фиксированной запятой не всегда дают такие же результаты, как соответствующие операции деления.
Как объясняется более подробно ниже, модуль 12 декодирования может использовать отрицательные числители в некоторых рациональных дробях для снижения ошибок округления. Использование отрицательных числителей может избавлять от необходимости в прибавлении значений среднего смещения до правого сдвига значений. Это может давать преимущество, поскольку прибавление значений среднего смещения может излишне усложнять применение обратного дискретного косинусного преобразования.
После генерации матрицы преобразованных коэффициентов модулем 12 декодирования модуль 12 декодирования генерирует матрицу отрегулированных коэффициентов путем правого сдвига каждого коэффициента в матрице преобразованных коэффициентов на число позиций, равное количеству битов, добавленных путем применения преобразования, плюс количество битов, добавленных путем масштабирования коэффициентов матрицы деквантованных коэффициентов. Затем модуль 12 декодирования может генерировать матрицу ограниченных коэффициентов путем ограничения коэффициентов в матрице отрегулированных коэффициентов. Ограничение коэффициентов в матрице отрегулированных коэффициентов изменяет отрегулированные коэффициенты таким образом, чтобы они находились в разрешенном диапазоне значений компонентов пикселя. Следовательно, матрицу ограниченных коэффициентов можно охарактеризовать как матрицу значений компонентов пикселя.
После генерации матрицы значений компонентов пикселя модуль 12 декодирования может генерировать блок пикселей путем объединения матрицы значений компонентов пикселя с матрицами, в которых хранятся другие значения компонентов пикселя для блока пикселей. Затем модуль 12 декодирования может объединять блоки пикселей в видеокадр.
Для декодирования прогнозирующего кадра модуль 12 декодирования может использовать вышеописанный метод пространственного декодирования для декодирования матриц квантованных коэффициентов в остаточном изображении для прогнозирующего кадра. Кроме того, модуль 12 декодирования может использовать схему энтропийного декодирования для декодирования векторов движения прогнозирующего кадра. Затем модуль 12 декодирования может генерировать реконструированный кадр путем “перемещения” макроблоков опорных кадров прогнозирующего кадра в соответствии с векторами движения. После генерации реконструированного кадра модуль 12 декодирования прибавляет значения компонентов пикселя в каждом пикселе декодированного остаточного кадра к соответствующим значениям компонентов пикселя в соответствующих пикселях реконструированного кадра. Результатом этого сложения является реконструированный прогнозирующий кадр.
Методики, описанные в этом раскрытии, могут обеспечивать ряд преимуществ. Например, снижение ошибок округления в ходе вычисления дискретных косинусных преобразований и обратных дискретных косинусных преобразований может снижать видимые ошибки в данных изображения и может снижать слышимые ошибки в аудиоданных. Кроме того, поскольку эти методики можно применять для вычислений с фиксированной запятой, эти методики можно применять в более компактных, менее сложных устройствах, например мобильных телефонах, карманных персональных компьютерах и персональных медиаплеерах. В частности, методики можно применять с использованием чисел с фиксированной запятой, которые имеют очень ограниченное количество битов в своих частях мантиссы (например, три бита), тем не менее, удовлетворяя требованиям точности, предписанным стандартом 1180 Института инженеров по электротехнике и радиоэлектронике (IEEE), который в полном объеме настоящим включен посредством ссылки. Кроме того, эти методики можно применять к форматам, которые включают в себя рекомендации H.261, H.263, H.264, T.81 (JPEG) International Telecommunication Union Standardization Sector (ITU-T), а также к медиаформатам International Organization for Standardization (ISO)/MEC Moving Pictures Experts Group (MPEG)-1, MPEG-2, и MPEG-4 Часть 2.
На фиг.2 показана подробная блок-схема иллюстративного модуля 8 кодирования. Модуль 8 кодирования могут содержать множество “модулей”. Эти модули могут содержать подмножество программных инструкций модуля 8 кодирования. Альтернативно эти модули могут содержать специализированное программное обеспечение. Согласно другой альтернативе эти модули могут содержать программные инструкции и специализированное программное обеспечение.
Как показано в примере, приведенном на фиг.2, модуль 8 кодирования включает в себя модуль 20 управления кадрами, который определяет, обрабатывает ли модуль 8 кодирования видеокадр как i-кадр, прогнозирующий кадр или дважды прогнозирующий кадр. Например, когда модуль 8 кодирования принимает видеокадр, модуль 20 управления кадрами может определять на основании флага битового потока, связанного с видеокадром, является ли кадр i-кадром, прогнозирующим кадром или дважды прогнозирующим кадром. Если модуль 20 управления кадрами определяет, что флаг битового потока указывает, что кадр является i-кадром, модуль 20 управления кадрами может предписывать обработку видеокадра посредством множества модулей, которые немедленно осуществляют пространственное кодирование на видеокадре. Если же модуль 20 управления кадрами определяет, что кадр является прогнозирующим кадром или дважды прогнозирующим кадром, модуль 20 управления кадрами может предписывать обработку видеокадра посредством множества модулей, которые осуществляют временное кодирование.
Модуль 8 кодирования включает в себя ряд модулей для применения пространственного кодирования к видеокадрам. Эти модули включают в себя модуль 22 разделения на блоки, модуль 24 выделения компонентов, модуль 26 прямого преобразования, модуль 28 квантования и модуль энтропийного кодирования 30. Модуль 22 разделения на блоки может принимать некодированные видеокадры от медиаисточника 4, сетевого интерфейса 16 или другого источника. Когда модуль 22 разделения на блоки принимает некодированный видеокадр, модуль 22 разделения на блоки может разделять кадр на блоки пикселей. Модуль 22 разделения на блоки может выдавать блоки пикселей на модуль 24 выделения компонентов.
Когда модуль 24 выделения компонентов принимает блок пикселей, модуль 24 выделения компонентов может преобразовывать значения компонентов пикселя для каждого пикселя в другой формат цвета. Например, модуль 24 выделения компонентов может преобразовывать каждый пиксель из формата цвета красный-зеленый-синий (RGB) в формат цвета YCrCb. Преобразовав пиксели в блоке к другому формату цвета, модуль 24 выделения компонентов может разделить значения компонентов пикселя для пикселей в блоке на матрицы значений компонентов пикселя. Например, модуль 24 выделения компонентов может выделить матрицу значений Y, матрицу значений Cr и матрицу значений Cb из одного блока пикселей. Значения Y указывают яркость пикселей, значения Cr указывают красную составляющую цветности пикселей, и значения Cb указывают синюю составляющую цветности пикселей. Когда модуль выделения компонентов 24 выделит матрицы значений компонентов пикселя, модуль 24 выделения компонентов сможет выдавать каждую из матриц по отдельности на модуль 26 прямого преобразования.
Когда модуль 26 прямого преобразования принимает матрицу значений компонентов пикселя, модуль 26 прямого преобразования генерирует матрицу преобразованных коэффициентов. Каждый коэффициент в этой матрице масштабированных коэффициентов аппроксимирует коэффициент, который был бы получен с использованием идеального прямого дискретного косинусного преобразования, для преобразования матрицы значений компонентов пикселя.
Модуль 26 прямого преобразования использует арифметику с фиксированной запятой для применения одномерного преобразования к матрицам значений компонентов пикселя. Использование арифметики с фиксированной запятой может иметь преимущество в ряде обстоятельств. Например, компактные устройства, например мобильные телефоны, могут не иметь блока арифметики с плавающей запятой, необходимого для выполнения арифметических операций с плавающей запятой. Модуль 26 прямого преобразования может начать процесс генерации матрицы масштабированных коэффициентов путем сдвига влево каждого значения компонентов пикселя. Например, модуль 26 прямого преобразования может генерировать матрицу отрегулированных коэффициентов путем сдвига влево каждого значения компонента пикселя на количество битов точности (т.е. количество битов мантиссы) для представлений с фиксированной запятой чисел, которые модуль 26 прямого преобразования использует при применении одномерного преобразования, плюс количество битов точности, удаленных путем масштабирования преобразованных коэффициентов, полученных с применением преобразования. После сдвига влево каждого значения компонентов пикселя модуль 26 прямого преобразования может осуществлять преобразование на каждом векторе-строке матрицы отрегулированных коэффициентов. Благодаря осуществлению дискретного косинусного преобразования на каждом векторе-строке матрицы отрегулированных коэффициентов, генерируется матрица промежуточных коэффициентов. Затем модуль 26 прямого преобразования может осуществлять преобразование на каждом векторе-столбце матрицы промежуточных коэффициентов. Благодаря осуществлению преобразования на каждом векторе-столбце матрицы промежуточных коэффициентов, получается матрица преобразованных коэффициентов.
После генерации матрицы преобразованных коэффициентов модуль 26 прямого преобразования масштабирует преобразованные коэффициенты в разных позициях в матрице преобразованных коэффициентов с разными масштабными коэффициентами. Как описано ниже, модуль 12 декодирования может использовать величины, обратные этим масштабным коэффициентам при применении обратного преобразования. Когда модуль 26 прямого преобразования заканчивает масштабирование преобразованных коэффициентов с помощью масштабных коэффициентов, модуль 26 прямого преобразования может выводить результирующую матрицу масштабированных коэффициентов на модуль 28 квантования.
Когда модуль 28 квантования принимает матрицу коэффициентов от модуля 26 прямого преобразования, модуль 28 квантования может квантовать масштабированные коэффициенты. Модуль 28 квантования может квантовать масштабированные коэффициенты по-разному в зависимости от используемого стандарта кодирования. Например, в соответствии со стандартом MPEG-4 часть 2 модуль 28 квантования может использовать следующую матрицу квантования для квантования коэффициентов в матрице масштабированных коэффициентов для i-кадра:
Кроме того, в этом примере модуль 28 квантования может использовать следующую матрицу квантования для квантования коэффициентов в матрице масштабированных коэффициентов для прогнозирующего или дважды прогнозирующего кадра:
После генерации матрицы квантованных коэффициентов модулем 28 квантования модуль энтропийного кодирования 30 может сжимать матрицу квантованных коэффициентов с использованием схемы энтропийного кодирования. Для сжатия матрицы квантованных коэффициентов с использованием схемы энтропийного кодирования модуль энтропийного кодирования 30 может организовать квантованные коэффициенты в виде вектора, расположив коэффициенты в виде зигзага. Другими словами, модуль энтропийного кодирования 30 может составить из всех квантованных коэффициентов в двумерной матрице квантованных коэффициентов одномерный вектор квантованных коэффициентов предсказуемым образом. Затем модуль энтропийного кодирования 30 может применять схему энтропийного кодирования, например кодирование по Хаффману или арифметическое кодирование, к вектору квантованных коэффициентов.
Модуль 8 кодирования также включает в себя один или несколько модулей для осуществления временного кодирования видеокадров. Как показано в примере, приведенном на фиг.2, модуль 8 кодирования включает в себя модуль 32 оценки движения, модуль 34 генерации реконструированных кадров и модуль 36 генерации остаточных кадров. Модуль 32 оценки движения пытается идентифицировать исходный макроблок в опорном изображении для каждого макроблока в текущем видеокадре. Модуль 32 оценки движения может пытаться идентифицировать исходный макроблок для макроблока в текущем кадре путем поиска макроблоков в опорном изображении, которые содержат примерно такие же пиксели, как макроблок. Модуль 32 оценки движения может искать области разных размеров в соответствии с разными стандартами кодирования для идентификации исходного макроблока для макроблока в текущем кадре. Например, модуль 32 оценки движения может искать исходный макроблок в области, которая имеет 32 пикселя в ширину и 32 пикселя в высоту, причем текущий макроблок находится в центре области поиска. Когда модуль 32 оценки движения идентифицирует исходный макроблок для макроблока в текущем кадре, модуль 32 оценки движения вычисляет вектор движения для макроблока в текущем кадре. Вектор движения для макроблока в текущем кадре указывает значение x, которое указывает разность в горизонтальной позиции между идентифицированным исходным макроблоком и макроблоком текущего кадра. После того как модуль 32 оценки движения либо вычислит вектор движения, либо окажется неспособным идентифицировать исходный макроблок для каждого макроблока в текущем кадре, модуль 32 оценки движения сможет выдать вычисленные векторы движения для текущего кадра на модуль 34 генерации реконструированных кадров.
Модуль 34 генерации реконструированных кадров может использовать векторы движения и опорный кадр для генерации реконструированного кадра. Модуль 34 генерации реконструированных кадров может генерировать реконструированный кадр путем применения векторов движения для каждого макроблока в текущем кадре к исходным макроблокам в опорных кадрах. В результате модуль 34 генерации реконструированных кадров создает кадр, в котором макроблоки опорных кадров “переместились” в позиции, указанные соответствующими векторами движения текущего кадра.
Модуль 36 генерации остаточных кадров может генерировать остаточный кадр путем вычитания значений компонентов пикселя в реконструированном кадре из соответствующих значений компонентов пикселя в текущем кадре. В общем случае остаточный кадр включает в себя меньше информации, чем реконструированный кадр или текущий кадр. После генерации остаточного кадра модулем 36 генерации остаточных кадров модуль 36 генерации остаточных кадров выдает остаточный кадр на модуль 22 разделения на блоки, чтобы начать процесс пространственного кодирования остаточного кадра. Кроме того, модуль 32 оценки движения может выдавать векторы движения для текущего кадра на модуль 30 энтропийного кодирования для сжатия векторов движения. После того как остаточный кадр пространственно закодирован и модуль 30 энтропийного кодирования закодировал векторы движения, модуль 38 вывода потока может форматировать пространственно-кодированный остаточный кадр и кодированные векторы движения как часть битового потока видеосигнала.
На фиг.3 показана подробная блок-схема иллюстративного модуля 12 декодирования. Модуль 12 декодирования может содержать модуль 44 энтропийного декодирования, модуль 46 деквантования, модуль 48 обратного преобразования, модуль 50 реконструкции пикселей, буфер 51 кадров, модуль 52 объединения блоков, модуль 53 управления кадрами, модуль 54 хранения опорных кадров, модуль 56 генерации реконструированных кадров и модуль 58 генерации прогнозирующих кадров. Некоторые или все из этих модулей могут содержать подмножество программных инструкций модуля 12 декодирования. Альтернативно некоторые или все из этих модулей могут содержать специализированное аппаратное обеспечение или программно-аппаратное обеспечение. Согласно другой альтернативе эти модули могут содержать программные инструкции и специализированное аппаратное обеспечение или программно-аппаратное обеспечение.
Когда модуль 12 декодирования принимает битовый поток, содержащий видеокадр, модуль 44 энтропийного декодирования может применять схему энтропийного декодирования к матрицам квантованных коэффициентов в видеокадре. Битовый поток может включать в себя значение, которое указывает модулю 44 энтропийного декодирования, какую схему энтропийного декодирования применять к матрицам квантованных коэффициентов в битовом потоке. Кроме того, модуль 44 энтропийного декодирования может применять ту же самую или другую схему энтропийного декодирования для декодирования векторов движения видеокадра.
После применения модулем энтропийного декодирования 44 схемы энтропийного декодирования к матрицам квантованных коэффициентов в видеофайле, модуль 46 деквантования может деквантовать коэффициенты в каждой матрице квантованных коэффициентов. В зависимости от стандарта кодирования модуль 46 деквантования может деквантовать коэффициенты по-разному. Например, в соответствии со стандартом MPEG-4 часть 2 модуль 46 деквантования может использовать две вышеописанные матрицы квантования двумя разными способами. Во-первых, модуль 46 деквантования может использовать эти матрицы квантования для осуществления деквантования типа H.263. При деквантовании типа H.263 модуль 46 деквантования получает реконструированные коэффициенты F”[v][u] из квантованных значений QF[v][u] следующим образом:
 F"[v][u]: F"[v][u]=Sign(QF[v][u])×|F"[v][u]|,
F"[v][u]: F"[v][u]=Sign(QF[v][u])×|F"[v][u]|,
что предусматривает только одно умножение на quantiser_scale, и, во-вторых, модуль 46 деквантования может использовать эти матрицы квантования для осуществления деквантования типа MPEG-1/2. При деквантовании типа MPEG-1/2 модуль 46 деквантования использует дополнительные взвешивающие матрицы W[w][v][u], где w указывает, какая взвешивающая матрица используется:
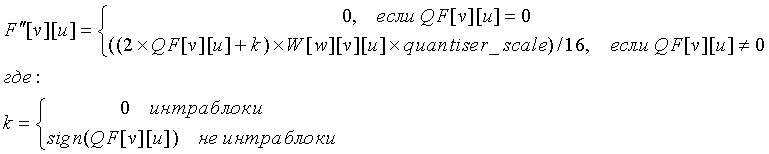
Когда модуль 48 обратного преобразования принимает матрицу деквантованных коэффициентов, модуль 48 обратного преобразования генерирует матрицу компонентов пикселя. Как описано более подробно ниже, модуль 48 обратного преобразования генерирует матрицу значений компонентов пикселя, сначала масштабируя каждый коэффициент в матрице деквантованных коэффициентов, прибавляя значение смещения к коэффициенту постоянной составляющей матрицы, применяя последовательность одномерных дискретных косинусных преобразований, сдвигая вправо результирующие значения, ограничивая сдвинутые вправо значения и затем выводя ограниченные значения.
После вывода модулем 48 обратного преобразования матрицы значений компонентов пикселя модуль 50 реконструкции пикселей может генерировать матрицу пикселей путем объединения матрицы значений компонентов пикселя с матрицами значений компонентов пикселя, связанными с эквивалентными позициями в видеокадре. Например, модуль 50 реконструкции пикселей может принимать матрицу значений компонента Y пикселя, матрицу значений компонента Cb пикселя и матрицу значений компонента Cr пикселя от модуля 48 обратного преобразования. Каждая из этих трех матриц может включать в себя компоненты пикселя для одного блока пикселей 8×8. Каждый пиксель может включать в себя значение компонента Y пикселя, значение компонента Cb пикселя и значение компонента Cr пикселя. После генерации матрицы пикселей модуль 50 реконструкции пикселей может выдавать блок пикселей на модуль 52 объединения блоков.
Когда модуль 52 объединения блоков принимает блок пикселей, модуль 52 объединения блоков может буферизовать блок пикселей прежде, чем модуль 52 объединения блоков принимает некоторые или все блоки пикселей в видеокадре. После получения одного или нескольких блоков пикселей модуль 52 объединения блоков может объединять блоки пикселей в видеокадр и может выводить видеокадр на буфер 51 кадров. Видеокадр может храниться в буфере 51 кадров, пока он не будет отображен блоком 51 представления медиа. Кроме того, модуль 52 объединения блоков может выводить видеокадр на модуль 54 хранения кадров. Видеокадры в модуле 54 хранения кадров можно использовать в качестве опорных кадров для реконструкции прогнозирующих и дважды прогнозирующих кадров. Кроме того, видеокадры в модуле 54 хранения кадров могут быть остаточными кадрами, которые используются при реконструкции прогнозирующих и дважды прогнозирующих кадров.
Для реконструкции прогнозирующего или дважды прогнозирующего кадра модуль 12 декодирования включает в себя модуль 56 генерации реконструированных кадров. Модуль 56 генерации реконструированных кадров принимает декодированные векторы движения от модуля 44 энтропийного декодирования. Кроме того, модуль 56 генерации реконструированных кадров извлекает опорные кадры текущего кадра из модуля 54 хранения кадров. Затем модуль 56 генерации реконструированных кадров “перемещает” макроблоки из их позиций в опорных кадрах в позиции, указанные векторами движения. Реконструированный кадр получается в результате подобного перемещения макроблоков. После генерации реконструированного кадра модулем 56 генерации реконструированных кадров модуль 56 генерации реконструированных кадров выдает реконструированный кадр на модуль 58 генерации прогнозирующих кадров.
Когда модуль 58 генерации прогнозирующих кадров принимает временный кадр, модуль генерации прогнозирующих кадров 58 может извлекать из модуля 54 хранения кадров остаточный кадр для текущего кадра. Извлекши остаточный кадр, модуль 58 генерации прогнозирующих кадров может суммировать соответствующие значения цветовых компонентов в каждом пикселе остаточного кадра и реконструированного кадра. В результате этого суммирования получается реконструированный видеокадр. Затем модуль 58 генерации прогнозирующих кадров может выводить этот реконструированный кадр в буфер 51 кадров для своевременного отображения в блоке 14 представления медиа.
На фиг.4 показана логическая блок-схема, иллюстрирующая принцип работы модуля 8 кодирования. Хотя принцип работы, представленный на фиг.4, описан в последовательном режиме, следует заметить, что работа может осуществляться в конвейерном режиме.
Первоначально модуль 8 кодирования принимает последовательность некодированных видеокадров (60). Например, модуль 8 кодирования может принимать последовательность некодированных кадров в виде множеств пикселей от медиаисточника 4. Когда модуль 8 кодирования принимает последовательность некодированных кадров, модуль 20 управления кадрами в модуле 8 кодирования может определять, подлежит ли текущий кадр в последовательности некодированных кадров кодированию как i-кадр или как прогнозирующий или дважды прогнозирующий кадр (62).
Если модуль 20 управления кадрами определяет, что текущий кадр подлежит кодированию как i-кадр, модуль 22 разделения на блоки в модуле 8 кодирования может делить текущий кадр на блоки пикселей (64). Например, модуль 8 кодирования может делить текущий кадр на блоки пикселей 2×2, 4×4 или 8×8.
Разделив текущий кадр на блоки пикселей, модуль 24 выделения компонентов может отделять значения компонентов пикселя в каждом блоке пикселей (66). В результате может получиться три блока значений компонентов пикселя для каждого блока пикселей: блок значений Y для представления яркости пикселей, блок значений Cb для представления синей составляющей цветности пикселей и блок значений Cr для представления красной составляющей цветности пикселей.
Затем модуль 26 прямого преобразования в модуле 8 кодирования может генерировать матрицу масштабированных коэффициентов для каждой матрицы значений компонентов пикселя (68). Коэффициенты в этих матрицах масштабированных коэффициентов являются аппроксимациями значений, которые были бы получены с использованием идеального двумерного прямого дискретного косинусного преобразования на соответствующих матрицах значений компонентов пикселя.
После генерации модулем 26 прямого преобразования матриц масштабированных коэффициентов для каждой матрицы компонентов пикселя модуль 28 квантования в модуле 8 кодирования может квантовать коэффициенты в каждой матрице масштабированных коэффициентов (70). После квантования модулем 28 квантования коэффициентов в каждой матрице масштабированных коэффициентов модуль 30 энтропийного кодирования может осуществлять процесс энтропийного кодирования на каждой матрице квантованных коэффициентов (72). Например, модуль 8 кодирования может применять схему кодирования по Хаффману или схему арифметического кодирования к каждой матрице квантованных коэффициентов. Процесс энтропийного кодирования дополнительно сжимает данные. Однако процессы энтропийного кодирования не приводят к потере информации. После осуществления процесса энтропийного кодирования на каждой матрице квантованных коэффициентов модуль 38 вывода потока в модуле 8 кодирования может прибавлять кодированные матрицы квантованных коэффициентов к битовому потоку для последовательности видеокадров (74). После прибавления модулем 38 вывода потока кодированных матриц к битовому потоку модуль 20 управления кадрами может определять, является ли текущий кадр последним видеокадром последовательности кадров (76). Если текущий кадр является последним кадром последовательности кадров (“Да” на 76), модуль 8 кодирования завершает кодирование последовательности кадров (78). Если же текущий кадр не является последним кадром последовательности кадров (“НЕТ” на 76), модуль 8 кодирования может возвратиться к началу цикла для определения, подлежит ли новый текущий кадр кодированию в качестве i-кадра (62).
Если текущий кадр не подлежит кодированию как i-кадр (“НЕТ” на 62), модуль 32 оценки движения в модуле 8 кодирования может делить текущий кадр на множестве макроблоков (80). Затем модуль 32 оценки движения может пытаться идентифицировать исходный макроблок в одном или нескольких опорных кадрах для каждого из макроблоков в текущем кадре (82). Затем модуль 32 оценки движения может вычислять вектор движения для каждого макроблока в текущем кадре, для которого модуль 32 оценки движения смог идентифицировать исходный макроблок (84). После вычисления векторов движения модулем 32 оценки движения модуль 34 генерации реконструированных кадров использует векторы движения для генерации реконструированного кадра, “перемещая” идентифицированные макроблоки в опорных кадрах в позиции, указанные векторами движения (86). Затем модуль 36 генерации остаточных кадров может генерировать остаточный кадр для текущего кадра, вычитая значения компонентов пикселя в реконструированном кадре из соответствующих значений компонентов пикселя в текущем кадре (88). После генерации остаточного кадра модулем 36 генерации остаточных кадров модуль 30 энтропийного кодирования может использовать схему энтропийного кодирования для кодирования векторов движения для текущего кадра (90). Кроме того, пространственное кодирование можно применять к остаточному кадру путем применения этапов (66)-(74) к остаточному кадру.
На фиг.5 показана логическая блок-схема, иллюстрирующая принцип действия модуля 12 декодирования. Хотя принцип действия, представленный на фиг.5, описан в последовательном режиме, следует заметить, что работа может осуществляться в конвейерном режиме.
Первоначально модуль 12 декодирования принимает кодированный видеокадр (100). Получив кодированный видеокадр, модуль 44 энтропийного декодирования в модуле 12 декодирования может осуществлять процесс энтропийного декодирования на блоках данных в кодированном кадре (102). Модуль 44 энтропийного декодирования может осуществлять процесс энтропийного декодирования, эквивалентный процессу энтропийного кодирования, используемому для кодирования кадра. Например, если модуль 8 кодирования использует кодирование по Хаффману для кодирования кадра, модуль 44 энтропийного декодирования использует декодирование по Хаффману для декодирования кадра. В результате применения процесса энтропийного декодирования к каждому блоку данных в кадре модуль 44 энтропийного декодирования создает множество матриц квантованных коэффициентов.
Затем модуль 46 деквантования в модуле 12 декодирования может деквантовать коэффициенты в каждой матрице квантованных коэффициентов (104). После деквантования каждого коэффициента в матрицах квантованных коэффициентов модуль 48 обратного преобразования в модуле 12 декодирования генерирует матрицы значений компонентов пикселя (106). Значения компонентов пикселя в одной из матриц значений компонентов пикселя являются аппроксимациями соответствующих значений, которые были бы получены путем преобразования одной из матриц квантованных коэффициентов с использованием идеального двумерного обратного дискретного косинусного преобразования.
После вычисления модулем 48 обратного преобразования матрицы значений компонентов пикселя для каждой матрицы коэффициентов модуль 50 реконструкции пикселей в модуле 12 декодирования может объединять соответствующие матрицы значений компонентов пикселя для создания блоков пикселей (108). Например, модуль 12 декодирования может объединять блок значений Y с соответствующим блоком значений Cr и соответствующим блоком значений Cb для создания блока пикселей YCrCb. После создания блоков пикселей модулем 50 реконструкции пикселей модуль 52 объединения блоков может восстанавливать видеокадр из блоков пикселей (110).
Затем модуль 53 управления кадрами в модуле 12 декодирования может определять, является ли текущий кадр i-кадром (114). Если текущий кадр является i-кадром (“Да” на 114), модуль 52 объединения блоков может выводить видеокадр в буфер 51 кадров (114). Если же текущий кадр не является i-кадром (т.е. текущий кадр является прогнозирующим или дважды прогнозирующим кадром) (“НЕТ” на 114), модуль 44 энтропийного декодирования использует схему энтропийного декодирования для декодирования векторов движения текущего кадра (116). Затем модуль генерации реконструированных кадров 56 использует декодированные векторы движения и один или несколько опорных кадров в модуле 54 хранения кадров для генерации реконструированного кадра (118). Затем модуль 58 генерации прогнозирующих кадров может использовать реконструированный кадр и кадр, сгенерированный модулем 52 объединения блоков для генерации реконструированного кадра (120).
На фиг.6 показана подробная блок-схема иллюстративного модуля 48 обратного преобразования. Как показано в примере, приведенном на фиг.6, модуль 48 обратного преобразования может содержать входной модуль 140. Входной модуль 140 может принимать матрицу коэффициентов от модуля 46 деквантования. Например, входной модуль 140 может принимать указатель, который указывает ячейку в модуле памяти устройства 2, где хранится матрица коэффициентов. Альтернативно входной модуль 140 может включать в себя внутренние структуры данных, в которых хранится матрица коэффициентов.
Когда входной модуль 140 принимает матрицу деквантованных коэффициентов, входной модуль 140 может выдавать матрицу коэффициентов на модуль 142 масштабирования в модуле 48 обратного преобразования. Модуль 142 масштабирования генерирует матрицу масштабированных коэффициентов путем масштабирования каждого коэффициента в матрице деквантованных коэффициентов. Модуль 142 масштабирования может масштабировать коэффициенты в матрице деквантованных коэффициентов путем сдвига влево каждого коэффициента на количество битов мантиссы, используемое модулем 146 обратного преобразования для представления чисел с фиксированной запятой. Биты мантиссы - это биты, которые располагаются слева от десятичной запятой (т.е. дробная часть числа). Таким образом, модуль 142 масштабирования эффективно преобразует представления коэффициентов в матрице деквантованных коэффициентов в представления с фиксированной запятой с надлежащим количеством битов мантиссы. Например, если модуль 146 обратного преобразования использует числа с фиксированной запятой, которые включают в себя три бита мантиссы, модуль 142 масштабирования генерирует матрицу масштабированных коэффициентов путем сдвига влево каждого коэффициента в матрице деквантованных коэффициентов на три позиции.
После генерации матрицы масштабированных коэффициентов модулем 142 масштабирования модуль 144 смещения коэффициентов может генерировать матрицу смещенных коэффициентов путем сложения значения среднего смещения и значения дополнительного смещения с коэффициентом постоянной составляющей матрицы масштабированных коэффициентов. Как описано выше, коэффициент постоянной составляющей матрицы обычно является коэффициентом в верхней левой позиции в матрице. В общем случае коэффициент постоянной составляющей представляет среднее значение других коэффициентов в матрице.
Значение дополнительного смещения - это значение, благодаря которому положительные ошибки и отрицательные ошибки, в среднем, равны по величине и, в среднем, симметричны относительно нуля. Например, значение дополнительного смещения может представлять собой значение смещения, адаптивное к знаку, которое равно нулю, когда коэффициент постоянной составляющей неотрицателен, и равно минус единице, когда коэффициент постоянной составляющей отрицателен. Для прибавления значения смещения, адаптивного к знаку, к коэффициенту постоянной составляющей в 16-битовом процессоре модуль 144 смещения коэффициентов может использовать следующую формулу:
DC_coefficient=DC_coefficient+(1<<(P+2))+(DC_coefficien >>15) (1)
(1)
В формуле (1) член (1<<(P+2)) прибавляется для обеспечения среднего смещения. P - это константа, равная количеству битов мантиссы с фиксированной запятой (т.е. битов справа от десятичной запятой), используемых в преобразовании, осуществляемом модулем 146 обратного векторного преобразования. Число 2 прибавляется к P, поскольку модуль 148 правого сдвига может сдвигать вправо все коэффициенты на (P+3), где число '3' это число битов точности, добавляемых путем осуществления обратного дискретного косинусного преобразования. В частности, если число x генерируется путем сдвига 1 влево на (P+2), а число z генерируется путем сдвига x вправо на (P+3), то z=½. (Иными словами, 2P+2/2P+3=20/21=½). Таким образом, прибавление (1<<(P+2)) к коэффициенту постоянной составляющей эквивалентно прибавлению (1<<(P+3))/2 к коэффициенту постоянной составляющей.
В формуле (1) член (DC_coefficient>>15) сдвигает вправо 16-битовый коэффициент постоянной составляющей на 15 позиций. Оставшийся один бит указывает знак коэффициента постоянной составляющей. Например, пусть коэффициент постоянной составляющей равен 0b1111 1100 0011 0101. В этом примере, со знаковым расширением, сдвиг коэффициента постоянной составляющей вправо на 15 позиций дает значение 0b1111 1111 1111 1111 (в десятеричной системе -1). Аналогично, если коэффициент постоянной составляющей равен 0b0111 1111 1111 1111, сдвиг коэффициента постоянной составляющей вправо на 15 позиций дает значение 0b0000 0000 0000 0000 (в десятеричной системе 0).
В другом примере значение дополнительного смещения может быть значением смешивающего смещения. Значение смешивающего смещения - это значение, которое равно -1 или 0. Для прибавления значения знакосмешивающего смещения к коэффициенту постоянной составляющей в 16-битовом процессоре модуль 34 IDCT может использовать следующую формулу:
DC_coefficient=DC_coefficient+(1<<(P+2))+dither(-1|0) (2)
(2)
В формуле (2) P указывает количество битов мантиссы в DC_coefficient. Член (1<<(P+2)) прибавляет среднее смещение. Член dither(-1|0) указывает, что модуль 34 IDCT выбирает -1 или 0 на псевдослучайной основе.
Модуль 144 смещения коэффициентов также может суммировать значение среднего смещения и значение дополнительного смещения с каждым из коэффициентов переменной составляющей в матрице масштабированных коэффициентов. Коэффициенты переменной составляющей матрицы - это все коэффициенты в матрице, отличные от коэффициента постоянной составляющей. Суммирование значения среднего смещения и масштабированного значения смещения с каждым из коэффициентов переменной составляющей может дополнительно снижать ошибки округления.
После генерации матрицы смещенных коэффициентов модулем 144 смещения коэффициентов модуль 146 обратного векторного преобразования генерирует матрицу преобразованных коэффициентов с использованием арифметики с фиксированной запятой для повторного применения одномерного преобразования к матрице смещенных коэффициентов. Например, модуль 146 обратного векторного преобразования может генерировать матрицу промежуточных значений с использованием арифметики с фиксированной запятой для применения одномерного преобразования к каждому вектору-строке коэффициентов в матрице смещенных коэффициентов. Затем модуль 146 обратного векторного преобразования может вычислять матрицу преобразованных коэффициентов с использованием арифметики с фиксированной запятой для применения одномерного преобразования к каждому вектору-столбцу в матрице промежуточных значений. Иллюстративные одномерные преобразования проиллюстрированы ниже на фиг.10 и 11.
После генерации матрицы преобразованных коэффициентов модулем 146 обратного векторного преобразования модуль 148 правого сдвига может генерировать матрицу отрегулированных коэффициентов путем правого сдвига каждого коэффициента в матрице преобразованных коэффициентов на число позиций, равное количеству битов, добавленных в ходе применения преобразования и в ходе масштабирования. Например, если применение преобразования дает три дополнительных бита и масштабирование коэффициентов добавляет три дополнительных бита, модуль 148 правого сдвига может сдвигать вправо каждый коэффициент на шесть (3+3) позиций.
Модуль 148 правого сдвига может осуществлять этот правый сдвиг вместо деления каждого коэффициента на 2b, где b равно количеству дополнительных битов, добавляемых модулем 146 обратного векторного преобразования, плюс количество битов, добавляемых к части мантиссы коэффициентов модулем 142 масштабирования в ходе масштабирования. Различия между данными исходного изображения и данными конечного изображения могут быть обусловлены разностью между x n/2b и x n>>b, где x n - это коэффициент в матрице в позиции n. Некоторые из этих разностей могут быть обусловлены ошибками округления, связанными с тем, что в арифметике ограниченной точности с фиксированной запятой (x n>>b) не равно (x n/2b) для всех значений x n. Например, модуль 8 кодирования может использовать шестнадцатибитные числа с фиксированной запятой и x n=63 (0000 0000 0011 1111 в двоичной системе) и b=6. В этом примере сдвиг 0000 0000 0011 1111 вправо на шесть позиций дает двоичное значение 0000 0000 0000 0000. Следовательно, 63>>6=0. Между тем, 63/26=31/64=0,984375. Разность между 0 и 0,984 может приводить к видимому различию между исходным изображением и конечным изображением.
Сложение значений смещения с коэффициентом постоянной составляющей снижает разности, обусловленные ошибками округления. Например, модуль 144 смещения коэффициентов может прибавлять значение среднего смещения c к x n. Значение среднего смещения c может быть равно 2b/2=2(b-1). Например, если b=6, то c=26/2=64/2=32. В этом примере если x n=63, то 63+32=95 (0b0000 0000 0101 1111). 95, сдвинутое вправо на 6 позиций=1 (0b0000 0000 0000 0001 в двоичной системе). Значение 1, полученное прибавлением значения среднего смещения, ближе к верному значению 0,984375, чем значение 0, полученное без прибавления значения среднего смещения.
Кроме того, для прибавления значения среднего смещения c модуль 144 смещения коэффициентов также может суммировать значение дополнительного смещения с коэффициентом постоянной составляющей. Например, модуль 144 смещения коэффициентов может прибавлять значение смещения, адаптивное к знаку, d(x n). Значение смещения, адаптивное к знаку, d(x n) может быть равно -1, когда x n отрицательно, и может быть равно 0 в противном случае. Прибавление значения смещения, адаптивного к знаку, d(x n) может давать более точные значения, чем значения без значения смещения, адаптивного к знаку, d(x n). Например, без значения смещения, адаптивного к знаку, d(x n), функция (x n+c)>>b не симметрична относительно 0. Например, если x n=32, b=6 и c=32, то (x n+c)>>b=1. Однако если x n=-32, b=6 и c=32, то (x n+c)>>b=0. Этот недостаток симметрии относительно нуля может приводить к нарастанию ошибок при вычислении последовательных прогнозирующих видеокадров. Кроме того, разности между x n>>b и x n/2b значительнее, когда x n больше нуля, чем когда x n меньше нуля. Это также может порождать ошибки.
Значение смещения, адаптивное к знаку, d(x n) может исправлять этот недостаток. Например, пусть x n=32, b=6, c=32, тогда d(x n)=0. Следовательно, (x n+c+d(x n ))>>b=1. Теперь, пусть x n=-32, b=6, c=32, тогда d(x n)=-1. Следовательно, (x n+c+d(x n))>>b=-1. Этот пример иллюстрирует, что функция (x n+c+d(x n))>>b теперь симметрична относительно 0 и не создает разности, которые больше, когда x n больше нуля, чем когда (x n) меньше нуля.
В альтернативной реализации модуль 144 смещения коэффициентов может прибавлять значение смешивающего смещения e вместо того, чтобы прибавлять значение смещения, адаптивное к знаку, d. Когда модуль 144 смещения коэффициентов суммирует значение смешивающего смещения e с коэффициентом постоянной составляющей, модуль 144 смещения коэффициентов может выбирать либо значение 0, либо значение -1 в качестве значения e на псевдослучайной основе. Для выбора значения смешивающего смещения e модуль 144 смещения коэффициентов может включать в себя следующие инструкции:
Многие стандарты кодирования видео используют так называемую группу изображений (“GOP”). GOP содержит i-кадр и множество прогнозирующих кадров и/или дважды прогнозирующих кадров, которые ссылаются на i-кадр и/или другие прогнозирующие или дважды прогнозирующие кадры в GOP. Например, медиафайл может включать в себя i-кадр, закодированный с использованием множества матриц коэффициентов. Для получения видеопоследовательности модуль 12 декодирования может создавать прогнозирующие кадры на основании этого i-кадра. Ошибки, обусловленные декодированием i-кадра, отражаются в прогнозирующем кадре, основанном на i-кадре. Кроме того, ошибки, обусловленные декодированием прогнозирующего кадра, внедряются в следующий прогнозирующий кадр. Если ошибки, обусловленные декодированием кадров, не симметричны относительно нуля или отклоняются в сторону положительных или отрицательных величин, эти ошибки могут быстро увеличивать или уменьшать значения компонентов пикселя в последовательных прогнозирующих кадрах. Например, если ошибкам свойственно иметь в большей степени положительные значения, эти ошибки могут накапливаться в последовательных прогнозирующих кадрах, приводя к тому, что значения компонентов пикселя оказываются больше верных значений компонентов пикселя. В результате, пиксели в последовательных прогнозирующих кадрах в GOP могут неверно изменять цвет или яркость. Это называется ошибкой дрейфа. Для уменьшения ошибки дрейфа из i-кадра можно генерировать лишь ограниченное количество кадров. Вследствие округления ошибки могут быть больше по величине при осуществлении преобразования с использованием чисел с фиксированной запятой, которые имеют ограниченное количество битов мантиссы (например, три бита мантиссы), чем при осуществлении преобразования с использованием чисел, имеющих более высокую точность. Следовательно, ошибка дрейфа может создавать особенно большие проблемы при осуществлении преобразования с использованием чисел с фиксированной запятой, которые имеют ограниченное количество битов мантиссы.
Выбор значения смешивающего смещения e на псевдослучайной основе означает, что каждый прогнозирующий кадр имеет равную вероятность иметь ошибки, которые имеют более высокую положительную величину, или ошибки, которые имеют более высокую отрицательную величину. Таким образом, в группе изображений положительные ошибки и отрицательные ошибки имеют тенденцию быть равными по величине и имеют тенденцию быть симметричными относительно нуля. Поскольку положительные ошибки и отрицательные ошибки, в среднем, симметричны относительно нуля и положительные ошибки и отрицательные ошибки, в среднем, равны по величине, маловероятно, что ошибки будут распространяться и усиливаться в последующих прогнозирующих кадрах. Это обусловлено тем, что ошибки с положительной величиной, скорее всего, будут компенсировать ошибки с отрицательной величиной в другом кадре и наоборот. Следовательно, поскольку значение смешивающего смещения имеет тенденцию иметь ошибки, симметричные относительно нуля, и имеет тенденцию иметь положительные ошибки и отрицательные ошибки, равные по величине, весьма вероятно, что ошибка дрейфа в пределах GOP будет уменьшаться. По этой причине больше изображений можно включить в GOP. Поскольку больше изображений можно включить в GOP, общая видеопоследовательность может иметь более высокую степень сжатия. Аналогично, прибавление значения смещения, адаптивного к знаку, приводит к ошибкам в каждом кадре, которые имеют тенденцию быть равными по величине и которые имеют тенденцию быть симметричными относительно нуля. В результате эти ошибки не будут распространяться и усиливаться в последующих прогнозирующих кадрах.
После сдвига вправо коэффициентов модулем 148 правого сдвига модуль 150 ограничения может “обрезать” коэффициенты для ограничения коэффициентов максимально допустимым диапазоном значений компонентов пикселя. Например, в типичном изображении JPEG значение цветового компонента может составлять от -256 до 255. Если матрица коэффициентов включает в себя коэффициент, равный 270, модуль 150 ограничения ограничивает этот коэффициент максимально допустимым диапазоном, снижая коэффициент до 255. После того как модуль 150 ограничения заканчивает ограничение коэффициентов, эти коэффициенты могут представлять значения компонентов пикселя. Когда модуль 150 ограничения заканчивает ограничение коэффициентов в матрице, модуль 150 ограничения может выдавать матрицу ограниченных коэффициентов на выходной модуль 152.
Когда выходной модуль 152 принимает матрицу коэффициентов (которые теперь являются значениями компонентов пикселя), выходной модуль 152 может выводить матрицу значений компонентов пикселя на модуль 50 реконструкции пикселей.
На фиг.7 показана логическая блок-схема, иллюстрирующая принцип работы модуля 34 обратного преобразования. Первоначально входной модуль 140 принимает матрицу деквантованных коэффициентов (170). Когда входной модуль 140 принимает матрицу деквантованных коэффициентов, модуль 142 масштабирования может масштабировать каждое значение в матрице деквантованных коэффициентов, тем самым генерируя матрицу масштабированных коэффициентов (172). Например, модуль 142 масштабирования может осуществлять операции, которые умножают каждый коэффициент в матрице деквантованных коэффициентов на эквивалентно расположенные значения в матрице масштабных коэффициентов.
После генерации матрицы масштабированных коэффициентов модулем 142 масштабирования модуль 144 смещения коэффициентов может прибавлять значение среднего смещения и значение дополнительного смещения к коэффициенту постоянной составляющей матрицы масштабированных коэффициентов, тем самым генерируя матрицу смещенных коэффициентов (174). После того как модуль 144 смещения коэффициентов прибавляет значение смещения к коэффициенту постоянной составляющей матрицы, модуль 146 обратного векторного преобразования может определять, меньше ли счетчик строк максимального счетчика строк (176). Первоначально счетчик строк можно задать равным нулю. Максимальный счетчик строк может быть статическим значением, которое равно количеству строк в матрице коэффициентов. Например, если матрица коэффициентов включает в себя восемь строк, максимальный счетчик строк равен восьми.
Если счетчик строк меньше максимального счетчика строк (“ДА” на 176), модуль 146 обратного векторного преобразования может использовать арифметику с фиксированной запятой для применения одномерного преобразования к вектору-строке матрицы коэффициентов, указанному счетчиком строк (178). Когда модуль 146 обратного векторного преобразования применяет преобразование к вектору-строке матрицы коэффициентов, модуль 146 обратного векторного преобразования может заменять исходные коэффициенты в векторе-строке коэффициентов вектором промежуточных коэффициентов. После применения модулем 146 обратного векторного преобразования преобразования к вектору-строке матрицы коэффициентов модуль 146 обратного векторного преобразования может увеличивать счетчик строк (180). Модуль 146 обратного векторного преобразования может затем возвращаться к началу цикла и снова определять, меньше ли счетчик строк максимального счетчика строк (176).
Если счетчик строк не меньше (т.е. больше или равен) максимального счетчика строк (“НЕТ” на 176), модуль 146 обратного векторного преобразования может определять, меньше ли счетчик столбцов максимального счетчика столбцов (182). Первоначально счетчик столбцов можно задать равным нулю. Максимальный счетчик столбцов может быть статическим значением, которое равно количеству столбцов в матрице коэффициентов. Например, если матрица коэффициентов включает в себя восемь столбцов, максимальный счетчик столбцов равен восьми.
Если счетчик столбцов меньше максимального счетчика столбцов (“ДА” на 182), модуль 146 обратного векторного преобразования может применять одномерное преобразование к вектору-столбцу матрицы промежуточных коэффициентов, указанному счетчиком столбцов (184). Когда модуль 34 обратного преобразования применяет преобразование к вектору-столбцу промежуточных коэффициентов, модуль 34 обратного преобразования заменяет промежуточные коэффициенты в векторе-столбце вектором преобразованных коэффициентов.
После применения модулем 146 обратного векторного преобразования преобразования к вектору-столбцу матрицы коэффициентов модуль 146 обратного векторного преобразования может увеличивать счетчик столбцов (186). Модуль 146 обратного векторного преобразования может затем возвращаться к началу цикла и снова определять, меньше ли счетчик столбцов максимального счетчика столбцов (182).
Если счетчик столбцов не меньше (т.е. больше или равен) максимального счетчика столбцов (“НЕТ” на 182), модуль 148 правого сдвига может сдвигать вправо каждый из преобразованных коэффициентов в матрице (188). Когда модуль 148 правого сдвига сдвигает вправо коэффициент, модуль 148 правого сдвига может сдвигать коэффициент вправо на определенное количество позиций. В результате правого сдвига каждого из вторых промежуточных коэффициентов в матрице получается матрица отрегулированных значений. После правого сдвига модулем 148 правого сдвига каждого из преобразованных коэффициентов модуль 150 ограничения может ограничивать отрегулированные коэффициенты, чтобы гарантировать, что отрегулированные коэффициенты находятся в пределах надлежащего диапазона значений компонентов пикселя (190). Например, модуль 150 ограничения может ограничивать отрегулированные коэффициенты, чтобы гарантировать, что отрегулированные коэффициенты находятся в диапазоне от -256 до 255. Когда модуль 150 ограничения заканчивает ограничение отрегулированных коэффициентов, выходной модуль 152 может выводить результирующую матрицу значений компонентов пикселя (192).
На фиг.8 показана подробная блок-схема иллюстративного модуля 26 прямого преобразования. Как показано в примере, приведенном на фиг.8, модуль 26 прямого преобразования содержит входной модуль 210, который принимает матрицу значений компонентов пикселя от модуля 24 выделения компонентов. Когда входной модуль 210 принимает матрицу значений компонентов пикселя, входной модуль 210 может выдавать матрицу значений компонентов пикселя на модуль 212 левого сдвига. Модуль 212 левого сдвига может сдвигать все значения компонентов пикселя в матрице значений компонентов пикселя влево на количество битов мантиссы, используемое в значениях, которое модуль 214 прямого векторного преобразования использует при осуществлении прямого преобразования, минус количество битов мантиссы, удаленных путем осуществления прямого преобразования. Например, если десять битов мантиссы используются в значениях при осуществлении прямого преобразования и три бита мантиссы удаляются путем осуществления прямого дискретного косинусного преобразования, модуль 212 левого сдвига может сдвигать значения компонентов пикселя влево на семь позиций. В другом примере, если три бита мантиссы используются в значениях при осуществлении прямого преобразования и три бита мантиссы удаляются путем осуществления прямого преобразования, модуль 212 левого сдвига может сдвигать значения компонентов пикселя влево на нуль позиций.
После того как модуль 212 левого сдвига сдвигает значения компонентов пикселя, модуль 214 прямого векторного преобразования может применять прямое преобразование к каждому вектору-столбцу в матрице значений компонентов пикселя для получения матрицы промежуточных значений. Затем модуль 214 прямого векторного преобразования может применять прямое преобразование к каждому вектору-строке в матрице промежуточных значений для получения матрицы преобразованных коэффициентов. Когда модуль 214 прямого векторного преобразования применяет прямое преобразование к вектору, модуль 214 прямого векторного преобразования может применять прямое преобразование, описанное на фиг.12 ниже. Заметим, что преобразование, описанное на фиг.12 ниже, является обратным по отношению к преобразованию, описанному на фиг.11.
После создания матрицы преобразованных коэффициентов модулем 214 прямого векторного преобразования модуль 216 масштабирования может применять масштабирующие множители к каждому преобразованному коэффициенту в матрице преобразованных коэффициентов. Модуль 216 масштабирования может применять величины, обратные масштабирующим множителям, используемым модулем 142 масштабирования, в модуле 48 обратного преобразования. Например, если одно или несколько значений было вынесено за скобки преобразования для повышения эффективности преобразования, эти значения могут стать базисом матрицы масштабных коэффициентов. Коэффициенты в матрице преобразованных коэффициентов можно корректировать путем умножения коэффициентов на эти значения.
Для снижения ошибок округления модуль 218 смещения коэффициентов в модуле 26 прямого преобразования может суммировать значение среднего смещения и значение дополнительного смещения с коэффициентами в матрице масштабированных коэффициентов. Прибавление значения смещения, адаптивного к знаку, или значения смешивающего смещения к коэффициентам в матрице преобразованных коэффициентов имеет эффект, аналогичный случаю, когда модуль 144 смещения коэффициентов в модуле 48 обратного преобразования прибавляет значение смещения, адаптивное к знаку, или значение смешивающего смещения. То есть в результате сложения значений смещения с коэффициентом положительные ошибки и отрицательные ошибки оказываются, в среднем, равными по величине и оказываются, в среднем, симметричными относительно нуля. Ошибки представляют разности между значениями, полученными в результате правого сдвига представлений ограниченной точности с фиксированной запятой для коэффициентов в матрице масштабированных коэффициентов на первую величину, и результатами деления коэффициентов в матрице масштабированных коэффициентов на 2 в степени первой величины, безотносительно к точности.
После генерации модулем 218 смещения коэффициентов матрицы смещенных коэффициентов модуль 220 правого сдвига в модуле 26 прямого преобразования может генерировать матрицу выходных коэффициентов путем правого сдвига коэффициентов в матрице смещенных коэффициентов. Модуль 220 правого сдвига может сдвигать вправо каждый коэффициент в матрице смещенных коэффициентов на количество битов мантиссы в коэффициентах матрицы смещенных коэффициентов плюс количество битов, добавленных к коэффициентам путем осуществления преобразования.
Следующее уравнение отражает воздействие модуля 216 масштабирования, модуля 218 смещения коэффициентов и модуля 220 правого сдвига на матрицу преобразованных коэффициентов, когда модуль 218 смещения коэффициентов прибавляет значение смещения, адаптивное к знаку:
F[v][u]=(F'[v][u]*S[v][u]+(1<<(P+Q)-((F'[v][u]>=0)?0:1))>>(P+Q),
где v=0..7, u=0..7; где S[v][u] - это элемент матрицы масштабных коэффициентов, F - это матрица масштабированных коэффициентов, F' - это матрица преобразованных коэффициентов, P указывает количество битов мантиссы в коэффициентах в матрице преобразованных коэффициентов и Q указывает количество битов, добавленных к коэффициентам в матрице преобразованных коэффициентов путем применения преобразования.
Следующее уравнение отражает воздействие модуля 216 масштабирования, модуля 218 смещения коэффициентов и модуля 220 правого сдвига на матрицу преобразованных коэффициентов, когда модуль 218 смещения коэффициентов прибавляет значение смешивающего смещения:
F[v][u]=(F'[v][u]*S[v][u]+(1<<19)-(dither(0:1))>>20,
где v=0..7, u=0..7; где S[v][u] - это элемент матрицы масштабных коэффициентов, F - это матрица масштабированных коэффициентов и F' - это матрица преобразованных коэффициентов.
После генерации матрицы масштабированных коэффициентов модулем 216 масштабирования выходной модуль 222 может выводить матрицу коэффициентов на модуль 28 квантования.
На фиг.9 показана логическая блок-схема, иллюстрирующая принцип действия модуля 26 прямого преобразования. Первоначально входной модуль 210 принимает матрицу значений компонентов пикселя (230). Когда входной модуль 140 принимает матрицу значений компонентов пикселя, модуль 212 левого сдвига может генерировать матрицу отрегулированных коэффициентов путем сдвига влево каждого значения в матрице значений компонентов пикселя (232). Например, модуль 212 левого сдвига может сдвигать все коэффициенты влево на десять позиций. В этом примере модуль 212 левого сдвига может сдвигать все коэффициенты вправо на десять позиций, поскольку модуль 214 прямого векторного преобразования может использовать арифметику с фиксированной запятой, в которой числа кодируются с использованием десяти битов в дробной части. Таким образом, сдвигая коэффициенты влево на десять позиций, модуль 212 левого сдвига эффективно преобразует значения компонентов пикселя в числа с фиксированной запятой с десятью битами мантиссы.
После сдвига влево каждого значения компонента пикселя в матрице отрегулированных значений модуль 214 прямого векторного преобразования может определять, меньше ли счетчик столбцов максимального счетчика строк (234). Первоначально счетчик столбцов можно задать равным нулю. Максимальный счетчик столбцов может быть статическим значением, которое равно количеству столбцов в матрице отрегулированных коэффициентов. Например, если матрица отрегулированных коэффициентов включает в себя восемь столбцов, максимальный счетчик столбцов равен восьми.
Если счетчик столбцов меньше максимального счетчика столбцов (“ДА” на 234), модуль 214 прямого векторного преобразования может вычислять одномерное прямое преобразование на векторе-столбце, указанном счетчиком столбцов (236). Когда модуль 214 прямого векторного преобразования вычисляет прямое преобразование на векторе-столбце матрицы отрегулированных коэффициентов, модуль 214 прямого векторного преобразования заменяет исходные отрегулированные коэффициенты в векторе-столбце промежуточными коэффициентами. После вычисления модулем 214 прямого векторного преобразования прямого преобразования на векторе-столбце матрицы отрегулированных коэффициентов модуль 214 прямого векторного преобразования может увеличивать счетчик столбцов (238). Модуль 214 прямого векторного преобразования может затем возвращаться к началу цикла и снова определять, меньше ли счетчик столбцов максимального счетчика столбцов (234).
Если счетчик столбцов не меньше (т.е. больше или равен) максимального счетчика столбцов (“НЕТ” на 234), модуль 214 прямого векторного преобразования может определять, меньше ли счетчик строк максимального счетчика строк (240). Первоначально счетчик строк можно задать равным нулю. Максимальный счетчик строк может быть статическим значением, которое равно количеству векторов-строк в матрице коэффициентов. Например, если матрица коэффициентов включает в себя восемь строк, максимальный счетчик строк равен восьми.
Если счетчик строк меньше максимального счетчика строк (“ДА” на 240), модуль 214 прямого векторного преобразования может вычислять одномерное дискретное косинусное преобразование на векторе-строке, указанном счетчиком строк (242). Поскольку модуль 214 прямого векторного преобразования уже вычислил прямое преобразование на векторе-строке матрицы, матрица коэффициентов теперь содержит промежуточные коэффициенты. Когда модуль 214 прямого векторного преобразования вычисляет прямое преобразование на векторе-строке промежуточных коэффициентов, модуль 214 прямого векторного преобразования заменяет промежуточные коэффициенты в векторе-столбце вектором преобразованных коэффициентов.
После вычисления модулем 214 прямого векторного преобразования дискретного косинусного преобразования на векторе-строке матрицы коэффициентов модуль 214 прямого векторного преобразования может увеличивать счетчик строк (244). Модуль 214 прямого векторного преобразования может затем возвращаться к началу цикла и снова определять, меньше ли счетчик строк максимального счетчика строк (240).
Если счетчик строк не меньше (т.е. больше или равен) максимального счетчика строк (“НЕТ” на 240), модуль 216 масштабирования может масштабировать каждый преобразованный коэффициент в матрице преобразованных коэффициентов (246). После того как модуль 216 масштабирования генерирует матрицу масштабированных коэффициентов, модуль 218 смещения коэффициентов может генерировать матрицу смещенных коэффициентов путем сложения одного или нескольких значений смещения с коэффициентами в матрице масштабированных коэффициентов (248). Например, модуль 218 смещения коэффициентов может прибавлять значение среднего смещения и адаптивное к знаку или смешивающее значение дополнительного смещения к каждому коэффициенту в матрице масштабированных коэффициентов. Затем модуль 220 правого сдвига может сдвигать вправо каждый коэффициент в матрице смещенных коэффициентов (250). Модуль 220 правого сдвига может генерировать матрицу отрегулированных коэффициентов путем правого сдвига каждого коэффициента на количество битов мантиссы в каждом коэффициенте плюс количество битов, добавленных к коэффициенту путем применения преобразования. После генерации модулем 220 правого сдвига матрицы отрегулированных коэффициентов выходной модуль 222 может выводить результирующую матрицу отрегулированных коэффициентов (252).
На фиг.10 показана схема первого иллюстративного одномерного преобразования 260. Как показано в примере, приведенном на фиг.10, преобразование 260 может брать в качестве входных значений X 0-X 7. Значения X 0-X 7 могут представлять коэффициенты одной строки или одного столбца матрицы входных коэффициентов. Преобразование 260 может вводить значения x 0-x 7. Когда значения X 0-X 7 являются значениями в строке коэффициентов в матрице входных коэффициентов, значения x 0-x 7 могут представлять строку промежуточных значений. Когда значения X 0-X 7 являются значениями в столбце коэффициентов, значения x 0-x 7 могут представлять столбец сдвинутых значений компонентов пикселя. Как показано в примере, приведенном на фиг.10, кружки, окружающие символы “+”, обозначают операции сложения и кружки, окружающие символы “X”, обозначают операции умножения. Буквенно-цифровые комбинации указывают значения, на которые умножается значение. Например, на линии X 2 символ “A1” символ располагается поверх кружка, окружающего символ “X”. Это указывает, что значение на линии X 2 умножается на значение A1.
Преобразование 260 включает в себя множество “операций типа бабочка”. “Операция типа бабочка” может представлять собой программную или аппаратную структуру, в которой первое выходное значение u вычисляется путем умножения первого входного значения x на первый множитель C для создания первого промежуточного значения, умножения второго входного значения y на второй множитель S для создания второго промежуточного значения, с последующим суммированием первого промежуточного значения и второго промежуточного значения. В этой более сложной “операции типа бабочка” второе выходное значение v может вычисляться путем умножения второго входного значения y на первый множитель для создания третьего промежуточного значения, умножения первого входного значения x на второй множитель S для создания четвертого промежуточного значения, с последующим вычитания третьего промежуточного значения из четвертого промежуточного значения. Следующие формулы представляют математический результат “операции типа бабочка”:
u=x*C+y*S;
v=x*S-y*C.
Операция 264 типа бабочка иллюстрирует одну операцию типа бабочка, используемую в преобразовании 260. Операции типа бабочка называются так потому, что операция типа бабочка выглядит как имеющая два “крыла” вследствие перекрещивания значений от первого входного значения ко второму входному значению и от второго входного значения к первому входному значению.
Первый множитель C и второй множитель S, используемые в преобразовании 260, могут быть иррациональными числами. Например, C может быть равен  и S может быть равен
и S может быть равен  . Поскольку модуль 146 обратного векторного преобразования может использовать арифметику с фиксированной запятой в 16-битовых регистрах и поскольку C и S часто являются иррациональными значениями, может быть вычислительно неудобно умножать входные значения x и y на C и S. По этой причине модуль 146 обратного векторного преобразования может использовать рациональные аппроксимации для C и S. Эти целочисленные аппроксимации могут иметь вид (C'/2j) и (S'/2k), где C' и S' являются целочисленными аппроксимациями для C и S и j и k являются целыми числами. Например, пусть C=
. Поскольку модуль 146 обратного векторного преобразования может использовать арифметику с фиксированной запятой в 16-битовых регистрах и поскольку C и S часто являются иррациональными значениями, может быть вычислительно неудобно умножать входные значения x и y на C и S. По этой причине модуль 146 обратного векторного преобразования может использовать рациональные аппроксимации для C и S. Эти целочисленные аппроксимации могут иметь вид (C'/2j) и (S'/2k), где C' и S' являются целочисленными аппроксимациями для C и S и j и k являются целыми числами. Например, пусть C= . В примере модуль 146 обратного векторного преобразования может использовать целочисленные значения C'=2217 и j=12 для аппроксимации
. В примере модуль 146 обратного векторного преобразования может использовать целочисленные значения C'=2217 и j=12 для аппроксимации  , поскольку 2217/212=0,541259766 и
, поскольку 2217/212=0,541259766 и  ≈0,5411961..... В этом примере ясно, что 0.5411961 примерно равно 0.541259766. Таким образом, вычисления в виде:
≈0,5411961..... В этом примере ясно, что 0.5411961 примерно равно 0.541259766. Таким образом, вычисления в виде:
u=x*C+y*S;
v=x*S-y*C
можно заменить вычислениями в виде:
u'=x*(C'/2j)+y*(S'/2k);
v'=x*(S'/2k)-y*(C'/2j).
Чтобы дополнительно упростить эти вычисления, операции деления на 2j и 2k можно заменить побитовыми операциями правого сдвига на j и k позиций, обозначаемыми символом “>>”:
U”=((x*C')>>j)+((y*S')>>k);
V"=((x*S')>>k)-((y*C')>>j).
Однако, как рассмотрено выше в связи с суммированием значений смещения с коэффициентом постоянной составляющей, замена операции деления побитовой операции правого сдвига может обуславливать разности между u' и u” и v' и v”. Суммирование значений среднего смещения с членами в этих вычислениях может снижать разности между u' и u” и между v' и v”. При прибавлении значений среднего смещения вычисления могут иметь вид:
U'''=((x*C'+(1<<(j-1))>>j)+((y*S'+(1<<(k-1))>>k);
v'''=((x*S'+(1<<(k-1))>>k)-((y*C'+(1<<(j-1))>>j).
В то время как прибавление значений среднего смещения может приводить к разностям между u и u''' и v и v''', меньшим, чем разности между u и u''' и v и v''', прибавление значений среднего смещения может добавлять вычислительную сложность операции типа бабочка. Кроме того, прибавление значений среднего смещения может делать вычисление u''' и v''' непрактичным, при использовании арифметики с фиксированной запятой в 16-битовых регистрах. Прибавление значений среднего смещения может делать вычисление u''' и v''' непрактичным, поскольку прибавление значений среднего смещения происходит до правого сдвига, и, следовательно, может приводить к переполнению регистров.
Средняя разность между v=x*S-y*C и v''=((x*S)>>k)-((y*C')>>j) примерно равна нулю. Другими словами, среднее всех значений (v''-v) для всех значений x и y примерно равно нулю. Кроме того, средняя разность между v=x*S-y*C и v'''=((x*S+(1<<(k-1))>>k)-((y*C'+(1<<(j-1))>>j) также примерно равна нулю. Это объясняется тем, что v'' и v''' всегда примерно равны. V'' и v''' всегда примерно равны, поскольку, когда j равно k, значение среднего смещения компенсируется путем вычитания:
V'''=((x*C+m)>>j)-((y*S'+m)>>k)≈
(x*C'+m)/2j-(y*S'+m)/2k=
(x*C')/2j+(m/2j)-(y*S')/2k-(m/2k)=
(x*C')/2j-(y*S')/2k≈
v''=((x*C')>>j)-((y*S')>>k),
где m представляет значение среднего смещения. Согласно этому примеру вычитание (m/2k) из (m/2j), когда j равно k, компенсирует значение среднего смещения m. Поскольку средняя разность между v и v'' примерно равна нулю, модуль 146 обратного векторного преобразования несимметрично вносит положительное или отрицательное смещение в значения, генерируемые путем вычисления v'' вместо v''', и поскольку v'' и v''' примерно равны, модуль 146 обратного векторного преобразования может использовать v'' вместо v'''.
Средняя разность между u=x*C+y*S и u'''=((x*C'+(1<<(j-1))>>j)+((y*S'+(1<<(k-1))>>k) также примерно равна нулю. В то же время разность между u=x*C+y*S и u''=((x*C')>>j)+((y*S')>>k) не равна примерно нулю. Напротив, средняя разность между u и u'' примерно равна - ½. Таким образом, u'' и u''' не являются примерно равными. U'' и u''' не являются примерно равными, поскольку значения среднего смещения не компенсируются, даже когда j равно k:
u'''=((x*C'+m)>>k)+((y*S'+m)>>k)≈
((x*C'+m)/2j)+((y*S'+m)/2k)=
((x*C')/2j)+(m/2j)+((y*S')/2k)+(m/2k) =
((x*C')/2j)+((y*S')/2k)+(m/2j)+(m/2k) ≠
u''=((x*C')>>j)+((y*S')>>k).
Поскольку u'' не равна примерно u''', u'' можно не использовать вместо u'''. Попытка использовать u'' вместо u''' может приводить к значительным отклонениям от u.
Во избежание сложности и перегрузки, связанных с прибавлением значения среднего смещения, в каждом вычислении вместо u''' и u'' можно использовать следующую формулу:
u''''=((x*C')>>j)-((y*-S')>>k).
u'''' равно u'' за исключением того, что в u'''' используется отрицательная версия S' и вычитается ((y*-S)>>k). По аналогии с u''' u'''' не прибавляет значения среднего смещения. Однако в отличие от u''' разности между u'''' и u сосредоточены вокруг 0. Поскольку разности между u'''' и u сосредоточены вокруг нуля, ошибки округления не увеличиваются при применении последующих операций типа бабочка. По этой причине модуль 146 обратного векторного преобразования может использовать u'''' для вычисления u в операции типа бабочка. По этой причине, когда j равно k, операции типа бабочка, используемые модулем 146 обратного векторного преобразования для применения преобразования 260, могут иметь следующий вид:
u''''=((x*C')>>j)-((y*-S')>>k);
v'''=((x*S')>>k)-((y*C)>>j).
Поэтому разности между результатами, полученными в подобной операции типа бабочка, и результатами, которые были бы получены посредством эквивалентной операции типа бабочка с использованием арифметики с неограниченной точностью, сосредоточены вокруг нуля и имеют положительную или отрицательную величину, равную 1 или менее.
Альтернативно, когда j равно k, модуль 146 обратного векторного преобразования может использовать операции типа бабочка, в которых сдвиги вправо отложены на конец операции типа бабочка:
u'=x*(C'/2k)+y*(S'/2k);
((x*C')/2k)+((y*S')/2k)=
((x*C')+(y*S'))/2k≈
u*=(((x*C')+(y*S')+(1<<(k-1)))>>k;
v'=x*(S'/2k)-y*(C'/2j)=
((x*S')/2k)-((y*C')/2k)=
((x*S')/2k)+((-1)(y*C')/2k)=
((x*S')/2k)+((y*-C')/2k)=
((x*S')+(y*-C'))/2k≈
v*=((x*S')+(y*-C')+(1<<(k-1)))>>k.
Отсрочка сдвигов вправо на конец операции типа бабочка может сокращать общее количество операций сдвига, необходимых для осуществления операции типа бабочка, и может повышать точность. Кроме того, 4-этапные инструкции умножения с накоплением, доступные в самом современном 16-битовом процессоре с одним потоком инструкций и множественными потоками данных (“SIMD”) и в цифровых сигнальных процессорах, можно использовать для эффективного вычисления u* и v*.
Операции умножения могут быть вычислительно дорогими по сравнению с операциями сложения, вычитания и побитового сдвига. По этой причине может быть проще использовать последовательность операций сложения, вычитания и побитового сдвига, которые дают такой же результат, как операция умножения. Например, пусть C'=2217. В этом примере r=x*C' можно заменить следующими этапами:
x2=(x<<3)-;
x3=x+(x2<<6);
x4=x3-x2;
r=x3+(x4<<2).
В этом примере x2, x3 и x4 - это промежуточные значения. Для примера рассмотрим случай, когда x=1:
7=(1<<3)-1;
449=1+(7<<6);
442=449-7;
2217=449+(442<<2).
2217=(1*2217)=(x*2217, где x=1).
В этом примере 1*2217=2217 и значение, полученное с помощью этой последовательности операций, где x=1, равно 2217.
В нижеследующей таблице приведено иллюстративное множество целочисленных аппроксимаций, которые модуль 146 обратного векторного преобразования может использовать для постоянных множителей A1, A2, B1, B2, C1, C2, D1 и D2.
Иллюстративные аппроксимации постоянных множителей, используемых в преобразовании 260
x=x*F1, y=x*F2:
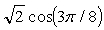
x3=x+(x2<<6),
x4=x3-x2,
(2217*x)=x3+(x4<<2);
(5352*x)*2=x4+(x2<<7);
4 сдвига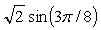
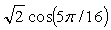
x3=x2+(x<<4),
x4=(x3<<5)-x,
(3218*x)*2=x2+(x3<<6);
(4816*x)*2=x4+x*2;
4 сдвига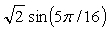
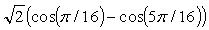
x3=(x2<<3)-x,
x4=x3+(x2<<6),
x5=x2+(x4<<1)
(2463*x)=x5;
(3686*x)=x4+x5;
4 сдвига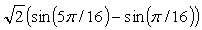

x3=x2<<5,
x4=x2+x3,
x5=x3+(x<<3)
(2088*x)=x5;
(10497*x)=x4+(x5<<2)
4 сдвига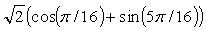
В Таблице 1 значения в столбце “Целое значение” аппроксимируют значения в столбце “исходное значение” при делении на 212=4096. Например, 2217/4096=0,541259766 и 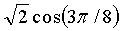 ≈0,5411961. Аналогично, 5352/4096=1,30664062 и
≈0,5411961. Аналогично, 5352/4096=1,30664062 и  ≈1,30656296. Формулы в столбце “Алгоритм вычисления произведений” представляют способы, которые модуль 146 обратного векторного преобразования может использовать вместо операций умножения на соответствующие целочисленные значения.
≈1,30656296. Формулы в столбце “Алгоритм вычисления произведений” представляют способы, которые модуль 146 обратного векторного преобразования может использовать вместо операций умножения на соответствующие целочисленные значения.
На фиг.11 показана схема второго иллюстративного алгоритма 270. Согласно фиг.10 значения X 0, X 1, X 2, X 3, X 4, X 5, X 6 и X 7 представляют входные коэффициенты и значения x 0, x 1, x 2, x 3, x 4, x 5, x 6 и x 7 представляют выходные значения. Значение, связанное с линией после кружка, окружающего символ “+”, является результатом суммирования значений, связанных со стрелками, указывающими на этот кружок. Значение, связанное с линией после кружка, окружающего символ “x”, является результатом умножения коэффициента, расположенного после кружка, и значений, связанных с линиями, проходящими через кружки. Символ “-“ после стрелки представляет смену знака значения, связанного со стрелкой. Например, если значение “10” связано со стрелкой до символа “-“, значение “-10” связано со стрелкой после символа “-“. Кроме того, следует заметить, что вышеописанные методы снижения ошибки округления с использованием коэффициентов с противоположным знаком и вычитания, можно использовать в алгоритме 190.
В преобразовании 270 значения α=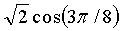 , β=
, β=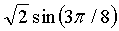 , γ=
, γ= , δ=
, δ=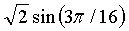 , ∈=
, ∈=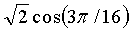 и ζ=
и ζ=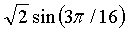 можно аппроксимировать с использованием рациональных дробей. Например, значения α, β, γ, δ, ∈ и ζ можно аппроксимировать с использованием целочисленных аппроксимаций, приведенных в нижеследующей Таблице 2.
можно аппроксимировать с использованием рациональных дробей. Например, значения α, β, γ, δ, ∈ и ζ можно аппроксимировать с использованием целочисленных аппроксимаций, приведенных в нижеследующей Таблице 2.
Иллюстративные аппроксимации постоянных значений, используемых в преобразовании 270
x=x*F1, y=x*F2:

x3=x2-(x<<5),
x4=(x3<<5)-x2,
α*x≈((x4+(x3<<4))<<1)+x,
β*x =(x3<<8)-x4
6 сдвигов
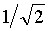
x3=x2<<7,
x4=x3-x2,
x5=x4+(x3<<2),
*x=x5+(x4<<3),
4 сдвига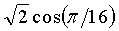
x3=x2-(x<<4),
y=x3+(x3<<2),
(δ*x)=y
x5=x2+y,
(γ*x)=x2+(x5<<3)
4 сдвига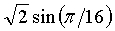

x3=x2-(x<<3),
x4=x2+(x3<<8),
(ζ*x)=((x4+(x<<2))<<1)-x,
(ε*x)=x4+(x3<<7)
6 сдвигов
В Таблице 2 значения в столбце “Целочисленное приближение” представляют целочисленную версию значений в столбце “Исходное значение”. Например, 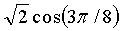 ≈0,5411961 и 8867/16384=0,54119873046875. Уравнения в столбце “Алгоритм вычисления произведений” Таблицы 2 представляют алгоритмы, посредством которых модуль 146 обратного векторного преобразования может использовать вместо операций умножения на значения в столбце “Целочисленное приближение”.
≈0,5411961 и 8867/16384=0,54119873046875. Уравнения в столбце “Алгоритм вычисления произведений” Таблицы 2 представляют алгоритмы, посредством которых модуль 146 обратного векторного преобразования может использовать вместо операций умножения на значения в столбце “Целочисленное приближение”.
На фиг.12 показана схема иллюстративного преобразования 200, которое может использоваться модулем 214 прямого векторного преобразования. Согласно фиг.12 значения X 0, X 1, X 2, X 3, X 4, X 5, X 6 и X 7 представляют выходные коэффициенты и значения x 0, x 1, x 2, x 3, x 4, x 5, x 6 и x 7 представляют входные значения. Кроме того, следует заметить, что вышеописанные методы снижения ошибки округления с использованием коэффициентов с противоположным знаком и вычитания можно использовать в преобразовании 270.
В примере, приведенном на фиг.12, значения α=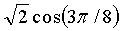 , β=
, β=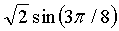 , γ=
, γ=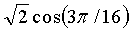 , δ=
, δ=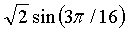 , ∈=
, ∈=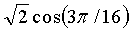 и ζ=
и ζ=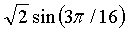 можно аппроксимировать с использованием рациональных дробей. Например, значения α, β, γ, δ, ∈ и ζ можно аппроксимировать с использованием целочисленных аппроксимаций, приведенных в Таблице 2.
можно аппроксимировать с использованием рациональных дробей. Например, значения α, β, γ, δ, ∈ и ζ можно аппроксимировать с использованием целочисленных аппроксимаций, приведенных в Таблице 2.
Описанные здесь методики можно реализовать посредством аппаратного обеспечения, программного обеспечения, программно-аппаратного обеспечения или любой их комбинации. Любые признаки, описанные как модули или компоненты, могут быть реализованы совместно в интегрированном логическом устройстве или раздельно как дискретные, но взаимодействующие между собой логические устройства. При программной реализации методики можно реализовать, по меньшей мере частично, в виде компьютерно-считываемого носителя, содержащего инструкции, которые при выполнении осуществляют один или несколько из вышеописанных способов. Компьютерно-считываемый носитель может составлять часть компьютерного программного продукта, которая может включать в себя упаковочные материалы. Компьютерно-считываемый носитель может содержать оперативную память (RAM), например синхронную динамическую оперативную память (SDRAM), постоянную память (ПЗУ), энергонезависимую оперативную память (NVRAM), электрически стираемую программируемую постоянную память (EEPROM), флэш-память, магнитные или оптические хранилища данных и пр. Методики, дополнительно или альтернативно, можно реализовать, по меньшей мере частично, посредством компьютерно-считываемой среды связи, которая переносит или передает код в форме инструкций или структур данных, к которым компьютер может обращаться, которые он может считывать и/или выполнять.
Код может выполняться одним или несколькими процессорами, например одним или несколькими цифровыми сигнальными процессорами (DSP), микропроцессорами общего назначения, специализированными интегральными схемами (ASIC), вентильными матрицами, программируемыми пользователем (FPGA), или другими эквивалентными интегральными или дискретными логическими схемами. Соответственно, используемый здесь термин “процессор” может относиться к любой из вышеупомянутых структур или любой иной структуре, пригодной для реализации описанных здесь методик. Кроме того, в некоторых аспектах, описанные здесь функции можно обеспечивать в специализированных программных модулях или аппаратных модулях, предназначенных для кодирования и декодирования или объединенных в комбинированный кодер-декодер (кодек) видеосигнала.
Описаны различные варианты осуществления изобретения. Эти и другие варианты осуществления отвечают объему нижеследующей формулы изобретения.
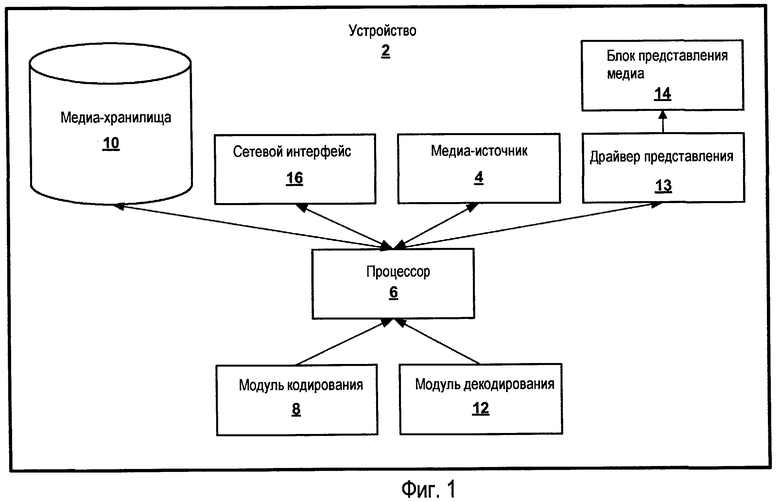
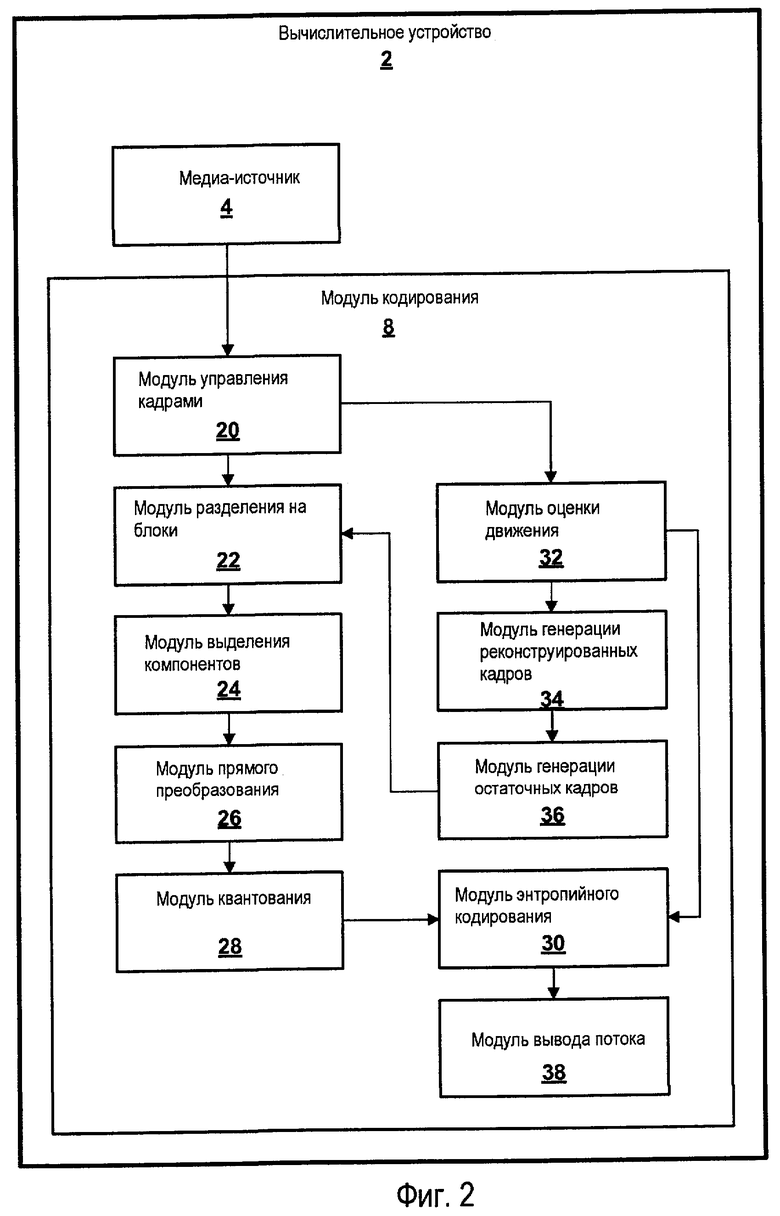
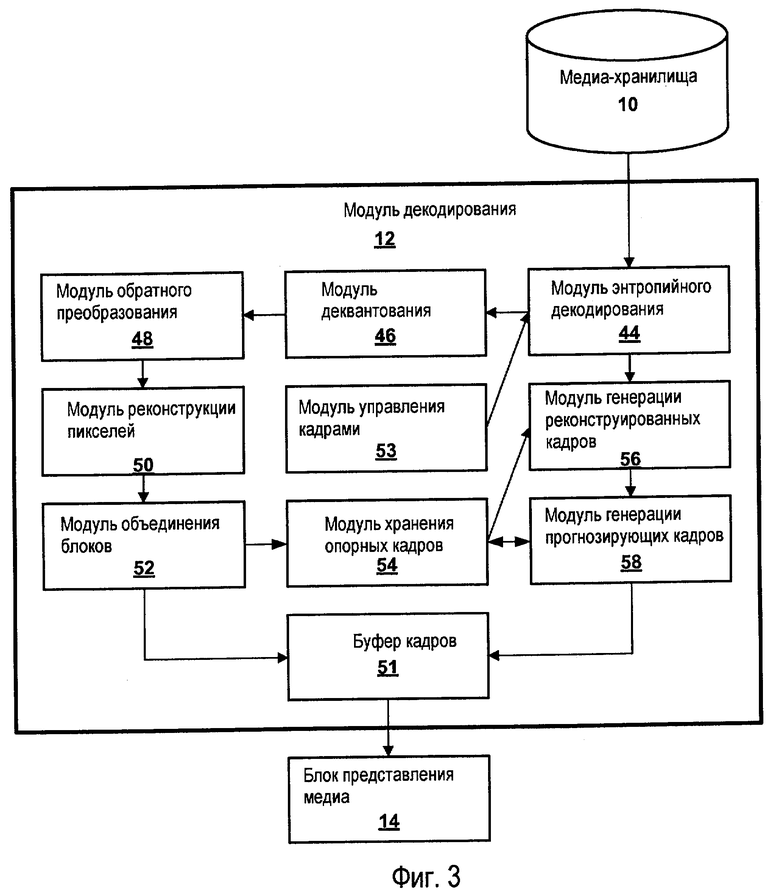
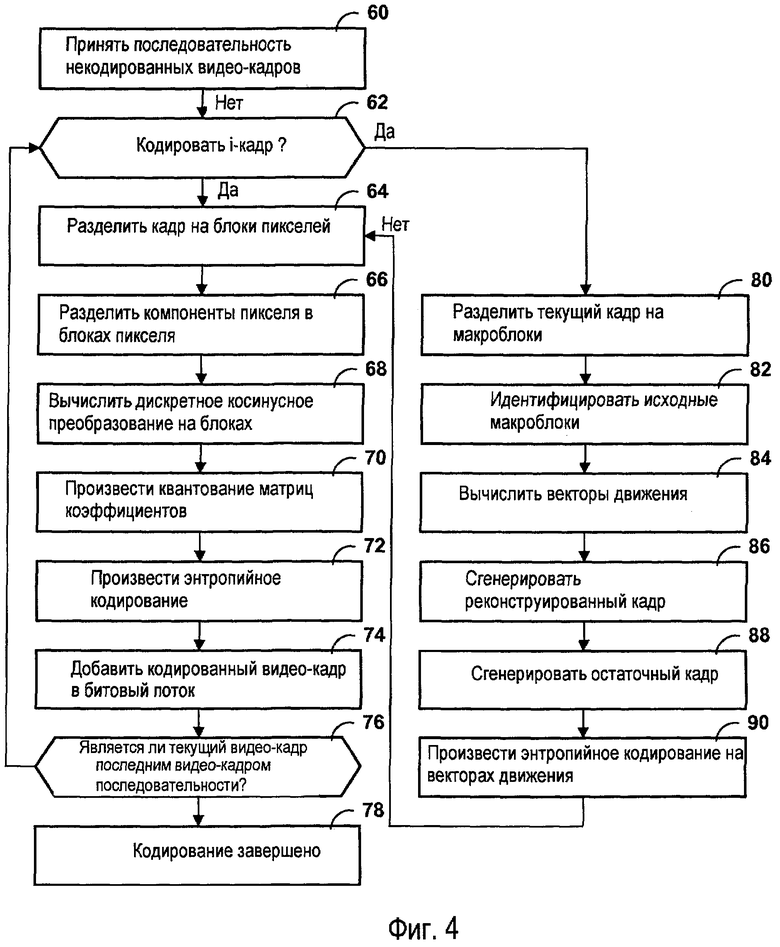
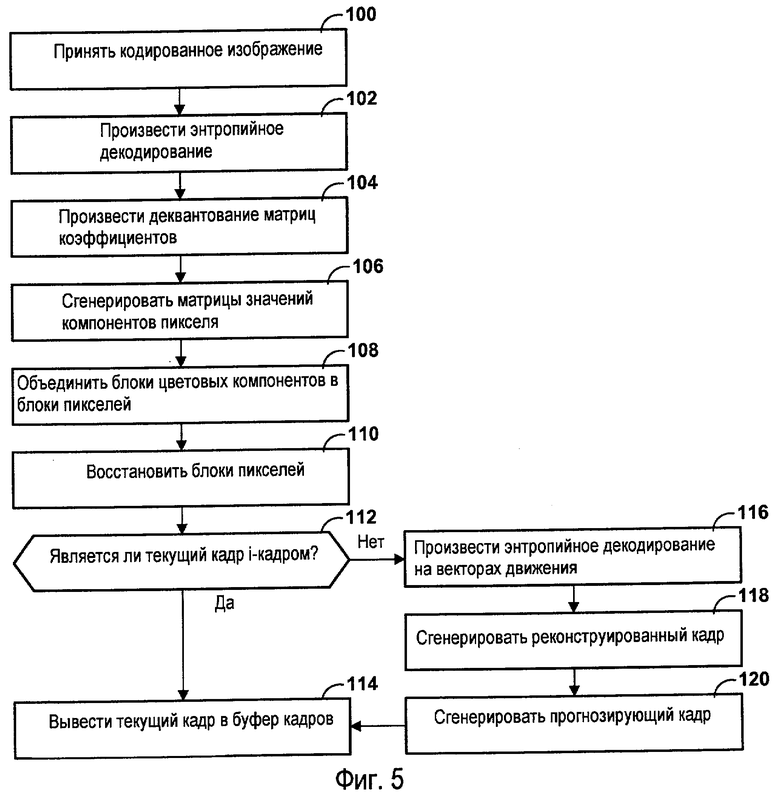
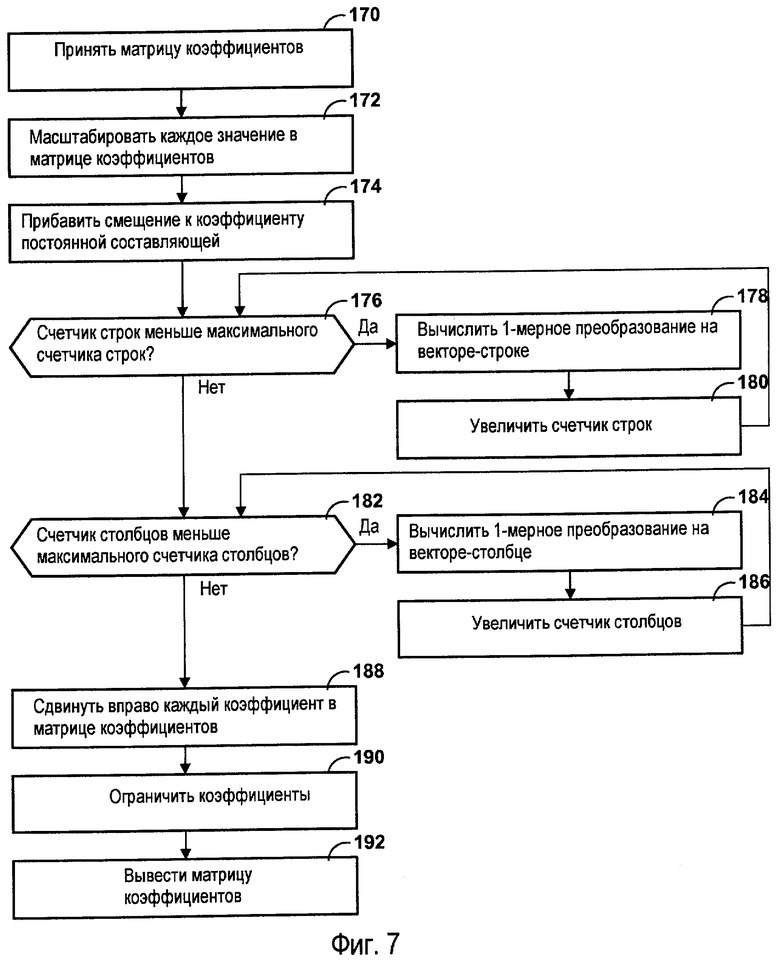
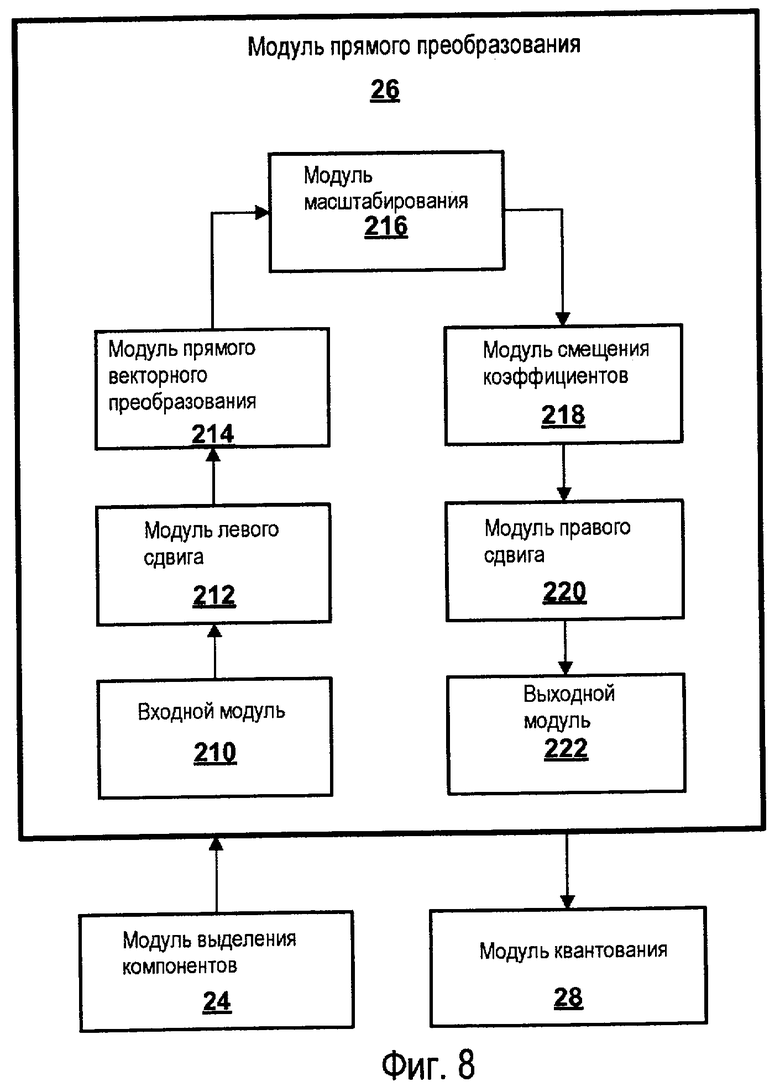
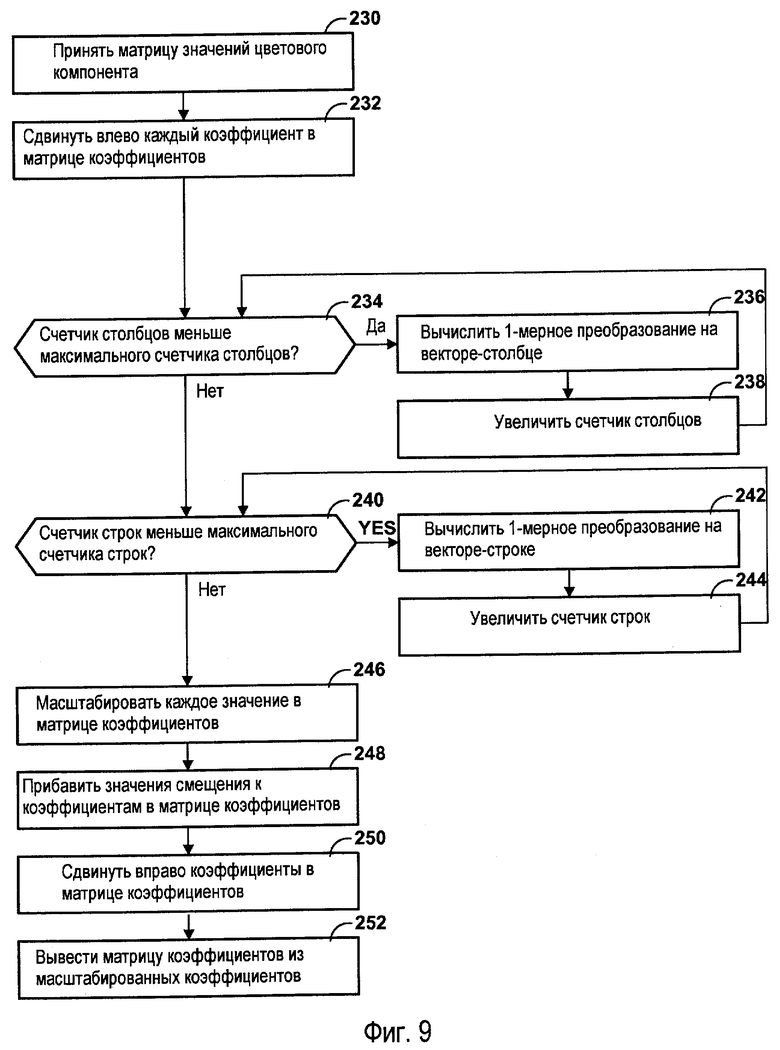



Изобретение относится к способам и устройствам для сжатия информации. Техническим результатом является снижение ошибок округления в ходе вычисления дискретного косинусного преобразования с использованием вычислений с фиксированной запятой. Способ содержит этапы: генерируют матрицу смещенных коэффициентов путем сложения одного или нескольких значений смещения с коэффициентом матрицы исходных коэффициентов, генерируют матрицу преобразованных коэффициентов с использованием арифметики с фиксированной запятой для повторного применения одномерного преобразования к коэффициентам в матрице смещенных коэффициентов, генерируют матрицу выходных коэффициентов путем правого сдвига коэффициентов в матрице преобразованных коэффициентов, причем коэффициенты в матрице выходных коэффициентов являются аппроксимациями значений, которые были бы получены путем преобразования матрицы исходных коэффициентов с использованием идеального обратного дискретного косинусного преобразования, предписывают блоку представления медиа выводить слышимые или видимые сигналы на основании матрицы выходных значений. 8 н. и 75 з.п. ф-лы, 12 ил.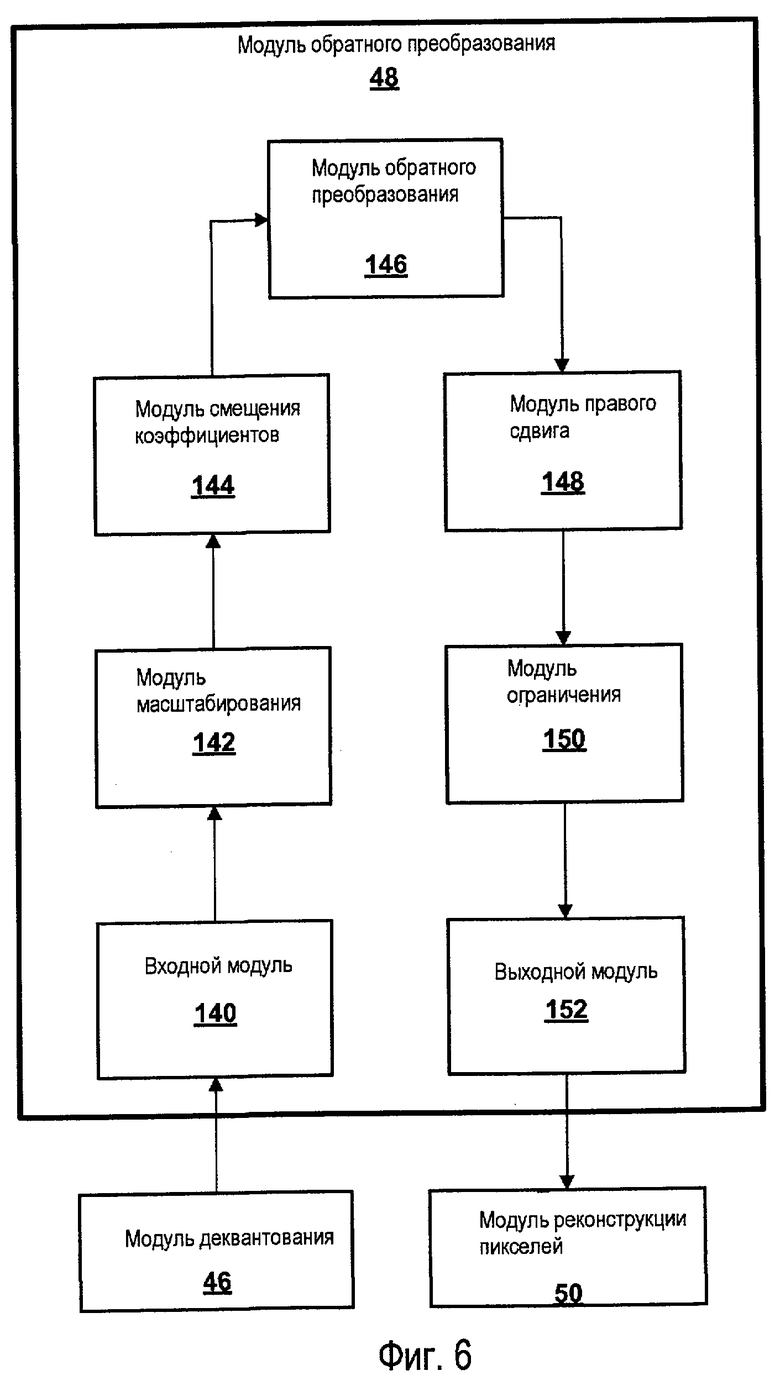
1. Способ снижения ошибок во время вычисления дискретного косинусного преобразования, содержащий этапы, на которых
генерируют матрицу смещенных коэффициентов путем сложения одного или нескольких значений смещения с коэффициентом матрицы исходных коэффициентов,
генерируют матрицу преобразованных коэффициентов с использованием арифметики с фиксированной запятой для повторного применения одномерного преобразования к коэффициентам в матрице смещенных коэффициентов,
генерируют матрицу выходных коэффициентов путем правого сдвига коэффициентов в матрице преобразованных коэффициентов, и
причем коэффициенты в матрице выходных коэффициентов являются аппроксимациями значений, которые были бы получены путем преобразования матрицы исходных коэффициентов с использованием идеального обратного дискретного косинусного преобразования,
предписывают блоку представления медиа выводить слышимые или видимые сигналы на основании матрицы выходных значений,
причем в результате сложения значений смещения с коэффициентом положительные ошибки и отрицательные ошибки оказываются, в среднем, равными по величине и оказываются, в среднем, симметричными относительно нуля, и
причем ошибки представляют разности между значениями, полученными в результате правого сдвига представлений ограниченной точности с фиксированной запятой для коэффициентов в матрице преобразованных коэффициентов на первую величину, и результатами деления коэффициентов в матрице преобразованных коэффициентов на 2 в степени первой величины, безотносительно к точности.
2. Способ по п.1, в котором коэффициенты в матрице выходных коэффициентов являются значениями компонентов пикселя, и
причем способ дополнительно содержит этап, на котором строят блок пикселей, который включает в себя значения компонентов пикселя.
3. Способ по п.2, в котором на этапе предписания блоку представления медиа выводить слышимые или видимые сигналы на основании матрицы выходных значений предписывают блоку представления медиа отображать блок пикселей.
4. Способ по п.2, в котором способ дополнительно содержит этапы, на которых
генерируют первый видеокадр путем объединения блоков пикселей с другими блоками пикселей, и
используют временное декодирование для генерации одного или нескольких последующих видеокадров, которые используют первый видеокадр как опорный видеокадр.
5. Способ по п.1, в котором коэффициент является коэффициентом постоянной составляющей матрицы исходных коэффициентов.
6. Способ по п.1, в котором способ дополнительно содержит этап, на котором суммируют член среднего смещения с коэффициентом, и
причем значение среднего смещения равно 2P-1, где Р равно количеству битов мантиссы в числах с фиксированной запятой, используемых в преобразовании, плюс количество битов, которые суммируются с коэффициентами в матрице преобразованных коэффициентов путем применения преобразования.
7. Способ по п.1, в котором первая величина равна 2P, причем Р равно количеству битов мантиссы в числах с фиксированной запятой, используемых в преобразовании, плюс количество битов, которые суммируются с коэффициентами в матрице преобразованных коэффициентов путем применения преобразования.
8. Способ по п.1, в котором на этапе генерации матрицы смещенных коэффициентов суммируют значение дополнительного смещения с коэффициентом,
причем значение дополнительного смещения равно -1, когда коэффициент отрицателен, и равно 0, когда коэффициент неотрицателен.
9. Способ по п.1, в котором способ дополнительно содержит этап, на котором выбирают на псевдослучайной основе значение, равное -1 или 0, и
в котором на этапе генерации матрицы смещенных коэффициентов суммируют выбранное значение с коэффициентом.
10. Способ по п.1, в котором способ дополнительно содержит этапы, на которых
генерируют матрицу деквантованных коэффициентов путем деквантования матрицы квантованных коэффициентов, и
генерируют матрицу исходных коэффициентов путем левого сдвига коэффициентов в матрице деквантованных коэффициентов на количество битов мантиссы чисел с фиксированной запятой, используемых при генерации матрицы преобразованных коэффициентов.
11. Способ по п.10, в котором количество битов мантиссы равно трем, и
причем для данной матрицы исходных коэффициентов матрица выходных коэффициентов удовлетворяет требованиям точности согласно стандарту 1180 Института инженеров по электротехнике и радиоэлектронике (IEEE).
12. Способ по п.1, в котором на этапе генерации матрицы преобразованных коэффициентов используют арифметику с фиксированной запятой для повторного применения преобразования к коэффициентам в матрице смещенных коэффициентов без использования операций умножения или деления.
13. Способ по п.1, в котором числа с фиксированной запятой, используемые при генерации матрицы преобразованных коэффициентов, являются 16-битовыми числами с фиксированной запятой.
14. Способ по п.1, в котором на этапе генерации матрицы преобразованных коэффициентов
генерируют матрицу промежуточных коэффициентов с использованием арифметики с фиксированной запятой для применения последовательности операций типа бабочка к каждому вектору-строке матрицы смещенных коэффициентов и
генерируют матрицу преобразованных коэффициентов с использованием арифметики с фиксированной запятой для применения последовательности операций типа бабочка к каждому вектору-столбцу матрицы промежуточных коэффициентов.
15. Способ по п.14, в котором при осуществлении любых операций типа бабочка осуществляют операции типа бабочка в виде
u=((x*C')+(y*S')+(1<<(k-1)))>>k;
ν=((x*S')+(y*-C')+(1<<(k-1)))>>k,
где u, ν, x и y - числа с фиксированной запятой,
где х и y - входные значения, и u и ν - выходные значения, и
где С, S и k являются целыми числами.
16. Способ по п.14, в котором разности между результатами, полученными посредством одной из операций типа бабочка, и результатами, которые были бы получены посредством эквивалентной операции типа бабочка с использованием арифметики с неограниченной точностью, центрированы вокруг нуля и имеют положительную или отрицательную величину, равную 1 или менее.
17. Способ по п.16, в котором при осуществлении любых операций типа бабочка осуществляют операции типа бабочка в виде
u=((x*C)>>k)-((y*-S)>>k);
ν=((x*S)>>k)-((y*C)>>k),
где u, ν, х и y - числа с фиксированной запятой,
где х и y - входные значения, и u и ν - выходные значения, и
где С, S и k являются целыми числами.
18. Устройство, снижающее ошибки во время вычисления дискретного косинусного преобразования, содержащее
модуль смещения коэффициентов, который генерирует матрицу смещенных коэффициентов путем сложения одного или нескольких значений смещения с коэффициентом матрицы исходных коэффициентов,
модуль обратного преобразования, который генерирует матрицу преобразованных коэффициентов с использованием арифметики с фиксированной запятой для повторного применения одномерного преобразования к коэффициентам в матрице смещенных коэффициентов,
модуль правого сдвига, который генерирует матрицу выходных коэффициентов путем правого сдвига коэффициентов в матрице преобразованных коэффициентов, и
причем коэффициенты в матрице выходных коэффициентов являются аппроксимациями значений, которые были бы получены путем преобразования матрицы исходных коэффициентов с использованием идеального обратного дискретного косинусного преобразования, и
драйвер представления, который предписывает блоку представления медиа выводить слышимые или видимые сигналы на основании матрицы выходных коэффициентов,
причем в результате сложения значений смещения с коэффициентом положительные ошибки и отрицательные ошибки оказываются, в среднем, равными по величине и оказываются, в среднем, симметричными относительно нуля, и
причем ошибки представляют разности между значениями, полученными в результате правого сдвига представлений ограниченной точности с фиксированной запятой для коэффициентов в матрице преобразованных коэффициентов на первую величину, и результатами деления коэффициентов в матрице преобразованных коэффициентов на 2 в степени первой величины, безотносительно к точности.
19. Устройство по п.18, в котором коэффициенты в матрице выходных коэффициентов являются значениями компонентов пикселя, и
причем устройство дополнительно содержит модуль реконструкции пикселей, который строит блок пикселей, который включает в себя значения компонентов пикселя.
20. Устройство по п.19, в котором драйвер представления предписывает блоку представления медиа отображать блок пикселей.
21. Устройство по п.19, в котором устройство дополнительно содержит
модуль объединения блоков, который генерирует первый видеокадр путем объединения блоков пикселей с другими блоками пикселей, и
модуль генерации прогнозирующих кадров, который генерирует один или несколько последующих видеокадров, которые используют первый видеокадр как опорный видеокадр.
22. Устройство по п.18, в котором коэффициент является коэффициентом постоянной составляющей матрицы коэффициентов.
23. Устройство по п.18, в котором модуль смещения коэффициентов генерирует матрицу смещенных коэффициентов путем сложения значения среднего смещения с коэффициентом, и
причем значение среднего смещения равно 2P-1, где Р равно количеству битов мантиссы в числах с фиксированной запятой, используемых в преобразовании, плюс количество битов, которые суммируются с коэффициентами в матрице преобразованных коэффициентов путем применения преобразования.
24. Устройство по п.18, в котором первая величина равна 2P, где Р равно количеству битов мантиссы в числах с фиксированной запятой, используемых в преобразовании, плюс количество битов, которые суммируются с коэффициентами в матрице преобразованных коэффициентов путем применения преобразования.
25. Устройство по п.18, в котором модуль смещения коэффициентов генерирует матрицу смещенных коэффициентов путем прибавления значения дополнительного смещения, которое равно -1, когда коэффициент отрицателен, и которое равно 0, когда коэффициент неотрицателен.
26. Устройство по п.18, в котором модуль смещения коэффициентов генерирует матрицу смещенных коэффициентов путем выбора, на псевдослучайной основе, значения, равного -1 или 0, и сложения выбранного значения с коэффициентом в качестве значений дополнительного смещения.
27. Устройство по п.18, в котором устройство дополнительно содержит
модуль деквантования, который генерирует матрицу деквантованных коэффициентов путем деквантования матрицы квантованных коэффициентов, и
модуль масштабирования, который генерирует матрицу исходных коэффициентов путем левого сдвига коэффициентов в матрице деквантованных коэффициентов на количество битов мантиссы чисел с фиксированной запятой, используемых при генерации матрицы преобразованных коэффициентов.
28. Устройство по п.27, в котором количество битов мантиссы равно трем, и
причем для данной матрицы исходных коэффициентов матрица выходных коэффициентов удовлетворяет требованиям точности согласно стандарту 1180 Института инженеров по электротехнике и радиоэлектронике (IEEE).
29. Устройство по п.18, в котором модуль обратного преобразования использует 16-битные числа с фиксированной запятой при использовании арифметики с фиксированной запятой для повторного применения одномерного преобразования к коэффициентам в матрице смещенных коэффициентов.
30. Устройство по п.18, в котором модуль обратного преобразования
использует арифметику с фиксированной запятой для применения последовательности операций типа бабочка к каждому вектору-строке матрицы масштабированных коэффициентов для получения матрицы промежуточных коэффициентов и
использует арифметику с фиксированной запятой для применения последовательности операций типа бабочка к каждому вектору-столбцу матрицы промежуточных коэффициентов для получения матрицы преобразованных коэффициентов.
31. Устройство по п.30, в котором операции типа бабочка выражаются в виде
u=((x*C')+(y*S')+(1<<(k-1)))>>k;
ν=((x*S')+(y*-C')+(1<<(k-1)))>>k,
где u, ν, x и y - числа с фиксированной запятой,
где х и y - входные значения, и u и ν - выходные значения, и
где С, S и k являются целыми числами.
32. Устройство по п.30, в котором разности между результатами, полученными посредством одной из операций типа бабочка, и результатами, которые были бы получены посредством эквивалентной операции типа бабочка с использованием арифметики с неограниченной точностью, центрированы вокруг нуля и имеют положительную или отрицательную величину, равную 1 или менее.
33. Устройство по п.32, в котором операции типа бабочка выражаются в виде
u=((x*C)>>k)-((y*-S)>>k);
ν=((x*S)>>k)-((y*C)>>k),
где u, ν, х и y - числа с фиксированной запятой,
где х и y - входные значения, и u и ν - выходные значения, и
где С, S и k являются целыми числами.
34. Устройство, снижающее ошибки во время вычисления дискретного косинусного преобразования, содержащее
средство для генерации матрицы смещенных коэффициентов путем сложения одного или нескольких значений смещения с коэффициентом матрицы исходных коэффициентов,
средство для генерации матрицы преобразованных коэффициентов с использованием арифметики с фиксированной запятой для повторного применения одномерного преобразования к коэффициентам в матрице смещенных коэффициентов,
средство для генерации матрицы выходных коэффициентов путем правого сдвига коэффициентов в матрице преобразованных коэффициентов,
причем коэффициенты в матрице выходных коэффициентов являются аппроксимациями значений, которые были бы получены путем преобразования матрицы исходных коэффициентов с использованием идеального обратного дискретного косинусного преобразования, и
средство для предписания блоку представления медиа выводить слышимые или видимые сигналы на основании матрицы выходных значений,
причем в результате сложения значений смещения с коэффициентом положительные ошибки и отрицательные ошибки оказываются, в среднем, равными по величине и оказываются, в среднем, симметричными относительно нуля, и
причем ошибки представляют разности между значениями, полученными в результате правого сдвига представлений ограниченной точности с фиксированной запятой для коэффициентов в матрице преобразованных коэффициентов на первую величину, и результатами деления коэффициентов в матрице преобразованных коэффициентов на 2 в степени первой величины, безотносительно к точности.
35. Устройство по п.34, в котором коэффициенты в матрице выходных коэффициентов являются значениями компонентов пикселя, и
причем устройство дополнительно содержит средство для построения блока пикселей, который включает в себя значения компонентов пикселя.
36. Устройство по п.35, в котором средство для предписания блоку представления медиа выводить слышимые или видимые сигналы на основании матрицы выходных значений содержит средство для предписания блоку представления медиа отображать блок пикселей.
37. Устройство по п.35, в котором устройство дополнительно содержит
средство для генерации первого видеокадра путем объединения блоков пикселей с другими блоками пикселей, и
средство для использования временного декодирования для генерации одного или нескольких последующих видеокадров, которые используют первый видеокадр как опорный видеокадр.
38. Устройство по п.34, в котором коэффициент является коэффициентом постоянной составляющей матрицы исходных коэффициентов.
39. Устройство по п.34, в котором средство для генерации матрицы смещенных коэффициентов содержит средство для сложения значения среднего смещения с коэффициентом, и
причем значение среднего смещения равно 2P-1, где Р равно количеству битов мантиссы в числах с фиксированной запятой, используемых в преобразовании, плюс количество битов, которые суммируются с коэффициентами в матрице преобразованных коэффициентов путем применения преобразования.
40. Устройство по п.39, в котором первая величина равна 2P, где Р равно количеству битов мантиссы в числах с фиксированной запятой, используемых в преобразовании, плюс количество битов, которые суммируются с коэффициентами в матрице преобразованных коэффициентов путем применения преобразования.
41. Устройство по п.34, в котором средство для генерации матрицы смещенных коэффициентов содержит средство для сложения значения дополнительного смещения с коэффициентом,
причем значение дополнительного смещения равно -1, когда коэффициент отрицателен, и равно 0, когда коэффициент неотрицателен.
42. Устройство по п.34, в котором способ дополнительно содержит этап, на котором выбирают на псевдослучайной основе значение, равное -1 или 0, и
причем средство для генерации матрицы смещенных коэффициентов содержит средство для сложения выбранного значения с коэффициентом.
43. Устройство по п.34, в котором устройство дополнительно содержит:
средство для генерации матрицы деквантованных коэффициентов путем деквантования матрицы квантованных коэффициентов, и
средство для генерации матрицы исходных коэффициентов путем левого сдвига коэффициентов в матрице деквантованных коэффициентов на количество битов мантиссы чисел с фиксированной запятой, используемых при генерации матрицы преобразованных коэффициентов.
44. Устройство по п.43, в котором количество битов мантиссы равно трем, и
причем для данной матрицы исходных коэффициентов матрица выходных коэффициентов удовлетворяет требованиям точности согласно стандарту 1180 Института инженеров по электротехнике и радиоэлектронике (IEEE).
45. Устройство по п.34, в котором средство для генерации матрицы преобразованных коэффициентов содержит средство для использования арифметики с фиксированной запятой для повторного применения преобразования к коэффициентам в матрице смещенных коэффициентов без использования операций умножения или деления.
46. Устройство по п.34, в котором средство для генерации матрицы преобразованных коэффициентов использует 16-битные числа с фиксированной запятой при использовании арифметики с фиксированной запятой для повторного применения одномерного преобразования к коэффициентам в матрице смещенных коэффициентов.
47. Устройство по п.34, в котором средство для генерации матрицы преобразованных коэффициентов содержит
средство для генерации матрицы промежуточных коэффициентов с использованием арифметики с фиксированной запятой для применения последовательности операций типа бабочка к каждому вектору-строке матрицы смещенных коэффициентов и
средство для генерации матрицы преобразованных коэффициентов с использованием арифметики с фиксированной запятой для применения последовательности операций типа бабочка к каждому вектору-столбцу матрицы промежуточных коэффициентов.
48. Устройство по п.47, в котором средство для осуществления любой из операций типа бабочка содержит средство для осуществления операции типа бабочка в виде
u=((x*C')+(y*S')+(1<<(k-1)))>>k;
ν=((x*S')+(y*-C')+(1<<(k-1)))>>k,
где u, ν, x и y - числа с фиксированной запятой,
где х и y - входные значения, и u и ν - выходные значения, и
где С, S и k являются целыми числами.
49. Устройство по п.47, в котором разности между результатами, полученными посредством одной из операций типа бабочка, и результатами, которые были бы получены посредством эквивалентной операции типа бабочка с использованием арифметики с неограниченной точностью, центрированы вокруг нуля и имеют положительную или отрицательную величину, равную 1 или менее.
50. Устройство по п.49, в котором средство для осуществления любой из операций типа бабочка содержит средство для осуществления операции типа бабочка в виде
u=((x*C)>>k)-((y*-S)>>k);
ν=((x*S)>>k)-((y*C)>>k),
где u, ν, x и y - числа с фиксированной запятой,
где х и y - входные значения, и u и ν - выходные значения, и
где С, S и k являются целыми числами.
51. Компьютерно-считываемый носитель, содержащий инструкции, которые, при выполнении, предписывают процессору
генерировать матрицу смещенных коэффициентов путем сложения одного или нескольких значений смещения с коэффициентом матрицы исходных коэффициентов,
генерировать матрицу преобразованных коэффициентов с использованием арифметики с фиксированной запятой для повторного применения одномерного преобразования к коэффициентам в матрице смещенных коэффициентов,
генерировать матрицу выходных коэффициентов путем правого сдвига коэффициентов в матрице преобразованных коэффициентов,
причем коэффициенты в матрице выходных коэффициентов являются аппроксимациями значений, которые были бы получены путем преобразования матрицы исходных коэффициентов с использованием идеального обратного дискретного косинусного преобразования, и
предписывать блоку представления медиа выводить слышимые или видимые сигналы на основании матрицы выходных значений,
причем в результате сложения значений смещения с коэффициентом положительные ошибки и отрицательные ошибки оказываются, в среднем, равными по величине и оказываются, в среднем, симметричными относительно нуля, и
причем ошибки представляют разности между значениями, полученными в результате правого сдвига представлений ограниченной точности с фиксированной запятой для коэффициентов в матрице преобразованных коэффициентов на первую величину, и результатами деления коэффициентов в матрице преобразованных коэффициентов на 2 в степени первой величины, безотносительно к точности.
52. Компьютерно-считываемый носитель по п.51, в котором коэффициенты в матрице выходных коэффициентов являются значениями компонентов пикселя, и
причем инструкции дополнительно предписывают процессору строить блок пикселей, который включает в себя значения компонентов пикселя.
53. Компьютерно-считываемый носитель по п.52, в котором инструкции предписывают процессору предписывать блоку представления медиа выводить слышимые или видимые сигналы на основании матрицы выходных значений путем предписания процессору предписывать блоку представления медиа отображать блок пикселей.
54. Компьютерно-считываемый носитель по п.52, в котором инструкции дополнительно предписывают процессору
генерировать первый видеокадр путем объединения блоков пикселей с другими блоками пикселей и
использовать временное декодирование для генерации одного или нескольких последующих видеокадров, которые используют первый видеокадр как опорный видеокадр.
55. Компьютерно-считываемый носитель по п.51, в котором коэффициент является коэффициентом постоянной составляющей матрицы коэффициентов.
56. Компьютерно-считываемый носитель по п.51, в котором инструкции дополнительно предписывают процессору суммировать значение среднего смещения с коэффициентом, и
причем значение среднего смещения равно 2P-1, где Р равно количеству битов мантиссы в числах с фиксированной запятой, используемых в преобразовании, плюс количество битов, которые суммируются с коэффициентами в матрице преобразованных коэффициентов путем применения преобразования.
57. Компьютерно-считываемый носитель по п.51, в котором первая величина равна 2P, где Р равно количеству битов мантиссы в числах с фиксированной запятой, используемых в преобразовании, плюс количество битов, которые суммируются с коэффициентами в матрице преобразованных коэффициентов путем применения преобразования.
58. Компьютерно-считываемый носитель по п.51, в котором инструкции, которые предписывают процессору генерировать матрицу смещенных коэффициентов, предписывают процессору суммировать значение дополнительного смещения с коэффициентом,
причем значение дополнительного смещения равно -1, когда коэффициент отрицателен, и равно 0, когда коэффициент неотрицателен.
59. Компьютерно-считываемый носитель по п.51, в котором инструкции дополнительно предписывают процессору выбирать на псевдослучайной основе значение, равное -1 или 0, и
в котором инструкции, которые предписывают процессору генерировать матрицу смещенных коэффициентов, предписывают процессору суммировать выбранное значение с коэффициентом.
60. Компьютерно-считываемый носитель по п.51, в котором инструкции дополнительно предписывают процессору
генерировать матрицу деквантованных коэффициентов путем деквантования матрицы квантованных коэффициентов, и
генерировать матрицу исходных коэффициентов путем левого сдвига коэффициентов в матрице деквантованных коэффициентов на количество битов мантиссы чисел с фиксированной запятой, используемых при генерации матрицы преобразованных коэффициентов.
61. Компьютерно-считываемый носитель по п.60, в котором количество битов мантиссы равно трем, и
причем для данной матрицы исходных коэффициентов матрица выходных коэффициентов удовлетворяет требованиям точности согласно стандарту 1179 Института инженеров по электротехнике и радиоэлектронике (IEEE).
62. Компьютерно-считываемый носитель по п.51, в котором инструкции предписывают процессору генерировать матрицу преобразованных коэффициентов путем предписания процессору повторно применять преобразования к коэффициентам в матрице смещенных коэффициентов без использования операций умножения или деления.
63. Компьютерно-считываемый носитель по п.51, в котором инструкции предписывают процессору использовать 16-битовые числа с фиксированной запятой, когда инструкции предписывают процессору использовать арифметику с фиксированной запятой для повторного применения одномерного преобразования к коэффициентам в матрице смещенных коэффициентов.
64. Компьютерно-считываемый носитель по п.51, в котором инструкции предписывают процессору генерировать матрицу преобразованных коэффициентов путем предписания процессору
генерировать матрицу промежуточных коэффициентов с использованием арифметики с фиксированной запятой для применения последовательности операций типа бабочка к каждому вектору-строке матрицы смещенных коэффициентов и
генерировать матрицу преобразованных коэффициентов с использованием арифметики с фиксированной запятой для применения последовательности операций типа бабочка к каждому вектору-столбцу матрицы промежуточных коэффициентов.
65. Компьютерно-считываемый носитель по п.64, в котором инструкции предписывают процессору осуществлять любую из операций типа бабочка путем предписания процессору осуществлять операции типа бабочка в виде
u=((х*С')+(y*S')+(1<<(k-1)))>>k;
ν=((x*S')+(y*-C')+(1<<(k-1)))>>k,
где u, ν, х и y - числа с фиксированной запятой,
где х и y - входные значения, и u и ν - выходные значения, и
где С, S и k являются целыми числами.
66. Компьютерно-считываемый носитель по п.64, в котором разности между результатами, полученными посредством одной из операций типа бабочка, и результатами, которые были бы получены посредством эквивалентной операции типа бабочка с использованием арифметики с неограниченной точностью, центрированы вокруг нуля и имеют положительную или отрицательную величину, равную 1 или менее.
67. Компьютерно-считываемый носитель по п.65, в котором инструкции предписывают процессору осуществлять любую из операций типа бабочка путем предписания процессору осуществлять операции типа бабочка в виде
u=((х*С)>>k)-((y*-S)>>k);
ν=((x*S)>>k)-((y*C)>>k),
где u, ν, x и y - числа с фиксированной запятой,
где х и y - входные значения, и u и ν - выходные значения, и
где С, S и k являются целыми числами.
68. Способ снижения ошибок во время вычисления дискретного косинусного преобразования, содержащий этапы, на которых
генерируют матрицу отрегулированных коэффициентов путем сдвига влево каждого коэффициента в матрице исходных коэффициентов,
генерируют матрицу преобразованных коэффициентов с использованием арифметики с фиксированной запятой для повторного применения одномерного преобразования к коэффициентам в матрице отрегулированных коэффициентов,
генерируют матрицу масштабированных коэффициентов путем масштабирования каждого коэффициента в матрице преобразованных коэффициентов,
генерируют матрицу смещенных коэффициентов путем сложения одного или нескольких значений смещения с одним или несколькими коэффициентами в матрице масштабированных коэффициентов и
генерируют матрицу выходных коэффициентов путем правого сдвига коэффициентов в матрице смещенных коэффициентов на первую величину,
причем матрица исходных коэффициентов представляет медиаданные,
причем коэффициенты в матрице выходных коэффициентов являются аппроксимациями значений, которые были бы получены путем преобразования матрицы исходных коэффициентов с использованием идеального прямого дискретного косинусного преобразования,
причем в результате сложения значений смещения с коэффициентом положительные ошибки и отрицательные ошибки оказываются, в среднем, равными по величине и оказываются, в среднем, симметричными относительно нуля, и
причем ошибки представляют разности между значениями, полученными в результате правого сдвига представлений ограниченной точности с фиксированной запятой для коэффициентов в матрице смещенных коэффициентов на первую величину, и результатами деления коэффициентов в матрице смещенных коэффициентов на 2 в степени первой величины, безотносительно к точности.
69. Способ по п.68, в котором первая величина равна 2P, где Р равно количеству битов мантиссы в числах с фиксированной запятой, используемых в преобразовании, плюс количество битов, которые суммируются с коэффициентами в матрице преобразованных коэффициентов путем применения преобразования.
70. Способ по п.68, в котором на этапе генерации матрицы смещенных коэффициентов суммируют значение дополнительного смещения с одним или несколькими коэффициентами в матрице масштабированных коэффициентов,
причем значение дополнительного смещения равно -1, когда коэффициент отрицателен, и равно 0, когда коэффициент неотрицателен.
71. Способ по п.68, в котором способ дополнительно содержит этап, на котором выбирают, на псевдослучайной основе, значение, равное -1 или 0, и
причем на этапе генерации матрицы смещенных коэффициентов суммируют выбранное значение с одним или несколькими коэффициентами в матрице масштабированных коэффициентов.
72. Устройство, снижающее ошибки во время вычисления дискретного косинусного преобразования, содержащее
модуль левого сдвига, который генерирует матрицу отрегулированных коэффициентов путем сдвига влево каждого коэффициента в матрице исходных коэффициентов,
модуль прямого преобразования, который генерирует матрицу преобразованных коэффициентов с использованием арифметики с фиксированной запятой для повторного применения одномерного преобразования к коэффициентам в матрице отрегулированных коэффициентов,
модуль масштабирования, который генерирует матрицу масштабированных коэффициентов путем масштабирования каждого коэффициента в матрице преобразованных коэффициентов,
модуль смещения коэффициентов, который генерирует матрицу смещенных коэффициентов путем сложения одного или нескольких значений смещения с одним или несколькими коэффициентами в матрице масштабированных коэффициентов, и
модуль правого сдвига, который генерирует матрицу выходных коэффициентов путем правого сдвига коэффициентов в матрице смещенных коэффициентов на первую величину,
причем матрица исходных коэффициентов представляет медиаданные,
причем коэффициенты в матрице выходных коэффициентов являются аппроксимациями значений, которые были бы получены путем преобразования матрицы исходных коэффициентов с использованием идеального прямого дискретного косинусного преобразования,
причем в результате сложения значений смещения с коэффициентом положительные ошибки и отрицательные ошибки оказываются, в среднем, равными по величине и оказываются, в среднем, симметричными относительно нуля, и
причем ошибки представляют разности между значениями, полученными в результате правого сдвига представлений ограниченной точности с фиксированной запятой для коэффициентов в матрице смещенных коэффициентов на первую величину, и результатами деления коэффициентов в матрице смещенных коэффициентов на 2 в степени первой величины, безотносительно к точности.
73. Устройство по п.72, в котором первая величина равна 2P, где Р равно количеству битов мантиссы в числах с фиксированной запятой, используемых в преобразовании, плюс количество битов, которые суммируются с коэффициентами в матрице преобразованных коэффициентов путем применения преобразования.
74. Устройство по п.72, в котором модуль смещения коэффициентов генерирует матрицу смещенных коэффициентов путем прибавления значения дополнительного смещения к одному или нескольким коэффициентам в матрице масштабированных коэффициентов,
причем значение дополнительного смещения равно -1, когда коэффициент отрицателен, и равно 0, когда коэффициент неотрицателен.
75. Устройство по п.72, в котором модуль смещения коэффициентов выбирает, на псевдослучайной основе, значение, равное -1 или 0, и суммирует выбранное значение с одним или несколькими коэффициентами в матрице масштабированных коэффициентов.
76. Устройство, снижающее ошибки во время вычисления дискретного косинусного преобразования, содержащее
средство для генерации матрицы отрегулированных коэффициентов путем сдвига влево каждого коэффициента в матрице исходных коэффициентов,
средство для генерации матрицы преобразованных коэффициентов с использованием арифметики с фиксированной запятой для повторного применения одномерного преобразования к коэффициентам в матрице отрегулированных коэффициентов,
средство для генерации матрицы масштабированных коэффициентов путем масштабирования каждого коэффициента в матрице преобразованных коэффициентов,
средство для генерации матрицы смещенных коэффициентов путем сложения одного или нескольких значений смещения с одним или несколькими коэффициентами в матрице масштабированных коэффициентов и
средство для генерации матрицы выходных коэффициентов путем правого сдвига коэффициентов в матрице смещенных коэффициентов на первую величину,
причем матрица исходных коэффициентов представляет медиаданные,
причем коэффициенты в матрице выходных коэффициентов являются аппроксимациями значений, которые были бы получены путем преобразования матрицы исходных коэффициентов с использованием идеального прямого дискретного косинусного преобразования,
причем в результате сложения значений смещения с коэффициентом положительные ошибки и отрицательные ошибки оказываются, в среднем, равными по величине и оказываются, в среднем, симметричными относительно нуля, и
причем ошибки представляют разности между значениями, полученными в результате правого сдвига представлений ограниченной точности с фиксированной запятой для коэффициентов в матрице смещенных коэффициентов на первую величину, и результатами деления коэффициентов в матрице смещенных коэффициентов на 2 в степени первой величины, безотносительно к точности.
77. Устройство по п.76, в котором первая величина равна 2Р, где Р равно количеству битов мантиссы в числах с фиксированной запятой, используемых в преобразовании, плюс количество битов, которые суммируются с коэффициентами в матрице преобразованных коэффициентов путем применения преобразования.
78. Устройство по п.76, в котором средство для генерации матрицы смещенных коэффициентов генерирует матрицу смещенных коэффициентов путем прибавления значения дополнительного смещения к одному или нескольким коэффициентам в матрице масштабированных коэффициентов,
причем значение дополнительного смещения равно -1, когда коэффициент отрицателен, и равно 0, когда коэффициент неотрицателен.
79. Устройство по п.76, в котором средство для генерации матрицы смещенных коэффициентов выбирает, на псевдослучайной основе, значение, равное -1 или 0, и суммирует выбранное значение с одним или несколькими коэффициентами в матрице масштабированных коэффициентов.
80. Компьютерно-считываемый носитель, содержащий инструкции, в котором инструкции предписывают программируемому процессору
генерировать матрицу отрегулированных коэффициентов путем сдвига влево каждого коэффициента в матрице исходных коэффициентов,
генерировать матрицу преобразованных коэффициентов с использованием арифметики с фиксированной запятой для повторного применения одномерного преобразования к коэффициентам в матрице отрегулированных коэффициентов,
генерировать матрицу масштабированных коэффициентов путем масштабирования каждого коэффициента в матрице преобразованных коэффициентов,
генерировать матрицу смещенных коэффициентов путем сложения одного или нескольких значений смещения с одним или несколькими коэффициентами в матрице масштабированных коэффициентов и
генерировать матрицу выходных коэффициентов путем правого сдвига коэффициентов в матрице смещенных коэффициентов на первую величину,
причем матрица исходных коэффициентов представляет медиаданные,
причем коэффициенты в матрице выходных коэффициентов являются аппроксимациями значений, которые были бы получены путем преобразования матрицы исходных коэффициентов с использованием идеального прямого дискретного косинусного преобразования,
причем в результате сложения значений смещения с коэффициентом положительные ошибки и отрицательные ошибки оказываются, в среднем, равными по величине и оказываются, в среднем, симметричными относительно нуля, и
причем ошибки представляют разности между значениями, полученными в результате правого сдвига представлений ограниченной точности с фиксированной запятой для коэффициентов в матрице смещенных коэффициентов на первую величину, и результатами деления коэффициентов в матрице смещенных коэффициентов на 2 в степени первой величины, безотносительно к точности.
81. Компьютерно-считываемый носитель по п.80, в котором первая величина равна 2P, где Р равно количеству битов мантиссы в числах с фиксированной запятой, используемых в преобразовании, плюс количество битов, которые суммируются с коэффициентами в матрице преобразованных коэффициентов путем применения преобразования.
82. Компьютерно-считываемый носитель по п.80, в котором инструкции предписывают процессору генерировать матрицу смещенных коэффициентов путем предписания процессору суммировать значение дополнительного смещения с одним или несколькими коэффициентами в матрице масштабированных коэффициентов,
причем значение дополнительного смещения равно -1, когда коэффициент отрицателен, и равно 0, когда коэффициент неотрицателен.
83. Компьютерно-считываемый носитель по п.80, в котором инструкции предписывают процессору генерировать матрицу смещенных коэффициентов путем предписания процессору
выбирать, на псевдослучайной основе, значение, равное -1 или 0, и
суммировать выбранное значение с одним или несколькими коэффициентами в матрице масштабированных коэффициентов.
| ДРЕНАЖ ДЛЯ ХИРУРГИЧЕСКОГО ЛЕЧЕНИЯ ГЛАУКОМЫ | 2005 |
|
RU2304946C2 |
| Способ обработки целлюлозных материалов, с целью тонкого измельчения или переведения в коллоидальный раствор | 1923 |
|
SU2005A1 |
| Прибор, замыкающий сигнальную цепь при повышении температуры | 1918 |
|
SU99A1 |
| СПОСОБ И УСТРОЙСТВО ДЛЯ КОДИРОВАНИЯ И ДЕКОДИРОВАНИЯ ИЗОБРАЖЕНИЯ В ЦИФРОВОЙ ФОРМЕ | 1998 |
|
RU2196391C2 |
Авторы
Даты
2011-05-27—Публикация
2007-06-25—Подача