ЦИЛИНДРИЧЕСКАЯ ЛИНЗА Российский патент 2014 года по МПК H01Q15/08 H01Q19/08 

Изобретение относится к антенной технике, а именно к устройствам для фокусировки радиоволн сантиметрового и миллиметрового диапазонов.

Из уровня техники известна линза Микаэляна [А.Л.Микаэлян Оптические методы в информатике: запись, обработка и передача информации. - М.: «Наука, 1990 г. стр.18-65, рис.2.30] в виде диэлектрического цилиндра, представляющего собой градиентную среду с цилиндрической симметрией, показатель преломления которой уменьшается в радиальном направлении по закону обратного гиперболического косинуса. В такой среде наблюдается явление самофокусировки, при котором все лучи, исходящие из одной осевой точки, на некотором расстоянии опять соберутся в осевом фокусе. При удалении от центра линзы интенсивность поля уменьшается по тому же закону, что и показатель преломления. Рассматриваемая линза имеет хорошие сканирующие свойства и свободна от сферической аберрации.

Случай, когда фокус вынесен с поверхности линзы, получил название обобщенной линзы Микаэляна.

Важно отметить, что поскольку рассмотренные линзы представляют собой отрезки самофокусирующих волноводов, их можно легко изготавливать в больших количествах.

На практике эксперимент по исследованию свойств обобщенной линзы Микаэляна, выполненной из искусственного (дырчатого) диэлектрика, был проведен в сантиметровом диапазоне волн. Линза была изготовлена из листов плексигласа толщиной 6.4 мм в виде дисков с цилиндрическими отверстиями, распределенными таким образом, чтобы обеспечивался требуемый закон изменения показателя преломления в радиальном направлении. Диаметры отверстий менялись от 6.4 до 9.6 мм, что соответствует изменению показателя преломления от 1.61 в центре до 1.24 на краях линзы. Диски плотно прилегали друг к другу, образуя участок кругового цилиндра длиной 7 см. Диаметр линзы составлял 25.6 см, источник располагался на расстоянии 256 мм от выходной плоскости линзы.

Было установлено, что в достаточно широкой полосе частот характеристики излучения сохраняются хорошими. Ширина главного лепестка соответствует формуле θ_0.5,=55λ/D, где D - диаметр линзы. На частоте 7000 МГц она составляла 9º,а на частоте 15000 МГц - 4,4º. Уровень боковых лепестков для этих случаев не превышал 20 и 19 дБ соответственно.

Линза имеет также неплохие характеристики при смещении источника из фокуса. Установлено, что наилучшие результаты при сканировании получаются в случае, когда источник перемещается по дуге с вершиной в центре линзы.

Известна конструкция цилиндрической диэлектрической линзы [патент JP 2001085936 (MATSUSHITA ELECTRIC IND CO LTD), МПК H01Q 15/02, H01Q 15/08, (реферат) [он-лайн] [найдено 2012-03-30] Найдено из: базы данных esp@cenet], выполненная в виде набора параллельных диэлектрических пластин с просверленными в них отверстиями равного диаметра, но различной плотности размещения в зависимости от расстояния до центральной оси линзы. Отверстия расположены так, что эффективная плотность полученной линзы увеличивается к середине.

Недостатком данной конструкции является большой продольный размер при заданной апертуре, который обусловлен тем, что между отверстиями необходимо оставлять минимально допустимой зазор для исключения наложения отверстий друг на друга. Это ведет к увеличению эффективного показателя преломления на краю линзы и, следовательно, необходимости увеличения толщины линзы.

Из статьи [Я.Р.Триандафилов, В.В.Котляр. Фотонно-кристаллическая линза Микаэляна. Компьютерная оптика, том 31, №3, стр.27-31] известно, что цилиндрическую градиентную микролинзу Микаэляна (ЛМ), показатель преломления которой меняется от центра к краю линзы по определенному закону:

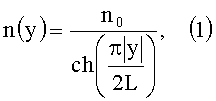
где n₀ - показатель преломления в центре;

L - ширина линзы вдоль оси z,

можно заменить на двухмерную фотонно-кристаллическую линзу (ФК-линзу) из материала с показателем преломления n и шириной а. В этом случае двухмерная ФК-линза состоит из фотонного кристалла, радиус дырочек в котором меняется по следующему закону:

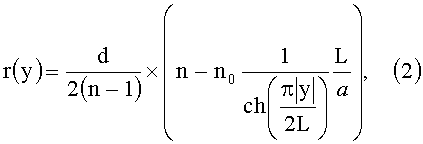
где d - постоянная кристалла.

Пусть в каждом столбике линзы М дырочек. Тогда полученная зависимость должна выполняться в точках y=±dm, m меняется от 0 до M/2. При этом на радиус дырочки также должны быть наложены определенные условия. Во-первых, радиус должен быть неотрицательным. Из формулы (1) видно, что минимальное значение радиуса достигается в точке y=0. Наложив на него условие неотрицательности, получим следующую связь для параметров ЛМ и соответствующей ей фотонной линзы:

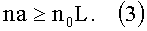
Во-вторых, диаметр дырочки, очевидно, должен быть меньше постоянной кристалла. Максимальное значение радиуса достигается в точке y=b/2, где b - апертура линзы. Указанное условие налагает следующее ограничение на апертуру линзы:

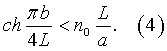
В-третьих, на период решетки, как уже было сказано выше, должно налагаться условие d<λ. Кроме того, при численном моделировании фотонно-кристаллической линзы шаг сетки должен выбираться настолько маленьким, чтобы радиус менялся от ряда к ряду. Дело в том, что может получиться так, что изменение радиуса от ряда кряду может оказаться меньшим, чем шаг дискретизации. В этом случае радиус не измениться и желаемый эффект достигнут не будет.

Недостатком данной конструкции является большой продольный размер при заданной апертуре.

Из статьи [Нестеренко Д.В. Металло-диэлектрическая линза Микаэляна. Компьютерная оптика, том 35, №1, стр.47-53] известно, что для преодоления ограничения снизу на значение показателя преломления в линзе Микаэляна и увеличение ее апертуры было предложено использовать композитную металлодиэлектрическую среду, включающую периодические массивы металлических стержней, технологически труднореализуемую в настоящее время.

В качестве ближайшего аналога выбрана цилиндрическая линза Люнеберга [Патент GB 131605 8, МПК H01Q 15/02, опубл. 09.05.1973 г.], состоящая из коаксиального набора параллельных элементов одинакового максимального радиуса r₀, изготовленных из одинакового диэлектрического материала, причем толщина каждого элемента меняется вдоль радиуса так, чтобы соответствовать заданному закону изменения эффективной диэлектрической проницаемости вдоль радиуса линзы. В данной конструкции закон изменения эффективной диэлектрической проницаемости соответствует цилиндрической линзе Люнеберга и достигается путем изменения толщины каждого из элементов по расстоянию от оси, перпендикулярной плоскости расположения элементов. Все элементы, изготовленные из одинакового диэлектрического материала, имеют одинаковые размеры и расположены на одинаковом расстоянии друг от друга. Верхняя поверхность каждого элемента имеет выпуклую форму, а его нижняя поверхность - выпуклую или иную форму. Расстояние между элементами выбрано таким образом, чтобы выполнялись необходимые отношения Люнеберга. В других вариантах плосковыпуклую форму элемента аппроксимируют с помощью трех дисков с уменьшающимся диаметром, которые либо контактируют друг с другом, либо отделены друг от друга на небольшое расстояние. В других вариантах диски могут быть изготовлены из разных диэлектрических материалов.

При заданной апертуре продольным размером цилиндрической линзы Люнеберга является диаметр цилиндра, а у цилиндрической линзы Микаэляна - толщина. Поэтому при заданной апертуре продольный размер цилиндрической линзы Люнеберга больше, чем продольный размер цилиндрической линзы Микаэляна. Кроме того, у цилиндрической линзы Микаэля в отличие от цилиндрической линзы Люнеберга фокусировка падающей волны одновременно осуществляется в двух плоскостях. Это обеспечивает симметричную форму диаграммы направленности (ДН).

Задачей изобретения является создание технологически простой в изготовлении конструкции цилиндрической линзы Микаэляна из однородного диэлектрического материала с минимальным продольным размером.

Поставленная задача решается тем, что в цилиндрической линзе, состоящей из коаксиального набора параллельных элементов одинакового максимального радиуса r₀, изготовленных из одинакового диэлектрического материала, согласно изобретению коаксиальный набор состоит из М диэлектрических плоских N-лепестковых элементов, повернутых относительно друг друга на угол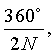

каждый лепесток i-го диэлектрического плоского N-лепесткового элемента, имеющий миндалевидную форму, радиально ориентирован относительно центральной оси данного элемента, причем количество элементов М в коаксиальном наборе рассчитывается по формуле:

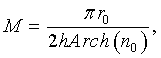
где n₀ - показатель преломления линзы в центре, равный показателю преломления n_M материала i-го диэлектрического плоского N-лепесткового элемента;

r₀ - максимальный радиус i-го диэлектрического плоского N-лепесткового элемента;

- толщина i-го диэлектрического плоского N-лепесткового элемента;

- минимальная рабочая длина волны.

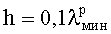
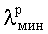
В целях получения при заданной апертуре минимального продольного размера минимальный показатель преломления n(r₀) на краю линзы должен быть равен единице.

Для того чтобы минимальный показатель преломления n(r₀) на краю заявляемой цилиндрической линзы был равен единице, каждый лепесток i-го диэлектрического плоского N-лепесткового элемента имеет миндалевидную форму.

Показатель преломления заявляемой цилиндрической линзы Микаэляна уменьшается в радиальном направлении по закону обратного гиперболического косинуса за счет того, что каждый лепесток i-го диэлектрического плоского N-лепесткового элемента радиально ориентирован относительно центральной оси данного элемента.

Для обеспечения высокой точности выполнения закона обратного гиперболического косинуса, по которому показатель преломления линзы уменьшается в радиальном направлении от значения показателя преломления (пм) материала до единицы, заявляемая цилиндрическая линза выполнена в виде коаксиального набора, состоящего из М диэлектрических плоских TV-лепестковых элементов, повернутых относительно друг друга на угол 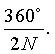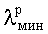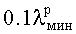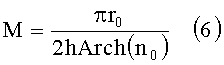Кроме того, толщина i-го диэлектрического плоского N-лепесткового элемента h должна быть на порядок меньше минимальной рабочей длина волны , т.е. толщина i-го диэлектрического плоского N-лепесткового элемента h равна .

Толщина заявляемой цилиндрической линзы вычисляется по формуле, которая выводится из выражения (1):

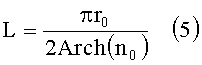
Разделив выражение (5) на толщину i-го диэлектрического плоского N-лепесткового элемента h, получим выражения для количества М в коаксиальном наборе:

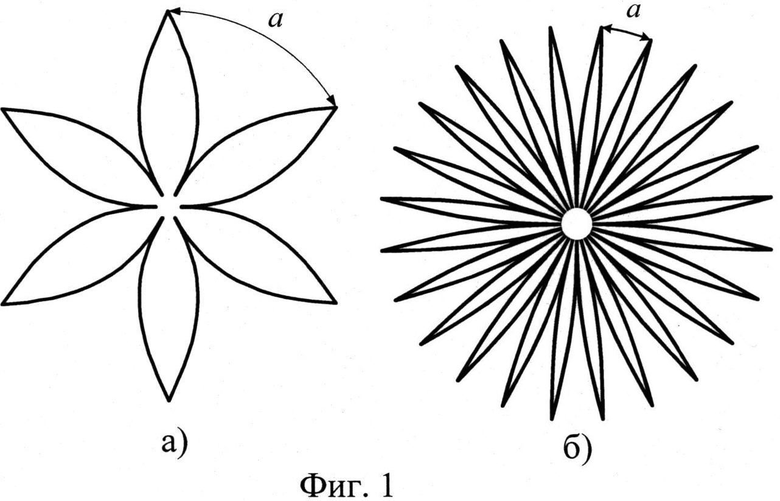
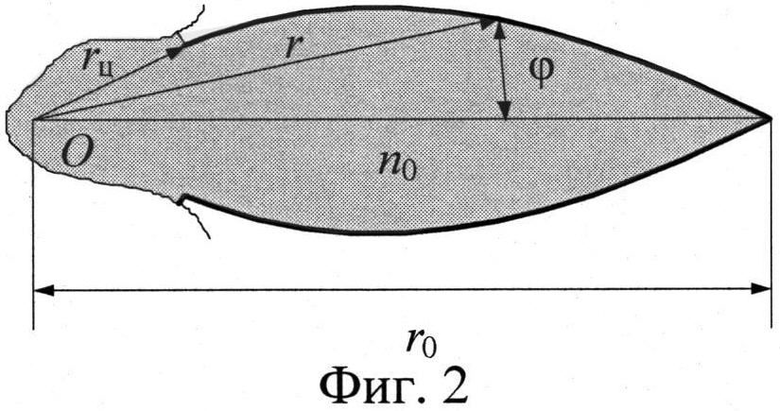
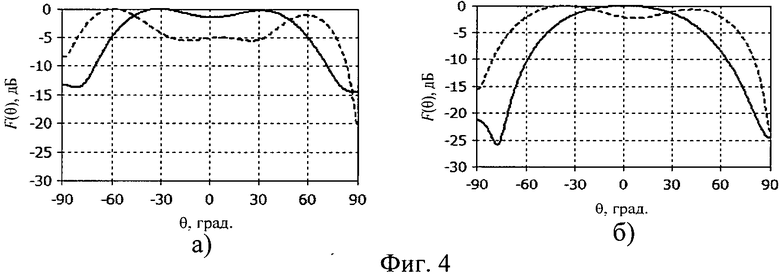
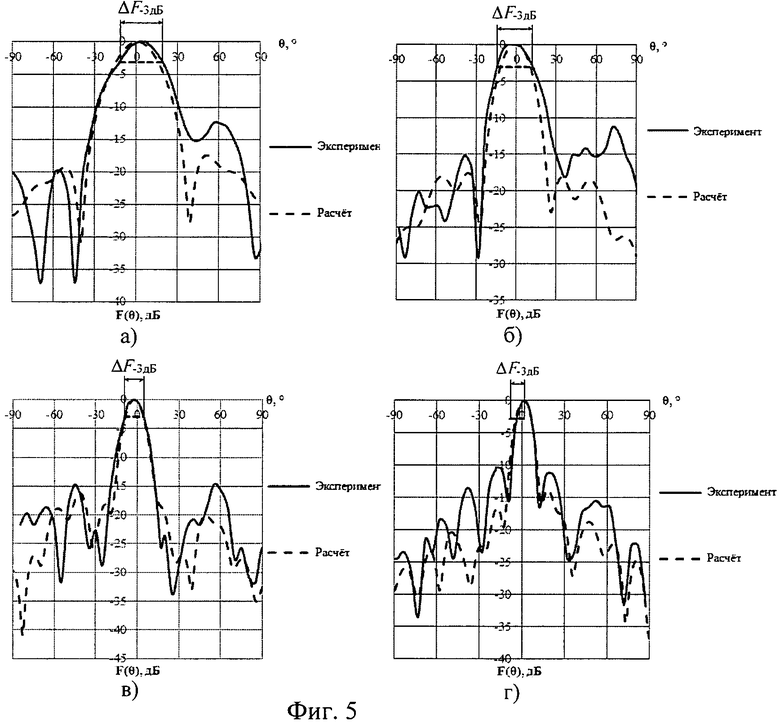
На фиг.1 а) и б) приведены формы i-ых 6- и 24-лепестковых элементов соответственно. На фиг.2 приведена форма отдельного лепестка i-го N-лепесткового элемента. На фиг.3 представлен пример конкретного выполнения заявляемой цилиндрической линзы из 6-лепестковых элементов (М=36). 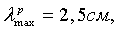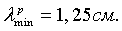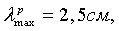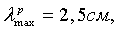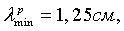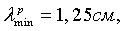На фиг.4 приведены нормированные расчетные и экспериментальные диаграммы направленности (ДН) широкополосного вибратора без линзы: а - максимальная рабочая длина волны б - минимальная рабочая длина волны На фиг.5 представлены нормированные расчетные и экспериментальные диаграммы направленности заявляемой цилиндрической линзы из 6-лепестковых элементов (М=36): а - максимальная рабочая длина волны плоскость Е; б - максимальная рабочая длина волны плоскость H; в - минимальная рабочая длина волны плоскость Е; г - минимальная рабочая длина волны плоскость H.

Отдельный i-ый элемент с максимальным радиусом r₀ представляет собой диэлектрическую монолитную плоскую фигуру, выполненную в виде цветка, состоящего из цветоложа с N лепестками, радиально ориентированными относительно центральной оси. При изготовлении i-го элемента радиус цветоложа r_ц не должен превышать 0.1r₀.

Число лепестков определяется следующим выражением:

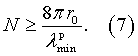
В соответствии с выражением (7) длина дуги а между вершинами соседних лепестков i-го элемента равна .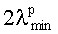

Как видно на фиг.1, при заданной минимальной рабочей длине волны 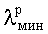с увеличением числа лепестков длина дуги a между вершинами соседних лепестков i-го элемента уменьшается. Так для i-го 6-лепесткового элемента длина дуги а составляет πr₀/3, а для i-ого 24-лепесткового элемента длина дуги а равна πr₀/12, т.е. вчетверо меньше.

Как видно на фиг.2, отдельный лепесток i-го N-лепесткового элемента имеет миндалевидную форму, которая описывается в полярных координатах следующим выражением:

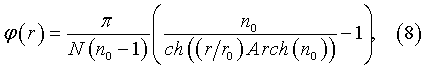
где φ - угловая полярная координата;

r - радиальная полярная координата.

Радиальная координата r отсчитывается от геометрического центра О элемента.

Заявляемая цилиндрическая линза представляет собой неразъемный коаксиальный набор, состоящий из М плоских монолитных N-лепестковых элементов одинакового максимального радиуса r₀, изготовленных из одинакового диэлектрического материала. Количество элементов М в коаксиальном наборе рассчитывается по формуле (6):

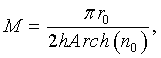
где 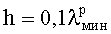- толщина i-го диэлектрического плоского N-лепесткового элемента.

В коаксиальном наборе диэлектрические плоские N-лепестковые элементы уложены параллельно и повернуты относительно друг друга на угол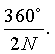

В качестве материала изготовления i-го N-лепесткового элемента используют листовой диэлектрик с малыми потерями (ПТФЭ, ПЭТ). Все TV-лепестковые элементы имеют одинаковые размеры и форму.

Цилиндрическая линза 1 (фиг.3) представляет собой неразъемный коаксиальный набор, состоящий из 36 плоских монолитных 6-лепестковых элементов одинакового максимального радиуса r₀, равного 310 мм. Толщина линзы L составляет 32 мм. Все элементы изготовлены из полиэтилентерефталата (ПЭТ) с показателем преломления (пм), равным 1.7. Цилиндрическая линза 1 размещена на фольгированной диэлектрической подложке 2 (материал RT/Duroid 5880 толщиной 0,5 мм) с металлическим экраном 3. На фольгированной диэлектрической подложке 2 выполнен печатный широкополосный вибратор 4, размещенный в фокусе цилиндрической линзы 1. Печатный широкополосный вибратор 4 соединен посредством печатной симметричной двухпроводной линии 5 с источником питания (не показан). Между подложкой и экраном оставлен воздушный зазор 5 мм, между линзой и подложкой зазор отсутствует. Площадь апертуры линзы равна 3068 мм².

Цилиндрическая линза работает следующим образом.

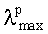
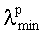
При максимальной рабочей длине волны , равной 2.5 см, широкополосный вибратор 4 имеет двунаправленную диаграмму направленности с провалом в центре (см. фиг.4, а), при минимальной рабочей длине волны , равной 1.25 см, диаграмма направленности вибратора 4 однонаправленная (см. фиг.4, б).

Сигнал со сферическим фазовый фронтом волны, формируемый широкополосным вибратором 4, попадает на поверхность цилиндрической линзы 1 из однородного диэлектрического материала, показатель преломления которой уменьшается в радиальном направлении по закону обратного гиперболического косинуса. Проходя через цилиндрическую линзу 1, лучи, составляющие сферический фазовый фронт, распространяются в соответствии с характеристиками линзы Микаэляна. Как видно на фигурах 5 а)-г), происходит сужение диаграммы направленности линзы 1 по сравнению с диаграммой направленности вибратора 4. 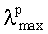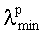При максимальной рабочей длине волны , равной 2,5 см, ширина диаграммы направленности ∆F_-3дд по уровню -3 дБ составляет 30,3º в плоскости Е (см. фиг.5, а)) и 26,7º в плоскости Н (см. фиг.5, б)), а при минимальной рабочей длине волны , равной 1,25 см, ширина диаграммы направленности ∆F_-3дд по уровню -3 дБ составляет 13,9º в плоскости Е (см. фиг.5, в)) и 10,9º в плоскости Н (см. фиг.5, г)). Данные значения ширин ДН соответствуют ДН синфазной апертуры площадью 3068 мм² с косинусоидальным распределением амплитуды. Разница между ширинами ДН в различных плоскостях обусловлена разной шириной ДН широкополосного вибратора 4 в двух плоскостях. Разница между расчетными и экспериментальными ДН в области бокового излучения обусловлена погрешностями измерений ДН антенны в закрытом помещении. Таким образом, линза 1 осуществляет преобразование сферического фронта волны широкополосного вибратора 4 в плоский фазовый фронт в раскрыве линзы 1, осуществляя фокусировку.

Заявляемая цилиндрическая линза может быть использована в конструкции широкополосных направленных антенн или элементов антенных решеток.

Изобретение относится к антенной технике, а именно к устройствам для фокусировки радиоволн сантиметрового и миллиметрового диапазонов. Техническим результатом является создание цилиндрической линзы Микаэляна из однородного диэлектрического материала с минимальным продольным размером. Цилиндрическая линза представляет собой коаксиальный набор, состоящий из М диэлектрических плоских N-лепестковых элементов одинакового максимального радиуса r₀, изготовленных из одинакового диэлектрического материала, повернутых относительно друг друга на угол Каждый лепесток i-го диэлектрического плоского N-лепесткового элемента, имеющий миндалевидную форму, радиально ориентирован относительно центральной оси данного элемента. 5 ил.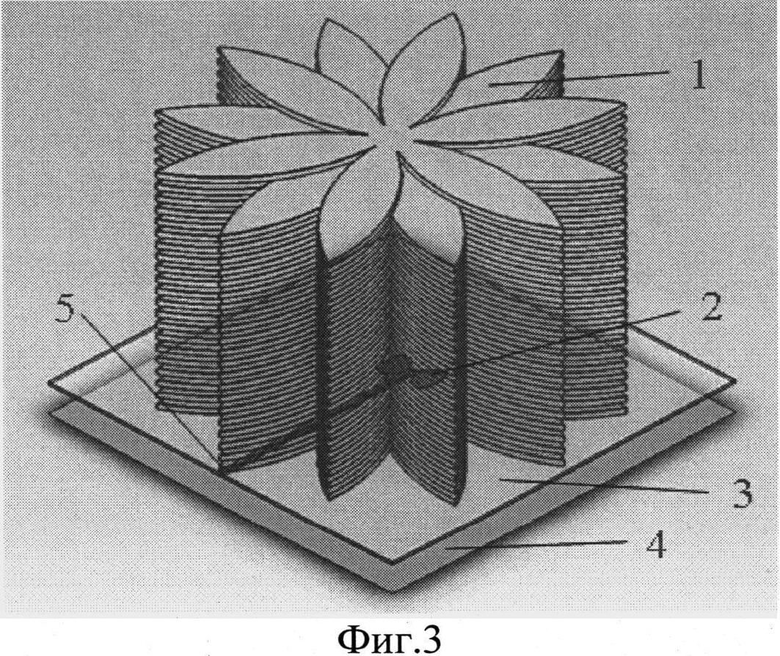

Цилиндрическая линза, состоящая из коаксиального набора параллельных элементов одинакового максимального радиуса r₀, изготовленных из одинакового диэлектрического материала, отличающаяся тем, что коаксиальный набор состоит из М диэлектрических плоских N-лепестковых элементов, повернутых относительно друг друга на угол 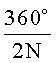, каждый лепесток i-го диэлектрического плоского N-лепесткового элемента, имеющий миндалевидную форму, радиально ориентирован относительно центральной оси данного элемента, причем количество элементов М в коаксиальном наборе рассчитывается по формуле:

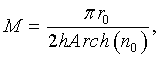
где n₀ - показатель преломления линзы в центре, равный показателю преломления n_M материала i-го диэлектрического плоского N-лепесткового элемента;
r₀ - максимальный радиус i-го диэлектрического плоского N-лепесткового элемента;
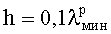- толщина i-го диэлектрического плоского N-лепесткового элемента;
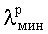- минимальная рабочая длина волны.