Предлагаемое изобретение относится к области метеорологии и гляциологии, а именно к способам дистанционного определения экспозиции склона, характеризующего пространственную ориентацию элементарного склона относительно сторон света, и может быть использовано при определении толщины снежного покрова на склонах для прогноза лавинной опасности и определения снегонакопления в горах.
Экспозиция склона является одной из важнейших морфометрических характеристик рельефа. Экспозиция склонов - расположение склонов горных хребтов, холмов и др. элементов рельефа по отношению к странам света или преобладающим ветрам. Согласно определению экспозиция точки на склоне равна азимуту проекции нормали точки на горизонтальную плоскость и выражается в градусах.
Известны различные способы определения экспозиции склона в горах с помощью таких простейших приборов, как компас [1].
Суть способа заключается в том, что предварительно с помощью компаса измеряют положение склона относительно частей света, т.е. азимут горизонтали склона в точке измерения, а затем определяют экспозицию склона как азимут проекции нормали склона в этой точке на горизонтальную плоскость.
Известный способ прост в реализации. Однако он не приемлем для определения экспозиции склона при наличии глубокого снежного покрова на склоне, да еще при наличии серьезной опасности, связанной со сходом лавин.
В последнее время для лыжников создан миниатюрный компас, который позволяет, находясь на склоне, измерить экспозицию и крутизну склона с помощью откидывающейся крышечки и отметок на его корпусе [2]. Однако данный прибор имеет те же недостатки, что и обычный компас.
Наиболее близким по технической сущности к заявленному объекту является способ дистанционного определения параметров склона и снежного покрова в лавинных очагах с использованием лазерной локации. Задача этих съемок - получение высокоточных цифровых моделей рельефа поверхности земли и поверхности снежного покрова [3].
К недостаткам известного способа можно отнести высокую стоимость авиационной техники и невозможность ее использования при снегопадах, что затрудняет реализацию способа для целей активного воздействия на снеголавинный режим в горах.
Техническим результатом, ожидаемым от использования заявленного способа, является снижение трудозатрат по его реализации и повышение точности дистанционного измерения экспозиции склона в лавинных очагах с использованием лазерного дальномера.
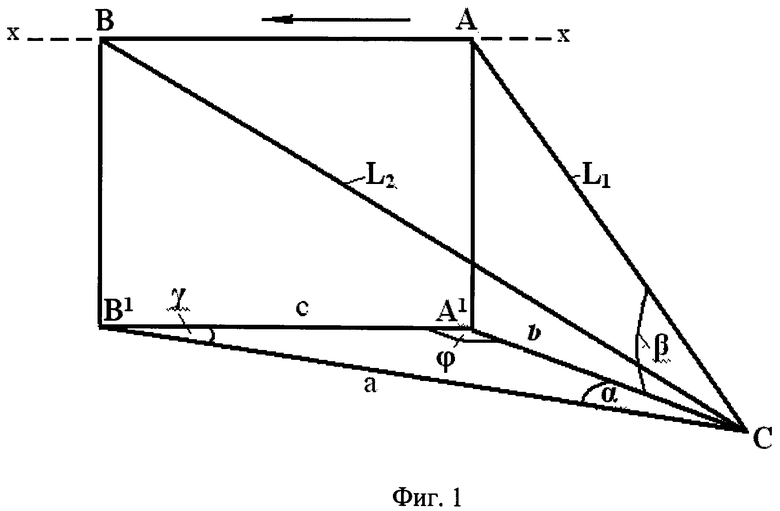
Технический результат достигается тем, что в известном способе дистанционного определения экспозиции склона в лавинных очагах путем измерения расстояния до контрольных точек (фиг.1, 2) с использованием лазерного дальномера, размещенного в долине, определяют расстояние до контрольной точки на склоне (L1), азимут (A1) и угол зондирования (β), затем, сместив зондирующий луч на некоторое расстояние АВ по горизонтали влево или вправо, определяют расстояние (L2) до произвольной вспомогательной точки на склоне и азимут зондирования этой точки (А2), затем из проекции на горизонтальную плоскость величин L1, L2 и АВ, образующих треугольник - А1В1С, определяют угол α между проекциями отрезков L1 и L2 на горизонтальную плоскость, а также значение проекции АВ и углы φ и γ, образованные соответственно на стыке проекций отрезков L1 и L2 с проекцией отрезка АВ на горизонтальную плоскость, после этого для случая А1>А2 определяют экспозицию склона (Э) через азимут зондирования контрольной точки на склоне по формуле
Э=А1+φ+90,
либо через азимут зондирования произвольной вспомогательной точки на склоне по формуле
Э=А2+270-γ,
а для случая, когда точка «В» выбирается справа от точки «А» {А1<А2), экспозицию склона находят через азимут зондирования контрольной точки на склоне по формуле
Э=А1+270-γ,
либо через азимут зондирования произвольной вспомогательной точки на склоне по формуле
Э=А2+γ+90,
где
А1 - азимут зондирования контрольной точки на склоне, град.;
А2 - азимут зондирования произвольной вспомогательной точки на склоне, град.;
φ - угол между проекциями на горизонтальную плоскость отрезков L1 и АВ, град.;
γ - угол между проекциями на горизонтальную плоскость отрезков L2 и АВ, град.;
90 - постоянная величина, характеризующая перпендикулярность нормали 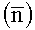
Технический результат достигается и тем, что проекцию L1 на горизонтальную плоскость (b) определяют по формуле
b=L1·cosβ,
а проекцию L2 на горизонтальную плоскость (b) определяют по формуле
а=L2·cosβ,
где β - угол зондирования контрольной и вспомогательной точек на склоне.
Технический результат достигается и тем, что угол α между проекциями на горизонтальную плоскость величин L1 и L2 находят: для случая А1>А2 по формуле
α=А1-A2,
а для случая А1<А2 по формуле
α=А2-A1.
Технический результат достигается также и тем, что проекцию отрезка АВ на горизонтальную плоскость определяют по теореме косинусов
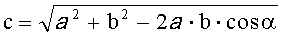
где
с - проекция отрезка АВ на горизонтальную плоскость;
а и b - проекции величин соответственно L2 и L1 на горизонтальную плоскость.
Технический результат достигается и тем, что угол φ между проекциями на горизонтальную плоскость величин L1 и АВ определяют по теореме синусов
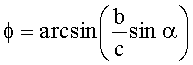
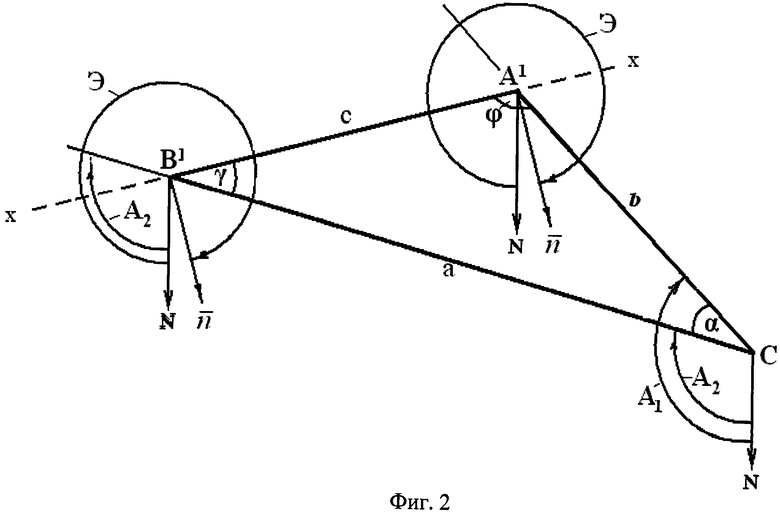
Сущность изобретения поясняется рисунками, где для случая А1>А2 представлена схема зондирования контрольной (А) и вспомогательной (В) точек на склоне (фиг.1) и проекции величин L1 L2 и АВ на горизонтальную плоскость (фиг.2).
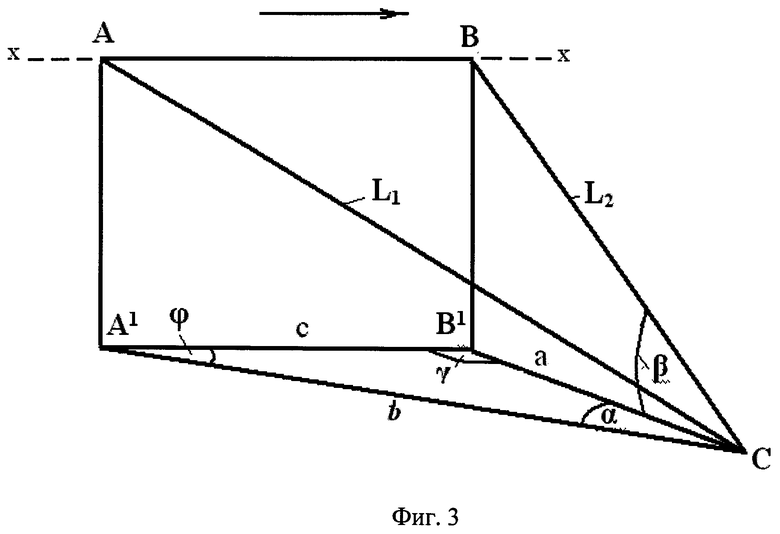
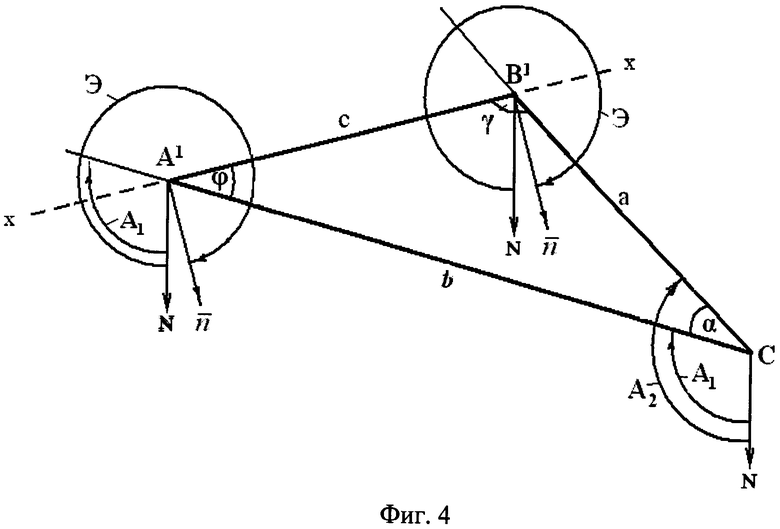
На рисунке (фиг.3) представлена аналогичная схема для случая А1<А2 и проекции величин L1, L2 и АВ на горизонтальную плоскость (фиг.4).
На рисунках приняты следующие обозначения: L1 и L2 - расстояние, измеренное лазерным дальномером соответственно до контрольной (А) и вспомогательной (В) точек на склоне. Угол зондирования (он один и тот же для рассматриваемых точек) обозначен позицией β. Величины L1, L2 и отрезок АВ, соединяющий точки «А» и «В» на склоне, образуют на рисунках треугольник ABC. Стороны данного треугольника обозначены через а, b и с, где b и а - проекции на горизонтальную плоскость соответственно величин L1 L2, а с - проекция отрезка АВ, соединяющего контрольную и вспомогательную точки на склоне. Стрелкой на рисунках (фиг.1 и фиг.3) обозначено направление перемещения зондирующего луча лазерного дальномера влево или вправо от контрольной точки при зондировании склона. Буквой «N» обозначено направление на Север. На рисунках горизонталь обозначена через «х-х». Экспозиция склона, которая согласно определению равна азимуту проекции нормали склона 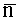
Предлагаемый способ реализуется следующим образом:
1) Предварительно в долине в точке «С», с которой хорошо просматривается контрольная точка «А» на склоне (фиг.1), устанавливается система измерений (теодолит с лазерным дальномером).
2) Затем с помощью лазерного дальномера определяют расстояние (L1) до контрольной точки «А» на склоне, азимут (А1) и угол зондирования (β).
3) После чего, сместив зондирующий луч на некоторое расстояние АВ по горизонтали влево (или вправо), определяют расстояние (L2) до произвольной вспомогательной точки (В) на склоне и азимут зондирования этой точки (А2). При этом расстояние АВ составляет ориентировочно 10-50 метров.
4) Затем определяют проекцию на горизонтальную плоскость величин L1, L2 (фиг.2) по формулам
b=L1·cosβ,
а=L2·cosβ,
где β - угол зондирования контрольной и вспомогательной точек на склоне.
5) После этого определяют угол α между проекциями на горизонтальную плоскость величин L1 и L2,
для случая А1>А2 по формуле
α=А1-A2,
а для случая А1<А2 по формуле
α=А2-А1,
где А1 и А2 - азимут зондирования контрольной (А) и вспомогательной (В) точек на склоне.
6) После этого, зная α, определяют проекцию отрезка АВ на горизонтальную плоскость по теореме косинусов
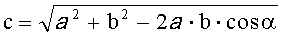
где
с - проекция отрезка АВ на горизонтальную плоскость; а и b - проекции величин соответственно L2 и L1 на горизонтальную плоскость.
7) Затем определяют угол ϕ между проекциями на горизонтальную плоскость величин L1 и АВ по теореме синусов
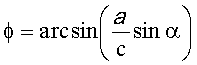
и угол γ между проекциями на горизонтальную плоскость величин L2 и АВ по формуле
φ=180-α-ϕ.
8) После этого определяют экспозицию склона в контрольной точке «А». При этом для случая А1>А2 экспозицию склона через азимут зондирования контрольной точки на склоне определяют по формуле
Э=А1+φ+90,
либо через азимут зондирования произвольной вспомогательной точки на склоне по формуле
Э=А2+270-γ,
а для случая А1<А2 экспозицию склона находят через азимут зондирования контрольной точки на склоне по формуле
Э=A1+270-φ,
либо через азимут зондирования произвольной вспомогательной точки на склоне по формуле
Э=A2+γ+90,
где
А1 - азимут зондирования контрольной точки на склоне, град.;
А2 - азимут зондирования произвольной вспомогательной точки на склоне, град.;
γ - угол между отрезками L1 и АВ в проекции на горизонтальную плоскость, град.;
φ - угол между отрезками L2 и АВ в проекции на горизонтальную плоскость, град;
90 - постоянная величина, характеризующая условие перпендикулярности нормали к отрезку АВ в проекции на горизонтальную плоскость, град.
Пример выполнения способа
В качестве примера дистанционного определения экспозиции склона в контрольной точке с использованием лазерного дальномера приведем результаты измерений, полученные в летний период при зондировании склона горы «Кизиловка», расположенного вблизи г.Нальчика. В качестве примера рассматривался случай, ограниченный условием A1>A2. Отсутствие снега на склоне при этом не играет никакой роли.
В соответствии с заявленным способом в летнее время был выбран склон на горе «Кизиловка», у основания которого была установлена система измерений (теодолит с лазерным дальномером) и выбрана контрольная точка на склоне «А».
В результате зондирования контрольной точки «А» были получены следующие результаты:
расстояние до контрольной точки L2=800 м;
азимут А1=120°;
угол зондирования β=60°.
После этого, сместив зондирующий луч на некоторое расстояние по горизонтали влево от точки «А», выбрали произвольную вспомогательную точку «В» на склоне. В результате зондирования данной точки «В» на склоне были получены следующие результаты:
расстояние до вспомогательной точки L2=805 м;
азимут A1=118°;
угол зондирования (как и в первом случае) β=60°.
Затем определили проекцию на горизонтальную плоскость величин L1 L2 по формулам
b=L1·cosβ=800·cos60=400 м,
a=L2·cosβ=805·cos60=402,5 м.
Затем нашли угол α между проекциями на горизонтальную плоскость величин L1 и L2 по формуле
α=A1-A2=120-118=2 град.
После нахождения угла α определили проекцию отрезка АВ на горизонтальную плоскость по теореме косинусов
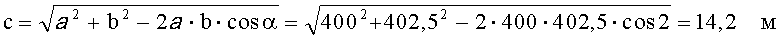
Затем нашли угол ϕ между проекциями на горизонтальную плоскость величин L1 и АВ по теореме синусов
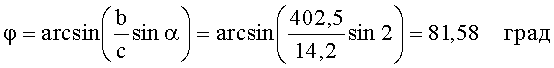
и угол γ между проекциями на горизонтальную плоскость величин L2 и АВ по формуле
γ=180-α-β=180-2-81,58=96,42 град.
После нахождения углов α и ϕ перешли к определению экспозиции склона в контрольной точке «А». По первому варианту расчета экспозицию склона «Э» нашли через азимут зондирования контрольной точки на склоне 4 по формуле
Э=А1+ϕ+90=120+81,58+90=291,58 град.,
а по второму варианту - через азимут зондирования произвольной вспомогательной точки на склоне А2 по формуле
Э=А2+270-γ=118+270-96,42=291,58 град.
По двум вариантам расчета получен один и тот же результат, что свидетельствует о правильности принципов, заложенных в основу способа.
Для случая А1<А2 расчеты производятся по соответствующим для этого случая формулам, приведенным выше.
Предлагаемый способ в отличие от известных существенно снижает трудоемкость операций и повышает точность дистанционного измерения экспозиции склона в лавинных очагах с использованием лазерного дальномера.
Источники информации
1. Сайт: 12/opredelenie-storon-sveta/#ixzz1GNEQZg4k.
2. Сайт: www.risk.ru/users/forest/9898/.
3. Бойко Е.С. Использование метода воздушной лазерной локации при оценке снегонакопления в горных условиях // Материалы VI международной конференции. «Лазерное сканирование и цифровая аэросъемка. Сегодня и завтра». - М.: 2006. С.29-30 - ПРОТОТИП.
| название | год | авторы | номер документа |
|---|---|---|---|
| СПОСОБ ДИСТАНЦИОННОГО ОПРЕДЕЛЕНИЯ ЭКСПОЗИЦИИ СКЛОНА В КОНТРОЛЬНЫХ ТОЧКАХ ЛАВИННОГО ОЧАГА С ИСПОЛЬЗОВАНИЕМ ЛАЗЕРНОГО ДАЛЬНОМЕРА | 2012 |
|
RU2515098C1 |
| СПОСОБ ДИСТАНЦИОННОГО ОПРЕДЕЛЕНИЯ КРУТИЗНЫ СКЛОНА В КОНТРОЛЬНЫХ ТОЧКАХ ЛАВИННОГО ОЧАГА С ИСПОЛЬЗОВАНИЕМ ЛАЗЕРНОГО ДАЛЬНОМЕРА | 2012 |
|
RU2509288C1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ ТОЛЩИНЫ СНЕЖНОГО ПОКРОВА В ЛАВИННЫХ ОЧАГАХ | 2013 |
|
RU2547000C1 |
| Оперативный способ определения угла наклона опор контактной сети железных дорог | 2024 |
|
RU2831589C1 |
| СПОСОБ ДИСТАНЦИОННОГО ОПРЕДЕЛЕНИЯ ТОЛЩИНЫ СНЕЖНОГО ПОКРОВА В ЛАВИННЫХ ОЧАГАХ | 2011 |
|
RU2454651C1 |
| УСТРОЙСТВО ДЛЯ ПРЕДУПРЕЖДЕНИЯ СТОЛКНОВЕНИЙ ПОЕЗДОВ | 1925 |
|
SU4525A1 |
| СПОСОБ БЕСКОНТАКТНОГО ИЗМЕРЕНИЯ ТОЛЩИНЫ ОБЪЕКТА | 1990 |
|
SU1826697A1 |
| СПОСОБ КОНТРОЛЯ ПАРАМЕТРОВ ТРУБЫ ПРИ МНОГОКОЛЕННОЙ ГИБКЕ | 1991 |
|
RU2025167C1 |
| РАЗНОСТНО-ДАЛЬНОМЕРНЫЙ СПОСОБ ПЕЛЕНГОВАНИЯ ИСТОЧНИКА РАДИОИЗЛУЧЕНИЯ | 2006 |
|
RU2325666C2 |
| СПОСОБ ОПРЕДЕЛЕНИЯ УГЛОВ НАКЛОНА БЛОКА ИНЕРЦИАЛЬНЫХ ИЗМЕРИТЕЛЕЙ КОМПЛЕКСНОЙ СИСТЕМЫ УГЛОВОЙ ОРИЕНТАЦИИ ОТНОСИТЕЛЬНО ПЛОСКОСТИ ГОРИЗОНТА | 2016 |
|
RU2646941C1 |
Изобретение относится к области метеорологии и гляциологии и может быть использовано при определении толщины снежного покрова на склонах для прогноза лавинной опасности и определения снегонакопления в горах.
Согласно заявленному способу с помощью лазерного дальномера, размещенного в долине, определяют расстояние до контрольной точки на склоне (L1), азимут (А1) и угол зондирования (β). Затем, сместив зондирующий луч на некоторое расстояние АВ по горизонтали влево или вправо, определяют расстояние (L2) до произвольной вспомогательной точки на склоне и азимут зондирования этой точки (А2). После этого из проекции на горизонтальную плоскость величин L1, L2 и АВ, образующих треугольник с соответствующими им сторонами b, а и с, определяют угол α между проекциями отрезков L1 и L2 на горизонтальную плоскость и по данному углу и проекциям сторон L1 и L2 находят истинное значение проекции АВ и углы φ и γ, образованные соответственно на стыке проекций отрезков L1 и L2 с проекцией отрезка АВ. Затем определяют экспозицию склона через азимут зондирования контрольной точки на склоне, либо через азимут зондирования произвольной вспомогательной точки на склоне или через азимут зондирования произвольной вспомогательной точки на склоне. Технический результат - повышение точности дистанционного измерения экспозиции склона. 4 з.п. ф-лы, 4 ил.
1. Способ дистанционного определения экспозиции склона в контрольных точках лавинного очага с использованием лазерного дальномера, отличающийся тем, что предварительно с помощью лазерного дальномера, размещенного в долине, определяют расстояние до контрольной точки на склоне (L1), азимут (А1) и угол зондирования (β), затем, сместив зондирующий луч на некоторое расстояние АВ по горизонтали влево или вправо, определяют расстояние (L2) до произвольной вспомогательной точки на склоне и азимут зондирования этой точки (А2), затем из проекции на горизонтальную плоскость величин L1, L2 и АВ, образующих треугольник, определяют угол α между проекциями отрезков L1 и L2 на горизонтальную плоскость и по данному углу находят истинное значение проекции отрезка АВ и углы φ и γ, образованные соответственно на стыке проекций отрезков L1 и L2 с проекцией отрезка АВ, после этого для случая А1>А2 определяют экспозицию склона через азимут зондирования контрольной точки на склоне (Эк) по формуле
Э=А1+φ+90,
либо через азимут зондирования произвольной вспомогательной точки на склоне по формуле
Э=А2+270-γ,
а для случая А1<А2 экспозицию склона находят через азимут зондирования контрольной точки на склоне по формуле
Э=А1+270-γ,
либо через азимут зондирования произвольной вспомогательной точки на склоне по формуле
где
А1 - азимут зондирования контрольной точки на склоне, град.;
А2 - азимут зондирования произвольной вспомогательной точки на склоне, град.;
φ - угол между отрезками L1 и АВ в проекции на горизонтальную плоскость, град.;
γ - угол между отрезками L2 и АВ в проекции на горизонтальную плоскость, град.;
90 - постоянная величина, характеризующая условие перпендикулярности нормали к отрезку АВ в проекции на горизонтальную плоскость, град.
2. Способ дистанционного определения экспозиции склона в контрольных точках лавинного очага по п.1, отличающийся тем, что проекцию L1 на горизонтальную плоскость (b) определяют по формуле
b=L1·cosβ,
а проекцию L2 на горизонтальную плоскость (а) определяют по формуле
а=L2·cosβ,
где β - угол зондирования контрольной и вспомогательной точек на склоне.
3. Способ дистанционного определения экспозиции склона в контрольных точках лавинного очага по п.1, отличающийся тем, что угол α между проекциями на горизонтальную плоскость величин L1 и L2 находят:
для случая А1>А2 по формуле
α=А1-А2,
а для случая А1<А2 по формуле
α=A2-A1.
4. Способ дистанционного определения экспозиции склона в контрольных точках лавинного очага по п.1, отличающийся тем, что проекцию отрезка АВ на горизонтальную плоскость определяют по теореме косинусов
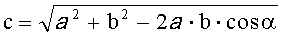
где
с - проекция отрезка АВ на горизонтальную плоскость;
а и b - проекции величин соответственно L2 и L1 на горизонтальную плоскость.
5. Способ дистанционного определения экспозиции склона в контрольных точках лавинного очага по п.1, отличающийся тем, что угол β между проекциями на горизонтальную плоскость величин L1 и АВ определяют по теореме синусов
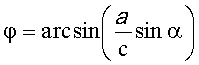
| ПОГОРЕЛОВ А.В., БОЙКО Е.С., РИЗАЕВ И.Г., "Применение воздушного лазерного сканирования для моделирования поля снежного покрова на горных склонах", журнал "ПРОСТРАНСТВЕННЫЕ ДАННЫЕ", 2007 г., N4, стр.34-38 | |||
| БОЙКО Е.С., ПОГОРЕЛОВ А.В., "Оперативная оценка снегонакопления по данным воздушного лазерного сканирования", электронный журнал " ГЕОПРОФИ", |
Авторы
Даты
2014-05-10—Публикация
2012-10-08—Подача