Изобретение относится к области силовой лазерной оптики и может быть использовано для детальной характеристики качества оптических поверхностей при проектировании и изготовлении мощных лазерных систем.
При облучении поверхности оптической детали пучком мощного лазерного излучения, интенсивность которого превосходит порог лучевой прочности, происходят разрушения оптической поверхности, возникающие на месте расположения поглощающих включений различной природы. Экспериментально наблюдаемые в единичной вспышке лазера разрушения зависят от размера, количества и физической природы случайным образом распределенных по поверхности включений, попавших в зону облучения. Как правило, чем больше размер включения, тем меньшая мощность излучения требуется для того, чтобы вызвать разрушение поверхности. Однако возникновение единственного или нескольких единичных разрушений на поверхности не всегда катастрофическим образом сказывается на эксплуатационных свойствах оптической детали или прибора, содержащего эту деталь. Поэтому наряду с лучевой прочностью важной характеристикой качества оптической поверхности является плотность дефектов поверхности детали. Наличие дефектов способствует быстрому разрушению поверхности под действием импульсного лазерного излучения. В общем случае под дефектами мы подразумеваем нарушающие оптическую однородность поверхности детали случайно распределенные микроскопические локальные поглощающие области (включения, примеси) в граничном приповерхностном слое оптического материала, из которого изготовлена деталь. Плотность же дефектов поверхности оптической детали D характеризуется поверхностной плотностью всего ансамбля дефектов, приводящих к разрушению поверхности при облучении пучком импульсного лазерного излучения.
Известен способ определения плотности дефектов поверхности оптической детали, приводящих к разрушению поверхности под действием импульсного лазерного излучения, изложенный в [Laurent Lamaignere, Stephane Reyne, Therry Donval at all, Review of Scientific Instruments, 78, 103105.1-103105.9, 2007]. При выполнении способа различные участки поверхности оптической детали облучают пучком импульсного лазерного излучения, имеющим гауссово распределение интенсивности в пятне облучения. Определяют величину максимальной интенсивности излучения в пятне облучения ε0 (здесь и далее эта величина представляет собой значение осевой интенсивности пучка в точке пересечения оси пучка с плоскостью пятна облучения), радиус пучка r0 по уровню ехр(-1) от ε0 и так называемую «эквивалентную» площадь пучка 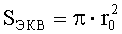
При возникновении разрушения поверхности в пятне облучения с интенсивностью ε0 его регистрируют, находят отношение числа облучений, в которых было зарегистрировано разрушение поверхности, к полному числу облучений. Разделив эту величину на SЭКВ, получают экспериментальную оценку вероятности разрушений j(ε0), приведенной к единице площади поверхности, при облучении пучком с интенсивностью ε0.
В известном способе используется следующее соотношение (получено авторами), связывающее распределение плотности дефектов D(ε0) по значениям интенсивности ε0 пучка с экспериментальной оценкой вероятности разрушений j(ε0), приведенной на единицу площади поверхности,
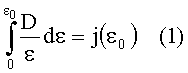
Дифференцируя обе части этого интегрального уравнения по переменной ε0, авторы приходят к уравнению:
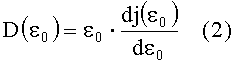
Авторами были проведены серии облучений оптической поверхности пучками лазерного излучения с различными значениями ε0k, получен статистический набор данных по j(ε0k) и построена зависимость вероятности разрушений, приведенная к единице площади поверхности детали, от максимальной интенсивности пучка в пятне облучения ε0k. Полученная экспериментально статистическая зависимость j(ε0) имеет разрывной характер и не является дифференцируемой. Чтобы ее можно было использовать для нахождения D(εθ) из соотношения (2), авторы аппроксимировали j(ε-0) гладкой степенной функцией вида J(ε)=α·εβ, где α и β - параметры подгонки. С использованием выбранной аппроксимирующей функции J(ε) выражение для определения D приобретает следующий вид:
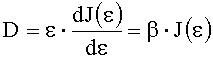
К причинам, препятствующим достижению указанного ниже технического результата при использовании известного способа, относятся следующие.
В способе величину D определяют косвенным путем. Для определения плотности дефектов необходимо осуществлять процедуру дифференцирования функции вероятности разрушений j(ε0), приведенной к единице площади поверхности, определенной экспериментально со значительными статистическими погрешностями. Такая процедура представляет собой типичную математически некорректную обратную задачу статистики. Как показано во многих работах, см., например, [А.А.Маненков, A.M.Прохоров. УФН, 1986, т.148 вып.1, с.179-211; М.Ф.Колдунов, М.Ф.Романов, Д.А.Филимонов. ДАН СССР, 1986, т.289, с.856-859], решение такой задачи применительно к статистике лазерного разрушения в общем случае неустойчиво, оно может не существовать, быть неоднозначным или даже нефизичным. Значительные погрешности возникают как на этапе выбора самой функциональной зависимости J(ε)=α·εβ, так и при последующей подгонке значений параметров α и β под экспериментальные данные. В результате оцененный в работе авторов дисперсионный разброс исходных экспериментальных данных оказывается сравним по амплитуде с рассчитанной величиной плотности дефектов поверхности.
Наиболее близким способом того же назначения к заявленному изобретению по совокупности признаков является способ определения плотности дефектов поверхности оптической детали, приводящих к разрушению поверхности под действием импульсного лазерного излучения, изложенный в [J.O. Porteus and Steven С.Seitel, Applied Optics / 1984., Vol.23, No.21, p.p.3796-3804], принятый за прототип. Способ включает облучение различных участков поверхности пучком импульсного лазерного излучения, имеющим гауссово распределение интенсивности в пятне облучения, определение величины максимальной интенсивности излучения в пятне облучения ε0 и радиуса пучка r0 по уровню ехр(-1) от ε0. При реализации способа проводят серии облучений оптической поверхности пучками лазерного излучения с различными значениями ε0. В каждой группе из Z(ε0k) облучений, отвечающих некоторому значению максимальной интенсивности ε0k, подсчитывают число облучений z(ε0k), в которых произошло разрушение поверхности оптической детали, и определяют вероятности разрушений p(ε0k)=z(ε0k)/Z(ε0k). По полученным значениям p(ε0k) находят экспериментальное статистическое распределение вероятности разрушения PЭКСП(ε0k).
Вводят теоретическое соотношение, связывающее плотность дефектов с вероятностью разрушения поверхности гауссовым лазерным пучком:
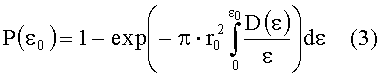
Уравнение (3) относительно неизвестной величины D(ε), как и в случае рассмотренного выше аналога, приводит к необходимости решать некорректную обратную задачу статистики, включающую процедуру дифференцирования статистической функции распределения вероятности разрушения поверхности PЭКСП(ε0), определенной экспериментально со значительными статистическими погрешностями и имеющей разрывной (ступенчатый) характер. Для решения этой некорректной задачи авторы моделируют плотность дефектов D(ε) распределением в виде 2-х или 3-х параметрической зависимости от ε, выраженной интегралом:
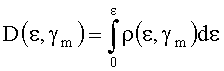
где функция ρ(ε,γm) включает в себя соответствующий набор подгоночных параметров γm. Например, для простейшей 2-х параметрической модели, описывающей «вырожденное» распределение, когда все дефекты характеризуются одним значением интенсивности пучка εt, инициирующим разрушение поверхности, функция имеет вид ρ(ε)=D0·d(ε-εt), где d(…) - дельта-функция, γ1=D0 - плотность дефектов; γ2=εt.
Поскольку распределение плотности дефектов, описываемое такой упрощенной моделью, практически не встречается на практике, авторы переходят к модели, которая описывает распределение плотности дефектов по интенсивности в виде непрерывной степенной функции и содержит 3 подгоночных параметра: γi=D1 - интегральная плотность всех дефектов, имеющих пороги разрушения ε≤εmax, где εmax - верхний предел диапазона интенсивностей, в котором проводятся измерения; γ2=q - показатель степени функции распределения плотности дефектов; γ3=ε't - нижний предел диапазона измерений (считают, что нет дефектов с порогом разрушения ε<ε't).
Методом наименьших квадратов осуществляют выбор значений параметров подгонки, добиваясь наибольшего сходства экспериментальной зависимости PЭКСП(ε) и той или иной описанной выше модели P(ε). При этом находят и значения плотностей дефектов D0 или D1, также являющихся параметрами подгонки.
К причинам, препятствующим достижению указанного ниже технического результата при использовании известного способа, принятого за прототип, относятся следующие.
Как и в способе-аналоге, величины D0 или D1 определяют косвенным путем, используя сложные, громоздкие соотношения и трудоемкие процедуры поиска подгоночных параметров, добиваясь наибольшего сходства экспериментальной и теоретической моделей. Используемое теоретическое соотношение (3), связывающее в прототипе распределение вероятности разрушений P(ε) и искомую плотность дефектов D, имеет вид, приводящий к необходимости решать математически некорректную обратную задачу статистики. Как указывалось выше, решение такой задачи обращения в общем случае неустойчиво, может не существовать, быть неоднозначным или даже нефизичным. В способе-прототипе оценку D получают путем подгонки параметров выбранной аналитической модели для распределения плотности дефектов при сравнении экспериментальной зависимости PЭКСП(ε) и расчетно - теоретической P(ε). При таком подходе в выборе значений параметров подгонки, если их несколько, может быть допущен большой произвол, поскольку изменение величины одного из них, например значения плотности дефектов D, легко скомпенсировать вариациями значений других параметров, не меняя при этом значения вычисляемого интеграла в уравнении (3). Это и происходит при применении способа-прототипа. Обе использованные разные модели подходят для аппроксимации экспериментальных данных с учетом дисперсионного разброса последних, однако определяемая по ним плотность дефектов оказывается существенно различной.
В совокупности реализация способа-прототипа не позволяет получить достаточно точную оценку искомой плотности дефектов, что типично для решений подобных некорректных задач.
Сущность изобретения заключается в следующем.
Задачей изобретения является определение плотности дефектов поверхности оптической детали, приводящих к разрушению поверхности под действием импульсного лазерного излучения, с высокой точностью, простотой и надежностью.
Технический результат, который может быть достигнут при осуществлении заявленного способа, заключается в определении плотности дефектов оптической поверхности, приводящих к ее разрушению под действием импульсного лазерного излучения, прямым методом и с высокой точностью. Способ отличается существенно меньшей трудоемкостью, простотой реализации и надежностью.
Указанный технический результат при осуществлении изобретения достигается тем, что в способе определения плотности дефектов поверхности оптической детали, включающем облучение разных участков поверхности оптической детали пучком импульсного лазерного излучения с гауссовым распределением интенсивности, определение максимальной интенсивности ε0 пучка импульсного лазерного излучения и радиуса r0 пучка по уровню ехр(-1) от ε0 в пятне облучения, регистрацию разрушения поверхности в пятне облучения, определение плотности дефектов поверхности, в соответствии с заявляемым техническим решением регистрируют разрушение поверхности, наиболее удаленное от точки максимальной интенсивности ε0 пучка импульсного лазерного излучения в пятне облучения, определяют соответствующее этому разрушению значение интенсивности εi пучка в пятне облучения, получают статистически представительную выборку значений εi, где i=1,…N; N - количество облучений детали, равное размеру статистической выборки, определяют экспериментальную зависимость плотности вероятности f(ε) разрушения поверхности оптической детали от интенсивности излучения ε, выбирают наименьшее значение εi min из полученных по всей выборке N значений εi, плотность дефектов поверхности оптической детали D определяют по формуле:
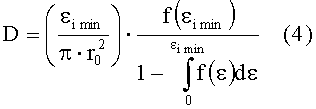
Если экспериментальную зависимость плотности вероятности f(ε) разрушения поверхности оптической детали от интенсивности излучения ε в пятне облучения аппроксимируют аналитической функцией:
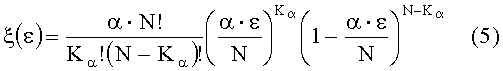
где α - параметр подгонки;
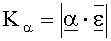
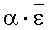
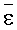
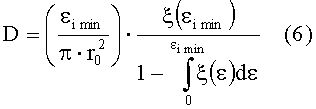
Совокупность вышеизложенных признаков изобретения связана причинно-следственной связью с техническим результатом изобретения.
Известно, что для гауссова пучка линии равной интенсивности представляют собой окружности в плоскости, перпендикулярной направлению распространения излучения, с радиусом r, значение интенсивности пучка ε(r) в каждой точке окружности удовлетворяет соотношению
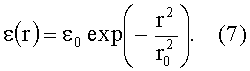
Такие линии равной интенсивности будем далее называть изолиниями интенсивности. Определяя в эксперименте максимальную интенсивность ε0 пучка импульсного лазерного излучения в пятне облучения, радиус пучка по уровню ехр(-1) от ε0 и расстояние r от центра гауссова пучка до точки разрушения в пятне облучения, мы можем рассчитать значение интенсивности ε(r) на любом расстоянии (радиусе) r от центра гауссова пучка (на любой изолинии).
Значение интенсивности пучка, соответствующее разрушению поверхности, наиболее удаленному от точки максимальной интенсивности ε0 пучка в пятне облучения, определяет изолинию интенсивности, разграничивающую разрушенный и неповрежденный участки поверхности в пятне облучения. При реализации способа различные участки поверхности оптической детали подвергают облучению, далее в каждом пятне облучения регистрируют разрушение поверхности, наиболее удаленное от точки максимальной интенсивности ε0 пучка, определяют значение интенсивности εi пучка в пятне облучения, соответствующее этому разрушению.
Получив статистически представительную выборку* значений εi, где i=1,…,N; N -количество облучений детали, равное размеру статистической выборки, строят экспериментальную зависимость плотности вероятности разрушений поверхности f(ε) на основе прямых измерений (*Подходы к определению размера статистически представительной выборки, т.е. определения числа экспериментальных значений случайной величины, необходимые для того, чтобы с удовлетворительной точностью получить распределение плотности вероятности случайной величины, известны [Е.С.Вентцель, Л.А.Овчаров. Теория вероятностей и ее приложения. // М.: Наука, 1988. -480 с.]).
В результате мы избегаем как необходимости дифференцирования статистической функции распределения вероятности разрушения поверхности, определяемой экспериментально со значительными статистическими погрешностями (как в способе-аналоге), так и необходимости использования неоднозначно определенных приближенных параметрических моделей (как в способе-прототипе). Исключение как некорректных, так и трудоемких, дающих неоднозначные результаты математических процедур из последовательности действий по определению плотности дефектов поверхности приводит к существенному повышению точности определения искомой величины и значительно упрощает реализацию способа.
При реализации способа среди N зарегистрированных значений интенсивности εi выбирают наименьшее значение εimin. Ни на одном из участков поверхности детали, облученном с интенсивностью меньшей этого значения, разрушений не появилось. С точки зрения оценки качества поверхности оптической детали наибольший интерес представляет то минимальное количество дефектов, при наличии которого уже будет осуществляться разрушение поверхности при облучении ее лазерным пучком. Если теперь определить плотность дефектов D, приводящих к разрушению поверхности при облучении ее именно на этом уровне интенсивности Simin, то это даст точную и достоверную оценку качества тестируемой оптической детали по плотности дефектов, позволит сравнивать детали, принадлежащие разным партиям продукции или изготовленные по разным технологиям.
Искомую плотность дефектов поверхности оптической детали D определяют, используя введенное нами соотношение (4), связывающее экспериментальное распределение плотности вероятности f(ε) разрушения поверхности и величину D. В основе вывода соотношения (4) лежит следующий подход.
Пусть точка М характеризует наиболее удаленное разрушение от точки максимума интенсивности в конкретном пятне облучения. Построим рядом с точкой разрушения М две изолинии интенсивности на расстояниях r1 и r2 от точки максимума интенсивности (центра гауссова пучка) в пятне облучения, ограничивающие узкое кольцо, внутри которого возникло это разрушение. Отвечающие изолиниям значения интенсивности определим из условий: ε1=ε-δε/2 и ε2=ε+δε/2, δε<<ε. В случае гауссова распределения интенсивности в пучке можно показать, что при условии δε→0 элементарная площадь кольца равна 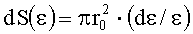
Разрушения внутри выделенной области происходят, когда на площади dS(ε) случайно оказываются дефекты, приводящие к разрушению поверхности под действием значений интенсивности облучающего пучка ε. Поскольку мы рассматриваем наиболее удаленное разрушение от точки максимума интенсивности в пятне облучения, то одновременно с попаданием соответствующих дефектов внутрь выделенной кольцевой зоны снаружи этой зоны не должны присутствовать дефекты, приводящие к разрушению поверхности. Эти два события независимы. Первое событие происходит с вероятностью D(ε)·dS(ε), поскольку попадание дефектов в пятно облучения можно рассматривать как пуассоновское поле событий. Второе же событие определяется вероятностью отсутствия разрушений снаружи выделенного кольца (1-Р(ε)), где p(ε) - вероятность появления хотя бы одного разрушения в этой области пятна облучения. Из этого следует, что элементарная вероятность dP(ε) появления разрушений внутри выделенного нами кольца есть:
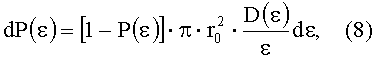
Учитывая, что 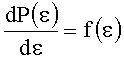
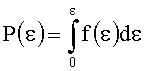
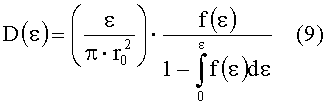
Как указывалось выше плотность дефектов D, приводящих к разрушению поверхности, мы определяем при облучении ее на уровне интенсивности εimin. Выбирая наименьшее значение εimin из полученных по всей выборке N значений εi и подставляя его в соотношение (9), мы получаем выражение (4) для определения поверхностной плотности дефектов D.
Соотношение (9) носит универсальный характер. В случае необходимости оценки поверхностной плотности ансамбля дефектов, приводящих к разрушению поверхности под действием импульсного лазерного излучения с интересующим пользователя значением интенсивности εi - это значение εi выбирают из полученных по всей выборке N значений, искомую величину D определяют по формуле (9), подставляя в нее значение εi.
Как видим, заявляемый способ достаточно прост. Математическое выражение для определения плотности дефектов D поверхности оптической детали включает минимальное число экспериментально измеряемых параметров. Величина D определяется из экспериментальных данных прямым методом, без необходимости решения математически некорректной обратной задачи путем дифференцирования статистических функций и осуществления трудоемких математических процедур, далеко не всегда дающих однозначные результаты. Получаемый результат не зависит от небольших вариаций энергии лазера, каждое пятно облучения используется для получения информации. Совокупное действие всех признаков изобретения позволяет определить плотность дефектов D поверхности оптической детали прямым путем, по сравнению с аналогом и прототипом с большей точностью, надежностью и меньшей трудоемкостью.
Если экспериментальную зависимость плотности вероятности f(ε) разрушения поверхности оптической детали от интенсивности излучения ε в пятне облучения аппроксимировать аналитической функцией (5):
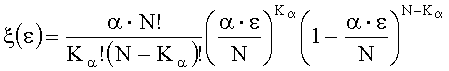
где α - параметр подгонки;
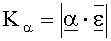
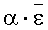
где 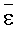
а плотность дефектов поверхности оптической детали определить по формуле (6):
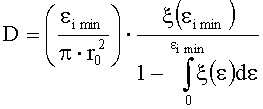
то выполнение этих операций способа позволяет достичь усиления технического результата - повысить точность и достоверность определения плотности дефектов поверхности оптической детали за счет устранения влияния случайных флуктуаций экспериментально регистрируемых статистических данных на точность определения зависимости f(ε).
На фиг.1 представлено зарегистрированное ПЗС-камерой изображение зоны разрушений поверхности оптической детали, полученное при облучении детали гауссовым пучком лазерного излучения, радиус пучка r0 по уровню ехр(-1) от ε0 составлял 0,2 мм. Центральная точка зоны O (центр гауссова пучка) является точкой максимальной интенсивности в пятне облучения. Точкой М отмечено разрушение, наиболее удаленное от точки максимальной интенсивности в пятне облучения; r - расстояние от центра гауссова пучка до точки разрушения окружности - линии, равной интенсивности с радиусами r1 и r2, выделяющие кольцевую зону, включающую разрушение.
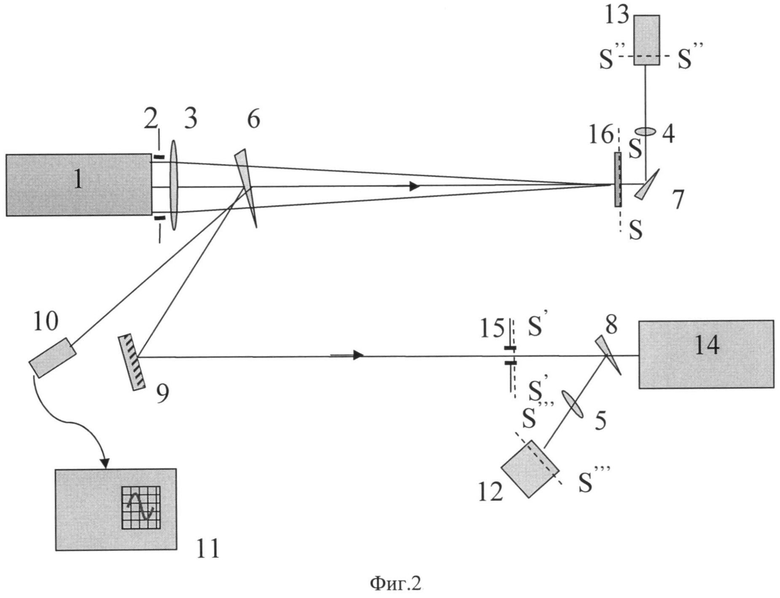
На фиг.2 приведена схема экспериментальной установки для измерения плотности дефектов поверхности оптической детали, где 1 - лазер, 2, 15 - диафрагмы, 3, 4, 5 - линзы, 6, 7, 8 - клинья, 9 - зеркало, 10 - фотодиод, 11 - осциллограф, 12,13 - ПЗС-камеры, 14 - калориметр, 16 - измеряемая деталь, S-S - плоскость, проходящая через заднюю (по ходу лазерного луча) поверхность оптической детали, S'-S',S”-S”,S'''-S''' - плоскости диафрагмы 15 и ПЗС - камер 13 и 12 соответственно, оптически сопряженные с плоскостью S-S.
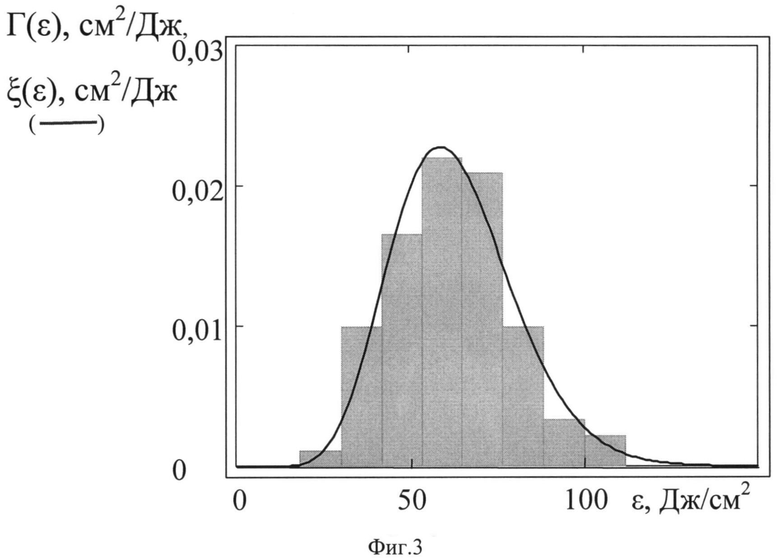
На фиг.3 приведена экспериментальная зависимость плотности вероятности разрушения поверхности оптической детали от интенсивности излучения е, полученная в виде гистограммы f(ε)=Г(ε) при облучении поверхности оптической детали гауссовым пучком лазерного излучения радиусом r0=0,2 мм. Сплошной линией представлена найденная аппроксимирующая функция плотности вероятности ξ(ε).
Заявленный способ был экспериментально осуществлен для измерения плотности дефектов поверхности оптической детали, представляющей собой плоскопараллельную пластину из стекла КГСС-0180.
Лазер 1 (фиг.2) генерирует моноимпульс длительностью τ=4,5 не по полувысоте и энергией до 1 Дж. Длина волны излучения 1,054 мкм. Пятно облучения с гауссовым распределением интенсивности формировалось с помощью соответствующего выбора диафрагмы 2 и фокусирующей линзы 3. Радиус пятна облучения r0 составлял 0,2 мм по уровню ехр(-1) от уровня максимальной интенсивности в пятне облучения на поверхности оптической детали. Энергия импульса излучения подбиралась таким образом, чтобы во всех вспышках лазера регистрировалось появление разрушения поверхности. Клинья 6,7 и зеркало 9 отводят часть излучения на фотодиод 10, калориметр 14 и ПЗС-камеры 12 и 13. Плоскость S''' ПЗС-камеры 12 с помощью линзы 5 оптически сопряжена с плоскостью S' диафрагмы 15, которая, в свою очередь, с помощью клина 6 является оптически сопряженной с плоскостью S задней поверхности тестируемой детали. Диаметр диафрагмы 15 выбирался немного больше размера пятна облучения. Изображение пятна облучения и диафрагмы 15, полученное ПЗС-камерой 12, и показания калориметра 14 использовались для вычисления максимального значения интенсивности (в нашем случае в качестве меры интенсивности мы используем плотность энергии) ε0 в пятне облучения по формуле:
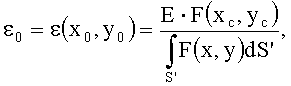
где
Е - энергия импульса лазерного излучения, зарегистрированная калориметром 14; F(x, y) - распределение уровней яркости в изображении пучка, облучающего поверхность оптической детали, полученное ПЗС-камерой 12, (x, y) - координаты пикселей ПЗС-камеры 12, (xc, yc) - координаты максимума распределения F(x, y), найденные путем сравнения уровней яркости в разных точках изображения пучка. Интегрирование в знаменателе уравнения осуществляется по площади диафрагмы 15. Перед проведением экспериментов определялся радиус пятна облучения путем определения координат пикселей (xe, ye) в изображении пучка с уровнем яркости F(xe,ye)=exp(-1)·F(xc,yc) и последующего вычисления значения 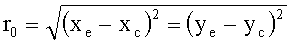
Контроль временных характеристик моноимпульса лазера осуществлялся с помощью фотодиода 10 и осциллографа 11. Плоскость ПЗС-камеры 13 с помощью клина 7 и линзы 4 оптически сопряжена с плоскостью задней поверхности тестируемой детали; ПЗС-камера 13 предназначена для регистрации в момент облучения распределения интенсивности в пятне облучения с наложенным на него изображением разрушения. Путем сопоставления полученного изображения разрушения поверхности и распределения интенсивности в облучающем пучке, зарегистрированных ПЗС-камерой 13, определяются координаты максимума интенсивности на картине разрушений (x0, y0).
Пример зарегистрированного разрушения приведен на фиг.1. Зная координаты максимума интенсивности в пятне облучения и определив координаты наиболее удаленного от точки максимума разрушения (x, y), находим соответствующее этому разрушению значение интенсивности пучка в пятне облучения в точке М по формуле 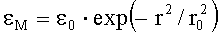
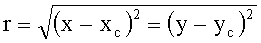
В результате многократного облучения различных участков поверхности оптической детали была получена выборка из 120 значений интенсивности для разрушений, наиболее удаленных от точки максимальной интенсивности ε0 пучка в пятне облучения для пучка радиусом r0=0,2 мм по уровню exp(-1) от ε0. Далее строилась экспериментальная зависимость плотности вероятности разрушения поверхности оптической детали от интенсивности излучения f(ε). Она была получена в нашем случае в виде гистограммы f(ε)=Г(ε).
Способ построения гистограммы традиционен (см., например, [Е.С.Вентцель, Л.А.Овчаров. Теория вероятностей и ее приложения. // М. Наука, - 1988. - 480 с.]). Полученный массив данных из N=120 значений интенсивности группировали по T разрядам значений Δεt, где T - количество разрядов, выбранное для группирования данных, t=1,…T - номер разряда. В нашем случае было выбрано значение T=8, ширина интервала была одинаковой для всех разрядов и равна Δεt=Δε=(εimax-εimin)/T, где εimax и εimin - наибольшее и наименьшее из значений εi интенсивности пучка, измеряемые в эксперименте для разрушений, наиболее удаленных от точки максимальной интенсивности εO пучка, во всех N облучениях. В каждом t-м разряде Δεt подсчитывали число попавших в него облучений nt, определяли случайную величину nt/N и строили гистограмму Г(ε) из значений (nt/N·Δε), которая по определению является экспериментальной или статистической оценкой функции распределения плотности вероятности разрушений поверхности. Полученная таким образом гистограмма Г(ε) приведена на фиг.3
Далее из полученных по всей выборке N значений εi было выбрано наименьшее значение εimin, которое составило 18 Дж/см2. Плотность дефектов поверхности оптической детали D определяли по формуле (4) с учетом того, что в этом случае f(εimin)=Г(εimin) и 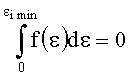
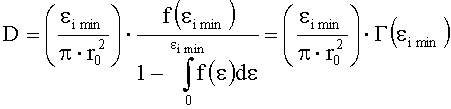
Найденная таким образом поверхностная плотность дефектов равна D≈19 см-2. Важно отметить, что такая процедура вычислений D не включает в себя математически некорректных операций.
Возможен вариант реализации способа, когда для вычисления плотности дефектов осуществляют аналитическую аппроксимацию экспериментально полученной функции плотности вероятности f(ε) разрушения поверхности оптической детали от интенсивности излучения ε, а искомую величину D определяют путем подстановки найденной аналитической функции плотности в соотношении (4) вместо f(ε). При этом достоверность и точность измерений D будет повышена за счет устранения влияния на результат случайных флуктуации, присущих экспериментальной гистограмме.
Сравнительный анализ различных вариантов аппроксимации гистограммы позволил найти функцию, не только демонстрирующую сходство с экспериментом по первым двум моментам статистического распределения, но и требующую подгонки всего лишь по одному параметру. Эта функция плотности вероятности, родственная биномиальному распределению, но не совпадающая с ним, имеет вид:
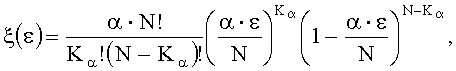
где α - параметр подгонки;
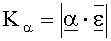
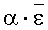
где 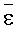
Определенное для описываемого эксперимента значение коэффициента α, минимизирующее расхождение аппроксимирующей функции с данными эксперимента в виде гистограммы, составило α=0,156 см2/Дж.
На фиг.3 сплошной линией представлена найденная аппроксимирующая функция плотности вероятности ξ(ε). Видно, что расхождение аппроксимирующей функции с данными эксперимента относительно невелико. Расчет с использованием ξ(ε) по формуле (6) дал искомое значение плотности D=17 см-2.
Нами были проведены количественные оценки точности измерений плотности дефектов поверхности по заявляемому способу.
Анализ точности полученного результата с учетом влияния основных факторов эксперимента (наиболее важными из которых являются погрешность калориметра, шум ПЗС-матрицы, погрешность определения радиуса пучка) на точность определения искомой величины D дает оценку относительной погрешности на уровне 15%.
Практическая ценность заявляемого способа заключается в том, что он существенно повышает точность измерений плотности дефектов. Это важно для получения более достоверных исходных данных, используемых при расчетно-теоретической имитации условий эксплуатации оптических элементов в мощных лазерных установках с целью определения их срока службы. Кроме того, этот метод расширяет возможности для контроля качества оптических элементов в процессе производства. Высокая точность измерений позволяет выборочно регистрировать отклонения концентрации дефектов от типичных значений в элементах, принадлежащих разным партиям продукции или изготовленным по разной технологии, и осуществлять при необходимости корректировку процесса их изготовления.
| название | год | авторы | номер документа |
|---|---|---|---|
| СПОСОБ ОПРЕДЕЛЕНИЯ ЛУЧЕВОЙ ПРОЧНОСТИ ПОВЕРХНОСТИ ОПТИЧЕСКОЙ ДЕТАЛИ | 2010 |
|
RU2430352C1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ ОПТИЧЕСКОЙ ПРОЧНОСТИ МАТЕРИАЛОВ ПРИ ОДНОКРАТНОМ ОБЛУЧЕНИИ | 2018 |
|
RU2694073C1 |
| Способ определения радиуса эффективного пятна облучения | 1989 |
|
SU1685146A1 |
| ПРИЕМНИК-ПРЕОБРАЗОВАТЕЛЬ КОНЦЕНТРИРОВАННОГО ЭЛЕКТРОМАГНИТНОГО ИЗЛУЧЕНИЯ | 2012 |
|
RU2499327C1 |
| СПОСОБ ОБРАБОТКИ ИНФОРМАЦИИ В ЛАЗЕРНОМ КОГЕРЕНТНОМ ЛОКАТОРЕ С МАТРИЧНЫМ ФОТОПРИЕМНИКОМ | 2007 |
|
RU2354994C1 |
| СПОСОБ ФОРМИРОВАНИЯ РАСПРЕДЕЛЕНИЯ ИНВЕРСИИ В АКТИВНОМ ЭЛЕМЕНТЕ ТВЕРДОТЕЛЬНОГО ЛАЗЕРА | 1994 |
|
RU2086058C1 |
| Приёмник-преобразователь лазерного излучения | 2016 |
|
RU2639738C2 |
| СПОСОБ ИЗМЕРЕНИЯ ПЛОТНОСТИ КВАЗИОДНОРОДНОГО ПУЧКА ИЗЛУЧАЕМЫХ ЧАСТИЦ, ЗАРЕГИСТРИРОВАННЫХ ПЛОСКИМ ТВЕРДОТЕЛЬНЫМ ДЕТЕКТОРОМ | 2021 |
|
RU2776093C1 |
| Перестраиваемый оптический формирователь масштабируемого плоского однородного лазерного пучка | 2019 |
|
RU2725685C1 |
| ЛАЗЕРНЫЙ ПРИБОР ДЛЯ ИЗБИРАТЕЛЬНОГО ЛЕЧЕНИЯ УГРЕЙ С УМЕНЬШЕННЫМ ПОВЫШЕНИЕМ ТЕМПЕРАТУРЫ КОЖИ | 2016 |
|
RU2727233C2 |
Изобретение относится к области силовой лазерной оптики и касается способа определения плотности дефектов поверхности оптической детали. Способ включает в себя облучение участков поверхности оптической детали пучком импульсного лазерного излучения с гауссовым распределением интенсивности, регистрацию разрушения поверхности, наиболее удаленного от точки максимальной интенсивности пучка лазерного излучения, определение соответствующего этому разрушению значения интенсивности пучка εi, определение зависимости плотности вероятности f(ε) разрушения поверхности оптической детали от интенсивности излучения и выбор наименьшего значения интенсивности пучка εimin. Плотность дефектов поверхности оптической детали D определяется по формуле: 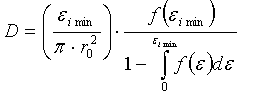 ,
,
где r0 - радиус пучка по уровню exp(-1) от максимальной интенсивности пучка излучения. Технический результат заключается в повышении точности и уменьшении трудоемкости измерений. 3 ил.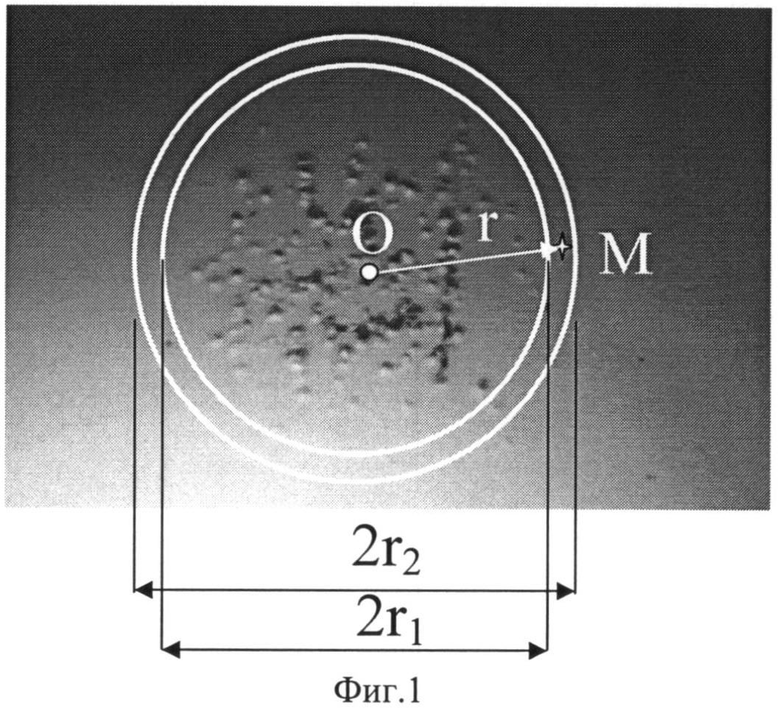
1. Способ определения плотности дефектов поверхности оптической детали, включающий облучение разных участков поверхности оптической детали пучком импульсного лазерного излучения с гауссовым распределением интенсивности, определение максимальной интенсивности ε0 пучка импульсного лазерного излучения и радиуса r0 пучка по уровню ехр(-1) от ε0 в пятне облучения, регистрацию разрушения поверхности в пятне облучения, определение плотности дефектов поверхности, отличающийся тем, что регистрируют разрушение поверхности, наиболее удаленное от точки максимальной интенсивности ε0 пучка импульсного лазерного излучения в пятне облучения, определяют соответствующее этому разрушению значение интенсивности εi пучка в пятне облучения, получают статистически представительную выборку значений εi, где i=1,…N; N - количество облучений детали, равное размеру статистической выборки, определяют экспериментальную зависимость плотности вероятности f(ε) разрушения поверхности оптической детали от интенсивности излучения ε, выбирают наименьшее значение εimin из полученных по всей выборке N значений εi, плотность дефектов поверхности оптической детали D определяют по формуле:
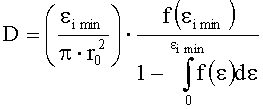
2. Способ по п.1, отличающийся тем, что экспериментальную зависимость плотности вероятности f(ε) разрушения поверхности оптической детали от интенсивности излучения ε в пятне облучения аппроксимируют аналитической функцией:
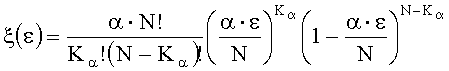 ,
,
где α - параметр подгонки;
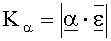 - наибольшее целое число, меньшее или равное значению
- наибольшее целое число, меньшее или равное значению 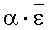 ,
,
где 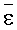 - среднеарифметическое значение εi по всей выборке,
- среднеарифметическое значение εi по всей выборке,
плотность дефектов поверхности оптической детали определяют по формуле:
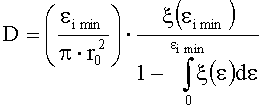
| J | |||
| 0 | |||
| Porteus and Steven C | |||
| Seitel "Absolute onset of optical surface damage using distributed defect ensembles", APPLIED OPTICS, Vol | |||
| Прибор для равномерного смешения зерна и одновременного отбирания нескольких одинаковых по объему проб | 1921 |
|
SU23A1 |
| МЯЛЬНАЯ МАШИНА ДЛЯ ЛУБОВЫХ РАСТЕНИЙ | 1916 |
|
SU3796A1 |
| H | |||
| Krol и др | |||
| "Investigation of nanoprecursors threshold distribution in laser-damage testing", OPTICS COMMUNICATIONS, т | |||
| Ножевой прибор к валичной кардочесальной машине | 1923 |
|
SU256A1 |
| Способ оценки оптической стойкости твердых прозрачных материалов | 1983 |
|
SU1150523A1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ ЛУЧЕВОЙ ПРОЧНОСТИ ПОВЕРХНОСТИ ОПТИЧЕСКОЙ ДЕТАЛИ | 2010 |
|
RU2430352C1 |
Авторы
Даты
2014-05-10—Публикация
2012-08-07—Подача